Review of Quaternion-Based Color Image Processing Methods
Abstract
1. Introduction
- A detailed overview of color image processing with a quaternion representation;
- A comprehensive survey of the different algorithms along with their benefits and limitations;
- A summary of each algorithm in detail, including objectives, goals, and weaknesses, and a discussion of recent challenges and their possible solutions.
2. Basic Theory
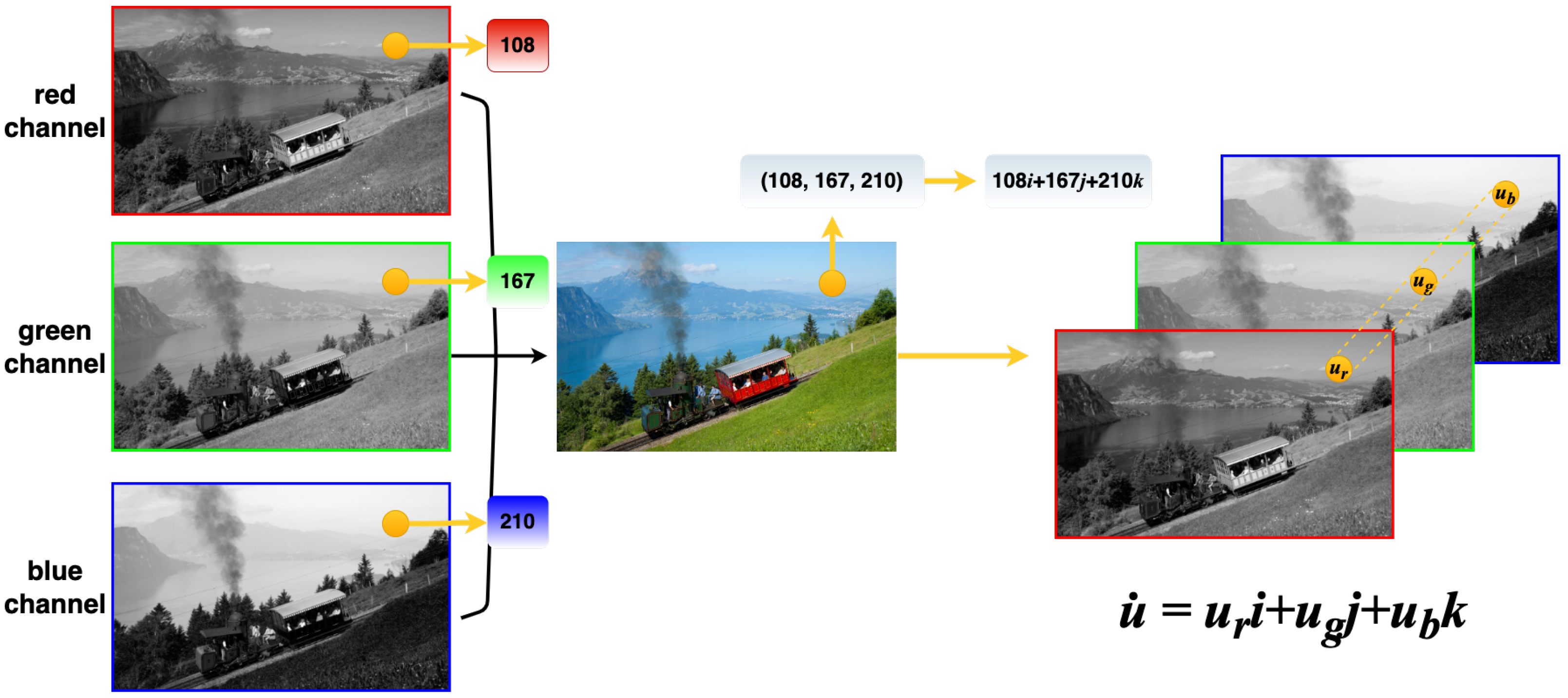
2.1. Color Image Processing Model
| Algorithm 1 ADMM for solving (3) |
|
2.2. Quaternion
2.3. Quaternion Modules
- Reduced network size: QCNNs can represent weights using fewer parameters than traditional CNNs, thereby reducing the overall size of the network.
- Improved performance: QCNNs outperform traditional CNNs on numerous tasks, particularly those involving 3D data, such as video analysis and computer vision.
- Efficient computation: Quaternion operations can be efficiently implemented using GPUs, resulting in fast training and inference times.
3. Traditional Methods
3.1. TV-Based Models
3.2. Low-Rank-Based and Sparse-Based Models
3.3. Moment-Based Models
3.4. Decomposition-Based Models
3.5. Transformation-Based Models
3.6. Other Models
4. Deep Learning
5. Discussion
6. Conclusions
Author Contributions
Funding
Conflicts of Interest
Abbreviations
| real space | |
| complex space | |
| quaternion space | |
| a | real/complex number |
| quaternion number | |
| A | real/complex matrix |
| quaternion matrix | |
| Q | quaternion |
| TV | total variation |
| QNLTV | quaternion non-local total variation |
| SV-TV | saturation-value total variation |
| LRQR | low-rank quaternion approximation |
| QWNNM | quaternion weighted nuclear norm minimization |
| QFT | quaternion Fourier transform |
| QWT | quaternion wavelet transform |
| CNN | convolutional neural network |
| QCNN | quaternion-based convolutional neural network |
| QTrans | quaternion-based transformer model |
| ADMM | alternating direction method of multipliers |
| FISTA | fast iterative shrinkage thresholding algorithm |
| DCA | difference of convex algorithm |
References
- García-Retuerta, D.; Casado-Vara, R.; Martin-del Rey, A.; De la Prieta, F.; Prieto, J.; Corchado, J.M. Quaternion neural networks: State-of-the-art and research challenges. In Proceedings of the Intelligent Data Engineering and Automated Learning–IDEAL 2020: 21st International Conference, Guimaraes, Portugal, 4–6 November 2020; pp. 456–467. [Google Scholar]
- Parcollet, T.; Morchid, M.; Linarès, G. A survey of quaternion neural networks. Artif. Intell. Rev. 2020, 53, 2957–2982. [Google Scholar] [CrossRef]
- Bayro-Corrochano, E. A survey on quaternion algebra and geometric algebra applications in engineering and computer science 1995–2020. IEEE Access 2021, 9, 104326–104355. [Google Scholar] [CrossRef]
- Voronin, V.; Semenishchev, E.; Zelensky, A.; Agaian, S. Quaternion-based local and global color image enhancement algorithm. In Proceedings of the Mobile Multimedia/Image Processing, Security, and Applications 2019, Baltimore, MD, USA, 15 April 2019; Volume 10993, pp. 13–20. [Google Scholar]
- Wang, H.; Wang, X.; Zhou, Y.; Yang, J. Color texture segmentation using quaternion-Gabor filters. In Proceedings of the 2006 International Conference on Image Processing, Atlanta, GA, USA, 8–11 October 2006; pp. 745–748. [Google Scholar]
- Yuan, S.; Wang, Q.; Duan, X. On solutions of the quaternion matrix equation AX = B and their applications in color image restoration. Appl. Math. Comput. 2013, 221, 10–20. [Google Scholar] [CrossRef]
- Li, Y. Color image restoration by quaternion diffusion based on a discrete version of the topological derivative. In Proceedings of the 2014 7th International Congress on Image and Signal Processing, Dalian, China, 14–16 October 2014; pp. 201–206. [Google Scholar]
- Wang, C.; Wang, X.; Xia, Z.; Zhang, C.; Chen, X. Geometrically resilient color image zero-watermarking algorithm based on quaternion exponent moments. J. Vis. Commun. Image Represent. 2016, 41, 247–259. [Google Scholar] [CrossRef]
- Rizo-Rodríguez, D.; Méndez-Vázquez, H.; García-Reyes, E. Illumination invariant face recognition using quaternion-based correlation filters. J. Math. Imaging Vis. 2013, 45, 164–175. [Google Scholar] [CrossRef]
- Bao, S.; Song, X.; Hu, G.; Yang, X.; Wang, C. Colour face recognition using fuzzy quaternion-based discriminant analysis. Int. J. Mach. Learn. Cybern. 2019, 10, 385–395. [Google Scholar] [CrossRef]
- Ranade, S.K.; Anand, S. Color face recognition using normalized-discriminant hybrid color space and quaternion moment vector features. Multimed. Tools Appl. 2021, 80, 10797–10820. [Google Scholar] [CrossRef]
- Gai, S.; Yang, G.; Zhang, S. Multiscale texture classification using reduced quaternion wavelet transform. AEU-Int. J. Electron. Commun. 2013, 67, 233–241. [Google Scholar] [CrossRef]
- Guo, L.; Dai, M.; Zhu, M. Quaternion moment and its invariants for color object classification. Inf. Sci. 2014, 273, 132–143. [Google Scholar] [CrossRef]
- Kumar, R.; Dwivedi, R. Quaternion domain k-means clustering for improved real time classification of E-nose data. IEEE Sens. J. 2015, 16, 177–184. [Google Scholar] [CrossRef]
- Lan, R.; Zhou, Y. Quaternion-Michelson descriptor for color image classification. IEEE Trans. Image Process. 2016, 25, 5281–5292. [Google Scholar] [CrossRef] [PubMed]
- Liu, L.; Chen, C.P.; Li, S. Learning quaternion graph for color face image super-resolution. In Proceedings of the 2019 IEEE International Conference on Image Processing (ICIP), Taipei, Taiwan, 22–25 September 2019; pp. 2846–2850. [Google Scholar]
- Hamilton, W.R. Theory of quaternions. Proc. R. Ir. Acad. (1836–1869) 1844, 3, 1–16. [Google Scholar]
- Wu, T.; Mao, Z.; Li, Z.; Zeng, Y.; Zeng, T. Efficient color image segmentation via quaternion-based L1/L2 regularization. J. Sci. Comput. 2022, 93, 9. [Google Scholar] [CrossRef]
- Murali, S.; Govindan, V.; Kalady, S. Quaternion-based image shadow removal. Vis. Comput. 2022, 38, 1527–1538. [Google Scholar] [CrossRef]
- Wu, L.; Zhang, X.; Chen, H.; Zhou, Y. Unsupervised quaternion model for blind colour image quality assessment. Signal Process. 2020, 176, 107708. [Google Scholar] [CrossRef]
- Yu, L.; Xu, Y.; Xu, H.; Zhang, H. Quaternion-based sparse representation of color image. In Proceedings of the 2013 IEEE International Conference on Multimedia and Expo (ICME), San Jose, CA, USA, 15–19 July 2013; pp. 1–7. [Google Scholar]
- Xiao, X.; Zhou, Y. Two-dimensional quaternion PCA and sparse PCA. IEEE Trans. Neural Netw. Learn. Syst. 2018, 30, 2028–2042. [Google Scholar] [CrossRef]
- Gai, S.; Wang, L.; Yang, G.; Yang, P. Sparse representation based on vector extension of reduced quaternion matrix for multiscale image denoising. IET Image Process. 2016, 10, 598–607. [Google Scholar] [CrossRef]
- Xiao, X.; Chen, Y.; Gong, Y.J.; Zhou, Y. 2D quaternion sparse discriminant analysis. IEEE Trans. Image Process. 2019, 29, 2271–2286. [Google Scholar] [CrossRef]
- Xiao, X.; Zhou, Y. Two-dimensional quaternion sparse principle component analysis. In Proceedings of the 2018 IEEE International Conference on Acoustics, Speech and Signal Processing (ICASSP), Calgary, AB, Canada, 15–20 April 2018; pp. 1528–1532. [Google Scholar]
- Bao, Z.; Gai, S. Reduced quaternion matrix-based sparse representation and its application to colour image processing. IET Image Process. 2019, 13, 566–575. [Google Scholar] [CrossRef]
- Yang, H.; Wang, Q.; Wang, Q.; Liu, P.; Huang, W. Facial micro-expression recognition using quaternion-based sparse representation. In Proceedings of the 2020 29th International Conference on Computer Communications and Networks (ICCCN), Honolulu, HI, USA, 3–6 August 2020; pp. 1–9. [Google Scholar]
- Ngo, L.H.; Luong, M.; Sirakov, N.M.; Viennet, E.; LeTien, T. Skin lesion image classification using sparse representation in quaternion wavelet domain. Signal Image Video Process. 2022, 16, 1721–1729. [Google Scholar] [CrossRef]
- Ngo, L.H.; Sirakov, N.M.; Luong, M.; Viennet, E.; LeTien, T. Image classification based on sparse representation in the quaternion wavelet domain. IEEE Access 2022, 10, 31548–31560. [Google Scholar] [CrossRef]
- Meng, B.; Liu, X.; Wang, X. Human action recognition based on quaternion spatial-temporal convolutional neural network and LSTM in RGB videos. Multimed. Tools Appl. 2018, 77, 26901–26918. [Google Scholar] [CrossRef]
- Shi, J.; Zheng, X.; Wu, J.; Gong, B.; Zhang, Q.; Ying, S. Quaternion Grassmann average network for learning representation of histopathological image. Pattern Recognit. 2019, 89, 67–76. [Google Scholar] [CrossRef]
- Wang, J.; Zhang, Y.; Ma, B.; Dui, G.; Yang, S.; Xin, L. Median filtering forensics scheme for color images based on quaternion magnitude-phase CNN. Comput. Mater. Contin. 2020, 62, 99–112. [Google Scholar] [CrossRef]
- Moya-Sánchez, E.U.; Xambo-Descamps, S.; Pérez, A.S.; Salazar-Colores, S.; Martinez-Ortega, J.; Cortes, U. A bio-inspired quaternion local phase CNN layer with contrast invariance and linear sensitivity to rotation angles. Pattern Recognit. Lett. 2020, 131, 56–62. [Google Scholar] [CrossRef]
- Singh, S.; Tripathi, B. Pneumonia classification using quaternion deep learning. Multimed. Tools Appl. 2022, 81, 1743–1764. [Google Scholar] [CrossRef] [PubMed]
- Wang, Z.; Xu, X.; Wang, G.; Yang, Y.; Shen, H.T. Quaternion relation embedding for scene graph generation. IEEE Trans. Multimed. 2023, 1–12. [Google Scholar] [CrossRef]
- Sfikas, G.; Giotis, A.P.; Retsinas, G.; Nikou, C. Quaternion generative adversarial networks for inscription detection in byzantine monuments. In Proceedings of the Pattern Recognition, ICPR International Workshops and Challenges, Virtual, 10–15 January 2021; pp. 171–184. [Google Scholar]
- Tay, Y.; Zhang, A.; Tuan, L.A.; Rao, J.; Zhang, S.; Wang, S.; Fu, J.; Hui, S.C. Lightweight and efficient neural natural language processing with quaternion networks. arXiv 2019, arXiv:1906.04393. [Google Scholar]
- Shahadat, N.; Maida, A.S. Adding quaternion representations to attention networks for classification. arXiv 2021, arXiv:2110.01185. [Google Scholar]
- Chen, W.; Wang, W.; Peng, B.; Wen, Q.; Zhou, T.; Sun, L. Learning to rotate: Quaternion transformer for complicated periodical time series forecasting. In Proceedings of the 28th ACM SIGKDD Conference on Knowledge Discovery and Data Mining, Washington, DC, USA, 14–18 August 2022; pp. 146–156. [Google Scholar]
- Zhang, A.; Tay, Y.; Zhang, S.; Chan, A.; Luu, A.T.; Hui, S.C.; Fu, J. Beyond fully connected layers with quaternions: Parameterization of hypercomplex multiplications with 1/n parameters. arXiv 2021, arXiv:2102.08597. [Google Scholar]
- Barthélemy, Q.; Larue, A.; Mars, J.I. Color sparse representations for image processing: Review, models, and prospects. IEEE Trans. Image Process. 2015, 24, 3978–3989. [Google Scholar] [CrossRef] [PubMed]
- Huang, Y.; Ng, M.K.; Wen, Y. A new total variation method for multiplicative noise removal. SIAM J. Imaging Sci. 2009, 2, 20–40. [Google Scholar] [CrossRef]
- Ng, M.K.; Weiss, P.; Yuan, X. Solving constrained total-variation image restoration and reconstruction problems via alternating direction methods. SIAM J. Sci. Comput. 2010, 32, 2710–2736. [Google Scholar] [CrossRef]
- Wen, Y.; Ng, M.K.; Huang, Y. Efficient total variation minimization methods for color image restoration. IEEE Trans. Image Process. 2008, 17, 2081–2088. [Google Scholar] [CrossRef] [PubMed]
- Boyd, S.; Parikh, N.; Chu, E.; Peleato, B.; Eckstein, J. Distributed optimization and statistical learning via the alternating direction method of multipliers. Found. Trends® Mach. Learn. 2011, 3, 1–122. [Google Scholar]
- Glowinski, R.; Le Tallec, P. Augmented Lagrangian and Operator-Splitting Methods in Nonlinear Mechanics; SIAM: Philadelphia, PA, USA, 1989. [Google Scholar]
- Gao, G.; Xu, G.; Li, J.; Yu, Y.; Lu, H.; Yang, J. FBSNet: A fast bilateral symmetrical network for real-time semantic segmentation. IEEE Trans. Multimed. 2022. [Google Scholar] [CrossRef]
- Gao, G.; Li, W.; Li, J.; Wu, F.; Lu, H.; Yu, Y. Feature distillation interaction weighting network for lightweight image super-resolution. In Proceedings of the AAAI Conference on Artificial Intelligence, Virtually, 22 February–1 March 2022; Volume 36, pp. 661–669. [Google Scholar]
- Li, J.; Fang, F.; Zeng, T.; Zhang, G.; Wang, X. Adjustable super-resolution network via deep supervised learning and progressive self-distillation. Neurocomputing 2022, 500, 379–393. [Google Scholar] [CrossRef]
- Zhu, X.; Xu, Y.; Xu, H.; Chen, C. Quaternion convolutional neural networks. In Proceedings of the European Conference on Computer Vision (ECCV), Munich, Germany, 8–14 September 2018; pp. 631–647. [Google Scholar]
- Parcollet, T.; Ravanelli, M.; Morchid, M.; Linarès, G.; Trabelsi, C.; Mori, R.D.; Bengio, Y. Quaternion Recurrent Neural Networks. 2019, 1–19. arXiv 2018, arXiv:1806.04418. [Google Scholar]
- Takahashi, K.; Isaka, A.; Fudaba, T.; Hashimoto, M. Remarks on quaternion neural network-based controller trained by feedback error learning. In Proceedings of the 2017 IEEE/SICE International Symposium on System Integration (SII), Taipei, Taiwan, 11–14 December 2017; pp. 875–880. [Google Scholar]
- Xu, D.; Mandic, D.P. The theory of quaternion matrix derivatives. IEEE Trans. Signal Process. 2015, 63, 1543–1556. [Google Scholar] [CrossRef]
- Huang, C.; Li, Z.; Liu, Y.; Wu, T.; Zeng, T. Quaternion-based weighted nuclear norm minimization for color image restoration. Pattern Recognit. 2022, 128, 108665. [Google Scholar] [CrossRef]
- Ma, L.; Xu, L.; Zeng, T. Low rank prior and total variation regularization for image deblurring. J. Sci. Comput. 2017, 70, 1336–1357. [Google Scholar] [CrossRef]
- Liu, X.; Chen, Y.; Peng, Z.; Wu, J.; Wang, Z. Infrared image super-resolution reconstruction based on quaternion fractional order total variation with Lp quasinorm. Appl. Sci. 2018, 8, 1864. [Google Scholar] [CrossRef]
- Li, X.; Zhou, Y.; Zhang, J. Quaternion non-local total variation for color image denoising. In Proceedings of the 2019 IEEE International Conference on Systems, Man and Cybernetics (SMC), Bari, Italy, 6–9 October 2019; pp. 1602–1607. [Google Scholar]
- Jia, Z.; Ng, M.K.; Wang, W. Color image restoration by Saturation-Value total variation. SIAM J. Imaging Sci. 2019, 12, 972–1000. [Google Scholar] [CrossRef]
- Voronin, V.; Semenishchev, E.; Zelensky, A.; Tokareva, O.; Agaian, S. Image segmentation in a quaternion framework for remote sensing applications. In Proceedings of the Mobile Multimedia/Image Processing, Security, and Applications 2020, Online, 27 April–8 May 2020; Volume 11399, pp. 108–115. [Google Scholar]
- Chen, Y.; Xiao, X.; Zhou, Y. Low-rank quaternion approximation for color image processing. IEEE Trans. Image Process. 2019, 29, 1426–1439. [Google Scholar] [CrossRef]
- Yu, Y.; Zhang, Y.; Yuan, S. Quaternion-based weighted nuclear norm minimization for color image denoising. Neurocomputing 2019, 332, 283–297. [Google Scholar] [CrossRef]
- Yang, L.; Miao, J.; Kou, K.I. Quaternion-based color image completion via logarithmic approximation. Inf. Sci. 2022, 588, 82–105. [Google Scholar] [CrossRef]
- Miao, J.; Kou, K.I.; Liu, W. Low-rank quaternion tensor completion for recovering color videos and images. Pattern Recognit. 2020, 107, 107505. [Google Scholar] [CrossRef]
- Elad, M.; Aharon, M. Image denoising via sparse and redundant representations over learned dictionaries. IEEE Trans. Image Process. 2006, 15, 3736–3745. [Google Scholar] [CrossRef]
- Yu, M.; Xu, Y.; Sun, P. Single color image super-resolution using quaternion-based sparse representation. In Proceedings of the 2014 IEEE International Conference on Acoustics, Speech and Signal Processing (ICASSP), Florence, Italy, 4–9 May 2014; pp. 5804–5808. [Google Scholar]
- Zou, C.; Kou, K.I.; Wang, Y. Quaternion collaborative and sparse representation with application to color face recognition. IEEE Trans. Image Process. 2016, 25, 3287–3302. [Google Scholar] [CrossRef]
- Xu, Y.; Yu, L.; Xu, H.; Zhang, H.; Nguyen, T. Vector sparse representation of color image using quaternion matrix analysis. IEEE Trans. Image Process. 2015, 24, 1315–1329. [Google Scholar] [CrossRef]
- Wu, T.; Huang, C.; Jin, Z.; Jia, Z.; Ng, M.K. Total variation based pure quaternion dictionary learning method for color image denoising. Int. J. Numer. Anal. Model. 2022, 19, 709–737. [Google Scholar]
- Huang, C.; Ng, M.K.; Wu, T.; Zeng, T. Quaternion-based dictionary learning and saturation-value total variation regularization for color image restoration. IEEE Trans. Multimed. 2021, 24, 3769–3781. [Google Scholar] [CrossRef]
- Liu, X.; Chen, Y.; Peng, Z.; Wu, J. Infrared image super-resolution reconstruction based on quaternion and high-order overlapping group sparse total variation. Sensors 2019, 19, 5139. [Google Scholar] [CrossRef] [PubMed]
- Zou, C.; Kou, K.I.; Wang, Y.; Tang, Y.Y. Quaternion block sparse representation for signal recovery and classification. Signal Process. 2021, 179, 107849. [Google Scholar] [CrossRef]
- Wang, Y.; Kou, K.I.; Zou, C.; Tang, Y.Y. Robust sparse representation in quaternion space. IEEE Trans. Image Process. 2021, 30, 3637–3649. [Google Scholar] [CrossRef]
- Jia, Z.; Ng, M.K.; Song, G. Robust quaternion matrix completion with applications to image inpainting. Numer. Linear Algebra Appl. 2019, 26, e2245. [Google Scholar] [CrossRef]
- Shi, L.; Funt, B. Quaternion color texture segmentation. Comput. Vis. Image Underst. 2007, 107, 88–96. [Google Scholar] [CrossRef]
- Jia, Z.; Jin, Q.; Ng, M.K.; Zhao, X. Non-local robust quaternion matrix completion for large-scale color image and video inpainting. IEEE Trans. Image Process. 2022, 31, 3868–3883. [Google Scholar] [CrossRef]
- Wang, M.; Song, L.; Sun, K.; Jia, Z. F-2D-QPCA: A quaternion principal component analysis method for color face recognition. IEEE Access 2020, 8, 217437–217446. [Google Scholar] [CrossRef]
- Sun, Y.; Chen, S.; Yin, B. Color face recognition based on quaternion matrix representation. Pattern Recognit. Lett. 2011, 32, 597–605. [Google Scholar] [CrossRef]
- Jia, Z.; Ling, S.; Zhao, M. Color two-dimensional principal component analysis for face recognition based on quaternion model. In Proceedings of the Intelligent Computing Theories and Application: 13th International Conference, ICIC 2017, Liverpool, UK, 7–10 August 2017; pp. 177–189. [Google Scholar]
- Chen, B.; Shu, H.; Coatrieux, G.; Chen, G.; Sun, X.; Coatrieux, J.L. Color image analysis by quaternion-type moments. J. Math. Imaging Vis. 2015, 51, 124–144. [Google Scholar] [CrossRef]
- Wang, X.; Niu, P.; Yang, H.; Wang, C.p.; Wang, A.l. A new robust color image watermarking using local quaternion exponent moments. Inf. Sci. 2014, 277, 731–754. [Google Scholar] [CrossRef]
- Hosny, K.M.; Darwish, M.M. Resilient color image watermarking using accurate quaternion radial substituted Chebyshev moments. ACM Trans. Multimed. Comput. Commun. Appl. (TOMM) 2019, 15, 1–25. [Google Scholar] [CrossRef]
- Yang, T.; Ma, J.; Miao, Y.; Wang, X.; Xiao, B.; He, B.; Meng, Q. Quaternion weighted spherical Bessel-Fourier moment and its invariant for color image reconstruction and object recognition. Inf. Sci. 2019, 505, 388–405. [Google Scholar] [CrossRef]
- El Alami, A.; Berrahou, N.; Lakhili, Z.; Mesbah, A.; Berrahou, A.; Qjidaa, H. Efficient color face recognition based on quaternion discrete orthogonal moments neural networks. Multimed. Tools Appl. 2022, 81, 7685–7710. [Google Scholar] [CrossRef]
- Guo, L.Q.; Zhu, M. Quaternion Fourier—Mellin moments for color images. Pattern Recognit. 2011, 44, 187–195. [Google Scholar] [CrossRef]
- Tsougenis, E.; Papakostas, G.A.; Koulouriotis, D.E.; Karakasis, E.G. Adaptive color image watermarking by the use of quaternion image moments. Expert Syst. Appl. 2014, 41, 6408–6418. [Google Scholar] [CrossRef]
- Li, M.; Yuan, X.; Chen, H.; Li, J. Quaternion discrete fourier transform-based color image watermarking method using quaternion QR decomposition. IEEE Access 2020, 8, 72308–72315. [Google Scholar] [CrossRef]
- Chen, Y.; Jia, Z.; Peng, Y.; Peng, Y.; Zhang, D. A new structure-preserving quaternion QR decomposition method for color image blind watermarking. Signal Process. 2021, 185, 108088. [Google Scholar] [CrossRef]
- Li, J.; Yu, C.; Gupta, B.B.; Ren, X. Color image watermarking scheme based on quaternion Hadamard transform and Schur decomposition. Multimed. Tools Appl. 2018, 77, 4545–4561. [Google Scholar] [CrossRef]
- Chen, Y.; Jia, Z.; Peng, Y.; Peng, Y. Robust dual-color watermarking based on quaternion singular value decomposition. IEEE Access 2020, 8, 30628–30642. [Google Scholar] [CrossRef]
- Zhang, M.; Ding, W.; Li, Y.; Sun, J.; Liu, Z. Color image watermarking based on a fast structure-preserving algorithm of quaternion singular value decomposition. Signal Process. 2023, 208, 08971. [Google Scholar] [CrossRef]
- He, Z.H.; Qin, W.L.; Wang, X.X. Some applications of a decomposition for five quaternion matrices in control system and color image processing. Comput. Appl. Math. 2021, 40, 205. [Google Scholar] [CrossRef]
- Xie, C.; Savvides, M.; Kumar, B.V. Quaternion correlation filters for face recognition in wavelet domain. In Proceedings of the ICASSP’05—IEEE International Conference on Acoustics, Speech, and Signal Processing, Philadelphia, PA, USA, 23 March 2005; Volume 2, p. ii-85. [Google Scholar]
- Kumar, V.V.; Vidya, A.; Sharumathy, M.; Kanizohi, R. Super resolution enhancement of medical image using quaternion wavelet transform with SVD. In Proceedings of the 2017 Fourth International Conference on Signal Processing, Communication and Networking (ICSCN), Chennai, India, 16–18 March 2017; pp. 1–7. [Google Scholar]
- Miao, J.; Kou, K.I.; Cheng, D.; Liu, W. Quaternion higher-order singular value decomposition and its applications in color image processing. Inf. Fusion 2023, 92, 139–153. [Google Scholar] [CrossRef]
- Cai, C.; Mitra, S.K. A normalized color difference edge detector based on quaternion representation. In Proceedings of the 2000 International Conference on Image Processing (Cat. No. 00CH37101), Vancouver, BC, Canada, 10–13 September 2000; Volume 2, pp. 816–819. [Google Scholar]
- Geng, X.; Hu, X.; Xiao, J. Quaternion switching filter for impulse noise reduction in color image. Signal Process. 2012, 92, 150–162. [Google Scholar] [CrossRef]
- Chanu, P.R.; Singh, K.M. A two-stage switching vector median filter based on quaternion for removing impulse noise in color images. Multimed. Tools Appl. 2019, 78, 15375–15401. [Google Scholar] [CrossRef]
- Huang, C.; Fang, Y.; Wu, T.; Zeng, T.; Zeng, Y. Quaternion screened Poisson equation for low-light image enhancement. IEEE Signal Process. Lett. 2022, 29, 1417–1421. [Google Scholar] [CrossRef]
- Bas, P.; Le Bihan, N.; Chassery, J.M. Color image watermarking using quaternion Fourier transform. In Proceedings of the 2003 IEEE International Conference on Acoustics, Speech, and Signal Processing (ICASSP’03), Hong Kong, China, 6–10 April 2003; Volume 3, p. III-521. [Google Scholar]
- Wang, X.; Wang, C.; Yang, H.; Niu, P. A robust blind color image watermarking in quaternion Fourier transform domain. J. Syst. Softw. 2013, 86, 255–277. [Google Scholar] [CrossRef]
- Ouyang, J.; Coatrieux, G.; Chen, B.; Shu, H. Color image watermarking based on quaternion Fourier transform and improved uniform log-polar mapping. Comput. Electr. Eng. 2015, 46, 419–432. [Google Scholar] [CrossRef]
- Niu, P.; Wang, L.; Shen, X.; Zhang, S.; Wang, X. A novel robust image watermarking in quaternion wavelet domain based on superpixel segmentation. Multidimens. Syst. Signal Process. 2020, 31, 1509–1530. [Google Scholar] [CrossRef]
- Grigoryan, A.M.; Agaian, S.S. Optimal color image restoration: Wiener filter and quaternion Fourier transform. In Proceedings of the Mobile Devices and Multimedia: Enabling Technologies, Algorithms, and Applications 2015, San Francisco, CA, USA, 10–11 February 2015; Volume 9411, pp. 215–226. [Google Scholar]
- Wang, H.; Li, C.; Guan, T.; Zhao, S. No-reference stereoscopic image quality assessment using quaternion wavelet transform and heterogeneous ensemble learning. Displays 2021, 69, 102058. [Google Scholar] [CrossRef]
- Xia, Z.; Wang, X.; Zhou, W.; Li, R.; Wang, C.; Zhang, C. Color medical image lossless watermarking using chaotic system and accurate quaternion polar harmonic transforms. Signal Process. 2019, 157, 108–118. [Google Scholar] [CrossRef]
- Wang, C.; Li, S.; Liu, Y.; Meng, L.; Zhang, K.; Wan, W. Cross-scale feature fusion-based JND estimation for robust image watermarking in quaternion DWT domain. Optik 2023, 272, 170371. [Google Scholar] [CrossRef]
- Subakan, Ö.N.; Vemuri, B.C. A quaternion framework for color image smoothing and segmentation. Int. J. Comput. Vis. 2011, 91, 233–250. [Google Scholar] [CrossRef]
- Subakan, Ö.N.; Vemuri, B.C. Color image segmentation in a quaternion framework. In Proceedings of the Energy Minimization Methods in Computer Vision and Pattern Recognition: 7th International Conference, EMMCVPR 2009, Bonn, Germany, 24–27 August 2009; pp. 401–414. [Google Scholar]
- Li, L.; Jin, L.; Xu, X.; Song, E. Unsupervised color—Texture segmentation based on multiscale quaternion Gabor filters and splitting strategy. Signal Process. 2013, 93, 2559–2572. [Google Scholar] [CrossRef]
- Zou, C.; Kou, K.I.; Dong, L.; Zheng, X.; Tang, Y.Y. From grayscale to color: Quaternion linear regression for color face recognition. IEEE Access 2019, 7, 154131–154140. [Google Scholar] [CrossRef]
- Liu, Z.; Qiu, Y.; Peng, Y.; Pu, J.; Zhang, X. Quaternion based maximum margin criterion method for color face recognition. Neural Process. Lett. 2017, 45, 913–923. [Google Scholar] [CrossRef]
- Risojević, V.; Babić, Z. Unsupervised learning of quaternion features for image classification. In Proceedings of the 2013 11th International Conference on Telecommunications in Modern Satellite, Cable and Broadcasting Services (TELSIKS), Nis, Serbia, 16–19 October 2013; Volume 1, pp. 345–348. [Google Scholar]
- Risojević, V.; Babić, Z. Unsupervised quaternion feature learning for remote sensing image classification. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2016, 9, 1521–1531. [Google Scholar] [CrossRef]
- Zeng, R.; Wu, J.; Shao, Z.; Chen, Y.; Chen, B.; Senhadji, L.; Shu, H. Color image classification via quaternion principal component analysis network. Neurocomputing 2016, 216, 416–428. [Google Scholar] [CrossRef]
- Gaudet, C.J.; Maida, A.S. Deep quaternion networks. In Proceedings of the 2018 International Joint Conference on Neural Networks (IJCNN), Rio de Janeiro, Brazil, 8–13 July 2018; pp. 1–8. [Google Scholar]
- Yin, Q.; Wang, J.; Luo, X.; Zhai, J.; Jha, S.K.; Shi, Y. Quaternion convolutional neural network for color image classification and forensics. IEEE Access 2019, 7, 20293–20301. [Google Scholar] [CrossRef]
- Waghmare, S.K.; Patil, R.B.; Waje, M.G.; Joshi, K.V.; Raut, V.P.; Shrivastava, P.C. Color image processing usingt modified quaternion neural network. J. Pharm. Negat. Results 2023, 13, 2954–2960. [Google Scholar]
- Parcollet, T.; Morchid, M.; Linarès, G. Quaternion convolutional neural networks for heterogeneous image processing. In Proceedings of the ICASSP 2019-2019 IEEE International Conference on Acoustics, Speech and Signal Processing (ICASSP), Brighton, UK, 12–17 May 2019; pp. 8514–8518. [Google Scholar]
- Jin, L.; Zhou, Y.; Liu, H.; Song, E. Deformable quaternion gabor convolutional neural network for color facial expression recognition. In Proceedings of the 2020 IEEE International Conference on Image Processing (ICIP), Abu Dhabi, United Arab Emirates, 25–28 October 2020; pp. 1696–1700. [Google Scholar]
- Zhou, Y.; Jin, L.; Liu, H.; Song, E. Color facial expression recognition by quaternion convolutional neural network with Gabor attention. IEEE Trans. Cogn. Dev. Syst. 2020, 13, 969–983. [Google Scholar] [CrossRef]
- Cao, Y.; Fu, Y.; Zhu, Z.; Rao, Z. Color random valued impulse noise removal based on quaternion convolutional attention denoising network. IEEE Signal Process. Lett. 2021, 29, 369–373. [Google Scholar] [CrossRef]
- Fang, F.; Li, J.; Zeng, T. Soft-edge assisted network for single image super-resolution. IEEE Trans. Image Process. 2020, 29, 4656–4668. [Google Scholar] [CrossRef] [PubMed]
- KM, S.K.; Rao, S.P.; Panetta, K.; Agaian, S.S. QSRNet: Towards quaternion-based single image super-resolution. In Proceedings of the Multimodal Image Exploitation and Learning 2022, Orlando, FL, USA, 3 April–12 June 2022; Volume 12100, pp. 192–205. [Google Scholar]
- Madhu, A.; Suresh, K. RQNet: Residual quaternion CNN for performance enhancement in low complexity and device robust acoustic scene classification. IEEE Trans. Multimed. 2023, 1–13. [Google Scholar] [CrossRef]
- Frants, V.; Agaian, S.; Panetta, K. QSAM-Net: Rain streak removal by quaternion neural network with self-attention module. arXiv 2022, arXiv:2208.04346. [Google Scholar]
- Frants, V.; Agaian, S.; Panetta, K. QCNN-H: Single-image dehazing using quaternion neural networks. IEEE Trans. Cybern. 2023. [Google Scholar] [CrossRef]
- Zhou, H.; Zhang, C.; Zhang, X.; Ma, Q. Image classification based on quaternion-valued capsule network. Appl. Intell. 2023, 53, 5587–5606. [Google Scholar] [CrossRef]
- Xu, T.; Kong, X.; Shen, Q.; Chen, Y.; Zhou, Y. Deep and low-rank quaternion priors for color image processing. IEEE Trans. Circuits Syst. Video Technol. 2023, 1–14. [Google Scholar] [CrossRef]
- Zhang, K.; Zuo, W.; Zhang, L. FFDNet: Toward a fast and flexible solution for CNN-based image denoising. IEEE Trans. Image Process. 2018, 27, 4608–4622. [Google Scholar] [CrossRef]
- Grassucci, E.; Cicero, E.; Comminiello, D. Quaternion generative adversarial networks. In Generative Adversarial Learning: Architectures and Applications; Springer: Berlin/Heidelberg, Germany, 2022; pp. 57–86. [Google Scholar]



| Note | ||
|---|---|---|
| 1 | ||
| , denotes the real part of | ||
| denotes the conjugation of | ||
| denotes the reciprocal of | ||
| – | ||
| Method | Model Structure | Prior | Algorithm | Testing Data | Task | |
|---|---|---|---|---|---|---|
| 2018–2011 | QGmF [107] | – | Gabor Filter + hypercomplex exponential basis functions | Closed Form Solution | Common Used | Denoising/Inpainting/ Segmentation |
| Xu et al. [67] | Sparse | Dictionary | KQSVD/QOMP | Animal Images | Reconstruction /Denoising/Inpainting/Super-resolution | |
| Zou et al. [66] | Sparse | CRC + Sparse RC | ADMM | AR/Caltech/SCface/ FERET/LFW | Face Recognition | |
| Kumar et al. [93] | Low-rank | QWT + QSVD | – | Biomedical Images | Super-resolution | |
| QPCANet [114] | Deep Network | Principal Component Analysis Network | Deep Learning | Caltech-101/Georgia Tech face/UC Merced Land Use | Classification | |
| QCNN [50] | Deep Network | Quaternion Representation | Deep Learning | COCO/Oxford flower102 | Classification/Denoising | |
| 2019 | QNLTV [57] | Non-local | Non-local Total Variation | Splitting Bargeman | Common Used | Denoising |
| LRQA [60] | Low-rank | Laplace/Geman/Weighted Schatten- | Difference of Convex | Common Used | Denoising/Inpainting | |
| QWNNM [61] | Low-rank | Nuclear Norm | QSVD | Berkeley | Denoising | |
| QPHTs [105] | – | Chaotic System+Polar Harmonic Transform | - | Whole Brain Atlas | Watermarking | |
| QMC [73] | Low-rank | Nuclear Norm/ Norm | ADMM | Berkeley | Inpainting | |
| HOGS4 [70] | Sparse | Total Variation+High-order Overlapping Group Sparse | ADMM | Infrared LTIR/IRData | Super-resolution | |
| QSBFM [82] | Orthogonal Moment | Weighted Spherical Bessel–Fourier Moment | QSBFM | CVG-UGR/Amsterdam Library/Columbia Library | Reconstruction /Recognition | |
| QCROC [110] | Linear Regression Classification | Linear Regression Classification+Collaborative Representation | Collaborative Representation Optimized Classification | SCface/AR/Caltech | Recognition | |
| Yin et al. [116] | Deep Network | QCNN+Attention Mechanism | Deep Learning | UCID | Classification/Forensics | |
| 2020 | Li et al. [86] | – | Discrete Fourier Transform+QR decomposition | Wavelet Transform+Just-noticeable Difference | Common Used | Watermarking |
| Voronin et al. [59] | – | Modified Chan and Vese Method | Anisotropic Gradient Calculation | Merced | Segmentation | |
| F-2D-QPCA [76] | Low-rank+Sparse | F-norm | Principal Component Analysis | Georgia Tech Face/FERET | Face Recognition | |
| DQG-CNN [119] | Deep Network | Deformable Gabor Filter | Deep Learning | Oulu-CASIA/MMI/SFEW | Facial Expression Recognition | |
| Zhou et al. [120] | Deep Network | Gabor Attention | Deep Learning | Oulu-CASIA/MMI/SFEW | Facial Expression Recognition | |
| 2021 | QBSR [71] | Sparse | Block Sparse Representation | ADMM | AR/SCface | Recognition |
| Huang et al. [69] | Sparse | Dictionary+Total Variation | ADMM | DIV2K | Denoising/Deblurring | |
| Shahadat et al. [38] | Deep Network | Axial-attention Modules | Deep Learning | ImageNet300k | Classification | |
| RQSVR [72] | Sparse | Welsch Estimator | HQS/ADMM | AR/SCface | Reconstruction/Recognition | |
| He et al. [91] | Low-rank | Matrix Decomposition | PSVD | Common Used | Watermarking | |
| 2022 | QSRNet [123] | Deep Network | Edge-Net | Deep Learning | DIV2K/Flickr2K /Set5/Set14/BSD100 /Urban100/UEC100 | Super-resolution |
| Yang et al. [62] | Low-rank | Logarithmic Norm | FISTA/ADMM | Common Used/Berkeley | Inpainting | |
| Wu et al. [18] | Total Variation | -norm | spADMM | Weizmann/Berkeley | Segmentation | |
| QSAM-Net [125] | Deep Network | QCNN+Self Attention | Deep Learning | LOL | Rain Streak Removal | |
| QDOMNN [83] | Deep Network | Discrete Orthogonal Moments | Deep Learning | Faces94/Faces95 /Faces96/Grimace /Georgia Tech Face/FEI | Recognition | |
| 2023 | RQNet [124] | Deep Network | Residual CNN | Deep Learning | DCASE19/DCASE20 | Classification |
| QHOSVD [94] | Low-rank | Higher-order SVD | Matrix Decomposition | Lytro/MFFW | Image Fusion/Denoising | |
| DLRQP [128] | Plug-and-play | FFDNet/Laplace | ADMM/DCA | Common Used | Denoising/Inpainting |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Huang, C.; Li, J.; Gao, G. Review of Quaternion-Based Color Image Processing Methods. Mathematics 2023, 11, 2056. https://doi.org/10.3390/math11092056
Huang C, Li J, Gao G. Review of Quaternion-Based Color Image Processing Methods. Mathematics. 2023; 11(9):2056. https://doi.org/10.3390/math11092056
Chicago/Turabian StyleHuang, Chaoyan, Juncheng Li, and Guangwei Gao. 2023. "Review of Quaternion-Based Color Image Processing Methods" Mathematics 11, no. 9: 2056. https://doi.org/10.3390/math11092056
APA StyleHuang, C., Li, J., & Gao, G. (2023). Review of Quaternion-Based Color Image Processing Methods. Mathematics, 11(9), 2056. https://doi.org/10.3390/math11092056






