Highly Dispersive Optical Solitons in Birefringent Fibers with Polynomial Law of Nonlinear Refractive Index by Laplace–Adomian Decomposition
Abstract
:1. Introduction
2. Governing Equation
Bright and Dark Solitons
3. Description and Application of the LADM
Convergence of the Proposed Method
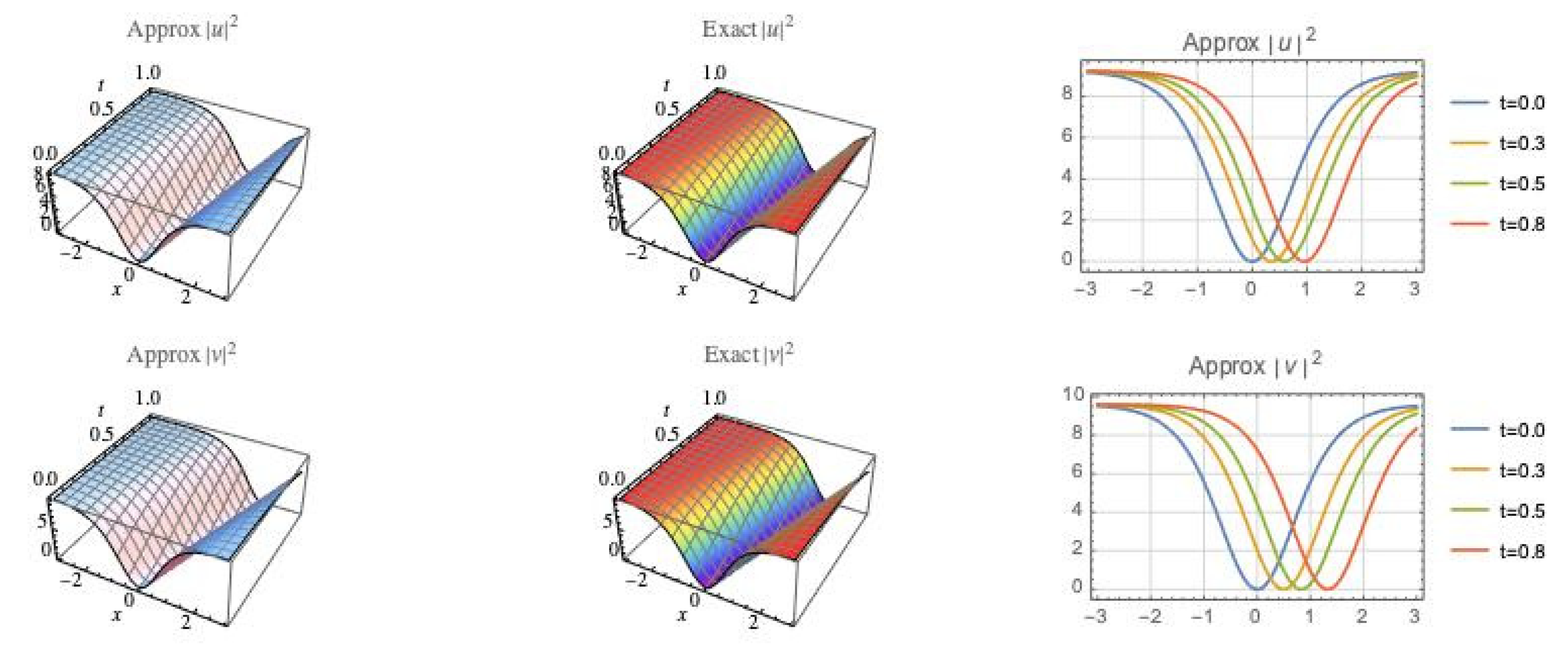
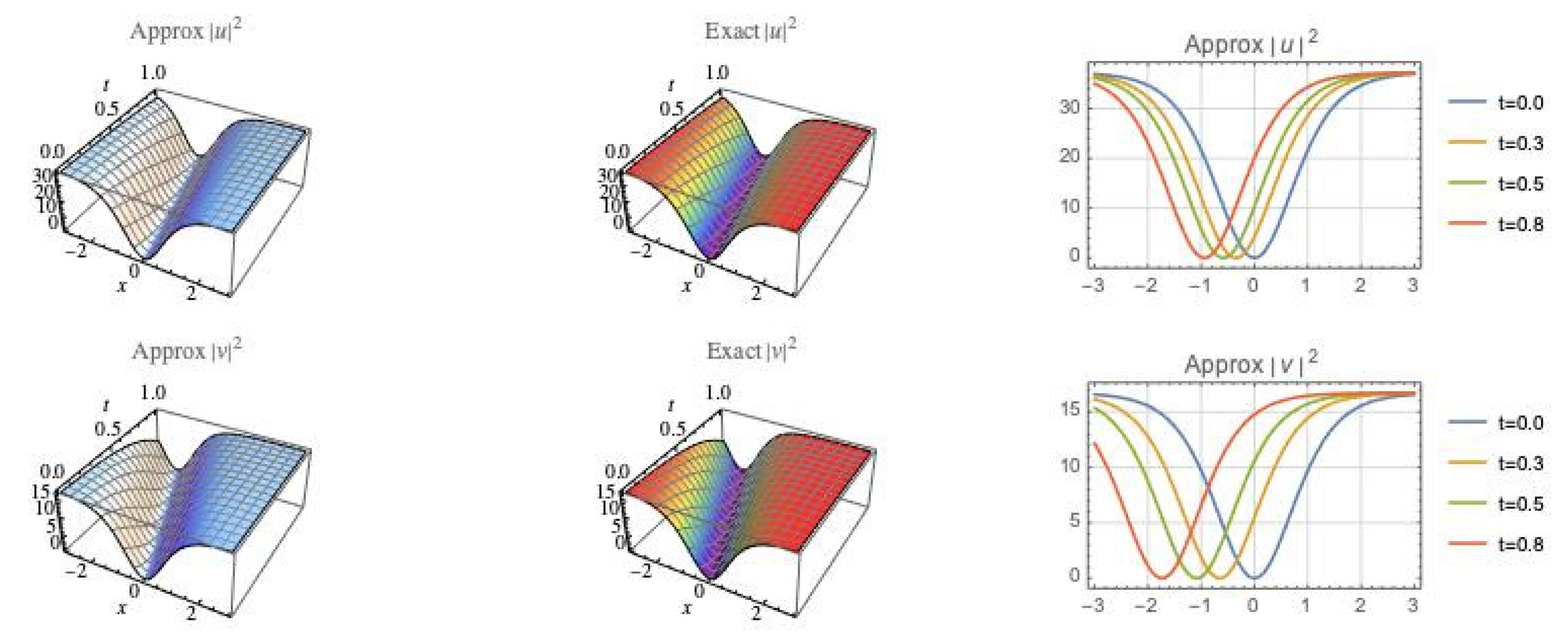
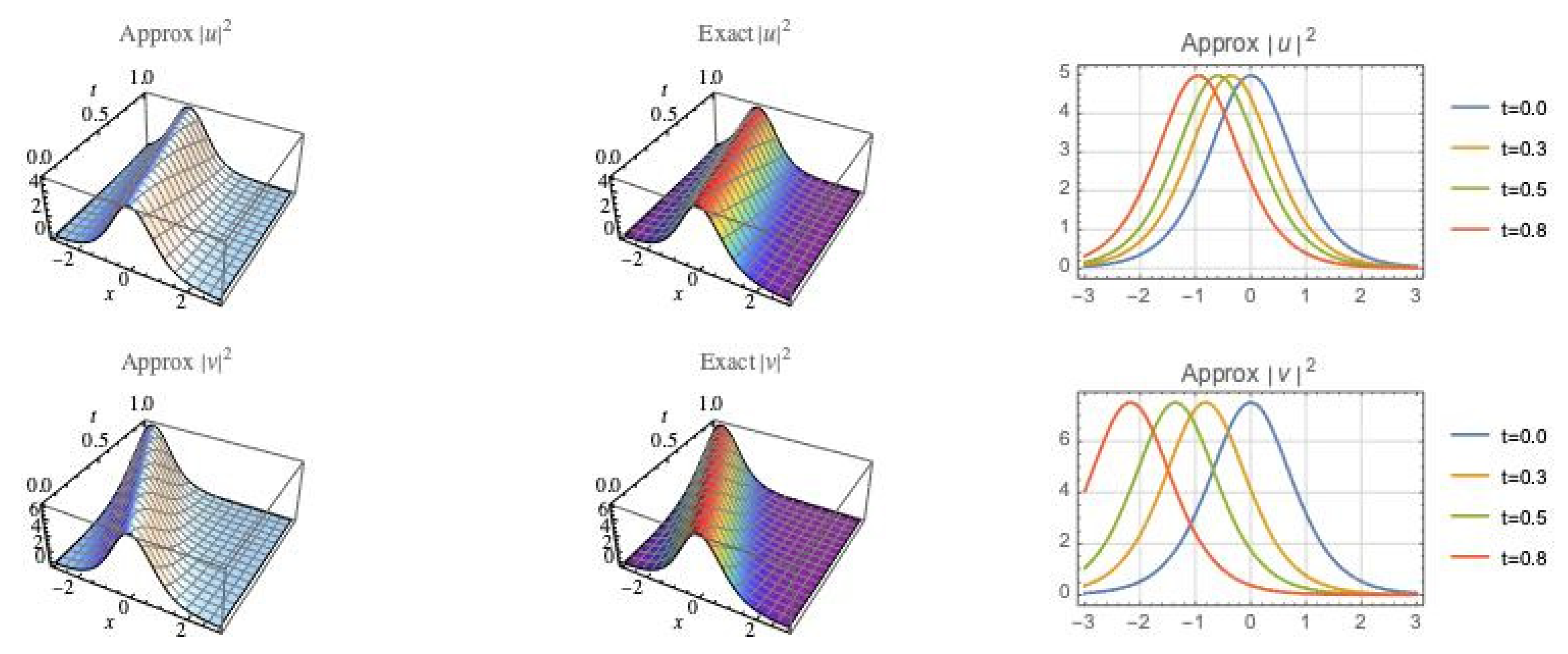
4. Graphical Representations
4.1. Dark Soliton Simulation
4.2. Bright Soliton Simulation
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Kudryashov, N.A. Highly dispersive optical solitons of an equation with arbitrary refractive index. Regul. Chaotic Dyn. 2020, 25, 537–543. [Google Scholar] [CrossRef]
- Kudryashov, N.A. Highly dispersive optical solitons of equation with various polynomial nonlinearity law. Chaos Soliton Fract. 2020, 140, 110202. [Google Scholar] [CrossRef]
- Kudryashov, N.A. Highly dispersive optical solitons of the generalized nonlinear eighth-order Schrödinger equation. Optik 2020, 206, 164335. [Google Scholar] [CrossRef]
- Kudryashov, N.A. Method for finding highly dispersive optical solitons of nonlinear differential equations. Optik 2020, 206, 163550. [Google Scholar] [CrossRef]
- Kudryashov, N.A. Highly dispersive solitary wave solutions of perturbed nonlinear Schrödinger equations. Appl. Math. Comput. 2020, 371, 124972. [Google Scholar] [CrossRef]
- Yildirim, Y.; Biswas, A.; Ekici, M.; Zayed, E.M.E.; Khan, S.; Moraru, L.; Alzahrani, A.K.; Belic, M.R. Highly dispersive optical solitons in birefringent fibers with four forms of nonlinear refractive index by three prolific integration schemes. Optik 2020, 220, 165039. [Google Scholar] [CrossRef]
- Wazwaz, A.M. Bright and dark optical solitons for (3+1)-dimensional Schrödinger equation with cubic–quintic-septic nonlinearities. Optik 2021, 225, 165752. [Google Scholar] [CrossRef]
- Wazwaz, A.M.; Khuri, S.A. Two (3+1)-dimensional Schrödinger equations with cubic–quintic–septic nonlinearities: Bright and dark optical solitons. Optik 2021, 235, 166646. [Google Scholar] [CrossRef]
- Mirzazadeh, M.; Akinyemi, L.; Senol, M.; Hosseini, K. A variety of solitons to the sixth-order dispersive (3+1)-dimensional nonlinear time-fractional Schrödinger equation with cubic-quintic-septic nonlinearities. Optik 2021, 241, 166318. [Google Scholar] [CrossRef]
- Kerbouche, M.; Hamaizi, Y.; El-Akrmi, A.; Triki, H. Solitary wave solutions of the cubic-quintic-septic nonlinear Schrödinger equation in fiber Bragg gratings. Optik 2016, 127, 9562–9570. [Google Scholar] [CrossRef]
- Rabie, W.B.; Ahmed, H.M. Optical solitons for multiple-core couplers with polynomial law of nonlinearity using the modified extended direct algebraic method. Optik 2022, 258, 168848. [Google Scholar] [CrossRef]
- Rabie, W.B.; Ahmed, H.M. Cubic-quartic optical solitons and other solutions for twin-core couplers with polynomial law of nonlinearity using the extended F-expansion method. Optik 2022, 253, 168575. [Google Scholar] [CrossRef]
- Wang, M.-Y. Optical solitons with perturbed complex Ginzburg–Landau equation in kerr and cubic–quintic–septic nonlinearity. Results Phys. 2022, 33, 105077. [Google Scholar] [CrossRef]
- Djoko, M.; Kofane, T.C. Dissipative optical bullets modeled by the cubic-quintic-septic complex Ginzburg–Landau equation with higher-order dispersions. Commun. Nonlinear Sci. Numer. Simulat. 2017, 48, 179–199. [Google Scholar] [CrossRef]
- Kutukov, A.A.; Kudryashov, N.A. Traveling wave solutions of the coupled nonlinear Schrödinger equation with cubic-quintic-septic and weak non-local nonlinearity. AIP Conf. Proc. 2022, 2425, 340002. [Google Scholar]
- Wang, F.; Liu, Y.C.; Zheng, H. A localized method of fundamental solution for numerical simulation of nonlinear heat conduction. Mathematics 2022, 10, 773. [Google Scholar] [CrossRef]
- Adomian, G. Nonlinear Stochastic Operator Equations; Academic Press: New York, NY, USA, 1986. [Google Scholar]
- Adomian, G.; Rach, R. On the solution of nonlinear differential equations with convolution product nonlinearities. J. Math. Anal. Appl. 1986, 114, 171–175. [Google Scholar] [CrossRef]
- Adomian, G. Solving Frontier Problems of Physics: The Decomposition Method; Kluwer Academic Publishers: Boston, MA, USA, 1994. [Google Scholar]
- Duan, J.S. Convenient analytic recurrence algorithms for the Adomian polynomials. Appl. Math. Comput. 2011, 217, 6337–6348. [Google Scholar] [CrossRef]
- González-Gaxiola, O.; Biswas, A.; Alshomrani, A.S. Highly dispersive optical solitons having Kerr law of refractive index with Laplace-Adomian decomposition. Rev. Mex. Fis. 2020, 66, 291–296. [Google Scholar] [CrossRef]
- González-Gaxiola, O.; Biswas, A.; Asma, M.; Alzahrani, A.K. Highly dispersive optical solitons with non-local law of refractive index by Laplace-Adomian decomposition. Opt. Quantum Electron. 2021, 53, 55. [Google Scholar] [CrossRef]
- González-Gaxiola, O.; Biswas, A.; Alzahrani, A.K.; Belic, M.R. Highly dispersive optical solitons with a polynomial law of refractive index by Laplace-Adomian decomposition. J. Comput. Electron. 2021, 20, 1216–1223. [Google Scholar] [CrossRef]
- Abbaoui, K.; Cherruault, Y. Convergence of Adomian’s method applied to differential equations. Comput. Math. Appl. 1994, 28, 103–109. [Google Scholar] [CrossRef] [Green Version]

Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
González-Gaxiola, O.; Biswas, A.; Yıldırım, Y.; Moraru, L. Highly Dispersive Optical Solitons in Birefringent Fibers with Polynomial Law of Nonlinear Refractive Index by Laplace–Adomian Decomposition. Mathematics 2022, 10, 1589. https://doi.org/10.3390/math10091589
González-Gaxiola O, Biswas A, Yıldırım Y, Moraru L. Highly Dispersive Optical Solitons in Birefringent Fibers with Polynomial Law of Nonlinear Refractive Index by Laplace–Adomian Decomposition. Mathematics. 2022; 10(9):1589. https://doi.org/10.3390/math10091589
Chicago/Turabian StyleGonzález-Gaxiola, Oswaldo, Anjan Biswas, Yakup Yıldırım, and Luminita Moraru. 2022. "Highly Dispersive Optical Solitons in Birefringent Fibers with Polynomial Law of Nonlinear Refractive Index by Laplace–Adomian Decomposition" Mathematics 10, no. 9: 1589. https://doi.org/10.3390/math10091589
APA StyleGonzález-Gaxiola, O., Biswas, A., Yıldırım, Y., & Moraru, L. (2022). Highly Dispersive Optical Solitons in Birefringent Fibers with Polynomial Law of Nonlinear Refractive Index by Laplace–Adomian Decomposition. Mathematics, 10(9), 1589. https://doi.org/10.3390/math10091589








