TPBF: Two-Phase Bloom-Filter-Based End-to-End Data Integrity Verification Framework for Object-Based Big Data Transfer Systems
Abstract
:1. Introduction
- A data- and layout-aware Bloom filter (DLBF) mechanism for effectively handling object and file level data integrity verification with object-based big data transfer systems.
- For efficiently handling dataset level integrity verification, we developed a two-phase Bloom-filter (TPBF)-based end-to-end data integrity verification framework for optimizing the memory and storage footprint when compared with state-of-the-art data integrity solutions.
- We utilized a Lustre file system [20,21,22] that interacts over an InfiniBand (IB) network [23,24] to evaluate the proposed design. Based on the experimental results, we can conclude that the proposed data integrity framework is very effective at detecting and resolving data integrity issues at all of object, file, and dataset levels.
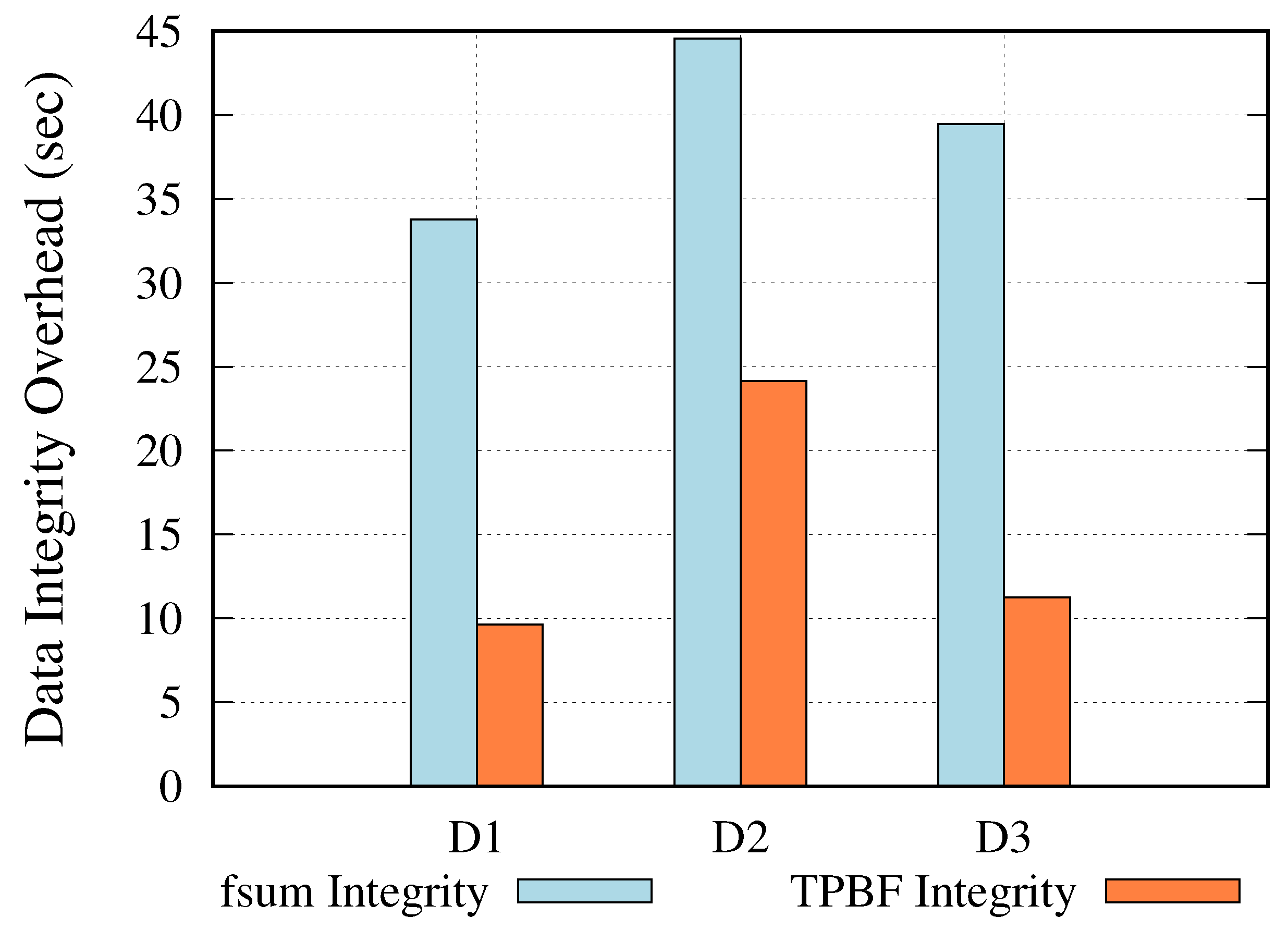
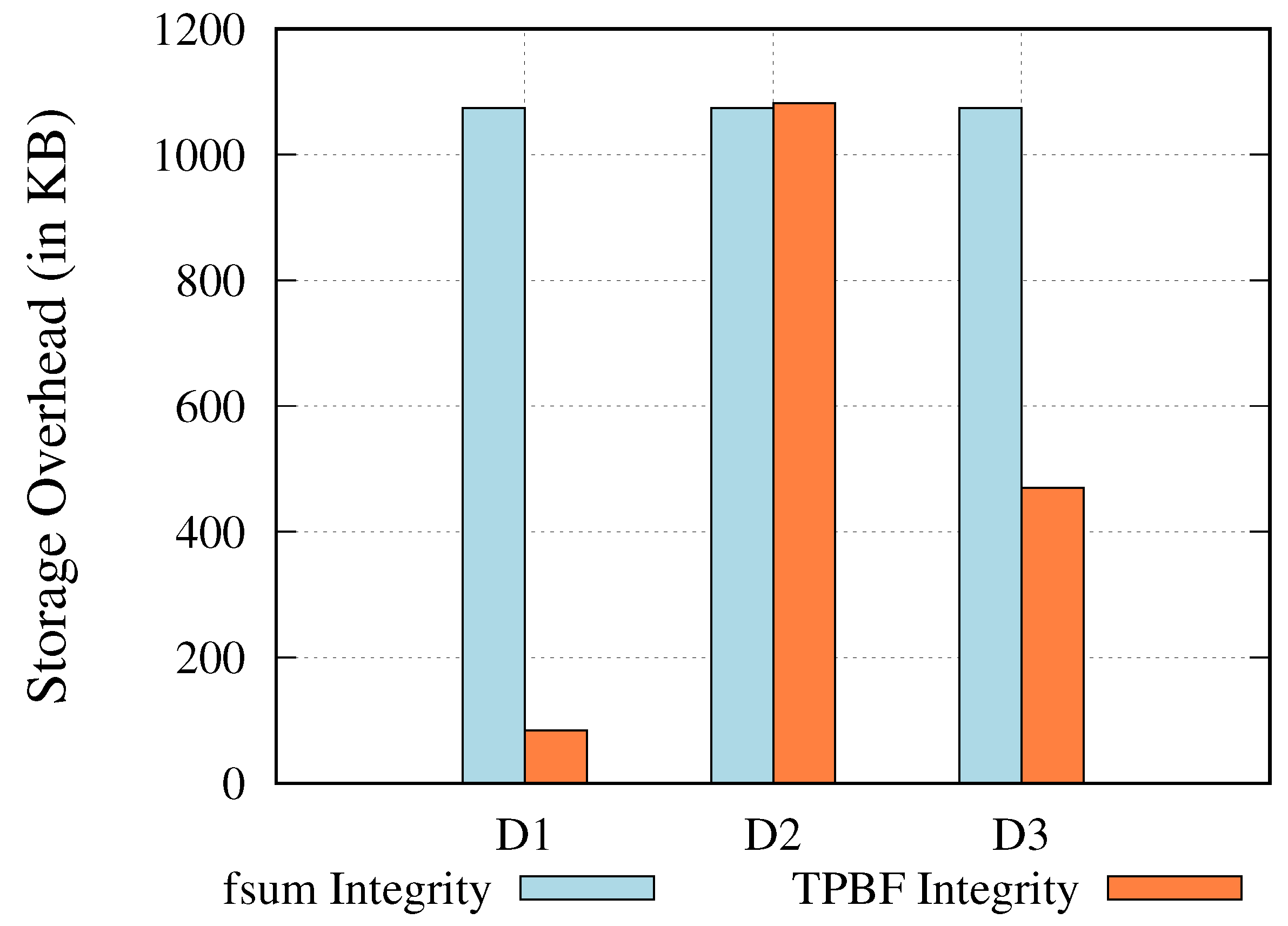
- Data transfer performance, memory, and storage overhead have been evaluated to assess the overhead of the proposed end-to-end integrity verification framework in the context of data transmission. The experimental findings show that the suggested framework had 5% and 10% overhead on the total data transmission rate and on the total memory usage, respectively. Moreover, we observed significant ≥50% savings in terms of storage requirements, when compared with state-of-the-art solutions.
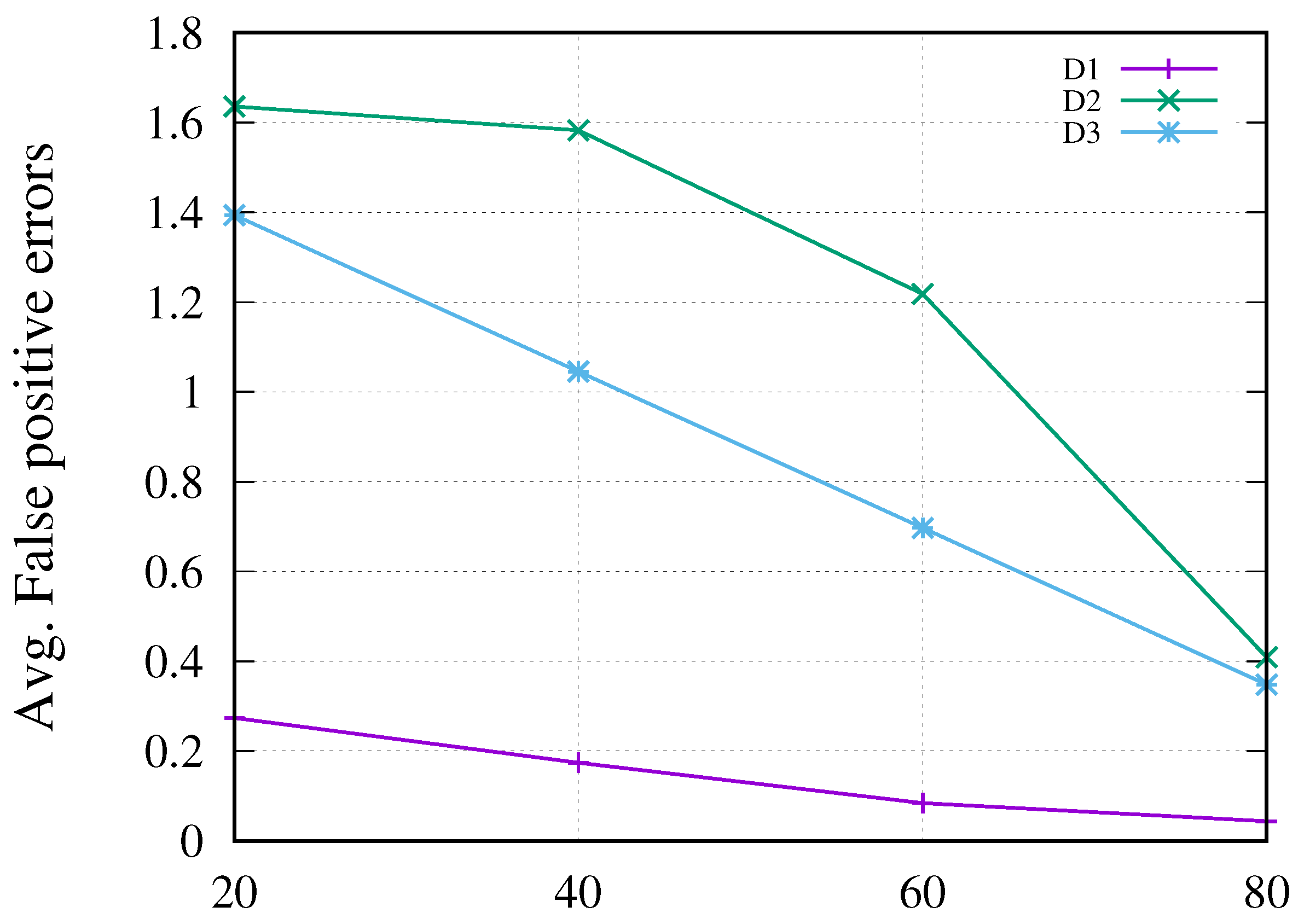
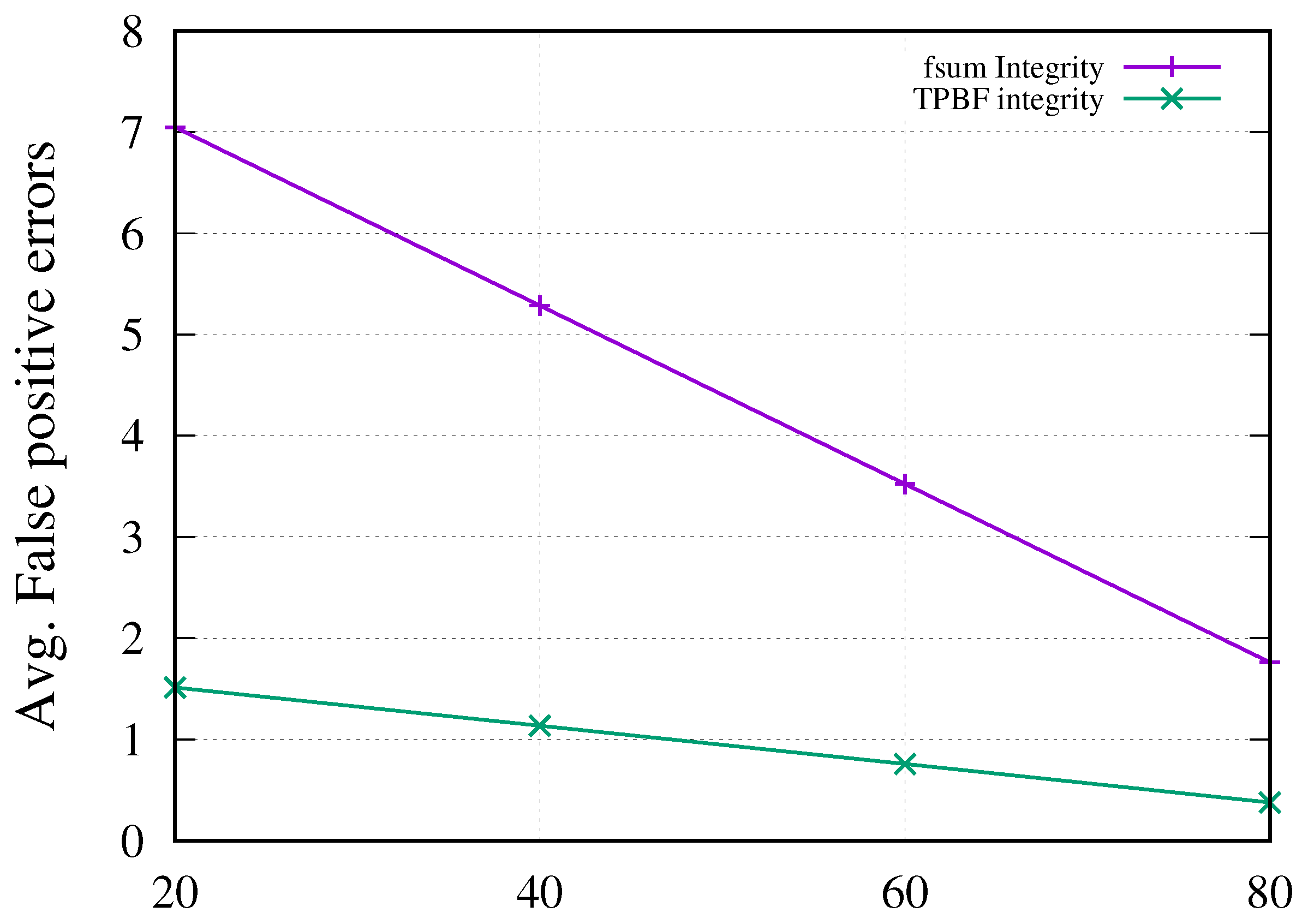
- The false-positive error rate was evaluated to assess the effectiveness of the proposed data integrity framework by manually inducing faults after transferring 20%, 40%, 60%, and 80% of the total data. Our experimental results showed that the proposed framework significantly reduced false-positive errors and was up to 80% more effective than current state-of-the-art solutions.
2. Background and Motivation
2.1. Background
2.1.1. Object-Based Big Data Transfer Systems
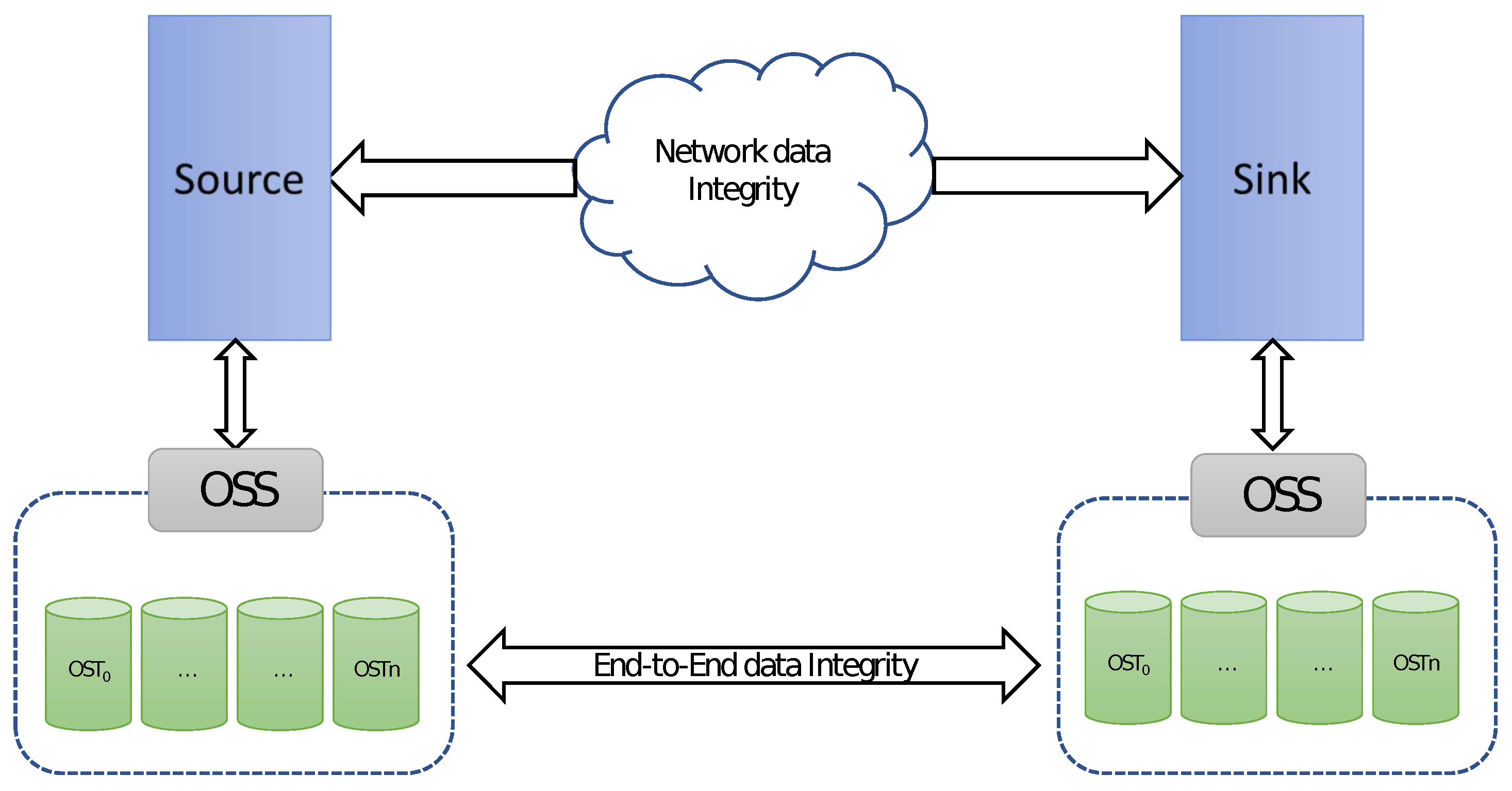
2.1.2. End-to-End Data Integrity
2.1.3. Big Data Transfer Frameworks
2.2. Motivation
- How can the impact of the data integrity framework on the overall data transfer rate of object-based big data transfer systems be minimized?
- How can the memory and storage requirements of the data integrity framework be reduced?
3. Related Work
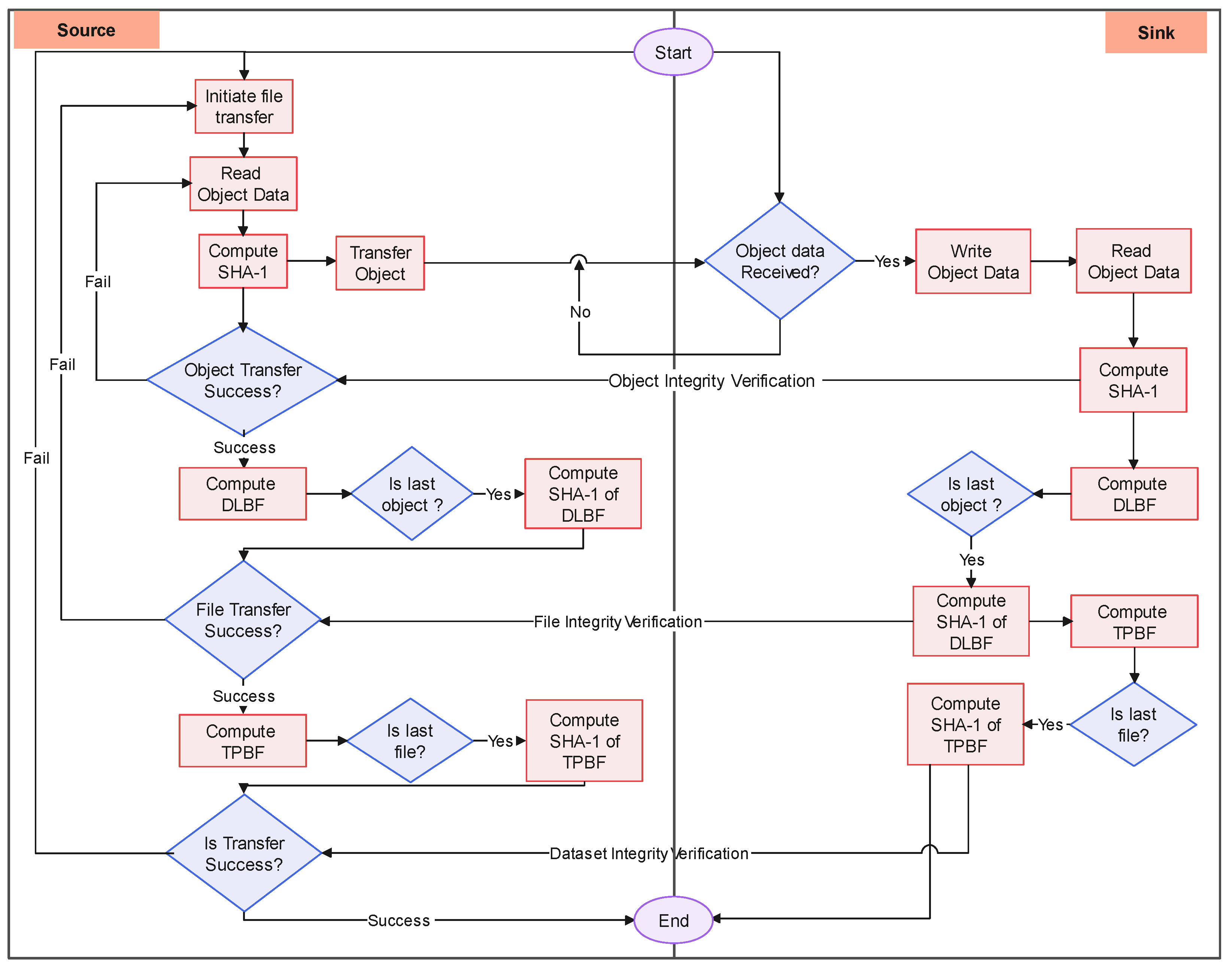
4. Data Integrity Verification Framework
4.1. Bloom Filter Design
4.1.1. Bloom Filter Data Structure
4.1.2. Hash Optimization
- i =
- m = Bloom filter size
4.1.3. Data- and Layout-Aware Bloom Filter (DLBF)
- Insert: For each object ∈S, compute and set .
- Query: To check whether an object, , is in S, compute . If , the answer is yes; otherwise, the answer is no. However, if ,…, in the bit vector B are set to 1 as a result of hash collisions, then it results in false-positive errors.
- Insert: For each object ∈S, compute , and set , and also set the object layout information bit, = 1. Where, ‘i’ represents the layout of the object.
- Query: To check whether an object, , is in S, compute . If and = 1, the answer is yes; otherwise, the answer is no.
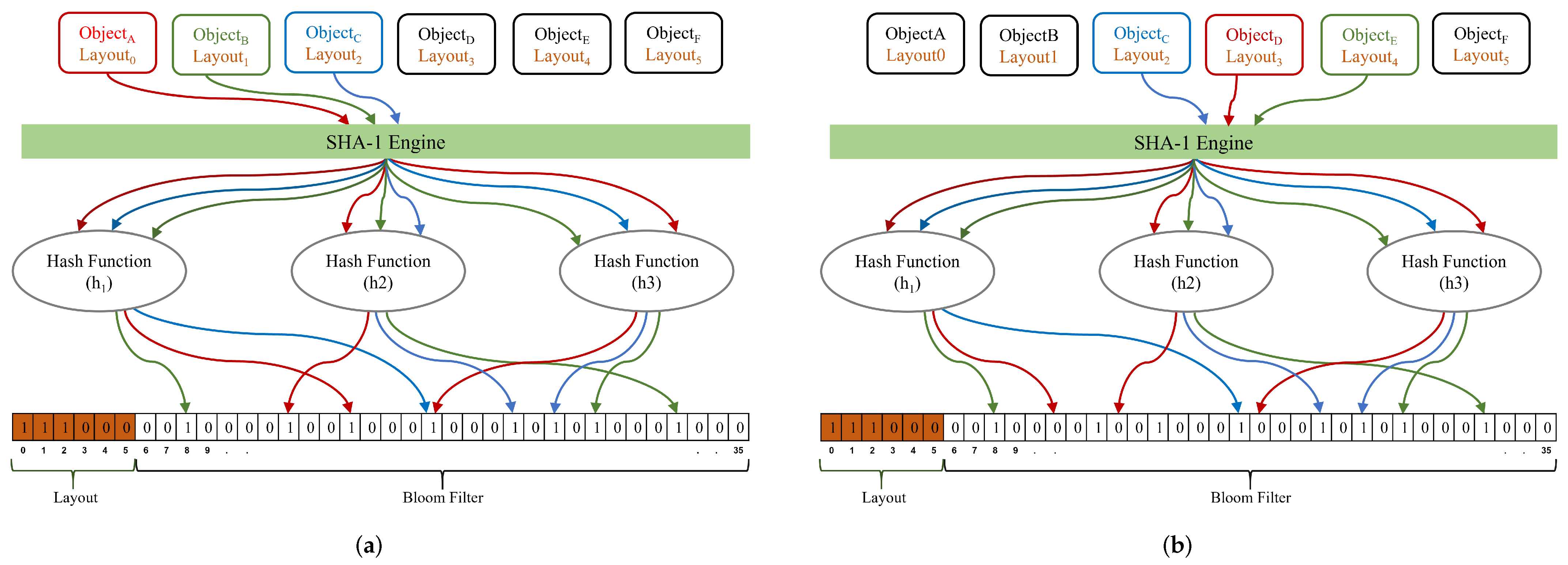
4.1.4. Illustration of Data and Layout Aware Bloom Filter
- Insert: The insert operation is shown in Figure 3a. To uniquely represent the object, the SHA-1 engine is employed to calculate the block hash on the dataset. In this illustrative example, objects A, B, and C are inserted into the Bloom filter. Hash functions {, , and } are employed on the hashed object data to uniformly map the objects into k random positions. The Bloom filter bits at positions {13, 16, and 20} are set to 1 using the {, , and } hash functions on hashed data. Additionally, bit {0} of the Bloom filter array is set to 1 as the layout of is zero. Similarly, bits at positions {1, 8, 28 32}, and {2, 20, 24, 26} are set to 1 for and , respectively.
- Query: The query operation is shown in Figure 3b. We considered objects C, D, and E for membership query operation. We presume the object membership if all the k bits in the Bloom filter section, along with the layout bit in the layout sections, are set to 1. For the Bloom filter returns “Positive” for membership query as the hash positions {20, 24, and 26} along with its layout bit at position {2} is set to 1. The membership query of returns “Negative” as the bit at position {11} is not set. On the other hand, membership query results in “Negative”, despite the fact that the bits at positions {8, 28, and 32} are all set. This is due to the fact that the object layout bit at position {4} is not set. Without the layout information, membership query may result in “False Positive” since the bits at positions {8, 28, and 32} are all set. Hence, we prevented false-positive matches of the Bloom filter by utilizing the object layout information in conjunction with the Bloom filter.
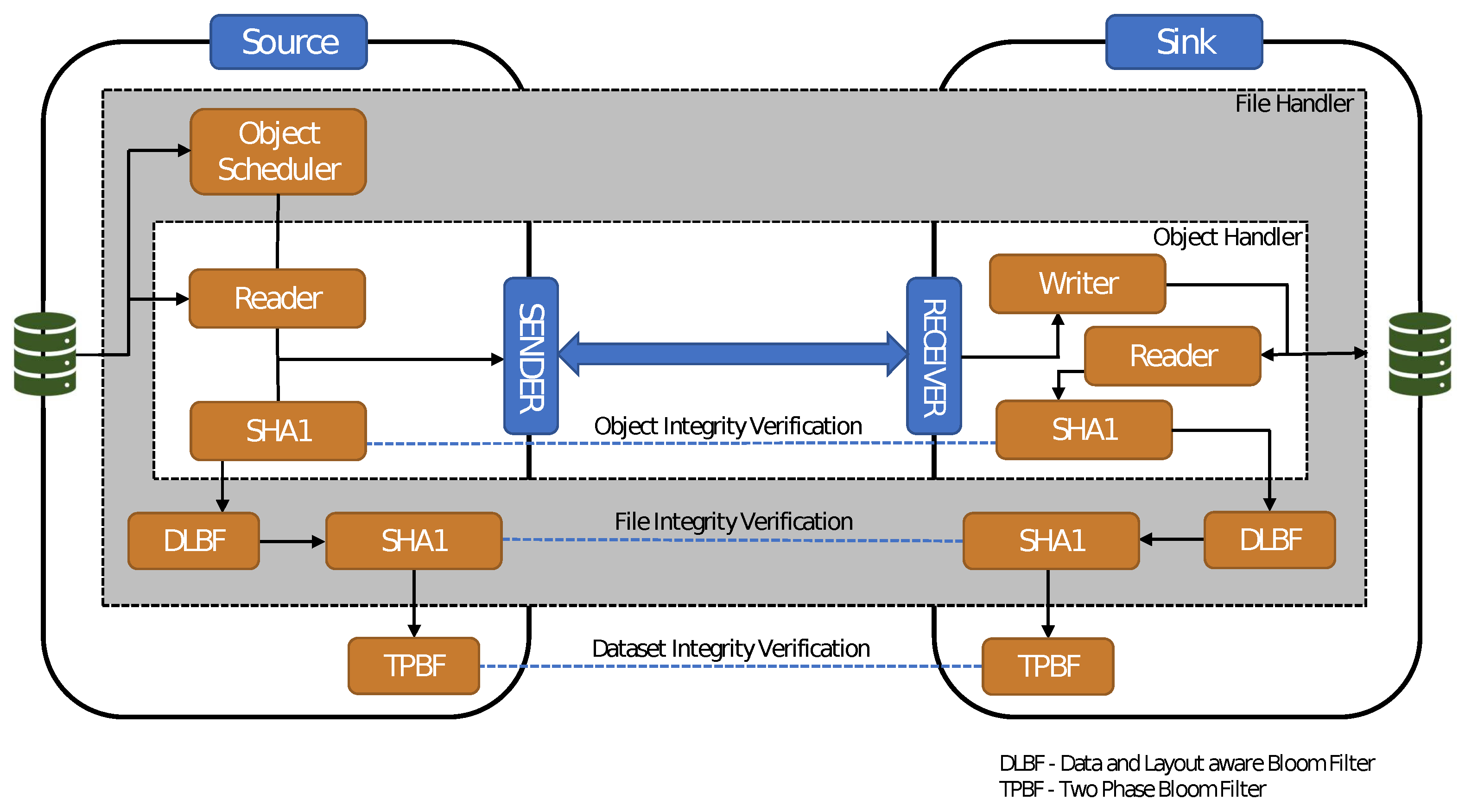
4.2. System Architecture
4.3. Design and Implementation
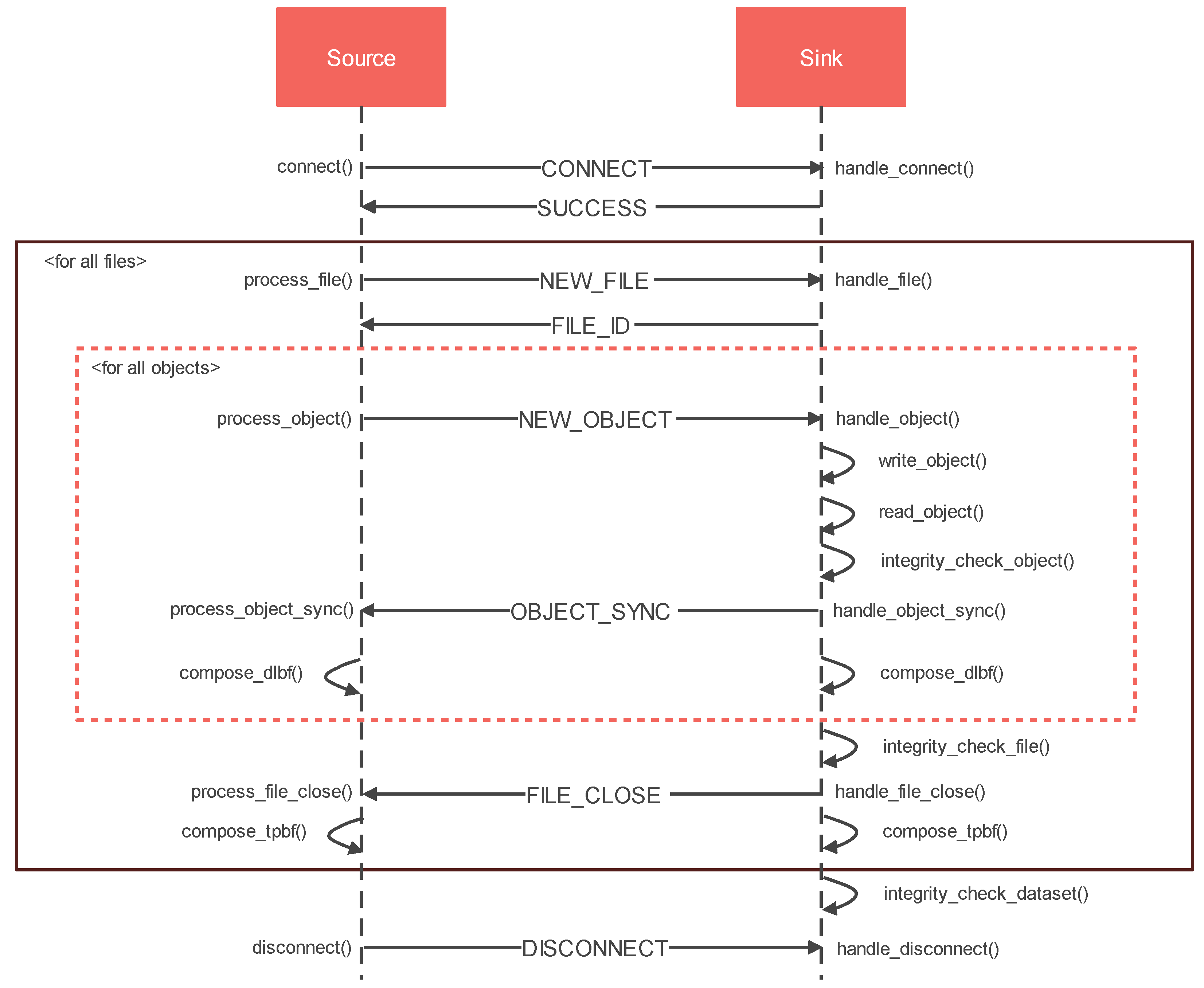
4.3.1. Communication Protocol
- The source endpoint sends a CONNECT request to the sink endpoint, and the sink endpoint responds with SUCCESS if the connection is successful.
- The source endpoint compiles a list of files to be transferred and then issues a NEW_FILE request for each file. The sink endpoint opens the file based on the information in the NEW_FILE request and adds the file descriptor to the FILE_ID response.
- The source endpoint schedules all the objects of a file and initiates object transfer using NEW_OBJECT request. The sink endpoint receives the object data and writes the same to the sink-end PFS. On successful write operation, the sink endpoint compares the block hash with the hash received in the NEW_OBJECT request and responds with OBJECT_SYNC.
- On successful integrity verification, both source and sink endpoints aggregate the file-based data and the layout-aware Bloom filter; otherwise, the source endpoint schedules the object for re-transfer.
- Steps 3 and 4 are repeated for all the objects in the file.
- On transferring all the objects of a file successfully, the sink endpoint compares the file hash with the hash received in the last object’s NEW_OBJECT request and responds with FILE_CLOSE response.
- On successful integrity verification, both source and sink endpoints aggregate the dataset level two phase Bloom filter; otherwise, the source endpoint schedules the file for re-transfer.
- Steps 2 to 7 are repeated for all the files in the dataset.
- After successfully transferring all of the files in the dataset, dataset level integrity verification is performed. If the integrity check is successful, the source endpoint will send a DISCONNECT request; otherwise, steps 2 to 9 will be repeated.
| Listing 1. Communication message type. | |
| typedef enum msg_type { | |
| CONNECT = 0, | //Connection Request |
| SUCCESS, | //Connection accepted |
| NEW_FILE, | //New File request |
| FILE_ID, | //Sink File ID. |
| NEW_OBJECT, | //Ready for object transfer |
| OBJECT_SYNC, | //Sync with Sink PFS |
| FILE_CLOSE, | //File close |
| DISCONNECT | //Ready to disconnect |
| } msg_type_t; | |
4.3.2. Data- and Layout-Aware Bloom Filter (DLBF)
| Algorithm 1 Two-phase Bloom Filter | |
| 1: procedure GenerateDLBF((S)) | |
| 2: for each do | ▹ For all objects in a file |
| 3: | ▹ Map object of arbitrary size to fixed size |
| 4: for each to do | ▹ k hash functions |
| 5: | ▹ Calculate k hash bit positions |
| 6: | ▹ Set k hash positions of DLBF to 1 |
| 7: end for | |
| 8: | ▹ Set the layout bit of DLBF to 1 |
| 9: end for | |
| 10: | ▹ File signature |
| 11: return | |
| 12: end procedure | |
| 13: procedure GenerateTPBF((N)) | |
| 14: for each do | ▹ For all files in a dataset |
| 15: | ▹ Generate file level DLBF |
| 16: for each to do | ▹ k hash functions |
| 17: | ▹ Calculate k hash bit positions |
| 18: | ▹ Set k hash positions of TPBF to 1 |
| 19: end for | |
| 20: end for | |
| 21: | ▹ Dataset signature |
| 22: return | |
| 23: end procedure |
4.3.3. Two-Phase Bloom Filter (TPBF)
4.4. Memory Overhead Analysis
- C = number of active file transfers
5. Evaluation
5.1. Testbed and Workload Specifications
5.1.1. Testbed
5.1.2. Workload
5.1.3. Bloom Filter Configuration
5.2. Performance Evaluation
5.2.1. Data Transfer Time
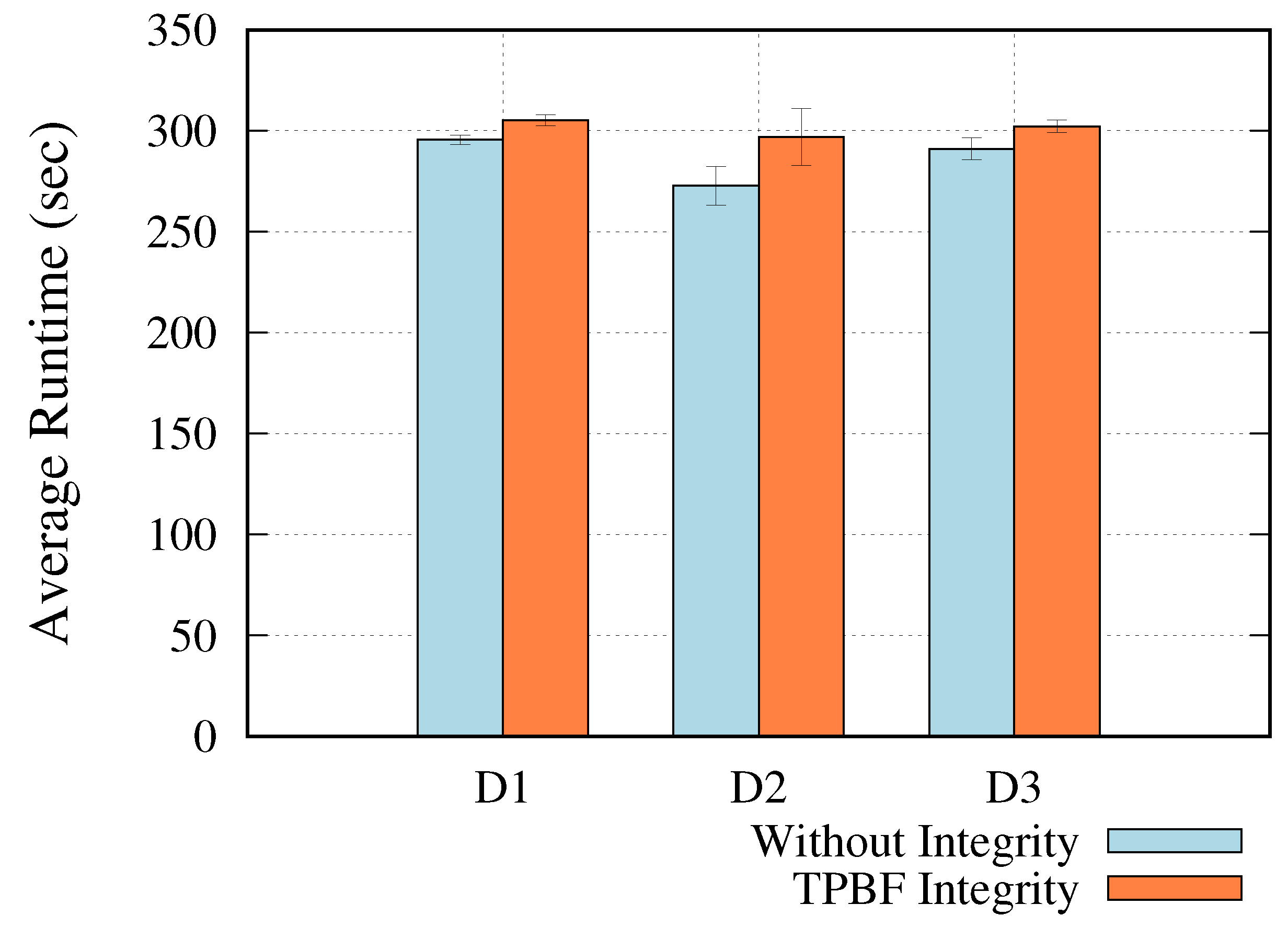
5.2.2. Computational Overhead
- = Estimated data integrity overhead
- = TPBF average runtime
- = Standalone average runtime
5.2.3. Memory Overhead
5.2.4. Storage Overhead
5.2.5. False-Positive Matches
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- ORNL. Available online: https://www.ornl.gov/ (accessed on 20 April 2021).
- CERN. Available online: https://home.cern/ (accessed on 20 April 2021).
- LIGO. Available online: https://www.ligo.caltech.edu/ (accessed on 20 April 2021).
- Data Never Sleeps 5.0. Available online: https://www.domo.com/learn/infographic/data-never-sleeps-5 (accessed on 25 May 2021).
- Carns, P.H.; Ligon, W.B., III; Ross, R.B.; Thakur, R. PVFS: A Parallel File System for Linux Clusters. In Proceedings of the 4th Annual Linux Showcase & Conference (ALS 2000), Atlanta, GA, USA, 10–14 October 2000. [Google Scholar]
- Enhancing Scalability and Performance of Parallel File Systems. Available online: https://www.intel.com/content/dam/www/public/us/en/documents/white-papers/enhancing-scalability-and-performance-white-paper.pdf (accessed on 25 February 2022).
- Welch, B.; Unangst, M.; Abbasi, Z.; Gibson, G.; Mueller, B.; Small, J.; Zelenka, J.; Zhou, B. Scalable Performance of the Panasas Parallel File System. In Proceedings of the 6th USENIX Conference on File and Storage Technologies, FAST’08, San Jose, CA, USA, 26–29 February 2008; pp. 1–17. [Google Scholar]
- Lofstead, J.; Zheng, F.; Liu, Q.; Klasky, S.; Oldfield, R.; Kordenbrock, T.; Schwan, K.; Wolf, M. Managing Variability in the IO Performance of Petascale Storage Systems. In Proceedings of the SC’10: 2010 ACM/IEEE International Conference for High Performance Computing, Networking, Storage and Analysis, New Orleans, LA, USA, 13–19 November 2010; pp. 1–12. [Google Scholar] [CrossRef]
- Kim, Y.; Atchley, S.; Vallee, G.R.; Shipman, G.M. Layout-aware I/O Scheduling for terabits data movement. In Proceedings of the 2013 IEEE International Conference on Big Data, Santa Clara, CA, USA, 6–9 October 2013; pp. 44–51. [Google Scholar] [CrossRef]
- Kim, Y.; Atchley, S.; Vallée, G.R.; Shipman, G.M. LADS: Optimizing Data Transfers using Layout-Aware Data Scheduling; Technical Report ORNL/TM-2014/251; Oak Ridge National Laboratory: Oak Ridge, TN, USA, 2015.
- Kim, Y.; Atchley, S.; Vallee, G.R.; Lee, S.; Shipman, G.M. Optimizing End-to-End Big Data Transfers over Terabits Network Infrastructure. IEEE Trans. Parallel Distrib. Syst. 2017, 28, 188–201. [Google Scholar] [CrossRef]
- Settlemyer, B.; Dobson, J.M.; Hodson, S.W.; Kuehn, J.A.; Poole, S.W.; Ruwart, T.M. A Technique for Moving Large Data Sets over High-Performance Long Distance Networks. In Proceedings of the IEEE Symposium on Massive Storage Systems and Technologies, MSST’11, Denver, CO, USA, 23–27 May 2011; pp. 1–6. [Google Scholar]
- Stone, J.; Partridge, C. When the CRC and TCP checksum disagree. ACM SIGCOMM Comput. Commun. Rev. 2001, 30, 309–319. [Google Scholar] [CrossRef]
- Meylan, A.; Cherubini, M.; Chapuis, B.; Humbert, M.; Bilogrevic, I.; Huguenin, K. A Study on the Use of Checksums for Integrity Verification of Web Downloads. ACM Trans. Priv. Secur. 2020, 24, 4. [Google Scholar] [CrossRef]
- Hash Functions: CSRC. Available online: https://csrc.nist.gov/projects/hash-functions (accessed on 25 February 2022).
- RFC 1321—The MD5 Message-Digest Algorithm. Available online: https://datatracker.ietf.org/doc/html/rfc1321 (accessed on 25 February 2022).
- Kettimuthu, R.; Liu, Z.; Wheeler, D.; Foster, I.; Heitmann, K.; Cappello, F. Transferring a Petabyte in a Day. Future Gener. Comput. Syst. 2018, 88, 191–198. [Google Scholar] [CrossRef]
- Jung, E.S.; LIU, S.; Kettimuthu, R.; CHUNG, S. High-Performance End-to-End Integrity Verification on Big Data Transfer. IEICE Trans. Inf. Syst. 2019, E102.D, 1478–1488. [Google Scholar] [CrossRef] [Green Version]
- Xiong, S.; Wang, F.; Cao, Q. A Bloom Filter Based Scalable Data Integrity Check Tool for Large-Scale Dataset. In Proceedings of the 1st Joint International Workshop on Parallel Data Storage & Data Intensive Scalable Computing Systems, PDSW-DISCS’16, Salt Lake City, UT, USA, 14 November 2016; pp. 55–60. [Google Scholar]
- Lustre: A Scalable, High-Performance File System Cluster. Available online: https://cse.buffalo.edu/faculty/tkosar/cse710/papers/lustre-whitepaper.pdf (accessed on 25 February 2022).
- Xie, B.; Chase, J.; Dillow, D.; Drokin, O.; Klasky, S.; Oral, S.; Podhorszki, N. Characterizing output bottlenecks in a supercomputer. In Proceedings of the SC’12: International Conference on High Performance Computing, Networking, Storage and Analysis, Salt Lake City, UT, USA, 11–15 November 2012; pp. 1–11. [Google Scholar] [CrossRef]
- Schwan, P. Lustre: Building a File System for 1,000-node Clusters. In Proceedings of the Linux Symposium, Ottawa, ON, Canada, 23–26 July 2003; p. 9. [Google Scholar]
- Introduction to InfiniBand. Available online: https://network.nvidia.com/sites/default/files/pdf/whitepapers/IB_Intro_WP_190.pdf (accessed on 25 February 2022).
- Wu, J.; Wyckoff, P.; Panda, D. PVFS over InfiniBand: Design and performance evaluation. In Proceedings of the 2003 International Conference on Parallel Processing, Kaohsiung, Taiwan, 6–9 October 2003; pp. 125–132. [Google Scholar] [CrossRef]
- Hanushevsky, A. BBCP. Available online: http://www.slac.stanford.edu/~abh/bbcp/ (accessed on 24 September 2021).
- Allcock, W.; Bresnahan, J.; Kettimuthu, R.; Link, M.; Dumitrescu, C.; Raicu, I.; Foster, I. The Globus Striped GridFTP Framework and Server. In Proceedings of the International Conference for High Performance Computing, Networking, Storage and Analysis, SC’05, Seattle, WA, USA, 12–18 November 2005; pp. 54–64. [Google Scholar] [CrossRef] [Green Version]
- Alliance, G. The Globus Toolkit. Available online: http://http://www.globus.org/toolkit/ (accessed on 24 September 2021).
- Malensek, M.; Pallickara, S.; Pallickara, S. Alleviation of Disk I/O Contention in Virtualized Settings for Data-Intensive Computing. In Proceedings of the 2015 IEEE/ACM 2nd International Symposium on Big Data Computing (BDC), Limassol, Cyprus, 7–10 December 2015; pp. 1–10. [Google Scholar] [CrossRef] [Green Version]
- Kim, Y.; Atchley, S.; Vallée, G.R.; Shipman, G.M. LADS: Optimizing Data Transfers using Layout-Aware Data Scheduling. In Proceedings of the 1st USENIX Conference on File and Storage Technologies, FAST’15, Santa Clara, CA, USA, 16–19 February 2015. [Google Scholar]
- Kasu, P.; Kim, T.; Um, J.; Park, K.; Atchley, S.; Kim, Y. FTLADS: Object-Logging Based Fault-Tolerant Big Data Transfer System Using Layout Aware Data Scheduling. IEEE Access 2019, 7, 37448–37462. [Google Scholar] [CrossRef]
- Bairavasundaram, L.N.; Goodson, G.; Schroeder, B.; Arpaci-Dusseau, A.C.; Arpaci-Dusseau, R.H. An Analysis of Data Corruption in the Storage Stack. In Proceedings of the 6th USENIX Conference on File and Storage Technologies (FAST 08), San Jose, CA, USA, 26–29 February 2008. [Google Scholar]
- Zhang, Y.; Rajimwale, A.; Arpaci-Dusseau, A.C.; Arpaci-Dusseau, R.H. End-to-end Data Integrity for File Systems: A ZFS Case Study. In Proceedings of the 8th USENIX Conference on File and Storage Technologies (FAST 10), San Jose, CA, USA, 23–26 February 2010. [Google Scholar]
- Lustre, ZFS, and Data Integrity. Available online: https://wiki.lustre.org/images/0/00/Tuesday_shpc-2009-zfs.pdf (accessed on 25 February 2022).
- Zhang, Y.; Myers, D.S.; Arpaci-Dusseau, A.C.; Arpaci-Dusseau, R.H. Zettabyte reliability with flexible end-to-end data integrity. In Proceedings of the 2013 IEEE 29th Symposium on Mass Storage Systems and Technologies (MSST), Long Beach, CA, USA, 6–10 May 2013; pp. 1–14. [Google Scholar] [CrossRef] [Green Version]
- Improvements in Lustre Data Integrity—Opensfs. Available online: https://www.opensfs.org/wp-content/uploads/2011/11/Improvements-in-Lustre-Data-Integrity.pdf (accessed on 25 February 2022).
- Sivathanu, G.; Wright, C.P.; Zadok, E. Ensuring Data Integrity in Storage: Techniques and Applications. In Proceedings of the 2005 ACM Workshop on Storage Security and Survivability, StorageSS’05, Fairfax, VA, USA, 11 November 2005; Association for Computing Machinery: New York, NY, USA, 2005; pp. 26–36. [Google Scholar] [CrossRef]
- Kumar, M.; Meena, J.; Singh, R.; Vardhan, M. Data outsourcing: A threat to confidentiality, integrity, and availability. In Proceedings of the 2015 International Conference on Green Computing and Internet of Things (ICGCIoT), Greater Noida, India, 8–10 October 2015; pp. 1496–1501. [Google Scholar] [CrossRef]
- Reyes-Anastacio, H.G.; Gonzalez-Compean, J.; Morales-Sandoval, M.; Carretero, J. A data integrity verification service for cloud storage based on building blocks. In Proceedings of the 2018 8th International Conference on Computer Science and Information Technology (CSIT), Amman, Jordan, 11–12 July 2018; pp. 201–206. [Google Scholar] [CrossRef]
- Sravan Kumar, R.; Saxena, A. Data integrity proofs in cloud storage. In Proceedings of the 2011 Third International Conference on Communication Systems and Networks (COMSNETS 2011), Bangalore, India, 4–8 January 2011; pp. 1–4. [Google Scholar] [CrossRef]
- George, A.S.; Nargunam, A.S. Multi-Replica Integrity Verification in Cloud: A Review and A Comparative Study. In Proceedings of the 2021 International Conference on Communication, Control and Information Sciences (ICCISc), Idukki, India, 16–18 June 2021; Volume 1, pp. 1–5. [Google Scholar] [CrossRef]
- Luo, W.; Bai, G. Ensuring the data integrity in cloud data storage. In Proceedings of the 2011 IEEE International Conference on Cloud Computing and Intelligence Systems, Beijing, China, 15–17 September 2011; pp. 240–243. [Google Scholar] [CrossRef]
- Wang, H.; Zhang, J. Blockchain Based Data Integrity Verification for Large-Scale IoT Data. IEEE Access 2019, 7, 164996–165006. [Google Scholar] [CrossRef]
- Ma, A.; Dragga, C.; Arpaci-Dusseau, A.C.; Arpaci-Dusseau, R.H. Ffsck: The Fast File System Checker. In Proceedings of the 11th USENIX Conference on File and Storage Technologies (FAST 13), San Jose, CA, USA, 12–15 February 2013; pp. 1–15. [Google Scholar]
- Abu-Rayyan, L.; Hacid, H.; Leoncé, A. Towards an End-User Layer for Data Integrity. In Proceedings of the 2019 IEEE/WIC/ACM International Conference on Web Intelligence (WI), Thessaloniki, Greece, 14–17 October 2019; pp. 317–320. [Google Scholar]
- Arasu, A.; Eguro, K.; Kaushik, R.; Kossmann, D.; Meng, P.; Pandey, V.; Ramamurthy, R. Concerto: A High Concurrency Key-Value Store with Integrity. In Proceedings of the 2017 ACM International Conference on Management of Data, SIGMOD’17, Chicago, IL, USA, 14–19 May 2017; Association for Computing Machinery: New York, NY, USA, 2017; pp. 251–266. [Google Scholar] [CrossRef]
- Liu, S.; Jung, E.S.; Kettimuthu, R.; Sun, X.H.; Papka, M. Towards optimizing large-scale data transfers with end-to-end integrity verification. In Proceedings of the 2016 IEEE International Conference on Big Data (Big Data), Washington, DC, USA, 5–8 December 2016; pp. 3002–3007. [Google Scholar] [CrossRef]
- Arslan, E.; Alhussen, A. A Low-Overhead Integrity Verification for Big Data Transfers. In Proceedings of the 2018 IEEE International Conference on Big Data (Big Data), Seattle, WA, USA, 10–13 December 2018; pp. 4227–4236. [Google Scholar] [CrossRef]
- Kasu, P.; Hamandawana, P.; Chung, T.S. DLFT: Data and Layout Aware Fault Tolerance Framework for Big Data Transfer Systems. IEEE Access 2021, 9, 22939–22954. [Google Scholar] [CrossRef]
- Bloom, B.H. Space/time trade-offs in hash coding with allowable errors. Commun. ACM 1970, 13, 422–426. [Google Scholar] [CrossRef]
- Broder, A.; Mitzenmacher, M. Survey: Network Applications of Bloom Filters: A Survey. Internet Math. 2003, 1, 485–509. [Google Scholar] [CrossRef] [Green Version]
- Bloom Filter. Available online: https://en.wikipedia.org/wiki/Bloom_filter (accessed on 20 April 2021).
- Kirsch, A.; Mitzenmacher, M. Less Hashing, Same Performance: Building a Better Bloom Filter. Random Struct. Algorithms 2008, 33, 187–218. [Google Scholar] [CrossRef] [Green Version]
- Lu, J.; Yang, T.; Wang, Y.; Dai, H.; Jin, L.; Song, H.; Liu, B. One-hashing Bloom filter. In Proceedings of the 2015 IEEE 23rd International Symposium on Quality of Service (IWQoS), Portland, OR, USA, 15–16 June 2015; pp. 289–298. [Google Scholar]
- Luo, L.; Guo, D.; Ma, R.T.B.; Rottenstreich, O.; Luo, X. Optimizing Bloom Filter: Challenges, Solutions, and Comparisons. IEEE Commun. Surv. Tutor. 2019, 21, 1912–1949. [Google Scholar] [CrossRef] [Green Version]
- Murmur Hash. Available online: https://en.wikipedia.org/wiki/MurmurHash (accessed on 25 May 2021).
- Hash Functions. Available online: http://www.cse.yorku.ca/~oz/hash.html (accessed on 25 May 2021).
- Tarkoma, S.; Rothenberg, C.E.; Lagerspetz, E. Theory and Practice of Bloom Filters for Distributed Systems. IEEE Commun. Surv. Tutor. 2012, 14, 131–155. [Google Scholar] [CrossRef] [Green Version]
- Jiang, M.; Zhao, C.; Mo, Z.; Wen, J. An improved algorithm based on Bloom filter and its application in bar code recognition and processing. EURASIP J. Image Video Process. 2018, 2018, 139. [Google Scholar] [CrossRef] [Green Version]
- George, A.; Mohr, R.; Simmons, J.; Oral, S. Understanding Lustre Internals Second Edition; Oak Ridge National Lab. (ORNL): Oak Ridge, TN, USA, 2021. [CrossRef]
- Atlas. Available online: https://github.com/ORNL-TechInt/Atlas_File_Size_Data (accessed on 20 April 2021).

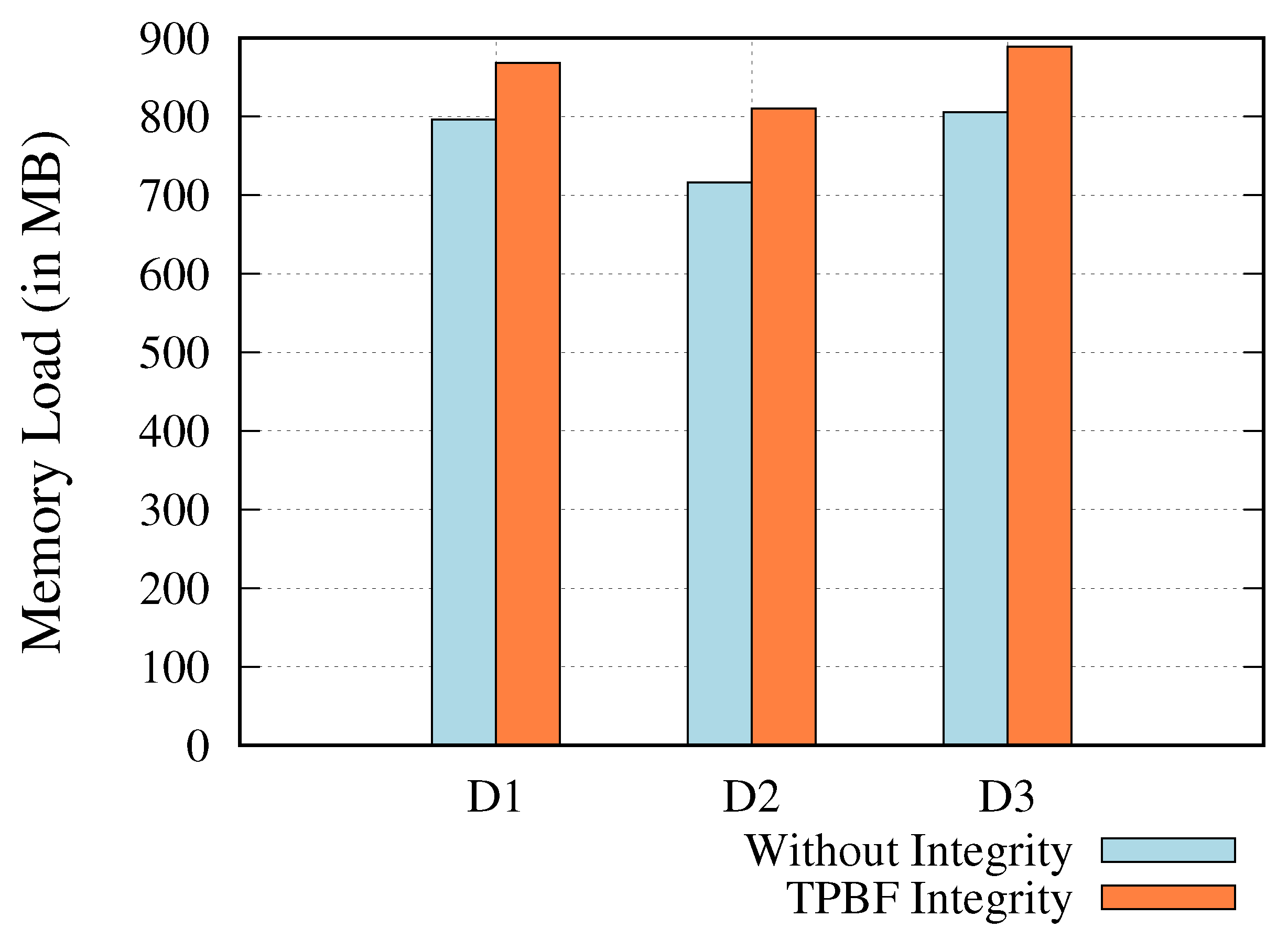
| Data Transfer Tool | Network Integrity | End-to-End Integrity | ||
|---|---|---|---|---|
| Object | File | Dataset | ||
| Grid FTP | Yes | No | Yes | No |
| BBCP | Yes | No | No | No |
| XDD | No | No | No | No |
| LADS | No | No | No | No |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Kasu, P.; Hamandawana, P.; Chung, T.-S. TPBF: Two-Phase Bloom-Filter-Based End-to-End Data Integrity Verification Framework for Object-Based Big Data Transfer Systems. Mathematics 2022, 10, 1591. https://doi.org/10.3390/math10091591
Kasu P, Hamandawana P, Chung T-S. TPBF: Two-Phase Bloom-Filter-Based End-to-End Data Integrity Verification Framework for Object-Based Big Data Transfer Systems. Mathematics. 2022; 10(9):1591. https://doi.org/10.3390/math10091591
Chicago/Turabian StyleKasu, Preethika, Prince Hamandawana, and Tae-Sun Chung. 2022. "TPBF: Two-Phase Bloom-Filter-Based End-to-End Data Integrity Verification Framework for Object-Based Big Data Transfer Systems" Mathematics 10, no. 9: 1591. https://doi.org/10.3390/math10091591
APA StyleKasu, P., Hamandawana, P., & Chung, T.-S. (2022). TPBF: Two-Phase Bloom-Filter-Based End-to-End Data Integrity Verification Framework for Object-Based Big Data Transfer Systems. Mathematics, 10(9), 1591. https://doi.org/10.3390/math10091591







