Dynamic Analysis of a COVID-19 Vaccination Model with a Positive Feedback Mechanism and Time-Delay
Abstract
:1. Introduction
2. Mathematical Modeling
3. Stability Analysis of Equilibrium and Existence of Hopf Bifurcation
4. Normal Form of Hopf Bifurcation
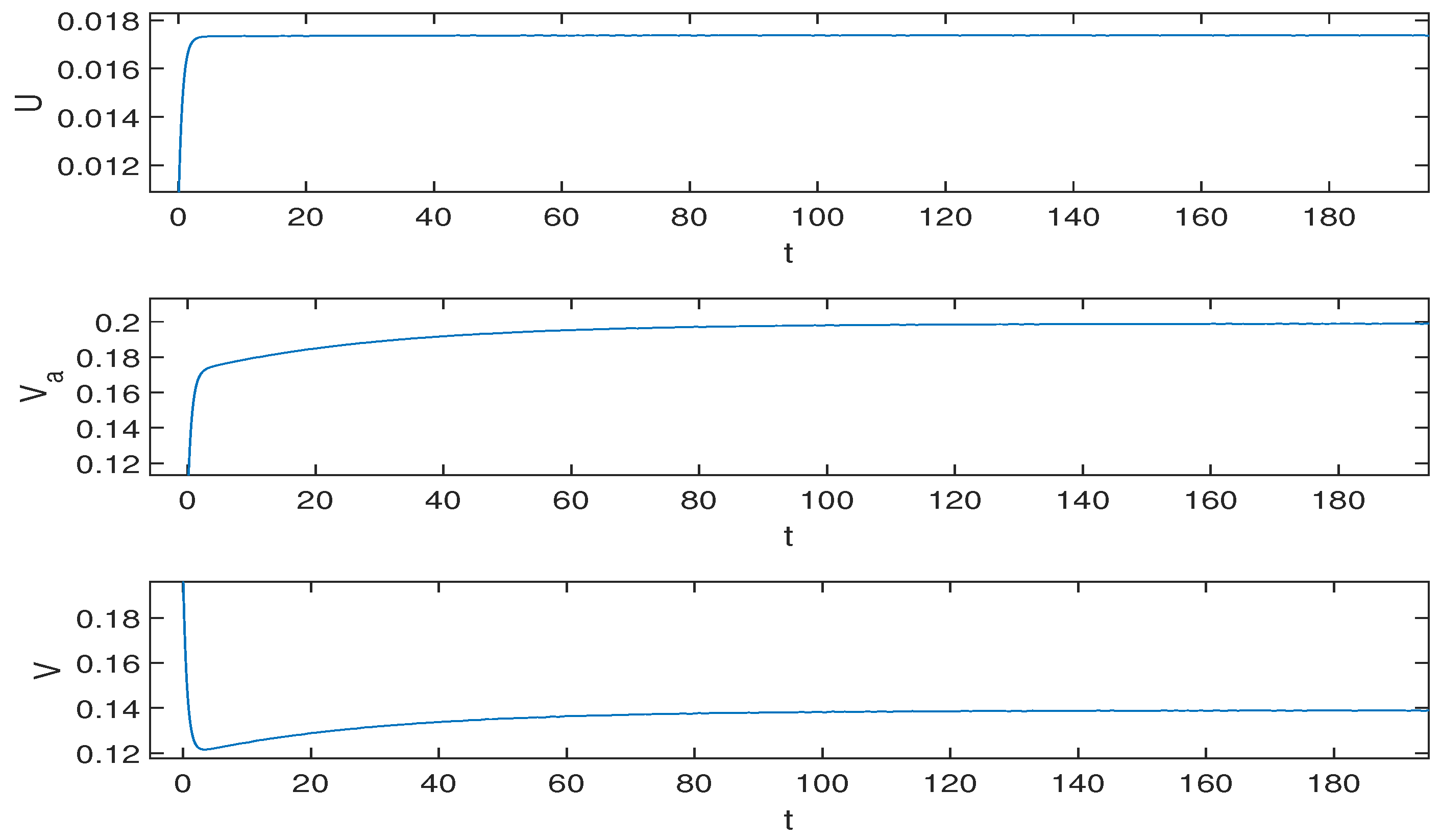
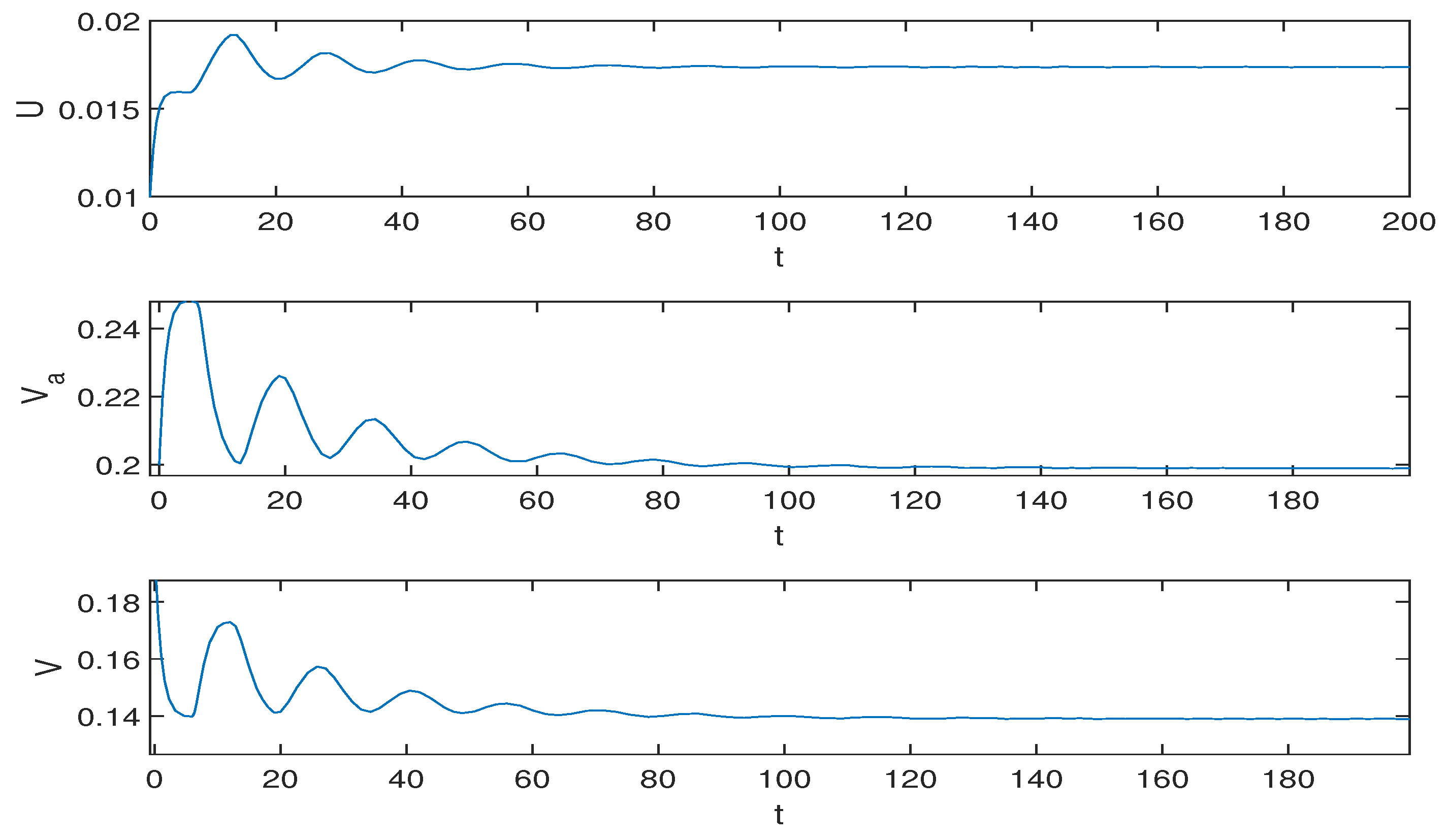
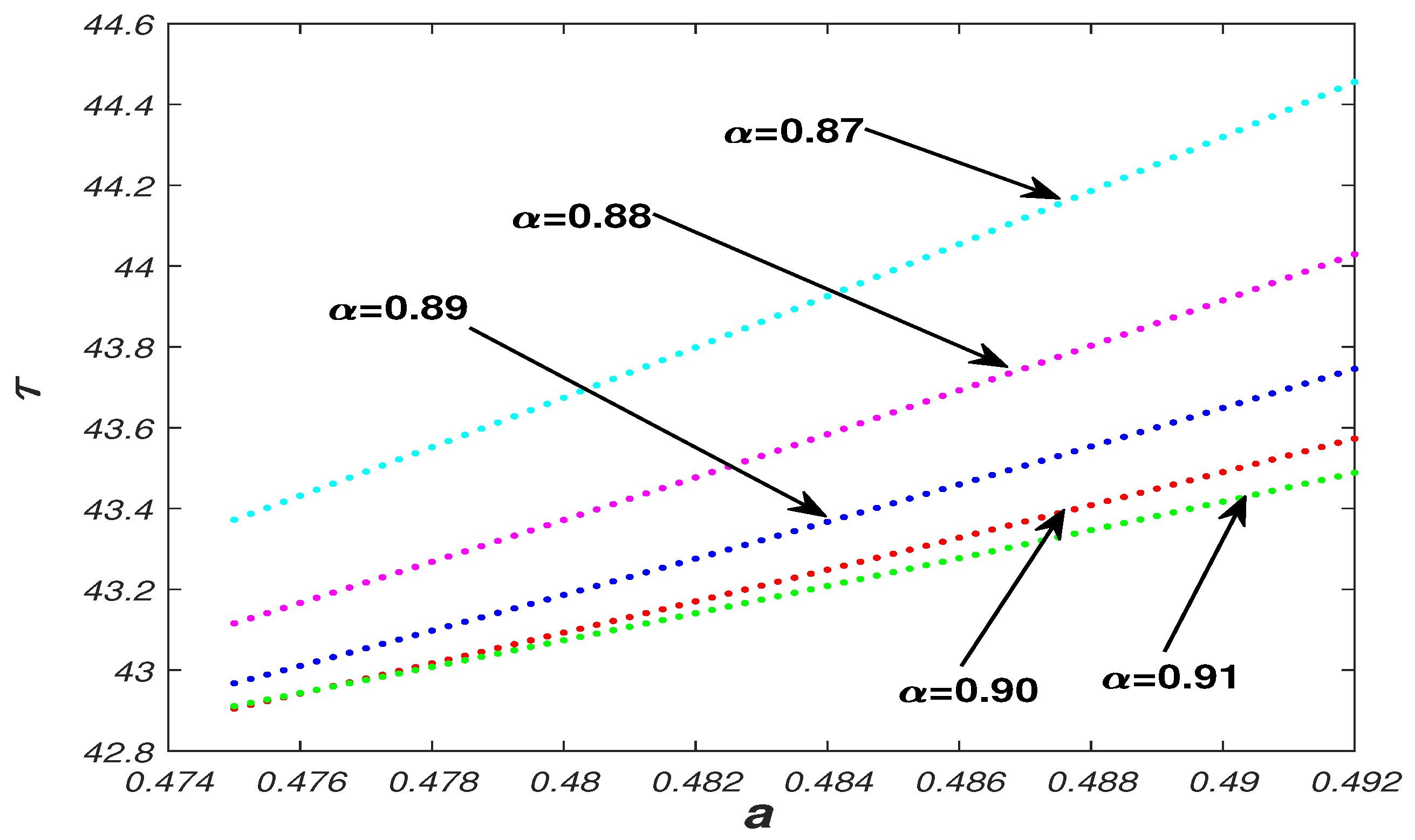
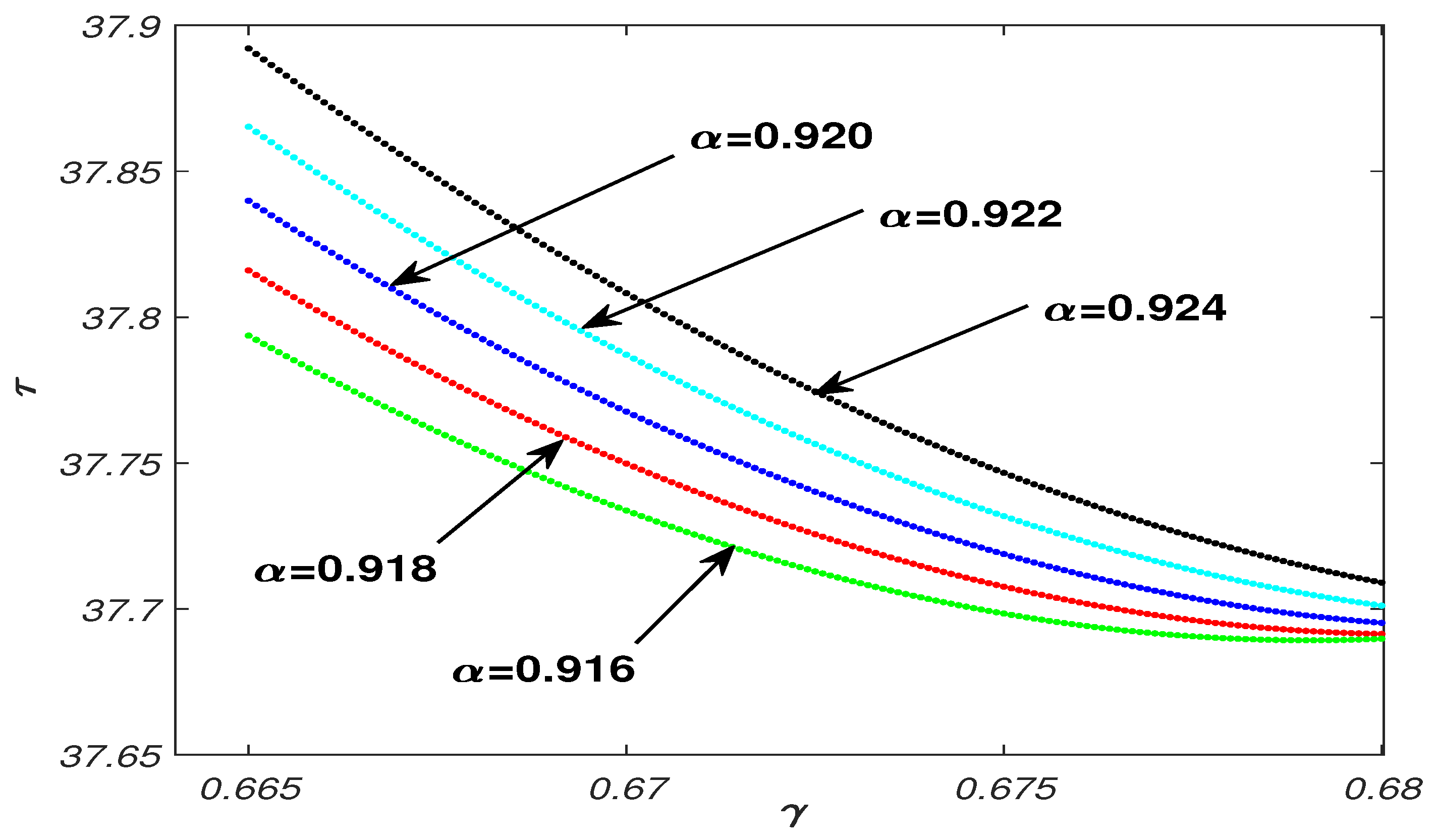
5. Numerical Simulations
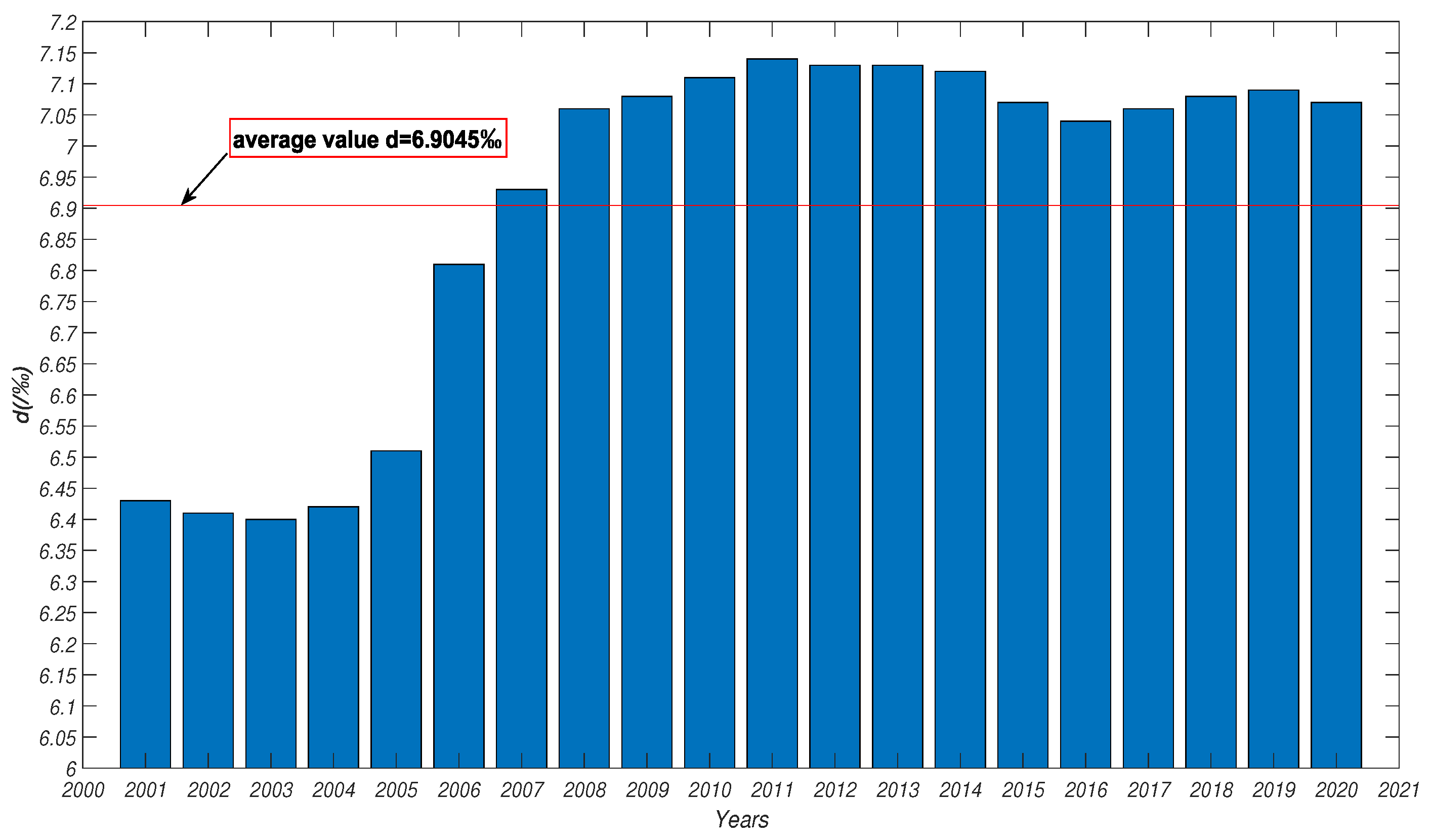
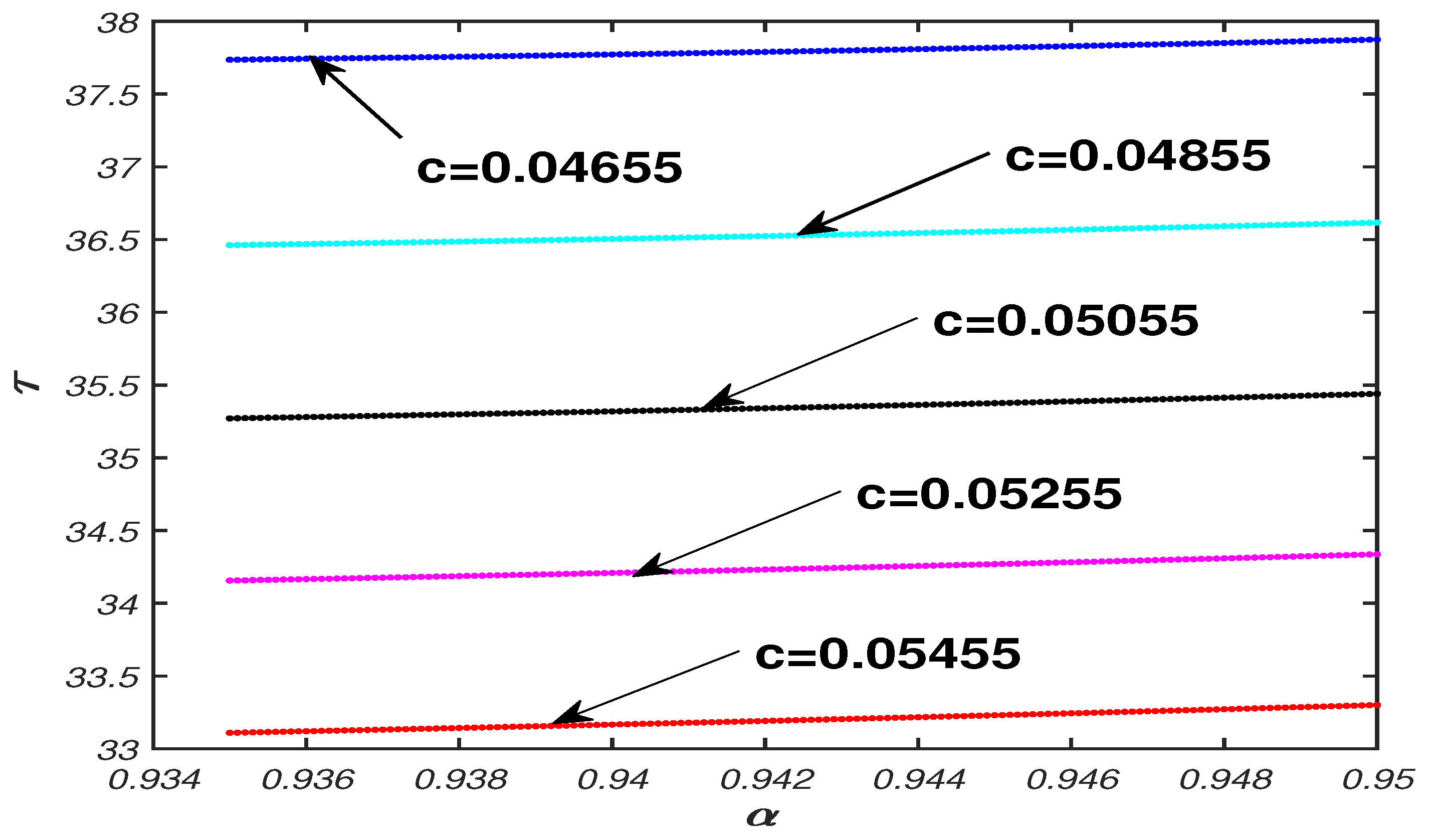
5.1. Parameter Analysis
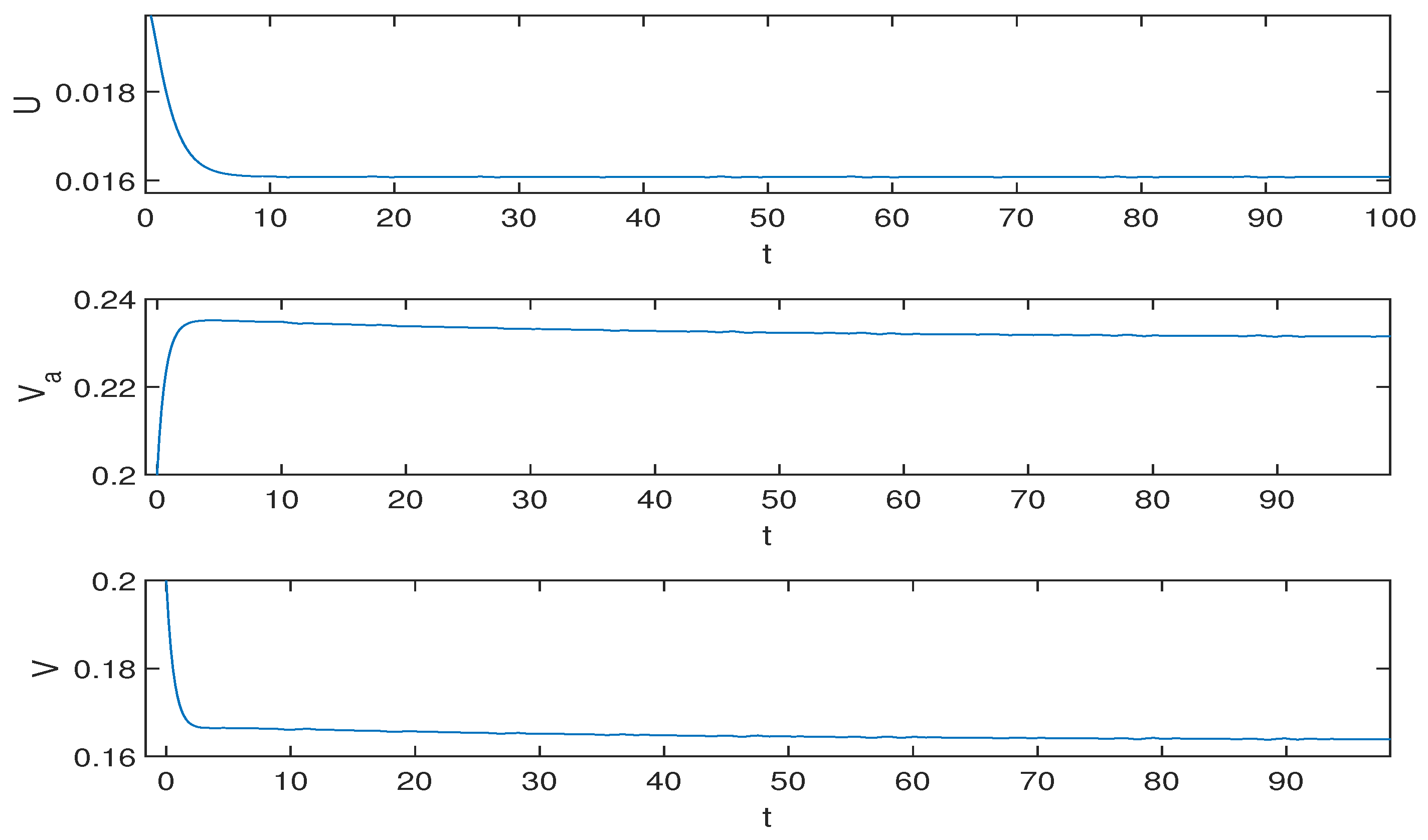
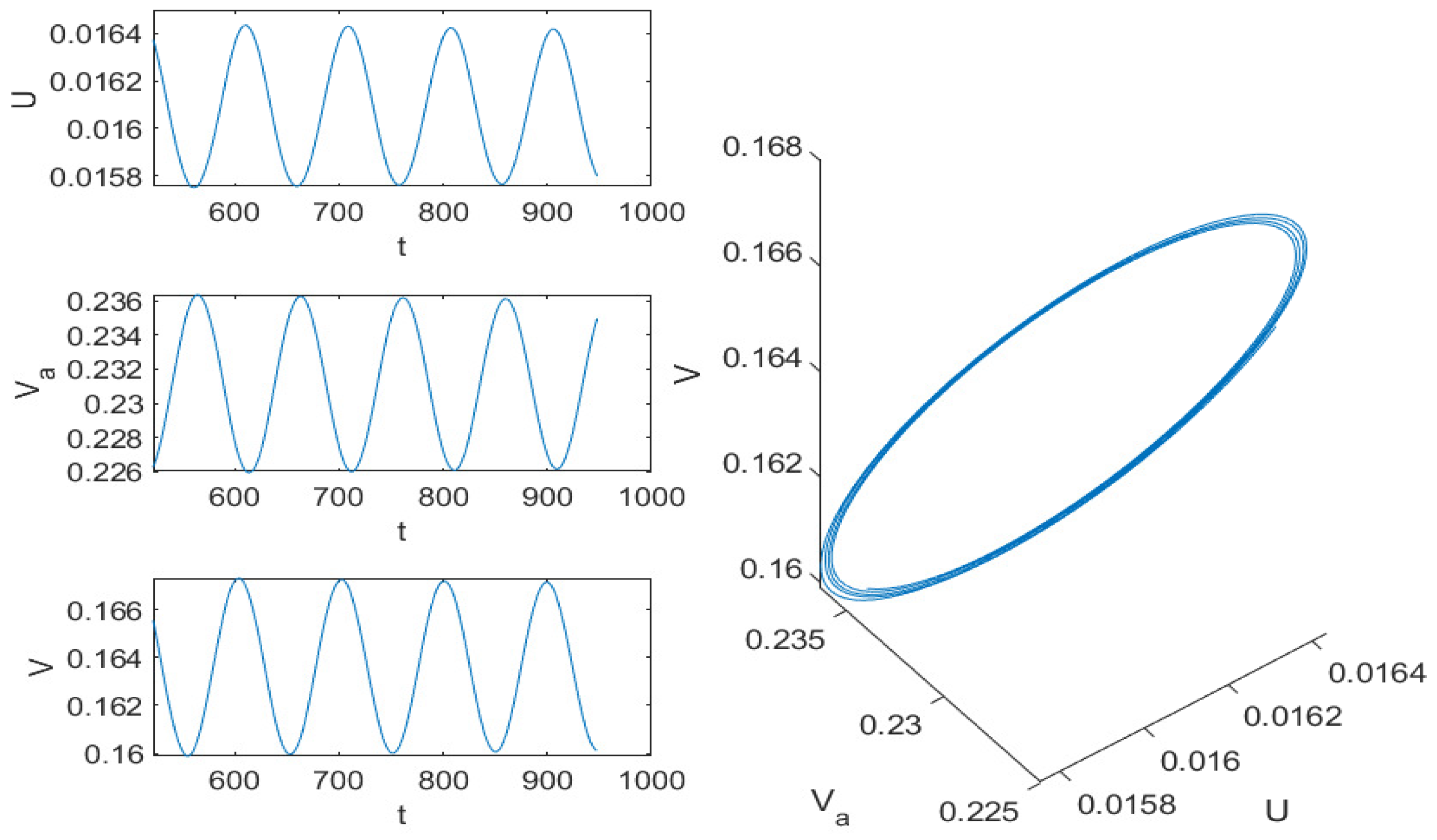
5.2. Numerical Simulation Results
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Maramattom, B.V.; Bhattacharjee, S. Neurological complications with COVID-19: A contemporaneous review. Ann. Indian Acad. 2020, 23, 468–476. [Google Scholar] [CrossRef] [PubMed]
- Zhao, D.H.; Lin, H.J.; Zhang, Z.R. Evidence-based framework and implementation of China’s strategy in combating COVID-19. Risk Manag. Healthc. Policy 2020, 13, 1989–1998. [Google Scholar] [CrossRef] [PubMed]
- Atalan, A. Is the lockdown important to prevent the COVID-19 pandemic? Effects on psychology, environment and economy-perspective. Ann. Med. Surg. 2012, 56, 38–42. [Google Scholar] [CrossRef] [PubMed]
- Acharya, S.R.; Moon, D.H.; Shin, Y.C. Assessing attitude toward COVID-19 vaccination in South Korea. Front. Psychol. 2021, 12, 694151. [Google Scholar] [CrossRef] [PubMed]
- Chakraborty, C.; Sharma, A.R.; Bhattacharya, M.; Agoramoorthy, G.; Lee, S.S. Asian-origin approved COVID-19 vaccines and current status of COVID-19 vaccination program in Asia: A critical analysis. Vaccines 2021, 9, 600. [Google Scholar] [CrossRef]
- Tagoe, E.T.; Sheikh, N.; Morton, A.; Nonvignon, J.; Sarker, A.R.; Williams, L.; Megiddo, I. COVID-19 vaccination in lower-middle income countries: National stakeholder views on challenges, barriers and potential solutions. Front. Public Health 2021, 9, 709127. [Google Scholar] [CrossRef]
- Van De Pas, R.; Van De Pas, M.A.; Ravinetto, R.; Srinivas, P.; Ochoa, T.J. COVID-19 vaccine equity: A health systems and policy perspective. Expert Rev. Vaccines 2021, 21, 25–36. [Google Scholar] [CrossRef]
- Zhu, F.; Li, Y.; Guan, X.; Hou, L.; Wang, W.; Li, J.X.; Wu, S.P.; Wang, B.S.; Wang, Z.; Wang, L.; et al. Safety, tolerability and immunogenicity of a recombinant adenovirus type-5 vectored COVID-19 vaccine: A dose-escalation, open-label, non-randomised, first-in-human trial. Lancet 2020, 395, 1845–1854. [Google Scholar] [CrossRef]
- Zhu, Y.; Wei, Y.; Sun, C.; He, H. Development of vaccines against COVID-19. Prev. Med. 2021, 33, 143–148. [Google Scholar]
- Hodgson, S.H.; Mansatta, K.; Mallett, G.; Harris, V.; Emary, K.R.W.; Pollard, A.J. What defines an efficacious COVID-19 vaccine? A review of the challenges assessing the clinical efficacy of vaccines against SARS-CoV-2. Lancet Infect. Dis. 2021, 21, E26–E35. [Google Scholar] [CrossRef]
- Grubaugh, N.D.; Hanage, W.P.; Rasmussen, A.L. Making sense of mutation: What D614G means for the COVID-19 pandemic remains unclear. Cell 2020, 182, 794–795. [Google Scholar] [CrossRef] [PubMed]
- Olaniyi, S.; Obabiyi, O.S.; Okosun, K.O.; Oladipo, A.T.; Adewale, S.O. Mathematical modelling and optimal cost-effective control of COVID-19 transmission dynamics. Eur. Phys. J. Plus 2020, 135, 938. [Google Scholar] [CrossRef] [PubMed]
- Abdy, M.; Side, S.; Annas, S.; Nur, W.; Sanusi, W. A SIR epidemic model for COVID-19 spread with fuzzy parameter: The case of Indonesia. Adv. Differ. Equ. 2021, 2021, 105. [Google Scholar] [CrossRef] [PubMed]
- Bardina, X.; Ferrante, M.; Rovira, C. A stochastic epidemic model of COVID-19 disease. Aims Math. 2020, 5, 7661–7677. [Google Scholar] [CrossRef]
- He, S.B.; Peng, Y.X.; Sun, K.H. SEIR modeling of the COVID-19 and its dynamics. Nonlinear Dynam. 2020, 101, 1667–1680. [Google Scholar] [CrossRef] [PubMed]
- Algehyne, E.A.; Din, R.U. On global dynamics of COVID-19 by using SQIR type model under nonlinear saturated incidence rate. Alex. Eng. J. 2021, 60, 393–399. [Google Scholar] [CrossRef]
- Li, N.; Wang, Z.Y.; Pei, Z. Sequential resource planning decisions in an epidemic based on an innovative spread model. IEEE T. Autom. Sci. Eng. 2022, 19, 677–691. [Google Scholar] [CrossRef]
- Li, M.Y.; Zhang, Y.J.; Zhou, X.H. Analysis of transimission pattern of COVID-19 based on EM algorithm and epidemiological data. Acta Math. Appl. Sin. 2020, 43, 427–439. [Google Scholar]
- Chong, P.Y.; Yin, H. System dynamics simulation on spread of COVID-19 by traffic and transportation. J. Traf. Trans. Eng. 2020, 20, 100–109. [Google Scholar]
- Cadoni, M.; Gaeta, G. Size and timescale of epidemics in the SIR framework. Phys. D 2020, 411, 132626. [Google Scholar] [CrossRef]
- Yang, L.L.; Su, Y.M.; Zhuo, X.J. Comparison of two different types of fractional-order COVID-19 distributed time-delay models with real data application. Int. J. Mod. Phys. B 2021, 35, 2150219. [Google Scholar] [CrossRef]
- Radha, M.; Radha, S. A study on COVID-19 transmission dynamics: Stability analysis of SEIR model with Hopf bifurcation for effect of time delay. Adv. Differ. Equ. 2020, 1, 523. [Google Scholar] [CrossRef] [PubMed]
- Chang, X.H.; Wang, J.R.; Liu, M.X.; Jin, Z.; Han, D. Study on an SIHRS model of COVID-19 pandemic with impulse and time delay under media coverage. IEEE Access 2021, 9, 49387–49397. [Google Scholar] [CrossRef] [PubMed]
- Zhu, C.C.; Zhu, J. Dynamic analysis of a delayed COVID-19 epidemic with home quarantine in temporal-spatial heterogeneous via global exponential attractor method. Chaos Solitons Fract. 2021, 143, 110546. [Google Scholar] [CrossRef] [PubMed]
- Yang, F.F.; Zhang, Z.Z. A time-delay COVID-19 propagation model considering supply chain transmission and hierarchical quarantine rate. Adv. Differ. Equ. 2021, 1, 191. [Google Scholar] [CrossRef]
- Hossain, M.K.; Hassanzadeganroudsari, M.; Apostolopoulos, V. The emergence of new strains of SARS-CoV-2. What does it mean for COVID-19 vaccines? Expert Rev. Vaccines 2021, 20, 635–638. [Google Scholar] [CrossRef]
- Tartof, S.Y.; Slezak, J.M.; Fischer, H.; Hong, V.; Ackerson, B.K.; Ranasinghe, O.N.; Frankland, T.B.; Ogun, O.A.; Zamparo, J.M.; Gray, S.; et al. Effectiveness of mRNA BNT162b2 COVID-19 vaccine up to 6 months in a large integrated health system in the USA: A retrospective cohort study. Lancet 2021, 398, 1407–1416. [Google Scholar] [CrossRef]
- Jara, A.; Undurraga, E.A.; Gonzalez, C.; Paredes, F.; Fontecilla, T.; Jara, G.; Pizarro, A.; Acevedo, J.; Leo, K.; Leon, F.; et al. Effectiveness of an inactivated SARS-CoV-2 vaccine in Chile. N. Engl. J. Med. 2021, 385, 875–884. [Google Scholar] [CrossRef]
- Xiao, L.L.; Zhang, Y.; Hu, X.W.; Liu, T.; Liu, Y. Analysis of global prevalence of SARS-CoV-2 varia. Chin. J. Front. Health Quar. 2022, 45, 10–12. [Google Scholar]
- Shi, Q.F.; Gao, X.D.; Hu, B.J. Research progress on characteristics, epidemiology and control measure of SARS-CoV-2 delta voc. Chin. J. Nosocomiol. 2021, 31, 3703–3707. [Google Scholar]
- Raman, R.; Patel, K.; Ran, K. COVID-19: Unmasking emerging SARS-CoV-2 variants, vaccines and therapeutic strategies. Biomolecules 2021, 11, 993. [Google Scholar] [CrossRef] [PubMed]
- Darvishi, M.; Rahimi, F.; Talebi, B.A. SARS-CoV-2 lambda (C.37): An emerging variant of concern. Gene. Rep. 2021, 25, 101378. [Google Scholar] [CrossRef] [PubMed]
- Choi, J.Y.; Smith, D.M. SARS-CoV-2 variants of concern. Yonsei Med. J. 2021, 62, 961–968. [Google Scholar] [CrossRef] [PubMed]
- Mohapatra, R.K.; Tiwari, R.; Sarangi, A.K.; Sharma, S.K.; Khandia, R. Twin combination of omicron and delta variants triggering a tsunami wave of ever high surges in COVID-19 cases: A challenging global threat with a special focus on the Indian subcontinent. J. Med. Virol. 2022, 94, 1761–1765. [Google Scholar] [CrossRef] [PubMed]
- Zhao, X.H.; Ning, Y.L.; Chen, M.I.C.; Cook, A.R. Individual and population trajectories of influenza antibody titers over multiple seasons in a tropical country. Am. J. Epidemiol. 2018, 187, 135–143. [Google Scholar] [CrossRef] [PubMed]
- Ibarrondo, F.J.; Fulcher, J.A.; Yang, O.O. Rapid decay of Anti-SARS-CoV-2 antibodies in persons with mild COVID-19. N. Engl. J. Med. 2020, 383, 1085–1087. [Google Scholar] [CrossRef] [PubMed]
- Li, J.; Ao, N.; Yin, J.H. Willingness for COVID-19 vaccination and its influencing factors among outpatient clinic attendees in Kunming city. China J. Public Health 2021, 37, 411–414. [Google Scholar]
- Sarwar, A.; Nazar, N.; Nazar, N.; Qadir, A. Measuring vaccination willingness in response to COVID-19 using a multi-criteria-decision-making method. Hum. Vaccines 2021, 17, 1–8. [Google Scholar] [CrossRef]
- Liu, R.G.; Liu, Y.X.; Nicholas, S.; Leng, A.L.; Maitland, E.; Wang, J. COVID-19 vaccination willingness among Chinese adults under the free vaccination policy. Vaccines 2021, 9, 292. [Google Scholar] [CrossRef]
- Lu, H.f.; Ding, Y.T.; Gong, S.L.; Wang, S.S. Mathematical modeling and dynamic analysis of SIQR model with delay for pandemic COVID-19. Math. Biosci. Eng. 2021, 18, 3197–3214. [Google Scholar] [CrossRef]
- Wang, J.W.; Cui, Z.W.; Dong, S. Simulation of COVID-19 propagation and transmission mechanism and intervention effect based on generalized SEIR model. Sci. Technol. Rev. 2020, 38, 130–138. [Google Scholar]
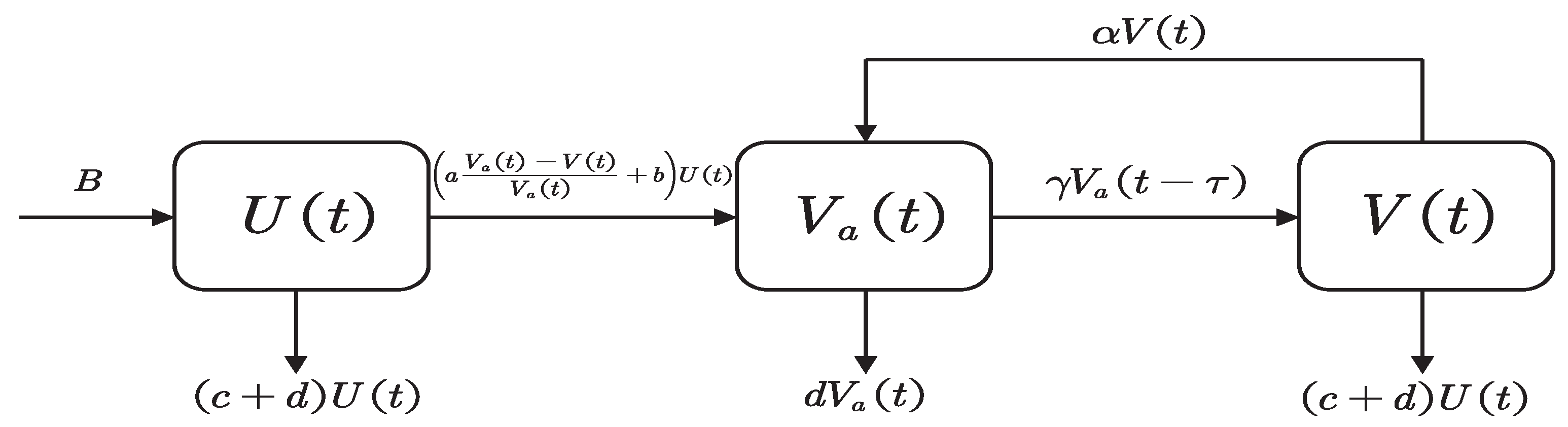



| Symbol | Descriptions |
|---|---|
| U | Number of unvaccinated individuals without antibodies |
| Number of vaccinated individuals who develop antibodies | |
| V | Number of vaccinated individuals whose antibodies failed |
| B | Natural increase of population |
| a | Factor affecting vaccine safety and efficacy |
| d | Natural mortality rate |
| b | Basic fixed vaccination rate |
| c | Mortality rate due to COVID-19 |
| Conversion rate from V to , secondary vaccination rate for COVID-19 vaccine | |
| The conversion rate from to V, the COVID-19 vaccine failure rate | |
| The time-delay between antibody production and antibody disappearance |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ai, X.; Liu, X.; Ding, Y.; Li, H. Dynamic Analysis of a COVID-19 Vaccination Model with a Positive Feedback Mechanism and Time-Delay. Mathematics 2022, 10, 1583. https://doi.org/10.3390/math10091583
Ai X, Liu X, Ding Y, Li H. Dynamic Analysis of a COVID-19 Vaccination Model with a Positive Feedback Mechanism and Time-Delay. Mathematics. 2022; 10(9):1583. https://doi.org/10.3390/math10091583
Chicago/Turabian StyleAi, Xin, Xinyu Liu, Yuting Ding, and Han Li. 2022. "Dynamic Analysis of a COVID-19 Vaccination Model with a Positive Feedback Mechanism and Time-Delay" Mathematics 10, no. 9: 1583. https://doi.org/10.3390/math10091583
APA StyleAi, X., Liu, X., Ding, Y., & Li, H. (2022). Dynamic Analysis of a COVID-19 Vaccination Model with a Positive Feedback Mechanism and Time-Delay. Mathematics, 10(9), 1583. https://doi.org/10.3390/math10091583







