Steady Flow of Burgers’ Nanofluids over a Permeable Stretching/Shrinking Surface with Heat Source/Sink
Abstract
1. Introduction
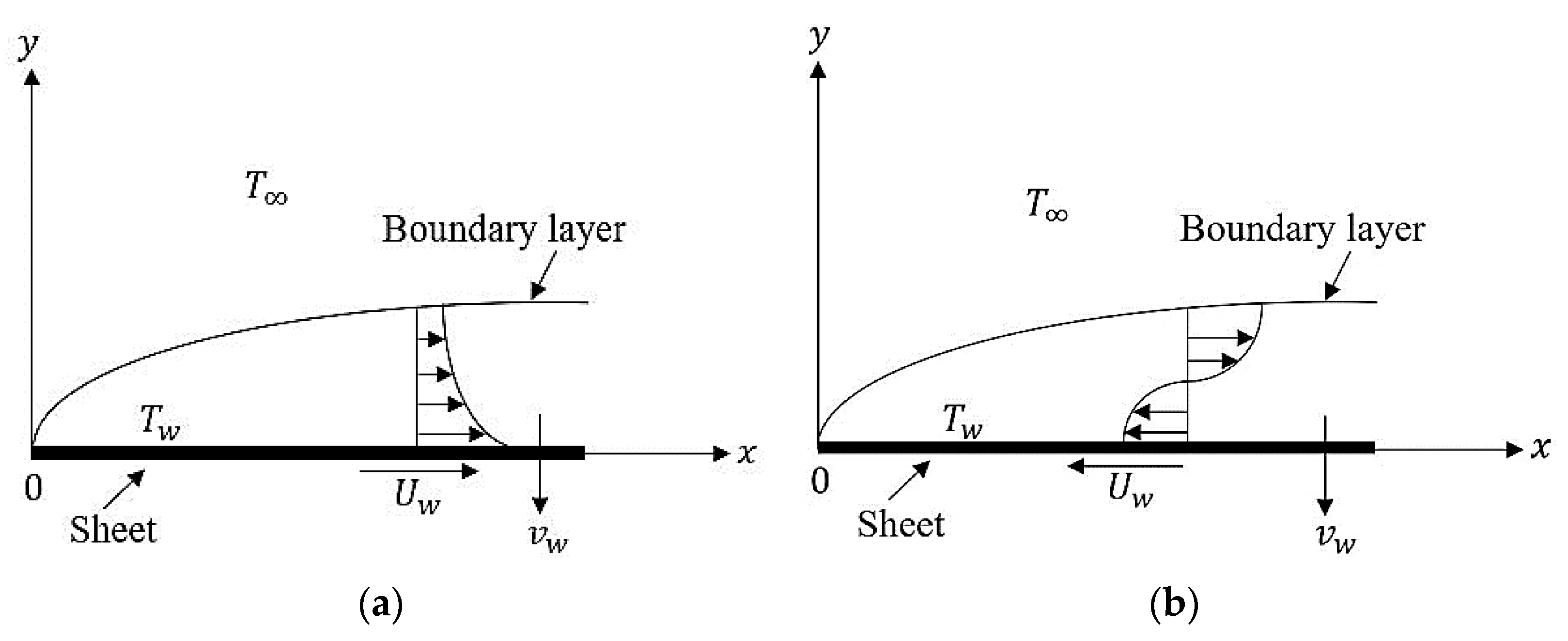
2. Mathematical Model
3. Stability Analysis
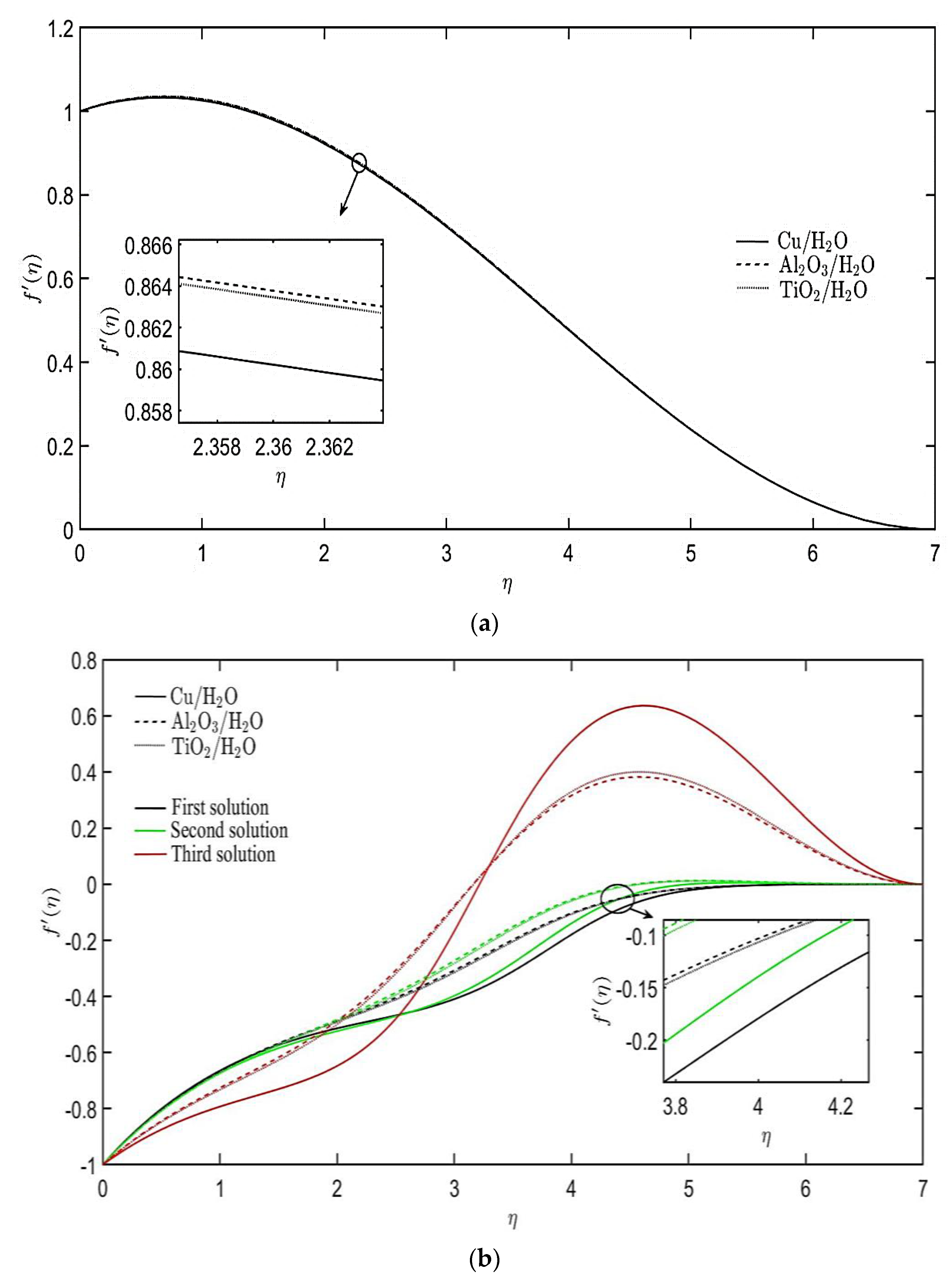
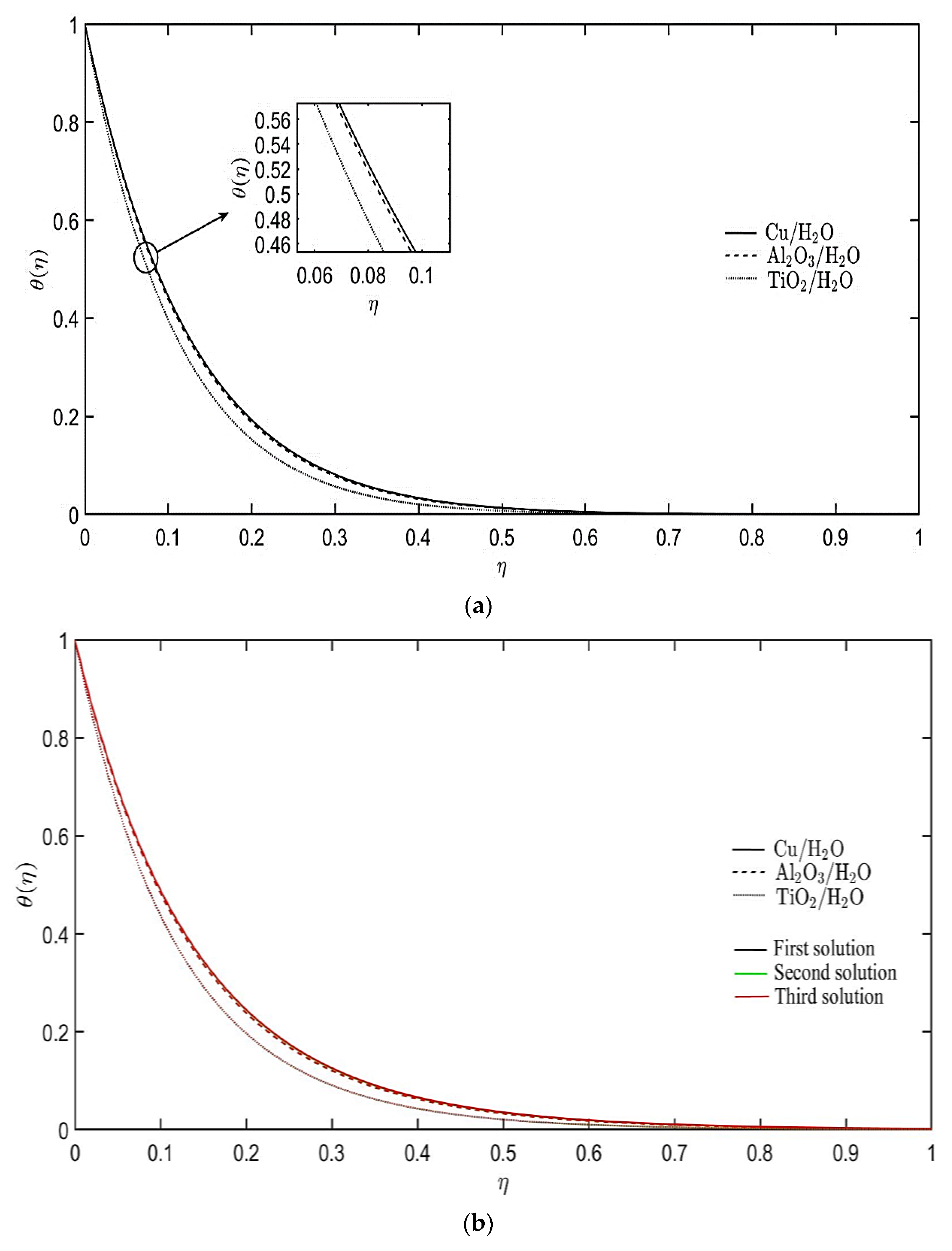
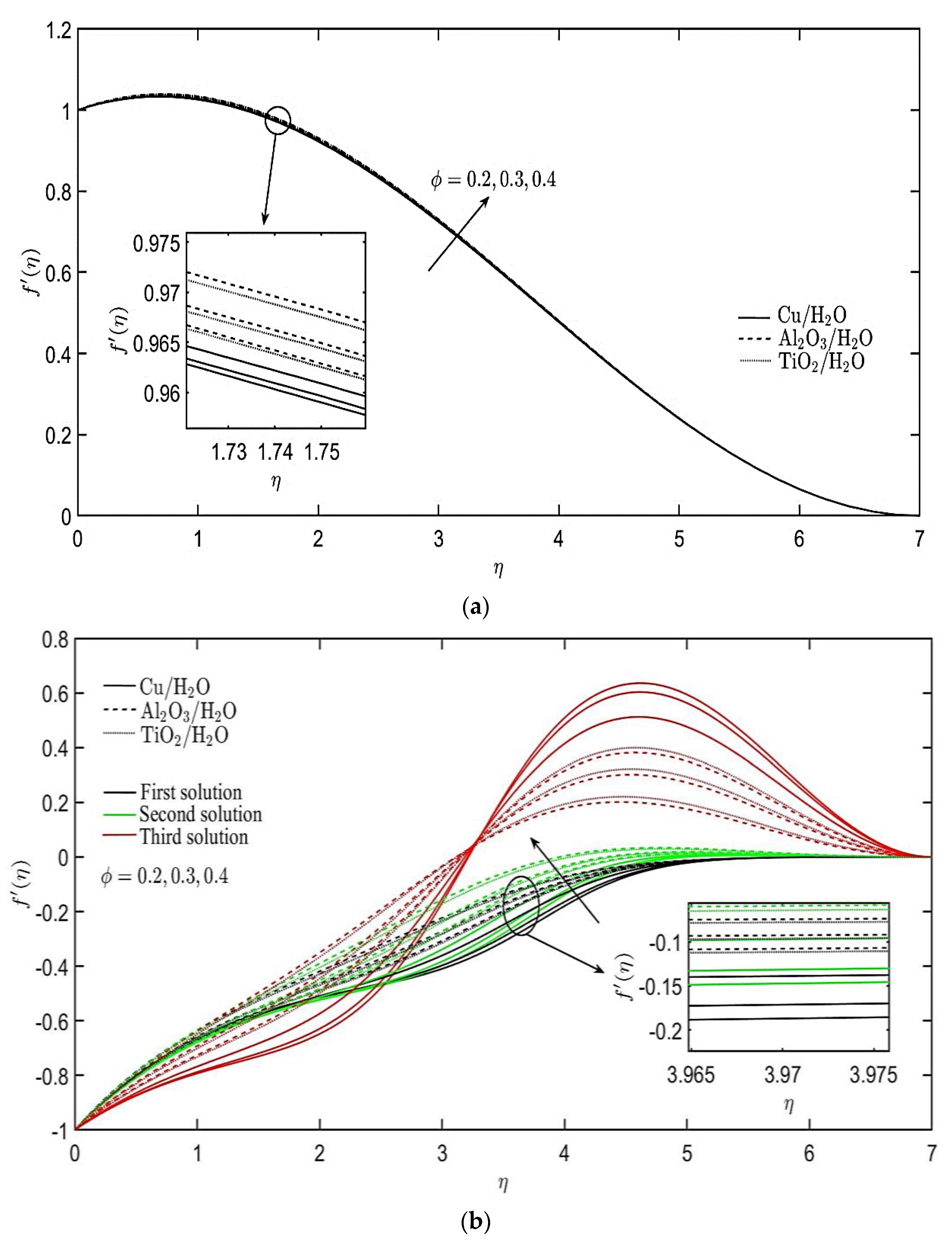
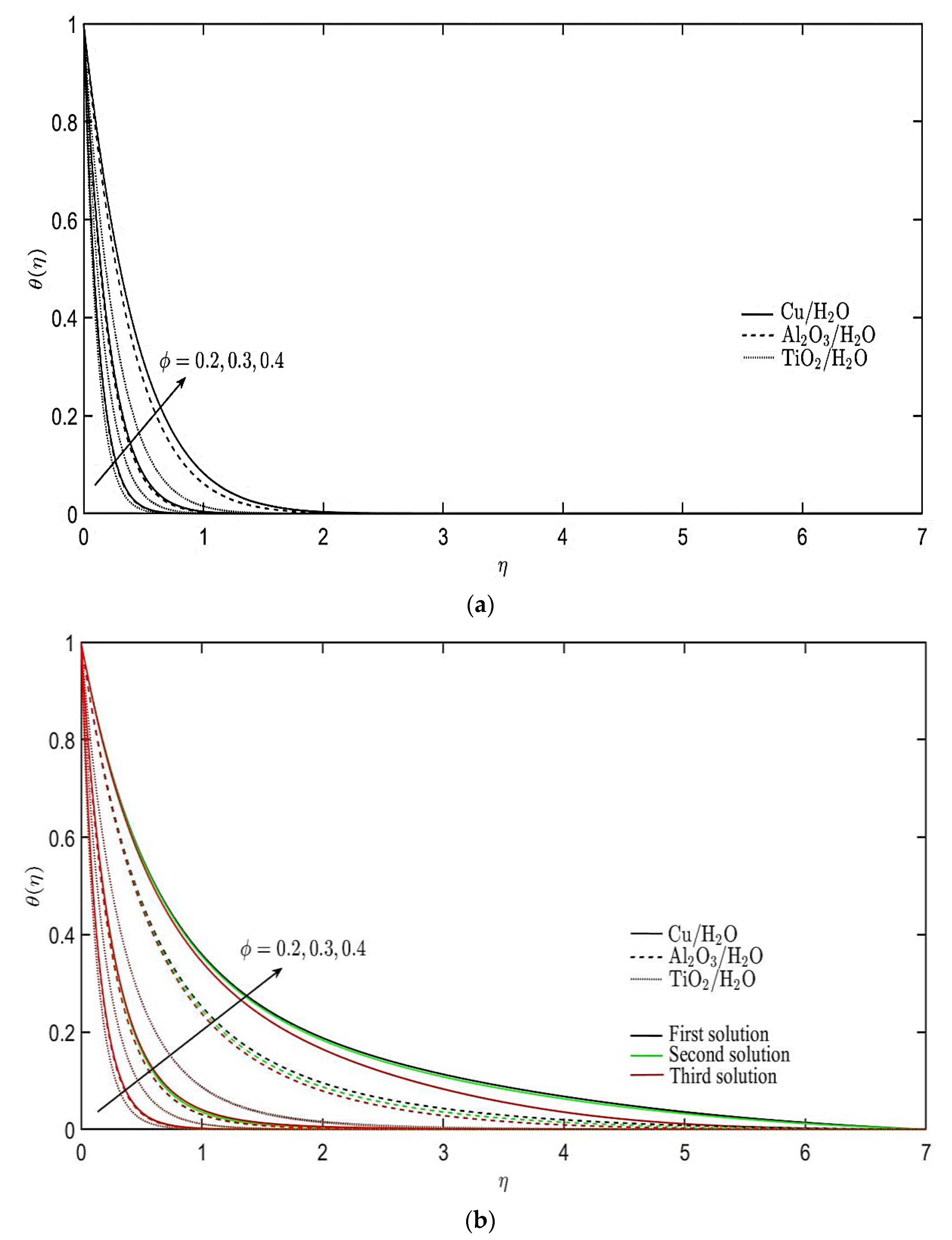
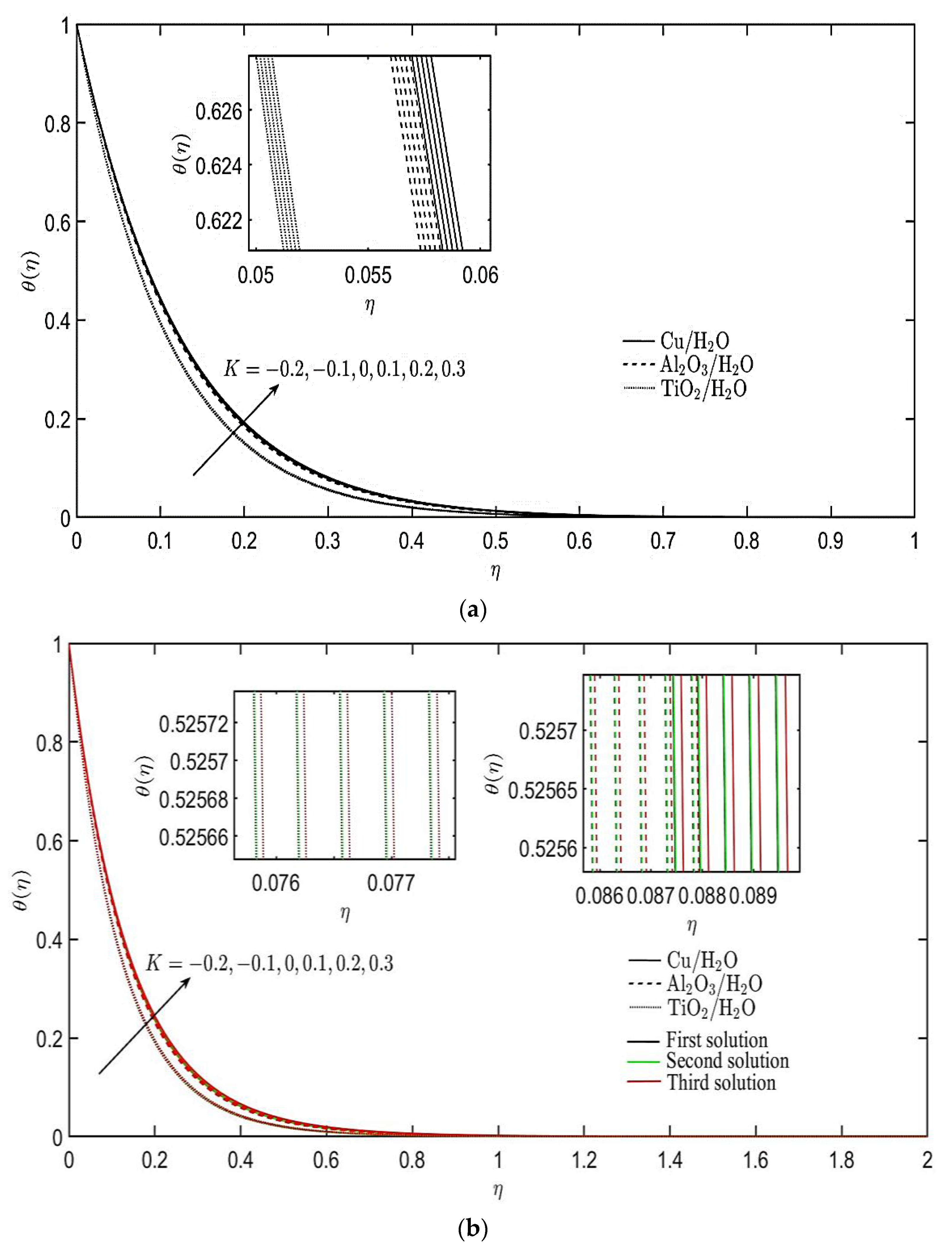
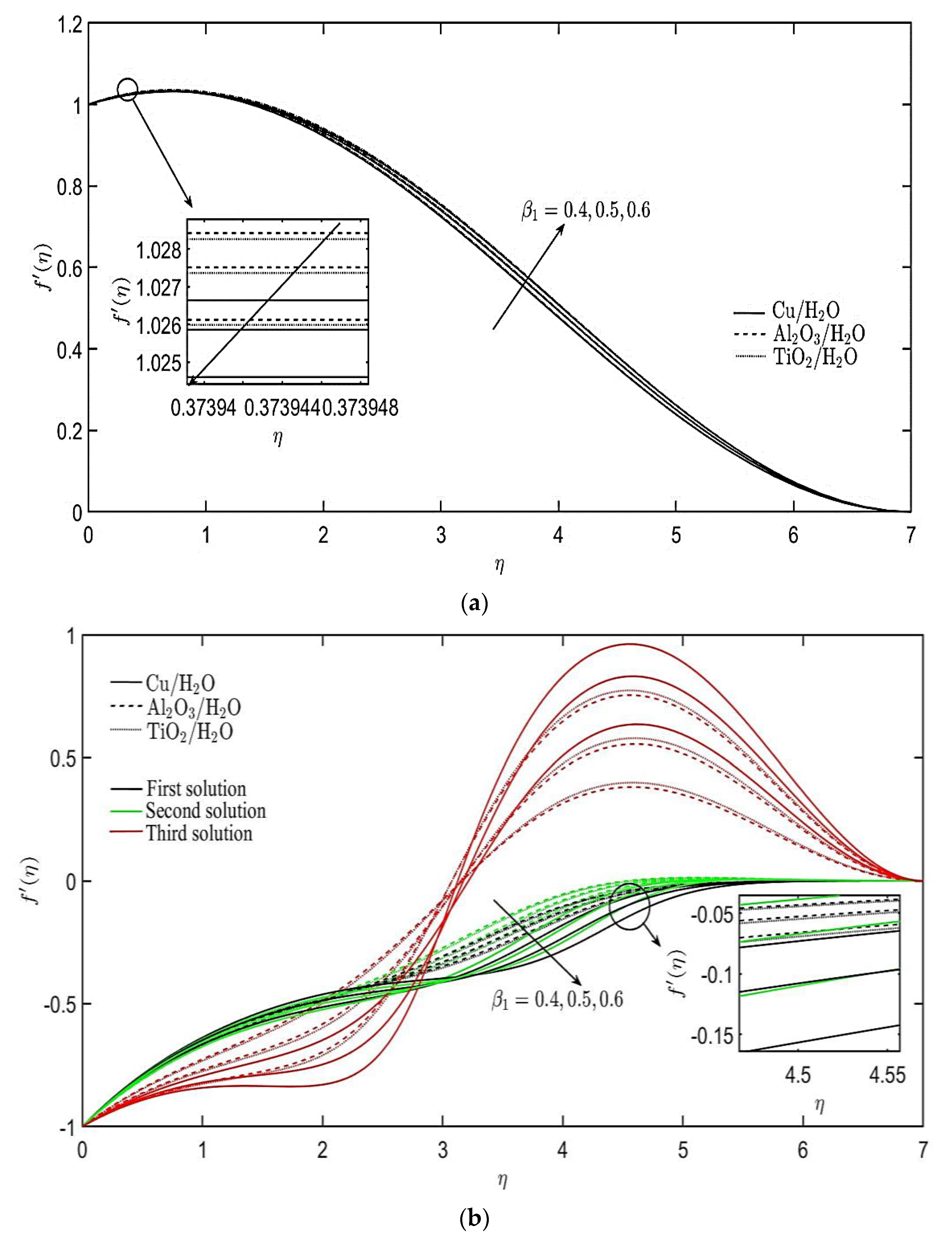
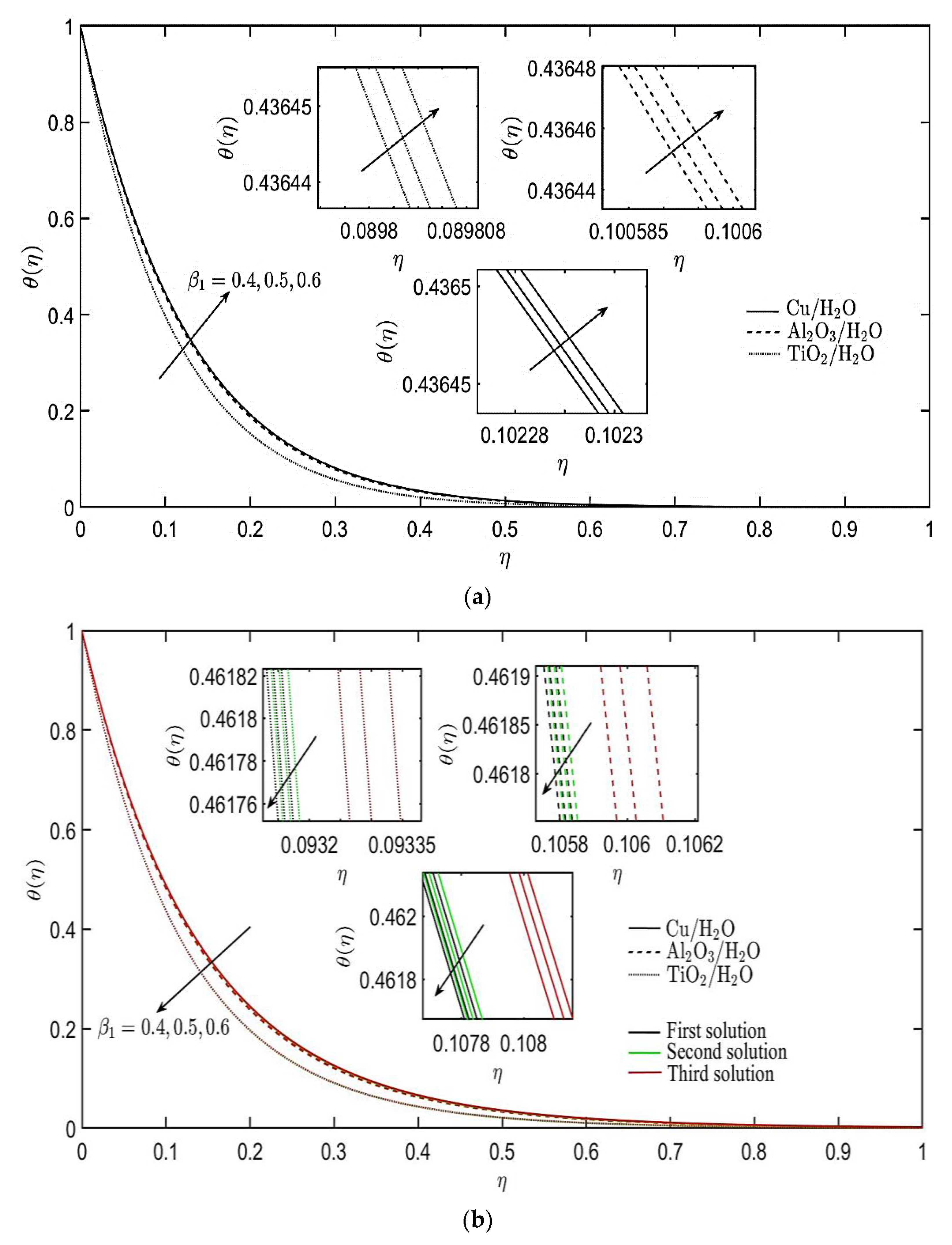
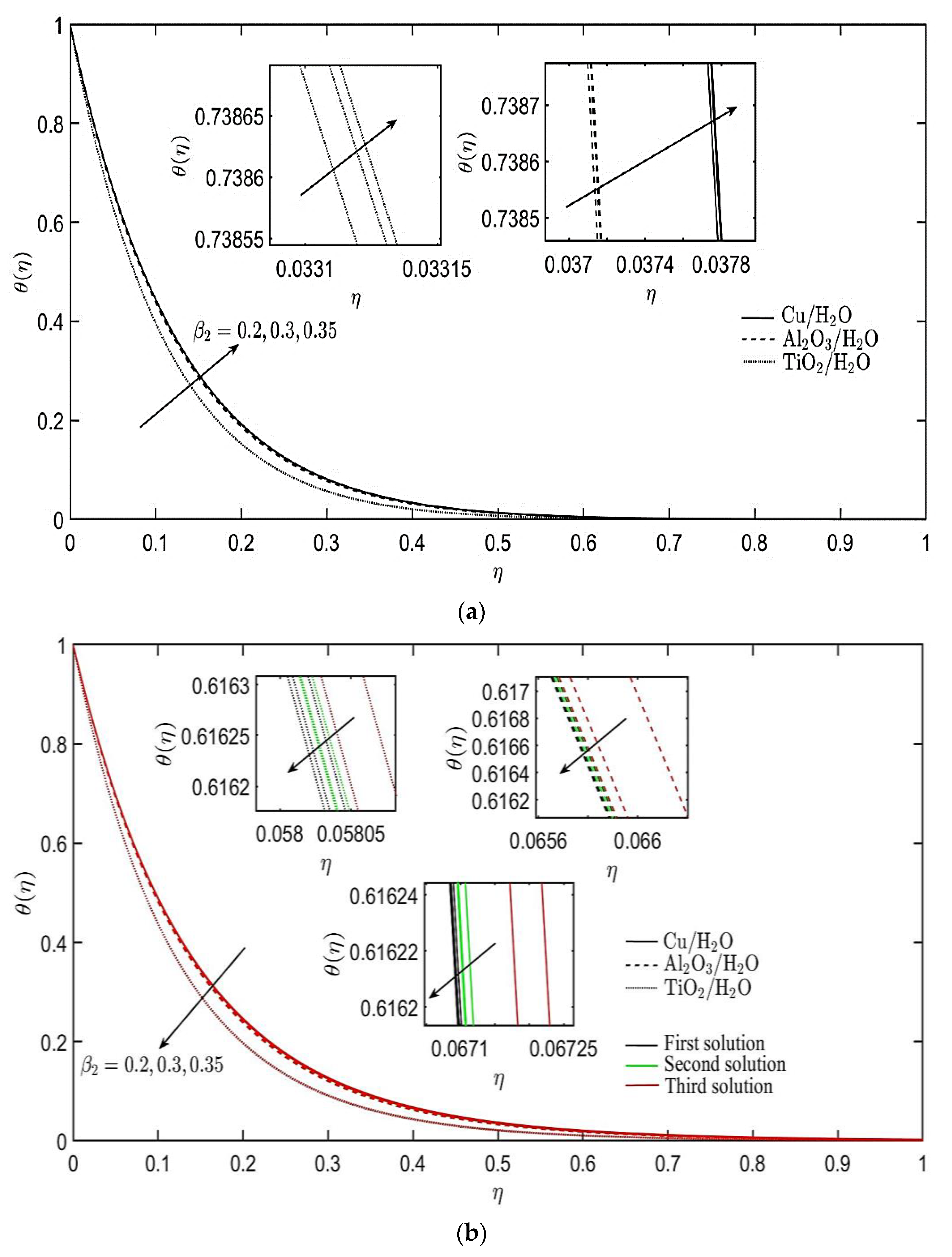
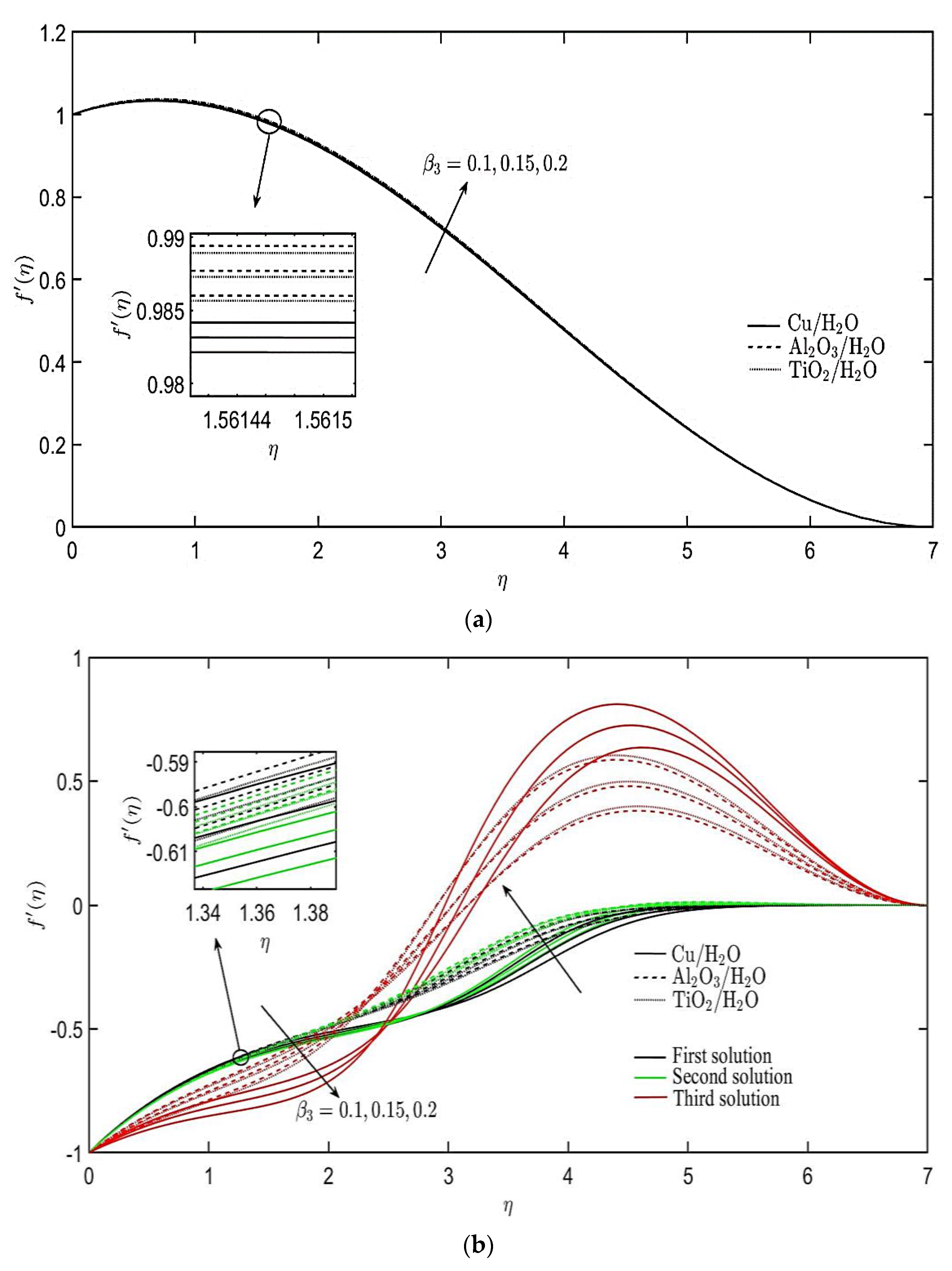
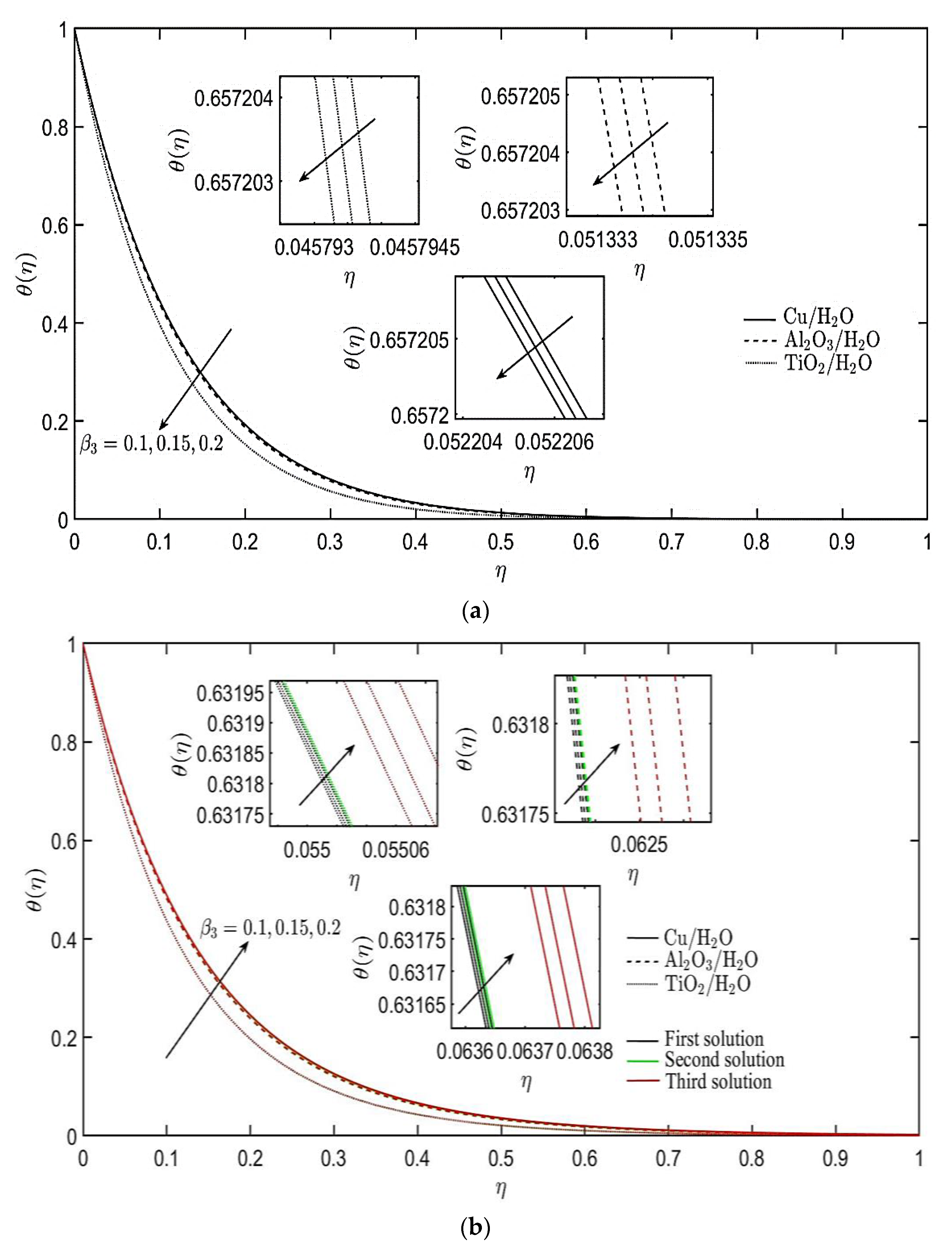
4. Results and Discussion
5. Conclusions
- A unique solution is found for the stretching sheet case, while triple solutions are generated for the shrinking sheet case.
- Stability analysis of solutions determined that only the first solution is stable and realizable in practice.
- Three different nanofluids are considered, and Cu/H2O nanofluid has the highest heat transfer rate compared to Al2O3/H2O and TiO2/H2O nanofluids.
- The application of Al2O3/H2O and Cu/H2O nanofluids in the flow over stretching and shrinking surfaces yield the highest skin friction coefficient, respectively.
- The inclusion of more nanoparticles into the base fluid boosts the velocity and temperature profiles of the nanofluids.
- The temperature profile is also augmented by the increment of the heat source parameter but diminished with the heat sink parameter.
- The non-Newtonian parameters related to Burgers’ fluid have different effects on the velocity and temperature profiles of the nanofluids for both cases of stretching and shrinking sheets.
Author Contributions
Funding
Conflicts of Interest
Nomenclature
| constant | |
| skin friction coefficient | |
| heat capacity (J/kg K) | |
| dimensionless velocity | |
| thermal conductivity (W/m·K) | |
| heat source/sink parameter | |
| local Nusselt number | |
| Prandtl number | |
| heat generation/absorption | |
| local Reynolds number | |
| mass flux parameter | |
| time (s) | |
| fluid temperature (K) | |
| Cartesian coordinates along the sheet and normal to it, respectively (m) | |
| velocity components along the -and -directions, respectively (m/s) | |
| velocity of the stretching/shrinking sheet (m/s) | |
| mass transfer velocity (m/s) | |
| Greek symbols | |
| non-Newtonian parameters | |
| stretching/shrinking parameter | |
| relaxation time | |
| material parameter | |
| retardation time | |
| unknown eigenvalue | |
| similarity variable | |
| fluid density (kg/m3) | |
| dynamic viscosity (kg/m2s) | |
| dimensionless time variable | |
| kinematic viscosity (m2/s) | |
| stream function | |
| dimensionless temperature | |
| nanoparticle volume fraction | |
| Superscript | |
| ′ | differentiation with respect to |
| Subscripts | |
| base fluid | |
| nanofluid | |
| nanoparticle | |
| sheet surface | |
| free stream |
References
- Khan, M.; Iqbal, Z.; Ahmed, A. Energy transport analysis in the flow of burgers nanofluid inspired by variable thermal conductivity. Pramana 2021, 95, 74. [Google Scholar] [CrossRef]
- Hayat, T.; Fetecau, C.; Asghar, S. Some simple flows of a burgers’ fluid. Int. J. Eng. Sci. 2006, 44, 1423–1431. [Google Scholar] [CrossRef]
- Rashidi, M.M.; Yang, Z.; Awais, M.; Nawaz, M.; Hayat, T. Generalized magnetic field effects in burgers’ nanofluid model. PLoS ONE 2017, 12, e0168923. [Google Scholar] [CrossRef] [PubMed]
- Alsaedi, A.; Alsaadi, F.E.; Ali, S.; Hayat, T. Stagnation point flow of burgers’ fluid and mass transfer with chemical reaction and porosity. J. Mech. 2012, 29, 453–460. [Google Scholar] [CrossRef]
- Hayat, T.; Ali, S.; Awais, M.; Obaidat, S. Stagnation point flow of burgers’ fluid over a stretching surface. Prog. Comput. Fluid Dyn. Int. J. 2013, 13, 48–53. [Google Scholar] [CrossRef]
- Hayat, T.; Ali, S.; Awais, M.; Alsaedi, A. Joule heating effects in mhd flow of burgers’ fluid. Heat Transf. Res. 2016, 47, 1083–1092. [Google Scholar] [CrossRef]
- Hayat, T.; Asad, S.; Alaseadi, A. Mhd mixed convection flow of burgers’ fluid in a thermally stratified medium. J. Aerosp. Eng. 2016, 29, 04016060. [Google Scholar] [CrossRef]
- Hayat, T.; Waqas, M.; Khan, M.I.; Alsaedi, A.; Shehzad, S.A. Magnetohydrodynamic flow of burgers fluid with heat source and power law heat flux. Chin. J. Phys. 2017, 55, 318–330. [Google Scholar] [CrossRef]
- Ahmad, I.; Ali, N.; Abbasi, A.; Aziz, W.; Hussain, M.; Ahmad, M.; Taj, M.; Zaman, Q. Flow of a burger’s fluid in a channel induced by peristaltic compliant walls. J. Appl. Math. 2014, 2014, 236483. [Google Scholar] [CrossRef]
- Khan, N.A.; Khan, S.; Ullah, S. Mhd flow of burger’s fluid over an off-centered rotating disk in a porous medium. AIP Adv. 2015, 5, 087179. [Google Scholar] [CrossRef]
- Imran, M.; Ching, D.L.C.; Safdar, R.; Khan, I.; Imran, M.A.; Nisar, K.S. The solutions of non-integer order burgers’ fluid flowing through a round channel with semi analytical technique. Symmetry 2019, 11, 962. [Google Scholar] [CrossRef]
- Safdar, R.; Imran, M.; Tahir, M.; Sadiq, N.; Imran, M.A. MHD Flow of Burgers’ Fluid under the Effect of Pressure Gradient Through a Porous Material Pipe. Punjab Univ. J. Math. 2018, 50, 73–90. [Google Scholar]
- Akram, S.; Anjum, A.; Khan, M.; Hussain, A. On stokes’ second problem for burgers’ fluid over a plane wall. J. Appl. Comput. Mech. 2021, 7, 1514–1526. [Google Scholar] [CrossRef]
- Jiang, Y.; Sun, H.; Bai, Y.; Zhang, Y. MHD flow, radiation heat and mass transfer of fractional Burgers’ fluid in porous medium with chemical reaction. Comput. Math. Appl. 2022, 115, 68–79. [Google Scholar] [CrossRef]
- Gangadhar, K.; Kumari, M.A.; Rao, M.V.S.; Alnefaie, K.; Khan, I.; Andualem, M. Magnetization for burgers’ fluid subject to convective heating and heterogeneous-homogeneous reactions. Math. Probl. Eng. 2022, 2022, 2747676. [Google Scholar] [CrossRef]
- Choi, S.U.S.; Eastman, J.A. Enhancing Thermal Conductivity of Fluids with Nanoparticles; Argonne National Lab. (ANL): Argonne, IL, USA, 1995.
- Alghamdi, M. Significance of arrhenius activation energy and binary chemical reaction in mixed convection flow of nanofluid due to a rotating disk. Coatings 2020, 10, 86. [Google Scholar] [CrossRef]
- Khan, M.I.; Alzahrani, F. Activation energy and binary chemical reaction effect in nonlinear thermal radiative stagnation point flow of walter-b nanofluid: Numerical computations. Int. J. Mod. Phys. B 2020, 34, 2050132. [Google Scholar] [CrossRef]
- Hayat, T.; Waqas, M.; Shehzad, S.A.; Alsaedi, A. On model of burgers fluid subject to magneto nanoparticles and convective conditions. J. Mol. Liq. 2016, 222, 181–187. [Google Scholar] [CrossRef]
- Hayat, T.; Waqas, M.; Shehzad, S.A.; Alsaedi, A. Mixed convection flow of a burgers nanofluid in the presence of stratifications and heat generation/absorption. Eur. Phys. J. Plus 2016, 131, 253. [Google Scholar] [CrossRef]
- Iqbal, Z.; Khan, M.; Ahmed, A.; Ahmed, J.; Hafeez, A. Thermal energy transport in burgers nanofluid flow featuring the cattaneo–christov double diffusion theory. Appl. Nanosci. 2020, 10, 5331–5342. [Google Scholar] [CrossRef]
- Xuan, Y.; Li, Q. Heat transfer enhancement of nanofluids. Int. J. Heat Fluid Flow 2000, 21, 58–64. [Google Scholar] [CrossRef]
- Das, S.K.; Choi, S.U.S.; Patel, H.E. Heat transfer in nanofluids—A review. Heat Transf. Eng. 2006, 27, 3–19. [Google Scholar] [CrossRef]
- Khattak, M.A.; Mukhtar, A.; Afaq, S.K. Application of nano-fluids as coolant in heat exchangers: A review. J. Adv. Res. Mater. Sci. 2020, 66, 8–18. [Google Scholar] [CrossRef]
- Das, S.K.; Choi, S.U.; Yu, W.; Pradeep, T. Nanofluids: Science and Technology; John Wiley & Sons: Hoboken, NJ, USA, 2007. [Google Scholar]
- Nield, D.A.; Bejan, A. Convection in Porous Media; Springer: Berlin/Heidelberg, Germany, 2006; Volume 3. [Google Scholar]
- Minkowycz, W.J.; Sparrow, E.M.; Abraham, J.P. Nanoparticle Heat Transfer and Fluid Flow; CRC Press: Boca Raton, FL, USA, 2012; Volume 4. [Google Scholar]
- Shenoy, A.; Sheremet, M.; Pop, I. Convective Flow and Heat Transfer from Wavy Surfaces: Viscous Fluids, Porous Media, and Nanofluids; CRC Press: Boca Raton, FL, USA, 2016. [Google Scholar]
- Manca, O.; Jaluria, Y.; Poulikakos, D. Heat Transfer in Nanofluids. Advances in Mechanical Engineering; Sage Publications: London, UK, 2010; p. 380826. [Google Scholar]
- Myers, T.G.; Ribera, H.; Cregan, V. Does Mathematics Contribute to the Nanofluid Debate? Int. J. Heat Mass Transf. 2017, 111, 279–288. [Google Scholar] [CrossRef]
- Mahian, O.; Kolsi, L.; Amani, M.; Estellé, P.; Ahmadi, G.; Kleinstreuer, C.; Marshall, J.S.; Siavashi, M.; Taylor, R.A.; Niazmand, H.; et al. Recent advances in modeling and simulation of nanofluid flows-part i: Fundamentals and theory. Phys. Rep. 2019, 790, 1–48. [Google Scholar] [CrossRef]
- Mahian, O.; Kolsi, L.; Amani, M.; Estellé, P.; Ahmadi, G.; Kleinstreuer, C.; Marshall, J.S.; Taylor, R.A.; Abu-Nada, E.; Rashidi, S. Recent advances in modeling and simulation of nanofluid flows—Part II: Applications. Phys. Rep. 2019, 791, 1–59. [Google Scholar] [CrossRef]
- Mahian, O.; Kianifar, A.; Kalogirou, S.A.; Pop, I.; Wongwises, S. A review of the applications of nanofluids in solar energy. Int. J. Heat Mass Transf. 2013, 57, 582–594. [Google Scholar] [CrossRef]
- Khan, M.; Khan, W.A. Forced convection analysis for generalized Burgers nanofluid flow over a stretching sheet. AIP Adv. 2015, 5, 107138. [Google Scholar] [CrossRef]
- Khan, M.; Khan, W.A. Steady flow of Burgers’ nanofluid over a stretching surface with heat generation/absorption. J Braz. Soc. Mech. Sci. Eng. 2016, 38, 2359–2367. [Google Scholar] [CrossRef]
- Buongiorno, J. Convective transport in nanofluids. J. Heat Transf. 2006, 128, 240–250. [Google Scholar] [CrossRef]
- Muhammad, S.; Ishaq, M.; Hussain, S.A.; Tahir, M.; Naeem, M.; Khan, H.; Jan, S.; Khan, K. Semi analytical solution of steady Burgers’ nanofluid flow between parallel channels with heat generation/absorption under the influence of thermal radiation. J. Nanofluids 2019, 8, 1468–1478. [Google Scholar] [CrossRef]
- Khan, M.; Iqbal, Z.; Ahmed, A. Stagnation point flow of magnetized burgers’ nanofluid subject to thermal radiation. Appl. Nanosci. 2020, 10, 5233–5246. [Google Scholar] [CrossRef]
- Khan, S.U.; Alabdan, R.; Al-Qawasmi, A.-R.; Vakkar, A.; ben Handa, M.; Tlili, I. Bioconvection applications for double stratification 3-d flow of burgers nanofluid over a bidirectional stretched surface: Enhancing energy system performance. Case Stud. Therm. Eng. 2021, 26, 101073. [Google Scholar] [CrossRef]
- Waqas, H.; Manzoor, U.; Shah, Z.; Arif, M.; Shutaywi, M. Magneto-burgers nanofluid stratified flow with swimming motile microorganisms and dual variables conductivity configured by a stretching cylinder/plate. Math. Probl. Eng. 2021, 2021, 8817435. [Google Scholar] [CrossRef]
- Ramzan, M.; Algehyne, E.A.; Saeed, A.; Dawar, A.; Kumam, P.; Watthayu, W. Homotopic simulation for heat transport phenomenon of the Burgers nanofluids flow over a stretching cylinder with thermal convective and zero mass flux conditions. Nanotechnol. Rev. 2022, 11, 1437–1449. [Google Scholar] [CrossRef]
- Wang, F.; Iqbal, Z.; Zhang, J.; Abdelmohimen, M.A.H.; Almaliki, A.H.; Galal, A.M. Bidirectional stretching features on the flow and heat transport of Burgers nanofluid subject to modified heat and mass fluxes. Waves Random Complex Media 2022, 1–18. [Google Scholar] [CrossRef]
- Tiwari, R.K.; Das, M.K. Heat transfer augmentation in a two-sided lid-driven differentially heated square cavity utilizing nanofluids. Int. J. Heat Mass Transf. 2007, 50, 2002–2018. [Google Scholar] [CrossRef]
- Pop, I.; Seddighi, S.; Bachok, N.; Ismail, F. Boundary layer flow beneath a uniform free stream permeable continuous moving surface in a nanofluid. J. Heat Mass Transf. Res. 2014, 1, 55–65. [Google Scholar] [CrossRef]
- Ejaz, A.; Abbas, I.; Nawaz, Y.; Arif, M.S.; Shatanawi, W.; Abbasi, J.N. Thermal analysis of mhd non-newtonian nanofluids over a porous media. CMES—Comput. Model. Eng. Sci. 2020, 125, 1119–1134. [Google Scholar] [CrossRef]
- Ho, C.J.; Liu, W.K.; Chang, Y.S.; Lin, C.C. Natural convection heat transfer of alumina-water nanofluid in vertical square enclosures: An experimental study. Int. J. Therm. Sci. 2010, 49, 1345–1353. [Google Scholar] [CrossRef]
- Sheremet, M.A.; Pop, I.; Rosca, A.V. The influence of thermal radiation on unsteady free convection in inclined enclosures filled by a nanofluid with sinusoidal boundary conditions. Int. J. Numer. Methods Heat Fluid Flow 2018, 28, 1738–1753. [Google Scholar] [CrossRef]
- Oztop, H.F.; Abu-Nada, E. Numerical study of natural convection in partially heated rectangular enclosures filled with nanofluids. Int. J. Heat Fluid Flow 2008, 29, 1326–1336. [Google Scholar] [CrossRef]
- Fang, T.; Yao, S.; Zhang, J.; Aziz, A. Viscous flow over a shrinking sheet with a second order slip flow model. Commun. Nonlinear Sci. Numer. Simul. 2010, 15, 1831–1842. [Google Scholar] [CrossRef]
- Vajravelu, K.; Rollins, D. Hydromagnetic flow of a second grade fluid over a stretching sheet. Appl. Math. Comput. 2004, 148, 783–791. [Google Scholar] [CrossRef]
- Cortell, R. Viscous flow and heat transfer over a nonlinearly stretching sheet. Appl. Math. Comput. 2007, 184, 864–873. [Google Scholar] [CrossRef]
- Crane, L.J. Flow past a stretching plate. Z. Angew. Math. Phys. ZAMP 1970, 21, 645–647. [Google Scholar] [CrossRef]
- Weidman, P.D.; Kubitschek, D.G.; Davis, A.M.J. The effect of transpiration on self-similar boundary layer flow over moving surfaces. Int. J. Eng. Sci. 2006, 44, 730–737. [Google Scholar] [CrossRef]
- Roşca, A.V.; Pop, I. Flow and heat transfer over a vertical permeable stretching/shrinking sheet with a second order slip. Int. J. Heat Mass Transf. 2013, 60, 355–364. [Google Scholar] [CrossRef]
- Wahid, N.S.; Arifin, N.M.; Khashi’ie, N.S.; Pop, I. Hybrid nanofluid slip flow over an exponentially stretching/shrinking permeable sheet with heat generation. Mathematics 2020, 9, 30. [Google Scholar] [CrossRef]
- Lund, L.A.; Omar, Z.; Khan, U.; Khan, I.; Baleanu, D.; Nisar, K.S. Stability analysis and dual solutions of micropolar nanofluid over the inclined stretching/shrinking surface with convective boundary condition. Symmetry 2020, 12, 74. [Google Scholar] [CrossRef]
- Yahaya, R.I.; Md Arifin, N.; Mohamed Isa, S.S.P.; Rashidi, M.M. Magnetohydrodynamics boundary layer flow of micropolar fluid over an exponentially shrinking sheet with thermal radiation: Triple solutions and stability analysis. Math. Methods Appl. Sci. 2021, 44, 10578–10608. [Google Scholar] [CrossRef]
- Harris, S.D.; Ingham, D.B.; Pop, I. Mixed convection boundary-layer flow near the stagnation point on a vertical surface in a porous medium: Brinkman model with slip. Transp. Porous Media 2009, 77, 267–285. [Google Scholar] [CrossRef]
- Zainal, N.A.; Nazar, R.; Naganthran, K.; Pop, I. Stability analysis of unsteady mhd rear stagnation point flow of hybrid nanofluid. Mathematics 2021, 9, 2428. [Google Scholar] [CrossRef]
- Khashi’ie, N.S.; Arifin, N.M.; Merkin, J.H.; Yahaya, R.I.; Pop, I. Mixed convective stagnation point flow of a hybrid nanofluid toward a vertical cylinder. Int. J. Numer. Methods Heat Fluid Flow 2021, 31, 3689–3710. [Google Scholar] [CrossRef]
- Yahaya, R.I.; Md Arifin, N.; Nazar, R.M.; Pop, I. Oblique stagnation-point flow past a shrinking surface in a Cu-Al2O3/H2O hybrid nanofluid. Sains Malays. 2021, 50, 3139–3152. [Google Scholar] [CrossRef]
- Pantokratoras, A. A common error made in investigation of boundary layer flows. Appl. Math. Model. 2009, 33, 413–422. [Google Scholar] [CrossRef]
- Rahman, M.M.; Ariz, A. Heat transfer in water based nanofluids (TiO2-H2O, Al2O3-H2O and Cu-H2O) over a stretching cylinder. Int. J. Heat Technol. 2012, 30, 31–42. [Google Scholar] [CrossRef]
- Dawar, A.; Bonyah, E.; Islam, S.; Alshehri, A.; Shah, Z. Theoretical analysis of Cu-H2O, Al2O3-H2O, and TiO2-H2O nanofluid flow past a rotating disk with velocity slip and convective conditions. J. Nanomater. 2021, 2021, 5471813. [Google Scholar] [CrossRef]

| Properties | kg/m3) | |||
|---|---|---|---|---|
| Cu | 8933 | 385 | 400 | - |
| Al2O3 | 3970 | 765 | 40 | - |
| TiO2 | 4250 | 686.2 | 8.9538 | - |
| H2O | 997.1 | 4179 | 0.613 | 6.2 |
| Present Study | Hayat et al. [8] | |
|---|---|---|
| 0 | 1.000000 | 1.000000 |
| 0.2 | 1.051890 | 1.051889 |
| 0.4 | 1.101903 | 1.101903 |
| 0.6 | 1.150137 | 1.150137 |
| Nanofluid | |||
|---|---|---|---|
| First Solution | Second Solution | Third Solution | |
| Cu/H2O | 0.3009 | −0.2486 | −0.3246 |
| Al2O3/H2O | 0.5468 | −0.1424 | −0.4223 |
| TiO2/H2O | 0.5254 | −0.1544 | −0.3289 |
| Nanofluid | |||||||
|---|---|---|---|---|---|---|---|
| First Solution | Second Solution | Third Solution | First Solution | Second Solution | Third Solution | ||
| 1 | Cu/H2O | 0.174834 | - | - | 18.530621 | - | - |
| Al2O3/H2O | 0.184990 | - | - | 18.148114 | - | - | |
| TiO2/H2O | 0.184073 | - | - | 17.977145 | - | - | |
| −1 | Cu/H2O | 0.834006 | 0.813087 | 0.537593 | 16.965115 | 16.963347 | 16.939337 |
| Al2O3/H2O | 0.823040 | 0.800393 | 0.640871 | 16.639103 | 16.637469 | 16.625451 | |
| TiO2/H2O | 0.820846 | 0.798131 | 0.628143 | 16.647590 | 16.646339 | 16.636665 | |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yahaya, R.I.; Md Arifin, N.; Pop, I.; Md Ali, F.; Mohamed Isa, S.S.P. Steady Flow of Burgers’ Nanofluids over a Permeable Stretching/Shrinking Surface with Heat Source/Sink. Mathematics 2022, 10, 1580. https://doi.org/10.3390/math10091580
Yahaya RI, Md Arifin N, Pop I, Md Ali F, Mohamed Isa SSP. Steady Flow of Burgers’ Nanofluids over a Permeable Stretching/Shrinking Surface with Heat Source/Sink. Mathematics. 2022; 10(9):1580. https://doi.org/10.3390/math10091580
Chicago/Turabian StyleYahaya, Rusya Iryanti, Norihan Md Arifin, Ioan Pop, Fadzilah Md Ali, and Siti Suzilliana Putri Mohamed Isa. 2022. "Steady Flow of Burgers’ Nanofluids over a Permeable Stretching/Shrinking Surface with Heat Source/Sink" Mathematics 10, no. 9: 1580. https://doi.org/10.3390/math10091580
APA StyleYahaya, R. I., Md Arifin, N., Pop, I., Md Ali, F., & Mohamed Isa, S. S. P. (2022). Steady Flow of Burgers’ Nanofluids over a Permeable Stretching/Shrinking Surface with Heat Source/Sink. Mathematics, 10(9), 1580. https://doi.org/10.3390/math10091580






