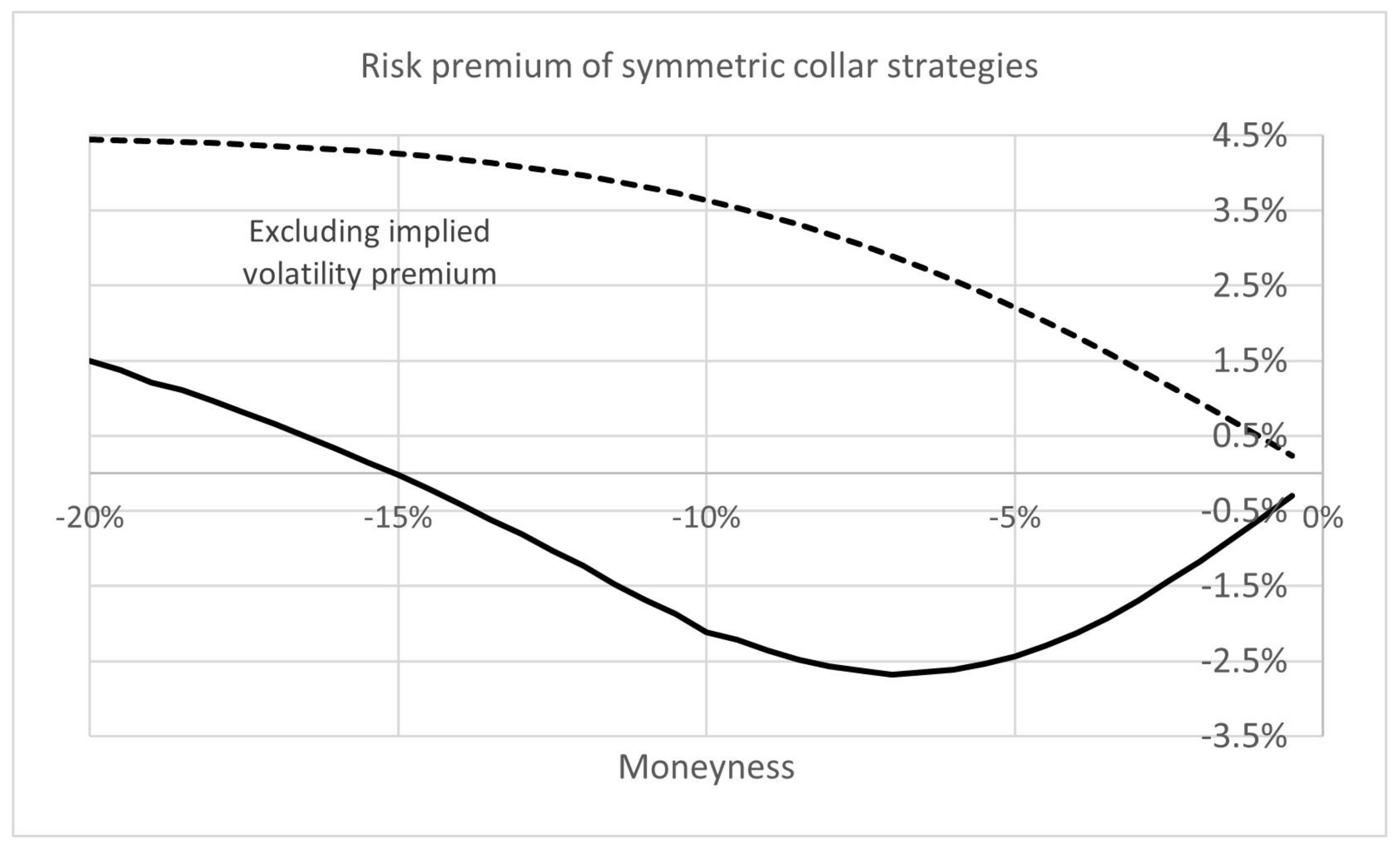
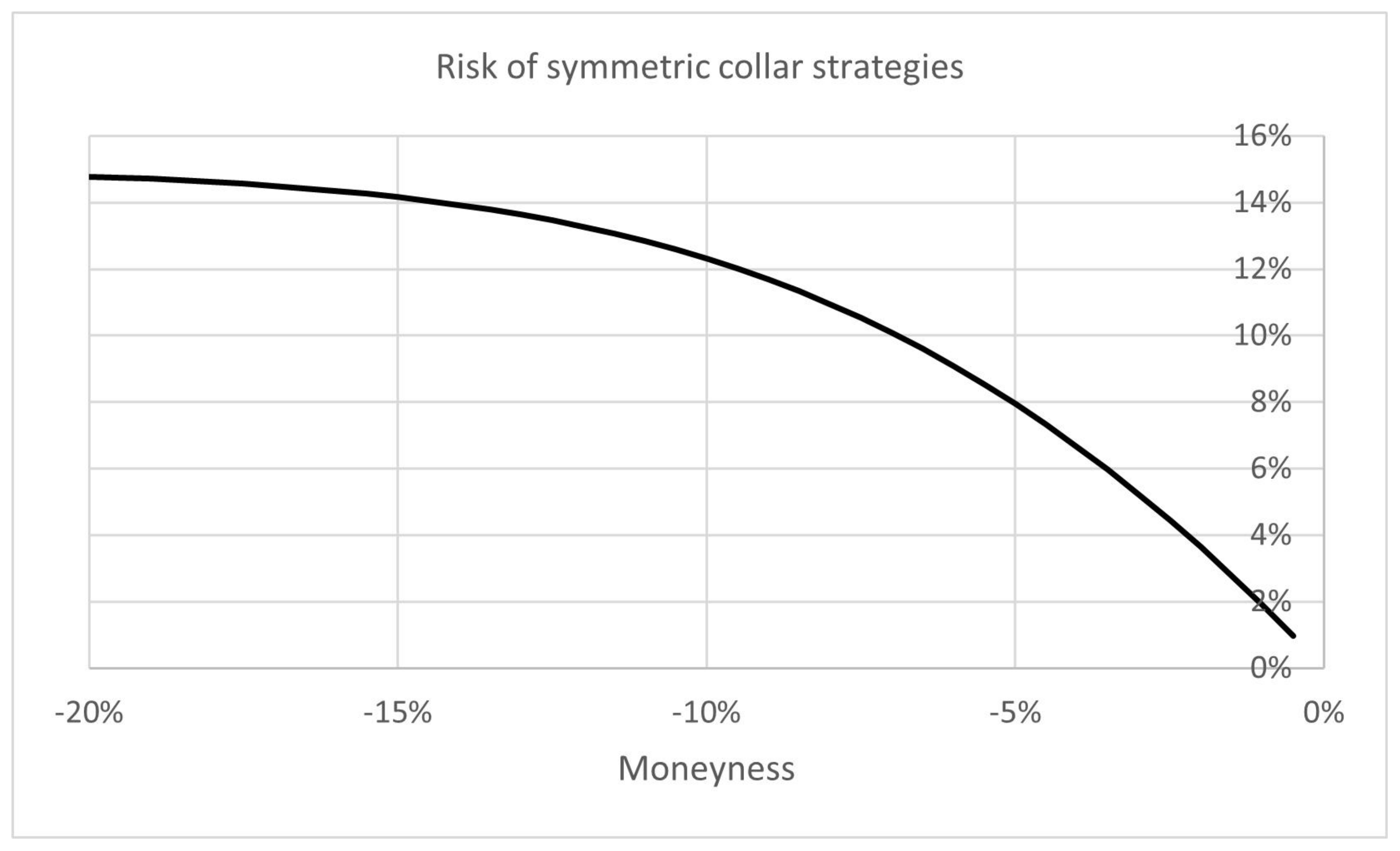
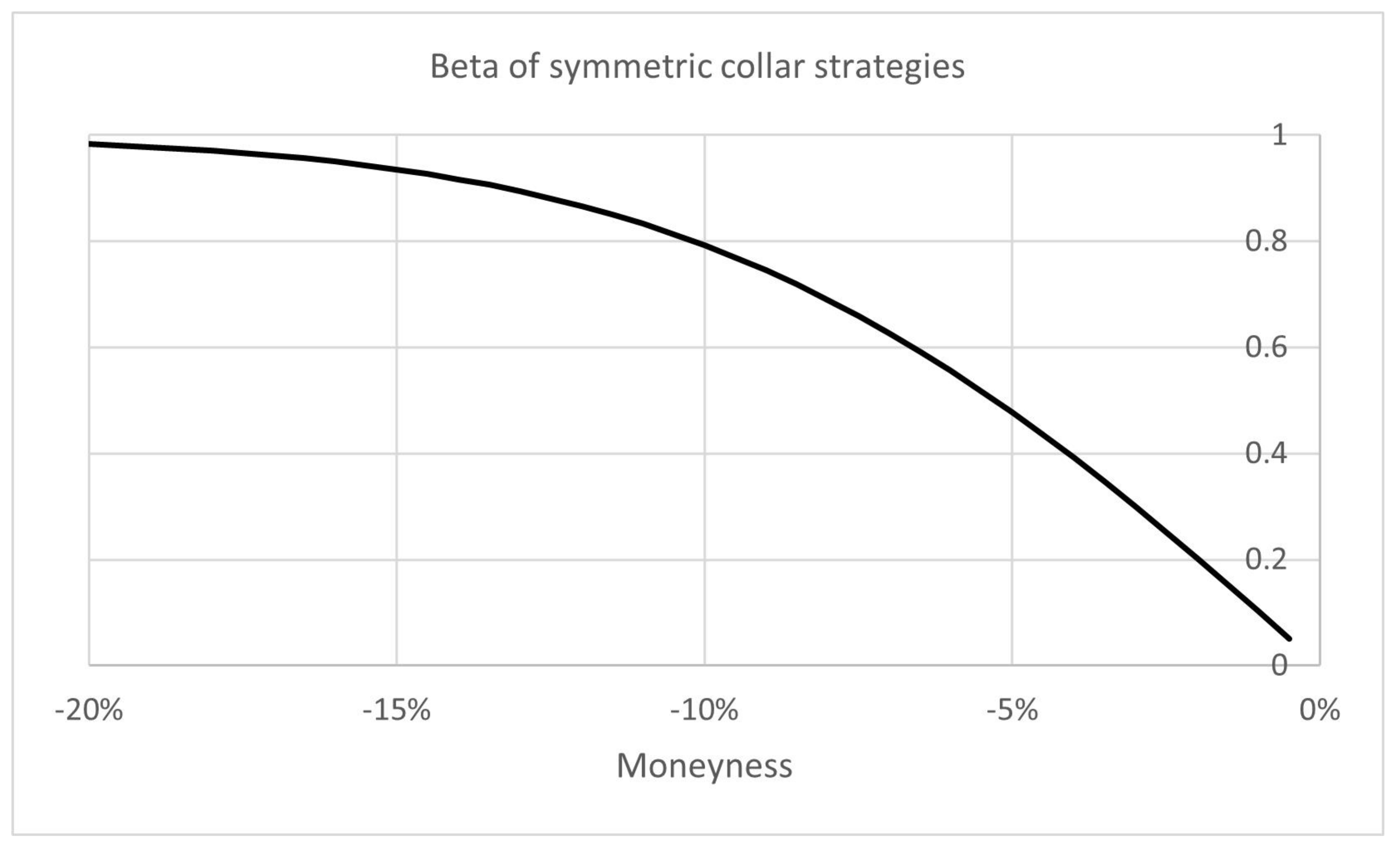
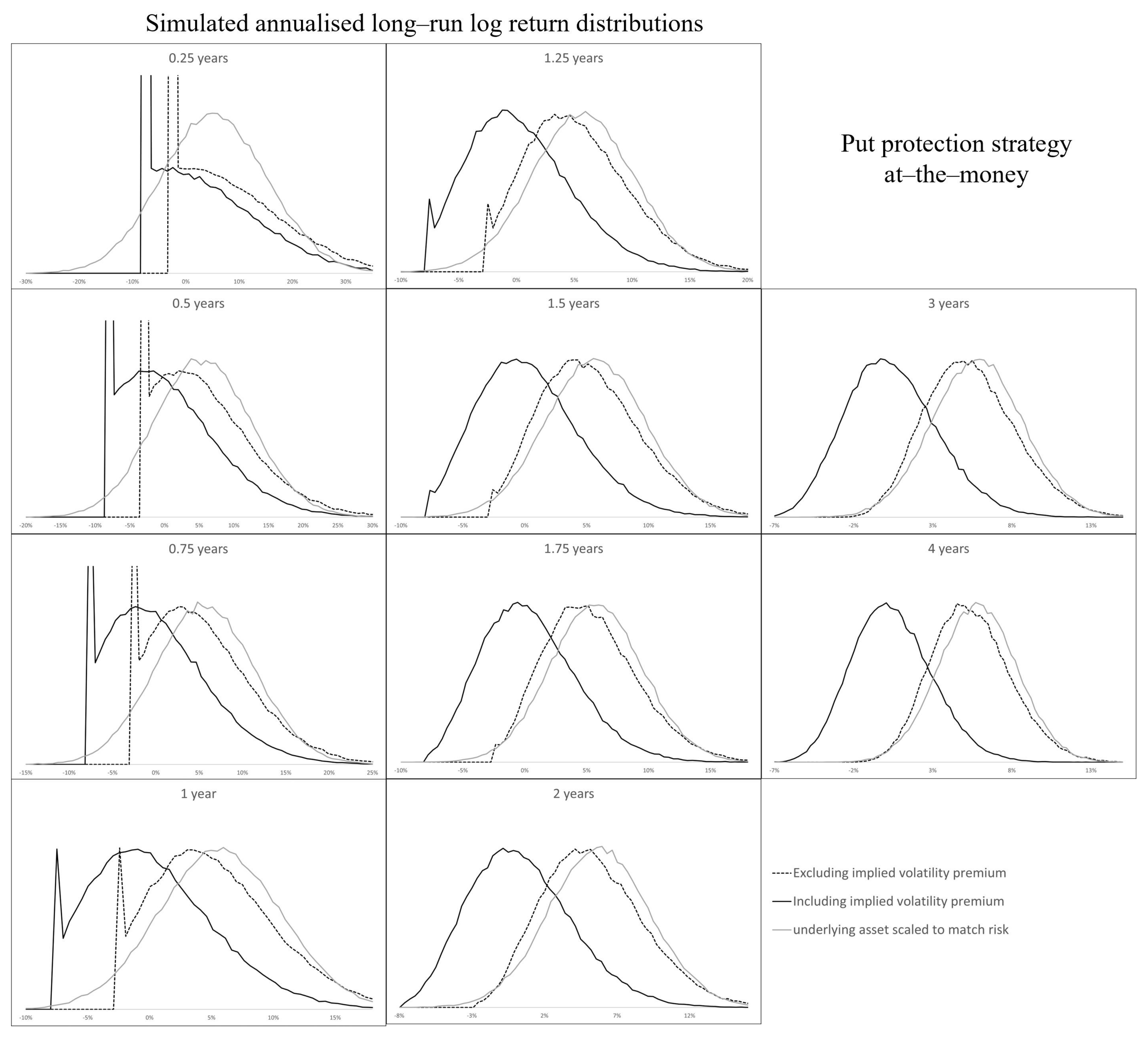
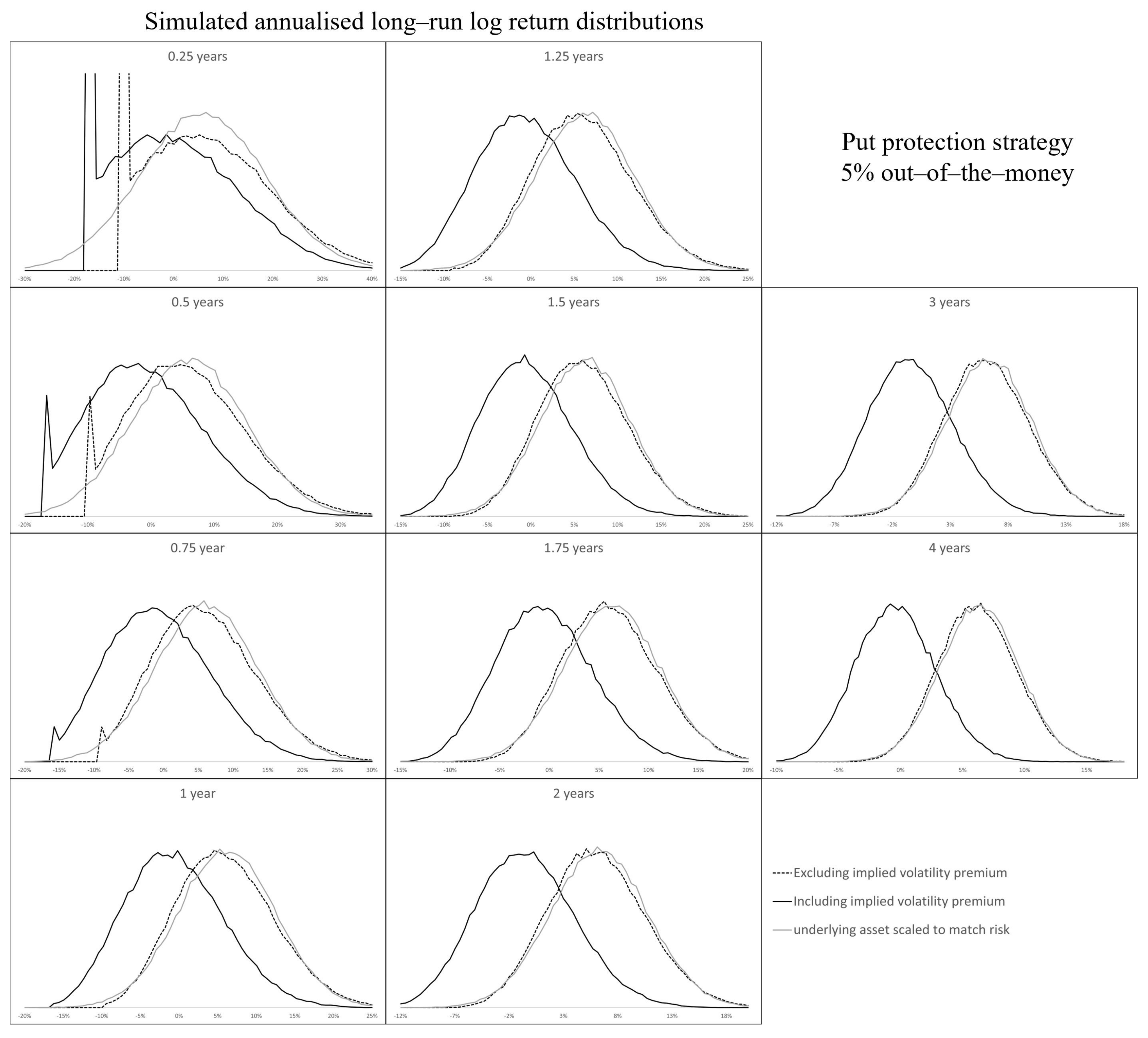
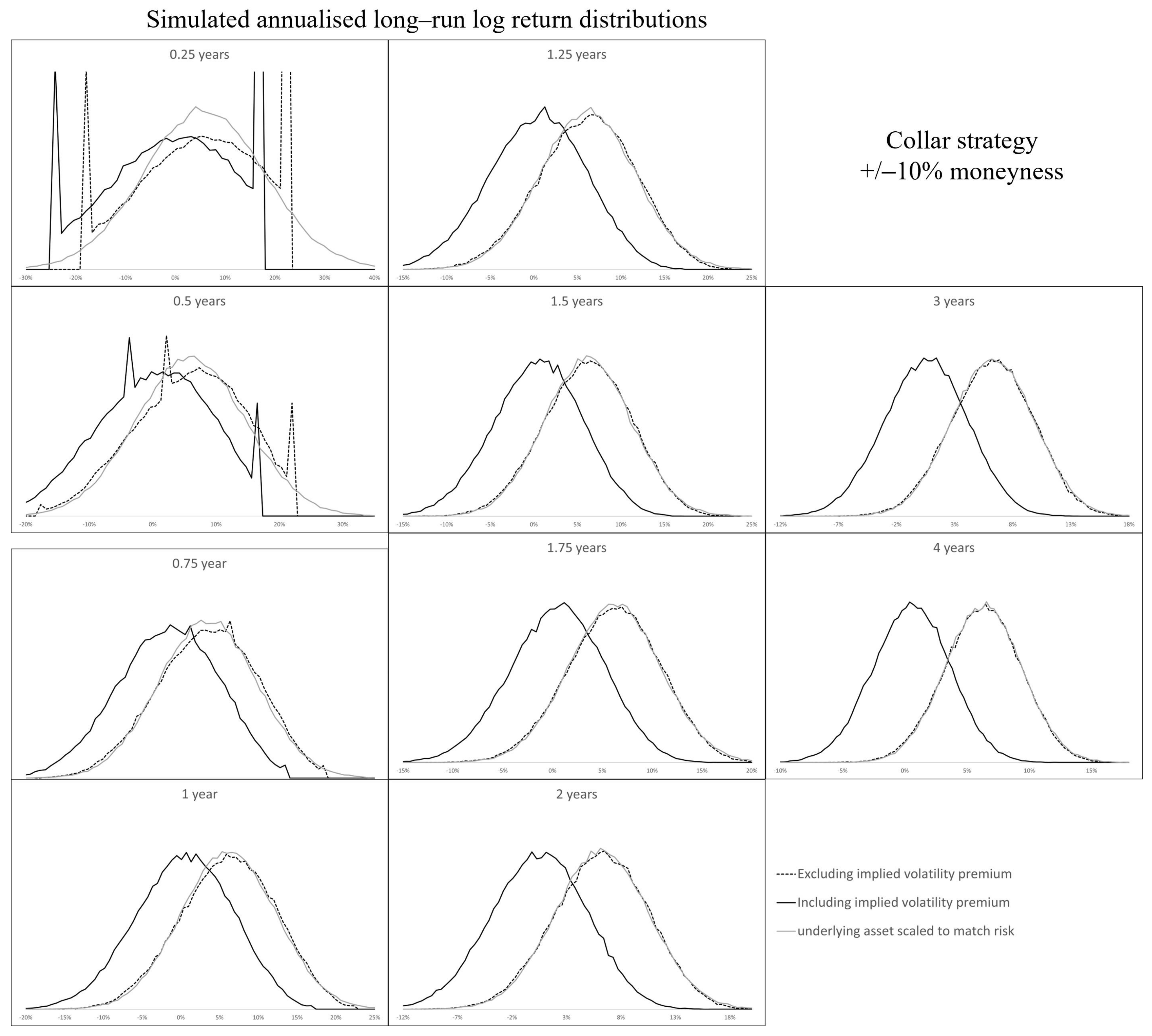
Appendix A
The purpose of
Appendix A is to detail the two key results in this article: (i) deriving formulae for the risk premium, risk, and beta of an option-adjusted portfolio, and (ii) deriving the long-term return of an option-adjusted portfolio.
To meet these objectives, we first show that put and call options are related (both having finite price) and therefore show that every option-adjusted portfolio can be considered as if the option component consists only of call options. We proceed by defining a continuous piecewise linear function and show that a portfolio containing call options has a value function of this form. With this, we derive the mean, variance, and covariance of the portfolio value function at expiry, which we prove are finite quantities. To meet our first objective, we use this result to express formulae for the risk premium, risk, and beta of a portfolio including options.
We then define an invariant option strategy and show that a time series of returns from invariant option strategies are identically distributed and that they are independent. Since the mean and variance exist, we show that the annualised long-run return must tend to a normal distribution.
Some of the properties in this
Appendix A are well-known. However, we have not seen proofs of all of them, certainly not in a single document, and we therefore prove all properties stated here to form a self-contained body of work and to enable us to develop notation and concepts used throughout
Appendix A.
Definition A1. Anassetis an item with value which can be bought or sold at a price [30]. Throughout
Appendix A, we will be considering the price change over a specific period of time and thus will denote the asset price at the start and the end of the time period as
s and
x, respectively. The symbol
s is strictly positive, and
x is non-negative but could be zero valued. Conceptually, the start of the time period is in the past and the end is in the future so that
s is known, but
x is a random variable.
Definition A2. Arisk-free assetis an asset whose end point price is known at the start point [30]. An asset that is not risk-free is termed ariskyasset. We will denote the risk-free asset’s start and end price by and , respectively. Both and are strictly positive.
Assumption A1. A risky asset and a risk-free asset are available to be bought and sold in any amount and without trading frictions.
Definition A3. Acall optionis the right, but not the obligation, to buy a unit of the risky asset on a specified date, termed theexpiry dateof the option, at a price agreed at the time of origination of the option, termed thestrike price. Aput optionis the right, but not the obligation, to sell a unit of the risky asset on a specified date at a specified price [1]. In
Appendix A, all options have an expiry date equal to the end point of the investment time period.
Definition A4. Aportfoliois a collection of assets and options [30]. An element of the portfolio is called aconstituent.
Multiple options can appear in a single portfolio, all potentially having different strike prices but all with the same expiry date. We will be specific about what is held in a portfolio, using statements such as ‘a portfolio consisting of the risk-free asset and a call option’, and where we need to be explicit, we will use the term option-adjusted portfolio to refer to a portfolio that contains options.
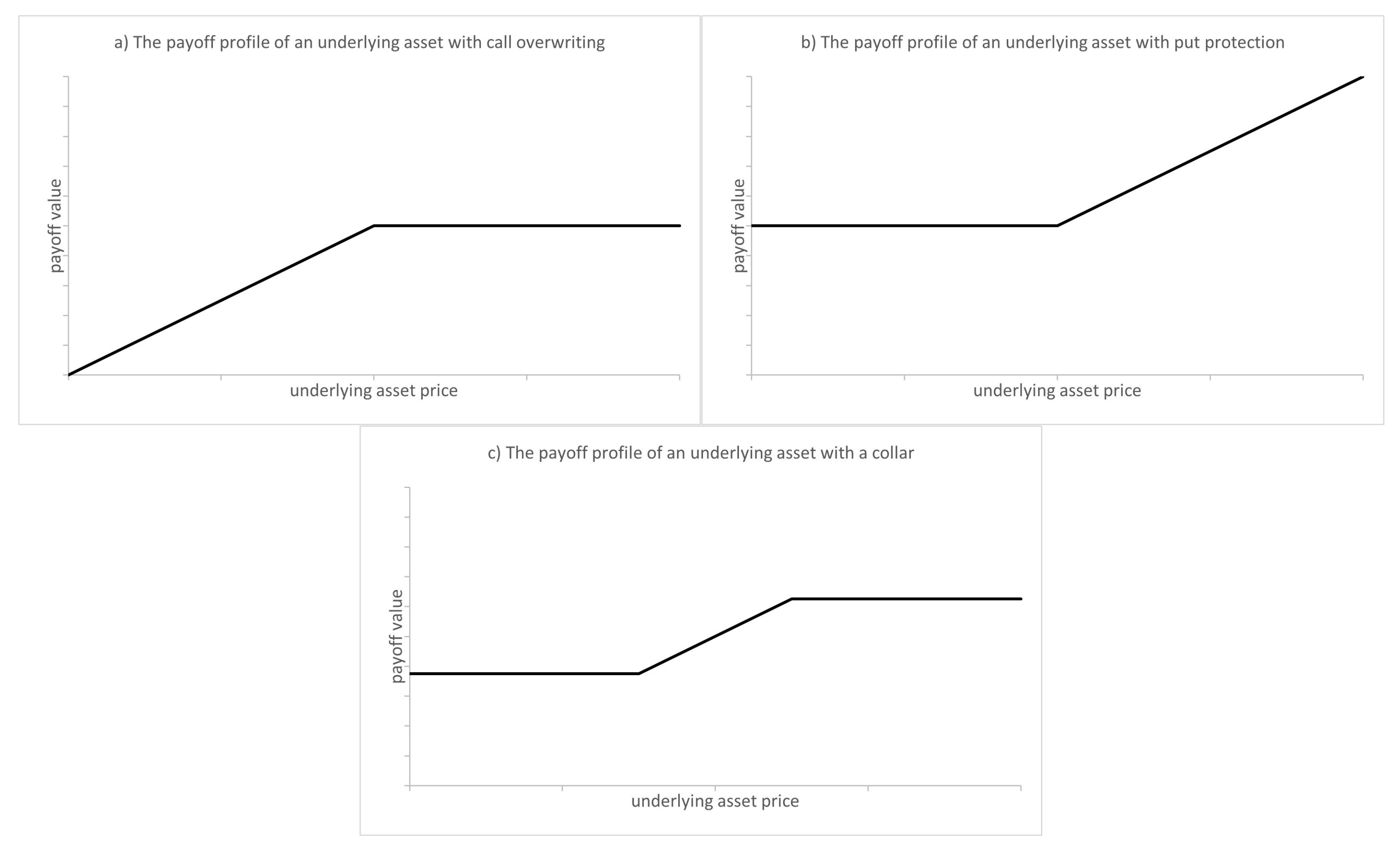
Definition A5. Avalue function, denoted in Appendix A by , is the value of an asset, option, or portfolio at the end of the time period, as a function of the underlying asset price, x. It is commonly referred to as the
payoff profile [
18], but in
Appendix A, we will use the term
value function to reinforce the fact that it is a function of the asset price.
Property A1 (Value of assets and options). The value functions of various assets are as follows:
For the risk-free asset, [18] For an asset, [18] For a call option, where k denotes the strike price [18] For a put option, where k denotes the strike price [1] For an option-adjusted portfolio consisting of put options, with units of the ith put option which has strike price , call options, with units of the ith call option with strike price , units of the underlying asset, and invested in the risk-free asset, the value function is Proof. By definition, the risk-free asset has a constant value at the end of the investment period and is not dependent on the risky asset. Therefore for the risk-free asset.
The value of an investment in the risky asset is its price. Therefore for the risky asset.
If the risky asset price x is lower than the strike price k of a call option, then the option will not be exercised and expires worthless. Otherwise, the option is exercised, and the option owner can buy the risky asset at price k and immediately sell it at its price of x. Therefore for a call option.
Similarly, if the risky asset price is greater than the strike price of a put option, then the option expires worthless. Otherwise, the option is exercised, and the option owner can sell the risky asset at price k and immediately buy it back at price x. Therefore for a put option.
The value of a portfolio is the sum of the value of its constituents. The value of each constituent is the value of a single unit of each constituent multiplied by the number of units owned. Therefore, the portfolio value function is
□
Property A2 (Put-call parity).
A portfolio consisting of an underlying asset and a put option on that asset has the same value function as a portfolio consisting of a call option and an amount invested in the risk-free asset to buy the underlying asset if it were called [1]. Proof. A portfolio consisting of an underlying asset and a put option on that asset has a value function of , where k denotes the strike price of the put, and x is the underlying asset price at expiry. This can be expressed as .
The amount needed to buy the underlying asset at the strike price on the expiry date must be k. Therefore a portfolio consisting of a call option and an amount invested in the risk-free asset to buy the underlying asset if it were called has a value function of . This also can be expressed as . □
Definition A6. Anarbitrageexists if a portfolio with zero price has a non-negative value function (and the value function is strictly positive somewhere) [30]. Assumption A2. There are no arbitrage opportunities.
Property A3 (Existence of option price).
The price of both put and call options exist [31]. Proof. We focus on a put option first. We will show that its price is bounded above and below and therefore must exist.
No arbitrage ensures that there cannot exist a portfolio with zero starting value whose value function at expiry is positive for every price of the underlying asset.
Consider the portfolio consisting of a put option and a short position in the risk-free asset equal in size to the put option price. This portfolio has zero starting value. Its value function at expiry is , where denotes the price of the put option. If then for every value of x, which breaches the no arbitrage condition.
Consider now the reverse of this portfolio: a long position in the risk-free asset equal in size to the put option price, and a short put option. Its value function is . If , then for every value of x which also breaches the no arbitrage condition. Therefore, is bounded and so must exist.
We now prove that a call option price exists. From the put-call parity property, the expiry value of a put option and the underlying asset equals the value of a call option and invested in the risk-free asset. Therefore , where denotes the price of the call option. Since and are finite quantities with strictly positive, and since we have shown that is bounded, then is also bounded and therefore must also exist. □
Property A4 (Sufficiency of call options). Every portfolio consisting of put and call options on an underlying asset, the underlying asset, and the risk-free asset can be expressed as a portfolio of solely call options, the underlying asset, and the risk-free asset.
Proof. This proof is based on put-call parity. The absence of arbitrage means that any two portfolios with the same value function must have the same price. Therefore, we need only demonstrate that the value function of any portfolio containing put options is equal to the value function of another portfolio not containing put options.
Let us suppose that the portfolio consists of
put options, with
units of the
ith put option which has strike price
,
call options, with
units of the
ith call option with strike price
,
units of the underlying asset, and
units of the risk-free asset.. The portfolio value function is
Now,
, and therefore we can write the value function as
This is the value function of a portfolio consisting of solely call options, the underlying asset, and the risk-free asset. □
Definition A7. A function f ispiecewise linearon if for some partition , it can be expressed aswhere and are finite constants [32]. (Note that the requirement that the constants are finite excludes vertical segments in the function). Definition A8. A function f iscontinuousat ξ if , and continuous everywhere
if it is continuous at every point on its domain [32]. Definition A9. Acontinuous piecewise linear functionis a piecewise linear function that is continuous everywhere on its domain.
Property A5 (Defining the intercepts of a continuous piecewise linear function).
A function f is a continuous piecewise linear function on if, and only if, it can be expressed aswhere for . Proof. By definition, if a function
f is piecewise linear on
, then it can be expressed as
If
f is continuous everywhere, then in particular it is continuous at
for
. That implies that
. Now,
Thus as required.
Conversely, if for and for where ), then . Since the function is piecewise linear, and the domain of each segment includes the lower point of its partition, then . Since , then and therefore f is continuous at for . Furthermore, since all other points on the domain lie in the open interior of a line segment, f must be continuous at those points. Therefore, f is continuous everywhere as required. □
Property A6 (Equivalence of the value of portfolios of options and continuous piecewise linear value functions). Every option-adjusted portfolio has a continuous piecewise linear value function, and every continuous piecewise linear function is the value function of some option-adjusted portfolio.
This property is a simple extension into the continuous domain of the well-known discrete case proven in [
33].
Proof. First we prove that every option-adjusted portfolio has a continuous piecewise linear value function:
From the Sufficiency of Call Options Property, we can assume without loss of generality that the portfolio of options, the underlying asset, and the risk-free asset contains no puts, only calls. It therefore has a value function expressed as
where
denotes the number of units of the risk-free asset owned,
denotes the number of units of the underlying asset owned,
n denotes the number of options, and
denotes the number of units of the
ith call option owned with strike price
for
. We order the
n options such that
and add
and
enabling us to write that every
satisfies
for some
i between 0 and
n. Therefore, we can state that when
This implies that when
By setting
and
we can write that when
and since this expression for
applies for
x in every partition, we have shown that
v is a piecewise linear function. Furthermore, for
This is the condition from the Defining the intercepts of a continuous piecewise linear function property, and therefore v is a continuous piecewise linear function.
Second, we prove that every continuous piecewise linear function is the value function of some option-adjusted portfolio:
By definition, if a function
v is continuous and piecewise linear on
then for some partition
, it can be expressed as
where
. From this recurrence relationship we can write that
and so
However, since
, we know that
which means that
This is the value function of an option-adjusted portfolio containing units of the risk-free asset, units of the underlying asset, and units of a call option with strike price , where . □
Definition A10. Theinvestment returnis the change in value of the investment over the investment period as a proportion of the starting value [2]. The risk-free asset return is .
The risky asset return is .
The option-adjusted portfolio return is where is the portfolio value function derived from the constituents of the portfolio, and p is the purchase price of the portfolio.
The intuition behind the option-adjusted portfolio return is that an investment is made in the risk-free asset, the price of the option portfolio is borrowed at the risk-free rate and used to purchase the option portfolio. Substituting the risk-free asset return allows us to rewrite
as
The returns and are a function of the random variable which we shall label q. We shall denote the probability density function of q by .
Property A7 (Mean and variance of an asset return).
The expectation and variance of the risky asset return, and , respectively, (where denotes the expectation operator, and denotes the variance operator), arewhere and Proof. where
where
Therefore . □
Property A8 (Mean, variance, and covariance of an option-adjusted portfolio return).
The return of an option-adjusted portfolio with a value function for and for has expectation, variance, and covariance with risky asset return, as follows:where and , with and .The variables and are defined as and for .
The variables and are defined as and , for .where , , and ,with , , and .where and , with and . The variable is defined as , for .
Proof. From the value function we have that
where for
,
and
.
The first moment is written as
where
and
, for
. These can be considered as partitions of probability and expectation, respectively, in that
and
.
By defining
and
, we can say
Finally, letting
and
we have that
Similarly, the second moment is written as
where
,
and
.
We can immediately write that and for .
For we expand the squared term of the integrand giving us that . Defining (which can be considered as a partition of the second moment satisfying ), we can write that, for , .
Finally, letting
,
and
, we have that
Combining these two expressions gives us that
In addition,
where
and
. Using the above definitions, we write
and
. Letting
and
Property A9 (Statistics under geometric Brownian motion).
When the underlying asset price follows a geometric Brownian motion process with instantaneous mean μ, and instantaneous standard deviation σ, thenwhere t denotes the length of time of the investment period, andwhere Proof. If the asset price follows geometric Brownian motion with instantaneous mean , and instantaneous standard deviation , then q, is log-normally distributed. Specifically is normally distributed with mean and variance .
Letting
we can write
where
, which can be expressed as
Therefore,
where
is the cumulative distribution function of a standard normal distribution. That is
Letting
, we can write
where
. which can be expressed as
Noting that
, and using identical logic to the above, we also have that
Therefore, .
Letting
, we can write
where
, which can be expressed as
Noting that
, and using identical logic to the above, we also have that
Therefore, . □
Definition A11. Theinstantaneous risk-free rate, denoted by , satisfies .
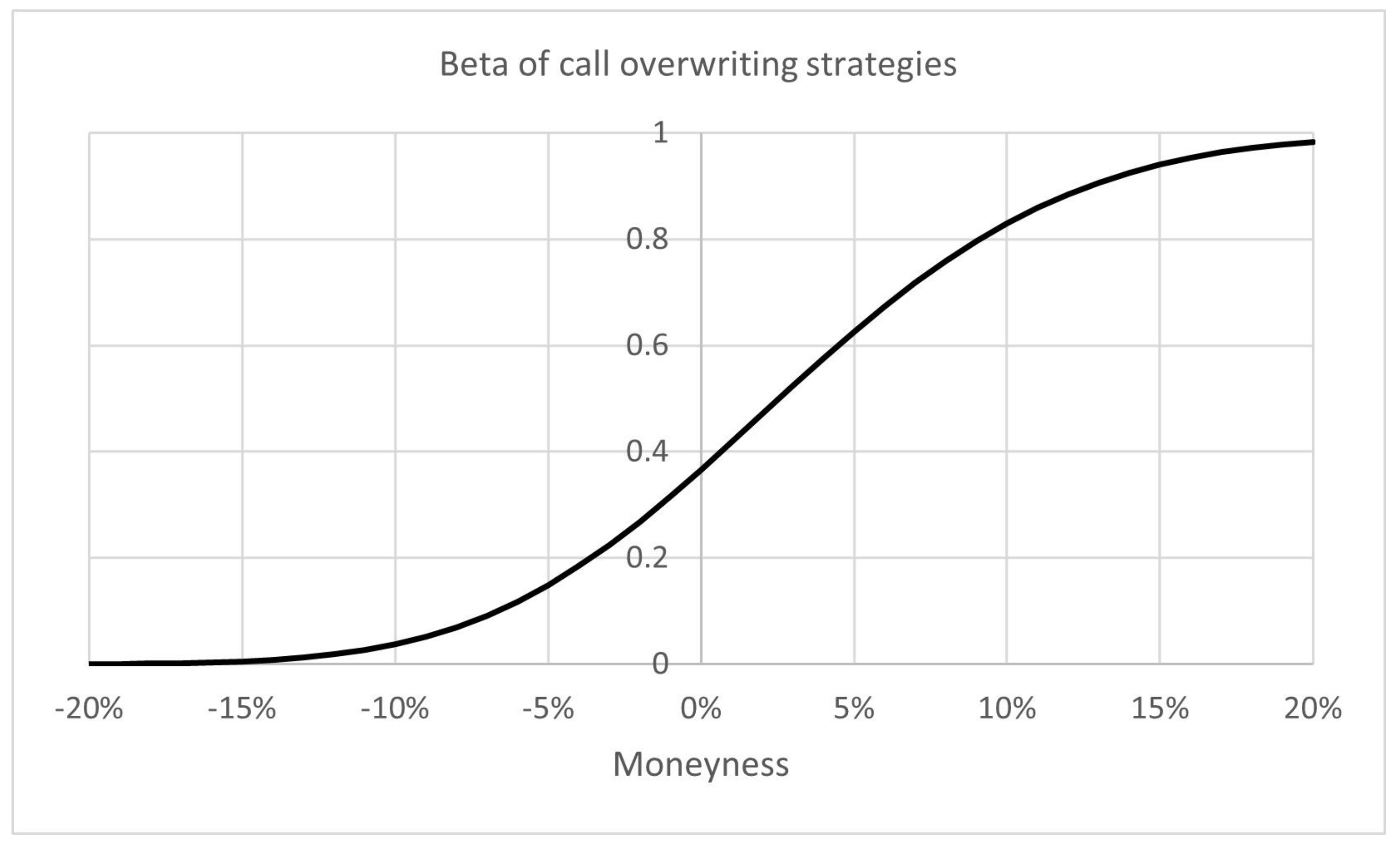
Property A10 (Option price under geometric Brownian motion). When the underlying asset price follows a geometric Brownian motion process with instantaneous mean μ, and instantaneous standard deviation σ, then where and are computed exactly as A and B were described in the Mean, variance, and covariance of an option-adjusted portfolio return property, but with μ replaced throughout by the instantaneous risk-free rate and σ by the implied volatility of the call option with the ith strike price.
Proof. If the asset price follows a geometric Brownian motion process, then a risk-neutral portfolio can be formed [
1]. Therefore, the options can be priced using risk-neutral valuation with the market’s price of volatility. Mathematically, this is expressed as
where the
represents the expectation operator using the risk-neutral distribution. Under the risk-neutral distribution
is normally distributed with mean
and variance
, where
denotes the implied volatility. Following the logic of the
Mean, variance, and covariance of an option-adjusted portfolio return property, we can write that
where
and
, for
, and
Furthermore, we can use the
statistics under geometric Brownian motion property to say
where
with
. □
Property A11 (Covariance of one option-adjusted asset with another asset).
The return of an option-adjusted asset (with a value function, , defined by intercepts , slopes , and strikes on an underlying asset with start and end prices of and , respectively) have a covariance with the return of another, non-option adjusted, asset (with start and end prices of and , respectively) given bywherewhere and with and for .whereand where , , and . The variables and denote the instantaneous mean and standard deviation of the price process of the underlying asset in the option-adjusted asset, and and denote the instantaneous mean and standard deviation of the price process of the other asset, and ρ denotes their instantaneous correlation.
Proof. The option-adjusted asset has value function denoted by
. Its return is
The covariance of this return with another asset is therefore
We can express this as
where
and
with
and
.
If
and
follow the bivariate the geometric Brownian motion process defined by
where
, then, for
,
is distributed normally with mean
and variance
, with correlation
, where
In this case we have that
where
and where
.
Let
, then
where
, which can be expressed as
Therefore, .
We also have that
where
.
Let
, then
where
, which can be expressed as
Therefore, □
Property A12 (Covariance of two option-adjusted assets). Consider two option-adjusted assets. The first has a value function, , defined by intercepts , slopes , and strikes , on an underlying asset with start and end prices of and , respectively. The second has a value function defined by has a value function, , defined by intercepts , slopes , and strikes on an underlying asset with start and end prices of and , respectively.
The covariance of returns of two option-adjusted assets iswherewhere , , , and withand where for ,and , and . The function is the cumulative distribution function of the bivariate standard normal distribution with correlation ρ.
The variables and denote the instantaneous mean and standard deviation of the price process of the underlying asset in the option-adjusted asset, and and denote the instantaneous mean and standard deviation of the price process of the other asset, and ρ denotes their instantaneous correlation.
Proof. For asset
k (
), the option-adjusted return is
The covariance of these returns is therefore
We can express this as
where
,
,
, and
with
If
and
follow the bivariate of the geometric Brownian motion process defined by
where
, then, for
,
is distributed normally with mean
and variance
, with correlation
, where
In this case we have that
where
, which can be expressed as
Therefore
where
is the cumulative distribution function of the bivariate standard normal distribution with correlation
. That is
Let
and
, then
where
and
, which can be expressed as
Therefore
where
.
Similarly,
where
and
Let
and
, then
where
and
, which can be expressed as
Therefore
where
. □
Property A13 (Existence of moments of a value function). If and exist, then and exist.
Proof. Since the probability density function of asset return, , is positive everywhere, , , and . By definition , so for , is bounded and therefore must exist. Furthermore, if the mean and variance of the underlying asset exist, then and also exist and therefore and are bounded for and so must exist.
From the Mean, variance, and covariance of an option-adjusted portfolio return property we know that and are quadratic functions of , , and for and therefore must exist. Since , also exists.
We have shown that any option-adjusted portfolio is a combination of the risk-free asset, the risky asset, and a set of call options. We have further shown that the price of every call option exists, and therefore the price of the option strategy, p, must also exist. Since , and exists, and , must also exist. □
Definition A12. An option-adjusted portfolio (with a non-negative initial price) isunleveragedif the value of the portfolio at the end of the time-period is non-negative everywhere.
Property A14 (unleveraged option-adjusted portfolio condition). An option-adjusted portfolio is unleveraged if, and only if, exists and .
Proof. The end value of an option-adjusted portfolio is .
If has a minimum, , and if then and since , for all x. Therefore, the portfolio is unleveraged.
If the portfolio is unleveraged then for all x. Therefore, . Since p is finite, must have a minimum. Furthermore and therefore . □
Definition A13. An unleveraged option-adjusted portfolio iswell-behavedif only when .
Property A15 (Existence of log moments of a value function). If and exist, and and exist, then and also exist for a well-behaved unleveraged portfolio.
Proof. Recall that
where
. Since
for all
we can write
Using the
Existence of moments of a value function property,
and
exist. Therefore, these upper bounds exist.
Since the portfolio is leveraged and well-behaved,
for all
q > 0 and
,
and so
When
,
, therefore
when
(where
). Moreover, since
for all
,
which means
when
. Therefore
Since
exists, both of these integrals exist. Therefore
Thus .
Finally, since for all x, .
Since and are bounded above and below, they must exist. Therefore and exist. □
In the remainder of this Appendix we shall be considering long-run returns of option-adjusted portfolios and will view these portfolios as a sequence of m single-period option strategies. We will let denote the single-period returns for the underlying asset, and let denote the single-period returns for the option-adjusted portfolio. The value functions of the options strategies in each single-period are denoted by . Furthermore, we will let denote the option-adjusted portfolio prices, denote the prices of the underlying asset at the start of the single periods, and denote the prices of the underlying asset at the end of the single-periods.
Property A16 (Independence of option-adjusted portfolio returns). If are mutually independent random variables, then are mutually independent.
Proof. Since each is a function solely of the random variable , if are mutually independent then must also be mutually independent. □
Definition A14. Two option strategies, deployed at different points in time, areidenticalif
- 1.
the initial amounts in invested in the risk-free rate are the same proportions of the starting underlying asset prices; and
- 2.
the number of units invested in the underlying asset are the same; and
- 3.
the number of options are the same; and
- 4.
every pair of corresponding options in the two strategies has the same moneyness.
If every pair of option strategies in a sequence over time are identical, then the option-adjusted portfolio is said to beinvariant.
Property A17 (Proportional value functions). If two option strategies are identical then their value functions, and , satisfy for all x.
Proof. If the two strategies are identical then their value functions are expressed as
Therefore
but since they are identical,
and the same moneyness means that
for
, therefore
. □
Property A18 (Identicality of option-adjusted returns). If are identically distributed, then are identically distributed for invariant option-adjusted portfolios.
Proof. For
, and for any real-valued
y, define the subset of the real numbers,
, as
Since
are identically distributed, so are
. We will label
as
X. Then we can write that for
Therefore, where is the probability density function of X. But for an invariant option-adjusted portfolio, , and the absence of arbitrage means that for any i and j. Therefore for all y and any i and j, and so . Thus and are identical. □
Definition A15. For a portfolio (or asset) with value at time i (for ), itsannualised long run-returnis Property A19 (Chain linked returns). The annualised long-run log return of a portfolio (or asset) is the average of the single-period log returns.
Proof.
where
denote the
m single-period returns.
□
Property A20 (Long-run option-adjusted portfolio return distribution). If are independent and identically distributed, then the annualised long-run log return of an invariant option-adjusted portfolio tends to a normal distribution as the number of single-periods constituting that long-run tends to infinity.
Proof. The long-run log return of the option-adjusted portfolio is defined as
The two previous properties have shown that if
are independent and identically distributed, and the option-adjusted portfolio is invariant, then
are independent and identically distributed. The
Existence of log moments of a value function property says that
and
exist (we have omitted the indexing as the expectation and variance will be the same for
). Therefore, by the central limit theorem [
34], in the limit as
, the long-run log return is normally distributed with mean
and variance
. □