Abstract
In shape analysis, the interpolation of shapes’ trajectories is often performed by means of geodesics in an appropriate Riemannian Shape Space. Over the past several decades, different metrics and shape spaces have been proposed, including Kendall shape space, LDDMM based approaches, and elastic contour, among others. Once a Riemannian space is chosen, geodesics and parallel transports can be used to build splines or piecewise geodesics paths. In a recent paper, we introduced a new Riemannian shape space named TPS Space based on the Thin Plate Spline interpolant and characterized by an appropriate metric and parallel transport rule. In the present paper, we further explore the geometry of the TPS Space by characterizing the properties of its geodesics. Several applications show the capability of the proposed formulation to conserve important physical properties of deformation, such as local strains and global elastic energy.
MSC:
53Z50
1. Introduction
In shape analysis, the interpolation of shapes’ trajectories is often performed by means of geodesics in appropriate Riemannian Shape Spaces. Different proposed metrics and shape spaces include Kendall shape space [1,2], LDDMM-based approaches [3,4,5,6], and elastic contour [7]. Once a Riemannian space is chosen, geodesics and parallel transports can be used to build splines or piecewise geodesics paths [1,8,9]. If the torsion of the connection defined on the Riemannian space does not vanish, then a difference can appear between geodesics and autoparallel lines [10]. In recent papers [11,12,13,14], the present authors introduced and developed a new Riemannian shape space named TPS Space based on the Thin Plate Spline interpolant and characterized by an appropriate metric and a parallel transport rule, and the efficiency of this TPS parallel transport was compared with other methods in [14]. One of the main features of the TPS connection is its independence from the path. In fact, TPS parallel transport is named Direct Transport. This feature leads to a flat space (vanishing Riemannian Curvature) with torsion. In previous contributions, the geodesics of the TPS Space have never been studied. The present paper aims at studying the characterization of geodesics and parallel lines in the TPS space together with numerical techniques to compute them. Looking for geodesics’ computation is of particular importance in a variety of morphological analyses, such as in spline regression, which have applications in a wide range of shape analysis tasks spanning fields from medical/clinical investigations to biological research. As will be clarified in the following pages, in a connection with torsion, geodesics and autoparallel lines can coincide; however, this is not a rule [10,15]. In particular, it happens only if the torsion is completely skew-symmetric. On the other hand, the TPS connection is defined by directly assigning a parallel transport rule without analytically defining the corresponding covariant derivative, ∇. For this reason, it is not possible to calculate the Christoffel symbols of the connection or the components of the torsion to establish whether it is completely skew-symmetric [15]. In the following, we exploit the qualitative definitions of Direct Transport and TPS metric in 2D to build the geodesics and the autoparallel lines of the TPS space numerically. In particular, geodesics are built by minimising the length of the path connecting two given points (the initial and final shapes), while autoparallel lines are calculated via shooting from a point (the initial configuration) and a vector (the initial deformation velocity). Our set of examples allows the geometry of the TPS Space to be explored by characterizing the properties of its geodesics and parallel lines. The paper is organised as follows:
- In Section 2, the general definitions of the two families of curves in Riemannian spaces are summarized.
- In Section 3, the main concept defining the TPS Space are recalled.
- In Section 4, the novel contribution of this paper is presented, that is, the construction of and comparison between autoparallel and geodesic lines in TPS Space.
- In Section 6, the numerical results are shown in order to discuss and compare the main features of autoparallel and geodesic lines in TPS Space.
2. Geodesics in Riemannian Manifolds
In this section, we sketch several concepts in differential geometry, referring to [10,15,16] for details.
In differential geometry, a Riemannian manifold is a smooth manifold equipped with a positive-definite inner product g on the tangent space at each point p.
A connection on the manifold is a rule allowing for parallel transport vectors along a smooth curve . This rule allows for the comparison of vectors belonging to different tangent spaces.
To be more precise, any parallel transport rule along a path from a to b has to fulfill the following properties:
moreover, for any point c on the path
It follows from this that is the identity on , and .
This procedure defines the connection, inducing a covariant derivative, ∇, that can be then calculated by the following limit:
A vector field V is said to be parallel along the curve if the following holds:
A connection is considered compatible with a metric g if the parallel transport is an isometry, i.e., if for each pair of vectors along each path.
In terms of connection, this means that:
The torsion of the connection ∇ is a tensor field defined as
with the Lie bracket.
A connection is called symmetric when the torsion is null for all . A fundamental result of Riemannian Geometry is the existence of a unique symmetric connection compatible with the metric g, named the Levi–Civita (LC) connection, which we call .
In its more general meaning, a geodesic is a curve the tangent field of which is parallel along the curve itself:
In other terms, a geodesic is the curve on the manifold where one walks, maintaining the same direction, according to the given parallel transport rule. In this general sense, the geodesic can be called an autoparallel line [10].
On the other hand, if the connection is the Levi–Civita one, the geodesics acquire an additional property. Given two points, , belonging to a convex neighbourhood of , a geodesic from p to q is the shortest path joining p and q according to the metric g. The distance between p and q can be calculated as .
In this paper, following [10], by geodesics we mean only those geodesics of the Levi–Civita connection, ; we refer to the geodesics of a different connection, ∇, as autoparallel lines.
In general, the difference between a Levi–Civita connection, , and any connection ∇ is a tensor field D [15]:
The symmetric and the antisymmetric part of D have direct geometric meanings:
- A connection ∇ is torsion-free if and only if D is symmetric.
- A connection ∇ has the same geodesics as the Levi–Civita connection if and only if D is skew-symmetric.
As a consequence of (4), the connection ∇ is compatible with the metric g if and only if D belongs to the space
3. Geometry of the TPS Space
In the present section, we summarize the formulation of the TPS Space presented and developed in [11,12,13]. Both the metric g and parallel transport are based on the interpolation function called Thin Plate Spline (TPS). Then, in order to introduce the Riemannian structure of the TPS Space, we need to first summarize the formulation of the TPS. Furthermore, in order to introduce the metric g we need to explain strain energy, bending energy, and body bending energy and how they are used to build g.
3.1. Thin Plate Spline
Let be the m-dimensional Euclidean space and be two regular regions representing the undeformed (source) and deformed (target) configurations of a body (Figure 1), respectively. We label as x the points in and as the points in . The displacement field is represented by the following difference vectors:
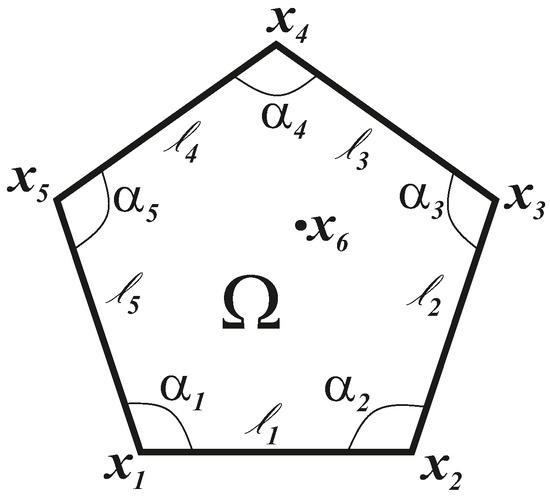
Figure 1.
Example of a 2D configuration made by six landmarks, with the first five lying on the boundary and one, , inside the region .
If the configurations are sampled in k points (landmarks), then and are named k-configurations and represented by the matrices X and , respectively. The displacements experienced by the k landmarks can be collected in the matrix . Because translations do not affect the shape, they are filtered out by centring configurations in the origin of . The set of all centred k-configurations is named Centred Configuration Space . Given a configuration X, the corresponding centred configuration can be represented in two different ways: by a matrix obtained as or, alternatively, by a matrix , where , is the identity matrix and is a column of ones, while H is the Helmert sub-matrix. The row of the Helmert sub-matrix H is obtained by
and thus, the row consists of repeated j times followed by and then zeros, . The notable property can be used to switch from one parametrization to the other. In the following we use only centred configurations; we therefore remove the subscript, C or H, by specifying, when necessary, which parametrization we are using. Let be a pair of centred configurations. The Thin Plate Spline (TPS) is a function that interpolates, in , the deformation from X to . The TPS is parametrized by the pair where is a linear transformation of represented by a matrix and is a matrix. Given a point and a centred configuration , we obtain
where is a matrix, is the position of the i-th landmark, and
Because X and are centred, Equation (12) represents interpolation constraints, while the matrices consist of parameters. In order to solve the interpolation problem we need to introduce more constraints on , uncoupling the affine and non-affine parts:
For a given pair there exists a unique set of parameters for the pair that solve the problem (12), constrained with (13):
where
are a and a matrices, respectively, which only depend on the source configuration X. We note that the inverse of the singular matrix is obtained by means of the Helmert matrix as
Finally the target can be represented as the deformation of X:
The matrix is called the Bending Energy matrix and is used to extract the non linear part of the deformation. Because it vanishes on affine deformations, its eigenvectors associated with non vanishing eigenvalues are only . These are called principal warp eigenvectors, and represent the principal modes of deformation of the shape X [11].
3.2. Energies
It has been proven [17] that TPS is the only interpolating function that minimizes the bending energy J, which gauges the second derivative of the displacement field:
Note that the bending energy is defined as an integral on the whole, . In [12], in order to provide a mechanical interpretation of bending energy, the concept of body-bending energy was introduced, allowing the integration to be performed entirely inside the body:
The body-bending energy is slightly smaller than the bending energy, and the decay can be used to quantify the difference. Both J and can be used as pseudo-metrics on , as they measure the difference between two configurations and vanish in affine deformations. In order to endow with a Riemannian metric we need a non-singular distance. Here, we propose slightly modifying the Dirichlet Energy used in the deformable templates method [18] to obtain the following expression for the strain energy, , stored by the body:
where
is the strain tensor (in the case of small displacements). We note that vanishes on the rotational part of the local deformation. On the other hand we stress that (19) is a global measure that should be calculated via integration, starting from local measures, by means of a discretization of the whole domain . In [12] it is shown that (19) can be calculated directly as a global quantity starting from landmark displacements, at least for bilinear deformations in 2D. In fact, in that case, when a rectangle bends in a generic trapezoid the deformation can be parametrized as follows:
where are the bending with respect to the two axes, A is a linear transformation, and I is the identity matrix. Then, the strain energy can be calculated as the sum of one contribution depending on the norm of A and a second contribution proportional to the bending energy, J. The proportionality coefficient depends only on geometrical quantities of :
where and are the polar inertia and the area of , respectively. In the next section, we show that both J and can be calculated by means of the TPS parameters and . Then, the expression (22) can be globally calculated starting from landmark displacements by means of TPS.
3.3. TPS Metric
In [11], it is shown that the value of the bending energy J associated with a displacement, U, of a configuration, X, obtained using the quadratic form
where for and is for . For this reason the matrix is called the Bending Energy Matrix of X. This fact allows us to evaluate the bending energy directly by means of a closed form expression, avoiding the need to discretize the configuration in a huge number of triangles. Furthermore we note that the Bending Energy Matrix depends only on X and can be used as a pseudo-metric on . Let two given configurations, X and , related landmark-wise by a bilinear deformation as (21); then, the strain energy (22) can be calculated as
and the average strain energy on the body can be obtained as
While this expression is valid only for bilinear deformations, it can be generalized by assuming certain approximations concerning, in particular, the decay, . In [13], it is further shown that for the body-bending energy calculation it is possible to define a symmetric matrix, , such that the following holds:
Then, in general, the decay, , is not isotropic and can be calculated by means of the Rayleigh quotient:
In the two-dimensional case, the BEB matrix is defined as follows:
where and the values of the angles are
while , is the vector rotated clockwise by , q is the number of landmarks that does not lie on the boundary , and is the number of landmarks lying on (see Figure 1). As can assume different values depending on the direction of the deformation, while we need a metric depending only on X, in the following we assume an isotropic decay :
where is the number of vanishing eigenvalues of . Then, in the following, we approximate the calculus of the BEB by assuming
Finally, we generalize (25), defining the distance between two generic configurations X and (called -Energy), as follows:
where
We note that depend only on the source configuration, X. From a mechanical point of view, we can define the -energy as the average strain energy , evaluated on a more simple deformation characterized by the same uniform component of U and a bilinear deformation storing the same body bending energy of , i.e., such that . In [12], it is shown that the -energy is a good approximation of the strain energy for more general deformations as well as bilinear ones. Then, the TPS Space [11,12,13] can be defined as the equipped with the TPS metric tensor:
In particular, the affine and non-affine components of the metric are defined by the sub-metrics
where
Alignments: OPA and MOPA Techniques
After the TPS metric tensor G is introduced, we introduce a technique for managing rotations in order to align two configurations, X and Y, based on minimization of the distance, defined as
The aligned configuration, , is obtained by means of an optimal rotation, , minimizing d.
where . According to this definition, turns out to be the rotational component of the polar decomposition of . When , we obtain the rotational component of , the classical Ordinary Procrustes Analysis (OPA). When , then . In the latter case, we define the alignment Modified OPA, or MOPA [11].
3.4. TPS Direct Transport
The connection called the TPS connection was introduced in [11] and developed in [13]. It has the following properties:
- It is compatible with the TPS metric;
- It is compatible with the decomposition provided in (12);
- It is independent of the path.
We assume all the configurations to be centred and represented by Helmertized landmarks; then, if not otherwise specified, each matrix is a matrix. Furthermore, deformation vectors have a subscript denoting the starting point, that is, the source configuration; for details, see [11].
Let X and Y be two source configurations and let and be the two associated deformation vectors, provided by
We can then say that is the parallel transport of a given , that is, , if and only if the uniform part of equals that of
and the non uniform part of solves the linear systems
where the body principal warps matrix collects all the body principal warps of X and is a suitable orthogonal matrix (i.e., ) defined on each configuration X and representing a rotation or reflection of the principal warps. After being chosen, a configuration P as a Pole for the space is estimated, minimising the Euclidean distance between the rotated principal warps of X and the corresponding basis on the pole, P.
The principal warps matrix can be built as follows:
- Perform a TPS analysis on X and find the and ;
- Perform an eigenvalue analysis on and obtain , where is the matrix containing the eigenvectors in column and is the diagonal matrix of the eigenvalues ordered by increasing magnitude (the first m eigenvalues will be equal to 0);
- Drop the first m columns from by obtaining the matrix , containing the principal warp eigenvectors by column;
- Drop the first m rows and the first m columns from by obtaining the matrix ;
- Define the matrix .
The same steps must be used to build the principal warps matrix on the target configuration.
The first equation of (40) constrains to be orthogonal to the affine part, while the second defines the isometry in the subspace of the non-affine deformations. This last requirement implies the conservation of the total bending energy. The system (40) can be written as
This can be re-written as
And so:
It is worth noting that Equation (41), characterizing as the parallel transport of , depends only on quantities related to the startpoint, X, and endpoint, Y, of the transport, and does not depend on the path. For this reason, the TPS connection is characterized by vanishing curvature and non-vanishing torsion. Moreover, it is easy to check that (41) is compatible with the TPS metric G and with the decomposition provided in (12).
4. Geodesics and Autoparallel Lines in TPS Space
In the present section, we introduce the main contribution of the present paper, that is, to show the most important features of the geodesics and autoparallel lines in the TPS space and compare the two families of lines.
In the previous section, the TPS connection has been defined by directly assigning the parallel transport rule (41) without analytically defining the corresponding covariant derivative ∇. For this reason, it is not immediately necessary to calculate the Christoffel symbols of the connection or the Christoffel symbols of the corresponding Levi–Civita connection , nor the components of the torsion for the purpose of establishing whether it is completely skew-symmetric [15] and thus whether or not the autoparallel lines and geodesic lines coincide.
After in (41) is substituted with and with , we obtain
Equation (42) can be integrated to shoot the autoparallel line starting from with initial velocity . In the general case, this integration is not simple because it involves the construction and inversion of the matrix and alignment with the pole, P. Fortunately, the integration of (42) is not as complicated in the case of purely affine deformations. In the next Section 4.1, we show the analytical solution of geodesic and autoparallel lines for the case of purely affine deformations. Then, in Section 4.2 and Section 4.3, we exploit the qualitative definitions of Direct Transport and TPS metrics in 2D to numerically build the geodesics and autoparallel lines of the TPS space, respectively, in the general case. In particular, geodesics are built by minimising the length of the path connecting two given points (initial and final shapes), while autoparallel lines are calculated via shooting from a point (initial configuration) and a vector (initial deformation velocity).
4.1. Analytical Solution for the Affine Subspace
A trajectory of affine transformations of can be represented as
with and
The trajectory is an autoparallel line if and only if
that is, by means of the (39)
that is,
we note that this equation is the same as that characterizing the autoparallel lines in . The solution is as follows:
as is well known, in geodesics and autoparallel lines coincide [15,19]; then, this property holds for TPS-geodesics and TPS-autoparallel lines as well in the case of affine deformations. The geodesic from to can be calculated as
4.2. Geodesics Calculation: Objective Function Optimisation and Equality Constraints
Given two configurations , we calculate the geodesics from to by exploiting the property of minimizing the Riemannian distance. The geodesic trajectory can be calculated by minimizing the functional:
In addition, we require that the curve has a constant speed, , and we enforce this constraint by adding a Lagrange multiplier, k, to the objective function:
The optimization problem is solved numerically by discretizing in a finite number n of steps using Algorithm 1, sketched below.
| Algorithm 1: geodesic algorithm. |
| Result: Geodesic path with initial configuration X0 and final configuration Xf using n discretization steps. |
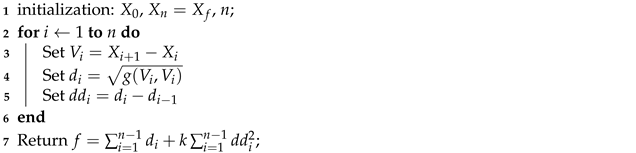 |
Then, the objective function is minimized by the R optimizer Solnp, R package version 1.16 [20]. The solver is an indirect solver implementing the augmented Lagrange multiplier method with an SQP interior algorithm.
4.3. Autoparallel Lines Calculation Algorithm via Shooting
Autoparallel lines do not minimize any distance, and are built directly by means of the parallel transport rule (41) via shooting. Let be the initial configuration and be the initial deformation velocity; V can be called shooting vector and the path such that is called shooting path of and V. In order to interpolate between and with an autoparallel line, shooting should be used iteratively to find a shooting vector such that a shooting path starting at and with as shooting vector reaches in a unit time (see [7]). In the present work, we are interested in comparing the behaviour of geodesics and autoparallel lines; thus, we avoid the iterative procedure by limiting ourselves to implementing a single shooting procedure starting from a configuration and a deformation and then using Algorithm 2, sketched below.
| Algorithm 2: shooting algorithm. |
| Result: Shooting path with initial position X0 and initial velocity V0 using n discretization steps. |
 |
5. Examples
We propose five experiments aimed at finding TPS geodesics and comparing them with original shapes, shapes inputted in the optimizer, and shapes from geodesic shooting. For each experiment, eight shapes were generated.
- Affine case, spherical: in this simple case, the starting rectangle experiences only a size increase.
- Affine case, general: in this case, the rectangle undergoes only a pure affine transformation.
- Non-affine case bending: in this case, the rectangle experiences pure bending parameterized according to the parameters specified below.
- Non-affine case bending+size: in this case, the rectangle experiences pure bending parameterized according to the parameters specified below, with the addition of a size increase.
- Non-affine case bending+general affine component: in this case, the rectangle experiences pure bending parameterized according to the parameters specified below, with the addition of the same parameters of affine transformation as in case 2.
5.1. Dataset
A set of parametric shape paths were generated, starting from a rectangle , by means of the following formula:
where parametrize the affine transformations and is the amount of bending. Each experiment is articulated in the following steps:
- A parametric trajectory is generated by the mean of the (54). In this way, the initial and final points, and , are identified.
- Linear interpolation between and .
- The geodesic , such that and are calculated following the procedure sketched in Section 4.2. The distance, , and the initial tangent, , are calculated.
- The autoparallel line , starting from , is built by shooting by means of Direct Transport for a distance of , following the procedure sketched in Section 4.3.
For all cases, we computed the linear interpolation between the first shape (the undeformed rectangle in all cases) and the last shape of any experiment. These linearized shapes (eight shapes) were the input for the optimizer, imposing as equality constraints the maintenance of the first and last shapes in order to force the geodesic to pass between these shapes. Finally, we performed a common Principal Component Analysis (PCA) for each experiment except for the first (which was trivial in terms of pure shape change), including all of the four sets of shapes: original, linearized, optimized, and shooted.
In each one of the experiments, we checked:
- The trend of the -energy.
- The trend of the components of the -energy.
5.2. Affine Case: Spherical
A parametric trajectory of eight configurations was generated by applying (54) to the initial rectangular shape by selecting eight values of the parameters in the following ranges: Figure 2 and Table 1 show the results for the size-only case. Geodesic searching via optimization satisfactorily recovers both the size change and the equally spaced -energy steps between consecutive shapes. The non-affine component of the -energy, , is of course equal to zero. Optimized geodesics and shooting quietly coincide. Figure 3 shows scatterplots of Table 1 values.
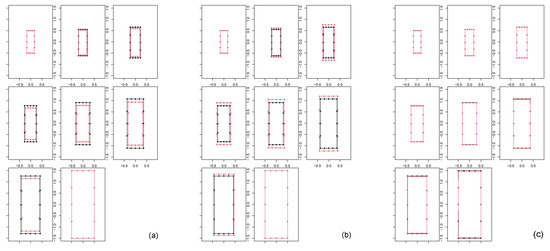
Figure 2.
Affine spherical case results. (a) Left panel: geodesic trajectory shapes (black) plotted against the original parametric shapes (red). (b) Center panel: geodesic trajectory shapes (black) plotted against the shapes found via linear interpolation between the first and last shapes of the parametric dataset (red). (c) Right panel: geodesic trajectory shapes (black) plotted against autoparallel trajectory (red) built via shooting of the first two configurations of the geodesic.

Table 1.
Values of the energies for the affine spherical case; represents the affine component of the -energy, the non-affine component and the total -energy.

Figure 3.
Trend of the energies for different interpolations: (a) Left: linear interpolation (b) Center: geodesics interpolation. (c) Right: autoparallel interpolation. Blue refers to , red to , grey to .
5.3. Affine Case: General Case
A parametric trajectory of eight configurations is generated by applying (54) to the initial rectangular shape by selecting eight values of the parameters in the following ranges:
Figure 4 and Table 2 show the results of the general affine-only case. Optimized geodesics correctly recover the original parameterized deformation, with equally spaced gamma-energy steps between consecutive shapes and db equal to zero. Figure 5 shows scatterplots of Table 2 values. Figure 6 shows the first two PCs resulting from PCA performed on all four types of datasets of the general affine case (parameterized, linearized, optimized geodesic, shooting).
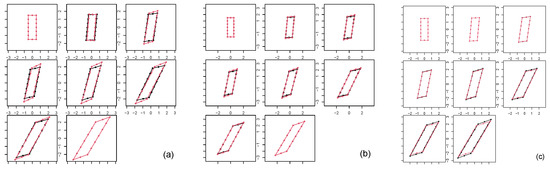
Figure 4.
Affine general case results. (a) Left panel: geodesic trajectory shapes (black) plotted against the original parametric shapes (red). (b) Center panel: geodesic trajectory shapes (black) plotted against the shapes found via linear interpolation between the first and last shapes of the parametric dataset (red). (c) Right panel: geodesic trajectory shapes (black) plotted against autoparallel trajectory (red) built via shooting of the first two configurations of the geodesic.

Table 2.
Values of the energies for the affine general case; represents the affine component of the -energy, the non-affine component, and the total -energy.

Figure 5.
Trend of the energies for different interpolations: (a) Left: linear interpolation (b) Center: geodesics interpolation. (c) Right: autoparallel interpolation. Blue refers to , red to , grey to .
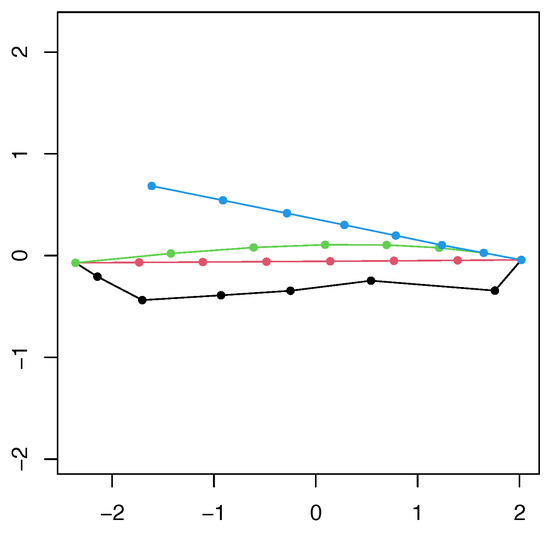
Figure 6.
PC1-PC2 scatterplot of the PCA perfomed on the four set of shapes resulting from the general affine case. PC1 explains 97.2% of total variance, while PC2 explains 2.66%. Black refers to the optimized shapes, red to the linearized, green to the original shapes, and cyan to the shooted shapes.
5.4. Non Affine Case: Bending
A parametric trajectory of eight configurations is generated by applying (54) to the initial rectangular shape by selecting eight values of the parameters in the following ranges:
The results of the general non-affine case are shown in Figure 7, Figure 8 and Figure 9 and Table 3. This simulation is particularly challenging due to the particular non-affine transformation experienced by the rectangle. Despite this, the geodesic optimization finds shapes characterized by approximately equally spaced steps in terms of both gamma energy and its two components, du and db. The PCA scatterplot in Figure 9 shows coherent behaviour for all datasets except, as expected, for the linearized shapes.
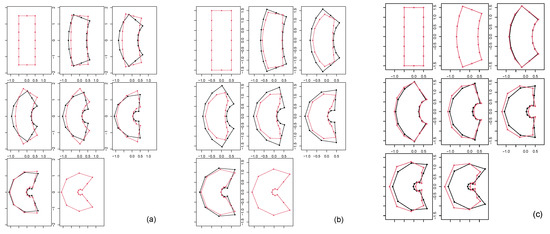
Figure 7.
Non-affine case bending-only results. (a) Left panel: geodesic trajectory shapes (black) plotted against the original parametric shapes (red). (b) Center panel: geodesic trajectory shapes (black) plotted against the shapes found via linear interpolation between the first and last shapes of the parametric dataset (red). (c) Right panel: geodesic trajectory shapes (black) plotted against autoparallel trajectory (red) built via shooting of the first two configurations of the geodesic.

Figure 8.
Trend of the energies for different interpolations: (a) Left: linear interpolation (b) Center: geodesics interpolation. (c) Right: autoparallel interpolation. Blue refers to , red to , grey to .
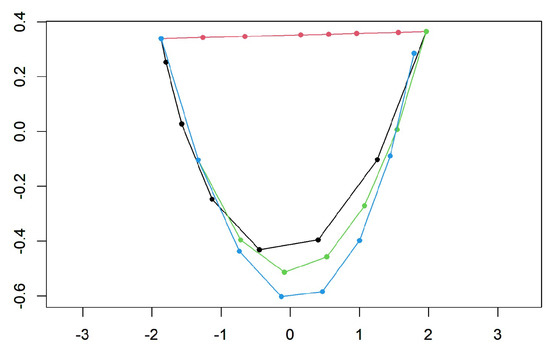
Figure 9.
PC1-PC2 scatterplot of the PCA perfomed on the four set of shapes resulting from the pure bending case. PC1 explains 91.11% of total variance, while PC2 explains 6.50%. Black refers to the optimized shapes, red to the linearized, green to the original shapes and cyan to the shooted shapes.

Table 3.
Values of the energies for the non-affine case of bending: represents the affine component of the -energy, the non-affine component, and the total -energy.
5.5. Non-Affine Case: Bending and Scaling
A parametric trajectory of eight configurations is generated by applying (54) to the initial rectangular shape by selecting eight values of the parameters in the following ranges:
Adding a significant size change to the previous experiment led to the results shown in Figure 10, Figure 11 and Figure 12 and Table 4. The equal spacing of the -energy of the optimized geodesics is rather acceptable, while its behaviour in the PCA space behaves more coherently than that of the parametrized or shooted shapes.
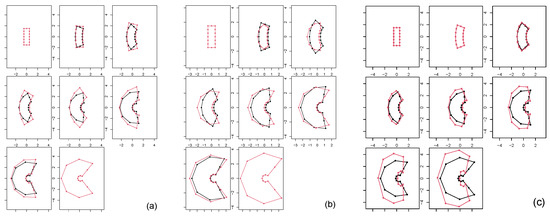
Figure 10.
Non-affine case bending+size results. (a) Left panel: geodesic trajectory shapes (black) plotted against the original parametric shapes (red). (b) Center panel: geodesic trajectory shapes (black) plotted against the shapes found via linear interpolation between the first and last shapes of the parametric dataset (red). (c) Right panel: geodesic trajectory shapes (black) plotted against autoparallel trajectory (red) built via shooting of the first two configurations of the geodesic.

Figure 11.
Trend of the energies for different interpolations: (a) Left: linear interpolation (b) Center: geodesics interpolation. (c) Right: autoparallel interpolation. Blue refers to , red to , grey to .
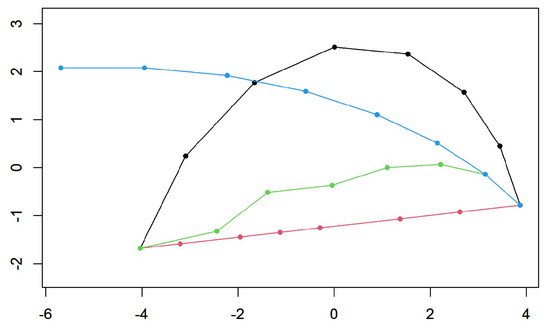
Figure 12.
PC1-PC2 scatterplot of the PCA perfomed on the four set of shapes resulting from the bending+size case. PC1 explains 79.36% of total variance, while PC2 explains 17.54%. Black refers to the optimized shapes, red to the linearized, green to the original shapes and cyan to the shooted shapes.

Table 4.
Values of the energies for the non-affine case of bending and scaling; represents the affine component of the -energy, the non-affine component, and the total -energy.
5.6. Non-Affine Case: Bending and General Affine Component
A parametric trajectory of eight configurations is generated by applying (54) to the initial rectangular shape by selecting eight values of the parameters in the following ranges:
The last experiment is represented by a combination of non-affine and affine components. Results relative to this deformation are shown in Figure 13, Figure 14 and Figure 15 and Table 5. Optimized geodesics struggle to find proper shape at fourth and fifth step of the deformation series; in the end, however, the final series results behave consistently in terms of both equal gamma energy spacing and general morphology.
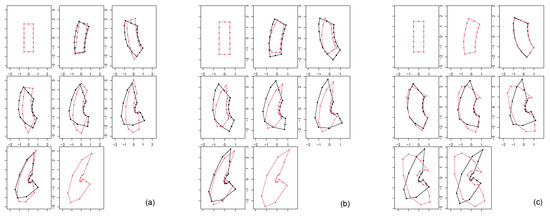
Figure 13.
Non-affine case, bending+general affine component, results. (a) Left panel: geodesic trajectory shapes (black) plotted against the original parametric shapes (red). (b) Center panel: geodesic trajectory shapes (black) plotted against the shapes found via linear interpolation between the first and last shapes of the parametric dataset (red). (c) Right panel: geodesic trajectory shapes (black) plotted against autoparallel trajectory (red) built via shooting of the first two configurations of the geodesic.

Figure 14.
Trend of the energies for different interpolations: (a) Left: linear interpolation (b) Center: geodesics interpolation. (c) Right: autoparallel interpolation. Blue refers to , red to , grey to .
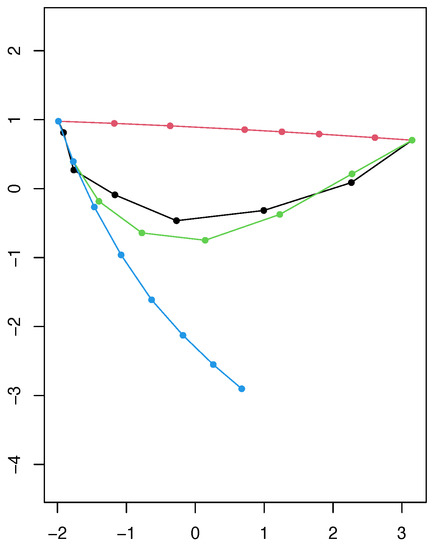
Figure 15.
PC1-PC2 scatterplot of the PCA perfomed on the four set of shapes resulting from the bending+general affine component case. PC1 explains 62.61% of total variance, while PC2 explains 25.48%. Black refers to the optimized shapes, red to the linearized, green to the original shapes and cyan to the shooted shapes.

Table 5.
Values of the energies for the non-affine case of bending and general affine deformation; represents the affine component of the -energy, the non-affine component, and the total -energy.
6. Discussion
The set of performed numerical analyses, together with the analytical results of Section 4.1, showed that: The TPS geodesics are able to catch important qualitative behaviours of the parametric deformations. In particular, in each example the horizontal sides of the initial rectangle remain straight for the whole path while the vertical sides bends, exactly as happens in the parametric path. For affine deformations, TPS geodesics coincide with TPS autoparallel lines and both coincide with the LC geodesics of the group GL(m). For non-affine deformations TPS geodesics and TPS autoparallel lines do not coincide. In particular, the autoparallel lines are not very similar, expecially in the last steps, to the parametric path. This was expected for the procedure of shooting used here. On the other hand, certain qualitative behaviours are lost, as was expected. TPS Autoparallel lines conserve the percentage of affine and non-affine energies, while this does not happen in optimized geodesic. Future directions of the present work will involve the use of 3D data. This will certainly depend on the possibility of its being independent of the body-bending energy matrix computation. Three-dimensional data offer many practical applications, spanning a wide range of scientific disciplines such as cardiology [11,12], vertebrate paleontology [21,22], and paleoanthropology.
Author Contributions
Conceptualization, V.V., P.P. and I.D.; software, P.P., F.M., S.G., S.S.; original draft preparation, V.V., P.P.; writing, review and editing, V.V. and P.P. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Data Availability Statement
Samples of the compounds are available from the authors.
Conflicts of Interest
The authors declare no conflict of interest.
Abbreviations
The following abbreviations are used in this manuscript:
| TPS | Thin Plate Spline |
| PT | Parallel Transport |
| DT | Direct Transport |
References
- Kim, K.R.; Dryden, I.; Le, H.; Severn, K. Smoothing splines on Riemannian manifolds, with applications to 3D shape space. J. R. Stat. Society. Ser. B Stat. Methodol. 2021, 83, 108–132. [Google Scholar] [CrossRef]
- Huckemann, S.; Hotz, T.; Munk, A. Intrinsic MANOVA for Riemannian manifolds with an application to Kendall’s space of planar shapes. IEEE Trans. Pattern Anal. Mach. Intell. 2010, 32, 593–603. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Trouvé, A. Diffeomorphisms groups and pattern matching in image analysis. Int. J. Comput. Vis. 1998, 28, 213–221. [Google Scholar] [CrossRef]
- Miller, M.I.; Younes, L.; Trouvé, A. Diffeomorphometry and geodesic positioning systems for human anatomy. Technology 2014, 2, 36–43. [Google Scholar] [CrossRef] [PubMed]
- Louis, M.; Charlier, B.; Jusselin, P.; Pal, S.; Durrleman, S. A fanning scheme for the parallel transport along geodesics on Riemannian manifolds. SIAM J. Numer. Anal. 2018, 56, 2563–2584. [Google Scholar] [CrossRef] [Green Version]
- Niethammer M., V.F. Riemannian metrics for statistics on shapes: Parallel transport and scale invariance. In Proceedings of the 4th MICCAI workshop on Mathematical Foundations of Computational Anatomy (MFCA), Nagoya, Japan, 22 September 2013. [Google Scholar]
- Xie, Q.; Kurtek, S.; Le, H.; Srivastava, A. Parallel transport of deformations in shape space of elastic surfaces. In Proceedings of the IEEE International Conference on Computer Vision, Sydney, NSW, Australia, 1–8 December 2013; pp. 865–872. [Google Scholar]
- Le, H. Unrolling shape curves. J. Lond. Math. Soc. 2003, 68, 511–526. [Google Scholar] [CrossRef]
- Louis, M.; Bône, A.; Charlier, B.; Durrleman, S.; The Alzheimer’s Disease Neuroimaging Initiative. Parallel transport in shape analysis: A scalable numerical scheme. In International Conference on Geometric Science of Information; Springer: Berlin, Germany, 2017; pp. 29–37. [Google Scholar]
- Marsland, S.; Twining, C. Data analysis in Weitzenbock space. In Proceedings of the 2017 International Joint Conference on Neural Networks (IJCNN), Anchorage, AK, USA, 14–19 May 2017; pp. 340–347. [Google Scholar]
- Varano, V.; Gabriele, S.; Teresi, L.; Dryden, I.; Puddu, P.; Torromeo, C.; Piras, P. The TPS Direct Transport: A new method for transporting deformations in the Size-and-shape Space. Int. J. Comput. Vis. 2017, 124, 384–408. [Google Scholar] [CrossRef]
- Varano, V.; Piras, P.; Gabriele, S.; Teresi, L.; Nardinocchi, P.; Dryden, I.; Torromeo, C.; Puddu, P. The decomposition of deformation: New metrics to enhance shape analysis in medical imaging. Med Image Anal. 2018, 46, 35–56. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Varano, V.; Piras, P.; Gabriele, S.; Teresi, L.; Nardinocchi, P.; Dryden, I.; Torromeo, C.; Schiariti, M.; Puddu, P. Local and global energies for shape analysis in medical imaging. Int. J. Numer. Methods Biomed. Eng. 2020, 36, e3252. [Google Scholar] [CrossRef] [PubMed]
- Piras, P.; Varano, V.; Louis, M.; Profico, A.; Durrleman, S.; Charlier, B.; Milicchio, F.; Teresi, L. Transporting Deformations of Face Emotions in the Shape Spaces: A Comparison of Different Approaches. J. Math. Imaging Vis. 2021, 63, 875–893. [Google Scholar] [CrossRef]
- Agricola, I.; Friedrich, T. A note on flat metric connections with antisymmetric torsion. Differ. Geom. Appl. 2010, 28, 480–487, cited By 18. [Google Scholar] [CrossRef] [Green Version]
- Kobayashi, S. 2: [Foundations of Differential Geometry]/Shoshichi Kobayashi and Katsumi Nomizu; Interscience Publishers: New York, NY, USA, 1969. [Google Scholar]
- Bookstein, F.L. Principal warps: Thin-plate splines and the decomposition of deformations. IEEE Trans. Pattern Anal. Mach. Intell. 1989, 11, 567–585. [Google Scholar] [CrossRef] [Green Version]
- Younes, L. Shapes and Diffeomorphisms; Springer: Berlin/Heidelberg, Germany, 2010; Volume 171. [Google Scholar]
- Guigui, N.; Pennec, X. A Reduced Parallel Transport Equation on Lie Groups with a Left-Invariant Metric. In Proceedings of the International Conference on Geometric Science of Information, Paris, France, 21–23 July 2021; pp. 119–126. [Google Scholar]
- Ghalanos, A.; Theussl, S. Rsolnp: General Non-linear Optimization Using Augmented Lagrange Multiplier Method; R Package Version 1.16; 2015. Available online: https://cran.r-project.org/web/packages/Rsolnp/Rsolnp.pdf (accessed on 15 March 2021).
- Piras, P.; Sansalone, G.; Teresi, L.; Moscato, M.; Profico, A.; Eng, R.; Cox, T.; Loy, A.; Colange, l.P.; Kotsakis, T. Digging adaptation in insectivorous subterranean eutherians. The enigma of Mesoscalops montanensis unveiled by geometric morphometrics and finite element analysis. J. Morphol. 2015, 276, 1157–1171. [Google Scholar] [CrossRef] [PubMed]
- Piras, P.; Marcolini, F.; Raia, P.; Curcio, M.; Kotsakis, T. Testing evolutionary stasis and trends in first lower molar shape of extinct Italian populations of Terricola savii (Arvicolidae, Rodentia) by means of geometric morphometrics. J. Evol. Biol. 2009, 22, 179–191. [Google Scholar] [CrossRef] [PubMed]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).