A High–Order WENO Scheme Based on Different Numerical Fluxes for the Savage–Hutter Equations
Abstract
1. Introduction
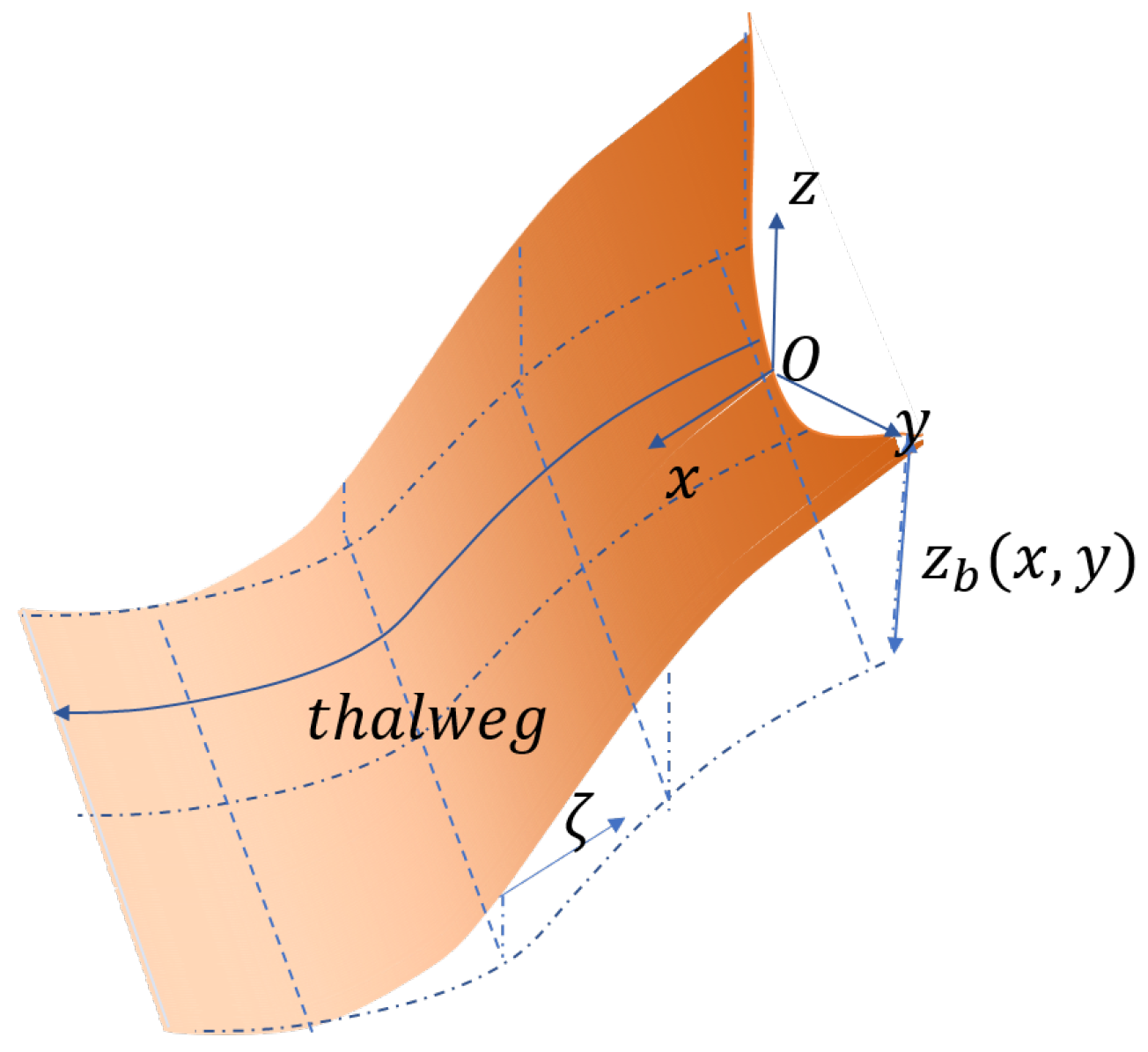
2. Governing Equations
3. Numerical Method
3.1. The Lax–Friedrichs Flux
3.2. The Harten–Lax–Van Leer Flux
3.3. The HLLC Flux
3.4. Review of WENO Reconstruction
3.5. Time Discretization and Time Stepping
3.6. Some Special Treatment
4. Numerical Examples
4.1. Traveling Shock Wave
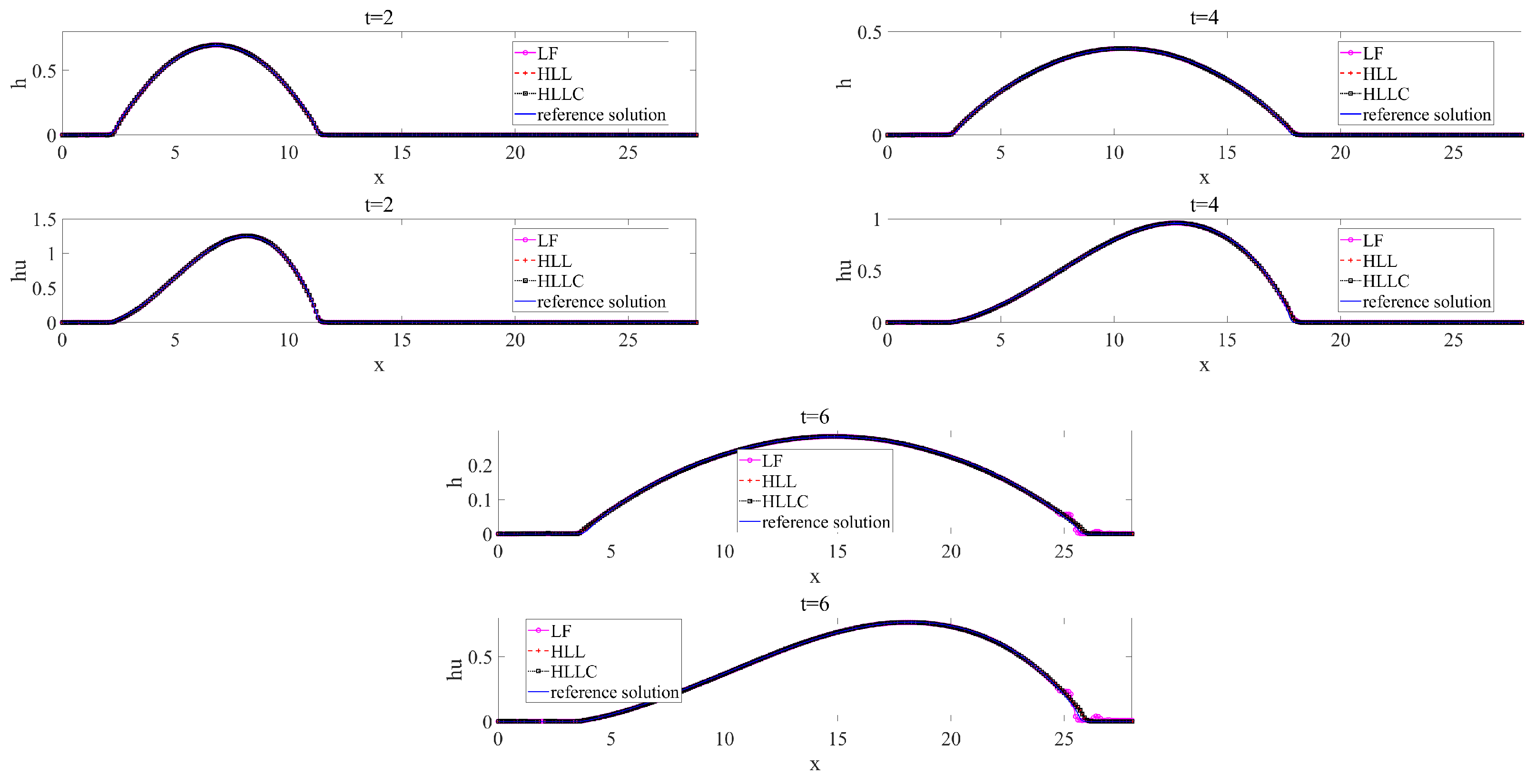
4.2. Parabolic Initial Solution
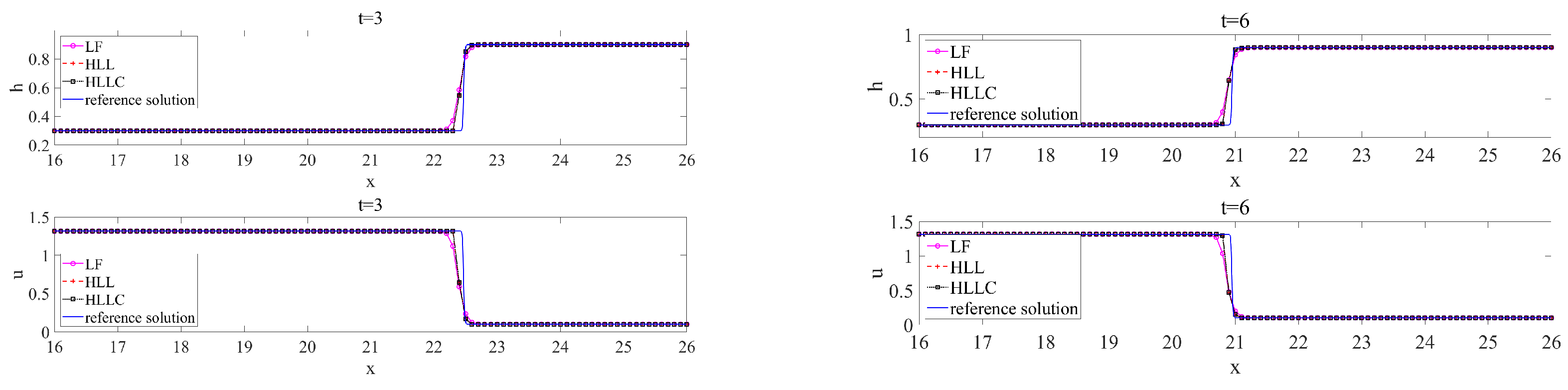
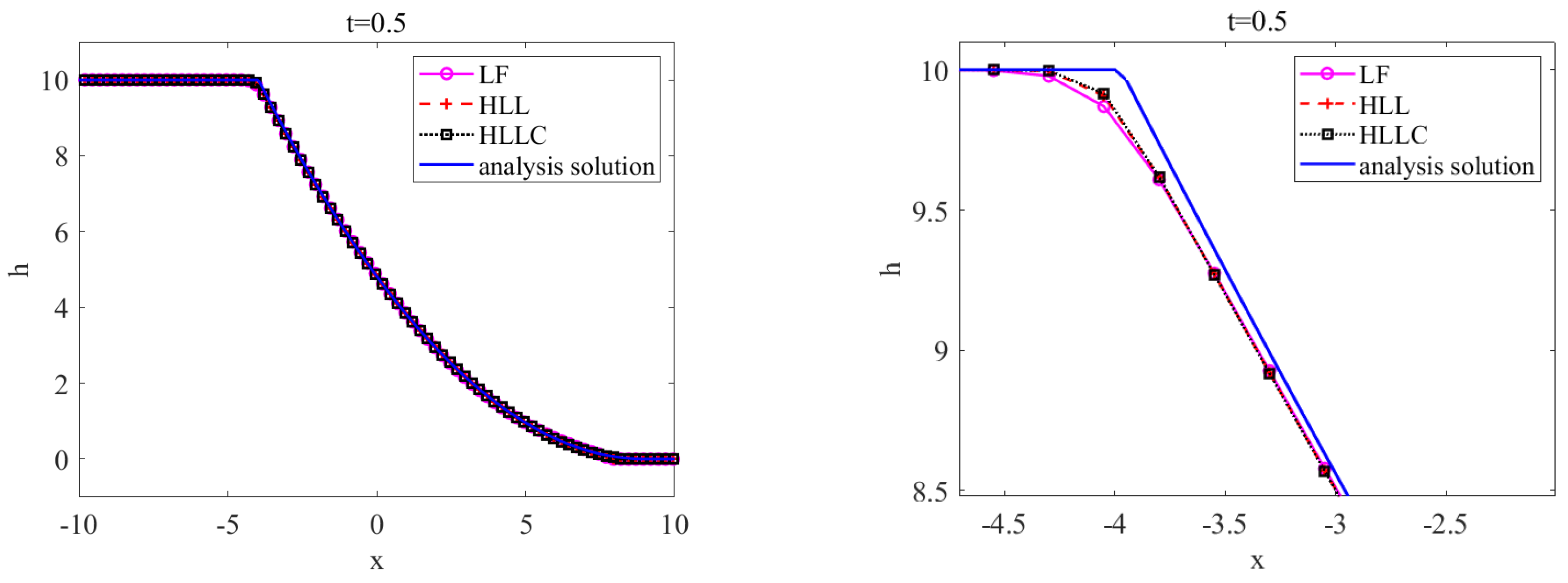
4.3. Dam Break with Exact Solution for 1D
4.4. Dam Break with Exact Solution for 2D
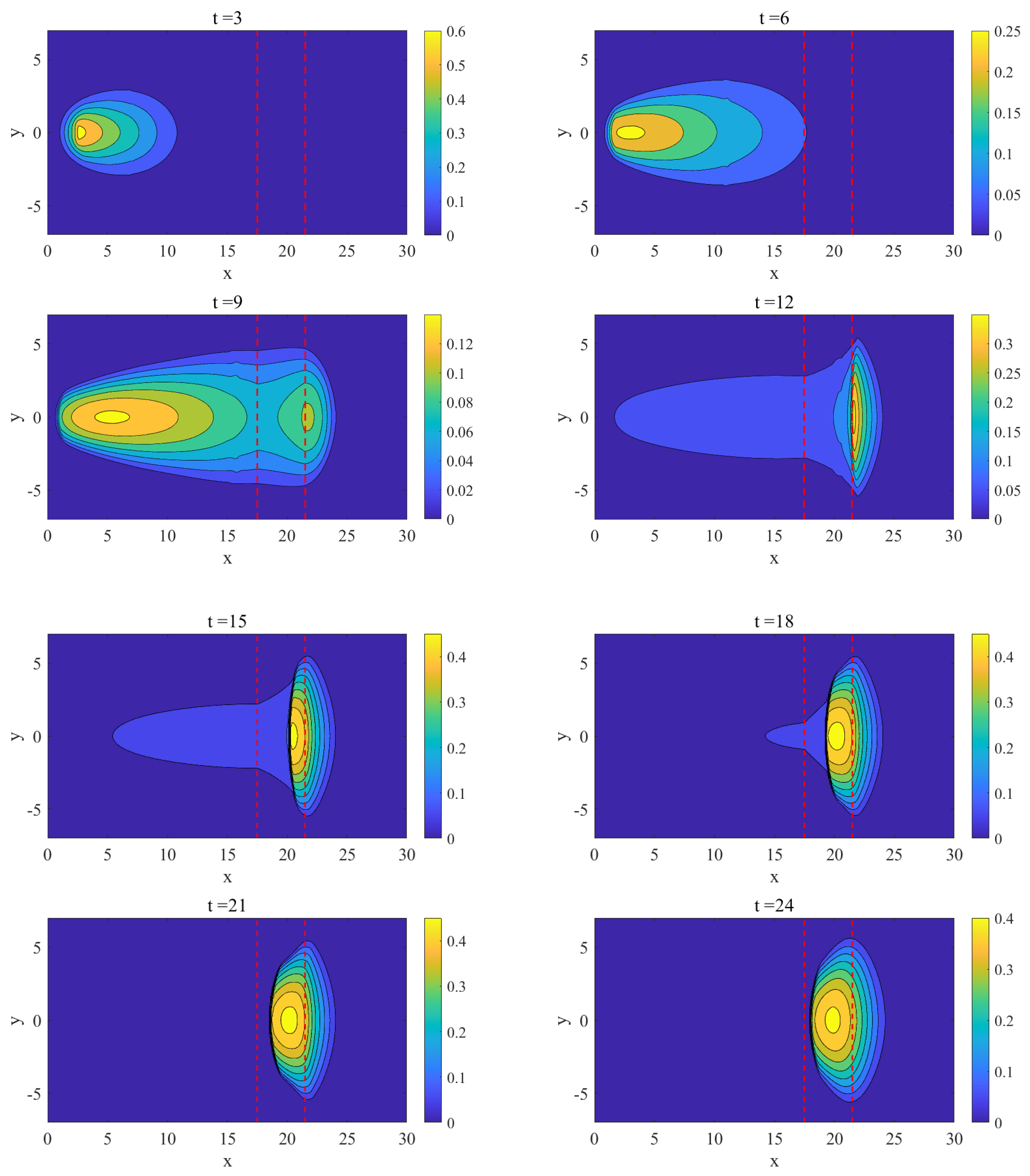
4.5. Avalanche Flows Slide down an Inclined Plane and Merge Continuously into a Horizontal Plane
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Savage, S.B.; Hutter, K. The motion of a finite mass of granular material down a rough incline. J. Fluid Mech. 1989, 199, 177–215. [Google Scholar] [CrossRef]
- Gray, J.M.; Tai, Y.C.; Noelle, S. Shock waves, dead zones and particle-free regions in rapid granular free-surface flows. J. Fluid Mech. 2003, 491, 161–181. [Google Scholar] [CrossRef]
- Hutter, K.; Wang, Y.; Pudasaini, S.P. The Savage–Hutter avalanche model: How far can it be pushed? Philos. Trans. R. Soc. Math. Phys. Eng. Sci. 2005, 363, 1507–1528. [Google Scholar] [CrossRef] [PubMed]
- Hutter, K.; Siegel, M.; Savage, S.B.; Nohguchi, Y. Two-dimensional spreading of a granular avalanche down an inclined plane Part I. theory. Acta Mech. 1993, 100, 37–68. [Google Scholar] [CrossRef]
- Greve, R.; Koch, T.; Hutter, K. Unconfined flow of granular avalanches along a partly curved surface. I. Theory. Proc. R. Soc. Lond. Ser. Math. Phys. Sci. 1994, 445, 399–413. [Google Scholar]
- Gray, J.M.; Wieland, M.; Hutter, K. Gravity-driven free surface flow of granular avalanches over complex basal topography. Proc. R. Soc. Lond. Ser. Math. Phys. Eng. Sci. 1999, 455, 1841–1874. [Google Scholar] [CrossRef]
- Paik, J. A high resolution finite volume model for 1D debris flow. J. Hydro-Environ. Res. 2015, 9, 145–155. [Google Scholar] [CrossRef]
- Pudasaini, S.P.; Hutter, K. Avalanche Dynamics: Dynamics of Rapid Flows of Dense Granular Avalanches; Springer Science & Business Media: Berlin/Heidelberg, Germany, 2007. [Google Scholar]
- Gray, J.M. Granular flow in partially filled slowly rotating drums. J. Fluid Mech. 2001, 441, 1–29. [Google Scholar] [CrossRef]
- Iverson, R.M. The physics of debris flows. Rev. Geophys. 1997, 35, 245–296. [Google Scholar] [CrossRef]
- Iverson, R.M.; Denlinger, R.P. Flow of variably fluidized granular masses across three-dimensional terrian: 1. Coulomb mixture theory. J. Geophys. Res. Solid Earth 2001, 106, 537–552. [Google Scholar] [CrossRef]
- Pitman, E.B.; Long, L.E. A two-fluid model for avalanche and debris flows. Philos. Trans. R. Soc. Math. Phys. Eng. Sci. 2005, 363, 1573–1601. [Google Scholar] [CrossRef]
- Koch, T.; Greve, R.; Hutter, K. Unconfined flow of granular avalanches along a partly curved surface. II. Experiments and numerical computations. Proc. R. Soc. Lond. Ser. Math. Phys. Sci. 1994, 445, 415–435. [Google Scholar]
- Denlinger, R.P.; Iverson, R.M. Flow of variably fluidized granular masses across three-dimensional terrain: 2. Numerical predictions and experimental tests. J. Geophys. Res. Solid Earth 2001, 106, 553–566. [Google Scholar] [CrossRef]
- Wang, Y.; Hutter, K.; Pudasaini, S. The Savage–Hutter theory: A system of partial differential equations for avalanche flows of snow, debris, and mud. Zamm-J. Appl. Math. Mech. FüR Angew. Math. Und Mech. Appl. Math. Mech. 2004, 84, 507–527. [Google Scholar] [CrossRef]
- Chiou, M.C.; Wang, Y.; Hutter, K. Influence of obstacles on rapid granular flows. Acta Mech. 2005, 175, 105–122. [Google Scholar] [CrossRef]
- Cui, X. Computational and experimental studies of rapid free-surface granular flows around obstacles. Comput. Fluids 2014, 89, 179–190. [Google Scholar] [CrossRef]
- Zhai, J.; Yuan, L.; Liu, W.; Zhang, X. Solving the Savage–Hutter equations for granular avalanche flows with a second-order Godunov type method on GPU. Int. J. Numer. Methods Fluids 2015, 77, 381–399. [Google Scholar] [CrossRef]
- Vollmöller, P. A shock-capturing wave-propagation method for dry and saturated granular flows. J. Comput. Phys. 2004, 199, 150–174. [Google Scholar] [CrossRef]
- Rosatti, G.; Begnudelli, L. Two-dimensional simulation of debris flows over mobile bed: Enhancing the TRENT2D model by using a well-balanced Generalized Roe-type solver. Comput. Fluids 2013, 71, 179–195. [Google Scholar] [CrossRef]
- Tai, Y.C.; Noelle, S.; Gray, J.M.N.; Hutter, K. An accurate shock-capturing finite-difference method to solve the Savage–Hutter equations in avalanche dynamics. Ann. Glaciol. 2001, 32, 263–267. [Google Scholar] [CrossRef][Green Version]
- Tai, Y.C.; Noelle, S.; Gray, J.M.; Hutter, K. Shock-capturing and front-tracking methods for granular avalanches. J. Comput. Phys. 2002, 175, 269–301. [Google Scholar] [CrossRef]
- Yavari-Ramshe, S.; Ataie-Ashtiani, B.; Sanders, B.F. A robust finite volume model to simulate granular flows. Comput. Geotech. 2015, 66, 96–112. [Google Scholar] [CrossRef]
- Lu, C.; Qiu, J.; Wang, R. A numerical study for the performance of the WENO schemes based on different numerical fluxes for the shallow water equations. J. Comput. Math. 2010, 28, 807–825. [Google Scholar] [CrossRef]
- Musa, O.; Huang, G.; Wang, M. A New Smoothness Indicator of Adaptive Order Weighted Essentially Non-Oscillatory Scheme for Hyperbolic Conservation Laws. Mathematics 2020, 9, 69. [Google Scholar] [CrossRef]
- Shu, C.W. Essentially non-oscillatory and weighted essentially non-oscillatory schemes for hyperbolic conservation laws. In Advanced Numerical Approximation of Nonlinear Hyperbolic Equations; Springer: New York, NY, USA, 1998; pp. 325–432. [Google Scholar]
- Shu, C.W. High order weighted essentially nonoscillatory schemes for convection dominated problems. Siam Rev. 2009, 51, 82–126. [Google Scholar] [CrossRef]
- Shu, C.W. High-order finite difference and finite volume WENO schemes and discontinuous galerkin methods for CFD. Int. J. Comput. Fluid Dyn. 2003, 17, 107–118. [Google Scholar] [CrossRef]
- Dumbser, M.; Käser, M. Arbitrary high order non-oscillatory finite volume schemes on unstructured meshes for linear hyperbolic systems. J. Comput. Phys. 2007, 221, 693–723. [Google Scholar] [CrossRef]
- Cooley, K.; Baeder, J. A central compact-reconstruction WENO method for hyperbolic conservation laws. In Proceedings of the AIAA Aerospace Sciences Meeting, Kissimmee, FL, USA, 8–12 January 2018. [Google Scholar] [CrossRef]
- Guerrero Fernández, E.; Escalante, C.; Castro Díaz, M.J. Well-Balanced High-Order Discontinuous Galerkin Methods for Systems of Balance Laws. Mathematics 2021, 10, 15. [Google Scholar] [CrossRef]
- Li, R.; Zhang, X. A Finite Volume Scheme for Savage–Hutter Equations on Unstructured Grids. Numer. Math. Theory Methods Appl. 2020, 13, 479–496. [Google Scholar]
- Toro, E.F. Riemann Solvers and Numerical Methods for Fluid Dynamics, 3rd ed.; Springer: Berlin/Heidelberg, Germany, 2009; pp. 1–749. [Google Scholar]
- Toro, E.F. Shock-Capturing Methods for Free-Surface Shallow Flows; Wiley-Blackwell: Hoboken, NJ, USA, 2001. [Google Scholar]
- Savage, S.B.; Hutter, K. The dynamics of avalanches of granular materials from initiation to runout. Part I: Analysis. Acta Mech. 1991, 86, 201–223. [Google Scholar] [CrossRef]
- Fraccarollo, L.; Capart, H.; Zech, Y. A Godunov method for the computation of erosional shallow water transients. Int. J. Numer. Methods Fluids 2003, 41, 951–976. [Google Scholar] [CrossRef]
- Hesthaven, J.S. Numerical Methods for Conservation Laws: From Analysis to Algorithms; SIAM: Philadelphia, PA, USA, 2018. [Google Scholar]
- Juez, C.; Murillo, J.; García-Navarro, P. 2D simulation of granular flow over irregular steep slopes using global and local coordinates. J. Comput. Phys. 2013, 255, 166–204. [Google Scholar] [CrossRef]
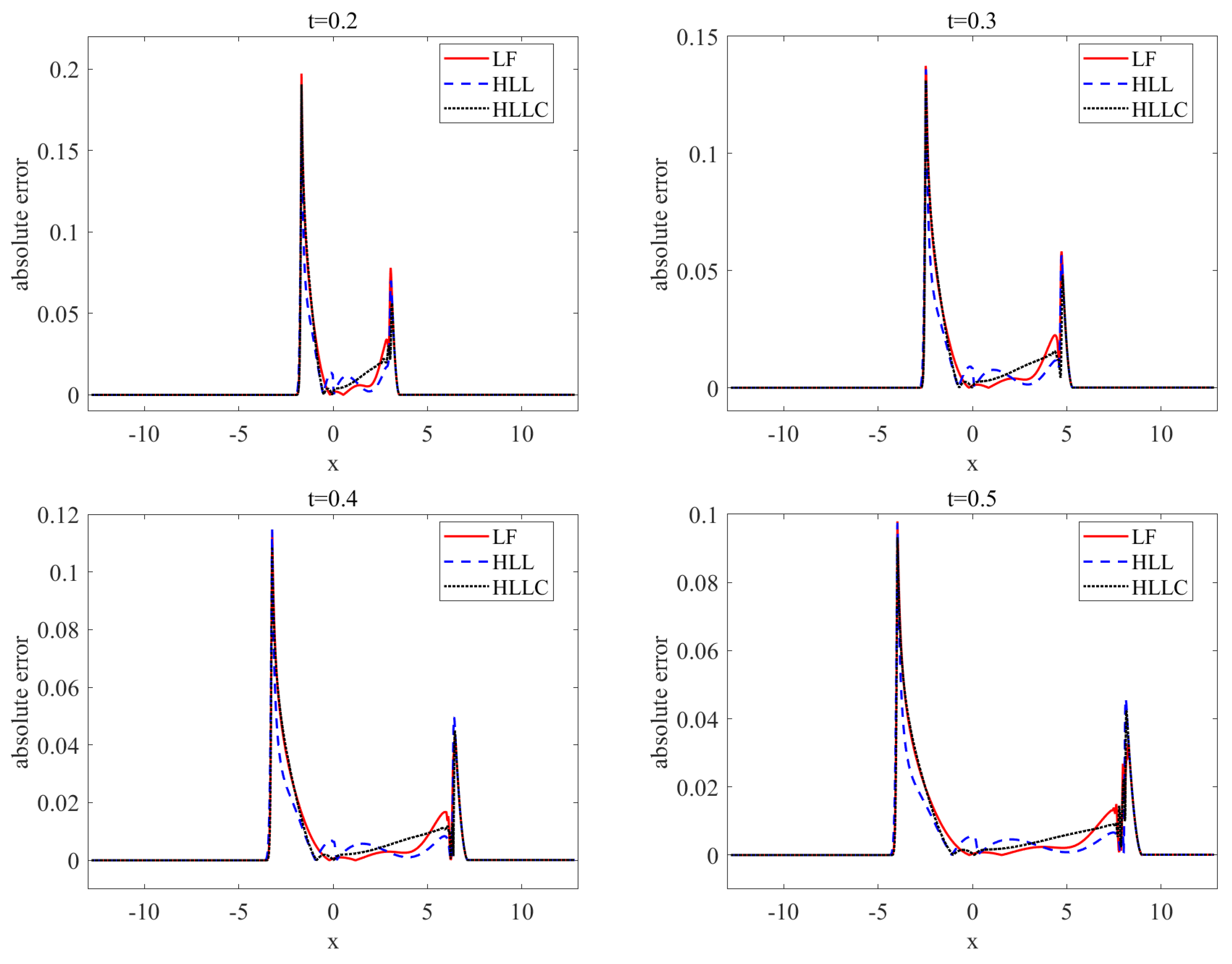
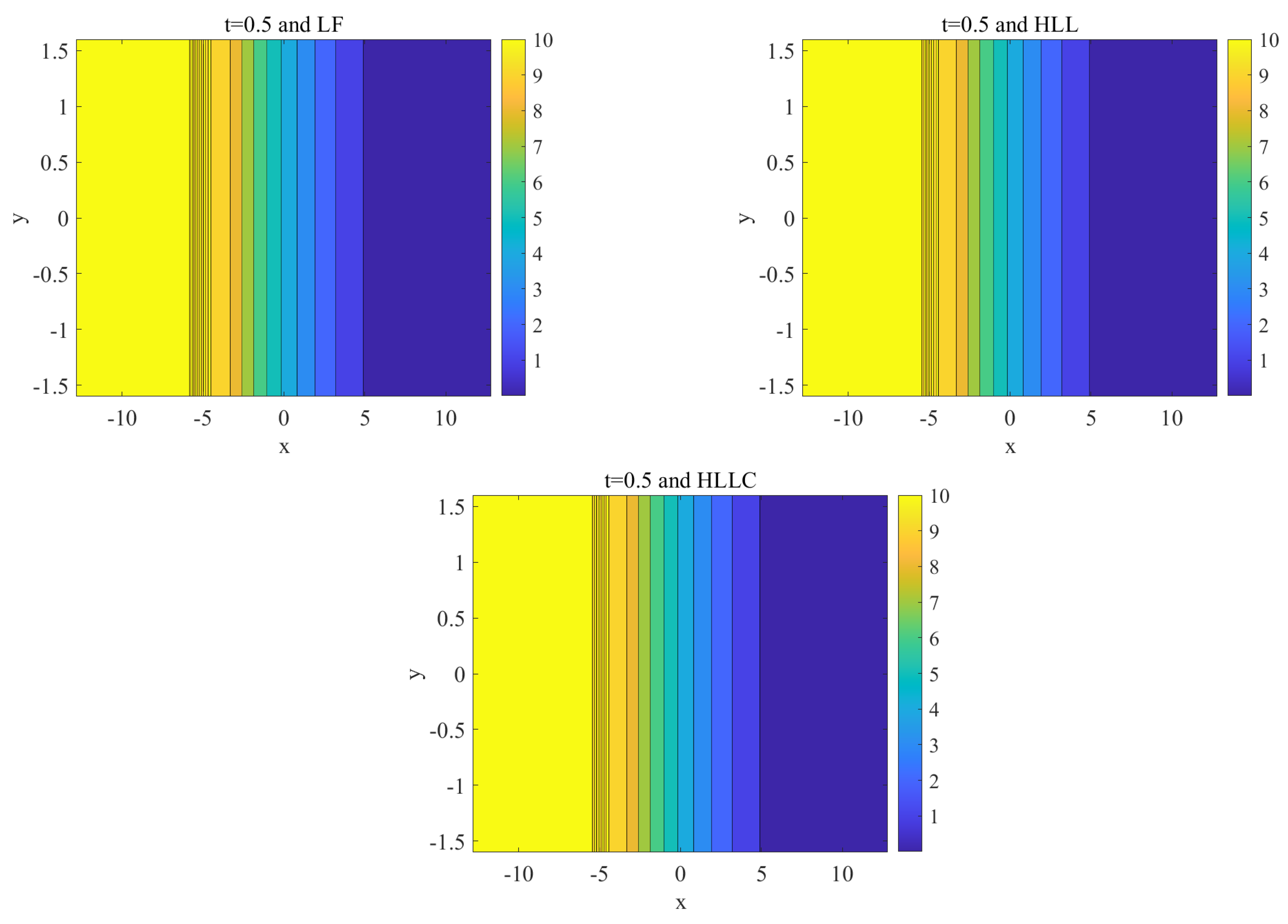



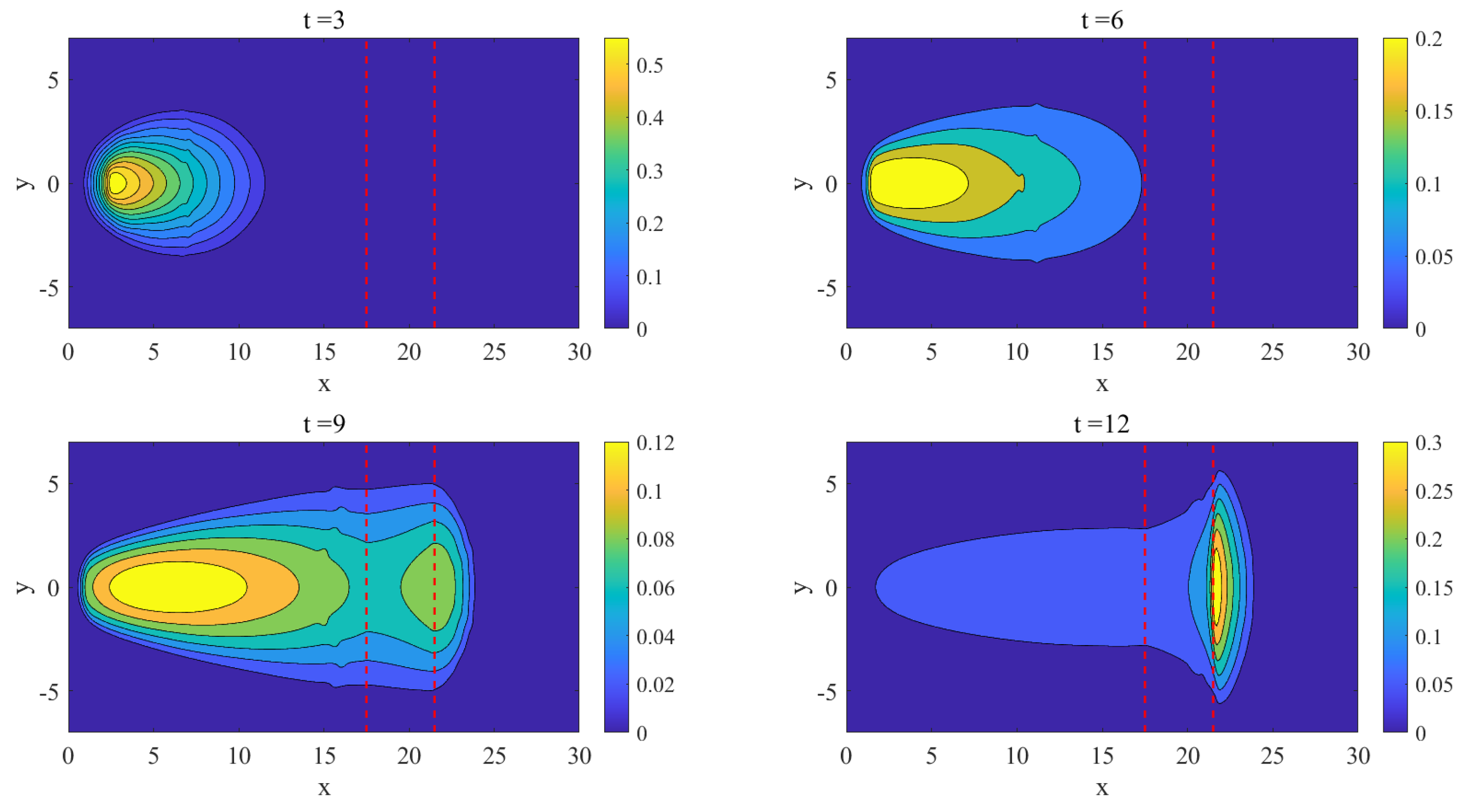
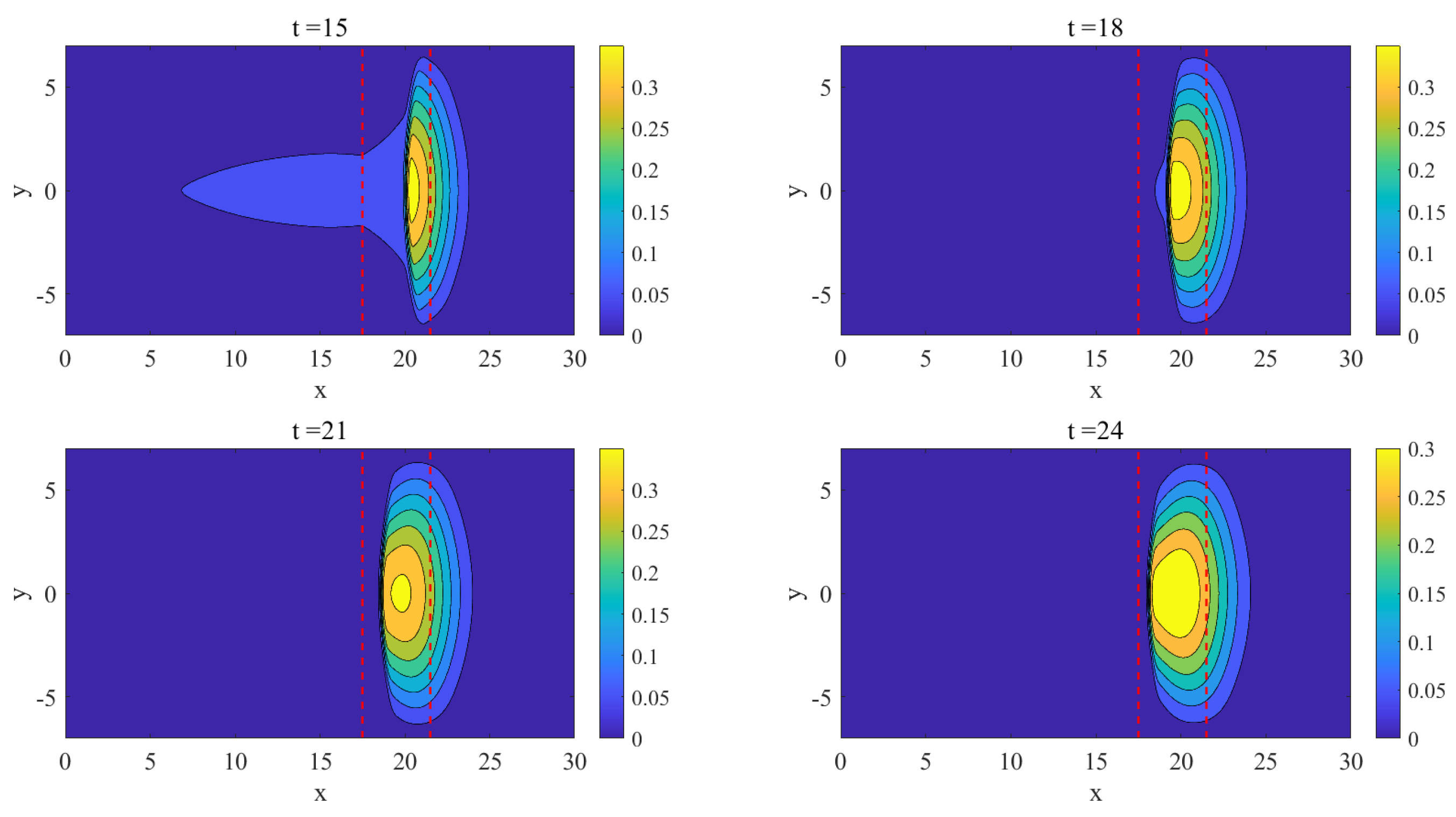

| N | WENO-LF | WENO-HLL | WENO-HLLC | |||
|---|---|---|---|---|---|---|
| Error | Order | Error | Order | Error | Order | |
| 180 | - | - | - | |||
| 360 | 2.8658 | 2.9635 | 3.0356 | |||
| 720 | 2.98 | 2.9486 | 3.0531 | |||
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, M.; Zhang, X. A High–Order WENO Scheme Based on Different Numerical Fluxes for the Savage–Hutter Equations. Mathematics 2022, 10, 1482. https://doi.org/10.3390/math10091482
Wang M, Zhang X. A High–Order WENO Scheme Based on Different Numerical Fluxes for the Savage–Hutter Equations. Mathematics. 2022; 10(9):1482. https://doi.org/10.3390/math10091482
Chicago/Turabian StyleWang, Min, and Xiaohua Zhang. 2022. "A High–Order WENO Scheme Based on Different Numerical Fluxes for the Savage–Hutter Equations" Mathematics 10, no. 9: 1482. https://doi.org/10.3390/math10091482
APA StyleWang, M., & Zhang, X. (2022). A High–Order WENO Scheme Based on Different Numerical Fluxes for the Savage–Hutter Equations. Mathematics, 10(9), 1482. https://doi.org/10.3390/math10091482






