Enhanced Unconditionally Positive Finite Difference Method for Advection–Diffusion–Reaction Equations

Abstract

In this study, we develop the enhanced unconditionally positive finite difference method (EUPFD), and use it to solve linear and nonlinear advection–diffusion–reaction (ADR) equations. This method incorporates the proper orthogonal decomposition technique to the unconditionally positive finite difference method (UPFD) to reduce the degree of freedom of the ADR equations. We investigate the efficiency and effectiveness of the proposed method by checking the error, convergence rate, and computational time that the method takes to converge to the exact solution. Solutions obtained by the EUPFD were compared with the exact solutions for validation purposes. The agreement between the solutions means the proposed method effectively solved the ADR equations. The numerical results show that the proposed method greatly improves computational efficiency without a significant loss in accuracy for solving linear and nonlinear ADR equations.

1. Introduction

Many problems in science and engineering are modeled by partial differential equations that are often difficult to solve for an exact solution and, in some cases, impossible. Numerical methods are a good alternative in providing approximate solutions close to the exact solution. As a result, several accurate numerical methods, such as the Crank–Nicolson [1], finite element [2], finite volume [3], spectral [4], and nonstandard finite difference [5,6] methods were developed. Developing better numerical methods continues to stimulate much interest among researchers. Motivated by the continued need for better-performing numerical methods, in this work, we propose a novel hybrid method that is based on combining elements of the unconditionally positive finite difference method (UPFD) and the proper orthogonal decomposition method (POD), called the enhanced unconditionally positive finite difference method (EUPFD).

The UPFD was developed by Chen-Charpentier and Kojouharov [7] for the advection–diffusion–reaction equation (ADR), and has since been used by several other researchers [8,9,10]. It is a finite difference-based method that guarantees the positivity of solutions independent of time step and mesh size. Numerical schemes that preserve the positivity of solutions are important in physical applications. To have significant meaning, quantities such as chemical species concentration, population sizes, and neutron numbers require positive solutions. On the other hand, the POD is a powerful technique widely used in statistics and image processing [11,12] to reduce a large number of interdependent variables to a much smaller number of uncorrelated variables while retaining as much possible of the variation in the original variables. By utilizing the POD, the EUPFD involves the extraction of a set of basis functions from the UPFD solution called the snapshot matrix; then, it uses a small subset of leading basis functions to construct state variable approximations. One of the most persistent challenges faced by several numerical methods when solving PDEs is that they require many grid points and numerous iterations to converge to the exact solution. That significantly affects their efficiency in terms of computational speed and memory requirement. The POD has been used to reduce the dimensions of numerical methods, such as the Crank–Nicolson method [13,14,15,16,17,18]. The POD is useful when it is impossible to perform numerical simulations due to large-scale computing requirements.

The POD modes are updated until the EUPFD satisfies the theoretical accuracy requirements. Luo and Sun [19] combined the POD with the finite volume, the finite element, and the finite difference methods to solve Navier–Stokes, Sobolev, Burger’s, and hyperbolic equations. In this work, we extend the POD coupling by hybridising it with the UPFD to obtain a novel numerical method that exhibits higher accuracy with less computing time, fewer degrees of freedom in numerical computations, and reduced truncation error, ensuring the positivity of the solutions.

We test the applicability of the EUPFD on the nonlinear ADR equations given below:

$$\begin{array}{cc}\hfill & {\displaystyle \frac{\partial u}{\partial t}}+U_a{\displaystyle \frac{\partial u}{\partial x}}-D{\displaystyle \frac{{\partial }^{2}u}{\partial x^2}}=f(t,x,u),(x,t)\in [a,b]\times [0,T]t>0.x\in \partial \mathsf{\Omega }\hfill \\ \hfill & u(0,x)=u_0\left(x\right)\ge 0,\hfill \\ \hfill & u(a,t)=u_a\left(t\right)u(b,t)=u_b\left(t\right).\hfill \end{array}$$

(1)

where $U_a$ is the advection coefficient, D is the diffusion coefficient, $u_t(t,x)$ is the rate at which the concentration of substances changes over time, $u_x(t,x)$ is the advection term, $u_{xx}(t,x)$ is the diffusion term, and $f(t,x,u)$ is the reaction term or the source [20]. The ADR equation governs the process of advection and diffusion simultaneously. It is used to model exponential travelling waves, absorption of pollutants in soil, semiconductors, modelling of biological systems, and diffusion of neutrons [21,22,23,24]. Among other numerical methods, the UPFD method has been used to solve ADR equations, is stable, accurate, and consistent in rectangular domains, and it guarantees the positivity of the solution that is independent of the step sizes [25]. The Rosenbrock scheme is another interesting approach that preserves solution accuracy and is mostly used to solve stiff ODEs problems. Al’shin, Al’shina, Kalitkin, and Koryagina [26] proposed the complex Rosenbrock schemes for the numerical integration of differential algebraic systems by the $\epsilon$-embedding method. The method converges quadratically, and the scheme applies even to superstiff systems. The method enables computations to be performed with guaranteed accuracy. However, as always, numerical methods need to be refined and improved to converge faster to the exact solution.

The rest of the paper is organised as follows. In Section 2, we present the UPFD method, and illustrate how it is used to solve linear and nonlinear ADR equations. We also provide the stability and consistency analysis of the UPFD scheme. In Section 3, we formulate the POD basis to optimise the UPFD scheme and this results in the EUPFD method. In Section 4, numerical results are presented to illustrate the efficiency and effectiveness of the EUPFD method to solve the discussed problems. Section 5 provides the conclusion of the study.

2. Unconditionally Positive Finite Difference Method

In this section, we present details of the unconditionally positive finite difference method (UPFD), and illustrate how it is utilized to solve linear and nonlinear ADR equations.

The discretization of the linear and nonlinear ADR equation is obtained by using the derivative schemes given below to obtain the UPFD schemes [7],

$$\begin{array}{cc}\hfill {\displaystyle \frac{\partial u}{\partial x}}& \approx {\displaystyle \frac{u_i^n-u_{i-1}^{n+1}}{\Delta x}}\hfill \end{array}$$

(2)

$$\begin{array}{cc}\hfill {\displaystyle \frac{\partial u}{\partial x}}& \approx {\displaystyle \frac{u_i^{n+1}-u_{i-1}^n}{\Delta x}}\hfill \end{array}$$

(3)

$$\begin{array}{cc}\hfill {\displaystyle \frac{\partial u}{\partial t}}& \approx {\displaystyle \frac{u_i^{n+1}-u_i^n}{\Delta t}},\hfill \end{array}$$

(4)

$$\begin{array}{cc}\hfill {\displaystyle \frac{{\partial }^{2}u}{\partial x^2}}& \approx {\displaystyle \frac{u_{i+1}^n-2u_i^{n+1}-u_{i-1}^n}{{(\Delta x)}^2}}.\hfill \end{array}$$

(5)

where the spatial step size $\Delta x={\displaystyle \frac{b-a}{m-1}}$, and the grid points are given as $x_i=a+\Delta x(i-1)$, $1\le i\le m$. Time step size $\Delta t={\displaystyle \frac{T}{N-1}}$ with the corresponding grid points are given as $t_n=\Delta t(n-1)$, $1\le n\le N$.

When approximating the first and second space derivatives, the terms in the finite difference schemes are evaluated at different time levels n and $n+1$. This is required to preserve the positivity of the solution. Equation (2) is used when the coefficient of the first space derivative is negative, while Equation (3) is used when the derivative is positive. On the other hand, Equation (5) is used whether the coefficient of the second space derivative is positive or negative.

2.1. Linear Advection–Diffusion–Reaction Equation

In this section, we set $f(t,x,u)=-u$, $U_a=1$, and $D=1$ in Equation (1) to obtain the equation given below.

$$\begin{array}{c}\hfill {\displaystyle \frac{\partial u}{\partial t}}+{\displaystyle \frac{\partial u}{\partial x}}={\displaystyle \frac{{\partial }^{2}u}{\partial x^2}}-u,\end{array}$$

(6)

subject to the following initial and boundary conditions:

$$\begin{array}{c}\hfill \left\{\begin{array}{c}u(x,0)=e^{-x}0\le x\le 6,\hfill \\ u(0,t)=e^{t}0\le t\le T,\hfill \\ u_x(6,t)=-u(6,t),\hfill \end{array}\right.\end{array}$$

(7)

with the exact solution given by $u(x,t)=e^{(t-x)}$ [7].

Since the coefficient of ${\displaystyle \frac{\partial u}{\partial x}}$ in Equation (6) is positive, we used Equation (3) to find the UPFD scheme. Therefore, the UPFD discretization of Equation (6) is given by

$$\begin{array}{c}\hfill {\displaystyle \frac{u_i^{n+1}-u_i^n}{\Delta t}}+{\displaystyle \frac{u_i^{n+1}-u_{i-1}^n}{\Delta x}}={\displaystyle \frac{u_{i+1}^n-2u_i^{n+1}+u_{i-1}^n}{{(\Delta x)}^2}}-u_i^{n+1}.\end{array}$$

(8)

Equation (8) can be written as

$$\begin{array}{c}\hfill u_i^{n+1}={\displaystyle \frac{u_i^n+(\lambda +\beta )u_{i-1}^n+\beta u_{i-1}^n}{1+\Delta t+\lambda +2\beta }}.\end{array}$$

(9)

where $\lambda ={\displaystyle \frac{\Delta t}{\Delta x}}$ and $\beta ={\displaystyle \frac{\Delta t}{{(\Delta x)}^2}}$.

2.1.1. Stability

To obtain the region of stability of the UPFD scheme, we used the Fourier series analysis of the form $u_i^n={\xi }^n{e}^{j\Delta ti\Delta x}$ on Equation (9). The amplification factor is then given by

$$\begin{array}{c}\hfill \xi ={\displaystyle \frac{1+(\lambda +2\beta )cos\omega }{1+\Delta t+\lambda +2\beta }}-I\left[{\displaystyle \frac{\lambda sin\omega }{1+\Delta t+\lambda +2\beta }}\right]\end{array}$$

(10)

where $\omega$ is the phase angle, $\omega =\theta \Delta x$ where $\theta$ is the wave number, and $\Delta t$ is the spatial step size, and $\xi ={\displaystyle \frac{{\xi }^{n+1}}{{\xi }^n}}$.

By using the $\mid \xi {\mid }^2\le 1$ in (10), where $\mid \xi \mid =\sqrt{{(\Re \left(\xi \right))}^2+{(\Im \left(\xi \right))}^2}$, the following is obtained.

$$\begin{array}{c}\hfill \mid \xi \mid =\sqrt{{\left({\displaystyle \frac{1+(\lambda +2\beta )cos\omega }{1+\Delta t+\lambda +2\beta }}\right)}^2+{\left({\displaystyle \frac{\lambda sin\omega }{1+\Delta t+\lambda +2\beta }}\right)}^2}\end{array}$$

(11)

The UPFD method presented here guarantees the positivity of the solutions independent of the time step and mesh size. The UPFD method works with terms that are the sum of a positive and negative function of the unknown, and one or both may be zero. The scheme is positive definite for all values of $\Delta t,\Delta x>0$, hence, the scheme is unconditionally stable for all $\Delta x,\Delta t>0$.

2.1.2. Consistency

In this section, we investigate the consistency of Equation (6). We use the Taylor expansion to approximate the $u_i^{n+1}$, $u_{i+1}^n$, $u_{i-1}^n$, thus

$$\begin{array}{c}\hfill u_i^{n+1}\approx u_i^n+\Delta t{\displaystyle \frac{\partial u}{\partial t}}+{\displaystyle \frac{{(\Delta t)}^2}{2}}{\displaystyle \frac{{\partial }^{2}u}{\partial t^2}}+{\displaystyle \frac{{(\Delta t)}^3}{6}}{\displaystyle \frac{{\partial }^{3}u}{\partial t^3}}+\cdots \\ \hfill u_{i-1}^n\approx u_i^n-\Delta x{\displaystyle \frac{\partial u}{\partial x}}+{\displaystyle \frac{{(\Delta x)}^2}{2}}{\displaystyle \frac{{\partial }^{2}u}{\partial x^2}}-{\displaystyle \frac{{(\Delta x)}^3}{6}}{\displaystyle \frac{{\partial }^{3}u}{\partial x^3}}+\cdots \\ \hfill u_{i+1}^n\approx u_i^n+\Delta x{\displaystyle \frac{\partial u}{\partial x}}+{\displaystyle \frac{{(\Delta x)}^2}{2}}{\displaystyle \frac{{\partial }^{2}u}{\partial x^2}}+{\displaystyle \frac{{(\Delta x)}^3}{6}}{\displaystyle \frac{{\partial }^{3}u}{\partial x^3}}+\cdots \end{array}$$

(12)

The UPFD scheme terms are approximated by using Equation (12), which are then substituted into Equation (8) to obtain the truncation error for the UPFD method. After simplification, we obtain the following.

$$\begin{array}{cc}\hfill {\displaystyle \frac{\partial u}{\partial t}}+{\displaystyle \frac{\partial u}{\partial x}}& ={\displaystyle \frac{{\partial }^{2}u}{\partial x^2}}-u-\left(\Delta t+{\displaystyle \frac{\Delta t}{\Delta x}}+{\displaystyle \frac{2\Delta t}{{(\Delta x)}^2}}\right){\displaystyle \frac{{\partial }^{2}u}{\partial t^2}}-\left({\displaystyle \frac{\Delta t}{2}}+{\displaystyle \frac{{(\Delta t)}^2}{2}}+{\displaystyle \frac{{(\Delta t)}^2}{2(\Delta x)}}+{\displaystyle \frac{{(\Delta t)}^2}{{(\Delta x)}^2}}\right){\displaystyle \frac{{\partial }^{2}u}{\partial t^2}}\hfill \\ \hfill & -\left({\displaystyle \frac{{(\Delta t)}^2}{6}}+{\displaystyle \frac{{(\Delta t)}^3}{6}}+{\displaystyle \frac{{(\Delta t)}^3}{6(\Delta x)}}+{\displaystyle \frac{{(\Delta t)}^3}{3{(\Delta x)}^2}}\right){\displaystyle \frac{{\partial }^{3}u}{\partial t^3}}+{\displaystyle \frac{\Delta x}{2}}{\displaystyle \frac{{\partial }^{2}u}{\partial x^2}}-{\displaystyle \frac{{(\Delta x)}^2}{6}}{\displaystyle \frac{{\partial }^{3}u}{\partial x^3}}+\cdots \hfill \end{array}$$

(13)

The above scheme is not consistent when $\Delta t\to 0$, $\Delta x\to 0$; as a result, $\Delta t={(\Delta x)}^3$ to obtain the following equation.

$$\begin{array}{cc}\hfill {\displaystyle \frac{\partial u}{\partial t}}+{\displaystyle \frac{\partial u}{\partial x}}& ={\displaystyle \frac{{\partial }^{2}u}{\partial x^2}}-u-\left({(\Delta x)}^3+{(\Delta x)}^2+2(\Delta x)\right){\displaystyle \frac{{\partial }^{2}u}{\partial t^2}}\hfill \\ \hfill & -{\displaystyle \frac{{(\Delta x)}^3}{2}}\left(1+{(\Delta x)}^2+2\Delta x+{(\Delta x)}^3\right){\displaystyle \frac{{\partial }^{2}u}{\partial t^2}}\hfill \\ \hfill & -{\displaystyle \frac{{(\Delta x)}^6}{6}}\left(1+{(\Delta x)}^2+2\Delta x+{(\Delta x)}^3\right){\displaystyle \frac{{\partial }^{3}u}{\partial t^3}}+{\displaystyle \frac{\Delta x}{2}}{\displaystyle \frac{{\partial }^{2}u}{\partial x^2}}-{\displaystyle \frac{{(\Delta x)}^2}{6}}{\displaystyle \frac{{\partial }^3}{\partial x^3}}+\cdots \hfill \end{array}$$

(14)

when $\Delta x⟶0$, $\Delta t⟶0$, Equation (14) reduces to Equation (6); hence, the UPFD scheme is consistent when $\Delta t={(\Delta x)}^3$.

2.2. Nonlinear Advection–Diffusion–Reaction Equation

In this section, we set $f(t,x,u)=ru(1-u)$, and $U_a=0$ in Equation (1) to obtain the nonlinear reaction diffusion equation given below.

$$\begin{array}{c}\hfill {\displaystyle \frac{\partial u}{\partial t}}-D{\displaystyle \frac{{\partial }^{2}u}{\partial x^2}}=ru(1-u)(x,t)\in [0,1]\times [0,T]\end{array}$$

(15)

with initial and boundary conditions given by

$$\begin{array}{c}\hfill u(x,0)=\left\{\begin{array}{c}0.7e^{-\sigma {(x-x_0)}^2},|x-x_0|\le 0.06\hfill \\ 0,\mathrm{otherwise}\hfill \end{array}\right.\end{array}$$

(16)

$$\begin{array}{cc}\hfill u(0,t)& =0,0\le t\le T\hfill \\ \hfill u(1,t)& =0,\hfill \end{array}$$

where $\sigma =80,x_0=0.5$ [7].

With the exact solution given as

$$\begin{array}{c}\hfill u(t,x)={\displaystyle \frac{1}{{\left[1+\left({\displaystyle \frac{1-\sqrt{u(x,0)}}{\sqrt{u(x,0)}exp\left({\displaystyle \frac{1}{6D}}\sqrt{6Dr}x\right)}}\right)exp\left(-{\displaystyle \frac{5}{6}}rt+{\displaystyle \frac{1}{6D}}\sqrt{6Dr}x\right)\right]}^2}}\end{array}$$

(17)

where $D=0.0002,r=0.05$.

The discretization of the nonlinear ADR Equation (15) using Equation (5) is given below.

$$\begin{array}{c}\hfill u_i^{n+1}={\displaystyle \frac{(1+r\Delta t)u_i^n+\lambda (u_{i+1}^n-u_i^n)}{1+2\lambda +r\Delta t{u}_i^n}}.\end{array}$$

(18)

where $\lambda ={\displaystyle \frac{D\Delta t}{{(\Delta x)}^2}}$.

2.2.1. Stability

By applying Fourier series analyses of the form $u_{i,n}={\xi }^n{e}^{j\Delta ti\Delta x}$, and freezing coefficient technique [27] to Equation (18), we obtain the following amplification factor.

$$\begin{array}{c}\hfill \xi ={\displaystyle \frac{1+\Delta tr+2\lambda cos\omega }{1+2\lambda +r\Delta t{u}_{\max }}}\end{array}$$

(19)

where by the freezing coefficient technique, $u^2$ is replace by $u{u}_{max}$, and u is frozen to a constant $u_{max}$, which represents the maximum value of the solution u.

The scheme is unconditionally stable for all $\Delta x$, $\Delta t>0$.

2.2.2. Consistency

Through the consistency of the UPFD scheme [25] by the Taylor expansion to Equation (18), we obtain the following.

$$\begin{array}{cc}\hfill {\displaystyle \frac{\partial u}{\partial t}}-D{\displaystyle \frac{{\partial }^{2}u}{\partial x^2}}& =ru(1-u)-{\displaystyle \frac{\Delta t}{2}}{\displaystyle \frac{{\partial }^{2}u}{\partial x^2}}-\left({(\Delta x)}^{3}ru+2\Delta xD\right){\displaystyle \frac{\partial u}{\partial t}}\hfill \\ \hfill & -{\displaystyle \frac{{(\Delta x)}^3}{2}}\left(1+2\Delta xD+r{(\Delta x)}^{3}u\right){\displaystyle \frac{{\partial }^{2}u}{\partial t^2}}-{\displaystyle \frac{{(\Delta x)}^6}{6}}\left(1+2\Delta xD+r{(\Delta x)}^{3}u\right){\displaystyle \frac{{\partial }^{3}u}{\partial t^3}}\cdots \cdots \hfill \end{array}$$

(20)

As $\Delta x⟶0$ and $\Delta t⟶0$, Equation (20) reduces to Equation (15); therefore, the scheme is consistent.

3. Formulation of the POD Basis

In this section, we discuss the POD basis that reduces the degree of freedom for numerical methods [28].

The POD is used to reduce the computational time accumulated in the UPFD method. The EUPFD method is built by extracting a snapshot matrix from the matrix solution of the UPFD method. The snapshot matrix is then used to construct a small subset of leading basis functions, which is an eigenvector generated by singular value decomposition (SVD), to approximate state variables ${\psi }_i$. The SVD technique is used to decompose a matrix into several component matrices, exposing many of the original matrix’s useful and interesting properties [29]. The POD method seeks a low-dimensional basis that could be used to approximate the state variables well. POD basis functions are typically the left singular vectors of the matrix.

From the standard UPFD solution, denoted by $u_i^n$, where $(1\le i\le m)$, $0\le n\le N$, we extract the first L sequence of solutions ${\left\{u_i^n\right\}}_{(n=1)}^L$$(1\le i\le m$, and $L\le N)$ as snapshots, yielding the formulated $m\times L$ snapshot matrix shown below.

$$\begin{array}{c}\hfill A=\left(\begin{array}{ccccccccc}{u}_1^1& u_1^2& ·& ·& ·& ·& ·& ·& u_1^L\\ u_2^1& u_2^2& ·& ·& ·& ·& ·& ·& u_2^L\\ ·& ·& & & & & & & ·\\ ·& ·& ·& & & & & & ·\\ ·& ·& & ·& & & & & ·\\ ·& ·& & & ·& & & & ·\\ ·& ·& & & & ·& & & ·\\ ·& ·& & & & & ·& & ·\\ ·& ·& & & & & & ·& ·\\ u_m^1& u_m^2& ·& ·& ·& ·& ·& ·& u_m^L\end{array}\right)\end{array}$$

(21)

where m and L are the mesh points of the snapshot. When the snapshot is tall and skinny, the method of snapshot is an efficient alternative way to compute the POD basis. The POD modes are computed by using the method of snapshots developed by Sirovich [30].

The SVD is then used to factorise snapshot matrix A.

$$\begin{array}{c}\hfill A=U\Sigma V^T=U\left(\begin{array}{cc}{\Sigma }_{l\times l}& O_{l\times (L-l)}\\ O_{(m-1)\times l}& O_{(m-l)\times (L-l)}\end{array}\right)V^T\end{array}$$

(22)

where l = $rankA$, ${\Sigma }_{l\times l}$ = $diag({\sigma }_1,{\sigma }_2,\dots ,{\sigma }_l)$ is a diagonal matrix that is generated from the SVD of A as arranged from the decreasing order ${\sigma }_1\ge {\sigma }_2\ge \dots \dots \ge {\sigma }_l>0$, $U=({\psi }_1,{\psi }_2,\dots ,{\psi }_m)$ is an $m\times m$ orthogonal matrix consisting of the eigenvectors of $A{A}^T$, whereas $V=({\varphi }_1,{\varphi }_2,\dots ,{\varphi }_L)$ is an $L\times L$ orthogonal matrix consisting of the orthogonal eigenvectors of $A^{T}A$ and O is a zero matrix [31].

The eigenvalues of $A^{T}A$ and $A{A}^T$ are identical and satisfy ${\Lambda }_j={\sigma }_j^2(j=1,2,\dots ,l)$. Therefore, we may first find the eigenvalues ${\Lambda }_1\ge {\Lambda }_2\ge \dots \dots \ge {\Lambda }_l>0(l=rankA)$ for matrices $A{A}^T$ and corresponding eigenvectors ${\psi }_j$. That means that the following relationship applies.

$$\begin{array}{c}\hfill {\psi }_j=A{\varphi }_j/\sqrt{{\Lambda }_j},j=1,2,\cdots \cdots ,l.\end{array}$$

(23)

Eigenvectors ${\varphi }_j(j=1,2,\cdots \cdots ,l)$ that correspond to the nonzero eigenvalues for matrix $A{A}^T$ are obtained. Therefore,

$$\begin{array}{c}\hfill A_M=U\Sigma V^T=U\left(\begin{array}{cc}{\Sigma }_{M\times M}& O_{M\times (L-M)}\\ O_{(m-M)\times M}& O_{(m-M)\times (L-M)}\end{array}\right)V^T\end{array}$$

(24)

where ${\Sigma }_{M\times M}=diag({\sigma }_1,{\sigma }_1,\cdots ,{\sigma }_m)$ represents the diagonal matrix that consists of the first M positive singular values of diagonal matrix ${\Sigma }_{l\times l}$. The 2-norm of matrix A is defined as follows: ${\parallel A\parallel }_2=su{p}_{u\in {\Re }^L}{\parallel Au\parallel }_2/{\parallel u\parallel }_2$ ( where ${\parallel u\parallel }_2$ is the $l^2$ norm for vector u).

Theorem 1.

Let $\varphi =({\psi }_1,{\psi }_2,\cdots ,{\psi }_M)$ consist of the first M eigenvectors $U=({\psi }_1,{\psi }_2,\cdots ,{\psi }_m)$; then, we have

$$\begin{array}{c}\hfill A_M=\sum _{i=1}^M{\sigma }_i{\psi }_i{\varphi }_i^T=\varphi {\varphi }^{T}A.\end{array}$$

(25)

Proof. 

$$A_M=\sum _{i=1}^M{\sigma }_i{\psi }_i{\varphi }_i^T=\left({\psi }_1,\cdots \cdots ,{\psi }_M\right)\left(\begin{array}{ccccccccc}{\sigma }_1& ·& ·& ·& ·& ·& ·& ·& 0\\ ·& ·& ·& ·& ·& ·& ·& ·& ·\\ ·& ·& & & & & & & ·\\ ·& ·& ·& & & & & & ·\\ ·& ·& & ·& & & & & ·\\ ·& ·& & & ·& & & & ·\\ ·& ·& & & & ·& & & ·\\ ·& ·& & & & & ·& & ·\\ ·& ·& & & & & & ·& ·\\ 0& ·& ·& ·& ·& ·& ·& ·& {\sigma }_M\end{array}\right)\left(\begin{array}{c}{\varphi }_1^T\\ ·\\ ·\\ ·\\ ·\\ ·\\ ·\\ ·\\ ·\\ {\varphi }_M^T\end{array}\right)$$

(26)

$$A=\left({\psi }_1,\cdots \cdots ,{\psi }_l\right)\left(\begin{array}{ccccccccc}{\sigma }_1& ·& ·& ·& ·& ·& ·& ·& 0\\ ·& ·& ·& ·& ·& ·& ·& ·& ·\\ ·& ·& & & & & & & ·\\ ·& ·& ·& & & & & & ·\\ ·& ·& & ·& & & & & ·\\ ·& ·& & & ·& & & & ·\\ ·& ·& & & & ·& & & ·\\ ·& ·& & & & & ·& & ·\\ ·& ·& & & & & & ·& ·\\ 0& ·& ·& ·& ·& ·& ·& ·& {\sigma }_l\end{array}\right)\left(\begin{array}{c}{\varphi }_1^T\\ ·\\ ·\\ ·\\ ·\\ ·\\ ·\\ ·\\ ·\\ {\varphi }_l^T\end{array}\right)$$

(27)

$$\varphi {\varphi }^{T}A=\varphi \left(\begin{array}{c}{\psi }_1\\ ·\\ ·\\ ·\\ ·\\ ·\\ ·\\ ·\\ ·\\ {\varphi }_M^T\end{array}\right)\left({\psi }_1,\cdots \cdots ,{\psi }_l\right)\left(\begin{array}{ccccccccc}{\sigma }_1& ·& ·& ·& ·& ·& ·& ·& 0\\ ·& ·& ·& ·& ·& ·& ·& ·& ·\\ ·& ·& & & & & & & ·\\ ·& ·& ·& & & & & & ·\\ ·& ·& & ·& & & & & ·\\ ·& ·& & & ·& & & & ·\\ ·& ·& & & & ·& & & ·\\ ·& ·& & & & & ·& & ·\\ ·& ·& & & & & & ·& ·\\ 0& ·& ·& ·& ·& ·& ·& ·& {\sigma }_l\end{array}\right)\left(\begin{array}{c}{\varphi }_1^T\\ ·\\ ·\\ ·\\ ·\\ ·\\ ·\\ ·\\ ·\\ {\varphi }_l^T\end{array}\right)$$

(28)

$$=\varphi \left(\begin{array}{cc}{I}_M& O\end{array}\right)\left(\begin{array}{ccccccccc}{\sigma }_1& ·& ·& ·& ·& ·& ·& ·& 0\\ ·& ·& ·& ·& ·& ·& ·& ·& ·\\ ·& ·& & & & & & & ·\\ ·& ·& ·& & & & & & ·\\ ·& ·& & ·& & & & & ·\\ ·& ·& & & ·& & & & ·\\ ·& ·& & & & ·& & & ·\\ ·& ·& & & & & ·& & ·\\ ·& ·& & & & & & ·& ·\\ 0& ·& ·& ·& ·& ·& ·& ·& {\sigma }_l\end{array}\right)\left(\begin{array}{c}{\varphi }_1^T\\ ·\\ ·\\ ·\\ ·\\ ·\\ ·\\ ·\\ ·\\ {\varphi }_l^T\end{array}\right)$$

(29)

$$=\varphi \left(\begin{array}{ccccccccc}{\sigma }_1& ·& ·& ·& 0& ·& ·& ·& 0\\ ·& & & & ·& & & & ·\\ ·& & & & ·& & & & ·\\ ·& & & & ·& & & & ·\\ ·& & & & ·& & & & ·\\ ·& & & & ·& & & & ·\\ ·& & & & ·& & & & ·\\ 0& ·& ·& ·& {\sigma }_M& ·& ·& ·& {\sigma }_l\end{array}\right)\left(\begin{array}{c}{\varphi }_1^T\\ ·\\ ·\\ ·\\ ·\\ ·\\ ·\\ {\varphi }_l^T\end{array}\right)$$

(30)

$$=\left({\psi }_1,\cdots \cdots ,{\psi }_M\right)\left(\begin{array}{ccccccccc}{\sigma }_1& ·& ·& ·& ·& ·& ·& ·& 0\\ ·& ·& ·& ·& ·& ·& ·& ·& ·\\ ·& ·& & & & & & & ·\\ ·& ·& ·& & & & & & ·\\ ·& ·& & ·& & & & & ·\\ ·& ·& & & ·& & & & ·\\ ·& ·& & & & ·& & & ·\\ ·& ·& & & & & ·& & ·\\ ·& ·& & & & & & ·& ·\\ 0& ·& ·& ·& ·& ·& ·& ·& {\sigma }_M\end{array}\right)\left(\begin{array}{c}{\varphi }_1^T\\ ·\\ ·\\ ·\\ ·\\ ·\\ ·\\ ·\\ ·\\ {\varphi }_M^T\end{array}\right)=A_M$$

(31)

Thus, by the relationship between the matrix norm and its spectral radius, we have

$$\underset{rank\left(B\right)\le M}{min}{\parallel A-B\parallel }_{2,2}={\parallel A-A_M\parallel }_{2,2}={\parallel A-\varphi {\varphi }^{T}A\parallel }_{2,2}=\sqrt{{\Lambda }_{M+1}}$$

(32)

where $\varphi =({\varphi }_1,{\varphi }_2,\cdots \cdots ,{\varphi }_M)$ consist of the first M eigenvectors $U=({\psi }_1,{\psi }_2,\cdots \cdots ,{\psi }_m)$.

If the L column vectors of A are denoted by $u^n={(u_1^n,u_2^n,\cdots \cdots ,u_m^n)}^T(n=1,2,\cdots \cdots ,L)$ we have

$$\begin{array}{c}\hfill {\parallel u^n-u_M^n\parallel }_2={\parallel (A-\varphi {\varphi }^{T}A){\xi }_n\parallel }_2\le {\parallel A-\varphi {\varphi }^{T}A\parallel }_{2,2}{\parallel \xi \parallel }_2=\sqrt{{\Lambda }_{M+1}},\end{array}$$

(33)

where

$$\begin{array}{c}\hfill u_M^n=\sum _{j=1}^M({\psi }_j,u^n){\psi }_j\end{array}$$

(34)

which represents the projection of $u^n$ onto $\varphi =({\varphi }_1,\varphi ,\cdots \cdots ,{\psi }_M)({\psi }_j,u^n)$ is the inner product of ${\psi }_j$ and $u^n$, and ${\xi }_n$ denotes the unit vector with the nth component being 1. Inequality (33) shows that $u_M^n$ is an optimal approximation $u^n$ whose error is no more than $\sqrt{{\Lambda }_{M+1}}$; thus, $\varphi$ is just an orthogonal optimal POD base of A. □

3.1. Formulation of the POD to Reduce the Order of the Finite Difference Scheme for the Advection–Diffusion–Reaction Equations

The EUPFD method is built on the basis of POD. The solution vector of the UPFD method is given by $u^n={(u_1^n,u_2^n,\dots ,u_m^n)}^T(n=1,2,\cdots \cdots ,L,L+1,\cdots \cdots ,N)$ and have a finite difference scheme, as follows:

$$\begin{array}{c}\hfill u^{n+1}=u^n+{\displaystyle \frac{\Delta t}{\Delta x^2}}B{u}^n+\Delta t{F}^n\end{array}$$

(35)

where $F^n=\left(f_1^n,f_2^n,\cdots \cdots ,f_m^n\right)$ and

$$\begin{array}{c}\hfill B=\left(\begin{array}{ccccccccc}-2& 1& 0& 0& ·& ·& ·& 0& 0\\ 1& -2& 1& 0& ·& ·& ·& 0& 0\\ 0& 1& -2& 1& ·& ·& ·& 0& 0\\ 0& 0& 1& -2& ·& ·& ·& 0& 0\\ ·& & & & & & & & ·\\ ·& & & & & & & & ·\\ ·& & & & & & & & ·\\ 0& 0& 0& 0& ·& ·& ·& -2& 1\\ 0& 0& 0& 0& ·& ·& ·& 1& -2\end{array}\right)\end{array}$$

(36)

Matrix B is a tridiagonal matrix with the following eigenvalues:

$$\begin{array}{c}\hfill {\Lambda }_j=-2+2cos\left[\left(2j-1\right)\pi /\left(2m+1\right)\right],j=1,2,\cdots \cdots \cdots ,m.\end{array}$$

(37)

Taking the norm of matrix B, we obtain the following.

$$\begin{array}{cc}\hfill {\parallel B\parallel }_{2,2}& =|2-2cos[(2m-1)\pi /(2m+1)\left]\right|\hfill \\ \hfill & =|2-2cos[\pi -2\pi /(2m+1)\left]\right|\hfill \\ \hfill & =|2+2cos[2\pi /(2m+1)\left]\right|<4\hfill \end{array}$$

(38)

Replacing $u^n$ in Equation (35) with $u^{\ast n}=\varphi {\varphi }^{T}A{\xi }_n$$(n=1,2,\cdots \cdots ,L)$, which is $u^{\ast n}=\varphi {\alpha }^n(n=L+1,L+2,\cdots \cdots ,N)$, where ${\alpha }^n={\varphi }^{T}A{\xi }_n$, we obtain the EUPFD scheme as follows.

$$\begin{array}{c}\hfill \left\{\begin{array}{c}{u}^{\ast n}=\varphi {\varphi }^{T}A{\xi }_n,\cdots \cdots ,n=1,2,\cdots \cdots ,L\hfill \\ \varphi {\alpha }^{n+1}=\varphi {\alpha }^n+{\displaystyle \frac{\Delta t}{\Delta x^2}}B\varphi {\alpha }^n+\Delta t{F}^n,\hfill \\ n=L,L+1,\cdots \cdots ,N-1\hfill \end{array}\right.\end{array}$$

(39)

where ${\alpha }^n={({\alpha }_1^n,{\alpha }_2^n,\cdots \cdots ,{\alpha }_M^n)}^T$ are vectors that are yet to be determined.

Using orthogonal vectors in ${\varphi }^T$ multiplied by (39), we obtain

$$\begin{array}{c}\hfill \left\{\begin{array}{c}{\alpha }^n={\varphi }^T{u}^n,,\cdots \cdots ,n=1,2,\cdots \cdots ,L\hfill \\ {\alpha }^{n+1}={\alpha }^n+{\displaystyle \frac{\Delta t}{\Delta x^2}}{\varphi }^{T}B\varphi {\alpha }^n+\Delta t{\varphi }^T{F}^n,\hfill \\ n=L,L+1,\cdots \cdots ,N-1\hfill \end{array}\right.\end{array}$$

(40)

We obtain the ${\alpha }^n(n=L,L+1,\cdots \cdots ,N)$ from Equation (40); then, we obtain the EUPFD solution as follows.

$$\begin{array}{c}\hfill u^{\ast n}=\varphi {\alpha }^n,n=1,2,\cdots \cdots ,N.\end{array}$$

(41)

Therefore, the EUPFD solution component of Equation (6) is given as follows.

$$\begin{array}{c}\hfill u_{j,k}^{\ast n}=u_i^{\ast n},\cdots \cdots 0\le j\le J,0\le k\le K,1\le i=k(J+1)+j+1\le m=(K+1)(J+1)\end{array}$$

3.2. Error Estimates of the EUPFD for the Advection–Diffusion–Reaction Equation

By finding the norm of Equations (39) and (40), we obtain the following.

$$\begin{array}{c}\hfill {\parallel u^n-u^{\ast n}\parallel }_2={\parallel u^n-u_M^n\parallel }_2={\parallel (A-\varphi {\varphi }^{T}A){\xi }_n\parallel }_2\le \sqrt{{\Lambda }_{M+1}}\end{array}$$

(42)

$n=1,2,\cdots \cdots ,L$

Theorem 2

(Accuracy). The errors between solutions $u_i^n$ from the UPFD scheme and solution $u_i^{\ast n}$ from the EUPFD scheme satisfy the following estimates:

$$\begin{array}{c}\hfill |u_i^n-u_i^{\ast n}{|\le (1+\delta )}^{n-L}\sqrt{{\Lambda }_M+1}for(L+1\le n\le N)\end{array}$$

(43)

where $\delta ={\displaystyle \frac{\Delta t}{\Delta x^2}}{\parallel B\parallel }_{2,2}$.

The errors between exact solution $u(x,t)$ and solution $u_m^n$ from the POD-reduced-order FD scheme satisfy the following estimates [31]

$$\begin{array}{c}\hfill |u(x_i,t_n)-u_i^{\ast n}|=O\left({(1+\delta )}^{n-L}\sqrt{{\Lambda }_M+1},\Delta t,\Delta x^2\right),1\le i\le M,1\le n\le N.\end{array}$$

(44)

Proof. 

$$\begin{array}{c}\hfill |u^n-u^{\ast n}{|}_2=|u^n-u_M^n{|}_2={|(A-\alpha {\alpha }^{T}A){ϵ}_n|}_2\le \sqrt{{\Lambda }_{M+1}},n=1,2,\cdots \cdots ,L.\end{array}$$

(45)

Equation (39) is rewritten as follows.

$$\begin{array}{c}\hfill u^{\ast n+1}=u^{\ast n}+{\displaystyle \frac{\Delta t}{{(\Delta x)}^2}}+\Delta t{F}^n,n=L,L+1,\cdots ,N-1.\end{array}$$

(46)

By putting $\delta ={\Delta t\left|B\right|}_2/{(\Delta x)}^2$, we obtain the following simplified equation of Equation (45).

$$|u^{n+1}-u^{\ast n+1}{|}_2\le (1+\delta )|u^n-u^{\ast n}{|}_2$$

(47)

$$\begin{array}{cc}\hfill & \le \cdots \hfill \\ \hfill & \le {(1+\delta )}^{n+1-L}{|u^L-u^{\ast L}|}_2\hfill \end{array}$$

$$\begin{array}{cc}\hfill & \le {(1+\delta )}^{n+1-L}\sqrt{{\Lambda }_{M+1}},n=L,L+1,\cdots ,N-1.\hfill \end{array}$$

(48)

□

Remark 1.

The error terms containing $\sqrt{{\Lambda }_{M+1}}$ are caused by the POD-based reduced-order for the classical FD scheme, which could be used to select the number of the POD basis, i.e., it is necessary to take M such that $\sqrt{{\Lambda }_{M+1}}=O(\Delta t,\Delta x^2)$. Whereas $E\left(n\right)={(1+\delta )}^{n-L}$$(L+1\le n\le N)$ are caused by extrapolating iterations that could be used as the guide for renewing the POD basis, i.e., if ${(1+\delta )}^{n-L}\sqrt{{\Lambda }_{M+1}}>max(\Delta t,\Delta x^2)$ it is necessary to update the POD basis. If we take ${\Lambda }_{M+1}$ that satisfies ${(1+\delta )}^{n-L}\sqrt{{\Lambda }_{M+1}}=O(\Delta t,\Delta x^2)$, then the EUPFD scheme converges; thus, we did not have to update the POD basis [31].

3.3. Implementation of the EUPFD Scheme Algorithm for Advection–Diffusion–Reaction Equations

In order to facilitate the use of the EUPFD scheme for the linear and nonlinear ADR equation, the following implementation steps of the algorithm for the EUPFD scheme are useful [31].

Step 1: Standard UPFD computation and extraction of snapshots:

Write the standard UPFD scheme in vector form and find solution vectors $u^n={(u_1^n,u_2^n,\cdots ,u_m^n)}^T(n=1,2,\cdots ,L)$ at the few L steps.

Step 2: Snapshot matrix A and eigenvalues of $A^{T}A$: Formulate snapshot matrix $A={\left(u_i^n\right)}_{x\times L}$ and compute eigenvalues ${\Lambda }_1\ge ,{\Lambda }_2\ge ,\cdots ,{\Lambda }_l>0(l=$ Rank $A)$ and eigenvectors ${\varphi }_j(j=1,2,\cdots ,\tilde{M})$ of matrix $A^{T}A$.

Step 3: Choice of POD basis: For error tolerance $\mu =O(\Delta t,\Delta x^2)$, decide the numbers $M\le \tilde{M}$ of POD basis, such that $\sqrt{{\Lambda }_{u(M+1)}}\le \mu$, and formulate the POD bases $\varphi =({\psi }_1,{\psi }_2,\cdots ,{\psi }_M)$(where ${\psi }_j={\displaystyle \frac{A{\varphi }_j}{\sqrt{{\Lambda }_j}}},j=1,2,\cdots ,M$).

Step 4: Solve or compute the EUPFD model:

Solve Equation (40) and use (41) to obtain the reduced-order solution vectors of the EUPFD given in a form of $u^{\ast n}=(u_1^{\ast n},u_2^{\ast n},\cdots ,u_m^{\ast n})$, further obtain the component forms $u_{j,k}^{\ast n}=u_i^{\ast n}$, where $(0\le j\le J,0\le k\le K,i=k(J+1)+j+1.1\le i\le m=(K+1\left)\right(J+1\left)\right)$.

Step 5: Check accuracy and renew POD basis to continue:

Set $\delta ={\displaystyle \frac{\Delta t\mid \mid B\mid {\mid }_{2,2}}{{(\Delta x)}^2}}$. If ${(1+\delta )}^{n-L}\sqrt{{\Lambda }_{u(M+1)}}\le \mu$, then $u^{\ast n}={(u_1^{\ast n},u_2^{\ast n},\cdots ,u_m^{\ast n})}^T$ is the solution vectors for the EUPFD scheme that satisfy the accuracy requirement. Else, if ${(1+\delta )}^{n-L}\sqrt{{\Lambda }_{u(M+1)}}>\mu$, put $u^1=u^{\ast (n-L)},u^2=u^{\ast (n-L+1)},\cdots ,u^L=u^{\ast (n-1)}$ and return to step 2.

4. Numerical Results

This section presents solutions to the linear and nonlinear ADR equations using the UPFD and EUPFD. Exact solutions are also used for comparison purposes. Convergence rates, absolute errors, and computational time were calculated to evaluate the methods’ performance. The numerical and analytical solutions are denoted by ${\overline{u}}_{i,n}$ and $u_{i,n}$, respectively. The error is denoted by $e_{i,n}$, and its magnitude is measured by the $L_{\infty }$-norm given by the formula below.

$$\begin{array}{c}\hfill \left|\right|e_{i,n}{\left|\right|}_{\infty }=\left|\right|u_{i,n}-{\overline{u}}_{i,n}{\left|\right|}_{\infty }=Max|u_{i,n}-{\overline{u}}_{i,n}|\end{array}$$

(49)

The convergence rate is calculated by using the formula below.

$$\begin{array}{c}\hfill q(\Delta t_k)={\displaystyle \frac{lo{g}_2\left(\frac{e_k}{e_{k+1}}\right)}{lo{g}_2\left(\frac{\Delta t}{\Delta t_{k+1}}\right)}}\mathrm{or}q(\Delta x_k)={\displaystyle \frac{lo{g}_2\left(\frac{e_k}{e_{k+1}}\right)}{lo{g}_2\left(\frac{\Delta x}{\Delta x_{k+1}}\right)}}\end{array}$$

(50)

The accuracy of the EUPFD relies on the size of the snapshot, L. Therefore, finding the best snapshot size such that the accuracy is maximal is paramount. To determine the best snapshot size, we first set $L=1$ and found the solution. We then produced increments of 1 on L until there was no significant change in the solution. For this, we set up a tolerance as follows.

$$\left|\right|u_{exact}-u_L{\left|\right|}_{\infty }\le ϵ,L=1,2,3,\dots$$

(51)

where $u_{exact}$ is the exact solution, and $u_L$ is the solution at the specific value of L. The first value of L that satisfies (51) is the optimal value of $L.$ In this work, we set $ϵ$ to be ${10}^{-10}$.

4.1. Numerical Results for the Linear Advection–Diffusion–Reaction Equation

The convergence rates of the UPFD and the EUPFD with respect to the time and spatial steps are shown in Table 1 and Table 2. The convergence rates of UPFD and EUPFD decreased with a decrease in time and spatial step sizes. Table 3 compares the exact, UPFD, and the EUPFD solutions at $(t,x)=\left(0.008,0.05\right),\left(0.016,0.1\right),$ and $\left(0.032,0.2\right)$, as well as the computational times for the UPFD and EUPFD methods. EUPFD took less computational time to converge to the solution of the linear ADR equation compared to the UPFD.

Table 1. Convergence rates for the linear ADR equation by the UPFD and EUPFD with respect to $\Delta t$ and a fixed $\Delta x=0.025$.

	$\mathit{q}(\Delta {\mathit{t}}_{\mathit{k}})$
$t_k$	UPFD	EUPFD
$0.001$	3.668	3.568
$0.002$	3.573	3.448
$0.004$	3.530	3.375

Table 2. Convergence rates for the linear ADR equation by the UPFD and EUPFD with respect to $\Delta x$ and a fixed $\Delta t=0.001$.

	$\mathit{q}(\Delta {\mathit{x}}_{\mathit{k}})$
$x_k$	UPFD	EUPFD
$0.0125$	3.269	3.320
$0.025$	3.001	3.075
$0.05$	3.074	3.146

Table 3. Numerical results of the linear ADR equation at a fixed $\Delta x=0.025$ and $\Delta t=0.004$.

$(\mathit{t},\mathit{x})$	Exact Solution	UPFD Solution	Error	EUPFD Solution	Error
$\left(0.008,0.05\right)$	0.979	0.975	0.003	0.975	0.003
$\left(0.016,0.1\right)$	0.938	0.928	0.010	0.928	0.010
$\left(0.032,0.2\right)$	0.9003	0.883	0.016	0.883	0.016
Time		0.008816		0.004314

In Table 4, we compare the infinity norms of the proposed EUPFD with the Crank–Nicolson method in solving the linear ADR equation. For this example, results show that Crank–Nicolson achieved better accuracy. However, Crank–Nicolson did not preserve the positivity of solutions, which is the main focus of this work.

Table 4. Infinity norm results of the linear ADR equation by using the exact, Crank Nicolson, and EUPFD solutions.

$(\mathit{t},\mathit{x})$	Exact	Crank–Nicolson	Error	EUPFD	Error
$u(:,0.05)$	0.9231	0.9246	0.0015	0.9056	0.0175
$u(:,0.1)$	0.9608	0.9621	0.0013	0.9071	0.0536
$u(:,0.2)$	1.0000	0.9987	0.0013	0.9087	0.0913

Figure 1a shows the contribution of each POD basis mode. The first 12 modes contained the predominant information where the EUPFD met the theoretical accuracy requirement. The 12 modes were significant in optimizing the linear ADR equation. Figure 1b shows the decreasing error when the number of modes increased.

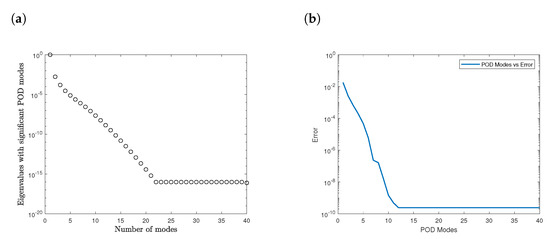
Figure 1. (a) POD modes for linear reaction diffusion equation. (b) Number of POD modes vs. error.

Figure 2a,b and Figure 3a show the surface plots of the exact, UPFD and EUPFD solutions of linear ADR. Figure 3b shows the increase in error when the POD modes increased.

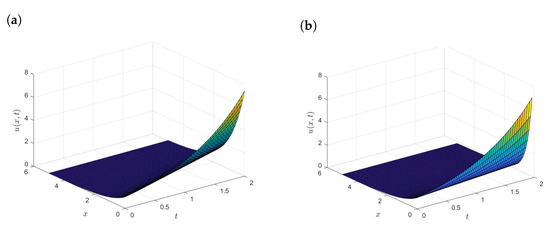
Figure 2. (a) Surface plot of the exact solution of the linear ADR equation. (b) Surface plot of the UPFD solution of the linear ADR equation.

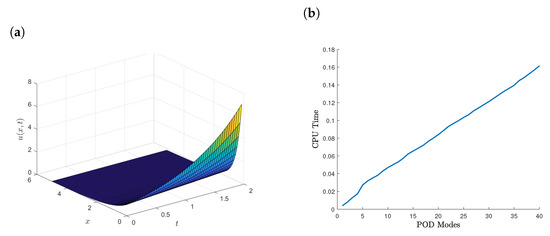
Figure 3. (a) Surface plot of the EUPFD solution of the linear ADR equation. (b) Number of POD modes vs. CPU time for the linear reaction diffusion equation.

Figure 4a,b show the absolute errors between the exact solution and EUPFD solution for the linear ADR against time and space, respectively.

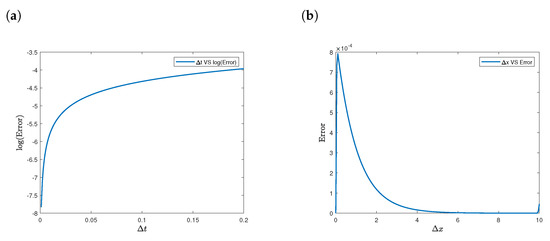
Figure 4. (a) Absolute error between the exact and EUPFD solutions of the linear ADR against time. (b) Absolute error between the exact and EUPFD solutions for the linear ADR against space.

4.2. Numerical Results for the Nonlinear Reaction Diffusion Equation

Table 5 and Table 6 show the convergence rates of the UPFD and EUPFD for the nonlinear reaction–diffusion equation with respect to time and spatial steps. In these tables, the convergence rate of the UPFD and the EUPFD decreases with the increasing time step, and increases with the increasing spatial step sizes.

Table 5. Convergence rates for the nonlinear diffusion reaction by the UPFD and EUPFD equations with respect to $\Delta t$ and a fixed $\Delta x=0.01$.

	$\mathit{q}(\Delta {\mathit{t}}_{\mathit{k}})$
$t_k$	UPFD	EUPFD
$0.00625$	2.041	2.041
$0.0125$	2.028	2.028
$0.025$	1.983 7	1.983

Table 6. Convergence rates for the nonlinear diffusion reaction equation by the UPFD and EUPFD with respect to $\Delta x$ and a fixed $\Delta t=0.025$.

	$\mathit{q}(\Delta {\mathit{x}}_{\mathit{k}})$
$x_k$	UPFD	EUPFD
$0.0005$	7.160	4.767
$0.001$	5.405	4.320
$0.002$	3.878	3.882

Table 7 shows the comparison of the exact, UPFD, and EUPFD solutions obtained at $(t,x)=\left(0.05,0.02\right),\left(0.1,0.04\right)$, and $\left(0.2,0.08\right)$, and the computational times taken by the UPFD and EUPFD methods. The EUPFD took less computational time to converge to the solution of the nonlinear reaction–diffusion equation than the UPFD did.

Table 7. Numerical results of the nonlinear ADR equation at a fixed $\Delta x=0.01$, $\Delta t=0.025$, $r=0.05$ and $D=0.002$.

$(\mathit{t},\mathit{x})$	Exact Solution	UPFD Solution	Error	EUPFD Solution	Error
$\left(0.05,0.02\right)$	3.191 × 10${}^{-9}$	3.214 × 10${}^{-9}$	2.281 × 10${}^{-11}$	3.214 × 10${}^{-9}$	2.285 × 10${}^{-11}$
$\left(0.1,0.04\right)$	1.488 × 10${}^{-8}$	1.603 × 10${}^{-8}$	1.152 × 10${}^{-9}$	1.603 × 10${}^{-8}$	1.152 × 10${}^{-9}$
$\left(0.2,0.08\right)$	6.508 × 10${}^{-8}$	7.285 × 10${}^{-8}$	7.764 × 10${}^{-9}$	7.285 × 10${}^{-8}$	7.764 × 10${}^{-9}$
Time		0.004314		0.002357

In this example, the infinity norms of the EUPFD and Crank–Nicolson errors are shown in Table 8. Results show that EUPFD was slightly more accurate than Crank–Nicolson.

Table 8. Infinity norm results of the nonlinear ADR equation by using the exact, Crank–Nicolson, and EUPFD solutions.

$(\mathit{t},\mathit{x})$	Exact	Crank Nicolson	Error	EUPFD	Error
$u(:,0.02)$	0.7103	0.6998	0.0105	0.7000	0.0101
$u(:,0.04)$	0.7103	0.6993	0.0110	0.7000	0.0101
$u(:,0.08)$	0.7103	0.6989	0.0114	0.7000	0.0101

Figure 5a,b and Figure 6 shows the surface plots of the exact, UPFD and EUPFD solutions of the nonlinear ADR equation. Figure 6b shows the increase in CPU time when the number with the increase in POD modes.

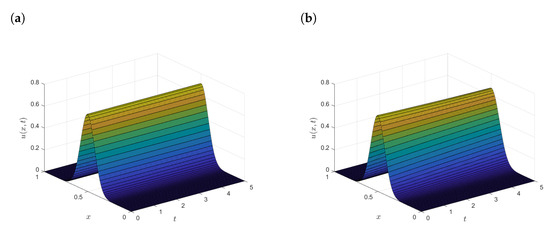
Figure 5. (a) Surface plot of the EUPFD solution of the nonlinear ADR equation. (b) Number of POD modes vs. CPU time for the nonlinear reaction diffusion equation.

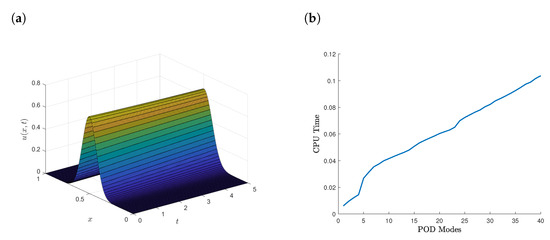
Figure 6. (a) Surface plot of the exact solution of the nonlinear reaction diffusion equation. (b) Surface plot of the UPFD solution of the nonlinear reaction diffusion equation.

Figure 7a shows the contribution of each of the POD basis modes. The first 9 modes contain the predominant information where the EUPFD met the theoretical accuracy requirement. The 9 modes were significant in optimising the nonlinear ADR equation.

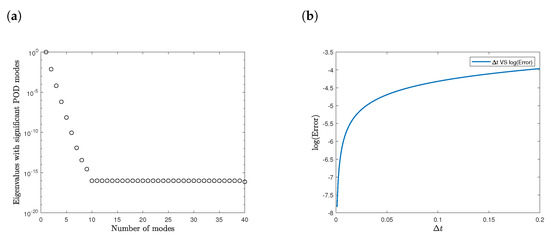
Figure 7. (a) Significant POD modes against number of modes. (b) Absolute error between the exact solution and EUPFD solution against time.

Figure 7b and Figure 8 shows the absolute error between the exact and EUPFD solutions for the nonlinear ADR against time and space, respectively.

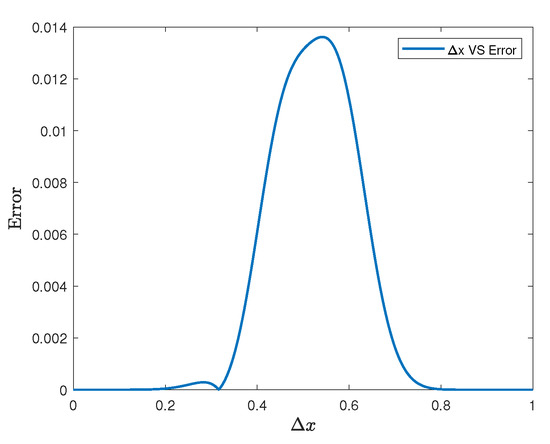
Figure 8. Absolute error between the exact and EUPFD solutions against space.

5. Conclusions

In this paper, we presented a new method, the enhanced unconditionally positive finite difference (EUPFD) method. The method uses the POD in conjunction with the unconditionally positive finite difference (UPFD) scheme. We used it to investigate the solutions to the linear and nonlinear diffusion reaction equations. The POD’s goal is to find the UPFD’s low-dimensional approximated solution. Results show that the EUPFD gives a good approximation to the solutions of these problems, and this validated its efficiency and effectiveness. Another remarkable result of the EUPFD is the reduced computational time compared to that of the UPFD. Besides the reduction in computational time and solution positivity that the EUPFD guarantees, only a small number of modes containing the predominant information are required to meet the theoretical accuracy. As the POD modes increased, the error of EUPFD measured against the exact solution significantly decreased. The spatial steps were taken to be $\Delta x=0.01,0.02$ and $0.04$, while the time step was $\Delta t=0.025,0.0125$ and $0.00625$. We had $\delta <1$; thus, we next took 50 snapshots from the UPFD. By performing POD on UPFD, we achieved $\sqrt{{\Lambda }_9}\le 4\times {10}^{-4}$ and $\sqrt{{\Lambda }_{35}}\le 4\times {10}^{-4}$ for the linear and nonlinear ADR equations, respectively. As long as the first 9 and 12 POD bases were used, the theoretical accuracy requirement could be met. Since the EUPFD only used 9 and 12 POD modes from the selected 50 classical solutions of the UPFD as the snapshot, this would mean that EUPFD saves computational time, reduces degrees of freedom in numerical computations, alleviates truncation error accumulation, and it preserves the positivity of the solution. These render the EUPFD more efficient and effective in solving linear and nonlinear PDEs. However, the accuracy of the EUPFD was less than that of Crank–Nicolson when solving the linear ADR equation.