New Monotonic Properties of the Class of Positive Solutions of Even-Order Neutral Differential Equations

Abstract

In this study, new asymptotic properties of positive solutions of the even-order neutral delay differential equation with the noncanonical operator are established. The new properties are of an iterative nature, which allows it to be applied several times. Using these properties, we obtain new criteria to exclude a class from the positive solutions of the studied equation, using the comparison principles.

1. Introduction

Differential equations (DE) are crucial for understanding real-life problems and phenomena, or at the very least for knowing the characteristics of the solutions to the equations resulting from modeling these phenomena. However, DEs, such as the ones presented, that are utilized to address real-world issues may not be explicitly solvable, i.e., may not have closed-form solutions. Only equations with simple forms accept the solutions supplied by explicit formulae. In recent decades, different models of DEs have been established in various fields, which have led to stimulate research in the qualitative theory of DEs. Qualitative properties of differential equations have received a lot of attention, such as existence, oscillation, periodicity, boundedness, stability; see for example [1,2].

Neutral differential equations (NDE) are a type of functional differential equation in which the highest derivative of the unknown function appears with and without delay. The qualitative analysis of such equations has a lot of practical use in addition to its theoretical value. This is due to the fact that NDEs appear in a variety of situations, such as problems involving lossless transmission lines in electric networks (as in high-speed computers, where such lines are used to interconnect switching circuits), the study of vibrating masses attached to an elastic bar, and the solution of variational problems with time delays; see Hale [2].

The essence of oscillation theory is to establish conditions for the existence of oscillatory (non-oscillatory) solutions and/or convergence to zero, studying the laws of distribution of the zeros, obtaining lower limits for the separation between successive zeros, and considering the number of zeros of each given span, as well as looking at the relationship between the oscillatory properties of solutions and corresponding oscillatory processes in a system. The oscillation theory has become a significant numerical mathematical tool for many disciplines and high technologies. The subject of finding oscillation criteria for certain functional DEs has been a highly active study area in recent decades, and the monographs by Agarwal et al. [3,4] and Győri and Ladas [5] contain many references and descriptions of known results.

Let us denote the composition of two functions f and g by $g\circ f$, that is, $\left(g\circ f\right)\left(t\right)=g\left(f\left(t\right)\right)$. Consider the NDE of the form

$${\left(a·{\left(x+p·\left(x\circ \tau \right)\right)}^{\left(n-1\right)}\right)}^{\prime }+q·\left(x\circ \zeta \right)=0,\mathfrak{k}\ge {\mathfrak{k}}_0,$$

(1)

where $n\ge 4$ is an even natural number, $a,$$p,$$\tau$ and $\zeta$ in $C^1\left(\left[{\mathfrak{k}}_0,\infty \right)\right)$, q in $C\left(\left[{\mathfrak{k}}_0,\infty \right)\right)$, $a\left(\mathfrak{k}\right)>0$, $a^{\prime }\left(\mathfrak{k}\right)\ge 0$, $0\le p\left(\mathfrak{k}\right)<1$, $q\left(\mathfrak{k}\right)\ge 0$, $\tau \left(\mathfrak{k}\right)\le \mathfrak{k}$, $\zeta \left(\mathfrak{k}\right)\le \mathfrak{k}$, ${\zeta }^{\prime }\left(\mathfrak{k}\right)\ge 0$, and ${lim}_{\mathfrak{k}\to \infty }\tau \left(\mathfrak{k}\right)=\infty ={lim}_{\mathfrak{k}\to \infty }\zeta \left(\mathfrak{k}\right)$. By a proper solution of (1), we mean a real-valued function x in $C^{n-1}\left(\left[{\mathfrak{k}}_0,\infty \right)\right)$ with

$$a·{\left(x+p\left(x\circ \tau \right)\right)}^{\left(n-1\right)}\in C^1\left(\left[{\mathfrak{k}}_0,\infty \right)\right),sup\{\left|x\left(\mathfrak{k}\right)\right|:\mathfrak{k}\ge {\mathfrak{k}}_{*}\}>0,\mathrm{for}{\mathfrak{k}}_{*}\ge {\mathfrak{k}}_0,$$

and x satisfies (1) on $\left[{\mathfrak{k}}_0,\infty \right)$. In this paper, we study the asymptotic and oscillatory behavior of solutions of (1) in the non-canonical case, that is

$${\int }_{{\mathfrak{k}}_0}^{\infty }{a}^{-1}\left(\eta \right)\mathrm{d}\eta <\infty .$$

Jacob Robert Emden (1862–1940), a Swiss astrophysicist, and Sir Ralph Howard Fowler (1889–1944), an English astronomer, are the namesakes of the famous Emden–Fowler equation. Fowler investigated the equation to explain many fluid mechanics phenomena [6]. Since then, there has been a surge of interest in generalizing this equation and using it to explain a variety of physical processes [7,8]. Equation (1) is a generalization of the Emden–Fowler equation in the higher-order and the neutral case.

Studying the qualitative behavior of solutions to differential equations is of great importance, especially in the case of an inability to find a solution to differential equations. On the other hand, numerical studies are important in understanding, analyzing and interpreting different phenomena (see, for example, [9,10]).

In 2011, Zhang et al. [11] presented conditions that ensure the convergence of non-oscillatory solutions to zero of the equation

$${\left(a·{\left(x^{\left(n-1\right)}\right)}^{\alpha }\right)}^{\prime }+q·\left(x^{\beta }\circ \zeta \right)=0,$$

(2)

where $\alpha$ and $\beta$ are ratios of odd positive integers. Zhang et al. [12] provided criteria for oscillation of all solutions of (2). Using the comparison technique, Baculíková [13] investigated the oscillation of the solutions of the equation

$${\left(a·{\left(x^{\left(n-1\right)}\right)}^{\alpha }\right)}^{\prime }+q·\left(f\circ x\circ \zeta \right)=0,$$

(3)

where $f^{\prime }\left(x\right)\ge 0$ and $-f\left(-xy\right)\ge f\left(xy\right)\ge f\left(x\right)f\left(y\right),$ for $xy>0.$ Moaaz and Muhib [14] studied the oscillation of (2) and presented improved results in [12,13].

On the other hand, the study of the oscillatory behavior of solutions of second-order delay differential equations was recently developed. To track this development, see [15,16,17,18,19]. Baculíková [15] established the monotonic properties of nonoscillatory solutions of the linear equation

$${\left(a·x^{\prime }\right)}^{\prime }+q·\left(x\circ \zeta \right)=0,$$

in the delay and advanced cases. He provided criteria for oscillation, which improved the results in [16]. For the NDE

$${\left(a·{\left({\left(x+p·\left(x\circ \tau \right)\right)}^{\prime }\right)}^{\alpha }\right)}^{\prime }+q·\left(x^{\alpha }\circ \zeta \right)=0,$$

(4)

Bohner et al. [18] and Moaaz et al. [19] verified the oscillatory behavior of this equation in the non-canonical case.

On the other hand, the study of the asymptotic behavior of delay differential equations in the non-canonical case differs greatly from the canonical case. The possibilities of signs of derivatives of positive solutions are more in the non-canonical case, and this opens the way for the use of different approaches and methods to exclude positive solutions. Anis and Moaaz [20] presented oscillation criteria for the equation

$${\left({\left(x+p·\left(x\circ \tau \right)\right)}^{\left(n-1\right)}\right)}^{\prime }+q·\left(x\circ \zeta \right)=0,$$

and Moaaz et al. [21] verified the oscillatory behavior of (4) in the canonical case.

The main objective of this study is to find the new monotonic properties of a class of positive solutions of (1) in the non-canonical case. Then, we improve these properties by establishing them in an iterative nature. By using these properties, we can obtain an iterative criterion that ensures that there are no solutions in the class of the positive solutions under study. The results in this paper extend the approach used in [15] for the higher order as well as the neutral equations. Finally, we test the effect of this improvement on a special case of (1).

Lemma 1.

Lemma 2.2.3 of [3]. If $\mathfrak{g}$is in $C^r(\left[{\mathfrak{k}}_0,\infty \right),\left(0,\infty \right))$ with derivatives up to order $r-1$ of constant sign, ${\mathfrak{g}}^{\left(\kappa -1\right)}\left(\mathfrak{k}\right){\mathfrak{g}}^{\left(\kappa \right)}\left(\mathfrak{k}\right)\le 0$for $\mathfrak{k}\ge {\mathfrak{k}}_1\ge {\mathfrak{k}}_0$, and ${lim}_{\mathfrak{k}\to \infty }\mathfrak{g}\left(\mathfrak{k}\right)\ne 0$, then there is a ${\mathfrak{k}}_{\mu }\ge {\mathfrak{k}}_1$ such that

$$\mathfrak{g}\left(\mathfrak{k}\right)\ge \frac{\mu }{\left(r-1\right)!}{\mathfrak{k}}^{r-1}\left|{\mathfrak{g}}^{\left(r-1\right)}\left(\mathfrak{k}\right)\right|,$$

for all $\mathfrak{k}\ge {\mathfrak{k}}_{\mu }$ and $\mu \in (0,1)$.

2. Main Results

Naturally, the qualitative study of the solutions of the NDDs begins with the classification of the signs of the derivatives of the function

$$\upsilon \stackrel{\mathrm{def}}{=}x+p·\left(x\circ \tau \right).$$

(5)

Assume that x is a positive solution to Equation (1). Since ${lim}_{\mathfrak{k}\to \infty }\tau \left(\mathfrak{k}\right)=\infty$ and ${lim}_{\mathfrak{k}\to \infty }\zeta \left(\mathfrak{k}\right)=\infty$, there is a ${\mathfrak{k}}_1>{\mathfrak{k}}_0$ such that $x\circ \tau$ and $x\circ \zeta$ are positive for all $\mathfrak{k}\ge {\mathfrak{k}}_1$. Thus, $\upsilon \left(\mathfrak{k}\right)>0$ and ${\left(a\left(\mathfrak{k}\right){\upsilon }^{\left(n-1\right)}\left(\mathfrak{k}\right)\right)}^{\prime }\le 0$. Taking into account Lemma 2.2.3 in [3], the following are the possible cases, eventually:

$$\begin{array}{cc}\mathbf{P}1:& {\upsilon }^{\left(r\right)}\left(\mathfrak{k}\right)>0\mathrm{for}r=0,1,n-1\mathrm{and}{\upsilon }^{\left(n\right)}\left(\mathfrak{k}\right)<0;\hfill \\ \mathbf{P}2:& {\upsilon }^{\left(r\right)}\left(\mathfrak{k}\right)>0\mathrm{for}r=0,1,n-2\mathrm{and}{\upsilon }^{\left(n-1\right)}\left(\mathfrak{k}\right)<0;\hfill \\ \mathbf{P}3:& {\left(-1\right)}^r{\upsilon }^{\left(r\right)}\left(\mathfrak{k}\right)>0\mathrm{for}r=0,1,\dots ,n-1.\hfill \end{array}$$

Here, we define the class ℑ as the set of all positive solutions of (1) with $\upsilon$ satisfying $\mathbf{P}2$. Further, we define the functions $B_m$ and Q by

$$B_0\left(\mathfrak{k}\right)\stackrel{\mathrm{def}}{=}{\int }_{\mathfrak{k}}^{\infty }{a}^{-1}\left(\eta \right)\mathrm{d}\eta ,B_m\left(\mathfrak{k}\right)\stackrel{\mathrm{def}}{=}{\int }_{\mathfrak{k}}^{\infty }{B}_{m-1}\left(\eta \right)\mathrm{d}\eta ,\mathrm{for}m=1,2,\dots ,n-2,$$

and

$$Q\left(\mathfrak{k}\right)\stackrel{\mathrm{def}}{=}q\left(\mathfrak{k}\right)\left(1-p\left(\zeta \left(\mathfrak{k}\right)\right)\right).$$

Lemma 2.

Assuming that x belongs to ℑ, we obtain the following cases, eventually:

$\begin{array}{cc}\left({\mathfrak{r}}_{1,1}\right)& x\left(\mathfrak{k}\right)>\left(1-p\left(\mathfrak{k}\right)\right)\upsilon \left(\mathfrak{k}\right);\hfill \\ \left({\mathfrak{r}}_{1,2}\right)& \upsilon \left(\mathfrak{k}\right)\ge {\left(\left(n-2\right)!\right)}^{-1}{\mu }_0{\mathfrak{k}}^{n-2}{\upsilon }^{\left(n-2\right)}\left(\mathfrak{k}\right)\mathit{for}\mathit{all}{\mu }_0\in \left(0,1\right);\hfill \\ \left({\mathfrak{r}}_{1,3}\right)& {\left(a\left(\mathfrak{k}\right){\upsilon }^{\left(n-1\right)}\left(\mathfrak{k}\right)\right)}^{\prime }\le -Q\left(\mathfrak{k}\right)\upsilon \left(\zeta \left(\mathfrak{k}\right)\right);\hfill \\ \left({\mathfrak{r}}_{1,4}\right)& \upsilon {}^{\left(n-2\right)}\left(\mathfrak{k}\right)\ge -B{}_0\left(\mathfrak{k}\right)a\left(\mathfrak{k}\right)\upsilon {}^{\left(n-1\right)}\left(\mathfrak{k}\right);\hfill \\ \left({\mathfrak{r}}_{1,5}\right)& {\upsilon }^{\left(n-2\right)}\left(\mathfrak{k}\right)/B_0\left(\mathfrak{k}\right)\mathit{is}\mathit{increasing}.\hfill \end{array}$

Proof. 

As a result of the facts that $x\in \Im$ and $\tau \left(\mathfrak{k}\right)\le \mathfrak{k}$, we get that ${\upsilon }^{\prime }\left(\mathfrak{k}\right)>0$ and $x\left(\tau \left(\mathfrak{k}\right)\right)\le \upsilon \left(\tau \left(\mathfrak{k}\right)\right)\le \upsilon \left(\mathfrak{k}\right)$. Thus, it follows from (5) that $x\left(\mathfrak{k}\right)>\left(1-p\left(\mathfrak{k}\right)\right)\upsilon \left(\mathfrak{k}\right)$ and therefore, $\left({\mathfrak{r}}_{1.1}\right)$ is proved.

Using Lemma 1 with $r=n-1$ and $\mathfrak{g}=\upsilon$, we obtain $\left({\mathfrak{r}}_{1,2}\right)$ for all ${\mu }_0\in \left(0,1\right)$. Next, Equation (1), with $\left({\mathfrak{r}}_{1,1}\right)$ becomes

$$\begin{array}{ccc}\hfill {\left(a\left(\mathfrak{k}\right){\upsilon }^{\left(n-1\right)}\left(\mathfrak{k}\right)\right)}^{\prime }& =& -q\left(\mathfrak{k}\right)x\left(\left(\zeta \left(\mathfrak{k}\right)\right)\right)\hfill \\ & \le & -q\left(\mathfrak{k}\right)\left(1-p\left(\zeta \left(\mathfrak{k}\right)\right)\right)\upsilon \left(\zeta \left(\mathfrak{k}\right)\right)\hfill \\ & =& Q\left(\mathfrak{k}\right)\upsilon \left(\zeta \left(\mathfrak{k}\right)\right).\hfill \end{array}$$

Moreover, we have

$${\int }_{\mathfrak{k}}^{\infty }{\upsilon }^{\left(n-1\right)}\left(s\right)\mathrm{d}s={\int }_{\mathfrak{k}}^{\infty }\frac{1}{a\left(s\right)}a\left(s\right){\upsilon }^{\left(n-1\right)}\left(s\right)\mathrm{d}s\le B_0\left(\mathfrak{k}\right)a\left(\mathfrak{k}\right){\upsilon }^{\left(n-1\right)}\left(\mathfrak{k}\right).$$

(6)

Since ${\upsilon }^{\left(n-2\right)}$ is a positive decreasing function, we conclude that ${\upsilon }^{\left(n-2\right)}$ converges to a non-negative constant, and this with (6) gives

$${\upsilon }^{\left(n-2\right)}\left(\mathfrak{k}\right)\ge -B_0\left(\mathfrak{k}\right)a\left(\mathfrak{k}\right){\upsilon }^{\left(n-1\right)}\left(\mathfrak{k}\right).$$

This also confirms the positivity of the numerator of the derivative of ${\upsilon }^{\left(n-2\right)}/B_0$, or otherwise,

$$\frac{\mathrm{d}}{\mathrm{d}\mathfrak{k}}\frac{{\upsilon }^{\left(n-2\right)}}{B_0}=\frac{B_0{\upsilon }^{\left(n-1\right)}+a^{-1}{\upsilon }^{\left(n-2\right)}}{B_0^2}\ge 0.$$

This completes the proof. □

Lemma 3.

Assuming that x belongs to ℑ and

$\left({\mathfrak{c}}_1\right)$ there are $\delta \in \left(0,1\right)$ and ${\mathfrak{k}}_1\ge {\mathfrak{k}}_0$ such that

$$a\left(\mathfrak{k}\right)B_0^2\left(\mathfrak{k}\right){\zeta }^{n-2}\left(\mathfrak{k}\right)Q\left(\mathfrak{k}\right)\ge \left(n-2\right)!\delta ,$$

we obtain, for $\mathfrak{k}\ge {\mathfrak{k}}_1$,

$\begin{array}{cc}\left({\mathfrak{r}}_{2,1}\right)& {\upsilon }^{\left(n-2\right)}\left(\mathfrak{k}\right)convergestozero;\hfill \\ \left({\mathfrak{r}}_{2,2}\right)& {\upsilon }^{\left(n-2\right)}\left(\mathfrak{k}\right)/B_0^{{\mathfrak{y}}_0}\left(\mathfrak{k}\right)isdecreasing;\hfill \\ \left({\mathfrak{r}}_{2,3}\right)& {\upsilon }^{\left(n-2\right)}\left(\mathfrak{k}\right)/B_0^{{\mathfrak{y}}_0}\left(\mathfrak{k}\right)converges\mathrm{to}zero;\hfill \\ \left({\mathfrak{r}}_{2,4}\right)& {\upsilon }^{\left(n-2\right)}\left(\mathfrak{k}\right)/B_0^{1-{\mathfrak{y}}_0}\left(\mathfrak{k}\right)isincreasing;\hfill \end{array}$

where ${\mathfrak{y}}_0={\mu }_0\delta ,$${\mu }_0\in \left(0,1\right)$.

Proof. 

First of all, since x belongs to ℑ, we can say that $\left({\mathfrak{r}}_{1,1}\right)-\left({\mathfrak{r}}_{1,5}\right)$ in Lemma 2 are satisfied for all $\mathfrak{k}\ge {\mathfrak{k}}_1$, with ${\mathfrak{k}}_1$ large enough. Now, since ${\upsilon }^{\left(n-2\right)}$ is a positive decreasing function, we conclude that ${\upsilon }^{\left(n-2\right)}$ converges to a non-negative constant, let us say l.

If we assume that $l>0$, then there is a ${\mathfrak{k}}_2\ge {\mathfrak{k}}_1$ with ${\upsilon }^{\left(n-2\right)}\left(\mathfrak{k}\right)\ge l$ for $\mathfrak{k}\ge {\mathfrak{k}}_2$, which with $\left({\mathfrak{r}}_{1,2}\right)$ gives

$$\upsilon \left(\mathfrak{k}\right)\ge \frac{{\mu }_{0}l}{\left(n-2\right)!}{\mathfrak{k}}^{n-2},$$

for all ${\mu }_0\in \left(0,1\right)$. Thus, from $\left({\mathfrak{r}}_{1,3}\right)$, we get

$${\left(a\left(\mathfrak{k}\right){\upsilon }^{\left(n-1\right)}\left(\mathfrak{k}\right)\right)}^{\prime }\le -\frac{{\mu }_{0}l}{\left(n-2\right)!}{\zeta }^{n-2}\left(\mathfrak{k}\right)Q\left(\mathfrak{k}\right),$$

which with $\left({\mathfrak{c}}_1\right)$ gives

$${\left(a\left(\mathfrak{k}\right){\upsilon }^{\left(n-1\right)}\left(\mathfrak{k}\right)\right)}^{\prime }\le -{\mathfrak{y}}_{0}l\frac{1}{a\left(\mathfrak{k}\right)B_0^2\left(\mathfrak{k}\right)}.$$

If we integrate the previous inequality from ${\mathfrak{k}}_2$ to $\mathfrak{k}$, then we obtain

$$\begin{array}{ccc}\hfill a\left(\mathfrak{k}\right){\upsilon }^{\left(n-1\right)}\left(\mathfrak{k}\right)& \le & a\left({\mathfrak{k}}_2\right){\upsilon }^{\left(n-1\right)}\left({\mathfrak{k}}_2\right)-{\mathfrak{y}}_{0}l{\int }_{{\mathfrak{k}}_2}^{\mathfrak{k}}\frac{1}{a\left(s\right)B_0^2\left(s\right)}\mathrm{d}s\hfill \\ & \le & {\mathfrak{y}}_{0}l\left(\frac{1}{B_0\left({\mathfrak{k}}_2\right)}-\frac{1}{B_0\left(\mathfrak{k}\right)}\right).\hfill \end{array}$$

(7)

Since $B_0^{-1}\left(\mathfrak{k}\right)\to \infty$ as $\mathfrak{k}\to \infty$, there is a ${\mathfrak{k}}_3\ge {\mathfrak{k}}_2$ such that $B_0^{-1}\left(\mathfrak{k}\right)-B_0^{-1}\left({\mathfrak{k}}_2\right)\ge ϵB_0^{-1}\left(\mathfrak{k}\right)$ for all $ϵ\in \left(0,1\right)$. Hence, (7) becomes

$${\upsilon }^{\left(n-1\right)}\left(\mathfrak{k}\right)\le -\frac{{\mathfrak{y}}_{0}lϵ}{a\left(\mathfrak{k}\right)B_0\left(\mathfrak{k}\right)},$$

for all $\mathfrak{k}\ge {\mathfrak{k}}_3$. By integrating the above inequality from ${\mathfrak{k}}_3$ to $\mathfrak{k}$, we obtain

$$\begin{array}{ccc}\hfill {\upsilon }^{\left(n-2\right)}\left(\mathfrak{k}\right)& \le & {\upsilon }^{\left(n-2\right)}\left({\mathfrak{k}}_3\right)-{\mathfrak{y}}_{0}lϵ{\int }_{{\mathfrak{k}}_3}^{\mathfrak{k}}\frac{1}{a\left(s\right)B_0\left(s\right)}\mathrm{d}s\hfill \\ & \le & {\upsilon }^{\left(n-2\right)}\left({\mathfrak{k}}_3\right)-{\mathfrak{y}}_{0}lϵln\frac{B_0\left({\mathfrak{k}}_3\right)}{B_0\left(\mathfrak{k}\right)},\hfill \end{array}$$

and therefore ${lim}_{\mathfrak{k}\to \infty }{\upsilon }^{\left(n-2\right)}\left(\mathfrak{k}\right)=-\infty$, which is a contradiction. Then, $l=0$.

Next, from $\left({\mathfrak{c}}_1\right),$$\left({\mathfrak{r}}_{1,2}\right)$ and $\left({\mathfrak{r}}_{1,3}\right)$, we have

$$\begin{array}{ccc}\hfill {\left(a\left(\mathfrak{k}\right){\upsilon }^{\left(n-1\right)}\left(\mathfrak{k}\right)\right)}^{\prime }& \le & -\frac{{\mu }_0}{\left(n-2\right)!}{\zeta }^{n-2}\left(\mathfrak{k}\right)Q\left(\mathfrak{k}\right){\upsilon }^{\left(n-2\right)}\left(\zeta \left(\mathfrak{k}\right)\right)\hfill \\ & \le & -\frac{{\mathfrak{y}}_0}{a\left(\mathfrak{k}\right)B_0^2\left(\mathfrak{k}\right)}{\upsilon }^{\left(n-2\right)}\left(\zeta \left(\mathfrak{k}\right)\right).\hfill \end{array}$$

By integrating this inequality from ${\mathfrak{k}}_1$ to $\mathfrak{k}$ and using the fact that ${\upsilon }^{\left(n-1\right)}\left(\mathfrak{k}\right)<0$, we obtain

$$\begin{array}{ccc}\hfill a\left(\mathfrak{k}\right){\upsilon }^{\left(n-1\right)}\left(\mathfrak{k}\right)& \le & a\left({\mathfrak{k}}_1\right){\upsilon }^{\left(n-1\right)}\left({\mathfrak{k}}_1\right)-{\int }_{{\mathfrak{k}}_1}^{\mathfrak{k}}\frac{{\mathfrak{y}}_0}{a\left(s\right)B_0^2\left(s\right)}{\upsilon }^{\left(n-2\right)}\left(\zeta \left(s\right)\right)\mathrm{d}s\hfill \\ & \le & a\left({\mathfrak{k}}_1\right){\upsilon }^{\left(n-1\right)}\left({\mathfrak{k}}_1\right)-{\mathfrak{y}}_0{\upsilon }^{\left(n-2\right)}\left(\mathfrak{k}\right){\int }_{{\mathfrak{k}}_1}^{\mathfrak{k}}\frac{1}{a\left(s\right)B_0^2\left(s\right)}\mathrm{d}s\hfill \\ & \le & a\left({\mathfrak{k}}_1\right){\upsilon }^{\left(n-1\right)}\left({\mathfrak{k}}_1\right)+\frac{{\mathfrak{y}}_0}{B_0\left({\mathfrak{k}}_1\right)}{\upsilon }^{\left(n-2\right)}\left(\mathfrak{k}\right)-\frac{{\mathfrak{y}}_0}{B_0\left(\mathfrak{k}\right)}{\upsilon }^{\left(n-2\right)}\left(\mathfrak{k}\right).\hfill \end{array}$$

(8)

As a result of ${\upsilon }^{\left(n-2\right)}\left(\mathfrak{k}\right)\to 0$ as $\mathfrak{k}\to \infty$, there is a ${\mathfrak{k}}_2\ge {\mathfrak{k}}_1$ such that

$$a\left({\mathfrak{k}}_1\right){\upsilon }^{\left(n-1\right)}\left({\mathfrak{k}}_1\right)+\frac{{\mathfrak{y}}_0}{B_0\left({\mathfrak{k}}_1\right)}{\upsilon }^{\left(n-2\right)}\left(\mathfrak{k}\right)\le 0,$$

for $\mathfrak{k}\ge {\mathfrak{k}}_2$. Therefore, we have

$$a\left(\mathfrak{k}\right){\upsilon }^{\left(n-1\right)}\left(\mathfrak{k}\right)B_0\left(\mathfrak{k}\right)+{\mathfrak{y}}_0{\upsilon }^{\left(n-2\right)}\left(\mathfrak{k}\right)\le 0,$$

(9)

and then

$$\begin{array}{ccc}\hfill {\left(\frac{{\upsilon }^{\left(n-2\right)}\left(\mathfrak{k}\right)}{B_0^{{\mathfrak{y}}_0}\left(\mathfrak{k}\right)}\right)}^{\prime }& =& \frac{1}{B_0^{2{\mathfrak{y}}_0}\left(\mathfrak{k}\right)}\left(B_0^{{\mathfrak{y}}_0}\left(\mathfrak{k}\right){\upsilon }^{\left(n-1\right)}\left(\mathfrak{k}\right)-{\mathfrak{y}}_0\frac{B_0^{{\mathfrak{y}}_0-1}\left(\mathfrak{k}\right)}{-a\left(\mathfrak{k}\right)}{\upsilon }^{\left(n-2\right)}\left(\mathfrak{k}\right)\right)\hfill \\ & =& \frac{1}{B_0^{{\mathfrak{y}}_0+1}\left(\mathfrak{k}\right)}\left(B_0\left(\mathfrak{k}\right){\upsilon }^{\left(n-1\right)}\left(\mathfrak{k}\right)+\frac{{\mathfrak{y}}_0}{a\left(\mathfrak{k}\right)}{\upsilon }^{\left(n-2\right)}\left(\mathfrak{k}\right)\right)\hfill \\ & \le & 0.\hfill \end{array}$$

Now, we have that ${\upsilon }^{\left(n-2\right)}/B_0^{{\mathfrak{y}}_0}$ is a positive decreasing function. Then, ${\upsilon }^{\left(n-2\right)}/B_0^{{\mathfrak{y}}_0}$ converges to a non-negative constant, let us say k.

Suppose that $k>0$. Hence,

$$\frac{{\upsilon }^{\left(n-2\right)}\left(\mathfrak{k}\right)}{B_0^{{\mathfrak{y}}_0}\left(\mathfrak{k}\right)}\ge k,$$

(10)

for $\mathfrak{k}\ge {\mathfrak{k}}_3$, where ${\mathfrak{k}}_3\ge {\mathfrak{k}}_2$ and is large enough.

From $\left({\mathfrak{r}}_{1,4}\right)$, we see that the function

$$\frac{{\upsilon }^{\left(n-2\right)}\left(\mathfrak{k}\right)+a\left(\mathfrak{k}\right){\upsilon }^{\left(n-1\right)}\left(\mathfrak{k}\right)B_0\left(\mathfrak{k}\right)}{B_0^{{\mathfrak{y}}_0}\left(\mathfrak{k}\right)}$$

(11)

is positive. Moreover,

$$\begin{array}{ccc}& & {\left(\frac{{\upsilon }^{\left(n-2\right)}\left(\mathfrak{k}\right)+a\left(\mathfrak{k}\right){\upsilon }^{\left(n-1\right)}\left(\mathfrak{k}\right)B_0\left(\mathfrak{k}\right)}{B_0^{{\mathfrak{y}}_0}\left(\mathfrak{k}\right)}\right)}^{\prime }\hfill \\ & =& \frac{{\upsilon }^{\left(n-1\right)}\left(\mathfrak{k}\right)+{\left(a\left(\mathfrak{k}\right){\upsilon }^{\left(n-1\right)}\left(\mathfrak{k}\right)\right)}^{\prime }{B}_0\left(\mathfrak{k}\right)+a\left(\mathfrak{k}\right){\upsilon }^{\left(n-1\right)}\left(\mathfrak{k}\right)B_0^{\prime }\left(\mathfrak{k}\right)}{B_0^{{\mathfrak{y}}_0}\left(\mathfrak{k}\right)}\hfill \\ & & +{\mathfrak{y}}_0\frac{{\upsilon }^{\left(n-2\right)}\left(\mathfrak{k}\right)+a\left(\mathfrak{k}\right){\upsilon }^{\left(n-1\right)}\left(\mathfrak{k}\right)B_0\left(\mathfrak{k}\right)}{a\left(\mathfrak{k}\right)B_0^{{\mathfrak{y}}_0+1}\left(\mathfrak{k}\right)}\hfill \\ & =& \frac{{\left(a\left(\mathfrak{k}\right){\upsilon }^{\left(n-1\right)}\left(\mathfrak{k}\right)\right)}^{\prime }}{B_0^{{\mathfrak{y}}_0-1}\left(\mathfrak{k}\right)}+{\mathfrak{y}}_0\frac{{\upsilon }^{\left(n-2\right)}\left(\mathfrak{k}\right)}{a\left(\mathfrak{k}\right)B_0^{{\mathfrak{y}}_0+1}\left(\mathfrak{k}\right)}+{\mathfrak{y}}_0\frac{{\upsilon }^{\left(n-1\right)}\left(\mathfrak{k}\right)}{B_0^{{\mathfrak{y}}_0}\left(\mathfrak{k}\right)}.\hfill \end{array}$$

(12)

From $\left({\mathfrak{r}}_{1,3}\right)$, $\left({\mathfrak{r}}_{1,4}\right)$ and $\left({\mathfrak{c}}_1\right)$, we get

$$\begin{array}{ccc}\hfill {\left(a\left(\mathfrak{k}\right){\upsilon }^{\left(n-1\right)}\left(\mathfrak{k}\right)\right)}^{\prime }& \le & -\frac{{\mu }_0}{\left(n-2\right)!}Q\left(\mathfrak{k}\right){\zeta }^{n-2}\left(\mathfrak{k}\right){\upsilon }^{\left(n-2\right)}\left(\zeta \left(\mathfrak{k}\right)\right)\hfill \\ & \le & -{\mathfrak{y}}_0\frac{1}{a\left(\mathfrak{k}\right)B_0^2\left(\mathfrak{k}\right)}{\upsilon }^{\left(n-2\right)}\left(\zeta \left(\mathfrak{k}\right)\right),\hfill \end{array}$$

(13)

which with (12) gives

$$\begin{array}{ccc}\hfill {\left(\frac{{\upsilon }^{\left(n-2\right)}\left(\mathfrak{k}\right)+a\left(\mathfrak{k}\right){\upsilon }^{\left(n-1\right)}\left(\mathfrak{k}\right)B_0\left(\mathfrak{k}\right)}{B_0^{{\mathfrak{y}}_0}\left(\mathfrak{k}\right)}\right)}^{\prime }& \le & -{\mathfrak{y}}_0\frac{{\upsilon }^{\left(n-2\right)}\left(\zeta \left(\mathfrak{k}\right)\right)}{a\left(\mathfrak{k}\right)B_0^{{\mathfrak{y}}_0+1}\left(\mathfrak{k}\right)}+{\mathfrak{y}}_0\frac{{\upsilon }^{\left(n-2\right)}\left(\mathfrak{k}\right)}{a\left(\mathfrak{k}\right)B_0^{{\mathfrak{y}}_0+1}\left(\mathfrak{k}\right)}+{\mathfrak{y}}_0\frac{{\upsilon }^{\left(n-1\right)}\left(\mathfrak{k}\right)}{B_0^{{\mathfrak{y}}_0}\left(\mathfrak{k}\right)}\hfill \\ & =& {\mathfrak{y}}_0\frac{{\upsilon }^{\left(n-2\right)}\left(\mathfrak{k}\right)-{\upsilon }^{\left(n-2\right)}\left(\zeta \left(\mathfrak{k}\right)\right)}{a\left(\mathfrak{k}\right)B_0^{{\mathfrak{y}}_0+1}\left(\mathfrak{k}\right)}+{\mathfrak{y}}_0\frac{{\upsilon }^{\left(n-1\right)}\left(\mathfrak{k}\right)}{B_0^{{\mathfrak{y}}_0}\left(\mathfrak{k}\right)}.\hfill \end{array}$$

(14)

Since ${\upsilon }^{\left(n-1\right)}\left(\mathfrak{k}\right)\le 0$ and $\zeta \left(\mathfrak{k}\right)\le \mathfrak{k}$, we obtain ${\upsilon }^{\left(n-2\right)}\left(\zeta \left(\mathfrak{k}\right)\right)\ge {\upsilon }^{\left(n-2\right)}\left(\mathfrak{k}\right)$, and then (14) becomes

$${\left(\frac{{\upsilon }^{\left(n-2\right)}\left(\mathfrak{k}\right)+a\left(\mathfrak{k}\right){\upsilon }^{\left(n-1\right)}\left(\mathfrak{k}\right)B_0\left(\mathfrak{k}\right)}{B_0^{{\mathfrak{y}}_0}\left(\mathfrak{k}\right)}\right)}^{\prime }\le {\mathfrak{y}}_0\frac{{\upsilon }^{\left(n-1\right)}\left(\mathfrak{k}\right)}{B_0^{{\mathfrak{y}}_0}\left(\mathfrak{k}\right)}.$$

Using (9) and (10), we conclude that

$${\left(\frac{{\upsilon }^{\left(n-2\right)}\left(\mathfrak{k}\right)+a\left(\mathfrak{k}\right){\upsilon }^{\left(n-1\right)}\left(\mathfrak{k}\right)B_0\left(\mathfrak{k}\right)}{B_0^{{\mathfrak{y}}_0}\left(\mathfrak{k}\right)}\right)}^{\prime }\le -\frac{{\mathfrak{y}}_0^{2}k}{a\left(\mathfrak{k}\right)B_0\left(\mathfrak{k}\right)}<0.$$

Then, the function defined in (11) is a positive decreasing function that converges to a non-negative constant. Furthermore, if we integrate the last inequality from ${\mathfrak{k}}_3$ to ∞, then we obtain

$$-\frac{{\upsilon }^{\left(n-2\right)}\left({\mathfrak{k}}_3\right)+a\left({\mathfrak{k}}_3\right){\upsilon }^{\left(n-1\right)}\left({\mathfrak{k}}_3\right)B_0\left({\mathfrak{k}}_3\right)}{B_0^{{\mathfrak{y}}_0}\left({\mathfrak{k}}_3\right)}\le -{\mathfrak{y}}_0^{2}k\underset{\mathfrak{k}\to \infty }{lim}\left(ln\frac{B_0\left({\mathfrak{k}}_3\right)}{B_0\left(\mathfrak{k}\right)}\right)\to \infty ,$$

which is a contradiction. This implies that $k=0$.

Finally, we have

$$\begin{array}{ccc}\hfill {\left(a\left(\mathfrak{k}\right){\upsilon }^{\left(n-1\right)}\left(\mathfrak{k}\right)B_0\left(\mathfrak{k}\right)+{\upsilon }^{\left(n-2\right)}\left(\mathfrak{k}\right)\right)}^{\prime }& =& {\left(a\left(\mathfrak{k}\right){\upsilon }^{\left(n-1\right)}\left(\mathfrak{k}\right)\right)}^{\prime }{B}_0\left(\mathfrak{k}\right)-a\left(\mathfrak{k}\right){\upsilon }^{\left(n-1\right)}\left(\mathfrak{k}\right)a^{-1}\left(\mathfrak{k}\right)+{\upsilon }^{\left(n-1\right)}\left(\mathfrak{k}\right)\hfill \\ & =& {\left(a\left(\mathfrak{k}\right){\upsilon }^{\left(n-1\right)}\left(\mathfrak{k}\right)\right)}^{\prime }{B}_0\left(\mathfrak{k}\right),\hfill \end{array}$$

which with (13) gives

$${\left(a\left(\mathfrak{k}\right){\upsilon }^{\left(n-1\right)}\left(\mathfrak{k}\right)B_0\left(\mathfrak{k}\right)+{\upsilon }^{\left(n-2\right)}\left(\mathfrak{k}\right)\right)}^{\prime }\le -{\mathfrak{y}}_0\frac{1}{a\left(\mathfrak{k}\right)B_0\left(\mathfrak{k}\right)}{\upsilon }^{\left(n-2\right)}\left(\zeta \left(\mathfrak{k}\right)\right).$$

(15)

By integrating this inequality from $\mathfrak{k}$ to ∞ and using $\left({\mathfrak{r}}_{1,5}\right)$, we obtain

$$\begin{array}{ccc}\hfill -a\left(\mathfrak{k}\right){\upsilon }^{\left(n-1\right)}\left(\mathfrak{k}\right)B_0\left(\mathfrak{k}\right)-{\upsilon }^{\left(n-2\right)}\left(\mathfrak{k}\right)& \le & -{\mathfrak{y}}_0{\int }_{\mathfrak{k}}^{\infty }\frac{1}{a\left(s\right)B_0\left(s\right)}{\upsilon }^{\left(n-2\right)}\left(\zeta \left(s\right)\right)\mathrm{d}s\hfill \\ & \le & -{\mathfrak{y}}_0{\int }_{\mathfrak{k}}^{\infty }\frac{1}{a\left(s\right)}\frac{{\upsilon }^{\left(n-2\right)}\left(s\right)}{B_0\left(s\right)}\mathrm{d}s\hfill \\ & \le & -{\mathfrak{y}}_0\frac{{\upsilon }^{\left(n-2\right)}\left(\mathfrak{k}\right)}{B_0\left(\mathfrak{k}\right)}{\int }_{\mathfrak{k}}^{\infty }\frac{1}{a\left(s\right)}\mathrm{d}s\hfill \\ & =& -{\mathfrak{y}}_0{\upsilon }^{\left(n-2\right)}\left(\mathfrak{k}\right).\hfill \end{array}$$

Then

$$\begin{array}{ccc}\hfill {\left(\frac{{\upsilon }^{\left(n-2\right)}\left(\mathfrak{k}\right)}{B_0^{1-{\mathfrak{y}}_0}\left(\mathfrak{k}\right)}\right)}^{\prime }& =& \frac{1}{B_0^{2-2{\mathfrak{y}}_0}\left(\mathfrak{k}\right)}\left(B_0^{1-{\mathfrak{y}}_0}\left(\mathfrak{k}\right){\upsilon }^{\left(n-1\right)}\left(\mathfrak{k}\right)-\left(1-{\mathfrak{y}}_0\right)\frac{B_0^{-{\mathfrak{y}}_0}\left(\mathfrak{k}\right)}{-a\left(\mathfrak{k}\right)}{\upsilon }^{\left(n-2\right)}\left(\mathfrak{k}\right)\right)\hfill \\ & =& \frac{1}{B_0^{2-{\mathfrak{y}}_0}\left(\mathfrak{k}\right)}\left(B_0\left(\mathfrak{k}\right){\upsilon }^{\left(n-1\right)}\left(\mathfrak{k}\right)+\left(1-{\mathfrak{y}}_0\right)\frac{1}{a\left(\mathfrak{k}\right)}{\upsilon }^{\left(n-2\right)}\left(\mathfrak{k}\right)\right)\hfill \\ & \ge & 0.\hfill \end{array}$$

which means that ${\upsilon }^{\left(n-2\right)}\left(\mathfrak{k}\right)/B_0^{1-{\mathfrak{y}}_0}\left(\mathfrak{k}\right)$ is increasing. This completes the proof. □

If ${\mathfrak{y}}_0\le 1/2$, we can improve the properties in Lemma 3, as stated in the following result.

Lemma 4.

Assume that x belongs to ℑ and $\left({\mathfrak{c}}_1\right)$ holds. If

$$\left({\mathfrak{c}}_2\right):\underset{\mathfrak{k}\to \infty }{liminf}\frac{B_0\left(\zeta \left(\mathfrak{k}\right)\right)}{B_0\left(\mathfrak{k}\right)}:=\kappa <\infty ,$$

and there exists an increasing sequence ${\left\{{\mathfrak{y}}_r\right\}}_{r=0}^m$ defined by

$${\mathfrak{y}}_r:={\mathfrak{y}}_0\frac{{\kappa }^{{\mathfrak{y}}_{r-1}}}{1-{\mathfrak{y}}_{r-1}},$$

with ${\mathfrak{y}}_0={\mu }_0\delta$, ${\mathfrak{y}}_{m-1}\le 1/2$ and ${\mathfrak{y}}_m,{\mu }_0\in \left(0,1\right)$, then, eventually,

$\begin{array}{cc}\left({\mathfrak{r}}_{3,1}\right)& {\upsilon }^{\left(n-2\right)}\left(\mathfrak{k}\right)/B_0^{{\mathfrak{y}}_m}\left(\mathfrak{k}\right)isdecreasing;\hfill \\ \left({\mathfrak{r}}_{3,2}\right)& {\upsilon }^{\left(n-2\right)}\left(\mathfrak{k}\right)/B_0^{{\mathfrak{y}}_m}\left(\mathfrak{k}\right)convergestozero;\hfill \\ \left({\mathfrak{r}}_{3,3}\right)& {\upsilon }^{\left(n-2\right)}\left(\mathfrak{k}\right)/B_0^{1-{\mathfrak{y}}_m}\left(\mathfrak{k}\right)isdecreasing;\hfill \end{array}$

Proof. 

First of all, since x belongs to ℑ, we can say that $\left({\mathfrak{r}}_{1,1}\right)-\left({\mathfrak{r}}_{1,5}\right)$ in Lemma 2 are satisfied for all $\mathfrak{k}\ge {\mathfrak{k}}_1$, with ${\mathfrak{k}}_1$ being large enough. Furthermore, from Lemma 3, we have that $\left({\mathfrak{r}}_{2,1}\right)-\left({\mathfrak{r}}_{2,4}\right)$ hold.

Now, assume that ${\mathfrak{y}}_0\le 1/2$, and

$${\mathfrak{y}}_1={\mathfrak{y}}_0\frac{{\kappa }^{{\mathfrak{y}}_0}}{1-{\mathfrak{y}}_0}.$$

Next, we will prove $\left({\mathfrak{r}}_{3,1}\right),$$\left({\mathfrak{r}}_{3,2}\right)$ and $\left({\mathfrak{r}}_{3,3}\right)$ for $m=1$. As in the proof of Lemma 3, we arrive at (13). Integrating (13) from ${\mathfrak{k}}_1$ to $\mathfrak{k}$ and using $\left({\mathfrak{r}}_{2,2}\right)$ and $\left({\mathfrak{c}}_2\right)$, we obtain

$$\begin{array}{ccc}\hfill a\left(\mathfrak{k}\right){\upsilon }^{\left(n-1\right)}\left(\mathfrak{k}\right)& \le & a\left({\mathfrak{k}}_1\right){\upsilon }^{\left(n-1\right)}\left({\mathfrak{k}}_1\right)-{\mathfrak{y}}_0{\int }_{{\mathfrak{k}}_1}^{\mathfrak{k}}\frac{1}{a\left(s\right)B_0^2\left(s\right)}{\upsilon }^{\left(n-2\right)}\left(\zeta \left(s\right)\right)\mathrm{d}s\hfill \\ & \le & a\left({\mathfrak{k}}_1\right){\upsilon }^{\left(n-1\right)}\left({\mathfrak{k}}_1\right)-{\mathfrak{y}}_0{\int }_{{\mathfrak{k}}_1}^{\mathfrak{k}}\frac{1}{a\left(s\right)B_0^2\left(s\right)}{B}_0^{{\mathfrak{y}}_0}\left(\zeta \left(s\right)\right)\frac{{\upsilon }^{\left(n-2\right)}\left(s\right)}{B_0^{{\mathfrak{y}}_0}\left(s\right)}\mathrm{d}s\hfill \\ & \le & a\left({\mathfrak{k}}_1\right){\upsilon }^{\left(n-1\right)}\left({\mathfrak{k}}_1\right)-{\mathfrak{y}}_0\frac{{\upsilon }^{\left(n-2\right)}\left(\mathfrak{k}\right)}{B_0^{{\mathfrak{y}}_0}\left(\mathfrak{k}\right)}{\int }_{{\mathfrak{k}}_1}^{\mathfrak{k}}\frac{B_0^{{\mathfrak{y}}_0-2}\left(s\right)}{a\left(s\right)}\frac{B_0^{{\mathfrak{y}}_0}\left(\zeta \left(s\right)\right)}{B_0^{{\mathfrak{y}}_0}\left(s\right)}\mathrm{d}s\hfill \\ & \le & a\left({\mathfrak{k}}_1\right){\upsilon }^{\left(n-1\right)}\left({\mathfrak{k}}_1\right)-{\mathfrak{y}}_0{\kappa }^{{\mathfrak{y}}_0}\frac{{\upsilon }^{\left(n-2\right)}\left(\mathfrak{k}\right)}{B_0^{{\mathfrak{y}}_0}\left(\mathfrak{k}\right)}{\int }_{{\mathfrak{k}}_1}^{\mathfrak{k}}\frac{B_0^{{\mathfrak{y}}_0-2}\left(s\right)}{a\left(s\right)}\mathrm{d}s\hfill \\ & \le & a\left({\mathfrak{k}}_1\right){\upsilon }^{\left(n-1\right)}\left({\mathfrak{k}}_1\right)+\frac{{\mathfrak{y}}_0{\kappa }^{{\mathfrak{y}}_0}}{1-{\mathfrak{y}}_0}\frac{{\upsilon }^{\left(n-2\right)}\left(\mathfrak{k}\right)}{B_0^{{\mathfrak{y}}_0}\left(\mathfrak{k}\right)}{B}_0^{{\mathfrak{y}}_0-1}\left({\mathfrak{k}}_1\right)-\frac{{\mathfrak{y}}_0{\kappa }^{{\mathfrak{y}}_0}}{1-{\mathfrak{y}}_0}\frac{{\upsilon }^{\left(n-2\right)}\left(\mathfrak{k}\right)}{B_0\left(\mathfrak{k}\right)}.\hfill \end{array}$$

(16)

Using $\left({\mathfrak{r}}_{2,3}\right)$, we have that

$$a\left({\mathfrak{k}}_1\right){\upsilon }^{\left(n-1\right)}\left({\mathfrak{k}}_1\right)+\frac{{\mathfrak{y}}_0{\kappa }^{{\mathfrak{y}}_0}}{1-{\mathfrak{y}}_0}\frac{{\upsilon }^{\left(n-2\right)}\left(\mathfrak{k}\right)}{B_0^{{\mathfrak{y}}_0}\left(\mathfrak{k}\right)}{B}_0^{{\mathfrak{y}}_0-1}\left({\mathfrak{k}}_1\right)\le 0,$$

which, with (16), results in

$$a\left(\mathfrak{k}\right){\upsilon }^{\left(n-1\right)}\left(\mathfrak{k}\right)\le -{\mathfrak{y}}_1\frac{{\upsilon }^{\left(n-2\right)}\left(\mathfrak{k}\right)}{B_0\left(\mathfrak{k}\right)}.$$

Then ${\left({\upsilon }^{\left(n-2\right)}\left(\mathfrak{k}\right)/B_0^{{\mathfrak{y}}_1}\left(\mathfrak{k}\right)\right)}^{\prime }\le 0.$ Proceeding exactly as in the proof of $\left({\mathfrak{r}}_{2,3}\right)$ and $\left({\mathfrak{r}}_{2,4}\right)$, we can verify that $\left({\mathfrak{r}}_{3,2}\right)$ and $\left({\mathfrak{r}}_{3,3}\right)$ hold.

Next, if ${\mathfrak{y}}_1\le 1/2$, then we define

$${\mathfrak{y}}_2={\mathfrak{y}}_0\frac{{\kappa }^{{\mathfrak{y}}_1}}{1-{\mathfrak{y}}_1}.$$

As in the proof of the case for $m=1$, we can prove $\left({\mathfrak{r}}_{3,1}\right),$$\left({\mathfrak{r}}_{3,2}\right)$ and $\left({\mathfrak{r}}_{3,3}\right)$ for $m=2$, and so on. The proof is complete. □

Theorem 1.

Assume that $\left({\mathfrak{c}}_1\right)$ and $\left({\mathfrak{c}}_2\right)$ hold. If there exists a positive integer m such that ${\mathfrak{y}}_m>1/2$ for some ${\mu }_0\in \left(0,1\right)$, then the class ℑ is empty, where ${\mathfrak{y}}_m$ is defined as in Lemma 4.

Proof. 

Assume the contrary, that x belongs to ℑ. From Lemma 4, we have that the functions ${\upsilon }^{\left(n-2\right)}/B_0^{{\mathfrak{y}}_m}$ and ${\upsilon }^{\left(n-2\right)}/B_0^{1-{\mathfrak{y}}_m}$ are decreasing and increasing for $\mathfrak{k}\ge {\mathfrak{k}}_1$, respectively. Then, ${\mathfrak{y}}_m\le 1/2$, which is a contradiction. The proof is complete. □

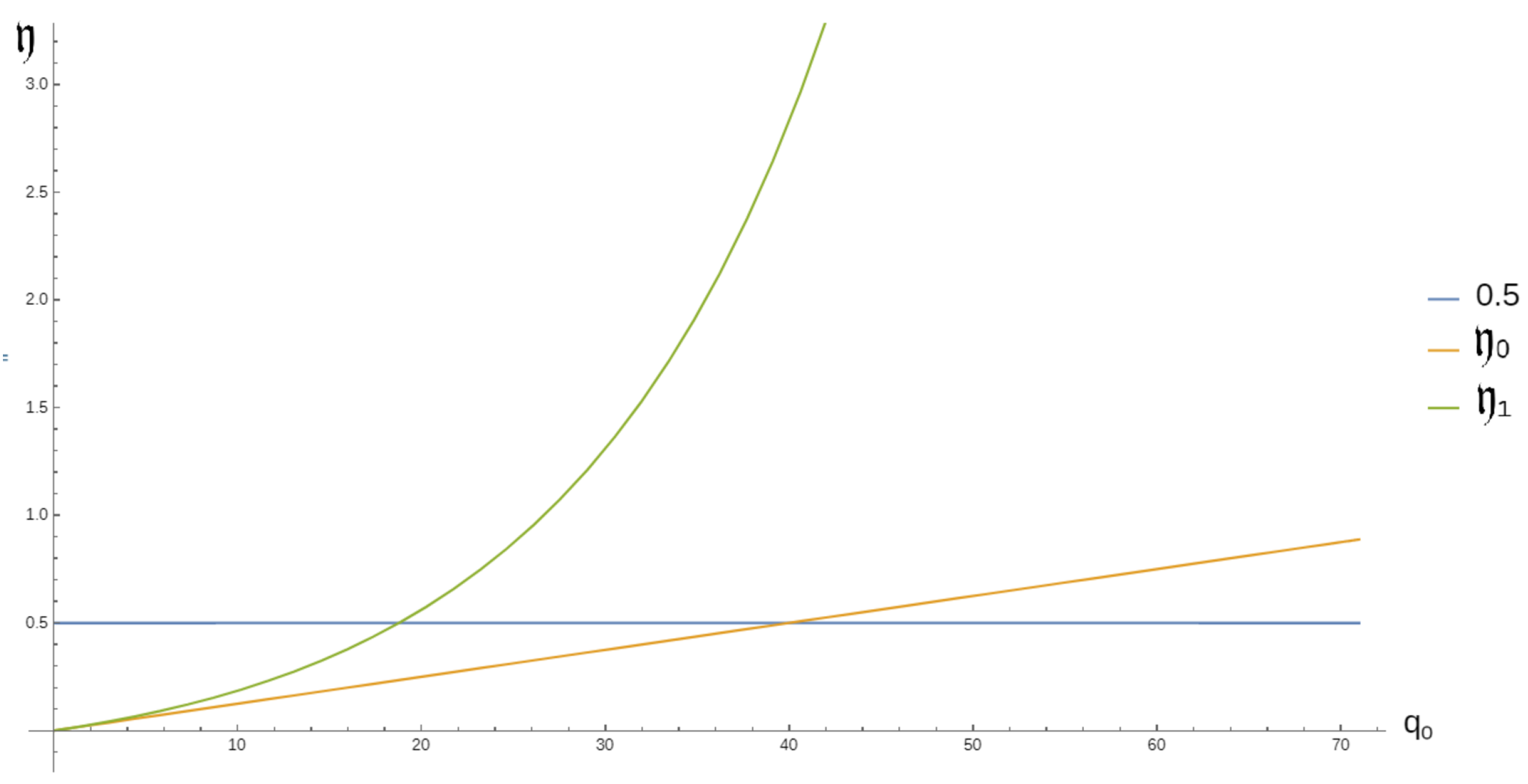
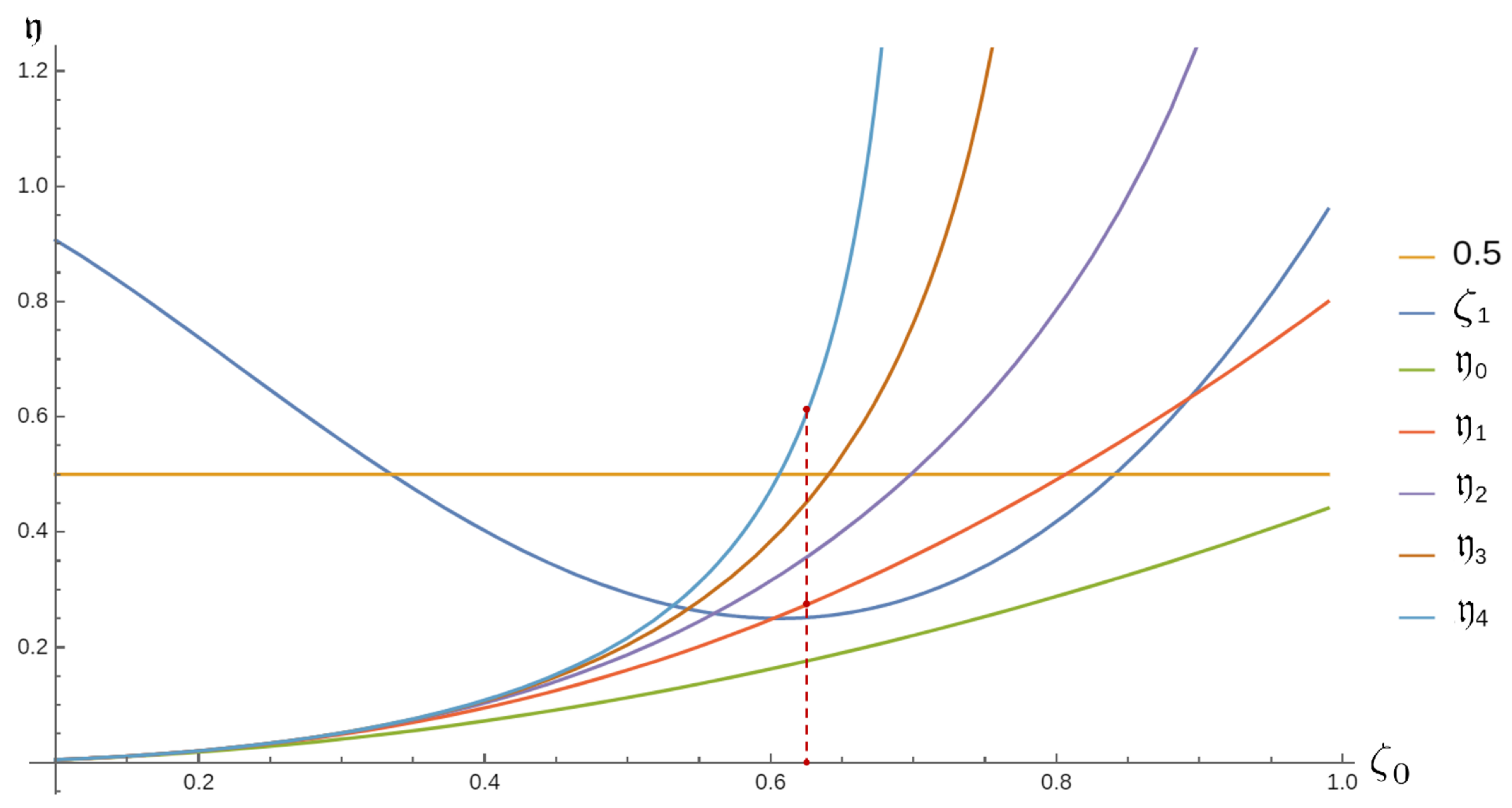
Example 1.

Consider the NDE

$${\left({\mathfrak{k}}^4{\left(x\left(\mathfrak{k}\right)+p_{0}x\left({\tau }_0\mathfrak{k}\right)\right)}^{‴}\right)}^{\prime }+q_{0}x\left({\zeta }_0\mathfrak{k}\right)=0,$$

(17)

where $\mathfrak{k}>0,$ $p_0\in \left[0,1\right),$ ${\tau }_0,{\zeta }_0\in \left(0,1\right)$ and $q_0>0$. By comparing (1) and (17), we note that $n=4,$ $a\left(\mathfrak{k}\right)={\mathfrak{k}}^4,$ $p\left(\mathfrak{k}\right)=p_0,$ $\tau \left(\mathfrak{k}\right)={\tau }_0\mathfrak{k},$ $q\left(\mathfrak{k}\right)=q_0,$ and $\zeta \left(\mathfrak{k}\right)={\zeta }_0\mathfrak{k}$. It is easy to verify that

$$B_0\left(\mathfrak{k}\right)=\frac{1}{3{\mathfrak{k}}^3},B_1\left(\mathfrak{k}\right)=\frac{1}{6{\mathfrak{k}}^2},B_2\left(\mathfrak{k}\right)=\frac{1}{6\mathfrak{k}},$$

and

$$Q\left(\mathfrak{k}\right)=q_0\left(1-p_0\right).$$

For $\left({\mathfrak{c}}_1\right)$, we set

$$\delta :=\frac{1}{18}{\zeta }_0^2{q}_0\left(1-p_0\right),$$

with

$${\zeta }_0^2{q}_0\left(1-p_0\right)<18.$$

(18)

For $\left({\mathfrak{c}}_2\right)$, we have

$$\kappa =\frac{1}{{\zeta }_0^3}.$$

Now, we define the sequence ${\left\{{\mathfrak{y}}_r\right\}}_{r=0}^m$ as

$${\mathfrak{y}}_r=\frac{{\mathfrak{y}}_0}{1-{\mathfrak{y}}_{r-1}}{\left(\frac{1}{{\zeta }_0}\right)}^{3{\mathfrak{y}}_{r-1}},$$

with

$${\mathfrak{y}}_0=\frac{1}{18}{\mu }_0{\zeta }_0^2{q}_0\left(1-p_0\right).$$

where ${\mu }_0\in \left(0,1\right)$.

Special case 1: Consider the NDE

$${\left({\mathfrak{k}}^4{\left(x\left(\mathfrak{k}\right)+\frac{1}{2}x\left({\tau }_0\mathfrak{k}\right)\right)}^{‴}\right)}^{\prime }+18x\left({\zeta }_0\mathfrak{k}\right)=0.$$

(19)

We note that (18) holds. If we set ${\mu }_0=0.9$, then ${\mathfrak{y}}_0=\frac{9}{20}{\zeta }_0^2$ and

$${\mathfrak{y}}_r=\frac{9}{20}\frac{{\left({\zeta }_0\right)}^{2-3{\mathfrak{y}}_{r-1}}}{1-{\mathfrak{y}}_{r-1}},$$

(see Figure 1). We note that ${\mathfrak{y}}_0<1/2$ for all ${\zeta }_0\in \left(0,1\right)$, while ${\mathfrak{y}}_1>1/2$ for all ${\zeta }_0\in \left(0.805,1\right).$

Figure 1. The iterations ${\mathfrak{y}}_r$, for $r=0,1,\dots ,6$ in the special case 1.

Special case 2: Consider the delay equation

$${\left({\mathfrak{k}}^4{x}^{‴}\left(\mathfrak{k}\right)\right)}^{\prime }+q_{0}x\left(\frac{1}{2}\mathfrak{k}\right)=0,$$

where $q_0<72$. If we set ${\mu }_0=0.9$, then ${\mathfrak{y}}_0=\frac{1}{80}{q}_0$ and

$${\mathfrak{y}}_r=\frac{1}{80}\frac{q_0}{1-{\mathfrak{y}}_{r-1}}{\left(2\right)}^{3{\mathfrak{y}}_{r-1}},$$

(see Figure 2). We note that if $q_0\in \left(40,72\right)$, then ${\mathfrak{y}}_0>1/2$. Moreover, ${\mathfrak{y}}_1>1/2$ for $q_0\in \left(19,72\right).$

Figure 2. The iterations ${\mathfrak{y}}_r$, for $r=0,1$ in the special case 2.

Theorem 2.

Assume that $\left({\mathfrak{c}}_1\right)$ and $\left({\mathfrak{c}}_2\right)$ hold. If there exists a positive integer m such that

$$\underset{\mathfrak{k}\to \infty }{liminf}{\int }_{\zeta \left(\mathfrak{k}\right)}^{\mathfrak{k}}{\zeta }^{n-2}\left(s\right)B_0\left(s\right)Q\left(s\right)\mathrm{d}s>\frac{\left(n-2\right)!\left(1-{\mathfrak{y}}_m\right)}{\mathrm{e}},$$

(20)

then the class ℑ is empty, where ${\mathfrak{y}}_m$ is defined as in Lemma 4.

Proof. 

Assume the contrary, that x belongs to ℑ. From Lemma 4, we have that $\left({\mathfrak{r}}_{3,1}\right)-\left({\mathfrak{r}}_{3,3}\right)$ hold.

Now, we define the function

$$\mathfrak{P}\left(\mathfrak{k}\right)=a\left(\mathfrak{k}\right){\upsilon }^{\left(n-1\right)}\left(\mathfrak{k}\right)B_0\left(\mathfrak{k}\right)+{\upsilon }^{\left(n-2\right)}\left(\mathfrak{k}\right).$$

From $\left({\mathfrak{r}}_{3,1}\right)$, we obtain $a\left(\mathfrak{k}\right){\upsilon }^{\left(n-1\right)}\left(\mathfrak{k}\right)B_0\left(\mathfrak{k}\right)\le -{\mathfrak{y}}_m{\upsilon }^{\left(n-2\right)}\left(\mathfrak{k}\right)$. Then, from the definition of $\mathfrak{P}\left(\mathfrak{k}\right)$, we arrive at

$$\mathfrak{P}\left(\mathfrak{k}\right)\le \left(1-{\mathfrak{y}}_m\right){\upsilon }^{\left(n-2\right)}\left(\mathfrak{k}\right).$$

(21)

Using Lemma 3, we obtain that $\left({\mathfrak{r}}_{1,1}\right)-\left({\mathfrak{r}}_{1,5}\right)$ hold. From $\left({\mathfrak{r}}_{1,2}\right)$ and $\left({\mathfrak{r}}_{1,3}\right)$, we arrive at

$${\mathfrak{P}}^{\prime }\left(\mathfrak{k}\right)={\left(a\left(\mathfrak{k}\right){\upsilon }^{\left(n-1\right)}\left(\mathfrak{k}\right)\right)}^{\prime }{B}_0\left(\mathfrak{k}\right)\le -\frac{{\mu }_0}{\left(n-2\right)!}{\zeta }^{n-2}\left(\mathfrak{k}\right)B_0\left(\mathfrak{k}\right)Q\left(\mathfrak{k}\right){\upsilon }^{\left(n-2\right)}\left(\zeta \left(\mathfrak{k}\right)\right),$$

which, with (21), gives

$${\mathfrak{P}}^{\prime }\left(\mathfrak{k}\right)+\frac{{\mu }_0{\zeta }^{n-2}\left(\mathfrak{k}\right)B_0\left(\mathfrak{k}\right)Q\left(\mathfrak{k}\right)}{\left(n-2\right)!\left(1-{\mathfrak{y}}_m\right)}\mathfrak{P}\left(\zeta \left(\mathfrak{k}\right)\right)\le 0.$$

(22)

It follows from $\left({\mathfrak{r}}_{1,4}\right)$ that $\mathfrak{P}\left(\mathfrak{k}\right)>0$ for $\mathfrak{k}\ge {\mathfrak{k}}_1$. Hence, $\mathfrak{P}$ is a positive solution of the differential inequality (22). However, from Theorem 2.1.1 in [22], condition (20) guarantees that (22) is oscillatory. This contradiction completes the proof. □

Example 2.

Consider the NDE (17). If (18) and

$$\frac{1}{3}{\zeta }_0^2{q}_0\left(1-p_0\right)ln\frac{1}{{\zeta }_0}>\frac{2\left(1-{\mathfrak{y}}_m\right)}{\mathrm{e}},$$

(23)

hold, then, from Theorem 2, the class ℑ is empty.

For the special case (19), condition (23) reduces to

$${\mathfrak{y}}_m>1-\frac{3\mathrm{e}}{2}{\zeta }_0^{2}ln\frac{1}{{\zeta }_0}:={\zeta }_1.$$

Remark 1.

Consider the NDE (19). We note that, with fewer iterations, condition ${\mathfrak{y}}_m>{\zeta }_1$ checks that class ℑ is empty, compared to condition ${\mathfrak{y}}_m>1/2$. For example, if ${\zeta }_0=0.625$, then we have that ${\mathfrak{y}}_i<1/2$ for $i=0,1,2,3$ and ${\mathfrak{y}}_4>1/2$; however, ${\mathfrak{y}}_1>{\zeta }_1$ (see Figure 3).

Figure 3. Comparison of the two criteria ${\mathfrak{y}}_m>{\sigma }_1$ and ${\mathfrak{y}}_m>1/2$.

Remark 2.

In the non-canonical case, Li and Rogovchenko [23] used the principle of comparison to obtain criteria for oscillation of all solutions of

$${\left(a·{\left({\left(x+p·\left(x\circ \tau \right)\right)}^{\prime }\right)}^{\alpha }\right)}^{\prime }+q·\left(x^{\alpha }\circ \zeta \right)=0.$$

Applying the results in [23] to Equation (1), we obtain that ℑ is empty if $p\left(t\right)\le p_0$,

$${\tau }^{\prime }\ge {\tau }_{*}>0\mathrm{and}\tau \circ \sigma =\sigma \circ \tau ,$$

(24)

and there exists a $\varrho \in C\left(\left[t_0,\infty \right)\right)$ with

$$\zeta \left(t\right)\le \varrho \left(t\right),\tau \left(t\right)\le t<\varrho \left(t\right),$$

such that

$$\frac{{\tau }^{*}}{\left(n-2\right)!\left({\tau }^{*}+p_0\right)}{\int }_t^{{\tau }^{-1}\left(\varrho \left(t\right)\right)}Q\left(s\right){\zeta }^{\left(n-2\right)}\left(s\right)B_0\left(\varrho \left(s\right)\right)\mathrm{d}s>\frac{1}{\mathrm{e}}.$$

Note that in this paper, we have obtained a new criterion without requiring the existence of the unknown functions ϱ and without requiring the condition in (24).

3. Conclusions

In the non-canonical case, new monotonic properties of the positive solutions of a class of even-order neutral differential equations were obtained. Using these properties, we have presented some criteria to guarantee that $\Im =⌀$. The new criteria are iterative in nature, which allows us to apply them more than once. The examples and figures show the importance of the new properties. It is interesting to extend the technique used in this work to advanced differential equations.