Abstract
Due to the fundamental solutions are employed as basis functions, the localized method of fundamental solution can obtain more accurate numerical results than other localized methods in the homogeneous problems. Since the inverse Cauchy problem is ill posed, a small disturbance will lead to great errors in the numerical simulations. More accurate numerical methods are needed in the inverse Cauchy problem. In this work, the LMFS is firstly proposed to analyze the inhomogeneous inverse Cauchy problem. The recursive composite multiple reciprocity method (RC-MRM) is adopted to change original inhomogeneous problem into a higher-order homogeneous problem. Then, the high-order homogeneous problem can be solved directly by the LMFS. Several numerical experiments are carried out to demonstrate the efficiency of the LMFS for the inhomogeneous inverse Cauchy problems.
Keywords:
localized method of fundamental solutions; meshless method; recursive composite multiple reciprocity method; inhomogeneous problems; inverse Cauchy problems MSC:
65D21
1. Introduction
The inverse Cauchy problem is well known for its numerically unstable characteristic; a small disturbance will lead to great errors in the numerical simulation. To develop a stable and accurate numerical method for the inverse Cauchy problem is very important. Different numerical methods are proposed and developed for solving the inverse Cauchy problems. One of the most popular methods for solving the inverse Cauchy problems is the finite element method (FEM), where the computational domain is divided into small meshes [1]. Similar to the FEM, the finite difference method (FDM) is also developed based on the mesh generation and has been used in inverse Cauchy problems [2]. However, these mesh-based methods have difficulties in the mesh generation when facing some complex geometry. Meanwhile, the boundary element method (BEM) has attracted some researchers’ attention and has been utilized in the inverse Cauchy problems [3,4,5]. Since the fundamental solutions are employed in the BEM, the discretization is only imposed on the boundary, and the accuracy of the BEM is generally higher than other methods. However, the fundamental solutions in the BEM have some troubles in dealing with the singularities, and the BEM are not easy to apply to nonlinear problems.
Besides the mesh-based methods, many meshless methods have also been proposed for inverse Cauchy problems in recent years [6,7,8,9]. The collocation method is one type of the strong meshless methods, which are very popular recently for their simplicity [10,11]. Similar to the classification of the FEM and BEM, the collocation methods can be divided into domain-type and boundary-type methods. Domain-type collocation methods employ interior nodes to discretize the governing equations. The boundary-type collocation methods employ the fundamental solutions or general solutions as the basis function, and the governing equations are analytically satisfied; thus, the accuracy of the boundary-type collocation methods is higher [12]. Many boundary-type collocation methods are developed for inverse Cauchy problems. For example, there are boundary-type methods available for inverse Cauchy problems including the boundary knot method (BKM) [13], the singular boundary method (SBM) [14], the boundary particle method (BPM) [15], and the method of fundamental solutions (MFS) [16,17].
The MFS was proposed by Karageorghis in 1964 [16] and has been utilized in different kinds of inverse Cauchy problems [17]. The MFS is powerful in dealing with engineering problems [18]; however, the full discretized matrix is always ill conditioned. Thus, the MFS is difficult to apply to the large-scale problems. Meanwhile, a finite difference approach is proposed into the global domain-type methods to localize the collocation methods [19,20], which makes the large-scale problems possible. Recently, the finite difference approach has been further applied to the MFS by considering the fictitious nodes [21], which is referred as the localized method of fundamental solutions (LMFS). Similar to the calculation process of the LRBFCM, the LMFS uses both of the interior nodes and boundary nodes at the same time to yield a sparse matrix. The LMFS can be applied to large-scale problems with higher accuracy than other domain-type methods. [22,23].
In general, the boundary-type methods cannot solve inhomogeneous PDEs directly. As such, several numerical techniques have been proposed to solve the inhomogeneous problems, such as the dual reciprocity method (DRM) [24,25], the multiple reciprocity method (MRM) [26,27], and the recursive composite multiple reciprocity (RC-MRM) technique [28]. The DRM and MRM solve the inhomogeneous problems by a linear combination of the homogeneous solution and the particular solution, and the accuracy is related to the approximation of the particular solutions. In order to avoid the errors caused by the particular solutions, the RC-MRM employs high-order differential operators to eliminate the inhomogeneous terms in the governing equations, so that the homogeneous problem can be solved by the LMFS directly. By using the RC-MRM, the accuracy of solving the inhomogeneous inverse Cauchy problem is only related to the numerical methods. The RC-MRM has been effectively applied to the Kirchhoff plate bending problems [29] and Winkler plate bending problems [30].
The paper is organized as follows: Section 2 mainly gives the details of numerical formation of the inhomogeneous inverse Cauchy problem. In Section 3, the RC-MRM is proposed to show how to eliminate the inhomogeneous terms in detail, and the numerical procedure of the LMFS is introduced clearly. In order to verify the effectiveness of this study, several numerical examples of 2D inhomogeneous inverse Cauchy problems are taken into consideration in Section 4. Finally, some conclusions and remarks are provided in Section 5.
2. The Inhomogeneous Inverse Cauchy Problem
In this section, the governing equation of the inverse problem is presented by a simple PDE given as follows,
with boundary conditions
where is a second-order differential operator, and represents the spatial position of nodes. is the inhomogeneous term of the governing equation. and are the Dirichlet boundary condition and Neumann boundary condition, respectively. As shown in Figure 1, is the computational domain with boundary . In addition, n = (nx, ny) is the unit outward normal vector.

Figure 1.
Schematic illustration for a computational domain.
There is no information along boundary in the inverse problems. The main aim for the inverse Cauchy problem is to find out the numerical solutions of the unknown parts, including the boundary and the computational domain .
3. Solution Procedure
In this section, the general idea of the RC-MRM and the details of the numerical discretization of the LMFS are presented.
3.1. The Recursive Multiple Reciprocity Technique (RC-MRM)
Since the fundamental solutions are evaluated from the homogeneous PDEs, the LMFS cannot be used directly to the inhomogeneous PDE. Therefore, the RC-MRM is applied to the LMFS to get the numerical solutions. The RC-MRM uses high-order differential operators to eliminate the inhomogeneous term in the governing equations as follows:
where denote some second-order differential operators, and M is the number of the differential operators that we used in Equation (4). The linear differential operators in Equation (4) are not unique, we mainly consider the Laplacian , the Helmholtz operator , and the modified Helmholtz operator , where is the wavenumber. The above three differential operators can be used on both side of Equation (1) until the inhomogeneous term is eliminated.
Since the re-formulated homogeneous governing equation becomes a higher-order PDE, as shown in Equation (4), extra boundary conditions are added to ensure the uniqueness of the numerical solution. According to principle of the RC-MRM, additional M boundary conditions are given as follows,
Therefore, the inhomogeneous problem described in Equations (1)–(3) can be changed to a higher-order homogeneous problem in Equation (4) with the boundary conditions described in Equations (2), (3) and (5). It should be noted that the new added boundary conditions are put along all the boundaries. Then, the homogeneous solution can be obtained directly by the LMFS. In order to illustrate the specific operation process of the RC-MRM, we propose a simple example below. If the original inhomogeneous governing equation is , when we set , a new homogeneous governing equation can be easily obtained. Moreover, the new boundary condition of the whole boundaries is added to ensure the uniqueness of the solution.
3.2. Introduction of the LMFS
Before introducing the LMFS, the fundamental solution is defined as G, which can be obtained according to the differential operators or Lm mentioned in Equations (1) and (4). Three fundamental solutions according to different differential operators can be found on the right side of Table 1 [31], where Y0 and K0 are the second kind of Bessel function and modified Bessel function, respectively. In addition, represents the distance between the ith filed node and the jth source node , which can be found in Figure 2.

Table 1.
Fundamental solutions of different differential operators in two-dimensional cases [31].
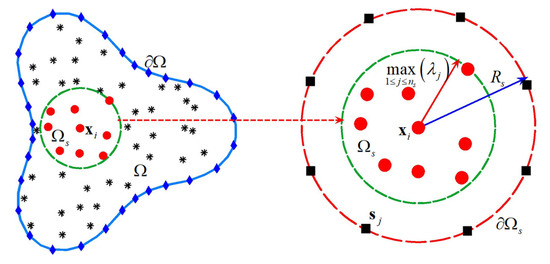
Figure 2.
Schematic of a local domain .
As shown in Figure 2, a local domain near the ith node is considered, where can be found inside the local domain . The numerical solutions of the nodes inside the local domain can be expressed by considering fictitious nodes uniformly distributed on an artificial circle as follows:
where are the fictitious source nodes uniformly distributed on an artificial circle , as shown on the right side of Figure 2. are the unknown coefficients of source nodes, which are related to . The radius of the artificial circle is defined as , which can be controlled by the following equation,
where is the distance between the ith node and jth nodes in the local domain, and R > 1 is usually called the scaling factor that can be given randomly in a considerable range. In this work, R = 10 is chosen for simplicity; thus, an artificial circle or surface centered at ith node can be generated with radius Rs. Equation (6) can be rewritten as
where
Then, the unknown coefficients at source nodes on the artificial circle can be interpolated in terms of the information at the local nodes, which can be expressed as
Reconsidering Equation (10) back to Equation (16), the phase field at ith node can be changed as follows,
where is the vector related to the fundamental solution by considering xi and sj. are the weighting coefficients of the nodes in the local domain at the ith node. By considering the sparse system of the weighting coefficients, the phase field inside domain is evaluated directly without knowing the unknown coefficients in the LMFS. This is different from the classical MFS.
Since is a full matrix during the computational process, the ill condition should be proper treated when dealing with the inverse of . In this work, the MATLAB command pinv (G, tol) is directly taken to solve the inverse of , where tol is the tolerance error. The command, pinv (G, tol), reduces the impact of the ill condition by using the singular value decomposition (SVD). Then, the representation of G becomes:
where U is a left singular matrix that contains eigenvectors of matrix GGT, V is a right singular matrix that contains eigenvectors of matrix GTG, and S is a diagonal matrix containing singular values {\displaystyle \mathbf {U^{*}U} =\mathbf {V^{*}V} =\mathbf {I} _{r}}. When the singular values along the diagonal of S are smaller than tol, the pseudoinverse of G is then given by:
The MATLAB command B = pinv (G, tol) returns the Moore–Penrose pseudoinverse of matrix G. It should be noted that the pseudoinverse B exists for any matrix G, and B has the same dimensions as GT.
Since Equation (11) is derived by assuming that the solution within the local domain of the ith node satisfies the governing equation, each interior node can be taken as the ith node, and the procedures of Equations (6)–(11) can be implemented. Thus, the following system of linear algebraic equations can be yielded,
Meanwhile, the Dirichlet boundary condition can be satisfied directly as follows,
where represents the number of interior nodes, and and represent the numbers of nodes located at boundary and boundary , respectively. The Dirichlet boundary conditions are given on , and there is no boundary information on . is defined as the total number of the nodes, and is the number of boundary nodes. Since the Neumann boundary conditions are usually expressed as the first-order derivatives, the numerical approximation of the first-order derivative can be presented as
where
and
are the vectors of the derivatives of fundamental solutions. and are the weighting coefficients related to derivative calculation. By considering the formulation of first-order derivative in Equations (17) and (18), the Neumann boundary condition can be discretized as
where is the unit outward normal vector at the ith node. Mapping from the local to global domain, the governing equations in Equation (15) and the boundary conditions in Equations (16) and (19) can be recast as the following sparse system
where A is the coefficient matrix, while b is the vector consist of the forcing term related to the governing equations and boundary conditions. The numerical solution can be obtained by solving the above sparse system. In this paper, a MATLAB command backslash is used to solve the above system [11].
4. Numerical Examples
In this section, several different inhomogeneous inverse Cauchy problems are presented to show the efficiency and stability of the proposed LMFS. Some noises are added to the boundary conditions to show the ability of the proposed LMFS. The noise data are introduced as follows:
where and are random numbers between [−1, 1], and l and p represent the index of the number of boundary nodes on the Dirichlet and the Neumann boundary, respectively, as shown in Figure 1. s is used to control the noise data, which are given by researchers. Since the noise is caused by boundary measurement and the additional boundary conditions are derived by the RC-MRM without any measurement, there is no need to consider the noise in the additional boundary conditions. It means that the boundary conditions presented in Equation (5) remain unchanged. The maximum average relative error Emaxr and global error Eglobal in this work are defined as follows:
where and are the analytical and numerical solutions at , respectively.
In order to find the optimal tolerance of MATLAB command pinv, the previous work by Wang et al. [32] is considered in this work, where tol = 10−3 is used in Examples 2 and 4 while tol = 10−4 is picked up for Examples 1 and 3. Since the LMFS can always get accurate results with a big range of R in the previous research [21], a fixed R = 10 is set in all the examples.
4.1. Example 1
In this example, a simple unit square domain is considered in Figure 3, where represents the interior domain, and represents the four boundaries, respectively. The Dirichlet boundary conditions with noise data are considered on , and . There is no information on , an additional Neumann boundary condition with noise data imposed on to guarantee the solvability of the system.

Figure 3.
Collocation nodes’ distribution.
The inhomogeneous governing equation subjected to mixed boundary conditions of Equations (2) and (3) is given as follows:
where is utilized. The following analytical solution is considered,
where the constant is simply used. The given boundary conditions without noise data can be obtained from Equation (26), which are presented as follows:
When considering noise in Equations (21) and (22), the given boundary conditions in Equations (27) and (28) can be rewritten as
where and are random numbers between [−1, 1], l = 1, 2, …, nb1 + nb2 + nb3 represents the index of number of boundary nodes on , and p = 1, 2, …, nb1 represents the index of number of boundary nodes on . In this paper, we chose s = 1%, 3%, 5%, and 7%. From Equations (25) and (26), the inhomogeneous forcing term can be expressed as,
Using the RC-MRM, the inhomogeneous term in the governing equation can be annihilated by three differential operators as
where and . Since Equation (32) is an eighth-order homogeneous problem, the LMFS can be used directly. According to the procedure in RC-MRM, three additional boundary conditions are required to guarantee the solvability of the eighth-order PDE, which are given as
Therefore, the discretized system in Equation (20) can be obtained by considering governing Equation (30), the additional boundary conditions described in Equations (30)–(35), and the given boundary conditions with noise data in Equations (29) and (30).
First, different noises controlled by s are considered to obtain the numerical results by using N = 3591, nb1 = nb2 = nb3 = nb4 = 57, and ns = 300. The analytical and numerical solutions in Figure 4 are depicted with black solid and red dashed curves, respectively. Since the noises are given on boundary , it can be found that the red dashed curves are obviously unstable near these three boundaries in Figure 4, especially when the value of s is large. Meanwhile, the numerical solutions near boundary show the most unstable results since there is zero information. From the results in Figure 4, we can find that the analytical and numerical solutions are almost identical in Figure 4a when s = 1%. Meanwhile, the deviation of the two curves increases as the value of s enlarges in the other parts of Figure 4. As there is no information on the boundary ,. the location of the maximum deviation always appears on . Therefore, the comparison between analytical and numerical solutions of the boundary nodes on is shown in Figure 5. By observation, the deviation between each numerical and analytical curve will increase when the value of s is enlarging. Additionally, when the value of u is large, a large deviation between the numerical and the analytical curve can be found, especially when s = 5% and s = 7%.
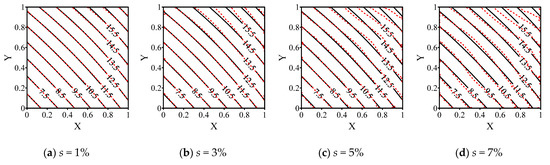
Figure 4.
The distribution of numerical (dashed curves) and analytical solutions (solid curves).

Figure 5.
Comparisons between the numerical and analytical solutions on .
The numerical tests above show that the LMFS can solve this inhomogeneous inverse Cauchy problem accurately with a group of fixed parameters. Furthermore, in order to test the stability of numerical solutions calculated by the LMFS, the numerical results obtained by using different ns and N will be discussed. The Emaxr and Eglobal are listed in Table 2 and Table 3. In Table 2, five different groups of ns varying from 200 to 360 with fixed N = 3591 are used for the calculation. In Table 3, ns = 300 is fixed, and N changes from 3591 to 7650. By observing the errors in Table 2 and Table 3, it can be found that the values of Emaxr are quite close to their corresponding values of s, which can validate the accuracy of the proposed method. In addition, the Eglobal obtained in Table 2 and Table 3 also show similar accuracy. In the considered range of the ns and N, the LMFS shows a strong stability in solving the inhomogeneous inverse Cauchy problem. By using the RC-MRM, although the order of the governing equation is raised, the numerical solutions are still quite accurate.

Table 2.
The numerical errors of different number of local nodes.

Table 3.
The numerical errors of different number of total nodes.
During our test, when a fixed N is given, ns < 200 leads to a Emaxr > s in Table 2. Meanwhile, the results in Table 3 show that when s = 1%, N changes from 6552 to 7560 with fixed ns, and Emaxr will be close to s. However, the accuracy will be reduced if N is increased. It means that when calculating a high-order governing equation, a large number of ns should be employed. Here, the order of PDE is the eighth, and more than 200 local nodes are required. In other examples, we discuss whether the accuracy of LMF can be proved by less than 200 local nodes when the order of the governing equation is less than the eighth.
4.2. Example 2
In this example, an inverse Cauchy problem in a double connected domain is presented. The computational domain consists of two concentric circles, where the inner unit circle locates at a center point x = [0, 0] and the radius of the outer circle is 1.5, as shown in Figure 6. There is no boundary information on outer boundary in this inverse Cauchy problem. At the same time, the boundary conditions on inner boundary are given with Cauchy noise data.
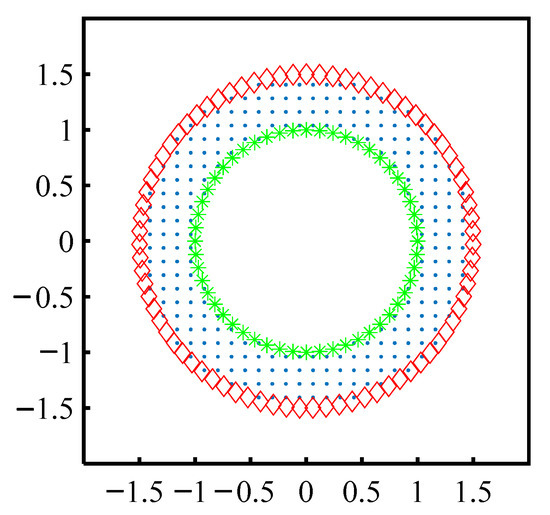
Figure 6.
Collocation nodes’ distribution.
The original governing equation is given as follows,
where the wavenumber is given. The inhomogeneous term in Equation (36), the Dirichlet and Neumann boundary conditions on the boundary can be directly obtained from the following analytical solution,
where the constant . The noises given in Equations (21) and (22) are considered in the given boundary conditions on boundary . By adopting the RC-MRM, a modified Helmholtz operator is used to annihilate the inhomogeneous term, . Thus, the inhomogeneous governing equation can be converted as follows,
Since the order of the governing equation is raised by the RC-MRM, the additional boundary conditions are required. The following boundary condition generated from the RC-MRM is used directly without any noise,
Firstly, N = 3259, and ns = 120 is used to test this inverse Cauchy problem. In Figure 7, the black solid contours represent the analytical solution, and the red dashed contours represent the numerical solution. Since the noises are given on boundary , the red dashed curves are unstable near the outer boundary in Figure 7, especially when the value of s is large. When s = 1%, the numerical and analytical solutions are almost close to each other in Figure 7a. When s increases to 3%, 5%, and 7%, the deviation between the numerical and analytical solutions keeps increasing. Meanwhile, due to the missing boundary conditions of boundary , the maximum deviation always appears on the outer boundary. Therefore, the details of numerical and analytical solutions on the boundary are shown in Figure 8, where θ is the angular coordinate of the outer boundary node in the polar coordinate system. From the Figure 8, we can see that the deviation between numerical and analytical curve increases when the value of s is enlarging, and a large deviation can always be found when the value of u is large.
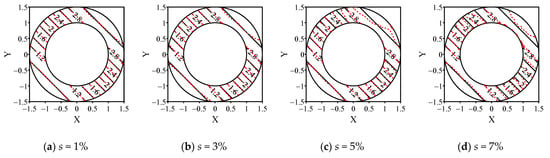
Figure 7.
The comparison of numerical (dashed curves) and analytical solutions (solid curves).
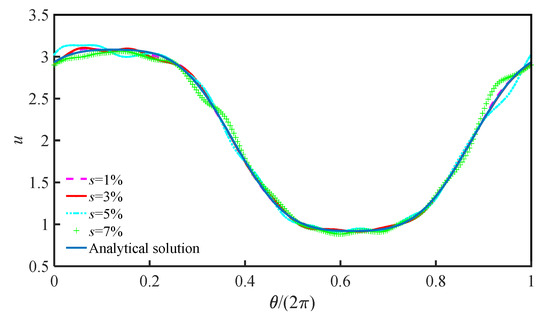
Figure 8.
Comparisons between the numerical and analytical solutions on .
Then, the stability of the LMFS with different parameters is discussed. In order to test the influence of ns, we selected five groups of local nodes with fixed N = 3259 to evaluate the numerical errors in Table 4. The accuracy of the numerical results can be validated by the comparing the values of Emaxr and the given noises s. In Table 4, the values of the Emaxr and s are very close to each other. Meanwhile, the values of Eglobal listed in the Table 4 are generally smaller. When N remains unchanged and ns increases, a larger ns makes the numerical errors smaller. However, more local nodes lead the system matrix to a full matrix, which increases the computational costs. Giving consideration to the accuracy and efficiency, ns = 120 is suggested in this example.

Table 4.
The numerical errors with different number of local nodes.
In the last part of this example, the influence of N is tested by using five different N with fixed ns = 120. The values of Emaxr are approximate to the values of given noises, and the values of Eglobal are quite small in Table 5. Numerical results validate that the LMFS can be applied to a big range of N. In addition, when the ns is fixed, the increase of N will lead to a slight increase of errors. Then, the Emaxr are not close to the value of given noise data, especially when N is too large. These results show that there is an upper limit on the selection of N with a fixed ns. Similar with the results obtained in Example 1, when a larger N is used, more local nodes should be used to guarantee the accuracy. Furthermore, although the order of the original governing equation is raised by the RC-MRM, the LMFS can still obtain very accurate numerical results by using 120 local nodes even when N = 8834. Compared with Example 1, less local nodes are required since the order of the governing equation is only the fourth.

Table 5.
The numerical errors with different number of total nodes.
The LMFS shows its stability and effectiveness of in a double connected computational domain in this example. Since the traditional MFS can hardly be applied in complex geometrics of the inverse problem, in the next example, we further study an inverse problem composed of a multi-connected domain.
4.3. Example 3
This example introduces another inhomogeneous problem in an irregular multi-connected domain, as shown in Figure 9. For some engineering problems, the boundaries of hidden holes are irregular, and their boundary conditions can be hardly measured. The multi-connected domain , which is the same as what was used in [32], is composed of a symmetrical outer boundary and three irregular inner boundaries , and . The parametric equations of the irregular boundaries can be defined as follows,
where θ represents the angles in polar coordinates of the boundary nodes along each boundary, , , , , , , and . The original governing equation can be written as,

Figure 9.
Collocation nodes’ distribution.
Unlike the boundary conditions in Example 2, the Cauchy data are used in the outer boundary , while no information is employed on , , and . Similar to the work in [32], the Cauchy problem with missing boundary conditions of the inner boundaries is solved. However, the numerical problem in this example is inhomogeneous, which means it cannot be solved directly by the LMFS. For the inhomogeneous term in Equation (41), the Dirichlet and Neumann boundary conditions can be obtained by the analytical solution as follows,
where the constant is used. The noise data in Equations (21) and (22) are imposed on the Dirichlet and Neumann boundary conditions on the boundary . By adopting the RC-MRM, a Helmholtz operator and a Laplace operator are used to annihilate the inhomogeneous term for Equation (41), which can be shown as . Therefore, a new homogeneous governing equation can be formed as follows,
The order of the original governing equation is increased by the RC-MRM, and the new homogeneous governing equation is transformed into a sixth-order PDE. Then, two additional boundary conditions without considering any additional noises are imposed on the whole boundaries as follows,
Firstly, N = 3144 and ns = 120 are used to test this problem. The analytical and numerical solutions are depicted by black solid contours and red dashed contours, respectively, in Figure 10. From the Figure 10, we can see that when s = 1%, the contours of numerical solution and analytical solution fit well. As the value of s increases, the deviation between the two kinds of contours is becoming larger. Although some unstable results appear on the outer boundary, the most unstable numerical results are located on the inner boundaries, where zero boundary information can be obtained. This phenomenon is similar with the previous examples. Therefore, in order to further show the detailed numerical results of each inner boundary, the numerical and analytical solutions on boundaries , and are presented in Figure 11, Figure 12 and Figure 13. In Figure 11, Figure 12 and Figure 13, when s = 1% the analytical and numerical solutions all are almost consistent with each other on the inner boundaries, the largest absolute deviation can be found on boundary . From the details in the last part of Figure 13, when s = 7%, the maximum relative error Emaxr is close to 6.67%. However, the maximum relative error on the inner boundary is still close to its given noise data, which validates the efficiency of the proposed LMFS.
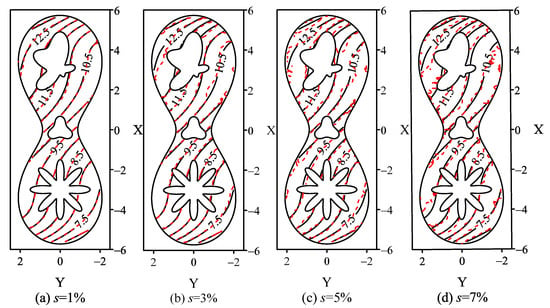
Figure 10.
The comparison of numerical (dashed curves) and analytical solutions (solid curves).
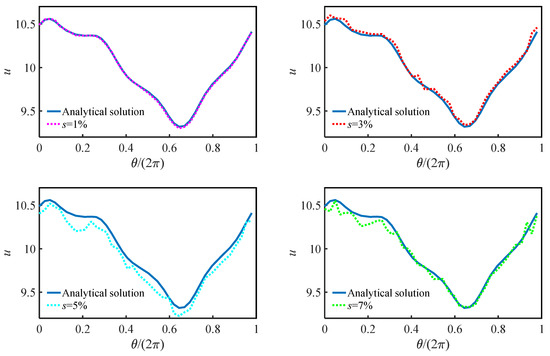
Figure 11.
Comparisons between the numerical and analytical solutions on boundary .
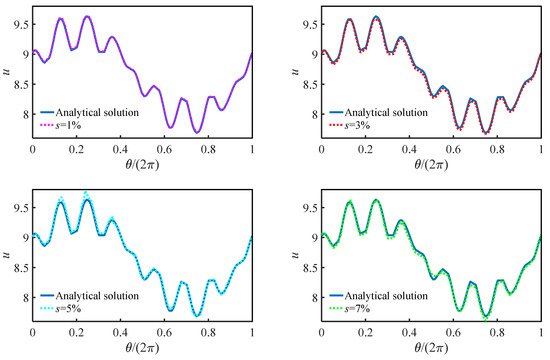
Figure 12.
Comparisons between the numerical and analytical solutions on boundary .
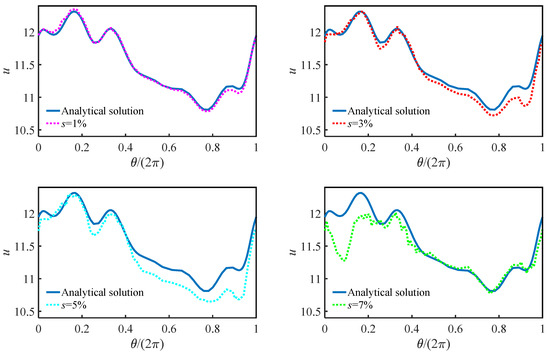
Figure 13.
Comparisons between the numerical and analytical solutions on boundary .
The convergence rate of the LMFS is presented in Table 6 and Table 7. In Table 6, different ns are tested with fixed N = 3144. When ns ranges from 100 to 200, the values of Emaxr and s are almost identical. Meanwhile, Eglobal is stable in the range of [0.001, 0.01]. These results show that, when ns ≥ 100 and N = 3144, the numerical results calculated by the LMFS are accurate. Then, considering the homogeneous governing equation is a sixth-order PDE, ns = 180 is used to test the influence of N in the Table 7.

Table 6.
The numerical errors with different number of local nodes.

Table 7.
The numerical errors with different number of local nodes.
As shown in Table 7, the value of Emaxr is slightly smaller or close to s, except when s = 1% and N = 7680, Emaxr =1.17%s. All the numerical errors show good accuracy of the LMFS. The values of Eglobal in Table 7 are all quite small and similar with those in Table 6. When the value of N is larger than 7860, more local nodes are needed to guarantee the accuracy. According to Equation (43), as the order of the final governing equation in this example is lower than that in Example 1, and higher than that in Example 2, the value of ns used in this example is smaller than Example 1 and larger than Example 2 when considering the same N. This can be validated by the numerical results calculated with N = 7560 in Table 3, N = 7405 in Table 5, and N = 7680 in Table 7. The results show that more local nodes are suggested for calculating when the order of the final governing equation is higher.
4.4. Example 4
In this part, an inhomogeneous inverse problem without an analytical solution is proposed. The mixed Dirichlet and Neumann boundary conditions are given in this problem. It should be emphasized that, in order to simulate the engineering problems, the two kinds of boundary conditions can neither be derived from each other nor meet the governing equations. The inverse Cauchy problem was proposed recently by Fan et al. [33], which can be introduced as two steps: the direct problem and inverse problem. Then, the details of the irregular boundary are shown in Figure 14, where represents the angles of polar coordinates of the boundary nodes. The formulas of the boundaries are presented as follows,
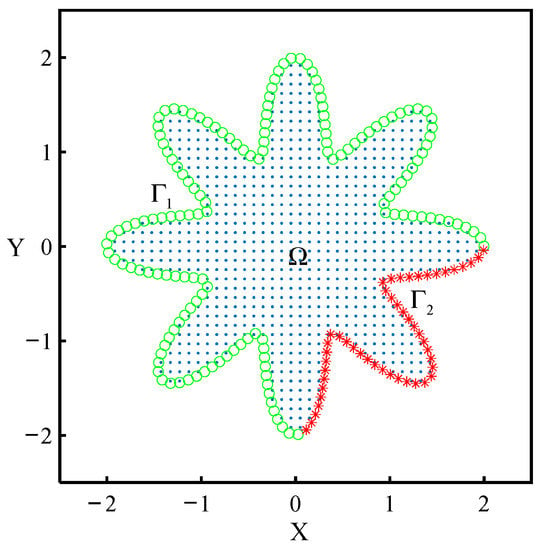
Figure 14.
Collocation nodes’ distribution.
- Step 1. Direct problem:
The direct problem introduces a Poisson equation as the governing equation. In addition, the Neumann boundary condition is given on the boundary and the Dirichlet boundary condition is given on the boundary . The governing equation and the boundary conditions are given as follows:
Meanwhile, through the using of RC-MRM, the inhomogeneous governing equation can be transformed into the following homogeneous form,
Therefore, the Poisson equation is changed into a biharmonic equation, which can be solved by the LMFS directly. Since the order of differential operator is increased, the additional boundary condition on the whole boundary is given as follows,
Then, the LMFS can solve the direct problem governed by the new governing equation, Equation (50), with the given boundary conditions and the additional boundary condition (Equation (51)) directly. Since no analytical solution can be used for comparison, it is hard to verify the accuracy of numerical results. Thus, an inverse Cauchy problem is introduced in Step 2 for solving this problem. It should be emphasized that the LMFS is still applied to this inverse Cauchy problem. In addition, the boundary data in Step 1 denoted as are used as the given information in Step 2.
- Step 2. Inverse problem:
By using the LMFS with RCMRM in Step 1, we have the numerical solutions of all the collocation nodes. In Step 2, we note the value of on boundary as . Thus, the new defined can be used as the Dirichlet boundary condition on boundary in Step 2. The above description can be summarized as the following formula,
Then, we remove the original boundary condition on boundary and regard it as a boundary with no information. Thus, the original governing Equation (47), the given Neumann boundary condition (48), and the new Dirichlet boundary condition (52) on boundary , consist of a new inhomogeneous inverse Cauchy problem. Similarly, the RC-MRM can be used to transform the governing equation from Equation (47) into a homogeneous Equation (50). Moreover, the additional boundary condition (51) can help the LMFS to solve this inverse Cauchy problem directly. Unlike the previous examples, we do not put any noise on boundary conditions in this example. Because the numerical solutions from Step 1 contain numerical errors, there is no need to add extra noise into the boundary conditions. The final numerical solution is denoted as in Step 2.
The comparison of the contours of and calculated by different N and ns can be seen in Figure 15 and Figure 16, respectively. In order to test the influence of N, ns = 100 is used to obtain numerical results in Figure 15. Since the final governing equation is a second-order PDE, the value of ns is suggested to be located in between 40 and 100, and the influence of the local nodes is tested in Figure 16. The contour maps show that no matter how many total nodes or local nodes are used, the numerical solutions between the direct problem and the inverse problem are close to each other. Since no noise is added, the contours of the direct problem and the inverse problem can be completely well fit with each other on boundary , while the deviation between the contours only occurs far away from this boundary. It is easy to find that almost all the maximum deviations occur near boundary , especially in the middle of this boundary. In order to further show the accuracy of the LMFS, we compare the numerical solutions on boundary to find out the specific value of the deviation in Figure 17 and Figure 18.
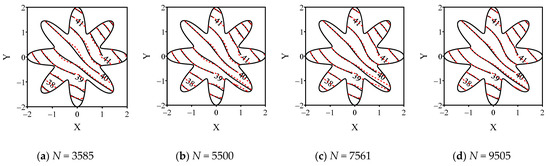
Figure 15.
The comparison of numerical solutions of direct problem (solid curve) and inverse problem (dashed curve).
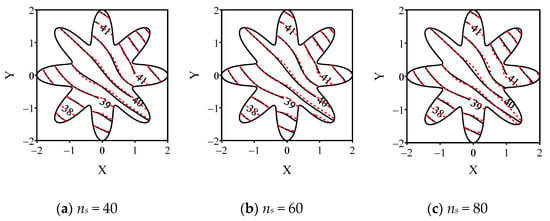
Figure 16.
The comparison of numerical solutions of direct problem (solid curve) and inverse problem (dashed curve).
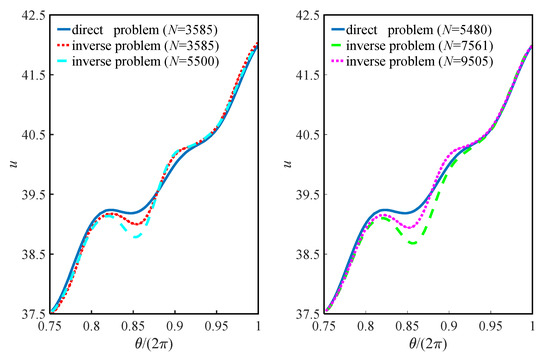
Figure 17.
Comparison between in Step 2 (dashed lines) and in Step 1 (solid line) on .

Figure 18.
Comparison between in Step 2 (dashed lines) and in Step 1 (solid line) on .
The numerical solution on boundary in Step 2 is defined as . Figure 17 and Figure 18 show the details of the numerical results from Figure 15 and Figure 16 on , respectively. The numerical curves of and can are compared in detail, where the curves in Figure 17 and Figure 18 fit well with each other, and only small deviations can be found between every two curves. The maximum deviation always appears in the middle of the curves, which draws the same conclusions as Figure 15 and Figure 16. These numerical results show that the most inaccurate position often appears at the position that is far away from the boundary with the given boundary conditions. Meanwhile, the maximum deviation appears on the curve when N = 7561 in Figure 17, where , and the maximum deviation can be found as less than 1. Then, the relative deviation is approximated to 1/39 < 3%, which is smaller than the allowable error in many engineering problems.
5. Conclusions
In this paper, the LMFS is firstly used for solving the inverse Cauchy problems of two-dimensional inhomogeneous problems based on the RC-MRM without considering any particular solutions. Four numerical examples with and without analytical solutions are provided in this paper. Different noise data are considered in our numerical examples. From the presented numerical results and analysis, it is clear that the proposed LMFS can solve the inverse Cauchy problem of different geometries accurately and stably. The number of the local nodes is related to the order of the formulated PDE in the RC-MRM. The numerical errors are convergent to the same level of the given noise data as the number of nodes increases. Some useful suggestions and experience are presented in detail for the LMFS in solving the inverse Cauchy problem.
Author Contributions
Formal analysis, J.Z., H.Z. and C.-M.F. and M.-F.F. All authors have read and agreed to the published version of the manuscript.
Funding
This work is supported by the National Natural Science Foundation of China (No: 12172159), National Natural Science Foundation of Jiangxi Provence (No: 20212BAB211022). The authors are very thankful for Jiangxi double thousand talents support (No: jxsq2018106027).
Conflicts of Interest
The authors declare no conflict of interest.
References
- Chakib, A.; Nachaoui, A. Convergence analysis for finite element approximation to an inverse Cauchy problem. Inverse Probl. 2006, 22, 1191–1206. [Google Scholar] [CrossRef]
- Vanrumste, B.; Van Hoey, G.; Van de Walle, R.; Michel, R.D.; Lemahieu, I.A.; Boon, P.A. The validation of the finite difference method and reciprocity for solving the inverse problem in EEG dipole source analysis. Brain Topogr. 2001, 14, 83–92. [Google Scholar] [CrossRef] [PubMed]
- Lesnic, D.; Elliott, L.; Ingham, D.B. An alternating boundary element method for solving Cauchy problems for the biharmonic equation. Inverse Probl. Eng. 1997, 5, 145–168. [Google Scholar] [CrossRef]
- Marin, L.; Elliott, L.; Ingham, D.B.; Lesnic, D. Boundary element method for the Cauchy problem in linear elasticity. Eng. Anal. Bound. Elem. 2001, 25, 783–793. [Google Scholar] [CrossRef]
- Marin, L.; Hao, D.N.; Lesnic, D. Conjugate gradient-boundary element method for a Cauchy problem in the Lame system. In BETECH XIV; Brebbia, C.A., Kassab, A.J., Eds.; WTT Press: Southampton, UK, 2001; pp. 229–238. [Google Scholar]
- Liu, C.S. A modified collocation Trefftz method for the inverse Cauchy problem of Laplace equation. Eng. Anal. Bound. Elem. 2008, 32, 778–785. [Google Scholar] [CrossRef]
- Liu, C.S.; Atluri, S.N. Numerical solution of the Laplacian Cauchy problem by using a better postconditioning collocation Trefftz method. Eng. Anal. Bound. Elem. 2013, 37, 74–83. [Google Scholar] [CrossRef]
- Yang, J.P.; Hsin, W.C. Weighted reproducing kernel collocation method based on error analysis for solving inverse elasticity problems. Acta Mech. 2019, 230, 3477–3497. [Google Scholar] [CrossRef]
- Zhang, T.; Dong, L.T.; Alotaibi, A.; Atluri, S.N. Application of the MLPG mixed collocation method for solving inverse problems of linear isotropic/anisotropic elasticity with simply/multiply-connected domains. CMES Comput. Model. Eng. Sci. 2013, 94, 1–28. [Google Scholar]
- Zheng, H.; Zhang, C.; Wang, Y.S.; Chen, W.; Sladek, J.; Sladek, V. A local RBF collocation method for band structure computations of 2D solid/fluid and fluid/solid phononic crystals. Int. J. Numer. Methods Eng. 2017, 110, 467–500. [Google Scholar] [CrossRef]
- Zheng, H.; Zhang, C.; Wang, Y.S.; Sladek, J.; Sladek, V. A meshfree local RBF collocation method for anti-plane transverse elastic wave propagation analysis in 2D phononic crystals. J. Comput. Phys. 2016, 305, 997–1014. [Google Scholar] [CrossRef]
- Cheng, H.D.; Hong, Y.X. An overview of the method of fundamental solutions—Solvability, uniqueness, convergence, and stability. Eng. Anal. Bound. Elem. 2020, 120, 118–152. [Google Scholar] [CrossRef]
- Jin, B.T.; Zheng, Y. Boundary knot method for the Cauchy problem associated with the inhomogeneous Helmholtz equation. Eng. Anal. Bound. Elem. 2005, 29, 925–935. [Google Scholar] [CrossRef]
- Gu, Y.; Chen, W.; Fu, Z.J. Singular boundary method for inverse heat conduction problems in general anisotropic media. Inverse Probl. Sci. Eng. 2014, 129, 124–136. [Google Scholar] [CrossRef]
- Chen, W.; Fu, Z.J. Boundary particle method for inverse Cauchy problems of inhomogeneous Helmholtz equations. J. Mar. Sci. Technol. 2009, 17, 157–163. [Google Scholar] [CrossRef]
- Karageorghis, A.; Fairweather, G. The method of fundamental solutions for the numerical solution of the biharmonic equation. J. Comput. Phys. 1987, 69, 433–459. [Google Scholar] [CrossRef]
- Karageorghis, A.; Lesnic, D.; Marin, L. A survey of applications of the MFS to inverse problems. Inverse Probl. Sci. Eng. 2011, 19, 309–336. [Google Scholar] [CrossRef]
- Rek, Z.; Sarler, B. The method of fundamental solutions for the Stokes flow with the subdomain technique. Eng. Anal. Bound. Elem. 2021, 128, 80–89. [Google Scholar] [CrossRef]
- Flyer, N.; Fornberg, B.; Bayona, V.; Barnett, G.A. On the role of polynomials in RBF-FD approximations: I. Interpolation and accuracy. J. Comput. Phys. 2016, 321, 21–38. [Google Scholar] [CrossRef] [Green Version]
- Bayona, V.; Flyer, N.; Fornberg, B.; Barnett, G.A. On the role of polynomials in RBF-FD approximations: II. Numerical solution of elliptic PDEs. J. Comput. Phys. 2017, 332, 257–273. [Google Scholar] [CrossRef] [Green Version]
- Fan, C.M.; Huang, Y.K.; Chen, C.S.; Kuo, S.R. Localized method of fundamental solutions for solving two-dimensional Laplace and biharmonic equations. Eng. Anal. Bound. Elem. 2019, 101, 188–197. [Google Scholar] [CrossRef]
- Qu, W.Z.; Fan, C.M.; Gu, Y.; Wang, F.J. Analysis of three-dimensional interior acoustic fields by using the localized method of fundamental solutions. Appl. Math. 2019, 76, 122–132. [Google Scholar] [CrossRef]
- Gu, Y.; Fan, C.M.; Qu, W.Z.; Wang, F.J. Localized method of fundamental solutions for large-scale modelling of three-dimensional anisotropic heat conduction problems. Comput. Struct. 2019, 220, 144–155. [Google Scholar] [CrossRef]
- Nowak, A.J.; Partridge, P.W. Comparison of the dual reciprocity and the multiple reciprocity methods. Eng. Anal. Bound. Elem. 1992, 10, 155–160. [Google Scholar] [CrossRef]
- Patridge, P.W.; Brebbia, C.A.; Wrobel, L.W. The Dual Reciprocity Boundary Element Method; Computational Mechanics Publication: Southampton, UK, 1992. [Google Scholar]
- Nowak, A.J.; Neves, A.C. (Eds.) The Multiple Reciprocity Boundary Element Method; Computational Mechanics Publication: Southampton, UK, 1994; pp. 1–41. [Google Scholar]
- Wei, X.; Huang, A.; Sun, L.L.; Chen, B. Multiple reciprocity singular boundary method for 3D inhomogeneous problems. Eng. Anal. Bound. Elem. 2020, 117, 212–220. [Google Scholar] [CrossRef]
- Chen, W.; Fu, Z.J.; Jin, B.T. A truly boundary-only meshfree method for inhomogeneous problems based on recursive composite multiple reciprocity technique. Eng. Anal. Bound. Elem. 2010, 34, 196–205. [Google Scholar] [CrossRef]
- Fu, Z.J.; Chen, W. A truly boundary-only meshfree method applied to Kirchhoff plate bending problems. Adv. Appl. Math. Mech. 2009, 1, 341–352. [Google Scholar]
- Fu, Z.; Chen, W.; Yang, W. Winkler plate bending problems by a truly boundary-only boundary particle method. Comput. Mech. 2009, 44, 757–763. [Google Scholar] [CrossRef]
- Cheng, A.H.-D.; Antes, H.; Ortner, N. Fundamental solutions of products of Helmholtz and polyharmonic operators. Eng. Anal. Bound. Elem. 1994, 14, 187–191. [Google Scholar] [CrossRef]
- Wang, F.J.; Fan, C.M.; Hua, Q.S.; Gu, Y. Localized MFS for the inverse Cauchy problems of two-dimensional Laplace and biharmonic equations. Appl. Math. Comput. 2020, 364, 124658. [Google Scholar] [CrossRef]
- Fan, C.M.; Li, P.W.; Yeih, W.C. Generalized finite difference method for solving two-dimensional inverse Cauchy problem. Inverse Probl. Sci. Eng. 2014, 23, 737–759. [Google Scholar] [CrossRef]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).