Pursuit Differential Game with Slow Pursuers on the 1-Skeleton Graph of the Icosahedron
Abstract
:1. Introduction
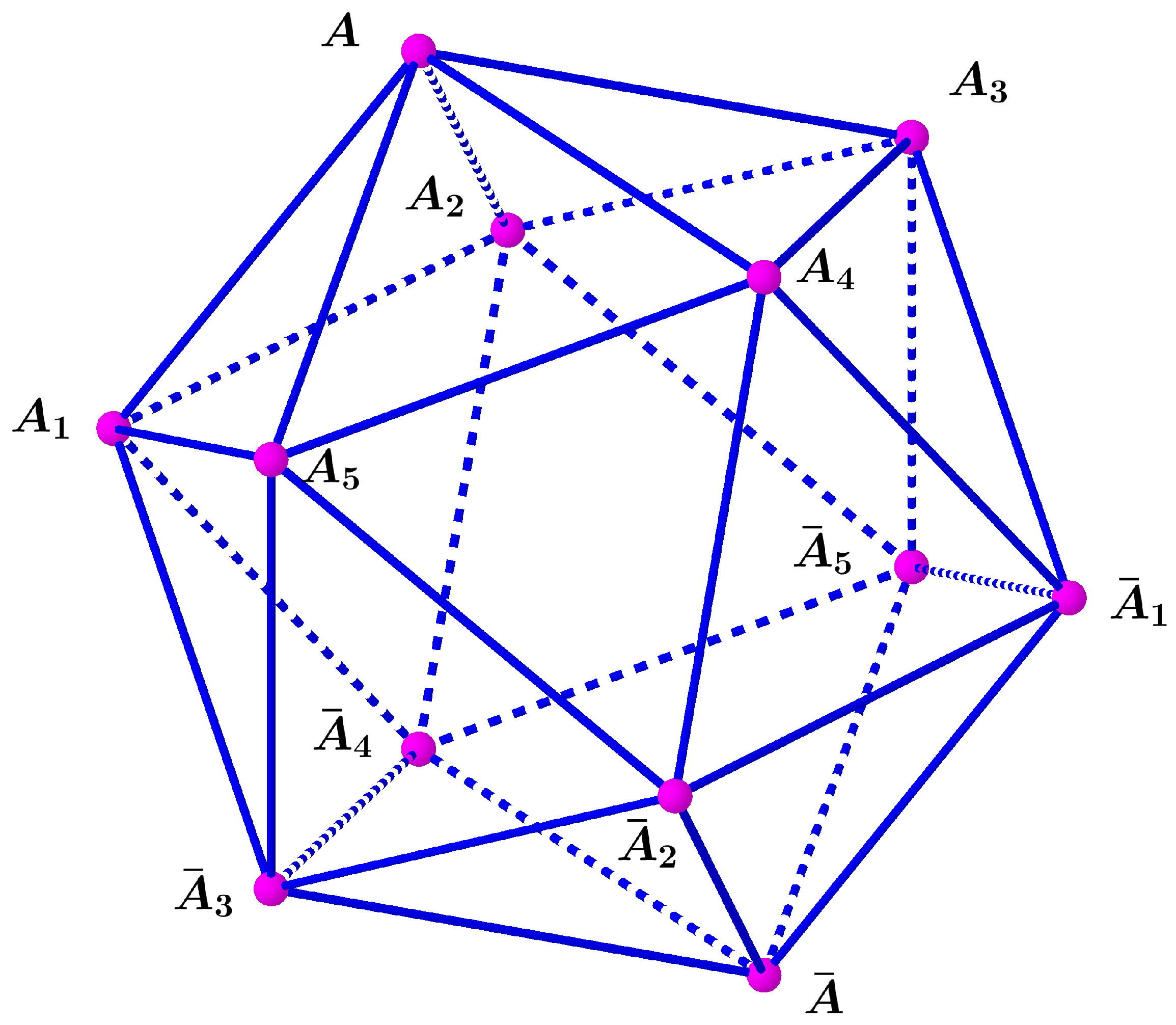
2. Statement of Problem
3. Main Result
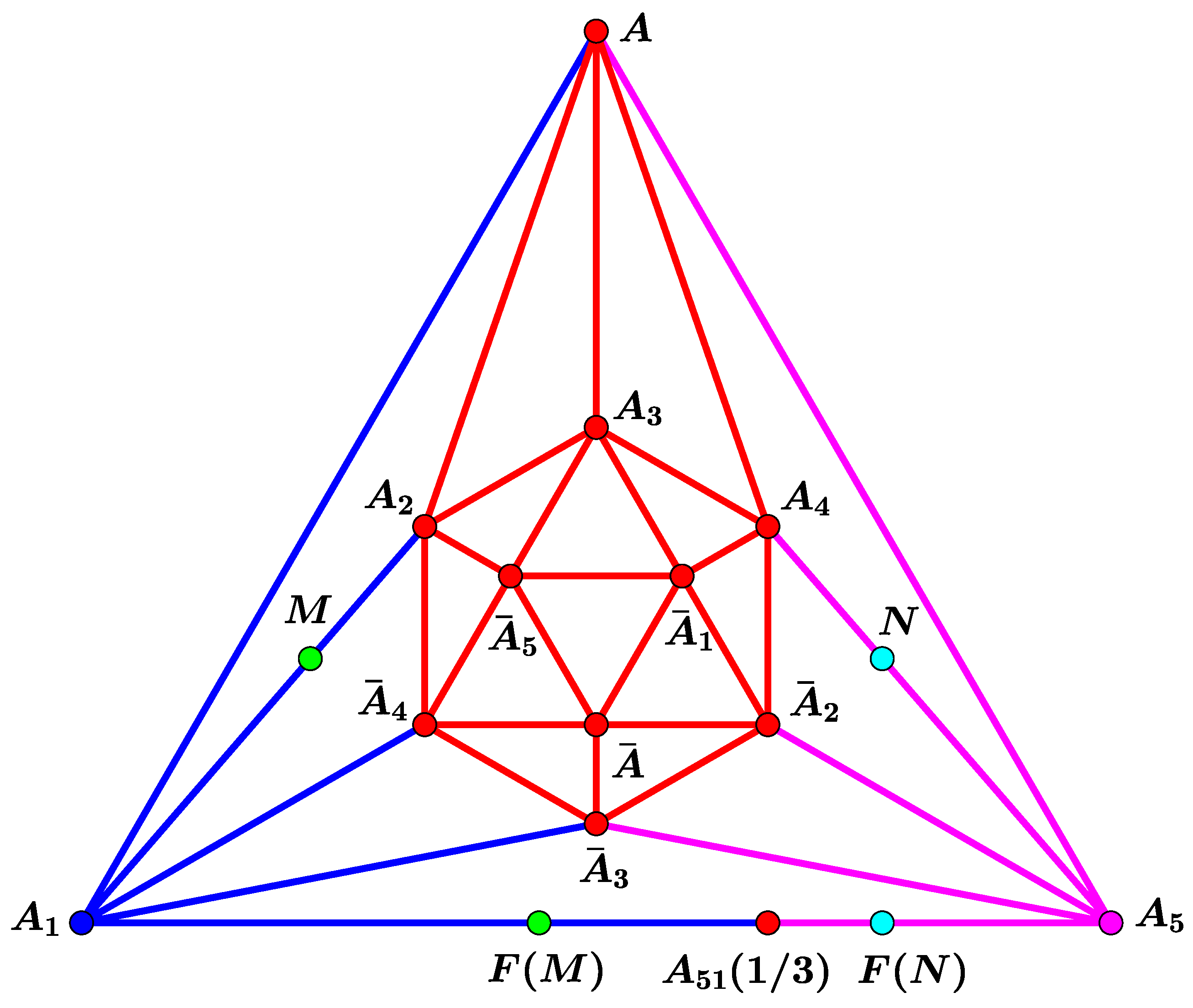
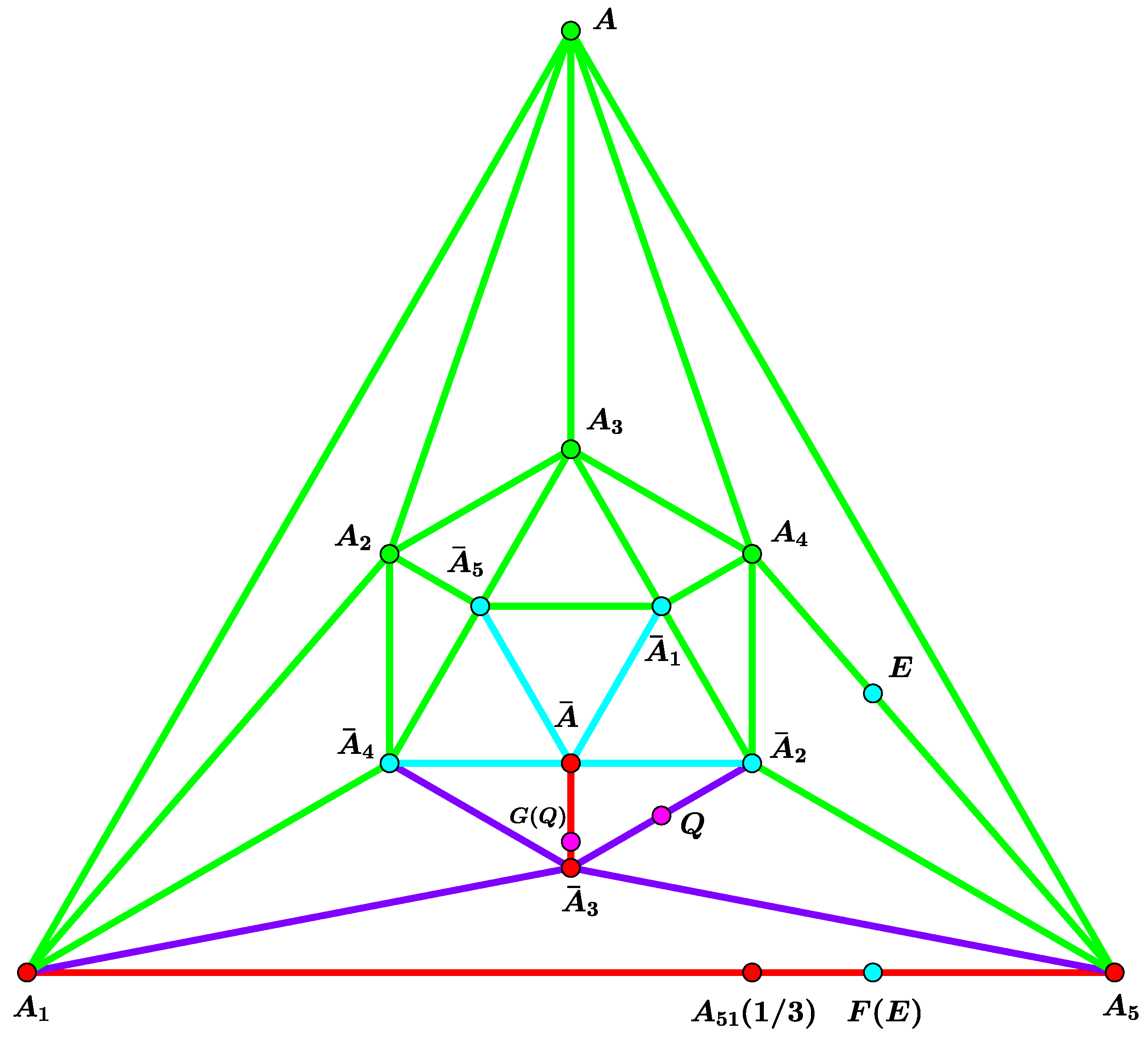
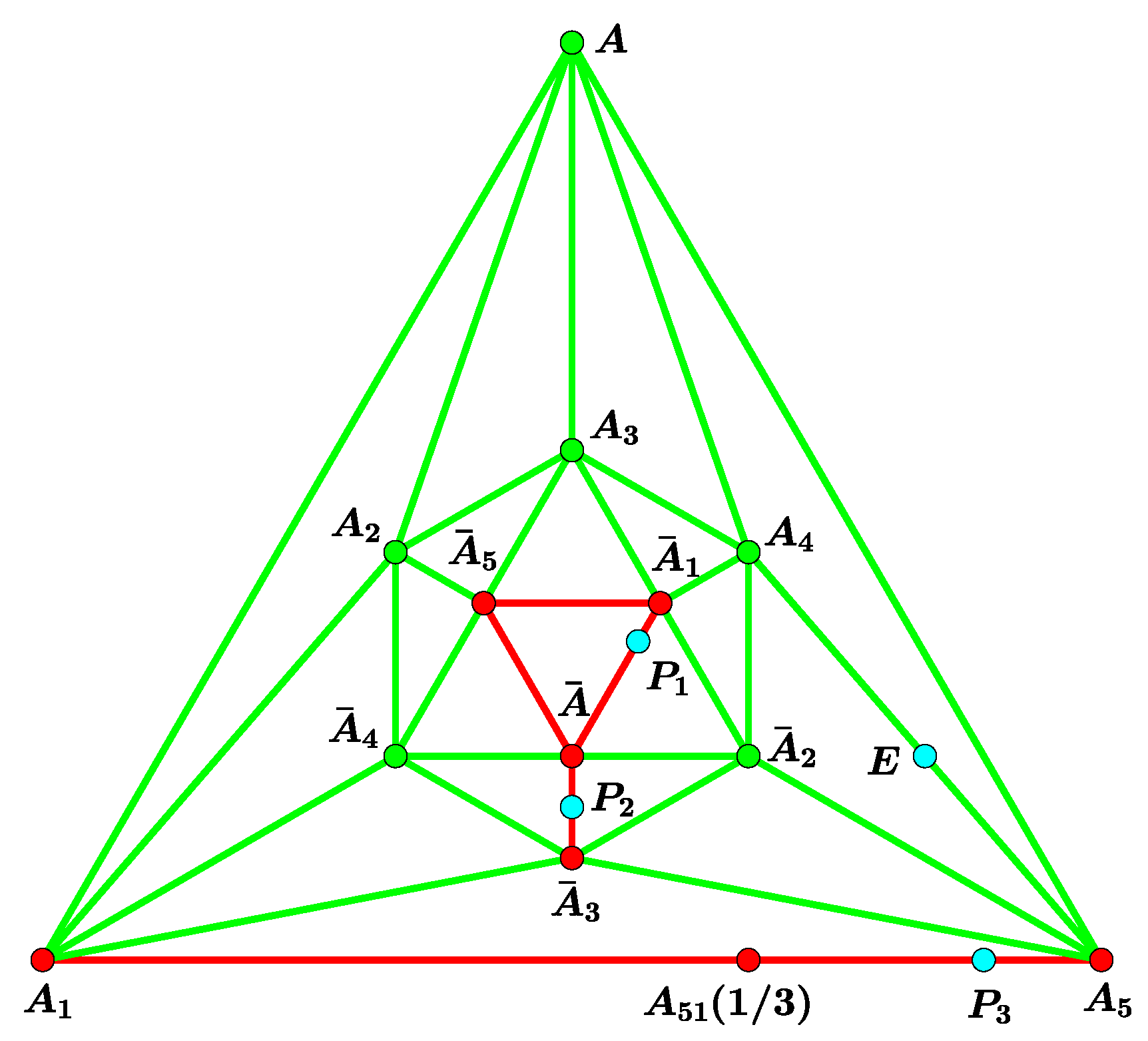
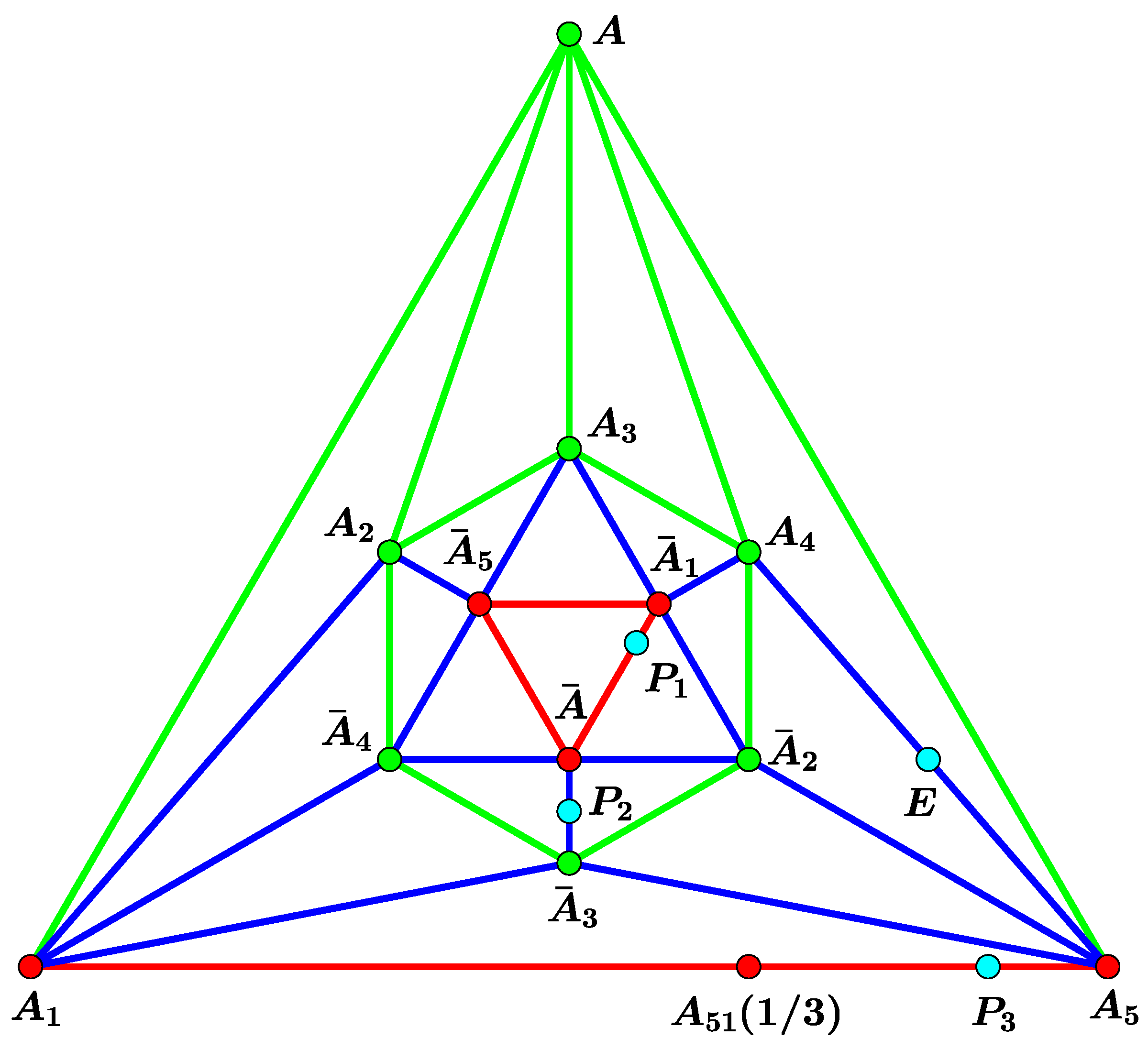
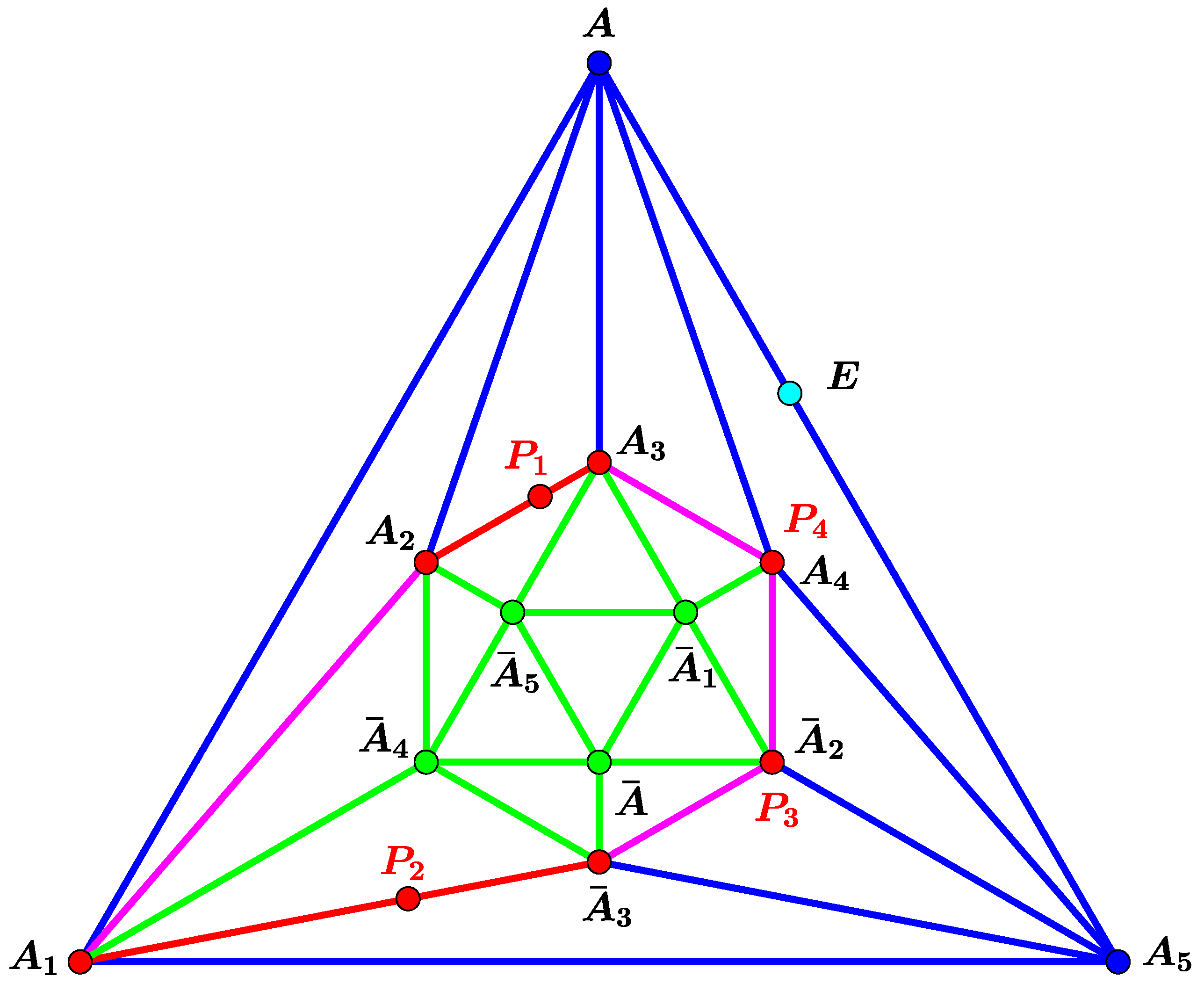
3.1. The Case of Three Pursuers
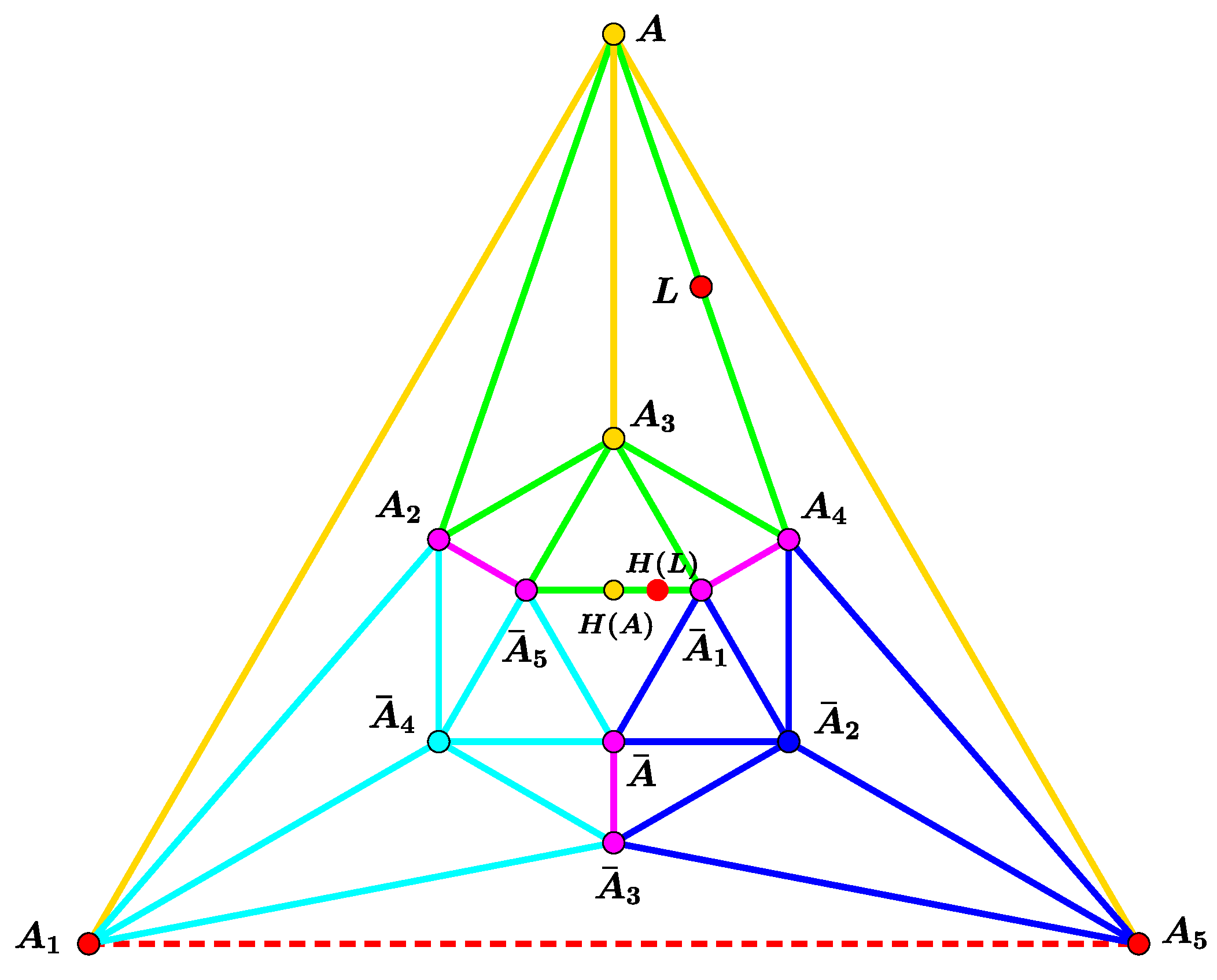
3.2. The Case of More than Three Pursuers
4. Conclusions and Discussion
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Bakolas, E.; Tsiotras, P. Relay Pursuit of a Maneuvering Target Using Dynamic Voronoi Diagrams. Automatica 2012, 48, 2213–2220. [Google Scholar] [CrossRef]
- Blagodatskikh, A.I.; Petrov, N.N. Simultaneous Multiple Capture of Rigidly Coordinated Evaders. Dyn. Games Appl. 2019, 9, 594–613. [Google Scholar] [CrossRef]
- Blagodatskikh, A.I. Multiple capture of rigidly coordinated evaders. Bull. Udmurt. Univ. Math. Mech. Comput. Sci. 2016, 26, 46–57. [Google Scholar]
- Borowko, P.; Rzymowski, W.; Stachura, A. Evasion from many pursuers in the simple motion case. J. Math. Anal. Appl. 1988, 135, 75–80. [Google Scholar] [CrossRef] [Green Version]
- Chernous’ko, F.L.; Zak, V.L. On differential games of evasion from many pursuers. J. Optim. Theory Appl. 1985, 46, 461–470. [Google Scholar] [CrossRef]
- Chikrii, A.A.; Prokopovich, P.V. Simple pursuit of one evader by a group. Cybern. Syst. Anal. 1992, 28, 438–444. [Google Scholar] [CrossRef]
- Chodun, W. Differential games of evasion with many pursuers. J. Math. Anal. Appl. 1989, 142, 370–389. [Google Scholar] [CrossRef] [Green Version]
- Ramana, M.V.; Mangal, K. Pursuit strategy to capture high-speed evaders using multiple pursuers. J. Guid. Control Dyn. 2017, 40, 139–149. [Google Scholar] [CrossRef]
- Scott, W.L.; Leonard, N.E. Optimal evasive strategies for multiple interacting agents with motion constraints. Autom. J. IFAC 2018, 94, 26–34. [Google Scholar] [CrossRef]
- Shaunak, B.; Subhash, S. k-capture in multiagent pursuit evasion, or the lion and the hyenas. Theor. Comput. Sci. 2014, 522, 13–23. [Google Scholar]
- Sun, W.; Tsiotras, P.; Yezzi, A.J. Multiplayer Pursuit-Evasion Games in Three-Dimensional Flow Fields. Dyn. Games Appl. 2019, 9, 1188–1207. [Google Scholar] [CrossRef]
- Kumkov, S.S.; Stéphane, L.M.; Patsko, V.P. Zero-sum pursuit-evasion differential games with many objects: Survey of publications. Dyn. Games Appl. 2017, 7, 609–633. [Google Scholar] [CrossRef]
- Alias, I.A.; Ibragimov, G.I.; Rakhmanov, A.T. Evasion Differential Game of Infinitely Many Evaders from Infinitely Many Pursuers in Hilbert Space. Dyn. Games Appl. 2016, 6, 1–13. [Google Scholar] [CrossRef]
- Ibragimov, G.I.; Ferrara, M.; Kuchkarov, A.S.; Bruno, A.P. Simple motion evasion differential game of many pursuers and evaders with integral constraints. Dyn. Games Appl. 2018, 8, 352–378. [Google Scholar] [CrossRef]
- Ibragimov, G.I.; Salleh, Y. Simple motion evasion differential game of many pursuers and one evader with integral constraints on control functions of players. J. Appl. Math. 2012, 8, 748096. [Google Scholar] [CrossRef]
- Alexander, S.; Bishop, R.; Christ, R. Capture pursuit games on unbounded domain. LËnseignement MathËmatique 2009, 55, 103–125. [Google Scholar] [CrossRef] [Green Version]
- Kuchkarov, A.S.; Risman, M.H.; Malik, A.H. Differential games with many pursuers when evader moves on the surface of a cylinder. ANZIAM J. 2012, 53, E1–E20. [Google Scholar] [CrossRef]
- Andreae, T.; Hartenstein, F.; Wolter, A. A two-person game on graphs where each player tries to encircle his opponent’s men. Theoret. Comput. Sci. 1999, 215, 305–323. [Google Scholar] [CrossRef] [Green Version]
- Azamov, A.A.; Kuchkarov, A.S.; Holboyev, A.G. The pursuit-evasion game on the 1-skeleton graph of the regular polyhedron. III. Mat. Teor. Igr Pril. 2019, 11, 5–23. [Google Scholar]
- Azamov, A.A.; Kuchkarov, A.S.; Holboyev, A.G. Pursuit-evasion game on edge graphs of regular polyhedrons in presence of slow pursuers. Uzb. Math. J. 2017, 1, 140–145. [Google Scholar]
- Azamov, A.A.; Kuchkarov, A.S.; Holboyev, A.G. The pursuit-evasion game on the 326 1-skeleton graph of the regular polyhedron. II. Mat. Teor. Igr Pril. 2016, 8, 3–13. Translated in Automation and Remote Control 2019, 80, 164–170. (In Russian) [Google Scholar]
- Azamov, A.A.; Kuchkarov, A.S.; Holboyev, A.G. The pursuit-evasion game on the 1-skeleton graph of the regular polyhedron. I. Mat. Teor. Igr Pril. 2015, 7, 3–15. Translated in Automation and Remote Control 2017, 78, 754–761. (In Russian) [Google Scholar] [CrossRef]
- Azamov, A.A.; Ibaydullaev, T.; Ibragimov, G.I.; Alias, I.A. Optimal number of pursuers in the differential games on the 1-skeleton of orthoplex. Symmetry 2021, 13, 2170. [Google Scholar] [CrossRef]
- Azamov, A.A.; Samatov, B.T. The Π-strategy: Analogies and applications. In Contribution to Game Theory and Management; St-Petersburg University: Saint Petersburg, Russia, 2011; Volume IV, pp. 33–46. [Google Scholar]
- Bulgakova, M.A.; Petrosyan, L.A. Multistage games with pairwise interactions on full 345 graph. Mat. Teor. Igr Pril. 2019, 11, 3–20. Translated in Automation and Remote Control 2020, 81, 1519–1530. (In Russian) [Google Scholar]
- Bonato, A.; Golovach, P.; Hahn, G.; Kratochvil, J. The capture time of a graph. Discret. Math. 2009, 309, 5588–5595. [Google Scholar] [CrossRef]
- Bonato, A.; Nowakowski, R.J. The game of cops and robbers on graphs. In Student Mathematical Library; American Mathematical Society: Providence, RI, USA, 2011; Volume 61, p. 276. [Google Scholar]
- Gavenčiak, T. Cop-win graphs with maximum capture-time. Discret. Math. 2010, 310, 1557–1563. [Google Scholar] [CrossRef] [Green Version]
- Nowakowski, R.J. Unsolved problems in combinatorial games. In Games of No Chance; Cambridge University Press: Cambridge, MA, USA, 2019; Volume 5, pp. 125–168. [Google Scholar]
- Petrosyan, L.A.; Sedakov, A.A. Multi-step network game with full information. Math. Theory Games Its Appl. 2009, 1, 66–81. Translated in Automation and Remote Control 2014, 75, 1532–1540. (In Russian) [Google Scholar]
- Azamov, A.A. Lower bound for the advantage coefficient in the graph search problem. Differ. Equations 2008, 44, 1764–1767. [Google Scholar] [CrossRef]

Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ibragimov, G.; Holboyev, A.; Ibaydullaev, T.; Pansera, B.A. Pursuit Differential Game with Slow Pursuers on the 1-Skeleton Graph of the Icosahedron. Mathematics 2022, 10, 1435. https://doi.org/10.3390/math10091435
Ibragimov G, Holboyev A, Ibaydullaev T, Pansera BA. Pursuit Differential Game with Slow Pursuers on the 1-Skeleton Graph of the Icosahedron. Mathematics. 2022; 10(9):1435. https://doi.org/10.3390/math10091435
Chicago/Turabian StyleIbragimov, Gafurjan, Azamat Holboyev, Tolanbay Ibaydullaev, and Bruno Antonio Pansera. 2022. "Pursuit Differential Game with Slow Pursuers on the 1-Skeleton Graph of the Icosahedron" Mathematics 10, no. 9: 1435. https://doi.org/10.3390/math10091435
APA StyleIbragimov, G., Holboyev, A., Ibaydullaev, T., & Pansera, B. A. (2022). Pursuit Differential Game with Slow Pursuers on the 1-Skeleton Graph of the Icosahedron. Mathematics, 10(9), 1435. https://doi.org/10.3390/math10091435






