Confidence-Interval-Based Fuzzy Testing for the Lifetime Performance Index of Electronic Product

Abstract

When the lifetime of an electronic component does not reach the required level, it can be enhanced by means of the paralleling current sharing backup system or the redundant backup system. The lifetime of the redundant backup system is the sum of lifetimes of all electronic components, which is the maximum of all the electronic components’ lifetimes, compared with the lifetime of the parallel current sharing backup system. For the purpose of enhancing products’ reliability, electronic goods are usually designed with spare electronic components. If it is assumed that there are $m-1$ redundant backup components for each electronic product, then the lifetime of the electronic product will be distributed as a Gamma distribution with two parameters—$m$ and $\lambda$, where $\lambda$ is the mean for each lifetime of each electronic component. According to numerous studies, the sample size is not large, as it takes a long time to test the lifetime of an electronic product, and enterprises consider cost and timeliness. This paper concerns the performance index of the lifetime of the electronic product. Therefore, based on the confidence interval, this paper aims to develop a fuzzy testing model. As this model can integrate past data and expert experience, the testing accuracy can be retained despite small-sized samples. In fact, through adopting the testing model proposed by this paper, companies can make precise and intelligent decisions instantly with the use of small-sized samples to grasp the opportunities for improvement.

1. Introduction

According to some studies, electronic products are usually designed with spare electronic components to increase the product reliability [1,2,3,4,5]. When an electronic product has only one electronic component without any spare electronic components, improving the lifetime of the electronic component can help prolong the lifetime of the electronic product. If the lifetime of the electronic component cannot be leveled up to the required level in a short time, the parallel current-sharing backup system or redundant backup system can be used to increase the lifetime of the electronic product. Based on the research of Chen et al. [6], the concept of the parallel current sharing system is that all the backup batteries run together until the maximum battery lifetime fails and stops working. Such products include high-power battery pack testers and digital parallel high-efficiency water-cooled power supplies. The redundant backup system is activated when the primary electronic component fails, and then the product will immediately switch the primary electronic component to a spare. Such products include the time synchronization system and the channel analog multiplexer (high electrostatic discharge protection multiplexer). Moreover, Chen et al. [6] indicated that during the failure of the primary component, the redundant backup system will be activated instantaneously, and the system will automatically switch to the spare component. Assume that for each electronic product, there are m electronic components; then, the lifetime of the electronic product is $T_m$$=$${\displaystyle {\sum }_{j=1}^m{T}_j}$ for the redundancy backup system, where $T_j$ represents the lifetime of the $j-th$ electronic component, $j$$=1,2,..,m$. The lifetime of the $j-th$ electronic component ($T_j$) follows an exponential distribution with mean λ [7,8]. Chen et al. [6] noted that the characteristic function of $T_j$ is ${\varphi }_{T_j}\left(\tau \right)={\left(1-i\lambda \tau \right)}^{-1}$, and the characteristic function of $T_m$ is ${\left(1-i\lambda \tau \right)}^{-m}$. Therefore, $T_m$ is distributed as a Gamma distribution with two parameters—$m$ and $\lambda$, denoted by $T_m$~$G\left(m,\lambda \right)$. The probability density function of $T_m$ is

$$f_{T_m}(t)=\frac{1}{\Gamma \left(m\right){\lambda }^m}{t}^{m-1}{e}^{\frac{-t}{\lambda }}, t>0.$$

(1)

Obviously, the lifetime of the electronic product belongs to the larger-the-best quality characteristic [9,10,11]. According to this condition, Chen et al. [6] proposed a lifetime performance index of the electronic product below:

$$C_{Lm}=1-\frac{L}{m\lambda },$$

(2)

where L represents the warranty period and $m\lambda$ is the expected value of $T_m$. When the average lifetime of electronic products is $m\lambda$ $\ge$ $L$, the lifetime performance index is $C_{Lm}$ $\ge$ 0; the larger the average lifetime value $m\lambda$, the greater the value of the lifetime performance index $C_{Lm}$. As the value of the lifetime performance index $C_{Lm}$ approaches infinity, the electronic component lifetime performance index $C_{Lm}$ also approaches 1 and $C_{Lm}$ $<$ 1. In addition, the product reliability $p_R$ is

$$p_R=p\left\{T_m>L\right\}=exp\left\{-m\left(1-C_{Lm}\right)\right\}\times {\displaystyle \sum _{j=0}^{m-1}\left(\frac{m^j{\left(1-C_{Lm}\right)}^j}{j!}\right)}.$$

(3)

Obviously, the product reliability $p_R$ is a function of index $C_{Lm}$. The partial differentiation of $p_R$ by $C_{Lm}$ is bigger than zero as follows:

$$\frac{\partial p_R}{\partial C_{Lm}}=e^{-m(1-C_{Lm})}\hspace{0.17em}\frac{m^m}{(m-1)!}{\left(1-C_{Lm}\right)}^{m-1}.$$

(4)

Therefore, $p_R$ is an increasing function of $C_{Lm}$. The higher the value of the lifetime performance index $C_{Lm}$, the higher the product reliability $p_R$. It is clearly seen that the electronic product lifetime performance index $C_{Lm}$ can reflect product reliability, which is an excellent index for evaluating the lifetime performance of electronic products. Moreover, Chen et al. [6] discovered the uniformly minimum variance unbiased estimator (UMVUE) and the uniformly most powerful (UMP) test for index $C_{Lm}$. As the data collection time of the electronic product lifetime is relatively long, some scholars have shortened the time of collecting sample data by means of accelerating tests. However, the shortcoming is that the lifetime data are not complete. In addition, according to various studies, the Internet of Things and big data analysis technologies have gradually matured, so fast, precise, and intelligent decision-making can help businesses grasp the opportunities for improvement [12,13,14,15]. To solve the above-mentioned problems, this paper proposes a fuzzy testing model built on the confidence interval of lifetime performance index $C_{Lm}$. The advantages of this fuzzy test proposed in this paper are as follows:

(1)

The sample data obtained from this model are more complete than the sample data received from the accelerated tests.

(2)

Obtaining the lifetime sample data through the tests is easier than receiving the triangular fuzzy number data. Then, the fuzzy membership function is constructed with the confidence interval, and the fuzzy evaluation rules are established by calculating easy simple ratios, convenient for the industry to apply.

(3)

The fuzzy testing based on the confidence interval can reduce the risk of misjudgment [16,17].

(4)

This model can integrate past data and expert experience. Despite small-sized samples, the testing accuracy can still be maintained [18].

The remainder of this paper is organized as follows: In Section 2, we derive the 100(1 $-$ $\alpha$)% confidence interval of index $C_{Lm}$. Next, we propose a confidence-interval-based fuzzy testing method to evaluate the electronic product lifetime performance and determine whether the performance needs to improve. Section 4 shows a numerical example, demonstrating the applicability of the approach proposed by this paper. Finally, Section 5 presents the conclusions.

2. Confidence Interval of Index $C_{Lm}$

Assuming that $T_{m,1},\dots ,T_{m,j},\dots ,T_{m,n}$ is a random sample of $T_m$ with sample size n, the uniformly minimum variance unbiased estimator of $C_{Lm}$ can be shown below [6]:

$$C_{Lm}^{\ast }=1-\frac{(n-m^{-1})L}{T_{SUM}},$$

(5)

where $T_{SUM}={\displaystyle {\sum }_{j=1}^n{T}_{m,j}}$. Assuming that the characteristic function of $T_{SUM}$ is ${(1-i\lambda t)}^{-mn}$, $T_{SUM}$ is distributed as $G\left(mn,\lambda \right)$.

Furthermore, let

$$W=\frac{T_{SUM}}{\lambda }=\left(mn-1\right)\frac{1-C_{Lm}}{1-C_{Lm}^{\ast }},$$

(6)

then $W$ is distributed as $\mathit{Gamma}\left(mn,1\right)$ and

$$\begin{array}{c}1-\alpha \\ =p\left\{GAMINV\left(\alpha /2,mn\right)\le W\le GAMINV\left(1-\alpha /2,mn\right)\right\}\\ =p\left\{GAMINV\left(\alpha /2,mn\right)\le \left(mn-1\right)\frac{1-C_{Lm}}{1-C_{Lm}^{\ast }}\le GAMINV\left(1-\alpha /2,mn\right)\right\}\hfill \\ =p\left\{1-\frac{GAMINV\left(1-\alpha /2,mn\right)}{mn-1}\left(1-C_{Lm}^{\ast }\right)\le C_{Lm}\le 1-\frac{GAMINV\left(\alpha /2,mn\right)}{mn-1}\left(1-C_{Lm}^{\ast }\right)\right\},\hfill \end{array}$$

where $GAMINV\left(a,mn\right)$ represents the lower quantile of $G(mn,1)$, $a=\alpha /2$, or $a=1-\alpha /2$. Thus, the $(1-\alpha )100\%$ confidence interval of $C_{Lm}$ is $\left[L{C}_{Lm},U{C}_{Lm}\right]$, which can be displayed as follows:

$$L{C}_{Lm}=1-\frac{GAMINV\left(1-\alpha /2,mn\right)}{mn-1}\left(1-C_{Lm}^{\ast }\right);$$

(7)

$$U{C}_{Lm}=1-\frac{GAMINV\left(\alpha /2,mn\right)}{mn-1}\left(1-C_{Lm}^{\ast }\right).$$

(8)

Let $(t_1,\dots ,t_j,\dots ,t_n)$ be the observed values of $T_{m,1},\dots ,T_{m,j},\dots ,T_{m,n}$, then the observed value of $C_{Lm}^{\ast }$ is

$$C_{Lm0}^{\ast }=1-\frac{(n-m^{-1})L}{t_{SUM}},$$

(9)

where $t_{SUM}={\displaystyle {\sum }_{j=1}^n{t}_j}$. Thus, the observed values of the lower confidence limit and upper confidence limit can be presented as follows:

$$L{c}_{Lm}=1-\frac{GAMINV\left(1-\alpha /2,mn\right)}{mn-1}\left(1-C_{Lm0}^{\ast }\right);$$

(10)

$$U{c}_{Lm}=1-\frac{GAMINV\left(\alpha /2,mn\right)}{mn-1}\left(1-C_{Lm0}^{\ast }\right).$$

(11)

3. Fuzzy Testing Method

As mentioned earlier, the fuzzy testing based on the confidence interval can still maintain the testing accuracy in the case of small samples. Therefore, based on the confidence interval of the lifetime performance index $C_{Lm}$ derived in Section 2, a fuzzy testing method is proposed to evaluate whether the lifetime performance of electronic products reaches the required level. If the lifetime performance index $C_{Lm}$ of electronic products is required to be at least k, then

$H_0:C_{Lm}\ge k$ (The lifetime performance of electronic products reaches the required level.)

$H_1:C_{Lm}<k$ (The lifetime performance of electronic products does not reach the required level.)

Based on Equations (10) and (11), using Buckley’s approach proposed by Buckley [19], the $\alpha -cuts$ of the triangular-shaped fuzzy number ${\tilde{C}}_{Lm}$ with $\left[L{c}_{Lm},U{c}_{Lm}\right]$ is

$${\tilde{C}}_{Lm}\left[\alpha \right]=\{\begin{array}{l}\left[C_{Lm1}(\alpha ),C_{Lm2}(\alpha )\right],0.01\le \alpha \le 1.00\\ \left[C_{Lm1}(0.01),C_{Lm2}(0.01)\right],0.00\le \alpha <0.01\end{array},$$

(12)

where

$$C_{Lm1}\left(\alpha \right)=1-\frac{GAMINV\left(1-\alpha /2,mn\right)}{mn-1}\left(1-C_{Lm0}^{\ast }\right);$$

(13)

$$C_{Lm2}\left(\alpha \right)=1-\frac{GAMINV\left(\alpha /2,mn\right)}{mn-1}\left(1-C_{Lm0}^{\ast }\right).$$

(14)

Thus, the triangular-shaped fuzzy number is ${\tilde{C}}_{Lm}=\left(C_L,C_M,C_R\right)$, where

$$C_L=1-\frac{GAMINV\left(0.995,mn\right)}{mn-1}\left(1-C_{Lm0}^{\ast }\right);$$

(15)

$$C_M=1-\frac{GAMINV\left(0.5,mn\right)}{mn-1}\left(1-C_{Lm0}^{\ast }\right);$$

(16)

$$C_R=1-\frac{GAMINV\left(0.005,mn\right)}{mn-1}\left(1-C_{Lm0}^{\ast }\right).$$

(17)

In addition, the membership function of ${\tilde{C}}_{Lm}$ is

$$\eta (x)=\{\begin{array}{l}0 \hspace{1em}if x\le C_L\\ {\alpha }_1\hspace{1em}if C_L<x<C_M\\ 1 \hspace{1em}if x=C_M\\ {\alpha }_2\hspace{1em}if C_M<x<C_R\\ 0 \hspace{1em}if C_R\le x\end{array},$$

(18)

where ${\alpha }_1$ and ${\alpha }_2$ are determined by

$$x=1-\frac{GAMINV\left(1-{\alpha }_1/2,mn\right)}{mn-1}\left(1-C_{Lm0}^{\ast }\right)$$

(19)

and

$$x=1-\frac{GAMINV\left({\alpha }_2/2,mn\right)}{mn-1}\left(1-C_{Lm0}^{\ast }\right).$$

(20)

Before the fuzzy testing method was proposed, the statistical testing rules were first reviewed and are listed below:

(1)

If the upper confidence limit is $U{c}_{Lm}\ge k$, then do not reject $H_0$ ($C_{Lm}$ $\ge$ $k$).

(2)

If the upper confidence limit is $U{c}_{Lm}<k$, then reject $H_0$ and assume that $C_{Lm}$ $<$ $k$.

Next, this paper constructed a fuzzy testing method based on the above-mentioned statistical testing rules. Figure 1 presents a diagram of membership functions of $\eta \left(x\right)$ with vertical line $x$ $=$ $k$.

Then, let the set $A_T$ represent the area sandwiched between the membership function $\eta (x)$ and the x-axis as follows:

$$A_T=\left\{\left(x,\alpha \right)|C_{Lm1}(\alpha )\le x\le C_{Lm1}(\alpha ),0\le \alpha \le 1\right\}.$$

(21)

Let $a_T$ denote the area of the set $A_T$. Based on Buckley [19], it is difficult to calculate the area of $A_T$ directly via the integration. Therefore, this paper adopted the method of Chen et al. [20] to cut set $A_T$ into 100 approximately trapezoidal blocks, and let set $A_{Tl}$ represent the lth block of $A_T$ and $l=\left[100\alpha \right]$, $l=1,\dots ,100$ for $0\le \alpha \le 1$, where $\left[100\alpha \right]$ represents the largest integer less than or equal to $100\alpha$. Then, $\alpha =0.01\times l$ and $l=1,\dots ,100$ cut set $A_T$ into 100 approximately trapezoidal blocks, and the lth block of $A_T$ can be shown as follows:

$$A_{Tl}=\left\{\left(x,l\right)|C_{Lm1}(0.01\times l)\le x\le C_{Lm2}(0.01\times l),l=1,\dots ,100\right\},$$

(22)

where

$$C_{Lm1}(0.01\times l)=1-\frac{GAMINV\left(1-0.005\times l,mn\right)}{mn-1}\left(1-C_{Lm0}^{\ast }\right);$$

(23)

$$C_{Lm2}(0.01\times l)d_0=d1-\frac{GAMINV\left(0.005\times l,mn\right)}{mn-1}\left(1-C_{Lm0}^{\ast }\right).$$

(24)

Let $d_l=C_{Lm2}(0.01\times l)-C_{Lm1}(0.01\times l)$, then

$$d_l=\frac{GAMINV\left(1-0.005\times l,mn\right)-GAMINV\left(0.005\times l,mn\right)}{mn-1}\left(1-C_{Lm0}^{\ast }\right).$$

(25)

Obviously, we have $d_0=d_1$ based on Equation (12) and $d_{100}=0$ based on Equation (25). Let $a_{Tl}$ denote the area of set $A_{Tl}$, then the approximate area of $A_{Tl}$ is

$$a_{Tl}=\left(\frac{d_{l-1}+d_l}{2}\right)\times \left(0.01\right), l=1,\dots ,100.$$

(26)

Thus,

$$a_T={\displaystyle \sum _{l=1}^{100}{a}_{Tl}}=(0.01)\times {\displaystyle \sum _{l=1}^{100}\left(\frac{d_{l-1}+d_l}{2}\right)}=\left(0.5\times d_1+{\displaystyle \sum _{l=10}^{99}{d}_l}\right)\times (0.01).$$

(27)

Let $A_R$ be the area in the graph of $\eta \left(x\right)$ but to the right of the vertical line $x=k$, then

$$A_R=\left\{\left(x,\alpha \right)|k\le x\le C_{Lm2}(\alpha ),0\le \alpha \le 0.01\times l^{\prime }\right\},$$

(28)

where $\alpha =0.01\times l^{\prime }$ such that $C_{Lm2}(0.01\times l^{\prime })=k$. Clearly, $\alpha =0.01\times l$ and $l=1,\dots ,l^{\prime }$ cut set $A_R$ into $l^{\prime }$ blocks, and the lth block of $A_{Rl}$ can be shown as follows:

$$A_{Rl}=\left\{\left(x,l\right)|k\le x\le C_{Lm2}(0.01\times l),l=1,\dots ,l^{\prime }\right\},$$

(29)

where $k=C_{Lm2}(0.01\times l^{\prime })$. Let $r_l=C_{Lm2}(0.01\times l)-k$, then

$$r_l=\frac{GAMINV\left(0.005\times l,mn\right)-GAMINV\left(0.005\times l^{\prime },mn\right)}{mn-1}\left(1-C_{Lm0}^{\ast }\right).$$

(30)

Obviously, we have $r_0=r_1$ based on Equation (12) and $r_{l^{\prime }}=0$ based on Equation (30). Let the area of $A_R$ be $a_R$, then the approximate area of $A_{Rl}$ is

$$a_{Rl}=\left(\frac{r_{l-1}+r_l}{2}\right)\times \left(0.01\right), l=1,\dots ,100.$$

(31)

Thus,

$$a_R={\displaystyle \sum _{l=1}^{100}{a}_{Rl}}=(0.01)\times {\displaystyle \sum _{l=1}^{l^{\prime }}\left(\frac{r_{l-1}+r_l}{2}\right)}=\left(0.5\times r_1+{\displaystyle \sum _{l=10}^{l^{\prime }}{r}_l}\right)\times (0.01).$$

(32)

Based on Equations (27) and (31), we have

$$\frac{a_R}{a_T}=\frac{0.5\times r_1+{\displaystyle \sum _{l=10}^{l^{\prime }}{r}_l}}{0.5\times d_1+{\displaystyle \sum _{l=10}^{99}{d}_l}}.$$

(33)

Note that we let $0 < {\varphi }_1<{\varphi }_2<0.5$, where the values of ${\varphi }_1$ and ${\varphi }_2$ can be determined based on the past accumulated production data or expert experience [21,22]. As noted by Yu et al. [23] and Buckley [19], we may obtain the following fuzzy testing rules:

• If $a_R/a_T$$\le$${\varphi }_1$, then reject $H_0$ and assume that $C_{Lm}$$<$$k$.
• If ${\varphi }_1$$<$$a_R/a_T$$<$${\varphi }_2$, then do not make any decision on whether to reject $H_0$ or not.
• If ${\varphi }_2$$\le$$a_R/a_T$, then do not reject $H_0$ and assume that $C_{Lm}$$\ge$$k$.

4. Numerical Example

A numerical example is presented in this section to illustrate the fuzzy testing method outlined in Section 3. To determine whether the lifetime performance index value of an electronic product is bigger than or equal to 0.75, the null hypothesis and alternative hypothesis can be displayed as follows:

$H_0: C_{Lm}\ge 0.75$;

$H_1: C_{Lm}<0.75$.

In this paper, we suppose that an enterprise adds an electronic component to the redundant backup system to increase the reliability of the electronic product, which means that the electronic product has a total of two electronic components ($m=2$). Let $(t_1,\dots ,t_j,\dots ,t_{18})$ be the observed values of $T_{2,1},\dots ,T_{2,j},\dots ,T_{2,18}$, then the observed value of $C_{Lm}^{\ast }$ is

$$C_{Lm0}^{\ast }=1-\frac{(n-m^{-1})L}{t_{SUM}}=1-\frac{(17.5)24}{1200}=0.65.$$

Thus, the triangular-shaped fuzzy number is ${\tilde{C}}_{Lm}=\Delta \left(C_L,C_M,C_R\right)=\Delta \left(0.467,0.643,0.776\right)$, where

$$C_L=1-\frac{GAMINV\left(0.995,mn\right)}{mn-1}\left(1-C_{Lm0}^{\ast }\right)=1-\frac{GAMINV\left(0.995,36\right)}{35}\left(0.35\right)=0.467;$$

$$C_M=1-\frac{GAMINV\left(0.5,mn\right)}{mn-1}\left(1-C_{Lm0}^{\ast }\right)=1-\frac{GAMINV\left(0.5,36\right)}{35}\left(0.35\right)=0.643;$$

$$C_R=1-\frac{GAMINV\left(0.005,mn\right)}{mn-1}\left(1-C_{Lm0}^{\ast }\right)=1-\frac{GAMINV\left(0.005,36\right)}{35}\left(0.35\right)=0.776.$$

In addition, the membership function of ${\tilde{C}}_{Lm}$ with triangular-shaped fuzzy number ${\tilde{C}}_{Lm}=\Delta \left(0.467,643,776\right)$ is

$$\eta (x)=\{\begin{array}{l}0 \hspace{1em}if x\le 0.467\\ {\alpha }_1\hspace{1em}if 0.467<x<0.643\\ 1 \hspace{1em}if x=0.643\\ {\alpha }_2\hspace{1em}if 0.643<x<0.776\\ 0 \hspace{1em}if 0.776\le x\end{array},$$

where ${\alpha }_1$ and ${\alpha }_2$ are determined by

$$x=1-GAMINV\left(1-{\alpha }_1/2,36\right)/10$$

and

$$x=1-GAMINV\left({\alpha }_2/2,36\right)/10.$$

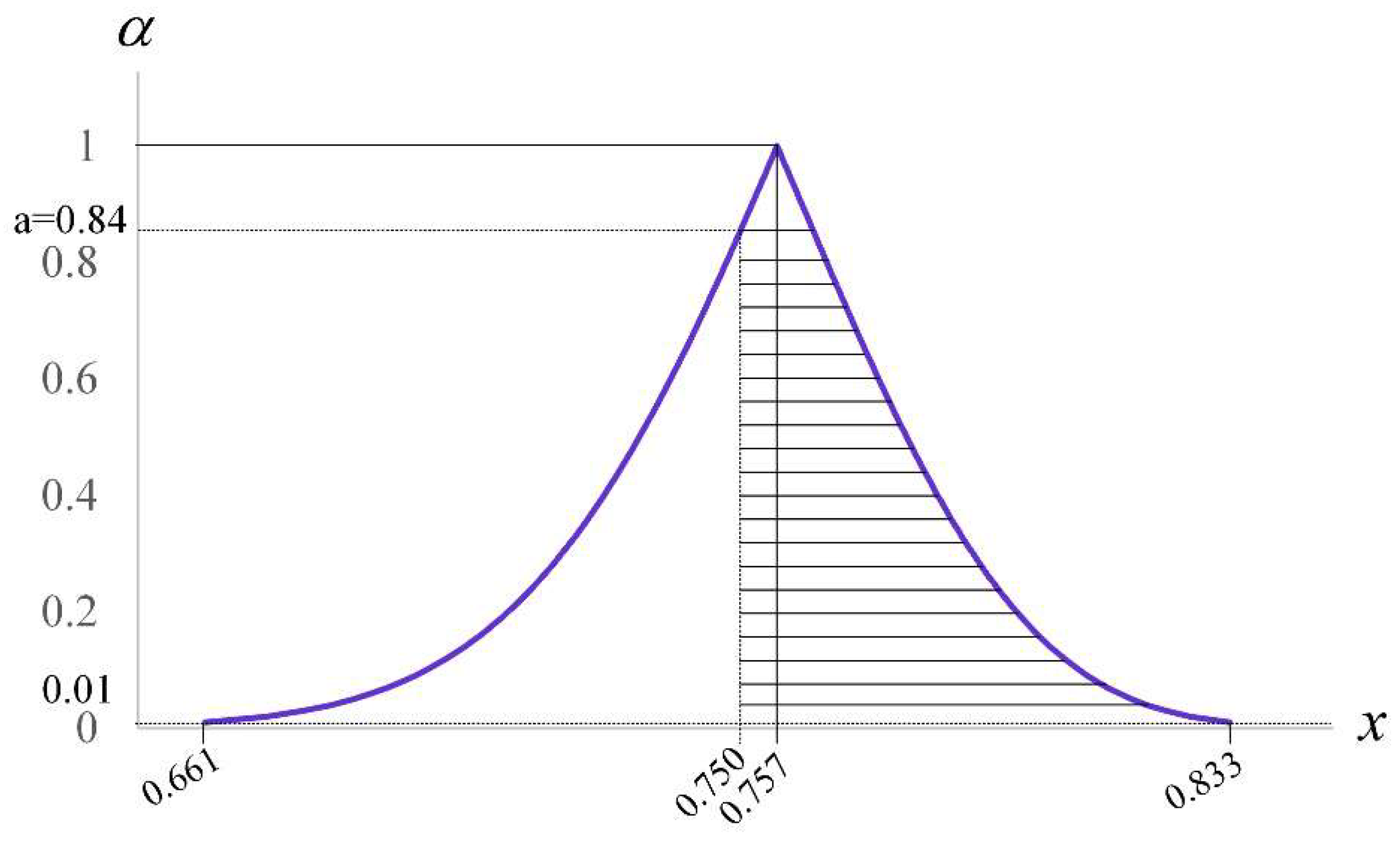
Figure 2 presents a diagram of membership functions of $\eta \left(x\right)$ with triangular-shaped fuzzy number ${\tilde{C}}_{Lm}=\Delta \left(0.467,0.643,0.776\right)$ and vertical line x $=$ 0.75.

When $l^{\prime }=5$, $C_{Lm2}(0.01\times l^{\prime })=C_{Lm2}(0.05)=k=0.75$. Based on Equation (31), we have

$$a_R=\left(0.5\times r_1+{\displaystyle \sum _{l=1}^4{r}_l}\right)\times (0.01)=0.063\times 0.01.$$

According to Equation (27), we have

$$a_T=\left(0.5\times d_1+{\displaystyle \sum _{l=1}^{99}{d}_l}\right)\times (0.01)=9.503\times 0.01.$$

Thus,

$$\frac{a_R}{a_T}=\frac{0.063\times 0.01}{9.503\times 0.01}=0.007.$$

Chen et al. [21] noted that the value of ${\varphi }_1$ that can be obtained from practice is equal to 0.2 and the value of ${\varphi }_2$ is 0.4. As $a_R/a_T$$=$0.007$<$${\varphi }_1$, reject $H_0$ and conclude that $C_{Lm}$ $<$ 0.75, showing that the lifetime performance of the electronic product does not reach the required level. Consequently, the operation must be improved.

As $C_{Lm0}^{\ast } =$ 0.65 is smaller than the minimum required value of index $C_{Lm}$ $=$ 0.75, it is obvious that the fuzzy evaluation model of this paper is used so that the opportunity for improvement will not be missed. The reliability engineer decided to add a spare electronic component, that is, $m=3$. Let $({t^{\prime }}_1,\dots ,{t^{\prime }}_j,\dots ,{t^{\prime }}_{18})$ be the observed values of $T_{3,1},\dots ,T_{3,j},\dots ,T_{3,18}$, then the observed value of $C_{Lm}^{\ast }$ is

$$C_{Lm0}^{\ast }=1-\frac{(n-m^{-1})L}{t_{SUM}}=1-\frac{(17\frac{2}{3})24}{1800}=0.76.$$

Thus,

$$C_L=1-\frac{GAMINV\left(0.995,mn\right)}{mn-1}\left(1-C_{Lm0}^{\ast }\right)=1-\frac{GAMINV\left(0.995,54\right)}{53}\left(0.24\right)=0.661;$$

$$C_M=1-\frac{GAMINV\left(0.5,mn\right)}{mn-1}\left(1-C_{Lm0}^{\ast }\right)=1-\frac{GAMINV\left(0.5,54\right)}{53}\left(0.24\right)=0.757;$$

$$C_R=1-\frac{GAMINV\left(0.005,mn\right)}{mn-1}\left(1-C_{Lm0}^{\ast }\right)=1-\frac{GAMINV\left(0.005,54\right)}{53}\left(0.24\right)=0.833.$$

Then, the triangular-shaped fuzzy number is ${\tilde{C}}_{Lm}=\Delta \left(C_L,C_M,C_R\right)=\Delta \left(0.661,0.757,0.833\right)$, and the membership function of ${\tilde{C}}_{Lm}$ is

$$\eta (x)=\{\begin{array}{l}0 \hspace{1em}if x\le 0.661\\ {\alpha }_1\hspace{1em}if 0.467<x<0.757\\ 1 \hspace{1em}if x=0.757\\ {\alpha }_2\hspace{1em}if 0.757<x<0.833\\ 0 \hspace{1em}if 0.833\le x\end{array},$$

where ${\alpha }_1$ and ${\alpha }_2$ are determined by

$$x=1-GAMINV\left(1-{\alpha }_1/2,54\right)\times (0.24)/53$$

and

$$x=1-GAMINV\left({\alpha }_2/2,54\right)\times (0.24)/53.$$

Figure 3 presents a diagram of membership functions of $\eta \left(x\right)$ with triangular-shaped fuzzy number ${\tilde{C}}_{Lm}=\Delta \left(0.661,0.757,0.833\right)$ and vertical line x $=$ 0.750.

When $l^{\prime }=5$, $C_{Lm2}(0.01\times l^{\prime })=C_{Lm2}(0.05)=k=0.750$. Based on Equation (31), we have

$$a_R=\left(0.5\times r_1+{\displaystyle \sum _{l=1}^4{r}_l}\right)\times (0.01)=3.048\times 0.01.$$

According to Equation (27), we have

$$a_T=\left(0.5\times d_1+{\displaystyle \sum _{l=1}^{99}{d}_l}\right)\times (0.01)=5.106\times 0.01.$$

Thus,

$$\frac{a_R}{a_T}=\frac{3.048\times 0.01}{5.106\times 0.01}=0.597.$$

As $a_R/a_T$$=$0.579 >${\varphi }_2$, do not reject $H_0$, and conclude that $C_{Lm}\ge 0.750$ with $m=3$, showing that the lifetime performance of the electronic product reaches the required level.

5. Conclusions

Several studies have noted that for the purpose of enhancing product reliability, electronic goods are usually designed with spare electronic components. In consideration of generality, this paper assumed that there are m electronic components for each electronic product. According to Chen et al. [6], during the failure of the primary component, the redundant backup system will be activated instantaneously, and the system will automatically switch to the spare component. Therefore, the lifetime of each electronic component follows an exponential distribution with mean λ, and the lifetime of the electronic products is distributed as $G\left(m,\lambda \right)$. Based on the above, this paper derived the 100($1-\alpha$) confidence interval of an electronic product lifetime performance index. Next, this paper proposed a confidence-interval-based fuzzy testing method to evaluate whether the reliability of the electronic product reaches the required level. This fuzzy evaluation method is based on the confidence interval of the index and thus can reduce the probability of misjudgment due to sampling error. In addition, according to many studies, this model can incorporate the past accumulated data or expert experience, so that the testing accuracy can still be maintained despite small-sized samples. Finally, a numerical example was provided to demonstrate the application of the fuzzy testing model proposed in this paper in order to help enterprises apply this fuzzy testing model to make fast, accurate, and intelligent decisions in the case of small samples, as well as grasp opportunities for improvement.

In fact, using the past accumulated data experience or expert experience to evaluate the data of small samples can meet companies’ expectations of rapid response, as well as maintain the accuracy of the evaluation. However, the limitation of the study is that this paper did not explore the reliability of data experience or expert experience verified by scientific methods, so a future research direction can focus on exploring the reliability of the verified data experience or expert experience. Meanwhile, when the lifetime is neither an exponent nor a Gamma distribution, it is also an important issue worth discussing in the future.