A Family of Position Values for Directed Communication Situations

Abstract

In this paper, we define a family of values for directed communication situations that are inspired by the position value. We use the concept of directed communication and related connectedness in directed graphs, under which a coalition of players in a game can only cooperate if these players form a directed path in a directed communication graph. By defining an arc game, which assesses the worth of coalitions of (directed) arcs in generating worth, we allocate the Shapley value payoff of each arc over the nodes incident with this arc, where we allow the head and tail to obtain a different share in this arc payoff. However, the way that the arc payoff is shared over its head and tail is uniform over all arcs. We characterize these values by connection efficiency and a modification of the classical balanced link contributions property for undirected communication situations, discriminating between the roles of the nodes as head and tail.

1. Introduction

A situation in which a finite set of players or agents can generate certain payoffs by cooperation can be described by a cooperative game with transferable utility (or simply a TU game). The characteristic function of a TU game assigns to every subset of the player set (coalition) a real worth, which is the transferable utility that the players in the coalition can earn when they agree to cooperate. In a TU game, there are no restrictions on the cooperation possibilities of the players, i.e., every coalition is feasible and can generate a worth. However, in many real-life situations, there are restrictions on coalition formation and not every coalition is feasible.

One of the most famous restrictions in coalition formation is communication restrictions. If players are not able to communicate directly with every other player, then some coalitions might not be feasible. This is modeled by the communication situations of [1] where the players in a game are also members of a communication network that is represented by an undirected (communication) graph. The idea, then, is that players can only cooperate and form a feasible coalition if its members are connected in the communication graph. As an allocation rule, Ref. [1] proposed to apply the Shapley value [2] to a modified game in which every feasible coalition can earn its worth, and every other coalition’s worth equals the sum of the worths of its connected components in the original game. This allocation rule is nowadays known as the Myerson value. He also gave an axiomatization of this allocation rule in terms of component efficiency (meaning that the sum of the payoffs of all players in a component equals the worth of that component) and fairness (meaning that breaking a link between two players has the same effect on the payoffs of these two players). Later, Ref. [3] provided another axiomatization, replacing fairness by balanced contributions (meaning that the effect of isolating a player on the payoff of another player is the same as the effect the other way around).

An alternative allocation rule for communication situations was introduced by [4,5], who first defined a link game, where the links are the players, and the worth of every coalition of links equals the worth of the grand coalition of all players in the Myerson-restricted game associated with the communication situation where only this coalition of links forms the communication graph. As an allocation rule, they proposed to (i) apply the Shapley value to this link game, and (ii) divide the Shapley value payoff of every link equally over the two players incident with this link. Later, Ref. [6] axiomatically characterized this allocation rule, called the position value, by component efficiency and balanced link contributions (meaning that the sum of the effects of breaking each individual link of a player on the payoff of another player is the same as the effect the other way around).

Instead of undirected communication graphs, where the communication links are symmetric, Ref. [7] consider directed communication situations where the players in a game belong to a directed network that is represented by a directed graph. Similar to [1], they introduce a restricted game that takes account of the communication restrictions, but in their case, these communication restrictions are determined by a notion of connectedness in directed graphs. Communication in undirected graphs is usually associated with connectedness in the graph, a coalition being connected if there is a path between any pair of players in this coalition using only players that belong to this coalition. However, there are several notions of connectedness in directed graphs, and different ways in which directed communication restricts the cooperation possibilities of players in a game where players can only communicate by one-direction communication. Ref. [7] assume that a coalition of players in a game can only cooperate if these players form a directed path in a directed communication graph. Based on this idea, they modify the restricted game of [1] in this setting, and apply the Shapley value to this restricted game. They characterize this value by connection efficiency, which is based on the new connectedness concept, and either fairness or balanced contributions.

In this paper, we use this concept of connectedness and, following [4,5], define an arc game and a family of position values for directed communication situations. In this arc game, the worth of coalitions of (directed) arcs in generating worth is assessed, and then we allocate the Shapley value payoff of each arc over the nodes incident with this arc, where we allow the head and tail to obtain a different share in this arc payoff. However, the way that the arc payoff is shared over its head and tail is uniform over all arcs. We characterize these values by the above-mentioned connection efficiency and a modification of balanced link contributions, discriminating between the roles of the nodes as head and tail.

Our motivation to combine our notion of connection efficiency with the balanced link contributions type of axioms is as follows. First, as described in [7], a connectedness concept based on directed (connection) paths is useful in applications such as supply chain management, attribution models and vaccination policy. In supply chains, value can be created when products produced by a manufacturer (source) are transported to a retailer (sink) by a sequence of intermediaries (wholesalers, shipping companies, etc.) In the other direction, to dampen the bullwhip effect (meaning that information about demand becomes less precise when moving up the supply chain from retailer to manufacturer), efficiency gains can be reached when the agents on a supply chain cooperate and share information. Thus, efficiency gains are realized by directed paths of players. Regarding our second example, advertisers are interested in measuring the success of their online advertising. Before conversion, customers may visit a path of advertisements containing multiple ads from the same advertiser. Attribution models assess the ‘value’ or ‘credit’ of each ad on the path leading to conversion. With respect to the third example, to ‘beat’ the COVID-19 pandemic, vaccination is an important strategy. However, in many countries, the vaccination rate stayed too low for too long. One reason for nonvaccination was that information from the government did not reach certain people. Intermediary social clubs, doctors, etc., helped in passing the information from the government to the people. Value is created by any directed path from the government to a (nonvaccinated) citizen.

Whereas [7] show the compatibility of connection efficiency with [1,3], type of fairness and balanced contributions axioms, in this paper, we investigate its compatibility with [6]’s balanced link contributions type of axiom. Whereas [6] considered undirected graphs and balanced link contributions considers an ‘equal’ mutual effect on the payoffs of pairs of players, by considering directed communication situations, we allow for different mutual effects on the payoffs of players, depending on whether we delete arcs where the player is a head or a tail. This makes sense for the applications mentioned above, since the role of heads and tails is different in different applications. To dampen the bullwhip effect in a supply chain, for example, it is crucial that the agents downstream (i.e., close to the retailer/sink) of the supply chain share information with agents more upstream (closer to the manufacturer/source). Therefore, one might give higher weight to the heads of the arcs. However, in marketing attribution, it is less clear how the weight between heads and tails must be allocated. On one hand, the channel starts at the first advertisement that a customer sees, stressing the role of the tails (who send the customer to the next advertisement). However, on the other hand, the last advertisements convince the customer to buy the project and realize a conversion, stressing the importance of the heads. Therefore, the weights between heads and tails are not beforehand known, but our axioms require that these weights are uniform across the network.

The remainder of this paper is organized as follows. After discussing some preliminaries on games, graphs, directed graphs and directed communication situations in Section 2, in Section 3, we introduce the arc game. In Section 4, we define our family of position values for directed communication situations, which are axiomatized in Section 5. Section 6 contains some concluding remarks.

2. Preliminaries

2.1. Cooperative TU Games

A cooperative n-person game with transferable utility (TU game) is a pair $(N,v)$ where $N=\{1,\cdots ,n\}$ is the set of players and, denoting $2^N=\left\{S\right|S\subseteq N\}$ as the set of all possible coalitions, $v:2^N\to {\mathbb{R}}^n$, verifying $v(\varnothing )=0$, is the characteristic function. For each $S\in 2^N$, $v\left(S\right)$ is the worth obtained by players in S if they cooperate.

We will denote by $G^N$ the vector space of all TU games with N fixed. In $G^N$, the family ${\left\{(N,u_S)\right\}}_{\varnothing \ne S\subseteq N}$ with

$$u_S\left(T\right)=\left\{\begin{array}{cc}1,& \mathrm{if}S\subseteq T\\ 0,& \mathrm{otherwise}.\end{array}\right.$$

is the unanimity games basis. Each v can be written uniquely as:

$$v=\sum _{\varnothing \ne S\subseteq N}{\Delta }_v\left(S\right)u_S,$$

where the coefficients ${\left\{{\Delta }_v\left(S\right)\right\}}_{\varnothing \ne S\subseteq N}$ are the Harsanyi dividends [8].

A TU game $(N,v)$ is zero-normalized if $v\left(\right\{i\left\}\right)=0$ for all $i\in N$. We will denote with $G_0^N$ the subspace of $G^N$ consisting of all zero-normalized games with player set N. A basis for $G_0^N$ is given by the games $(N,u_S)$ with $S\subseteq N$ and $s\ge 2$. In the following, for each $S\subseteq N$, s represents the cardinality of S.

An allocation rule in $G^N$ is a map $\psi :G^N\to {\mathbb{R}}^n$. For each $(N,v)\in G^N$, ${\psi }_i(N,v)$ represents the outcome or payoff for player $i\in N$ in the game $(N,v)$.

One of the more prominent allocation rules for TU games was proposed by [2], later called the Shapley value. It assigns to each player the following weighted mean of his marginal contributions to different coalitions:

$$S{h}_i(N,v)=\sum _{S\subseteq N\backslash \left\{i\right\}}\frac{(n-s-1)!s!}{n!}\left[v(S\cup \{i\left\}\right)-v\left(S\right)\right],i\in N.$$

2.2. Graphs

A $graph$ or a $network$ is a pair $(N,\gamma )$ in which $N=\{1,2,\cdots ,n\}$ is the set of nodes and $\gamma \subseteq {\gamma }_N=\left\{\{i,j\}\right|i,j\in N,i\ne j\}$, which is the complete graph. ${\Gamma }^N$ denotes the set of all graphs with node set N. A $subgraph$ of $(N,\gamma )$ is a graph $(N,{\gamma }^{\prime })$ with ${\gamma }^{\prime }\subseteq \gamma$. The restriction of the graph $(N,\gamma )\in {\Gamma }^N$ to $\varnothing \ne S\subseteq N$ is the graph $(S,{\gamma }_{{|}_S})$ with ${\gamma }_{{|}_S}=\{\{i,j\}\in \gamma |i,j\in S\}.$

We will say that two nodes i and j are directly connected in $(N,\gamma )$, if $\{i,j\}\in \gamma$. If i and j are not directly connected, they might be connected using a sequence of nodes (intermediaries) $i_1,i_2,\cdots i_k$ with $i_1=i$, $i_k=j$, and such that $\{i_l,i_{l+1}\}\in \gamma$, for $l=1,\cdots ,k-1$.

A connected component, C, in the graph $(N,\gamma )$ is a maximal connected subset. We will denote by $N/\gamma$ the partition of N in connected components in $(N,\gamma )$, and by $S/\gamma$ the set of the connected components of S in $(S,{\gamma }_{{|}_S})$. The graph $(N,\gamma )$ is connected if the cardinality of $N/\gamma$ is 1. Similarly, a set $\varnothing \ne S\subseteq N$ is connected in $\gamma$ if $|S/\gamma |=1$. We will consider $S\subseteq N$ to be connected whenever $s=1$.

2.3. Communication Situations and Allocation Rules

Ref. [1] introduced the possibility that players in a TU game have restrictions in their communication given by a graph. This model is known as a communication situation and it is mathematically formalized by means of a triple $(N,v,\gamma )$, $(N,v)$ being a TU game and $(N,\gamma )$ being a graph. $\mathcal{C}{\mathcal{S}}^N$ will denote the set of all communication situations with player–node set $N,$ and $\mathcal{C}{\mathcal{S}}_0^N$ will denote the subset of those elements in $\mathcal{C}{\mathcal{S}}^N$ in which the game is zero-normalized.

An allocation rule $\psi$ on $\mathcal{C}{\mathcal{S}}^N$ is a map $\psi :\mathcal{C}{\mathcal{S}}^N\to {\mathbb{R}}^n$, ${\psi }_i(N,v,\gamma )$ representing the outcome for player i in $(N,v,\gamma )$.

Ref. [1] also defined the graph-restricted game for a communication situation $(N,v,\gamma )$ as the TU game $(N,v^{\gamma })$ with the characteristic function given by:

$$v^{\gamma }\left(S\right)=\sum _{C\in S/\gamma }v\left(C\right), \mathrm{for}\mathrm{all} S\subseteq N.$$

In this restricted game, the worth of a coalition is the sum of the worths of its maximally connected subcoalitions. As an allocation rule for communication situations, he introduced the Myerson value, obtained by applying the Shapley value to the graph-restricted game.

In [1]’s framework, for communication situations in $\mathcal{C}{\mathcal{S}}_0^N$, Refs. [4,5] introduced a link game where the undirected edges (or links) are the players, and the worth of every coalition (of links) is determined by what the grand coalition of all players N can earn if exactly the links in that coalition are present. Formally, given a communication situation $(N,v,\gamma )\in \mathcal{C}{\mathcal{S}}_0^N$, the associated link game is the game $(\gamma ,r_{\gamma }^v)$ with the characteristic function given by:

$${\displaystyle r_{\gamma }^v\left(\eta \right)=v^{\eta }\left(N\right)=\sum _{C\in N/\eta }v\left(C\right), \mathrm{for}\mathrm{all} \eta \subseteq \gamma .}$$

They proposed another allocation rule, the position value $\pi$, that assigns to a player i in a communication situation half of the sum of the Shapley values of the links (in the link game) incident with it. Thus, this allocation rule is given by:

$${\displaystyle {\pi }_i(N,v,\gamma )=\frac{1}{2}\sum _{l\in {\gamma }_i}S{h}_l(\gamma ,r_{\gamma }^v), \mathrm{for}\mathrm{all} i\in N,}$$

where, for $i\in N$ and $(N,\gamma )\in {\Gamma }^N$, ${\gamma }_i=\{l\in \gamma |i\in l\}$ is the set of links incident with $i.$

Ref. [6] characterized the position value in terms of the following two properties.

An allocation rule $\psi$ on $\mathcal{C}{\mathcal{S}}^N$ satisfies component efficiency [1] if, $\mathrm{for}\mathrm{all}(N,v,\gamma )\in \mathcal{C}{\mathcal{S}}^N$ and all $C\in N/\gamma ,{\sum }_{i\in C}{\psi }_i(N,v,\gamma )=v\left(C\right)$.

An allocation rule $\psi$ on $\mathcal{C}{\mathcal{S}}^N$ satisfies balanced link contributions [6] if, $\mathrm{for}\mathrm{all}(N,v,\gamma )\in \mathcal{C}{\mathcal{S}}^N$ and all $i,j\in N$,

$${\displaystyle \sum _{l\in {\gamma }_i}\left[{\psi }_j(N,v,\gamma )-{\psi }_j(N,v,\gamma \backslash \left\{l\right\})\right]=\sum _{l\in {\gamma }_j}\left[{\psi }_i(N,v,\gamma )-{\psi }_i(N,v,\gamma \backslash \left\{l\right\})\right],}$$

where $(N,\gamma \backslash \{l\left\}\right)$ is the subgraph of $(N,\gamma )$ obtained when the relation l is broken.

2.4. Directed Graphs or Digraphs

A digraph (directed graph) is a pair $(N,D)$ (occasionally D when there is no ambiguity with respect to N), where $N=\{1,2,\cdots ,n\}$ is a (finite) set of nodes and $D\subseteq N\times N$ is a binary relation on N. Each $(i,j)\in D$ is an directed edge or arc, and i and j are called endpoints, the tail and the head, respectively. It is said that i is a predecessor of j and j a successor of i.

We will assume the digraph to be (i) irreflexive, i.e., with no loops (edges with equal endpoints), and (ii) simple, i.e., with no multiple edges (those having identical tails and identical heads). ${\mathcal{D}}^N$ denotes the set of all irreflexive, simple digraphs with node set N.

Given $(N,D)\in {\mathcal{D}}^N$ and $i\in N$, $D_i^O=\left\{(i,j)\right|(i,j)\in D\}$ is the set of directed edges in $(N,D)$ in which i is the tail, and $D_i^I=\left\{(j,i)\right|(j,i)\in D\}$ is the set of directed edges in $(N,D)$ in which i is the head. Moreover, given $(N,D)\in {\mathcal{D}}^N$ and $i\in N$, the out-degree, $d_i^O\left(D\right)=\left|D_i^O\right|$ (respectively, the in-degree, $d_i^I\left(D\right)=\left|D_i^I\right|$) is the number of edges with i as the tail (respectively, i as the head). Further, $d_i\left(D\right)=d_i^O\left(D\right)+d_i^I\left(D\right)$ is the degree of node i in $(N,D)$.

The total out-degree, respectively, the total in-degree, in the digraph $(N,D)$, will be denoted by ${\displaystyle d^O\left(D\right)=\sum _{i\in N}{d}_i^O\left(D\right)}$, respectively, ${\displaystyle d^I\left(D\right)=\sum _{i\in N}{d}_i^I\left(D\right)}$. It is easy to see that $d^O\left(D\right)=d^I\left(D\right)=\left|D\right|,$ as every edge has one tail and one head.

The relative out-degree of node i in $(N,D)$, denoted $r{d}_i^O\left(D\right)$, is defined as

$$r{d}_i^O\left(D\right)=\frac{d_i^O\left(D\right)}{{\displaystyle \sum _{j\in N}{d}_j^O\left(D\right)}}=\frac{d_i^O\left(D\right)}{d^O\left(D\right)}.$$

Similarly,

$$r{d}_i^I\left(D\right)=\frac{d_i^I\left(D\right)}{{\displaystyle \sum _{j\in N}{d}_j^I\left(D\right)}}=\frac{d_i^I\left(D\right)}{d^I\left(D\right)}$$

denotes the relative in-degree of node $i\in N$ in the digraph $(N,D)$.

A subdigraph of $(N,D)\in {\mathcal{D}}^N$ is a digraph $(N,D^{\prime })$ with $D^{\prime }\subseteq D$. The restriction of $(N,D)$ to $\varnothing \ne S\subseteq N$ is the directed graph $(S,D_{{|}_S})$ in which $D_{{|}_S}=\{(i,j)\in D|i,j\in S\}$. For $L\subseteq D$, we will abuse notation $\left\{L\right\}$ to indicate the nodes incident with the edges in L, i.e., $\left\{L\right\}=\{i\in N| \mathrm{there}\mathrm{is}a j\in N\mathrm{with} (i,j)\in L or (j,i)\in L\}$. Notice that the restriction $(\left\{L\right\},D_{{|}_{\left\{L\right\}}})$ coincides with $\left(\right\{L\},L)$.

Given a digraph $(N,D)$, a (directed) path from i to j is a sequence of distinct nodes $P=(i_1,\cdots ,i_t)$ with $i_1=i$, $i_t=j$ and such that $(i_j,i_{j+1})\in D$ for $j=1,\cdots ,t-1$. We assume that $\left(i\right)$, $i\in N$, is a path. For convenience, we will sometimes abuse the notation $\left\{P\right\}$ to denote the set of nodes of a path $P=(i_1,i_2,\cdots ,i_{t-1},i_t)$, and thus $\left\{P\right\}=\{i_1,\cdots ,i_t\}$.

A Hamiltonian path is a path that visits each node exactly once. Thus, if $P=(i_1,\cdots ,i_t)$ is a Hamiltonian path, then $t=n$ and $\left\{P\right\}=N$.

Given two paths $P=(i_1,\cdots ,i_t)$ and $Q=(j_1,\cdots ,j_r)$ in $(N,D)$, with $t\le r$, we say that P is a subpath of Q, denoted by $P\tilde{\subseteq }Q$, if for each $k=1,\cdots ,t-1$ there exists $l=1,\cdots ,r-1$ such that $j_l=i_k$ and $j_{l+1}=i_{k+1}$. Notice that $\tilde{\subseteq }$ is a partial order in the set of paths of $(N,D)\in D^N$. A path P in $(N,D)$ is maximal if it is maximal for this defined order, meaning that P is a path in $(N,D)$ and there is no other path Q in $(N,D)$ such that $P\tilde{\subseteq }Q$. We will denote by $\mathcal{P}(N,D)$ the set of all maximal paths of $(N,D)$ for $\tilde{\subseteq }$. Similarly, for $\varnothing \ne S\subseteq N$, we denote the family of the maximal paths in $(S,D_{{|}_S})$ by $\mathcal{P}(S,D_{{|}_S})$.

Given a digraph $(N,D)$ and $\varnothing \ne S\subseteq N$, we say that a path P in $(N,D)$ is a connection path of S in $(N,D)$ if $S\subseteq \left\{P\right\}$. We will say that a path P is a minimal connection path of S in $(N,D)$ if P is a connection path of S and there does not exist another connection path $P^{\prime }\ne P$ of S such that $P^{\prime }\tilde{\subseteq }P.$ By $\mathcal{M}\mathcal{C}\mathcal{P}(S,N,D)$, we will denote the family (occasionally empty) of all minimal connection paths of S in $(N,D)$.

We illustrate these notions with an example.

Example 1

([7]). Consider the digraph $(N,D)\in {\mathcal{D}}^N$ with $N=\{1,2,3,4\}$, and $D=\{a=(1,2),b=(2,4),c=(1,3),d=(3,4\left)\right\}$; see Figure 1.

In this case, the set of maximal paths in $(N,D)$ is

$$\mathcal{P}(N,D)=\left\{\right(1,2,4),(1,3,4\left)\right\}$$

and in $(S,D_{{|}_S})$ for $S=\{1,2,3\}$ is

$$\mathcal{P}(S,D_{{|}_S})=\{(1,2),(1,3)\}.$$

There is no Hamiltonian path in $(N,D).$

Moreover,

$$\begin{array}{cc}\hfill & \mathcal{M}\mathcal{C}\mathcal{P}\left(\right\{1,4\},N,D)=\left\{\right(1,2,4),(1,3,4\left)\right\}\hfill \\ \hfill & \mathcal{M}\mathcal{C}\mathcal{P}\left(\right\{2,3\},N,D)=\varnothing \hfill \\ \hfill & \mathcal{M}\mathcal{C}\mathcal{P}\left(\right\{1,2\},N,D)=\left\{\right(1,2\left)\right\}.\hfill \end{array}$$

2.5. Directed Communication Situations

A situation where cooperation among players in a TU game is restricted because of restricted directed communication possibilities can be modeled by a directed communication situation.

A directed communication situation is a triple $(N,v,D)$ in which $(N,v)$ is a TU game and $(N,D)$ is a directed graph, the nodes in the digraph being the players in the game.

The set of all directed communication situations with player set N will be denoted by $\mathcal{D}\mathcal{C}{\mathcal{S}}^N$. $\mathcal{D}\mathcal{C}{\mathcal{S}}_0^N$ will be the subset of those directed communication situations in which the underlying game is zero-normalized.

As mentioned in [7], the model of a directed communication situation is mathematically identical to other models of a game with an order (or digraph) on the player set, but, because of the interpretation of the directed graph as a directed communication network, we refer to it as a directed communication situation. See [7] for a discussion.

In [7], given a directed communication situation, a digraph-restricted game is introduced in which the worth of a coalition is obtained from the classical inclusion–exclusion principle applied to the values of the players connected by the maximal paths existing in the coalition.

Given $(N,v,D)\in \mathcal{D}\mathcal{C}{\mathcal{S}}^N$, the digraph-restricted game is defined as the TU game $(N,v^D)$ with the characteristic function given by:

$$\begin{array}{cc}\hfill & {\displaystyle v^D\left(S\right)=\sum _{i=1}^{r\left(S\right)}v\left(\left\{P_i^S\right\}\right)-\sum _{i=1}^{r\left(S\right)-1}\sum _{j=i+1}^{r\left(S\right)}v(\left\{P_i^S\right\}\cap \left\{P_j^S\right\})}\hfill \\ \hfill & {\displaystyle +\sum _{i=1}^{r\left(S\right)-2}\sum _{j=i+1}^{r\left(S\right)-1}\sum _{k=j+1}^{r\left(S\right)}v(\left\{P_i^S\right\}\cap \left\{P_j^S\right\}\cap \left\{P_k^S\right\})+\cdots +}\hfill \\ \hfill & +{(-1)}^{r\left(S\right)-1}v(\left\{P_1^S\right\}\cap \cdots \cap \left\{P_{r\left(S\right)}^S\right\}),\hfill \end{array}$$

where, for $\varnothing \ne S\subseteq N$, $\mathcal{P}(S,D_{{|}_S})=\{P_1^S,\cdots ,P_{r\left(S\right)}^S\}$ is the family of the maximal paths in $(S,D_{{|}_S})$, and $v^D(\varnothing )=0$.

3. An Arc Game for Directed Communication Situations

As mentioned in the preliminaries, Refs. [4,5] introduced a link game for communication situations, in which the links are the players and the worth of each coalition of links is determined by the worth of the coalition of all players in the digraph-restricted game corresponding to this set of links. Following their ideas, we define an arc game for directed communication situations based on the restricted game $v^D$ defined in Section 2.5.

Definition 1.

Given $(N,v,D)$ in $\mathcal{D}\mathcal{C}{\mathcal{S}}_0$, the arc game is defined as the TU game $(D,r_D^v)$ with characteristic function given by:

$${\displaystyle r_D^v\left(L\right)=v^L\left(N\right)=v^L\left(\left\{L\right\}\right)=\sum _{i=1}^{r\left(\right\{L\left\}\right)}v\left(\left\{P_i^{\left\{L\right\}}\right\}\right)-\sum _{i=1}^{r\left(\right\{L\left\}\right)-1}\sum _{j=i}^{r\left(\right\{L\left\}\right)}v(\left\{P_i^{\left\{L\right\}}\right\}\cap \left\{P_j^{\left\{L\right\}}\right\})}$$

$${\displaystyle +\sum _{i=1}^{r\left(\right\{L\left\}\right)-2}\sum _{j=i}^{r\left(\right\{L\left\}\right)-1}\sum _{k=j+1}^{r\left(\right\{L\left\}\right)}v(\left\{P_i^{\left\{L\right\}}\right\}\cap \left\{P_j^{\left\{L\right\}}\right\}\cap \left\{P_k^{\left\{L\right\}}\right\})}$$

$$+\cdots +{(-1)}^{r\left(\right\{L\left\}\right)-1}v(\left\{P_1^{\left\{L\right\}}\right\}\cap \left\{P_2^{\left\{L\right\}}\right\}\cap \cdots \cap \left\{P_{r\left(\right\{L\left\}\right)}^{\left\{L\right\}}\right\}), for all L\subseteq D,$$

with $\mathcal{P}(\left\{L\right\},L)=\{P_1^{\left\{L\right\}}\cdots P_{r\left(\right\{L\left\}\right)}^{\left\{L\right\}}\}$ being the set of all maximal paths in the digraph $\left(\right\{L\},L)$.

To clarify the previous definition, let us consider the next example.

Example 2.

Consider $(N,v,D)\in \mathcal{D}\mathcal{C}{\mathcal{S}}_0$ with $N=\{1,2,3,4\}$, $D=\{a=(1,2),b=(2,4),c=(1,3),d=(3,4\left)\right\}$ as in Example 1, and $(N,v)$ a zero-normalized game.

The characteristic function $r_D^v$ is given by:

$$r_D^v\left(L\right)=\left\{\begin{array}{cc}v\left(\right\{1,2\left\}\right)+v\left(\right\{1,3\left\}\right)-v\left(\right\{1\left\}\right),& if L=\{a,c\},\\ v\left(\right\{1,2\left\}\right)+v\left(\right\{3,4\left\}\right),& if L=\{a,d\},\\ v\left(\right\{2,4\left\}\right)+v\left(\right\{1,3\left\}\right),& if L=\{b,c\},\\ v\left(\right\{2,4\left\}\right)+v\left(\right\{3,4\left\}\right)-v\left(\right\{4\left\}\right),& if L=\{b,d\},\\ v\left(\right\{1,2,4\left\}\right)+v\left(\right\{1,3\left\}\right)-v\left(\right\{1\left\}\right),& if L=\{a,b,c\},\\ v\left(\right\{1,2,4\left\}\right)+v\left(\right\{3,4\left\}\right)-v\left(\right\{4\left\}\right),& if L=\{a,b,d\},\\ v\left(\right\{1,2\left\}\right)+v\left(\right\{1,3,4\left\}\right)-v\left(\right\{1\left\}\right),& if L=\{a,c,d\},\\ v\left(\right\{2,4\left\}\right)+v\left(\right\{1,3,4\left\}\right)-v\left(\right\{4\left\}\right),& if L=\{b,c,d\},\\ v\left(\right\{1,2,4\left\}\right)+v\left(\right\{1,3,4\left\}\right)-v\left(\right\{1\left\}\right)-v\left(\right\{4\left\}\right),& if L=\{a,b,c,d\},\\ v\left(\right\{L\left\}\right),& otherwise.\end{array}\right.$$

In the following proposition, we give an expression for the arc game associated with a zero-normalized unanimity game.

Proposition 1.

Given $(N,u_S,D)\in \mathcal{D}\mathcal{C}{\mathcal{S}}_0^N$ with $S\subseteq N$, $s\ge 2$, the characteristic function $r_D^{u_S}$ is given by

$${\displaystyle r_D^{u_S}=1-\prod _{i=1}^{t\left(S\right)}(1-u_{Q_i^S})if\mathcal{M}\mathcal{C}\mathcal{P}(S,N,D)=\{Q_1^S\cdots Q_{t\left(S\right)}^S\}\ne \varnothing ,}$$

and $r_D^{u_S}\equiv 0$, the null game, otherwise.

We denote by $(N,1)\in G^N$ the game with characteristic function given by $1\left(S\right)=1$ for all $\varnothing \ne S\subseteq N$ and $1(\varnothing )=0$. Similarly, we denote by $(N,0)\in G^N$ the game with characteristic function given by $0\left(S\right)=0$ for all $S\subseteq N$.

Proof. 

The result for $L=\varnothing$ is trivial. Consider $\varnothing \ne L\subseteq D$. Using Definition 1 of the arc game,

$${\displaystyle r_D^{u_S}\left(L\right)=u_S^L\left(\left\{L\right\}\right)=\sum _{i=1}^{r\left(\right\{L\left\}\right)}{u}_S\left(\left\{P_i^{\left\{L\right\}}\right\}\right)-\sum _{i=1}^{r\left(\right\{L\left\}\right)-1}\sum _{j=i}^{r\left(\right\{L\left\}\right)}{u}_S(\left\{P_i^{\left\{L\right\}}\right\}\cap \left\{P_j^{\left\{L\right\}}\right\})}$$

$${\displaystyle +\sum _{i=1}^{r\left(\right\{L\left\}\right)-2}\sum _{j=i}^{r\left(\right\{L\left\}\right)-1}\sum _{k=j+1}^{r\left(\right\{L\left\}\right)}{u}_S(\left\{P_i^{\left\{L\right\}}\right\}\cap \left\{P_j^{\left\{L\right\}}\right\}\cap \left\{P_k^{\left\{L\right\}}\right\})}$$

$$+\cdots +{(-1)}^{r\left(\right\{L\left\}\right)-1}{u}_S(\left\{P_1^{\left\{L\right\}}\right\}\cap \left\{P_2^{\left\{L\right\}}\right\}\cap \cdots \cap \left\{P_{r\left(\right\{L\left\}\right)}^{\left\{L\right\}}\right\}),$$

with $\mathcal{P}(\left\{L\right\},L)=\{P_1^{\left\{L\right\}}\cdots P_{r\left(\right\{L\left\}\right)}^{\left\{L\right\}}\}$ the set of all maximal paths in the digraph $\left(\right\{L\},L)$. Let $r^{\prime }\left(\left\{L\right\}\right)\le r\left(\left\{L\right\}\right)$ be the cardinality of the subset of $\mathcal{P}\left(\right\{L\},L)$ with node set $\left\{L\right\}$ containing S. If $r^{\prime }\left(\left\{L\right\}\right)=0,$ then $r_D^{u_S}\left(L\right)$ is clearly the null game, $\mathcal{M}\mathcal{C}\mathcal{P}(S,N,D)=\varnothing$, and thus the statement holds in this case.

If $r^{\prime }\left(\left\{L\right\}\right)\ge 1$, then we have

$$u_S^L\left(\left\{L\right\}\right)=\left(\genfrac{}{}{0pt}{}{r^{\prime }\left(\left\{L\right\}\right)}{1}\right)-\left(\genfrac{}{}{0pt}{}{r^{\prime }\left(\left\{L\right\}\right)}{2}\right)+\cdots +{(-1)}^{r^{\prime }\left(\left\{L\right\}\right)-1}\left(\genfrac{}{}{0pt}{}{r^{\prime }\left(\left\{L\right\}\right)}{r^{\prime }\left(\left\{L\right\}\right)}\right)$$

$$=-\left(\genfrac{}{}{0pt}{}{r^{\prime }\left(\left\{L\right\}\right)}{0}\right)+\left(\genfrac{}{}{0pt}{}{r^{\prime }\left(\left\{L\right\}\right)}{1}\right)-\left(\genfrac{}{}{0pt}{}{r^{\prime }\left(\left\{L\right\}\right))}{2}\right)+\cdots +{(-1)}^{r^{\prime }\left(\left\{L\right\}\right)-1}\left(\genfrac{}{}{0pt}{}{r^{\prime }\left(\left\{L\right\}\right)}{r^{\prime }\left(\left\{L\right\}\right)}\right)+\left(\genfrac{}{}{0pt}{}{r^{\prime }\left(\left\{L\right\}\right)}{0}\right)$$

$$=-\left[\left(\genfrac{}{}{0pt}{}{r^{\prime }\left(\left\{L\right\}\right)}{0}\right)-\left(\genfrac{}{}{0pt}{}{r^{\prime }\left(\left\{L\right\}\right)}{1}\right)+\left(\genfrac{}{}{0pt}{}{r^{\prime }\left(\left\{L\right\}\right))}{2}\right)+\cdots +{(-1)}^{r^{\prime }\left(\left\{L\right\}\right)}\left(\genfrac{}{}{0pt}{}{r^{\prime }\left(\left\{L\right\}\right)}{r^{\prime }\left(\left\{L\right\}\right)}\right)\right]+\left(\genfrac{}{}{0pt}{}{r^{\prime }\left(\left\{L\right\}\right)}{0}\right)$$

$$=-{(1-1)}^{r^{\prime }\left(\left\{L\right\}\right)}+\left(\genfrac{}{}{0pt}{}{r^{\prime }\left(\left\{L\right\}\right))}{0}\right)=1.$$

On the other hand, for $\varnothing \ne L\subseteq D$, ${\displaystyle \prod _{i=1}^{t\left(S\right)}(1-u_{Q_i}^S)\left(L\right)=0}$, and thus ${\displaystyle [1-\prod _{i=1}^{t\left(S\right)}(1-u_{Q_i}^S)]\left(L\right)=1}$ if there is at least one path contained in L whose node set contains S. Thus, the result is proven. □

4. A Family of Position Values for Directed Communication Situations

In this section, we introduce a family of allocation rules for directed communication situations based on the idea of the position value.

Definition 2.

An allocation rule on $\mathcal{D}\mathcal{C}{\mathcal{S}}_0^N$ is a function $\psi :\mathcal{D}\mathcal{C}{\mathcal{S}}_0^N\to {\mathbb{R}}^n$ that assigns to each $i\in N$ in a directed communication situation $(N,v,D)\in \mathcal{D}\mathcal{C}{\mathcal{S}}_0^N$ his reward ${\psi }_i(N,v,D)$.

Next, we define a class of allocation rules that is based on the idea behind the position value, using the arc game associated with a directed communication situation; see Definition 1. Whereas the position value for undirected communication situations shares the Shapley value payoff of every link in the link game equally between the two players on the link, in the case of directed communication, it is not obvious why the Shapley value payoff of every arc should be shared equally between the two nodes on the arc. The head and tail of an arc are clearly in an asymmetric position, and therefore discrimination in the payoff allocation seems plausible. In the definition below, we allow any split of the payoff of an edge between the head and the tail, but requires a uniform sharing across all arcs. Recall from the preliminaries that $D_i^O=\left\{(i,j)\right|(i,j)\in D\}$ and $D_i^I=\left\{(j,i)\right|(j,i)\in D\}$.

Definition 3.

Let $\alpha \in [0,1]$. The value ${\pi }^{\alpha }$ is defined, for every $(N,v,D)\in \mathcal{D}\mathcal{C}{\mathcal{S}}_0^N$, as:

$${\pi }_i^{\alpha }(N,v,D)=\alpha {\displaystyle \sum _{a\in D_i^I}S{h}_a(D,r_D^v)}+(1-\alpha ){\displaystyle \sum _{a\in D_i^O}S{h}_a(D,r_D^v)}for i=1,\cdots ,n.$$

The family of values $\{{\pi }^{\alpha }\mid \alpha \in [0,1]\}$ is called the family of position values.

Notice that, in the definition above, we can give the arc payoff fully to the head (if $\alpha =1$), fully to the tail (if $\alpha =0$) or allow an equal sharing between head and tail (if $\alpha =\frac{1}{2}$). However, we use the same means of splitting on every arc. We illustrate this allocation rule with an example.

Example 3.

Consider $(N,v,D)\in \mathcal{D}\mathcal{C}{\mathcal{S}}_0^N$ with $N=\{1,2,3,4\}$ and $D=\{a=(1,2),b=(2,4),c=(1,3),d=(3,4\left)\right\}$; see Figure 1.

(a)Let v be the messages game of [9] given by

$$v\left(S\right)=\left\{\begin{array}{cc}\frac{s(s-1)}{2},\hfill & ifs\ge 2\hfill \\ 0,\hfill & otherwise\hfill \end{array}\right.$$

This game reflects the importance of bilateral connection, since the worth of a coalition equals the number of unordered pairs in the coalition.

As

$$v=u_{\{1,2\}}+u_{\{1,3\}}+u_{\{1,4\}}+u_{\{2,3\}}+u_{\{2,4\}}+u_{\{3,4\}},$$

we have, using Proposition 1, that

$$r_D^v=\left(u_{\left\{a\right\}}\right)+\left(u_{\left\{c\right\}}\right)+(u_{\{a,b\}}+u_{\{c,d\}}-u_{\{a,b,c,d\}})+\left(u_{\left\{b\right\}}\right)+\left(u_{\left\{d\right\}}\right)$$

$$=u_{\left\{a\right\}}+u_{\left\{b\right\}}+u_{\left\{c\right\}}+u_{\left\{d\right\}}+u_{\{a,b\}}+u_{\{c,d\}}-u_{\{a,b,c,d\}}.$$

Notice that $r_D^{u_{\{2,3\}}}\equiv 0$ as there is no path connecting 2 and 3.

Thus, $Sh(D,r_D^v)=(\frac{5}{4},\frac{5}{4},\frac{5}{4},\frac{5}{4})$ and

$${\pi }_1^{\alpha }(N,v,D)=(1-\alpha )(\frac{5}{4}+\frac{5}{4})=\frac{5(1-\alpha )}{2}$$

$${\pi }_2^{\alpha }(N,v,D)=\alpha \frac{5}{4}+(1-\alpha )\frac{5}{4}=\frac{5}{4}$$

$${\pi }_3^{\alpha }(N,v,D)=\alpha \frac{5}{4}+(1-\alpha )\frac{5}{4}=\frac{5}{4}$$

$${\pi }_4^{\alpha }(N,v,D)=\alpha (\frac{5}{4}+\frac{5}{4})=\frac{5\alpha }{2}.$$

We emphasize the following intuitive behavior of these allocation rules in this example:

(i) 

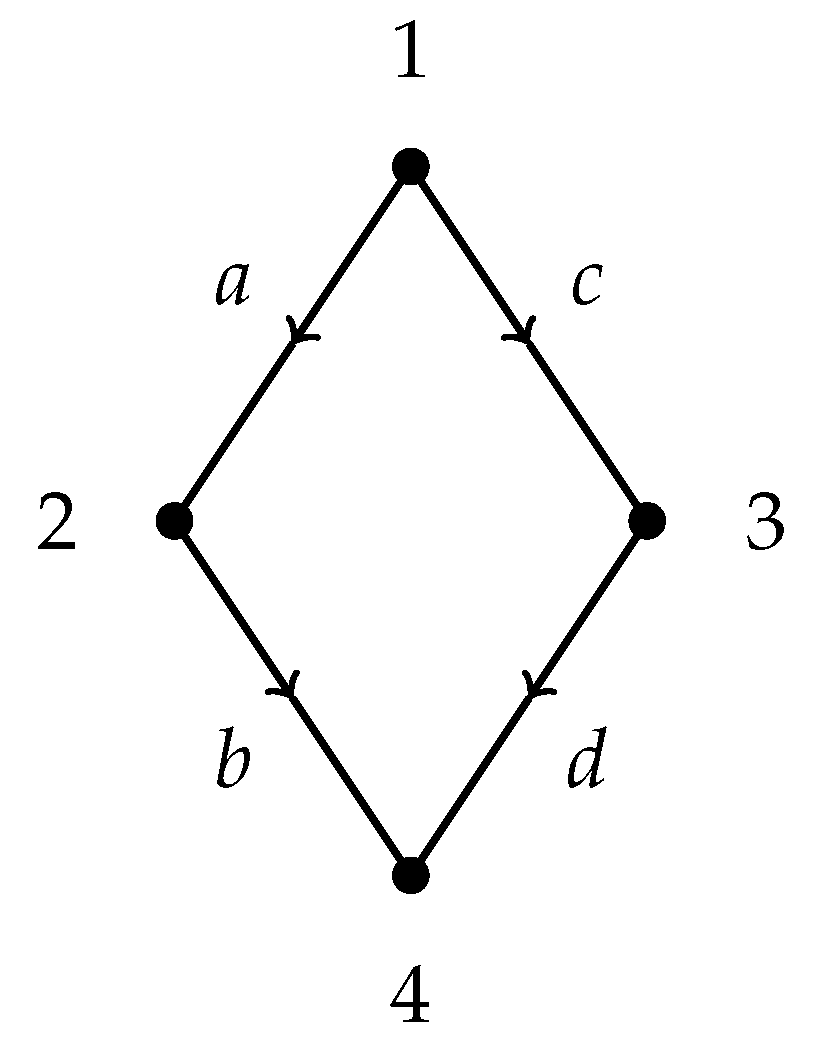
Given that all players are symmetrical in the game, and that players 2 and 3 are also symmetrical in the digraph, it is not surprising that the payoff is equal for both of them and it does not depend on α because the payoff lost (increased) being the tail is compensated by the payoff increased (lost) being the head.

(ii) 

The payoff for 1 is greater than the payoff for 4 when $\alpha <\frac{1}{2}$, illustrating that, in this case, the tail is better paid. Reciprocally, for $\alpha >\frac{1}{2}.$

(iii) 

The sum of the payoffs is 5 as only 5 of the 6 bilateral connections are feasible given the digraph. Notice that connection of 2 and 3 is not possible.

(b)Consider the conference game $(N,w),$ with characteristic function given by

$$w\left(S\right)=\left\{\begin{array}{cc}\left(\genfrac{}{}{0pt}{}{s}{2}\right)+\left(\genfrac{}{}{0pt}{}{s}{3}\right)+\cdots +\left(\genfrac{}{}{0pt}{}{s}{s}\right)=2^s-s-1,\hfill & ifs\ge 2\hfill \\ 0,\hfill & otherwise,\hfill \end{array}\right.$$

or equivalently

$${\displaystyle w=\sum _{S\subseteq N,s\ge 2}{u}_S.}$$

We have, using Proposition 1, that

$$r_D^w=\left(u_{\left\{a\right\}}\right)+\left(u_{\left\{c\right\}}\right)+(u_{\{a,b\}}+u_{\{c,d\}}-u_{\{a,b,c,d\}})+\left(u_{\left\{b\right\}}\right)+\left(u_{\left\{d\right\}}\right)+\left(u_{\{a,b\}}\right)+\left(u_{\{c,d\}}\right)$$

$$=u_{\left\{a\right\}}+u_{\left\{b\right\}}+u_{\left\{c\right\}}+u_{\left\{d\right\}}+2u_{\{a,b\}}+2u_{\{c,d\}}-u_{\{a,b,c,d\}},$$

and $Sh(D,r_D^w)=(\frac{7}{4},\frac{7}{4},\frac{7}{4},\frac{7}{4})$. In this case,

$${\pi }_1^{\alpha }(N,w,D)=(1-\alpha )\left(\frac{7}{4}+\frac{7}{4}\right)=\frac{7(1-\alpha )}{2}$$

$${\pi }_2^{\alpha }(N,w,D)=\alpha \frac{7}{4}+(1-\alpha )\frac{7}{4}=\frac{7}{4}$$

$${\pi }_3^{\alpha }(N,w,D)=\alpha \frac{7}{4}+(1-\alpha )\frac{7}{4}=\frac{7}{4}$$

$${\pi }_4^{\alpha }(N,w,D)=\alpha \left(\frac{7}{4}+\frac{7}{4}\right)=\frac{7\alpha }{2}.$$

In the following, we obtain some useful results relating the particular (extreme) values ${\pi }^0$ and ${\pi }^1$ to the relative out-degree and the relative in-degree, respectively.

Proposition 2.

Let $(N,v,D)\in \mathcal{D}\mathcal{C}{\mathcal{S}}_0^N$. Then, for $i\in N$,

$${\displaystyle {\pi }_i^0(N,v,D)=\sum _{A\subseteq D}{\Delta }_{r_D^v}\left(A\right)r{d}_i^O\left(A\right)}$$

where, for each $A\subseteq D$, ${\Delta }_{r_D^v}\left(A\right)$ is the Harsanyi dividend of the coalition (of directed edges) A in the arc game $r_D^v$, and $r{d}_i^O\left(A\right)$ is the relative out-degree of node i in the directed graph $(N,A)$.

Proof. 

The game $(N,r_D^v)$ admits the following expression in terms of the Harsanyi dividends:

$${\displaystyle r_D^v=\sum _{\varnothing \ne A\subseteq D}{\Delta }_{r_D^v}\left(A\right)u_A.}$$

Then, using the definition of ${\pi }_i^0(N,v,D)$ (see Definition 3), for $(N,v,D)\in \mathcal{D}\mathcal{C}{\mathcal{S}}_0^N$ and $i\in N$, we have

$${\displaystyle {\pi }_i^0(N,v,D)=\sum _{a\in D_i^O}S{h}_a(D,r_D^v)=\sum _{a\in D_i^O}S{h}_a\left[{\displaystyle D,\sum _{A\subseteq D}{\Delta }_{r_D^v}\left(A\right)u_A}\right]}$$

$${\displaystyle =\sum _{a\in D_i^O}\sum _{A\subseteq D}{\Delta }_{r_D^v}\left(A\right)S{h}_a(D,u_A),}$$

(1)

the last equality holding because of linearity of the Shapley value.

Rearranging the terms in (1), we obtain

$${\displaystyle \sum _{a\in D_i^O}\sum _{A\subseteq D}{\Delta }_{r_D^v}\left(A\right)S{h}_a(D,u_A)=\sum _{A\subseteq D}{\Delta }_{r_D^v}\left(A\right)\sum _{a\in D_i^O}S{h}_a(D,u_A)}$$

$${\displaystyle =\sum _{A\subseteq D}{\Delta }_{r_D^v}\left(A\right)\sum _{a\in D_i^O\cap A}S{h}_a(D,u_A)=\sum _{A\subseteq D}{\Delta }_{r_D^v}\left(A\right)\frac{|D_i^O\cap A|}{\left|A\right|}}$$

$${\displaystyle =\sum _{A\subseteq D}{\Delta }_{r_D^v}\left(A\right)\frac{d_i^O\left(A\right)}{\left|A\right|}=\sum _{A\subseteq D}{\Delta }_{r_D^v}\left(A\right)\frac{d_i^O\left(A\right)}{d^O\left(A\right)}=\sum _{A\subseteq D}{\Delta }_{r_D^v}\left(A\right)r{d}_i^O\left(A\right),}$$

where the second equality follows since $a\in D\backslash A$ implies that $S{h}_a(D,u_A)=0$, the fifth equality holding as the out-degree in $(N,A)$ equals the number of edges in A (each edge has one tail and one head), and the last equality holding as $\frac{d_i^O\left(A\right)}{d^O\left(A\right)}$, by definition, is the relative out-degree of node i in the digraph $(N,A)$, $r{d}_i^O\left(A\right)$. The result is proven. □

The proof of the following proposition follows similar lines as the previous one and is therefore omitted.

Proposition 3.

Let $(N,v,D)\in \mathcal{D}\mathcal{C}{\mathcal{S}}_0^N$ and $i\in N.$ Then,

$${\displaystyle {\pi }_i^1(N,v,D)=\sum _{A\subseteq D}{\Delta }_{r_D^v}\left(A\right)r{d}_i^I\left(A\right)}$$

where, for each $A\subseteq D$, ${\Delta }_{r_D^v}\left(A\right)$ is the Harsanyi dividend of $A\subseteq D$, and $r{d}_i^I\left(A\right)$ is the relative in-degree of i in $(N,A)$.

Since, by definition, for all $\alpha \in [0,1]$

$${\pi }_i^{\alpha }(N,v,D)=\alpha {\pi }_i^1(N,v,D)+(1-\alpha ){\pi }_i^0(N,v,D),$$

(i.e., ${\pi }^{\alpha }$ is a convex combination of ${\pi }^0$ and ${\pi }^1$) the following corollary is a direct consequence of the previous propositions.

Corollary 1.

For each $\alpha \in (0,1)$, $(N,v,D)\in \mathcal{D}\mathcal{C}{\mathcal{S}}_0^N$ and $i\in N$,

$${\displaystyle {\pi }_i^{\alpha }(N,v,D)=\sum _{A\subseteq D}{\Delta }_{r_D^v}\left(A\right)[\alpha r{d}_i^I\left(A\right)+(1-\alpha )r{d}_i^O\left(A\right)].}$$

We illustrate this result with an example.

Example 4.

Consider ${\pi }_1^{\alpha }(N,v,D)$ in Example 3.

(a)If v is the messages game, then, by Corollary 1, we have:

$${\pi }_1^{\alpha }(N,v,D)={\Delta }_{r_D^v}\left(\left\{a\right\}\right)\left[\alpha r{d}_1^I\left(\left\{a\right\}\right)+(1-\alpha )r{d}_1^O\left(\left\{a\right\}\right)\right]$$

$$+{\Delta }_{r_D^v}\left(\left\{b\right\}\right)\left[\alpha r{d}_1^I\left(\left\{b\right\}\right)+(1-\alpha )r{d}_1^O\left(\left\{b\right\}\right)\right]$$

$$+{\Delta }_{r_D^v}\left(\left\{c\right\}\right)\left[\alpha r{d}_1^I\left(\left\{c\right\}\right)+(1-\alpha )r{d}_1^O\left(\left\{c\right\}\right)\right]$$

$$+{\Delta }_{r_D^v}\left(\left\{d\right\}\right)\left[\alpha r{d}_1^I\left(\left\{d\right\}\right)+(1-\alpha )r{d}_1^O\left(\left\{d\right\}\right)\right]$$

$$+{\Delta }_{r_D^v}\left(\{a,b\}\right)\left[\alpha r{d}_1^I\left(\{a,b\}\right)+(1-\alpha )r{d}_1^O\left(\{a,b\}\right)\right]$$

$$+{\Delta }_{r_D^v}\left(\{c,d\}\right)\left[\alpha r{d}_1^I\left(\{c,d\}\right)+(1-\alpha )r{d}_1^O\left(\{c,d\}\right)\right]$$

$$+{\Delta }_{r_D^v}\left(\{a,b,c,d\}\right)\left[\alpha r{d}_1^I\left(\{a,b,c,d\}\right)+(1-\alpha )r{d}_1^O\left(\{a,b,c,d\}\right)\right]$$

$$=(1-\alpha )+0+(1-\alpha )+0+\frac{(1-\alpha )}{2}+\frac{(1-\alpha )}{2}-\frac{2(1-\alpha )}{4}=\frac{5(1-\alpha )}{2}.$$

Similarly,

$${\pi }_2^{\alpha }(N,v,D)=\alpha +(1-\alpha )+\left(\frac{\alpha }{2}+\frac{(1-\alpha )}{2}\right)-\left(\frac{\alpha }{4}+\frac{(1-\alpha )}{4}\right)=\frac{5}{4}$$

$${\pi }_3^{\alpha }(N,v,D)=\alpha +(1-\alpha )+\left(\frac{\alpha }{2}+\frac{(1-\alpha )}{2}\right)-\left(\frac{\alpha }{4}+\frac{(1-\alpha )}{4}\right)=\frac{5}{4}$$

$${\pi }_4^{\alpha }(N,v,D)=0+\alpha +0+\alpha +\frac{\alpha }{2}+\frac{\alpha }{2}-\frac{2\alpha }{4}=\frac{5\alpha }{2}.$$

Notice that these outcomes coincide with those in Example 3 (a).

(b)If w is the conference game, then, by Corollary 1, we have:

$${\pi }_1^{\alpha }(N,w,D)=(1-\alpha )+0+(1-\alpha )+0+\frac{2(1-\alpha )}{2}+\frac{2(1-\alpha )}{2}-\frac{2(1-\alpha )}{4}=\frac{7(1-\alpha )}{2}$$

$${\pi }_2^{\alpha }(N,w,D)=\alpha +(1-\alpha )+0+0+\frac{2(\alpha +(1-\alpha \left)\right)}{2}+0-\frac{\alpha +(1-\alpha )}{4}=\frac{7}{4}$$

$${\pi }_3^{\alpha }(N,w,D)=0+0+\alpha +(1-\alpha )+0+\frac{2(\alpha +(1-\alpha \left)\right)}{2}-\frac{\alpha +(1-\alpha )}{4}=\frac{7}{4}$$

$${\pi }_4^{\alpha }(N,w,D)=0+\alpha +0+\alpha +\frac{2\alpha }{2}+\frac{2\alpha }{2}-\frac{2\alpha }{4}=\frac{7\alpha }{2}$$

Notice that these outcomes coincide with those in Example 3 (b).

5. Characterization of the Position Values

In this section, we characterize the family of values defined in Definition 3 in terms of two properties, connection efficiency and $\alpha$-balanced arc contributions, which are defined as follows.

Given a digraph $(N,D)\in {\mathcal{D}}^N$, its underlying (undirected) graph $(N,{\gamma }_D)\in {\Gamma }^N$ is obtained by replacing all directed edges with corresponding undirected links, i.e., ${\gamma }_D=\left\{\{i,j\}\right|(i,j)\in D\}$.

Definition 4

([7]). An allocation rule $\psi :\mathcal{D}\mathcal{C}{\mathcal{S}}_0^N\to {\mathbb{R}}^n$ satisfies connection efficiency if, for all $(N,v,D)\in \mathcal{D}\mathcal{C}{\mathcal{S}}_0^N$ and all $C\in N/{\gamma }_D$,

$${\displaystyle \sum _{i\in C}{\psi }_i(N,v,D)=v^D\left(C\right).}$$

As mentioned in the Introduction, Ref. [7] motivated the use of connection efficiency in situations where worth is generated by (maximal) paths. This is a very useful concept of efficiency in, for example, marketing attribution or supply chains. In these applications, worth is generated when, through a sequence of advertisements—respectively, a sequence of intermediary retailers and other agents (such as transportation companies) on the supply chain—a conversion takes place when a consumer (sink of the path) buys a product that is produced by a producer (source of the path). Another situation where this occurs is in communications (e.g., sending messages), when the only aspect that matters is whether a message from a sender reaches the intended receiver, possibly through a chain of intermediaries. In recent years, this occurred, for example, in COVID-19 vaccination policy, where governments tried to reach to people who lived somewhat isolated through intermediaries such as doctors and social workers. Specifically, Ref. [7] use this notion of connection efficiency to define game theoretical measures of centrality, efficiency and vulnerability for directed networks.

Proposition 4.

Let $\alpha \in [0,1]$. The allocation rule ${\pi }^{\alpha }$$:\mathcal{D}\mathcal{C}{\mathcal{S}}_0^N\to {\mathbb{R}}^n$ satisfies connection efficiency.

Proof. 

Let $(N,v,D)\in \mathcal{D}\mathcal{C}{\mathcal{S}}_0^N$ and $C\in N/{\gamma }_D$. Then, using Corollary 1,

$${\displaystyle \sum _{i\in C}{\pi }_i^{\alpha }(N,v,D)=\sum _{i\in C}\sum _{A\subseteq D}{\Delta }_{r_D^v}\left(A\right)\left[\alpha r{d}_i^I\left(A\right)+(1-\alpha )r{d}_i^O\left(A\right)\right]}$$

$${\displaystyle =\sum _{i\in C}\sum _{{A\subseteq D|}_C}{\Delta }_{r_D^v}\left(A\right)\left[\alpha r{d}_i^I\left(A\right)+(1-\alpha )r{d}_i^O\left(A\right)\right]}$$

$${\displaystyle =\sum _{{A\subseteq D|}_C}{\Delta }_{r_D^v}\left(A\right)\sum _{i\in C}\left[\alpha r{d}_i^I\left(A\right)+(1-\alpha )r{d}_i^O\left(A\right)\right]}$$

$${\displaystyle =\sum _{{A\subseteq D|}_C}{\Delta }_{r_D^v}\left(A\right)\left[{\displaystyle \alpha \sum _{i\in C}r{d}_i^I\left(A\right)+(1-\alpha )\sum _{i\in C}r{d}_i^O\left(A\right)}\right]}$$

$${\displaystyle =\sum _{{A\subseteq D|}_C}{\Delta }_{r_D^v}\left(A\right)\left[\alpha +(1-\alpha )\right]=\sum _{{A\subseteq D|}_C}{\Delta }_{r_D^v}\left(A\right)=r_D^v\left(D{|}_C\right)}$$

where ${D|}_C=\{(k,l)\in D|k,l\in C\}$, the second equality holding because the dividend of a coalition in the game $(D,r_D^v)$ is zero if the coalition contains arcs from different components, and the fifth equality holding because the sum of the relative (in- and out-) degrees in a set of arcs that all belong to the same component is equal to one.

Finally, $r_D^v\left(D{|}_C\right)=v^D\left(C\right)$ by the definition of $r_D^v$, and, thus, the result is proven. □

Before defining an extension of the balanced link contribution property for directed communication situations, we first define two special cases focussing on the nodes’ out-arcs, respectively, the in-arcs. First, balanced out-arc contributions require that the sum of the effects of breaking each outgoing arc of a player on the payoff of another player is the same as the effect the other way around.

Definition 5.

An allocation rule $\psi :\mathcal{D}\mathcal{C}{\mathcal{S}}_0^N\to {\mathbb{R}}^n$ satisfies balanced out-arc contributions if, for all $(N,v,D)\in \mathcal{D}\mathcal{C}{\mathcal{S}}_0^N$ and all $i,j\in N$,

$${\displaystyle \sum _{a\in D_j^O}[{\psi }_i(N,v,D)-{\psi }_i(N,v,D\backslash \left\{a\right\})]=\sum _{a\in D_i^O}[{\psi }_j(N,v,D)-{\psi }_j(N,v,D\backslash \left\{a\right\})].}$$

The extreme position value where $\alpha =0$ satisfies balanced out-arc contributions.

Proposition 5.

The allocation rule ${\pi }^0:\mathcal{D}\mathcal{C}{\mathcal{S}}_0^N\to {\mathbb{R}}^n$ satisfies balanced out-arc contributions.

Proof. 

Let $(N,v,D)\in \mathcal{D}\mathcal{C}{\mathcal{S}}_0^N$ and $i,j,\in N$. Using Proposition 2, we have that ${\displaystyle {\pi }_i^0(N,v,D)=\sum _{A\subseteq D}{\Delta }_{r_D^v}\left(A\right)r{d}_i^O\left(A\right)}$ and similarly for j. Then,

$${\displaystyle \sum _{a\in D_j^O}\left[{\pi }_i^0(N,v,D)-{\pi }_i^0(N,v,D\backslash \left\{a\right\})\right]}$$

$${\displaystyle =\sum _{a\in D_j^O}\left[{\displaystyle \sum _{A\subseteq D}{\Delta }_{r_D^v}\left(A\right)r{d}_i^O\left(A\right)-\sum _{A\subseteq D\backslash \left\{a\right\}}{\Delta }_{r_D^v}\left(A\right)r{d}_i^O\left(A\right)}\right]}$$

$${\displaystyle =\sum _{a\in D_j^O}\sum _{A\subseteq D,a\in A}{\Delta }_{r_D^v}\left(A\right)r{d}_i^O\left(A\right)=\sum _{A\subseteq D,a\in A}{\Delta }_{r_D^v}\left(A\right)d_j^O\left(A\right)r{d}_i^O\left(A\right)}$$

$${\displaystyle =\sum _{A\subseteq D,a\in A}{\Delta }_{r_D^v}\left(A\right)\frac{d_j^O\left(A\right)d_i^O\left(A\right)}{d^O\left(A\right)}.}$$

As this last expression is symmetric in i and j, it coincides with

$${\displaystyle \sum _{a\in D_i^O}\left[{\pi }_j^0(N,v,D)-{\pi }_j^0(N,v,D\backslash \left\{a\right\}\right]}$$

and, thus, the result is proven. □

Similarly, we can define balanced in-arc contributions, and have the next proposition for $\alpha =1$. The proof mimics the previous one and, therefore, it is omitted.

Definition 6.

An allocation rule $\psi :\mathcal{D}\mathcal{C}{\mathcal{S}}_0^N\to {\mathbb{R}}^n$ satisfies balanced in-arc contributions if, for all $(N,v,D)\in \mathcal{D}\mathcal{C}{\mathcal{S}}_0^N$ and all $i,j\in N$,

$${\displaystyle \sum _{a\in D_j^I}[{\psi }_i(N,v,D)-{\psi }_i(N,v,D\backslash \left\{a\right\})]=\sum _{a\in D_i^I}[{\psi }_j(N,v,D)-{\psi }_j(N,v,D\backslash \left\{a\right\})].}$$

Proposition 6.

The allocation rule ${\pi }^1:\mathcal{D}\mathcal{C}{\mathcal{S}}_0^N\to {\mathbb{R}}^n$ satisfies balanced in-arc contributions.

As mentioned in the Introduction, which type of balanced arc contributions is appropriate depends on the application that one considers. In some cases, such as sharing information to dampen the bullwhip effect in a supply chain, it seems that the heads (which are closer to the retailer) should receive higher weight. However, in other cases, such as channels in marketing attribution, it is less clear how the weight between heads and tails must be allocated since the tails are closer to the origin of the marketing channel, but the heads are closer to the point of conversion. To allow a compromise between the effect on heads and tails, next, we state a balanced arc contribution property for any $\alpha \in [0,1]$ with a balanced out-arc, and balanced in-arc contributions as two extreme cases.

Definition 7.

Let $\alpha \in [0,1]$. An allocation rule $\psi :\mathcal{D}\mathcal{C}{\mathcal{S}}_0^N\to {\mathbb{R}}^n$ satisfies the α-balanced arc contributions property if, for all $(N,v,D)\in \mathcal{D}\mathcal{C}{\mathcal{S}}_0^N$ and all $i,j\in N$,

$${\displaystyle \alpha \sum _{a\in D_j^I}[{\psi }_i(N,v,D)-{\psi }_i(N,v,D\backslash \left\{a\right\})]}$$

$${\displaystyle +(1-\alpha )\sum _{a\in D_j^O}[{\psi }_i(N,v,D)-{\psi }_i(N,v,D\backslash \left\{a\right\})]}$$

$${\displaystyle =\alpha \sum _{a\in D_i^I}[{\psi }_j(N,v,D)-{\psi }_j(N,v,D\backslash \left\{a\right\})]}$$

$${\displaystyle +(1-\alpha )\sum _{a\in D_i^O}[{\psi }_j(N,v,D)-{\psi }_j(N,v,D\backslash \left\{a\right\})].}$$

Before exploring the implications of these properties, in the following lemma, we first state a property relating the rules ${\pi }^0$ and ${\pi }^1$. This property is a kind of cross-balanced arc contribution, in the sense that the sum of the differences in ${\pi }^0$ that a player experiences when another player breaks the edges in which he is head is equal to the differences experienced in ${\pi }^1$ for the second player when the other breaks the edges in which he is tail.

Lemma 1.

Let $(N,v,D)\in \mathcal{D}\mathcal{C}{\mathcal{S}}_0^N$ and $i,j\in N$. Then,

$${\displaystyle \sum _{a\in D_j^I}\left[{\pi }_i^0(N,v,D)-{\pi }_i^0(N,v,D\backslash \left\{a\right\})\right]=\sum _{a\in D_i^O}\left[{\pi }_j^1(N,v,D)-{\pi }_j^1(N,v,D\backslash \left\{a\right\})\right].}$$

Proof. 

For $(N,v,D)\in \mathcal{D}\mathcal{C}{\mathcal{S}}_0^N$ and $i,j\in N$,

$${\displaystyle \sum _{a\in D_j^I}\left[{\pi }_i^0(N,v,D)-{\pi }_i^0(N,v,D\backslash \left\{a\right\}\right]}$$

$${\displaystyle =\sum _{a\in D_j^I}\left[{\displaystyle \sum _{A\subseteq D}{\Delta }_{r_D^v}\left(A\right)r{d}_i^O\left(A\right)-\sum _{A\subseteq D\backslash \left\{a\right\}}{\Delta }_{r_D^v}\left(A\right)r{d}_i^O\left(A\right)}\right]}$$

$${\displaystyle =\sum _{a\in D_j^I}\sum _{A\subseteq D,a\in A}{\Delta }_{r_D^v}\left(A\right)r{d}_i^O\left(A\right)=\sum _{A\subseteq D}{\Delta }_{r_D^v}\left(A\right)d_j^I\left(A\right)r{d}_i^O\left(A\right)}$$

$${\displaystyle =\sum _{A\subseteq D}{\Delta }_{r_D^v}\left(A\right)\frac{d_j^I\left(A\right)d_i^O\left(A\right)}{d^O\left(A\right)}}$$

where the first equality follows from Proposition 2.

Similarly, we can obtain, for $(N,v,D)\in \mathcal{D}\mathcal{C}{\mathcal{S}}_0^N$ and $i,j\in N$, that

$${\displaystyle \sum _{a\in D_i^O}\left[{\pi }_j^I(N,v,D)-{\pi }_j^I(N,v,D\backslash \left\{a\right\}\right]}$$

$${\displaystyle =\sum _{a\in D_i^O}\left[{\displaystyle \sum _{A\subseteq D}{\Delta }_{r_D^v}\left(A\right)r{d}_j^I\left(A\right)-\sum _{A\subseteq D\backslash \left\{a\right\}}{\Delta }_{r_D^v}\left(A\right)r{d}_j^I\left(A\right)}\right]}$$

$${\displaystyle =\sum _{a\in D_i^O}\sum _{A\subseteq D,a\in A}{\Delta }_{r_D^v}\left(A\right)r{d}_j^I\left(A\right)=\sum _{A\subseteq D}{\Delta }_{r_D^v}\left(A\right)d_i^O\left(A\right)r{d}_j^I\left(A\right)}$$

$${\displaystyle =\sum _{A\subseteq D}{\Delta }_{r_D^v}\left(A\right)\frac{d_i^O\left(A\right)d_j^I\left(A\right)}{d^I\left(A\right)},}$$

showing the result since $d^O\left(A\right)=d^I\left(A\right)$. □

Using this lemma and Propositions 5 and 6, we have the following proposition.

Proposition 7.

Let $\alpha \in [0,1]$. The allocation rule ${\pi }^{\alpha }:\mathcal{D}\mathcal{C}{\mathcal{S}}_0^N\to {\mathbb{R}}^n$, satisfies the α-balanced arc contributions property.

Proof. 

Given $(N,v,D)\in \mathcal{D}\mathcal{C}{\mathcal{S}}_0^N$ and $i,j\in N$,

$${\displaystyle \alpha \sum _{a\in D_j^I}\left[{\pi }_i^{\alpha }(N,v,D)-{\pi }_i^{\alpha }(N,v,D\backslash \left\{a\right\})\right]}$$

$${\displaystyle +(1-\alpha )\sum _{a\in D_j^O}\left[{\pi }_i^{\alpha }(N,v,D)-{\pi }_i^{\alpha }(N,v,D\backslash \left\{a\right\})\right]}$$

$${\displaystyle =\alpha \sum _{a\in D_j^I}[\alpha {\pi }_i^1(N,v,D)+(1-\alpha ){\pi }_i^0(N,v,D)}$$

$$-\alpha {\pi }_i^1(N,v,D\backslash \left\{a\right\})-(1-\alpha ){\pi }_i^0(N,v,D\backslash \left\{a\right\})]$$

$${\displaystyle +(1-\alpha )\sum _{a\in D_j^O}[\alpha {\pi }_i^1(N,v,D)+(1-\alpha ){\pi }_i^0(N,v,D)}$$

$$-\alpha {\pi }_i^1(N,v,D\backslash \left\{a\right\})-(1-\alpha ){\pi }_i^0(N,v,D\backslash \left\{a\right\})]$$

$${\displaystyle ={\alpha }^2\sum _{a\in D_j^I}\left[{\pi }_i^1(N,v,D)-{\pi }_i^1(N,v,D\backslash \left\{a\right\})\right]}$$

$${\displaystyle +{(1-\alpha )}^2\sum _{a\in D_j^O}\left[{\pi }_i^0(N,v,D)-{\pi }_i^0(N,v,D\backslash \left\{a\right\})\right]}$$

$${\displaystyle +\alpha (1-\alpha )\sum _{a\in D_j^I}\left[{\pi }_i^0(N,v,D)-{\pi }_i^0(N,v,D\backslash \left\{a\right\})\right]}$$

$${\displaystyle +(1-\alpha )\alpha \sum _{a\in D_j^O}\left[{\pi }_i^1(N,v,D)-{\pi }_i^1(N,v,D\backslash \left\{a\right\})\right],}$$

where the first equality follows from the definition of ${\pi }^{\alpha }$. Taking into account that ${\pi }^0$ and ${\pi }^1$ satisfy balanced out-arc contributions and balanced in-arc contributions, respectively, and using Lemma 1, the last expression coincides with

$${\displaystyle {\alpha }^2\sum _{a\in D_i^O}\left[{\pi }_j^1(N,v,D)-{\pi }_j^1(N,v,D\backslash \left\{a\right\})\right]}$$

$${\displaystyle +{(1-\alpha )}^2\sum _{a\in D_i^I}\left[{\pi }_j^0(N,v,D)-{\pi }_j^0(N,v,D\backslash \left\{a\right\})\right]}$$

$${\displaystyle +\alpha (1-\alpha )\sum _{a\in D_j^I}\left[{\pi }_i^1(N,v,D)-{\pi }_i^1(N,v,D\backslash \left\{a\right\})\right]}$$

$${\displaystyle +(1-\alpha )\alpha \sum _{a\in D_j^O}\left[{\pi }_i^0(N,v,D)-{\pi }_i^0(N,v,D\backslash \left\{a\right\})\right].}$$

A similar calculation as above shows that the last expression is equal to

$${\displaystyle \alpha \sum _{a\in D_i^O}\left[{\pi }_j^{\alpha }(N,v,D)-{\pi }_j^{\alpha }(N,v,D\backslash \left\{a\right\})\right]}$$

$${\displaystyle +(1-\alpha )\sum _{a\in D_i^I}\left[{\pi }_j^{\alpha }(N,v,D)-{\pi }_j^{\alpha }(N,v,D\backslash \left\{a\right\})\right]}$$

and thus ${\pi }^{\alpha }$ satisfies $\alpha$-balanced arc contributions, for $\alpha \in [0,1]$. □

Finally, we can characterize the allocation rules ${\pi }^{\alpha },\alpha \in [0,1]$, by connection efficiency and the corresponding $\alpha$-balanced arc contributions property.

Theorem 1.

Let $\alpha \in [0,1]$. The allocation rule ${\pi }^{\alpha }:\mathcal{D}\mathcal{C}{\mathcal{S}}_0^N\to {\mathbb{R}}^n$ is the unique allocation rule satisfying connection efficiency and α-balanced arc contributions.

Proof. 

It is already proven that ${\pi }^{\alpha }$ satisfies connection efficiency and $\alpha$-balanced arc contributions; see Propositions 4 and 7. Therefore, it is sufficient to show the uniqueness of an allocation rule satisfying the two properties. Let $\psi :\mathcal{D}\mathcal{C}{\mathcal{S}}_0^N\to {\mathbb{R}}^n$ be an allocation rule satisfying these two properties. We will prove that $\psi (N,v,D)$ is uniquely determined for all $(N,v,D)\in \mathcal{D}\mathcal{C}{\mathcal{S}}_0^N$ by induction on $\left|D\right|$, the cardinality of D. The proof follows similar steps as in [6].

If $\left|D\right|=0$, uniqueness is trivial by connection efficiency. Proceeding by induction, suppose that uniqueness holds for $(N,v,D)$ with $\left|D\right|\le k$ and consider $(N,v,D)$ such that $\left|D\right|=k+1$. Let $C\in N/{\gamma }_D$ and suppose, without loss of generality, that $C=\{1,2,\cdots ,c\}$. If $c=\left|C\right|=1$, uniqueness holds using connection efficiency. Thus, let us consider the case in which $c=\left|C\right|>1$. Take any $j\in C\backslash \left\{1\right\}$. Applying the $\alpha$-balanced arc contributions property to players–nodes 1 and j, we have

$${\displaystyle \alpha \sum _{a\in D_j^I}\left[{\psi }_1(N,v,D)-{\psi }_1(N,v,D\backslash \left\{a\right\})\right]}$$

$${\displaystyle +(1-\alpha )\sum _{a\in D_j^O}\left[{\psi }_1(N,v,D)-{\psi }_1(N,v,D\backslash \left\{a\right\})\right]}$$

$${\displaystyle =\alpha \sum _{a\in D_1^I}\left[{\psi }_j(N,v,D)-{\psi }_j(N,v,D\backslash \left\{a\right\})\right]}$$

$${\displaystyle +(1-\alpha )\sum _{a\in D_1^O}\left[{\psi }_j(N,v,D)-{\psi }_j(N,v,D\backslash \left\{a\right\})\right]}$$

or, alternatively, by rearranging the terms,

$${\displaystyle \alpha \sum _{a\in D_j^I}{\psi }_1(N,v,D)+(1-\alpha )\sum _{a\in D_j^O}{\psi }_1(N,v,D)-\alpha \sum _{a\in D_1^I}{\psi }_j(N,v,D)}$$

$${\displaystyle -(1-\alpha )\sum _{a\in D_1^O}{\psi }_j(N,v,D)}$$

$${\displaystyle =\alpha \sum _{a\in D_j^I}{\psi }_1(N,v,D\backslash \left\{a\right\})}$$

$${\displaystyle +(1-\alpha )\sum _{a\in D_j^O}{\psi }_1(N,v,D\backslash \left\{a\right\})-\alpha \sum _{a\in D_1^I}{\psi }_j(N,v,D\backslash \left\{a\right\})}$$

$${\displaystyle -(1-\alpha )\sum _{a\in D_1^O}{\psi }_j(N,v,D\backslash \left\{a\right\}).}$$

Notice that the left-hand side can be written as

$$\alpha d_j^I\left(D\right){\psi }_1(N,v,D)+(1-\alpha )d_j^O\left(D\right){\psi }_1(N,v,D)$$

$$-\alpha d_1^I\left(D\right){\psi }_j(N,v,D)-(1-\alpha )d_1^O\left(D\right){\psi }_j(N,v,D),$$

and the right-hand side is determined by the induction hypothesis.

Since this holds for every $j\in C\backslash \left\{1\right\}$, we have $c-1$ linear independent equations in the c unknown payoffs ${\psi }_i(N,v,D),i\in C$. Moreover, connection efficiency gives the equation

$${\displaystyle \sum _{i=1}^c{\psi }_i(N,v,D)=v^D\left(C\right).}$$

Thus, we have c linear independent equations in the c unkown payoffs ${\psi }_i(N,v,D)$, $i\in C$, which thus are uniquely determined.

(It is straightforward to prove that the determinant of the coefficient matrix is equal to ${\displaystyle \sum _{i=1}^c\left(\alpha d_i^I\left(D\right)+(1-\alpha )d_i^O\left(D\right)\right)}$${\displaystyle {\left[-\alpha d_1^I\left(D\right)-(1-\alpha )d_1^O\left(D\right)\right]}^{c-2}=-\sum _{i=1}^c{d}_i^O\left(D\right){\left[\alpha d_1^I\left(D\right)+(1-\alpha )d_1^O\left(D\right)\right]}^{c-2}=-\left|D_{{|}_C}\right|}$${\left[\alpha d_1^I\left(D\right)+(1-\alpha )d_1^O\left(D\right)\right]}^{c-2}\ne 0$, for all $\alpha \in (0,1)$.

If $\alpha =0$, $-|D_{{|}_C}|d_1^O{\left(D\right)}^{c-2}$ is also different from zero when node 1 is such that $d_1^O\left(D\right)>0$. If $d_1^O\left(D\right)=0$. This can be shown by taking another node with positive out-degree in C.

If $\alpha =1$, $-|D_{{|}_C}|d_1^I{\left(D\right)}^{c-2}$ is also different from zero when node 1 is such that $d_1^I\left(D\right)>0$. If $d_1^I\left(D\right)=0$. This can be shown by taking another node with positive in-degree in C.)

Since ${\pi }^{\alpha }$ satisfies the two properties, it must be that $\psi (N,v,D)={\pi }^{\alpha }(N,v,D)$. □

6. Concluding Remarks

In this paper, we introduce a family of position values for directed communication situations, based on the idea of the position value for (undirected) communication situations introduced in [4,5] and axiomatically characterized in [6]. Specifically, we characterize each position value in our family by the connection efficiency of [7] and a corresponding version of balanced arc contributions weighing out- and in-arcs in a different way, but uniform across arcs.

An idea for future research is to evaluate whether, in the expression of our family of position values in Corollary 1, the (relative) out- or in-degree can be replaced by other power or centrality measures for directed graphs, similarly to [10] for (undirected) communication situations. Instead of power or centrality measures, also other weights determined exogenously by, for example, bargaining, political, military, etc., power can be taken into consideration, as done in [11], who defines a family of weighted position values for undirected communication situations. Moreover, other types of axioms can be considered, such as monotonicity axioms related to adding/deleting arcs, as in [1] for undirected graph games, or related to changes in contributions in the game, as in [12] for TU games.

Another open issue concerns the computational efficiency of the proposed approach. Is is known from, for example, [13], that computing the Shapley value for arbitrary games is an NP-complete problem. As our value is in fact a linear combination of Shapley values, the problem of computing our values is NP-complete. Using sampling methods, such as the ones in [14], our values might be approximated in polynomial time.