Abstract
This survey starts with a general overview of the strategies for stock price change predictions based on market data and in particular Limit Order Book (LOB) data. The main discussion is devoted to the systematic analysis, comparison, and critical evaluation of the state-of-the-art studies in the research area of stock price movement predictions based on LOB data. LOB and Order Flow data are two of the most valuable information sources available to traders on the stock markets. Academic researchers are actively exploring the application of different quantitative methods and algorithms for this type of data to predict stock price movements. With the advancements in machine learning and subsequently in deep learning, the complexity and computational intensity of these models was growing, as well as the claimed predictive power. Some researchers claim accuracy of stock price movement prediction well in excess of 80%. These models are now commonly employed by automated market-making programs to set bids and ask quotes. If these results were also applicable to arbitrage trading strategies, then those algorithms could make a fortune for their developers. Thus, the open question is whether these results could be used to generate buy and sell signals that could be exploited with active trading. Therefore, this survey paper is intended to answer this question by reviewing these results and scrutinising their reliability. The ultimate conclusion from this analysis is that although considerable progress was achieved in this direction, even the state-of-art models can not guarantee a consistent profit in active trading. Taking this into account several suggestions for future research in this area were formulated along the three dimensions: input data, model’s architecture, and experimental setup. In particular, from the input data perspective, it is critical that the dataset is properly processed, up-to-date, and its size is sufficient for the particular model training. From the model architecture perspective, even though deep learning models are demonstrating a stronger performance than classical models, they are also more prone to over-fitting. To avoid over-fitting it is suggested to optimize the feature space, as well as a number of layers and neurons, and apply dropout functionality. The over-fitting problem can be also addressed by optimising the experimental setup in several ways: Introducing the early stopping mechanism; Saving the best weights of the model achieved during the training; Testing the model on the out-of-sample data, which should be separated from the validation and training samples. Finally, it is suggested to always conduct the trading simulation under realistic market conditions considering transactions costs, bid–ask spreads, and market impact.
Keywords:
survey/review of the literature; experiments reproducibility evaluation; microstructure market data; limit order book; time series analysis; deep learning; convolutional neural network; LSTM MSC:
68T07
1. Introduction
Since the inception of the stock capital markets investors have attempted to forecast the share price movements. However, at that time, the data available to them was quite limited and the approaches to processing this data were quite simple. Since then, the amount of data available to the investors has expanded significantly and new ways of processing this data have been introduced. Currently, even with all the technical progress and advanced trading algorithms, the ability to correctly predict the stock price movements still remains an extremely challenging task for most researchers and investors. Traditional models based on fundamental analysis, technical analysis, and statistical methods, e.g., regression in [1], which were used for decades, often can not fully capture the complexity of the issue at hand. In particular, they are not suitable for the data with high cardinality, such as the Limit Order Book (LOB) data.
The recent advancement in the Machine Learning methods and proliferation of the market, fundamental and alternative data in the digital format led to numerous attempts to adopt these models for the stock price prediction task, e.g., [2,3,4]. Some researchers were already able to demonstrate quite impressive results in this area, in particular using LOB data as a main source, e.g., [5]. In this paper, the focus is on the critical evaluation of the practical usefulness of state-of-the-art Machine Learning and Deep Learning models based on LOB data for stock price predictions. A more detailed formulation of the research problem, motivation, goals, and the structure of this paper is presented in the paragraphs below.
Progress in the machine and deep learning opened new opportunities for building stock price movement prediction models based on time-series data characterised by high cardinality, such as the LOB data. As a consequence this area has been the focus of increasing research interest over the recent years. Prediction performance of the suggested models is usually claimed to be rather high, for some state-of-the-art Machine Learning and Deep Learning models (e.g., [6,7]), according to the authors, accuracy is above 80%. From the practical perspective these results look too good to be actually reproducible in real world stock trading. Thus, these models require a detailed investigation, which we conduct in this paper.
This survey is focused on the critical evaluation of the current studies in the subject area of stock price movement predictions based on LOB data and identification of the improvements required and directions for further research.
In addition to this introductory section, the paper is organised into three main sections:
Section 2 contains an overview of the strategies for stock prediction based on the market data. At the beginning there is an introduction to the three core types of data used in trading: market data, fundamental data, and alternative data. The subsequent discussion will focus on market data such as stock execution prices and volumes and LOB data. Next there is an overview of the market data-based trading approaches, with their comparison, evolution trends analysis, and the respective conclusions. Among those conclusions are that the most promising data type for further analysis is LOB and the most promising model classes are Machine Learning and Deep Learning.
Section 3 is focused on a critical review of the empirical research on the Benchmark LOB dataset. At the beginning of this section there is a detailed description of the benchmark LOB dataset with the evaluation of its merits and issues. Next, there is a subsection devoted to the comparison and critical evaluation of the Machine Learning and Deep Learning models based on the Benchmark LOB dataset. At the end of this section there is a discussion of the data processing approach, experimental setup, and results for one of the state-of-the-art models, for which the experiment was reproduced.
Finally, Section 4 summarises the findings from the evaluation of the stock price prediction models and data used in these experiments. Based on these a number of improvements are suggested and potential directions for future work in this area are defined.
2. Overview of Strategies for Stock Prediction Based on Market Data
2.1. Introduction to the Input Data for Stock Trading
Broadly, the source data for the stock trading strategies can be divided into three major classes: fundamental data, alternative data, and market data.
The financial metrics, such as revenue, profit, free cash flow, etc., which define the equity value of a particular company, are considered as company-specific fundamental data. The second category is the external fundamental data, which include the macroeconomic and industrial indicators relevant to the selected company, such as GDP of the country of operations, or the iron ore price for a steel producing company. The main assumption of the trading strategies relying on fundamental data is that the stock price will converge towards its fair value defined by the above-mentioned factors. For example, Bartov et al. [2] concluded that the well-known post-earnings announcement drift phenomenon is caused by the unsophisticated investors’ delayed response to the new information. This suggests that trading strategies could exploit this market inefficiency and generate excess returns by rapidly and correctly responding to the new fundamental data inflows. Similarly, a more recent study [3] proved that the trading strategy exploiting the slow reaction of oil companies’ investors to the changing oil price can be profitable.
The proliferation of the internet and the production of large quantities of digital data in recent years created a highly valuable source of insights on potential stock price movements. The variety of this alternative data is unprecedented, it can be any insightful information about the company, starting from such obvious examples as announcements on a companies’ websites, rumours in the news blogs and on social media about a company, and ending with much more exotic data, such as the number of new positions posted on the company’s recruiting section of the website, number of the visitors in the online store, or even satellite photos of the number of cars parked near the company’s store or of the fields of a grain producing company. For example, the authors of this research [4] concluded that the satellite photos of the parking lots near a company’s stores provide useful information for assessing a retailer’s performance. According to the authors, the trading strategies utilising this data can generate extra profit at the expense of less informed market participants, who are making their investment decisions based on the earnings announcements. This is possible since only some investors have exclusive access to this information, while others have to rely on the official financial results announcements, which happen with a substantial time lag compared to the almost real-time satellite photos collection.
Market data comprises all the trade-related statistics that can be collected from the exchanges or other trading platforms, such as the flow of the orders, stock price, and trading volume. This type of data plays a pivotal role in intra-day trading and especially in High-Frequency Trading (HFT). HFT firms generated enormous profits in recent years, which provides empirical evidence that this type of data deserves the attention of researchers. In addition, this market data is often available at an extremely fine scale. With a time series interval that can be under 1 millisecond, a reasonable number of points for analysis can be collected even for a period as short as one trading day. Further to this, the trading strategies relying on fundamental data and alternative data generally need a longer investment horizon with unpredictable duration since the period of convergence to the target price in these strategies depends on how fast other market participants will process and react to this information, which could vary substantially and could be difficult to predict.
Taking into account the above-mentioned considerations the focus of this paper will be on the market data as a core input source for stock price prediction models.
2.2. Market Data Classification Overview
In this paper, market data has a narrow definition; this is stock trading related statistics that can be collected from the exchanges or other trading platforms, such as stock quotes, trade prices, and volumes. This data can be classified by type, frequency, and depth.
In technical terms, the type of market data can be considered as a feature. The two most basic market data types are the stock price and the traded volume. More advanced ones could be the information about particular orders placed, such as type of the order, buy/sell indicator, timestamp, etc.
The frequency of market data is defined based on the period between data points. The shorter this period the higher the frequency of the data. The highest frequency market data is tick-by-tick data, which means that the interval between the data points can be extremely small (below 1 millisecond) and is defined by the recorded time stamps of quote updates, order submissions, trades, etc. Often intra-day market data is provided with a lower frequency and recorded with a predefined time interval, for example 10 s or 1 min. The most common example of non-intra-day market data is the end of day prices and volumes, provided only on a daily basis.
The concept of depth of market data is mostly relevant for the LOB data which comprises the bid and offer limit order prices and sizes up to a certain level. For example, the most shallow Level 1 data provide just the best bid and ask quotes and their sizes for the stock under consideration. In contrast the deepest market data could be the complete LOB, including the price and size data for all the limit orders placed. Please refer to Table 1 for an illustrative example of LOB data structure.

Table 1.
Limit Order Book dataset illustrative example.
2.3. Market Data-Based Trading Approaches and Their Evolution
Market Data-Based trading strategies are leveraging the above-described data so as to infer the expected stock price change. In order to identify the most promising types of market data as well as an experimental approaches and models for stock price movement predictions, an analysis of the state-of-the-art studies in this field is conducted below. Approaches are compared both quantitatively and qualitatively and presented in chronological order to better demonstrate the evolution in this area. In the review, papers published in the last 15 years are considered. The discussion is built around the following three key pillars:
- Input data used in these experiments;
- Models applied for the stock price prediction;
- Results achieved, their comparability and practicality assessment.
The reviewed papers taxonomy along these three categories is presented in the Figure 1.
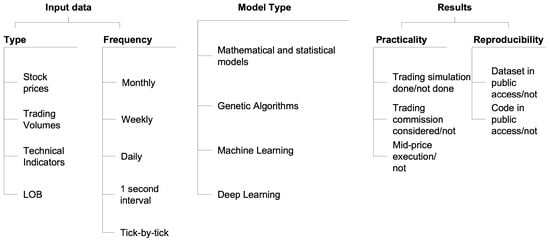
Figure 1.
The reviewed papers taxonomy.
2.3.1. Model
As can be seen from Table 2, at an earlier stage classical mathematical and statistical models, such as Hidden Markov Models (HMM) or linear regressions were often applied, as well as some basic machine learning models such as the Back Propagation Neural Network (BPNN) and Support Vector Machine (SVM). Furthermore, genetic algorithms (GA), such as traditional/hierarchical GA [8], Improved Bacterial Chemotaxis Optimisation (IBCO) [9], or BFO [10] were widely applied for stock price predictions. From Table 2 it is clear that models applied for stock prediction are evolving into deeper machine learning models with more complex structures. Basic machine learning models such as SVM [5], RR, and [11] were succeeded by the deeper machine learning architectures such as CNN [12], LSTM [13]. In more recent studies, authors were offering custom deep learning models consisting of layers of different types, refs. [6,14] are setting out combinations of convolution and LSTM layers. It is claimed that these models should improve the performance in stock price prediction compared to the earlier models, which were more shallow. However, the more complex models are also more prone to over-fitting, which can substantially limit their generalising capability.

Table 2.
State-of-the-art stock price prediction models based on market data.
2.3.2. Data
As can be seen from Table 2, earlier studies [15,16,17] were using low frequency, usually daily, data or sometimes even weekly or monthly data. Data samples were also relatively small, often in the range of 500–2500 data points. With rare exceptions such as [25], where the high frequency tick-by-tick market data was used with an extensive one-year long dataset of more than 450,000 data points. As a features from this data in addition to the prices and volumes, technical indicators, such as Moving Average (MA), Moving Average Convergence/Divergence (MACD), Average Directional Index (ADX), Relative Strength factor (RS), Relative Strength Index (RSI), Schaff Trend Cycle (STC), etc., were often used. In some studies, such as [17], the underlying model assumptions were unrealistically simplistic, for example, taking the prior day price as the only predictor for the next day price. Others [10,19,25], were using the extensive set of technical indicators as features, where for the feature selection mechanism the genetic algorithms were applied in combination with basic statistical models for the stock price prediction. More recent studies have tended to focus on the high-frequency market data and explore this data in greater depth. For example, instead of fully relying only on the level 1 data, up to 10 levels of LOB data were used. The average data sample size also increased substantially, from thousands of data points to hundreds of thousands. Some studies, such as [42], were using datasets consisting of more than a million of data-points or even more than a hundred millions like in [6]. This tendency could be explained by the fact that as the models applied are becoming more complex, larger datasets are required to properly train them. However, even for some studies utilising the LOB data the small sample size was still an issue. For example, ref. [49] was based on the data for just one day making it difficult to draw general conclusions on the general effectiveness of the methodology.
2.3.3. Experimental Setup, Results Comparability, Practicality and Reproducibility
Earlier studies were using predominantly different datasets, experiment setups and even the metrics measuring the models performance, were varying widely. All these factors are making them almost incomparable. Reproducibility of many of these experiments was also poor since datasets and code were made publicly available for only a few of the studies considered. The situation was improved after the first public benchmark LOB dataset was published [11] in 2017. This work established a common platform for the research in this area by allowing a greater standardisation of experiment setup and performance metrics in addition to the benchmark LOB dataset itself. Recent state-of-the-art studies are often using this dataset to compare the results against the other models. However, only a few authors were used their models to conduct trading simulations such as in these studies [5,6,43] and to calculate potential profits from the strategy based on the model predictions. Thus, it is possible to assess the practical value of just a few of the model suggested. The other problem affecting the practicality of these studies is that the transaction costs were often not taken into consideration even when this trading simulation was undertaken, with rare exceptions [15,24]. The other unrealistic assumption, which is embedded in the above-mentioned benchmark LOB dataset [11] and thus affecting all the studies using this data, is that transactions could be executed at the mid-price. The mid-price is just a simplifying approximation of the actual execution price. The former is calculated as an average of the best bid and offer prices, while the latter would be the best offer for buying and best bid for selling using market orders. This type of order would be required to ensure timely execution. It is clear that a round trip transaction in either direction with buying at best offer and selling at best bid would results in larger spread-related transaction costs than if the mid-price execution is assumed. At the same time, mid-price is still important for market-making strategies for properly positioning the bid and ask limit orders relative to the expected mid-price.
2.3.4. Key Takeaways
Our analysis of prior studies, as set out above, leads to the conclusion that machine/deep learning models using the high-frequency and high-depth market data such as LOB data, are the most promising direction in the research area of stock price prediction, that is why they are explored in the rest of this paper. Since the recent state-of-the-art models in this research area were often trained on the above-mentioned benchmark LOB dataset, which helped to substantially improve their predictive performance comparability, it was decided to focus in the next chapter on the review of studies that were leveraging this dataset, to identify the most promising studies.
3. Critical Review of the Experiments with the Benchmark LOB Dataset
3.1. Benchmark LOB Dataset
The above-mentioned benchmark LOB dataset contains high frequency LOB data for 10 trading days (1 June 2010–14 June 2010) for five stocks (Kesko, Outokumpu, Sampo, Rautaruukki, Wärtsilä) traded on the Helsinki Stock Exchange. As can be seen from Figure 2, there was generally an upward trend during this period with just a few days of price declines, also the movements of prices for these five stocks were fairly similar. Except Kesko, all these stocks demonstrated better performance than the market (based on the MSCI Finland Index) on average.
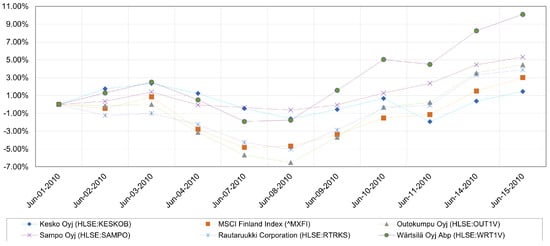
Figure 2.
Stocks performance against the market index.
The pre-processed LOB dataset contains timing, volume, and price information for the first 10 levels of bid and ask sides of the LOB. In Table 1, the structure of the dataset before the normalisation is illustrated. Timestamps are in milliseconds from 1 January 1970. Prices are in EUR with 4 decimal places after the decimal point. In addition to the above-described features, the dataset also contains the labels for 1, 2, 3, 5, and 10 predicted horizons. Labels values are ‘1’ (upward movement) or ‘2’ (no movement) or ‘3’ (downward movement).
The publication of this dataset became an important milestone in this area of research by providing other authors with the publicly available input data for their experiments and by enabling them to benchmark the performance of their models.
However, in the course of our empirical analysis, we identified a series of problems and limitations in this dataset which may either bias or reduce the practical relevance of the results obtained when using it:
- The underlying order flow data provided by NASDAQ is more than ten years old, so this data may not be a good indicator of the current situation in the dynamically evolving stock markets.
- Authors combined all the five stocks data into one dataset, making them indistinguishable from each other. As a results of this, at multiple data points in the experiments, the models are learning the price movement outcome for one stock based on the LOB features of the other stock, which does not make much sense from the market operations perspective. This could introduce some bias in the models and their conclusions.
- The other potential biases could have been introduced during the processing of the raw order flow data and further data clean-ups and normalisation. Analysis of the of raw data from NASDAQ, led to the conclusion that there could be some outliers and errors in this data that need to be adjusted before feeding this to the models to avoid biased results. It is not clear if this was actually performed by the authors of the benchmark LOB dataset, since the data in the benchmark LOB dataset is normalised using three different methods: min-max, z-score, and decimal-precision) and combined for all the stocks, making it hard to identify potentially erroneous data points.
- The dataset is inherently unbalanced among its three classes of movement (“upward”, “flat”, “downward”). As we can see from Figure 3 the “flat” class is dominant for the prediction horizons of 1, 2, 3 events. With the increasing length of the prediction horizon the proportion of the “flat” class is gradually shrinking, so for the prediction horizon of 5 events the dataset is more or less balanced between the three classes, while for 10 events the “flat” class is positioned as the smallest one. This requires appropriate adjustments to the experimental setup, such as over-sampling, under-sampling and etc. Based on the review of prior studies, some of the results reported were based on experimental procedures that did not include dynamically responsive sampling of datapoints; this could have potentially biased such results.
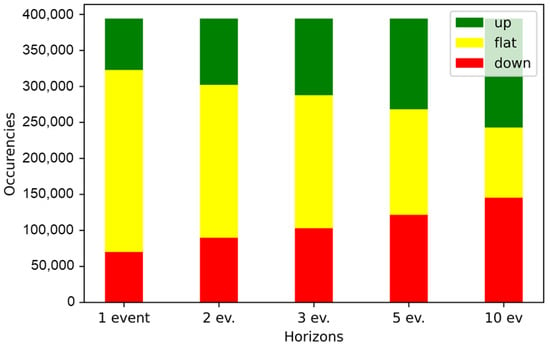 Figure 3. Dataset distribution among three classes of labels.
Figure 3. Dataset distribution among three classes of labels. - “upward”, “flat” and “downward” labels in this dataset are determined based on the mid-price movement, which is an average between the best bid and offer prices. This assumption could be valid if the buy or sell part of the transaction is executed using the limit orders instead of market orders. Since there is no guarantee that the limit orders would be actually executed in the required time slot, this assumption is unrealistic.
3.2. Comparison and Critical Evaluation of the ML/DL Models Based on the Benchmark LOB Dataset in Chronological Order
A number of state-of-the-art models in Table 3 below were compared based on the following statistical metrics as Accuracy, Precision, Recall, and F1 for the same benchmark dataset [11]. All the models considered were trained on the data for the first 7 days of the dataset for at least 150 epochs and tested on the last 3 days. The prediction horizon selected is 10 LOB events.

Table 3.
State-of-the-art stock price prediction models performance on the benchmark LOB dataset.
In the work of Tran et al. [48], the authors were comparing the stock price prediction models based on the methods presented in Table 4 below. As in previous papers, the same LOB benchmarks dataset was the source for features extraction.

Table 4.
Performance comparison of the methods applied in [48].
As can be seen from Table 3 and even more clearly from Figure 4, the performance in terms of F1 score, Accuracy, Precision, and Recall was gradually improving over time with more and more complex models applied. For the basic linear and non-linear classification (Ridge Regression (RR) and Support Vector Machines (SVM)) models the F1 score was around 40 percent. Shallow neural network architectures, such as Multilayer Perceptron (MLP) improved the F1 score to almost 50 percent. The resulting F1 score was even further improved by the deep learning models, such as Long Short-Term Memory (LSTM).
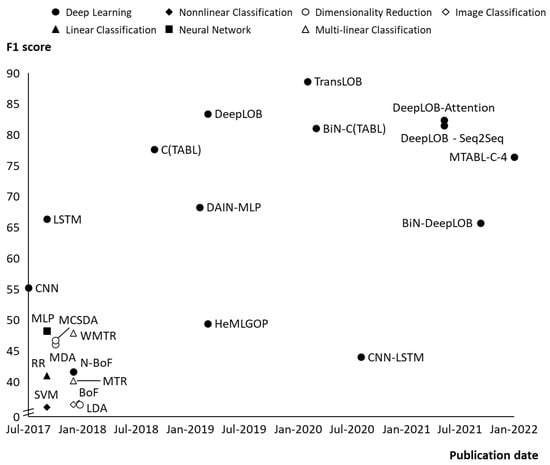
Figure 4.
F1 score evolution over time for the state-of-the-art stock price prediction models trained on the benchmark LOB dataset.
The best performance among those deep learning models was demonstrated by the DeepLOB [6] and TransLOB architectures [7]. Each of them according to their authors demonstrating Accuracy and F1 scores well in excess of 80%. If these results are reproducible in real stock trading, these models could be potentially employed by market makers for setting their bid and ask quotes. However, we are interested in assessing whether these models could be used to generate buying and selling signals which could be incorporated in the trading strategies of active traders. Thus, the question is whether these models can be used to develop profitable arbitrage strategies. In practice there are serious concerns that this could be the case. Firstly, because of the earlier described issues with the benchmark dataset. Secondly, because of the potential flaws in the experiment setups. Thirdly, because of the ignored transaction costs and assumed mid-price execution the expected profitability of the trading strategies based on these models could be overestimated. As it would be proved later these two factors alone can make the strategies based on the suggested models unprofitable. In the work of Zhang et al. [6], they set out a the deep neural network method with a combination of convolution layers and Long Short-Term Memory (LSTM) units—DeepLOB, which was exploited to develop stock trading strategy based on the LOB data. This approach demonstrates better prediction power than any other existing algorithms relying on the LOB as a source for the feature extraction at the time of publication. Authors claimed higher F1 score of DeepLOB compared with the following models: RR, SLFN, LDA, MDA, MCSDA, MTR, WMTR, BoF, N-BoF, B(TABL), and C(TABL). The authors tested their results on the two datasets, one of them was the benchmark LOB dataset, the other was a massive one year long sample with 134 million data points based on the London Stock Exchange LOB data. A trading simulation was also conducted which demonstrated the profitability to be statistically higher than zero.
From all the models tested on the benchmark LOB dataset to the best of our knowledge, the highest F1 score was demonstrated by the TransLOB model [7], which applied the deep learning architecture called Transformer to the LOB data for stock price movement prediction. The authors of this paper only tested the model on one dataset and did not conduct any trading simulation, which limits the credibility of the work.
For the last two studies, the authors kindly provided access to their code. However, the full code allowing the reproduction of the experiment was shared only for the DeepLOB. That is why it was decided to reproduce this experiment and make a detailed evaluation of the model architecture, experiment setup, and the conclusions drawn from it.
3.3. Reproducibility of Earlier LOB Predictions
3.3.1. Model, Experimental Setup and Results Analysis
DeepLOB work [6] demonstrated one of the best prediction performances and its code is available to the public (https://github.com/zcakhaa, 30 December 2021). The author’s experiment was reproduced on a Tesla V100 (PCIE card with 16GByte of memory) using the provided code and feeding in the benchmark LOB dataset [11]. This dataset contains the LOB data for five stocks for ten consecutive days. The model is trained on the data for the first seven days for 200 epochs and tested based on the data for the last 3 days. The prediction horizon was assumed to be five events.
F1 score, Accuracy, Precision, and Recall metrics were calculated for each of the 200 epochs of training for both training and validation datasets. Generally, they are consistent with what the authors are claiming in their paper. Furthermore, to better understand the performance for each of the three label classes (“up”, “flat”, “down”) separately, the confusion matrix for training—Figure 5a and validation—Figure 5b datasets were built. As it could be seen from Figure 5a, the model is demonstrating better accuracy in predicting the upward movements, and worst at predicting downward movement. For the validation dataset, the accuracy of prediction is significantly lower for all three classes as depicted in Figure 5b.
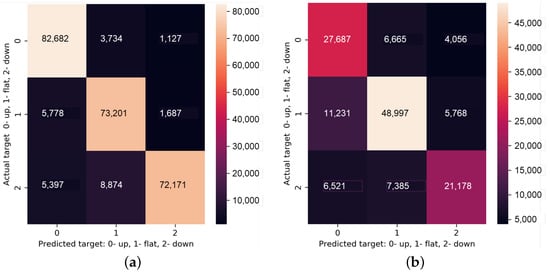
Figure 5.
Confusion matrix for the reproducibility experiment. (a) Training data sample. (b) Validation data sample.
As can be seen from Figure 6, after the first 50 epochs there is an over-fitting occurring as a validation Accuracy (“acc”), F1 score (“f1_m”), Precision (“precision_m”) and Recall (“recall_m”) are going down in parallel with the growing Categorical Cross-Entropy Loss (“loss”), while the respective training metrics continue to improve: Categorical Cross-Entropy Loss is reducing, while Accuracy, F1 score, Precision, and Recall are increasing. As Zhang et al. mentioned in their paper [6], training of the model is stopped if the validation accuracy does not improve for more than 20 epochs, which happens after 100 epochs, according to them. However, from Figure 6 it is clear that over-fitting already starts after epoch 50, so the weights taken at epoch 100 by the authors are not optimal.
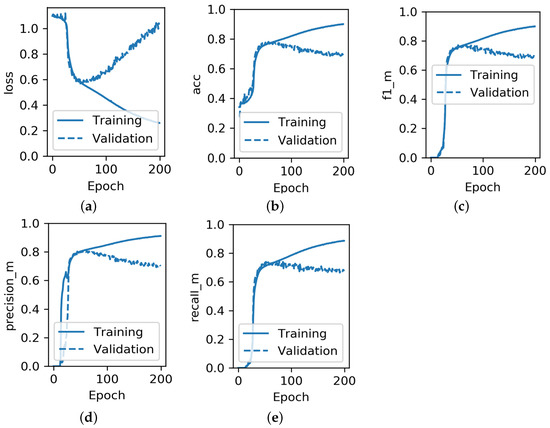
Figure 6.
Development of performance metrics for the DeepLOB model during the training phase on training and validation dataset: (a) Categorical Cross-Entropy Loss; (b) Accuracy; (c) F1 score; (d) Precision; (e) Recall.
In order to avoid over-fitting, the following actions could be considered:
- Increase the size of the dataset. Authors of DeepLOB (recognising the over-fitting issue that can result from the fact that the LOB benchmark dataset has only LOB data for 10 consecutive days) trained their model, in addition, on the larger dataset based on the one year long data from the London Stock Exchange (LSE). Depending on the type of security and prediction horizon, accuracy for the LSE dataset is in the range of 62–70%, which is substantially lower than for the benchmark LOB dataset. This could suggest that the performance of the model on the benchmark LOB dataset was overestimated.
- Remove some of the features, optimise feature space. Authors are using price and volume data for 10 levels of the bid and ask sides of LOB, which results in 40 features. Usually, higher level orders have less effect on the future price changes, so the reduction of the number of levels from the LOB taken as an input to the model. The other aspect is the number of the latest LOB events taken into account for the price movement prediction. In the DeepLOB work, it is taken as 100, but again there could be the potential to optimise that number. The respective optimisations of the feature space could help to reduce over-fitting.
- Model simplification. The DeepLOB model consists of convolution layer with 15 filters of size ; inception module (concatenation of five convolution layers with 32 filters and max-pooling layer with stride 1 and zero padding); LSTM with 64 units. The total number of parameters of this model is around 60,000. Probably, there is potential to further optimise this complex architecture to minimise over-fitting.
- Early stopping mechanism. This was mentioned by the authors of DeepLOB model in their paper. The script is stopping the training of the model if the validation accuracy does not improve for more than 20 epochs. As a result, early stopping happens after 100 epochs. However, as was earlier mentioned, there are symptoms of over-fitting happening already after the first 50 epochs, so the early stopping mechanism could be further optimised, by reducing the allowed number of epochs without improvement.
- Save the best weights of the model achieved during the training. Functionality in many Python machine learning libraries, including TensorFlow, enables the saving of the best weights of the model achieved during the training based on the selected metric performance. For example, as can be seen from Figure 6, if the condition for saving the model weights was the maximisation of the validation accuracy, the weights from somewhere around epoch 50 would be taken as the best. Thus, likewise for an early stopping mechanism the model would not suffer from over-fitting.
- Apply dropout. Dropout functionality is probabilistically removing inputs during training. This could be undertaken as an alternative to the removal of some features or in addition to that to solve the over-fitting problem.
3.3.2. Practical Value of the Model for Trading
The authors also conducted a simple trading simulation to test whether the DeepLOB model can be actually maximised. LOB data for 10 stocks traded on LSE were included in this simulation, namely: Lloyds Bank, Barclays, Tesco, Vodafone, HSBC, Glencore, Centrica, BT, BP, and ITV. The trading strategy applied was as follows: when output of the DeepLOB model is upward, the respective stock is acquired and position held until the model provides a downward signal, after which it is sold. For the short selling the opposite strategy is applied. At the end of each trading day all the positions are closed and no trading during the auction is allowed. The authors of the article claimed that the demonstrated profits are statistically higher than zero. However, they made two assumptions that are not realistic.
The first of them is absence of transaction costs. UK brokers typically either charge a flat fee of around GBP 15 per trade or a percentage of the transaction value of around 0.5% with some minimum commission (https://the-international-investor.com/investment-faq/stock-broker-charges, 10 January 2022). At the same time, it should be mentioned that a relatively new trend of zero-fee trading model is becoming a standard for the brokerage industry in the US. According to [61], Robinhood was the first brokerage firm that offered this, and others had to follow to stay competitive. Currently, many US brokers claim that their commissions are zero, however there are still some hidden costs for the traders for margin services, transfer costs, SEC fees, etc.
A second unrealistic assumption of the authors is that they can buy and sell stock at the mid-price. In reality execution is not guaranteed at this price. If trader wants a guaranteed execution of his order he would need to buy stock at the current best offer, which is higher than mid-price or sell at the current best bid, which is lower than the mid-price. The authors explain their mid-price approach assuming that it is possible to submit the limit order at the better price instead of executing a market order. Although, it could be possible that this limit order will be executed in the desired time-frame, it is not guaranteed. Thus, mid-price assumption as well as an absence of transaction costs are potentially overestimating the profitability of the trading strategy based on the DeepLOB model.
Depending on the type of stock and prediction horizon the average profit per trade for the above-described trading simulation is in the range of GBX (penny sterling) −0.01 to 0.03, with a median of around GBX 0.01. For example, for the Tesco stock the average profit per trade is close to this median of GBX 0.01. At the moment of preparation of this paper, the spread for this stock (difference between the best bid and ask prices) was around GBX 0.1. Assuming the spread is stable at this level and the trader has to use market orders to execute the intended transaction in the defined time-frame, even if brokers fees are ignored, this GBX 0.1 becomes an additional costs. This is more than ten times higher than the average profit per trade for Tesco. For the other nine stocks this spread is at least a few times higher than the average profit per trade as computed by the authors.
Another area for further improvement of this trading simulation could be to conduct the trading simulation for the stock index exchange-traded fund as well in addition to individual stocks. A stock index exchange-traded fund due to its diversified nature is less volatile than individual stocks. It would be interesting to explore how the lower volatility would impact the profitability of this strategy.
Thus, even though the DeepLOB model is demonstrating a promising performance in predicting stock price movements for the datasets tested, in its current form with a basic trading strategy it is unlikely to generate a consistent profit in the active stock trading. The DeepLOB model is also prone to over-fitting as was identified during the reproduced experiment, so there is room for improvement in the generalising capability of this model by applying the above-described methods.
4. Conclusions and Future Work
The LOB as an input data for the intra-day stock price prediction has received substantial academic attention over the last decade and proved to be one of the most valuable data sources for features extraction. After the first benchmark LOB dataset was published in 2017 the number of studies and their comparability substantially increased. However, this dataset suffers from a number of issues, such as dated information, inherently unbalanced distribution between three classes, five stocks comprising this dataset are indistinguishable, potential processing issues and unrealistic mid-price execution assumption embedded in the classes labels. All these could substantially bias the results of experiments performed with this dataset. Nevertheless, a number of the Deep learning models [7], ref. [6] have demonstrated a strong performance on this dataset based on standard statistical metrics such as Accuracy, Precision, Recall, and F1 score. However, further analysis has revealed that strategies based on these models can generate consistent profit only if some unrealistic conditions are assumed. One of them is the absence of transaction costs and the second is mid-price execution. Further, it was noted that some of these deep learning models are prone to over-fitting, which is limiting their generalising capability. The above-described issues in the data, models and experimental setups suggest that there is room for further research in each of these three domains.
In terms of the input data, the following steps are recommended:
- Use more recent LOB data for the input features;
- Do not implicitly assume the mid-price execution;
- To properly train the deep learning models, an extensive dataset should be used, otherwise the over-fitting problem could become severe;
- Careful pre-processing of the dataset should be performed as required to filter out erroneous data;
- Data for different stocks should be distinguishable in the dataset;
- It is advocated by a number of authors in recent studies [56,62] that Order Flow in addition to the LOB data can slightly improve the performance of the stock price prediction models.
In terms of model architectures, it is clear that deep learning architectures demonstrate a stronger performance than classical models. However, they are also more prone to over-fitting. Thus, this problem should be addressed by one of following methods:
- Removal of the relatively less significant features, optimisation of the feature space;
- Optimisation of the model architecture. This could be achieved by limiting the number of neurons and removing the relatively less critical layers;
- Applying the dropout functionality for probabilistically removing inputs during training
LSTM models for many years were a standard way of time series forecasting, and proved to work well for stock price prediction in particular. Authors of these studies [14], ref. [6] also suggested that a combination of CNN with LSTM can further improve the performance. A new deep learning architecture, Transformer has demonstrated a better performance than LSTM for the translation problem [63]. Wallbridge [7] developed the version of Transformer adopted for the stock price predicting based on LOB and claimed that it demonstrates the best performance on the benchmark LOB dataset.
Two broad directions could be undertaken to develop the next state-of-the-art model, either finding ways to improve the above-mentioned models or suggesting a new model architecture, or at least one that has not yet been used for this type of problem, that could demonstrate a superior performance without suffering from over-fitting.
The experimental setup plays a critical role in the quality of the research results obtained. In particular, a number of improvements in it could be made to address the earlier mentioned over-fitting problem:
- Increasing the size of the data sample;
- Introducing the early stopping mechanism in model training;
- Saving the best weights of the model achieved during the training.
It is also important to test the results on out of sample data, and not just on the validation data, that has already been used in the training process to find optimal model parameters. Unfortunately, this is often ignored by many researchers. If this is not done, the existing over-fitting problem can be hidden.
For the stock prediction task it is critically important not to limit the experiment to the standard statistical performance metrics such as accuracy, F1 score and etc., but also conduct the trading simulation. Profit is the ultimate measure of success of these algorithms, and if the model can not help to consistently generate it under real market conditions, which include transactions costs, bid–ask spreads, and market impact, then its practical value is rather limited.
Author Contributions
Conceptualization, I.Z. and J.K.; methodology, I.Z., J.K., A.D. and A.B.; software, I.Z. and J.K.; validation, J.K., A.D. and A.B.; formal analysis, I.Z.; investigation, I.Z.; resources, I.Z.; data curation, I.Z.; writing—original draft preparation, I.Z.; writing—review and editing, J.K., A.D. and A.B.; visualization, I.Z.; supervision, J.K., A.D. and A.B.; project administration, I.Z.; funding acquisition, I.Z. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
Please refer to the Benchmark Dataset for Mid-Price Forecasting of Limit Order Book Data used in this article: https://etsin.fairdata.fi/dataset/73eb48d7-4dbc-4a10-a52a-da745b47a649 (accessed on 5 March 2022).
Conflicts of Interest
The authors declare no conflict of interest.
Abbreviations
The following abbreviations are used in this manuscript:
| %D | 3-day moving average of Stochastic %K. |
| ADO | Accumulation Distribution Oscillator. |
| ADX | Average Directional Index. |
| ANFIS | Adaptive Network-Based Fuzzy Inference System. |
| ANN | Artificial Neural Network. |
| ARIMA | Autoregressive Integrated Moving Average. |
| BB | Bollinger Band. |
| BFO | Bacterial foraging optimisation. |
| BiN-DeepLOB | DeepLOB model with Bilinear Input Normalization layer. |
| BiN-C(TABL) | Neural network consisting of Bilinear normalisation layer and three Temporal Attention augmented Bilinear Layers. |
| BoF | Bag-of-Features. |
| bp | Basis points. |
| BPN | Back-Propagation Networks. |
| BPNN | Back Propagation Neural Network. |
| C(TABL) | Neural network consisting of three Temporal Attention augmented Bilinear Layers. |
| C4.5 DT | C4.5 decision tree. |
| CCI | Commodity Channel Index. |
| CMF | Chaikin Money Flow. |
| CNN | Convolutional Neural Network. |
| CNN-LSTM | Deep learning architecture combining Convolutional Neural Network with Long Short-Term Memory. |
| CPACC | Closing Price Acceleration. |
| CPI | Consumer price index. |
| CV | Chaikin’s volatility. |
| CX | Convexity. |
| DAIN MLP | Neural network architecture consisting of the Deep Adaptive Input normalisation Layer and Multilayer Perceptron. |
| DAN2 | Dynamic Artificial Neural network. |
| DeepLOB | Deep neural network method with Long Short-Term Memory units. |
| DeepLOB-Attention | DeepLOB model with Attention mechanism. |
| DeepLOB-Seq2Seq | DeepLOB model with sequence-to-sequence mechanism. |
| DI | Directional Indicator. |
| DL | Deep Learning. |
| DOA | Difference of averages. |
| DPS | Dividends Per Share. |
| EMA | Exponential Moving Average. |
| Ensemble-MBO-LOB | Deep learning model combining Ensemble-MBO and Ensemble-LOB models. |
| Ensemble-MBO | Deep learning model combining MBO-LSTM and MBO-Attention models. |
| EnsembleLOB | Deep learning model combining LOB-LSTM, LOB-CNN, and LOB-DeepLOB models. |
| EPS | Earnings Per Share. |
| ESN | Recurrent neural network–Echo State Network. |
| EWO | Elliott Wave Oscillator. |
| GA | Genetic Algorithms. |
| GARCH-DAN2 | Hybrid Dynamic Artificial Neural network which use generalised Autoregressive Conditional Heteroscedasticity. |
| GARCH-MLP | Hybrid Multi-Layer Perceptron which use generalised Autoregressive Conditional Heteroscedasticity. |
| GA-SVM | Hybrid Genetic Algorithm Support Vector Machine. |
| GAIS | Genetic Algorithm approach to Instance Selection in artificial neural networks. |
| GCHP | General Compound Hawkes Processes. |
| GCL | Genetic complementary learning (GCL) fuzzy neural network. |
| GDB | Gradient Boosting Classifier. |
| GDP | Gross Domestic Product. |
| GNB | Guassian Naive Bayes. |
| GRU | Gated recurrent unit. |
| HDT-RSB | Hybrid Decision Tree-Rough Set Based trend prediction system. |
| HeMLGOP | Heterogeneous Multi-layer generalised Operational Perceptron. |
| HFT | High-Frequency Trading. |
| HMM | Hidden Markov Models. |
| HMM-FM | Combination of Hidden Markov Model and Fuzzy Model. |
| HPACC | High Price Acceleration. |
| IBCO | Improved Bacterial Chemotaxis optimisation. |
| IFFS | Improved Fractal Feature Selection. |
| IG | Information Gain. |
| IP | Industrial Production. |
| IPI | Industrial production index. |
| KNN | Kth nearest neighbour. |
| LDA | Linear Discriminant Analysis. |
| LOB | Limit Order Book. |
| LS-SVM | Least Squares Support Vector Machine. |
| LSTM | Long Short-Term Memory. |
| LW %R | Larry William’s %R. |
| M1 | Money Supply level. |
| MA | Moving Average. |
| MACD | Moving Average Convergence/Divergence. |
| MAD | Moving Average Deviation rate. |
| MAE | Mean absolute error. |
| MAP-HMM | Combination of Maximum a Posteriori Approach with Hidden Markov Model. |
| MAPE | Mean Absolute Percentage Error. |
| MBO | Market by order data. |
| MCC | Matthews Correlation Coefficient. |
| MC-fuzzy | Markov-fuzzy Combination Model. |
| MCSDA | Multilinear Class-Specific Discriminant Analysis. |
| MDA | Multilinear Discriminant Analysis. |
| MFI | Money Flow Index. |
| ML | Machine Learning. |
| MLP | Multilayer Perceptron. |
| MSE | Mean Squared Error. |
| MSM | Mathematical and Statistical models. |
| MTABL-C-4 | Multi-head Temporal Attention Bilinear Layer with 4 attention heads and topology C. |
| MTR | Multi-channel Time-series Regression. |
| N-BoF | Neural Bag-of-Features. |
| NB | Naïve Bayes. |
| NMSE | normalised mean squared error. |
| NVI | Negative volume index. |
| OBV | On Balance Volume. |
| OSCP | Price Oscillator. |
| PL | Psychological Line. |
| PPI | Producer Price Index. |
| PROC | Price Rate of Change. |
| PVI | Positive volume index. |
| PVT | Price Volume Trend. |
| QDA | Quadratic Discriminant Analysis. |
| RBFN | Radial Basis Function Networks. |
| RCI | Rank Correlation Index. |
| RCNK | Recurrent Convolutional Neural Kernel. |
| RF | Random Forest. |
| RMSE | Root-Mean-Square Error. |
| ROC | Rate Of Change. |
| RR | Ridge Regression. |
| RRS | Rate of returns of Stocks. |
| RS | Relative Strength factor. |
| RSB | Rough Set Based trend prediction system. |
| RSI | Relative Strength Index. |
| SGD | Stochastic Gradient Descent. |
| SLEMA | Short/Long Exponential Moving Average. |
| SLMA | Short/Long Moving Average. |
| STC | Schaff Trend Cycle. |
| STI | Stochastic Indicator. |
| SU | Symmetrical Uncertain. |
| SVM | Support Vector Machine. |
| SVR | Support Vector Regression. |
| T-Bill3 | 3-month Treasury bill rate. |
| TBY-1 | One year Treasury Bill Yield. |
| TR | True Range of price movements. |
| TransLOB | Deep learning architecture based on the Transformer model. |
| TRIX | Triple Exponentially Smoothed Average. |
| TSK | Takagi–Sugeno–Kang type Fuzzy Rule Based System. |
| VR | Volume Ratio. |
| VRSI | Volume Relative Strength Index. |
| W.A.S.P | Wave Analysis Stock Prediction. |
| WMTR | Weighted Multi-channel Time-series Regression. |
References
- Chang, P.C.; Liu, C.H. A TSK type fuzzy rule based system for stock price prediction. Expert Syst. Appl. 2008, 34, 135–144. [Google Scholar] [CrossRef]
- Bartov, E.; Radhakrishnan, S.; Krinsky, I. Investor sophistication and patterns in stock returns after earnings announcements. Account. Rev. 2000, 75, 43–63. [Google Scholar] [CrossRef]
- Moore, J.; Velikov, M. Oil Price Exposure, Earnings Announcements, and Stock Return Predictability. Earnings Announcements, and Stock Return Predictability (20 January 2019) 2019. Available online: https://papers.ssrn.com/sol3/papers.cfm?abstract_id=3164353 (accessed on 10 December 2021).
- Katona, Z.; Painter, M.; Patatoukas, P.N.; Zeng, J. On the capital market consequences of alternative data: Evidence from outer space. In Proceedings of the 9th Miami Behavioral Finance Conference, Coral Gables, FL, USA, 14–15 December 2018. [Google Scholar]
- Kercheval, A.N.; Zhang, Y. Modelling high-frequency limit order book dynamics with support vector machines. Quant. Financ. 2015, 15, 1315–1329. [Google Scholar] [CrossRef]
- Zhang, Z.; Zohren, S.; Roberts, S. Deeplob: Deep convolutional neural networks for limit order books. IEEE Trans. Signal Process. 2019, 67, 3001–3012. [Google Scholar] [CrossRef]
- Wallbridge, J. Transformers for limit order books. arXiv 2020, arXiv:2003.00130. [Google Scholar]
- Fu, T.C.; Chung, C.P.; Chung, F.L. Adopting genetic algorithms for technical analysis and portfolio management. Comput. Math. Appl. 2013, 66, 1743–1757. [Google Scholar] [CrossRef]
- Zhang, Y.; Wu, L. Stock market prediction of S&P 500 via combination of improved BCO approach and BP neural network. Expert Syst. Appl. 2009, 36, 8849–8854. [Google Scholar]
- Majhi, R.; Panda, G.; Sahoo, G.; Dash, P.K.; Das, D.P. Stock market prediction of S&P 500 and DJIA using bacterial foraging optimization technique. In Proceedings of the 2007 IEEE Congress on Evolutionary Computation, Singapore, 25–28 September 2007; pp. 2569–2575. [Google Scholar]
- Ntakaris, A.; Magris, M.; Kanniainen, J.; Gabbouj, M.; Iosifidis, A. Benchmark dataset for mid-price prediction of limit order book data. arXiv 2017, arXiv:1705.03233. [Google Scholar]
- Tsantekidis, A.; Passalis, N.; Tefas, A.; Kanniainen, J.; Gabbouj, M.; Iosifidis, A. Forecasting stock prices from the limit order book using convolutional neural networks. In Proceedings of the 2017 IEEE 19th Conference on Business Informatics (CBI), Thessaloniki, Greece, 24–27 July 2017; Volume 1, pp. 7–12. [Google Scholar]
- Tsantekidis, A.; Passalis, N.; Tefas, A.; Kanniainen, J.; Gabbouj, M.; Iosifidis, A. Using deep learning to detect price change indications in financial markets. In Proceedings of the 2017 25th European Signal Processing Conference (EUSIPCO), Kos, Greece, 28 August–2 September 2017; pp. 2511–2515. [Google Scholar]
- Tsantekidis, A.; Passalis, N.; Tefas, A.; Kanniainen, J.; Gabbouj, M.; Iosifidis, A. Using deep learning for price prediction by exploiting stationary limit order book features. Appl. Soft Comput. 2020, 93, 106401. [Google Scholar] [CrossRef]
- Armano, G.; Marchesi, M.; Murru, A. A hybrid genetic-neural architecture for stock indexes forecasting. Inf. Sci. 2005, 170, 3–33. [Google Scholar] [CrossRef]
- Klassen, M. Investigation of Some Technical Indexes inStock Forecasting Using Neural Networks. Int. J. Comput. Inf. Eng. 2007, 1, 1438–1442. [Google Scholar]
- Hassan, M.R.; Nath, B. Stock market forecasting using hidden Markov model: A new approach. In Proceedings of the 5th International Conference on Intelligent Systems Design and Applications (ISDA’05), Warsaw, Poland, 8–10 September 2005; pp. 192–196. [Google Scholar]
- Tan, T.Z.; Quek, C.; Ng, G.S. Brain-inspired genetic complementary learning for stock market prediction. In Proceedings of the 2005 IEEE Congress on Evolutionary Computation, Edinburgh, UK, 2–5 September 2005; Volume 3, pp. 2653–2660. [Google Scholar]
- Kim, K.J. Artificial neural networks with evolutionary instance selection for financial forecasting. Expert Syst. Appl. 2006, 30, 519–526. [Google Scholar] [CrossRef]
- Huang, W.; Wang, S.; Yu, L.; Bao, Y.; Wang, L. A new computational method of input selection for stock market forecasting with neural networks. In International Conference on Computational Science; Springer: Berlin/Heidelberg, Germany, 2006; pp. 308–315. [Google Scholar]
- Sheta, A. Software effort estimation and stock market prediction using takagi-sugeno fuzzy models. In Proceedings of the 2006 IEEE International Conference on Fuzzy Systems, Vancouver, BC, Canada, 16–21 July 2006; pp. 171–178. [Google Scholar]
- Ince, H.; Trafalis, T.B. Kernel principal component analysis and support vector machines for stock price prediction. Iie Trans. 2007, 39, 629–637. [Google Scholar] [CrossRef]
- Shah, V.H. Machine learning techniques for stock prediction. Found. Mach. Learn. Spring 2007, 1, 6–12. [Google Scholar]
- Tsang, P.M.; Kwok, P.; Choy, S.O.; Kwan, R.; Ng, S.C.; Mak, J.; Tsang, J.; Koong, K.; Wong, T.L. Design and implementation of NN5 for Hong Kong stock price forecasting. Eng. Appl. Artif. Intell. 2007, 20, 453–461. [Google Scholar] [CrossRef]
- Tanaka-Yamawaki, M.; Tokuoka, S. Adaptive use of technical indicators for the prediction of intra-day stock prices. Phys. A Stat. Mech. Its Appl. 2007, 383, 125–133. [Google Scholar] [CrossRef]
- Choudhry, R.; Garg, K. A hybrid machine learning system for stock market forecasting. World Acad. Sci. Eng. Technol. 2008, 39, 315–318. [Google Scholar]
- Huang, C.J.; Yang, D.X.; Chuang, Y.T. Application of wrapper approach and composite classifier to the stock trend prediction. Expert Syst. Appl. 2008, 34, 2870–2878. [Google Scholar] [CrossRef]
- Ke, J.; Liu, X. Empirical analysis of optimal hidden neurons in neural network modeling for stock prediction. In Proceedings of the 2008 IEEE Pacific-Asia Workshop on Computational Intelligence and Industrial Application, Wuhan, China, 19–20 December 2008; Volume 2, pp. 828–832. [Google Scholar]
- Lin, X.; Yang, Z.; Song, Y. Short-term stock price prediction based on echo state networks. Expert Syst. Appl. 2009, 36, 7313–7317. [Google Scholar] [CrossRef]
- Lee, M.C. Using support vector machine with a hybrid feature selection method to the stock trend prediction. Expert Syst. Appl. 2009, 36, 10896–10904. [Google Scholar] [CrossRef]
- Ou, P.; Wang, H. Prediction of stock market index movement by ten data mining techniques. Mod. Appl. Sci. 2009, 3, 28–42. [Google Scholar] [CrossRef]
- Rao, S.; Hong, J. Analysis of Hidden Markov Models and Support Vector Machines in Financial Applications; University of California at Berkeley: Berkeley, CA, USA, 2010. [Google Scholar]
- Nair, B.B.; Mohandas, V.; Sakthivel, N. A decision tree—Rough set hybrid system for stock market trend prediction. Int. J. Comput. Appl. 2010, 6, 1–6. [Google Scholar] [CrossRef]
- Naeini, M.P.; Taremian, H.; Hashemi, H.B. Stock market value prediction using neural networks. In Proceedings of the 2010 International Conference on Computer Information Systems and Industrial Management Applications (CISIM), Krakow, Poland, 8–10 October 2010; pp. 132–136. [Google Scholar]
- Boyacioglu, M.A.; Avci, D. An adaptive network-based fuzzy inference system (ANFIS) for the prediction of stock market return: The case of the Istanbul stock exchange. Expert Syst. Appl. 2010, 37, 7908–7912. [Google Scholar] [CrossRef]
- Ni, L.P.; Ni, Z.W.; Gao, Y.Z. Stock trend prediction based on fractal feature selection and support vector machine. Expert Syst. Appl. 2011, 38, 5569–5576. [Google Scholar] [CrossRef]
- Guresen, E.; Kayakutlu, G.; Daim, T.U. Using artificial neural network models in stock market index prediction. Expert Syst. Appl. 2011, 38, 10389–10397. [Google Scholar] [CrossRef]
- Atsalakis, G.S.; Dimitrakakis, E.M.; Zopounidis, C.D. Elliott Wave Theory and neuro-fuzzy systems, in stock market prediction: The WASP system. Expert Syst. Appl. 2011, 38, 9196–9206. [Google Scholar] [CrossRef]
- Enke, D.; Grauer, M.; Mehdiyev, N. Stock market prediction with multiple regression, fuzzy type-2 clustering and neural networks. Procedia Comput. Sci. 2011, 6, 201–206. [Google Scholar] [CrossRef]
- Gupta, A.; Dhingra, B. Stock market prediction using hidden markov models. In Proceedings of the 2012 Students Conference on Engineering and Systems, Allahabad, India, 16–18 March 2012; pp. 1–4. [Google Scholar]
- Bing, Y.; Hao, J.K.; Zhang, S.C. Stock market prediction using artificial neural networks. In Advanced Engineering Forum; Trans Tech Publications Ltd.: Stafa-Zurich, Switzerland, 2012; Volume 6, pp. 1055–1060. [Google Scholar]
- Cont, R.; Kukanov, A.; Stoikov, S. The price impact of order book events. J. Financ. Econom. 2014, 12, 47–88. [Google Scholar] [CrossRef]
- Palguna, D.; Pollak, I. Non-parametric prediction in a limit order book. In Proceedings of the 2013 IEEE Global Conference on Signal and Information Processing, Austin, TX, USA, 3–5 December 2013; p. 1139. [Google Scholar]
- Palguna, D.; Pollak, I. Mid-price prediction in a limit order book. IEEE J. Sel. Top. Signal Process. 2016, 10, 1083–1092. [Google Scholar] [CrossRef]
- Gould, M.D.; Bonart, J. Queue imbalance as a one-tick-ahead price predictor in a limit order book. Mark. Microstruct. Liq. 2016, 2, 1650006. [Google Scholar] [CrossRef]
- Ky, D.X.; Tuyen, L.T. A Markov-fuzzy Combination Model For Stock Market Forecasting. Int. J. Appl. Math. Stat. 2016, 55, 110–121. [Google Scholar]
- Tran, D.T.; Gabbouj, M.; Iosifidis, A. Multilinear class-specific discriminant analysis. Pattern Recognit. Lett. 2017, 100, 131–136. [Google Scholar] [CrossRef][Green Version]
- Tran, D.T.; Magris, M.; Kanniainen, J.; Gabbouj, M.; Iosifidis, A. Tensor representation in high-frequency financial data for price change prediction. In Proceedings of the 2017 IEEE Symposium Series on Computational Intelligence (SSCI), Honolulu, HI, USA, 27 November–1 December 2017; pp. 1–7. [Google Scholar]
- Qureshi, F. Investigating Limit Order Book Features for Short-Term Price Prediction: A Machine Learning Approach. SSRN 3305277. 2018. Available online: https://papers.ssrn.com/sol3/papers.cfm?abstract_id=3305277 (accessed on 5 March 2022).
- Tran, D.T.; Iosifidis, A.; Kanniainen, J.; Gabbouj, M. Temporal attention-augmented bilinear network for financial time-series data analysis. IEEE Trans. Neural Netw. Learn. Syst. 2018, 30, 1407–1418. [Google Scholar] [CrossRef]
- Passalis, N.; Tefas, A.; Kanniainen, J.; Gabbouj, M.; Iosifidis, A. Deep adaptive input normalization for price forecasting using limit order book data. arXiv 2019, arXiv:1902.07892. [Google Scholar]
- Thanh Tran, D.; Kanniainen, J.; Gabbouj, M.; Iosifidis, A. Data-driven Neural Architecture Learning For Financial Time-series Forecasting. arXiv 2019, arXiv:1903.06751. [Google Scholar]
- Tran, D.T.; Kanniainen, J.; Gabbouj, M.; Iosifidis, A. Data Normalization for Bilinear Structures in High-Frequency Financial Time-series. arXiv 2020, arXiv:2003.00598. [Google Scholar]
- Liu, S.; Zhang, X.; Wang, Y.; Feng, G. Recurrent convolutional neural kernel model for stock price movement prediction. PLoS ONE 2020, 15, e0234206. [Google Scholar] [CrossRef] [PubMed]
- Shahi, T.B.; Shrestha, A.; Neupane, A.; Guo, W. Stock price forecasting with deep learning: A comparative study. Mathematics 2020, 8, 1441. [Google Scholar] [CrossRef]
- Zhang, Z.; Lim, B.; Zohren, S. Deep Learning for Market by Order Data. arXiv 2021, arXiv:2102.08811. [Google Scholar] [CrossRef]
- Zhang, Z.; Zohren, S. Multi-Horizon Forecasting for Limit Order Books: Novel Deep Learning Approaches and Hardware Acceleration using Intelligent Processing Units. arXiv 2021, arXiv:2105.10430. [Google Scholar]
- Tran, D.T.; Kanniainen, J.; Gabbouj, M.; Iosifidis, A. Bilinear Input Normalization for Neural Networks in Financial Forecasting. arXiv 2021, arXiv:2109.00983. [Google Scholar]
- Sjogren, M.; DeLise, T. General Compound Hawkes Processes for Mid-Price Prediction. arXiv 2021, arXiv:2110.07075. [Google Scholar]
- Shabani, M.; Tran, D.T.; Magris, M.; Kanniainen, J.; Iosifidis, A. Multi-head Temporal Attention-Augmented Bilinear Network for Financial time series prediction. arXiv 2022, arXiv:2201.05459. [Google Scholar]
- Eaton, G.W.; Green, T.C.; Roseman, B.; Wu, Y. Zero-Commission Individual Investors, High Frequency Traders, and Stock Market Quality. High Frequency Traders, and Stock Market Quality (January 2021) 2021. Available online: https://microstructure.exchange/slides/RobinhoodSlides_TME.pdf (accessed on 5 February 2022).
- Doering, J.; Fairbank, M.; Markose, S. Convolutional neural networks applied to high-frequency market microstructure forecasting. In Proceedings of the 2017 9th Computer Science and Electronic Engineering (CEEC), Colchester, UK, 27–29 September 2017; pp. 31–36. [Google Scholar]
- Vaswani, A.; Shazeer, N.; Parmar, N.; Uszkoreit, J.; Jones, L.; Gomez, A.N.; Kaiser, L.; Polosukhin, I. Attention is all you need. arXiv 2017, arXiv:1706.03762. [Google Scholar]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).