Towards Describing Student Learning of Abstract Algebra: Insights into Learners’ Cognitive Processes from an Acceptance Survey
Abstract
:1. Introduction
- Key Notion 1: In the first unit, the students explore the dihedral group of the equilateral triangle and get in touch with the basic notions of group theory, such as inverses, the identity element, and commutativity. They do so by working with a plexiglass triangle, so the isometries can be experienced in a haptic way (Figure 1). The isometries are described from a geometrical point of view (i.e., rotation by or reflecting on the bisecting line through vertex 1), resulting in .
- Key Notion 2: In the second unit, the dihedral group of the square as well as its substructures and the Cayley Tables are explored. The fact provides new problems to solve, i.e., discussions of why certain permutations do not describe isometries of the square.
- Key Notion 3: The concluding unit deals with modular arithmetic and isomorphisms by looking at the cyclic groups . Examples from everyday life, such as calculating times and dates, serve as the motivation to introduce “new” additions. A crucial point in this regard is realizing that only differs in terms of notation from the subgroup generated by .
2. Theoretical and Methodological Framework
2.1. Design-Based Research
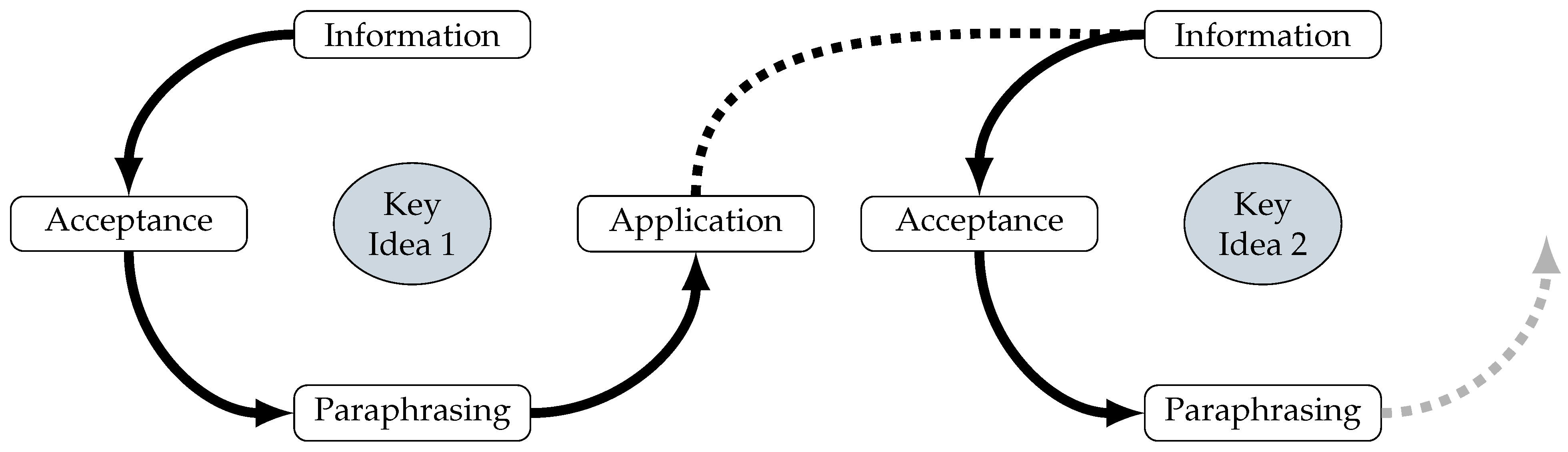
- Sequential cycles of design, evaluation and re-design: DBR is characterized by an iterative process. DBR projects consist of sequential cycles of design, implementation, and evaluation followed by re-design cycles which are based on the evaluation results of the previous cycle [31], as shown in Figure 2.
- Real educational contexts: DBR ensures that research findings are transferable to real educational contexts [19,29,33], which is why DBR projects do not only comprise (experimental) laboratory studies but also field studies, e.g., research questions “about the nature of learning in authentic learning environments” [32] (p. 3). In particular, researchers often conduct qualitative surveys in the early stages of their DBR projects to (a) identify possible learning difficulties, and (b) refine their innovation based on the results of such formative assessments. This may serve as a starting point for field studies to evaluate the innovation’s learning effectiveness in a later DBR cycle.
- Use of mixed-methods: In addition to the abovementioned point, in DBR projects, researchers take advantage of a pluralism of quantitative and qualitative methods to complement insights into learning processes and complex educational situations from different perspectives, e.g., via triangulation [34].
- Theory building and design of educational innovation: In DBR projects, researchers build on theories from the literature for the design of an educational innovation (e.g., a new teaching concept, method or media) on the one hand (cf. Figure 2). On the other hand, the evaluation of such innovations in authentic classroom settings may lead to refinement of the developed instructional elements. However, these evaluation results may also result in the derivation of new research questions, and hence, in stimuli for new research questions in the field under investigation [35].
- Close interactions between researchers and practitioners: Lastly, DBR is characterized by a close collaboration between researchers and practitioners [19]. ”This contributes toward creating ownership and commitment from teachers and learners” [32] (p. 2). Furthermore, such close cooperation may help to uncover how new teaching innovations are used in educational practice [36]. These insights are particularly important, since empirical research has revealed that teachers often use innovative materials in a different way than intended by the material developers [37].
2.2. Acceptance Survey as a Method for Formative Evaluation
“Evaluation may be done to provide feedback to people who are trying to improve something (formative evaluation); or to provide information for decision-makers who are wondering whether to fund, terminate, or to purchase something (summative evaluation).”[38] (pp. 6–7)
- Providing information: The interviewer provides information input in a similar way as in a classroom lesson. Media can be used and any questions from the interviewee are addressed.
- Survey of acceptance: The interviewer asks the interviewee to assess the information presented in terms of whether the explanations were comprehensible and understandable: “What do you think about this topic?” or “Was there anything you could not understand?” [41] (p. 857). The interviewee can, hence, also express criticism at this point.
- Paraphrasing: In this phase, the interviewer asks the interviewee to paraphrase the presented information in their own words or to independently repeat previously heard explanations.
- Application: In this final phase, the respondent is given a short task that allows the researcher to observe the student in a problem-solving situation. The student uses the information provided in previous phases in their problem-solving process, which enables the researcher to identify learning difficulties that might occur with specific instructional elements.
2.3. Research Questions and Key Ideas
- RQ1:
- How do students accept the instructional elements within the Hildesheim Teaching Concept of Abstract Algebra…
- (a)
- …with regard to introducing dihedral groups?
- (b)
- …with regard to introducing permutations as a tool to describe isometries?
- (c)
- …with regard to introducing the Cayley Tables?
- RQ2:
- Do students prefer to work with the abstract symbols of the dihedral group , or do they prefer to work with permutations presented by matrices?
- RQ3:
- What learning difficulties can be expected in the implementation of the Hildesheim Teaching Concept of Abstract Algebra?
- …abstract symbols, such as or , etc., or
- …concrete mapping rules presented in matrices, such as
3. Methods
3.1. Study Design and Sample
3.2. Data Analysis
3.2.1. Rating Acceptance
- Perfect acceptance (coded with numeric value 1): The explanations were accepted by the participant without reservation and classified as plausible or understandable.
- Partial acceptance (coded with numeric value ): The explanations were accepted by the participant, but criticism was voiced.
- No acceptance (coded with numeric value 0): The explanations were not accepted by the participant. This means that the contents were not explained in a comprehensible way or seemed implausible.
3.2.2. Rating Paraphrasing
- Fully adequate (coded with numeric value 1): The paraphrasing included all core aspects of the content according to the coding guide.
- Partially adequate (coded with numeric value ): The paraphrasing mentioned some core aspects of the contend but misses others. The mathematical object was only partially successfully described.
- Not adequate (coded with numeric value 0): The paraphrasing mentioned no core aspect of the content or was wrong.
3.2.3. Rating Application
- Successfully solved (coded with numeric value 1): The problem was solved independently and without any help. The application was also evaluated as 1 if the student made an error but immediately realized it and corrected it.
- Solved with help (coded with numeric value ): Solving the task independently was not possible. A correct solution could be found, however, after one clue was given by the interviewer.
- Not solved (coded with numeric value 0): Solving the task was either impossible or required more than one clue from the interviewer.
4. Results
4.1. Results of the Acceptance Phase
“the arrows and reflection lines that were drawn inside the triangles helped me understand. […] With the arrows and the angles where you reflect, one could well imagine it. That’s how it was for me at least.”
“I liked that we always had these vivid illustrations. That’s good for starters. I also liked that we summarized all isometries in the first tabular, so one could take a peek every now and then.”
“the pictures used when composing permutations were very helpful for understanding it.”
“I liked the visualization with the real triangles. […] It was very comprehensible. I think it’s good that everything is first presented pictorially—first the non-mathematical level and then later it’s easier to understand the mathematical level”.
hinting that skills and knowledge required to understand the key ideas has always been established previously.“if it is designed in a consecutive way, it is very comprehensible”,
4.2. Results of Paraphrasing
“you get a magma if you take two elements of a set and you compose them or multiply or add them, and by doing so, you again get an element of the set.”
“a set of elements, in our example isometries, that is presented by an action, and if we compose those actions, for example by reflecting along a bisecting line and then rotating, we get a magma.”
“when you have a given set and you compose two elements you get another element of the set. Then, we have a composed set.”
4.3. Results of Application
4.4. Perceived Difficulty and Plausibility of Notation
- What is the perceived difficulty of each content area? (0 = highest difficulty)
- How plausible were the notations and symbols of each content area? (0 = unplausible)
5. Discussion
- RQ1:
- How do students accept the instructional elements within the Hildesheim Teaching Concept of Abstract Algebra…
- (a)
- …with regard to introducing dihedral groups?
- (b)
- …with regard to introducing permutations as a tool to describe isometries?
- (c)
- …with regard to introducing Cayley Tables?
- RQ2:
- Do students prefer to work with the abstract symbols of the dihedral group , or do they prefer to work with permutations presented by matrices?
- RQ3:
- What learning difficulties can be expected in the implementation of the Hildesheim Teaching Concept of Abstract Algebra?
5.1. Discussion of RQ1
5.1.1. Discussion of RQ1 (a)
C: “An isometry tells us which area the triangle covers, and if we manipulate the triangle, the area still remains the same.”
I: “An isometry for me is the projection of the triangle onto the paper, and it doesn’t matter how I rotate the triangle, it will always have the same projection. It doesn’t matter which vertex is where, because the triangle will always cover the same area.”
5.1.2. Discussion of RQ1 (b)
5.1.3. Discussion of RQ1 (c)
A: “To be honest, I first thought about coordinate systems […] If you search for a point, you first look for the x coordinate and then y.
E: “Because it is maths, I think I would have read it just like a coordinate system, so first x and then y.”
F: “I learned in primary school that if you have a coordinate system you first look in which house you are and then in which floor you are. […] I would have first looked at the rows and then the columns.”
I: “I’m unsure because in a coordinate system, you first go horizontally.”
5.2. Discussion of RQ2
“got me confused with all the numbers”.
5.3. Discussion of RQ3
5.4. Implications for Revising the Concept in the Sense of Design-Based Research
- For the introduction of dihedral groups, the approach via permutations has turned out to be inferior. Composing isometries was possible without ever introducing permutations, and students perceived them as more complex compared to just working with the abstract symbols. We conclude that this content can be dropped if time restrictions enforce a selection.
- Since students had strong associations with coordinate systems when dealing with tables, they reversed the order in which such tables are usually read (rows first, columns second). We did not anticipate this confusion. However, since the reading order is more or less arbitrary from a mathematical point of view, we can simply reverse it for our teaching concept, avoiding this problem by simply adapting the reading order to the experience of the students.
- The biggest learning difficulties were caused by linguistic disparities. Mathematical terms like image, map, and (the German version of) operation that are used with a different meaning in common parlance caused students to transfer those different meanings into mathematics, resulting in incorrect descriptions/paraphrasing and misconceptions. We conclude that, when implementing the teaching concept, the instructional elements need to address those disparities from the beginning and clearly outline the differences.
5.5. Comparison with Related Research
6. Conclusions and Outlook
- To what extent does the technical language impede learning processes? In other words, what is the magnitude of the problem entailed by linguistic preconceptions?
- How can associations from common parlance be avoided so that misuse of the mathematical language can be prevented?
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Appendix A
| Abbreviation | Description |
|---|---|
| A1-1 | Do you understand what an isometry of the triangle is? |
| A1-2 | Are the symbols to describe the isometries plausible to you? |
| P1-1 | Can you describe in your own words what an isometry of the triangle is? |
| P1-2 | Can you describe in your own words what the isometry does? |
| E1 | Can you find the missing isometry in the table? |
| Abbreviation | Description |
|---|---|
| A2-1 | Do you understand how to compose isometries of the triangle? |
| A2-2 | Is it plausible to you that composing isometries yields isometries? |
| P2 | Can you describe in your own words what a composition is? |
| E2-1 | What expression describes “I first use on my triangle and then ”? |
| E2-2 | Please compute . |
| E2-3 | Previously, we computed . Do you notice anything? |
| Abbreviation | Description |
|---|---|
| A3 | Do you understand what a permutation is and how it is used to describe isometries? |
| P3 | Can you describe, in your own words, what a permutation is? |
| E3-1 | Can you describe with a permutation? |
| E3-2 | Which isometry is described by ? |
| Abbreviation | Description |
|---|---|
| A4 | Do you understand how to compose permutations? |
| P4 | Can you describe, in your own words, how two permutations are composed? |
| E4 | Can you compute ? |
| Abbreviation | Description |
|---|---|
| A5-1 | Do you understand what a Cayley Table is? |
| A5-2 | Do you find it plausible to choose columns first? |
| P5 | Can you describe in your own words what a Cayley Table is? |
| E5-1 | Can you complete this Cayley Table? |
| E5-2 | Can you tell me where in the Cayley Table the composition is? |
| E5-3 | What would a Cayley Table look like if ∘ was commutative? |
| Abbreviation | Description |
|---|---|
| A6 | Do you understand what a Magma is? |
| P6 | Can you describe, in your own words, what a Magma is? |
| E6-1 | Can you give an example of a Magma that you already know from school mathematics? |
| E6-2 | Can you give an example for ∘ such that becomes a magma? |
| Abbreviation | Clues |
|---|---|
| E1 | Did you find a position for the vertices that we haven’t seen yet? |
| We have already seen a rotation by 120 degrees. Does that give you an idea? | |
| E2-1 | There are only two possibilities. You have to figure out which one it is |
| E2-2 | First, apply to your triangle, and then apply . |
| E3-1 | Compare the positions of the vertices before and after the isometry. |
| E3-2 | We can see, for example, that vertex 1 switched positions with vertex 3. This already excludes some isometries. |
| E4 | First, only focus on vertex 1. Which final position does it go to? |
| E5-1 | Remember that we read rows first and columns second |
| E5-2 | There are only two possible cells. The correct one is determined by the reading order. |
| E5-3 | If the composition order did not matter, then and would be equal and, thus, the reading order would not matter. How would the table look like in that case? |
| E6-1 | We have already seen some examples. Can you maybe switch out sets or compositions and still get a magma? |
| E6-2 | Which geometrical construction would yield a third point by two given points? |
| P1-1: | Can You Describe in Your Own Words What an Isometry of the Triangle Is? | ||
|---|---|---|---|
| Fully Adequate | Partially Adequate | Not Adequate | |
| Criteria |
|
|
|
| P1-2: | Can You Describe in Your Own Words What the Isometry does? | ||
|---|---|---|---|
| Fully Adequate | Partially Adequate | Not Adequate | |
| Criteria |
|
|
|
| P2: | Can You Describe in Your Own Words What a Composition Is? | ||
|---|---|---|---|
| Fully Adequate | Partially Adequate | Not Adequate | |
| Criteria |
|
|
|
| P3: | Can You Describe in Your Own Words What a Permutation Is? | ||
|---|---|---|---|
| Fully Adequate | Partially Adequate | Not Adequate | |
| Criteria |
|
|
|
| P4: | Can You Describe in Your Own Words How Two Permutations Are Composed? | ||
|---|---|---|---|
| Fully Adequate | Partially Adequate | Not Adequate | |
| Criteria |
|
|
|
| P5: | Can You Describe, in Your Own Words, What a Cayley Table Is? | ||
|---|---|---|---|
| Fully Adequate | Partially Adequate | Not Adequate | |
| Criteria |
|
|
|
| P6: | Can You Describe in Your Own Words What a Magma Is? | ||
|---|---|---|---|
| Fully Adequate | Partially Adequate | Not Adequate | |
| Criteria |
|
|
|
References
- Wasserman, N.H. Introducing Algebraic Structures through Solving Equations: Vertical Content Knowledge for K-12 Mathematics Teachers. PRIMUS 2014, 24, 191–214. [Google Scholar] [CrossRef]
- Even, R. The relevance of advanced mathematics studies to expertise in secondary school mathematics teaching: Practitioners’ views. ZDM Math. Educ. 2011, 43, 941–950. [Google Scholar] [CrossRef]
- Hunkler, R.F. Achievement of Sixth-Grade Pupils in Modern Mathematics as Related to Theri Teachers’ Mathematics Preparation. Ph.D. Thesis, Texas A and M University, College Station, TX, USA, 1968. [Google Scholar]
- Hurst, D. The Relationship between Certain Teacher-Related Variables and Student Achievement in Third Grade Arithmetic. Ph.D. Thesis, Oklahoma State University, Stillwater, OK, USA, 1967. [Google Scholar]
- Norris, F.R. Pupil Achievement as a Function of an Inservice Training Program on Mathematics Concepts for Sixth Grade Teachers. Ph.D. Thesis, George Peabody College for Teachers, Nashville, TN, USA, 1969. [Google Scholar]
- Rouse, W.M. A Study of the Correlation between the Academic Preparation of Teachers of Mathematics and the Mathematics Achievement of Their Students in Kindergarten through Grade Eight. Ph.D. Thesis, Michigan State University, East Lansing, MI, USA, 1967. [Google Scholar]
- Eisenberg, T.A. Begle revisited: Teacher knowledge and student achievement in algebra. J. Res. Math. Educ. 1977, 8, 216–222. [Google Scholar] [CrossRef]
- Wasserman, N.H.; Galarza, P. Exploring an Instructional Model for Designing Modules for Secondary Mathematics Teachers in an Abstract Algebra Course. In Connecting Abstract Algebra to Secondary Mathematics, for Secondary Mathematics Teachers; Springer: Cham, Switzerland, 2018; pp. 335–361. [Google Scholar]
- Copeland, W.D.; Doyle, W. Laboratory skill training and student teacher classroom performance. J. Exp. Educ. 1973, 42, 16–21. [Google Scholar] [CrossRef]
- Veith, J.M.; Bitzenbauer, P. What Group Theory Can Do for You: From Magmas to Abstract Thinking in School Mathematics. Mathematics 2022, 10, 703. [Google Scholar] [CrossRef]
- Griesel, H. Die Leitlinie Menge—Struktur im gegenwärtigen Mathematikunterricht. Mathematikunterricht 1965, 1, 40–53. [Google Scholar]
- Leppig, M. Beispiele zum Rechnen in endlichen Gruppen. Mathematikunterricht 1966, 2, 39–49. [Google Scholar]
- Freudenthal, H. Was ist Axiomatik und welchen bildenden Wert kann sie haben? Mathematikunterricht 1963, 4, 5–29. [Google Scholar]
- Freudenthal, H. What groups mean in mathematics and what they should mean in mathematical education. In Developments in Mathematical Education; Howson, A.G., Ed.; Cambridge University Press: Cambridgeshire, UK, 1973; pp. 101–114. [Google Scholar]
- Wasserman, N.H. Exploring Advanced Mathematics Courses and Content for Secondary Mathematics Teachers. In Connecting Abstract Algebra to Secondary Mathematics, for Secondary Mathematics Teachers; Springer: Cham, Switzerland, 2018; pp. 1–15. [Google Scholar]
- Lee, Y.; Heid, M.K. Developing a Structural Perspective and Its Role in Connecting School Algebra and Abstract Algebra: A Factorization Example. In Connecting Abstract Algebra to Secondary Mathematics, for Secondary Mathematics Teachers; Springer: Cham, Switzerland, 2018; pp. 291–318. [Google Scholar]
- Berliner, D.C. Educational research: The hardest science of all. Educ. Res. 2002, 31, 18–20. [Google Scholar] [CrossRef]
- Levrini, O.; Levin, M.; Fantini, P. Fostering appropriation through designing for multiple access points to a multidimensional understanding of physics. Phys. Rev. Phys. Educ. Res. 2020, 16, 020154. [Google Scholar] [CrossRef]
- Barab, S.; Squire, K. Design-Based Research: Putting a Stake in the Ground. J. Learn. Sci. 2004, 13, 1–14. [Google Scholar] [CrossRef]
- Collins, A. Towards a design science of education. In New Directions in Educational Technology; Scanlon, E., O’Shea, T., Eds.; Springer: Berlin, Germany, 1992; pp. 15–22. [Google Scholar]
- Collins, A. The changing infrastructure of education research. In Issues in Education Research; Lagemann, E., Shulman, L., Eds.; Jossey-Bass: San Francisco, CA, USA, 1999; pp. 289–298. [Google Scholar]
- Bereiter, C. Design Research for Sustained Innovation. Cogn. Stud. 2002, 9, 321–327. [Google Scholar]
- Edelson, D.C. Design research: What we learn when we engage in design. J. Learn. Sci. 2002, 11, 105–121. [Google Scholar] [CrossRef]
- Oha, E.; Reeves, T. The implications of the differences between design research and instructional systems design for educational technology researchers and practitioners. Educ. Med. Int. 2010, 47, 263–275. [Google Scholar] [CrossRef]
- van den Akker, J. Principles and methods of development research. In Design Methodology and Developmental Research in Education and Training; van den Akker, J., Nieveen, N., Branch, R.M., Gustafson, K.L., Plomp, T., Eds.; Kluwer Academic Publishers: Dordrecht, The Netherlands, 1999; pp. 1–14. [Google Scholar]
- Conceicao, S.; Sherry, L.; Gibson, D. Using developmental research to design, develop and evaluate an urban education portal. J. Int. Learn. Res. 2004, 15, 271–286. [Google Scholar]
- Richey, R.C.; Klein, J.D.; Nelson, W.A. Development research: Studies of instructional design and development. In Handbook of Research for Educational Communications and Technology; Jonassen, D.H., Ed.; Lawrence Erlbaum Associates: Mahwah, NJ, USA, 2003; pp. 1099–1130. [Google Scholar]
- Brown, A.L. Design Experiments: Theoretical and Methodological Challenges in Creating Complex Interventions in Classroom Settings. J. Learn. Sci. 1992, 2, 141–178. [Google Scholar] [CrossRef]
- Anderson, T.; Shattuck, J. Design-Based Research: A Decade of Progress in Education Research? Educ. Res. 2012, 41, 16–25. [Google Scholar] [CrossRef] [Green Version]
- Fraefel, U. Professionalization of pre-service teachers through university-school partnerships. Partner schools for Professional Development: Development, implementation and evaluation of cooperative learning in schools and classes. In Proceedings of the WERA Focal Meeting, Edinburgh, Scotland, 19–21 November 2014. [Google Scholar]
- Design-Based Research Collective. Design-Based Research: An Emerging Paradigm for Educational Inquiry. Educ. Res. 2003, 32, 5–8. [Google Scholar] [CrossRef]
- Dolmans, D.H.J.M.; Tigelaar, D. Building bridges between theory and practice in medical education using a design-based research approach: AMEE Guide No. 60. Med. Teach. 2012, 34, 1–10. [Google Scholar] [CrossRef]
- Collins, A.; Joseph, D.; Bielaczyc, K. Design research: Theoretical and methodological issues. J. Learn. Sci. 2004, 13, 15–42. [Google Scholar] [CrossRef]
- Jick, T.D. Mixing Qualitative and Quantitative Methods: Triangulation in Action. Admin. Sci. Quart. 1979, 24, 602–611. [Google Scholar] [CrossRef] [Green Version]
- Wilhelm, T.; Hopf, M. Design-Forschung. In Methoden in der Naturwissenschaftsdidaktischen Forschung; Krüger, D., Parchmann, I., Schecker, H., Eds.; Springer: Berlin, Germany, 2014; pp. 31–42. [Google Scholar]
- Bitzenbauer, P. Practitioners’ views on new teaching material for introducing quantum optics in secondary schools. Phys. Educ. 2021, 56, 055008. [Google Scholar] [CrossRef]
- Davis, E.A.; Palincsar, A.S.; Smith, P.; Arias, A.K.S. Educative Curriculum Materials: Uptake, Impact, and Implications for Research and Design. Educ. Res. 2017, 46, 293–304. [Google Scholar] [CrossRef]
- Scriven, M. The Logic of Evaluation, 1st ed.; Edgepress: Iverness, CA, USA, 1980. [Google Scholar]
- Steffe, L.P.; Thompson, P.W. Teaching Experiment Methodology. In Handbook of Research Design in Mathematics and Science Education; Kelly, A.E., Lesh, R.A., Eds.; Rouledge: Mahwah, NJ, USA, 2000; pp. 267–306. [Google Scholar]
- Jung, W. Probing acceptance, a technique for investigating learning difficulties. In Research in Physics Learning: Theoretical Issues and Empirical Studies; Duit, R., Goldberg, F., Niedderer, H., Eds.; IPN: Kiel, Germany, 1992; pp. 278–295. [Google Scholar]
- Wiener, G.J.; Schmeling, S.; Hopf, M. The technique of probing acceptance as a tool forteachers’ professional development: A PCK study. J. Res. Sci. Teach. 2018, 55, 849–875. [Google Scholar] [CrossRef]
- Blumör, R. Schülerverständnisse und Lernprozesse in der Elementaren Optik, 1st ed.; Westarp: Hohenwarsleben, Germany, 1993. [Google Scholar]
- Haagen-Schützenhöfer, C. Lehr- und Lernprozesse im Anfangsoptikunterricht der Sekundarstufe I; Universität Wien: Habilitationsschrift, Austria, 2016. [Google Scholar]
- Wiener, G.J.; Schmeling, S.; Hopf, M. Can Grade-6 students understand quarks? Probing acceptance of the subatomic structure of matter with 12-year-olds. Eur. J. Sci. Math. Ed. 2015, 3, 313–322. [Google Scholar] [CrossRef]
- Komorek, M.; Duit, R. The teaching experiment as a powerful method to develop and evaluate teaching and learning sequences in the domain of non-linear systems. Int. J. Sci. Educ. 2017, 26, 619–633. [Google Scholar] [CrossRef]
- Burde, J.-P.; Wilhelm, T. Teaching electric circuits with a focus on potential differences. Phys. Rev. Phys. Educ. Res. 2020, 16, 020153. [Google Scholar] [CrossRef]
- Haagen-Schützenhöfer, C.; Hopf, M. Design-based research as a model for systematic curriculum development: The example of a curriculum for introductory optics. Phys. Rev. Phys. Educ. Res. 2020, 16, 020152. [Google Scholar] [CrossRef]
- Bitzenbauer, P.; Meyn, J.-P. A new teaching concept on quantum physics in secondary schools. Phys. Educ. 2020, 55, 055031. [Google Scholar] [CrossRef]
- Wiener, G.J.; Schmeling, S.M.; Hopf, M. Why not start with quarks? Teachers investigate a learning unit on the subatomic structure of matter with 12-year-olds. Eur. J. Sci. Math. Educ. 2017, 5, 134–157. [Google Scholar] [CrossRef]
- Dresing, T.; Pehl, T. Praxisbuch Interview, Transkription & Analyse. Anleitungen und Regelsysteme für Qualitativ Forschende, 8th ed.; Eigenverlag: Marburg, Germany, 2018. [Google Scholar]
- Mayring, P. Qualitative Inhaltsanalyse: Grundlage und Techniken, 12th ed.; Beltz Verlag: Weinheim Basel, Switzerland, 2010. [Google Scholar]
- Landis, J.R.; Koch, G.G. The Measurement of Observer Agreement for Categorial Data. Biometrics 1977, 33, 159–174. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Bitzenbauer, P. Quantenoptik an Schulen. Studie im Mixed-Methods Design zur Evaluation des Erlanger Unterrichtskonzepts zur Quantenoptik, 1st ed.; Logos Verlag Berlin: Berlin, Germany, 2020. [Google Scholar]
- Weber, K.; Larsen, S. Teaching and Learning Group Theory. In Making The Connection; Carlson, M.P., Rasmussen, C., Eds.; Mathematical Association of America: Washington, DC, USA, 2008; pp. 139–151. [Google Scholar]
- Wasserman, N.H. Connecting Abstract Algebra to Secondary Mathematics, for Secondary Mathematics Teachers; Springer: Cham, Switzerland, 2018. [Google Scholar]
- Suominen, A.L. Abstract Algebra and Secondary School Mathematics Connections as Discussed by Mathematicians and Mathematics Educators. In Connecting Abstract Algebra to Secondary Mathematics, for Secondary Mathematics Teachers; Springer: Cham, Switzerland, 2018; pp. 149–173. [Google Scholar]
- Shimizu, J.K. The Nature of Secondary Mathematics Teachers’ Efforts to Make Ideas of School Algebra Accessible. Ph.D. Thesis, The Pennsylvania State University, State College, PA, USA, 2013. [Google Scholar]
- Zbiek, R.M.; Heid, M.K. Making Connections from the Secondary Classroom to the Abstract Algebra Course: A Mathematical Activity Approach. In Connecting Abstract Algebra to Secondary Mathematics, for Secondary Mathematics Teachers; Springer: Cham, Switzerland, 2018; pp. 189–209. [Google Scholar]
- Leron, U.; Dubinsky, E. An abstract algebra story. Am. Math. Mon. 1995, 102, 227–242. [Google Scholar] [CrossRef]
- Melhuish, K.; Fagan, J. Connecting the Group Theory Concept Assessment to Core Concepts at the Secondary Level. In Connecting Abstract Algebra to Secondary Mathematics, for Secondary Mathematics Teachers; Springer: Cham, Switzerland, 2018; pp. 19–45. [Google Scholar]
- Wasserman, N.H. Making Sense of Abstract Algebra: Exploring Secondary Teachers’ Understandings of Inverse Functions in Relation to Its Group Structure. Math. Think. Learn. 2017, 19, 181–201. [Google Scholar] [CrossRef]
- Baldinger, E.E. Learning Mathematical Practices to Connect Abstract Algebra to High School Algebra. In Connecting Abstract Algebra to Secondary Mathematics, for Secondary Mathematics Teachers; Springer: Cham, Switzerland, 2018; pp. 211–239. [Google Scholar]
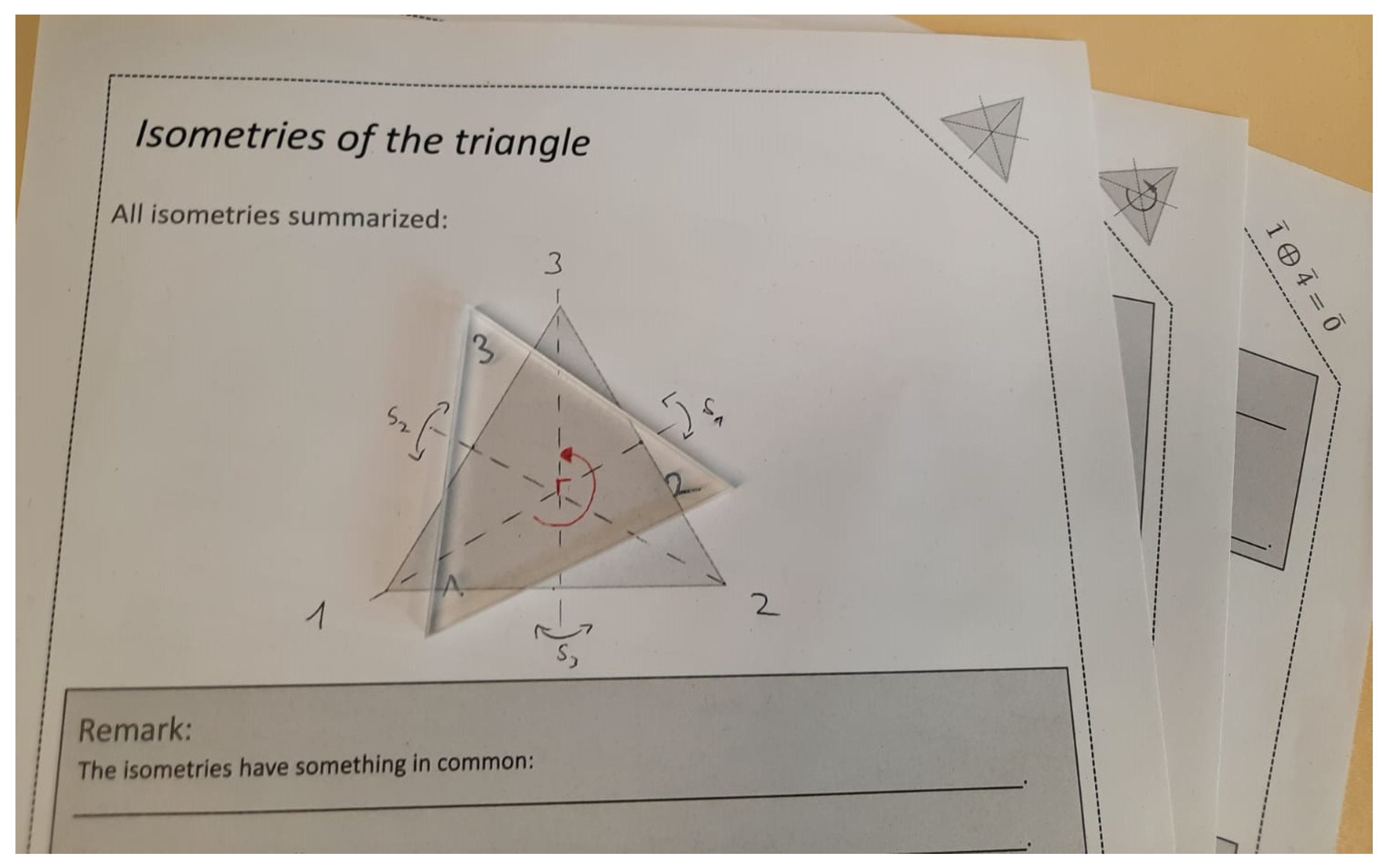

| Key Idea | Description | Research Question |
|---|---|---|
| K1 | Isometries of the triangle | RQ1 (a), RQ2, RQ3 |
| K2 | Composition of isometries | RQ1 (a), RQ2, RQ3 |
| K3 | Permutations | RQ1 (b), RQ2, RQ3 |
| K4 | Composition of permutations | RQ1 (b), RQ2, RQ3 |
| K5 | Cayley Tables | RQ1 (c) RQ3 |
| K6 | Magmas | RQ3 |
| Participant | Score 1 | Score 2 | Profile |
|---|---|---|---|
| A | 6 | 7 | PM |
| B | 7 | 6 | PM |
| C | 11 | 10 | PM |
| D | 10 | 11 | NM |
| E | 9 | 11 | M |
| F | 12 | 14 | M |
| G | 8 | 10 | NM |
| H | 10 | 11 | NM |
| I | 15 | 14 | M |
| Phase of the Acceptance Survey | %-Agreement | Judgement According to [52] | |
|---|---|---|---|
| Acceptance | substantial agreement | ||
| Paraphrasing | fair agreement | ||
| Application | substantial agreement |
| Anchor Example for Perfect Acceptance | |
|---|---|
| (I): | Do you find the symbols we’ve chosen to describe the isometries plausible? |
| (S): | Yes, of course. For each vertex, we have , , and depending on which vertex we reflected, and the other thing with the rotation was also plausible. |
| Anchor Example for Partial Acceptance | |
|---|---|
| (I): | Do you find the symbols we’ve chosen to describe the isometries plausible? |
| (S): | Yes, but only with the descriptions next to them in the table, because in mathematics, everybody uses their own symbols, which can be confusing. But with the description in the table, it’s fine. |
| Anchor Example for Fully Adequate Paraphrasing | |
|---|---|
| (I): | Can you describe in your own words what a permutation is? |
| (S): | For me a permutation is, let’s say, some kind of table where you can look up for each vertex how it got manipulated. For example, we can see where vertex 1 went as well as vertices 2 and 3. |
| Anchor Example for Partially Adequate Phrasing | |
|---|---|
| (I): | Can you describe in your own words what a Magma is? |
| (S): | Well, if we have a set, and composing two things gives another thing of the set, then we have a set which we composed. |
| Anchor Example for Not Adequate Phrasing | |
|---|---|
| (I): | Can you describe in your own words what an isometry of the triangle is? |
| (S): | An isometry of the triangle is a form of the triangle that has the same orientation and the same area as before, but we can move it and change it. |
| A1-1 | A1-2 | A2-1 | A2-2 | A3 | A4 | A5-1 | A5-2 | A6 | |
|---|---|---|---|---|---|---|---|---|---|
| A | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 0.5 | 1 |
| B | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 0.5 | 1 |
| C | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 |
| D | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 |
| E | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 0 | 1 |
| F | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 0 | 1 |
| G | 1 | 0.5 | 1 | 1 | 1 | 1 | 1 | 1 | 1 |
| H | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 |
| I | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 0 | 1 |
| Mean | 1.00 | 0.94 | 1.00 | 1.00 | 1.00 | 1.00 | 1.00 | 0.56 | 1.00 |
| P1-1 | P1-2 | P2 | P3 | P4 | P5 | P6 | |
|---|---|---|---|---|---|---|---|
| A | 1 | 1 | 0 | 1 | 1 | 0.5 | 0.5 |
| B | 1 | 1 | 0.5 | 1 | 0.5 | 1 | 1 |
| C | 0.5 | 1 | 0.5 | 0.5 | 1 | 1 | 1 |
| D | 1 | 1 | 0.5 | 1 | 0.5 | 1 | 1 |
| E | 0 | 0.5 | 1 | 1 | 1 | 1 | 0 |
| F | 0.5 | 1 | 1 | 1 | 1 | 1 | 1 |
| G | 1 | 0.5 | 1 | 1 | 0.5 | 1 | 1 |
| H | 1 | 1 | 1 | 1 | 1 | 1 | 0.5 |
| I | 0.5 | 1 | 1 | 1 | 1 | 1 | 0.5 |
| Mean | 0.72 | 0.94 | 0.72 | 0.94 | 0.83 | 0.94 | 0.72 |
| E1 | E2-1 | E2-2 | E2-3 | E3-1 | E3-2 | E4 | E5-1 | E5-2 | E5-3 | E6-1 | E6-2 | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| A | 1 | 1 | 0.5 | 1 | 1 | 1 | 0.5 | 1 | 1 | 0 | 1 | 0 |
| B | 1 | 1 | 1 | 1 | 1 | 0.5 | 1 | 1 | 0 | 0.5 | 1 | 0 |
| C | 0 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 0 | 1 | 0.5 |
| D | 1 | 1 | 1 | 1 | 1 | 0.5 | 1 | 1 | 1 | 1 | 1 | 1 |
| E | 1 | 1 | 1 | 1 | 1 | 0.5 | 1 | 1 | 0.5 | 1 | 0.5 | 0.5 |
| F | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 0.5 | 1 | 0.5 |
| G | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 0.5 |
| H | 1 | 1 | 1 | 1 | 1 | 0 | 1 | 1 | 1 | 1 | 1 | 1 |
| I | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 |
| Mean | 0.89 | 1.00 | 0.94 | 1.00 | 1.00 | 0.72 | 0.94 | 1.00 | 0.83 | 0.67 | 0.94 | 0.56 |
| Perceived Difficulty | Plausibility of the Notation | ||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| K1 | K2 | K3 | K4 | K5 | K6 | K1 | K2 | K3 | K5 | K6 | |
| A | 0.5 | 1 | 0.5 | 0 | 1 | 0.5 | 1 | 1 | 0.5 | 1 | 0.5 |
| B | 1 | 1 | 1 | 0.5 | 1 | 1 | 1 | 0.5 | 1 | 1 | 1 |
| C | 1 | 1 | 1 | 0.5 | 1 | 1 | 1 | 1 | 1 | 1 | 1 |
| D | 1 | 1 | 0.5 | 1 | 1 | 0.5 | 1 | 1 | 0.5 | 1 | 0.5 |
| E | 1 | 1 | 1 | 0.5 | 1 | 0.5 | 1 | 1 | 1 | 1 | 0.5 |
| F | 1 | 1 | 0.5 | 0.5 | 1 | 0.5 | 1 | 0.5 | 1 | 1 | 0.5 |
| G | 0.5 | 1 | 0.5 | 0.5 | 1 | 1 | 1 | 1 | 1 | 1 | 1 |
| H | 1 | 1 | 0.5 | 1 | 1 | 1 | 1 | 0.5 | 1 | 1 | 1 |
| I | 1 | 0.5 | 0.5 | 1 | 1 | 0.5 | 1 | 1 | 1 | 1 | 0.5 |
| Mean | 0.89 | 0.94 | 0.67 | 0.61 | 1.00 | 0.72 | 1.00 | 0.83 | 0.89 | 1.00 | 0.72 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Veith, J.M.; Bitzenbauer, P.; Girnat, B. Towards Describing Student Learning of Abstract Algebra: Insights into Learners’ Cognitive Processes from an Acceptance Survey. Mathematics 2022, 10, 1138. https://doi.org/10.3390/math10071138
Veith JM, Bitzenbauer P, Girnat B. Towards Describing Student Learning of Abstract Algebra: Insights into Learners’ Cognitive Processes from an Acceptance Survey. Mathematics. 2022; 10(7):1138. https://doi.org/10.3390/math10071138
Chicago/Turabian StyleVeith, Joaquin Marc, Philipp Bitzenbauer, and Boris Girnat. 2022. "Towards Describing Student Learning of Abstract Algebra: Insights into Learners’ Cognitive Processes from an Acceptance Survey" Mathematics 10, no. 7: 1138. https://doi.org/10.3390/math10071138
APA StyleVeith, J. M., Bitzenbauer, P., & Girnat, B. (2022). Towards Describing Student Learning of Abstract Algebra: Insights into Learners’ Cognitive Processes from an Acceptance Survey. Mathematics, 10(7), 1138. https://doi.org/10.3390/math10071138






