Abstract
In this paper, we introduce a general family of distributions based on Whittaker function. The properties of obtained distributions, moments, ordering, percentiles, and unimodality are studied. The distributions’ parameters are estimated using methods of moments and maximum likelihood. Furthermore, a generalization of Whittaker distribution that contains a wider class of distributions is developed. Validation of the obtained results is applied to real life data containing four data sets.
1. Introduction
There is no single definition of “special functions”, as the term has been used for a variety of functions. They are important to many mathematicians, such as mathematical analysis, functional analysis, applied mathematics, and distribution theory. Such functions can be written as a summation or an integration. Examples include the relatively exponential, gamma, Bessel, hypergeometric, and Whittaker functions. For more instances of special functions, see [1,2,3]. Most of these functions are non-negative and finite over a certain range, and thus can be used to define probability distributions. Typical examples are the Poisson, gamma, and Bessel distributions.
There was an early interest in special functions in the theory of distribution. This included studies by [4,5], who introduced Bessel function distributions of types I and II. The exact distribution of the product of two independent generalized gamma variables with the same shape parameters using the modified Bessel function of the second kind was given by [6]. A power series distribution generated by the first type of modified Bessel function has been studied [7]. The generalized beta of the first and second kinds of distribution was considered by [8]. The Kummer-beta distribution in the problem of common value action, which features confluent hypergeometric functions, was defined [9]. The type I distribution of the inverted hypergeometric function that includes a Gaussian hypergeometric function is obtained [10]. A generalized Laplacian distribution using the modified Bessel function of second kind has been introduced [11]. The product distribution of two independent random variables featuring the Kummer-beta distribution was obtained by [12] using a confluent hypergeometric series of a two-variable function. The distribution of the product of two independent random variables, beta type II (beta prime) and beta type III, featuring the hypergeometric function of two variables is derived [13]. The distribution of the difference between independent gamma random variables with different shapes and scale parameters, called the bilateral gamma, is introduced [14]. This distribution has used the Whittaker function. The density of the product of type I variables of the Kummer–beta and the inverted hypergeometric functions containing a confluent hypergeometric series of a two-variable function was developed by [15]. They also derived the distribution of the product of the beta type III and type I variables of the inverted hypergeometric function that uses the hypergeometric function of two variables. Several properties of the extended Gauss hypergeometric and extended confluent hypergeometric functions have been studied [16]. The distribution of the products of independent central normal variables involving Meijer G-functions has been developed [17]. A new distribution was obtained as a solution of the generalized Pearson differential equation by [18], and a generalization of this distribution was also defined using the Whittaker functions. This Distribution includes as special cases distributions obtained as the product of well-known distributions. A distribution based on the generalized Pearson differential equation using a modified Bessel function of the second kind was introduced by [19] and named as generalized inverse Gaussian distribution (GGIG). The GGIG distribution is also defined in terms of the Whittaker function.
The current paper belongs to the above studies. We use the Whittaker function to introduce a new life distribution called the Whittaker distribution. This distribution is a generalization of many important continuous distributions. The gamma, exponential, chi-square, generalized Lindley, Lindley, beta prime, and Lomax are special cases of the Whittaker distribution. In some applications, the Whittaker distribution has outperformed the generalized gamma and log-normal distributions. We also define the generalized Whittaker distribution as , where is the Whittaker distribution and c ≠ 0. The generalized gamma, half-normal, Weibull, half-t, half-Cauchy, Nakagami, Rayleigh, Dagum, Lévy, type-2 Gumbel, inverse gamma, inverse chi-square, inverse exponential, inverse Weibull, and inverse-Rayleigh distributions are special cases of the proposed generalized Whittaker distribution.
The current paper is organized as follows: In Section 2, we proposed the Whittaker distribution and examined some of its properties. Several important special distributions are presented in Section 3. The parameters are estimated by methods of moments and maximum likelihood in Section 4. To illustrate the usefulness of the proposed Whittaker distribution, four data sets are analyzed in Section 5. Finally, some concluding remarks are given in Section 6.
2. Whittaker Distribution
The Whittaker function is defined as in [2] (Ch. Confluent Hypergeometric Functions, page 1024),
This function can be used to introduce a probability distribution on as follows:
Theorem 1.
The function:
where , andis a probability density function.
Proof of Theorem 1.
As and , the Whittaker function is non-negative and finite, hence , and .
To show that , we will use the following relation [3] (Ch. Laplace Transforms-Arbitrary Powers p. 139 Equation (22),
for .
Therefore, by setting , and . The proof is complete. □
Definition 1.
Let X be a non-negative random variable with probability density function (pdf) (2). Then, we say that has a Whittaker distribution and is denoted by .
Figure 1 gives sample plots of the Whittaker probability density function for different values of the relevant parameters. We first note that is a scale parameter as exhibited in Figure 1. In Figure 1b–k, we fix .
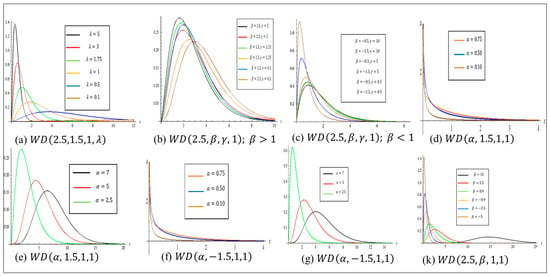
Figure 1.
Plots of density function for some parameters values.
From the plot in Figure 1b, when , we note that the change in the value of has a negligible effect on the shape of the Whittaker probability density function. In Figure 1c, when , note that the change in the value of is taken as a scale parameter, and has a greater effect when . For (), the distribution peaks further as increases (decreases). In Figure 1d–k, we fix . For , the Whittaker pdf attains ∞ and decreases sharply to zero as shown in Figure 1d,f. In Figure 1e,g, as the value of decreases, the distribution peaks more.
From the plot in Figure 1k, we note that when the value of increases, the mode increases. Finally, we note that the Whittaker distribution is unimodal.
Theorem 2.
The cumulative distribution function of the is given by,
where , , and is the confluent hypergeometric series of two variables defined in [2] (Ch. Exponentials and arbitrary powers, page 349),
Proof of Theorem 2.
, where .
Using one acquires,
. □
Using the properties of the cumulative distribution function, the following lemma provides new properties of the confluent hypergeometric series of two variables:
Lemma 1.
Let , the confluent hypergeometric series of two variables satisfies the following conditions:
- 1-
- 2-
- 3-
- is a non-decreasing and right continuous function.
The proof is straightforward using the properties of the cumulative distribution function (cdf).
3. Statistical Properties
This section presents the statistical properties and main characteristics of . We summarize these properties in the following theorem:
Theorem 3.
- The Laplace transformation is.
- The rth moment about the origin is
- The mean is .
- The variance is .
- The mode of for is .
- The measures of skewness , kurtosis , and the coefficient of variation of distribution are, respectively, , , and .
- The survival function is .
- The hazard function is .
Proof of Theorem 3.
- The Laplace transformation: , by using (3).
- The rth moment function is, By using (3).
- We have from II that, and
- The variance is given by
- The mode can be obtained by differentiating the pdf of with respect to as follows, .
However, the mode is obtained as the solution of . Therefore, we have , that leads to , or .
By solving , one acquires, .
Since the distribution is defined on the set , we acquire as in the form, . □
Note: The skewness , kurtosis , and the coefficient of variation of do not depend on .
Some recurrence relations of the Whittaker function are provided in [1]. From the above theorem, we can deduce other recurrence relations for the Whittaker function as follows.
Corollary 1.
For and, we have,
- 1-
- .
- 2-
- 3-
- .
Proof of Corollary 1.
From Theorem 3, one can acquire the mean and the second order moment using the Laplace transformation as follows,
The mean and the second order moment can also be derived from the rth moment formula in Theorem 3,
Hence, by equating the two formulas of , we acquire .
By replacing , and with , and , respectively, we acquire, .
Similarly, by equating the two formulas of , we acquire,
By replacing , and with , and , respectively, we acquire,
Since
By replacing , and with , and , respectively, we acquire,
The proof is complete. □
Corollary 2.
Forand, the Whittaker function satisfies the following conditions,
Proof of Corollary 2.
- .
- . □
Corollary 3.
Forand, the confluent hypergeometric function of the second kind satisfies the relation,
Proof of Corollary 3.
The confluent hypergeometric function of the second kind is defined in [1] (Ch. Confluent Hypergeometric functions/Integral Representations page 505),
At , we acquire □
Theorem 4.
Let . Then,
- (a)
- Forandis log-concave.
- (b)
- Forandis log-convex.
Proof of Theorem 4.
It is simple to see that, .
It is a decreasing (increasing) function for , and . Thus, is log-concave (convex). □
Theorem 4 does not cover all ranges of and as shown in Figure 2. In the following example, we illustrate that there is no obvious conclusion outside the above ranges.
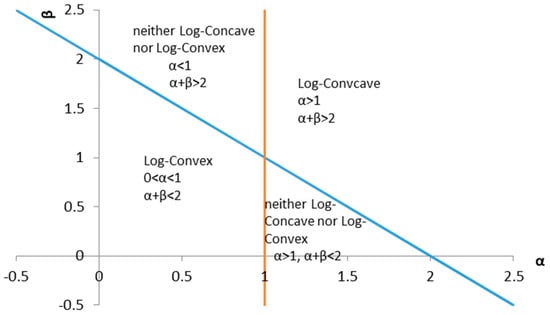
Figure 2.
The relation between and , and the concavity of .
Example: The second derivative of the log of density is,
Figure 3 shows the function for the two cases where and When , is positive for , and for is negative. Therefore is neither log-convex nor log-concave. Further, when , is negative for , and for is positive. Therefore, is neither log-convex nor log-concave.
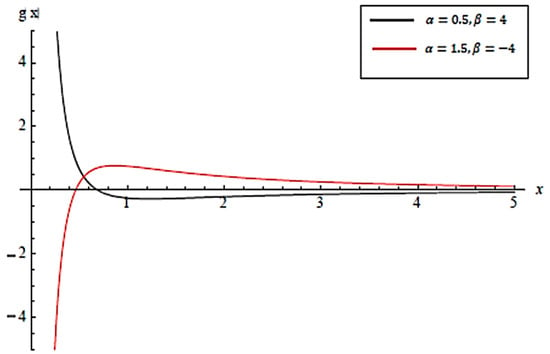
Figure 3.
for .
The distributions with log-concave density are unimodal and have increasing failure rate property.
Theorem 5.
- The Whittaker distribution has a monotonic likelihood ratio in x with respect towhen the other parameters are constant.
- The Whittaker distribution has a monotonic likelihood ratio in x with respect towhen the other parameters are constant.
- The Whittaker distribution has a monotonic likelihood ratio in x with respect towhen the other parameters are constant and .
Proof of Theorem 5.
- I
- Let . Then, where .
- II.
- The proof is similar to that of I.
- II.
- For , we acquire where
If then . □
Note: The Whittaker distribution is not a member of the monotonic likelihood ratio family with respect to when other parameters are constant.
Percentiles
Now, we compute the percentiles of Whittaker distribution. For any , the -th percentile is a number such that the area under to the left of is . That is, is any root of the equation,
Using numerical simulation, the percentage points associated with the cdf of X are computed for some selected values of the parameters using Mathematica software (The code is provided in Appendix A).
Definition 2.
Let and, then,is defined as the generalized Whittaker distribution given by,
where ,, and. For simplicity, we use the notation .
4. Special Cases
Many well-known distributions can be viewed as special cases of the WD and GWD. Figure 4 summarizes all these findings. Whereas the distribution defined in [18,19] are neither a generalization nor a special cases of the WD.
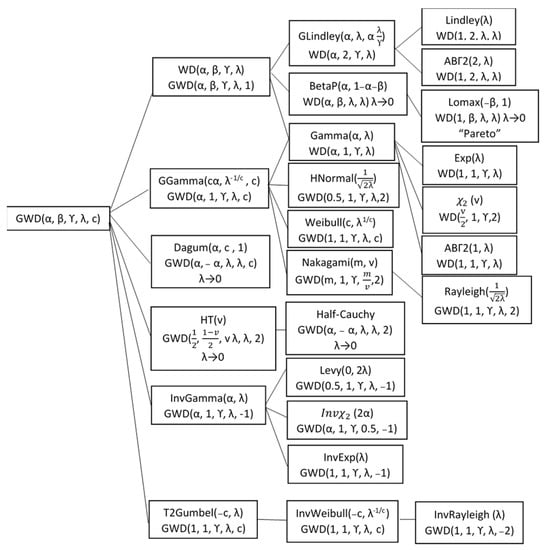
Figure 4.
The special cases of and .
4.1. Generalized Lindley Distribution
If , then the Whittaker distribution is reduced to the generalized Lindley distribution proposed by [20], as follows:
At , the mgf .
By using Corollary 2(II) at , we acquire .
Then,
Thus, if and , the Whittaker distribution is reduced to the Lindley distribution [21].
4.2. Beta Prime Distribution
If , = , and , the Whittaker distribution is reduced to the beta prime distribution [22].
For , the pdf of is reduced to .
By using [1] (Ch. Confluent Hypergeometric functions, page 505),
we acquire
Then, . By taking the limit as tends to zero, one acquires
Using Corollary 3, we acquire the pdf
Thus, if , = , and , the Whittaker distribution is reduced to Lomax [23] and the Pareto distribution [24].
4.3. Generalized Gamma Distribution
If , then follows a generalized gamma distribution [25]. Hence the corresponding pdf is,
From Corollary 2 (I), we acquire .
Therefore,
Notes:
- (a)
- If and , the generalized Whittaker distribution is reduced to the Nakagami distribution [26].
- (b)
- If , and , the generalized Whittaker distribution is reduced to Rayleigh distribution [27].
- (c)
- If , and , the generalized Whittaker distribution is reduced to the half-normal distribution.
- (d)
- If and , the generalized Whittaker distribution is reduced to the Weibull distribution.
- (e)
- If and , the generalized Whittaker distribution is reduced to the gamma distribution.
- (f)
- If and , the Whittaker distribution is reduced to an exponential distribution.
- (g)
- If , and , the Whittaker distribution is reduced to a chi-square distribution with n degrees of freedom.
4.4. Dagum Distribution
If , follows the Dagum distribution [28] with
Recalling Corollary 3, we acquire the pdf as
4.5. Half-t Distribution
If follows a generalized Whittaker distribution with , and at , the generalized Whittaker distribution is reduced to the half-t distribution.
The pdf of is given by .
From (8), we acquire . Then,
From Corollary 3, at , we acquire
Therefore,
Thus, if , = , and , the generalized Whittaker distribution is reduced to a half-Cauchy distribution.
4.6. Inverse Gamma Distribution
If , follows the inverse gamma distribution [23], as,
From Corollary 2 (I), we acquire .
Therefore,
Notes:
- (a)
- If and , the generalized Whittaker distribution is reduced to Lévy distribution [29].
- (b)
- If , and , the generalized Whittaker distribution is reduced to the inverse exponential distribution.
- (c)
- If , , and , the generalized Whittaker distribution is reduced to the inverse chi-square distribution.
4.7. Type-2 Gumbel Distribution
If , then follows a Type-2 Gumbel distribution [30], as,
From Corollary 2 (I), we acquire .
Therefore,
Note: If and , then the generalized Whittaker distribution is reduced to inverse Rayleigh distribution [31].
5. Estimation
In this section, we focus on the estimation of the parameters and of the Whittaker distribution. We introduce the estimation of parameters via the moments’ and the maximum likelihood methods, denoted by MME and MLE, respectively.
Let be i.i.d. , the we have the following estimates.
5.1. Method of Moments
5.2. Maximum Likelihood Estimates
The log-likelihood function is given by,
.
The MLE of and can be obtained by solving numerically the equations and , respectively:
where,
In addition,
where,
and is the di-gamma function.
6. Validations
In this section, we consider the application of and to four different data sets to study the behavior of the parameters and . Mathematica software is adopted to find the parameter estimates (The computer codes are provided in Appendix B). The four data sets are described below.
Data set 1: The data set consisted of third-party motor insurance data for Sweden (1977), described and analyzed in [32].
Data set 2: The data set represented an uncensored data set corresponding to remission times (in months) of a random sample of 128 patients of bladder cancer reported in [33].
Data set 3: It represented the survival times (in days) of 72 guinea pigs infected with virulent tubercle bacilli, observed and reported in [34].
Data set 4: It represented waiting times (in minutes) before service of 100 bank customers as discussed [35].
Table 1 lists the model evaluation statistics for fitting the and the together with some other distributions. The best model is shown in bold.

Table 1.
Estimation results for all data sets.
Table 2 presents the values of the Vuong test for against normal, Johnson , and log-normal distributions for all data sets.

Table 2.
Vuong test of vs. some models for all data sets.
The variance covariance matrix of the MLEs under the Whittaker distribution for data set 1 are computed as,
Thus, the 95% confidence intervals for , and were (0, 21.1722), (42.6242, 134.978), (39.733, 40.2333), and (3.6761, 5.8683), respectively. Since is always nonegative, the lower bound of the confidence interval of was set to zero.
For (), the value of Pearson’s chi-square test was with p-value 0.1849 (0.3351), which implies that () fits the data well. Regarding the maximum values of the log-likelihood, and the minimum values of the AIC and BIC for and , the results of both models are nearly identical. From the result of fitting , the estimated value is . Therefore, we perform an LRT for the hypothesis against . The value of the test statistic is with a p-value of 0.671, providing . This implies that we can reduce the model to the model with fewer parameters. Figure 5 illustrates the estimated density of for data set 1.
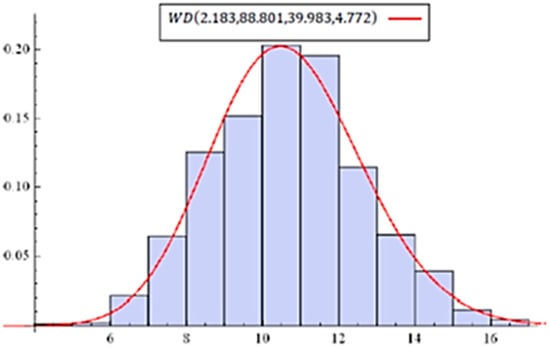
Figure 5.
Estimated density of for data set 1.
The distribution is better than the log-normal distribution in terms of log-likelihood, AIC, and BIC. The value of the Vuong test for versus log-normal is (p-value = 0.0041), which implies that the yielded a significantly better fit than the log-normal distribution. While the distribution outperforms the normal distribution in terms of log-likelihood and AIC, this was not the case in terms of BIC. The value of the Vuong test for the distribution versus the normal distribution is (p-value = 0.3834), indicating no significant difference between the models.
The generalized gamma distribution and Weibull distributions are special cases of the generalized Whittaker distribution. Therefore, there is no need to fit these distributions. The gamma and generalized Lindley distributions are special cases of the Whittaker distribution at and , respectively. It is clear that in the is neither one nor two. For the gamma distribution, the value of LRT is (p-value = 0.0104). Then, . The same conclusion is obtained under the generalized Lindley, , where the value of the test statistic is (p-value = 0.003).
The variance covariance matrix of the MLEs under the Whittaker distribution for data set 2 was computed as,
Thus, the 95% confidence intervals of , and are (0.7937, 1.3981), (−9.684, −0.1094), (0.09735, 0.1087), and (0, 0.0076), respectively. The lower bound of the confidence interval of is negative. Since is always non-negative, zero is considered the lower bound.
The results of Pearson’s chi-square test for () yield = 12.0676 (12.3476) with a p-value 0.0984 (0.1944), which implies that () fits the data well. The result of shows that the estimated value of is 1.09, and the other parameters are nearly the same as those of . Therefore, we perform the LRT for hypotheses and . The value of the test statistic is (p-value = 0.7447). This implies that we can reduce to , which has fewer parameters. Figure 6 illustrates the estimated density of for data set 2.
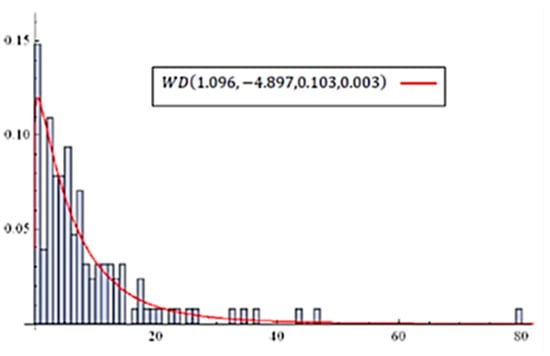
Figure 6.
Estimated density of for data set 2.
According to the Vuong test, we can conclude that fits the data better than the normal distribution and Johnson’s with (V = 4.47 with p-value < 0.001) and (V = 2.31 with p-value = 0.021), respectively. There is no significant difference between the WD distribution and the log-normal distribution with a p-value of 0.156.
The generalized gamma and Weibull distributions are special cases of , and thus are eliminated from the comparison. Using the LRT to check where the data had been drawn from an exponential distribution, the value of the test statistic becomes (p-value = 0.2318). This implies that the exponential distribution fits the data.
The variance covariance matrix of the MLEs under the Whittaker distribution for data set 3 is computed as follows.
Thus, the 95% confidence intervals of , and were (0, 6.4892), (−15.8852, 17.8852), (2.7513, 3.1339), and (0, 4.4875), respectively. The lower bounds of the confidence intervals of and are negative; and as both and are always non-negative, zero is used as lower bound.
We fit the models and to data on survival times. The results of Pearson’s chi-square test for () yield a value = 3.766 (3.8114) with p-value 0.1521 (0.2826), which implies that () fits the data well. The results (in Table 1) of show that the estimated value of is 0.97, and the other parameters are nearly identical to those of . Using the LRT, the value of the test statistic is (p-value = 0.946). This implies that we can reduce the model to , which has fewer parameters. Figure 7 illustrates the estimated density of for data set 3.
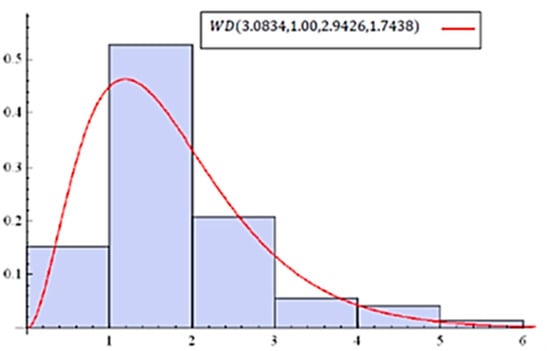
Figure 7.
Estimated density of for data set 3.
Using the Vuong test (in Table 2), there is no significant difference between the fitted model using the distribution and all remaining tested distributions.
The generalized gamma and Weibull distributions are a special case of , and thus are eliminated from the comparison. From the results of fitting , we note that the estimated value of is one, and the other fitting measures of and are identical to those of . Therefore, we perform the LRT () with a p-value of one, with providing . The generalized Lindley is a special case of the WD when is two. Without testing, we know that the gamma distribution yields a better fit than the generalized Lindley for this data set.
The variance covariance matrix of the MLEs under the Whittaker distribution for data set 4 is computed as follows.
Thus, the 95% confidence intervals for , and are (0, 106.00), (−104.35, 46.4446), (0.0047, 0.0053), and (0.0922, 0.2627), respectively. The lower bound of the confidence interval of α is negative. As α is non-negative, zero is used as lower bound.
We fit the models and to data of waiting times. The results of Pearson’s chi-square test for () yield a value of = 10.9955 (11.0327) with a p-value 0.202 (0.2735), which implies that () fits the data well. The result (in Table 1) for shows that the estimated value of is 0.97. Using the LRT for , the value of the test statistic is (p-value = 0.964). This implies that we can reduce the model to , which has fewer parameters. Figure 8 illustrates the estimated density of for data set 4.
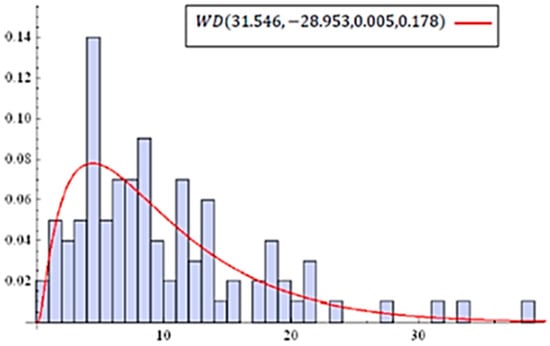
Figure 8.
Estimated density of for data set 4.
According to the Vuong test, we can conclude that yields a better fit than the normal with (V = 4.47 with p-value < 0.001), and there is no significant difference between the fitted model using the distribution, and the log-normal and Johnson’s distributions. The generalized gamma and Weibull distributions are special cases of and thus are eliminated from the comparison. Using the LRT, the value of the test statistic of was (p-value = 0.179). This implies that the generalized Lindley distribution fits the data. Finally, the value of the test statistic of the LRT for is (p-value = 0.691). This implies that the gamma distribution fits the data as well.
7. Conclusions
Based on Whittaker function a modified life distribution that is called Whittaker distribution has been introduced. The Whittaker distribution is a generalization of many well-known continuous distributions such as gamma, exponential, chi-square, generalized Lindley, Lindley, beta prime, and Lomax distributions. Furthermore, we have defined the generalized Whittaker distribution that also has the generalized gamma, half-normal, Weibull, half-t, half-Cauchy, Nakagami, Rayleigh, Dagum, Lévy, type-2 Gumbel, inverse gamma, inverse chi-square, inverse exponential, inverse Weibull, and inverse-Rayleigh distributions as special cases. We Validated the proposed distributions on four real data sets. The results of Pearson’s chi-square test confirmed that the Generalized Whittaker distribution and the Whittaker distribution fit the data well for all the four data sets. In some applications, the vuong test showed that the Whittaker distribution has significantly better fit than the normal, log-normal and Jhonson distributions.
Author Contributions
Conceptualization, A.A.A.; methodology, A.A.A., M.A.O. and Y.A.T.; software, Y.A.T. and M.A.O.; validation, M.A.O. and A.A.A.; formal analysis, Y.A.T. and M.A.O.; investigation, S.A. and A.A.A.; resources, Y.A.T.; data curation, Y.A.T. and M.A.O.; writing—original draft preparation, M.A.O. and Y.A.T.; writing—review and editing, A.A.A. and S.A.; visualization, A.A.A.; supervision, A.A.A.; project administration, S.A.; funding acquisition, Y.A.T. All authors have read and agreed to the published version of the manuscript.
Funding
This research project was supported by the Researchers Supporting Project Number (RSP2022R488), King Saud University, Riyadh, Saudi Arabia.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
Data set 1: The third-party motor insurance data for Sweden for the year 1977 described and analyzed by Hallin and Ingenbleek (1983) in The Swedish automobile portfolio in 1977 [DATA TYPE: the logarithm of the total number which had at least one claim]. The data can be found in www.math.uni.wroc.pl/~dabr/R/motorins.html (1 March 2022). Data set 2: The data set represents an uncensored data set corresponding to remission times (in months) of a random sample of 128 bladder cancer patients reported in Lee and Wang (2003) in Statistical Methods for Survival Data Analysis [DATA TYPE: the remission times (in months)]. The data can be found in http://www.naturalspublishing.com/files/published/j9wsil53h390x8.pdf (1 March 2022). Data set 3: The data are given in Bjerkedal (1960) in Acquisition of resistance in guinea pies infected with different doses of virulent tubercle bacilli [DATA TYPE: the survival times (in days)]. The data can be found in https://rivista-statistica.unibo.it/article/viewFile/6282/6061 (1 March 2022). Data set 4: The data represent the waiting times (in minutes) before service of 100 bank customers as discussed by Ghitany et al. (2008). The data can be found in http://biomedicine.imedpub.com/on-generalized-lindley-distribution-and-its-applications-to-model-lifetime-data-from-biomedical-science-and-engineering.pdf (1 March 2022).
Conflicts of Interest
The authors declare no conflict of interest. The funders had no role in the design of the study; in the collection, analyses, or interpretation of data; in the writing of the manuscript, or in the decision to publish the results.
Appendix A
The code for calculating the 25th percentiles of the Whittaker distribution:
(Code file)
Clear[a1,a2,b1,b2,x,f,g,cf]
a1 = 10.5; a2 = 1.25; b = 3.5; v = 2.5;
f[x_]:= Exp[−v/2]/Gamma[a1] b^a1/v^((a1 + a2)/2 − 1)*(x^(a1 − 1) (v + b*x)^(a2 − 1))/WhittakerW[(a2 − a1)/2,(a1 + a2 − 1)/2,v] Exp[−x*b]
cf[u_]: = Exp[−v/2]/Gamma[a1] b^a1/v^((a1 + a2)/2 − 1)*1/WhittakerW[(a2 − a1)/2,(a1 + a2−1)/2,v] NIntegrate[x^(a1 − 1) (v + b*x)^(a2 − 1) Exp[−x*b],{x,0,u}]
w1 = FindRoot[Exp[−v/2]/Gamma[a1] b^a1/v^((a1 + a2)/2−1)*1/WhittakerW[(a2−a1)/2,(a1 + a2−1)/2,v] NIntegrate[x^(a1 − 1) (v + b*x)^(a2 − 1) Exp[−x*b],{x,0,u}]−0.25,{u,0.12}]
q1 = u//.w1
cf[q1]
{u− > 2.38469}
2.38469
0.25
Appendix B
The computer codes for the maximum likelihood estimation, the Voung test and for the variance covariance matrix of the MLEs under the Whittaker distribution for data set 2:
(Code file)
y = {0.08,0.52,0.22,0.82,0.62,0.39,0.96,0.19,0.66,0.4,0.26,0.31,0.73,3.48,6.97,25.74,2.54,5.32,14.83,1.05,4.26,17.14,4.34,19.13,6.54,3.36,6.94,13.29,2.46,5.17,10.06,0.9,4.23,7.63,1.35,7.93,3.25,12.03,8.65,13.11,2.26,5.09,9.74,32.15,4.18,7.62,46.12,5.62,18.1,6.25,2.02,22.69,0.2,5.06,9.47,26.31,3.88,7.59,16.62,2.83,11.64,4.4,12.02,6.76,2.09,4.98,13.8,0.51,3.82,10.34,36.66,2.75,11.25,3.02,11.98,4.51,2.07,4.87,9.02,0.5,3.7,7.32,34.26,2.69,5.41,79.05,5.71,1.76,8.53,6.93,8.66,0.4,3.64,7.28,14.77,2.69,5.41,17.12,2.87,11.79,4.5,20.28,12.63,23.63,3.57,7.26,14.76,2.64,5.34,10.75,1.26,7.87,1.46,8.37,3.36,5.49,2.23,7.09,14.24,0.81,5.32,10.66,43.01,4.33,17.36,5.85,2.02,12.07};
n = 128;
w1 = FindRoot[{c*Sum[Log[y[[i]]], {i, 1, n}] − (n*((1/2)*Derivative[0, 1, 0][WhittakerW][(a2 − a1)/2, (1/2)*(a1 + a2 − 1), v] −
(1/2)*Derivative[1, 0, 0][WhittakerW][(a2 − a1)/2, (1/2)*(a1 + a2 − 1), v]))/WhittakerW[(a2 − a1)/2, (1/2)*(a1 + a2 − 1), v] − n*PolyGamma[0, a1] + n*Log[b] − (1/2)*n*Log[v], Sum[Log[b*y[[i]]^c + v], {i, 1, n}] − (n*((1/2)*Derivative[0, 1, 0][WhittakerW][(a2 − a1)/2, (1/2)*(a1 + a2 − 1), v] +
(1/2)*Derivative[1, 0, 0][WhittakerW][(a2 − a1)/2, (1/2)*(a1 + a2 − 1), v]))/WhittakerW[(a2 − a1)/2, (1/2)*(a1 + a2 − 1), v] − (1/2)*n*Log[v],
(a2 − 1)*Sum[1/(b*y[[i]]^c + v), {i, 1, n}] − (n*((1/2 − (a2 − a1)/(2*v))*WhittakerW[(a2 − a1)/2, (1/2)*(a1 + a2 − 1), v] − WhittakerW[(a2 − a1)/2 + 1, (1/2)*(a1 + a2 − 1), v]/v))/WhittakerW[(a2 − a1)/2, (1/2)*(a1 + a2 − 1), v] − (n*((a1 + a2)/2 − 1))/v − n/2, (a2 − 1)*Sum[y[[i]]^c/(b*y[[i]]^c + v), {i, 1, n}] − Sum[y[[i]]^c, {i, 1, n}] + (a1*n)/b && a1 > 0 && v > 0 && b > 0}, {{a1, 1.08}, {a2, −4.57}, {b, 0.005}, {v, 0.15}}]
{a1− > 1.09587,a2− > −4.89705,b− > 0.00331532,v− > 0.103035}
Clear[a1, a2, v, b, c]
w = FindRoot[{n*Log[b] − (1/2)*n*Log[v] − n*PolyGamma[0, a1] + c*Sum[Log[y[[i]]], {i, 1, n}] − (n*((1/2)*Derivative[0, 1, 0][WhittakerW][(1/2)*(−a1 + a2), (1/2)*(−1 + a1 + a2), v] − (1/2)*Derivative[1, 0, 0][WhittakerW][(1/2)*(−a1 + a2), (1/2)*(−1 + a1 + a2), v]))/ WhittakerW[(1/2)*(−a1 + a2), (1/2)*(−1 + a1 + a2), v], (−(1/2))*n*Log[v] + Sum[Log[v + b*y[[i]]^c], {i, 1, n}] − (n*((1/2)*Derivative[0, 1, 0][WhittakerW][(1/2)*(−a1 + a2), (1/2)*(−1 + a1 + a2), v] + (1/2)*Derivative[1, 0, 0][WhittakerW][(1/2)*(−a1 + a2), (1/2)*(−1 + a1 + a2), v]))/ WhittakerW[(1/2)*(−a1 + a2), (1/2)*(−1 + a1 + a2), v], −(n/2) − ((−1 + (a1 + a2)/2)*n)/v + (−1 + a2)*Sum[1/(v + b*y[[i]]^c), {i, 1, n}] − (n*((1/2 − (-a1 + a2)/(2*v))*WhittakerW[(1/2)*(−a1 + a2), (1/2)*(−1 + a1 + a2), v] − WhittakerW[1 + (1/2)*(−a1 + a2), (1/2)*(−1 + a1 + a2), v]/v))/ WhittakerW[(1/2)*(−a1 + a2), (1/2)*(−1 + a1 + a2), v], (a1*n)/b − Sum[y[[i]]^c, {i, 1, n}] + (−1 + a2)*Sum[y[[i]]^c/(v + b*y[[i]]^c), {i, 1, n}], n/c + a1*Sum[Log[y[[i]]], {i, 1, n}] − b*Sum[Log[y[[i]]]*y[[i]]^c, {i, 1, n}] + (−1 + a2)*Sum[(b*Log[y[[i]]]*y[[i]]^c)/(v + b*y[[i]]^c), {i, 1, n}] && a1 > 0 && v > 0 && b > 0}, {{a1, 0.98}, {a2, −3.47}, {b, 0.005}, {v, 0.15}, {c, 1.5}}]
{a1− > 0.967908,a2− > −3.52849,b− > 0.00510853,v− > 0.166534,c− > 1.09214}
“Vuong test”
k = 4;
a1 = 1.09587;
a2 = −4.897054;
b = 0.0033153184;
v = 0.103034;
f[x_]:= (Exp[−v/2]/Gamma[a1])*(b^a1/v^((a1 + a2)/2 − 1))*((x^(a1 − 1)*(v + b*x)^(a2 − 1))/WhittakerW[(a2 − a1)/2, (a1 + a2 − 1)/2, v])*Exp[(−x)*b]
“Log-normal”
Clear[u, se]
wln = FindRoot[{−(n/se) − Sum[−((−u + Log[y[[i]]])^2/se^3), {i, 1, n}], −Sum[−((−u + Log[y[[i]]])/se^2), {i, 1, n}]}, {{u, 2.3}, {se, 0.2}}]
se = se //. wln;
u = u //. wln;
fln[x_]:= (1/(x*se*Sqrt[2*Pi]))*Exp[−((Log[x] − u)^2/(2*se^2))];
lln = (−n)*Log[Sqrt[2*Pi]] − Sum[Log[y[[i]]], {i, 1, n}] − n*Log[se] − Sum[(Log[y[[i]]] − u)^2/(2*se^2), {i, 1, n}]
lrln = Sum[Log[f[y[[i]]]/fln[y[[i]]]], {i, 1, n}] − (k − 2);
wnln = (1/n)*Sum[Log[f[y[[i]]]/fln[y[[i]]]]^2, {i, 1, n}] − ((1/n)*Sum[Log[f[y[[i]]]/fln[y[[i]]]], {i, 1, n}])^2;
vln = lrln/Sqrt[n*wnln]
2*(1 − CDF[NormalDistribution[], Abs[vln]])
“Normal”
Clear[sn, un, w1, vnor, lrnor, wnnor, fn, lnor]
w1 = FindRoot[{−(n/sn) + Sum[(−un + y[[i]])^2, {i, 1, n}]/sn^3, −(Sum[−2*(−un + y[[i]]), {i, 1, n}]/(2*sn^2))}, {{un, 1}, {sn, 1}}]
un = un //. w1;
sn = sn //. w1;
fn[x_]:= (1/Sqrt[2*Pi*sn^2])*Exp[−((x − un)^2/(2*sn^2))]
lnor = (−(n/2))*Log[2*Pi] − n*Log[sn] − Sum[(y[[i]] − un)^2, {i, 1, n}]/(2*sn^2)
lrnor = Sum[Log[f[y[[i]]]/fn[y[[i]]]], {i, 1, n}] − (k − 2);
wnnor = (1/n)*Sum[Log[f[y[[i]]]/fn[y[[i]]]]^2, {i, 1, n}] − ((1/n)*Sum[Log[f[y[[i]]]/fn[y[[i]]]], {i, 1, n}])^2;
vnor = lrnor/Sqrt[n*wnnor]
2*(1 − CDF[NormalDistribution[], Abs[vnor]])
“Johnson”
Clear[bj, tj, cj]
vjo = −2.25315;
cj = 1.1633;
tj = −1.37569;
fj[x_]:= (cj/Sqrt[2*Pi])*(1/(x − tj))*Exp[(−2^(−1))*(vjo + cj*Log[x − tj])^2]
lnj = n*Log[cj/Sqrt[2*Pi]] − Sum[Log[y[[i]] − tj], {i, 1, n}] − (1/2)*Sum[(vjo + cj*Log[y[[i]] − tj])^2, {i, 1, n}]
lrj = Sum[Log[f[y[[i]]]/fj[y[[i]]]], {i, 1, n}] − (k − 3);
wnj = (1/n)*Sum[Log[f[y[[i]]]/fj[y[[i]]]]^2, {i, 1, n}] − ((1/n)*Sum[Log[f[y[[i]]]/fj[y[[i]]]], {i, 1, n}])^2;
vj1 = lrj/Sqrt[n*wnj]
2*(1 − CDF[NormalDistribution[], Abs[vj1]])
Vuong test0e
Log-normal
{u− > 1.51087,se− > 1.28189}
−406.802
1.41883
0.155948
Normal
{un− > 8.56875,sn− > 10.5191}
−482.833
4.46717
7.92596 × 10−6
Johnson
−406.447
2.30962
0.0209092
“CI”
a11 = n*((v^((a1 + a2)/2)*Exp[−v/2])/Gamma[a1])*(NIntegrate[Exp[(−v)*t]*t^(a1 − 1)*(1 + t)^(a2 − 1)*Log[t]^2, {t, 0, Infinity}]/WhittakerW[(a2 − a1)/2, (a1 + a2 − 1)/2, v]) − n*(((v^((a1 + a2)/2)*Exp[-v/2])/Gamma[a1])*(NIntegrate[Exp[(−v)*t]*t^(a1 − 1)*(1 + t)^(a2 − 1)*Log[t], {t, 0, Infinity}]/WhittakerW[(a2 − a1)/2, (a1 + a2 − 1)/2, v]))^2;
a12 = n*((v^((a1 + a2)/2)*Exp[−v/2])/Gamma[a1])*(NIntegrate[Exp[(−v)*t]*t^(a1 − 1)*(1 + t)^(a2 − 1)*Log[t]*Log[1 + t], {t, 0, Infinity}]/WhittakerW[(a2 − a1)/2, (a1 + a2 − 1)/2, v]) − n*((v^((a1 + a2)/2)/Gamma[a1])*(Exp[−v/2]/WhittakerW[(a2 − a1)/2, (a1 + a2 − 1)/2, v]))^2*NIntegrate[Exp[(-v)*t]*t^(a1 − 1)*(1 + t)^(a2 − 1)*Log[t], {t, 0, Infinity}]* NIntegrate[Exp[(−v)*t]*t^(a1 − 1)*(1 + t)^(a2 − 1)*Log[1 + t], {t, 0, Infinity}];
a13 = −(−(n/v) − n*(a2 − v)*((v^((a1 + a2)/2 − 1)*Exp[−v/2])/Gamma[a1])*(NIntegrate[Exp[(−v)*t]*t^(a1 − 1)*(1 + t)^(a2 − 1)*Log[t], {t, 0, Infinity}]/
WhittakerW[(a2 − a1)/2, (a1 + a2 − 1)/2, v]) + n*((v^((a1 + a2)/2)*Exp[-v/2])/Gamma[a1])*(NIntegrate[Exp[(−v)*t]*t^a1*(1 + t)^(a2 − 1)*Log[t], {t, 0, Infinity}]/ WhittakerW[(a2 − a1)/2, (a1 + a2 − 1)/2, v]) − n*((v^((a1 + a2)/2 − 1)*Exp[-v/2])/Gamma[a1])*WhittakerW[(a2 − a1)/2 + 1, (a1 + a2 − 1)/2, v]*
(NIntegrate[Exp[(−v)*t]*t^(a1 − 1)*(1 + t)^(a2 − 1)*Log[t], {t, 0, Infinity}]/WhittakerW[(a2 − a1)/2, (a1 + a2 − 1)/2, v]^2));
a14 = −(n/b);
a22 = n*((v^((a1 + a2)/2)*Exp[-v/2])/Gamma[a1])*(NIntegrate[Exp[(−v)*t]*t^(a1 − 1)*(1 + t)^(a2 − 1)*Log[1 + t]^2, {t, 0, Infinity}]/WhittakerW[(a2 − a1)/2, (a1 + a2 − 1)/2, v]) − n*(((v^((a1 + a2)/2)*Exp[−v/2])/Gamma[a1])*(NIntegrate[Exp[(−v)*t]*t^(a1 − 1)*(1 + t)^(a2 − 1)*Log[1 + t], {t, 0, Infinity}]/WhittakerW[(a2 − a1)/2, (a1 + a2 − 1)/2, v]))^2;
a23 = −(−(n/v) + Sum[1/(v + b*y[[i]]), {i, 1, n}] + n*((v^((a1 + a2)/2)*Exp[-v/2])/Gamma[a1])*(NIntegrate[Exp[(-v)*t]*t^a1*(1 + t)^(a2 − 1)*Log[1 + t], {t, 0, Infinity}]/WhittakerW[(a2 − a1)/2, (a1 + a2 − 1)/2, v]) + n*(1 − a2/v)*((v^((a1 + a2)/2)*Exp[-v/2])/Gamma[a1])*(NIntegrate[Exp[(-v)*t]*t^(a1 − 1)*(1 + t)^(a2 − 1)*Log[1 + t], {t, 0, Infinity}]/WhittakerW[(a2 − a1)/2, (a1 + a2 − 1)/2, v]) − (n/v)*((v^((a1 + a2)/2)*Exp[-v/2])/Gamma[a1])*WhittakerW[(a2 − a1)/2 + 1, (a1 + a2 − 1)/2, v]* (NIntegrate[Exp[(-v)*t]*t^(a1 − 1)*(1 + t)^(a2 − 1)*Log[1 + t], {t, 0, Infinity}]/WhittakerW[(a2 − a1)/2, (a1 + a2 − 1)/2, v]^2));
a24 = −(n/b − Sum[v/((v + b*y[[i]])*b), {i, 1, n}]);
a33 = −((n/v^2)*(a1 − 1) + (n/v^2)*(v/2 − (a2 − a1)/2 − 2)*(WhittakerW[(a2 − a1)/2 + 1, (a1 + a2 − 1)/2, v]/WhittakerW[(a2 − a1)/2, (a1 + a2 − 1)/2, v]) −
(n/v^2)*(WhittakerW[(a2 − a1)/2 + 2, (a1 + a2 − 1)/2, v]/WhittakerW[(a2 − a1)/2, (a1 + a2 − 1)/2, v]) − (a2 − 1)*Sum[1/(v + b*y[[i]])^2, {i, 1, n}]);
a34 = (a2 − 1)*Sum[y[[i]]/(v + b*y[[i]])^2, {i, 1, n}];
a44 = −(−((n*(a1 + a2 − 1))/b^2) + (−1 + a2)*Sum[(y[[i]]*v)/(b*(v + b*y[[i]])^2), {i, 1, n}] + (−1 + a2)*Sum[v/(b^2*(v + b*y[[i]])), {i, 1, n}]);
beta = {{a11, a12, a13, a14}, {a12, a22, a23, a24}, {a13, a23, a33, a34}, {a14, a24, a34, a44}};
inbeta = Inverse[beta];
MatrixForm[inbeta]
CI
(_{{0.0237651, 0.139018, −2.65017 × 10−6, 0.00020543},
{0.139018, 5.96683, −0.0000375354, 0.00511258},
{−2.65017 × 10−6, −0.0000375354, 8.32295 × 10−6, 2.16077 × 10−7},
{0.00020543, 0.00511258, 2.16077 × 10−7, 4.85993 × 10−6}}_)
“a1”
Sqrt[inbeta[[1,1]]]
“p-value”
2*(1 − CDF[NormalDistribution[], a1/Sqrt[inbeta[[1,1]]]])
a1 + 1.96*Sqrt[inbeta[[1,1]]]
a1 − 1.96*Sqrt[inbeta[[1,1]]]
“a2”
Sqrt[inbeta[[2,2]]]
“p-value”
2*(1 − CDF[NormalDistribution[], Abs[a2/Sqrt[inbeta[[2,2]]]]])
a2 + 1.96*Sqrt[inbeta[[2,2]]]
a2 − 1.96*Sqrt[inbeta[[2,2]]]
“v”
Sqrt[inbeta[[3,3]]]
“p-value”
2*(1 − CDF[NormalDistribution[], v/Sqrt[inbeta[[3,3]]]])
v + 1.96*Sqrt[inbeta[[3,3]]]
v − 1.96*Sqrt[inbeta[[3,3]]]
“b”
Sqrt[inbeta[[4,4]]]
“p-value”
2*(1 − CDF[NormalDistribution[], b/Sqrt[inbeta[[4,4]]]])
b + 1.96*Sqrt[inbeta[[4,4]]]
b − 1.96*Sqrt[inbeta[[4,4]]]
a1
0.154159
p-value
1.16995 × 10−12
1.39805
0.793748
a2
2.44271
p-value
0.0449863
−0.10939
−9.68481
v
0.00288495
p-value
0.
0.108655
0.0973455
b
0.00220453
p-value
0.134414
0.00762087
−0.00102087
References
- Abramowitz, M.; Stegun, I.A. Handbook of Mathematical Functions with Formulas, Graphs, and Mathematical Tables; 9th Printing; Dover: New York, NY, USA, 1972. [Google Scholar]
- Gradshteyn, I.S.; Ryzhik, I.M. Table of Integrals, Series, and Products, 7th ed.; Elsevier: Burlington, MA, USA, 2007. [Google Scholar]
- Bateman, H. Tables of Integral Transforms [Volumes I & II]; McGraw-Hill Book Company: New York, NY, USA, 1954; Volume 1. [Google Scholar]
- McKay, A.T. A Bessel function distribution. Biometrika 1932, 1, 39–44. [Google Scholar] [CrossRef]
- Laha, R.G. On some properties of the Bessel function distributions. Bull. Calcutta. Math. Soc. 1954, 46, 59–72. [Google Scholar]
- Malik, H.J. Exact distribution of the product of independent generalized gamma variables with the same shape parameter. Ann. Math. Stat. 1968, 39, 1751–1752. [Google Scholar] [CrossRef]
- Pitman, J.; Yor, M.A. decomposition of Bessel bridges. Z. Wahrscheinlichkeit. 1982, 59, 425–457. [Google Scholar] [CrossRef]
- McDonald, J.B. Some generalized functions for the size distribution of income. In Modeling Income Distributions and Lorenz Curves; Springer: New York, NY, USA, 2008; pp. 37–55. [Google Scholar]
- Gordy, M.B. Computationally convenient distributional assumptions for common-value auctions. Comput. Econ. 1998, 12, 61–78. [Google Scholar] [CrossRef]
- Gupta, A.K.; Nagar, D.K. Matrix Variate Distributions; Chapman & Hall/CRC: Washington, DC, USA, 2000. [Google Scholar]
- McNeil, A.J. The Laplace Distribution and generalizations: A revisit with applications to communications, economics, engineering, and finance. J. Am. Stat. Assoc. 2002, 97, 1210–1211. [Google Scholar] [CrossRef]
- Nagar, D.Y.; Zarrazola, E. Distributions of the product and the quotient of independent Kummer-beta variables. Sci. Math. Jpn. 2005, 61, 109–118. [Google Scholar]
- Sánchez, L.E.; Nagar, D.K. Distributions of the product and the quotient of independent beta type 3 variables. Far. East. J. Theor. Stat. 2005, 17, 239. [Google Scholar]
- Küchler, U.; Tappe, S. Bilateral gamma distributions and processes in financial mathematics. Stoch. Process. Appl. 2008, 118, 261–283. [Google Scholar] [CrossRef] [Green Version]
- Zarrazola, E.; Nagar, D.K. Product of independent random variables involving inverted hypergeometric function type I variables. Ing. Cienc. 2009, 5, 93–106. [Google Scholar]
- Nagar, D.K.; Morán-Vásquez, R.A.; Gupta, A.K. Properties and applications of extended hypergeometric functions. Ing. Cienc. 2014, 10, 11–31. [Google Scholar] [CrossRef] [Green Version]
- Gaunt, R.E. Products of normal, beta and gamma random variables: Stein operators and distributional theory. Braz. J. Probab. Stat. 2018, 32, 437–466. [Google Scholar] [CrossRef] [Green Version]
- Shakil, M.; Singh, J.N.; Kibria, B.G. On a family of product distributions based on the Whittaker functions and generalized Pearson differential equation. Pak. J. Statist. 2010, 26, 111–125. [Google Scholar]
- Shakil, M.; Kibria, B.G.; Singh, J.N. A new family of distributions based on the generalized Pearson differential equation with some applications. Austrian J. Stat. 2010, 39, 259–278. [Google Scholar] [CrossRef]
- Zakerzadeh, H.; Dolati, A. Generalized Lindley distribution. J. Math. Ext. 2009, 3, 13–25. [Google Scholar]
- Lindley, D.V. Fiducial distributions and Bayes’ theorem. J. R Stat. Soc. Ser. B Stat. Methodol. 1958, 1, 102–107. [Google Scholar] [CrossRef]
- Johnson, N.L.; Kotz, S.; Balakrishnan, N. Continuous Univariate Distributions, 2nd ed.; Wiley: Hoboken, NJ, USA, 1995; Volume 2, ISBN 0-471-58494-0. [Google Scholar]
- Lomax, K.S. Business failures: Another example of the analysis of failure data. J. Am. Stat. Assoc. 1954, 49, 847–852. [Google Scholar] [CrossRef]
- Arnold, B.C. Pareto Distributions; International Co-operative Publishing House: Fairlan, MD, USA, 1983. [Google Scholar]
- Stacy, E.W. A generalization of the gamma distribution. Ann. Math. Stat. 1962, 33, 1187–1192. [Google Scholar] [CrossRef]
- Nakagami, M. The m-Distribution—A General Formula of Intensity Distribution of Rapid Fading. Stat. Methods Radio Wave Propag. 1960, 1, 3–36. [Google Scholar]
- Beckmann, P. Rayleigh distribution and its generalizations. Radio Sci. J. Res. NBS/USNC-URSIs 1962, 68d, 927–932. [Google Scholar] [CrossRef]
- Dagum, C. A model of income distribution and the conditions of existence of moments of finite order. Bull. Int. Stat. Inst. 1975, 46, 199–205. [Google Scholar]
- Lévy, P. Calcul des probabilités. Rev. Metaphys. Morale 1926, 33, 3–6. [Google Scholar]
- Gumbel, E.J. Statistics of Extremes; Columbia University Press: New York, NY, USA, 1958. [Google Scholar]
- Treyer, V.N. Doklady Acad. Nauk, Belorus, U.S.S.R., 1964.
- Hallin, M.; Ingenbleek, J.F. The swedish automobile portfolio in 1977: A statistical study. Scand. Actuar. J. 1983, 1, 49–64. [Google Scholar] [CrossRef]
- Lee, E.T.; Wang, J.W. Statistical Methods for Survival Data Analysis, 3rd ed.; Wiley: Hoboken, NJ, USA, 2003. [Google Scholar]
- Bjerkedal, T. Acquisition of Resistance in Guinea Pies infected with Different Doses of Virulent Tubercle Bacilli. Am. J. Hyg. 1960, 72, 130–148. [Google Scholar] [PubMed]
- Ghitany, M.E.; Al-Mutairi, D.K.; Nadarajah, S. Zero-truncated Poisson–Lindley distribution and its application. Math. Comput. Simul. 2008, 79, 279–287. [Google Scholar] [CrossRef]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).