Varieties of Selective Influence: Toward a More Complete Taxonomy and Implications for Systems Identification

Abstract

All science, including psychological science, is subject to what Townsend and Ashby have called the principle of correspondent change which ensures that experimental manipulations act as informed agents with respect to predictions and testing critical theoretical features. Mostly, this type of program goes unspoken. Within the general field known as the information processing approach, S. Sternberg invented the additive factors method in which the aforesaid feature plays a major and explicit role. We call this approach a theory driven methodology because the scientist formulates a set of theories or models and then formulates experimental variables that will permit strong tests among the hypothetical alternatives. Our term for the general approach is systems factorial technology. Often, these tests can be accomplished with qualitative, non-parametric, distribution free methods, but our so-called sieve method advocates, once the initial qualitative steps are accomplished, a move to assessing more detail parametric versions of the model classes. Over the decades, the meta-theory underpinning SFT and like approaches has evidenced dramatic growth in both expanse and depth. Particularly, the critical assumption of selective influence, testable to some extent, has received extensive and sophisticated treatment. The various central allied concepts are interlinked but do not form a simple linearly-ordered chain. This study carries on exploration of the central concepts and relationships and their implications for psychological research.

1. Introduction

An essential aspect of mathematical models in psychology is that the structure and parameters of the quantitative ingredients be related to specific aspects of nature, that is, measurable features of stimuli and physiological or behavioral responses. Anything short of that smacks of triviality, metaphor or, at best, curve fitting. Although almost always unspoken, almost all hypothesis testing proceeds by attempts to provoke expected reactions via the effects of experimental manipulations on suspected structures and mechanisms. We have characterized this vital element as the principle of correspondent change [1].

In the early heydays following the birth of the information processing approach, one very popular direction hypothesized that a larger processing workload, such as presenting a longer list of n items for search in short-term memory, would produce a linear increasing mean response time (hereafter RT) function of the load size n if the system was acting as a serial processor [2]. Scores of experiments were run on this basis, although it was soon pointed out that these tests were weak in the sense that reasonable models from the other class were mathematically equivalent to the serial models, and vice versa [3,4,5]. Despite the demonstrated frailty of this argument, identical experimental designs, with the exception that the probe was presented before the longer list which appeared in a visual display, began to recur in vision science within two decades of the original S. Sternberg designs in short term memory (e.g., [6]). An early warning of pitfalls of that approach in a visual context had been already voiced in Atkinson, Holmgren and Juola [7]. However, once again, this track of faulted reasoning led to a plethora of conclusions of questionable validity (see also the discussion in [8,9,10]).

A much more redoubtable use of the principle of correspondent change was proffered, also by S. Sternberg, termed the additive factors method in the late 1960s [11]. This version of the principle stipulated that if individual factors only influenced separate psychological processes arranged in a series that did not overlap in their processing times, then the mean RTs must be additive functions of the experimental factors. It stands as a ground-breaking exemplar of the principle of correspondent change, alluded to above. Sternberg’s conceptualization of selective influence operates at what we may refer to as a qualitative level. That is, specific parameterized models are avoided. However, parameterized models may and, in modern days, usually are also subjected to and tested principles of selective influence. For instance, models of signal detection assume that bias parameters should be influenced by experimental variables such as reward structures and frequency of stimulus presentations, whereas parameters reflecting sensitivity should only be affected by variables such as stimulus intensity, their similarity and so on. This concept has been generalized and studied by R. Thomas [12]. A number of popular parameterized stochastic models capable of predicting both accuracy and response times have been subjected to tests of selective influence in an important study by Dutilh et al. [13].

The notion of selective influence is perhaps the deepest and most critical aspect of the later theory-driven methodology referred to as systems factorial technology, or simply SFT [14]. SFT adheres to the qualitative approach first espoused explicitly by S. Sternberg [15] as mentioned above. By now, SFT has been applied to almost all major disciplines of psychology and cognitive science. Introductions are now widely available, for instance, in Townsend, Houpt and Wenger [16], Algom et al. [8] and Harding, B., Goulet, M.A., Jolin, S., Tremblay, C., Villeneuve, S.-P. and Durand, G. [17]. Up to date applications and surveys can be found in Little et al. [18] and Houpt, Little and Eidels [19].

Two principal targets of selective influence manipulations are mental architecture and decisional stopping rule. It has turned out that the notion of selective influence as seen in psychology has deep connections to important concepts in other regions of science and mathematics, including physics, for example, quantum theory (e.g., [20]). Many of these versions do not require that the random entities be positive real numbers. For that reason, although we use language and notation suggestive of time, we will not always require that the observables be positive numbers. Another valuable dimension is how alterations in required effort affect efficiency of performance, usually as indexed by response times (RT) or accuracy and reflected in the workload capacity index [21] or the assessment function [22]. This latter dimension will not be under consideration in this study.

As noted above, Sternberg’s original primary objective was that of serial systems, wherein one and only one process could take place at a time [15]. Each constituent process, say the ith., starts immediately after process $i-1$ completes, continues without interruption until it is finished and then process $i+1$ begins instantaneously. Of course, some of these axioms can be relaxed. For example, in some circumstances, lag between successive processes might be present without harm to the major predictions but the foregoing assumptions are now standard [8,16].

The notion, selective influence, seems eminently straightforward. However, it turns out to be a much more subtle and fascinating concept that has continuously evolved over the years. In fact, we think it now makes sense to offer a menu of several types of selective influence. In addition, some might be more observable than others in any given observational context. This philosophy will help guide us in the present enterprise.

The typical approach to utilization of selective influence has been to define if and how an external factor, usually experimental, might alter some dependent variable associated with a psychological process. That observable variable has historically usually been RT. We shall therefore concentrate on RT and, in particular, the way individual processes are affected by such factors. However, then we are immediately faced with the question of, assuming stochasticity of the processes, what aspect of the probability distribution is so affected? Initially, S. Sternberg [15] assumed that the means (expectations) of processing times were manipulated through the factors with each subprocess being uniquely affected by a single factor. This was sufficient to falsify or support the inference of serial processing. Sternberg assumed that an external factor A could slow down or speed up a process in such a way that the means would be affected in a detectable way. This operation could then be employed to affirm or deny serial processing. A huge number of studies were carried out applying the additive factors method (for limited reviews, see [1,8,23]).

Schweickert [24] subsequently applied the notion of selective influence to mean RTs of complex systems based on forward-flow graphs known in the engineering literature as PERT networks (literally, program evaluation and review technique). These were mostly deterministic systems, but there were extensions that included stochastic inequalities [25]. Egeth and Dagenbach [26] put the mean RT predictions for serial and parallel systems to effective use.

A stronger but also theoretically more powerful assumption is to simply assume that if two values of a factor, called A, are different, then the cumulative distribution functions (hereby designated by capital $F\left(t\right)$) are also different in some sufficiently potent way. In fact, it was discovered around the same time in the 1980s that factorial influence could occur at the distributional level in the sense that if $A_H>A_L$ where $H=high$ and $L=low$, then $F_A(t;A_H)>F_A(t;A_L)$, that is, the $F\left(t\right)$s would also be ordered [23,27,28]. However, then it transpired that other systems and their stopping rule could be distinguished also at the level of mean RTs but now including not only parallel systems but PERT networks more generally [23,29,30].

It was not observed until the late 1980s and 1990s that the same facets that could be employed to make predictions at the mean RT level actually propelled results at a much more formidable echelon. Thus, an assumption on the distributional orderings, given just above, led to predictions on the RT probability distributions themselves [14,31]. These findings provided tests of architectures and stopping rules that were in several important cases, invisible in mean RTs alone.

The influence of factors on a distribution function is certainly key, but in the great preponderance of experiments meant to identify architecture, the experimenter cannot espy the underlying joint distributions on the multiple processes directly (but see [32,33] for experimental designs that can). Thus, what is visible in data usually is an RT distribution on an architecture with a decision rule that yields overall completion time (plus a random variable, usually stochastically independent of the other sequentially arranged subprocesses, representing a sum of early sensory and later motor intervals) as a function of the underlying, individual processing times. We shall later visit those statistics in the required detail.

The raison d’être, at least originally, that motivated the development of the concept of selective influence was to identify mental architecture and stopping rule. Our treatment and implied taxonomy here envision a taxonomy that differs somewhat from the field’s previous way of thinking about selective influence, including our own. The prior philosophy, whether conscious or not, seems to have focused pretty much on finding “the best” definition of selective influence. While Sternberg noted that stochastic independence along with manipulation of mean RTs could assess serial processing, he mentioned that, in some cases, distributions might be mutually dependent. Examples, though not really suited for processing times, are joint Gaussian distributions with non-zero covariance. There, the means might be affected by experimental factors, but not the covariances, therefore rendering nice observable predictions as long as the covariances are not influenced by the experimental factors. We shall have cause to explore multivariate Gaussian distributions a bit further in our discourse.

Our survey of current and past theoretical studies and surveys, in conjunction with the present venture, convince us that there are several meaningful definitions of, perhaps, types of selective influence. Each variety might have its own strengths and weaknesses and serve somewhat distinct purposes. We will see how this plays out. As theoretical efforts on selective influence have blossomed into regions rather remote from response times, this proposition becomes more and more tenable (see, e.g., [32,33]).

The purview of systems considered herein will be circumscribed in certain respects to lay bare the essence in readily communicable fashion, with the expectation of subsequent expansion. This has proven to be a useful tactic in previous research such as the assumption of stochastic independence with an arbitrary number of subsystems, channels, etc. (e.g., [34]).

Suppose then that there are two processes with names ${\mathbb{S}}_a$ and ${\mathbb{S}}_b$. We note that these $\mathbb{S}$’s are distinct from the later symbols we will use for the survivor functions, the plain “S”. In addition, within the current investigation, we assume that the systems will not terminate until the completion of both processes. That is, the systems employ an exhaustive stopping rule.

The names for processes ${\mathbb{S}}_a$ and ${\mathbb{S}}_b$ will not distinguish their architecture. We will assume that readers are familiar with the basic concepts of serial and parallel processing so that we need not use distinct notation for a serial processing time vs. a parallel processing duration (for a more formal tutorial on these concepts, please see Chapters 2, 3 of [1] or, more recently, [8]; those seeking an axiomatic treatment of fundamental concepts, which evinces the foundational principals at the level of measure theory, are referred to [35]).

$T_a$ and $T_b$ will be employed to exhibit processing time random variables for the corresponding processes, regardless of whether they are in serial or parallel conformation. To render this important distinction, “$f\left(t\right)$” and “$F\left(t\right)$” will denote the density and cumulative distribution functions for serial architectures, whereas “$g\left(t\right)$” and “$G\left(t\right)$” will denote those for parallel architectures. When needed, $P_{PAR}(T_a\le t_a\cap T_b\le t_b)=P(T_a\le t_a,T_b\le t_b)$ can be used to indicate the joint distribution for a 2-channel parallel system and also $P_{SER}(T_a\le t_a\cap T_b\le t_b)=P(T_a\le t_a,T_b\le t_b)$ for a serial system. Note that these look the same but are not, since in the parallel case, the “t”s refer to processing that is ongoing simultaneously, but in the serial case, they refer to sequential and non-overlapping times.

Moreover, if a system is serial, we further assume that ${\mathbb{S}}_a$ always goes first. That is, its operation always precedes that of ${\mathbb{S}}_b$. This assumption, that of a single processing order, specifies a special case of the more general situation where ${\mathbb{S}}_a$ precedes ${\mathbb{S}}_b$ with probability p, but ${\mathbb{S}}_b$ precedes ${\mathbb{S}}_a$ with probability $1-p$. In general, it may be that $p\ne 1$ or 0 (see [1], Definition 4.1, p. 50). Yet, in the current investigation, we introduce the key serial concepts confined to single order systems. That is, in formal language, $p=1$. We shall call this notion “1-Directionality”. In fact, this class of two-stage serial systems will serve to erect the foundational scaffolding that generates several of our theoretical inferences.

We shall also almost always focus our attention on systems with only two processors, $n=2$, and, without exception, assume that all our stochastic processes possess continuous densities defined on the positive real line, usually including the origin, 0, so $T\ge 0$. The exception will be a few examples where the random variable’s support is the entire real line. These postulates will avert a lot of pedantic notation. We shall hereafter assume that experimental factors, A and B, are effective in the sense that the probability distributions for the random variables $T_a$ and $T_b$ are actually changed with any change in A, B, respectively, in the sense that, for example, on some measurable interval of time, $f(t_a;A_1)\ne f(t_a;A_2)$, and the same goes for the parallel densities. More consequential assumptions about how experimental factors affect our distributions will be made forthwith. Finally, in conditional probability elements, for example, in $f_b(t_b;B,A|t_a)$, to be visited below, it will always be assumed that this term is a non-trivial function of $t_a$.

2. Definitions of Primary Concepts and Taxonomy

2.1. Selective Influence

We express canonical notions of serial vs. parallel processing in slightly different ways to emphasize the “forward motion” in seriality as opposed to simultaneity in parallelism. Of course, no harm could come from writing the terms in mathematically equivalent forms. Let the experimental factor that the researcher hopes will affect system ${\mathbb{S}}_a$ be designated A and that for system ${\mathbb{S}}_b$ be B.

Definition 1.

Canonical Serial Expressions for 1-Direction Systems. We say that the formula for the joint probability density function in a 1-direction serial system is in canonical form if it is written as:

$$\begin{array}{cc}\hfill & P(T_a=t_a,T_b=t_b;A,B)\hfill \\ \hfill =& f_{a,b}(t_a,t_b;A,B)\hfill \\ \hfill =& f_a(t_a;A,B)f_b(t_b;B,A|t_a),t_a,t_b\ge 0.\hfill \end{array}$$

Rigorous measurement axioms are given in Houpt et al. [35] to ensure there is no measure that allows overlap in the serial processing durations.

Definition 2.

Canonical Parallel Expressions. We say that the formula for the joint probability density function in a parallel system is in canonical form if it is written as:

$$P(T_a=t_a,T_b=t_b;A,B)=g_{a,b}(t_a,t_b;A,B),t_a,t_b\ge 0.$$

Deeper postulates that ensure $T_a$ and $T_b$ possess non-zero probability of occurrence, until one finishes, over a shared time interval are given in Houpt et al. [35].

This notation is explicitly compatible with that of Townsend and Ashby [1] and Townsend [23]. Observe that, so far, $f_a$ might be a direct function of both factors A and B and similarly for $f_b$. Our treatment of the concept of selective influence continues the evolution of our thinking as expressed in Townsend, Y. Liu and R. Zhang [36]. We start our forward march by putting down the Sternbergian definition of selective influence [15].

Definition 3.

The Sternbergian Definition of Selective Influence.

Consider two processes ${\mathbb{S}}_a$ and ${\mathbb{S}}_b$ with processing time random variables $T_a$ and $T_b$. Sternbergian selective influence holds if and only if there exist two experimental variables, A and B, such that the mean of $T_a$ is affected only by A and the mean of $T_b$ is affected only by B.

It has long been tacitly acknowledged that the most quintessential form of selective influence occurs in the context of stochastic independence of the separate subprocesses. Our current thinking emphasizes that there may exist a spectrum of types of selective influence and therefore that selective influence cum independence should occupy a special place in this taxonomy.

Definition 4.

Pure Selective Influence

Pure selective influence is in force in the serial 1-direction systems if we can write

$$f_{a,b}(t_a,t_b,A,B)=f_a(t_a;A,)f_b(t_b;B)$$

That is, the joint probability density function for $T_a$ and $T_b$ is independent in these variables and each term is a function of its respective factor.

Pure selective influence is in force in the parallel systems if we can write

$$g_{a,b}(t_a,t_b;A,B)=g_a(t_a;A)g_b(t_b;B).$$

That is, the joint density function for $T_a$ and $T_b$ is independent in these variables and each is a function only of its respective factor.

2.2. Nonselective Influence

We now move to present the major types of nonselective influence. efinition

Definition 5.

Direct and Indirect Nonselective Influence.

In the 1-direction serial systems,

(1). If both direct and indirect nonselective influence are in force, the joint probability density function will be expressed in canonical form as

$$f_{a,b}(t_a,t_b;A,B)=f_a(t_a;A,B)f_b(t_b;B,A|t_a).$$

(2). If only direct nonselective influence is afoot in process ${\mathbb{S}}_a$, then we have $fa(t_a;A,B)$ for that stage. That is, $f_a(t_a;A,B)$ is a function of the “other” factor B. If only direct nonselectivity in ${\mathbb{S}}_b$, we have

$$f_b(t_b;B,A|t_a)=f_b(t_b;B,A).$$

That is, $f_b(t_b;B,A|t_a)$ is a function of the factor but is stochastically independent of processing-time variable of the other process ${\mathbb{S}}_a$.

(3). If only indirect nonselective influence occurs in a 1-direction serial system, it can only happen in stage ${\mathbb{S}}_b$ to yield $f_b(t_b;B|t_a)$ by definition.

In the parallel systems,(1). If both direct and indirect nonselective influence are in force, we have

$$g_{a,b}(t_a,t_b;A,B)=g_a(t_a;A,B)g_b(t_b;B,A|t_a)=g_b(t_b;B,A)g_a(t_a;A,B|t_b).$$

Unlike in serial systems, similar remarks occur for the opposite order.

(2). If only direct nonselective influence is afoot in process ${\mathbb{S}}_a$, then we have $g_a(t_a;A,B)$ as a function of B with no dependencies on $t_b$. If only direct nonselective influence is afoot in process ${\mathbb{S}}_b$, then $g_b(t_b;B,A)$ is a function of A with no dependencies on $t_a$.

(3). If only indirect nonselective influence is present in Channel ${\mathbb{S}}_a$, then we can write

$$g_a(t_a;A,B|t_b)=g_a(t_a;A|t_b)$$

which is a function of $t_b$ but not B, and similarly for Channel ${\mathbb{S}}_b$.

The reader may have noticed that due to our empirical distinction between seriality and parallelism, when only one order is possible in the former, we always write $f_a(t_a;A,B)f_b(t_b;B,A|t_a)$ rather than $f_a(t_a;A,B|t_b)f_b(t_b;B,A)$. This is a convention and has no impact on further developments.

Earlier work established how stochastic dependence of $T_b$ on $T_a$ (that is, indirect nonselective influence) could perpetrate a visible failure of selective influence in the sense that mean response times would be seriously affected. Thus, Townsend and R. Thomas [37] showed how such indirect influences could devastate the expected response time signatures of serial vs. parallel processing through failure of selective influence. In fact, the latter investigation demonstrated that, at the mean processing time level, one could obtain over-additivity or under-additivity by either negative or positive interactions and in either parallel or serial systems. Even if it turned out that a failure of indirect selective influence somehow failed to affect architecture identification, we now take the position that someday and in some experimental designs, perhaps with the aid of neuroscientific procedures, it may be possible to detect such probabilistic perturbations (i.e., $T_b$ is influenced by the current-trial value of $T_a$).

Dzhafarov [38] has chosen to use the term conditional selectivity for what we have always labeled indirect nonselective influence. He also proves a number of theorems on that topic including conditions for its satisfaction. As far as names go of course, neither is either right or wrong. Logically, any restriction on the influences of the factors could be styled either as a type of selectivity or, in contrast, as a version of nonselectivity, as long as pure selective influence is not obeyed in our lexicon. We prefer to adhere to our original terminology while noting the chimerical essence of the concept. It is important to not conflate this concept with his much later new definition of selective influence, though both include the term “conditional”. We introduce the latter momentarily.

At this juncture, we call up the definition of selective influence proffered by Dzhafarov [39]. To date, this definition is the most potent in terms of still perpetrating useful consequences, such as identification of architecture and stopping rule in a number of valuable architectures, while affording a type of stochastic dependence. It is particularly germane in the present context because it implies, but is not implied by, a primary target of our investigation—a type of marginal selective influence which will be dealt with in detail in what follows.

Definition 6

([39]). The Conditional Independence Definition of Selective Influence. In serial systems, two factors selectively influence ${\mathbb{S}}_a$ and ${\mathbb{S}}_b$ if and only if the joint density of the two associated times can be expressed as $P(T_a=t_a,T_b=t_b;A,B,C=c)=f_a(t_a;A|c)f_b(t_b;B|c)f_c\left(c\right)$, where C is a random variable stochastically independent of $T_a$ and $T_b$ and functionally independent of A, B.

In parallel systems, two factors selectively influence ${\mathbb{S}}_a$ and ${\mathbb{S}}_b$ if and only if the joint density of the two associated times can be expressed as $P(T_a=t_a,T_b=t_b;A,B,C=c)=g_a(t_a;A|c)g_b(t_b;B|c)g_c\left(c\right)$, where C is a random variable stochastically independent of $T_a$ and $T_b$ and functionally independent of A, B.

This definition clearly generalizes the demands of pure selective influence to include a certain type of dependence. Observe the distinction between this concept and his earlier term “conditionally selective influence” which is our “indirect nonselective influence”. The earlier one requires statement of any type of stochastic dependence between the random variables of the processes, while the later one only allows the dependence between the processes through a third source. There exists other, but mathematically equivalent, ways of defining the concept (e.g., [33]). We view this one as the most pellucid and intuitive. The notion of conditional independence is one found in many areas of applied statistics including psychometrics in general and test theory in particular as well as in machine learning (look for the so called naive Bayesian approach), economics and physics. Dzhafarov and colleagues (e.g., [33,39]) have established conditions that can test for selective influence (see definition in [39]). However, these methods typically assume that the joint distributions of the random variables are observable. Given the quintessential importance of selective influence in identification of psychological mechanisms, those results are quite fundamental. Yet, in many psychological milieus, as intimated earlier, the joint distributions are not observable, and this has been the situation in most, if not all, cases where the uncovering of mental architectures is the goal through the employment of response times (e.g., as in [11,14,19,23,24,29,30,37,40]).

A simple example propaedeutic to Dzhafarov’s definition offers some intuition. In fact, Townsend and Ashby ([1], Chapter 11, pp. 368–370) considered a special case of that concept, where we conceived of the random variable C as denoting capacity. This capacity was distributed between ${\mathbb{S}}_a$ and ${\mathbb{S}}_b$ in a serial system where A and B directly affected their appropriate processes and, just as in Dzhafarov’s definition ([39]), $f_a$ and $f_b$ were, given $C=c$, conditionally independent. It was demonstrated that the canonical prediction on the mean interaction contrasts ($MIC$) for serial systems with direct selective influence was fulfilled, namely $MIC=0$ (see Propositions 8 and 9). Dzhafarov and colleagues subsequently proved their more general results and made conditional independence a cornerstone of their approach to factor selectivity.

We next move on to one of the key concepts in the present discourse as alluded to above. It is called marginal selective influence, or marginal selectivity for short. It is implied by some other types of selective influence, most pointedly, the aforementioned Dzhafarov definition, and in some circumstances may allay certain avenues of nonselective influence in discriminating mental architectures. It seems to have made its first formal appearance in Townsend and Schweickert ([29]; also see [30]). It turns out to be an intriguing condition.

Its presence or absence may bear consequences for systems identification. In addition, though, it might be useful in its own right. For instance, when a person is asked to make two responses on experimental trials, the marginal selectivity would perforce be immediately available for inspection and offer critical information concerning the underlying processing mechanisms. A recent example of a new design in systems factorial technology which employs two responses is Howard, Garrett, Little, Townsend and Eidels [41].

Definition 7.

Marginal Selective Influence.

In 1-direction serial systems where ${\mathbb{S}}_a$ always occur before ${\mathbb{S}}_b$, marginal selectivity is said to hold if and only if(1)$f_a(t_a;A,B)=f_a(t_a;A)$ and(2)$f_b(t_b;B)={\int }_0^{\infty }{f}_a(t_a;A,B)f_b(t_b;B,A|t_a)d{t}_a$.

In parallel systems, the marginal selectivity is said to hold if and only if(1)$g_a(t_a;A)={\int }_0^{\infty }{g}_a(t_a;A,B|t_b)g_b(t_b;B,A)d{t}_b$ and(2)$g_b(t_b;B)={\int }_0^{\infty }{g}_b(t_b;B,A|t_a)g_a(t_a;A,B)d{t}_a$.

We were surprised to discover, as in the next definition, that the concept of marginal selective influence can be further disassembled into two sub-types and that these differ in their implications for systems identification.

Definition 8.

Strong and Weak Marginal Selective Influence.

(1).Strong marginal selectivity restricts the effect of any factor to its impact on the appropriate marginal distribution.(2).Weak marginal selectivity, in our sense, demands that one or more of the experimental factors influences the joint distribution outside their impact on the pertinent marginal distribution.

As was the case for indirect nonselective influence, the presence of marginal selectivity may be of import for other types of influence as well as drawing inferences regarding mental mechanisms.

3. Key Propositions on Satisfaction of Marginal Selectivity

This section will focus on when marginal selectivity is or is not satisfied (Definition 7), without regard to strictness conditions (Definition 8). In preparation for Propositions 1A and 1B, and Propositions 2A and 2B, we continue reference to Townsend and R. Thomas [37]. In general, their manifold demonstrations of failure of selective influence, even at the level of means, implied that the distributions themselves were severely perturbed. That is, marginal selectivity was destroyed by their examples. We can exhibit the havoc, even at the distributional level, that can be wrought by indirect nonselective influence alone on $T_b$.

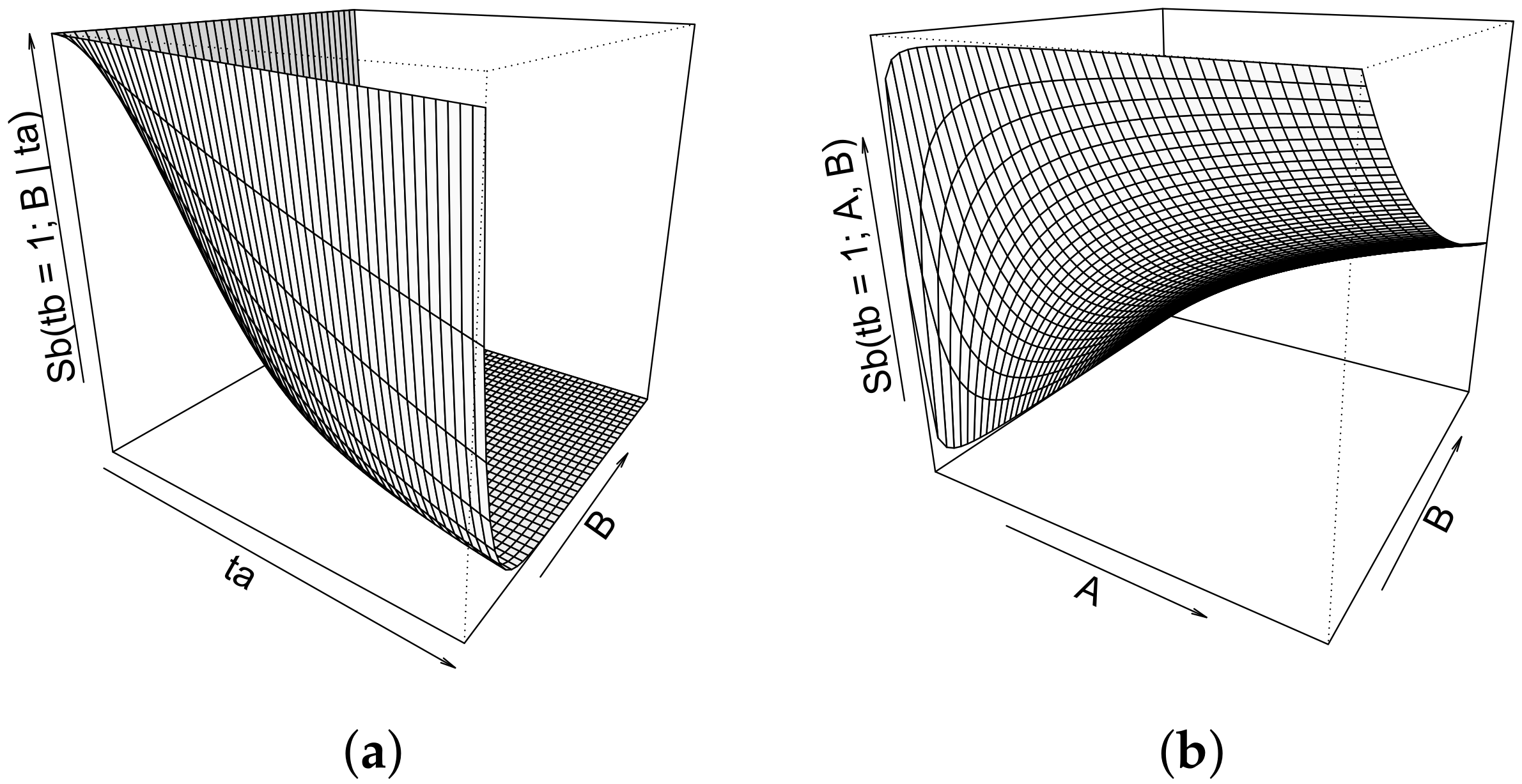
Example 1.

Suppose $A,B>0$, $S_a(t_a;A)=Exp(-A{t}_a)$ and $S_b(t_b;B|t_a)=Exp(-B{t}_a{t}_b^2)$. Note that there is no direct affliction from A, but the second stage is a function of $t_a$ indicating indirect nonselective influence. Then, we can see that the longer stage ${\mathbb{S}}_a$ takes, the faster stage ${\mathbb{S}}_B$ will be, in a stochastic sense, provoking a negative correlation on these stages. We can intuit that since A makes the first stage faster, there should ultimately be discovered a negative relationship between A and $T_b$. Thus, deriving the marginal survivor function for $T_b$, we have

$$\begin{array}{cc}\hfill & S_b(t_b;B)\hfill \\ \hfill =& {\int }_0^{\infty }AExp(-A{t}_a)Exp(-B{t}_a{t}_b^2)d{t}_a\hfill \\ \hfill =& \frac{A}{B{t}_b^2+A}.\hfill \end{array}$$

Figure 1a shows how the survivor function for $T_b$ conditioned on $T_a$ is a function of $t_a$. Then, Figure 1b exhibits how the marginal for $T_b$ is a function of both A and B. Obviously, since $S_b$ is an increasing function of A as we suspected, the slower we make ${\mathbb{S}}_a$ go, the faster will go ${\mathbb{S}}_b$ (because the survivor function on $T_b$ will be smaller), and this happens both at the within-trial as well as the across-trial levels. The reader will note that an even simpler example works in principle, that is, where $S_b(t_b;B|t_a)=Exp(-B{t}_a{t}_b)$. However, this model suffers from not possessing a mean in ${\mathbb{S}}_B$.

Proposition 1A(a) indicates the trivial-to-show but interesting feature that, with both 1-directional seriality and no direct nonselectivity from the second to first stage in a 1-direction serial system, overall selectivity is found on $T_a$. Proposition 1A(b) exhibits the rather patent result that if pure selective influence (see Definition 4) is true, then marginal selectivity perforce occurs. Proposition 1A(c) establishes the somewhat curious but important outcome that if perturbation of selective influence is both direct and indirect, then marginal selectivity can also be valid. Finally, Proposition 1A(d) discovers that this type of cancellation can go in both directions, a result that we will see also pertains to parallel systems.

Proposition 1

(A). On Satisfaction of Marginal Selectivity in 1-Direction Serial Systems.

Under the assumptions of 1-directional seriality,

(a). If direct nonselective influence of B on ${\mathbb{S}}_a$ is absent, then it is impossible that the marginal distribution on $T_a$ be a function of the “wrong” factor B in either the weak or strong sense. Hence, indirect nonselective influence on ${\mathbb{S}}_a$ is ruled out and selective influence of A on ${\mathbb{S}}_a$ is assured. Thus, $f_a(t_a;A)$ is no function of B and marginal selectivity holds for $T_a$.

(b). If neither indirect nor direct nonselective influence are present in the ${\mathbb{S}}_a\to {\mathbb{S}}_b$ or the opposite direction, then strong marginal selectivity on $T_b$ is true.

(c). Suppose that $f_b(t_b;B,A|t_a)$ is a non-trivial function of A, B and $t_a$. Then, even strong marginal selectivity on $T_b$ may succeed.

(d). We can construct a case where both factors cancel out and we are left with no influence, selective or nonselective at all.

Proof. 

(a): For every value of $t_a$, $f_b(t_b;B,A|t_a)$, integration over all values of $t_b$ yields 1, leaving the marginal distribution of $t_a$ to be a function only of A. So, marginal selectivity is determined in Stage ${\mathbb{S}}_a$ if there is no direct nonselective influence there.

(b): Obvious, because the hypothesis is tantamount to stochastic independence plus direct selective influence, that is pure selective influence is in power. This could be seen as a corollary to part (a).

(c): It is helpful to picture the integral of the product $f_a(t_a;A)f_b(t_b;B,A|t_a)$ over all values of $t_a$ as a linear transformation $\mathbf{T}$ in continuous function space, arising from the Markov kernel $f_a(t_a;A)$. Then, we require that the marginal on $T_b$ be invariant over the factor A: $f_b(t_b;B,A)=f_b(t_b;B)={\int }_0^{\infty }{f}_b(t_b;B,A|t_a)f_a(t_a;A)d{t}_a$.

An example shows that this is possible. One is straightaway found by setting $f_a(t_a,A)=AExp(-A{t}_a)$ and $S_b(t_b;B,A|t_a)=Exp(-AB{t}_a{t}_b^2)$. Integration over the interval from 0 to ∞ finds the marginal survivor function to be $S_b(t_b;B,A)=\frac{1}{1+B{t}_b^2}$ which is obviously a function only of $t_b$ and B and therefore satisfies marginal selectivity. Rewriting the joint distribution function using the copula trick (detailed in the next section) of inverting the marginals finds that no factorial influence outside of the marginal distribution resides.

(d): Prove with an example. Let $f_a\left(t_a\right)=ABExp(-AB{t}_a)$ and $S_b\left(t_b\right|t_a)=Exp(-AB{t}_a{t}_b)$. Now, calculate the marginal of $T_b$:

$$\begin{array}{cc}\hfill & {\int }_0^{\infty }{f}_b(t_b;B,A|t_a)f_a(t_a;A,B)d{t}_a\hfill \\ \hfill & ={\int }_0^{\infty }Exp(-AB{t}_a{t}_b)ABExp(-AB{t}_a)d{t}_a\hfill \\ \hfill & =AB{\int }_0^{\infty }Exp[-AB{t}_a(1+t_b)]d{t}_a\hfill \\ \hfill & =\frac{1}{1+t_b}\hfill \end{array}$$

which is a function of neither factor A (no direct nonselectivity), B (no direct selectivity) nor $t_a$ (no indirect nonselectivity). □

Figure 2 illustrates Proposition 1A(c) by exhibiting that the conditional survivor $S_b(t_b;B,A|t_a)$ is a function of A, B and $t_a$ but then reveals that its marginal form is a function only of B.

Now, taking up parallelism, since processing is going on simultaneously, we cannot obtain the hypothesis in Proposition 1A(a) through any principle such as causality. However, we can just impose something like it by fiat in Proposition 1A(a).

Proposition 1

(B). On Satisfaction of Marginal Selectivity in Parallel Exhaustive Systems.

Under the assumptions of parallel exhaustive processing:

(a). If $T_a$ is afflicted by neither indirect nor direct nonselective influence, then its marginal distribution is selective. As intimated in the prologue just above, we simply impose an absence of direct and indirect nonselective influence on $T_a$. Then, integrating over $T_b$ yields a marginal on $T_a$ that is selective.

(b). If neither indirect nor direct nonselective influence are present, then marginal selectivity on $T_a$ and $T_b$ is true.

(c). Suppose that either $g_a(t_a;A,B|t_b)$ is a non-trivial function of A, B and $t_b$, or $g_b(t_b;B,A|t_a)$ is a non-trivial function of A, B and $t_a$, then even strong marginal selectivity may succeed.

(d). As in Proposition 1A(d), if both channels are directly and indirectly influenced by the “other” factor, then the result could have complete freedom from either type of influence on either channel.

Proof. 

(a).: The marginal distribution of $T_a$ is:

$$\begin{array}{cc}\hfill & {\int }_0^{\infty }{g}_{ab}(t_a,t_b;B,A)d{t}_b\hfill \\ \hfill & ={\int }_0^{\infty }{g}_a(t_a;A)g_b(t_b;B,A|t_a)d{t}_b\hfill \\ \hfill & =g_a(t_a;A){\int }_0^{\infty }{g}_b(t_b;B,A|t_a)d{t}_b,(\because \mathrm{direct}\mathrm{and}\mathrm{indirect}\mathrm{selectivity})\hfill \\ \hfill & =g_a(t_a;A)\hfill \end{array}$$

(b): Obvious. Because the hypothesis is tantamount to stochastic independence plus direct selective influence, that is, pure selective influence is in power.

(c): We can employ a similar example to that used in Proposition 1. Let $g_a(t_a;A)=AExp(-A{t}_a)$ and the survivor function ${\overline{G}}_b(t_b;B,A|t_a)=Exp(-AB{t}_a{t}_b)$. Then, the marginal survivor for $T_b$ is:

$$\begin{array}{cc}\hfill & {\overline{G}}_b(t_b;B,A)\hfill \\ \hfill & ={\int }_0^{\infty }{\overline{G}}_b(t_b;B,A|t_a)g_a(t_a,A)d{t}_a\hfill \\ \hfill & ={\int }_0^{\infty }Exp(-AB{t}_a{t}_b)AExp(-A{t}_a)d{t}_a\hfill \\ \hfill & =\frac{1}{1+B{t}_b}\hfill \\ \hfill & ={\overline{G}}_b(t_b;B)\hfill \end{array}$$

which proves marginal selectivity. An analogous tactic to that in Proposition 1(c) works to infer that this is the strong form of marginal selectivity.

(d): We perform the demonstration for ${\mathbb{S}}_b$. The other direction is the same. Let $g_a(t_a;A,B|t_b)=ABExp(-AB{t}_b{t}_a)$ and ${\overline{G}}_b(t_b;B,A|t_a)=Exp(-AB{t}_a{t}_b)$. Then, the marginal survivor for $T_b$ is:

$$\begin{array}{cc}\hfill & {\int }_0^{\infty }Exp(-AB{t}_a{t}_b)ABExp(-AB{t}_b{t}_a)d_{t}a\hfill \\ \hfill & =\frac{1}{2t_b}\hfill \end{array}$$

which is a function of $t_b$ only. □

We find it intriguing the way in which the direct effect of factor A from ${\mathbb{S}}_a$ can counteract the perturbing indirect effect of $T_a$ in both parallel as well as serial systems. We deem it of sufficient import to endow it with a name offset.

Definition 9.

Offset.

The offset effect is referred as an instance where the presence of direct and indirect nonselective influence from a process, say ${\mathbb{S}}_a$, on the other process, say ${\mathbb{S}}_b$, eliminate each other.

The reader may observe that, as intimated earlier, in a parallel system, there is the possibility that a double-cancelling offset can occur ending with no influence in the system at all (Proposition 1B(d)). Within the 1-direction serial systems, the next Proposition 2A(a) indicates the fairly evident fact that direct nonselective influence by itself can cause failure of marginal selectivity. Proposition 2A(b) states that marginal selectivity can fail if both indirect and direct nonselective influence intrude. That is, offset is far from mandatory. Finally, Proposition 2A(c) strengthens the Townsend and R. Thomas [37] developments by proving the rather startling result that marginal selectivity in the second stage is impossible in 1-direction serial systems if indirect nonselectivity does occur but direct nonselectivity does not. That is, without offset, and with the presence of contamination from $T_a$, marginal selectivity is impossible. This will be the most curious, yet vital, result of the next proposition.

Proposition 2

(A). On Failure of Marginal Selectivity in 1-Direction Serial Systems.

Marginal selectivity of either type can fail through:

(a). Direct nonselective influence only on ${\mathbb{S}}_a$, or only on ${\mathbb{S}}_b$ or both.

(b). Indirect and direct nonselectivity on ${\mathbb{S}}_b$ with direct selective influence on ${\mathbb{S}}_a$.

(c). It must fail when only indirect nonselectivity on ${\mathbb{S}}_b$ occurs. Note that we also assume $T_a$ is neither directly influenced by B or indirectly by $T_b$.

Proof. 

(a): Obvious.

(b): Here, we see the intuitive statement that offset is by no means guaranteed. Again, let $f_a(t_a;A)=Exp(-A{t}_a)$, but now let the conditional survivor function on $S_b$ be $S_b(t_b;B|t_a)=Exp(-\frac{B{t}_a{t}_b^2}{A})$. It will be found that the marginal survivor on $S_b$ will be $S_b(t_b;B,A)=\frac{A^2}{B{t}_b^2+A^2}$, revealing a critical dependence in ${\mathbb{S}}_b$ on the wrong factor A. In fact, now, A slows down the second stage even more than in the example at the beginning of this section.

(c): Due to its importance and its additional subtlety, we briefly rephrase this issue and proceed with care.

Suppose $f_b(t_b;B|t_a)\ne f_b(t_b;B)$, that is, indirect nonselective influence is present, but A is absent from $f_b(t_b;B|t_a)$ indicating that $T_b$ is not directly nonselectively affected by A. Then, marginal selectivity of $T_b$ is impossible. Consider then the transformation $\mathbf{T}\left[f_b(t_b;B|t_a)\right]={\int }_0^{\infty }{f}_b(t_b;B|t_a)f_a(t_a;A)d{t}_a$. We can interpret $f_a(t_a;A)$ as a Markov kernel which maps $A\times t_a$ into the measure space on $B\times t_b$. We also can regard the latter measure as coming immediately from the parametric density $f_b(t_b;B)$.

Let the symbol 1 represent the constant function $f\left(t\right)\equiv 1$. It is easy to see that $T\mathbf{1}=1$ is the constant function because that is just the integral over the ordinary density $f_b(t_b;B|t_a)$ over the domain of $t_b$ from 0 to ∞.

Now, assume marginal selectivity is to be true, that is, ${\int }_0^{\infty }{f}_b(t_b;B|t_a)f_a(t_a;A)d{t}_a=f_b(t_b;B)$, and observe that the right-hand side is constant across values of A. Then, it follows that $\mathbf{T}\left[f_b(t_b;B|t_a)\right]=f_b(t_b;B)\mathbf{1}$. Note that the right hand side is invariant over all values of the A factor. We can re-express this fact as $\mathbf{T}\left[f_b(t_b;B|t_a)\right]-f_b(t_b;B)\mathbf{1}={\int }_0^{\infty }[f_b(t_b;B,A|t_a)f_a(t_a;A)-f_b(t_b;B)\mathbf{1}]d{t}_a=0$.

Since T does not kill any function that is not already zero almost everywhere, then it implies that $f_b(t_b,B|t_a)=f_b(t_b;B)$. That is, this outcome contradicts our hypothesis that $t_a$ is effective in $fb(t_b;B|t_a)$. Therefore, we conclude that marginal selectivity is false. □

An analogous proposition for the parallel exhaustive systems is presented in Proposition 2B.

Proposition 2

(B). On Failure of Marginal Selectivity in Parallel Exhaustive Systems.

Marginal selectivity of either type can fail through:

(a). Direct nonselective influence only on ${\mathbb{S}}_a$, or ${\mathbb{S}}_b$ or both.

(b). Indirect and direct nonselectivity on ${\mathbb{S}}_b$ with direct selective influence on ${\mathbb{S}}_a$; or indirect and direct nonselectivity on ${\mathbb{S}}_a$ with direct selective influence on ${\mathbb{S}}_b$

(c). It must fail when only indirect nonselectivity occurs either on ${\mathbb{S}}_a$ or ${\mathbb{S}}_b$.

Proof. 

Proofs are similar to those in Proposition 2A. □

Again, we emphasize the part (c) of the above propositions that, in the presence only of indirect nonselectivity, marginal selectivity is impossible, as exemplified in earlier examples.

Sometimes, things that work for continuous functions do not for discrete, even finite cases. For instance, difference equations with certain properties expressed as functional equations do not always generalize to their “natural” continuous counterparts expressed in terms of differential equations [42,43]. In the present situation, the proven statement is actually a bit stronger in the discrete version, as we show in Appendix A (Proposition A1). The next observation, though obvious, is so important that we render it as a proposition.

Proposition 3.

Indirect Nonselectivity and the Dzhafarov Definition of Selectivity.(a). In 1-direction serial systems ${\mathbb{S}}_a\to {\mathbb{S}}_b$, if indirect influence only afflicts ${\mathbb{S}}_b$, then the Dzhafarov definition of selective influence fails.(b)In parallel systems, if indirect influence only afflicts either ${\mathbb{S}}_a$ or ${\mathbb{S}}_b$, then the Dzhafarov definition of selective influence fails.

Proof. 

The falsity of marginal selectivity implies the failure of the Dzhafarov definition. □

Previously, we chose exponential distributions for Ts in the proof for Proposition 1A(c) and 1B(c) to show that systems having both direct and indirect nonselective influences can still have marginal selectivity. This is because the exponential distribution possesses high intuitive value in response time modeling and enjoys an exceedingly rich history in the employment of exponential distributions in that venue (e.g., [1,37]). Next, we show that a Gaussian example can also accomplish precisely this type of result.

In Sternberg’s original statements [15], it was allowed that selective influence on $T_b$ might still occur even with the stochastic dependence on $T_a$. This is a natural impulse because of one of the backbones of classical statistical analyses: Multivariate Gaussian distributions possess mathematically independent parameters of means and covariances. Gaussian distributions, though ill-suited for response times (due to being defined for $T<0$), figure heavily in theory and applications to non-response time data (e.g., [38,39,44]). This leads to an example where there exists both direct and indirect nonselective influence, yet marginal selectivity is found. For instance, consider a bivariate Gaussian distribution where the means are taken as the experimental factors and there is a non-zero correlation. The correlation could be a function of both factors as well. This is a case where we should consider the Ts as other than time variables so that they can take on negative values.

A key component of linear regression is that the mean of $T_b$ conditional on $T_a=t_a$ is just the Gaussian distribution $f_b(t_b;B,A|t_a)$ and thus is distributed as $N({\mu }_b+\rho (t_a-{\mu }_a),(1-{\rho }^2){\sigma }^2)$ where ${\mu }_a=A,{\mu }_b=B$ are the respective factors, $\sigma$ is the mutual standard deviation and $\rho$ is the correlation coefficient. Notice that the conditional distribution is a function of the experimental factor A and B and is dependent on $t_a$. Therefore, under our defined structure, both direct and indirect nonselective influence are present. Yet, integrating over $T_a=t_a$ would leave $T_b$ to be a function only of its variance and mean parameters (${\sigma }_a^2$ and ${\mu }_b$), thus satisfying marginal selectivity. Therefore, we have another instance of offset here. That is, a case of both direct as well as indirect nonselective influence, yet overall marginal selectivity, is found in the end.

Finally, for this section, a brief excursion shows how the Dzhafarov conditional independence conception of selective influence can be viewed as a case of offset with regard to marginal selectivity. To conjoin the concept of conditional independence to our general line of attack, let us write the critical conditional probability of the ${\mathbb{S}}_b$ duration on $T_a$ in the context of the former condition. It will not do serious harm to the generality of our inference to assume that the random variable C is defined on the positive real line. Let us check the status of indirect nonselective influence: $f_b(t_b;B,A|t_a)=\frac{{\int }_0^{\infty }{f}_b(t_b;B,A|t_a,c)f_a(t_a;A,B|c)f_c\left(c\right)dc}{{\int }_0^{\infty }{f}_a(t_a;A,B|c)dc}$. This expression reveals that, in general, $T_b$ given $T_a=t_a$ is not independent of $t_a$ or, equivalently, $T_b$ is a non-trivial function of $t_a$, regardless of whether or not direct nonselective influence is existent. How about the latter, that is, is $f_b(t_b;B,A|t_a)$ a function of A in general, after integration over values of $C=c$, as opposed to indirect dependence through integration of $t_a$?

Apparently, even if $f_a(t_a;A,B|c)=f_a(t_a;A|c)$ for all $t_a$ and even if $f_b(t_b;B,A|t_a,c)$ is not a function of A, still in general, $f_b(t_b;B|t_a)$ can be a function not only of B but also of A. We rewrite the above integral to facilitate the reader’s scrutiny with these restrictions: $f_b(t_b;B,A|t_a)=\frac{{\int }_0^{\infty }{f}_b(t_b;B|t_a,c)f_a(t_a;A|c)f_c\left(c\right)dc}{{\int }_0^{\infty }{f}_a(t_a;A|c)d_c}$. The reader will notice that $f_b(t_b;B,A|t_a)$ is a function of both A as well as $t_a$ and therefore meets the requirement for offset (Definition 9).

4. Canonically Shaped Distribution Interaction Contrasts and Marginal Selectivity

As observed in the introduction, an absolutely essential aspect of almost any discussion of selective influence is that of its implications for identification of psychological structure and mechanisms and its own experimental testability. As also mentioned in the introduction, the root of SFT via its leveraging of selective influence in experiments lies in the original additive factors method as invented by S. Sternberg [15]. We have already limned in the way in which his early notion of selective influence not only provided for hundreds of studies testing for serial processing in mean RTs but instigated a deep and massive evolution of the notion of that concept.

A key attendant axiom in almost all applications of selective influence in SFT since the late 1970s is the added requirement that an experimental factor acts to order cumulative distribution functions on processing times of the associated entity (e.g., a perceptual, cognitive or motor subprocess involved in a task; see [23,27,28]). While the advent of distribution ordering turned out to carry with it much more penetrating consequences for system identification than did mean orderings alone, it is far less demanding than other even more intense forms of ordering but putting more constraints on nature. For example, an ordering of hazard functions implies the distributional ordering but not vice versa, and a monotonic likelihood function implies the hazard ordering but also not in reverse [28].

The present section will provide new developments regarding the relationships of distinct notions of selective influence on the canonical signatures of architecture recapped below. For the authors, the place in the armamentarium of SFT that marginal selectivity enjoys was especially intriguing. Candidly, we had long thought, without any proof whatsoever, that it might be quite formidable in its consequences for systems identification, particularly through the canonical classical SFT predictions. In the early stages of the present theoretical developments, we had anticipated that this tenet would be false. It simply seemed too coarse of a condition. As the story unfolds, we will find that the true nature of marginal selectivity vis-a-vis the survivor interaction contrast (or equivalently, the distributional interaction contrast, see below) predictions seems more complex and subtle than we had anticipated, and the denouement is not yet complete.

At this point, we need to repeat once again for the general reader, the basic concept of the double difference or so-called interaction contrast. Using only a finite number of statistical functions, it is straightforward to implement with data. However, it turns out to be highly useful in certain theoretical contexts, to utilize its continuous analogue, the second order, mixed partial derivative. This tactic permits the immediate employment of elegant tools from the calculus.

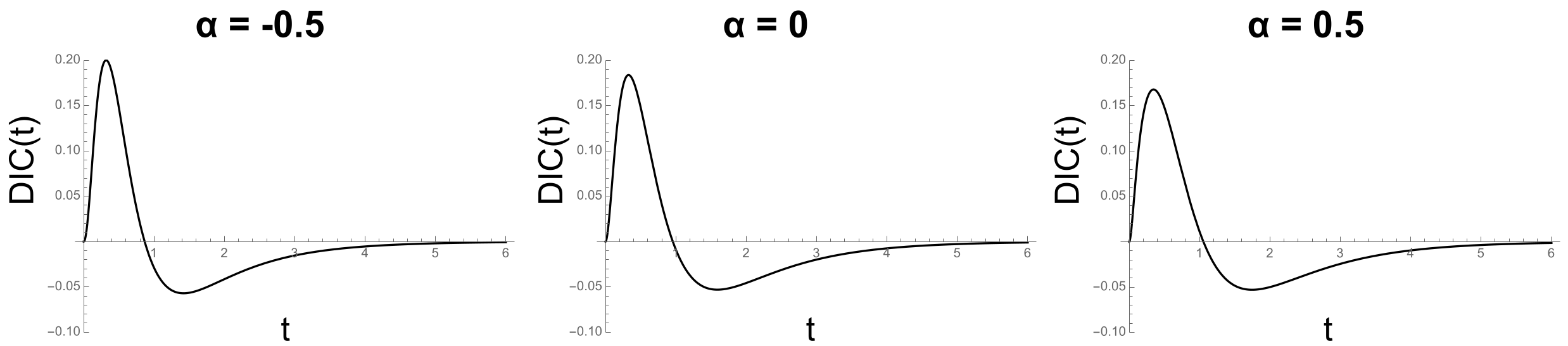
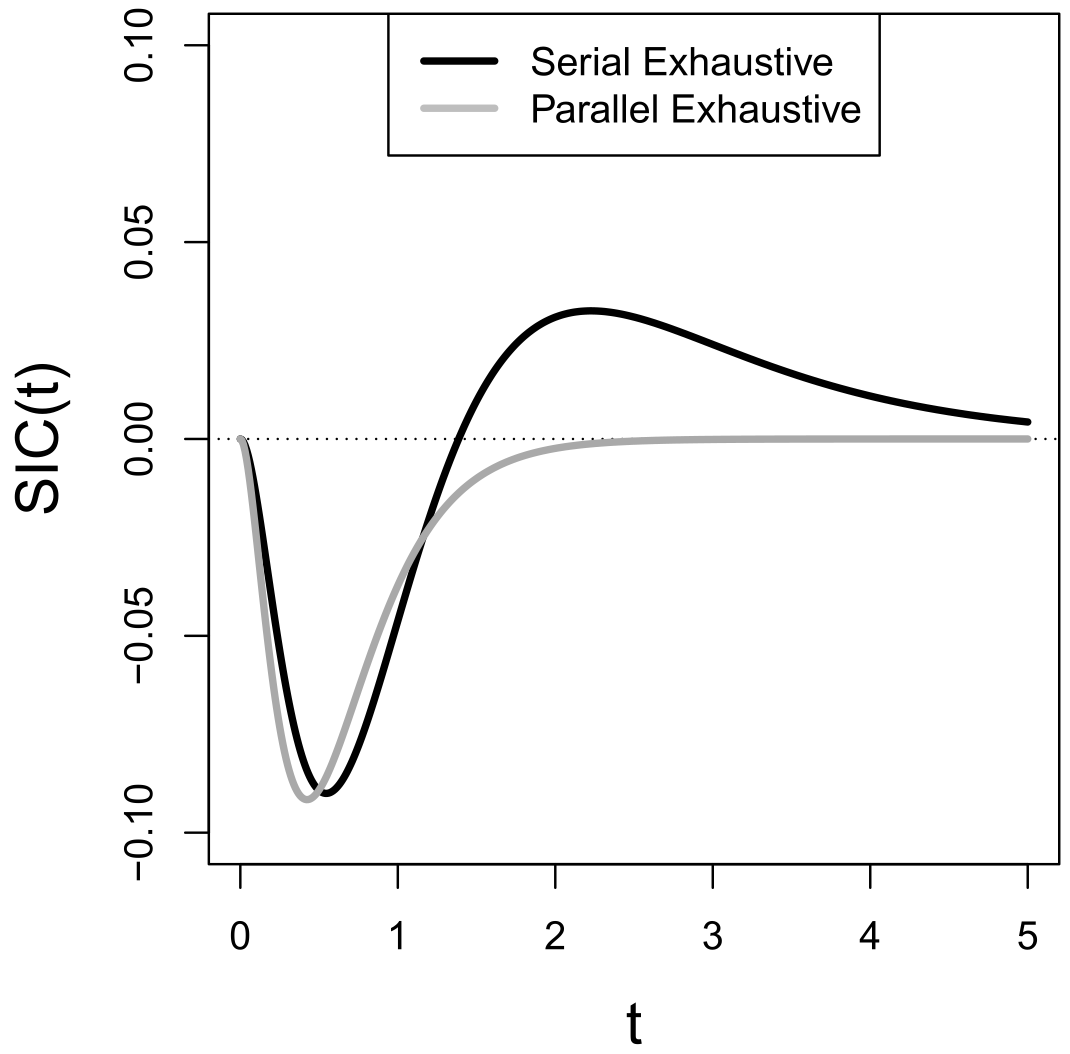
The mean interaction contrast ($MIC$; Figure 3) has been employed since its inception in the 1960s to test for the presence of serial processing. If selective influence holds in serial systems, then the $MIC$ is predicted to be 0, irrespective of the attendant stopping rule [15]. As long as the means are ordered through the experimental factors, even without an ordering of the distributions themselves, this prediction is in force. However, even at the mean response time level, other architectures necessitate more impactful means of influence (e.g., [23]).

Definition 10.

Mean Interaction Contrast.

$$MIC=[E\left(T_{LL}\right)-E\left(T_{HL}\right)]-[E\left(T_{LH}\right)-E\left(T_{HH}\right)],$$

(1)

where L = low salience level and H = high salience level.

Next, it is required to recall the vital statistical function that differentiates various stopping rules and architectures, the so-called survivor interaction contrast ($SIC\left(t\right)$). The survivor function itself is straightforwardly defined as $S\left(t\right)=1-F\left(t\right)$ where $F\left(t\right)$ is the well-known cumulative distribution function as used above. That is, $F\left(t\right)=P(T\le t)$. Thus, interpreted at the level of $F\left(t\right)$ and $S\left(t\right)$, the faster the processing time, the larger $F\left(t\right)$ is and the smaller $S\left(t\right)$ is for a given t. As formally defined in Definition 11, $SIC\left(t\right)$ is just a double difference of the survivor functions under distinct combinations of the two experimental factors at different salience level, low (L) and high (H) [14].

Definition 11.

Distributional Contrast Functions.

(a). The survivor interaction contrast: Let $A,B$ be the experimental factors and write the survivor function on the underlying processing times as $S_{AB}\left(t\right)$. Then, the survivor interaction contrast function is defined as:

$SIC\left(t\right)=[S_{LL}\left(t\right)-S_{HL}\left(t\right)]-[S_{LH}\left(t\right)-S_{HH}\left(t\right)],\forall t\ge 0$.

(b). The distribution interaction contrast: Using a similar notation as in (A), we can exhibit the distribution interaction contrast ($DIC\left(t\right)$) as:

$$DIC\left(t\right)=[F_{HH}\left(t\right)-F_{HL}\left(t\right)]-[F_{LH}\left(t\right)-F_{LL}\left(t\right)]=-SIC\left(t\right),\forall t\ge 0.$$

(2)

Figure 4 shows the well-known signatures for the prototypical 1-direction serial and parallel architectures with a conjunctive (AND, exhaustive) stopping rule under the assumption of pure selective influence. Note that the total processing time of the system is the sum of all stages for serial and is the maximum time for parallel.

Another highly beneficial tool from previous work, and as intimated earlier, is the substitution of second-order, mixed partial derivatives for the second-order, mixed differences (even used some by [14]). Basically, as intimated just above, we assume that what is going on at the macro level extends in the limit to the local-level derivatives for well-behaved processes. Thus, the signatures for the various architectures and their stopping rules follow the qualitative properties of the finite differences and vice versa.

Before advancing to in-depth exploration of marginal selectivity, we pause to exhibit a strong consequence of the Dzhafarov definition of selective influence (see Definition 6) which will play an intriguing role in what follows.

Proposition 4.

Single Signed Distribution Interaction Contrast. Consider any joint distribution on $T_a$, $T_b$ and any well-defined function of $T_a$, $T_b$, say $R(T_a,T_b)$. Suppose pure selective influence for the architecture and stopping rule produce R that is single signed over all values of $T_a$, $T_b$. Under the Dzhafarov definition of selective influence, if the second order mixed partial derivative (mixed partial difference) on $R(T_b,T_b)$ is single signed with the same sign over $T_a$, $T_b$ values for all Dzhafarov mixing parameter C, then the same holds for the marginal distribution over $C=c$ and the canonical $DIC\left(t\right)$ function is preserved.

Proof. 

Consider $P(R(T_a,T_b)\le r;A,B|C=c)$ and then $\frac{{\partial }^2\left[R(t_a,t_b;A,B,c)\right]}{\partial A\partial B}\ge 0$ without loss of generality. Then, the overall signature is the marginal, ${\int }_{-\infty }^{\infty }\frac{{\partial }^2[R(t_a,t_b;A,B,c)}{\partial A\partial B}dc\ge 0$ as well. □

This rather obvious result has powerful consequences and immediately implies the canonical predictions, under the Dzhafarov condition, for parallel systems. However, by the same token, we will see that the absence of the constant sign bears portent for systems identification as well. The theorems of Dzhafarov, Schweickert and Sung [45] cover cases of distributional double differences which are not themselves single signed but by formulating integrals of these are. However, we shall adduce some new theorems below which broaden the spectrum of canonical $DIC\left(t\right)$s delivered through the Dzhafarov [39] condition.

Next, in order to explore the consequences of marginal selectivity for the signatures of architectures cum stopping rules, it is helpful, if not obligatory, to be able to generate compliant joint distributions without independence. As the reader may be persuaded by such attempts, it can be taxing to come up with distributions with non-trivial dependencies that do satisfy marginal selectivity.

Mercifully, a deus ex machina takes the stage in the form of copula theory. Copula theory, as we will shortly see, does not mandate marginal selectivity, but it does offer a rather crafty way of producing it, at least in parallel systems. Copula theory has become a valuable strategy in applied mathematics areas such as finance, actuarial theory, reliability engineering, turbulence and even medicine. It has recently been introduced into psychology and cognitive science by H. Colonius and colleagues [46,47,48]. The Colonius doctrine has contributed much in the way of rigorous theory and methodology to the field of redundant signals research in general and of multi-sensory perception in particular. He formulated powerful theorems regarding workload capacity comparing response times when an observer is confronted with, say, one vs. several signals, and detection of any determines a decision by assuming the marginal distributions remain invariant when moving from one to several signals ([48]; see also [49]). This is tantamount to marginal selective influence when the number of signals is interpreted as an experimental factor [36]. However, the usage to which he put copulas does not broach the strong vs. weak distinction. In any event, we again repurpose copulas here in such a way as to help provide answers to some of our critical issues, although not all derivations require their usage.

We have no space for even a tutorial here, but suffice it to say, this approach permits the development of joint distributions with specified marginals. Let $G_a(t_a;A)$ be the marginal cumulative distribution function for ${\mathbb{S}}_a$ and similarly for the other process, ${\mathbb{S}}_b$, and then by the provenance of copula theory, the joint cumulative distribution function may be expressed as $P_{ab}(T_a\le t_a,T_b\le t_b;A,B)=F_{ab}(t_a,t_b;A,B)=H[G_a(t_a;A),G_b(t_b;B)]$. This result, known as Sklar’s theorem (e.g., see [50]), can be viewed as a generalization to multi-dimensions of the so-called integral transform since the arguments of H can be interpreted as random variables $U_a,U_b$ each uniformly distributed on $[0,1]$ (see, e.g., [51]). The dependency structure of the original joint distribution $P_{ab}$ is inherent in H. Conditions for the existence of H are extremely weak and we shall make the further common assumption that $P_{ab}$ is built upon a continuous joint density function. The marginals of H are naturally just $G_a$ and $G_b$, and the reader will observe that in the above formular, we have imposed our rule that the marginal distributions conform to marginal selectivity a fortiori. This constraint will be relaxed in some of what follows.

Recall that the distribution interaction contrast function for parallel models with exhaustive processing is always greater than or equal to 0. The very next result makes good use of copulas and might mislead the theorist into hoping for very great benefits with the satisfaction of marginal selectivity. There are, indeed, substantial benefits but perhaps not so all-encompassing as the theorist might wish.

The distinction between strong and weak marginal selectivity is instrumental in Propositions 5 and 6.

Recall that the canonical mixed partial difference (or derivative) of the cumulative distribution function for exhaustive processing is greater than or equal to 0. The implications from Proposition 4 are all to the good. The less appealing results emerge below.

Proposition 5.

When Experimental Factors Affect the Joint Distribution of Parallel Exhaustive Systems only Through the Marginal Distributions: The Case with Strong Marginal Selectivity. Consider the class of joint parallel distribution functions.

(a). Every parallel system with a joint distribution whose copula indicates that the experimental factors influence the distribution only through the marginals (strong marginal selectivity) predicts that the second order mixed partial derivative of the joint distribution itself will be non-negative.

(b). Every parallel system enjoying strong marginal selectivity predicts that the second order mixed partial derivative of the cumulative distribution on the maximum processing time will be non-negative. Thus, this situation entails the canonical $DIC$ function.

Proof. 

(a). First, construct the copula for the joint cumulative distribution of a 2-channel parallel system: $G_{ab}(t_a,t_b;A,B)$. It can be expressed as $H[G_a(t_a;A),G_b(t_b;B)]$. Then,

$$\begin{array}{cc}\hfill \frac{{\partial }^2{G}_{ab}}{\partial t_a\partial t_b}& =\frac{{\partial }^{2}H}{\partial t_a\partial t_b}\hfill \\ \hfill & =\frac{{\partial }^{2}H}{\partial G_a\partial G_b}\frac{\partial G_a}{\partial t_a}\frac{\partial G_b}{\partial t_b}\hfill \\ \hfill & =g_{ab}(t_a,t_b)\hfill \\ \hfill & >0(\because g_{ab}(t_a,t_b)\mathrm{is}\mathrm{the}\mathrm{actual}\mathrm{joint}\mathrm{probability}\mathrm{density}\mathrm{function}\mathrm{of}{T}_a\mathrm{and}.T_b)\hfill \end{array}$$

By hypothesis that the experimental factors only influence the distribution through the marginals, $\frac{\partial G_a}{\partial t_a}$ and $\frac{\partial G_b}{\partial t_b}$ are > 0. Therefore, it must be that $\frac{{\partial }^2{H}_{ab}}{\partial G_a\partial G_b}>0$. Again, use the chain rule, we have

$$\begin{array}{cc}\hfill & \frac{{\partial }^2{H}_{ab}}{\partial A\partial B}\hfill \\ \hfill =& \frac{{\partial }^2{H}_{ab}}{\partial G_a\partial G_b}\frac{\partial G_a}{\partial A}\frac{\partial G_b}{\partial B}\hfill \\ \hfill >& 0.\hfill \end{array}$$

If the support is not the entire positive real line, then $\frac{{\partial }^2{H}_{ab}}{\partial A\partial B}=0$.

(b). Obvious. □

The next corollary can be regarded as part B of the Proposition 5. We restate it to emphasize its interpretation in terms of distributional contrast functions.

Corollary 1

(1). The second mixed partial derivative of the CDF: $P(T_a\le t,T_b\le t;A,B)=P(max(T_a,T_b)\le t)$ is $\frac{{\partial }^2{G}_{MAX}\left(T_{max}\right)}{\partial A\partial B}>0$.

Proof. 

Obvious. □

In addition, the next corollary simply states the implied result for the finite $DIC\left(t\right)$ function.

Corollary 1

(2). The $DIC\left(t\right))$ for $MAX(T_a,T_b)$ is

$$DIC\left(t\right)=[G(t,t;A_H{B}_H)-G(t,t;A_H{B}_L)]-[G(t,t;A_L{B}_H)-G(t,t;A_L{B}_L)]>0,\forall t>0.$$

Proof. 

Obvious. □

The upshot is that the canonical $DIC$ (or $SIC$) holds for any possibly dependent parallel model that satisfies marginal selectivity and selective influence only works through the marginal distributions.

The reader will espy that Proposition 5(a) establishes an even stronger result than that for which we sought. Namely, the mixed partial differences are always positive (or 0) even for the precise joint distribution function. Due to obscurations of processing times by residual processes and the like, we do not usually have these available, but they might be in some of Dzhafarov and colleagues’ designs (see, e.g., [52,53,54]) and other future extensions such as the RT designs with two responses on every trial, as intimated earlier.

This is all to the good—strong marginal selectivity forces the canonical signature for exhaustive parallel processing if the only locus where the experimental factors influence speed is through the marginal distributions. We must confess pleasant surprise by this finding. However, we soon discover that relinquishing that seemingly innocent constraint unleashes destruction on the canonical signatures.

Proposition 6.

When Experimental Factors Affect Joint Distributions in Ways Outside the Marginals: The Case with Weak Marginal Selectivity.

Consider the class of joint parallel distribution functions.

(a). If the experimental factors satisfy only weak marginal selectivity, then it is possible that canonical parallel predictions can fail.

(b)If weak marginal selectivity holds, then it may be that the canonical parallel predictions still are in force.

Proof. 

(a). Prove with a counter example. If the canonical prediction on $DIC$ holds for the parallel system when experimental factors affect the joint distribution, then for any $H_{ab}(t_a,t_b;A,B)$ which is monotone in A and B (and, of course, also in $t_a$ and $t_b$), its second mixed partial derivative must be > 0.

The Gumbel’s copula ([55], Vol. 2) is:

$$C_{\alpha }(G_a,G_b)=G_a{G}_b[1+\alpha (1-G_a)(1-G_b)],\forall 0\le G_a,G_b\le 1,\left|\alpha \right|\le 1,$$

(3)

where $\alpha$ is some function of A and B.

We derived that:

$$\begin{array}{cc}\hfill \frac{{\partial }^2{H}_{a,b}(t_a,t_b;A,B)}{\partial A\partial B}& =\frac{\partial \alpha (A,B)}{\partial A\partial B}D(G_a,G_b)\hfill \\ \hfill & +\frac{\partial \alpha (A,B)}{\partial A}\frac{\partial D(G_a,G_b)}{\partial G_b}\frac{\partial G_b}{\partial B}\hfill \\ \hfill & +\frac{\partial \alpha (A,B)}{\partial B}\frac{\partial D(G_a,G_b)}{\partial G_a}\frac{\partial G_a}{\partial A}\hfill \\ \hfill & +\frac{{\partial }^2{C}_{\alpha }(G_a,G_b)}{\partial G_a\partial G_b}\frac{\partial G_a}{\partial A}\frac{\partial G_b}{\partial B},\hfill \end{array}$$

where $D(G_a,G_b)=\frac{\partial C_{\alpha }(G_a,G_b)}{\partial \alpha }$.

Let us have the experimental factors influence both the joint and the marginals by taking $\alpha (A,B)=\sqrt{A+B}$, $G_a(t_a;A)=1-e^{-\theta (1+A)t_a}$, $G_b(t_b;B)=1-e^{-\theta (1+B)t_b}$. Following the derived formula for $\frac{{\partial }^2{H}_{a,b}(t_a,t_b;A,B)}{\partial A\partial B}$, we have:

$$\begin{array}{cc}\hfill \frac{{\partial }^2{H}_{a,b}(t_a=t,t_b=t;A,B)}{\partial A\partial B}& =\frac{-1}{4{(A+B)}^{3/2}}{G}_a{G}_b(1-G_a)(1-G_b)\hfill \\ \hfill & +\frac{1}{2{(A+B)}^{1/2}}{G}_a(1-G_a)(1-2G_b)\theta t(1-G_b)\hfill \\ \hfill & +\frac{1}{2{(A+B)}^{1/2}}{G}_b(1-G_b)(1-2G_a)\theta t(1-G_a)\hfill \\ \hfill & +\frac{{\partial }^2{C}_{\sqrt{a+b}}(G_a,G_b)}{\partial G_a\partial G_b}{\theta }^2{t}^2(1-G_a)(1-G_b),\hfill \end{array}$$

where $\frac{{\partial }^2{C}_{\alpha }(G_a,G_b)}{\partial G_a\partial G_b}\ge 1-\frac{\alpha }{4},\forall \alpha \ge 0$.

If $a+b\to 0$, then $\frac{{\partial }^2{H}_{a,b}(t_a=t,t_b=t;A,B)}{\partial A\partial B}\to -\infty$. If $a+b=1$ and $\theta \to \infty$, then $\frac{{\partial }^2{C}_{\alpha }(G_a,G_b)}{\partial G_a\partial G_b}\ge \frac{3}{4}$ and $\frac{{\partial }^2{H}_{a,b}(t_a=t,t_b=t;A,B)}{\partial A\partial B}\to +\infty$. Thus, the second mixed derivative $\frac{{\partial }^2{H}_{a,b}(t_a=t,t_b=t;A,B)}{\partial A\partial B}$ has a sign inversion with difference values of experimental factors A and B, which violates the canonical prediction on parallel systems.

(b). Prove with an example. Let us set a parallel exhaustive system whose joint cumulative distribution follows a Gumbel’s distribution with the joint part $\alpha (A,B)=\frac{B}{A}$:

$$\begin{array}{cc}\hfill & P(T_a\le t,T_b\le t;A,B)\hfill \\ \hfill =& G_{a,b}(t;A,B)\hfill \\ \hfill =& 1-e^{-At}-e^{-Bt}+e^{-At-Bt-\frac{B{t}^2}{A}}\hfill \end{array}$$

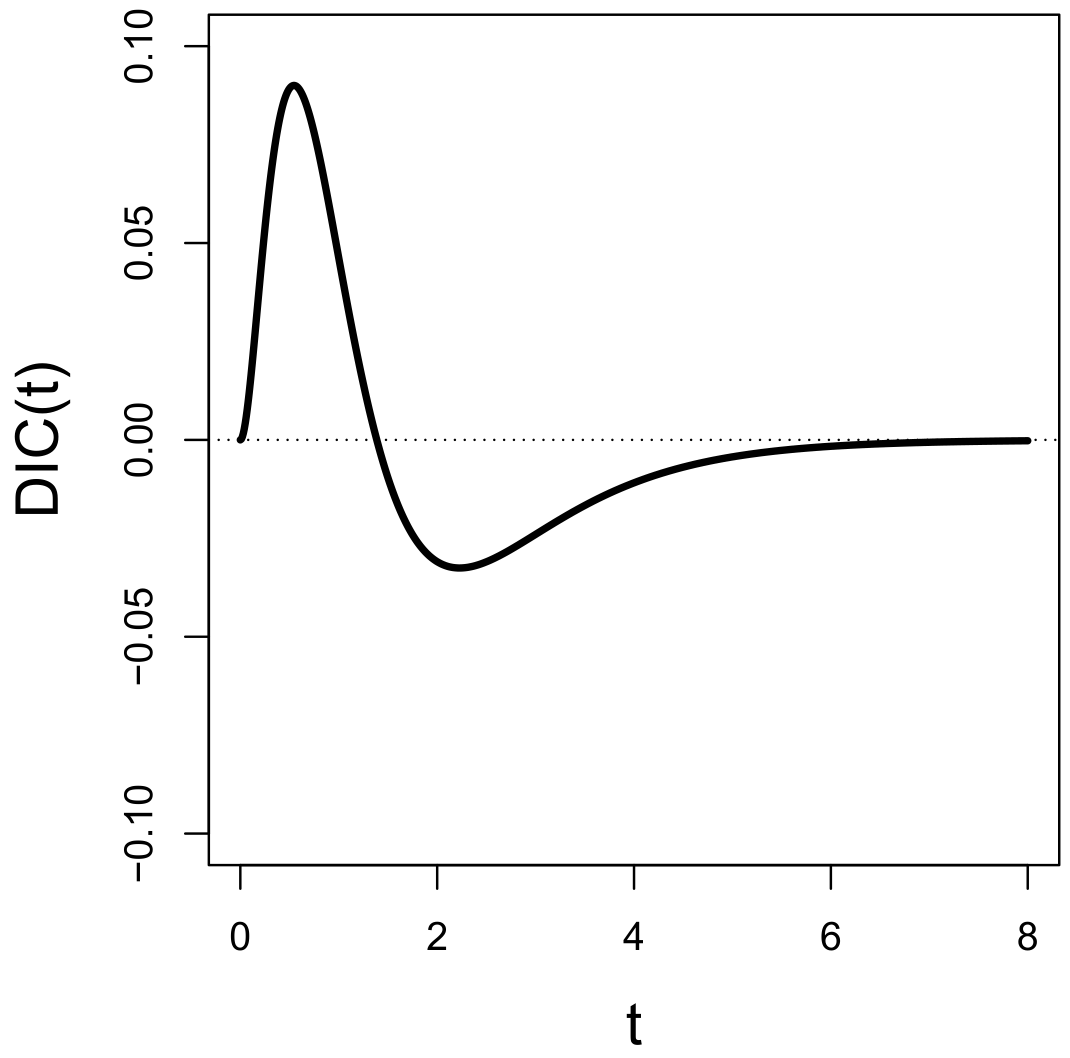
In such a system, the joint distribution is influenced by both experimental factors, yet the marginals are still influenced by their pertinent factors. That is, the weak marginal selectivity holds. As shown in Figure 5, the $DIC\left(t\right)$ produced from this system follows the canonical pattern of the parallel exhaustive system.

This concludes the proof. □

The two foregoing theorems imply that if factors influence a parallel joint distribution only through the marginals and strong marginal selectivity is present, then all is well but may not be if the influence spreads beyond the marginals as in weak marginal selectivity.

We next have a corollary regarding implications for the mean interaction contrast ($MIC$).

Corollary 2.

Implications of where the Experimental Factors Affect the Joint Distribution for Mean Interaction Contrast Statistics in Exhaustive Parallel Processing.

Consider the class of parallel joint distribution functions.

(a). If the conditions in Proposition 5 are met, that is, the factors only influence the distributions through the marginal distributions, then the mean interaction contrasts are canonical: $MIC<0$.

(b). If the conditions in Proposition 6 are met, that is, the factors influence the joint distribution outside of the marginal distributions, then the canonical mean interaction contrast sign may also be violated.

Proof. 

(a). First, recall that the mean processing time is just the integral from 0 to ∞ of the survivor function: $E\left(T\right)={\int }_0^{\infty }S\left(t\right)dt$. Moreover, as shown in Equation (2), the distributional interaction contrast is simply the negative of the survivor interaction contrast: $DIC\left(t\right)=-SIC\left(t\right)$. Then, as proved that the $DIC\left(t\right)$ is canonical and single valued under the condition of Proposition 5, so in the $SIC\left(t\right)$. Thus, the mean interaction contrast’s canonical nature ensues: $MIC<0$.

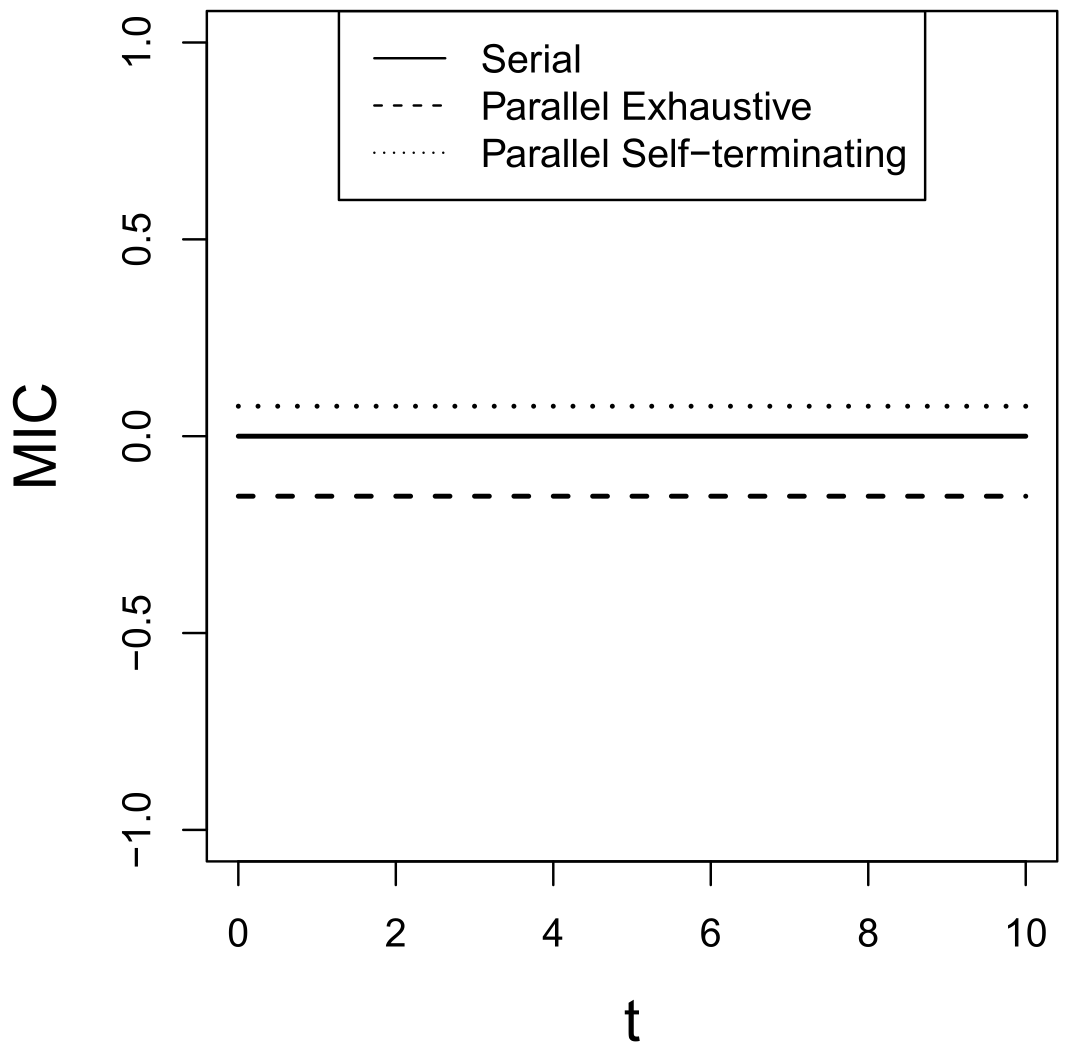
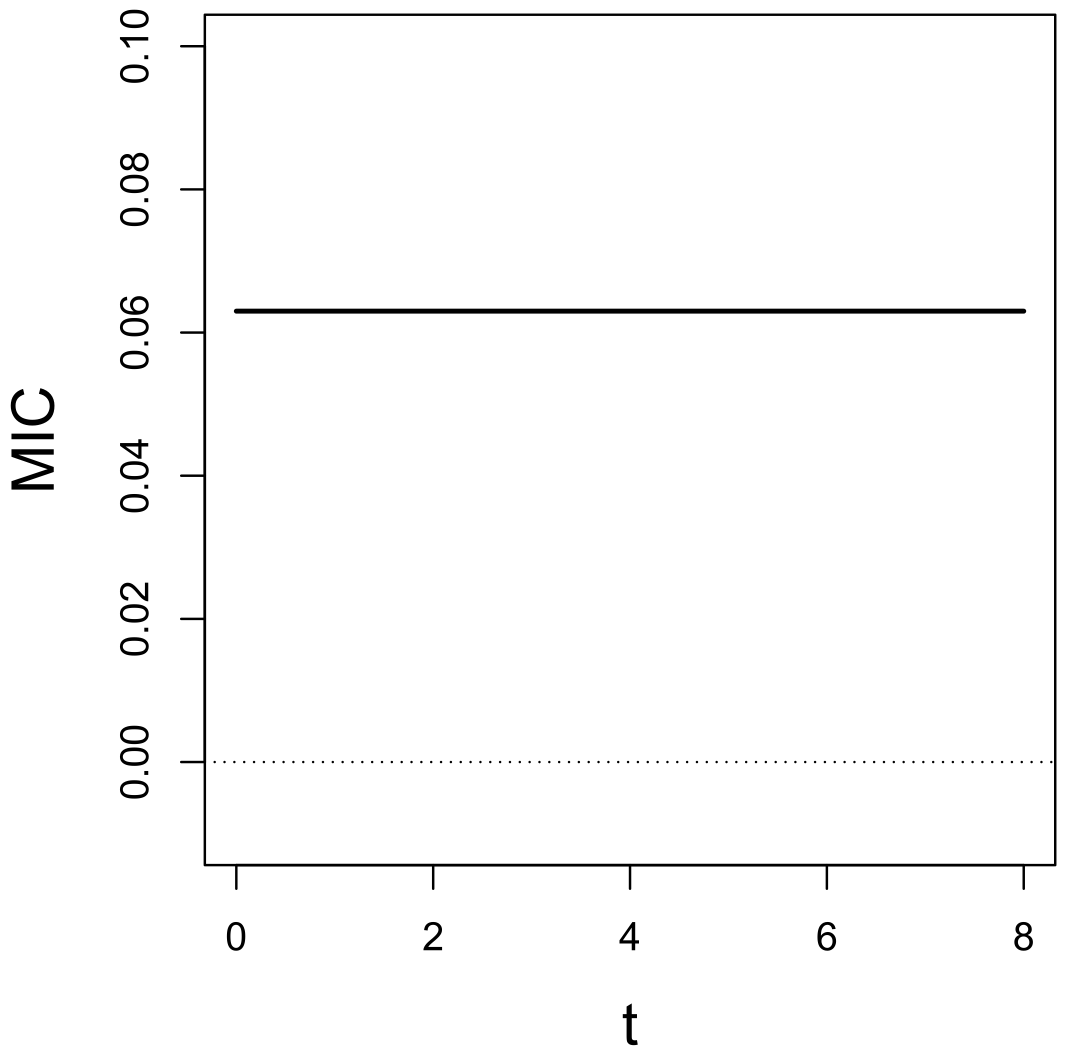
(b). Prove with a counter example. Let us construct the parallel joint cumulative function following Gumbel’s distribution (see Equation (3) in the proof of Proposition 6) by having $A_L=0.005$, $A_H=0.01$, $B_L=0.1$, $B_H=0.8$ and $\theta =5$. Then, compute the MIC following Equation (1) and the result is positive (Figure 6), which contradicts the canonical prediction on $MIC$ for parallel exhaustive systems. □

Now, the previous two propositions and their corollaries not only specify a range of when parallel systems can and cannot predict canonical $DIC$ functions, they tell us how to formulate models which do vs. do not obey marginal selectivity. We can take note especially from Corollary 2(1) that even the $MIC$s are not assured to be proper if the conditions in Propositions 1A and 1B are violated.

How do these latest results relate to the Dzhafarov definition? We include known results from Dzhafarov and colleagues for completeness sake.

Proposition 7.

Relationship of how the Experimental Factors Affect the Joint Distribution and the Dzhafarov Definition of Selective Influence in Parallel Systems. Consider the class of parallel systems with an exhaustive stopping rule.(a). The Dzhafarov definition of selective influence implies strong marginal selectivity.(b). Strong marginal selectivity does not imply the Dzhafarov condition.(c). The Dzhafarov condition does not imply weak marginal selectivity.(d). Weak marginal selectivity does not imply the Dzhafarov condition.

Proof. 

(a). The proof that marginal selectivity is forced by the Dzhafarov definition of selective influence ([33]) in fact entails the strong version can be seen through the fact that the latter only allows factor effects through the pairwise combining of the random variable with a factor—there is no other accompanying factorial influence.

(b). Observe that lots of joint distributions in copula form may have dependencies not expressed simply via conditional independence.

(c). If this was not the case, then absence of weak marginal selectivity would imply falsity of the Dzhafarov condition, but we know this is not true because strong marginal selectivity and weak marginal selectivity are incompatible.

(d). If weak marginal selectivity implied the Dzhafarov condition then weak marginal selectivity would imply canonical $DIC$s, but we know this is wrong.

□

At first glance, one might think that Proposition 7 contradicts Proposition 4. However, the insertion of the extra perturbations caused by influences of factors on non-marginal aspects of the joint distributions, in fact, violates the original terms of Dzhafarov’s definition.

Now that we have valuable information concerning parallel systems, what is the situation for serial systems? At this point, we have not been able to effectively utilize copula theory for assistance with serial models. Compared with certain other topics, even independent serial processing (thereby fomenting convolutions) has not been much treated, and we are not aware of any results regarding stochastically dependent serial events in relation to selective influence. We have been able to discover some facts as follows, but the story is far from complete as we will learn.

Because the canonical signature for exhaustive serial systems is not single signed but rather guarantees an odd number of crossovers (see [56]), we fully expected to find that even in the presence of the Dzhafarov ([39]) condition, we could find violating $DIC$ functions. We were rather astonished to discover that all 1-direction serial systems that obey the Dzhafarov dictum perforce generate canonical $DIC$ signatures. The following result goes beyond previous theorems regarding Dzhafarov’s definition of selective influence.

Proposition 8.

1-Direction Serial Systems and the Dzhafarov Definition of Selective Influence. Consider the class of 1-direction, two-stage serial systems which meet the Dzhafavov ([39]) definition of selective influence. Then, the $DIC$ will be canonical, that is, the number of crossovers will be odd.

Proof. 

Following Dzhafarov’s definition, the joint cumulative function of T of the 1-direction serial systems is: $F_{ab}(t;A,B,C=c)={\int }_0^t{F}_b(t-t_a;B|t_a,C=c)f_a(t_a;A|C=c)f_c(C=c)d{t}_a$.

Then, the $DIC\left(t\right)$ is:

$$\begin{array}{cc}\hfill & DI{C}_{1-\mathrm{direction},\mathrm{serial}}\left(t\right)\hfill \\ \hfill =& {\int }_0^t{F}_b(t-t_a;B_H|t_a,c)f_a(t_a;A_H|c)f_c(C=c)d{t}_a-{\int }_0^t{F}_b(t-t_a;B_H|t_a,c)f_a(t_a;A_L|c)f_c\left(c\right)d{t}_a\hfill \\ \hfill -& {\int }_0^t{F}_b(t-t_a;B_L|t_a,c)f_a(t_a;A_H|c)f_c(C=c)d{t}_a+{\int }_0^t{F}_b(t-t_a;B_L|t_a,c)f_a(t_a;A_L|c)f_c\left(c\right)d{t}_a\hfill \\ \hfill =& f_c\left(c\right){\int }_0^t[F_b(t-t_a;B_H|t_a,c)-F_b(t-t_a;B_L|t_a,c)][f_a(t_a;A_H|c)-f_a(t_a;A_L|c)]d{t}_a.\hfill \end{array}$$

Since $f_c$ is a density function for C, $f_c\left(c\right)>0$. By definition, $F_b(t-t_a;B_H|t_a,c)-F_b(t-t_a;B_L|t_a,c)>0$. When $t<t^{*}$ where $t*$ is the crossover point of the density functions, $f_a(t_a;A_H|c)-f_a(t_a;A_L|c)>0$. Thus, for small t that $0<t<t^{*}$, $DIC\left(t\right)$ must be positive. In addition, following the proof for Proposition 2.1 in H. Yang et al. ([56]), we can show that when $t\to \infty$, ${\int }_0^t[F_b(t-t_a;B_H|t_a,c)-F_b(t-t_a;B_L|t_a,c)][f_a(t_a;A_H|c)-f_a(t_a;A_L|c)]d{t}_a$ must approach 0 from the negative side. Therefore, the $DI{C}_{1-\mathrm{direction},\mathrm{serial}}\left(t\right)$ of the systems satisfying Dzhafarov’s definition on selective influence must be a function that is positive for small ts and converges to 0 from the negative side for $t\to +\infty$, for every value of c, which implies that it must have an odd number of crossovers.

Any function which starts negative and ends positive must have an odd number of crossovers. To see this is valid for the present circumstance, recall that the Dzhafarov definition of selective influence basically postulates a probability mixture on the pertinent density functions. Each one of these starts with a positive departure so the first one to be visible must also. The reverse holds in the sense that all densities in the mixture end with its functions being negative. So, will also be the last to appear. □

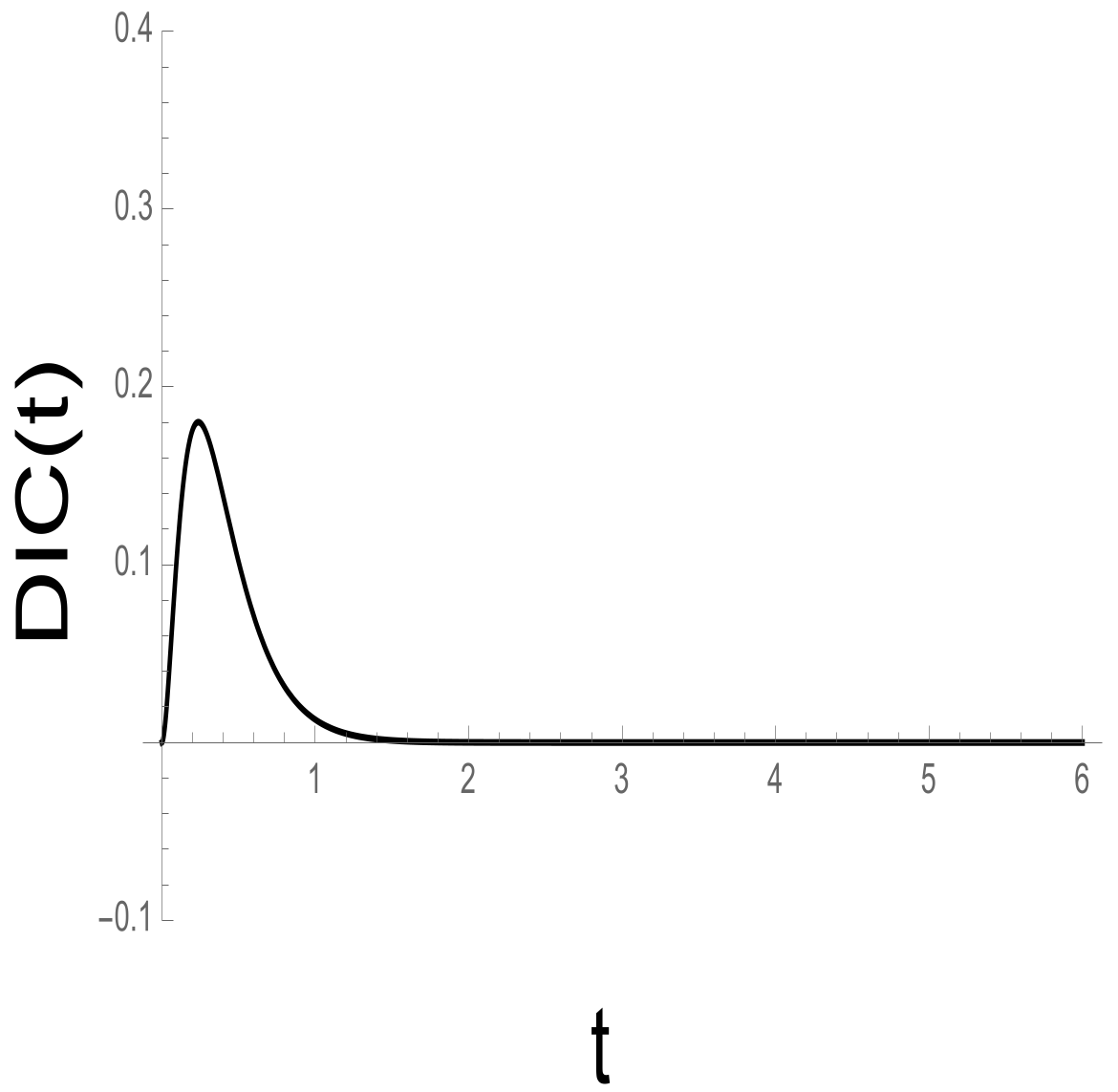
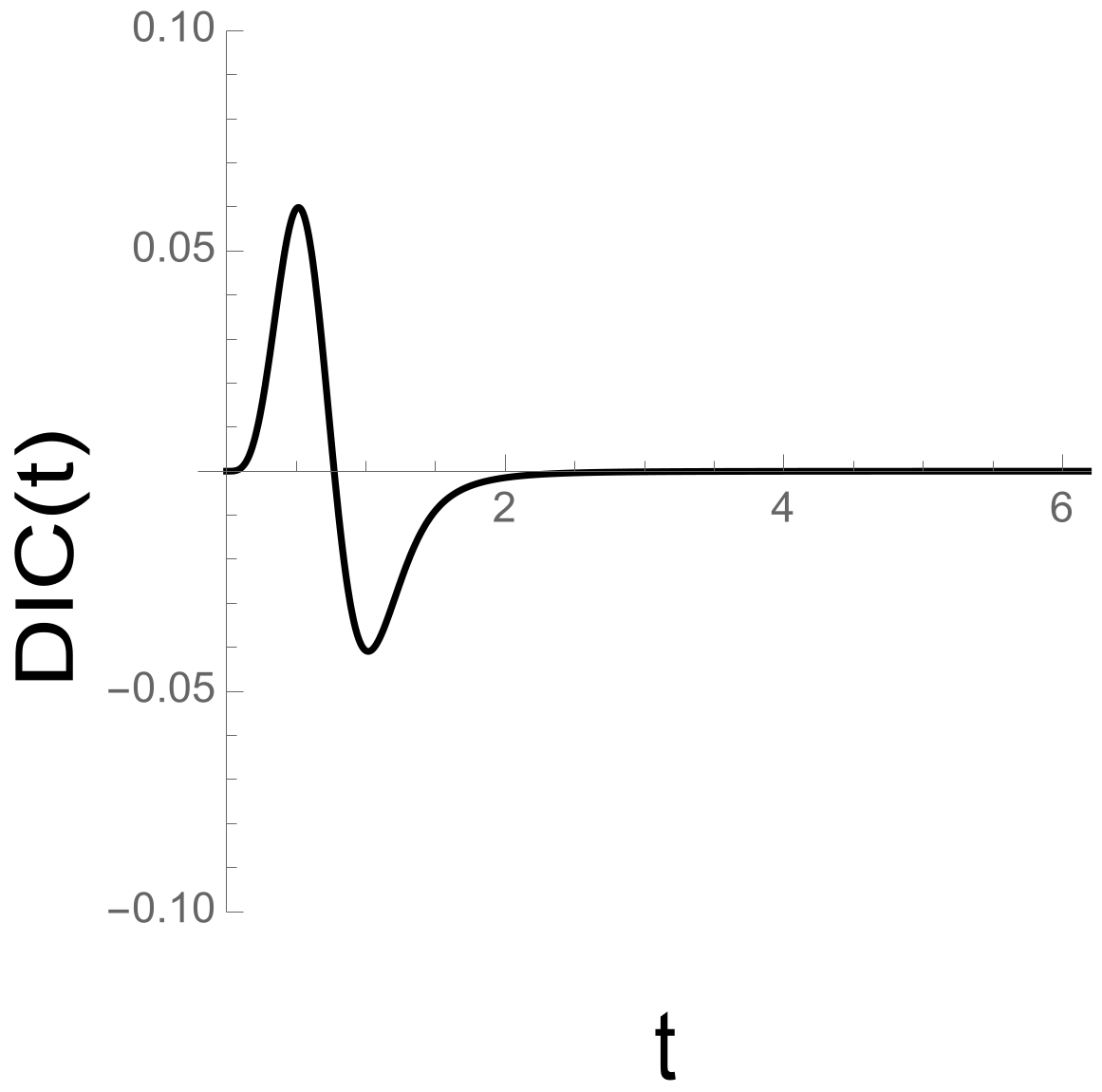
Together with Proposition 5, we have the pleasant result that the Dzhafarov selective influence condition ensures that both parallel and serial systems will evince canonical $DIC$ signatures, as long as pernicious influences do not arise via affecting aspects of the joint (parallel) distributions outside of the marginal. Figure 7 takes an earlier example of a 1-direction serial system which obeys the Dzhafarov definition and demonstrates that its $DIC$ function is canonical.

The next derivation, featured in Proposition 9, shows that marginal selectivity is sufficient to evince canonical $MIC$s with serial exhaustive processing.

Proposition 9.

Marginal Selectivity and 1-Direction Serial Systems. If even weak marginal selectivity is in force, regardless of satisfaction of the Dzhafarov condition, mean interaction contrast is canonical: $MIC=0$.

Proof. 

We provide the proof for exhaustive processing.

For exhaustive systems, the mean RT is:

$$\begin{array}{cc}\hfill E\left(T\right)& =E(T_a+Tb)\hfill \\ & ={\int }_0^{\infty }{\int }_0^{\infty }(t_a+t_b)f_a(t_a;A)f_b(t_b;B,A|t_a)d{t}_{a}d{t}_b\hfill \\ \hfill & ={\int }_0^{\infty }{t}_a{f}_a(t_a;A)d{t}_a+{\int }_0^{\infty }{t}_b{f}_b(t_b;B)d{t}_b(\because \mathrm{marginal}\mathrm{selectivity})\hfill \\ \hfill & =E(T_a;A)+E(T_b;B).\hfill \end{array}$$

Taking the factorial combinations of $A_L$, $A_H$, $B_L$, $B_H$ and figuring the double difference clearly yields:

$$\begin{array}{cc}\hfill & MIC\hfill \\ \hfill =& E(T_a;A_L)+E(T_b;B_L)-[E(T_a;A_H)+E(T_b;B_L)]\hfill \\ \hfill -& [E(T_a;A_L)+E(T_b;B_H)]+[E(T_a;A_H)+E(T_b;B_H)]\hfill \\ \hfill =& 0\hfill \end{array}$$

□

So, weak marginal selectivity, a rather coarse type of influences, to say the least, is all it takes to guarantee a proper mean interaction contrast result in a 1-direction serial system. Naturally, strong marginal selectivity will also do the trick, but we do not bother to make that a formal statement.

Our final question for this study is still an enigma: Does strong marginal selectivity imply canonical $DIC$s in exhaustive serial systems? We do not know the answer. On the one hand, even strong marginal selectivity would seem to be incapable of forcing canonical $DIC$s. Why should a condition where the dependencies are integrated out imply something formidable on a generalized convolution (i.e., the sum of the two random variables but with stochastic dependence) of the joint distribution? Although it certainly did with the class of exhaustive parallel systems, the sum function appears less directly affected, for example, than in the parallel models (recall that just letting $T_a=T_b=T$ altered the joint distribution into the distribution on the maximum function). In addition, the relative ease with which Townsend and R. Thomas ([37]) came up with dependencies that disrupted even the canonical $MIC$s would not seem to suggest very robust $DIC$s.

On the other hand, we have analyzed and performed computations with numerous dependent serial systems that obey strong marginal selectivity but that (so far) produce canonical $DIC$s. Some of the classic distributions in copula form, and made to satisfy strong marginal selectivity, form impressive examples. In addition, we do have our earlier example from Proposition 1A(c) which indicates a felicitous type of offset and evinces proper $DIC$s. 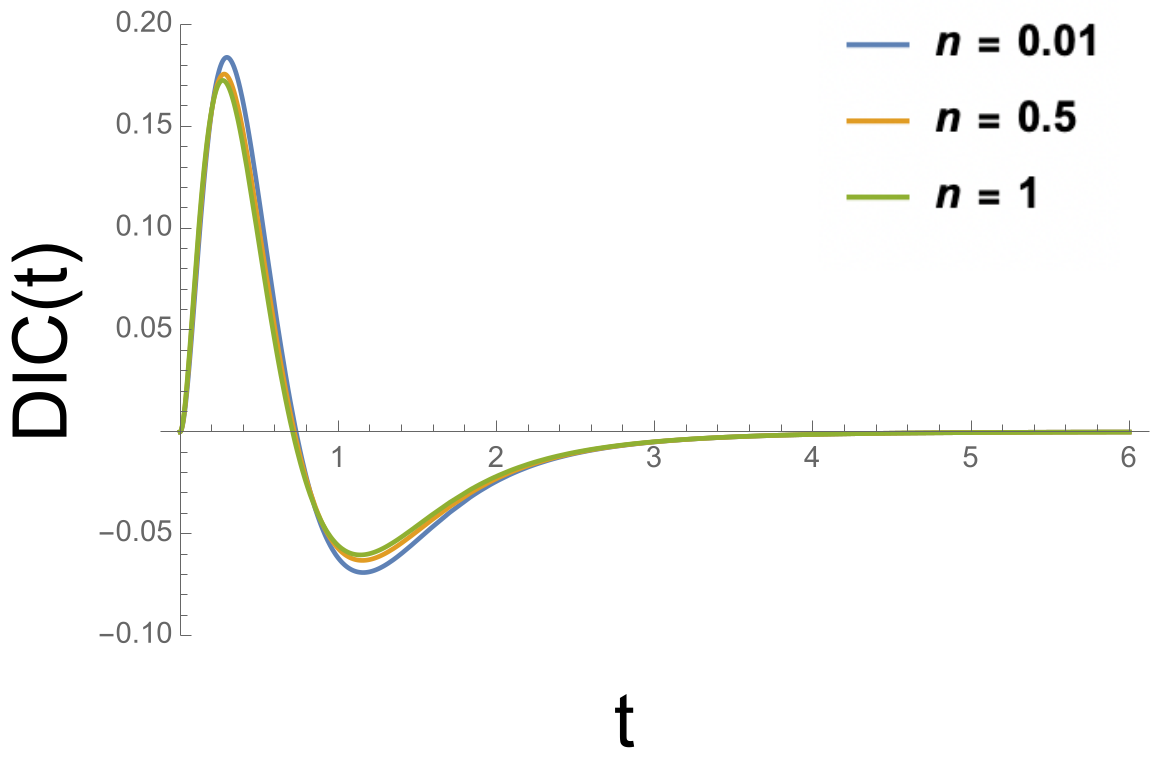In fact, we begin our final exploration by exhibiting the $DIC$s for several parameter settings of this rather classic example of offset, in Figure 8. In each of these cases, as predicted, the $MIC$s equal 0.

Next, we outline our reasoning with respect to features of what a counter example (i.e., possessing strong marginal selectivity but failing to reveal a canonical $DIC$) might logically possess and end with an example discussing what happens when we try that with a modification of a classic copula-interpreted distribution. It ends in failure, but perhaps a reader may see their way through to a counterexample or even to a proof to the contrary.

One way in which to try to perturb canonicality would be to simply predict an incorrect $MIC$. However, that is a non-starter since, as already demonstrated, a canonical $MIC$ in the case of seriality (and specifically here, exhaustive seriality) is guaranteed by strong marginal selectivity. To more readily appreciate the logic, consider first the special version where we can separate the first ${\mathbb{S}}_a$ density from that for ${\mathbb{S}}_b$ and assume direct selectivity on $f_a\left(t\right)$. In addition, we start by assuming no direct nonselective influence of A on ${\mathbb{S}}_b$. We know that this cannot end with marginal selectivity.

First, set $P(T_a=t_a,T_b\le t_b;A,B)=f_a(t_a;A)F_b(t_b;B|t_a)$. Next, we transform this to the conditional convolution: $P(T_a+T_b\le t;A,B)={\int }_0^t{f}_a(t_a;A)F_b(t-t_a;B|t_a)d{t}_a$ and then $DIC\left(t\right)={\int }_{t_a=0}^t[f_a(t_a;A_H)-f_a(t_a;A_L)][F_b(t-t_a;B_H|t_a)-F_b(t-t_a;B_L|t_a)]d{t}_a$.

Observe that the second difference in the integral is always positive. In addition, in order to produce $F_a(t_a;A_H)>F_a(t_a;A_L)$ for small $t_a$, the first difference must also be positive. Under positive circumstances, this ensures that the $DIC$ begins its trajectory as a positive function. We believe this type of machinery has to be overcome if a counter example were to be forthcoming.

Of course, when we insert direct nonselectivity in the second stage here:

$$\begin{array}{cc}\hfill DIC\left(t\right)& ={\int }_{t_a=0}^t{f}_a(t_a;A_H)[F_b(t-t_a;A_H,B_H)-F_b(t-t_a;A_H,B_L)]\hfill \\ \hfill & -f_a(t_a;A_L)[F_b(t-t_a;A_L,B_H)-F_b(t-t_a;A_L,B_L)]d{t}_a\hfill \end{array}$$

the expression becomes even more complicated.

Now, we currently know of no algorithm to even produce marginal selectivity from such expressions, although we do know that both indirect as well as direct nonselectivity must be present to induce marginal selectivity.

One natural tactic, given the success with copulas with parallel processing, might be to take such joint distributions but now interpret the random variables as serial duration rather than parallel processing times. We can then convert the expression to a generalized convolution as just above. One starts with the joint distribution and differentiates with regard to $t_a$. Then, substitute $t-t_a$ for $t_b$ and integrate the expression (integrand) over $t_a$ from 0 to t.

This approach possesses the advantage of generating a number of cases with automatic marginal selectivity characteristics. Nonetheless, so far, we have not been able to find a counterexample or to use the copula technique to find a proof that even strong marginal selectivity entails canonical $DIC$ functions. Yet, all our considered examples have turned out to engender canonical $DIC$s.

We now offer an example endowed with machinery that we had hoped might perturb the initial positivity alluded to above. Basically, we must transform the general expression $P(T_a\le t_a,T_b\le t_b;A,B)$ to $P(T_a=t_a,T_b\le t_b;A,B)$ via differentiation with respect to $t_a$ and then to convert to our generalized convolution and taking the double difference.

$$\begin{array}{cc}\hfill DIC\left(t\right)& ={\int }_0^t\{[P(T_a=t_a,T_b\le t-t_a;A_H,B_H)-P(T_a=t_a,T_b\le t-t_a;A_H,B_L)]\hfill \\ \hfill & -[P(T_a=t_a,T_b\le t-t_a;A_L,B_H)-P(T_a=t_a,T_b\le t-t_a;A_L,B_L)]\}d{t}_a\hfill \end{array}$$

The present copula distribution is slightly modified from the classic Gumbel’s bivariate exponential distribution (e.g., see [48]). Set:

$$\begin{array}{cc}\hfill & P(T_a\le t_a,T_b\le t_b;A,B)=1-e^{-A{t}_a}-e^{-B{t}_b}+e^{-A{t}_a-B{t}_b-q(A,B)t_a{t}_b},\hfill \\ \hfill & where0\le q(A,B)\le 1.\hfill \end{array}$$

Then, we take the derivative of the joint CDF with respect to $t_a$ to calculate $P(T_a=t_a,T_b\le t_b;A,B)$:

$$\begin{array}{cc}\hfill \frac{\partial P(T_a\le t_a,T_b\le t_b;A,B)}{\partial t_a}& =P(T_a=t_a,T_b\le t_b;A,B)\hfill \\ \hfill & =A{e}^{-A{t}_a}+(-A-q(A,B)t_b)e^{-A{t}_a-B{t}_b-q(A,B)t_a{t}_b}\hfill \end{array}$$

The cumulative distribution of the 1-directional serial exhaustive system: $P(T_a+T_b\le t;A,B)$ is calculated by replacing $t_b$ with $t-t_a$ and integrating $P(T_a=t_a,Tb\le t_b;A,B)$ with respect to $t_a$ from 0 to t:

$$\begin{array}{cc}\hfill & P(T_a+T_b\le t;A,B)\hfill \\ \hfill & ={\int }_0^t\{A{e}^{-A{t}_a}+(-A-q(A,B)(t-t_a))e^{-A{t}_a-B(t-t_a)-q(A,B)t_a(t-t_a)}\}d{t}_a\hfill \end{array}$$

We now try to find a counterexample by countering the earlier tilt toward a $DIC$. We do this by searching for a function $q(A,B)$ that satisfies its constraint but tends to lessen the early density’s ($t_a=0+ϵ$, when $ϵ$ is small) trend to be larger for $A_H$ than $A_L$. We performed calculations of $DIC$ assuming, say, $q(A,B)=\frac{B}{A^n}$ such that $\frac{B}{A^n}\in [0,1]$. Several of these are given in Figure 9. Clearly, this track did not pay off.

Appendix B presents other distributions that possess well-know copula form (and thereby immediately satisfy marginal selectivity). Putting them into proper form of 1-direction serial systems finds that they also induce canonical $DIC$s. We still suspect there must be a counterexample there. Two other examples based on the copula strategy are offered in the appendix. Perhaps one or more readers will solve this puzzler.

5. Summary and Discussion

Our introduction outlines some of the previous history and scientific philosophy regarding selective influence. We began with the apparently indisputable claim that any theoretical venture in psychology that goes beyond pure description or in a quantitative sense, curve fitting, must impart some notion of what we have called the “principle of correspondent change”. The latter, of course, includes symmetry and conservation laws of modern physics which can arguably be referred to as the linchpins of the science.

Due to the inextricable relationship of selective influence and mental architectures, we began our more rigorous developments with definitions of canonical serial and parallel systems (see Definitions 1 and 2). On seriality, we confine ourselves to “1-direction serial systems”, which assume a single processing order, say, “${\mathbb{S}}_a\to {\mathbb{S}}_b$”. We believe this tactic helps unveil essential structures and serial-parallel distinctions in a reasonably clear and cogent fashion. When in the realm of initial forays into complex territories, we have found this approach to be useful, as in the investigation of $DIC$s (recall, distributional interaction contrasts) for the number of channels or stages greater than two. Multi-order serial processes, self-terminating stopping rules (e.g., single-target, self-terminating and minimum time) and more-than-two subprocesses in the system (see, [56]) await extension of the present results.

The groundbreaking concept of selective influence was first formally proposed by S. Sternberg ([15]). The formulation indicated that if experimental factors selectively influence two or more successive and temporally non-overlapping processing durations, then the mean response times would be an additive function of those experimental factors. Our next definition (Definition 3) captures what we now refer to as Sternbergian selective influence. We move to our definition (Definition 4) of “pure selective influence” which is more general than the Sternbergian version in that it pertains to either a parallel or a serial architecture but, unlike the latter, explicitly assumes stochastic independence.

Perturbations caused by nonselective influences come in two major forms, direct and indirect, which are defined in Definition 5. Direct nonselective influence occurs when a probability distribution on processing time is an explicit, deterministic function of the “other” factor acting as parameter. Indirect nonselective influence is propagated by a process duration being stochastically dependent on the duration of a separate process.

When we give up pure selective influence, it might seem as if the proverbial doors to perdition itself might be opened. However, a robust generalization of the conception of selective influence which permits a type of stochastic dependence was proposed by Dzhafarov ([39]). We refer to this as “conditional independence selective influence” (Definition 6). We reviewed some of what is known about its ability to expose architecture and stopping rules and prove some novel ones. The reader is referred to the numerous references to his and his colleagues’ work for detail.

Yet another species of selective influence comes in the guise where the marginal distributions are only functions of the “proper” factor and are irrespective of potential nonselectivity of either the direct or indirect sort (Definition 7). The basic intuition is that, although the processes may be stochastically dependent and possibly even subject to direct nonselectivity, somehow the pernicious influences average out. It was lurking in the background at least back to Townsend ([23]) and, as admitted earlier in the present study, we incorrectly (and implicitly) believed if it held, then canonical $DIC$s would perforce always be propagated. Subsequently, it began to be explicitly named “marginal selective influence”. When more than two subprocesses are present, Dzhafarov ([39]) introduced a more strict definition of marginal selectivity that implies the version for $n=2$. It turns out that there is another way to further deconstruct marginal selectivity which can impact systems identification as exhibited in Definition 8. Definition 8 breaks down the concept of marginal selectivity into two separate and mutually exclusive cases, strong vs. weak marginal selectivity. Marginal selectivity in either guise is not ordinarily accessible in standard RT experiments. However, there exist designs where it can itself be assessed (e.g., [52,54]). Its relationships with other forms of selectivity and structural features turn out to be intriguing as well.

Returning to the concept of indirect nonselectivity, Dzhafarov ([38]) investigated a number of fundamental properties and consequences of this concept (i.e., nonselectivity caused through stochastic dependence). However, it remained unknown as to its relationship to marginal selectivity. Proposition 1A and 1B establish how it can be satisfied. The most intriguing aspect is that it can still be true even if both indirect and direct nonselective influence hold. This ability of direct nonselective influence to compensate for indirect perturbations is then defined as “offset” (Definition 9).

Propositions 1A and 1B limn in conditions that suffice for marginal selectivity in serial and parallel systems. Propositions 2A and 2B do the same regarding failure. Sealing the importance of offset in allowing (though not forcing) marginal selectivity is discovered in the portion of Proposition 2A(c), which proves that, lacking offset and in the presence of indirect nonselective influence, marginal selectivity is impossible. An immediate inference deriving from Proposition 2A and 2B comes with Proposition 3: Since the Dzhafarov definition of selective influence implies marginal selectivity, without offset but with indirect nonselective influence, the Dzhafarov condition must fail.

After deliberation and explication through more examples comes the inevitable issue of the impact of all these results on identification of architecture, the backbone of systems factorial technology ([14]). The next section ensues with reminders of the foundational definitions of the double difference statistics which, under proper conditions of selective influence, permit such identification. These form the distinguishing characteristics of the mean interaction contrast ($MIC$) and the much more potent distributional interaction contrast ($DIC$ or its complement, survivor interaction contrast, $SIC$). These remind the reader in Definitions 10 and 11.

We consider that the qualitative features of the architecture (and the pertinent) stopping rule predicted under pure selective influence to be characterized by the term “canonical”. For instance, under pure selective influence, exhaustive parallel systems produce survivor interaction contrasts that are always negative ([14]). Exhaustive serial systems’ survivor interaction contrasts start negative, cross the abscissa an odd number of times and end positive ([56]) and so on.

Proposition 4 states the fact employed earlier by Dzhafarov, Schweickert and Sung ([45]) that if the $DIC$ is single valued, then the Dzhafarov definition of selective influence preserves the canonical $DIC$ signature. In the case of some architectures, integration was called upon by these authors to produce the single signed property. Although very useful, this device can also bring forth more $DIC$ mimicking of signature. We revisit our new theorem on serial exhaustive processing below.

As acknowledged in the earlier text, we had, for a long spell, supposed that marginal selective influence would force canonical $DIC$ functions. One of the stark and surprising outcomes of the present theoretical enterprise was the finding that this belief might not be universally valid. On the one hand, we discovered for exhaustive parallel processing, with marginal selectivity and the imposed condition, that factors influence the joint distributions only through the marginals, then canonical results do indeed emerge. That is, strong marginal selectivity is well named. Yet, if the factors can exert influence in ways outside the marginals as with weak marginal selectivity, there can be (and probably usually will be) failure of the classical predictions. These findings are captured in Propositions 5 and 6. These discoveries we made possible through the use of copula theory, introduced into mathematical psychology by Colonius ([46,47,48]). Presently, we have not found a path to their exploitation with serial systems excepting for the means.

Proposition 7 explores the relationships of the two tiers of marginal selectivity to the Dzhafarov ([39]) definition of selective influence. Moving on to serial systems, we observed that the earlier Dzhafarov, Schweickert and Sung ([45]) results did not include the canonical serial predictions, perhaps because these are not single valued $DIC$ functions. We frankly expected that the canonical serial predictions would therefore not be valid even when the Dzhafarov condition was in force. Therefore, we were surprised to espy a simple proof that exhaustive serial systems enjoying selective influence of the Dzhafarov variety would indeed effectuate the canonical signature. This is Proposition 8.

A final fairly patent result may also be viewed as a partial, if weak, justification for our earlier belief in the impact marginal selectivity can have on system identifiability. Namely, marginal selectivity does imply the canonical MIC result for exhaustive serial systems, namely $MIC=0$. This statement partly, but only partly, helps justify our earlier belief in the force of marginal selectivity.

We finally investigated the linkages of marginal selectivity and distributions on the serial sum of times in serial exhaustivity, with very minor success. We trust that future work by mathematical psychologists can cut the Gordian knot on this one.

The seemingly simple unadorned notion of selective influence has turned out to be rather more complex and multifaceted than perhaps earlier appreciated. We now advocate for more of a rich, multi-tiered and not necessarily linearly ordered-by-implication set of concepts. Various types of influence may come to be most appropriate or observable in somewhat distinct circumstances. We look forward to further advances in this quest in the near future.