Abstract
Nowadays, there are a plethora of services that are provided and paid for online, such as video streaming subscriptions, car-share, vehicle parking, purchasing tickets for events, etc. Online services usually issue tokens that are directly related to the identities of their users after they sign up to a platform; users need to authenticate themselves by using the same credentials each time they use the service. Likewise, when using in-person services, such as going to a concert, after paying for this service, the user usually receives a ticket, which proves that he/she has the right to use that service. In both scenarios, the main concerns surround the centralization of these systems and that they do not ensure customers’ privacy. The involved service providers are trusted third parties—authorities that offer services and handle private data about users. In this paper, we designed and implemented FORT, a decentralized system that allows customers to prove their rights to use specific services (either online or in-person) without revealing sensitive information. To achieve decentralization, we proposed a solution where all of the data are handled by a blockchain. We describe and uniquely identify users’ rights using non-fungible tokens (NFTs), and possession of these rights is demonstrated by using zero-knowledge proofs—cryptographic primitives that allow us to guarantee customers’ privacy. Furthermore, we provide benchmarks of FORT, which show that our protocol is efficient enough to be used in devices with low computing resources, such as smartphones or smartwatches, which are devices commonly used in our use case scenario.
1. Introduction
Smart cities have evolved, with the inclusion of static internet-connected devices [1,2,3], such as pollution sensors, traffic lights, surveillance cameras, etc. Moreover, other mobile Internet of Things (IoT) [4] devices, such as autonomous cars, will soon populate across cities. If we consider all of the computers, smartphones, smartwatches, etc., we can observe how the density of devices achieves high numbers. Technically speaking, handling a large amount of connections will be possible thanks to 5G communications [5], which introduce network slicing to split the network into many virtual and logical networks, providing specific features for different services.
A high density of devices also translates to more data shared over the network. One concerning fact is what happens with the data shared by users, especially when such data are sensitive or can simply be used to profile users with no permission. Even with the increasing use of internet technologies, some security and privacy concerns [6,7] still need to be addressed. In this paper, we address the problem of trusted third parties (TTPs), which are still required in many scenarios [8]. For instance, GPS or autonomous driving applications trace our locations and collect much data about us. Even if a company says no personal data are collected, we can only trust them, with no possibility of detecting misbehavior. Other examples include medical devices that share sensitive information about patients through trusted web servers or any other service that requires a TTP.
One natural solution to avoid the need for a TTP involves the decentralization of its role. In this direction, several approaches [9,10] were explored in the last decade, involving the use of blockchain technologies to connect devices, skipping the need for a TTP in many cases. In the same context, new digital services have appeared on the market, changing how users interact with them. Among many use cases, we find car sharing, buying tickets for events, subscriptions to streaming services, etc. As centralization was a property of these applications, which used to lead to the control of the network by some individuals, blockchains [11] began to change the way people interacted with online services. The most common example, cryptocurrencies, has become a payment method without central authorities (i.e., banks) controlling the streams of the issued transactions and all of the collateral information. Moreover, beyond being a payment solution, some blockchains, such as Ethereum [12], offer a way to execute programs on-chain. Those programs, called smart contracts, allow issuing a payment to a specific party as soon as this party proves that he/she meets requirements specified in a contract. This same approach is used in many decentralized applications (DApps) [13] nowadays, such as paying for subscriptions to some service.
1.1. Motivation
Decentralization implies that public data stored in the blockchain can be accessed by anyone. This leads to some privacy concerns. As blockchains publicly store all network activity, user tracking or profiling becomes an issue. The problem is worse when users of a blockchain-based service need to interact with real-world services (i.e., proving to event staff that you paid for a ticket); if anyone learns about your blockchain identity, he/she will learn about all of your history.
Zero-knowledge proofs (ZKPs) are integrated within some blockchain projects, such as Zcash [14], to solve the privacy concerns from blockchain applications. ZKPs are cryptographic primitives, allowing users to prove to others that a statement regarding some secret information is true, without leaking such information. In the Zcash example, these primitives allow users to issue transactions without leaking their identities nor the amount of money they are spending, while proving that they are solvent.
Dusk Network [15], another blockchain, introduced a way to program private-by-design smart contracts—programs where executions and parameters are kept private while being validated by the network. This leads to a toolset capable of building new privacy-preserving applications, solving many privacy and security concerns.
In such a scenario, the concept of self-sovereign authentication [16] has appeared: authentication systems where users can manage their identities in a fully transparent way, deciding which information they are willing to reveal to other parties. Some solutions, such as SANS [17], allow users to prove to service providers (SP) that they own a token that proves their right to use a specific service. Such a solution is suitable in many scenarios, but some use cases can have efficiency drawbacks, since it relies on a ZKP construction called zk-SNARKs [18], which requires high computing power. This scheme is executable on Internet of Things (IoT) devices, thanks to implementations, such as ZPiE [19], but taking a fair amount of time. This fact makes such a solution infeasible in use cases where IoT devices must prove several things in a short amount of time (i.e., willing to use a smartwatch to prove a right, having a door sensor with a cheap CPU verifying proofs, etc.). Besides, this solution is still centralized, which means that if the SP disappears, the user no longer owns the right.
1.2. Our Contributions
In this paper, we introduce FORT, a novel self-sovereign authentication protocol, combined with blockchain technologies to provide a solution where users of a service acquire rights, which are a set of different provable blinded attributes. Such attributes are portions of personal information that have been blinded: they are invisible to the SP, and only the user can decide how much information about them has to be leaked. These attributes are represented by non-fungible tokens (NFT) [20] on the blockchain, which can be granted on-chain by entities providing services, the SPs, and verified off-chain. For instance, a car willing to access a smart city would have to prove its right to do so, having two attributes: a certificate stating that the car has a low-emissions level and a fee payment receipt for entering the city. Once the right is represented in the blockchain using an NFT, the car will be able to prove off-chain the possession of such a right, by using a ZKP [21]. Such proof will state the possession of a valid NFT, without leaking the identifier of such NFT nor the identity of the car owner. Furthermore, our solution also skips third-party fees: for instance, in the scenario of buying tickets online for some event, in many cases, the ticket is issued by a third party who handles ticketing management, and who needs to be trusted. Furthermore, this party charges the users a service fee. Our solution relies on the blockchain. Thus, the event organizer does not need to rely on third parties, and the user does not share his identity nor pay a service fee.
Moreover, even when ZKPs require high computing resources, our solution can be deployed in IoT devices thanks to ZPiE [19], the library we used to implement a proof-of-concept of our solution. This allows users to use our protocol, using devices with low computing resources, such as smartwatches.
Our contribution relies on zk-SNARKs, as well as on range proofs, another ZKP scheme where users prove that a value lies within a given range, without leaking such a value to other parties. In particular, we use the bulletproofs [22] range proofs scheme. For that reason, our second contribution in this paper involves the implementation of a bulletproofs module for ZPiE. Our implementation achieves excellent benchmarks, and using such a module, we implement our protocol and show its efficiency in IoT devices.
1.3. Roadmap
In Section 2, we present the background needed to understand the paper. In Section 3, we present the related works to our solution. In Section 4, we present the cryptographic building blocks of our solution. In Section 5, we present FORT, our solution. The implementation is detailed in Section 6, along with its security analysis and several benchmarks. Section 7 presents future works that could be conducted to integrate our solution into more use cases. We conclude in Section 8.
2. Background
In this section, we introduce the building blocks of our solution. We first introduce blockchain technologies and their applications to IoT, and later we focus on the details and the specific use cases of smart contracts. We finally review ZKPs and how they are used to scale blockchains by means of zk-rollups.
2.1. Blockchain
A blockchain [23] is a decentralized set of interconnected nodes, which share unique and immutable sets of data, called a ledger. Such a ledger is split into small portions of data called transactions, which are issued by different nodes in the network. In the scenario of cryptocurrencies, such as Bitcoin [11], these transactions are cryptographically validated by the network (i.e., a user sending bitcoins has enough funds to do so). Moreover, the whole network is ruled by a consensus agreed among all users of the network to keep the network safe (i.e., proof-of-work [24], proof-of-stake [25], etc.). The decentralization properties of blockchains and their security and privacy features have led toward their integration with smart cities and IoT scenarios. This has been a hot research topic in recent years, for instance, in surveys, such as the one provided in [26], where some of the challenges and opportunities in such regard are stated. Many use cases have emerged in recent years, including renting, sharing, or selling specific assets, such as cars or apartments. Other approaches are blockchains applied to wireless sensor networks [27] or e-health devices [28], among many others.
As such, large amounts of data regarding IoT devices can be found in blockchains—data that could be useful for improving traffic control, energy consumption, or pollution in smart cities. Interesting approaches, such as the one proposed in [29], allow for easy IoT discovery in blockchains. Regarding the security model, there are contributions, such as trust systems for IoT [10], where nodes of a blockchain can be trusted upon checking their reputation, which changes depending on the behavior of the nodes in the network.
2.2. Smart Contracts
One of the most useful blockchains in regards to our scenario is Ethereum [12]. It is a network whose purpose is not a currency for making payments, but rather a way to run distributed applications (DApps). DApps are possible thanks to smart contracts [30], pieces of code executed on the Ethereum virtual machine (EVM) [31]. Such contracts and the EVM allow users, for instance, to be paid upon fulfilling some conditions. For instance, distributed exchanges: applications where users buy or sell their cryptocurrencies to other users.
In order to execute transactions, Ethereum requires gas. This is the amount of Ether (Ethereum coin) per amount of bytes needed to run a transaction. Depending on how busy the Ethereum network is, the price of gas increases or decreases. This can make using Ethereum very expensive. To overcome such a problem, zero-knowledge-rollups (zk-rollups) have recently been proposed [32]. They basically group several transactions into a single transaction on the main Ethereum blockchain. Whereas the Ethereum network is called layer 1, the zk-rollup is commonly called an application of layer 2. The zk-rollups are possible thanks to ZKPs. Both ZKPs and zk-rollups are introduced in Section 2.3 and Section 2.4, respectively.
Similarly, as with Ethereum, Dusk Network [15] is a layer 1 blockchain that provides a virtual machine called Rusk, enabling the deployment and execution of smart contracts. However, they have introduced the confidential security contract standard (XSC), which ensures the preservation of transactional confidentiality while simultaneously guarantees compliance through the use of ZKPs. This opens the door to a wide variety of use cases where privacy is a must, but accountability is required at the very same time.
2.3. Zero-Knowledge Proofs
A zero-knowledge proof [21] is a cryptographic primitive that allows a prover P to convince a verifier V that a statement is true, without leaking any secret information. A statement is a set of elements known by both parties, defined as u, and the secret information only known by P is called the witness w. P wants to convince V that he knows w, which makes a set of operations involving u, to hold. Such operations are defined by a circuit, a graph composed of different wires and gates, which leads to a set of equations relating to the inputs and the outputs of these gates. Each of these equations is called constraint. As depicted in Figure 1, P executes a proving algorithm, using u as the set of public inputs and w as the private inputs. This execution outputs a set of elements of an elliptic curve defined over a finite field, which we call the proof . We send to V, who will use a verifying algorithm to verify that u is true, for a given w only known by P. Formally speaking, ZKPs must satisfy three properties:
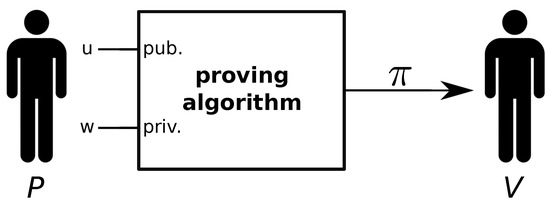
Figure 1.
Zero-knowledge proof scenario.
- Completeness: If the statement is true, P must be able to convince V.
- Soundness: If the statement is false, P must not be able to convince V that the statement is true, except with negligible probability.
- Zero-knowledge: V must not learn any information from the proof beyond the fact that the statement is true.
Even when first schemes required P and V to interact several times, non-interactive ZKPs (NIZKPs) [33] emerged, allowing P to prove statements to V by sending him a single message. However, the first schemes were expensive in terms of computing resources, and this made them not useful in real applications. More recently, zk-SNARKs appeared, which are zero-knowledge succinct and non-interactive arguments of knowledge [34]. This kind of proof is short and succinct: it can be verified in a few milliseconds, which makes it suitable for on-chain verification on blockchains using smart contracts, being relatively cheaper in terms of gas consumption than other solutions.
2.4. zk-rollups
zk-rollups [32], as depicted in Figure 2, create batches of several transactions in a layer 2 scenario, and publish the whole batch into a single layer 1 transaction. This saves a lot of gas that would be consumed if each transaction was executed directly on the main blockchain. To do so, we have two actors, the transactors willing to create a rollup transaction and the relayers computing the required operations to make the rollup work. In such regard, transactors send transactions to the relayers containing information about the sender, the receiver, the amount of tokens to be sent, etc. Such transactions also include a signature of the transaction. As stated previously, ZKPs require an elliptic curve, as proofs are sets of elements on such curves. For instance, the Barreto–Naehrig elliptic curve [35], called BN128, is the currently used curve for zk-SNARKs in Ethereum. The signature scheme used is EdDSA [36], which also requires an additional elliptic curve where parameters are compatible with the zk-SNARKs elliptic curve (BN128). In this scenario, the Baby Jubjub [37] elliptic curve is used for its compatibility with the parameters of BN128.
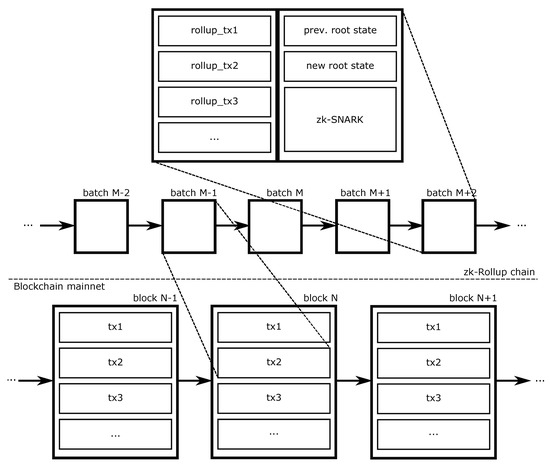
Figure 2.
zk-rollups overview.
Once the relayer has received a bunch of transactions, he computes a Merkle tree of the previous accounts’ state and the new state. Later, he computes a zk-SNARK, which verifies all signatures, and posts on the blockchain a transaction containing this batch: the rollup transactions, the previous and new root states, and the zk-SNARK. This transaction is verified by a smart contract previously deployed on the blockchain.
3. Related Work
Self-sovereign identity systems [38] have the premise of deploying protocols where users of different services can manage their identities in secure, transparent, and private ways. A general idea in this regard, and similar to our solution, was envisioned as a system where users can claim and prove possession of different rights associated with their identities, without compromising their privacy [39]. Furthermore, the combination of self-sovereign identity systems with ZKPs has become a new research topic in recent years [40]. In this regard, solutions, such as SANS [17], introduce a private authentication mechanism based on ZKPs. Using such tools, SANS allows users to prove their rights to access several services, without the service provider (SP) knowing the identity of the users, while guaranteeing that the users are allowed to use the service (e.g., the users have paid a subscription fee).
There are some differences between SANS and this work. In all cases, ownership of a given token can be proved (proof of ownership). Moreover, this work can prove that the token exists in the blockchain (proof of transaction). Our solution is meant to have protection against malleability: we allow the service providers (SP) to be sure that a given token has been used only once. We also deploy blinding attributes, where our solution becomes full self-sovereign: users reveal their data in transparent and private ways. Furthermore, the efficiency of our scheme is increased and its usage in IoT devices is totally feasible.
Regarding privacy in online transactions, other research papers, such as [41], explore interesting ways to provide a privacy-preserving authentication protocol by means of physical unclonable functions (PUFs), providing a solid and efficient protocol.
Moreover, research regarding how zk-SNARKs can contribute to blockchains scalability is being conducted [42], with the research focused on distributed proof generation making use of recursive zk-SNARKs.
However, combining IoT devices and NFTs is not an unexplored research area. Recently, researchers [43] introduced a solution to manage IoT devices securely. They associated NFTs stored in blockchains with IoT devices, to grant them unique and indivisible identities.
Finally, to the best of our knowledge, there are no other solutions that provide a private-by-design and self-sovereign system to authenticate users, providing, at the very same time, a decentralized architecture, just like FORT does.
4. Cryptographic Building Blocks
In this section, we provide the necessary background on zk-SNARKs and bulletproofs needed for the rest of the paper. We begin with a very high-level description of commitment schemes, and later move to an explanation of bulletproofs and zk-SNARKs.
4.1. Preliminaries
We begin by discussing a cryptographic primitive, which is at the core of almost all modern cryptographic constructions, commitment schemes. A commitment scheme allows us to select a secret value and commit to it, in the sense that the party performing the commitment cannot change that value for another in the future. The scheme gives the capability of revealing the value later on, but this is not a mandatory task. We are particularly interested in non-interactive commitment schemes, defined as follows:
Definition 1
(Non-interactive commitment schemes). A non-interactive commitment scheme consists of a pair of probabilistic polynomial time algorithms (setup, commit). The setup algorithm generates public parameters given the security parameter λ. Given the public parameters , the commitment algorithm, Commit, defines a function for message space , randomness space , and commitment space . Given a message , the commitment algorithm samples uniformly at random and computes
A useful commitment scheme for us is the Pedersen commitment, which we define as follows:
Definition 2
(Pedersen commitment scheme). Let be a group of order p and set and . The setup and commit algorithms for Pedersen commitments are defined as follows:
- Setup: Sample uniformly at random.
- : For a given , and a random value , we compute .
4.2. Bulletproofs
Bulletproofs [22] are short non-interactive zero-knowledge arguments of knowledge that require no trusted setup. This means that the prover P sends a single message to the verifier V, and this is enough to prove knowledge of the secret information. There is no need to rely on any prior information generated by a trusted party.
Bulletproofs were designed to enable efficient confidential transactions in cryptocurrencies, but they have found many other applications, such as shortening proofs of solvency or enabling confidential smart contracts [44]. The main technical feature of bulletproofs involves proving that a committed value lies within a certain interval. For example, in the context of blockchains, it is very useful to have an efficient protocol to prove that a secret value lies in the interval for some large value of . In the cryptographic community, this feature is called a range proof. Range proofs allow us to prove that a secret value (previously committed to) lies within a certain range. They do not leak any information about the secret value but the fact that it lies within the desired range.
Let be a cyclic group of prime order p and let be the ring of integers modulo p. An inner-product argument lets P convince V that he/she knows two vectors (bold font denotes a vector) such that
where are independent generators, , and . Now, let and let be a Pedersen commitment to c using randomness r. An inner-product range proof allows P to convince V that by proving the relation
Now consider the case where P needs to provide multiple range proofs at the same time. The idea of aggregated range proofs is to build a system that can provide a proof for multiple secret values and its efficiency is better than doing one proof for each of the secrets. Since the inner-product range proofs provided by bulletproofs have logarithmic size, it is possible to build efficient aggregated logarithmic range proofs. That is, it is possible to efficiently prove the relation
where m corresponds to the number of proofs. Bulletproofs can be computed in , and verified in linear time as well. The communication complexity (the size of the proofs) is .
4.3. zk-SNARKs
One of the most used ZKP systems in practice is zk-SNARKs [18]. This kind of proof is short and succinct: it can be verified in only a few milliseconds. zk-SNARKs require a trusted setup that is used both by the prover and the verifier to generate and verify proofs. The set of parameters obtained during the setup phase is commonly called the common reference string (CRS). If an attacker is able to get the secret random values used to generate the CRS, it would be able to generate false proofs. For this reason, the initial setup is commonly made through a secure multi-party computation (MPC) protocol [45], which generates the required parameters using a distributed computation protocol.
Definition 3
(zk-SNARKs). A zero-knowledge succinct non-interactive argument of knowledge involves a triple of algorithms (setup, prove, verify) that work as follows:
- : the setup algorithm outputs a proving key and a verification key given the security parameter λ and a circuit. Both keys (the CRS) are made public and can be used by the prover and the verifier to generate and verify proofs.
- : the proving algorithm produces a proof π using the proving key that attests that a statement u and a witness w are a correct solution to the set of equations derived from the circuit.
- : the verification algorithm uses the verification key to check whether π is a correct proof for the public statement u.
zk-SNARKs can be computed in . Both the verification and the communication complexity are .
5. Our Solution: FORT
In this section, we introduce our solution. We begin with an overall description of our protocol, and later present the specific details and its security analysis.
5.1. Overall Description
Our solution is meant to be used in scenarios where a user needs to prove his/her right to use a service, for instance, accessing a house rented online. In such a scenario, we envision the usage of a certificate installed in the user’s smartphone (or smartwatch, or any similar device), which can be validated by some sensor installed in the door of the house. Once validated, the SP might want a proof of meeting some requirements, linked with the previously validated certificate. We detail this workflow (as depicted in Figure 3) in this section, as follows:
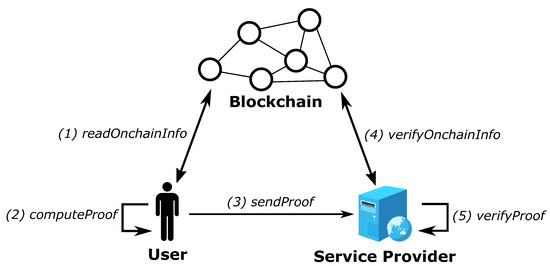
Figure 3.
FORT protocol scenario overview.
- Read on-chain information: the user acquires some attributes granted by third parties, which can be a SP to whom the user is buying a ticket or subscription, a governmental entity verifying personal information, a bank providing a proof of solvency, etc. Such attributes are granted through an NFT stored in a blockchain. The SP issues an NFT representing user attributes. The SP mints this NFT on-chain, and later transfers it to the user’s address. Now, the user can read these attributes from the blockchain.
- Compute proof (the certificate): the user acts as a prover, and computes a ZKP from the information collected from the NFT, as detailed in the circuit of Figure 4, and installs this certificate on his/her device.
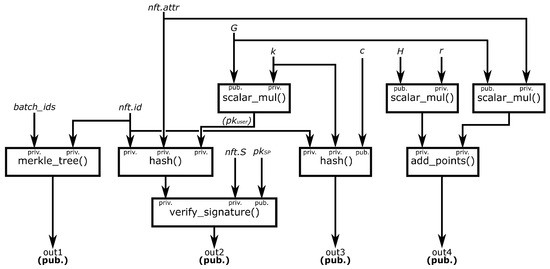 Figure 4. Circuit for our solution.
Figure 4. Circuit for our solution. - Send proof (read certificate): the user attempts to use the service by showing the certificate to the SP, who reads it.
- Verify on-chain information: the SP needs to partially read the Merkle tree of the blockchain (as detailed in the next section) to verify (in the next step) that the attributes the user wants to prove are really on-chain (the NFT).
- Verify proof (validate the certificate): the SP verifies the ZKP; thus, verifying the rights of the user.
After performing this protocol, the SP can ask the user for some information about the attributes, for instance, if they lay within a specific range. To do it, the user computes a bulletproof and sends it to the SP, the verifier. Then, the SP verifies that the bulletproof sent by the user is correct, and knows for sure that the value is within a specific range.
Ideally, a desirable way to implement our protocol would be by creating the NFTs directly using a blockchain, proving that we own them by using the signature details, involving the blockchain transaction representing each NFT. However, this has some constraints regarding scalability and efficiency: first, the gas fees in the case of Ethereum can become very expensive, so using a transaction for a single right is far from being optimal. Second, the elliptic curve used to sign Ethereum transactions, the secp256k1, is not pairing-friendly, so generating proofs proving ownership of the private key used to sign the transaction will not be efficient. To solve this problem, FORT relies on zk-rollups for scalability and on EdDSA for proofs off-chain.
5.2. Protocol Details
To prove rights to access the service, the first thing a user needs to do is to receive an NFT stating some attributes about him/her. To do so, the user needs to contact the SP and provide him/her a proof of meeting some requirements. Then, the SP executes Algorithm 1: after validating the requirements, it issues an NFT representing the user’s attributes. The SP mints this NFT on-chain, and later transfers it to the user’s address.
| Algorithm 1: Create NFT |
 |
Upon receiving the NFT, the user is ready to anonymously prove possession of such an NFT. To do so, the user will follow the Algorithm 2. Then, at some point, the user will want to prove some rights; to do so, he/she will send/show the proof to the SP, and it will execute Algorithm 3.
| Algorithm 2: Create certificate |
Env: User and service provider (SP).
|
| Algorithm 3: Verify certificate |
Env: User and Service Provider (SP).
|
| Algorithm 4: Verify right |
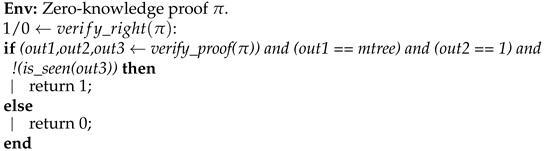 |
The proof used in Algorithm 2 uses the circuit depicted in Figure 4. As can be seen, the circuit includes a verification of the signature , using the public key of the SP . The inputs of the signature were the attributes along with the ID and the public key of the user . The challenge c is hashed along with and the user’s private key k. is also hashed along with .
Finally, and before the SP grants the service, the prover might have to create a bulletproof to reveal some information about the attributes. This is done using , a Pedersen commitment. This process is detailed in Algorithm 5.
| Algorithm 5: Create bulletproof |
Env: secret key k; vector of x attributes: ; vector of x commitments: : fori in x do end |
5.3. Security Analysis
An important element to consider when analyzing the security of FORT is the ZKP scheme to use. The main drawback of some ZKP constructions, such as zk-SNARKs, when used in some scenarios, such as cryptocurrencies, is the need for a trusted setup. An untrusty setup could lead to huge losses of money if a malicious party gets the seed used to compute it, so it could create false transactions. This is not a problem in our solution: a different setup can be generated by each SP, as the proofs are verified off-chain by a single entity, the SP, and he is the main interested in not leaking the secret seed.
Moreover, the soundness property of each scheme relies on different security assumptions [46] (e.g., zk-SNARKs in [47] use a strong assumption, the q-power knowledge of exponent (q-PKE) assumption). Furthermore, the security of these schemes relies on the security of elliptic curves, where breaking the security of the selected curve would lead to being able to generate false proofs. One of the most used curves in ZKPs is the BN128, which security level in practice is estimated to be 110-bits [48]. Other curves, such as BLS12-381 [14], estimate around 128-bits of security, with the drawback of heavier group operations. More recent research is introduced in [49], where a new curve called BW6-761 is introduced. As stated by its authors, verification of proofs is at least five times faster than other state-of-the-art curves.
Regarding the circuit we designed, our solution grants several privacy and authentication features:
- Proof of ownership: the circuit used in FORT verifies a signature of an input , using the public key of SP, . Moreover, is the output of the scalar multiplication , where k is the user’s private key. This ensures that the user owns the NFT, as only he/she can compute the public key using the private key, while keeping both values private, so the SP cannot learn the identity of the user.
- Proof of transaction: the circuit computes a Merkle tree of two private inputs: the and the IDs of some other issued NFTs in the same batch . This ensures that the NFT the user is proving ownership of has been transacted in the blockchain. The SP can compute the Merkle tree itself, and check if it equals as stated in Algorithm 4.
- Malleability protection: the circuit computes the hash of , the private key k, and a challenge c. The format of this value could change in different scenarios. Taking the example of proving ownership of a ticket for an event, ideally, c would be the date of such event. If , it means that someone already entered the event with the same NFT. This is true because neither nor k can change, so will always be the same for a given public input c. This prevents a user to use the same right multiple times, and to compute valid proofs for other users.
- Attribute blinding: the private information the user wants to share only when required, the attributes, are private inputs of the circuit. Such values are committed using a Pedersen commitment (i.e., , but as many as required can be included in the circuit), so the verifier learns these commitments, and the prover later uses a bulletproof to prove knowledge of them, and to prove that they are within a specific range.
FORT, as introduced in this section, can also be seen as a framework to be modified to match the needs of every use case our solution could be deployed to. This means, selecting the proper ZKP scheme to be used, recompute the certificate each time instead of using bulletproofs, select a different challenge c, etc.
6. Implementation and Benchmarks
In this section, we explain the capabilities and implementation details of the bulletproofs module we developed, and later explain how we implemented our specific solution using our module.
6.1. Bulletproofs Module
We implemented bulletproofs as a module integrated into ZPiE, a ZKPs library coded in C. The library uses GMP and MCL as dependencies: GMP is a pure C library used to handle big numbers and operations involving them, and MCL is a library written in C++, which offers a C wrapper for using it in pure C projects, used to do elliptic curve operations. The library also supports the elliptic curves BN128 and BLS12-381, which are also supported by our implementation. We implemented an API that allowed us to generate aggregated range proofs using the bulletproofs scheme above referred, and to verify them. The instructions on how to compile and use the library can be found in the README of the repository. The code can be used as explained in Listing 1.

Listing 1.
Bulletproof generation example. Generation of 2 aggregated proofs of 64 bits.
We benchmarked our implementation as depicted in Figure 5. Moreover, we improved the efficiency of our solution by using multi-threading in several parts of the prover and the verifier, where splitting the operations in different cores was possible. As one can see, we benchmarked the time it takes by the prover, in single-core (SC) or multi-core (MC), to compute the proofs. We performed the experiments for several amounts of aggregated proofs of 64 bits, using a 4-core CPU, and BN128.
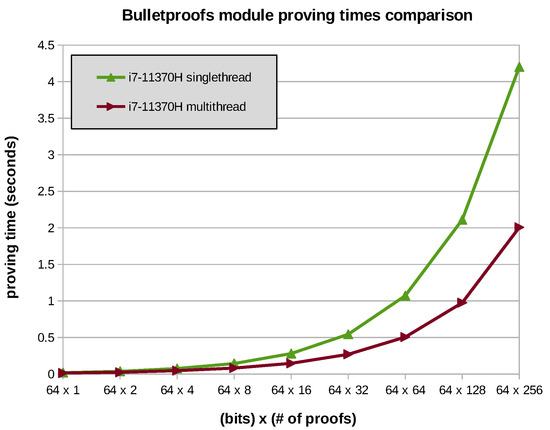
Figure 5.
CPU proving times of our solution.
6.2. Solution Deployment
In this subsection, we detail the deployment of the three main parts of our protocol, generate rights, generate the certificate, and prove the attributes.
6.2.1. Generate Rights
The first step to use our solution is to generate the rights that our users will need to prove. To do so, a SP needs to provide a service and sell its subscription using an NFT minted to a smart contract-based blockchain. For testing purposes, we used an Ethereum testnet where we created test NFTs using a reference implementation of ERC-721 (the Ethereum NFT standard) (https://github.com/nibbstack/erc721, accessed on 28 September 2021). After deploying an NFT to the blockchain, a user can buy it. Once done, he is ready to generate the certificate.
The computational costs for generating the NFTs are negligible, as no heavy cryptographic computations are involved in the process. Regarding the time it takes to be reflected on the blockchain, it would depend on how crowded it is (typically it will take only a few minutes). On the other hand, one of the main concerns regarding this step when deploying it into the mainnet is the amount of gas required to execute the smart contract that mints the NFT. As discussed before, using zk-rollups would be the best choice to reduce the cost when moving our solution to a production environment.
In Section 7, we discuss further work to be done regarding the deployment of our solution into a blockchain network, considering how to boost even further the capabilities of our solution when using other blockchains as the backbone of FORT.
6.2.2. Generate the Certificate
As explained previously, the prover precomputes the certificate, which is a zk-SNARK, required to use a specific service. The SP will verify the certificate and will be sure of the prover’s right to use the service. We used circomlib (https://github.com/iden3/circomlib, accessed on 28 September 2021) to estimate the number of constraints of the circuit used in our solution and, thus, its efficiency. To create our circuit, we rely on four main functions:
- scalar_mul(): the circuit needs to multiply a number k by a point on an elliptic curve G. To do this scalar multiplication using BN128, circomlib uses 776 constraints.
- hash(): the circuit needs to perform two fixed hashes, plus a variable number of hashes to compute a Merkle tree. A fairly secure and efficient hash function is Poseidon [50], which only uses 210 constraints in circomlib.
- verify_signature(): we used the state-of-the-art signature scheme EdDSA [36] over BN128 provided in circomlib, which uses 4018 constraints.
- merkle_tree(): the circuit needs to compute a Merkle tree. Assuming that , our solution will need to compute eight Poseidon hashes. This sums up to 1680 constraints.
In total, our circuit can be implemented using 6894 constraints. We coded a proof-of-concept using ZPiE (https://github.com/xevisalle/zpie, accessed on 28 September 2021), and executed the code using a laptop, a smartphone, and a Raspberry Pi Zero. To demonstrate the scalability of our solution, we also executed the circuit using snarkjs (https://github.com/iden3/snarkjs, accessed on 28 September 2021), a JavaScript implementation of zk-SNARKs, which can be executed in web browsers. This is perfect for scalability in web applications, with the performance drawback it involves, compared with binaries executed directly in the kernel. Table 1 shows the results.

Table 1.
Performance results of FORT in different devices using different implementations. All experiments used Groth16 and BN128.
As can be seen, either in high-end devices (a laptop CPU, such as i7-11370H) or in mobile CPUs (snapdragon 732 G), the proofs used in our protocol can be computed in a fair small amount of time using ZPiE. On the other hand, the time increases when talking about extremely low-end CPUs, such as the one used in the Raspberry Pi Zero. Nevertheless, computing the proof in about a minute, taking into account the single-core 700 MHz CPU that it uses (approximately 10$), is a good result. Furthermore, an advantage of FORT is that proofs can be precomputed prior to being used. Even in worst-case scenarios, protocols, such as the one introduced in [51], would allow those devices to rely computations on other servers owned by the same user, using a secure channel.
Regarding the verification of these proofs, as we stated previously, the verifier is succinct: all proofs can be verified in just a few milliseconds, with no relation to the size of the circuit. As can be seen, ZPiE outperforms here, even in Raspberry Pi, where it takes roughly 0.1 s to verify proofs.
Finally, we can see how the prover and the verifier in snarkjs are much slower than ZPiE for the same CPU. However, such a result was expected; taking into account the trade-off between performance and scalability, it is still a great result.
6.2.3. Prove the Attributes
The SP, after verifying the certificate, might want to be sure that some of the attributes meet some additional requirements (e.g., being within a given range). For such a purpose, we computed a bulletproof from the Pedersen commitment described in the zk-SNARK circuit. We used the module introduced in the last section to achieve this outcome. In Listing 2, we show how to deploy our solution, where the prover proves knowledge of the Pedersen commitment; the secret lies within the range .

Listing 2.
Implementation of our solution.
The above code for proving knowledge of an 8-bit attribute takes only 0.3 s on a Raspberry Pi Zero. This time increases as the size of the attributes increases, but with a fair amount of time, to be able to use our solution in IoT devices without problems. Executing the same approach using a zk-SNARK will require around 776 constraints, and the benchmark gives us 10.5 s. As such, it is clear that bulletproofs are a much better approach for this specific use case, where provers will be able to execute the protocol instantly using low-powered devices.
7. Discussion on Future Works
We introduced a protocol that allows a user to get some rights to be used in different scenarios: the right to use a service (i.e., demonstrate having some attributes, such as not being underage, having a salary above some threshold, etc.) or the right to access an event (i.e., demonstrate to have the attribute, in this case, the ticket for entering to an event, a performance, etc.). Our protocol works as-it-is in such scenarios. Needless to say, some changes shall be made if other constraints arise, or in other use cases. The usage of standard NFTs on Ethereum opens up a wide range of features to implement. For instance, NFTs offer the feature of being transferred from one user to another, while charging a percentage of the selling price to the original creator of the token (e.g., the event planner). At the very same time, a SP organizing a performance could allow users to resell the tickets if they cannot attend, but prevent them from increasing the price, while preventing price speculations as well.
We have seen how FORT could be easily deployed using blockchains, such as Ethereum or Dusk. Regarding the latter, which, at the time of writing, is still under development, we have to take into account the private nature of the execution of the smart contracts. We envision how future work in a fully integrated solution within their network could lead to new privacy models, enhancing our protocol by even blinding the data we need to store on-chain.
8. Conclusions
In this paper, we introduced a protocol to prove the right to use a service or access an event, in a self-sovereign manner. Our protocol grants one the chance to buy or request to be granted different attributes, which are grouped into rights, using a blockchain. We can prove ownership of such rights using zero-knowledge proofs, the main element of our FORT protocol. After stating the details of FORT and its security analysis, we performed several tests to show that—using only 6894 constraints—it can be executed very efficiently in a wide variety of devices and environments: desktop, mobile, and web applications. We saw how we could compute a certificate with a user’s rights in less than one second using a conventional smartphone. Later, the attributes of the certificate could be proved in just a few milliseconds. In the future work section, we discussed how our protocol could be modified to fit in other use cases, such as ticket reselling or rights transferring, and how integrating our solution into the Dusk Network blockchain could lead to a higher level of privacy.
Author Contributions
Conceptualization, X.S.; methodology, X.S. and S.R.; software, X.S.; investigation, X.S. and S.R.; writing—original draft preparation, X.S. and S.R.; writing—review and editing, X.S., S.R. and V.D.; supervision, V.D.; project administration, V.D.; funding acquisition, V.D. All authors have read and agreed to the published version of the manuscript.
Funding
Project RTI2018-102112-B-100 (AEI/FEDER, UE) and H2020 PRESENT grant agreement no. 856879.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
Not applicable.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Ramos, F.; Trilles, S.; Muñoz, A.; Huerta, J. Promoting Pollution-Free Routes in Smart Cities Using Air Quality Sensor Networks. Sensors 2018, 18, 2507. [Google Scholar] [CrossRef] [Green Version]
- Misbahuddin, S.; Zubairi, J.A.; Saggaf, A.; Basuni, J.; A-Wadany, S.; Al-Sofi, A. IoT based dynamic road traffic management for smart cities. In Proceedings of the 2015 12th International Conference on High-Capacity Optical Networks and Enabling/Emerging Technologies (HONET), Islamabad, Pakistan, 21–23 December 2015; pp. 1–5. [Google Scholar] [CrossRef]
- Al-Turjman, F.; Lemayian, J.P. Intelligence, security, and vehicular sensor networks in internet of things (IoT)-enabled smart-cities: An overview. Comput. Electr. Eng. 2020, 87, 106776. [Google Scholar] [CrossRef]
- Painuly, S.; Kohli, P.; Matta, P.; Sharma, S. Advance Applications and Future Challenges of 5G IoT. In Proceedings of the 2020 3rd International Conference on Intelligent Sustainable Systems (ICISS), Thoothukudi, India, 3–5 December 2020; pp. 1381–1384. [Google Scholar] [CrossRef]
- ETSI (3GPP). Procedures for the 5G System (5GS), v15.5.1, Release 15. 2019. Available online: https://www.etsi.org/deliver/etsi_ts/123500_123599/123502/15.05.01_60/ts_123502v150501p.pdf (accessed on 28 September 2021).
- Ijaz, S.; Shah, M.A.; Khan, A.; Ahmed, M. Smart cities: A survey on security concerns. Int. J. Adv. Comput. Sci. Appl. 2016, 7, 612–625. [Google Scholar] [CrossRef]
- Van Zoonen, L. Privacy concerns in smart cities. Gov. Inf. Q. 2016, 33, 472–480. [Google Scholar] [CrossRef] [Green Version]
- Zhu, L.; Li, M.; Zhang, Z.; Qin, Z. ASAP: An anonymous smart-parking and payment scheme in vehicular networks. IEEE Trans. Dependable Secur. Comput. 2018, 17, 703–715. [Google Scholar] [CrossRef]
- Ayoade, G.; Karande, V.; Khan, L.; Hamlen, K. Decentralized IoT Data Management Using BlockChain and Trusted Execution Environment. In Proceedings of the 2018 IEEE International Conference on Information Reuse and Integration (IRI), Salt Lake City, UT, USA, 6–9 July 2018; pp. 15–22. [Google Scholar] [CrossRef]
- Di Pietro, R.; Salleras, X.; Signorini, M.; Waisbard, E. A blockchain-based Trust System for the Internet of Things. In Proceedings of the 23nd ACM on Symposium on Access Control Models and Technologies, New York, NY, USA, 13–15 June 2018; pp. 77–83. [Google Scholar]
- Nakamoto, S. Bitcoin: A Peer-to-Peer Electronic Cash System. 2008. Available online: https://bitcoin.org/bitcoin.pdf (accessed on 28 September 2021).
- Wood, G. Ethereum: A Secure Decentralised Generalised Transaction Ledger. 2014. Available online: https://gavwood.com/paper.pdf (accessed on 28 September 2021).
- Shamili, P.; Muruganantham, B.; Sriman, B. Understanding Concepts of Blockchain Technology for Building the DApps. In Intelligent Computing and Applications; Dash, S.S., Das, S., Panigrahi, B.K., Eds.; Springer: Singapore, 2021; pp. 383–394. [Google Scholar]
- Hopwood, D.; Bowe, S.; Hornby, T.; Wilcox, N. Zcash Protocol Specification—Version 2019.0.2. 2019. Available online: https://github.com/zcash/zips/blob/master/protocol/protocol.pdf (accessed on 28 September 2021).
- Maharramov, T.; Khovratovich, D.; Francioni, E. The Dusk Network Whitepaper. 2021. Available online: https://dusk.network/uploads/The_Dusk_Network_Whitepaper_v3_0_0.pdf (accessed on 28 September 2021).
- Fedrecheski, G.; Rabaey, J.M.; de Paula Costa, L.C.; Calcina-Ccori, P.C.; Pereira, W.T.; Zuffo, M.K. Self-Sovereign Identity for IoT environments: A Perspective. In Proceedings of the 2020 Global Internet of Things Summit (GIoTS), Dublin, Ireland, 3 June 2020; pp. 1–6. [Google Scholar]
- Salleras, X.; Daza, V. SANS: Self-Sovereign Authentication for Network Slices. Secur. Commun. Netw. 2020, 2020, 8823573. [Google Scholar] [CrossRef]
- Groth, J. On the Size of Pairing-Based Non-interactive Arguments. In Advances in Cryptology—EUROCRYPT 2016; Fischlin, M., Coron, J.S., Eds.; Springer: Berlin/Heidelberg, Germany, 2016; pp. 305–326. [Google Scholar]
- Salleras, X.; Daza, V. ZPiE: Zero-Knowledge Proofs in Embedded Systems. Mathematics 2021, 9, 2569. [Google Scholar] [CrossRef]
- Entriken, W.; Shirley, D.; Evans, J.; Sachs, N. EIP-721: ERC-721 Non-Fungible Token Standard. 2018. Available online: https://eips.ethereum.org/EIPS/eip-721 (accessed on 28 September 2021).
- Goldwasser, S.; Micali, S.; Rackoff, C. The Knowledge Complexity of Interactive Proof-systems. In Proceedings of the Seventeenth Annual ACM Symposium on Theory of Computing; ACM: New York, NY, USA, 1985; pp. 291–304. [Google Scholar] [CrossRef] [Green Version]
- Bünz, B.; Bootle, J.; Boneh, D.; Poelstra, A.; Wuille, P.; Maxwell, G. Bulletproofs: Short Proofs for Confidential Transactions and More. In Proceedings of the 2018 IEEE Symposium on Security and Privacy (SP), San Francisco, CA, USA, 20–24 May 2018; pp. 315–334. [Google Scholar] [CrossRef]
- Leible, S.; Schlager, S.; Schubotz, M.; Gipp, B. A Review on Blockchain Technology and Blockchain Projects Fostering Open Science. Front. Blockchain 2019, 2, 16. [Google Scholar] [CrossRef]
- Gervais, A.; Karame, G.O.; Wüst, K.; Glykantzis, V.; Ritzdorf, H.; Capkun, S. On the security and performance of proof of work blockchains. In Proceedings of the 2016 ACM SIGSAC Conference on Computer and Communications Security, Vienna, Austria, 24–26 October 2016; pp. 3–16. [Google Scholar]
- Bentov, I.; Lee, C.; Mizrahi, A.; Rosenfeld, M. Proof of activity: Extending bitcoin’s proof of work via proof of stake [extended abstract] y. ACM Sigmetrics Perform. Eval. Rev. 2014, 42, 34–37. [Google Scholar] [CrossRef]
- Reyna, A.; Martín, C.; Chen, J.; Soler, E.; Díaz, M. On blockchain and its integration with IoT. Challenges and opportunities. Future Gener. Comput. Syst. 2018, 88, 173–190. [Google Scholar] [CrossRef]
- Cui, Z.; Fei, X.; Zhang, S.; Cai, X.; Cao, Y.; Zhang, W.; Chen, J. A hybrid BlockChain-based identity authentication scheme for multi-WSN. IEEE Trans. Serv. Comput. 2020, 13, 241–251. [Google Scholar] [CrossRef]
- Rifi, N.; Rachkidi, E.; Agoulmine, N.; Taher, N.C. Towards using blockchain technology for eHealth data access management. In Proceedings of the 2017 Fourth International Conference on Advances in Biomedical Engineering (ICABME), Beirut, Lebanon, 19–21 October 2017; pp. 1–4. [Google Scholar] [CrossRef]
- Daza, V.; Di Pietro, R.; Klimek, I.; Signorini, M. CONNECT: CONtextual NamE disCovery for blockchain-based services in the IoT. In Proceedings of the 2017 IEEE International Conference on Communications (ICC), Paris, France, 21–25 May 2017; pp. 1–6. [Google Scholar] [CrossRef] [Green Version]
- Mavridou, A.; Laszka, A. Designing secure ethereum smart contracts: A finite state machine based approach. In Proceedings of the International Conference on Financial Cryptography and Data Security, Nieuwpoort, Curaçao, 26 February–2 March 2018; pp. 523–540. [Google Scholar]
- Hildenbrandt, E.; Saxena, M.; Rodrigues, N.; Zhu, X.; Daian, P.; Guth, D.; Moore, B.; Park, D.; Zhang, Y.; Stefanescu, A.; et al. Kevm: A complete formal semantics of the ethereum virtual machine. In Proceedings of the 2018 IEEE 31st Computer Security Foundations Symposium (CSF), Oxford, UK, 9–12 July 2018; pp. 204–217. [Google Scholar]
- Reports, E. Zero-Knowledge Blockchain Scalability. 2020. Available online: https://ethworks.io/assets/download/zero-knowledge-blockchain-scaling-ethworks.pdf (accessed on 28 September 2021).
- Blum, M.; Feldman, P.; Micali, S. Non-interactive Zero-knowledge and Its Applications. In Proceedings of the Twentieth Annual ACM Symposium on Theory of Computing; ACM: New York, NY, USA, 1988; pp. 103–112. [Google Scholar] [CrossRef]
- Ben-Sasson, E.; Chiesa, A.; Tromer, E.; Virza, M. Succinct Non-Interactive Zero Knowledge for a von Neumann Architecture. Cryptology ePrint Archive, Report 2013/879. 2013. Available online: https://eprint.iacr.org/2013/879 (accessed on 28 September 2021).
- Barreto, P.S.L.M.; Naehrig, M. Pairing-Friendly Elliptic Curves of Prime Order. Cryptology ePrint Archive, Report 2005/133. 2005. Available online: https://eprint.iacr.org/2005/133 (accessed on 28 September 2021).
- Bernstein, D.J.; Duif, N.; Lange, T.; Schwabe, P.; Yang, B.Y. High-speed high-security signatures. J. Cryptogr. Eng. 2012, 2, 77–89. [Google Scholar] [CrossRef] [Green Version]
- Baylina, J.; Bellés, M. EdDSA For Baby Jubjub Elliptic Curve with MiMC-7 Hash. Available online: https://iden3-docs.readthedocs.io/en/latest/_downloads/a04267077fb3fdbf2b608e014706e004/Ed-DSA.pdf (accessed on 28 September 2021).
- Allen, C. The Path to Self-Sovereign Identity. Available online: http://www.lifewithalacrity.com/2016/04/the-path-to-self-soverereign-identity.html (accessed on 7 July 2020).
- Sovrin Foundation. Sovrin: A Protocol and Token for Self-Sovereign Identity and Decentralized Trust. 2018. Available online: https://sovrin.org/wp-content/uploads/Sovrin-Protocol-and-Token-White-Paper.pdf (accessed on 28 September 2021).
- Mühle, A.; Grüner, A.; Gayvoronskaya, T.; Meinel, C. A survey on essential components of a self-sovereign identity. Comput. Sci. Rev. 2018, 30, 80–86. [Google Scholar] [CrossRef] [Green Version]
- Fragkos, G.; Minwalla, C.; Plusquellic, J.; Tsiropoulou, E.E. Artificially Intelligent Electronic Money. IEEE Consum. Electron. Mag. 2021, 10, 81–89. [Google Scholar] [CrossRef]
- Bespalov, Y.; Garoffolo, A.; Kovalchuk, L.; Nelasa, H.; Oliynykov, R. Probability Models of Distributed Proof Generation for zk-SNARK-Based Blockchains. Mathematics 2021, 9, 3016. [Google Scholar] [CrossRef]
- Arcenegui, J.; Arjona, R.; Baturone, I. Secure Management of IoT Devices Based on Blockchain Non-fungible Tokens and Physical Unclonable Functions. In Applied Cryptography and Network Security Workshops; Springer International Publishing: Cham, Switzerland, 2020; pp. 24–40. [Google Scholar]
- Bünz, B.; Agrawal, S.; Zamani, M.; Boneh, D. Zether: Towards Privacy in a Smart Contract World. Cryptology ePrint Archive, Report 2019/191. 2019. Available online: https://eprint.iacr.org/2019/191 (accessed on 28 September 2021).
- Bowe, S.; Gabizon, A.; Miers, I. Scalable Multi-party Computation for zk-SNARK Parameters in the Random Beacon Model. Cryptology ePrint Archive, Report 2017/1050. 2017. Available online: https://eprint.iacr.org/2017/1050 (accessed on 28 September 2021).
- Goldwasser, S.; Tauman Kalai, Y. Cryptographic Assumptions: A Position Paper. In Theory of Cryptography; Kushilevitz, E., Malkin, T., Eds.; Springer: Berlin/Heidelberg, Germany, 2016; pp. 505–522. [Google Scholar]
- Groth, J. On the Size of Pairing-based Non-interactive Arguments. Cryptology ePrint Archive, Report 2016/260. 2016. Available online: https://eprint.iacr.org/2016/260 (accessed on 28 September 2021).
- Menezes, A.; Sarkar, P.; Singh, S. Challenges with Assessing the Impact of NFS Advances on the Security of Pairing-based Cryptography. Cryptology ePrint Archive, Report 2016/1102. 2016. Available online: https://eprint.iacr.org/2016/1102 (accessed on 28 September 2021).
- Housni, Y.E.; Guillevic, A. Optimized and secure pairing-friendly elliptic curves suitable for one layer proof composition. Cryptology ePrint Archive, Report 2020/351. 2020. Available online: https://eprint.iacr.org/2020/351 (accessed on 28 September 2021).
- Grassi, L.; Khovratovich, D.; Rechberger, C.; Roy, A.; Schofnegger, M. Starkad and Poseidon: New Hash Functions for Zero Knowledge Proof Systems. Cryptology ePrint Archive, Report 2019/458. 2019. Available online: https://eprint.iacr.org/2019/458 (accessed on 28 September 2021).
- Wu, H.; Zheng, W.; Chiesa, A.; Popa, R.A.; Stoica, I. DIZK: A Distributed Zero Knowledge Proof System. Cryptology ePrint Archive, Report 2018/691. 2018. Available online: https://eprint.iacr.org/2018/691 (accessed on 28 September 2021).
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).