GeoStamp: Detail Transfer Based on Mean Curvature Field
Abstract
:1. Introduction
- Robustness: We formulate the transfer of the shape details as finding the solutions to a Poisson equation of a sparse symmetric linear system. By employing an efficient numerical solver, we can guarantee robust solutions to the problem.
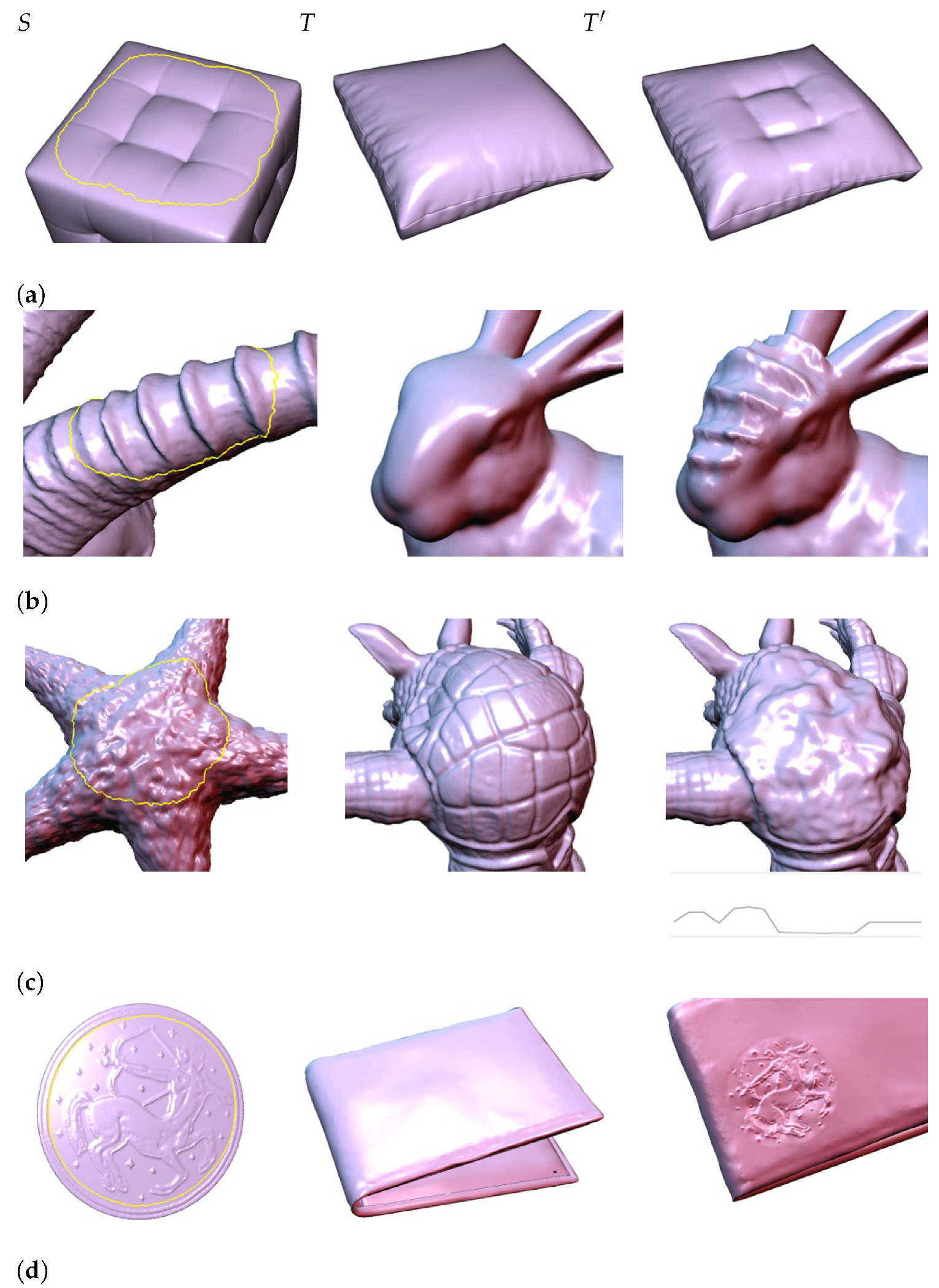
- Effectiveness: By analyzing the mean curvatures, any shape details such as regular patterns or irregular bumps can be effectively transferred to a target region. Moreover, our method can effectively and easily be combined with conventional methods such as the hole-filling of a triangular mesh to generate sophisticated results to match the shape details around a hole (see Supplementary Video).
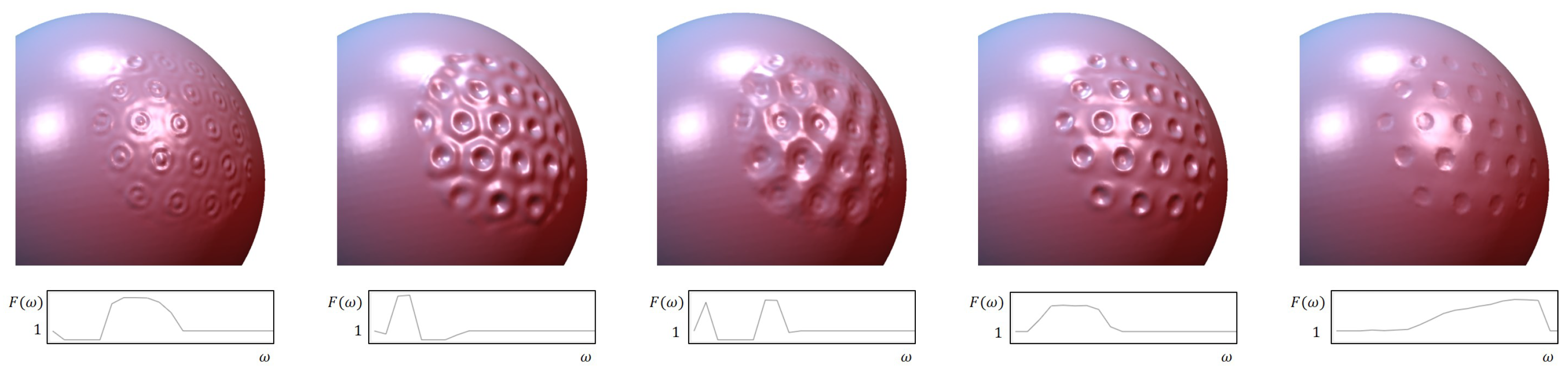
- Controllability: Our method provides the user with several control parameters for the shape detail intensity and orientation. The shape details can be thought of as a grayscale image on the parameter domain and thus analyzed within the frequency domain by applying a fast Fourier transformation (FFT). In the frequency domain, the user can edit the shape details interactively and transfer them to the target region in the spatial domain.
2. Related Work
2.1. Discrete Differential Property
2.2. Detail Transfer
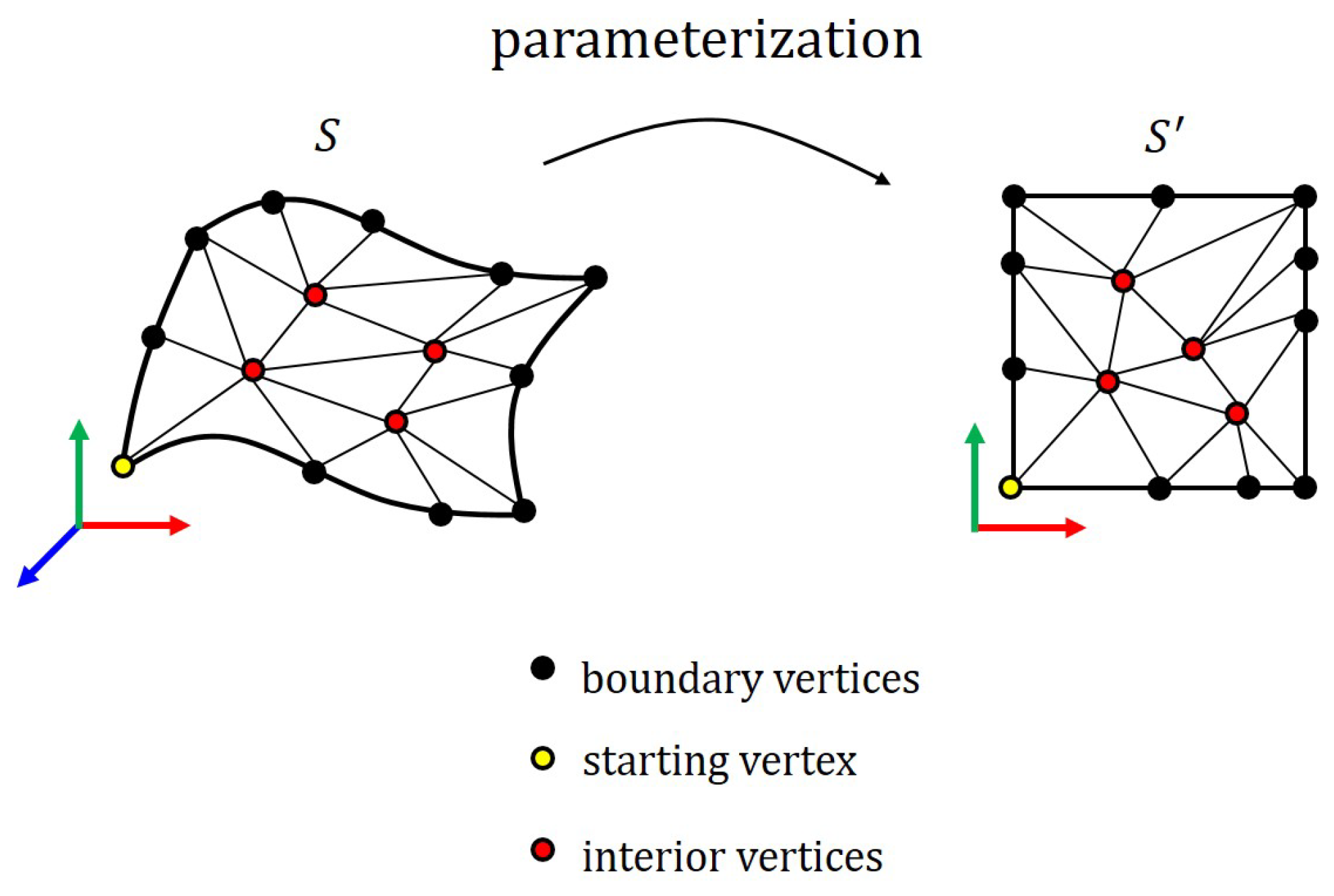
3. Representation of Shape Details
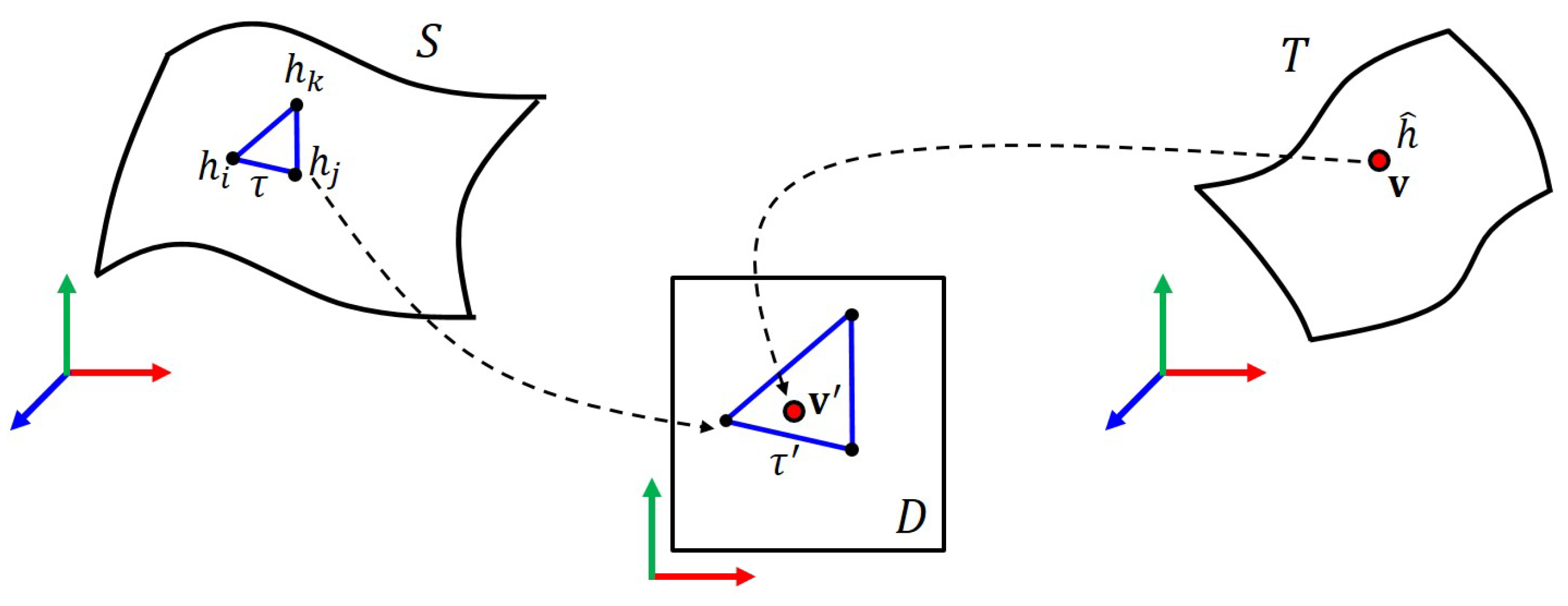
4. Transferring Shape Details
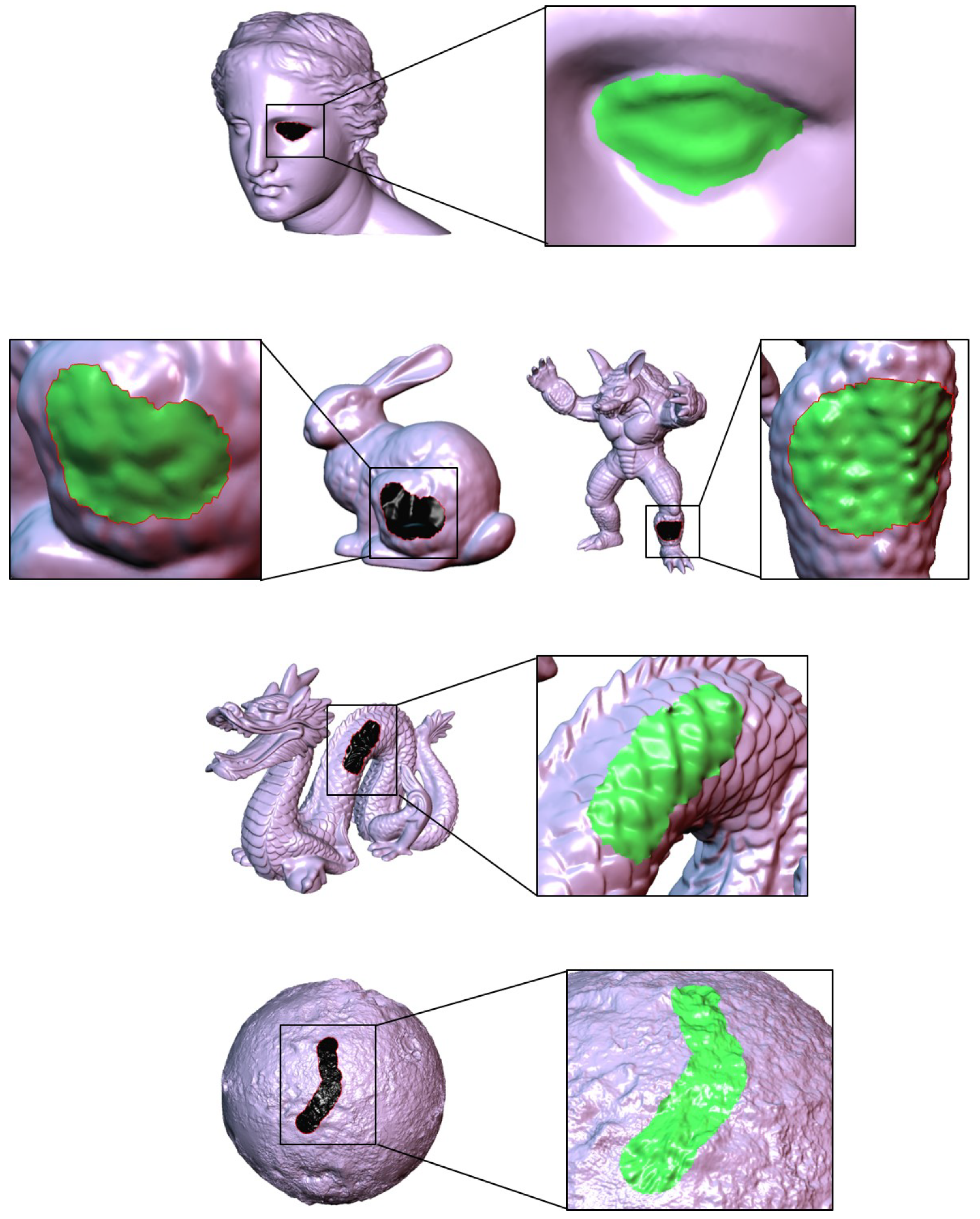
4.1. Shape Details for Target Region
4.2. Reconstruction of Target Region
4.3. Controlling Shape Details
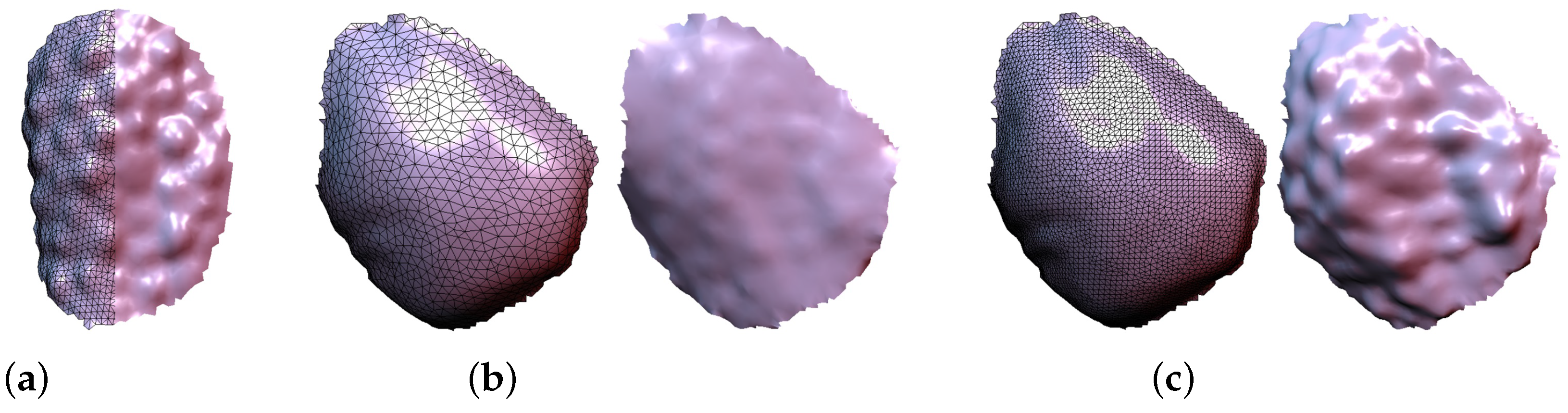
5. Experimental Results
6. Conclusions and Future Work
Supplementary Materials
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Botsch, M.; Sorkine, O. On linear variational surface deformation methods. IEEE Trans. Vis. Comput. Graph. 2007, 14, 213–230. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Alexa, M. Differential coordinates for local mesh morphing and deformation. Vis. Comput. 2003, 19, 105–114. [Google Scholar] [CrossRef]
- Lipman, Y.; Sorkine, O.; Cohen-Or, D.; Levin, D.; Rossi, C.; Seidel, H.P. Differential coordinates for interactive mesh editing. In Proceedings of the Shape Modeling Applications, Genova, Italy, 7–9 June 2004; pp. 181–190. [Google Scholar]
- Sorkine, O. Laplacian mesh processing. In Proceedings of the Eurographics 2005—State of the Art Reports. The Eurographics Association, Vienna, Austria, 3–7 May 2005. [Google Scholar]
- Sorkine, O.; Cohen-Or, D.; Lipman, Y.; Alexa, M.; Rössl, C.; Seidel, H.P. Laplacian surface editing. In Proceedings of the 2004 Eurographics/ACM SIGGRAPH Symposium on Geometry Processing. Association for Computing Machinery, Nice, France, 8–10 July 2004; pp. 175–184. [Google Scholar] [CrossRef] [Green Version]
- Taubin, G. Estimating the tensor of curvature of a surface from a polyhedral approximation. In Proceedings of the IEEE International Conference on Computer Vision, Cambridge, MA, USA, 20–23 June 1995; pp. 902–907. [Google Scholar]
- Taubin, G. A signal processing approach to fair surface design. In Proceedings of the 22nd Annual Conference on Computer Graphics and Interactive Techniques, Los Angeles, CA, USA, 6–11 August 1995; pp. 351–358. [Google Scholar]
- Meyer, M.; Desbrun, M.; Schröder, P.; Barr, A.H. Discrete differential-geometry operators for triangulated 2-manifolds. In Visualization and mathematics III; Springer: Berlin/Heidelberg, Germany, 2003; pp. 35–57. [Google Scholar]
- Desbrun, M.; Meyer, M.; Schröder, P.; Barr, A.H. Implicit fairing of irregular meshes using diffusion and curvature flow. In Proceedings of the 26th Annual Conference on Computer Graphics and Interactive Techniques, Los Angeles, CA, USA, 8–13 August 1999; pp. 317–324. [Google Scholar]
- Pinkall, U.; Polthier, K. Computing discrete minimal surfaces and their conjugates. Exp. Math. 1993, 2, 15–36. [Google Scholar] [CrossRef]
- Cohen-Steiner, D.; Morvan, J.M. Restricted delaunay triangulations and normal cycle. In Proceedings of the 9th Annual Symposium on Computational Geometry, San Diego, CA, USA, 8–10 June 2003; pp. 312–321. [Google Scholar]
- Rusinkiewicz, S. Estimating curvatures and their derivatives on triangle meshes. In Proceedings of the 2nd International Symposium on 3D Data Processing, Visualization and Transmission, Thessaloniki, Greece, 9 September 2004; pp. 486–493. [Google Scholar]
- Gatzke, T.D.; Grimm, C.M. Estimating curvature on triangular meshes. Int. J. Shape Model. 2006, 12, 1–28. [Google Scholar] [CrossRef] [Green Version]
- Kalogerakis, E.; Simari, P.; Nowrouzezahrai, D.; Singh, K. Robust statistical estimation of curvature on discretized surfaces. In Proceedings of the 5th Eurographics Symposium on Geometry Processing. Eurographics Association, Barcelona, Spain, 4–6 July 2007; pp. 13–22. [Google Scholar]
- Botsch, M.; Kobbelt, L.; Pauly, M.; Alliez, P.; Lévy, B. Polygon Mesh Processing; CRC Press: Boca Raton, FL, USA, 2010. [Google Scholar]
- Biermann, H.; Martin, I.; Bernardini, F.; Zorin, D. Cut-and-paste editing of multiresolution surfaces. ACM Trans. Graph. 2002, 21, 312–321. [Google Scholar] [CrossRef] [Green Version]
- Liu, Z.; Zhang, Z.; Shan, Y. Image-based surface detail transfer. IEEE Comput. Graph. Appl. 2004, 24, 30–35. [Google Scholar] [PubMed]
- Takayama, K.; Schmidt, R.; Singh, K.; Igarashi, T.; Boubekeur, T.; Sorkine-Hornung, O. GeoBrush: Interactive mesh geometry cloning. Comput. Graph. Forum 2011, 30, 613–622. [Google Scholar] [CrossRef]
- Berkiten, S.; Halber, M.; Solomon, J.; Ma, C.; Li, H.; Rusinkiewicz, S. Learning detail transfer based on geometric features. Comput. Graph. Forum 2017, 36, 361–373. [Google Scholar] [CrossRef]
- Floater, M.S.; Hormann, K. Surface parameterization: A tutorial and survey. In Advances in Multiresolution for Geometric Modelling; Springer: Berlin/Heidelberg, Germany, 2005; pp. 157–186. [Google Scholar]
- Pérez, P.; Gangnet, M.; Blake, A. Poisson image editing. ACM Trans. Graph. 2003, 22, 313–318. [Google Scholar] [CrossRef]
- Yu, Y.; Zhou, K.; Xu, D.; Shi, X.; Bao, H.; Guo, B.; Shum, H.Y. Mesh editing with Poisson-based gradient field manipulation. ACM Trans. Graph. 2004, 23, 644–651. [Google Scholar] [CrossRef]
- Bloor, M.I.; Wilson, M.J. Using partial differential equations to generate free-form surfaces. Comput.-Aided Des. 1990, 22, 202–212. [Google Scholar] [CrossRef]
- Moreton, H.P.; Séquin, C.H. Functional optimization for fair surface design. SIGGRAPH Comput. Graph. 1992, 26, 167–176. [Google Scholar] [CrossRef]
- Chen, Y.; Davis, T.A.; Hager, W.W.; Rajamanickam, S. Algorithm 887: CHOLMOD, supernodal sparse Cholesky factorization and update/downdate. ACM Trans. Math. Softw. 2008, 35, 1–14. [Google Scholar] [CrossRef]
- Botsch, M.; Kobbelt, L. An intuitive framework for real-time freeform modeling. ACM Trans. Graph. 2004, 23, 630–634. [Google Scholar] [CrossRef]
- Botsch, M.; Kobbelt, L. A remeshing approach to multiresolution modeling. In Proceedings of the 2004 Eurographics/ACM SIGGRAPH Symposium on Geometry Processing, Nice, France, 8–10 July 2004; pp. 185–192. [Google Scholar]
- Kobbelt, L.P.; Bareuther, T.; Seidel, H.P. Multiresolution shape deformations for meshes with dynamic vertex connectivity. Comput. Graph. Forum 2000, 19, 249–260. [Google Scholar] [CrossRef]
- Vorsatz, J.; Rössl, C.; Seidel, H.P. Dynamic remeshing and applications. In Proceedings of the 8th ACM Symposium on Solid Modeling and Applications, Seattle, WA, USA, 16–20 June 2003; pp. 167–175. [Google Scholar] [CrossRef] [Green Version]
- Park, J.H.; Park, S.; Yoon, S.H. Parametric blending of hole patches based on shape difference. Symmetry 2020, 12, 1759. [Google Scholar] [CrossRef]
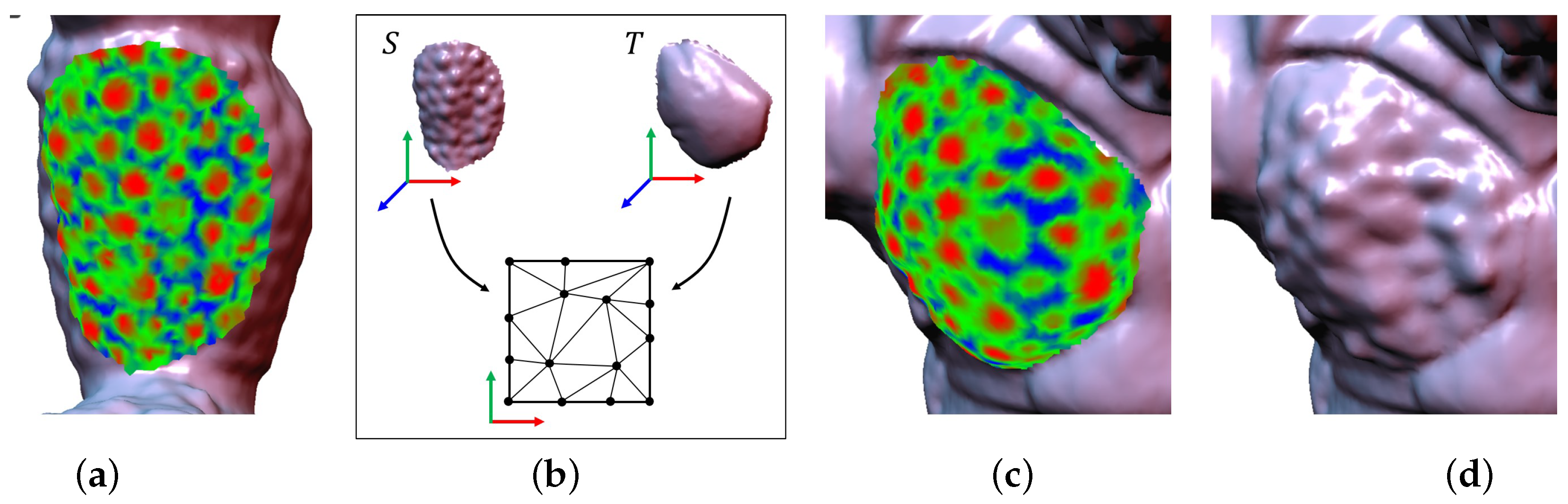



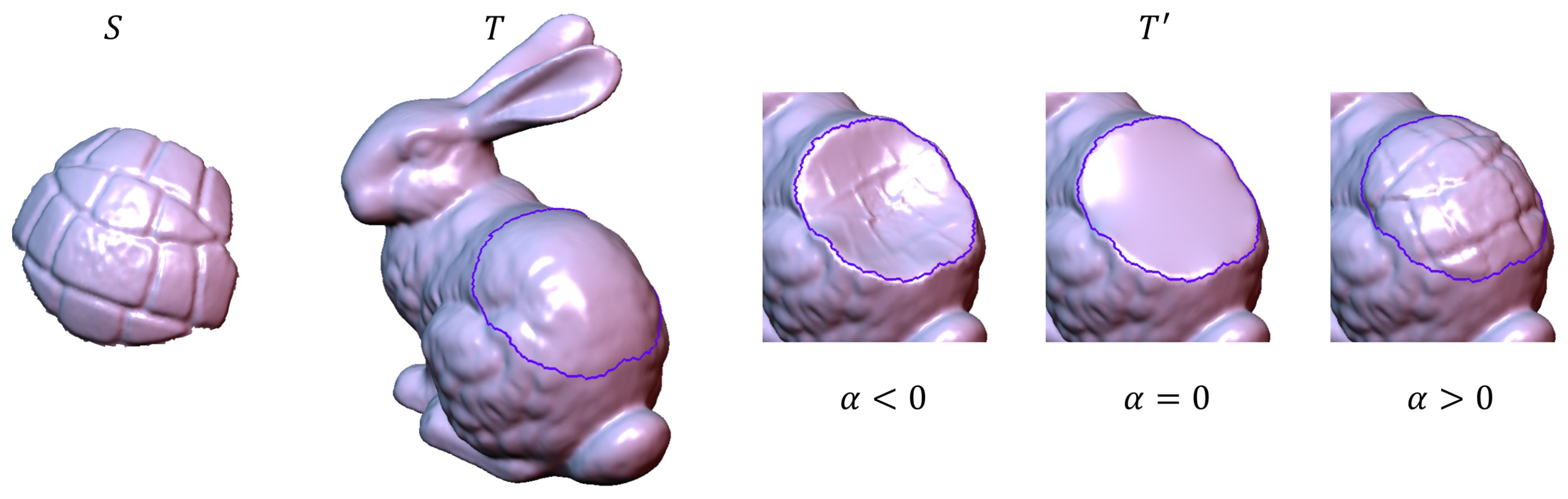




| Examples | # Vertices of Source | # Vertices of Target | Computation Time (in ms) | |
|---|---|---|---|---|
| Sorkine et al. [5] | Our Method | |||
| Figure 14a | 4731 | 4032 | 345 | 246 |
| Figure 14b | 3507 | 1039 | 212 | 158 |
| Figure 14c | 2001 | 21329 | 676 | 521 |
| Figure 14d | 37187 | 46640 | 4235 | 2488 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Park, J.-H.; Moon, J.-H.; Park, S.; Yoon, S.-H. GeoStamp: Detail Transfer Based on Mean Curvature Field. Mathematics 2022, 10, 500. https://doi.org/10.3390/math10030500
Park J-H, Moon J-H, Park S, Yoon S-H. GeoStamp: Detail Transfer Based on Mean Curvature Field. Mathematics. 2022; 10(3):500. https://doi.org/10.3390/math10030500
Chicago/Turabian StylePark, Jung-Ho, Ji-Hye Moon, Sanghun Park, and Seung-Hyun Yoon. 2022. "GeoStamp: Detail Transfer Based on Mean Curvature Field" Mathematics 10, no. 3: 500. https://doi.org/10.3390/math10030500
APA StylePark, J.-H., Moon, J.-H., Park, S., & Yoon, S.-H. (2022). GeoStamp: Detail Transfer Based on Mean Curvature Field. Mathematics, 10(3), 500. https://doi.org/10.3390/math10030500







