Integrating a Stabilized Radial Basis Function Method with Lattice Boltzmann Method
Abstract
1. Introduction
2. Lattice Boltzmann Method
3. Radial Basis Function Method
3.1. RBF for Solving the Streaming Step
3.2. Basis Function
4. Results and Discussions
4.1. One-Dimensional Problems
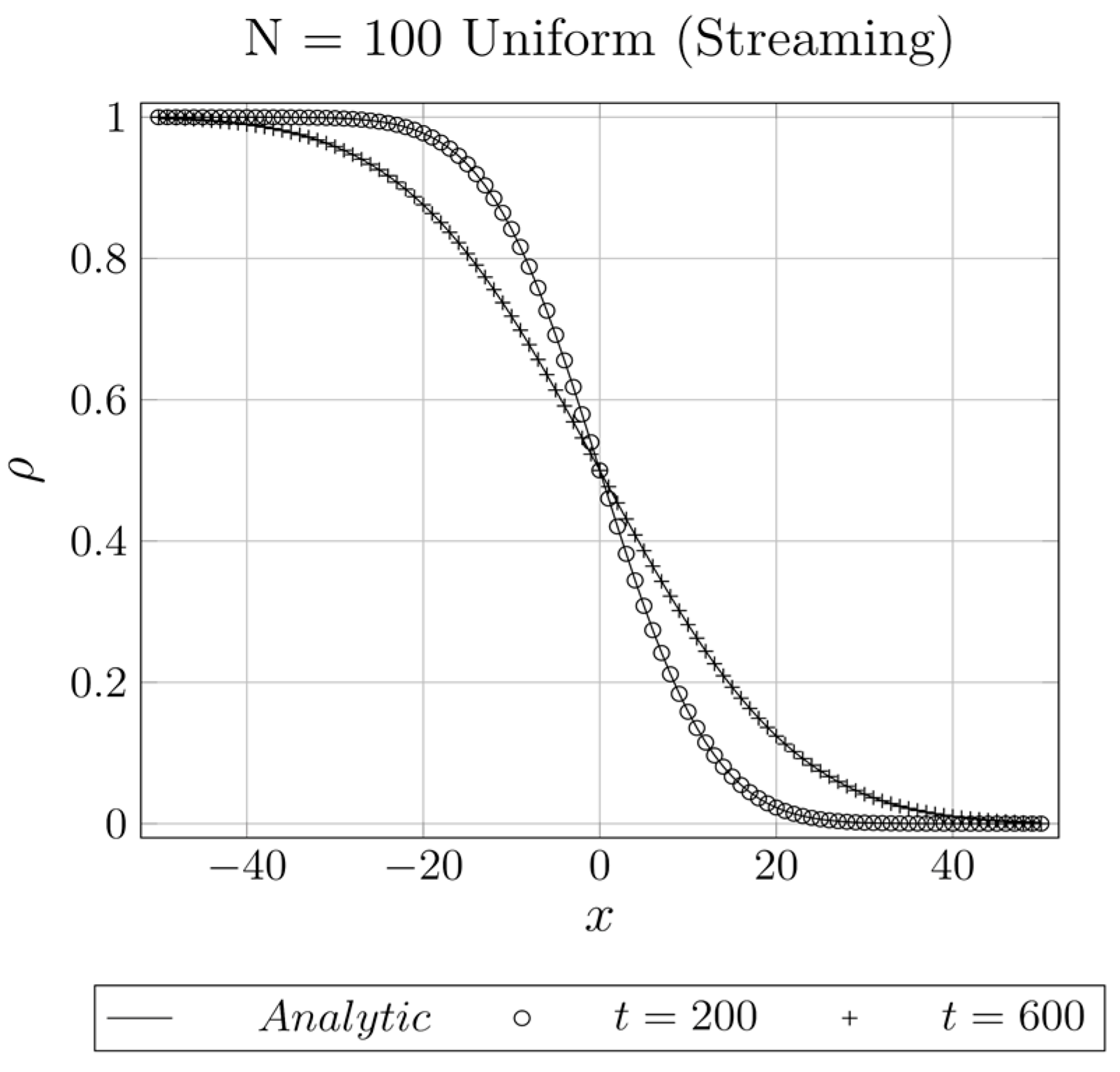
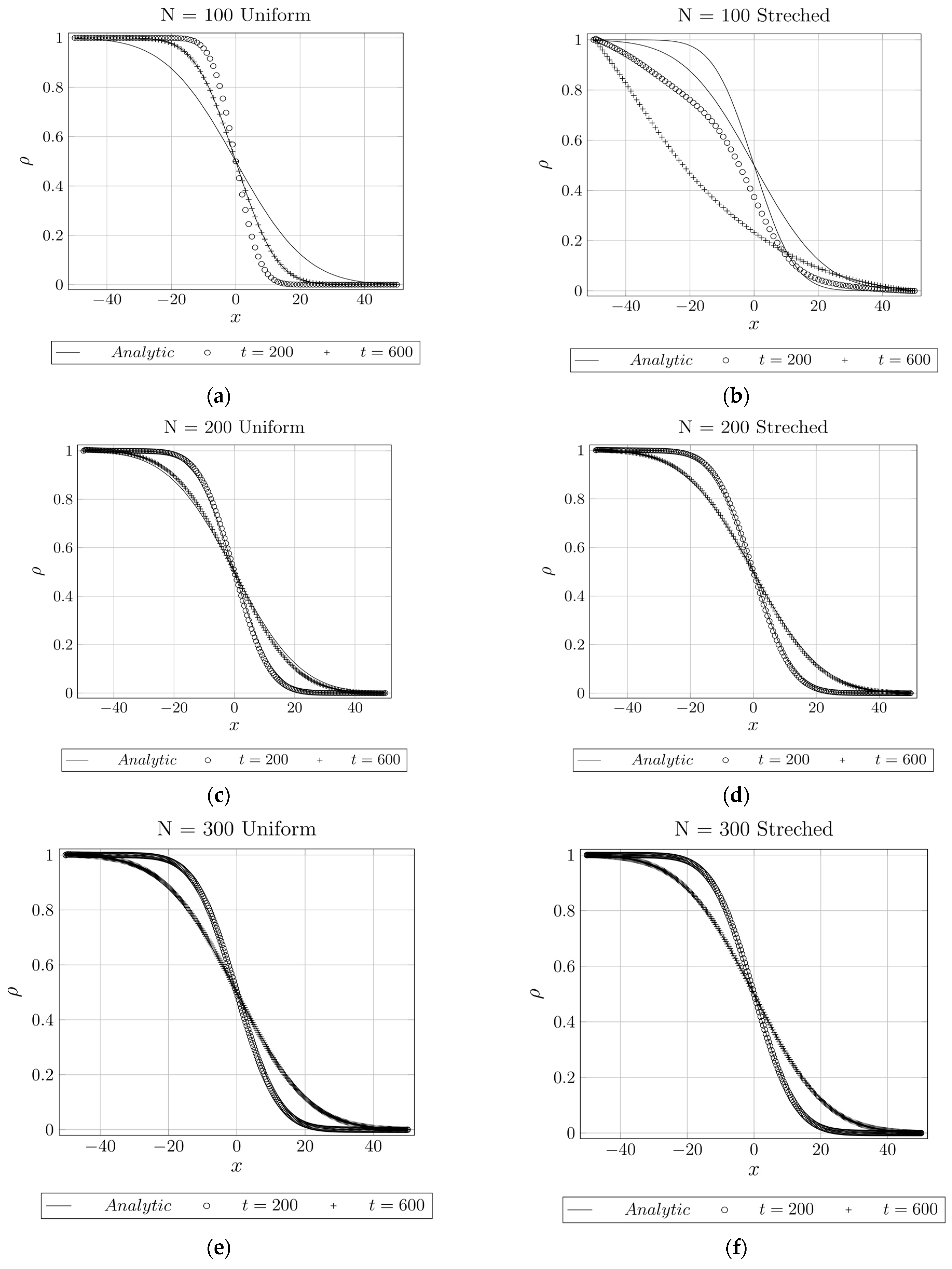
4.1.1. 1D Diffusion
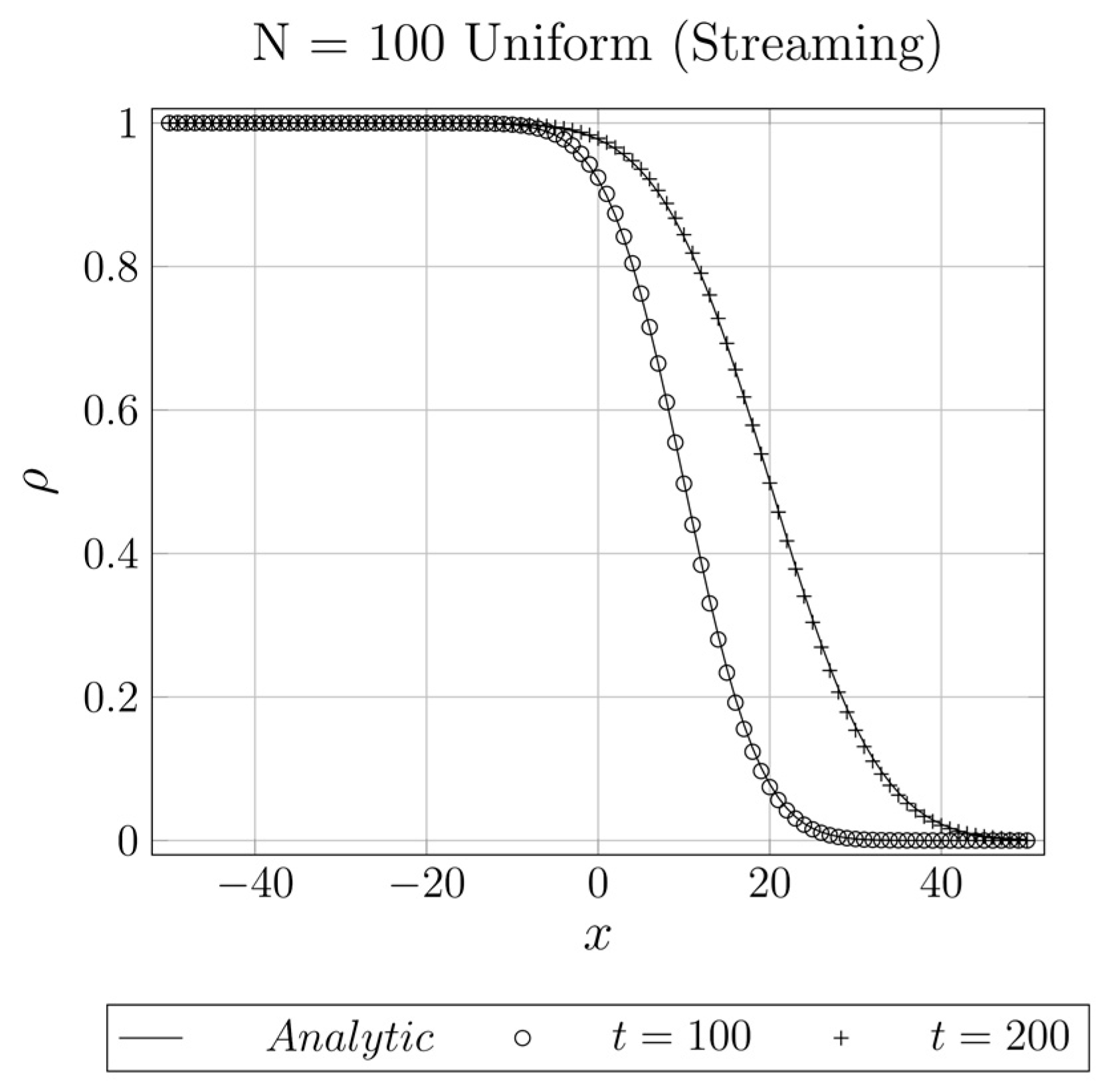
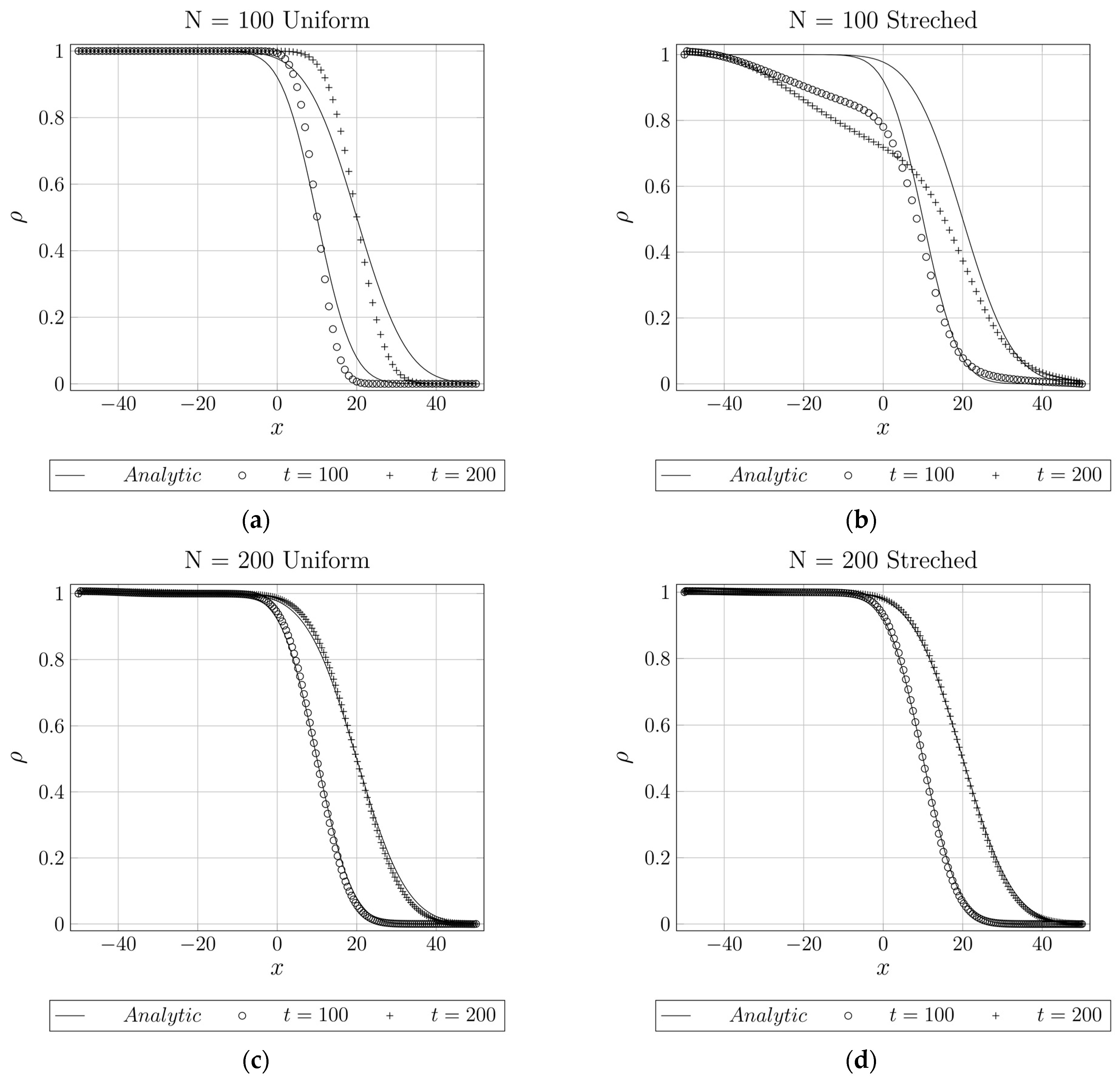
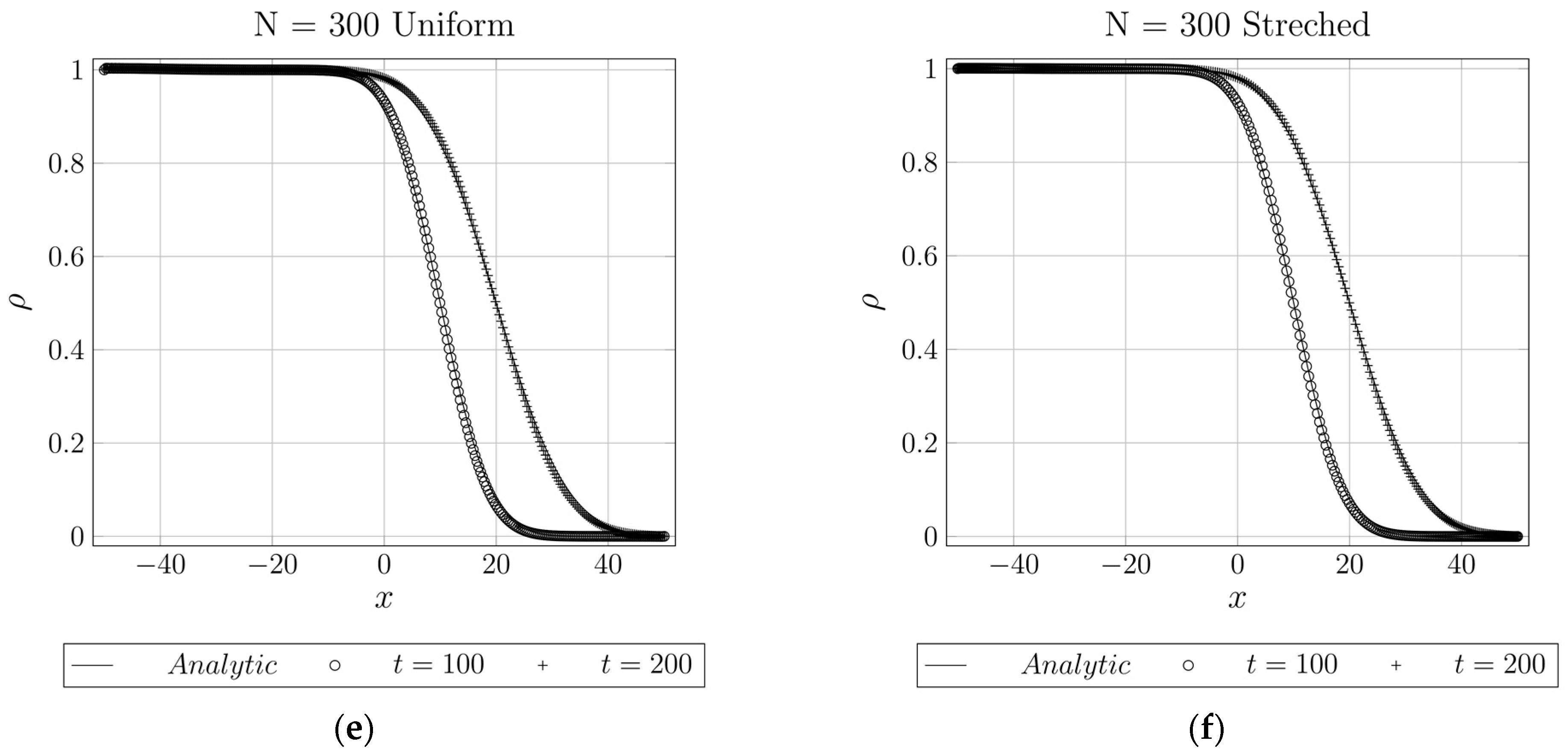
4.1.2. 1D Advection–Diffusion
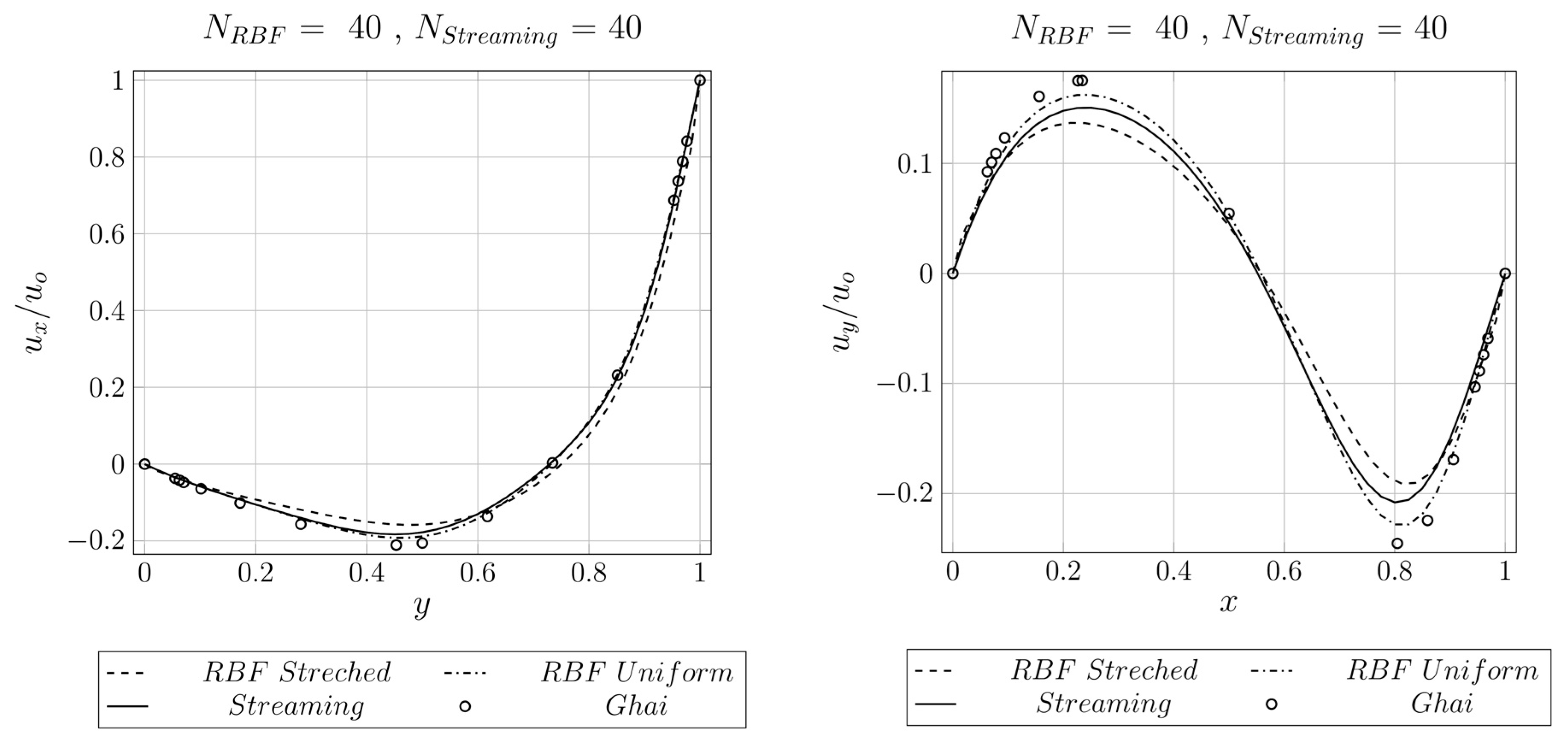
4.2. 2D Lid-Driven Cavity
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Bawazeer, S.; Mohamad, A.; Oclon, P. Natural convection in a differentially heated enclosure filled with low prandtl number fluids with modified lattice boltzmann method. Int. J. Heat Mass Transf. 2019, 143, 118562. [Google Scholar] [CrossRef]
- Mohamad, A.A. Lattice Boltzmann Method: Fundamentals and Engineering Applications with Computer Codes, 2nd ed.; Springer: New York, NY, USA, 2019. [Google Scholar]
- Mohamad, A.; Tao, Q.; He, Y.; Bawazeer, S. Treatment of transport at the interface between multilayers via the lattice boltzmann method. Numer. Heat Transf. Part B Fundam. 2015, 67, 124–134. [Google Scholar] [CrossRef]
- Bawazeer, S. Lattice Boltzmann Method with Improved Radial Basis Function Method; University of Calgary: Calgary, AB, Canada, 2019. [Google Scholar]
- Filippova, O.; Hänel, D. Grid refinement for lattice-bgk models. J. Comput. Phys. 1998, 147, 219–228. [Google Scholar] [CrossRef]
- Kandhai, D.; Soll, W.; Chen, S.; Hoekstra, A.; Sloot, P. Finite-difference lattice-bgk methods on nested grids. Comput. Phys. Commun. 2000, 129, 100–109. [Google Scholar] [CrossRef]
- Yu, D.; Mei, R.; Shyy, W. A multi-block lattice boltzmann method for viscous fluid flows. Int. J. Numer. Methods Fluids 2002, 39, 99–120. [Google Scholar] [CrossRef]
- Yu, Z.; Fan, L.-S. An interaction potential based lattice boltzmann method with adaptive mesh refinement (amr) for two-phase flow simulation. J. Comput. Phys. 2009, 228, 6456–6478. [Google Scholar] [CrossRef]
- Crouse, B.; Rank, E.; Krafczyk, M.; Tölke, J. A lb-based approach for adaptive flow simulations. Int. J. Mod. Phys. B 2003, 17, 109–112. [Google Scholar] [CrossRef]
- Wu, J.; Shu, C. A solution-adaptive lattice boltzmann method for two-dimensional incompressible viscous flows. J. Comput. Phys. 2011, 230, 2246–2269. [Google Scholar] [CrossRef]
- Chen, Y.; Kang, Q.; Cai, Q.; Zhang, D. Lattice boltzmann method on quadtree grids. Phys. Rev. E 2011, 83, 026707. [Google Scholar] [CrossRef]
- Lagrava, D.; Malaspinas, O.; Latt, J.; Chopard, B. Advances in multi-domain lattice boltzmann grid refinement. J. Comput. Phys. 2012, 231, 4808–4822. [Google Scholar] [CrossRef]
- Eitel-Amor, G.; Meinke, M.; Schröder, W. A lattice-boltzmann method with hierarchically refined meshes. Comput. Fluids 2013, 75, 127–139. [Google Scholar] [CrossRef]
- Fakhari, A.; Lee, T. Numerics of the lattice boltzmann method on nonuniform grids: Standard lbm and finite-difference lbm. Comput. Fluids 2015, 107, 205–213. [Google Scholar] [CrossRef]
- Fakhari, A.; Lee, T. Finite-difference lattice boltzmann method with a block-structured adaptive-mesh-refinement technique. Phys. Rev. E 2014, 89, 033310. [Google Scholar] [CrossRef] [PubMed]
- Guzik, S.M.; Weisgraber, T.H.; Colella, P.; Alder, B.J. Interpolation methods and the accuracy of lattice-boltzmann mesh refinement. J. Comput. Phys. 2014, 259, 461–487. [Google Scholar] [CrossRef]
- Succi, S.; Amati, G.; Benzi, R. Challenges in lattice boltzmann computing. J. Stat. Phys. 1995, 81, 5–16. [Google Scholar] [CrossRef]
- Nannelli, F.; Succi, S. The lattice boltzmann equation on irregular lattices. J. Stat. Phys. 1992, 68, 401–407. [Google Scholar] [CrossRef]
- Xi, H.; Peng, G.; Chou, S.-H. Finite-volume lattice boltzmann schemes in two and three dimensions. Phys. Rev. E 1999, 60, 3380. [Google Scholar] [CrossRef]
- Peng, G.; Xi, H.; Duncan, C.; Chou, S.-H. Finite volume scheme for the lattice boltzmann method on unstructured meshes. Phys. Rev. E 1999, 59, 4675. [Google Scholar] [CrossRef]
- Shrestha, K.; Mompean, G.; Calzavarini, E. Finite-volume versus streaming-based lattice boltzmann algorithm for fluid-dynamics simulations: A one-to-one accuracy and performance study. Phys. Rev. E 2016, 93, 023306. [Google Scholar] [CrossRef]
- Cevik, F.; Albayrak, K. A fully implicit finite volume lattice boltzmann method for turbulent flows. Commun. Comput. Phys. 2017, 22, 393–421. [Google Scholar] [CrossRef]
- Cao, N.; Chen, S.; Jin, S.; Martinez, D. Physical symmetry and lattice symmetry in the lattice boltzmann method. Phys. Rev. E 1997, 55, R21. [Google Scholar] [CrossRef]
- Mei, R.; Shyy, W. On the finite difference-based lattice boltzmann method in curvilinear coordinates. J. Comput. Phys. 1998, 143, 426–448. [Google Scholar] [CrossRef]
- Guo, Z.; Zhao, T.-S. Explicit finite-difference lattice boltzmann method for curvilinear coordinates. Phys. Rev. E 2003, 67, 066709. [Google Scholar] [CrossRef] [PubMed]
- Sofonea, V.; Sekerka, R.F. Viscosity of finite difference lattice boltzmann models. J. Comput. Phys. 2003, 184, 422–434. [Google Scholar] [CrossRef]
- Sofonea, V.; Lamura, A.; Gonnella, G.; Cristea, A. Finite-difference lattice boltzmann model with flux limiters for liquid-vapor systems. Phys. Rev. E 2004, 70, 046702. [Google Scholar] [CrossRef]
- El-Amin, M.; Sun, S.; Salama, A. On the stability of the finite difference based lattice boltzmann method. Procedia Comput. Sci. 2013, 18, 2101–2108. [Google Scholar] [CrossRef][Green Version]
- Hejranfar, K.; Ezzatneshan, E. Implementation of a high-order compact finite-difference lattice boltzmann method in generalized curvilinear coordinates. J. Comput. Phys. 2014, 267, 28–49. [Google Scholar] [CrossRef]
- Polasanapalli, S.R.G.; Anupindi, K. A high-order compact finite-difference lattice boltzmann method for simulation of natural convection. Comput. Fluids 2019, 181, 259–282. [Google Scholar] [CrossRef]
- Yoshida, H.; Nagaoka, M. Lattice boltzmann method for the convection–diffusion equation in curvilinear coordinate systems. J. Comput. Phys. 2014, 257, 884–900. [Google Scholar] [CrossRef]
- Rao, P.R.; Schaefer, L.A. Numerical stability of explicit off-lattice boltzmann schemes: A comparative study. J. Comput. Phys. 2015, 285, 251–264. [Google Scholar] [CrossRef]
- Hejranfar, K.; Saadat, M.H. Preconditioned weno finite-difference lattice boltzmann method for simulation of incompressible turbulent flows. Comput. Math. Appl. 2018, 76, 1427–1446. [Google Scholar] [CrossRef]
- Krivovichev, G.V.; Mikheev, S.A. On the stability of multi-step finite-difference-based lattice boltzmann schemes. Int. J. Comput. Methods 2019, 16, 1850087. [Google Scholar] [CrossRef]
- Lee, T.; Lin, C.-L. A characteristic galerkin method for discrete boltzmann equation. J. Comput. Phys. 2001, 171, 336–356. [Google Scholar] [CrossRef]
- Li, Y.; LeBoeuf, E.J.; Basu, P. Least-squares finite-element scheme for the lattice boltzmann method on an unstructured mesh. Phys. Rev. E 2005, 72, 046711. [Google Scholar] [CrossRef] [PubMed]
- Li, Y.; LeBoeuf, E.J.; Basu, P. Least-squares finite-element lattice boltzmann method. Phys. Rev. E 2004, 69, 065701. [Google Scholar] [CrossRef] [PubMed]
- Bardow, A.; Karlin, I.V.; Gusev, A.A. General characteristic-based algorithm for off-lattice boltzmann simulations. EPL 2006, 75, 434. [Google Scholar] [CrossRef]
- Jo, J.C.; Roh, K.W.; Kwon, Y.W. Finite element based formulation of the lattice boltzmann equation. Methods 2008, 6, 7. [Google Scholar] [CrossRef]
- Krivovichev, G. On the finite-element-based lattice boltzmann scheme. Appl. Math. Sci. 2014, 8, 1605–1620. [Google Scholar] [CrossRef]
- Patel, S.; Lee, T. A new splitting scheme to the discrete boltzmann equation for non-ideal gases on non-uniform meshes. J. Comput. Phys. 2016, 327, 799–809. [Google Scholar] [CrossRef]
- Shu, C.; Peng, Y.; Chew, Y. Simulation of natural convection in a square cavity by taylor series expansion-and least squares-based lattice boltzmann method. Int. J. Mod. Phys. C 2002, 13, 1399–1414. [Google Scholar] [CrossRef]
- Shu, C.; Niu, X.; Chew, Y. Taylor series expansion and least squares-based lattice boltzmann method: Three-dimensional formulation and its applications. Int. J. Mod. Phys. C 2003, 14, 925–944. [Google Scholar] [CrossRef]
- Shu, C.; Niu, X.; Chew, Y. Taylor-series expansion and least-squares-based lattice boltzmann method: Two-dimensional formulation and its applications. Phys. Rev. E 2002, 65, 036708. [Google Scholar] [CrossRef]
- Shu, C.; Chew, Y.; Niu, X. Least-squares-based lattice boltzmann method: A meshless approach for simulation of flows with complex geometry. Phys. Rev. E 2001, 64, 045701. [Google Scholar] [CrossRef]
- Lin, X.; Wu, J.; Zhang, T. A mesh-free radial basis function–based semi-Lagrangian lattice Boltzmann method for incompressible flows. Int. J. Numer. Methods Fluids 2019, 91, 198–211. [Google Scholar] [CrossRef]
- Musavi, S.H.; Ashrafizaadeh, M. Meshless lattice boltzmann method for the simulation of fluid flows. Phys. Rev. E 2015, 91, 023310. [Google Scholar] [CrossRef]
- He, X.; Luo, L.-S.; Dembo, M. Some progress in lattice boltzmann method. Part i. Nonuniform mesh grids. J. Comput. Phys. 1996, 129, 357–363. [Google Scholar] [CrossRef]
- He, X.; Doolen, G.D. Lattice boltzmann method on a curvilinear coordinate system: Vortex shedding behind a circular cylinder. Phys. Rev. E 1997, 56, 434. [Google Scholar] [CrossRef]
- He, X.; Doolen, G. Lattice boltzmann method on curvilinear coordinates system: Flow around a circular cylinder. J. Comput. Phys. 1997, 134, 306–315. [Google Scholar] [CrossRef]
- Chen, H. Volumetric formulation of the lattice boltzmann method for fluid dynamics: Basic concept. Phys. Rev. E 1998, 58, 3955. [Google Scholar] [CrossRef]
- Guo, P.; Qian, F.; Zhang, W.; Yan, H.; Wang, Q.; Zhao, C. Radial basis function interpolation supplemented lattice Boltzmann method for electroosmotic flows in microchannel. Electrophoresis 2021, 42, 2171–2181. [Google Scholar] [CrossRef]
- Bawazeer, S.A.; Baakeem, S.S.; Mohamad, A. A new radial basis function approach based on hermite expansion with respect to the shape parameter. Mathematics 2019, 7, 979. [Google Scholar] [CrossRef]
- Bawazeer, S. Stability and Accuracy of Lattice Boltzmann Method. Master’s Thesis, University of Calgary, Calgary, AB, Canada, 2013. [Google Scholar]
- Lee, H.; Bawazeer, S.; Mohamad, A. Boundary conditions for lattice boltzmann method with multispeed lattices. Comput. Fluids 2018, 162, 152–159. [Google Scholar] [CrossRef]
- Baakeem, S.S.; Bawazeer, S.A.; Mohamad, A. Comparison and evaluation of shan-chen model and most commonly used equations of state in multiphase lattice boltzmann method. Int. J. Multiph. Flow 2020, 128, 103290. [Google Scholar] [CrossRef]
- Bawazeer, S.A.; Baakeem, S.S.; Mohamad, A. A critical review of forcing schemes in lattice boltzmann method: 1993–2019. Arch. Comput. Methods Eng. 2021, 28, 4405–4423. [Google Scholar] [CrossRef]
- Lee, T.; Lin, C.-L. An eulerian description of the streaming process in the lattice boltzmann equation. J. Comput. Phys. 2003, 185, 445–471. [Google Scholar] [CrossRef]
- Carslaw, H.S.; Jaeger, J.C. Conduction of Heat in Solids; Clarendon Press: Oxford, UK, 1992. [Google Scholar]
- Ghia, U.; Ghia, K.N.; Shin, C. High resolutions for incompressible flow using the navier-stokes equations and a multigrid method. J. Comput. Phys. 1982, 48, 387–411. [Google Scholar] [CrossRef]


| Model | Mesh | Error | Time per Iteration (s) | ||
|---|---|---|---|---|---|
| Distribution | Size | Norm | Norm per Node | ||
| Streaming | Uniform | 100 | 0.004746 | 4.75 × 10−5 | 1.58 × 10−4 |
| Interpolation | Uniform | 100 | 0.734430 | 7.34 × 10−3 | 2.26 × 10−4 |
| Interpolation | Stretched | 100 | 2.186103 | 2.19 × 10−2 | 2.28 × 10−4 |
| Interpolation | Uniform | 200 | 0.197118 | 9.81 × 10−4 | 2.70 × 10−4 |
| Interpolation | Stretched | 200 | 0.074056 | 3.68 × 10−4 | 2.50 × 10−4 |
| Interpolation | Uniform | 300 | 0.108697 | 3.56 × 10−4 | 2.92 × 10−4 |
| Interpolation | Stretched | 300 | 0.046173 | 1.53 × 10−4 | 2.79 × 10−4 |
| Model | Mesh | Error | Time per Iteration (s) | ||
|---|---|---|---|---|---|
| Distribution | Size | Norm | Norm per Node | ||
| Streaming | Uniform | 100 | 0.018873 | 1.89 × 10−4 | 1.66 × 10−4 |
| Interpolation | Uniform | 100 | 0.567023 | 5.67 × 10−3 | 2.31 × 10−4 |
| Interpolation | Stretched | 100 | 1.317779 | 1.32 × 10−2 | 2.43 × 10−4 |
| Interpolation | Uniform | 200 | 0.179421 | 8.93 × 10−4 | 2.54 × 10−4 |
| Interpolation | Stretched | 200 | 0.087822 | 4.37 × 10−4 | 2.59 × 10−4 |
| Interpolation | Uniform | 300 | 0.117243 | 3.88 × 10−4 | 2.79 × 10−4 |
| Interpolation | Stretched | 300 | 0.071195 | 2.36 × 10−4 | 2.92 × 10−4 |
| Model | Mesh | No. of Steps | Time | Error w.r.t Ghai et al.’s Results | |||
|---|---|---|---|---|---|---|---|
| Distribution | Size | Total (s) | Per Iteration (s) | ||||
| Streaming | Uniform | 40 | 7227 | 173.9970 | 0.0241 | 0.0410 | 0.0367 |
| Interpolation | Uniform | 40 | 8332 | 256.7160 | 0.0308 | 0.0353 | 0.0368 |
| Interpolation | Stretched | 40 | 7620 | 237.4643 | 0.0312 | 0.1529 | 0.1028 |
| Interpolation | Uniform | 60 | 8395 | 564.0292 | 0.0672 | 0.1214 | 0.0806 |
| Interpolation | Stretched | 60 | 8629 | 616.4658 | 0.0714 | 0.0453 | 0.0448 |
| Interpolation | Uniform | 80 | 9000 | 1285.9117 | 0.1429 | 0.0372 | 0.0315 |
| Interpolation | Stretched | 80 | 8906 | 1302.6666 | 0.1463 | 0.0668 | 0.0532 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Bawazeer, S.A.; Baakeem, S.S.; Mohamad, A.A. Integrating a Stabilized Radial Basis Function Method with Lattice Boltzmann Method. Mathematics 2022, 10, 501. https://doi.org/10.3390/math10030501
Bawazeer SA, Baakeem SS, Mohamad AA. Integrating a Stabilized Radial Basis Function Method with Lattice Boltzmann Method. Mathematics. 2022; 10(3):501. https://doi.org/10.3390/math10030501
Chicago/Turabian StyleBawazeer, Saleh A., Saleh S. Baakeem, and Abdulmajeed A. Mohamad. 2022. "Integrating a Stabilized Radial Basis Function Method with Lattice Boltzmann Method" Mathematics 10, no. 3: 501. https://doi.org/10.3390/math10030501
APA StyleBawazeer, S. A., Baakeem, S. S., & Mohamad, A. A. (2022). Integrating a Stabilized Radial Basis Function Method with Lattice Boltzmann Method. Mathematics, 10(3), 501. https://doi.org/10.3390/math10030501







