Knots and Knot-Hyperpaths in Hypergraphs

Abstract

This paper deals with some theoretical aspects of hypergraphs related to hyperpaths and hypertrees. In ordinary graph theory, the intersecting or adjacent edges contain exactly one vertex; however, in the case of hypergraph theory, the adjacent or intersecting hyperedges may contain more than one vertex. This fact leads to the intuitive notion of knots, i.e., a collection of explicit vertices. The key idea of this manuscript lies in the introduction of the concept of the knot, which is a subset of the intersection of some intersecting hyperedges. We define knot-hyperpaths and equivalent knot-hyperpaths and study their relationships with the algebraic space continuity and the pseudo-open character of maps. Moreover, we establish a sufficient condition under which a hypergraph is a hypertree, without using the concept of the host graph.

1. Introduction

Being a generalization of graphs and yet having its own unique complexity and utility, hypergraph theory has emerged as a completely new dynamic research area. The fundamental concepts of path, tree, trail, cycle and their different well-known properties have already found plenty of applications in real-world problems in networking systems [1,2] of different types or in the field of bioinformatics [3,4,5]. The concept of the hyperpath, called also the path (both terms being used in a synonymous way), in a hypergraph represents the foundation of many research works. In the majority of these studies, the hypergraphs are considered to be directed, though there are papers related to paths in the case of undirected hypergraphs as well. Nguyen and Pallottino [6], in their work based on directed hypergraphs, have given some efficient algorithms in connection to some shortest path properties. In the same direction, we recall the work of Nielsen, Andersen and Pretolani [7], where the authors present the procedures for finding the K-shortest hyperpaths in a directed hypergraph. It is worth underlining that the area of research related to hyperpaths, shortest hyperpaths [6] and their links with vehicle navigation [1], network systems based on transit schedules [2], cellular networks [3], etc., is flourishing.

In this paper, we deal with two different problems related to hypergraphs. One concerns the behavior of hyperpaths under hyper-continuous mappings and pseudo-open mappings, while the other one is related to hyperpaths and hypertrees. Our study was motivated by the definition of the so-called algebraic space [8], introduced as a pair $(X,S_X)$, where X is a non-empty arbitrary set and $S_X\subseteq \mathcal{P}\left(X\right)$ a non-empty family of subsets of X. An algebraic space can be seen as an extended version of a topological space but without having any closure property with respect to union or intersection, and it recalls the definition of the hypergraph to a great extent. As a result, the concept of pseudo-map or pseudo-continuity could be then defined between two hypergraphs. The key element of this parallel study is the new concept of the knot, which is a subset of hyperedge intersection vertices. Since, in a hypergraph, the hyperedges appear as some subsets of the vertex set, it is trivial to note that the intersections of all possible adjacent hyperedges may contain more than one vertex. This fact leads to the intuitive notion of the knot that is the collection of explicit vertices. This notion further changes the dimension of perceiving the different concepts of hypergraphs such as walk, trail, path, tree, etc., where each of the adjacent hyperedge intersections gives rise to knots.

In graph theory, another important concept is that of the tree, which has been extensively used in networking, especially in theoretical computer science [9]. A graph G is a tree if there exists a unique path between any two vertices. Recall that the concept of the hypertree was introduced in hypergraph theory in terms of its host graph, as the hypergraph that admits a host graph that is a tree [10]. We emphasize that this fundamental characterization of trees is not generalized in hypergraph theory, in the sense that there is no characterization of hypertrees merely in terms of hyperpaths. This motivated us to present, in the second part of the paper, a characteristic of hypertrees in terms of hyperpaths, without using the concept of the host graph.

The structure of this work can be summarized as follows. First, in Section 2, we introduce the new concepts of point-hyperwalk, point-hypertrail and point-hyperpath, showing their differences in one illustrative example. Next, the key concepts of the knot and knot-hyperpath are defined. In Section 3, the notions of the hyper-continuous map, strictly hyper-continuous map and pseudo-open map between two hypergraphs are introduced and the behavior of point-hyperpaths and knot-hyperpaths under these notions is observed. In particular, we prove that the image of a point-hyperpath under an injective pseudo-open mapping is a point-hyperpath, while the image of a knot-hyperpath under a pseudo-open map is again a knot-hyperpath. Regarding the inverse image, we show that the inverse image of a knot-hyperpath under a surjective hyper-continuous map is a weak knot-hyperpath, or a knot-hyperpath if the map is surjective and strictly hyper-continuous. Section 4 is dedicated to the study of hypertrees. Based on the concept of equivalent entire knot-hyperpaths, we establish a sufficient condition under which a hypergraph becomes a hypertree. Moreover, we present an algorithm that extracts a host graph from a hypertree. A concluding section ends our study.

2. Preliminaries

Many definitions of hypergraphs exist; here, we will adopt the original one, given by Berge [11]. A hypergraph is a couple $H=(V,E)$ defined by a finite set of vertices (called also nodes) $V=\{v_1,\dots ,v_n\}$, with $n\in \mathbb{N}$, and the set $E={\left\{E_i\right\}}_{i\in \mathbb{N}}$ of non-empty subsets of V, called hyperedges. Two hyperedges $E_j,E_k\in E$, with $j\ne k$, such that $E_j=E_k$ are called repeated hyperedges [12]. In this paper, all hypergraphs are considered to be with no repeated hyperedges.

Definition 1

([13]). Let $H=(V,E)$ be a hypergraph. By a hyperpath between two distinct vertices $v_1$ and $v_k$ in V, we mean a sequence $v_1{E}_1{v}_2{E}_2\dots v_{k-1}{E}_{k-1}{v}_k$ of vertices and hyperedges having the following properties:

(i) 

k is a positive integer;

(ii) 

$v_1,v_2,\dots ,v_k$ are distinct vertices;

(iii) 

$E_1,E_2,\dots ,E_{k-1}$ are hyperedges (not necessarily distinct);

(iv) 

$v_j,v_{j+1}\in E_j$ for $j=1,2,\dots ,k-1$.

We call this sequence a $v_1-v_k$–hyperpath.

Definition 2

([13]). A hypercycle in a hypergraph $H=(V,E)$ on a vertex $v_1$ is a sequence $v_1{E}_1{v}_2{E}_2\dots v_{k-1}{E}_{k-1}{v}_k{E}_k{v}_1$, having the following properties:

(i) 

k is a positive integer $\ge 3$;

(ii) 

$v_1{E}_1{v}_2{E}_2\dots v_{k-1}{E}_{k-1}{v}_k$ is a $v_1-v_k$–hyperpath;

(iii) 

at least one of the hyperedges $E_1,E_2,\dots ,E_{k-1}$ is distinct from $E_k$;

(iv) 

$v_j,v_{j+1}\in E_j$ for $j=1,\dots ,k-1$.

It is important to note that a path in a graph does not contain repeated edges, while this property is not retained in the definition of a hyperpath in a hypergraph as it appears in Definition 1. Since, in some cases, it is necessary to distinguish this special case; we define the following types of hyperpaths.

Definition 3.

A point-hyperwalk in a hypergraph $H=(V,E)$ is a hyperpath as defined in Definition 1, where the vertices may be repeated. A point-hyperwalk where no hyperedge is repeated (but vertices may be repeated) is called a point-hypertrail. A point-hyperpath is a point-hypertrail in which vertices are not repeated.

In other words, a point-hyperpath is a point-hyperwalk where neither the edges nor the vertices are repeated.

The above definitions are illustrated in the following example.

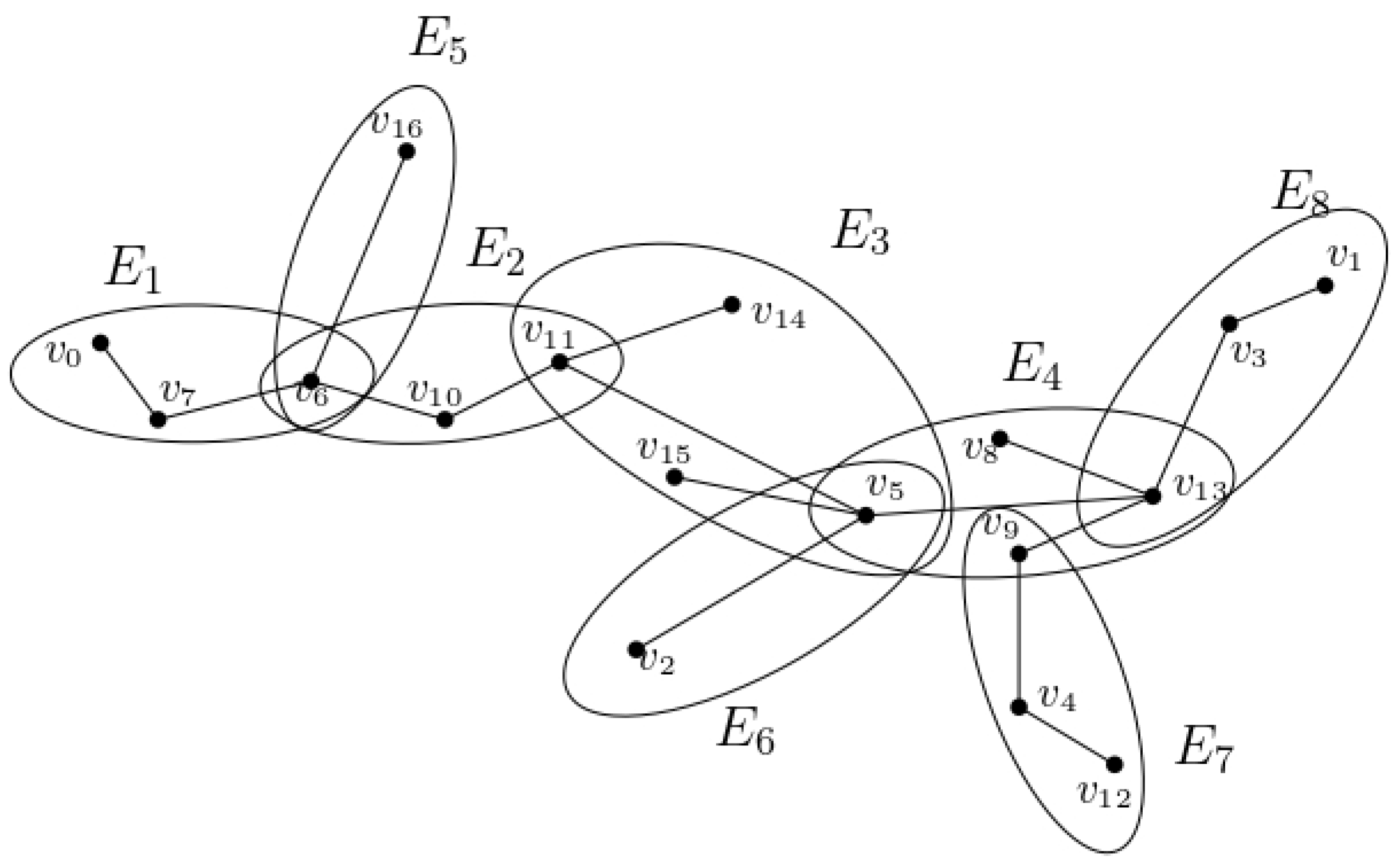
Example 1.

Let $H=(V,E)$ be a hypergraph with the vertex set $V=\left\{v_i\right|i=1,2,\dots ,50\}$ and hyperedges $E=\{E_1,E_2,\dots ,E_{10}\}$ such that

$$\begin{gathered} E_1=\{v_1,v_2,v_3,v_4,v_5,v_{47},v_9,v_{10}\}, \\ {E}_2=\{v_{12},v_{11},v_{15},v_9,v_{10},v_8,v_6,v_{16},v_7\}, \\ {E}_3=\{v_{11},v_{12},v_{15},v_{13},v_{46},v_{14},v_{30}\}, \\ {E}_4=\{v_{14},v_{30},v_{31},v_{34},v_{33}\}, \\ {E}_5=\{v_{14},v_{30},v_{20},v_{32},v_{22},v_{21}\}, \\ {E}_6=\{v_{21},v_{22},v_{44},v_{48},v_{49},v_{50},v_{43}\}, \\ {E}_7=\{v_{50},v_{43},v_{41},v_{42},v_{36},v_{45},v_{37}\}, \\ {E}_8=\{v_{36},v_{45},v_{37},v_{46},v_{40},v_{27},v_{29}\}, \\ {E}_9=\{v_{28},v_{23},v_{24},,v_{27},v_{29},v_{25},v_{26}\}, \\ {E}_{10}=\{v_{16},v_7,v_{18},v_{17},v_{28},v_{23},v_{24}\} \end{gathered}$$.

We represent this hypergraph in Figure 1.

We notice that

• $P\equiv v_1{E}_1{v}_9{E}_2{v}_{12}{E}_3{v}_{14}{E}_5{v}_{21}{E}_6{v}_{50}{E}_7{v}_{37}{E}_8{v}_{20}{E}_9{v}_{28}{E}_{10}{v}_7{E}_2{v}_{12}$ is a point-hyperwalk, but not a point-hypertrail, because the hyperedge $E_2$ is repeated.
• $P\equiv v_{12}{E}_3{v}_{30}{E}_5{v}_{22}{E}_6{v}_{43}{E}_7{v}_{37}{E}_8{v}_{29}{E}_9{v}_{28}{E}_{10}{v}_7{E}_2{v}_{12}$ is a point-hypertrail. Here, the vertex $v_{12}$ is repeated, but there is no repetition of the hyperedges.
• $P\equiv v_{16}{E}_{10}{v}_{28}{E}_9{v}_{27}{E}_8{v}_{36}{E}_7{v}_{50}{E}_6{v}_{22}$ is a point-hyperpath, since hyperedges and vertices are not repeated.

Suppose that $H=(V,E)$ and $H^{\prime }=(V^{\prime },E^{\prime })$ are two hypergraphs. Let $f:V\to V^{\prime }$ be a mapping and let $P\equiv v_1{E}_1{v}_2{E}_2\dots v_{k-1}{E}_{k-1}{v}_k$ denote an alternating sequence of vertices and edges in the hypergraph H. Then, we denote the f-image of this sequence as $f\left(P\right)\equiv f\left(v_1\right)f\left(E_1\right)f\left(v_2\right)f\left(E_2\right)\dots f\left(v_{k-1}\right)f\left(E_{k-1}\right)f\left(v_k\right)$, where $f\left(E_i\right),i=1,2,\dots ,k$ is the f-image of $E_i,i=1,2,\dots ,k$, respectively.

Generalizing the notions in Definition 1, we are ready to introduce the concepts of the knot and knot-hyperpath, where the vertices are replaced by a cluster of vertices, each of them behaving in a significant manner.

Definition 4.

A knot K in a hypergraph $H=(V,E)$ is a non-empty subset of the intersections of some intersecting hyperedges. In other words, if $H=(V,E)$ is a hypergraph and K is a knot, then $K(\ne \varnothing )\subseteq \cap E_i$ for some intersecting hyperedges $E_i,i=1,2,\dots ,k$ and $k\ge 2$. In particular, if $K=\cap E_i$, then K is called an entire knot.

Definition 5.

A knot-hyperpath in a hypergraph $H=(V,E)$ between two vertices $v_1$ and $v_n$ is an alternating sequence of knots and hyperedges of the following type:

$$\left\{v_1\right\}{E}_1{K}_1{E}_2{K}_2{E}_3\dots E_{n-1}{K}_{n-1}{E}_n\left\{v_n\right\},$$

(1)

where $K_i\subseteq (E_i\cap E_{i+1})\backslash \left({\cup }_{t=1}^{i-1}{K}_t\right)$, with $i=1,\dots ,n-1$, $v_1\in E_1,v_n\in E_n$ and $E_i$s are distinct hyperedges.

If $K_i=E_i\cap E_{i+1}$ for all $i=1,2,\dots ,n-1$, then the knot-hyperpath is called the entire knot-hyperpath.

Although the entire knot-hyperpath is a particular case of the knot-hyperpath, its significance can be seen in Section 4.

From the constructions of knots, it is clear that knots are mutually disjointed. Here, n is called the length of the knot-hyperpath.

Example 2.

By taking the hypergraph defined in Example 1, we can observe that

$$\left\{v_4\right\}{E}_1\{v_9,v_{10}\}{E}_2\{v_{11},v_{12},v_{15}\}{E}_3\{v_{14},v_{30}\}{E}_5\left\{v_{22}\right\}{E}_6\left\{v_{50}\right\}$$

is a knot-hyperpath of length 5.

Definition 6.

Two knot-hyperpaths

$$P_1\equiv \left\{v_1\right\}{E}_1{K}_1{E}_2{K}_2{E}_3\dots E_{n-1}{K}_{n-1}{E}_n\left\{v_n\right\}$$

and

$$P_2\equiv \left\{v_1\right\}{E}_1^{{}^{\prime }}{K}_1^{{}^{\prime }}{E}_2^{{}^{\prime }}{K}_2^{{}^{\prime }}{E}_3^{{}^{\prime }}\dots E_{n-1}^{{}^{\prime }}{K}_{n-1}^{{}^{\prime }}{E}_n^{{}^{\prime }}\left\{v_n\right\}$$

of the same length of a hypergraph $H=(V,E)$ are called equivalent or isomorphic if

(i) 

$E_i\cap E_i^{{}^{\prime }}\ne \varnothing$,

(ii) 

$K_i\cap K_i^{{}^{\prime }}\ne \varnothing$ for all $i=1,2,\dots ,n-1$.

The above definition further can be generalized to a finite number of knot-hyperpaths (entire knot-hyperpaths) $P_1,P_2,\dots ,P_k$, where $k\ge 2$ and the intersections in items (i) and (ii) are taken as follows:

(i)

${\bigcap }_{j=1}^k{E}_i^j\ne \varnothing$

(ii)

${\bigcap }_{j=1}^k{K}_i^j\ne \varnothing$ for all $i=1,2,\dots ,n-1$.

Example 3.

Consider the hypergraph H, with the vertex set

$$V=\{v_1,v_2,v_3,v_4,v_5,v_6,v_7,v_8,v_9,v_{10},v_{11},v_{12},v_{13}\}$$

and the hyperedges $E_1=\{v_1,v_2,v_3,v_4\},E_2=\{v_3,v_4,v_5,v_7,v_9\},E_3=\{v_2,v_3,v_4,v_7,v_8,v_9\},E_4=\{v_8,v_9,v_{10},v_{11},v_{12}\},E_5=\{v_{11},v_{12},v_{13}\}$.

It can be easily verified that the following two knot-hyperpaths

$$P_1\equiv \left\{v_1\right\}{E}_1\{v_2,v_3,v_4\}{E}_3\{v_8,v_9\}{E}_4\{v_{11},v_{12}\}{E}_5\left\{v_{13}\right\}$$

and

$$P_2\equiv \left\{v_1\right\}{E}_1\{v_3,v_4\}{E}_2\left\{v_9\right\}{E}_4\{v_{11},v_{12}\}{E}_5\left\{v_{13}\right\}$$

are equivalent. We notice also that $P_1$ and $P_2$ are entire knot-hyperpaths, while

$$P_1^{{}^{\prime }}\equiv \left\{v_1\right\}{E}_1\{v_2,v_3,v_4\}{E}_3\{v_8,v_9\}{E}_4\left\{v_{11}\right\}{E}_5\left\{v_{13}\right\}$$

and

$$P_2^{{}^{\prime }}\equiv \left\{v_1\right\}{E}_1\{v_3,v_4\}{E}_2\left\{v_9\right\}{E}_4\left\{v_{12}\right\}{E}_5\left\{v_{13}\right\}$$

are not equivalent because the last two knots of the knot-hyperpaths $P_1^{{}^{\prime }}$ and $P_2^{{}^{\prime }}$ have empty intersections.

Definition 7

([8]). A mapping $f:V\to V^{{}^{\prime }}$ from the vertex set of a hypergraph $H=(V,E)$ to the vertex set of another hypergraph $K=(V^{{}^{\prime }},E^{{}^{\prime }})$ is said to be pseudo-open (in short, ps-open) if, for each hyperedge $E_i$ in E, the corresponding image $f\left(E_i\right)$ is a hyperedge in $E^{{}^{\prime }}$.

Example 4.

Let $H=(V,E)$ and $K=(V^{{}^{\prime }},E^{{}^{\prime }})$ be two hypergraphs with the vertex sets $V=\{v_1,v_2,v_3,v_4,v_5,v_6\}$ and $V^{{}^{\prime }}=\{v_1^{{}^{\prime }},v_2^{{}^{\prime }},v_3^{{}^{\prime }},v_4^{{}^{\prime }},v_5^{{}^{\prime }}\}$ and the hyperedge sets $E=\{\{v_1,v_2\},$$\{v_2,v_3,v_4\},$$\{v_3,v_4,v_5\}\}$, $E^{{}^{\prime }}=\{\left\{v_1^{{}^{\prime }}\right\},\{v_2^{{}^{\prime }},v_5^{{}^{\prime }}\},\{v_1^{{}^{\prime }},v_2^{{}^{\prime }},v_5^{{}^{\prime }}\}\}$, respectively. Define the map $f:V\to V^{{}^{\prime }}$ such that $f\left(v_1\right)=v_1^{{}^{\prime }}=f\left(v_2\right)$, $f\left(v_3\right)=v_2^{{}^{\prime }}=f\left(v_5\right)$, $f\left(v_4\right)=v_5^{{}^{\prime }}$, $f\left(v_6\right)=v_3^{{}^{\prime }}$. Then, $f\left(\{v_1,v_2\}\right)=\left\{v_1^{{}^{\prime }}\right\}$, $f\left(\{v_2,v_3,v_4\}\right)=\{v_1^{{}^{\prime }},v_2^{{}^{\prime }},v_5^{{}^{\prime }}\}$, $f\left(\{v_3,v_4,v_5\}\right)=\{v_2^{{}^{\prime }},v_5^{{}^{\prime }}\}$. Thus, for each $E_i\in E$, we have $f\left(E_i\right)\in E^{{}^{\prime }}$. Hence, f is a ps-open mapping.

Definition 8.

A hypergraph $H=(V,E)$ is called connected if, for any two distinct vertices $v_1$ and $v_2$, there exists a hyperpath joining $v_1$ and $v_2$.

Definition 9.

In a hypergraph $H=(V,E)$, a sequence

$$\left\{v_1\right\}{G}_1{K}_1{G}_2{K}_2{G}_3\dots G_{n-1}{K}_{n-1}{G}_n\left\{v_n\right\}$$

is called a weak knot-hypergraph if each $G_i\supset E_i$, ($E_i\in E$) with $K_i\subseteq (G_{i-1}\cap G_i)\backslash \left({\cup }_{t=1}^{i-1}{K}_t\right)$ for all $i=1,2,\dots ,n-2$.

3. Hyperpaths and Hypercontinuity

In this section, we check whether the pseudo-open maps preserve the notion of the point-hyperpath and knot-hyperpath between two hypergraphs and under which conditions. Then, the notions of the hyper-continuous map and strictly hyper-continuous map between two hypergraphs are stated and various possible relationships between any two knot-hyperpaths under these notions are investigated.

Definition 10.

A mapping $f:V\to V^{{}^{\prime }}$ between the vertex sets of two hypergraphs $H=(V,E)$ and $K=(V^{{}^{\prime }},E^{{}^{\prime }})$ is called hyper-continuous if, for any $E_i^{{}^{\prime }}\in E^{{}^{\prime }}$, there is some $E_j\in E$ such that the corresponding inverse image satisfies $f^{-1}\left(E_i^{{}^{\prime }}\right)\supseteq E_j$.

Example 5.

Suppose that $H=(V,E)$ and $K=(V^{{}^{\prime }},E^{{}^{\prime }})$ are two hypergraphs, where $V=\{v_1,v_2,v_3,v_4,v_5,v_6\}$ and $V^{{}^{\prime }}=\{v_1^{{}^{\prime }},v_2^{{}^{\prime }},v_3^{{}^{\prime }},v_4^{{}^{\prime }},v_5^{{}^{\prime }}\}$ and $E=\{\{v_1,v_2\},\left\{v_3\right\},\{v_3,v_4,v_5\}\}$, $E^{{}^{\prime }}=\{\left\{v_1^{{}^{\prime }}\right\},\{v_2^{{}^{\prime }},v_3^{{}^{\prime }},v_4^{{}^{\prime }}\},\{v_1^{{}^{\prime }},v_2^{{}^{\prime }},v_3^{{}^{\prime }}\}\}$. A map $f:V\to V^{{}^{\prime }}$ is defined such that $f\left(v_1\right)=v_1^{{}^{\prime }}=f\left(v_2\right)$, $f\left(v_3\right)=v_2^{{}^{\prime }}=f\left(v_5\right)$, $f\left(v_4\right)=v_5^{{}^{\prime }}$, $f\left(v_6\right)=v_3^{{}^{\prime }}$. Now, we have $\left\{v_1^{{}^{\prime }}\right\}\in E^{{}^{\prime }}$ and $f^{-1}\left(\left\{v_1^{{}^{\prime }}\right\}\right)=\{v_1,v_2\}\supseteq \{v_1,v_2\}(\in E)$. Again, $\{v_2^{{}^{\prime }},v_3^{{}^{\prime }},v_4^{{}^{\prime }}\}\in E^{{}^{\prime }}$ and $f^{-1}\left(\{v_2^{{}^{\prime }},v_3^{{}^{\prime }},v_4^{{}^{\prime }}\}\right)=\{v_3,v_5,v_6\}\supseteq \left\{v_3\right\}(\in E)$. Moreover, $\{v_1^{{}^{\prime }},v_2^{{}^{\prime }},v_3^{{}^{\prime }}\}\in E^{{}^{\prime }}$ and $f^{-1}\left(\{v_1^{{}^{\prime }},v_2^{{}^{\prime }},v_3^{{}^{\prime }}\}\right)=\{v_1,v_2,v_3,v_5\}\supseteq \{v_1,v_2\},\left\{v_3\right\}(\in E)$.

Thus, for each $E_i^{{}^{\prime }}\in E^{{}^{\prime }},i=1,2,3$, there is one $E_j\in E,j=1,2,3$, such that $f^{-1}\left(E_i^{{}^{\prime }}\right)\supseteq E_j(\in E)$. Thus, f is a hyper-continuous map from V to $V^{{}^{\prime }}$.

Definition 11.

A mapping $f:V\to V^{{}^{\prime }}$ between the vertex sets of two hypergraphs $H=(V,E)$ and $K=(V^{{}^{\prime }},E^{{}^{\prime }})$ is called strictly hyper-continuous if, for each $E_i^{{}^{\prime }}\in E^{{}^{\prime }}$, there is an $E_j\in E$, such that $f^{-1}\left(E_i^{{}^{\prime }}\right)=E_j$.

Example 6.

Suppose that $H=(V,E)$ and $K=(V^{{}^{\prime }},E^{{}^{\prime }})$ are two hypergraphs, where $V=\{v_1,v_2,v_3,v_4,v_5,v_6\}$ and $V^{{}^{\prime }}=\{v_1^{{}^{\prime }},v_2^{{}^{\prime }},v_3^{{}^{\prime }},v_4^{{}^{\prime }},v_5^{{}^{\prime }}\}$ and $E=\{\{v_1,v_2\},\{v_2,v_3,v_4\},$$\{v_3,v_4,v_5\}\}$, $E^{{}^{\prime }}=\{\left\{v_1^{{}^{\prime }}\right\},\{v_2^{{}^{\prime }},v_5^{{}^{\prime }}\},\{v_1^{{}^{\prime }},v_4^{{}^{\prime }}\}\}$. A map $f:V\to V^{{}^{\prime }}$ is defined such that $f\left(v_1\right)=v_1^{{}^{\prime }}=f\left(v_2\right)$, $f\left(v_3\right)=v_2^{{}^{\prime }}=f\left(v_5\right)$, $f\left(v_4\right)=v_5^{{}^{\prime }}$, $f\left(v_6\right)=v_3^{{}^{\prime }}$. Now, we have $\left\{v_1^{{}^{\prime }}\right\}\in E^{{}^{\prime }}$ and $f^{-1}\left(\left\{v_1^{{}^{\prime }}\right\}\right)=\{v_1,v_2\}\in E$. Again, $\{v_2^{{}^{\prime }},v_5^{{}^{\prime }}\}\in E^{{}^{\prime }}$ and $f^{-1}\left(\{v_2^{{}^{\prime }},v_5^{{}^{\prime }}\}\right)=\{v_3,v_4,v_5\}\in E$. Moreover, we have $\{v_1^{{}^{\prime }},v_4^{{}^{\prime }}\}\in E^{{}^{\prime }}$ and $f^{-1}\left(\{v_1^{{}^{\prime }},v_4^{{}^{\prime }}\}\right)=\{v_1,v_2\}\in E$.

Thus, for each $E_i^{{}^{\prime }}\in E^{{}^{\prime }}$, $i=1,2,3$, there exists an $E_j\in E$ such that $f^{-1}\left(E_i^{{}^{\prime }}\right)=E_j$. Thus, f is strictly hyper-continuous.

Theorem 1.

Suppose that $H=(V,E)$ and $K=(V^{{}^{\prime }},E^{{}^{\prime }})$ are two hypergraphs and f is a mapping from V into $V^{{}^{\prime }}$. If f is a ps-open mapping, then the f-image of a point-hyperwalk in H is a point-hyperwalk in K.

Proof. 

Let

$$P\equiv v_1{E}_1{v}_2{E}_2{v}_3{E}_3\dots v_{n-1}{E}_n{v}_n$$

be a point-hyperwalk in H. Then, we obtain its f-image

$$f\left(P\right)\equiv f\left(v_1\right)f\left(E_1\right)f\left(v_2\right)f\left(E_2\right)f\left(v_3\right)f{\left(E\right)}_3\dots f\left(v_{n-1}\right)f\left(E_n\right)f\left(v_n\right).$$

Since P is a point-hyperwalk, it follows that $v_1\in E_1,v_2\in E_1\cap E_2,\dots ,v_{n-1}\in E_{n-1}\cap E_n$ and $v_n\in E_n$. Thus, $f\left(v_1\right)\in f\left(E_1\right),f\left(v_2\right)\in f(E_1\cap E_2),\dots ,f\left(v_{n-1}\right)\in f(E_{n-1}\cap E_n)$, $f\left(v_n\right)\in E_n$. Now, $E_1\cap E_2\subseteq E_1,E_2$ implies that $f(E_1\cap E_2)\subseteq f\left(E_1\right),f\left(E_2\right)$, whence $f(E_1\cap E_2)\subseteq f\left(E_1\right)\cap f\left(E_2\right)$. Therefore, $f\left(v_2\right)\in f(E_1\cap E_2)\subseteq f\left(E_1\right)\cap f\left(E_2\right)$. Similarly, $f\left(v_3\right)\in f\left(E_2\right)\cap f\left(E_3\right),\dots ,f\left(v_n\right)\in f\left(E_n\right)$. Hence, $f\left(P\right)$ is a point-hyperwalk in K. □

Corollary 1.

In Theorem 1, if f is an injective mapping, then the f-image of a point-hyperpath in H is a point-hyperpath in K, too.

Theorem 2.

Suppose that $H=(V,E)$ and $K=(V^{{}^{\prime }},E^{{}^{\prime }})$ are two hypergraphs and f is a ps-open mapping from V to $V^{{}^{\prime }}$. Then, the f-image of a knot-hyperpath in H is a knot-hyperpath in K, too.

Proof. 

Let $P\equiv \left\{v_1\right\}{E}_1{K}_1{E}_2{K}_2{E}_3{K}_3\dots K_{n-1}{E}_n\left\{v_n\right\}$ be a knot-hyperpath in H with $K_0=\left\{v_1\right\}\subseteq E_1,K_n=\left\{v_n\right\}\subseteq E_n$ and $K_i\subseteq (E_{i+1}\cap E_i)\backslash \left({\cup }_{t=1}^{i-1}{K}_t\right),i=1,2,\dots ,n-1$. Then, we have the f-image

$$f\left(P\right)\equiv f\left(K_0\right)f\left(E_1\right)f\left(K_1\right)f\left(E_2\right)f\left(K_2\right)f\left(E_3\right)f\left(K_3\right)\dots f\left(K_{n-1}\right)f\left(E_n\right)f\left(K_n\right).$$

In order to prove that $f\left(P\right)$ is a knot-hyperpath, we first show that $f\left(K_0\right)\subseteq f\left(E_1\right)$ and $f\left(K_n\right)\subseteq f\left(E_n\right)$. Since $K_0\subseteq E_1$ and $K_n\subseteq E_n$, we have $f\left(K_0\right)\subseteq f\left(E_1\right)$ and $f\left(K_n\right)\subseteq f\left(E_n\right)$.

Since $K_2\subseteq (E_2\cap E_3)\backslash E_1$, we have $K_2\subseteq (E_2\cap E_3)\cap K_1^c$. It follows that $f\left(K_2\right)\subseteq f((E_2\cap E_3)\cap K_1^c)$$\subseteq f(E_2\cap E_3)\cap f\left(K_1^c\right)$$\subseteq f(E_3\cap E_2)\cap {\left(f\left(K_1\right)\right)}^c\subseteq f(E_3\cap E_2)\backslash f\left(K_1\right)$. Hence, $f\left(K_2\right)\subseteq f(E_3\cap E_2)\backslash f\left(K_1\right)$.

Similarly, $K_3\subseteq (E_4\cap E_3)\backslash (K_1\cup K_2)$ implies that $f\left(K_3\right)\subseteq f(E_4\cap E_3)\backslash f\left(K_1\right)\cup f\left(K_2\right)$ and so on. Thus, $K_i\subseteq (E_i\cap E_{i+1})\backslash \left({\cup }_{t=1}^{i-1}{K}_t\right)$ implies that

$$\begin{array}{c}\hfill f\left(K_i\right)\subseteq f(E_i\cap E_{i+1})\backslash {\cup }_{t=1}^{i-1}f\left(K_t\right)\end{array}$$

(2)

for any $i=1,2,\dots ,n-1$. Hence, we conclude that $f\left(P\right)$ is a knot-hyperpath in K. □

Theorem 3.

Suppose that $H=(V,E)$ and $K=(V^{{}^{\prime }},E^{{}^{\prime }})$ are two hypergraphs. If f is a hyper-continuous map from V onto $V^{{}^{\prime }}$, then the inverse image of a knot-hyperpath in K under f is a weak knot-hyperpath in H.

Proof. 

Let $P^{{}^{\prime }}\equiv K_0^{{}^{\prime }}{E}_1^{{}^{\prime }}{K}_1^{{}^{\prime }}{E}_2^{{}^{\prime }}{K}_2^{{}^{\prime }}\dots K_{n-1}^{{}^{\prime }}{E}_n^{{}^{\prime }}{K}_n^{{}^{\prime }}$ be a knot-hyperpath in K. As f is hyper-continuous, we have $f^{-1}\left(E_1^{{}^{\prime }}\right)\supseteq E_1,f^{-1}\left(E_2^{{}^{\prime }}\right)\supseteq E_2,\dots ,f^{-1}\left(E_n^{{}^{\prime }}\right)\supseteq E_n$, for some hyperedges $E_1,E_2,\dots ,E_n\in E$. Moreover, the sets $f^{-1}\left(K_i\right),i=0,1,2,\dots ,n$ are nonempty because f is an onto mapping. Now, the inverse image of the knot-hyperpath can be written as

$$f^{-1}(K_0^{{}^{\prime }})f^{-1}(E_1^{{}^{\prime }})f^{-1}(K_1^{{}^{\prime }})f^{-1}(E_2^{{}^{\prime }})\dots f^{-1}(K_{n-1}^{{}^{\prime }})f^{-1}(E_n^{{}^{\prime }})f^{-1}(K_n^{{}^{\prime }}),$$

where $f^{-1}\left(E_i^{{}^{\prime }}\right)\supseteq E_i$, for $i=1,2,3,\dots ,n$. Since the inverse set function behaves well for union, intersection and complement, it follows that the conditions of a knot-hyperpath are easily satisfied. Hence, $f^{-1}\left(P^{{}^{\prime }}\right)$ is a weak knot-hyperpath. □

Corollary 2.

The inverse image of an onto strictly hyper-continuous map of a knot-hyperpath is again a knot-hyperpath.

Proof. 

Consider the knot-hyperpath

$$P^{{}^{\prime }}\equiv K_0^{{}^{\prime }}{E}_1^{{}^{\prime }}{K}_1^{{}^{\prime }}{E}_2^{{}^{\prime }}{K}_2^{{}^{\prime }}\dots K_{n-1}^{{}^{\prime }}{E}_n^{{}^{\prime }}{K}_n^{{}^{\prime }}$$

as in the proof of Theorem 3. As f is strictly hyper-continuous, each $f^{-1}\left(E_i\right)$ belongs to E and, by using similar arguments, we can conclude that

$$f^{-1}(P^{{}^{\prime }})\equiv f^{-1}\left(K_0^{{}^{\prime }}\right)f^{-1}\left(E_1^{{}^{\prime }}\right)f^{-1}\left(K_1^{{}^{\prime }}\right)\dots f^{-1}\left(K_{n-1}^{{}^{\prime }}\right)f^{-1}\left(E_n^{{}^{\prime }}\right)f^{-1}\left(K_n^{{}^{\prime }}\right)$$

is a knot-hyperpath. □

Theorem 4.

Let $f:V\to V^{{}^{\prime }}$ be a ps-open mapping from a hypergraph $H=(V,E)$ onto a hypergraph $K=(V^{{}^{\prime }},E^{{}^{\prime }})$. If H is connected, then K is connected, too.

Proof. 

Let $v_1^{{}^{\prime }}$ and $v_2^{{}^{\prime }}$ be two any vertices in K. Since f is onto, there exists $v_1$, $v_2\in V$ such that $f\left(v_1\right)=v_1^{{}^{\prime }}$ and $f\left(v_2\right)=v_2^{{}^{\prime }}\in V$. Moreover, since H is connected and $v_1$, $v_2\in V$, there exists a knot-hyperpath P from $v_1$ to $v_2$. Because the image of a knot-hyperpath under a ps-open mapping is again a knot-hyperpath in K, starting at $f\left(v_1\right)={v_1}^{{}^{\prime }}$ and ending at $f\left(v_2\right)={v_2}^{{}^{\prime }}$, we immediately conclude that K is connected. □

4. Hyperpaths and Hypertrees

In this section, we will present a sufficient condition, only involving hyperpaths, under which a hypergraph is a hypertree. Till now, the definition of a hypertree has been based on the concept of the host graph.

Definition 12

([14]). Suppose that $H=(V,E)$ is a hypergraph and $G=(V,F)$ is a graph over the same vertex set V. We say that G is a host graph of H if each hyperedge $E_i\in E$ induces a connected subgraph in G.

Lemma 1.

There exists at least one host graph G of the hypergraph H in which the induced subgraph obtained from any two equivalent knot-hyperpaths never forms a cycle.

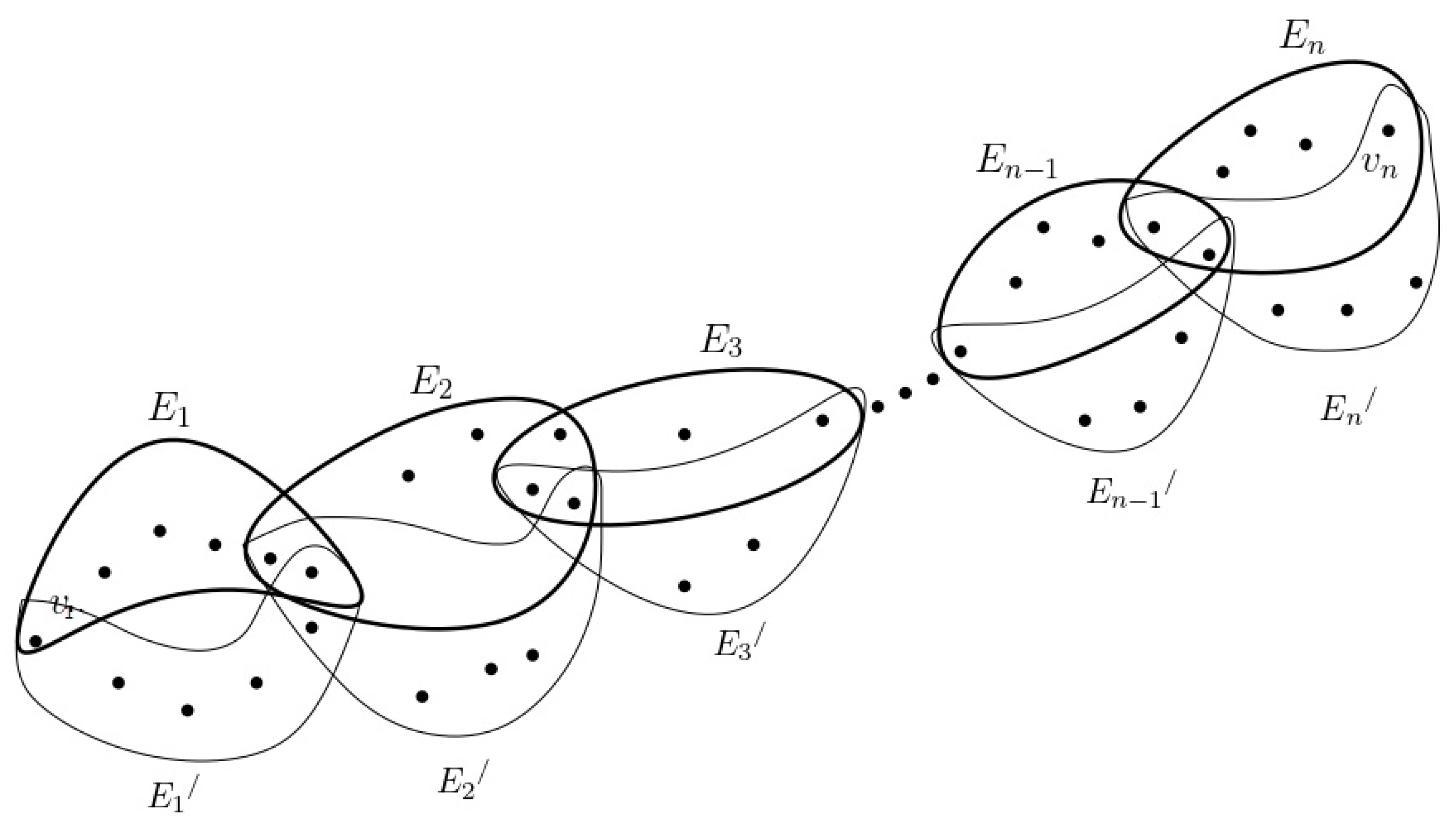
Proof. 

Let $P_1$ and $P_2$ be any two equivalent knot-hyperpaths of the hypergraph H, which may be denoted as follows:

$$P_1\equiv K_0=\left\{v_1\right\}{E}_1{K}_1{E}_2{K}_2{E}_3{K}_3\dots K_{n-1}{E}_n{K}_n=\left\{v_n\right\}$$

and

$$P_2\equiv {K_0}^{{}^{\prime }}=\left\{v_1\right\}{E_1}^{{}^{\prime }}{K_1}^{{}^{\prime }}{E_2}^{{}^{\prime }}{K_2}^{{}^{\prime }}{E_3}^{{}^{\prime }}{K_3}^{{}^{\prime }}\dots {K_{n-1}}^{{}^{\prime }}{E_n}^{{}^{\prime }}{K_n}^{{}^{\prime }}=\left\{v_n\right\}$$

and graphically represented in Figure 2.

Since they are equivalent knot-hyperpaths, it follows that $K_i\cap {K_i}^{{}^{\prime }}\ne \varnothing$, $E_i\cap {E_i}^{{}^{\prime }}\ne \varnothing$, $K_i\cap K_{i+1}=\varnothing$, and ${K_i}^{{}^{\prime }}\cap {K_{i+1}}^{{}^{\prime }}=\varnothing$.

We note that $E_1\cup E_1^{{}^{\prime }}$ can be expressed as the disjoint union of $E_1\backslash {E_1}^{{}^{\prime }}$, ${E_1}^{{}^{\prime }}\backslash E_1$ and $E_1\cap {E_1}^{{}^{\prime }}$. As we know that, in any host graph of a hypergraph, all the vertices in a hyperedge are connected, and since $E_1\cap {E_1}^{{}^{\prime }}$ is contained in $E_1$ and ${E_1}^{{}^{\prime }}$, it follows that all the vertices in $E_1\cap {E_1}^{{}^{\prime }}$ can be connected to form a graph without cycles. Moreover, since $E_1\cap {E_1}^{{}^{\prime }}$ and $E_1\backslash {E_1}^{{}^{\prime }}$ are contained in $E_1$, a graph can be drawn by connecting all the vertices in $E_1\backslash {E_1}^{{}^{\prime }}$ without forming a cycle, which can be further connected with the cycle-free graph drawn in $E_1\cap {E_1}^{{}^{\prime }}$ in the previous step. By connecting vertices in such a manner, the resultant graph will never form a cycle. Similarly, a graph can be drawn by connecting the cycle-free graph drawn in $E_1\cap {E_1}^{{}^{\prime }}$ with a cycle-free graph in ${E_1}^{{}^{\prime }}\backslash E_1$. All these constructions are depicted in Figure 3.

The model is constructed in such a way that the vertex $v_1$ is connected to $K_1\cap {K_1}^{{}^{\prime }}$ and $K_1\cap {K_1}^{{}^{\prime }}$ is connected to both $E_1\backslash {E_1}^{{}^{\prime }}$ and ${E_1}^{{}^{\prime }}\backslash E_1$ through $K_1\cup {K_1}^{{}^{\prime }}$ without forming a cycle. Furthermore, it is to be noted that because $K_1\cap {K_1}^{{}^{\prime }}$ is connected to $E_1\backslash {E_1}^{{}^{\prime }}$, in the next step, $K_2\cap {K_2}^{{}^{\prime }}$ will connect to those vertices of $E_2\backslash {E_2}^{{}^{\prime }}$ that are not in $E_1$, in order to not create a cycle. Similarly, $K_2\cap {K_2}^{{}^{\prime }}$ will connect to those vertices of ${E_1}^{{}^{\prime }}\backslash E_1$ that are not in ${E_1}^{{}^{\prime }}$. This further continues till the last vertex $v_n$, where $v_n$ is connected to $K_{n-1}\cap K_{n-1}^{{}^{\prime }}$ and $K_{n-1}\cap K_{n-1}^{{}^{\prime }}$ is connected to $E_n\backslash {E_n}^{{}^{\prime }}$ and ${E_n}^{{}^{\prime }}\backslash E_n$ through $K_1\cup {K_1}^{{}^{\prime }}$, without forming a cycle. In this manner, a host graph can be drawn from the hypergraph H, where the induced subgraph obtained from the vertices in the edges of the two paths is cycle-free. We conclude that there exists at least one host graph G of H in which the induced subgraph obtained from the two equivalent knot-hyperpaths will never form a cycle. □

Remark 1.

If the induced subgraph obtained from the vertex set of two knot-hyperpaths joining the same vertices of any host graph of a hypergraph always produces a cycle, then the knot-hyperpaths are not equivalent.

Theorem 5.

Suppose that H is a connected hypergraph, which is a hypertree. Then, any entire knot-hyperpaths having the same length and connecting any two vertices are equivalent.

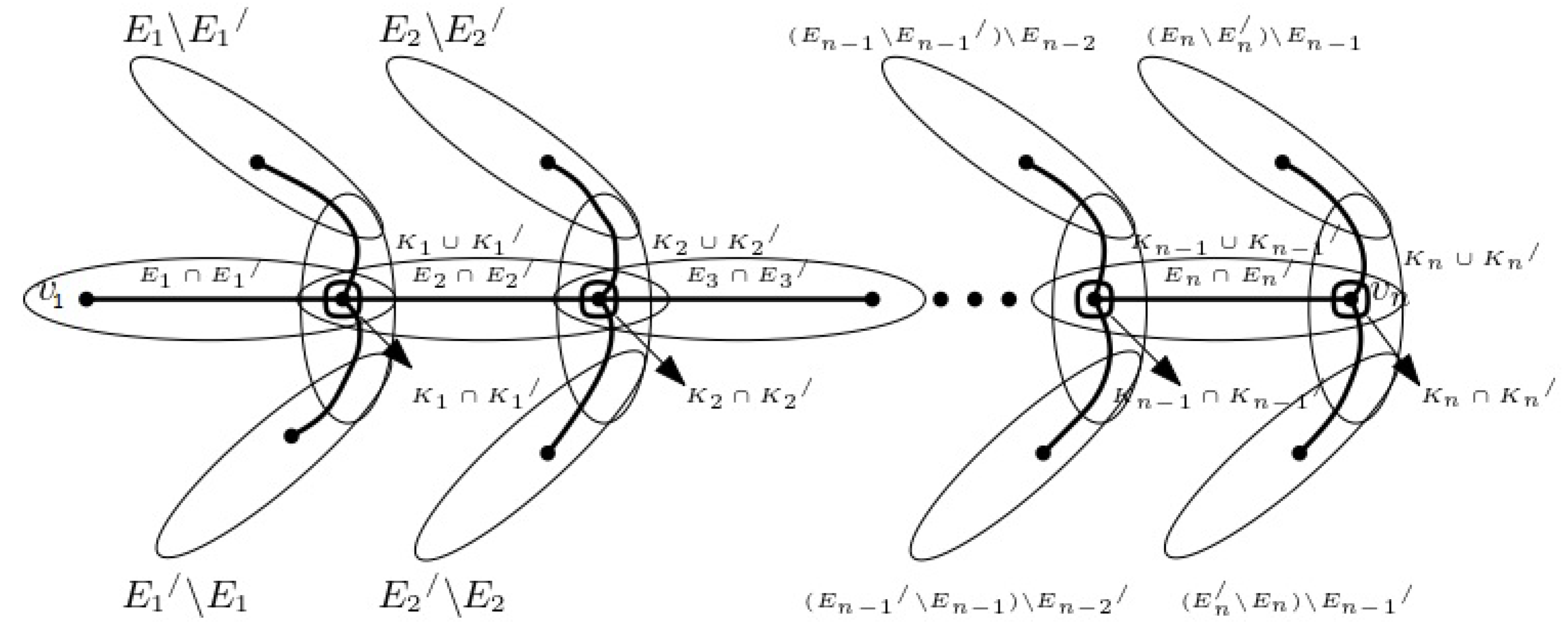
Proof. 

Let $P_1$ and $P_2$ be any two entire knot-hyperpaths of the hypergraph H, which may be denoted as follows:

$$P_1\equiv K_0=\left\{v_1\right\}{E}_1{K}_1{E}_2{K}_2{E}_3{K}_3\dots K_{n-1}{E}_n{K}_n=\left\{v_n\right\}$$

and

$$P_2\equiv K_0^{{}^{\prime }}=\left\{v_1\right\}{E}_1^{{}^{\prime }}{K}_1^{{}^{\prime }}{E}_2^{{}^{\prime }}{K}_2^{{}^{\prime }}{E}_3^{{}^{\prime }}{K}_3^{{}^{\prime }}\dots K_{n-1}^{{}^{\prime }}{E}_n^{{}^{\prime }}{K}_n^{{}^{\prime }}=\left\{v_n\right\}.$$

If $P_1$ and $P_2$ are equivalent knot-hyperpaths, then the result is proven.

On the contrary, if $P_1$ and $P_2$ are not equivalent, then there exists a pair of edges $(E_{i_0},E_{i_0}^{{}^{\prime }})$, where $E_{i_0}$ is from $P_1$ and $E_{i_0}^{{}^{\prime }}$ is from $P_2$, such that $E_{i_0}\cap E_{i_0}^{{}^{\prime }}=\varnothing$. Since $K_{i_0-1},K_{i_0}\subseteq E_{i_0}$ and $K_{i_0-1}^{{}^{\prime }},K_{i_0}^{{}^{\prime }}\subseteq E_{i_0}^{{}^{\prime }}$, we have $K_{i_0-1}\cap K_{i_0-1}^{{}^{\prime }}=\varnothing =K_{i_0}\cap K_{i_0}^{{}^{\prime }}$. Moreover, let $E_{j_0},E_{j_0}^{{}^{\prime }}$ be the edges such that $E_{j_0}\cap E_{j_0}^{{}^{\prime }}\ne \varnothing$, while $E_k\cap E_k^{{}^{\prime }}=\varnothing ,$ for any $k\in \{i_0,i_0+1,\dots ,j_0-1\}$. Then, the edges $E_{i_0-1}$ to $E_{j_0}$ and $E_{i_0-1}^{{}^{\prime }}$ to $E_{j_0}^{{}^{\prime }}$ will always form a cycle (see Figure 4) in any host graph of H, which is a contradiction. Therefore, $P_1$ and $P_2$ are equivalent. Thus, we can conclude that if H is a hypertree, then, between any two vertices, the entire knot-hyperpaths having the same length are unique up to isomorphism. □

It is to be noted that two knot-hyperpaths joining two vertices in a hypertree may not always be equivalent. This can be observed in Example 7 by introducing an extra edge $\{v_6,v_7,v_{10}\}$ to the hypergraph, which subsequently produces two knot-hyperpaths joining $v_0$ and $v_1$, but with different lengths.

Theorem 6.

Suppose that H is a hypergraph such that, between any two vertices, there exists a unique entire knot-hyperpath up to isomorphism. Then, H is a hypertree.

Proof. 

By hypothesis, between any two vertices $v_1$ and $v_2$ of H, there exists an entire knot-hyperpath, which is unique up to isomorphism. It follows that H is connected. To show that H is a hypertree, it is enough to show that H admits a host graph that is a tree. Let

$$P\equiv K_0=\left\{v_1\right\}{E}_1{K}_1{E}_2{K}_2{E}_3{K}_3\dots K_{n-1}{E}_n{K}_n=\left\{v_2\right\}$$

be an entire knot-hyperpath joining the vertices $v_1$ and $v_2$. Then, the vertices contained in the edges of this knot-hyperpath can be joined without forming a cycle, in such a way that the constructed graph $G_1$ is an induced subgraph with vertex set $V_1=\cup E_i$ of some host graph G of the given hypergraph H. Now, if $\cup E_i=V$, then we can take $G=G_1$, which is a tree. Hence, in this case, H is a hypertree and the theorem is proven.

If $\cup E_i\ne V$, then let $v_3\in V$ be such that $v_3\notin \cup E_i$. Let

$$P^{{}^{\prime }}\equiv \left\{v_1\right\}{E}_1^{{}^{\prime }}{K}_1^{{}^{\prime }}{E}_2^{{}^{\prime }}\dots K_{k-1}^{{}^{\prime }}{E}_k^{{}^{\prime }}\left\{v_3\right\}$$

be an entire knot-hyperpath joining the vertices $v_1$ and $v_3$. We note that there may exist some hyperedges in $P^{{}^{\prime }}$ that coincide with the hyperedges of P. Now, excluding these common hyperedges, the rest of the hyperedges of $P^{{}^{\prime }}$ can be joined without forming a cycle. In this way, an induced subgraph $G_2$ can be formed with vertex set $\cup E_j^{{}^{\prime }}$ and the edges set as the union of those edges common with $G_1$ and the edges newly formed from hyperedges of $P^{{}^{\prime }}$, which are not in P. It is clear from the construction that both subgraphs $G_1$ and $G_2$ are not cyclic and the union $G_1\cup G_2$ is connected; otherwise, H would have two entire knot-hyperpaths joining the same vertices, but not equivalent (see proof of Theorem 5). Now, if $(\cup E_i)\cup (\cup E_j^{{}^{\prime }})=V$, then $G=G_1\cup G_2$ is the host graph of H that is a tree and hence H is again a hypertree.

If $(\cup E_i)\cup (\cup E_j^{{}^{\prime }})\ne V$, then there exists a vertex $v_4\in V$ that is not in $(\cup E_i)\cup (\cup E_j^{{}^{\prime }})$. Then, we will have an entire knot-hyperpath $P^{{}^{″}}$ joining $v_1$ and $v_4$ as follows:

$$P^{{}^{″}}\equiv \left\{v_1\right\}{E}_1^{{}^{″}}{K}_1^{{}^{″}}{E}_2^{{}^{″}}\dots K_{l-1}^{{}^{″}}{E}_l^{{}^{″}}\left\{v_4\right\}.$$

Now, excluding those hyperedges of $P^{{}^{″}}$ that are common with P and $P^{{}^{\prime }}$, the rest of the hyperedges of $P^{{}^{″}}$ can be joined without forming a cycle. In this way, an induced subgraph $G_3$ can be formed with vertex set $\cup E_l^{{}^{″}}$ and the edges set as the union of those edges common with $G_1\cup G_2$ and the edges newly formed from hyperedges of $P^{{}^{″}}$ that are not in P and $P^{{}^{\prime }}$. It is clear from the construction that all the subgraphs $G_1,G_2$ and $G_3$ are not cyclic and the union $G_1\cup G_2\cup G_3$ is connected. Now, if $(\cup E_i)\cup (\cup E_j^{{}^{\prime }})\cup (\cup E_l^{{}^{″}})=V$, then $G=G_1\cup G_2\cup G_3$ is the host graph of H that is a tree and hence H is a hypertree.

As the vertex set of the hypergraph is finite, the process has a finite number of steps. Thus, we can conclude that if H is a hypergraph such that, between any two vertices, there exists an entire knot-hyperpath unique up to isomorphism, then H is a hypertree. □

Remark 2.

We can notice that the hypergraph considered in Example 3 is a hypertree, but the two knot-hyperpaths $P_1^{{}^{\prime }}$ and $P_2^{{}^{\prime }}$ joining the vertices $v_1$ and $v_{13}$ are not equivalent, even though they have the same length, while all the entire knot-hyperpaths (for example, $P_1$ and $P_2$) are equivalent. Hence, the property of knots of being entire, in the above two theorems, is an important hypothesis to be considered.

To illustrate the algorithm stated in the proof of Theorem 6, we present the following example, where the considered hypergraph is a hypertree and a host graph is drawn using the technique used in the proof of Theorem 6. This hypertree is represented in Figure 5.

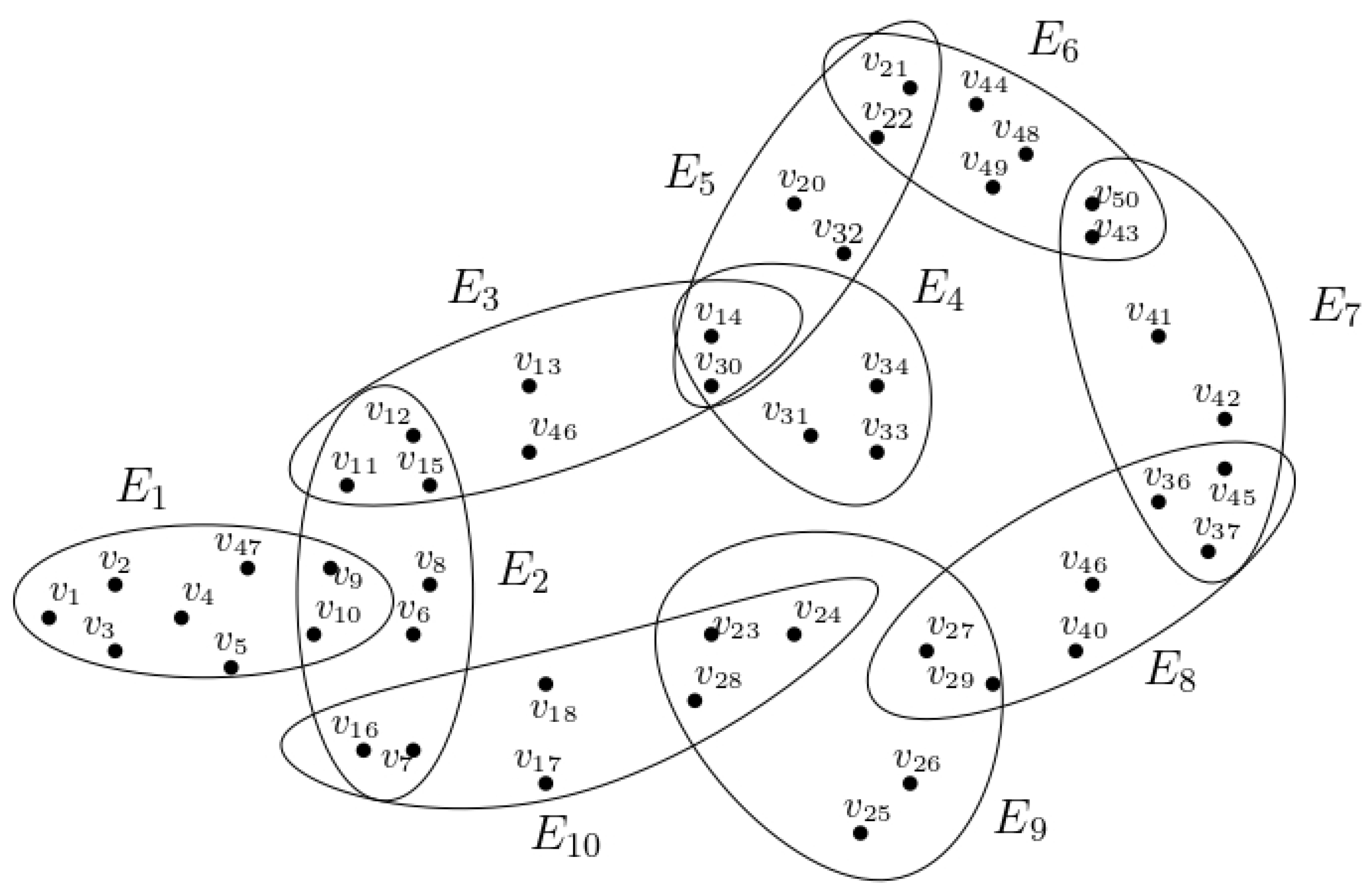
Example 7.

Consider the hypergraph $H=(V,E)$, where $V=\{v_0,v_1,v_2,\dots ,v_{16}\}$ and $E=\{E_1=\{v_0,v_7,v_6\},E_2=\{v_6,v_{10},v_{11}\},E_3=\{v_{11},v_{14},v_{15},v_5,v_{16}\},E_4=\{v_3,v_1,v_{13}\},E_5=\{v_6,v_2\},E_6=\{v_5,v_{16}\},E_7=\{v_4,v_9,v_{12}\},E_8=\{v_5,v_8,v_{13},v_9\}\}$. One can easily verify that H is a hypertree and, between any two vertices, there exists an entire knot-hyperpath, unique up to isomorphism. Now, we will use the technique used in the proof of Theorem 6, in order to obtain a host graph that is a tree.

Let us consider the vertices $v_0$ and $v_1$ and the knot-hyperpath

$$P\equiv \left\{v_0\right\}{E}_1\left\{v_6\right\}{E}_2\left\{v_{11}\right\}{E}_3\left\{v_5\right\}{E}_4\left\{v_{13}\right\}{E}_8\left\{v_1\right\}$$

joining $v_0$ and $v_1$. Now, the vertices in all hyperedges are connected and form a graph $G_1$ in such a way that it is not cyclic and it is an induced subgraph with vertex set $V_1=E_1\cup E_2\cup E_3\cup E_4\cup E_8$ of some host graph G of H.

Clearly, $V\ne V_1$, and so we consider the vertex $v_2\in V$, which is not in $V_1$. Now, a hyperpath $P^{{}^{\prime }}$ from $v_0$ to $v_2$ is constructed as follows:

$$P^{{}^{\prime }}\equiv \left\{v_0\right\}{E}_1\left\{v_6\right\}{E}_2\left\{v_{11}\right\}{E}_3\left\{v_5\right\}{E}_6\left\{v_2\right\}.$$

Clearly, except $E_6$, all other hyperedges of this knot-hyperpath appear in the previous knot-hyperpath, and so vertices of $E_6$ are joined in an acyclic way and represent a graph $G_2$ with vertex set $V_2=E_1\cup E_2\cup E_3\cup E_6$.

Here, we note that the union of the two graphs $G_1$ and $G_2$ is acyclic and connected. Moreover, $V_1\cup V_2\ne V$. Therefore, we consider an arbitrary vertex from $v_4,v_{12},v_{16}$ that is not in $V_1\cup V_2$. Let us consider the vertex $v_4$ and the knot-hyperpath $P^{{}^{″}}$ constructed as follows:

$$P^{{}^{″}}\equiv \left\{v_0\right\}{E}_1\left\{v_6\right\}{E}_2\left\{v_{11}\right\}{E}_3\left\{v_5\right\}{E}_4\left\{v_9\right\}{E}_7\left\{v_4\right\}.$$

Clearly, except $E_7$, all other hyperedges of this knot-hyperpath appear in the previous knot-hyperpaths, and so vertices of $E_7$ are joined in an acyclic way that represents a graph $G_3$ with vertex set $V_3=E_1\cup E_2\cup E_3\cup E_4\cup E_7$. Thus, $G_1\cup G_2\cup G_3$ is connected and acyclic. Since $V_1\cup V_2\cup V_3\ne V$, we consider the vertex $v_{16}$, the only one that is not in this union and the knot-hyperpath

$$P^{{}^{‴}}\equiv \left\{v_0\right\}{E}_1\left\{v_6\right\}{E}_5\left\{v_{16}\right\}.$$

Clearly, except $E_5$, all other hyperedges of this knot-hyperpath appear in the previous knot-hyperpaths, and so vertices of $E_5$ are joined in an acyclic way that represents a graph $G_4$ with vertex set $V_4=E_1\cup E_5$. Now, $G_1\cup G_2\cup G_3\cup G_4$ is connected and acyclic, and $V_1\cup V_2\cup V_3\cup V_4=V$. Therefore, $G=G_1\cup G_2\cup G_3\cup G_4$ is the required host graph, which is a tree.

5. Conclusions

Based on the definition of a knot in a hypergraph H, which is a subset of the intersections of some intersecting hyperedges of H, we have introduced the notion of the knot-hyperpath, in order to better characterize the hyper-continuity and pseudo-continuity of functions between two hypergraphs. Moreover, in the second part of the paper, we have characterized the hypertrees without using the concept of a host graph. A sufficient condition is established to check whether or not a hypergraph is a hypertree. Furthermore, an algorithm is designed in order to extract from a hypertree a host graph that is a tree. This algorithm has the potential to determine whether a hypergraph is a hypertree or not. As we know, hypergraphs and hypertrees are extensively used in different branches of applied sciences, including networking and theoretical computer science, and therefore this investigation will give more future ideas towards the applicability of hypergraphs and hypertrees in these fields.