Abstract
The preservice primary school mathematics teacher needs training that focuses on school mathematics and its didactics. Research has shown the importance of developing mathematical content knowledge as well as adequate didactic knowledge. Teacher education programs must address both to provide an effective teaching-learning process. The present research aims to assess the mathematical content knowledge of 194 prospective teachers about fraction word problems faced by students at the Primary Education stage, based on the Mathematics Teachers′ Specialized Knowledge (MTSK) model. By means of the preservice teachers’ written answers, we explored their knowledge and identified the associated error to fraction word problems (one-step and multistep) in which the fraction has a meaning as an operator. Preservice teachers showed some difficulties when working with this content, difficulties that were intensified when they solved multistep problems. The most common error founded in both types of problems is related to the meaning of fraction as operator. The results show a weak prior mathematical content knowledge and as a consequence, it is necessary to establish preventive actions in the training degrees since an insufficient mathematical content knowledge prevents them having a proper didactic knowledge.
1. Introduction
On 25 September 2015, the General Assembly of the United Nations presented the 2030 Agenda for Sustainable Development, in which one of the goals is [1] (p. 16) “Ensure inclusive and equitable quality education and promote lifelong learning opportunities for all”. Accordingly, it is emphasized that children in Primary Education should receive quality education, with relevant and effective learning outcomes. Likewise, emphasis is placed on teacher training because of its role in the teaching-learning process. Several researchers highlight the relationship between adequate student learning and the teachers’ knowledge of content and discipline [2,3]. As researchers and trainers of future teachers, we deem it necessary to investigate whether future teachers have learned the mathematical knowledge that they will later teach in schools.
The area of mathematics in Primary Education is developed around four large blocks of content (Numbers, Geometry, Measurement and Statistics and Probability). The Numbers block takes on greater prominence as it points out the need to achieve effective numerical literacy, understood as the ability to successfully face situations in which numbers and their relationships intervene [4]. Therefore, it is not enough to master written calculation algorithms; it is necessary to be confident with numbers and quantities, to use them whenever necessary and to identify the basic relationships between them. With regard to fractions, the Spanish curriculum proposes that students from 8 to 10 years of age begin to work on the concept of fraction as a part-whole relationship, and they use fractional numbers to express partitions and relationships in real contexts. Subsequently, in the successive years of Primary Education, fractions should be used as operators in the problem interpretation and resolution and the correspondence between simple fractions, decimals and percentages has to be studied. Comparing the Spanish curriculum with the principles and standards proposed by the National Council of Teachers of Mathematics (NCTM) for school Mathematics [5], we found similarities, since the NCTM proposes to develop the understanding of fractions as parts of unit wholes, as parts of a collection, as locations on number lines, and as divisions of whole numbers for students from 8 to 10 years. Moreover, for older students (10–12 years old), the NCTM suggests working flexibly with fractions, decimals, and percentages to solve problems.
Some research highlights the role of fractions in the understanding of other mathematical concepts, such as algebraic and probabilistic concepts [6]. Generally, the studies developed around this numerical set are focused on three aspects: the conceptualization and meanings of fractions [7,8,9,10], the knowledge of primary school students, including their difficulties and errors [11,12,13], and the knowledge of teachers [14,15,16]. The aim of this research is to explore the prior knowledge of a group of preservice elementary teachers about the meaning of the fraction as an operator in fraction word problems (one-step and multistep). Given that our objective is to analyze the knowledge of preservice teachers, Section 2 includes some of the models that address the teacher’s knowledge. Section 3 gives an overview of research on the different meanings for the fraction concept and on some errors made when working with fractions. Section 4 describes the characteristics of the participants as well as the instrument and codifications used for getting the results that are subsequently analyzed in Section 5. Finally, the main conclusions and their implications for the field of Mathematics Education are presented.
2. Teachers’ Knowledge
Fennema and Franke [17] underlined the importance of the knowledge that a teacher must have and therefore must be acquired by preservice teachers during their training. The authors state “What a teacher knows is one of the most important influences on what is done in the classroom and, ultimately, on what students learn” [17] (p. 147). In Mathematics Education, the research line on teacher training has focused for many years on characterizing the knowledge that future teachers should know or acquire [18], defining different theoretical models on mathematical, didactic and curricular knowledge, among others. However, several authors have pointed out the difficulty of determining the connection between the different types of knowledge that mathematics teachers should have [19,20,21]. Hence, what a future mathematics teacher should learn in their initial training is also a complex issue.
Shulman’s ideas were innovative on this question and were an important reference for later research [22]. Three categories of knowledge are proposed: (1) knowledge of the content to be taught, which is related to the body of knowledge of the subject and its organization; (2) curricular knowledge, referring to the teacher’s knowledge of the institutional curriculum that guides their teaching process; and (3) didactic knowledge of the content, understood as the knowledge necessary for teaching the subject. This last knowledge must be related to the two previous ones, as well as to the knowledge of the students’ cognitive characteristics in relation to the content.
Other research groups based on Shulman’s ideas, but focusing more on mathematics education, generated new models of the knowledge that a mathematics teacher should have. Ball and collaborators from the University of Michigan [23] developed the Mathematical Knowledge for Teaching (MKT) model, defined as “the mathematical knowledge that teachers use in the classroom to produce instruction and student growth” [24] (p. 374). The authors divide knowledge into two large domains, content knowledge and content didactic knowledge, each of them structured by three subdomains. Content knowledge includes: (1) common content knowledge, (2) specialized content knowledge, and (3) knowledge at the mathematical horizon. In turn, didactic content knowledge is determined by: (1) knowledge of content and students, (2) knowledge of content and teaching, and (3) knowledge of the curriculum.
In this paper, we rely on the model proposed by the research group in Didactics of Mathematics at the University of Huelva, led by José Carrillo, called Mathematics Teacher’s Specialized Knowledge (MTSK), which includes the domain of beliefs about mathematics and mathematics teaching and learning [25]. As with the MKT model, the MTSK is divided into two broad domains: mathematical knowledge (MK) and pedagogical content knowledge (PCK), but they differ in the specific subdomains.
Mathematical knowledge (MK) is structured by three subdomains of knowledge:
- (a)
- Knowledge of topics (KoT) is the knowledge of school mathematics, but without neglecting the knowledge of mathematics as a discipline, that is, knowing the content in greater depth than that which corresponds to a specific educational level. In the case of fractions, for example, it corresponds to knowing the conceptual structure of rational numbers or the different meanings of fractions.
- (b)
- Knowledge of the structure of mathematics (KSM) is understood as the teacher’s knowledge of the relationships of mathematical content, so that concepts should not only be included as isolated elements. For example, knowing the relations among the different fraction representations, ½ = 0.5.
- (c)
- The knowledge of practices in mathematics (KPM) implies knowing how to proceed in mathematics, understanding practice as doing mathematics, linked to knowing how to think in mathematics. Example, the way in which the rational numbers set is constructed from the equivalence relations.
Pedagogical knowledge of mathematical content (PCK) encompasses the features of teaching and learning mathematics and is broken down into:
- (a)
- Knowledge of the features of learning mathematics (KFLM) is related to the specific learning of mathematical topics, so the teacher must know how students learn those topics, taking into account errors and difficulties. For example: understanding the fraction as the pair of numbers forming a number and not seeing it as two whole numbers separated by a horizontal line.
- (b)
- Knowledge of mathematics teaching (KMT) is the knowledge that the teacher has to acquire in relation to how teaching should be carried out, taking into account different strategies, resources and materials to enhance the development of procedural and conceptual mathematical skills. In the case of fractions, to know the different ways of representing a fraction (discrete models and continuous models).
- (c)
- The knowledge of the mathematical learning standards (KMLS) includes knowing the curricular guidelines on the contents to be learned at each level, as well as the knowledge of the research findings in the area of didactics of mathematics. For example, knowing that, in the Spanish curriculum, the concept of fraction is introduced in the second cycle of Primary Education (students aged 8–10 years) [4].
As teacher trainers, we consider that a balance must be ensured between the above mentioned types of knowledge, because of the important role they play in their training [26]. Given the characteristics of our study, we focus specifically on the knowledge of the topics (KoT), since the teacher must possess a deeper mathematical knowledge than the one the students have to achieve [27], that is, concepts, properties, procedures, phenomenology and representation systems linked to a mathematical content [28]. In our case, we consider that, by working with the subconstruct of fraction as operator in a contextualized problem (one-step or multistep), we are relating those elements contemplated by the KoT.
3. Background
The teaching and learning of fractions have been topics of interest due to the difficulties that Primary Education students have with this content [29,30,31,32]. This situation is remarkable, since fractions are involved in different situations of daily life, such as following the steps of a food recipe, interpreting supermarket offers, etc. Moreover, fractions are a key content in primary school to address other mathematical contents (probabilistic, proportional and algebraic reasoning). Much of the research focused on addressing this problem points to a lack of conceptual understanding as the main difficulty, which is due to the diversity of meanings associated with this concept. Initially, Kieren [33] differentiated four meanings for the concept of fraction: measure, ratio, quotient and operator, expanding to five with the inclusion of the part–whole meaning [29,34,35,36]. Authors such as Lamon [34] underlined the importance of establishing and differentiating the five fraction subconstructs and their interpretation as an essential element for the conceptual understanding of fractions [37,38] (see Table 1).

Table 1.
Meaning of fractions.
Olanoff et al. [39] performed a review of 43 articles focused on the fraction knowledge of prospective elementary teachers at different time periods, to compare the aspects of fractions that have been researched and thus determine the difficulties faced by future teachers. Among the most noteworthy results, the authors pointed out that early research (before 1998) focused on knowledge of multiplication and division of fractions (operations). This situation has changed and now it has been extended to research on representation, comparison, problem solving and invention with fractions. A situation highlighted by these authors is that the par–whole meaning is the one that has been most researched, as it is the one that is most worked on in Primary Education. Likewise, the authors found that, despite not presenting difficulties in procedural aspects, the preservice teachers showed a certain lack of understanding of the meanings associated with fractions.
In the same vein, Vula and Kingji-Kastrati [40] administered a test to 58 prospective teachers to assess both knowledge about the different meanings of fractions and procedural knowledge when adding and subtracting fractions. They emphasized the misconception of the meanings of fractions when solving situations that required conceptual development. The authors also pointed out the disconnection between conceptual and procedural knowledge, as the majority of participants identified the procedure to be performed (addition or subtraction of fractions) without incorporating the corresponding conceptual explanation.
The conceptual understanding of the meanings of fractions is related to problem-solving competence. For this reason, several studies have focused on studying this aspect with preservice teachers [41,42,43,44,45]. Authors such as Yang et al. [46] analyzed the answers of 280 preservice teachers to the problem, “Vicky used 30/31 of a metre for her tape, and Mary used 36/37 of a metre for hers. Who used more tape? Why?” [46] (p. 388), in which fractions possess a measurement meaning. The results showed that most of the participants chose to represent the fraction in decimal form or to reduce the fractions to a common denominator, strategies that led to the emergence of arithmetical errors.
The Trends in International Mathematics and Science Study (TIMSS 2015) shows the difficulties in two-step fraction problems [47]. This fact has led to the need to delve into this issue by analyzing the type of instruction that students receive from teachers and the development of their competence in problem solving [48]. Likewise, it has been decided to deepen the mathematical knowledge that preservice and in-service primary teachers possess regarding the strategies for solving fraction problems [49,50,51,52], because teachers tend to replicate the strategies they have learned in their specific learning experience [53].
Behr et al. [54] described the strategies of a group of preservice primary school teachers on the rational number operator subconstruct, within a problem-solving contest involving finding three fourths of a quantity presented as eight bundles of four sticks. Most of the answers were categorized in two types of strategies: duplicator/partition-reducer (DPR), the effect is that of partitive division; and stretcher/shrinker (SS), the effect is that of quotitive division. However, the authors highlighted an increased presence of DPR versus SS due to the fact that the duplication of a quantity is psychologically more demanding than the partitioning of this quantity, among others [54].
By examining the answers of 350 fourth-and fifth-grade teachers in the U.S.A. about their mathematical knowledge of strategic competence for multistep fraction word problems, Copur-Gencturk and Doleck [53] provided evidence for the role that strategic competence played in solving word problems, in order to understand and describe teachers’ mathematical knowledge. The authors established three indicators to define the strategic competence to solve problems consisting of elaborating a solution strategy, modeling the problem and getting to the correct answer [53]. As part of capturing the teachers’ strategic competence, the errors were also coded according to the relationship between them. It was stated that incorrect strategies give evidence of the difficulties and errors (conceptual and procedural) that teachers may have. Specifically, the authors considered that a translation error (when teachers try out several operations that do not allow them to obtain a suitable solution strategy) provides evidence of the first indicator; a mathematization error (conceptual or interpretation errors) offers insights into the second indicator; and an arithmetic error (computational errors) into the third indicator. From their results, they highlighted the incorrect interpretation of the problem as the most common error, resulting in a translation error, and underlined the conceptual difficulties that teachers had about fractions. The authors associated the presence of these errors with the nature of the problems, since they had to bring into play more concepts about fractions as they were multistep problems.
Results from the literature on fraction problem solving, both from the point of view of meanings and operations [16,41,46,55,56], show that preservice teachers have more procedural knowledge based on rules than conceptual knowledge.
4. Methods
Since our aim is to explore the knowledge of a group of preservice elementary school teachers about the meaning of the fraction as an operator, we used a quantitative and qualitative methodology. The use of the mixed design allowed us to find out which are the most frequent problems related to the object of study, as well as to know the typology of these problems. The results with this type of design enabled us to obtain complementary knowledge [57] about the reality addressed. From the quantitative paradigm, we identified and analyzed the correct and incorrect answers and the qualitative methodology gave us the opportunity to investigate the types of difficulties and errors based on the answers given. Therefore, the mixed design contributed to deepen the knowledge and understanding of the topic studied.
The participants in this study were 194 preservice teachers (denoted by PT) who were undertaking the third grade of Primary Education Degree at the University of Almería, in Spain. The participants’ average age was 21.42 years with a standard deviation of 3.84. Table 2 shows the distribution of participants in relation to the group and gender. We can observe that almost three fifths of participants are women, which is very common in these studies at universities of Spain.

Table 2.
Distribution of participants according to group and gender.
In Almería, preservice elementary school teachers follow a four-year professional degree and they are trained in all school subjects, including mathematics. This study was carried out in three groups during the academic year 2021/2022, one week before students started a practice period in primary schools for two and a half months. The participants were taking the subject “Teaching and Learning of Arithmetic, Statistics and Chance”. At the end of this subject, students know and establish relationships among the main concepts, properties and procedures that make up the topics of the content blocks of “Numbers” and “Statistics and probability” of Primary Education. Furthermore, they receive specific training on the fundamentals of Didactics of Mathematics, specified in cognitive aspects (mathematical learning, errors and difficulties) and instructional (design and sequencing of tasks, materials and resources).
The participants had not been trained in rational numbers at the time of taking the test since the aim was to know their prior knowledge about this topic. The teachers informed the students about the test at least one month in advance and recommended them to review the mathematical contents included in the Primary Education curriculum.
4.1. Instrument
The main purpose of the instrument is to assess preservice teachers’ mathematical knowledge of the contents of arithmetic, statistics and probability included in the Primary Education curriculum. Fractions have a lot of applications in different domains of real-life situations, as well as in other subjects. In these contexts, the concept of fraction has different meanings and it is important that preservice teachers master them all. Many studies have focused on studying the part–whole relationship and, for that reason, we decided to conduct research on the fraction as an operator and to present our results in this paper. To do this, the researchers used 10 tasks sampled from primary mathematics textbooks, similar to the ones the teachers can encounter whilst teaching mathematics. Each task was scored on “the mathematical content” and not on their didactical value, thus the answers were scored correct (1) or incorrect (0). Three tasks were related to rational numbers: fraction as operator, fraction into percentage transformation, and decimal number writing.
We proposed four varieties of tasks, all of them similar to each other. Table 3 shows the four fraction word problems used to investigate students’ knowledge about the fraction as an operator, FWP1 is a one-step fraction word problem, and the rest are multistep fraction word problems. The different combinations of operations allowed us to identify errors in their solutions.

Table 3.
Fraction word problems.
To analyze qualitatively the procedure and identify the participants’ difficulties, their answers were categorized into six categories, from C0 to C5, by depending on whether the participants used the meaning of fraction as operator and whether they obtained the correct solution. Initially, this categorization was carried out individually by the three authors. Later, it was discussed amongst them and there were no discrepancies.
The answer categories defined are:
- C0, no procedure and incorrect solution. We classified in this category those answers in which the participant included only the numerical solution of the task without accompanying it with the procedure that allows obtaining this value. In this particular case, the solution given does not correspond to the correct solution. For example, PT157′s written solution to FWP4 only includes the sentence: “She has EUR 300 left over”.
- C1, no procedure and correct solution. In contrast to the previous category, in this case we considered those answers in which the correct solution was obtained without incorporating the procedure followed. For example, PT122’s answer to the task FWP1 was “She bought six red peppers”.
- C2, incorrect procedure and incorrect solution. This category includes answers where both the procedure followed and the final solution are not correct. We considered that the procedure was not adequate when there was not a correct use of the meaning of the fraction as operator. Figure 1 shows the answer given by PT30 in which the preservice teacher adds the two fractions and does not identify the meaning of fraction as operator.
 Figure 1. PT30’s written answer to problem FWP3. (Translation of P30’s solution: “The restaurant is short of kilos of flour [harina]. When adding up the fractions, there is no excess.”).
Figure 1. PT30’s written answer to problem FWP3. (Translation of P30’s solution: “The restaurant is short of kilos of flour [harina]. When adding up the fractions, there is no excess.”). - C3, correct procedure and incorrect solution. Answers in which the prospective teacher used the fraction as operator on a given quantity, but did not obtain the correct solution because they did not identify the quantity on which the fraction acts as an operator (see Figure 2) or because of miscalculations were considered (see Figure 3).
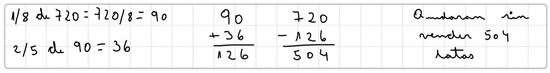 Figure 2. PT21’s written answer to problem FWP2. (Translation of PT21’s solution: “504 cans will remain unsold.”).
Figure 2. PT21’s written answer to problem FWP2. (Translation of PT21’s solution: “504 cans will remain unsold.”). Figure 3. PT3’s written answer to problem FWP2. (Translation of PT3’s solution: “388 cans remain unsold.”).
Figure 3. PT3’s written answer to problem FWP2. (Translation of PT3’s solution: “388 cans remain unsold.”). - C4, correct procedure and correct solution. Those written solutions where participants used a correct procedure and obtained the required solution. Figure 4, Figure 5, Figure 6 and Figure 7 show an example of each one of the tasks.
 Figure 4. PT94’s written answer to problem FWP1. (Translation of PT94’s solution: “¾ were green peppers. Solution: He bought ¼ of red peppers. This is equivalent to 6 red peppers.”).
Figure 4. PT94’s written answer to problem FWP1. (Translation of PT94’s solution: “¾ were green peppers. Solution: He bought ¼ of red peppers. This is equivalent to 6 red peppers.”). Figure 5. PT37’s written answer to problem FWP2. (Translation of PT37’s solution: “During the week 90 cans are sold. At the weekend 252 cans are sold. Solution: 378 cans remain unsold.”).
Figure 5. PT37’s written answer to problem FWP2. (Translation of PT37’s solution: “During the week 90 cans are sold. At the weekend 252 cans are sold. Solution: 378 cans remain unsold.”). Figure 6. PT1’s written answer to problem FWP3. (Translation of PT1’s solution: “12 kg for pasta. 18 kg for pizza. Solution: 6 kg a week left over.”).
Figure 6. PT1’s written answer to problem FWP3. (Translation of PT1’s solution: “12 kg for pasta. 18 kg for pizza. Solution: 6 kg a week left over.”). Figure 7. PT178’s written answer to problem FWP4. (Translation of PT178’s solution: “EUR 150 left over.” (VIAJE is translated as Trip, and Ropa as clothe)]).
Figure 7. PT178’s written answer to problem FWP4. (Translation of PT178’s solution: “EUR 150 left over.” (VIAJE is translated as Trip, and Ropa as clothe)]). - C5, undone. This category included blank answers, that is, answers in which the participants, after attempting to solve the task, decided not to include any procedure or solution in their written answers.
Of the answers coded as categories 2 and 3 (C2 and C3), we analyzed the types of errors made by the prospective teachers. This information enabled us to identify the errors of prospective teachers’ knowledge of fraction word problems where the fraction has the meaning as operator. To do this, we examined the previous literature on errors that preservice and in-service teachers made in those activities. Subsequently, we carried out a content analysis of the written answers to identify error categories and classify the participants’ answers into those categories. On the basis of recent studies [53] and through a cyclical and inductive process, the error categories defined below were refined. The three authors coded separately the errors reaching total agreement among them.
- AE, Arithmetic error: An arithmetic error made during the execution of the solution strategy. See for example Figure 3, in which PT3 successfully performs the whole process showing an adequate knowledge of the fraction as an operator. However, when subtracting 252 from 630, PT3 obtains 388 as a result, a very common error in the subtraction algorithm.
- CE, Conceptual error: An error made in the solution strategy related to the meaning of fraction as an operator (fraction as a number that operates and transforms an amount). See for example Figure 1, in which PT30 does not identify the meaning of fraction as operator, thus proceeding with the addition of the two fractions. In this situation we can guess that the participant considers the fractions as part–whole because he concludes that “there is no excess”, since the result of the addition is an improper fraction.
- IE, Interpretation error: An error made in the solution strategy by missing some information or interpreting it incorrectly. An interpretation error includes responses that overlooked some of the information provided in the problem even if the solution strategy was correct. See for example Figure 2, in which PT21 evidences an adequate knowledge of the fraction as an operator, but the student does not take into account that the task says “2/5 of the remainder”. That is, the participant does not identify the quantity on which the fraction acts as an operator. In addition to this interpretation error, he also makes an arithmetic error in the subtraction. However, this answer has been coded only as IE.
- OE, Other error: An error that could not be placed into any other error category. However, only 2 out of 72 errors have been coded in this category: one related to the non-inclusion of the solution and other to an incomplete procedure. For example, PT9 properly performs the entire procedure by correctly identifying the meaning of the fraction, without arithmetic errors, but does not complete the task.
As the participants were in the third year of the Primary Education degree, we considered that arithmetic errors are generally not associated with errors related to mathematical content knowledge. After analyzing the errors, the authors found that, if a participant could be classified into two categories, one of them was always AE. In order to not distort the information obtained from the results, we considered it convenient that, if a pupil presented two types of errors, one of them being AE, we would classify them in the other error.
5. Results
We carried out a quantitative and qualitative analysis of the participants’ written solutions. The four problems presented were randomly distributed among the participants so that each participant solved only one of them. Table 4 shows the frequency of correct and incorrect answers by fraction word problem. We can observe the difficulties to solve this kind of problems because 44.8% of the answers were scored zero. When we analyzed the existence of discrepancies in preservice teachers’ performance when they were asked to solve one-step problems (FWP1) versus multistep problems (FWP2, FWP3 and FWP4), the number of tasks marked with zero increased by 12% in the case of multistep.

Table 4.
Frequency (percentage) of participants according to the score for each fraction word problem.
The average score for the one-step fraction word problem was 0.63 (Standard Deviation = 0.48) and 0.50 (Standard Deviation = 0.50) for multistep ones. The study of the gender effect on the task score shows the existence of significant differences with a p-value = 0.024 and a confidence interval (−0.31, −0.02).
Table 5 shows the frequency analysis of the categories described in Section 4.1. It is worth remembering that, in order to deepen the study, preservice elementary teachers’ answers are coded according to the procedure followed and whether the solution obtained is correct. We observe that those whose solutions do not include the procedure or justification are associated with problems FWP1 and FPW4. In the case of the five participants who did not include the procedure in FWP1, but wrote down the correct solution, we can assume that they have a good conceptual understanding, according to Lee [50] and Newton [43], and they did not need to perform written calculations to solve the problem, although we do not really know what strategy they followed to get the solution. We can think that the non-justification of these five participants to FWP1 may be associated with the fact that it is a one-step problem and it can be solved by means of a reasoning that does not rely on a written mathematical procedure. However, the two answers to FWP4 are particularly striking because this task corresponds to a multistep problem in which a greater number of elements are involved in its resolution. Therefore, we can deduce that the participants did not know how to solve the task and decided to give a random value, for example, PT157 gave as a solution “She has EUR 300 left over” and PT163 pointed out that “Maria has EUR 350 left over from what she had saved at the beginning”.

Table 5.
Distribution of the number of participants’ written answers according to task types and categories.
Note that the sum of the responses coded C1 and C4 corresponds to the number of participants who obtained the maximum score on the task. Scoring was carried out in this way, as the test instructions did not explicitly ask participants to justify the procedure followed to obtain the solution nor included indications on how to solve it. Of particular concern is the fact that 13 participants left the task blank (C5). This action suggests the lack of knowledge that some preservice elementary teachers present in relation to fractions in word problems. Furthermore, we have noticed that six of them correspond to the FWP1 task, which is usually presented in primary school at the age of 8–9 years.
The 37.11% of the preservice school teachers (72 out of 194) presented some kind of error, either by having both the procedure and the solution incorrect (C2) or by making errors in determining the solution (C3). Note that 22 of them are associated with FWP1, a one-step problem. We can deduce these results because, unlike two-stage problems, in FWP1 the total quantity is unknown, which makes it difficult to interpret how the fraction acts on the given quantity. Particularly impressive is the fact that, even whilst making a correct use of the fraction, some participants did not achieve the expected final solution. In general, in two-step problems, it follows that these results are caused by not identifying the quantity on which the second fraction acts. In order to further explore this issue, from categories 2 and 3 (C2 and C3), we analyzed the participants’ errors in their written solutions in relation to fraction word problems. For this purpose, as we commented above, we classified the answers of these 72 participants in 1, and only 1, of these categories: arithmetic errors (AE), conceptual errors (CE), interpretation errors (IE), and other errors (OE).
As already mentioned, if a participant made both arithmetic and conceptual or interpretation errors, their answer was coded as the most serious error. Under this consideration, data analysis revealed that the most common errors were conceptual errors (34%) or interpretation errors (36%). To a lesser extent, the preservice teachers showed arithmetic errors (26%). Focusing on the 26 participants who performed incorrectly the procedure (C2), 19 out of them made a conceptual error. The results were different in the case where the preservice teachers devised a valid strategy; most of them had interpretation errors (21 out of 46) or arithmetical errors (17 out of 46).
We observed that the one-step fraction word problem caused a higher number of conceptual errors than the multistep ones, since preservice teachers did not make a correct use of the meaning of the fraction as an operator (see Figure 8). However, in the multistep fraction word problems, a higher number of errors associated with interpretation were observed, although there was no homogeneity in the distribution of error types in the three multistep problems. The presence of these interpretation errors was generally due to the fact that, in the second step, the fraction acted as an operator on a wrong quantity or because they did not identify the meaning of the results obtained after applying the first operator. In these latter cases, it is thought that the error may be caused by mechanizing the process of solving such problems.
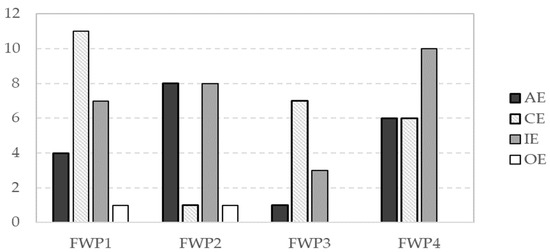
Figure 8.
Distribution of the errors (arithmetic errors, conceptual errors, Interpretation errors and other errors) in the written solution of preservice primary teachers according to the fraction word problem.
6. Conclusions
The teacher’s mathematical knowledge is a key factor in ensuring adequate student learning in elementary education [58]. Among the different mathematical contents, one interesting element is the study of fractions due to, among other reasons, their importance in the learning of several science areas. Students possess the knowledge that allows them to represent fractions, establish equivalences and operate with them, but they do not identify the meaning of the mathematical procedures involved, a situation that is fundamental for a deep and lasting learning of fractions [59,60]. Furthermore, the research on preservice teachers’ conceptual knowledge of fraction showed that from the five sub-constructs considered, the participants were most successful with part–whole, presenting little knowledge of the rest [37]. Because of this scenario, we must guarantee that the people involved in the teaching–learning process of the subject possess adequate knowledge of topic (KoT) [25]. If teachers are not able to address the mathematical content properly, then the learning experiences they offer their children will remain restricted to the lower level of the contents [61].
In our study, we focus on preservice school teachers’ knowledge of fraction word problems, in which the fraction is referred to as the operator sub-construct. The use of word problems (one-step and multistep) makes it possible to analyze not only the students’ prior conceptual knowledge, but also their strategic competence, which is of great interest to teacher trainers. Therefore, working from contextualization contributes to connecting the different elements of content knowledge.
Concerning the gender effect, our results coincide with the ones obtained by Van Steenbrugge et al. [37], who reported that there was a significant main effect of gender in a fraction test to analyze procedural and conceptual knowledge of fraction with preservice secondary school teachers. Referring to correct answers, the participants’ written solution revealed some difficulties because only 55% obtained the desired answer. However, if the arithmetic errors are not considered, the percentage increases to 65%. Our results are slightly worse than those obtained by Van Steenbrugge et al. [37] in which the authors stated that the level of knowledge about the operator (processor) meaning of the fraction was found to be 78% with 290 preservice teachers.
Another contribution of our research is the analysis of multistep word problems and not only one-step problems, which has been requested by previous research. Significant differences were found between those two types of problems, both in terms of their correct resolution by the participants and in terms of the type of error most frequently committed by them. In the same way, Li and Kulm [49] also delved into the difficulties of 46 preservice teachers in solving one-step and multistep problems and obtained the worst results to solve multistep problems. The discrepancy between the results of both types of problems indicates that preservice teachers have a fragile knowledge of the fraction as an operator. Likewise, our work shows that in multistep problems, even though the majority of participants make a correct use of the fraction from a conceptual perspective, they do not mathematize the situation posed in the problem. This fact reveals that, in general, students mechanically applied the learned procedure, leaving aside the meaning of the mathematical content with which they were working. The use of both types of problems revealed a greater presence of conceptual errors in the one-step problem compared to a predominance of interpretation errors in the multistep problems. Regarding the resolution strategies, the preservice teachers did not identify the relationship between fractions in multistep problems, in other words, they did not use the fraction multiplication to obtain the solution, these results being similar to those described in [54].
A qualitative analysis allowed us to identify three main error types: arithmetic, conceptual and interpretation errors. The results showed that the most frequent error was conceptual (47.82%) in one-step problem, while interpretation errors (41.2%) were the most repeated in multistep problems. In relation to arithmetic errors, these were more numerous in the multistep than in the one-step problems, which is logical because more operations had to be performed. Our results are highly worrying because the tasks were taken from primary school mathematics textbooks for pupils aged from 8 to 11.
We consider that prospective teachers need to be given multistep word problems, so they learn how to sort out the data and not give up after the first step. If they are presented with tasks that are designed to develop their competence, then it is likely that they will also develop the confidence to use these types of tasks in their teaching [50,61]. Our results show that the preservice teachers have an insufficient mathematics knowledge, which may limit their ability to teach this topic. The majority of existing research has tended to use one-step word problem [50], so studies such as the one we present can contribute to clarify the difficulties and errors of future teachers when they face one-step or multistep fraction word problems. The information obtained suggests continuing in this line of research by delving into preservice school teachers’ knowledge about this topic. Given that in this study each participant only responded to one fraction word problem, a future line of research could consist of designing instruments with which the same participant could tackle one-step and multistep fraction word problems in order to analyze strategic competence in more detail.
The review of previous research reveals a gap in the research agenda regarding prospective teachers’ prior knowledge of the meaning of fraction as an operator. Our research tried to address this weakness by identifying the difficulties and errors that preservice teachers present when solving situations in which the fraction acquires this meaning. In teacher education, there is a need for a balance between specific knowledge and practical skills [26]. In this sense, teacher trainers assume that students master these contents, having studied them in primary and secondary education, focusing mostly on didactical knowledge. However, the results reveal the obstacles that prospective teachers face when solving problems identical to those tackled by primary school children. This fact suggests that the learning process of future teachers was not always successful. Therefore, the access to Degree in Primary Education in some Spanish universities should be reviewed in order to diminish this problematic as much as possible due to the impact it has on our society.
Author Contributions
Conceptualization, M.d.M.L.-M. and C.G.A.-A.; methodology, M.d.M.L.-M., C.G.A.-A. and M.d.M.G.L.; software, M.d.M.L.-M.; validation, M.d.M.L.-M., C.G.A.-A. and M.d.M.G.L.; formal analysis, M.d.M.L.-M., C.G.A.-A. and M.d.M.G.L.; investigation, M.d.M.L.-M. and C.G.A.-A.; resources, M.d.M.L.-M. and C.G.A.-A.; data curation, M.d.M.L.-M., C.G.A.-A. and M.d.M.G.L.; writing—original draft preparation, M.d.M.L.-M., C.G.A.-A. and M.d.M.G.L.; writing—review and editing, M.d.M.L.-M., C.G.A.-A. and M.d.M.G.L.; visualization, M.d.M.L.-M., C.G.A.-A. and M.d.M.G.L.; supervision, M.d.M.L.-M., C.G.A.-A. and M.d.M.G.L. All authors have read and agreed to the published version of the manuscript.
Funding
This research has received external funding from Junta de Andalucía research group HUM886 of the University of Almería.
Data Availability Statement
Not applicable.
Acknowledgments
Preservice school teachers (students of third grade of Primary Education Degree at the University of Almeria).
Conflicts of Interest
The authors declare no conflict of interest.
References
- UN. General Assembly United Nations O_Cial Document—Transforming Our World: The 2030 Agenda for Sustainable Development—Resolution Adopted by the General Assembly on 25 September 2015. Available online: https://www.un.org/ga/search/view_doc.asp?symbol=A/RES/70/1&Lang=E (accessed on 15 September 2021).
- Haciomeroglu, G. Prospective secondary teachers’ subject matter knowledge and pedagogical content knowledge of the concept of function. Unpublished Ph.D. Thesis, The Florida State University College of Education, Tallahassee, FL, USA, 2006. [Google Scholar]
- Ma, L. Conocimiento y enseñanza de las matemáticas elementales. In La Comprensión de Las Matemáticas Fundamentales que Tienen Los Profesores en China y Los EE.UU, 1st ed.; Academia Chilena de Ciencias: Santiago, Chile, 2010. [Google Scholar]
- BOE. Real Decreto 126/2014, de 28 de febrero, por el que se establece el currículo básico de la Educación Primaria. BOE 2014, 52, 19349–19420. [Google Scholar]
- National Council of Teachers of Mathematics (NCTM). Principles and Standards for School Mathematics; National Council of Teachers of Mathematics: Reston, VA, USA, 2020. [Google Scholar]
- Clarke, D.M.; Mitchell, A.; Roche, A. Year six fraction understanding: A part of the whole story. In Mathematics: Essential Research, Essential Practice, Proceedings of the 30th Annual Conference of the Mathematics Education Research Group of Australasia, Mathematics Education Research Group of Australasia, Wrest Point Hotel Casino, Hobart, Tasmania, 2–6 July 2007; Watson, J., Beswick, K., Eds.; MERGA: Adelaide, SA, Australia, 2007; pp. 207–216. [Google Scholar]
- Brousseau, G.; Brousseau, N.; Warfield, V. Rationals and decimals as required in the school curriculum. Part 1: Rationals as measurements. J. Math. Behav. 2004, 23, 1–20. [Google Scholar]
- Gabriel, F.; Coché, F.; Szucs, D.; Carette, V.; Rey, B.; Content, A. A componential view of children’s difficulties in learning fractions. Front. Psychol. 2013, 4, 715. [Google Scholar] [CrossRef] [PubMed]
- Hansen, N.; Jordan, N.C.; Rodrigues, J. Identifying learning difficulties with fractions: A longitudinal study of student growth from third through sixth grade. Contemp. Educ. Psychol. 2017, 50, 45–59. [Google Scholar] [CrossRef]
- Hecht, S.A.; Vagi, K.J. Sources of group and individual differences in emerging fraction skills. J. Educ. Psychol. 2010, 102, 843–859. [Google Scholar] [CrossRef] [PubMed]
- Brown, G.; Quinn, R.J. Fraction proficiency and success in algebra: What does research say? Aust. Math. Teach. 2007, 63, 23–30. [Google Scholar]
- Hecht, S.A.; Vagi, K.J. Patterns of strengths and weaknesses in children’s knowledge about fractions. J. Exp. Child. Psychol. 2012, 111, 212–229. [Google Scholar] [CrossRef]
- Torbeyns, J.; Schneider, M.; Xin, Z.; Siegler, R.S. Bridging the gap: Fraction understanding is central to mathematics achievement in students from three different continents. Learn. Instr. 2015, 37, 5–13. [Google Scholar] [CrossRef]
- Castro-Rodríguez, E.; Pitta-Pantazi, D.; Rico, L.; Gómez, P. Prospective teachers’ understanding of the multiplicative part-whole relationship of fraction. Educ. Stud. Math. 2016, 92, 129–146. [Google Scholar] [CrossRef]
- Isiksal, M.; Cakiroglu, E. The nature of prospective mathematics teachers’ pedagogical content knowledge: The case of multiplication of fractions. J. Math. Teach. Educ. 2011, 14, 213–230. [Google Scholar] [CrossRef]
- Tirosh, D. Enhancing prospective teacher’ knowledge of children’s conceptions: The case of division of fractions. J. Res. Math. Educ. 2000, 31, 5–25. [Google Scholar] [CrossRef]
- Fennema, E.; Franke, M.L. Teachers’ knowledge and its impact. In Handbook of Research on Mathematics Teaching and Learning; Grouws, D.A., Ed.; Macmillan: New York, NY, USA, 1992; pp. 147–164. [Google Scholar]
- Sánchez, M. A review of research trends in mathematics teacher education. PNA 2011, 5, 129–145. [Google Scholar] [CrossRef]
- Godino, J.D.; Batanero, C.; Font, V. The onto-semiotic approach to research in mathematics education. ZDM-Math. Educ. 2007, 39, 127–135. [Google Scholar] [CrossRef]
- Ponte, J.P.; Oliveira, H. Remar contra a maré: A construção do conhecimento e da identidade profissional na formação inicial. Rev. Educ. 2002, 11, 145–163. [Google Scholar]
- Silverman, J.; Thompson, P. Toward a framework for the development of mathematical knowledge for teaching. J. Math. Teach. Educ. 2008, 11, 499–511. [Google Scholar] [CrossRef]
- Shulman, L.S. Those who understand: Knowledge growth in teaching. Educ. Res. 1986, 15, 4–14. [Google Scholar] [CrossRef]
- Ball, D.L.; Thames, M.H.; Phelps, G. Content knowledge for teaching: What makes it special. J. Teach. Educ. 2008, 59, 389–407. [Google Scholar] [CrossRef]
- Hill, H.C.; Ball, D.L.; Schilling, S.G. Unpacking pedagogical content knowledge: Conceptualizing and measuring teachers’ topic-specific knowledge of students. J. Res. Math. Educ. 2008, 39, 372–400. [Google Scholar] [CrossRef]
- Carrillo, J.; Climent, N.; Contreras, L.C.; Muñoz-Catalán, M.C. Determining specialized knowledge for mathematics teaching. In Proceedings of the Eighth Congress of the European Society for Research in Mathematics Education 8, Ankara, Turkey, 6–10 February 2013; Ubuz, B., Haser, C., Mariotti, M.A., Eds.; CERME: Ankara, Turquía, 2013; pp. 2985–2994. [Google Scholar]
- Nieto, L.J.B. Learning to teach mathematics: Types of knowledge. In Becoming a Primary Teacher: Issues from Mathematics Educa-tion; Giménez, J., Llinares, S., Sánchez, V., Eds.; Gracia Alvarez: Sevilla, Spain, 1996; pp. 159–177. [Google Scholar]
- Semanišinová, I. Multiple-Solution Tasks in Pre-Service Teachers Course on Combinatorics. Mathematics 2021, 9, 2286. [Google Scholar] [CrossRef]
- Muñoz Catalán, M.C.; Contreras, L.C.; Carrillo, J.; Rojas, N.; Montes, M.Á.; Climent, N. Conocimiento especializado del profesor de matemáticas (MTSK): Un modelo analítico para el estudio del conocimiento del profesor de matemáticas. Gac. Real Soc. Matemática Española 2015, 18, 1801–1817. [Google Scholar]
- Behr, M.J.; Lesh, R.; Post, T.; Silver, E.A. Rational number concepts. In Acquisition of Mathematics Concepts and Processes; Lesh, R., Landau, M., Eds.; Academic Press: New York, NY, USA; London, UK, 1983; pp. 91–126. [Google Scholar]
- Charalambous, C.Y.; Pitta-Pantazi, D. Drawing on a theoretical model to study students’ understandings of fractions. Educ. Stud. Math. 2007, 64, 293–316. [Google Scholar] [CrossRef]
- Grégoire, J.; Meert, G. L’apprentissage des nombres rationnels et ses obstacles. In La Dyscalculie: Trouble du Développement Numérique Chez L’enfant; Noël, M.P., Ed.; Solal: Marseille, France, 2005; pp. 223–251. [Google Scholar]
- Moss, J.; Case, R. Developing children’s understanding of the rational numbers: A new model and an experimental curriculum. J. Res. Math. Educ. 1999, 30, 122–147. [Google Scholar] [CrossRef]
- Kieren, T.E. On the mathematical, cognitive and instructional foundations of the rational numbers. In Number and Measurement: Papers from a Research Workshop; Lesh, R.A., Ed.; ERIC/SMEAC: Athens, GA, USA, 1976; pp. 101–144. [Google Scholar]
- Lamon, S.J. Teaching fractions and ratios for understanding, 3rd ed.; Taylor & Francis: New York, NY, USA; London, UK, 2012. [Google Scholar]
- Mack, N. Building on informal knowledge through instruction in a complex content domain: Partitioning, units, and understanding multiplication of fractions. J. Res. Math. Educ. 2001, 32, 267–295. [Google Scholar] [CrossRef]
- Simon, M.A. Prospective elementary teachers’ knowledge of division. J. Res. Math. Educ. 1993, 24, 233–254. [Google Scholar] [CrossRef]
- Van Steenbrugge, H.; Lesage, E.; Valcke, M.; Desoete, A. Preservice elementary school teachers’ knowledge of fractions: A mirror of students’ knowledge? J. Curric. Stud. 2014, 46, 138–161. [Google Scholar] [CrossRef]
- Lin, C.Y.; Becker, J.; Byun, M.R.; Ko, Y.Y. Enhancing pre-service teachers’ fraction knowledge through open approach instruction. J. Math. Behav. 2013, 32, 309–330. [Google Scholar] [CrossRef]
- Olanoff, D.; Lo, J.J.; Tobias, J. Mathematical Content Knowledge for Teaching Elementary Mathematics: A Focus on Fractions. TME 2014, 11, 267–310. [Google Scholar] [CrossRef]
- Vula, E.; Kingji-Kastrati, J. Pre-service teacher procedural and conceptual knowledge of fractions. In Research Advances in the Mathematical Education of Pre-Service Elementary Teachers, ICME-13 Monographs; Stylianides, G.J., Hino, K., Eds.; Springer: Cham, Switzerland, 2018; pp. 111–123. [Google Scholar]
- Chinnappan, M. Preservice teachers’ understanding and representation of fractions in a Java Bars environment. Math. Educ. Res. J. 2000, 12, 234–253. [Google Scholar] [CrossRef]
- Luo, F. Evaluating the effectiveness and insights of pre-service elementary teachers’ abilities to construct word problems for fraction. J. Math. Educ. 2009, 2, 83–98. [Google Scholar]
- Newton, K.J. An extensive analysis of preservice elementary teachers’ knowledge of fractions. Am. Educ. Res. J. 2008, 45, 1080–1110. [Google Scholar] [CrossRef]
- Rizvi, N.F.; Lawson, M.J. Prospective teachers’ knowledge: Concept of division. Int. Educ. J. 2007, 8, 377–392. [Google Scholar]
- Young, E.; Zientek, L.R. Fraction operations: An examination of prospective teachers’ errors, confidence, and bias. Investig. Math. Learn. 2011, 4, 1–23. [Google Scholar] [CrossRef]
- Yang, D.C.; Reys, R.; Reys, B.J. Number sense strategies used by preservice teachers in Taiwan. Int. J. Sci. Math. Educ. 2009, 7, 383–403. [Google Scholar] [CrossRef]
- Mullis, I.V.S.; Martin, M.O.; Foy, P.; Hooper, M. TIMSS 2015 International Results in Mathematics; TIMSS and PIRLS International Study Center: Boston, MA, USA, 2016. [Google Scholar]
- Verschaffel, L.; Schukajlow, S.; Star, J.; Van Dooren, W. Word problems in mathematics education: A survey. ZDM-Math. Educ. 2020, 52, 1–16. [Google Scholar] [CrossRef]
- Li, Y.; Kulm, G. Knowledge and confidence of pre-service mathematics teachers: The case of fraction division. ZDM-Math. Educ. 2008, 40, 833–843. [Google Scholar] [CrossRef]
- Lee, M. Pre-service teachers’ flexibility with referent units in solving a fraction division problem. Educ. Stud. Math. 2017, 96, 327–348. [Google Scholar] [CrossRef]
- Miller, A.; Tobias, J.; Safak, E.; Kirwan, J.V.; Enzinger, N.; Wickstrom, M.; Baek, J. Preservice teachers’ algebraic reasoning and symbol use on a multistep fraction word problem. Int. J. Math. Teach. Learn. 2017, 18, 109–131. Available online: https://digitalcommons.georgefox.edu/soe_faculty/165 (accessed on 15 September 2021).
- Perdomo-Díaz, J.; Felmer, P.; Randolph, V.; González, G. Problem solving as a professional development strategy for teachers: A case study with fractions. EURASIA J. Math. Sci. T. Educ. 2016, 13, 987–999. [Google Scholar] [CrossRef]
- Copur-Gencturk, Y.; Doleck, T. Strategic competence for multistep fraction word problems: An overlooked aspect of mathematical knowledge for teaching. Educ. Stud. Math 2021, 107, 49–70. [Google Scholar] [CrossRef]
- Behr, M.J.; Khoury, H.A.; Harel, G.; Post, T.; Lesh, R. Conceptual units analysis of preservice elementary school teachers’ strategies on a rational-number-as-operator task. J. Res. Math. Educ. 1997, 28, 48–69. [Google Scholar] [CrossRef]
- Chinnappan, M.; Forrester, T. Generating procedural and conceptual knowledge of fractions by pre-service teachers. Math. Educ. Res. J. 2014, 26, 871–896. [Google Scholar] [CrossRef]
- Domoney, B. Student teachers’ understanding of rational number: Part-whole and numerical constructs. Res. Math. Educ. 2002, 4, 53–67. [Google Scholar] [CrossRef]
- Ortí, A. La confrontación de modelos y nivels epistemológicos en la génesis e historia de la investigación social. In Métodos y Técnicas Cialitativas de Ivestigación Social en CC.SS; Delgado, J.M., Gutiérrez, J., Eds.; Síntesis: Madrid, España, 1995; pp. 85–95. [Google Scholar]
- Pincheira, N.; Alsina, Á. Teachers’ Mathematics Knowledge for Teaching Early Algebra: A Systematic Review from the MKT Perspective. Mathematics 2021, 9, 2590. [Google Scholar] [CrossRef]
- Fazio, L.; Siegler, R. Teaching fractions. In Vol. 22 of Educational Practices Series, 1st ed.; International Academy of Educational-International Bureau of Education: Geneva, Switzerland, 2011. [Google Scholar]
- Kërënxhi, S.; Gjoci, P. Involvement of Algebraic-Geometrical Duality in Shaping Fraction’s Meaning and Calculation Strategies with Fractions. J. Educ. Soc. Res. 2017, 7, 151. [Google Scholar] [CrossRef][Green Version]
- Taplin, M. Preservice teachers’ problem-solving processes. Math. Educ. Res. J. 1998, 10, 59–75. [Google Scholar] [CrossRef]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).