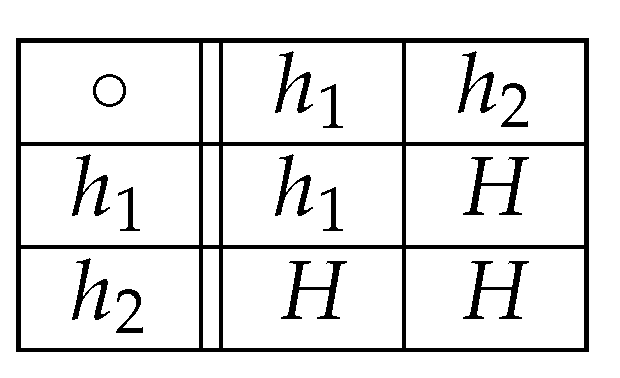From Automata to Multiautomata via Theory of Hypercompositional Structures

Abstract

In this paper, we study two important problems related to quasi-multiautomata: the complicated nature of verification of the GMAC condition for systems of quasi-multiautomata, and the fact that the nature of quasi-multiautomata has deviated from the original nature of automata as seen by the theory of formal languages. For the former problem, we include several new conditions that simplify the procedure. For the latter problem, we close this gap by presenting a construction of quasi-multiautomata, which corresponds to deterministic automata of the theory of formal languages and is based on the operation of concatenation.

1. Introduction

The theory of formal languages is closely linked to the theory of automata. An automaton is a finite representation of a formal language that can consist of an infinite number of words. Automata are often classified by means of a class of formal languages that they can accept; see, e.g., [1], a paper dealing with the automata theory from the point of view of our present paper, or papers such as [2,3]. The algebraic theory of automata studies various types of such structures, which are linked to actions of groups on sets. In the case of algebraic automata, the way of functioning is rather straightforward and simple: the automaton has a set of states and a set of inputs and, after we apply a certain input on a certain state, the automaton switches to a new state as specified by the transition function. However, in the theory of formal languages, automata are regarded as devices reading strings of words instead of single input symbols only. In other words, inputs (or characters) are catenated and one-by-one put into the automaton, which causes changes of states. In the algebraic definition, this can be seen in the definition of automaton, where the input alphabet is a free monoid over the input set, i.e., for each nonempty set A, we denote $A^{\ast }$ the set of all finite sequences $a_1{a}_2\dots a_n$, $a_i\in A$, i.e., finite words made of symbols from A. Moreover, $A^{\ast }$ regards the usual binary operation of concatenation: $u=a_1\dots a_n,v=b_1\dots b_k,uv=a_1\dots a_n{b}_1\dots b_k$. With this, $A^{\ast }$ is a free monoid over A with a neutral element e, the empty word.

In the course of time, the algebraic theory of automata began to regard automata without output, the operation of concatenation has been replaced by an arbitrary group operation, and monoid or a group have been used instead of the free monoid. Definition 2 complies with traditional books such as [4,5,6,7] or recent papers such as [8]. One can see that the conditions are constructed in such a way that both monoid and free monoid are applicable.

Since the late 1930s, the group theory has been generalized in the sense that the synthesis of elements of the carrier set need no longer to be an element of that carrier set. When subsets are permitted (such as a line segment being a result of an “operation” on its endpoints), we arrive at a concept of hypercompositional structures. For a basic introduction to the topic stressing its context from a historical perspective—see, e.g., an easy-to-follow overview paper [9].

The generalizations of algebraic automata in the sense of the theory of hypercompositional structures first focused on constructions of commutative hypergroups on their state sets. Properties of automata have been described by means of properties of such hypergroups over their state sets; see, e.g., [5,10,11,12]. The next step is to construct hypercompositional structures on the input sets and generalize the MAC condition to GMAC. Since there are no unique neutral elements in hypercompositional structures, the UC condition is omitted; see, e.g., [13,14]. The concept of quasi-multiautomaton originated in conference proceedings [15] while the GMAC condition was used for the first time (in the context of dynamical systems) in [12]—e.g., in [16,17]. In this respect, notice also suffix automata, which accept all suffixes of a given string and belong to the basic stringologic principles. When generalizing their transitions to include specific buffer operations, we obtain new subtree pushdown automata, which accept all subtrees of a given tree in the prefix notation; see, e.g., [18].

In 1959, M. O. Rabin and D. Scott introduced the concept of nondeterministic finite automata in [19] and proved their equivalence to deterministic finite automata. A nondeterministic automaton, such as a deterministic one, consumes a string of input symbols. It enters a new state for each input symbol until all input symbols are consumed. Unlike in deterministic finite automata, the way symbols are consumed is nondeterministic, i.e., for a state and an input symbol, the next state may be the original or one, two, or more possible states. Thus, in the formal definition, another state is an element of a potential set of states, which is a set of states that must be considered simultaneously. In this respect, the connection with the theory of hypercompositional structures is rather obvious. However, introducing hypergroups on input sets does not lead to nondeterministic quasi-multiautomata because the transition function $\delta :H\times S⟶S$ used in Definition 5 of a quasi-multiautomaton maps to the state set S instead of the set of its subsets $\mathcal{P}\left(S\right)$.

2. Basic Definitions

In order to clarify terminology used throughout the paper, in this section, we collect all basic definitions.

Definition 1.

[1] A deterministic automaton is a 5-tuple $(A,S,s_0,\delta ,F)$, where A is input alphabet, S is a finite nonempty set of states, $s_0\in S$ is the initial (or start) state, $\delta :A\times S⟶S$ is the state transition function, and $F\subseteq S$ is the set of final states. Sometimes it is convenient to use, instead of δ, the extended transition function ${\delta }^{\ast }:A^{\ast }\times S⟶S$, where $A^{\ast }$ is the set of words over the alphabet A, which is defined recursively as follows:

1. 

$(\forall s\in S)(\forall a\in A){\delta }^{\ast }(a,s)=\delta (a,s)$,

2. 

$(\forall s\in S){\delta }^{\ast }(a,\lambda )=s$ where λ is the empty string,

3. 

$(\forall s\in S)(\forall x\in A^{\ast })(\forall a\in A){\delta }^{\ast }(ax,s)={\delta }^{\ast }(\delta (a,s),x)$.

One can see that the conditions of the following definition are constructed in such a way that both monoid and free monoid are applicable.

Definition 2.

By automaton, we mean a structure $\mathbb{A}=(I,S,\delta )$ such that $I\ne \varnothing$ is a free monoid, $S\ne \varnothing$, and $\delta :I\times S\to S$ satisfies the following condition:

1. 

There exists an element $e\in I$ such that $\delta (e,s)=s$ for any state $s\in S$.

2. 

$\delta (y,\delta (x,s\left)\right)=\delta (xy,s)$ for any pair $x,y\in I$ and any state $s\in S.$

The set I is called the input set or input alphabet, the set S is called the state set, and the mapping δ is called next-state or transition function.

Remark 1.

Condition 1 is often called the unit condition (UC) while condition 2 is often called the Mixed Associativity Condition (MAC).

Notice that, in our paper, we write “$xy$” instead of “$x·y$”. However, in order to stress the difference between concatenation and arbitrary operation, we write “$x·y$” in Definition 3. For a deeper insight including historical perspective and terminology issues (e.g., “quasi-automaton” vs. “semiautomaton”), see [16].

Definition 3.

By quasi-automaton, we mean a structure $\mathbb{A}=(I,S,\delta )$ such that $I\ne \varnothing$ is a monoid, $S\ne \varnothing$, and $\delta :I\times S\to S$ satisfies the following condition:

1. 

There exists an element $e\in I$ such that $\delta (e,s)=s$ for any state $s\in S$.

2. 

$\delta (y,\delta (x,s\left)\right)=\delta (x·y,s)$ for any pair $x,y\in I$ and any state $s\in S.$

The set I is called the input set or input alphabet, the set S is called the state set, and the mapping δ is called next-state or transition function.

The following definition is a standard introductory definition of the theory of hypercompositional structures (or algebraic hyperstructures as they are also known).

Definition 4.

A hypergroupoid is a pair $(H,\ast )$, where H is a nonempty set and the mapping $\ast :\mathit{H}\times \mathit{H}⟶{\mathcal{P}}^{\ast }\left(H\right)$ is a binary hyperoperation (or hypercomposition) on $\mathit{H}$ (here, ${\mathcal{P}}^{\ast }\left(H\right)$ denotes the system of all nonempty subsets of $\mathit{H}$). If $a\ast (b\ast c)=(a\ast b)\ast c$ holds for all $a,b,c\in \mathit{H}$, then $(H,\ast )$ is called a semi-hypergroup. Moreover, if the reproduction axiom—i.e., relation $a\ast H=H=H\ast a$ for all $a\in H$—is satisfied, then the semi-hypergroup $(H,\ast )$ is called hypergroup.

The following definition transfers the concept of quasi-automaton into the theory of hypercompositional structures.

Definition 5.

[15] A quasi–multiautomaton is a triad $\mathbb{MA}=(H,S,\delta )$, where $(H,\ast )$ is a semi-hypergroup, S is a nonempty set and $\delta :H\times S\to S$ is a transition function satisfying the following condition:

$$\delta (b,\delta (a,s\left)\right)\in \delta (a\ast b,s)\mathrm{for}\mathrm{all}a,b\in H,s\in S.$$

(1)

The semi-hypergroup $(H,\ast )$ is called the input semi-hypergroup of the quasi–multiautomaton $\mathbb{A}$ (H alone is called the input set or input alphabet), the set S is called the state set of the quasi–multiautomaton $\mathbb{A}$, and δ is called next-state or transition function. Elements of the set S are called states; elements of the set H are called input symbols or letters. Condition (1) is called Generalized Mixed Associativity Condition (abbr. as GMAC).

Finally, we recall the notion of nondeterministic automaton.

Definition 6.

If, in Definition 1, we have $\delta :A\times S⟶\mathcal{P}\left(S\right)$ instead of $\delta :A\times S⟶S$, then the 5-tuple $(A,S,s_0,\delta ,F)$ is called nondeterministic automaton.

3. GMAC Condition in the Definition of Quasi-Multiautomata

This section aims at facilitating verifications of the GMAC condition. When doing so, we use ideas included in [1], where the notion of order of a state is defined in the context of deterministic automata of Definition 1. Notice that in [1], the term word length—meaning the number of concatenated input symbols—is used. For example, if we consider the word $aaabba$ on the set $a,b$, then its length is 6.

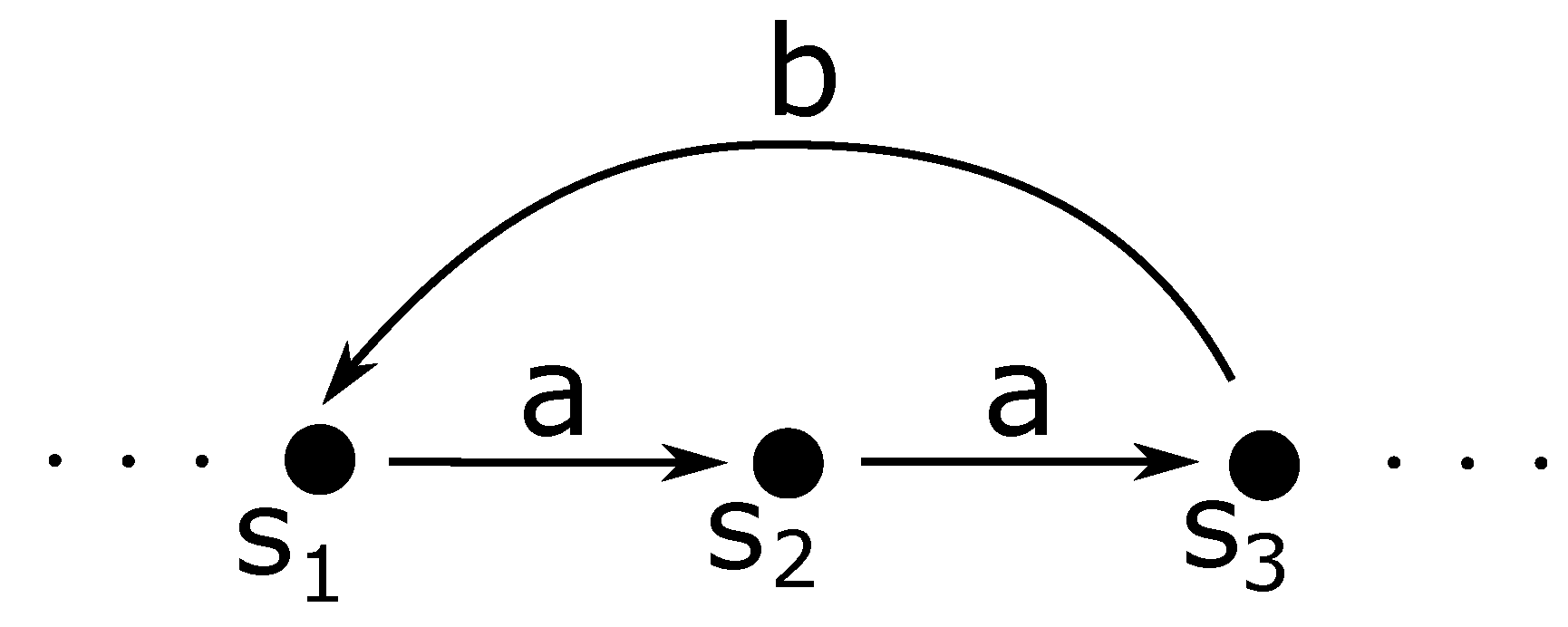
Definition 7.

[1] The order of a state $s\in S$ of the deterministic automaton in Definition 2, denoted by $ords$, is the minimum of the lengths of words that lead from the start state $s_0$ to s.

Example 1.

Consider an automaton as defined in Definition 1. Now, let $s_0$ be the initial state and $s_5$ the final state. The input alphabet is a free monoid over the set $\{a,b\}$. It is clear from Figure 1 that $ord{s}_0=0$, $ord{s}_1=ord{s}_2=1$, $ord{s}_3=ord{s}_4=2$, and $ord{s}_5=3$.

Obviously, the order of a state is related to the operation of concatenation of words. Thus, in Example 1, we have that $ord{s}_3=2$ because the shortest word taking us from $s_0$ to $s_3$ is $aa$. However, if we generalize the concatenation operation to an arbitrary associative operation, i.e., move to Definition 3, we have that $a·a$ is an element of I (say a). Thus, the “length of the word” becomes either 1 or 0 depending on whether the element is or is not isolated. The situation becomes even more complicated for quasi-multiautomata of Definition 5.

However, in both cases, we observe a discrepancy when transferring the intuitive notion of order tailored to the classical case of deterministic automata to quasi-automata or quasi-multiautomata of Definitions 3 and 5. The reason for such a discrepancy lies in the visualization of the algebraic concept by graphs and the fact that we no longer distinguish between start and end states. Therefore, further on, we will focus on the “descriptions of graphs” by “counting arrows” rather than attempts to stress the algebraic part of the notion. As a result, we cannot use the notion of order (based on word length) anymore (because, technically speaking, there are no words anymore). Notice that the forthcoming definitions once again enable us to “count arrows” of the graphs.

Definition 8.

By the transition number of states $s,t\in S$ (in this order), denoted by $tn(s,t)$, we mean the smallest number of transitions that take us from the state s to the state t.

It is easy to see that in Figure 1, $tn(s_0,s_5)=2$. Indeed, applying input b takes us from $s_0$ to $s_2$; then, applying input a takes us from $s_2$ to $s_5$, which means that the smallest number of transitions that take us from $s_0$ to $s_5$ is 2.

Notice that, from Definition 8, it does not follow that $tn(s,t)=tn(t,s)$. This is evident in Figure 2, where $tn(s_1,s_3)=2$ while $tn(s_3,s_1)=1$. Next, if there is no input that would take us from one state to another, we say that the respective transition number is 0. An example is depicted in Figure 1, where $tn(s_3,s_1)=0$.

Before introducing Theorem 1, recall the definition of a reversible automaton from [5].

Definition 9.

An automaton $\mathbb{A}=(A,S,\delta )$ is called reversible, if for every state $s\in S$ and every input $a\in A$ (or word $a\in A^{\ast }$) there exists an input $b\in A$ (or a word $b\in A^{\ast }$) such that $\delta (b,\delta (a,s\left)\right)=s$ (or $\delta (ab,s)=s$).

Now, we generalize the notion to the case of quasi-multiautomata.

Definition 10.

A quasi-multiautomaton $\mathbb{MA}=(H,S,\delta )$ is called reversible, if for every state $s\in S$ and every input $a\in H$ there exists an input $b\in H$ such that $\delta (b,\delta (a,s\left)\right)=s$.

Remark 2.

Notice that in every reversible quasi-multiautomaton there is $tn(s,t)=tn(t,s)$ for all $s,t\in S$.

To fully clarify the above notion and its application to quasi-multiautomata, we present the following example, in which two multiautomata are given. The first one is not reversible while the second one, with a modified input set, is.

Example 2.

Consider the interval of real numbers $I_1=[1,\infty )$ and the hyperoperation ${\circ }_1:I_1\times I_1\to {\mathcal{P}}^{\ast }\left(I_1\right)$ defined by

$$a\circ b=\{c\in I,c\ge a·b\},for all a,b\in I_1.$$

It is obvious that the associative law holds. Therefore, the structure $(I_1,{\circ }_1)$ is a semi-hypergroup. Then, the triad $((I_1,{\circ }_1),{\mathbb{R}}^{+}\setminus \left\{0\right\},{\delta }_1)$, where the transition function ${\delta }_1:I_1\times {\mathbb{R}}^{+}\setminus \left\{0\right\}\to {\mathbb{R}}^{+}\setminus \left\{0\right\}$ is defined by

$$\delta (a,r)=a·r,for all a\in I_1,r\in {\mathbb{R}}^{+}\setminus \left\{0\right\}.$$

which is a quasi-multiautomaton. Now, for input $a=5.2$ and state $r=10$, we have ${\delta }_1(5.2,20)=104$. Thus, the quasi-multiautomaton is not reversible, because there is no input b such that ${\delta }_1(b,104)=5.2$.

Now, consider the interval $I_2=(0,\infty )$ instead and the hyperoperation “${\circ }_2$” defined in the same way as “${\circ }_1$”. For the transition function ${\delta }_2$, defined in the same way as ${\delta }_1$, the triad $((I_2,{\circ }_2),{\mathbb{R}}^{+}\setminus \left\{0\right\},{\delta }_2)$ is a reversible quasi-multiautomaton because, for each input symbol a, there exists an input symbol $\frac{1}{a}$ such that ${\delta }_2\left(\frac{1}{a},{\delta }_2(a,r)\right)=r$.

At this point, using the notion of a reversible quasi-multiautomaton and the transition number of two states, we can provide the following theorem regarding the validity of the GMAC condition 1.

Theorem 1.

In every reversible quasi-multiautomaton $(H,S,\delta )$, there is $tn(s,t)=tn(t,s)=1$ for every two states $s,t\in S$.

Proof. 

Recall that the GMAC condition (1) is $\delta \left(b,\delta (a,s)\right)\in \delta (a\ast b,s)$ for all inputs and states. In a reversible quasi-multiautomaton, there is $tn(s,t)=tn(t,s)$ for all $s,t\in S$. Suppose that there exists at least one pair of states $(t,s)\in S$, such that $tn(t,s)=2$—i.e., from the state t we can reach the state s after application of at least two inputs. Denote such inputs as $a,b\in H$. Therefore, on the left-hand side of the condition GMAC, we have $\delta (a,\delta (b,t\left)\right)=r$. However, on the right-hand side, for all $c\in a\ast b$, we never obtain the state r, because this would mean that $tn(t,s)=1$, which would be a contradiction to the assumption that $tn(t,s)=2$. Naturally, the same is true for transition numbers greater than 2. □

In the following example, we show that the implication in Theorem 1 cannot be reversed, i.e., it is not true that if for every two states there is $tn(s,t)=tn(t,s)=1$, we obtain a reversible quasi-multiautomaton (or a quasi-multiautomaton).

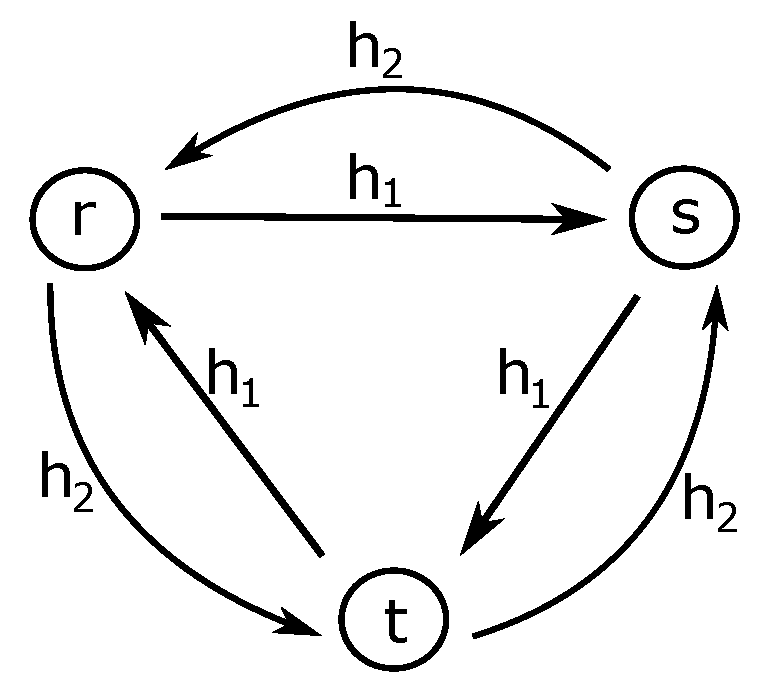
Example 3.

Consider the structure $(H,S,\delta )$. In this structure, we show that there is a path between each two states, yet the GMAC condition does not hold, i.e., from the fact that $tn(s,t)=1$ for all $s,t\in S$, it cannot be deduced that $(H,S,\delta )$ is a quasi-multiautomaton. Consider the set $H=\{h_1,h_2\}$, the hyperoperation “∘” defined by the following Figure 3, and the transition function δ defined by the transition diagram in Figure 4.

It is clear from the transition diagram that for each pair of states $r,s\in S$ there is $tn(r,s)=1$. However, the GMAC condition does not hold. Indeed, on the left-hand side, we have $\delta (h_2,\delta (h_1,r))=\delta (h_1,t)=r$ while on the right-hand side, we have $\delta (h_1\circ h_2,r)=\delta (h_1,r)\cup \delta (h_2,r)=\{s,t\}$ and obviously the left-hand side is not included in the right-hand side.

Notice that the above example also shows that the validity of the GMAC condition depends on the transition function as well as on the definition of the hyperoperation.

Theorem 2.

If in a quasi-multiautomaton $\left(\right(H,\ast ),S,\delta )$ there is $tn(r,s)=1$ and $tn(s,t)=1$ for some $r,s,t\in S$, then there is $tn(r,t)=1$.

Proof. 

Suppose that there is $tn(r,s)=1$ and also $tn(s,t)=1$ for some $r,s,t\in S$. Then, there exists such an input $i\in H$ for which there is $\delta (i,r)=s$, and also an input $j\in H$ for which there is $\delta (j,s)=t$. Since the GMAC condition holds, i.e., the state $t=\delta (j,\delta (i,r\left)\right)$ is included in the right-hand side $\delta (i\ast j,r)={\displaystyle \bigcup _{c\in i\ast j}}\delta (c,r)$, there is an input $k\in i\ast j$, where ${\displaystyle \bigcup _{c\in i\ast j}}\delta (c,r)\ni \delta (k,r)=t$. Thus, there must be $tn(r,t)=1$. □

In the following Example 4, we present a trivial quasi-multiautomaton, where the order of each pair of states is 1. The nontrivial quasi-multiautomaton is presented in Example 5.

Example 4.

Consider a quasi-multiautomaton, which was first presented in Example 5 of [16]. By coincidence, the order of each pair of states is 1, i.e., Theorem 2 holds for an arbitrary triad of elements.

One can see that in the automaton with a free monoid, in the MAC condition of Definition 2, we have links in the sequence of states that coincide with the “links” of strings, i.e., concatenation. In other words, in order to reach a given state, the automaton passes through the same states regardless of whether we regard the left- or the right-hand side of the MAC condition of Definition 2. However, this is not the case for the quasi-multiautomaton, where the GMAC condition suggests that there must exist a shorter, or more efficient input that enables us to reach the same state as when applying two different catenated inputs. Indeed, in Figure 5, we can get from $b_1$ to $b_2$ and from $b_2$ to $b_3$ or directly from $b_1$ to $b_3$. Notice that without the input $e_4$ applied to $b_1$, the GMAC condition would not hold.

Example 5.

In this example, we summarize our above considerations and also explain why Theorems 1 and 2 cannot be given as one even though they are semantically similar. In order to maintain clarity, the quasi-multiautomaton in Figure 6 does not have evaluated transitions. However, it is evident that the inputs could be easily supplemented as in Example 4. For this quasi-multiautomaton, it is obvious that Theorem 2 applies. Furthermore, it is obvious that the multi-automaton in Figure 6 is not reversible because there are no arrows in the opposite direction in the transition diagram—i.e., from the state $s_1$, we go to the state $s_2$, but from the state $s_2$ it is not possible go to $s_1$. If we considered bidirectional arrows in Figure 6, the quasi-multiautomaton would be reversible. In such a case, we would be able to get from state $s_2$ to state $s_4$ via state $s_1$, which corresponds to the left side of the GMAC condition. This must be met, so we must go directly from the state $s_2$ to the state $s_4$.

Another indicator that would help to decide whether the GMAC condition is met or not are identities (neutral elements) of the input hyperstructure. Recall that by an identity of a semi-hypergroup $(H,\ast )$, we mean such an element $e\in H$ that there is $x\in x\circ e\cap e\circ x$ for all $x\in H$. Although, in the definition of the quasi-multiautomaton, the UC condition of Definition 2 is not required, it does not mean that no elements fulfilling it exist. If they do, they are identities of the input semi-hypergroup.

Theorem 3.

If in the quasi-multiautomaton $\left(\right(H,\ast ),S,\delta )$ there exists an element $e\in H$ with the property $\delta (e,s)=s$ for all $s\in S$, then there is $a\in a\ast e\cap e\ast a$ for all $a\in H$—i.e., e is an identity of $(H,\ast )$.

Proof. 

Suppose that there is $\delta (e,s)=s$ for some $e\in H$ and all $s\in S$ and that the GMAC condition $\delta (a,\delta (b,s\left)\right)\in \delta (a\ast b,s)$ is satisfied for all $a,b\in H$ and for all $s\in S$.

For an element $e\in H$, and arbitrary $a\in H$ and $s\in S$, we have

$$\begin{array}{cc}\hfill \delta (a,\delta (e,s\left)\right)\in \delta (a\ast e,s)& \wedge \delta (e,\delta (a,s\left)\right)\in \delta (e\ast a,s)\hfill \\ \hfill \delta (a,s))\in \delta (a\ast e,s)& \wedge \delta (a,s))\in \delta (e\ast a,s)\hfill \\ \hfill \delta (a,s))\in \bigcup _{c\in a\ast e}\delta (c,s)& \wedge \delta (a,s))\in \bigcup _{d\in e\ast a}\delta (d,s).\hfill \end{array}$$

It is obvious that the state $\delta (a,s)$ belongs to the set of states on the right-hand side if and only if $a\in a\ast e\wedge a\in e\ast a$, i.e., $a\in a\ast e\cap a\in e\ast a$, for all $a\in H$. □

When the Cartesian composition of two quasi-multiautomata was constructed in [17], the necessary condition of Theorem 1 was not satisfied. As a result, the GMAC condition was not satisfied. The authors solved the problem by modifying the condition by adding an extension to its right-hand side. Notice that the Cartesian composition of two automata were introduced by Dörfler in [20], the composition was subsequently generalized to the case of quasi-multiautomata in [17].

We conclude this section with the definition of products of automata introduced by Dörfler.

Definition 11.

[21] Let ${\mathbb{A}}_1=(I,S,\delta )$, ${\mathbb{A}}_2=(I,R,\tau )$, and $\mathbb{B}=(J,T,\sigma )$ be quasi-automata. By the homogeneous product ${\mathbb{A}}_1\times {\mathbb{A}}_2$, we mean the quasi-automaton $(I,S\times R,\delta \times \tau )$, where $\delta \times \tau :I\times (S\times R)\to S\times R$ is a mapping satisfying, for all $s\in S,r\in R,a\in H$, $(\delta \times \tau )(a,(s,r))=({\delta }_1(a,s),\tau (a,r))$, while the heterogeneous product ${\mathbb{A}}_1\otimes \mathbb{B}$ is the quasi-automaton $(I\times J,S\times T,\delta \otimes \sigma )$, where $\delta \otimes \tau :(I\times J)\times (S\times T)\to S\times T$ is a mapping satisfying, for all $a\in I,b\in J,s\in S,t\in T$, $\delta \otimes \sigma \left(\right(a,b),(s,t\left)\right)=\left(\delta \right(a,s),\sigma (b,t\left)\right)$. For $I,J$ disjoint, by $\mathbb{A}·\mathbb{B}$, we denote the Cartesian composition of $\mathbb{A}$ and $\mathbb{B}$, i.e., the quasi-automaton $(I\cup J,S\times T,\delta ·\sigma )$, where $\delta ·\sigma :(I\cup J)\times (S\times T)\to S\times T$ is defined, for all $x\in I\cup J$, $s\in S$, and $t\in T$, by

$$(\delta ·\sigma )\left(x,(s,t)\right)=\left\{\begin{array}{cc}\left(\delta \right(x,s),t)\hfill & \mathrm{if}x\in I,\hfill \\ (s,\sigma (x,t\left)\right)\hfill & \mathrm{if}x\in J.\hfill \end{array}\right.$$

Generalizing the homogeneous or heterogeneous products of quasi-automata to the case of quasi-multiautomata is straightforward because, in these two cases, the condition used in Theorem 2 holds. However, in the case of the Cartesian composition, the situation is different. Since in the definition of the Cartesian composition the state set is created as the Cartesian product of the state set of the respective quasi-multiautomata, it is obvious from Figure 7 that the necessary condition $tn(r,t)=1$ is not satisfied in the resulting quasi-multiautomaton, as there is no direct path from state $(s_0,t_0)$ to state $(s_1,t_1)$ because the respective input elements can affect one component only. For a deeper insight into this issue, we refer the reader to Example 1 in [17], the proof of Theorem 2 in [22], or Example 4 in [16], where the GMAC condition is not satisfied anywhere and we consider modified GMAC conditions, called E-GMAC.

4. Nondeterministic Quasi-Multiautomata

First of all, we provide an example of a nondeterministic automaton.

Example 6.

Consider a nondeterministic finite automaton depicted in Figure 8. For input a applied to the state $s_0$ there is a transition to $s_1$, or the automaton can remain in the state $s_0$. As a result, the machine must “decide” how to behave. The same situation applies to the input b and the state $s_1$. Nondeterminism means ambiguity—from a given state, more transitions can lead to the same symbol. A nondeterministic automaton always chooses (sometimes we also say “guess”) the transition that will lead to accepting the word—if that is possible. If we insert the word $aba$ into the automaton in Figure 8, then it has the following options for dealing with it:

$$\begin{array}{c}\hfill s_0⟶s_0⟶s_0⟶s_0\\ \hfill s_0⟶s_1⟶s_3⟶s_3\\ \hfill s_0⟶s_1⟶s_2⟶s_3\end{array}$$

In the first case, the automaton will remain in the state of $s_0$; it certainly can because the rules of transition allow this. In the second case, the automaton moves to other states and eventually reaches $s_3$, which is the final one. The third case has the same final state. In the second and third cases, the automaton accepts the word. Notice that a nondeterministic automaton always automatically selects the branch in which it accepts a word, if such a branch exists.

The following definition transfers the notion of nondeterministic automaton from the context of automata to the context of quasi-multiautomata.

Definition 12.

By nondeterministic quasi-multiautomaton (denoted by ${}_N\mathbb{MA}$), we mean a triad ${}_N\mathbb{MA}=(\mathcal{C}\left(H\right),S,\delta )$, where $(H,\ast )$ is a semi-hypergroup, S is a nonempty set, and $\delta :\mathcal{C}\left(H\right)\times S\to \mathcal{P}\left(S\right)$, where $\mathcal{C}\left(H\right)\subseteq {\mathcal{P}}^{\ast }\left(H\right)$ is a transition function satisfying the following condition:

$$\delta (B,\delta (A,s\left)\right)\subseteq \delta (A\ast B,s)\mathrm{for}\mathrm{all}A,B\in \mathcal{C}\left(H\right),s\in S.$$

(2)

Notation 1.

We will call the condition (2) big-GMAC.

In Figure 9, we can see the basic concepts of deterministic quasi-automata, i.e., automaton with the free monoid, automaton with a monoid, and quasi-multiautomaton.

In the case of an automaton with a free monoid, if we apply the string $adf$ to $s_0$ then $\delta (adf,s_0)=s_3$, and the string $ij$ to $s_3$, we reach the state $s_6$. This is the same as applying $adfij$ directly to $s_0$.

In the case of an automaton with a monoid, if we apply the input (character) b to the state $s_0$, we reach the state $s_4$, where we apply g, which gets us to the state $s_3$. In order for the MAC condition to hold, there must exist an input (character) by which the automaton goes directly from $s_0$ to $s_3$. In our case, such an input (character) is c (on condition that $b·g$ is defined as c).

The case of a quasi-multiautomaton is similar with the difference that there must be $c\in b\ast g$. Therefore, in Theorem 1, this is only a necessary condition, as it does not take into account the fact that $c\in b\ast g$.

While in nondeterministic finite automata of the formal language theory nondeterminism occurs in the transition function, i.e., after we apply one input we can reach multiple states (see Figure 8), nondeterministic quasi-multiautomata of Definition 12 provide nondeterminism for the input set and leave the transition function single-valued.

In Figure 10, we consider the minimal extensive hyperoperation, where, for all $a,b$, there is $a\circ b=\{a,b\}$. Using Definition 6, we regard the element of the potent set, which we—by means of the transition function—apply on a state. Thus, in Figure 10, we apply on $s_0$ the input in the form of the hypercomposition (hyperproduct) $e\ast f$, which takes us to two states: $s_3$ and $s_6$. Thus, we obtain a similar result to that after application of input a to $s_0$ in Figure 8.

Now, consider input $e\ast f=\{e,f\}$ applied on state $s_0$ in Figure 10. Application of condition (2) brings ${}_N\mathbb{MA}$ into two states: $s_3$ and $s_6$. If we apply $c\ast d=\{c,d\}$ on each of these two states, ${}_N\mathbb{MA}$ turns into states $s_4,s_5,s_6$, which are the results of the left-hand side of the GMAC condition. On the right-hand side of this condition, we first evaluate $\{e,f\}\ast \{c,d\}=\{e,f,c,d\}$, which takes us to the set of states $\{s_3,s_4,s_5,s_6\}$. Obviously, the set of states on the left-hand side is the subset of the set of states on the right-hand side of GMAC.

5. Quasi-Multiautomata with the Input Semi-Hypergroup Based on Concatenation

In this section, inspired by [23], we present the construction of a quasi-multiautomata, in which the input semi-hypergroup is based on the original concatenation operation, as is the case of the classical concept of automata. For this type of construction, the necessary condition of Theorem 2, $tn(r,s)=1$ for all $r,s\in S$, is not required.

First, we recall the necessary concepts from the theory of formal languages. String length $\left|x\right|$ is the total number of symbols in the string x. A substring of a string is a sequence of symbols that is contained in the original string—i.e., if x and y are strings, then x is a substring of y if there exist strings $z,z^{\prime }$ such that $zx{z}^{\prime }=y$. Prefix of the string a, denoted by $pref\left(a\right)$, is such a substring of the string a that there exists a substring z of a (which can be empty, however) such that $pref\left(a\right)z=a$. Suffix of the string b, denoted $suf\left(b\right)$, is such a substring of the string b that there exists a substring z of a (which can be empty, however) where $zsuf\left(a\right)=a$. The set of all prefixes of the string x will be denoted $S_{pref}\left(x\right)$; the empty word will be denoted by $\epsilon$ (see also notation used for binary trees in [24]).

Now, denote $H^{\ast }$ as the set of all strings over the set of symbol H and define a hyperoperation $\star :H^{\ast }\times H^{\ast }⟶{\mathcal{P}}^{\ast }\left(H^{\ast }\right)$ by

$$x\star y=\left\{ab\in H^{\ast }\mid a\in S_{pref}\left(x\right),b\in S_{pref}\left(y\right)\right\}$$

(3)

In other words, $x\star y$ is in fact a set of all mutual concatenations of prefixes of x and y.

Example 7.

Consider set $M=\{0,1,2\}$ and the set $M^{\ast }$ of all strings over M. Further, consider strings $a,b\in M^{\ast }$, where $a=1010$ and $b=22$. For these, we have

$$\begin{array}{c}\hfill S_{pref}\left(a\right)=\{\epsilon ,1,10,101,1010\}and{S}_{pref}\left(b\right)=\{\epsilon ,2,22\}.\end{array}$$

Thus, we obtain

$$\begin{array}{c}\hfill a\star b=\{\epsilon ,2,22,1,12,122,10,102,1022,101,1012,10122,1010,10102,101022\}.\end{array}$$

Theorem 4.

Let $H^{\ast }$ by an arbitrary nonempty set of strings over H and let “⋆” be a defined by (3). Then, $(H^{\ast },\star )$ is a hypergoup.

Proof. 

First, we show that the associative law applies. For all strings $a,b,c\in H^{\ast }$, we have

$$(a\star b)\star c=\bigcup _{\genfrac{}{}{0pt}{}{x\in S_{pref}\left(a\right)}{y\in S_{pref}\left(b\right)}}xy\star c=\bigcup _{\genfrac{}{}{0pt}{}{\genfrac{}{}{0pt}{}{x\in S_{pref}\left(a\right)}{y\in S_{pref}\left(b\right)}}{z\in S_{pref}\left(c\right)}}xyz=a\star \bigcup _{\genfrac{}{}{0pt}{}{y\in S_{pref}\left(b\right)}{z\in S_{pref}\left(c\right)}}yz=a\star (b\star c).$$

The reproductive axiom holds automatically because “⋆” is extensive, i.e., $a,b\in a\star b$ for all $a,b\in H^{\ast }$. Indeed, each set of prefixes contains an empty word and the original word, if we perform the concatenation operation of the empty string and the original string from the second set of prefixes, we obtain the original string. Thus, the structure $(H^{\ast },\star )$ is a hypergoup. □

In the following two examples, Examples 8 and 10, we use the above hypergroup as the input sets for two quasi-multiautomata. We will consider two types of transition function. In the first case, it has the role of a “pointer”, i.e., it points to the follower of $s_0$, which is the result of the transition $s_1=\delta (a,s_0)$. In this case, the transition function is usually specified by a table or a transition diagram as in Figure 4 and there is no formula or rule to calculate the transition. In the second case, the transition function has the form of an “operation”, i.e., we obtain the new state by means of calculation (as in Example 2).

Example 8.

Consider the hypergroup $(M^{\ast },\star )$ from Example 7 and the set of states $T=$$\{a,b,c,d,\dots ,m\}$. The transition function ${\delta }_T$ is defined by means of the transition diagram in Figure 8. It is easy to verify that the structure $\mathbb{MA}=((M^{\ast },\star ),T,{\delta }_T)$ is a multiautomaton satisfying the GMAC condition. In Figure 11, we use different colors to highlight the following: processing the input word 1010, i.e., ${\delta }_T(1010,a)$, (blue); the left-hand side of GMAC ${\delta }_T(22,{\delta }_T(1010,a)$ (blue and red); right-hand side of GMAC ${\delta }_T(1010\star 20,a)$ (yellow).

Theorem 5.

Let $(H^{\ast },\star )$ be a hypergroup from Theorem 4 and S be a set of states. Then, it is possible to define a transition function δ such that $((H^{\ast },\star ),S,\delta )$ is a quasi-multiautomaton.

Proof. 

Proof of the condition GMAC is obvious from the presented scheme in Figure 8 and from the definition of hyperoperation, where for two strings a and b, there is $ab\in a\star b$. Indeed, suppose that $a=a_1\dots a_n$, $b_{=}{b}_1\dots b_n$. Then, the left-hand side of GMAC is

$$\delta (a,\delta (b,s))=\delta (a_1\dots a_n,\delta (b_1\dots b_n,s))=\delta (a_n,\delta (a_{n-1},\dots \delta (a_1,\delta (b_n,\delta \left(b_{n-1,\dots \delta (b_1,s)}\right))\left)\right))$$

while on the right-hand side, we have

$$\delta (b\ast a,s)=\delta (b_1,s)\cup \delta (b_1{a}_1,s)\cup \delta (b_1{a}_2,s)\cup \dots \cup \delta (b_1{b}_2{a}_1,s)\cup \delta (b_1{b}_2{a}_1{a}_2,s)\cup \dots \cup \delta (b_1\dots b_n{a}_1\dots a_n,s),$$

where the last term of the union is $\delta (a_n,\delta (a_{n-1},\delta (a_1,\delta (b_n\dots ,\delta (b_1,s))))))$, which is the left-hand side of the GMAC condition. □

Of course, the transition function cannot be arbitrary.

Example 9.

Consider a quasi-multiautomaton with the same input hyprergroup $(M^{\ast },\star )$. However, instead of the state set T, consider the set of all natural numbers $\mathbb{N}$. Next, define the transition function ${\delta }_O:M^{\ast }\times \mathbb{N}⟶\mathbb{N}$ by

$${\delta }_O(a,r)=a·r$$

for all $a\in M^{\ast }$ and $r\in \mathbb{N}$. We can afford to define the transition function δ in such a way because we treat numeric strings (1010 and 2020 below) as numbers. The GMAC condition is not satisfied in this case. Indeed,

$${\delta }_O(22,{\delta }_O(1010,2)={\delta }_O(22,2020)=44440,$$

yet for the right-hand side of GMAC—i.e., ${\delta }_O(1010\star 22,2)$—we require the string 22220 to belong to $1010\star 22$. Yet, we could see in Example 7 that $22220\notin 1010\star 22$.

Next, we will use the construction of a multiautomaton of Theorem 5 and construct a nondeterministic quasi-multiautomaton of Definition 12. There, the element of the power set will be used as the input word, which we will obtain as a result of two elements (strings) $a,b\in H^{\ast }$. In this context, on the right-side of the GMAC condition, the hypercomposition of two sets will be required. It is therefore desirable to first prove the following lemma.

Lemma 1.

In the hypergroup $(H^{\ast },\star )$, where “⋆” is defined by (3), there is $S_{pref}(a\star b)=a\star b$ for all $a,b\in H^{\ast }$.

Proof. 

Obviously, there is $S_{pref}(x\star y)={\displaystyle \bigcup _{z\in x\star y}}{S}_{pref}\left(z\right)$. Moreover, it is obvious that $x\in a\star b$ implies that $x\in S_{pref}(a\star b)$. Proving the other inclusion is also simple. Indeed, the fact that $x\in S_{pref}(a\star b)={\displaystyle \bigcup _{c\in a\star b}}{S}_{pref}\left(c\right)$ implies that there exist words $y,z\in H^{\ast }$ such that $x=yz$, where $y\in S_{pref}\left(a\right)$, $z\in S_{pref}\left(b\right)$. Yet, this means that $x\in a\star b$. □

Example 10.

Consider the quasi-multiautomaton $\mathbb{MA}=((M^{\ast },\star ),T,{\delta }_T)$ from Example 8 and sets $A=a\star b$ and $C=c\star d$, where $a,b,c,d\in M^{\ast }$. For $a=1010,b=22,c=1,d=\epsilon$, we have $A=\{\epsilon ,2,22,1,12,122,10,102,1022,101,1012,10122,1010,10102,101022\}$ (see Example 7) and $B=\{\epsilon ,1\}$. Proving that $\mathbb{MA}$ is a nondeterministic quasi-multiautomaton is rather difficult because one needs to show validity of big-GMAC (2) for all states and inputs. However, we outline the idea of the proof for our specific choice of states and inputs.

We need to show that there is $\delta (B,\delta (A,a\left)\right)\subseteq \delta (A\star B,a)$. From the transition diagram, we calculate the left-hand side of big-GMAC (2):

$$\begin{array}{c}\delta (B,\delta (A,a\left)\right)=\delta (B,\{a,b,d,f,g,j,k,l,m\left\}\right)=\{a,b,d,e,f,g,i,j,k,l,m\}\end{array}$$

(4)

Before calculating the right-hand side, we first establish $A\star B$. This is quite easy (given the specific choice of the set B and Lemma 1):

$$\begin{array}{c}A\star B=\{\epsilon ,1,2,10,12,22,101,102,122,1010,1012,1022,10102,10122,101022\}\cup \\ \{\epsilon ,11,21,101,121,221,1011,1021,1221,10101,10121,10221,101021,101221,1010221\}=\\ \{\epsilon ,1,2,10,11,12,21,22,101,102,121,122,221,1010,1011,1012,1021,1022,1221,10101,\\ 10102,10121,10221,101021,101221,101022,1010221\}\end{array}$$

Now, again using the transition diagram, we compute

$$\begin{array}{c}\delta (A\star B,a))=\{a,b,d,e,f,g,i,j,k,l,m\},\end{array}$$

(5)

and we can see that $\delta (B,\delta (A,a\left)\right)\subseteq \delta (A\star B,a)$; in this case, even $\delta (B,\delta (A,a\left)\right)=\delta (A\star B,a)$.

Lemma 2.

A set $H\subseteq H^{\ast }$ is reflexive in a hypergroup $(H^{\ast },\star )$.

Proof. 

Reflexivity of a subset H of $H^{\ast }$, where $(H^{\ast },\ast )$ is a hypergroupoid, is defined by validity of implication $x\star y\cap A\ne \varnothing \Rightarrow y\star x\cap A\ne \varnothing$ for all $x,y\in H^{\ast }$.

Suppose that $x=a_1\dots a_n$ and $y=b_1\dots b_m$, where $a_i,b_j\in H$ for all $i\in \{1,\dots ,n\}$ and $j\in \{1,\dots ,m\}$. Obviously, $a_1\in S_{pref}\left(x\right)$ and $b_1\in S_{pref}\left(y\right)$. Next, thanks to the fact that $ϵ\in H^{\ast }$, there is $S_{pref}\left(x\right)\subseteq x\star y$ and $S_{pref}\left(y\right)\subseteq x\star y$. Even though “⋆” is not commutative, there is $S_{pref}\left(x\right)\subseteq y\star x$ and $S_{pref}\left(y\right)\subseteq y\star x$. Thus, we have the two-element sets $\{a_1,b_1\}=x\star y\cap H$ and $\{a_1,b_1\}=y\star x\cap H$. □

In the end of this section, we are going to discuss nondeterminism, which is caused by the input structure as stated in Definition 12. In order to do so, we are going to use the hypergroup constructed using Theorem 4. We want to show that for such a structure, there exists a nondeterminism that is “controlled” due to the nature of the hyperoperation. (Recall that in the theory of formal languages, nondeterminism is caused by the transition function.) In order to do so, we are going to use the hypergroup constructed using Theorem 4. The following example shall thus be read within the context of Definition 12 and Theorem 4.

Example 11.

Regard a string $a=a_1\dots a_n\in H^{\ast }$. The transition function produces

$$\delta (a,r)=\delta (a_1\dots a_n,r)=\delta (a_n,\delta (a_{n-1}\dots \delta (a_1,r)).$$

(6)

If we now regard a nondeterministic quasi-multiautomaton, where the nondeterminism is provided in the input by hyperoperation (3), the nondeterminism is “controlled” because from each state in the sequence followed by the automaton, there are at most two paths. Indeed, for $a=a_1\dots a_n$ and $b=b_1\dots b_n$, their hypercomposition is a set of strings, which are concatenations of prefixes of a and b. Thus, e.g., at the second position (which of course exists), the symbol $a_1$ is followed by $a_2$ or $b_1$. As Figure 12 suggests, this idea holds for all positions.

Figure 12 shows that the first position of an arbitrary string from $a\ast b$ (which can be regarded as input) will be occupied by $a_1$ or $b_1$, the second position by $a_2$ or $b_1$, etc. Thus, given the input $a\ast b$, the quasi-multiautomaton will pass at most $2n$ paths (where $a_1{b}_1$ is included in $a_1{b}_1{b}_2$, i.e., these two are counted as one path).

Showing that the big-GMAC condition holds for all strings $a\in H^{\ast }$ such as in Figure 10, where the transition function is given by a diagram (or by a table yet not a rule) is complicated. There exists Light’s associativity test invented by F. W. Light for testing whether a binary operation defined on a finite set is associative. Miyakawa, Rosenberg, and Tatsumi [25] generalized this test for semi-hypergroups. We are not aware of any such test for finite quasi-multiautomata with a transition diagram or table. Finding such tests might be our next objective and the subject of further research.

6. Discussion

Currently, the combinations of algebraic multiautomata into higher entities, using various rules suggested by Dörfler [20,26], are studied—see, e.g., [27]. Such combinations seem to be suitable tools for modeling various real-life systems—see, e.g., [16,21,28]—or are even tools to control such systems [22]. However, two main problems appeared in this respect:

• When constructing algebraic quasi-multiautomata of Definition 5, one needs to show that the GMAC condition (1) is satisfied. This in fact means that one has to prove that if two arbitrary inputs are applied sequentially to a certain state $s_1$, we obtain a state that is contained in the subset of states given by the application potential determined by the hyperoperation of the inputs and the state $s_1$. In this respect, the proof of validity of the GMAC condition is not always straightforward. In [17], the proof is computationally demanding. If we consider various combinations of such quasi-multiautomata, the proofs become even more complicated. For these reasons, in Section 3, we search for conditions that could facilitate such proofs. Moreover, we show why, in some previous cases, the GMAC condition of the composition failed even though each separate quasi-multiautomata fulfilled it. This approach constitutes a sufficiently solid base for further research and the identification of conditions equivalent to GMAC. Note that the way transition number of states (see Definition 8), or even the whole concept of quasi-multiautomaton, is understood is similar to considerations of [29], where, in oriented graphs, one of the vertices is considered as the initial state while selected vertices are final states and the path from state $q_0$ to state $q_f$ (denoted $q_0{\to }^{a^m}{q}_f$) is simply a sequence of edges in the transition graph without any specific structure.
• The abovementioned generalizations of the original concept of automaton have deviated from the original idea of concatenation of input symbols. In Definition 5, H is a semi-hypergroup, which is called input alphabet. However, under this consideration, this “alphabet” cannot create words. Indeed, if $a,b$ are elements of H, i.e., letters, then $a\ast b$ is a subset of H; so, it is a set of letters, not words. This might be seen as a weak point of the theory, which diminishes its applicability. Therefore, in Section 4 and especially in Section 5, we construct quasi-multiautomata based on standard techniques of the theory of formal languages. In Section 4, we modify Definition 5 in such a way that quasi-multiautomata will work nondeterministically. However, being aware of the fact that nondeterministic automata are of no real added value, our concept is designed to include a limited degree of nondeterminism only. Moreover, since this paper deals with the generalization of the automaton, the quasi-multiautomaton can be further generalized by considering H to be an arbitrary hypergroupoid. This enhances possibilities to create input hypercompositional structures reflecting needs of automata of the theory of formal languages. In other words, weakening requirements of the input structure provides us a wider range of choices to construct quasi-multiautomata based on concatenation. For example, consider that $(H,\ast )$ is a hypergroupoid if $x\ast y=\{z,w\}$, where z is formed by deleting the odd-positioned letters from the word $xy$ and w is formed by deleting the even-positioned letters from the word $xy$. However, one needs to discuss the impact of losing associativity on GMAC, which is based on it. In Section 5, we show a construction of quasi-multiautomata, which corresponds to automata of the theory of formal languages and is based on the idea of concatenation of strings with associativity preserved. For quasi-automata, this is possible thanks to the free monoid. For quasi-multiautomata, i.e., structures making use of hypercompositional structures, we concatenate words for input. We present a specific example. However, thanks to the multivalued nature of the hypercomposition, a whole range of similar schemes might be thought of.

7. Conclusions

In our paper, we defined conditions that the GMAC condition must satisfy. We also constructed algebraic a quasi-multiautomaton related to automata of the theory of formal languages. On top of that, we constructed a quasi-multiautomaton with a limited degree of nondeterminism. In contrast to nondeterministic automata of the theory of formal languages, where nondeterminism is caused by the transition function, the nondeterminism in our construction follows from the input hyperstructure. It is properties of the input hyperstructure that have the potential to yield interesting results in such nondeterministic quasi-multiautomata, which suggest a potential line of further research.