1. Introduction
It has been more than three decades since computer spreadsheets became known as a tool of education [
1]. Designed in 1979 for non-educational purposes on the foundation of the computer program VisiCalc, the spreadsheet, nonetheless, was conceptualized in educational terms as “an electronic blackboard and electronic chalk in the classroom” [
2]. Whereas a spreadsheet is not the only digital tool discussed in this paper, it played an initial role in the development of mathematical ideas that the author, a mathematics educator of teacher candidates, intends to share. One of the earliest uses of a spreadsheet in tertiary mathematical education was in the context of numerical modeling of Fibonacci numbers [
3], motivated, perhaps, by the ideas about a laboratory course in calculus and linear algebra in which “one student found experimentally that the limit of the ratio of terms in a Fibonacci sequence is independent of the two given initial values” [
4] (p. 293). That is, as shown in [
3] towards launching the use of a spreadsheet in mathematics education, both for the sequence 1, 1, 2, 3, 5, 8, 13, … (Fibonacci numbers) and for the sequence 2, 1, 3, 4, 7, 11, 18, … (Lucas numbers), the ratios mentioned in the above quote tend to the number
, known as the Golden Ratio.
As an aside, according to [
5] (p. 5), it was Lucas, a French mathematician of the 19th century, who in 1876 introduced the term Fibonacci numbers for the former sequence. For example, in [
6] (p. 8, italics in the original) the sequence was also referred to as the series of Lamé, e.g., “la célèbre série de Lamé ou de
Fibonacci”. From an educational perspective, the Golden Ratio is an example of one of the big ideas of mathematics demonstrating “a property of a mathematical object which remains unchanged when the object undergoes some form of transformation” [
7] (p. 7); namely, the invariance of the limiting value of the ratio of two consecutive terms of the (Fibonacci-like) sequence
to the change (a numeric transformation) of the initial values of
a and
b. When
a =
b = 1, sequence (1) turns into Fibonacci numbers. Put another way, the sums of the coefficients in
a and
b in the terms of sequence (1) are Fibonacci numbers.
A recursive definition of sequence (1) has the form
and, as it was experimentally “discovered” by a tertiary mathematics student half a century ago,
for any positive values of
a and
b (one of which may be zero). Apparently, the student recognized a decimal approximation to the Golden Ratio, not the right-hand side of (3). Nowadays, one can come across the Golden Ratio (including its approximate values) in other contexts using different computer programs. Besides Excel, several commonly available digital tools can generate the Golden Ratio and its approximations. One such tool is
Wolfram Alpha, a computational knowledge engine available free online (
https://www.wolframalpha.com/; accessed on 18 November 2021). It displays various symbolic representations of the Golden Ratio, including its connection to circular functions which “proved to be admirably suited for the study of sound, electricity, radio, and the host of other oscillatory phenomena” [
8] (p. 417). Perhaps, this connection is not surprising as the ratios of two consecutive Fibonacci and Fibonacci-like numbers exhibit oscillatory behavior when approaching the Golden Ratio. Furthermore, the use of dynamic geometry software (e.g.,
The Geometer’s Sketchpad [
9]) makes it possible to discover the phenomenon of invariance exemplified by the Golden Ratio in a regular pentagon (by constructing the pentagon and exploring the ratio of its diagonal to its side) and in a regular decagon (by constructing the decagon and exploring the ratio of its radius to its side). Entering the ratio of any two consecutive terms of sequence (1) into the
Graphing Calculator [
10], a program capable of graphing a relation from any two-variable equation or inequality, while keeping
a and
b as parameters, yields an approximation to the Golden Ratio, and the higher the ranks of the terms, the better the approximation.
These discoveries, representing computational experiments made possible by the modern-day educational software tools which are transforming the mathematical practices of learners and teachers [
11,
12,
13,
14], open a window to students’ learning methods of mathematical machinery, including trigonometry and complex numbers, as a way of using theory to confirm the results of the experiments. Among those students are prospective elementary teachers [
15], impelling mathematics educators “to construct experiences which lead to the growth of subject matter knowledge in learners” [
16] (p. 331). Other geometric contexts for the Golden Ratio can be found in The Online Encyclopedia of Integer Sequences (OEIS
®), a rich source of information not all of which is mathematically grade appropriate. In particular, using this source requires certain competence in managing the abundance of information provided online [
17]. Such interplay of classic (and, according to OEIS
®, recently discovered) mathematics and contemporary mathematical education is a characteristic of the important role of the technological advancement in making the learning environment of the subject matter more user friendly and, thereby, enjoyable. Furthermore, whatever a grade level, there should be an astute didactic awareness of the importance of connecting mathematical topics to be studied and concrete problems from which the topics stem [
18,
19]. Indeed, as the authors of the last two publications argued, from psychological and mathematical positions, respectively, students are interested in the study of mathematics if they are confident in the usefulness of material in concrete applications. In more specific contexts describing the interplay of mathematical education and real life, one can find research-based suggestions about the importance of local culture for a better grasp of mathematics taught in the classroom [
20] and the need for careful attention to linguistic coherence in the use of terminology involved in formulating mathematical activities and problems when teaching diverse learners [
21].
Relation (3) can be proved formally by using an explicit representation of Fibonacci numbers
, (referred to since 1843 as Binet’s formula). In the capstone course taught by the author and used as the background for this paper, Binet’s formula was derived by representing Equation (2) in the matrix form and finding the corresponding eigenvalues needed for the transition to the Jordanian form of the matrix involved (see [
22] and the comment by a teacher candidate included below before Proposition 1). Other approaches to the formula may include the generating function approach or the method of the characteristic equation. This was known a century earlier to Euler, enabling one to show that there exists
, which is the Golden Ratio. One can also rewrite recurrence (2) in the form
and, after transitioning to the limit (knowing of its existence) in both sides of the last equation, to find
as the positive root of the equation
, whence
. It is a unique feature of the Golden Ratio to differ from its reciprocal by the unity (see an alternative representation of this property in
Section 8 below). To conclude this introductory section, note that all the facts mentioned above are well known and were prerequisite knowledge for this paper.
2. Materials and Methods
Two types of materials have been used by the author when working on this paper as a reflection on teaching the capstone course titled “Topics and Research in Mathematics Education”. The first type deals with the theory of education and it includes recommendations for mathematical preparation of secondary teacher candidates in the United States [
23,
24], classic treatises by John Dewey [
25,
26], and an article [
16] (closely related to the topic of the special issue for which the present paper was written) about the interplay of a subject matter and its pedagogy. The second type of material (used to support the capstone course) is digital and it includes a computer spreadsheet (Microsoft Excel), a free version of computational knowledge engine Wolfram Alpha (
https://www.wolframalpha.com/; accessed on 18 November 2021), Maple, a symbolic and numeric mathematics and engineering software program (
https://en.wikipedia.org/wiki/Waterloo_Maple; accessed on 18 November 2021), and the Graphing Calculator, produced by Pacific Tech [
10], capable of graphing relations defined by either equation or inequality.
Methods specific for mathematics education used in this paper include computer-based mathematics education, standards-based mathematics, and problem solving. Methods specific for mathematics used with secondary teacher candidates include the machinery of matrices, difference equations, one/two-variable polynomials, and continued fractions—topics studied by the candidates as undergraduate mathematics majors [
23]. The university where the author works is located in upstate New York in close proximity to Canada, and many of the author’s students have been Canadians pursuing their master’s degrees in education. This diversity of students suggests the importance of aligning mathematics education courses with multiple international perspectives on teaching mathematics to future teachers [
27]. In accord with those perspectives, activities described and analyzed in the paper are aimed at developing deep conceptual understanding of mathematics in teacher candidates and may be characterized as action learning [
28,
29]. Action learning begins with a query into a real problem, and it continually emphasizes conceptual learning, regardless of whether the problem is aimed at pragmatic or epistemic development. The paper is supported by the candidates’ reflections solicited through individual portfolios and various assignments of the capstone course (discussed in detail in [
22]) in which they describe their experience using technology and mathematical methods when working on the assignments.
The enrollment in the secondary mathematics teacher education graduate program and, consequently, into the capstone course has always been relatively small (about ten teacher candidates) reflecting a small size of the campus. The class setting was a combination of a lecture-type theoretical discussion and an exploratory work on assignments in a computer lab equipped by about 20 machines allowing the candidates, while not sharing a computer, to still work in pairs split across the lab. The class had the luxury of simultaneous reservation of a computer lab and a room with tables and a spacious white board, the use of which was alternated by the author and the candidates enabling mathematical truth to stem from a dialogue and be accepted when the latter made sense for everyone. More specifically, the correctness of reasoning, being supervised by the author, was decided at the white board through teacher candidates’ interactions with each other to include in the dialogue the use of trial-and-error and the recourse to counterexamples. In the lab, during experimentation with mathematical assignments requiring the use of digital tools, didactic intervention in the form of a dialogue was mostly between the author and a pair of participants and it could evolve into the whole class discussion of an issue important for the attention of all participants.
3. Mathematical and Educational Framework of the Paper
In what follows, the author reflects on his work with secondary mathematics teacher candidates in a technology-rich graduate capstone course designed to “develop deep understanding of mathematics they will teach … [through] a sustained immersion in mathematics that includes performing experiments and grappling with problems” [
23] (pp. 7, 65). Research in mathematics education is often carried out “through reflection on the status of mathematical constructs” [
30] (p. 2), attests that schoolteachers’ experience of learning mathematics “becomes grist for reflection” [
31] (p. 65), and emphasizes the “pivotal role of reflections in mathematising and didactising” [
32] (p. 163). The author’s reflections that span over several years—from the time a teacher candidate accidentally found a new phenomenon within the classic context of Fibonacci-like numbers (see
Section 5), something that required the revision of the course content by conceptualizing this experimental finding and turning it into a teachable material (see
Section 6)—are augmented by the candidates’ reflections on the revised course, on future work with their own students using ideas of the course and on the interplay of the subject matter and ways of teaching it in the digital era. This made it possible to diversify and to balance a possible subjectivity of the author’s perspective on the content of the capstone course developed for and taught to prospective teachers of secondary mathematics.
The main idea to be shared below is how the use of technology by teacher candidates led to the discovery (not to be confused with re-discovery) of apparently unknown mathematical knowledge. This discovery, made by a candidate through a careful observation of accidentally obtained numerical data, demonstrated the importance of paying attention to the interplay of mathematics and education as a possible source of new knowledge in the digital era. Dewey [
26] (p. 252) made the following distinction between recognizing something and observing something: “Recognition deals with already mastered; observation is concerned with delving in the unknown”. So, using Dewey’s terminology, the discovery (or better, re-discovery) of the limiting value of the ratio of two consecutive Fibonacci-like numbers being invariant of the first two numbers was a recognition by a calculus student mentioned above rather than observation. Indeed, this property of invariance was well known, perhaps from the time of Johannes Kepler, a notable German contributor to the 17th century Scientific Revolution, who observed the connection of the Golden Ratio to what we call nowadays Fibonacci numbers.
In the context of the interplay of mathematics and education, it is interesting to note that Dewey’s educational perspective on the nature of observation is very similar to the perspective of Leonhard Euler—the father of all modern mathematics—who emphasized the importance of thought processes (so-called quasi-experiments) that stem from observations, as cited in [
33] (p. 3): “the properties of the numbers known today have been mostly discovered by observations, and discovered long before their truth has been confirmed by rigid demonstration”. Almost identical meaning ascribed to observations by the great mathematician and the great educator suggests that reflection is critical for dealing with an unknown. It is through reflection, described in [
34] (p. 225) as moving “from action to the representation of the action—that is, from just being able to do something to thinking about the doing of that thing”, on what happens in the context of technology-enhanced mathematical education that hidden mathematics accidentally revealed by a student within a computational experiment and recognized by the instructor as worthy of paying avid attention can be shared. Indeed, as will be shown below, reflection “impels to inquiry” [
26] (p. 7), especially in mathematics and, by implication, in mathematics education. It is through reflection followed by inquiry into what happened in the classroom that mathematical knowledge for teaching teachers, the importance of which was emphasized in [
35], develops. From a pedagogical perspective, teacher candidates’ interest in didactic reflection on their mathematical work has to be fostered even if this work was different from what they will be teaching in their own classroom [
36]. Nonetheless, one teacher candidate suggested that “
teachers at the high school level can teach Fibonacci numbers in depth in order to strengthen students’ abilities to “think outside the box,” and to challenge mathematics students using multiple problem solving strategies. A number of these explorations and additional activities may be used as extra-credit, a unit project, in cooperative learning groups and also for technology integrated projects”. With the interplay of mathematics and education being under the reflective radar, this comment brings to mind the notion of PCK (pedagogical content knowledge) which, according to [
37] (p. 9) includes “the most regularly taught topics in one’s subject area … the ways of representing and formulating the subject that makes it comprehensible to others”. Whereas exploring mathematics in depth often requires that a teacher goes beyond those “regularly taught topics”, a care should still be taken to make the pedagogy of a less traditional and infrequently taught content “comprehensible to others”. With the advent of technology, the concept of PCK was extended to the concept of TPCK (technological pedagogical context knowledge) or, alternatively, TPACK [
38,
39]. Thus, one can see in the above comment by a teacher candidate not only willingness to teach mathematics in depth using their enriched PCK but also aspiration to integrate technology into various secondary school mathematical activities.
4. Generalizing Fibonacci-like Numbers
A possible direction towards computer-enabled explorations in the context of Fibonacci-like numbers is to change the rule through which the numbers develop; that is, to modify the rule that every number beginning from the third is the sum of the previous two numbers. For example, consider the sequence 1, 1, 5, 13, 41, 121, …, in which every number beginning from the third is two times the previous number plus three times the number before the previous one. Such sequence can be defined recursively as follows:
Teacher candidates were asked to use a spreadsheet to explore the behavior of the ratio of two consecutive terms of recurrence (4). As a result, they found that the ratio approaches pretty fast the number 3. The candidates were curious to see that by slightly amplifying the complexity of the rule through which the terms of the sequence develop, the ratio of consecutive terms approaches an integer rather than a non-integer (in fact, a non-terminating non-repeating decimal). Furthermore, one of the candidates recognized that when in recurrence Equation (4)
, the resulting sequence 1, 3, 9, 27, 81, 243, …, looks familiar as it consists of consecutive powers of the number 3; in other words, each power of 3 beginning from 9 is twice the previous power of 3 plus three times the power of 3 before the previous one. For example, 243 = 2·81 + 3·27. This was a not commonly thought of mathematical fact which came to light in the context of education. Of course, this is a special case of a pretty obvious identity
. Another important aspect of coming across this fact was its accidental nature—the candidates were just playing with initial values in (4) to see how the change of the first two values changes the limiting value of the ratio of two consecutive terms of the sequence. This is an example of collateral creativity [
40]—an educational phenomenon of accidental discovery of a certain mathematical fact and, most importantly, of its recognition and subsequent reflection. This finding prompted other candidates to be creative and, as a way of reflection on the finding of their peer, to search for an alternative recursive definition of the sequence which generates the powers of the number 3. Then do the same for the powers of the number 4, and, in general, of the number
k. Using trial and error as “the first stage of contact with any new material” [
25] (p. 181), the class came across the recurrences of the form
;
;
; and, more generally,
;
, each of which generates consecutive powers of
k and when
k = 4 turns into the corresponding recurrence with the coefficients (3, 4) and (8, −16). That is, consecutive powers of
n can be generated by the recurrence
, of the first order as well as by the recurrences of the second order, not to mention a closed formula
fk,n =
kn. One can see how the practice of mathematics education emphasizing reflection on an accidental discovery as an inquiry-driven activity [
26] brings us closer to doing mathematics. The next section will show how seeing classroom practice through the lens of mathematical education research [
41] enhanced by realization that experimental mathematics is deeply embedded “not only in the field of artificial intelligence, but also in the mathematical education and pedagogy community” [
42] (p. ix), has potential to develop the interplay of educational and research activities in the digital era, and, in the spirit of Dewey [
26], to advance the outcomes of mathematical activities from recognition to observation.
5. Parametrization of Fibonacci Recursion
The above considerations and the kudos of an accidental recognition served as a motivation for the class to explore a more general recurrent relation by parametrizing the coefficients in the right-hand side of (4) and the initial values as follows:
Setting the initial values
and using the activities described in detail in [
22] (skipped here for the sake of brevity), the following proposition about the existence of a generalized golden ratio was developed. (About those activities, one teacher candidate noted: “
… we connected Fibonacci numbers with Binet’s formula, the golden mean, matrices, and eigenvalues. We investigated Fibonacci numbers from many different avenues and perspectives, through experimental and theoretical practices”).
Proposition 1. For any pair, there exists a real number l (called a generalized golden ratio) such that the system of equationshas a single solutionand the corresponding ratiosconverge to l as n grows large.
Note that
when
a =
b = 1. In that way, Proposition 1 extends the experimental discovery of a student in a calculus and linear algebra course more than half a century ago [
4] and it provides the generalization of this discovery to any pair of parameters
a and
b such that
However, the power of educational artifacts that support computational experiments allows students not to be entirely controlled by instructors and, as appropriate, to satisfy their natural (mathematical) curiosity with ease. This educationally congenial state of affairs transpired when one teacher candidate, by playing with the coefficients
a and
b, reported to the author the following observation: there exists a pair of parameters
a and
b for which the ratio of consecutive terms of sequence (5) does not have a number as a limiting value. Instead, the ratio expands into a string of numbers that repeats over and over as the terms of the corresponding sequence change (
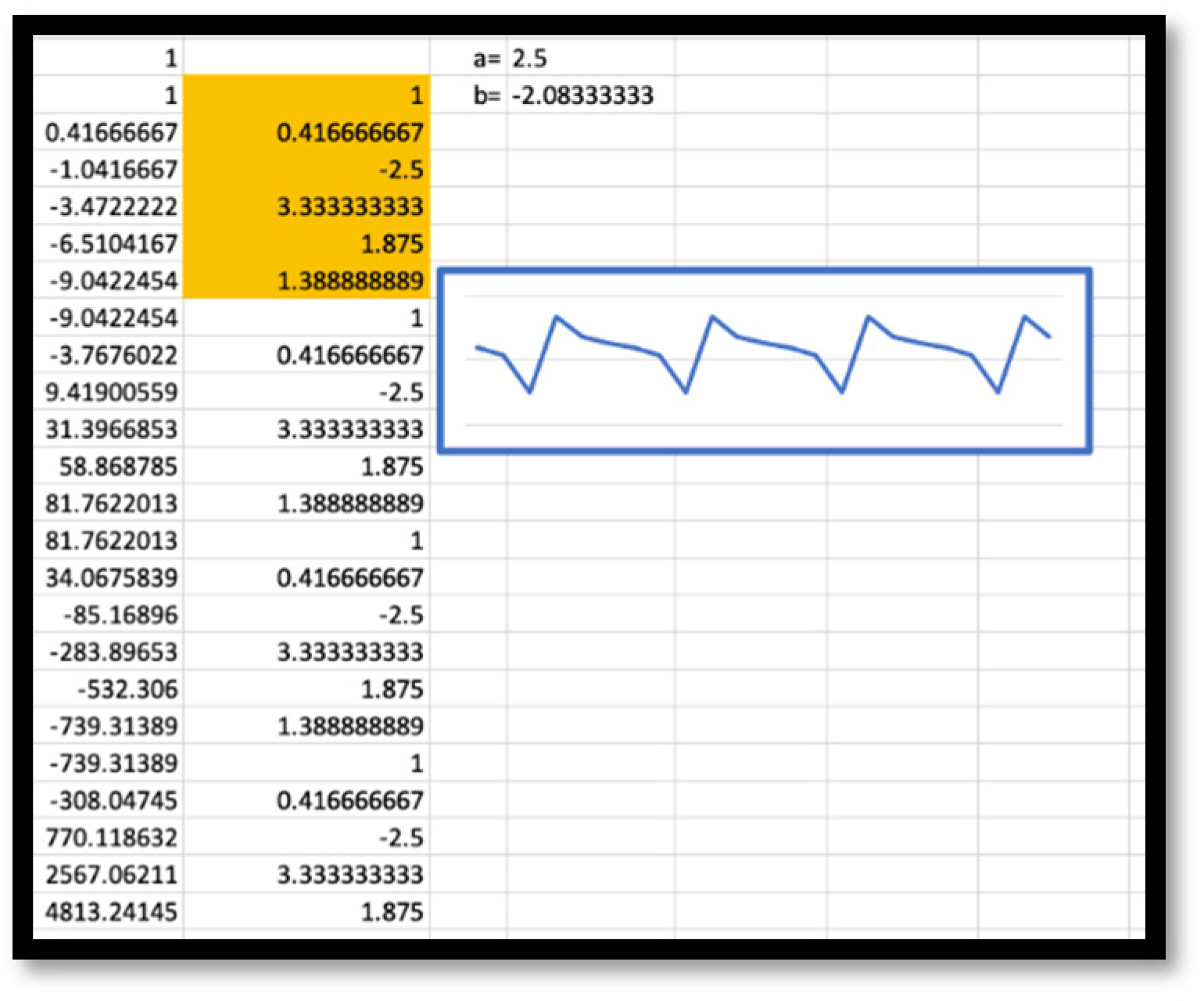
Figure 1). That is, once again, accidentally, the equation
was found in which the ratio
was not attracted by a number but rather by the string of three numbers, (1, −2, 4). This time, unlike the case of powers of the number 3, nothing looked familiar. Both Euler and Dewey would have described this finding as an observation. Therefore, being aware of almost identical mathematical and educational meanings ascribed to observations, it was the author’s didactic responsibility to act on the wonder of a mathematical unknown provided by a computational experiment which facilitated “the picking out of significant elements in a gross, vague whole” [
26] (p. 197). Once again, like in the case of accidental discovery that a second order linear difference equation can generate consecutive powers of natural numbers so that their ratio converges to a generalized golden ratio on the first iteration, the significant element of the latter observation, requiring intervention of the “more knowledgeable other”, was that there exist values of parameters
a and
b in Equation (5) so that the ratio of its consecutive terms may be attracted by a string of three numbers which are not invariant to the change of the initial values. In other words, in true agreement with the “opinion that exemplary teaching is a form of research” [
16] (p. 330), the class was curious to
observe that a generalized golden ratio may be a string of numbers.
This observation raised several conceptual questions to which no immediate answers were available even with the presence of the “more knowledgeable other”, thus pointing at the challenging nature of the interplay of mathematics and mathematics education in the digital era.
How can one find the relationship between a and b in (5) so that the ratio is attracted by a string of three numbers; alternatively, the ratio forms a cycle of period three?
Do there exist cycles of period larger than three that the ratio can form?
How can one find relations between a and b that are responsible for such cycles?
Do there exist cycles with an arbitrary large period?
That is, in the context of mathematics education, due to advances in digital technology, new mathematical knowledge was set to be developed. Answering the above questions required significant mathematical work that resulted in publication of a book [
43]. Educationally, after knowing answers to those questions, the next step within the interplay of mathematics and education was to find a way to communicate this new knowledge to the learners of mathematics, including secondary mathematics teacher candidates, in a grade-appropriate manner. Indeed, whereas “subject matter has instrumental value as a means of promoting discovery” [
16] (p. 362), the interplay implies the need for an educator to be concerned with making the concepts so discovered teachable. The next sections will show a way of turning the discovery into an instrument of teaching.
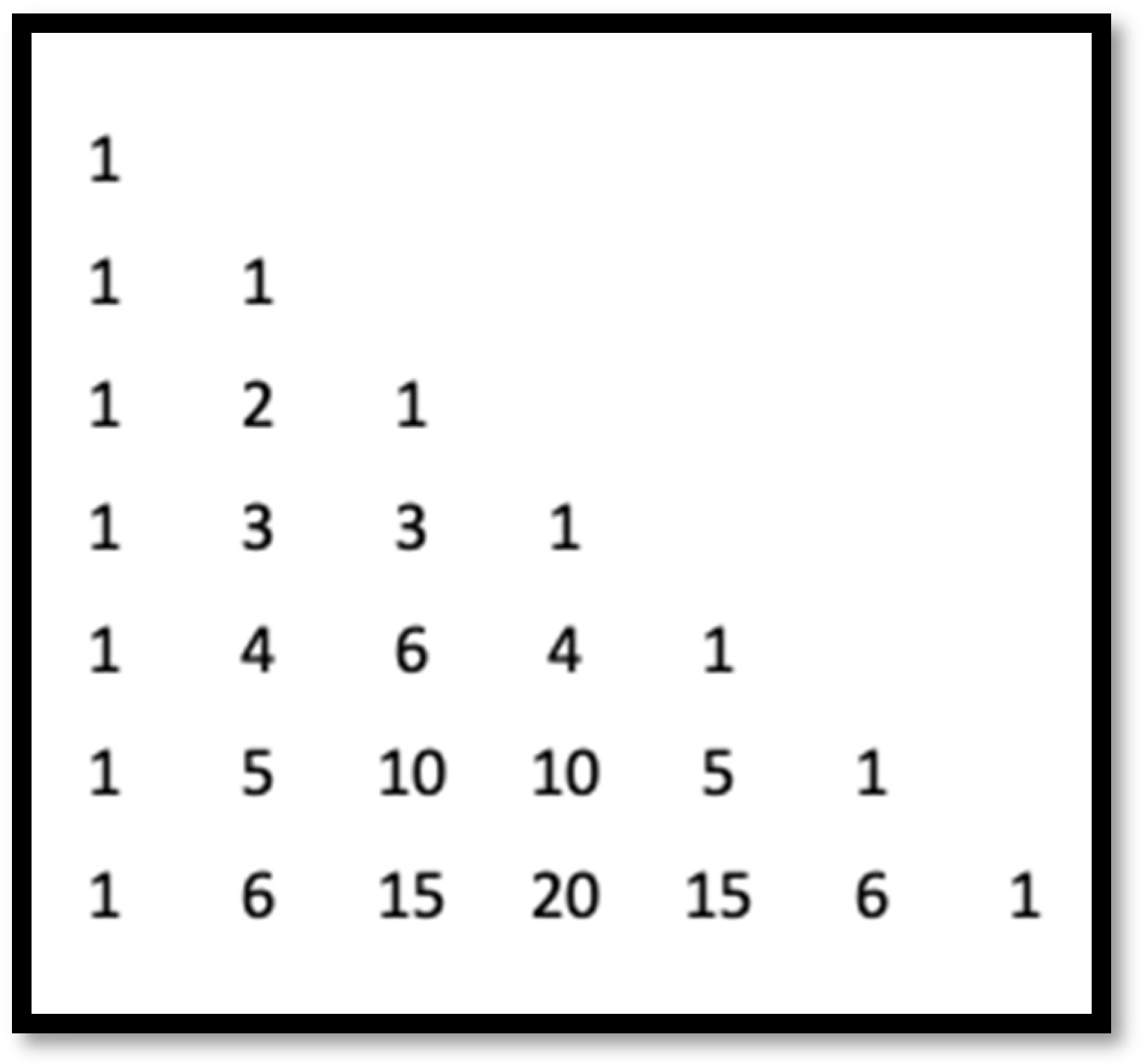
6. A Rearranged Pascal’s Triangle with Staggered Rows and Fibonacci-like Polynomials
It is well known that Fibonacci numbers can be found in Pascal’s triangle if one adds the entries of the latter along the so-called shallow diagonals [
42]. According to [
8], the triangle was used by Pascal, one of the founders of probability theory, for recording sample spaces of experiments of coin tossing. The image of Pascal’s triangle with staggered rows is shown in
Figure 2 and it can be found in [
44]. For example, the quadruple (1, 3, 3, 1) in the fourth row (
Figure 2) represents the case of tossing three coins when there is one case only to have either three heads or three tails, and only three cases to have either two heads and one tail or one head and two tails.
Consider a modification of the table of
Figure 2 by shifting each column (except the first column) one position down as shown in
Figure 3. Each column beginning from the second one consists of partial sums of numbers in the column immediately to its left. As a result, the sums of numbers in each (staggered) row represent Fibonacci numbers because the rows of the table of
Figure 3 coincide with the shallow diagonals of Pascal’s triangle. Apparently, before the questions listed at the end of the last section were formulated, such modification of Pascal’s triangle was never considered. However, this modification, when explored through the lens of a computational experiment, an instance of which was shown in the spreadsheet of
Figure 1, turned out to be truly consequential, both mathematically and pedagogically. In the words of Dewey [
26] (p. 289), “the familiar and the near do not excite or repay thought in their own account, but only as they are adjusted to mastering the strange and remote”. A possible explanation of the novelty of knowledge that is “strange and remote” for the well-investigated mathematics of Pascal’s triangle and Fibonacci numbers, deals with the virtue of digital tools (such as
Wolfram Alpha) that enabled observation (rather than recognition) of special properties of polynomials the coefficients of which have been traditionally located along the shallow diagonals of Pascal’s triangle and now located in the staggered rows of the rearranged triangle. Indeed, the interplay of mathematics and mathematical education “has less to do with how subject matter directly influences instruction and more to do with how teachers create activities and organize learning environment” [
16] (p. 329). As Dewey [
26] (p. 290, italics in the original), when encouraging teachers not to be afraid of activities which are new to students, put it: “The old, the near, the accustomed, is not that
to which but that
with which we attend; it does not furnish the material of a problem, but of its solution”. Nowadays, in true agreement with the statement that “intellectual individualism is tolerated … in subjects like mathematics” [
25] (p. 348), the academic environment of a pre-college mathematics classroom is often challenged with students’ ideas which may be foreign to the common practice, and teachers in the United States are expected to “have the intellectual courage and mathematical disposition to not reject the challenge but to investigate the proposed idea, applying their own critical thinking and using all available resources” [
24] (p. 9). Such resources include a variety of digital tools available to teachers through the generosity of numerous educational initiatives and grants. Despite or perhaps due to their variety, the tools have to be used appropriately to ensure both pragmatic and epistemic development of learners. The importance of the interplay between the pragmatic and the epistemic in the context of using computational experiments as one of the main instruments of the 21st century mathematics education “is rooted in the fact that nowadays the very act of mathematical thinking is enhanced through the power of technology” [
14] (p. 841).
With these pedagogic ideas in mind, mathematical teaching of the “strange and remote” begins with constructing one-variable polynomials, the coefficients of which are the numbers in the staggered rows of the rearranged Pascal’s triangle (
Figure 3). These polynomials, referred to as Fibonacci-like polynomials [
43], are as follows:
The term Fibonacci polynomial was used in [
45,
46] for another class of polynomials associated with Fibonacci numbers. Using
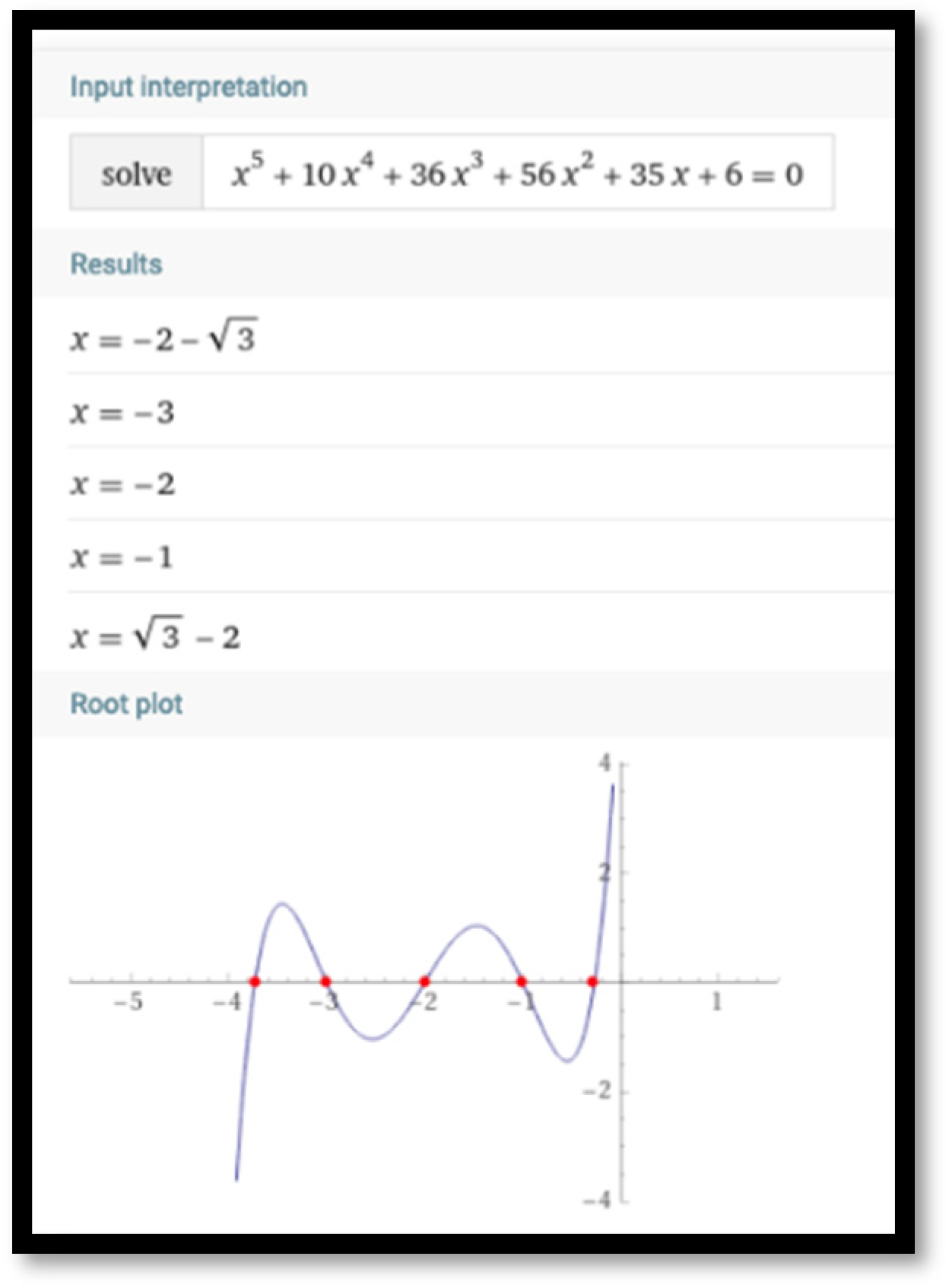
Wolfram Alpha, teacher candidates were able to see that all the polynomials do not have complex roots and, furthermore, all the roots belong to the interval (−4, 0). For example, as shown in
Figure 4, the polynomial
of degree five has five roots in the interval (−4, 0). Furthermore, some of the roots coincide with the roots of polynomials of degree smaller than five. Indeed, the values
and
are the roots of the polynomials
and
, respectively. Furthermore,
and
. This connection among three consecutive Fibonacci-like polynomials can be generalized to the following recursive formula:
where the notation
mod(
n, 2) stands for the remainder of
n upon the division by 2; therefore, the coefficient
assumes either the value of 1 or
x.
Simple (paper-and-pencil) calculations allow one to see that
To continue, the candidates were demonstrated the use of
Maple, another powerful computational tool, in calculating the values of
(
Figure 5). One can see that
. Because a Fibonacci-like polynomial
is associated with a cycle of length
p =
n + 2, we have 3
m − 2 =
p − 2 whence
p = 3
m. That is, there exist cycles of any length that are multiples of three. For example, as shown in
Figure 5, the cycle of length 993 as a product of two prime numbers, 3 and 331, consists of trivial 993-cycles and proper 993-cycles. This allows one to formulate the following technology-supported generalization in the form of
Proposition 2. For any integer N there exists integer p > N such that in Equation (7) generalized golden ratios form a cycle of period p.
7. Connecting Fibonacci-like Polynomials to Cycles Using Multiple Tools
Now, one has to explain how Fibonacci-like polynomials are connected to Equation (5) and how one can use them to generate cycles formed by the ratios. Originally, the polynomials came to light with no connection to Pascal’s triangle and the subsequent modification of the latter was used to make new mathematical ideas teachable to diverse learners of mathematics. Therefore, an explanation to be provided would allow one to see how reflection on the interplay of mathematics and mathematical education demonstrates the use of the tools of the subject matter in applications to the development of new knowledge and what it may mean that “success in science … is an inherently pedagogic affair … [because] ideas are themselves intrinsically pedagogic” [
16] (p. 332). The last quote is in line with the above-mentioned quote from the Standards of Preparing Teachers of Mathematics [
24] which confirmed that ideas are often born as one listens to a teacher and the latter is expected to appreciate that it is the teaching that motivated student ideas and, thereby, not to be indifferent, but rather enthusiastic about the opportunity of any idea, challenging or not, to be investigated. It is through mathematics education courses that teacher candidates are supposed to acquire such types of pedagogic experience. The following comment indicates one teacher candidate’s appreciation of pedagogy as an art of teaching through which ideas are presented as the birthplace of a subject matter so that “
in combination with quality instruction, the gap between disconnected mathematical ideas could be closed, providing a rich learning environment for all students.”
To connect Equation (5) and Fibonacci-like polynomials, let
and
, so that Equation (5) can be rewritten in the form
As noted by a teacher candidate, “
Looking at the Fibonacci numbers 1, 1, 2, 3, 5, 8, 13, 21, 34, etc.
we see that we cannot have a cycle less than period three because a cycle of one would be 1, 1, 1, 1, and a cycle of period two would also be 1, 1, 1, 1 which represents a cycle of period 1”. In order to find all values of
a and
b for which the sequence
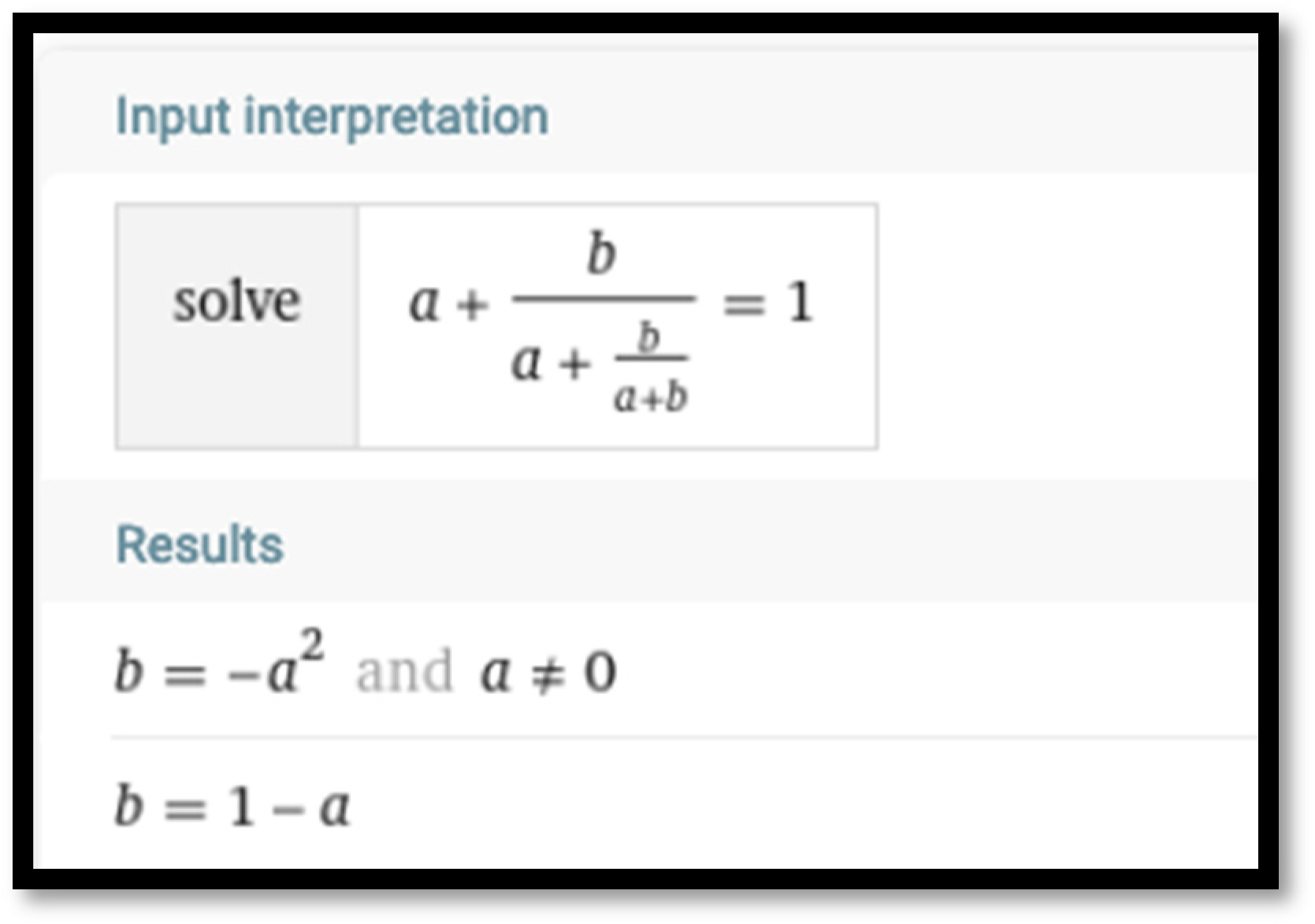
forms a three-cycle, one has to write
and then solve the equation
. The solution of the last equation can be outsourced to
Wolfram Alpha (
Figure 6) yielding
and
. The latter solution when substituted in Equation (7) yields the trivial case of
for all
n = 1, 2, 3, …. The former solution under the substitution
yields the equation
. Likewise,
and solving the equation
using
Wolfram Alpha (
Figure 7) yields the only non-trivial solution
which under the substitution
is equivalent to the equation
. This allowed for the formulation of
Proposition 3. All values of parameters a and b responsible for three-cycles formed by the solutions of Equation (7) belong to the parabola. All values of parameters a and b responsible for four-cycles formed by the solutions of Equation (7) belong to the parabola. Alternatively, the root of the equationis responsible for three-cycles in Equation (7) and the root of the equationis responsible for four-cycles in Equation (7).
Continuing in the same vein, the candidates found that the roots of Fibonacci-like polynomials are responsible for all five-cycles, the roots of Fibonacci-like polynomials are responsible for all six-cycles and so on, so that the roots of are responsible for all twelve-cycles which may consist of cycles of lengths three, four and six.
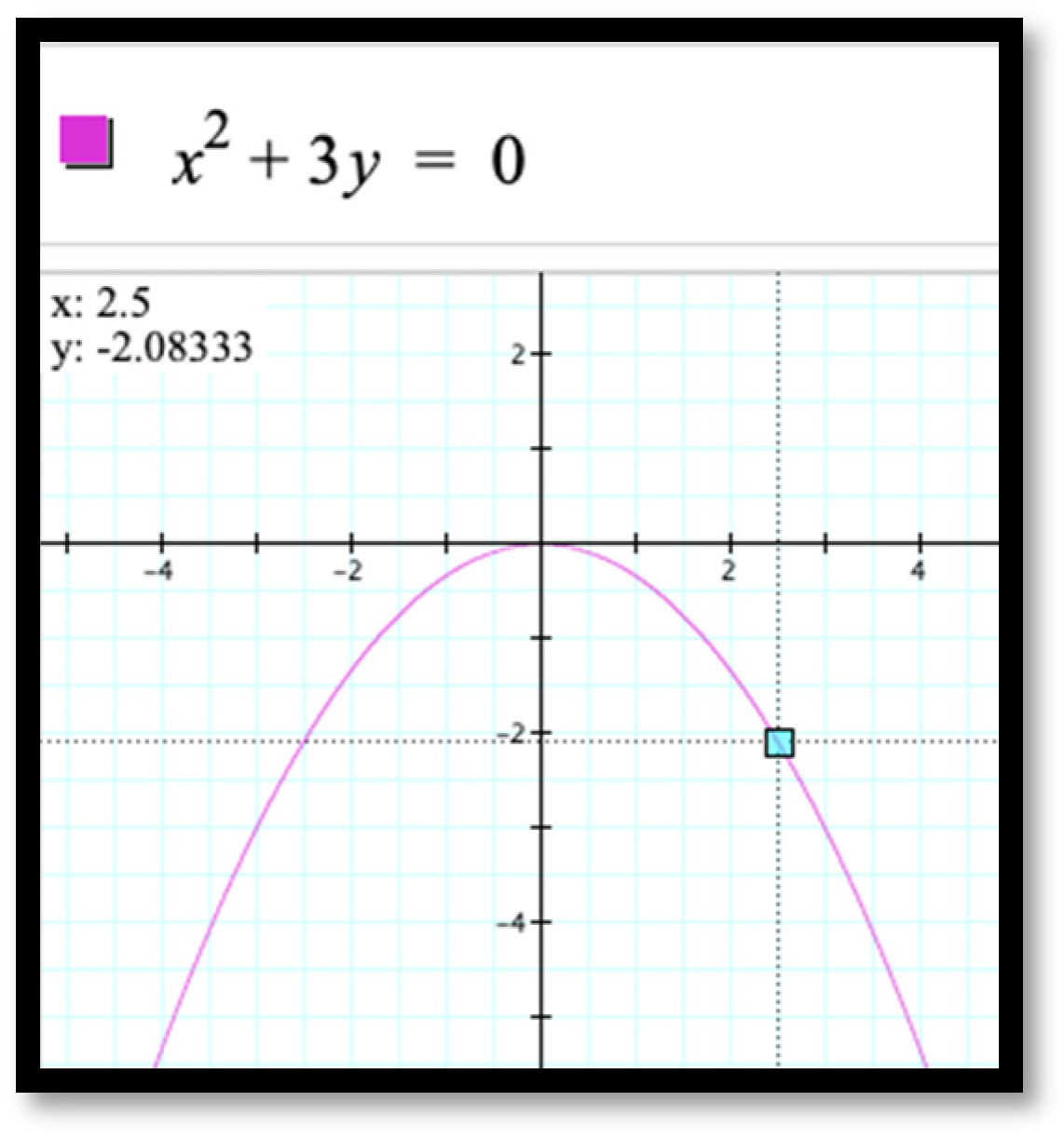
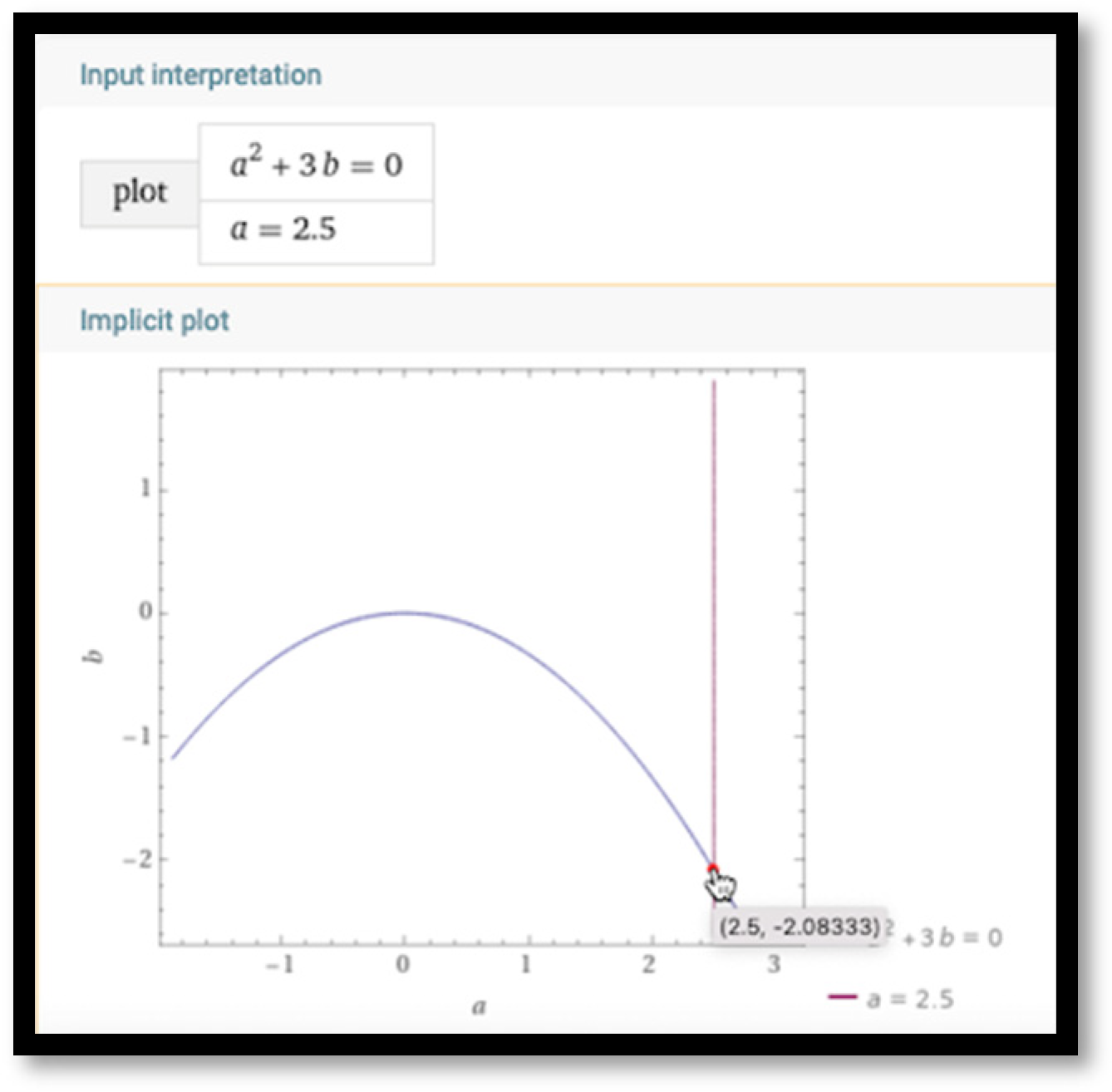
Figure 4 shows the presence of cycles of lengths three, four and six (
) as trivial cycles of length twelve. One can graph the equation
using the
Graphing Calculator (
Figure 8), select a point on the graph (parabola) by using a cursor and plug the coordinates of this point into a spreadsheet (
Figure 9) as values of
a and
b. By plugging
a = 2.5 and
into the spreadsheet, the tool displays a six-cycle generated by Equation (7), thus confirming theory through an experiment. Note that
Wolfram Alpha can graph relations without the use of the (
x,
y) notation; however, the program does not allow for the use of a cursor to select a point on a graph. Instead, one locates a point by graphing the vertical (or horizontal) line to which it belongs (
Figure 10). Such small-scale discrepancies in the functioning of different educational artifacts in response to identical mathematical assignments constitute an important part of the interplay of mathematics and education in the digital era that mathematical educators must be aware of. This awareness gives special meaning to a pre-digital era credence that “it is independency of new experiments that enhances credibility” [
47] (p. 193). Using multiple tools in having students regard as credible computationally obtained results has a valuable educational advantage over the use of a single tool as the sense of authenticity of new information with seemingly scattered mathematical ideas motivates learners to go on learning mathematics with technology. In the words of a teacher candidate, “
The use of technology demonstrated not only efficiency, but also touched at the heart of pedagogy. If used appropriately, technology does not hinder student learning, but rather allows students to delve deeper into mathematical learning and thinking, rather than approaching learning at a surface level”. In the spirit of Dewey [
26], the appropriate use of technology allows students, under the guidance of a “more knowledgeable other”, to advance their problem-solving skills from recognition to observation; that is, to learn how to proceed from dealing with the known to delving into the unknown.
As an example of deeper learning with technology, the notion of necessary and sufficient conditions can be discussed. To this end, note that the relation
implies
. Likewise, because all the roots,
, of Fibonacci-like polynomials belong to the interval
we have
, whence
or
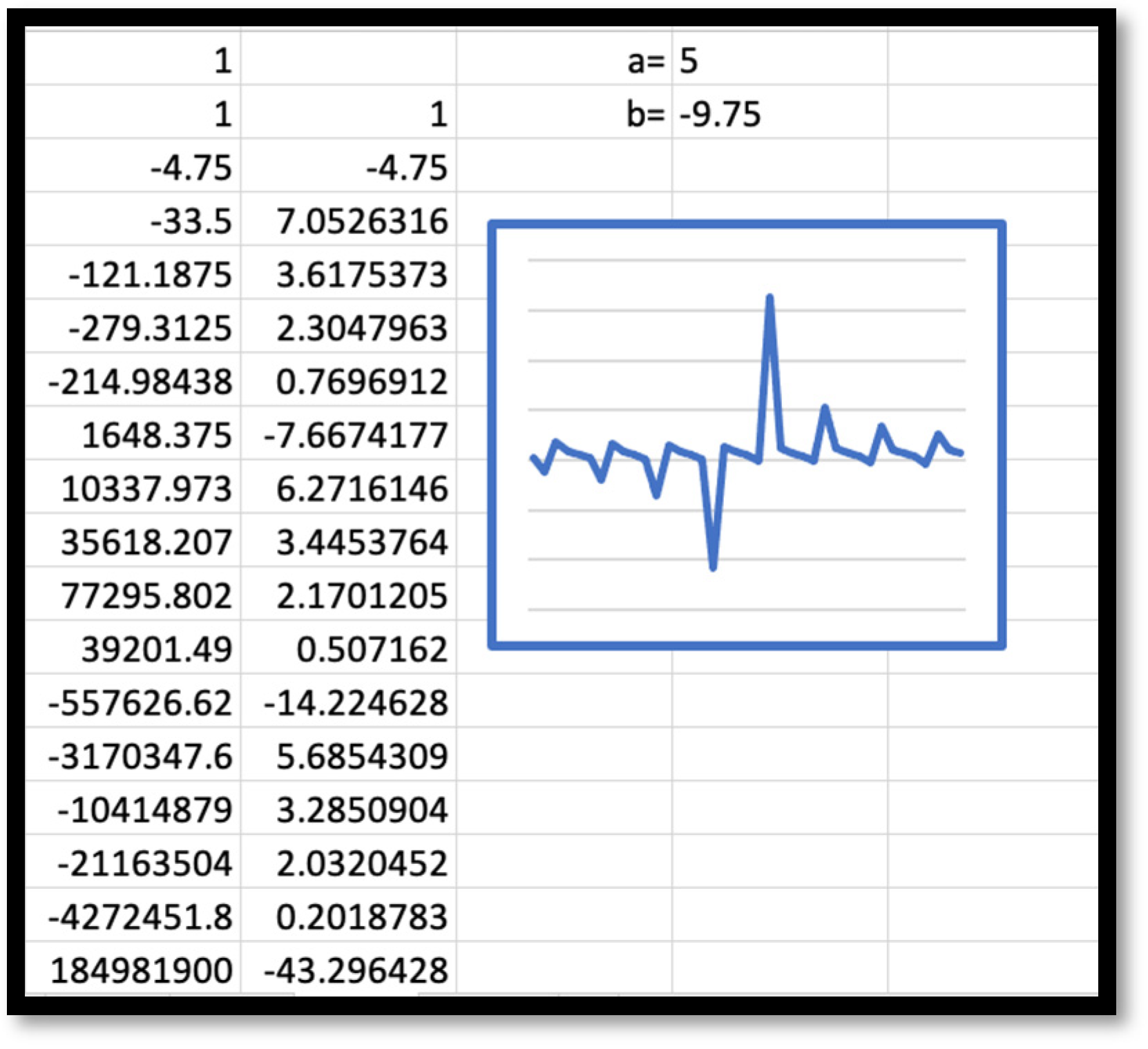
That is, inequality (8) provides a necessary condition for Equation (7) to generate cycles of different lengths that serve as generalized golden ratios. Inequality (8) is indeed necessary but apparently not sufficient for Equation (7) to generate cycles of different lengths that serve as generalized golden ratios. For example, when
a = 5 and
inequality (8) is satisfied but iterations generated by Equation (7) exhibit what may be perceived as irregular behavior shown in the spreadsheet of
Figure 11. At the same time, a computational experiment with tools used in this paper does not allow one to determine whether the seemingly irregular behavior of ratios displayed by a spreadsheet both numerically and graphically is, in fact, a part of a cycle of a much larger length than the spreadsheet displays. Indeed, as was mentioned above in the context of the
Maple-based computational experiment (
Figure 4), there exist proper cycles with length being a sufficiently large number.
This uncertainty in interpreting experimental data, amplified by the use of technology, indicates the duality of the interplay between experiment and theory. On the one hand, advanced technology can provide data the need for interpreting which gives birth to a theory which, in turn, was subject to technological verification. On the other hand, keeping in mind that suggestion is one of “the essential functions of reflective activity” [
26] (p. 106), the insufficiency of technology in prompting one to come up with a plausible conjecture suggests the need for a theory as a deeper reflection on mathematical meaning of a computational experiment. As it was mentioned in the introduction, some experimental findings, like the convergence of the ratio of two consecutive Fibonacci-like numbers to the Golden Ratio or the presence of the latter in a regular pentagon, can be confirmed using a grade-appropriate mathematical machinery. Yet, some findings of experimental mathematics, especially within a new conceptual domain, can be used as a motivation for seeking to grasp their meaning through developing new methods of theoretical mathematics.
8. The Interplay of Pragmatic and Epistemic Uses of Technology
As was mentioned above, the appropriate use of digital tools offers both pragmatic and epistemic development of learners. When
Wolfram Alpha was used to define the relationships between parameters
a and
b that are responsible for cycles of certain lengths, it was a pragmatic use of the program enabling one to avoid rather tedious algebraic transformations leading to polynomials which, quite unexpectedly, turned out to be factorable. At the same time, the appropriate use of technology with pragmatic intention in mind provided a collateral epistemic outcome—Fibonacci-like polynomials are factorable. Nonetheless, the algebra-free pragmatic use of
Wolfram Alpha by teacher candidates might have eluded their important epistemic development associated with an alternative representation of numbers through continued fractions. Once again, this is a case when the role of the “more knowledgeable other” in the teaching process is critical. The interplay of pragmatic and epistemic uses of technology is not straightforward in the sense that one cannot assume that any use is of one type only at any given moment. The pragmatic should always find a way to inform the epistemic and vice versa. Just as “ideas are themselves intrinsically pedagogic” [
16] (p. 332), pragmatic uses of technology always directly or collaterally influence epistemic development of the user. The opposite relation is also true.
As an illustration, note that whereas the exact value of the Golden Ratio is given by the fraction that requires three operations to be completed before its decimal representation is revealed and the position on the number line is located, one can consider the sequence 2/1, 3/2, 5/3, 8/5, 13/8, and refer to the fractions formed by the pairs of consecutive Fibonacci numbers as convergents to the Golden Ratio. Furthermore, the fraction 13/8 can be written as the sum 1 + 5/8 = 1 + 1/(8/5). That is, . The last equality is a special case of recursive relation (7) with a = b = 1, thereby indicating a recursive development of the convergents. Furthermore, the candidates recognized that the relationship between two consecutive convergents to the Golden Ratio is similar, if not identical, to the relationship between the Golden Ratio and its reciprocal.
This allows one to continue developing the special case numerically in much the same way as
Wolfram Alpha did it algebraically. As a result, a new representation of a rational number different from a decimal representation can be constructed. To this end, using a simple idea of representing a number as a sum of its integer and fractional parts, one can write:
Thus,
. The far-right representation of 13/8 is called the linear representation of continued fraction where the number 2 is used instead of the sum 1 + 1. Because 13/8 is a convergent to the Golden Ratio (something that was
recognized in the early 1970s by a student in a computer laboratory calculus and linear algebra course), one can try to use the same algorithm for expressing the Golden Ratio through a continued fraction as follows:
with an infinite number of ones which the continued fraction consists of. Note that
Wolfram Alpha provides the following continued fraction representation for the reciprocal of the Golden Ratio
. These two reciprocals have very similar continued fraction representations (reflecting, alternatively, their representation through an algebraic equation mentioned at the end of the introduction section and providing an unexpected example of a mathematical connection) and decimal representations as
and
. At the same time, using
Wolfram Alpha, one can write
and
. The similarity in the former case deals with the Golden Ratio being a very special number. In general, unlike continued fraction representations, decimal representations of reciprocals are very different and this difference explains what it might mean that continued fractions offer “insights that are not revealed by the decimal representation” [
48] (p. 186). For example, the reciprocals
and
have similar continued fraction representations and different decimal representations. Furthermore,
. Yet, the last fraction is not just a slight modification of the Golden Ratio; it represents the generalized golden ratio for the sequence 1, 2, 5, 13, 34, 89, … which consists of every other Fibonacci number and is described by the difference equation
. This is another example of how, in the digital era, seemingly pragmatic computations aimed at illustrating a certain property of numbers can be used collaterally towards one’s epistemic development. By paying attention to the interplay of pragmatic and epistemic uses of technology, secondary mathematics teacher candidates develop a better grasp of the interplay between educational instruments and mathematical ideas. As mentioned by one of the candidates: “
By experimenting first through graphs or some other way, one can perhaps induct an idea for a solution that can be backed by mathematical theory. I also learned that exploring problems both experimentally and theoretically is interesting for someone who enjoys mathematics, because connections can be discovered that are unexpected. If a teacher can incorporate such experimental and theoretical problems in his or her classroom perhaps more students would become intrigued and interested in mathematics”.
9. Conclusions
This paper was written to give a modern-day mathematical example of what Dewey [
26] meant by distinguishing between recognition and observation in terms of dealing with facts already known and delving into something apparently unknown. Some 150 years before Dewey, Euler, as mentioned in [
33], saw observations as a foundation for the discovery of new properties of numbers in mathematics. Such historically notable similarity of mathematical and educational perspectives on observations set a perfect context for writing a paper on the interplay of mathematics and education. As a background for the interplay discussed, an accidental discovery of certain properties of Fibonacci numbers that happened in a technology-rich classroom of secondary teacher candidates taught by the author was used. This discovery and the follow-up reflective discussion of how mathematical ideas inform a capstone mathematics education course was supported by multiple digital tools, including a spreadsheet,
Wolfram Alpha,
Maple, and the Graphing Calculator. Each tool played a mutually complementary role in advancing computational experiments from recognition to observation. Some recognitions were due to the candidates’ collateral creativity, some observations were due to their reflective inquiry encouraged and advised by a “more knowledgeable other”. Reflection in teacher education as a field of disciplined inquiry is aimed at the improvement of teacher quality [
49,
50]. Experiencing mathematics in the making, especially in the context of technology-rich pedagogy, does improve the subject matter qualifications of the 21st century teaching workforce.
All activities described in the paper were part of the course designed with the goal to address current world-wide standards emphasizing the need for a deep knowledge of mathematics by classroom teachers. The importance of such knowledge for the success of schoolchildren was recognized by a teacher candidate using the following statement: “
This project allows a prospective math teacher to achieve a deeper understanding of content material which translates to a better educational experience for students in the classroom. Furthermore, the use of technology, present in in these explorations is stressed as an essential component of education. It is for these reasons that this project, through its relation to the goals and expectations set forth by the standards serves as an appropriate capstone experience”. The teacher candidate did not mention, but according to [
27] (p. 147), “teacher knowledge should be particularly important for the learning gains of weaker students”. Often, among the “weaker students” are those whose mathematical “weakness” resulted from losing interest in the subject matter due to the lack of pedagogical content knowledge on the part of a teacher. In that case, the lost interest can be reviewed through the grade-appropriate presentation of infrequently taught topics by teachers who have “the intellectual courage and mathematical disposition … [to use] all available resources” [
24] (p. 9), digital tools included.
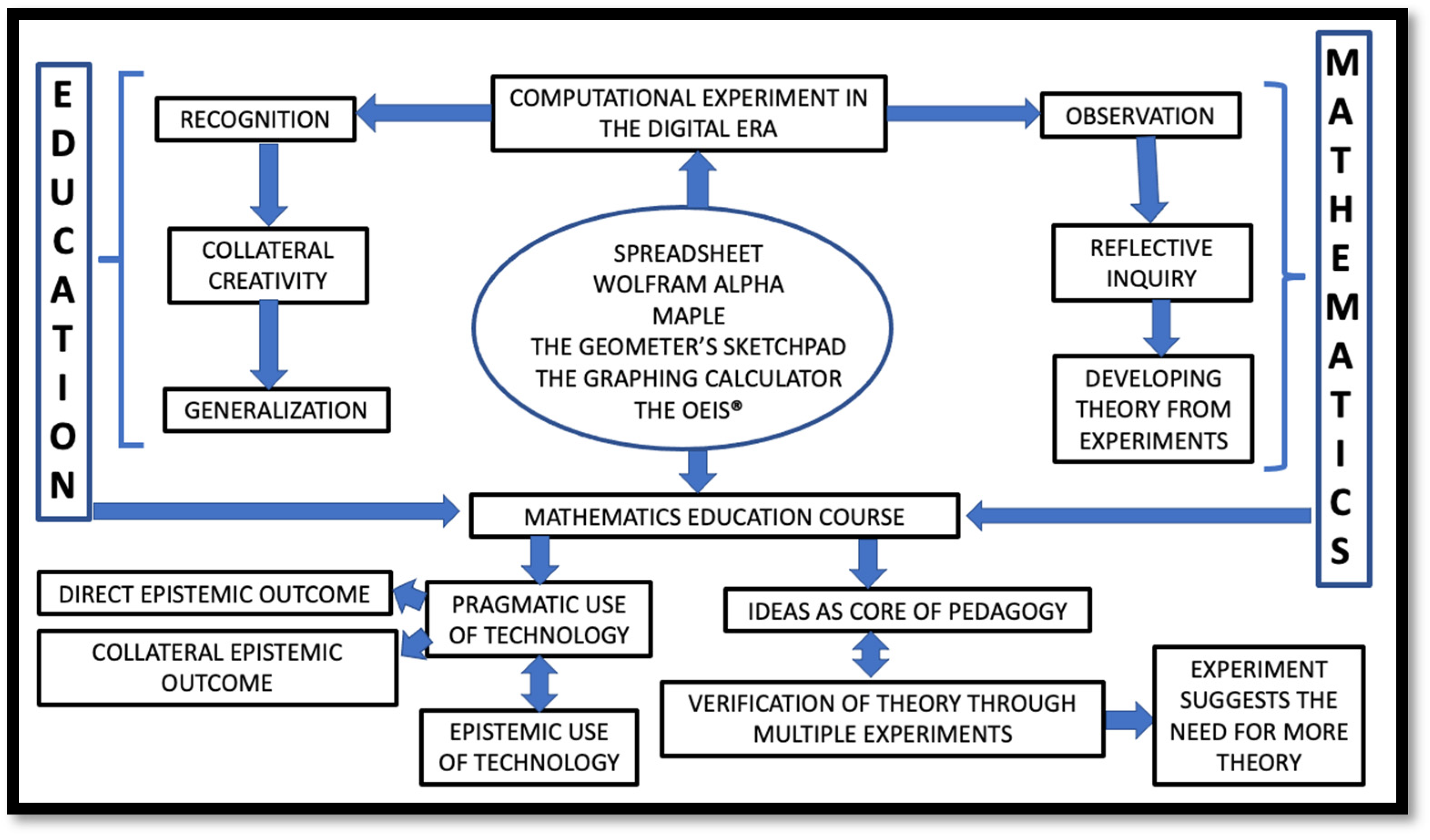
The diagram of
Figure 12 shows a possible application of the interplay of mathematics (top right) and education (top left) to the practice of teaching a technology-rich capstone mathematics education course (bottom). A computational experiment, being the pivot of the course fosters skills responsible for both recognition and observation. The former instrument of learning mathematics opens a window to students’ collateral creativity and motivates their desire to move towards generalization. The latter instrument of discovering new properties of mathematical structures brings about reflective inquiry which leads one to understand the need for the development of theory capable of explaining the meaning of the experiment.
A limitation to the study of the interplay of mathematics and mathematical education described in this paper is the accidental nature of the discovery of cycles which provided new knowledge about the behavior of generalized golden ratios. However, the author’s intent in the future offerings of the course was not to test whether such discovery could be replicated through an appropriate educational intervention. Rather, the accidental discovery of the cyclic nature of generalized golden ratios, like any other finding of experimental mathematics, has created a unique opportunity for the author to entertain the idea of the interplay of the subject matter and its educational layout supporting current standards emphasizing the intricacy of learning with technology. At the same time, secondary teacher candidates in each successive section of the course were informed that it is due to an accidental discovery by an ordinary yet observant student that part of the course has been modified in order to demonstrate an uncommon outcome of mathematical education research—the discovery of new mathematical knowledge. This information was communicated to teacher candidates with the goal to serve as a motivation to work towards new discoveries thus reducing the above-mentioned limitation to the study.
The paper discussed the pragmatic vs. epistemic duality of the use of technology by the learners of mathematics. Using the context of a pedagogical introduction of continued fractions, it was shown that pragmatic uses of technology always have either direct or collateral effect on the epistemic development of a learner. The bottom part of the diagram of
Figure 12 shows that pragmatic uses of the tools of technology, such as
Wolfram Alpha, may have two types of epistemic outcomes—direct (when recognition is not followed by reflection) and collateral (when observation implies reflection). The diagram also shows how the verification of theoretical ideas through multiple computational experiments belongs to the heart of the pedagogy of a technology-rich mathematics education course and how one can design pedagogical activities for a capstone course.
The interplay of mathematics and education in the age of technology can be analyzed through different lenses and take several routes. One route, as described in this paper, goes along the line of advancing mathematical activities, in the spirit of Dewey [
26], from recognition of the known to observation of the unknown. Facing the unknown by a classroom teacher happens every day when schoolchildren are allowed and even encouraged to ask questions. Their questions may just seek simple information (like, is my answer correct?), yet can be quite challenging when requesting explanation (like, why is my answer incorrect?). Whereas for a student any new topic taught by a teacher is presumably unknown, a pedagogy of connecting the unknown to the known helps students to elevate their recognition skills to the level of observation. Such elevation is not possible without students asking questions the answers to which might be unknown to the teacher. Therefore, when a technology-rich mathematics education capstone course for secondary mathematics teacher candidates is designed with the goal of advancing computational experiment from recognition of the known to observation of the unknown, the course contributes to forming the cornerstone of the interplay of mathematics and mathematical education.