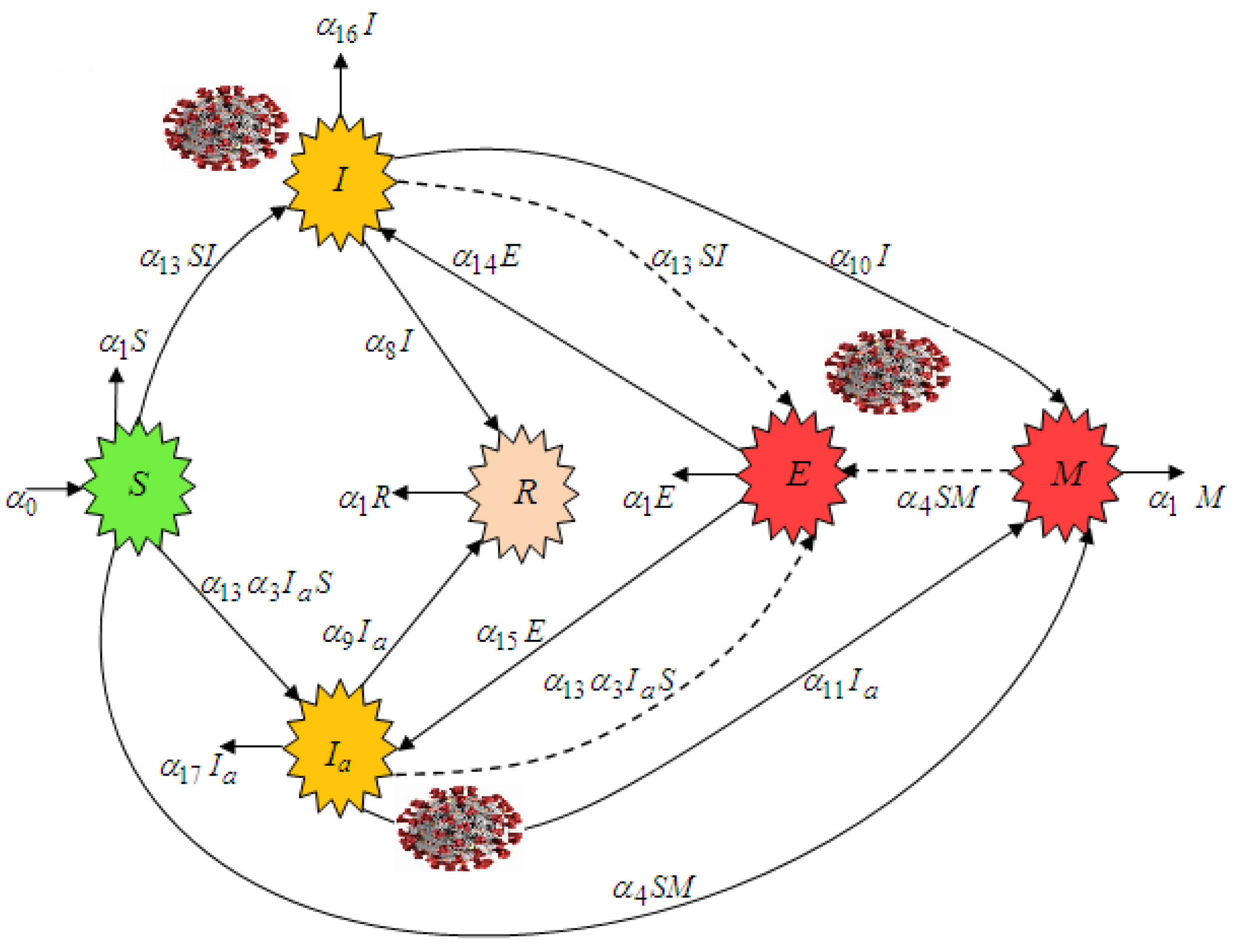
1. Introduction
COVID-19 spread is increasing in urban areas across India and Omicron cases are also increasing. In December 2021, Omicron is the leading variants compare to other variants. So for, each state has increased the cases of Omicron spread. Now COVID-19 active cases were increased in India and it is very soon end for this pandemic. COVID-19 cases in India as of 30 December 2021, collected from the WHO (World Health Organization) is as follows: via passengers screened at the airport (1,524,266), active cases (82,402), cured or discharged (34,258,778), deaths (480,860), total active cases (160,989), last total cured (33,614,434), last total death (456386), and total samples tested (605,885,769). The total vaccination doses as of the current date is 1,438,322,742.
The Omicron variant of COVID-19 has been detected in 653 cases across India by Union Health Ministry data updated in December 2021. As of 30 December 2021, COVID-19 cases are increasing in India. On 29 December 2021, there were 13187 new cases identified, a 77% increase from the previous week. Cases are surging in other states such as Mumbai, Delhi, Pune, Bengaluru, Chennai, Thane, Kolkata and Ahmedabad. Mumbai identified 2510 cases on 29 December 2021; this was an 80% increase from the previous day and 400% rise from a week previous. Similarly, Delhi identified 923 cases (600% rise), Bengaluru 400 cases (90%), Chennai 294 (100%), Mumbai (15%), etc. The current high rate is due to the Omicron variant. It is a type of the SARS-CoV-2 virus and dominant in India in the last few days of December 2021. The percentage of vaccination is 63% of its adults and 89% of partial in India.
Even though there are some vaccinations and medicines for control this pandemic treated at COVID-19 gives a big challenge to the people. Moreover, we discuss equilibrium points of COVID-19 to lessen the infected individuals in India. We have given the convergent, comparable and most appropriate solution of each and every compartment involved in the model by using the most powerful and elegant method via the homotopy perturbaton method. Particularly in India, many control strategies and policies were decided on and had to be followed by the people, including the quarantine period measures such as lockdowns, social distancing, the acceleration of treatment, the wearing of masks, sanitizer usage, and the frequent washing of hands.
Chakraborty T, Ghosh I. [
1], discuss the real life data and dangerous assessment of COVID-19 by using data-driven analysis. The analysis of prediction of COVID-19 spreads are in China, Italy and France in [
2]. The isolation of cases and contacts are to control COVID-19 outbreaks [
3]. We collected the Indian data separately in the Indian council of medical research (ICMR) [
4]. Dynamics and bifurcation approaches are defined in [
5]. Kucharski AJ et al. [
6], it gives a spread model study on transmission and infected data on COVID-19. The
of COVID-19 is calculated and data fluctuations to other viruses [
7,
8]. Ndariou F, et al. [
9], the COVID-19 model in Wuhan which is considered and control strategies in [
10] with similar to Brazil [
11]. The mathematical modelling of the improved SIR model with real life government control strategies [
12] with SARSCoV-2 in India [
13]. We collected the tracker data from crowd sourcing in India [
14]. SEIR is a good model which enables the COVID-19 outbreak in all countries with government polices and other endemic models for source data [
15,
16,
17,
18]. M. A. Khan, A. Atangana [
19], A Mathematical Modeling of novel Corona-virus (2019-nCoV) is studied with numerical simulation and asymptomatic carrier transmission [
20]. The compartment models are defined by [
21] with phase based [
22]. The numerical data’s are in all countries, we used this procedure the calculations [
23,
24,
25]. It helps to all the analysis such as control in Wuhan, China [
26,
27]. The Indian dynamics are of transmission and control strategy are derived from the mathematical modeling [
28] with New dynamical behavior in [
29]. In this regard, we calculated the active cases from the mathematical modeling and then created a new model in the second wave with the Omicron variant. We obtained the infected ratio for the period October 2021 to December 2021 and the parameter estimation of the model. The described model is solved numerically as well as approximated analytically by using the homotopy perturbation method.
In general, we collected all data from the WHO [
30] with optimal control theories [
31,
32,
33]. The supporting data collected from other government recongnised websites [
34,
35,
36,
37]. The four states (Kerala, Sikkim, Mizoram and Meghalaya) are an exception to the endemic state (they are not yet endemic). It will soon change and become endemic. Almost the majority of population is infected state. The affected population had 68 percentage (nearly 1000 million) antibodies from 4th ICMR survey by end of December 2021. The cumulative COVID-19 cases had 30,410,577 (3.2 percentage out of affected population).
Finally, we concluded that the five highly affected states of Maharashtra, kerala, Karnataka, Tamilnadu and Andra Pradesh need more attention to decrease the spread to the infected populations. The number of people infected with COVID-19 was still high in many areas, and transmission of the virus was easily regenerated once people increased their activities and contact with each other. The current pandemic situation is to reduce the infection of COVID-19 cases in India. Scientists are currently working to find opt vaccine for corona virus disease from various countries.
This research paper is written as follows: In
Section 2, we have given the detailed mathematical modeling of the second wave of the Indian COVID-19 pandemic. In
Section 3, Stability analysis of the model like uniformly bounded of the system, equilibrium analysis such as disease free equilibrium and endemic free equilibrium and basic reproduction number is studied.
In
Section 4 and
Section 5, the approximate analytical expressions of each and every compartment appeared in the given model are derived using HPM. Also, we briefly discuss the numerical analysis and error analysis for the
Section 6 and
Section 7. The concluding remarks are provided in
Section 7.
8. End of Second Wave Validity Checking
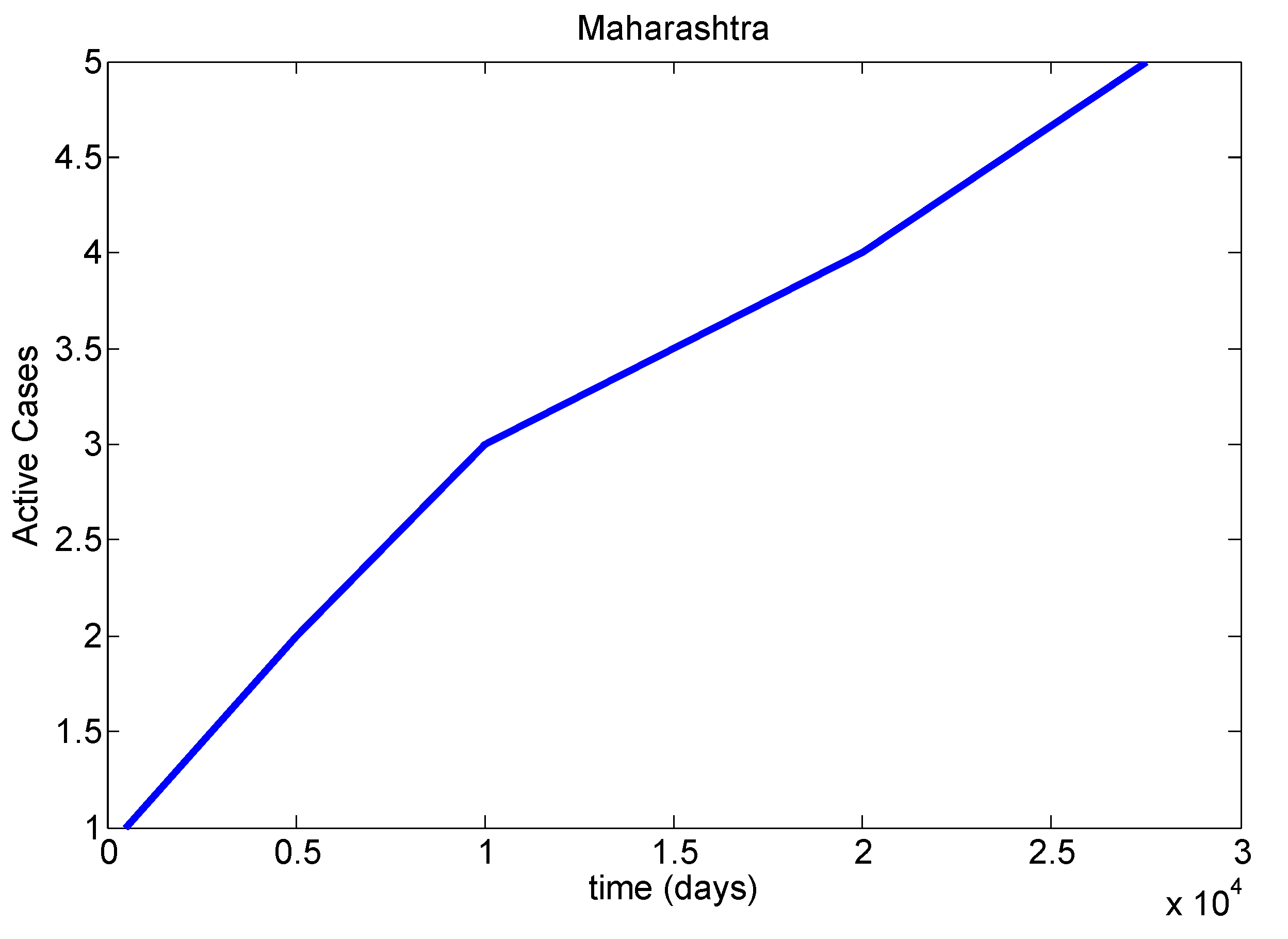
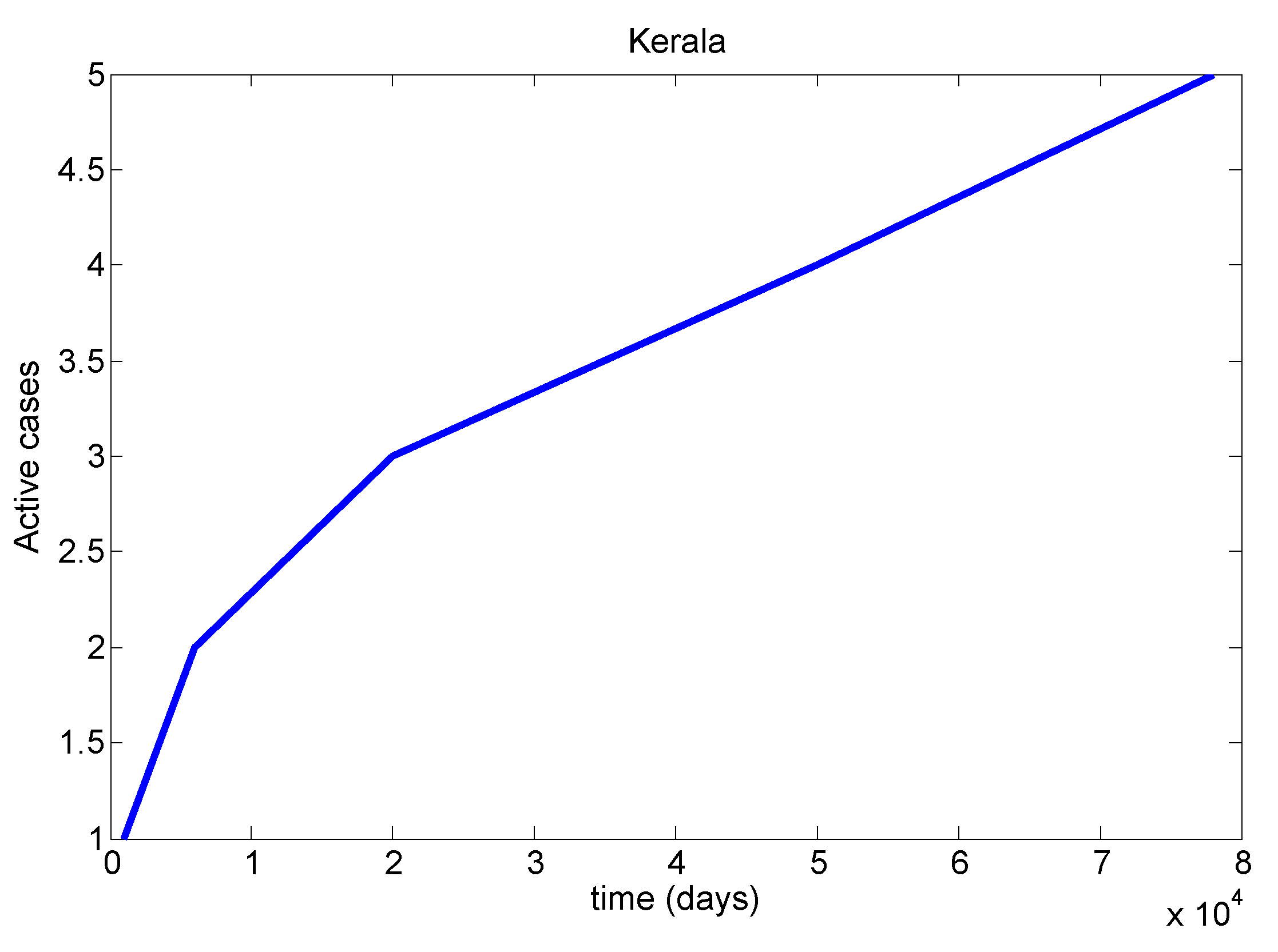
In this section, we discussed five affected states (Maharashtra, Kerala, Karnataka, Tamil Nadu, Andra Pradesh) in India. The four important parameter values (confirmed, active, recovered, deceased) are given in
Table 5.
Table 6 shows an initial values of the parameters in the states of Maharashtra, Kerala, Karnataka, Tamil Nadu and Andhra Pradesh. We have discussed the Omicron number of cases and initial values (See
Table 7 and
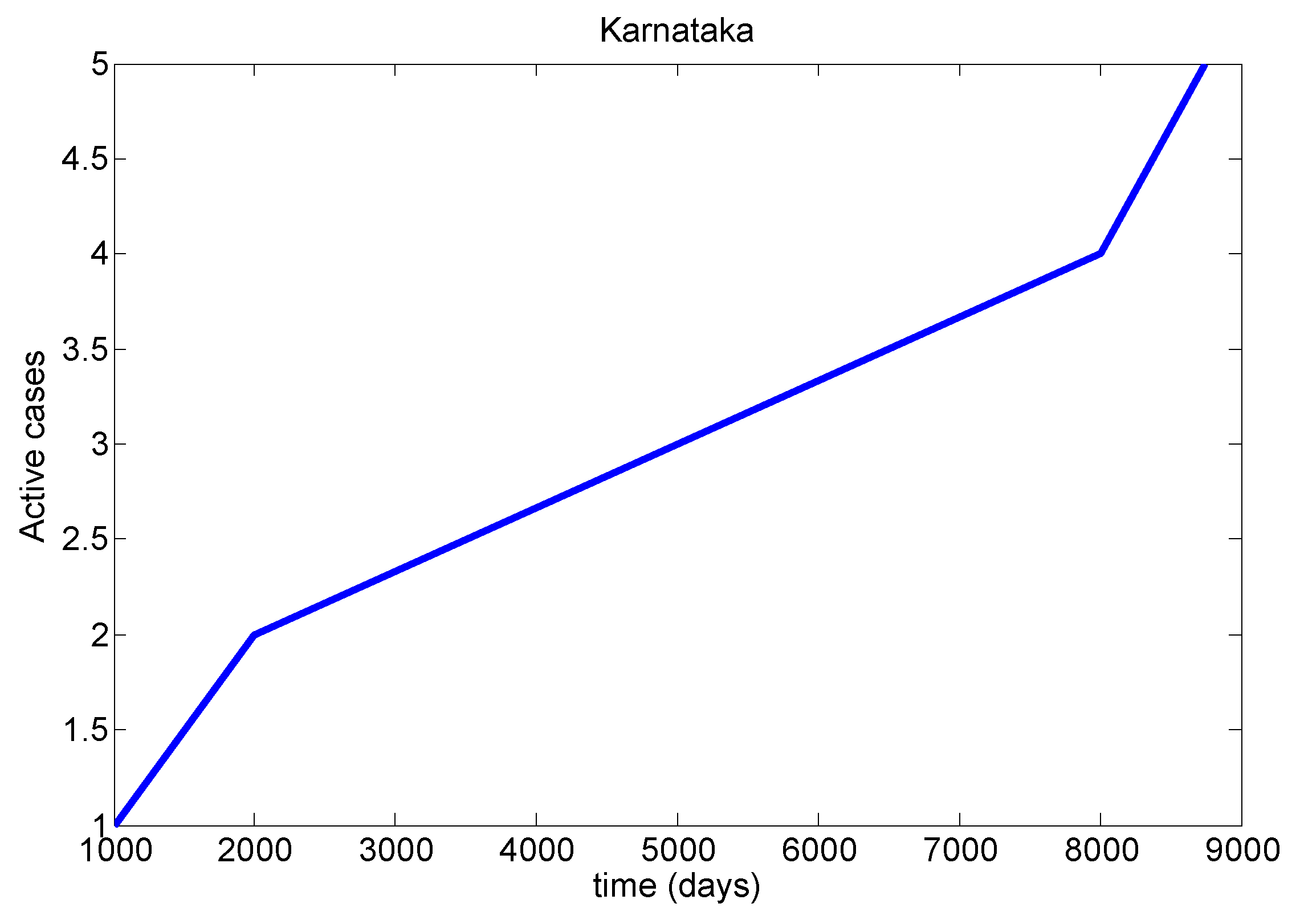
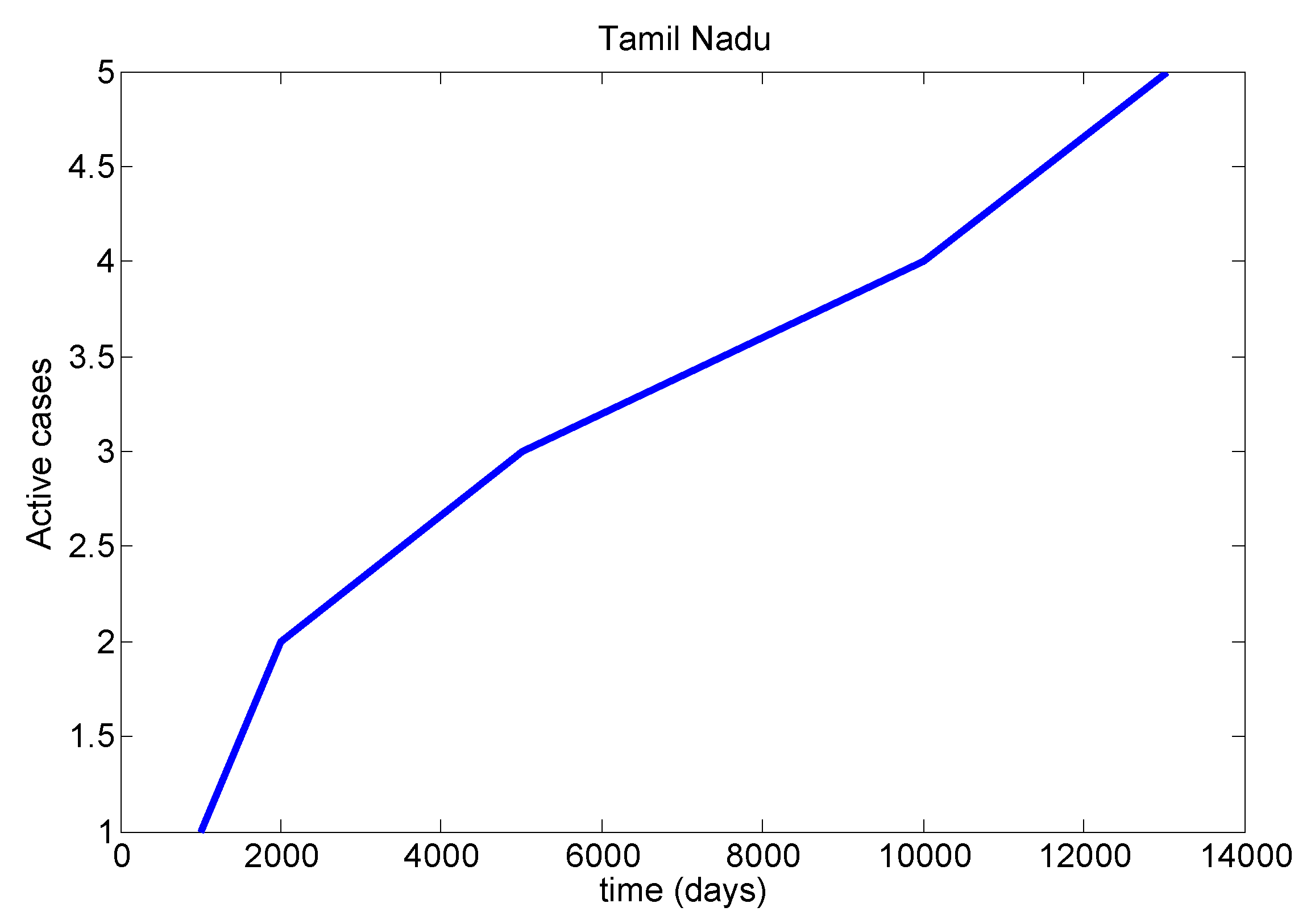
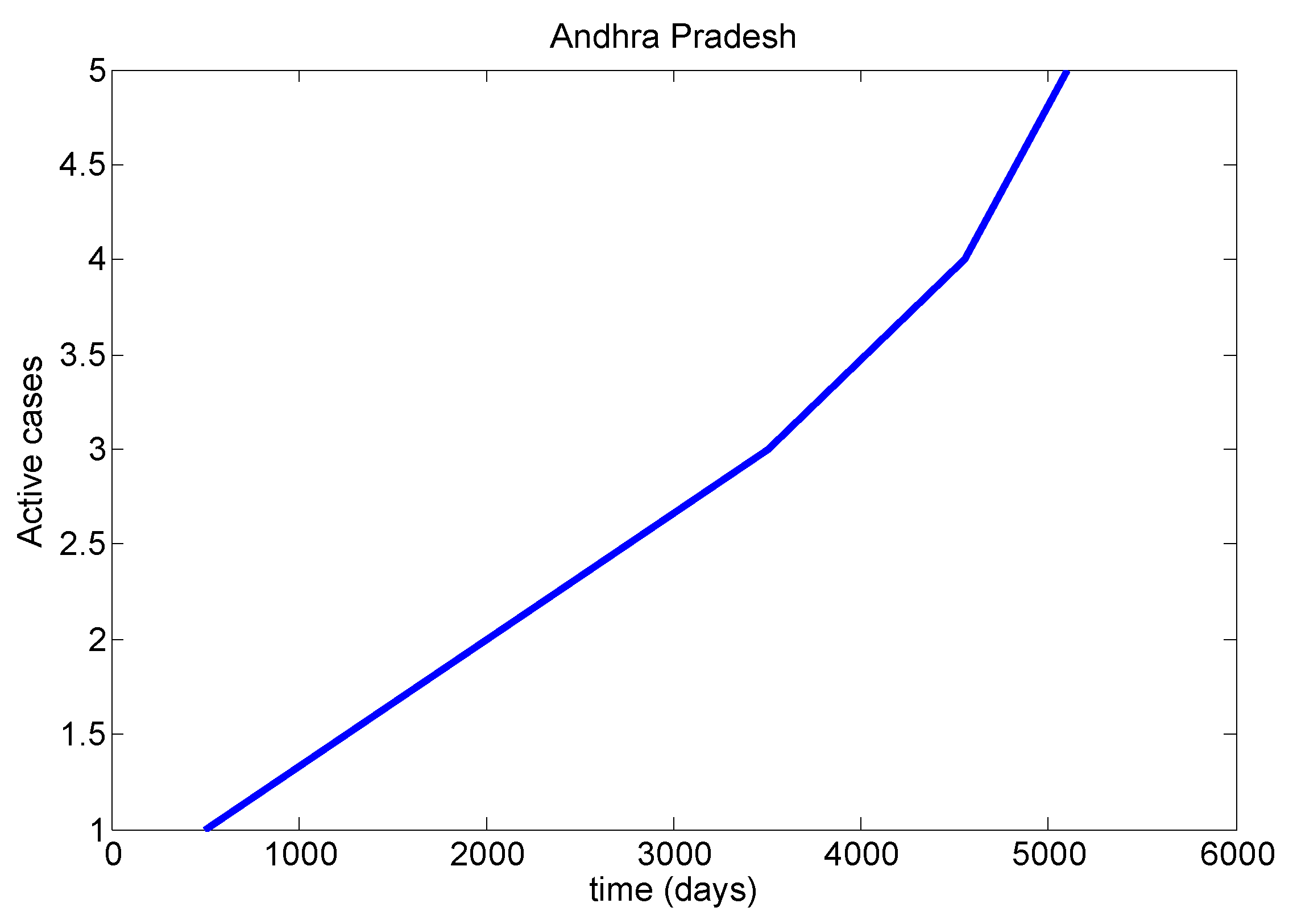
Table 8). We mainly discussed one parameter for active cases in Maharashtra, Kerala, Karnataka, Tamil Nadu and Andhra Pradesh. We have drawn a diagram for all states at active cases (see
Figure 7,
Figure 8,
Figure 9,
Figure 10 and
Figure 11). It has given guidelines for international arrivals from January 2022. It is mandatory for self declaration form and RT-PCR test. This approach is given by algorithmic model [
38]. If it is negative, home quarantine for one week. If suppose positive, we can send for genomic test and provide isolation facility. It used for proposed model validation from real life data and this case approximately equal to the proposed mathematical model. So this model helps for our future prediction from current data.
We have verified real life data for five highly affected states with other states in India. There are several authors published research articles based on the COVID-19 data details taken from their own countries. It is important to say that still there is no common COVID-19 equation to be utilized in Indian pandemic and to eradicate this disease. Right now, there is no common COVID-19 equation in Indian pandemic. Therefore, we propose a Common Indian COVID-19 Equation which can predict the infection rate and give the control strategies of spread. The aim of the paper is to find out a new model that is common to the Indian COVID-19 pandemic. This model remains the same in India but the parameter values and data will be different based on the present COVID-19 pandemic reports. The required data of COVID-19 will be collected from the WHO (World Health Organization) & Ministry of Health and Family Welfare (MoHFW) up to till date. The nonlinear least square algorithm will be used for getting values to calculate all parameters of the developing model. In our model there is no assumed data. When the data collection and parameter estimation is completed, we have to analyze the stability analysis, analytical solutions, numerical solutions, error analysis and statistical approach. Finally, the statistical approach is compared to real life data to check the validity of the theoretical outcome of new COVID-19 equations. As per the proposed plan, it is assumed that the infection rate of COVID-19 will be decreased very soon, based on government control policy. The proposed model is very useful for the current Indian pandemic to predict the future spread and control strategies with great impact. In the current situation, the infected cases of COVID-19 get changed daily. Our model is valid only for the fixed population. We fix the required time in days. Parameter estimation is done by collecting the data up to date. There are two important cases to find the new parameter values for their own countries. The first case is existence of unique solution of all parameters or important parameters. Another case is the individual’s rate of values in unknown parameters. In particular, COVID-19 equations have lot of parameters in current pandemic situation. Few parameter values are exactly and others may be in approximate solutions. It is very difficult to get the unique solutions for all parameters. Dynamic models have to be developed on related identification property. In this paper, our aim is to find out the common model. We believe that this model works well and will be useful for the Indian people. Based on the data, the model will be changed the susceptible cases, exposed cases, Infective cases, Recovery cases, etc., (SIR, SEIR, SEIRS, etc.). Finally, our model compares to COVID-19 data and validates the outcome system. The proposed model helps the Indian government and other researchers with COVID-19. In the third wave, it sweeps positive surges to 15%. The spread of the third wave is fast and be careful to this current situation.