Spreading of Infections on Network Models: Percolation Clusters and Random Trees
Abstract
:1. Introduction
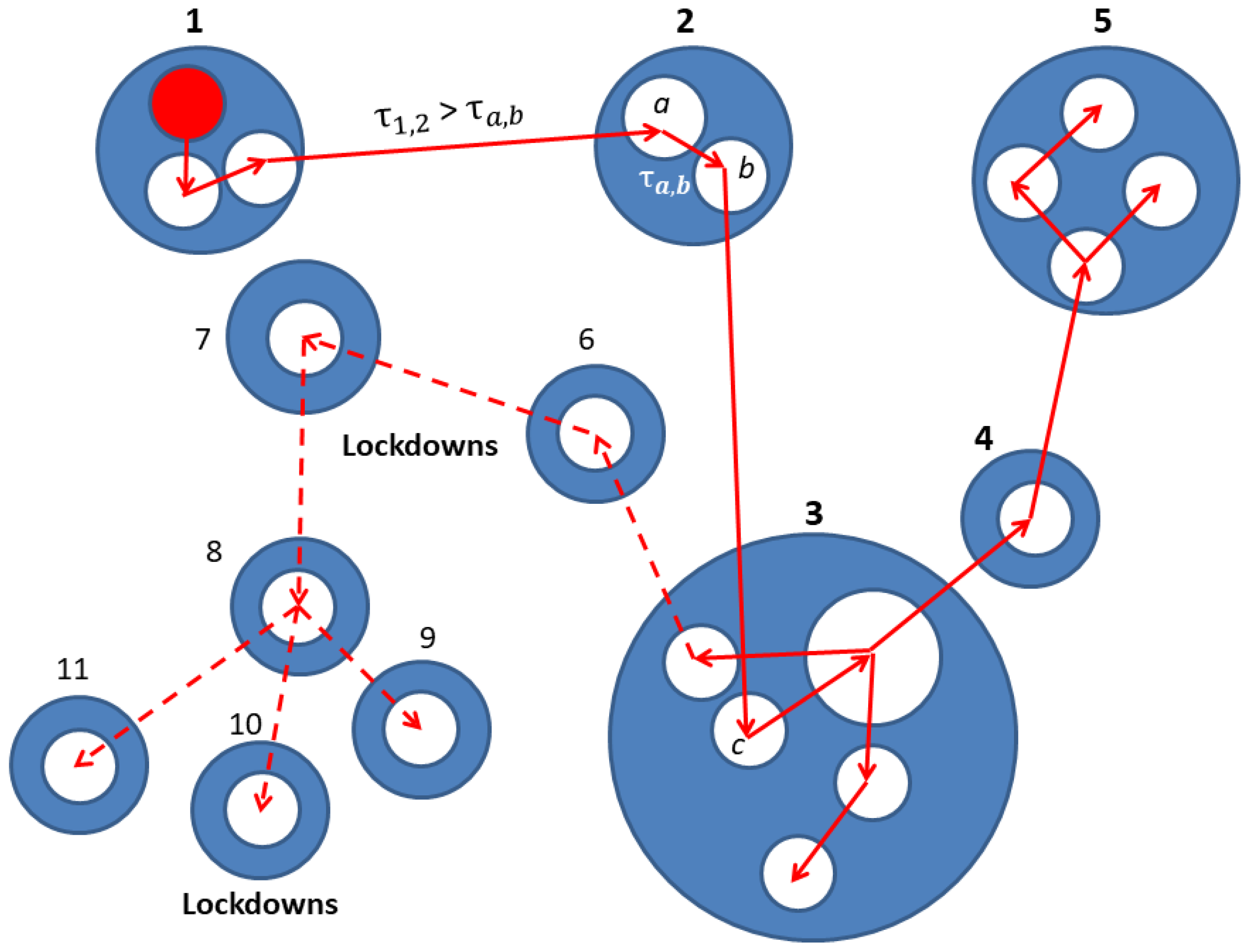
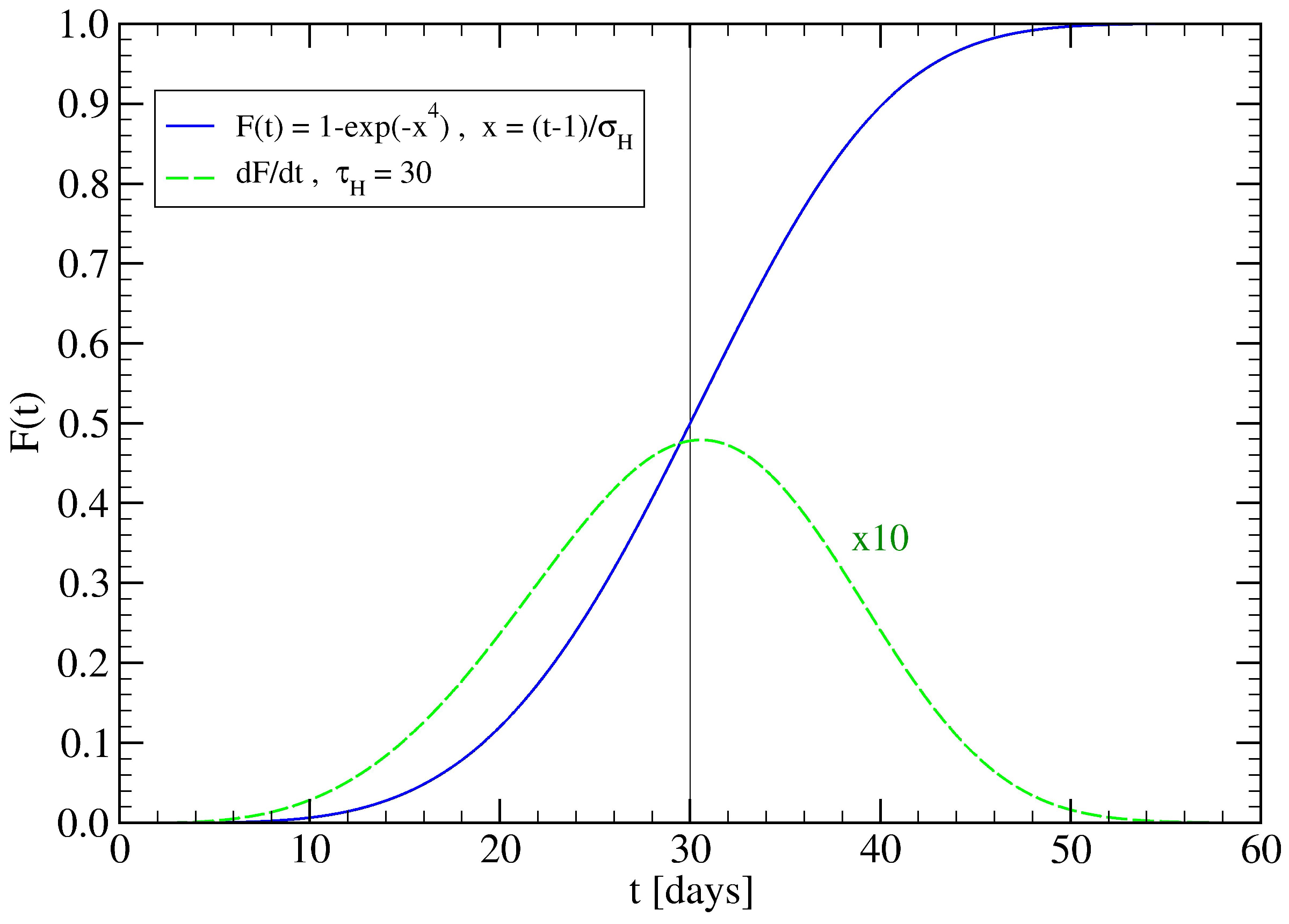
2. Network Model: A Hierarchical Structure of Transmission Times
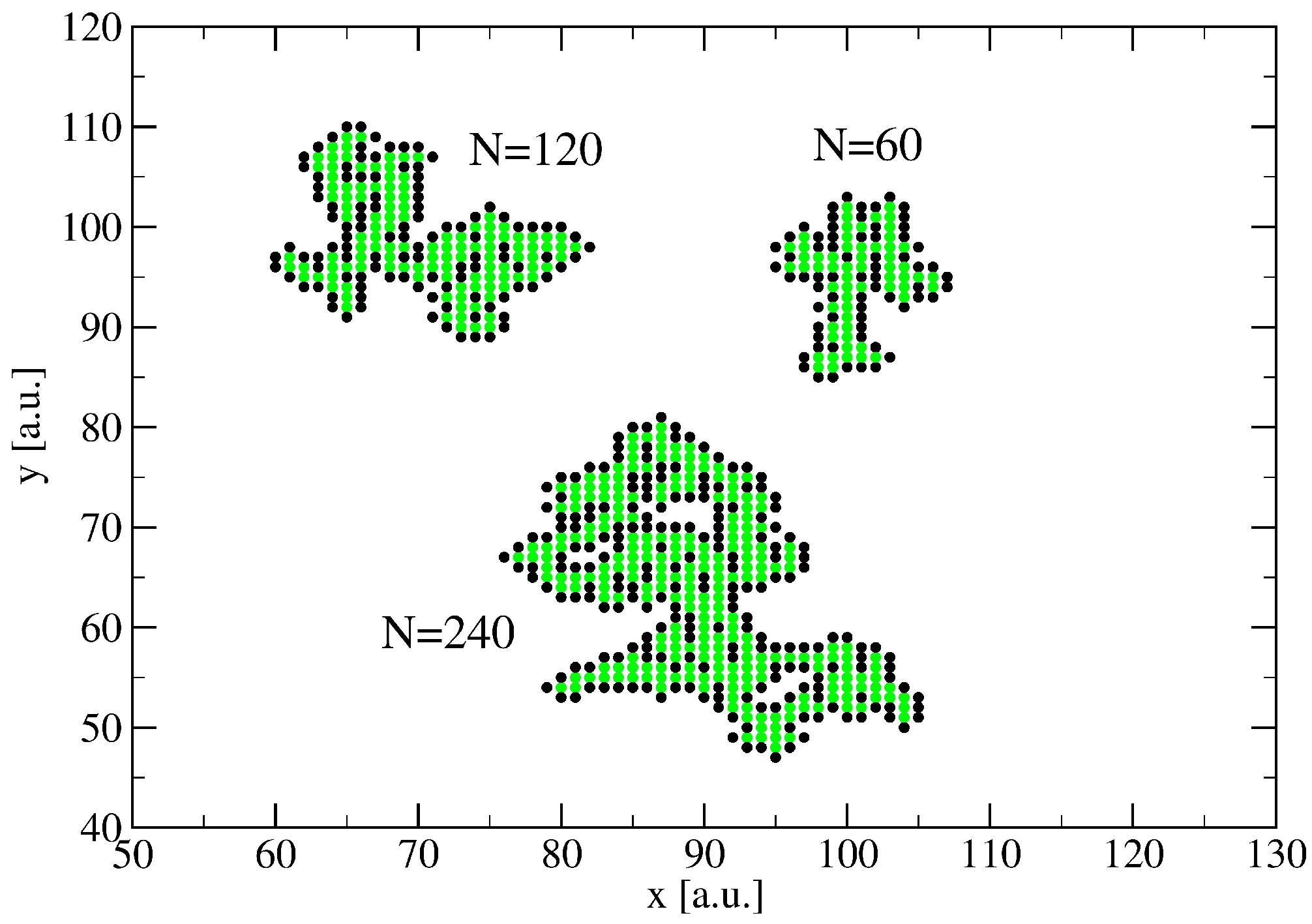
3. A Percolation Model for Minor Clusters: Cluster Sizes
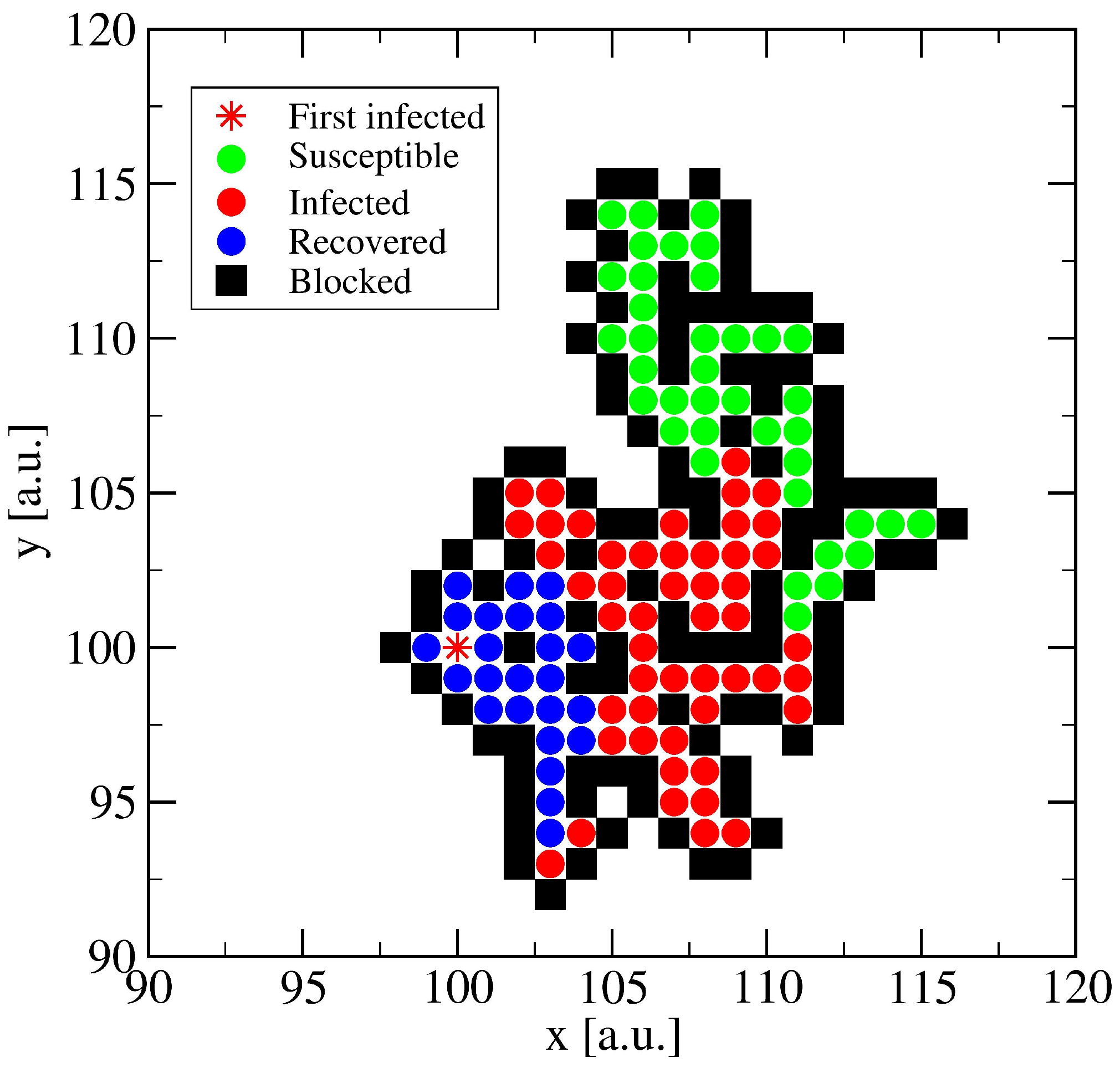
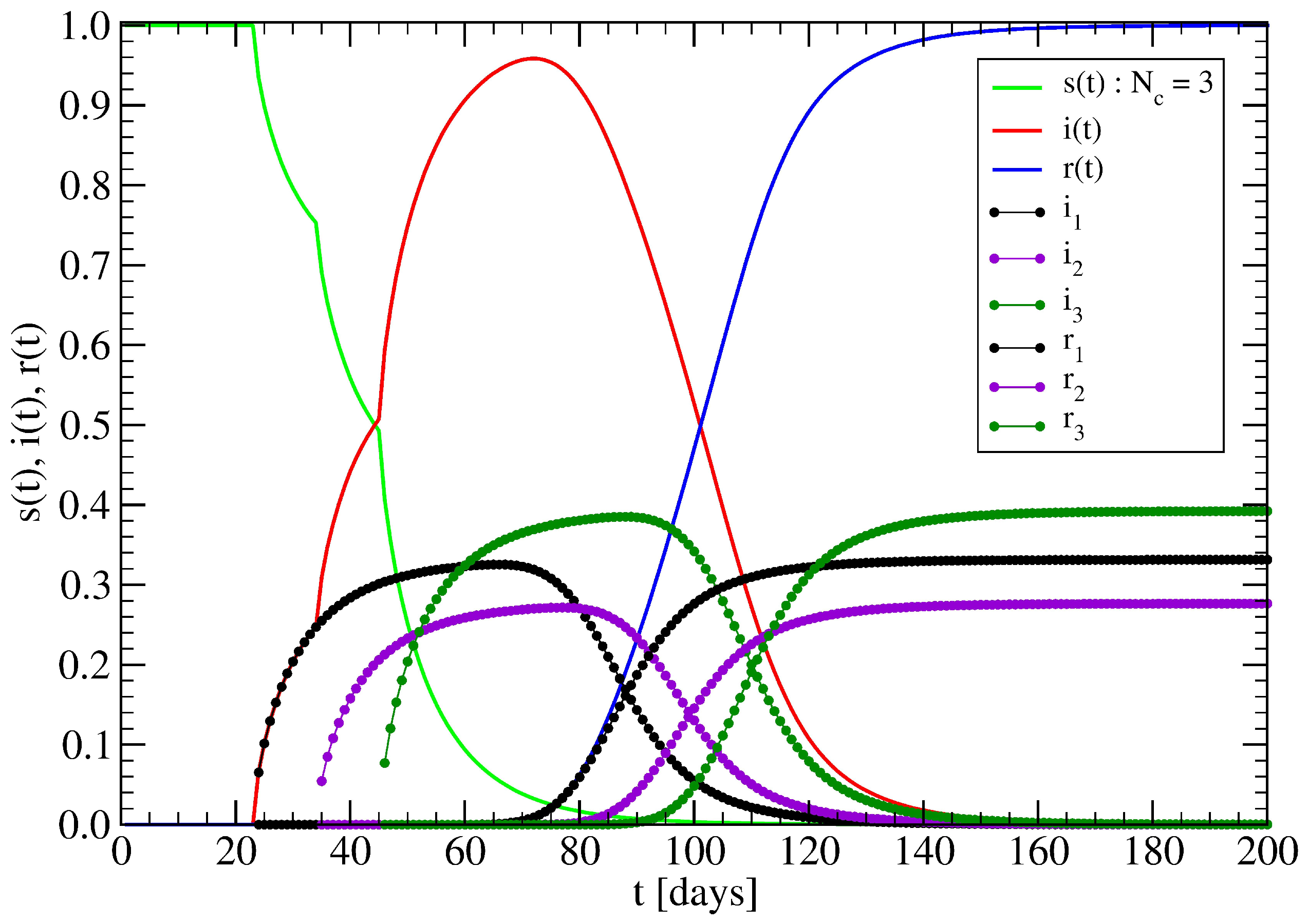
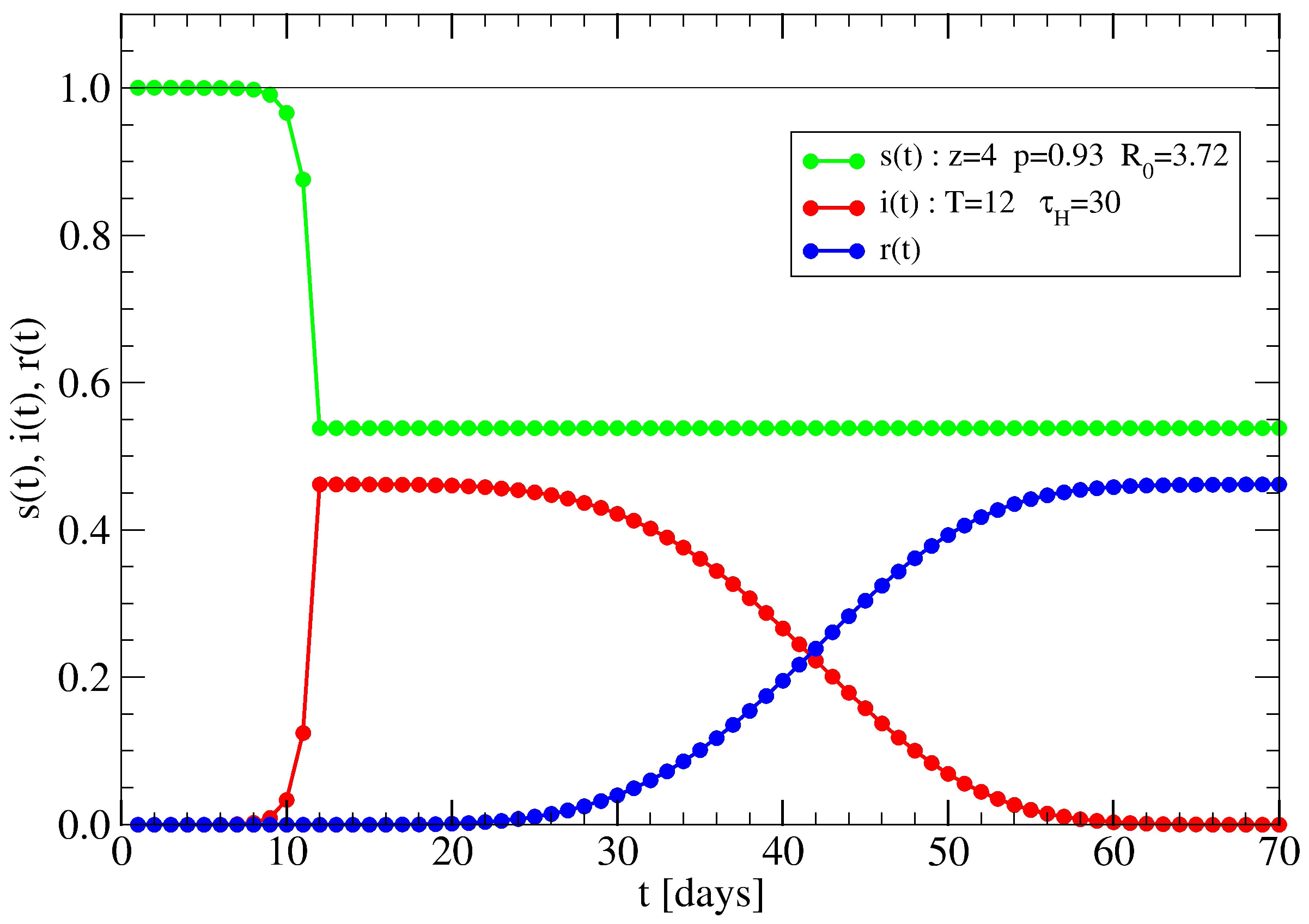
3.1. The Spreading Dynamics on a Minor Cluster
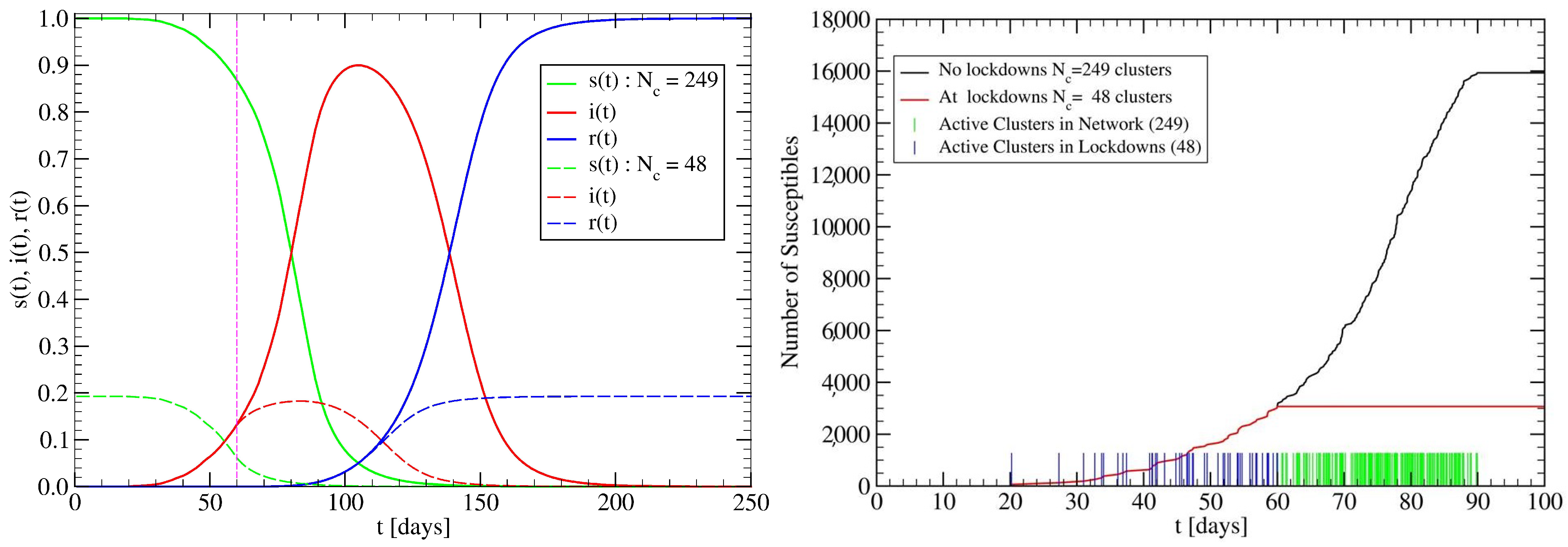
3.2. The Spreading Dynamics on a Network: Effects of Lockdowns
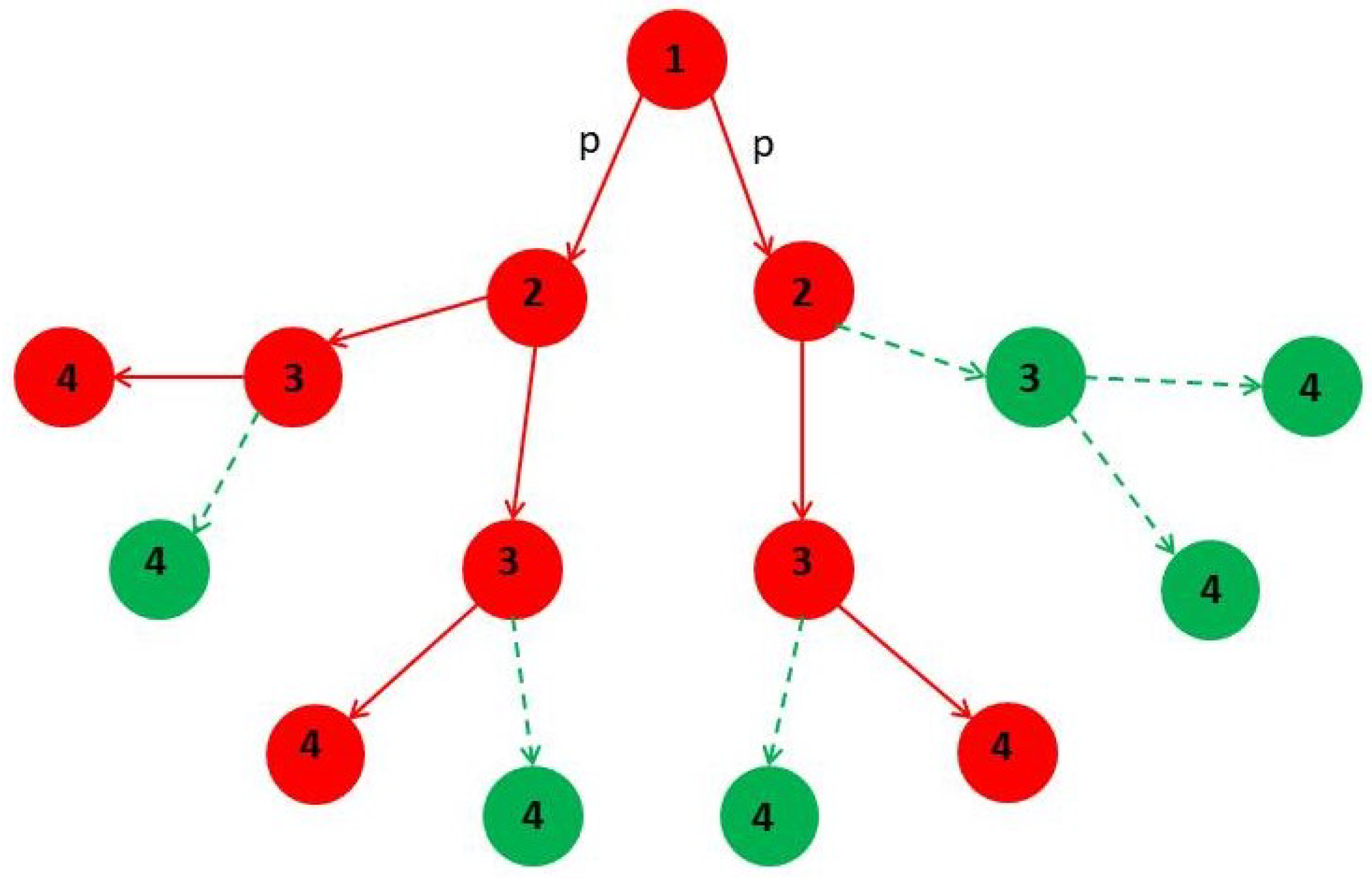
4. Minor Clusters Modeled as Random Trees
4.1. Effect of Healings Inside a Random Tree
4.2. Effect of Lockdowns Inside a Random Tree without Healings
- : In this case, , and using the asymptotic expansion, , for , yields , consistent with when and .
- : In this case, and , yielding , consistent with the stop of infection spreading at time .
4.3. Effect of Lockdowns Inside a Random Tree with Healings
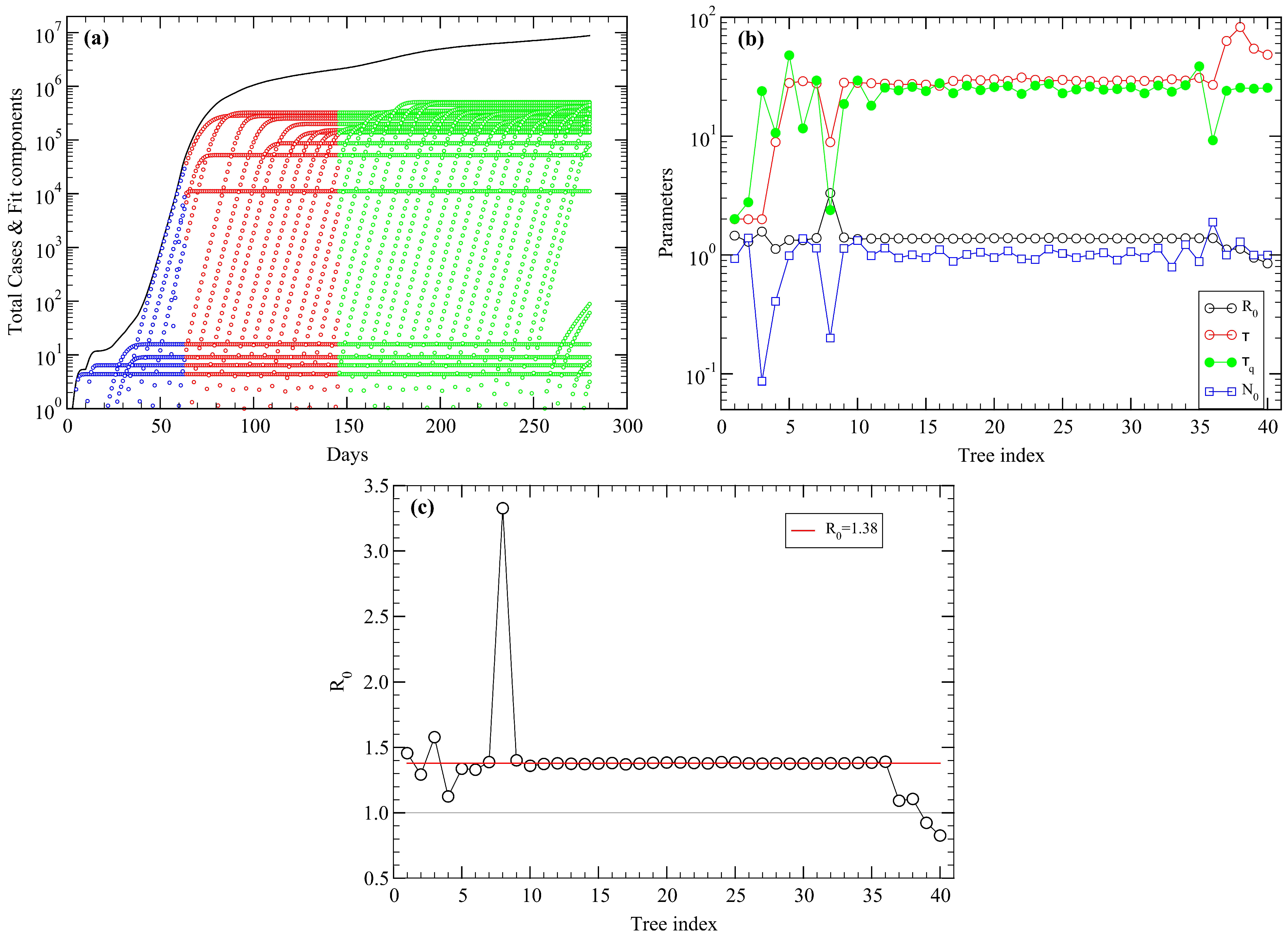
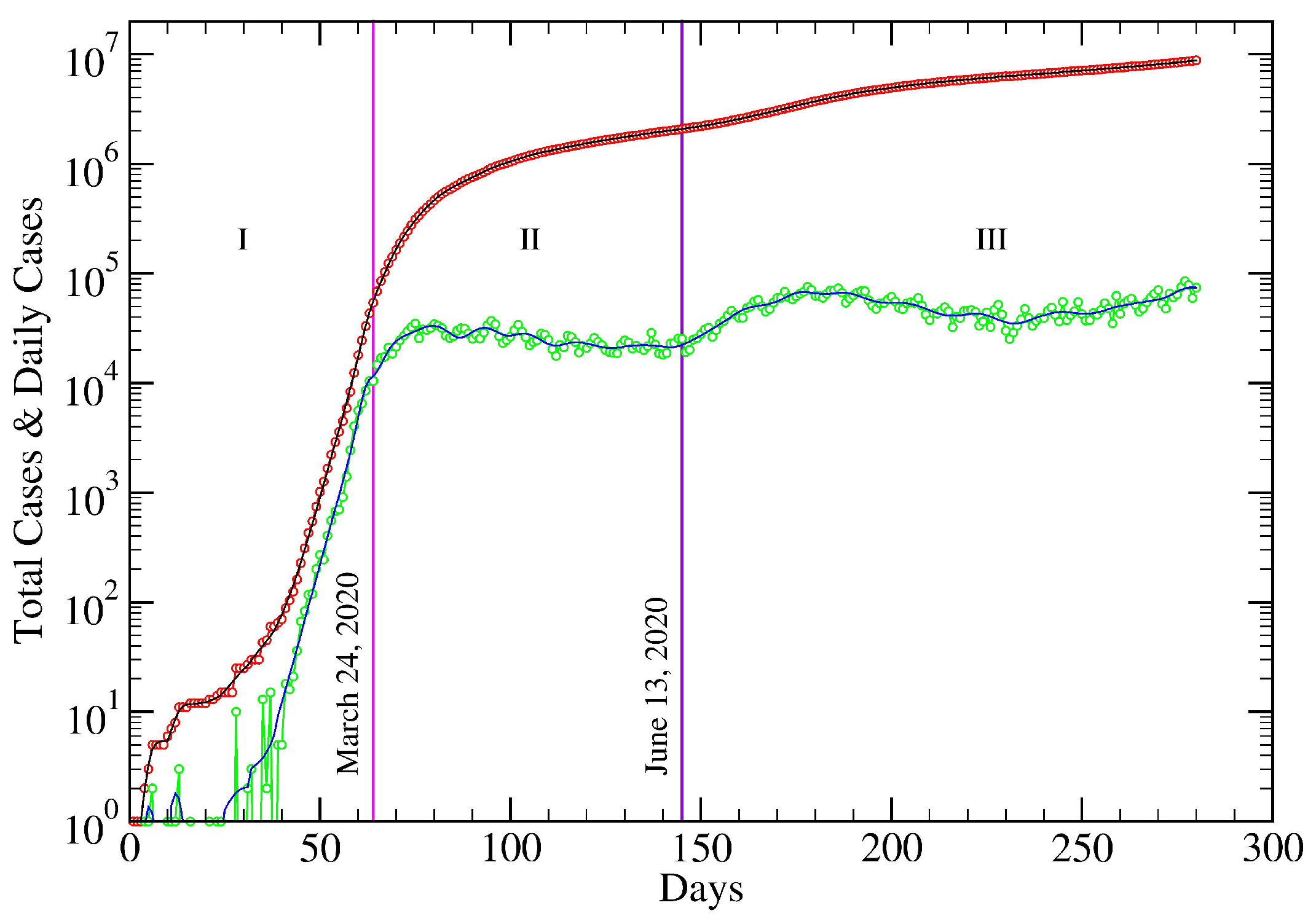
5. USA COVID-19 Data Revisited
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| NN | Nearest Neighbors. |
| SD | Standard Deviation. |
| SIR | Susceptibles, Infected, Recovered individuals. |
| Infecteds | Infected individuals (idiom). |
| Recovereds | Recovered individuals (idiom). |
Appendix A. Fitting Procedure
References
- Dong, E.; Du, H.; Gardner, L. An interactive web-based dashboard to track COVID-19 in real time. Lancet Infect. Dis. 2020, 20, 533–534. [Google Scholar] [CrossRef]
- Xu, Z.; Shi, L.; Wang, Y.; Zhang, J.; Huang, L.; Zhang, C.; Liu, S.; Zhao, P.; Liu, H.; Zhu, L.; et al. Pathological findings of COVID-19 associated with acute respiratory distress syndrome. Lancet Respir. Med. 2020, 8, 420–422. [Google Scholar] [CrossRef]
- Fernández-Villaverde, J.; Jones, C.I. Estimating and Simulating a SIRD Model of COVID-19 for Many Countries, States, and Cities. Natl. Bur. Econ. Res. Work. Pap. Ser. 2020, 27, 128. [Google Scholar]
- Chen, Y.C.; Lu, P.E.; Chang, C.S.; Liu, T.H. A Time-dependent SIR model for COVID-19 with Undetectable Infected Persons. IEEE Trans. Netw. Sci. Eng. 2020, 7, 3279–3294. [Google Scholar] [CrossRef]
- Wu, J.T.; Leung, K.; Bushman, M.; Kishore, N.; Niehus, R.; de Salazar, P.M.; Cowling, B.J.; Lipsitch, M.; Leung, G.M. Estimating clinical severity of COVID-19 from the transmission dynamics in Wuhan, China. Nat. Med. 2020, 26, 506–510. [Google Scholar] [CrossRef] [Green Version]
- Yang, Z.; Zeng, Z.; Wang, K.; Wong, S.S.; Liang, W.; Zanin, M.; Liu, P.; Cao, X.; Gao, Z.; Mai, Z.; et al. Modified SEIR and AI prediction of the epidemics trend of covid-19 in China under public health interventions. J. Thorac. Dis. 2020, 12, 165. [Google Scholar] [CrossRef]
- Chinazzi, M.; Davis, J.T.; Ajelli, M.; Gioannini, C.; Litvinova, M.; Merler, S.; Piontti, A.P.; Mu, K.; Rossi, L.; Sun, K.; et al. The effect of travel restrictions on the spread of the 2019 novel coronavirus (COVID-19) outbreak. Science 2020, 368, 395–400. [Google Scholar] [CrossRef] [Green Version]
- Palladino, A.; Nardelli, V.; Atzeni, L.G.; Cantatore, N.; Cataldo, M.; Croccolo, F.; Estrada, N.; Tombolini, A. Modelling the spread of Covid19 in Italy using a revised version of the SIR model. arXiv 2020, arXiv:2005.08724. [Google Scholar]
- Croccolo, F.; Roman, H.E. Spreading of infections on random graphs: A percolation-type model for COVID-19. Chaos Solitons Fractals 2020, 139, 110077. [Google Scholar] [CrossRef]
- Kermack, W.O.; McKendrick, A.G. A Contribution to the Mathematical Theory of Epidemics. Proc. R. Soc. Lond. Ser. A 1927, 115, 700–721. [Google Scholar]
- Hethcote, H.W. The Mathematics of Infectious Diseases. SIAM Rev. 2000, 42, 599–653. [Google Scholar] [CrossRef] [Green Version]
- Chen, D. Modeling the spread of infectious diseases: A review. In Analyzing and Modeling Spatial and Temporal Dynamics of Infectious Diseases; Chen, D., Moulin, B., Wu, J., Eds.; John Wiley & Sons: Hoboken, NJ, USA, 2014; pp. 19–42. [Google Scholar]
- Bailey, N.T.J. The Mathematical Theory of Epidemics, 1st ed.; Charles Griffin & Company: London, UK, 1957. [Google Scholar]
- Anderson, R.M.; May, R.M. Infectious Diseases of Humans: Dynamics and Control; Oxford University Press: Oxford, UK, 1991; Volume 757. [Google Scholar]
- Fraser, C.; Riley, S.; Anderson, R.M.; Ferguson, N.M. Factors that make an infectious disease outbreak controllable. Proc. Natl. Acad. Sci. USA 2004, 101, 6146–6151. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Pellis, L.; Ball, F.; Trapman, P. Reproduction numbers for epidemic models with households and other social structures. I. Definition and calculation of R0. Math. Biosci. 2012, 235, 85–97. [Google Scholar] [CrossRef] [PubMed]
- Ben-Avraham, D.; Havlin, S. Diffusion and Reactions in Fractals and Disordered Systems; Cambridge University Press: Cambridge, UK, 2000. [Google Scholar]
- Bunde, A.; Havlin, S. Fractals and Disordered Systems; Springer Science & Business Media: Berlin/Heidelberg, Germany, 2012. [Google Scholar]
- Stauffer, D.; Aharony, A. Introduction to Percolation Theory; Taylor & Francis: London, UK, 2018. [Google Scholar]
- Matouk, A.E. Complex dynamics in susceptible-infected models for COVID-19 with multi-drug resistance. Chaos Solitons Fractals 2020, 140, 110257. [Google Scholar] [CrossRef] [PubMed]
- Moussaoui, A.; Zerga, E.H. Transmission dynamics of COVID-19 in Algeria: The impact of physical distancing and face masks. AIMS Public Health 2020, 7, 816. [Google Scholar] [CrossRef]
- Kasinathan, P.; Montoya, O.D.; Gil-González, W.; Arul, R.; Moovendan, M.; Dhivya, S.; Kanimozhi, R.; Angalaeswari, S. Application of soft computing techniques in the analysis of COVID-19: A Review. Eur. J. Mol. Clin. Med. 2020, 7, 2480–2503. [Google Scholar]
- Tuteja, G.S. Stability and Numerical Investigation of modified SEIR model with Vaccination and Life-long Immunity. Eur. J. Mol. Clin. Med. 2020, 7, 3034–3044. [Google Scholar]
- Manríquez, R.; Guerrero-Nancuante, C.; Martínez, F.; Taramasco, C. Spread of Epidemic Disease on Edge-weighted Graphs from a Database: A Case Study of COVID-19. Int. J. Environ. Res. Public Health 2021, 18, 4432. [Google Scholar] [CrossRef]
- Czypionka, T.; Greenhalgh, T.; Bassler, D.; Bryant, M.B. Masks and face coverings for the lay public: A narrative update. Ann. Intern. Med. 2021, 174, 511–520. [Google Scholar] [CrossRef]
- Frank, T.D. Simplicity From Complexity: On The Simple Amplitude Dynamics Underlying Covid-19 Outbreaks In China. Adv. Complex Syst. 2021, 23, 2050022. [Google Scholar] [CrossRef]
- Schlickeiser, R.; Kröger, M. Analytical solution of the SIR-model for the temporal evolution of epidemics: Part B. Semi-time case. J. Phys. A Math. Theor. 2021, 54, 175601. [Google Scholar] [CrossRef]
- Ramaswamy, H.; Oberai, A.A.; Yortsos, Y.C. A comprehensive spatial-temporal infection model. Chem. Eng. Sci. 2021, 233, 116347. [Google Scholar] [CrossRef] [PubMed]
- Hemmer, C.J.; Hufert, F.; Siewert, S.; Reisinger, E. Protection from COVID-19: The efficacy of face masks. Dtsch. Ärztebl. Int. 2021, 118, 59. [Google Scholar] [CrossRef] [PubMed]
- Dogan, O.; Tiwari, S.; Jabbar, M.A.; Guggari, S. A systematic review on AI/ML approaches against COVID-19 outbreak. Complex Intell. Syst. 2021, 7, 2655–2678. [Google Scholar] [CrossRef] [PubMed]
- Huang, B.; Yang, J.X.; Li, X. Identifying influential links to control spreading of epidemics. Phys. A Stat. Mech. Its Appl. 2021, 583, 126291. [Google Scholar] [CrossRef]
- Pavan Kumar, S.T.; Lahiri, B.; Alvarado, R. Multiple change point estimation of trends in Covid-19 infections and deaths in India as compared with WHO regions. Spat. Stat. 2021, 44, 100538. [Google Scholar]
- Buzea, C.G.; Eva, L.; Prelipceanu, M.; Cazacu, M.M.; Garofalide, S.; Agop, M. Coronavirus disease COVID-19 tracking the global outbreak. SEIR compartmental model applied to SARS-CoV-2 epidemic in Romania. In Biomedical Engineering Tools for Management for Patients with COVID-19; Elsevier: Amsterdam, The Netherlands, 2021; pp. 87–102. [Google Scholar]
- Kröger, M.; Schlickeiser, R. Verification of the accuracy of the SIR model in forecasting based on the improved SIR model with a constant ratio of recovery to infection rate by comparing with monitored second wave data. R. Soc. Open Sci. 2021, 8, 211379. [Google Scholar] [CrossRef]
- Gandzha, I.S.; Kliushnichenko, O.V.; Lukyanets, S.P. Modeling and controlling the spread of epidemic with various social and economic scenarios. Chaos Solitons Fractals 2021, 148, 111046. [Google Scholar] [CrossRef]
- Barthélemy, M.; Barrat, A.; Pastor-Satorras, R.; Vespignani, A. Dynamical patterns of epidemic outbreaks in complex heterogeneous networks. J. Theor. Biol. 2005, 235, 275–288. [Google Scholar] [CrossRef] [Green Version]
- Colizza, V.; Vespignani, A. Invasion Threshold in Heterogeneous Metapopulation Networks. Phys. Rev. Lett. 2007, 99, 148701. [Google Scholar] [CrossRef] [Green Version]
- Shao, Q.; Han, D. Epidemic spreading in metapopulation networks with heterogeneous mobility rates. Appl. Math. Comput. 2022, 412, 126559. [Google Scholar] [CrossRef]
- Kraemer, M.U.G.; Yang, C.H.; Gutierrez, B.; Wu, C.H.; Klein, B.; Pigott, D.M.; Open COVID-19 Data Working Group; du Plessis, L.; Faria, N.R.; Li, R.; et al. The effect of human mobility and control measures on the COVID-19 epidemic in China. Science 2020, 368, 493–497. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Ordemann, A.; Roman, H.E.; Bunde, A. Cluster growth at the percolation threshold with a finite lifetime of growth sites. Phys. A Stat. Mech. Appl. 1999, 266, 92–95. [Google Scholar] [CrossRef]
- Roman, H.E. Diffusion in three-dimensional random systems at their percolation thresholds. J. Stat. Phys. 1990, 58, 375–382. [Google Scholar] [CrossRef]
- Bollobás, B. Modern Graph Theory; Springer Science & Business Media: Berlin/Heidelberg, Germany, 2013; Volume 184. [Google Scholar]






| N | () | N | () | ||||
|---|---|---|---|---|---|---|---|
| 64 | 1 | 1.40 (0.58) | 44.9 | All | 1 | 1.42 (0.55) | 46.6 |
| 64 | 4 | 1.40 (0.58) | 44.9 | All | 4 | 1.42 (0.55) | 46.6 |
| 64 | 10 | 1.40 (0.57) | 44.5 | All | 10 | 1.41 (0.54) | 45.6 |
| 64 | 30 | 1.35 (0.52) | 19.9 | All | 30 | 1.34 (0.47) | 16.1 |
| 64 | 40 | 1.30 (0.46) | 11.7 | All | 40 | 1.27 (0.41) | 9.42 |
| 64 | 50 | 1.23 (0.39) | 7.64 | All | 50 | 1.20 (0.35) | 6.16 |
| 64 | 60 | 1.15 (0.34) | 5.31 | All | 60 | 1.12 (0.29) | 4.41 |
| 64 | 90 | 0.97 (0.21) | 2.66 | All | 90 | 0.92 (0.17) | 2.23 |
| z | Infection degree | |
| p | Transmission probability | |
| Reproduction number | ||
| N | Total population in cluster | |
| T | Cluster infection time | |
| Characteristic healing time | ||
| Width of | ||
| Lockdown starting time | ||
| Quarantine reaction time | ||
| Effective (lockdowns) | ||
| Reference reaction time |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Roman, H.E.; Croccolo, F. Spreading of Infections on Network Models: Percolation Clusters and Random Trees. Mathematics 2021, 9, 3054. https://doi.org/10.3390/math9233054
Roman HE, Croccolo F. Spreading of Infections on Network Models: Percolation Clusters and Random Trees. Mathematics. 2021; 9(23):3054. https://doi.org/10.3390/math9233054
Chicago/Turabian StyleRoman, Hector Eduardo, and Fabrizio Croccolo. 2021. "Spreading of Infections on Network Models: Percolation Clusters and Random Trees" Mathematics 9, no. 23: 3054. https://doi.org/10.3390/math9233054
APA StyleRoman, H. E., & Croccolo, F. (2021). Spreading of Infections on Network Models: Percolation Clusters and Random Trees. Mathematics, 9(23), 3054. https://doi.org/10.3390/math9233054







