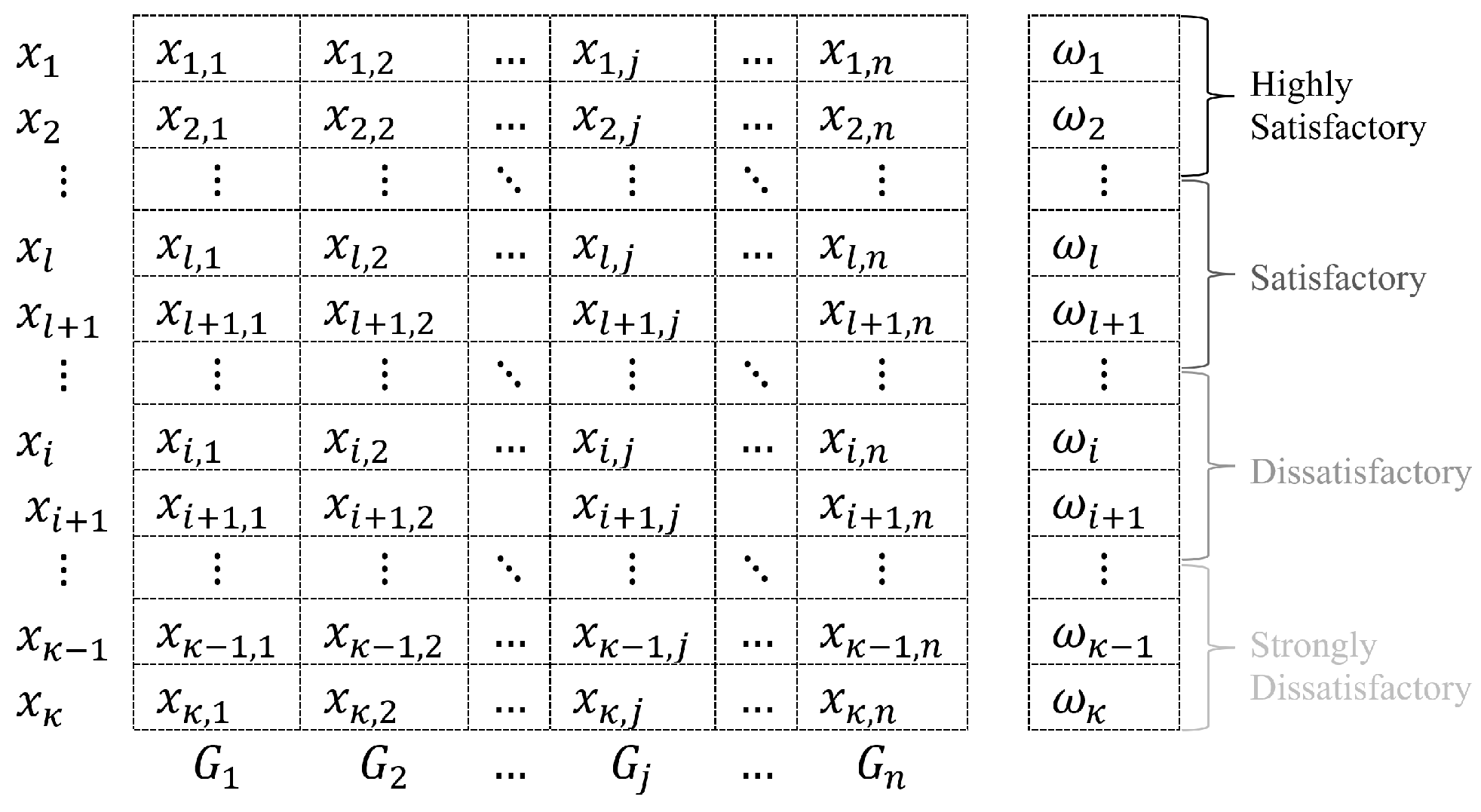Hybridisation of Swarm Intelligence Algorithms with Multi-Criteria Ordinal Classification: A Strategy to Address Many-Objective Optimisation

Abstract

This paper introduces a strategy to enrich swarm intelligence algorithms with the preferences of the Decision Maker (DM) represented in an ordinal classifier based on interval outranking. Ordinal classification is used to bias the search toward the Region of Interest (RoI), the privileged zone of the Pareto frontier containing the most satisfactory solutions according to the DM’s preferences. We applied this hybridising strategy to two swarm intelligence algorithms, i.e., Multi-objective Grey Wolf Optimisation and Indicator-based Multi-objective Ant Colony Optimisation for continuous domains. The resulting hybrid algorithms were called GWO-InClass and ACO-InClass. To validate our strategy, we conducted experiments on the DTLZ problems, the most widely studied test suit in the framework of multi-objective optimisation. According to the results, our approach is suitable when many objective functions are treated. GWO-InClass and ACO-InClass demonstrated the capacity of reaching the RoI better than the original metaheuristics that approximate the complete Pareto frontier.

1. Introduction

Organisations from different sectors and domains often face problems with multiple conflicting objectives to optimise. The scientific literature classifies these problems according to the number of objectives as Multi-objective Optimisation Problems (MOPs) for problems with 2–4 objectives and Many-objective Optimisation Problems (MaOPs) for problems with more than four objectives. Typically, MOPs and MaOPs are addressed through the so-called a posteriori approach, which consists of the following two phases:

• A set of efficient solutions is approximated (the Pareto optimal set).
• The Decision Maker (DM) has to choose the best compromise: the solution that best matches their preferences.

Metaheuristic algorithms are promising alternatives to address Phase 1. Multi-objective Evolutionary Algorithms (MOEAs) and Multi-objective Swarm Intelligence Algorithms (MOSIAs) are quite popular because their application does not demand particular mathematical properties on the objective functions, the geometry of the Pareto frontier or the constraints of the problem [1,2,3].

Even though MOEAs and MOSIAs have been widely used in addressing MOPs, most of them cannot adequately approximate the Pareto frontier for MaOPS. They have to cope with severe difficulties as the number of objectives increases; remarkably, the number of dominance resistant solutions, the high cost to ensure diversity, and the low effectiveness of the genetic operators. Studies on the difficulties and challenges found by MOEAs in addressing MaOPs are discussed by Bechikh et al. [4], López Jaimes and Coello Coello [5], Sudeng and Wattanapongsakorn [6], and Ikeda et al. [7]. One of the main criticisms of the a posteriori approaches is that they require reaching a sufficiently representative approximation of the complete Pareto front before the multi-criteria decision making.

Even supposing a good approximation of the Pareto frontier, the DM has to solve a multi-criteria selection problem in this set to address Phase 2. An alternative is to make a heuristic selection; the DM is supposed to consistently compare solutions on the approximated Pareto frontier until the best compromise is identified. This task is likely to become pretty hard and impractical in problems with many objective functions because of the human mind cognitive limitations (as stated by Miller [8]). Another alternative is to apply a Multi-Criteria Decision Analysis (MCDA) method that articulates the preferences of the DM. Again, this approach assumes that the solution set effectively contains the most preferred solutions, which is questionable under the presence of many objective functions.

As a consequence of the above discussion, there has been an increasing interest in combining MOEAs and MCDA methods in recent years. One way is to consider the preferences to bias the search toward the Region of Interest (RoI). The RoI is the region of the Pareto frontier with the solutions that best match the DM’s preferences; accordingly, the best compromise is a solution belonging to the RoI.

The preference incorporation requires considering non-trivial aspects such as defining the model of the DM’s preferences, characterising the RoI, and determining the relevance of the solutions [9]. Most methods for preference incorporation admit at least one of the following kinds of information on the preferences [10,11]: weights, e.g., [12]; ranking of solutions, e.g., [13]; ranking of objective functions, e.g., [14]; reference points, e.g., [15]; trade-offs between objective functions, e.g., [16]; desirability thresholds, e.g., [17]; solution classification, e.g., [18]; and pairwise comparisons based on preference relations, e.g., [19,20].

The two alternatives to incorporate the above strategies are the interactive approach and the a priori approach, and both have advantages over the a posteriori one. On the one hand, better solutions are found because there is an increment in the selective pressure toward the RoI [21]. On the other hand, preference incorporation can alleviate the DM’s cognitive effort to select the best compromise because the number of candidate solutions is relatively short. Still, the interactive approaches are strongly criticised because they require preference relations with full comparability and transitivity (as the dimensionality increases, these properties become unlikely) [22]. Contrastingly, the a priori preference incorporation does not mandatorily require such properties. However, it demands a model that reflects the DM’s preferences about the solutions.

In many real-world MaOPs, the models should support imprecision and vagueness in the DM’s preferences. For instance, if the DM is a heterogeneous group (e.g., a board of directors) or an ill-defined entity (e.g., a community in social networks). In those circumstances, the task of eliciting the parameters of a preference model is highly difficult and is only reachable with some level of imprecision. If such imperfect knowledge is not considered, the best compromise could hardly be identified among the existing alternatives. Interval mathematics is a straightforward but effective way to express imprecision [23].

Fernandez et al. [24] introduced an extension of the outranking method by incorporating interval numbers in the preference parameters. This MCDA method can handle incomparability, veto situations, and non-transitive preferences. These properties become critical to address real-world MaOPs because many DMs have non-transitive and non-compensatory preferences. Additionally, the DM feels more comfortable eliciting the values of the parameters as interval numbers than as precise values. If the DM cannot (or not want to) directly give a value for some required parameters, they may use an indirect elicitation method to infer them, e.g., [25].

In light of the above discussions, this paper presents a further analysis to observe how incorporating interval outranking in MOSIAs impacts the performance. We propose embedding multi-criteria ordinal classification based on interval outranking (strictly speaking, the INTERCLASS-nC method [26]) into many-objective optimisation algorithms. Similar to previous approaches based on ordinal classification, e.g., [11], our proposal also requires representative samples of solutions classified by the DM as ‘Satisfactory’ or ‘Dissatisfactory’. However, we extended this notion with two artificial classes (for internal use of the algorithms) that increase the selective pressure toward the RoI. By applying this strategy, we introduce the a priori versions of two relevant a posteriori algorithms based on swarm intelligence; specifically, Multi-objective Grey Wolf Optimisation (MOGWO) [27] and Indicator-based Multi-objective Ant Colony Optimisation for continuous domains (${\mathrm{iMOACO}}_{\mathbb{R}}$) [28]. The a priori preference incorporation significantly increased the performance of the MOSIAs according to a non-parametric test (Mann–Whitney–Wilcoxon).

The remainder of this paper is organised as follows. Section 2 includes some preliminaries on multi-objective optimisation, interval outranking, ordinal classification, and the MOSIAs taken as baseline. Section 3 details the proposed algorithms with preference incorporation. Section 4 shows the experimental results. Lastly, Section 5 discusses the conclusions and provides some directions for future research.

2. Background

This section presents an overview of the theoretical foundations. Section 2.1 presents some preliminaries on optimisation with multiple objectives. Section 2.2 briefly describes the baseline versions of the MOSIAs used in this paper. Lastly, Section 2.3 presents the model for multi-criteria ordinal classification based on interval outranking.

2.1. Preliminaries on Multi-Objective Optimisation

Optimisation refers to finding the values in the decision variables (independent variables) that provoke extreme values of one or more objective functions (dependent variables). It is called ‘mono-objective’ optimisation if a single function is treated. In contrast, it is called ‘multi-objective’ optimisation if a few objective functions are treated (typically, up to four). Farina and Amato [29] recognised that most MOEAs are severely affected when they address problems with more than four objective functions, named them ‘many-objective’ optimisation problems.

Real-world applications often involve optimising several functions that are essentially conflicting [30]. As a consequence, no point is simultaneously optimal in all objective functions.

Here, $x=〈x_1,x_2,x_3,\dots ,x_n〉$ represents a solution of a MOP/MaOP: a vector of decision variables that optimises a vector function $f\left(x\right)$ whose components represent the values of the objectives. Equation (1) defines $f\left(x\right)$, where m is the number of objectives (dimensionality of the problem), and n is the number of decision variables. Applied optimisation models usually add constraints to Equation (1) to reflect real situations.

$$f\left(x\right)=〈f_1\left(x\right),f_2\left(x\right),f_3\left(x\right),\dots ,f_m\left(x\right)〉f_k:{\mathbb{R}}^n\to \mathbb{R}$$

(1)

Pareto dominance is widely accepted to compare two solutions, determining which of them is better. Thus, Pareto dominance discriminates between solutions by comparing their $f\left(x\right)$. Without loss of generality, let us consider minimising the m objectives; the Pareto dominance relation, represented by the symbol ≼, may be expressed as [31]

$$\begin{array}{cc}\hfill x\preccurlyeq y=\left\{\right(x,y):& f_k\left(x\right)⩽f_k\left(y\right)\forall k\in \{1,2,3,\dots ,m\}\wedge \hfill \\ \hfill & f_k\left(x\right)<f_k\left(y\right)\exists k\in \{1,2,3,\dots ,m\}\}.\hfill \end{array}$$

(2)

The non-dominated solutions make up the Pareto set, expressed as

$$PS=\left\{x\in R_F:y\preccurlyeq x\nexists y\in R_F\right\},$$

(3)

where $R_F$ is the feasible region.

The Pareto frontier, $PF=\left\{f\left(x\right):x\in PS\right\}$, is the image of the Pareto set. In the absence of information on the preferences of the DM, a sufficiently representative sample of the Pareto frontier should be calculated.

Identifying a set of Pareto efficient solutions is indeed necessary to solve MOPs and MaOPS. Still, it is not sufficient since the DM must select the best compromise (the solution to implement). The DM chooses the best compromise according to their personal preferences about the objective functions. In practice, the best compromise is the ultimate solution to the problem.

2.2. An Overview of Two Swarm Intelligence Algorithms to Address MaOPs

In this section, we provide a brief description of MOGWO [27] and ${\mathrm{iMOACO}}_{\mathbb{R}}$ [28].

2.2.1. Multi-Objective Grey Wolf Optimisation

Mirjalili et al. [27] proposed MOGWO—Multi-Objective Grey Wolf Optimiser—which extends the mono-objective algorithm Grey Wolf Optimiser (GWO) [32] to treat multiple objectives. This swarm intelligence algorithm is inspired by nature, specifically by the behaviour of grey wolves in tracking and hunting their prey. By analogy, the solution with the best value in the objective function is named the $\mathsf{\alpha }$ wolf. The second-best and the third-best solutions are named $\mathsf{\beta }$ and $\mathsf{\delta }$ wolves, respectively. The remaining solutions are known as Ω wolves. The leaders ($\mathsf{\alpha }$, $\mathsf{\beta }$, and $\mathsf{\delta }$) guide the optimisation process, and the Ω wolves follow the leaders in the search for the global optimum.

Let n be the number of decision variables, $\iota$ be the number of the current iteration, $x_i^{\iota }=〈x_{i,1}^{\iota },x_{i,2}^{\iota },x_{i,3}^{\iota },\dots ,x_{i,n}^{\iota }〉$ be the n-dimensional location point of the ith wolf during the $\iota$th iteration, and $x^{\iota }=〈x_1^{\iota },x_2^{\iota },x_3^{\iota },\dots ,x_{\hslash }^{\iota }〉$ be the positions of a pack with ℏ wolves. The following equation simulates how the Ω wolves are relocated to siege their prey during hunt following the social leadership:

$$x_i^{\iota +1}=\frac{{\mathfrak{x}}_1^{\iota }+{\mathfrak{x}}_2^{\iota }+{\mathfrak{x}}_3^{\iota }}{3}\forall i\in \{1,2,3,\dots ,\hslash \},$$

(4)

where ${\mathfrak{x}}_1^{\iota }$, ${\mathfrak{x}}_2^{\iota }$, and ${\mathfrak{x}}_3^{\iota }$ are n-dimensional vectors reflecting the influence of the three leader wolves during the $\iota$th iteration. Each component of them is calculated as

$${\mathfrak{x}}_{1,j}^{\iota }=x_{\mathsf{\alpha },j}-A_j·D_{\mathsf{\alpha },j}\forall j\in \{1,2,3,\dots ,n\},\mathrm{where}{D}_{\mathsf{\alpha },j}=\left|C_j·x_{\mathsf{\alpha },j}-x_{i,j}^{\iota }\right|,$$

(5)

$${\mathfrak{x}}_{2,j}^{\iota }=x_{\mathsf{\beta },j}-A_j·D_{\mathsf{\beta },j}\forall j\in \{1,2,3,\dots ,n\},\mathrm{where}{D}_{\mathsf{\beta },j}=\left|C_j·x_{\mathsf{\beta },j}-x_{i,j}^{\iota }\right|,$$

(6)

$${\mathfrak{x}}_{3,j}^{\iota }=x_{\mathsf{\delta },j}-A_j·D_{\mathsf{\delta },j}\forall j\in \{1,2,3,\dots ,n\},\mathrm{where}{D}_{\mathsf{\delta },j}=\left|C_j·x_{\mathsf{\delta },j}-x_{i,j}^{\iota }\right|.$$

(7)

In Equations (4)–(7), $x_{\mathsf{\alpha },j}$, $x_{\mathsf{\beta },j}$ and $x_{\mathsf{\delta },j}$ are the positions of the leader wolves at the jth coordinate, $\iota +1$ is the number of the next iteration, and A and $D_{\mathsf{\alpha }}$ are coefficient vectors modelling the encircling behaviour of wolves as

$$A_j=2a_j·r_{1,j}-a_j\forall j\in \{1,2,3,\dots ,n\},$$

(8)

and

$$D_{\mathsf{\alpha },j}=\left|C_j·x_{\mathsf{\alpha },j}-x_{i,j}^{\iota }\right|\forall j\in \{1,2,3,\dots ,n\},\mathrm{where}{C}_j=2·r_{2,j}.$$

(9)

In Equations (8) and (9), a is an n-dimensional vector whose elements linearly decrease from two to zero throughout the run of the algorithm, and $r_1$ and $r_2$ are random n-dimensional vectors with values in $[0,1]$. The components of $D_{\mathsf{\beta }}$ and $D_{\mathsf{\delta }}$ are similarly calculated as those of $D_{\mathsf{\alpha }}$ in Equation (9).

Exploration is promoted by A with values greater than one (or less than –1); with that setting, the Ω wolves diverge from the leaders. C is another component of GWO that favours exploration, whose components represent weights and are generated at random to emphasise ($C_j>1$) or de-emphasise ($C_j<1$) the influence of the $\mathsf{\alpha }$, $\mathsf{\beta }$ and $\mathsf{\delta }$ wolves in defining the distance in Equations (5)–(7). According to Mirjalili et al. [27], p. 109: “C is not linearly decreased in contrast to A. The C parameter was deliberately required to provide random values at all times in order to emphasise exploration not only during initial iterations but also final iterations”.

GWO exploits the search space if $|A_j|<1$ because, when the components of A are in $[-1,1]$, the position of the ith wolf in the next iteration will be located between its current position and the position of the leader. This setting assists Ω wolves to converge toward an estimated position of their prey, provided by $x_{\mathsf{\alpha }}$, $x_{\mathsf{\beta }}$ and $x_{\mathsf{\delta }}$.

GWO starts the optimisation process by generating solutions at random during the first population. Then, the three best solutions so far are considered as the $\mathsf{\alpha }$, $\mathsf{\beta }$ and $\mathsf{\delta }$ wolves. In the next iteration, each Ω wolf updates its position by applying Equations (4)–(7). Simultaneously, the components of a are linearly decreased in each iteration. Therefore, the pack of wolves tends to widely explore the search space during the first iterations and intensively exploit it during the last iterations. The algorithm stops when a maximum number of iterations is reached, and $x_{\mathsf{\alpha }}$ is returned as the best solution obtained throughout the optimisation process.

To treat MOPs via GWO, MOGWO integrates the following two extensions into GWO: (i) an archive with the Pareto optimal solutions obtained so far, and (ii) a criterion for picking the leaders ($x_{\mathsf{\alpha }}$, $x_{\mathsf{\beta }}$ and $x_{\mathsf{\delta }}$) from the archive.

If the archive is full of non-dominated solutions (note that there is a predefined size) and there is a new solution to be entered; then, a grid technique determines the region in the Pareto frontier that is the most crowded by the archive. A solution is removed from this region at random; then, the new solution may be added to the archive. Thus, the probability of a solution being deleted is proportional to the number of points in each hypercube (region).

Complementarily, the criterion to select $x_{\mathsf{\alpha }}$, $x_{\mathsf{\beta }}$ and $x_{\mathsf{\delta }}$ favours the least crowded regions in the Pareto front. The selection is based on a roulette-wheel method with the following probability for each hypercube:

$$p_l=\frac{\mathcal{C}}{N_l},$$

(10)

where $\mathcal{C}$ is a constant ($\mathcal{C}⩾1$), and $N_l$ is the number of solutions in the lth hypercube. The two extensions of MOGWO jointly promote the representativeness in the sample of the Pareto frontier.

2.2.2. Indicator-Based Multi-Objective Ant Colony Optimisation for Continuous Domains

Socha and Dorigo [33] proposed ${\mathrm{ACO}}_{\mathbb{R}}$, an extension of Ant Colony Optimisation (ACO) [34] to optimise mono-objective problems with continuous decision variables. In ${\mathrm{ACO}}_{\mathbb{R}}$, the pheromone matrix ($\tau$) is an archive that stores the best-so-far solutions. Here, a vector $x_l=〈x_{l,1},x_{l,2},x_{l,3},\dots ,x_{l,n}〉$ represents a solution of a problem with n decision variables, and $f\left(x_l\right)$ is the objective function to minimise. The $\kappa$ best-evaluated solutions are stored in $\tau$, following the implicit order given by $f\left(x_l\right)$. The position in $\tau$ of each $x_l$ determines a weight (${\omega }_l$) that measures the quality of $x_l$, defined in Equation (11).

$${\omega }_l=\frac{e^{-\phi \left(l\right)}}{\varsigma ·\kappa \sqrt{2\pi }},\mathrm{where}\phi \left(l\right)=\frac{{(l-1)}^2}{2{\varsigma }^2{\kappa }^2}$$

(11)

Equation (11) defines ${\omega }_l$ as a value of the Gaussian function with standard deviation $\varsigma ·\kappa$, mean 1.0, and argument l. Here, $\kappa$ is the number of solutions in $\tau$, and $\varsigma$ is a parameter ($0⩽\varsigma ⩽1$). The effect of $\varsigma$ is to establish the proper balance between the pressures exerted by the best-so-far solution (with values close to one) and the iteration-best solutions (with values close to zero).

Furthermore, a Gaussian kernel ($G_j$) is calculated for each decision variable $(1⩽j⩽n)$ as

$$G_j\left(x\right)=\sum _{l=1}^{\kappa }{\omega }_l{g}_l^j\left(x\right),$$

(12)

where

$$g_l^j\left(x\right)=\frac{e^{-{\varphi }_j\left(l\right)}}{s_l^j\sqrt{2\pi }},\mathrm{where}{\varphi }_j\left(l\right)=\frac{{\left(x-x_{l,j}\right)}^2}{2{\left(s_l^j\right)}^2}.$$

(13)

According to Equation (13), $g_l^j\left(x\right)$ is a normal distribution, where $s_l^j$ is the standard deviation, and $x_{l,j}$ is the mean. The former is calculated in each iteration as ants construct solutions. Then, $G_j$ in Equation (12) is a weighted sum of $g_l^j\left(x\right)\forall l\in \{1,2,3,\dots \kappa \}$, which defines the one-dimensional Gaussian function for the jth decision variable of the lth solution in $\tau$.

Ants construct solutions by performing n steps. The ith ant sets the value for the variable $x_{i,j}$ at the jth step. Here, only $G_j$—the resulting Gaussian kernel—is needed. Then, the weights ${\omega }_l$ are computed through Equation (11) and used to sample, by following two phases:

• One Gaussian function is picked from the Gaussian kernel. The probability $p_l$ of choosing the lth Gaussian function is given by

  $$p_l=\frac{{\omega }_l}{{\sum }_{r=1}^{\kappa }{\omega }_r}.$$

  (14)
  To exploit the synergy among decision variables, $g_l^j\left(x\right)$ is the single Gaussian function ants use to construct a solution incrementally during a complete iteration.
• The chosen Gaussian function (l) is used to sample new solutions. At the jth step, the standard deviation ($s_l^j$) is required to calculate the Gaussian function, $g_l^j\left(x\right)$, picked in Phase 1 (de facto, the sampled Gaussian function will be different in each jth construction step). Here, $s_l^j$ is dynamically calculated by Equation (15).

  $$s_l^j=\xi \sum _{r=1}^{\kappa }\frac{\left|x_{r,j}-x_{l,j}\right|}{\kappa -1}$$

  (15)
  Equation (15) defines the standard deviation as the average distance from $x_l$ (the picked solution) to other solutions ($x_r$) in $\tau$. The parameter $\xi$ weights this distance ($0⩽\xi ⩽1$). The effect of the parameter $\xi$ is similar to the pheromone evaporation in ACO, influencing the behaviour of the colony: with low values, exploitation is more promoted than exploration. The value of the jth decision variable is inferred by the ith ant by following

  $$x_{i,j}\sim g_l^j\left(x\right).$$

  (16)

2.3. Multi-Criteria Ordinal Classification Based on Interval Outranking

The notion behind outranking is that the credibility of the proposition ‘x is at least as good as y’—represented as $\sigma (x,y)$—may be calculated by analysing each pair of their criteria scores [35]. ELECTRE is the most representative MCDA method of the outranking approaches. Typically, ELECTRE defines $\sigma (x,y)=c(x,y)·d(x,y)$, where

• $c(x,y)$, the concordance index, cumulates the weights of the criteria in favour of the statement ‘x is at least as good as y’; and
• $d(x,y)$, the discordance index, assesses the combined strength of the criteria against ‘x is at least as good as y’.

Both indexes are calculated in function of a series of parameters that must be appropriately inferred so that $\sigma$ models the preferences of the DM. Interval outranking generalises the classic outranking to the framework of interval numbers, providing support when the values of the preference parameters are imprecisely known.

If the reader is be unfamiliar with interval mathematics, Appendix A compiles the basic notions to understand interval outranking. Note that interval numbers in this paper are written in boldface italic letters.

Let O be a set of alternatives (solutions). Each $x\in O$ is evaluated with an m-dimensional objective function $f\left(x\right)=〈f_1\left(x\right),f_2\left(x\right),f_3\left(x\right),\dots ,f_m\left(x\right)〉$. Without loss of generality, we suppose that each $f_k\left(x\right)$ is a minimising objective and, consequently, the preference of the DM increases as the value of $f_k\left(x\right)$ decreases. The parameters of the outranking model are:

• The vector of weights, ${\mathit{w}}_{\mathit{k}}=\left[\underline{w_k},\overline{w_k}\right]\forall k\in \{1,2,3,\dots ,m\}$, where ${\displaystyle \sum _{k=1}^m\underline{w_k}⩽1}$ and ${\displaystyle \sum _{k=1}^m\overline{w_k}⩾1}$;
• The vector of veto thresholds, ${\mathit{v}}_{\mathit{k}}=\left[\underline{v_k},\overline{v_k}\right]\forall k\in \{1,2,3,\dots ,m\}$;
• The majority threshold, $\mathit{\lambda }=\left[\underline{\lambda },\overline{\lambda }\right]$, where $0.5⩽\underline{\lambda }⩽\overline{\lambda }⩽1$; and
• The credibility threshold, $\beta$, where $0.5⩽\beta ⩽1$.

The concordance coalition of two solutions $(x,y)$, denoted as $C_{x,y}=\{k\in \{1,2,3,\dots ,m\}:$$P\left(f_k\left(y\right)⩾f_k\left(x\right)\right)⩾0.5\}$, is the subset of objectives favouring the statement ‘x is at least as good as y’. The concordance index for the statement ‘x is at least as good as y’ is the interval number $\mathit{c}(\mathit{x},\mathit{y})=\left[\underline{c(x,y)},\overline{c(x,y)}\right]$, defined as

$$\underline{c(x,y)}=\left\{\begin{array}{cc}{\displaystyle \sum _{k\in C_{x,y}}\underline{w_k}}\hfill & {\displaystyle \mathrm{if}\sum _{k\in C_{x,y}}\underline{w_k}+\sum _{k\in D_{x,y}}\overline{w_k}⩾1,}\hfill \\ \\ {\displaystyle 1-\sum _{k\in D_{x,y}}\overline{w_k}}\hfill & \mathrm{otherwise},\hfill \end{array}\right.$$

(17)

and

$${\displaystyle \overline{c(x,y)}=\left\{\begin{array}{cc}{\displaystyle \sum _{k\in C_{x,y}}\overline{w_k}}\hfill & {\displaystyle \mathrm{if}\sum _{k\in C_{x,y}}\overline{w_k}+\sum _{k\in D_{x,y}}\underline{w_k}⩽1,}\hfill \\ \\ {\displaystyle 1-\sum _{k\in D_{x,y}}\underline{w_k}}\hfill & \mathrm{otherwise}.\hfill \end{array}\right.}$$

(18)

Moreover, the discordance coalition consists of the objectives that are not in the concordance coalition, defined as $D_{x,y}=\left\{1,2,3,\dots ,m\right\}\backslash C_{x,y}$. These objectives justify arguments invalidating the outranking relation ‘x is at least as good as y’. The value $P\left(f_k\left(x\right)-f_k\left(y\right)⩾{\mathit{v}}_{\mathit{k}}\right)$ models the degree of credibility of the proposition ‘the kth criterion alone vetoes the statement x outranks y’. The discordance index, $d(x,y)$, is calculated appraising the credibility of veto of each objective in $D_{x,y}$, and is expressed as

$$d(x,y)=1-\underset{k\in D_{x,y}}{max}\left\{P\left(f_k\left(x\right)-f_k\left(y\right)⩾{\mathit{v}}_{\mathit{k}}\right)\right\}.$$

(19)

Accordingly, $\sigma (x,y)$ is redefined as

$$\sigma (x,y)=min\left\{P\left(\mathit{c}(\mathit{x},\mathit{y})⩾\mathit{\lambda }\right),d(x,y)\right\}.$$

(20)

By following Equation (20), Fernandez et al. [24] introduced a pair of binary preference relations. First, the crisp outranking relation ($\mathrm{S}$) is presented in Equation (21), where $\beta$ is a threshold on the credibility of ‘x is at least as good as y’. Lastly, Equation (22) presents the crisp relation ‘x is preferred to y’.

$$x\mathrm{S}y=\left\{(x,y):\sigma (x,y)⩾\beta \right\}$$

(21)

$$x\mathrm{Pr}y=\left\{(x,y):x\preccurlyeq y\vee \left(x\mathrm{S}y\wedge \neg y\mathrm{S}x\right)\right\}$$

(22)

Fernandez et al. [26] proposed INTERCLASS-nC, an extension of ELECTRE TRI-nC [36] in the framework of interval outranking to multi-criteria ordinal classification. INTERCLASS-nC is applicable in circumstances in which other MCDA methods fail, specifically when the DM does not want to (or cannot) set precise values for the model parameters (majority threshold, veto thresholds, and weights). INTERCLASS-nC is especially advantageous if the DM has only a vague idea about the boundaries between adjacent classes; nonetheless, they can quickly identify one representative solution at least in each category, which may be characterised by intervals.

INTERCLASS-nC considers the array of classes $C=〈C_1,C_2,C_3,\dots ,C_{\varpi }〉$, increasingly sorted by preference ($\varpi ⩾2$), and the subset of reference solutions introduced to characterise each $C_{\ell }$, $R_{\ell }= \left\{r_{\ell ,\mathsf{𝚥}}\right\}$ (where $1⩽\mathsf{𝚥}⩽ \left|R_{\ell }\right|$, and $1⩽\ell ⩽\varpi$). Additionally, $〈r_0,R_1,R_2,R_3,\dots ,R_{\varpi },r_{\varpi +1}〉$ is the array of all reference solutions sorted by preference, where $r_0$ is the anti-ideal point and $r_{\varpi +1}$ is the ideal point. Following the interval outranking, the following condition is true for $1⩽\ell <\varpi$:

$$\neg x\mathrm{S}y\forall x\in R_{\ell },y\in R_{\ell +1}.$$

(23)

Then, Equations (24) and (25) are used to define the categorical credibility indices between an alternative x and the category $C_{\ell }$.

$$\vartheta \left(x,R_{\ell }\right)=\underset{1⩽\mathsf{𝚥}⩽\left|R_{\ell }\right|}{max}\left\{\sigma \left(x,r_{\ell ,\mathsf{𝚥}}\right)\right\}$$

(24)

$$\vartheta \left(R_{\ell },x\right)=\underset{1⩽\mathsf{𝚥}⩽\left|R_{\ell }\right|}{max}\left\{\sigma \left(r_{\ell ,\mathsf{𝚥}},x\right)\right\}$$

(25)

The crisp relation of interval outranking is extended to compare actions with the sets of characteristic actions as

• $x\mathsf{S}{R}_{\ell }=\left\{\left(x,R_{\ell }\right):\vartheta \left(x,R_{\ell }\right) ⩾ \beta \right\}$;
• $R_{\ell }\mathsf{S}x=\left\{\left(R_{\ell },x\right):\vartheta \left(R_{\ell },x\right) ⩾ \beta \right\}$.

To suggest a class for a new alternative x, INTERCLASS-nC uses the selection function $S_f(x,R_{\ell })=min\left\{\vartheta \left(x,R_{\ell }\right),\vartheta \left(R_{\ell },x\right)\right\}$ and two heuristics—the ascending rule and the descending rule—that are conjointly used. Each one of these heuristics proposes a class for an alternative x. If the classes do not coincide, they define a range of assignments for x (any category within such a range is admissible as the class of x).

The steps of the ascending rule are the following

• Compare x to $R_{\ell }$ for $\ell =1,2,3,\dots ,\varpi +1$ until the first ℓ such that $R_{\ell }\mathsf{S}x$;
• If $\ell =1$, select $C_1$ as a possible class for x;
• If $1<\ell <\varpi +1$, select $C_{\ell }$ as a possible class for x if $S_f(x,R_{\ell })⩾S_f(x,R_{\ell -1})$; otherwise, select $C_{\ell -1}$.
• If $\ell =\varpi +1$, select $C_{\varpi }$ as a possible class for x.

The descending rule has the following steps

• Compare x to $R_{\ell }$ for $\ell =\varpi ,\varpi -1,\varpi -2,\dots ,0$ until the first ℓ such that $x\mathsf{S}{R}_{\ell }$;
• If $\ell =\varpi$, select $C_{\varpi }$ as a possible class for x;
• If $0<\ell <\varpi$, select $C_{\ell }$ as a possible class for x if $S_f(x,R_{\ell })⩾S_f(x,R_{\ell +1})$; otherwise, select $C_{\ell +1}$.
• If $\ell =0$, select $C_1$ as a possible class for x.

3. Proposed Algorithms

In this section, we describe how ordinal classification based on interval outranking was embedded in MOGWO and ${\mathrm{iMOACO}}_{\mathbb{R}}$ to incorporate the preferences of the DM. The primary strategy is to measure the quality of the solutions in terms of the class suggested by INTERCLASS-nC. Consequently, the selective pressure increases toward the solutions the DM is highly satisfied with. Note that both proposed algorithms are not intended for searching representative approximations of the complete Pareto frontier; instead, they search for the RoI: a relatively short subset of Pareto optimal solutions that best match the DM’s preferences. Here, we propose that the RoI is made of solutions classified as ‘Highly Satisfactory’, and the best compromise—the final prescription chosen by the DM—should be a solution belonging to the RoI. Section 3.1 introduces the Grey Wolf Optimiser with Interval outranking-based ordinal Classification, abbreviated as GWO-InClass. Section 3.2 introduces Ant Colony Optimisation with Interval outranking-based ordinal Classification, abbreviated as ACO-InClass.

3.1. The GWO-InClass Algorithm

GWO-InClass extends MOGWO by classifying the solutions in each iteration utilising INTERCLASS-nC before picking the leaders from the archive, keeping the solutions ranked in the following order: ‘Highly Satisfactory’, ‘Satisfactory’, ‘Dissatisfactory’, and ‘Strongly Dissatisfactory’.

We suggest using an ordinal classifier that has already been validated in an evolutionary algorithm for many-objective optimisation [37]. In this approach, the DM should classify the reference solutions (input) in two classes, ‘Dissatisfactory’ and ‘Satisfactory’ (respectively, $C_1$ and $C_2$), the minimum number of classes to apply INTERCLASS-nC. Then, the model is extended by artificially adding the classes ‘Highly Satisfactory’ and ‘Strongly Dissatisfactory’. Each new solution x generated during the evolutionary search is classified according to the following assumptions:

• If $x\mathrm{Pr}y\forall y\in R_2$, then the DM is highly satisfied with x; otherwise, the DM is satisfied with x.
• If $y\mathrm{Pr}x\forall y\in R_1$, then the DM is strongly dissatisfied with the solution x; otherwise, the DM is dissatisfied with x.

Algorithm 1 presents an outline of the ordinal classifier proposed by Balderas et al. [37].

A crucial process of GWO-InClass is to update the archive and select the $\mathsf{\alpha }$, $\mathsf{\beta }$ and $\mathsf{\delta }$ wolves; this process is presented in Algorithm 2. Here, Lines 1–2 initialise the variables; Lines 3–12 rank the solutions according to the class suggested by Algorithm 1; Lines 13–15 make sure that the archive ($\mathcal{A}$) is not larger than the maximum size allowed by the parameter ℏ; and, lastly, Lines 16–20 pick three different solutions from the non-empty best-evaluated class to be the leader wolves.

Algorithm 3 provides an algorithmic outline of GWO-InClass. Unlike MOGWO, GWO-InClass needs information about the preferences of the DM, which is exploited to become closer to the RoI. The preferences of the DM are articulated through an interval outranking model. We suggest using the proposal by Fernandez et al. [25] to infer the model parameters that reflect the preferences of the DM. Furthermore, GWO-InClass also needs the reference sets with solutions labelled by the DM as ‘Satisfactory’ or ‘Dissatisfactory’. Initially, synthetic solutions are helpful to perform this task; however, if the DM is not confident about those initial sets, they may additionally have some interactions with GWO-InClass throughout the optimisation process and directly classify the solutions in the archive, updating the reference sets. Binary classification of solutions is one of the least cognitively demanding ways to interact with the DM.

Algorithm 1 Ordinal classifier based on interval outranking

Input: Number of objectives (m), parameters of the outranking model ($\mathit{\lambda }$, $\beta$, $\mathit{v}$, $\mathit{w}$), a solution x, representative sets $R_1$ and $R_2$ Output: The class for x ($class$)  1: $c_{nc}\leftarrow \mathrm{INTERCLASS}-\mathrm{nC}(x,R_1,R_2)$                   ▹ Descending and ascending rules  2: if  $c_{nc}=‘\mathrm{Satisfactory}’$  then  3:     if $x\mathrm{Pr}y\forall y\in R_2$ then  4:         $class\leftarrow ‘\mathrm{Highly}\mathrm{Satisfactory}’$  5: else  6:     if $y\mathrm{Pr}x\forall y\in R_1$ then  7:         $class\leftarrow ‘\mathrm{Strongly}\mathrm{Dissatisfactory}’$  8: return  $class$

Algorithm 2 Selection of the leader wolves

Input: Archive ( $\mathcal{A}$ ), solutions of the current iteration ($x^{\iota }$), maximum size of the archive (ℏ) Output: The leader wolves ($x_{\mathsf{\alpha }},x_{\mathsf{\beta }},x_{\mathsf{\delta }}$)   1: $\mathcal{R}\leftarrow 〈\varnothing ,\varnothing ,\varnothing ,\varnothing 〉$   2: $\mathcal{T}\leftarrow PS\left(\mathcal{A}\cup x^{\iota }\right)$   ▹ Filtering only Pareto efficient solutions, see Equation (3)   3: for $x_i\in \mathcal{T}$ do                  ▹ Main loop for ranking solutions   4:     $class\leftarrow \mathtt{extended}\_\mathtt{INTERCLASS}-\mathtt{nC}\left(x_i\right)$     ▹ Classifying by Algorithm 1   5:     if $class=‘\mathrm{Highly}\mathrm{Satisfactory}’$ then   6:         ${\mathcal{R}}_1\leftarrow {\mathcal{R}}_1\cup \left\{x_i\right\}$   7:     if $class=‘\mathrm{Satisfactory}’$ then   8:         ${\mathcal{R}}_2\leftarrow {\mathcal{R}}_2\cup \left\{x_i\right\}$   9:     if $class=‘\mathrm{Dissatisfactory}’$ then  10:         ${\mathcal{R}}_3\leftarrow {\mathcal{R}}_3\cup \left\{x_i\right\}$  11:     if $class=‘\mathrm{Strongly}\mathrm{Dissatisfactory}’$ then  12:         ${\mathcal{R}}_4\leftarrow {\mathcal{R}}_4\cup \left\{x_i\right\}$  13: if  $\left|\mathcal{T}\right|>\hslash$  then  14:     Remove the $\left|\mathcal{T}\right|-\hslash$ worst solutions according to the ranking  15: $\mathcal{A}\leftarrow \mathcal{T}$  16: $leaders\leftarrow 〈x_{\mathsf{\alpha }},x_{\mathsf{\beta }},x_{\mathsf{\delta }}〉$  17: for $x_i\in leaders$ do               ▹ Main loop for picking the leaders  18:     $topRanked\leftarrow \left\{\begin{array}{cc}{\mathcal{R}}_1\hfill & \mathrm{if} {\mathcal{R}}_1\ne \varnothing \hfill \\ {\mathcal{R}}_2\hfill & \mathrm{if} {\mathcal{R}}_1=\varnothing \wedge {\mathcal{R}}_2\ne \varnothing \hfill \\ {\mathcal{R}}_3\hfill & \mathrm{if} {\mathcal{R}}_1={\mathcal{R}}_2=\varnothing \wedge {\mathcal{R}}_3\ne \varnothing \hfill \\ {\mathcal{R}}_4\hfill & \mathrm{otherwise}\hfill \end{array}\right.$  ▹ Choosing the best evaluated set that is not empty  19:     $x_i\leftarrow \mathtt{roulette}\_\mathtt{wheel}\left(topRanked\right)$   ▹ Probabilities calculated by Equation (10)  20:     Remove $x_i$ from $\mathcal{R}$        ▹ To avoid selecting the same solution as $x_{\mathsf{\alpha }}$, $x_{\mathsf{\beta }}$ or $x_{\mathsf{\delta }}$  21: return  $x_{\mathsf{\alpha }},x_{\mathsf{\beta }},x_{\mathsf{\delta }}$

In Algorithm 3, Lines 1–5 initialise the parameters and generate the initial positions of the wolves. Line 6 picks the first leader wolves. Lines 7–12 present the iterated process of GWO-InClass; here, Line 8 applies Equations (4)–(9) to update the positions of the Ω wolves, following the social leadership of the $\mathsf{\alpha }$, $\mathsf{\beta }$ and $\mathsf{\delta }$ wolves; Line 10 updates the archive and obtains the latest positions of the leader wolves; and lastly, Lines 11–12 update the parameters and variables to perform the next iteration.

Algorithm 3 The Grey Wolf Optimiser with Interval outranking-based ordinal Classification

Input Number of objectives (m), number of decision variables (n), parameters of the outranking model (${\mathit{w}}_{\mathit{k}},{\mathit{v}}_{\mathit{k}}\forall k\in \{1,2,3,\dots ,m\}$, $\mathit{\lambda }$, $\mathit{\beta }$), reference solution sets ($R_1$, $R_2$), maximum size of the archive (ℏ) Output: An approximation of the RoI ($\mathcal{A}$)  1: Initialise the parameters of MOGWO (a, A, and C)  2: $x_i^0\leftarrow \mathtt{random}\_\mathtt{solution}\left(\right)\forall i\in \{1,2,3,\dots ,\hslash \}$ ▹ Generating the initial pack of wolves at random  3: Calculate $f_k\left(x_i^0\right)\forall k\in \{1,2,3,\dots ,m\},i\in \{1,2,3,\dots ,\hslash \}$   ▹ Getting the values of the objective functions for each wolf  4: $\mathcal{A}\leftarrow \varnothing$  5: $\iota \leftarrow 1$  6: $\left(x_{\mathsf{\alpha }},x_{\mathsf{\beta }},x_{\mathsf{\delta }}\right)\leftarrow \mathtt{get}\_\mathtt{leaders}(\mathcal{A},x^0,\hslash )$                  ▹ Algorithm 2  7: while $\iota ⩽ite{r}_{\max }$ do              ▹ Main loop of the optimisation process  8:     $x_i^{\iota }\leftarrow \frac{{\mathfrak{x}}_1^{\iota -1}+{\mathfrak{x}}_2^{\iota -1}+{\mathfrak{x}}_3^{\iota -1}}{3}\forall i\in \{1,2,3,\dots ,\hslash \}$  ▹ Updating the pack of wolves by applying Equations (4)–(9)  9:       Calculate $f_k\left(x_i^{\iota }\right)\forall k\in \{1,2,3,\dots ,m\},i\in \{1,2,3,\dots ,\hslash \}$ 10:     $\left(x_{\mathsf{\alpha }},x_{\mathsf{\beta }},x_{\mathsf{\delta }}\right)\leftarrow \mathtt{get}\_\mathtt{leaders}(\mathcal{A},x^{\iota },\hslash )$            ▹ Algorithm 2 11:     Update a, A, and C 12:     $\iota \leftarrow \iota +1$ 13: return  $\mathcal{A}$

3.2. The ACO-InClass Algorithm

Like GWO-InClass, ACO-InClass stores the best solutions in the pheromone matrix $\tau$—its archive—considering the class suggested by Algorithm 1. Figure 1 depicts the pheromone representation used in ACO-InClass; here, $\kappa$ is the size of the archive, n is the number of decision variable, $x_l\forall l\in \{1,2,3,\dots ,\kappa \}$ is the vector of the lth solution in the archive, $x_{l,j}$ is the value of the jth decision variable of $x_l$, $G_j\forall j\in \{1,2,3,\dots ,n\}$ is the Gaussian kernel for the jth decision variable, and ${\omega }_l\forall l\in \{1,2,3,\dots ,\kappa \}$ is the weight of the lth solution.

The chief difference between ${\mathrm{iMOACO}}_{\mathbb{R}}$ and ACO-InClass is the criteria to sort $\tau$. Falcón-Cardona and Coello Coello [28] suggested $R_2$ scores [38] as the primary criterion to rank the solutions in $\tau$. Contrarily, in this paper, we propose the class indicated by Algorithm 1 as the primary criterion, and $R_2$ scores as the secondary criterion (intra-class solutions are sorted using the $R_2$ metric). The archive is set to store the $\kappa$ top-ranked solutions.

Algorithm 4 provides an algorithmic outline of ACO-InClass. Lines 1 and 7 initialise the parameters and variables of the algorithm; Lines 2–6 generate and evaluate the initial random solutions of the colony. Lines 8–16 present the iterated process of ACO-InClass; here, Lines 9–10 generate the solutions of the colony by following the equations provided in Section 2.2.2, particularly Equations (14)–(16); Lines 11–14 evaluate and rank the solutions; and, lastly, Lines 15–16 update the data structures to perform the next iteration.

Algorithm 4 Ant Colony Optimisation with Interval outranking-based ordinal Classification

Input Number of objectives (m), number of decision variables (n), parameters of the outranking model (${\mathit{w}}_{\mathit{k}},{\mathit{v}}_{\mathit{k}}\forall k\in \{1,2,3,\dots ,m\}$, $\mathit{\lambda }$, $\mathit{\beta }$), reference solution sets ($R_1$, $R_2$), maximum size of the archive ($\kappa$) Output: An approximation of the RoI ($\tau$)  1: Initialise the parameters of ${\mathrm{iMOACO}}_{\mathbb{R}}$ ($\xi$ and $\varsigma$)  2: $x_i\leftarrow \mathtt{random}\_\mathtt{solution}\left(\right)\forall x_i\in \tau$ ▹ Generating the initial solutions of the pheromone trail at random  3: Calculate $f_k\left(x_i\right)\forall k\in \{1,2,3,\dots ,m\},x_i\in \tau$    ▹ Getting the values of the objective functions for each ant  4: $\tau \leftarrow PS\left(\tau \right)$          ▹ Filtering only Pareto efficient solutions, see Equation (3)  5: $\mathtt{Normalise}(\tau$)  6: Rank solutions in $\tau$                          ▹ See Algorithm 1  7: $\iota \leftarrow 1$  8: while $\iota ⩽ite{r}_{\max }$ do              ▹ Main loop of the optimisation process  9:     for $x_i\in \Lambda$ do                     ▹$\Lambda$ is the colony (with $\kappa$ ants) 10:         Generate a new solution based on $\tau$             ▹ Applying Equation (16) 11:     Calculate $f_k\left(x_i\right)\forall k\in \{1,2,3,\dots ,m\},x_i\in \Lambda$ ▹ Getting the values of the objective functions for each ant 12:     $\mathcal{O}\leftarrow PS\left(\Lambda \cup \tau \right)$     ▹ Filtering only Pareto efficient solutions, see Equation (3) 13:     $\mathtt{Normalise}(\mathcal{O}$) 14:     Rank solutions in $\mathcal{O}$                       ▹ See Algorithm 1 15:     Copy into $\tau$ the $\kappa$ first solutions of $\mathcal{O}$ 16:     $\iota \leftarrow \iota +1$ 17: return  $\tau$

4. Experimental Validation

We implemented GWO-InClass and ACO-InClass in Java using OpenJDK 11.0.10, on a computer with an Intel Core i7-10510U CPU 1.80 GHz, 16 GB of RAM, and Manjaro 5.10 as operating system. This computer setting applies to all experiments reported in this section.

GWO-InClass has three main parameters to be adjusted: a, C, and ℏ. The components of the vector a are initially set in two, and are linearly decreased to reach zero in the last iteration. The vector C is dynamically generated during each iteration, providing random numbers (cf. [27]). The parameter setting of ACO-InClass is $\varsigma =0.1$ and $\xi =0.5$ (cf. [28]). The parameter settings of the reference algorithms—NSGA-III, MOGWO and ${\mathrm{iMOACO}}_{\mathbb{R}}$—are also those originally published by the authors in the articles [27,28,39]. A particular case is the size of the population (ℏ in GWO-InClass and $\kappa$ in ACO-InClass), which depends on the number of objective functions (m): $\hslash =\kappa =92$ for $m=3$, $\hslash =\kappa =212$ for $m=5$, and $\hslash =\kappa =276$ for $m=10$. These values were inspired by the discussion of Deb and Jain [39] on suitable population sizes for evolutionary algorithms. The maximum number of iterations for all the algorithms reported in this section is $ite{r}_{\max }=1000$ for $m\in \{3,5\}$ and $ite{r}_{\max }=1500$ for $m=10$.

The adjective ‘significant’ is used in this section if a non-parametric U test (also know as Mann–Whitney test or Wilcoxon rank-sum test) with a 0.95-confidence level validates the difference as statistically significant. Furthermore, we performed all tests for statistical significance through STAC [40].

The rest of this section is organised as follows. Section 4.1 presents the test suite used to validate the results, as well as the indicators to measure the quality of the solutions. Section 4.2 describes the results obtained by GWO-InClass. Lastly, Section 4.3 presents the results by ACO-InClass.

4.1. Benchmark Problems and Performance Indicators

DTLZ [41] has become the standard test suite most broadly accepted to assess the performance of MOEAs and MOSIAs. Accordingly, we ran our algorithms on the nine problems in the DTLZ suite, named DTLZ1–DTLZ9. These problems have continuous decision variables, and are scalable regarding the number of decision variables and objective functions, offering Pareto frontiers with challenging properties (e.g., bias, concavity, convexity, degeneration, multi-frontality, and separability). We explored the dimensionality of each DTLZ problem by considering 3, 5, and 10 objective functions (m); accordingly, there are 27 different instances to validate our algorithms. The numbers of position-related variables (k) and decision variables (n) for each problem are the following:

• DTLZ1: $k=5$ and $n=m+k-1$.
• DTLZ2–DTLZ6: $k=10$ and $n=m+k-1$.
• DTLZ7: $k=20$ and $n=m+k-1$.
• DTLZ8 and DTLZ9: $k=m-1$ and $n=10m$.

As GWO-InClass and ACO-InClass consider the DM’s preferences, each of the 27 test instances was validated using ten interval outranking models, representing different DMs. Some state-of-the-art studies [42,43,44] have proposed and used these synthetic DMs to validate a priori optimisation methods run on the DTLZ suite. The primary motivation behind this choice is that an acceptable approximation to the true RoI is known for these synthetic DMs, and these Approximated RoIs (abbreviated as ‘A-RoI’ from hereon) are in compliance with the interval outranking model described in Section 2.3, which is the keystone of the interval ordinal classifier GWO-InClass and ACO-InClass use (see Algorithm 1).

The A-RoI should contain the most preferred solutions in terms of interval outranking; Rivera et al. [44] followed this underlying principle to calculate the A-RoI as follows (cf. [42,43]):

• A representative sample with $\mathrm{100,000}$ Pareto optimal points is generated, represented by the set $\mathcal{O}$.
• Considering the preference relation $x\mathrm{Pr}y$, the set of the ‘least weak’ solutions is calculated as

  $$NW\left(\mathcal{O}\right)=arg\underset{y\in \mathcal{O}}{min}\left\{\sum _{x\in \mathcal{O}\backslash \left\{y\right\}}{\varrho }_{\mathrm{Pr}}(x,y)\right\},\mathrm{where}{\varrho }_{\mathrm{Pr}}(x,y)=\left\{\begin{array}{cc}\hfill 1& \mathrm{if}x\mathrm{Pr}y,\hfill \\ \hfill 0& \mathrm{otherwise}.\hfill \end{array}\right.$$
• Then, the A-RoI is finally calculated as

  $$A-RoI\left(\mathcal{O}\right)=arg\underset{x\in NW\left(\mathcal{O}\right)}{max}\left\{\sum _{y\in \mathcal{O}\backslash \left\{x\right\}}{\varrho }_{\mathrm{S}}(x,y)\right\},\mathrm{where}{\varrho }_{\mathrm{S}}(x,y)=\left\{\begin{array}{cc}\hfill 1& \mathrm{if}x\mathrm{S}y,\hfill \\ \hfill 0& \mathrm{otherwise}.\hfill \end{array}\right.$$

The proposed algorithms ran 30 times on each test instance using each synthetic DM (as a consequence, each algorithm was run 300 times per instance). The benchmark algorithms—NSGA-III, MOGWO and ${\mathrm{iMOACO}}_{\mathbb{R}}$—were also run 300 times.

There are several indicators for evaluating the performance of a multi-objective optimiser that approximates the complete Pareto frontier (e.g., hypervolume, spacing, spread, and inverted generational distance). However, these indicators are inadequate for assessing the performance of preference-based multi-objective algorithms because no metric can be directly applied when only a partial Pareto frontier is considered [45]. Furthermore, some attempts to assess the quality of a preferred solution adapt these indicators in an oversimplified way, making the assessments misleading. In line with this notion, we measured the performance via three indicators that consider the solutions that maximise the preferences of the DM. Let $X^{*}$ be the latest set of solutions of an algorithm, the following three indicators are utilised:

• Minimum Euclidian distance. The distance from the A-RoI to the closest point in $X^{*}$.
• Average Euclidian distance. The average distance from the points in the A-RoI to those in $X^{*}$.
• Satisfaction. The proportion of solutions in $X^{*}$ belonging to the class ‘Highly Satisfactory’.

On the one hand, the distance-based indicators measure the quality in terms of the similarity between $X^{*}$ and the A-RoI; the minimum distance considers the best solution alone, and the average distance considers the overall trend. For these indicators, the lower the values, the closer the approximation. On the other hand, the satisfaction-based indicator measures the quality of the algorithm considering the number of solutions that could potentially become the best compromise solution. For this indicator, greater values are preferred.

4.2. On the Performance of GWO-InClass

Table 1. Average results obtained by GWO-InClass and MOGWO.

			Benchmark Problems
m	Indicator	Algorithm	DTLZ1	DTLZ2	DTLZ3	DTLZ4	DTLZ5	DTLZ6	DTLZ7	DTLZ8	DTLZ9
3	Min. Euclid.	MOGWO	1164.89	4.99	606.87	11.94	0.91	3.73	0.25	0.04	5.39
		GWO-InClass	37.01	2.12	374.02	21.14	0.90	5.16	0.35	0.05	5.21
	Avg. Euclid.	MOGWO	1283.63	5.61	776.68	26.70	0.95	4.53	1.56	0.36	7.23
		GWO-InClass	74.11	2.85	487.44	21.69	0.93	6.06	1.66	0.40	6.98
	Satisfaction	MOGWO	1.28	25.17	1.89	23.22	0.00	2.71	48.59	48.37	1.60
		GWO-InClass	8.84	48.40	3.49	50.96	1.61	7.44	48.51	50.00	1.62
5	Min. Euclid.	MOGWO	131.74	693.38	8201.95	0.00	0.17	74.29	0.61	0.76	9.09
		GWO-InClass	24.04	1.61	193.63	6.37	0.00	2.64	0.56	0.76	9.05
	Avg. Euclid.	MOGWO	168.45	693.91	8226.69	0.64	5.73	76.75	2.81	2.68	9.45
		GWO-InClass	78.02	3.03	414.04	17.69	0.26	3.08	2.68	1.28	9.48
	Satisfaction	MOGWO	0.84	12.91	0.28	33.00	1.61	0.18	48.49	49.36	1.61
		GWO-InClass	14.05	48.92	19.84	50.26	49.83	31.84	51.39	50.63	1.61
10	Min. Euclid.	MOGWO	20.16	148.91	189.48	7.03	3.94	2.64	1.96	1.48	7.97
		GWO-InClass	14.12	1.64	186.59	6.26	0.02	0.02	1.89	1.48	8.25
	Avg. Euclid.	MOGWO	84.21	920.18	435.90	16.45	4.82	4.79	5.98	2.22	8.45
		GWO-InClass	87.16	4.67	425.63	16.86	0.08	0.11	5.79	2.22	8.73
	Satisfaction	MOGWO	4.32	0.15	30.69	49.14	1.61	0.00	47.93	48.61	1.59
		GWO-InClass	49.63	53.45	53.70	50.81	50.90	50.18	50.45	51.38	1.63

shows the results of GWO-InClass in comparison with MOGWO. Given a number of objectives (Column 1), Table 1 presents the average performance in terms of the indicators (referred to in Column 2) obtained by each algorithm (referred to in Column 3) on each DTLZ problem (referred to in Columns 4–12); here, the cells were shaded if the difference is statistically significant: in blue if it is in favour of GWO-InClass, in yellow if it is in favour of MOGWO.

The information in Table 1 may be summarised in the following points:

• Considering the satisfaction-based indicator: The results of GWO-InClass were significantly better than those of MOGWO in DTLZ1, DTLZ2, and DTLZ6 regardless of the number of objectives. In other problems (DTLZ3, DTLZ5, and DTLZ7), the advantage of including ordinal classification only became significant when m increased. On the whole, our strategy had a greater impact on the ‘satisfaction’ indicator in many-objective optimisation ($m\in \{5,10\}$) than in multi-objective optimisation ($m=3$).
• Considering the Euclidean indicators: The results on DTLZ1–3 were particularly encouraging because the averages of GWO-InClass were consistently lower than those of MOGWO, having statistical significance in the great majority of the instances. In DTLZ5 and DTLZ6, GWO-InClass became closer to the RoI only in many-objective instances. Contrastingly, when $m=3$, our strategy was inconvenient to treat DTLZ4 and DTLZ6.
• Considering DTLZ8 and DTLZ9: The embedding of ordinal classification in MOGWO does not yield any significant benefit. It is worth noting that they are the only problems with side constraints in this benchmark [46].

As a partial conclusion, we would recommend using GWO-InClass instead of MOGWO to address MaOPS. GWO-InClass was at least as good as MOGWO; what is more, it was significantly better on a regular basis. A test for statistical significance supports this hypothesis on the DTLZ test suit.

Additionally, we compared the results of GWO-InClass with NSGA-III, which has been widely accepted by the scientific community as a benchmark algorithm for evolutionary many-objective optimisation.

Table 2. Average results obtained by GWO-InClass and NSGA-III.

			Benchmark Problems
m	Indicator	Algorithm	DTLZ1	DTLZ2	DTLZ3	DTLZ4	DTLZ5	DTLZ6	DTLZ7	DTLZ8	DTLZ9
3	Min. Euclid.	GWO-InClass	$45.82$	$2.13$	$8589.97$	$21.14$	$0.01$	$56.40$	$0.1$	$0.05$	$8.83$
		NSGA-III	$0.55$	$0.01$	$0.17$	$0.0$	$0.0$	$0.00$	$0.0$	$0.00$	$0.17$
	Avg. Euclid	GWO-InClass	$80.58$	$2.85$	$8617.98$	$21.7$	$7.30$	$56.40$	$1.43$	$0.40$	$15.14$
		NSGA-III	$1.01$	$0.97$	$0.99$	$0.81$	$0.03$	$0.00$	$1.32$	$0.41$	$0.78$
	Satisfaction	GWO-InClass	$5.57$	$48.35$	$1.91$	48	$1.6$	$0.03$	$48.44$	$50.11$	$1.61$
		NSGA-III	$5.12$	$35.29$	$20.78$	$34.66$	$0.94$	$2.26$	$44.70$	$32.99$	$5.31$
5	Min. Euclid.	GWO-InClass	$35.86$	$1.61$	$400.36$	$16.43$	$0.0$	$2.91$	$0.56$	$0.76$	$38.57$
		NSGA-III	$0.31$	$0.04$	$0.33$	$0.01$	$0.0$	$0.44$	$0.20$	$0.84$	$1.69$
	Avg. Euclid	GWO-InClass	$102.66$	$3.03$	$627.42$	$27.26$	$0.26$	$3.18$	$2.68$	$1.28$	$39.05$
		NSGA-III	$0.80$	$0.98$	$1.10$	$0.8$	$0.13$	$0.58$	$2.53$	$1.33$	$2.15$
	Satisfaction	GWO-InClass	$7.07$	$48.74$	$5.26$	$48.55$	$49.93$	$22.54$	$50.01$	$48.97$	$1.61$
		NSGA-III	$14.49$	$3.06$	$10.97$	$1.12$	$10.46$	$0.83$	$48.35$	$51.02$	$27.30$
10	Min. Euclid.	GWO-InClass	$0.18$	$1.64$	$0.04$	$1.50$	$0.02$	$0.02$	$1.90$	$1.85$	$8.25$
		NSGA-III	$0.22$	$0.34$	$0.79$	$0.16$	$1.35$	$8.73$	$1.13$	$1.46$	$15.25$
	Avg. Euclid	GWO-InClass	$1.04$	$2.50$	$4.40$	$6.26$	$0.08$	$0.11$	$5.79$	$2.02$	$8.73$
		NSGA-III	$0.54$	$2.11$	$1.49$	$1.17$	$1.99$	$9.73$	$5.66$	$2.10$	$15.85$
	Satisfaction	GWO-InClass	$45.22$	$49.90$	$55.39$	$51.48$	$67.50$	$45.73$	$51.61$	$89.02$	$2.82$
		NSGA-III	$48.72$	$47.90$	$28.59$	$39.93$	$0.43$	$42.69$	$48.38$	$10.97$	$0.39$

presents the results of both algorithms on the DTLZ test suit. Again, the three indicators—the average Euclidean distance, the minimum Euclidean distance, and satisfaction—are considered, and the cells with significant differences are shaded (blue in favour of GWO-InClass, yellow in favour of NSGA-III).

According to Table 2, the worst performance was observed when $m=3$. Contrarily, GWO-InClass approximated the RoI significantly better than NSGA-III in most of the 10-objective instances. Considering the satisfaction-based indicator, DTLZ1, DTLZ7, and DTLZ9 are especially challenging for GWO-InClass. To conclude, the performance of GWO-InClass becomes competitive as the number of objectives increases according to this standard of the literature.

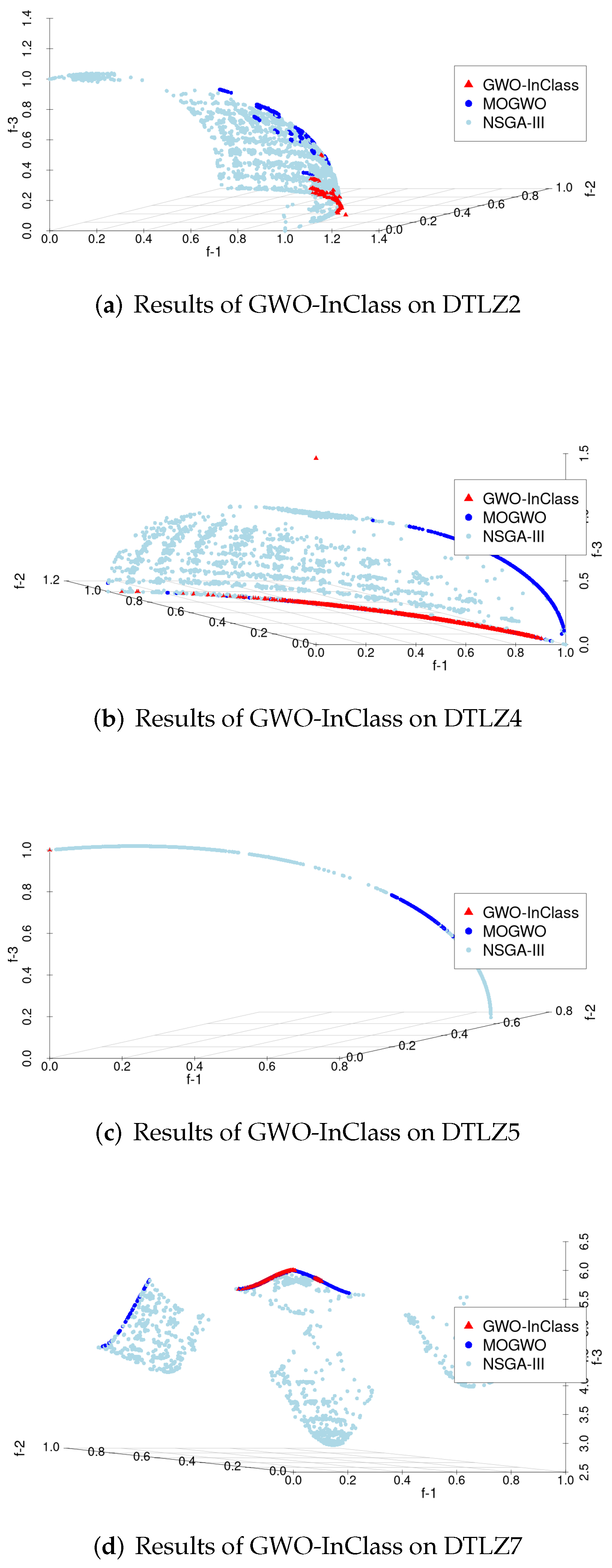
Lastly, we plotted the results of some single runs of GWO-InClass in Figure 2. We took those runs on the three-objective problems with the results closest to the A-RoI. Although such runs are not representative, they clearly depict how GWO-InClass biases the search toward a privileged region in the Pareto frontier. The best compromise would be a solution belonging to such region (coloured in red in Figure 2).

4.3. On the Performance of ACO-InClass

Table 3. Average results obtained by ACO-InClass and ${\mathrm{iMOACO}}_{\mathbb{R}}$.

			Benchmark Problems
m	Indicator	Algorithm	DTLZ1	DTLZ2	DTLZ3	DTLZ4	DTLZ5	DTLZ6	DTLZ7	DTLZ8	DTLZ9
3	Min. Euclid.	${\mathrm{iMOACO}}_{\mathbb{R}}$	35.33	2.84	506.46	12.77	0.00	5.46	1.30	0.43	14.04
		ACO-InClass	47.72	0.19	497.91	7.28	0.00	5.70	1.21	0.44	13.61
	Avg. Euclid.	${\mathrm{iMOACO}}_{\mathbb{R}}$	73.25	3.70	633.16	6.21	3.26	5.74	8.16	0.91	14.71
		ACO-InClass	79.33	1.33	634.59	14.12	2.99	5.98	7.72	0.91	14.23
	Satisfaction	${\mathrm{iMOACO}}_{\mathbb{R}}$	11.62	28.51	24.42	32.82	1.37	2.47	23.37	46.21	0.00
		ACO-InClass	11.18	32.21	15.38	31.79	2.08	2.64	24.27	52.14	3.22
5	Min. Euclid.	${\mathrm{iMOACO}}_{\mathbb{R}}$	44.73	0.94	256.49	0.00	0.00	6.50	2.01	7.62	18.28
		ACO-InClass	30.93	1.19	200.61	4.29	0.00	6.78	1.88	11.95	17.74
	Avg. Euclid.	${\mathrm{iMOACO}}_{\mathbb{R}}$	93.16	3.73	305.69	0.81	0.15	7.59	13.75	51.32	19.28
		ACO-InClass	77.75	4.22	275.32	6.79	0.17	7.97	14.47	83.02	18.73
	Satisfaction	${\mathrm{iMOACO}}_{\mathbb{R}}$	21.26	18.22	24.56	23.50	16.63	3.99	33.71	60.70	0.00
		ACO-InClass	22.91	18.92	22.77	24.55	15.54	3.97	34.43	38.26	3.22
10	Min. Euclid.	${\mathrm{iMOACO}}_{\mathbb{R}}$	20.57	0.39	224.90	6.28	0.09	8.13	7.85	56.96	25.79
		ACO-InClass	6.44	0.19	148.08	7.59	0.16	7.09	2.34	1.16	26.22
	Avg. Euclid.	${\mathrm{iMOACO}}_{\mathbb{R}}$	53.85	1.23	308.24	6.95	0.21	9.45	26.70	217.89	26.82
		ACO-InClass	33.53	1.22	220.34	9.09	0.49	9.12	17.06	2.48	27.34
	Satisfaction	${\mathrm{iMOACO}}_{\mathbb{R}}$	28.47	28.61	22.27	40.27	16.13	15.19	48.16	12.24	3.22
		ACO-InClass	49.84	47.47	61.03	59.72	11.94	25.63	49.13	87.75	2.21

presents the results of ACO-InClass in comparison with ${\mathrm{iMOACO}}_{\mathbb{R}}$; its columns should be interpreted with the same meaning provided for Table 1. As a summary of the information provided, let us discuss the following remarks:

• Considering ten objective functions: The advantage of embedding ordinal classification became statistically significant only when $m=10$. Taking DTLZ1–4 and DTLZ6–8, ACO-InClass outperformed ${\mathrm{iMOACO}}_{\mathbb{R}}$ in at least one indicator, performing especially well in DTLZ1, DTLZ3, DTLZ6, and DTLZ8.
• Considering three and five objective functions: With the only exception of a specific setting (DTLZ6, average Euclidean distance, and $m=5$), ACO-InClass was at least as good as ${\mathrm{iMOACO}}_{\mathbb{R}}$ regardless of the number of objectives.
• Considering DTLZ5 and DTLZ9: Like in the case of GWO-InClass, no advantage was observed in DTLZ9. Additionally, this situation also occurred in DTLZ5.

We would strongly recommend using ACO-InClass instead of ${\mathrm{iMOACO}}_{\mathbb{R}}$ to address MaOPS with about ten objective functions. This insight is relevant because the efficiency of MOSIAs and MOEAs is degraded as the number of objectives increases. The strategy proposed in this paper could become a viable means of mitigating this severe drawback. Still, the DM should be prepared to devote the necessary time to express their preferences.

Furthermore,

Table 4. Average results obtained by ACO-InClass and NSGA-III.

			Benchmark Problems
m	Indicator	Algorithm	DTLZ1	DTLZ2	DTLZ3	DTLZ4	DTLZ5	DTLZ6	DTLZ7	DTLZ8	DTLZ9
3	Min. Euclid.	ACO-InClass	$1782.09$	$0.00$	$478.51$	$12.80$	$0.00$	$0.00$	$70.01$	$40.91$	$9.12$
		NSGA-III	$0.56$	$0.01$	$0.17$	$0.00$	$0.00$	$0.00$	$0.01$	$0.01$	$0.18$
	Avg. Euclid	ACO-InClass	$1786.36$	$0.93$	$612.73$	$16.15$	$3.18$	$0.12$	$78.33$	$53.03$	$15.64$
		NSGA-III	$1.02$	$0.98$	$0.99$	$0.82$	$0.04$	$0.01$	$1.32$	$0.42$	$0.79$
	Satisfaction	ACO-InClass	$0.27$	$28.04$	$2.80$	$31.89$	$1.86$	$0.00$	$1.11$	$0.03$	$0.00$
		NSGA-III	$5.48$	$37.86$	$20.59$	$33.40$	$0.44$	$2.18$	$88.27$	$66.34$	$6.49$
5	Min. Euclid.	ACO-InClass	$58.84$	$0.01$	$3.38$	$4.29$	$0.00$	$1.44$	$6.83$	$41.87$	$2.83$
		NSGA-III	$0.31$	$3.05$	$0.33$	$0.02$	$0.00$	$0.44$	$0.20$	$0.85$	$1.33$
	Avg. Euclid	ACO-InClass	$122.12$	$0.08$	$327.58$	$4.81$	$0.13$	$9.10$	$17.02$	$40.31$	$5.61$
		NSGA-III	$0.81$	$10.99$	$1.10$	$2.80$	$3.18$	$0.59$	$2.54$	$2.15$	$2.69$
	Satisfaction	ACO-InClass	$15.39$	$15.76$	$11.42$	$1.21$	$10.18$	$1.95$	$7.98$	$0.14$	$28.91$
		NSGA-III	$2.91$	$3.35$	$2.97$	$19.94$	$12.44$	$1.08$	$8.63$	$9.77$	$0.00$
10	Min. Euclid.	ACO-InClass	$0.45$	$0.20$	$0.79$	$0.17$	$0.00$	$7.04$	$2.70$	$1.46$	$25.25$
		NSGA-III	$0.23$	$0.35$	$5.06$	$7.59$	$22.54$	$8.94$	$1.13$	$25.30$	$26.22$
	Avg. Euclid	ACO-InClass	$0.72$	$1.23$	$1.49$	$1.17$	$0.25$	$9.04$	$5.66$	$2.10$	$25.85$
		NSGA-III	$0.55$	$1.11$	$33.26$	$9.10$	$26.48$	$9.68$	$16.85$	$71.46$	$27.35$
	Satisfaction	ACO-InClass	$85.44$	$54.43$	$77.10$	$55.70$	$24.74$	$44.58$	$68.46$	$96.62$	$0.00$
		NSGA-III	$10.38$	$35.42$	$4.31$	$32.38$	$0.00$	$28.60$	$29.24$	$3.38$	$3.23$

shows the results of ACO-InClass in comparison with those of NSGA-III. The columns of Table 4 should be analogously interpreted as in Table 2. These results together with the statistical tests allow concluding that ACO-InClass is competitive to address 10-objective problems according to the standard established by NSGA-III; in fact, ACO-InClass outperformed NSGA-III in the vast majority of these instances. As a welcome side effect, ACO-InClass can also support the a posteriori decision analysis; this feature would reduce the DM’s cognitive effort invested in identifying the best compromise. Adversely, these results clearly imply that ACO-InClass was unsuitable for treating three-objective instances.

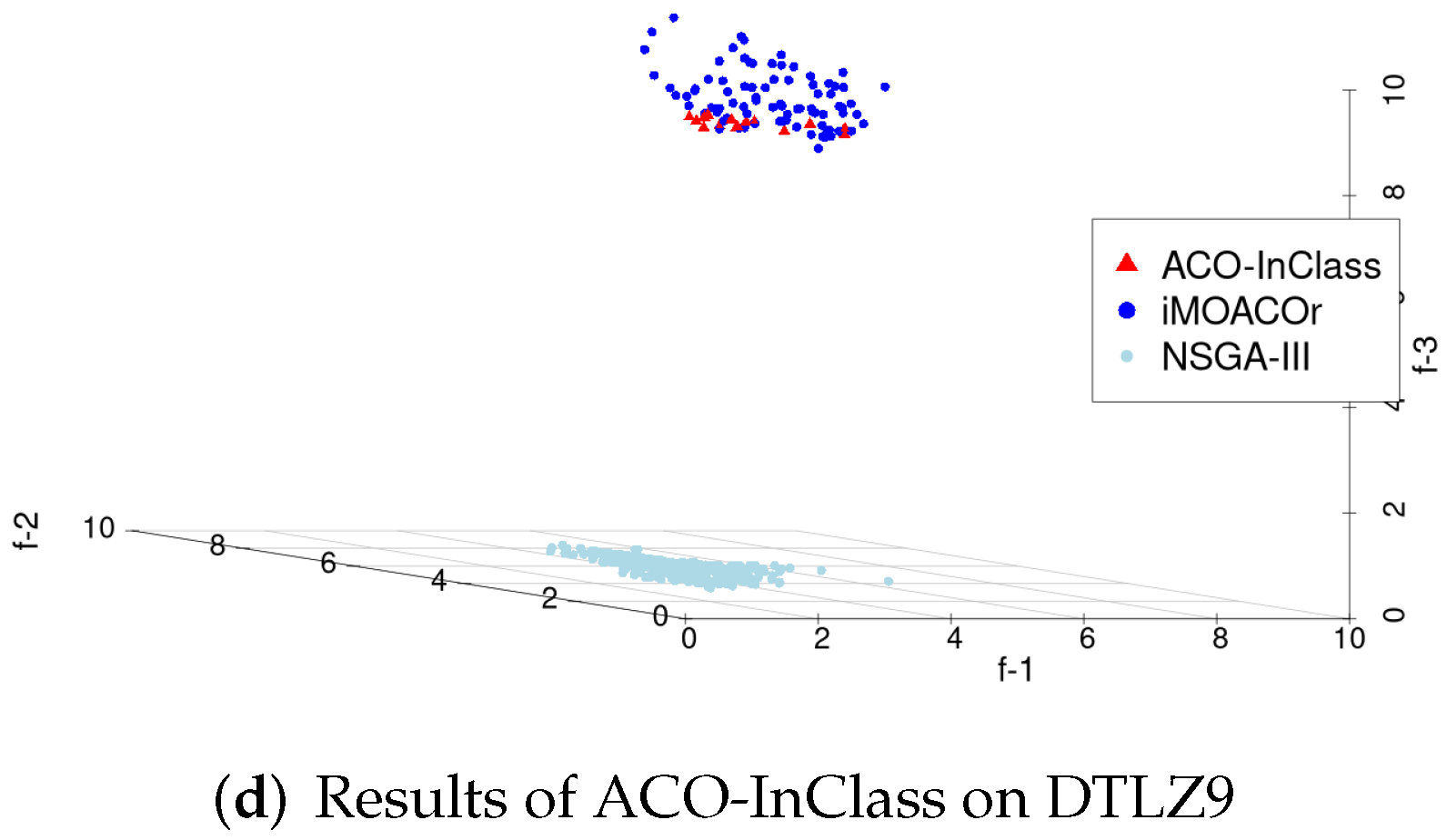
Again, we plotted the results of some runs of ACO-InClass, which are shown in Figure 3. These runs presented the best results on the three-objective instances and clearly depicted how ACO-InClass biases the search toward the A-RoI. Here, the best compromise would be a solution obtained by ACO-InClass (coloured in red in Figure 3).

5. Conclusions and Directions for Future Research

This paper introduces a novel strategy to incorporate preferences into swarm intelligence algorithms. Following the taxonomy of Bechikh et al. [4], the proposed strategy falls into the category of ‘solution classification’. Initially, the DM should express their preferences about the solutions by classifying them as ‘Satisfactory’ or ‘Dissatisfactory’. The proposed strategy is one of the least cognitively demanding in the framework of solution classification because the DM must merely classify solutions into just two categories.

Then, we suggest that the optimisation algorithms additionally identify two artificial classes—‘Highly Satisfactory’ and ‘Strongly Dissatisfactory’—through an ordinal classifier based on interval outranking to model different levels of intensity in the DM’s preferences. Consequently, the classifier increases its ability to discriminate. Here, we hypothesised that swarm intelligence algorithms can obtain the edge by increasing the selective pressure toward the region of the Pareto frontier containing ‘Highly Satisfactory’ solutions. A straightforward way to achieve it is to consider ordinal classification as the major criterion to rank the solutions in the archive.

Typically, swarm intelligence algorithms use an archive with the best so-far approximation of the Pareto frontier. These solutions are sorted to pick the solution(s) whose patterns will be exploited in the next iteration, hence its relevance.

By applying this strategy, ordinal classification was embedded in two swarm intelligence algorithms, expressly Multi-objective Grey Wolf Optimisation and Indicator-based Multi-objective Ant Colony Optimisation for continuous domains. The extended versions were called Grey Wolf Optimiser with Interval outranking-based ordinal Classification (GWO-InClass) and Ant Colony Optimisation with Interval outranking-based ordinal Classification (ACO-InClass). We used ten synthetic DMs to validate the results; we also considered each problem in the DTLZ test suite and explored different numbers of objective functions (three, five, and ten). The algorithms ran 30 times for each setting.

The impact of our strategy depended on several factors: the number of objectives, the baseline algorithm, and the properties of the test problem. Despite this, our strategy conferred marked benefits when many objective functions were treated. In the case of GWO-InClass, such benefits became significant in six of the nine DTLZ problems when the number of objectives was at least five. In the case of ACO-InClass, the ordinal classifier impacted the performance in seven DTLZ problems only when ten objective functions were considered.

Although our strategy requires that the DM is well-disposed to spend the necessary time to elicit their preferences, such an effort can be favourably compensated when problems with many objective functions are treated; especially, keeping in mind that these problems are still highly challenging for a posteriori algorithms (that approximate the complete Pareto frontier). The embedding of ordinal classification based on interval outranking contributed to coping with these difficulties. Numerical results and tests for statistical significance supported these conclusions.

Perhaps, the major criticism of our approach is that it is only applicable when the preferences of the DM are compatible with the underlying principles of outranking. That is, the DM admits veto effects and has a non-compensatory preference about the objectives.

Further research is needed to draft conclusions with a greater generalisation. First, it is necessary to know the impact of this strategy on other swarm intelligence algorithms (e.g., particle swarm optimisation, artificial bee colony, and elephant herding optimisation). Second, it is also necessary to conduct more experimentation with a deeper analysis to connect the performance with the properties of the problem, providing plausible explanations for those problems in which no advantage was observed (e.g., DTLZ9).