A Modified Coronavirus Herd Immunity Optimizer for the Power Scheduling Problem
Abstract
:1. Introduction
2. Power Scheduling Problem in Smart Home
2.1. Related Work
2.2. PSPSH Formulation
2.2.1. Power Consumption
2.2.2. Electricity Bill (EB)
2.2.3. Peak-to-Average Ratio (PAR)
2.2.4. User Comfort (UC) Level
2.3. Multi-Objective Function
3. Coronavirus Herd Immunity Optimizer
3.1. Inspiration
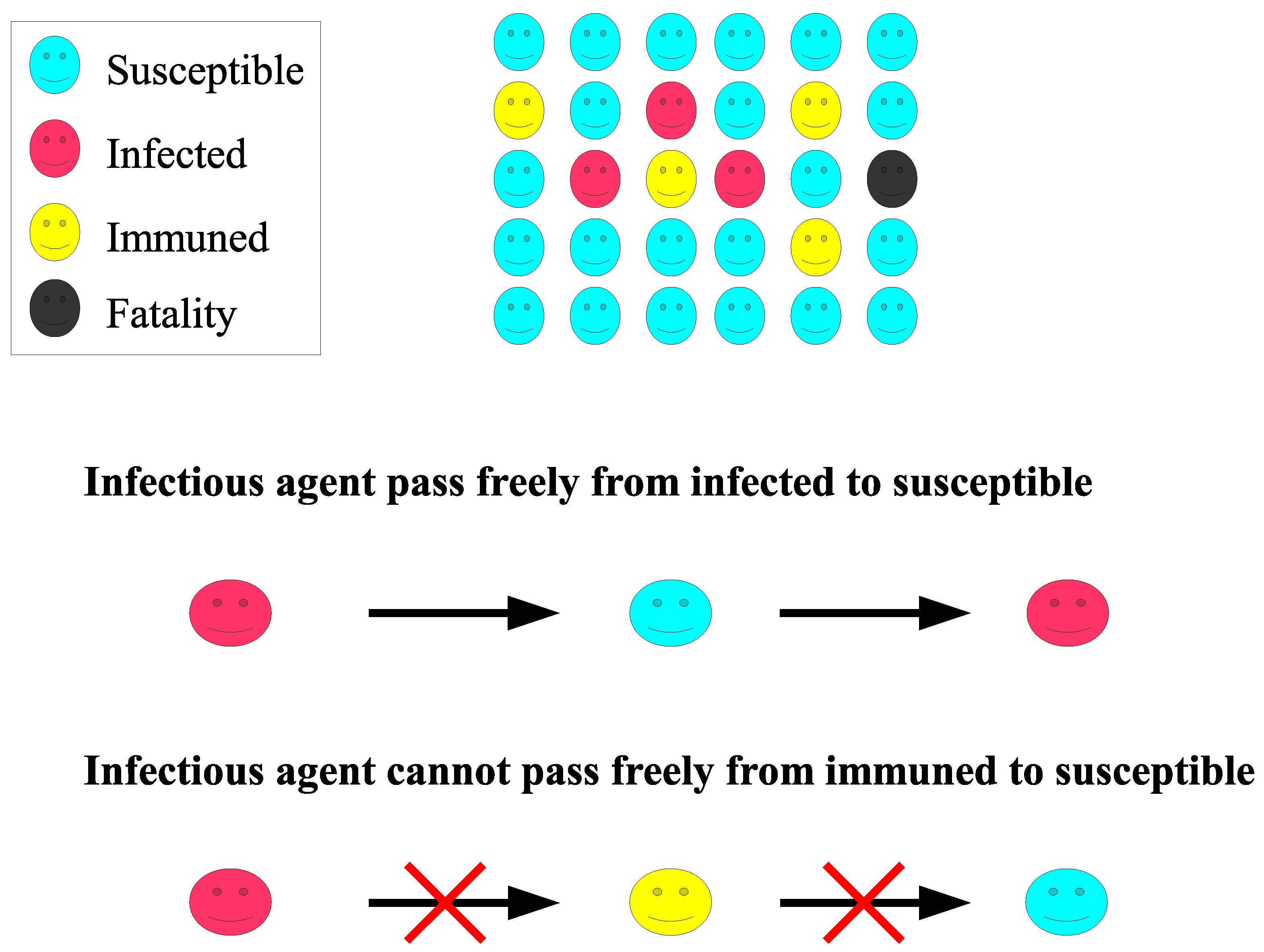
- A group of infected individuals infects a group of susceptible individuals.
- The majority of the infected people recover and gain immunity against COVID-19, and a low rate are dying.
- The immune individual will stop the virus from spreading; thus, the population is protected.
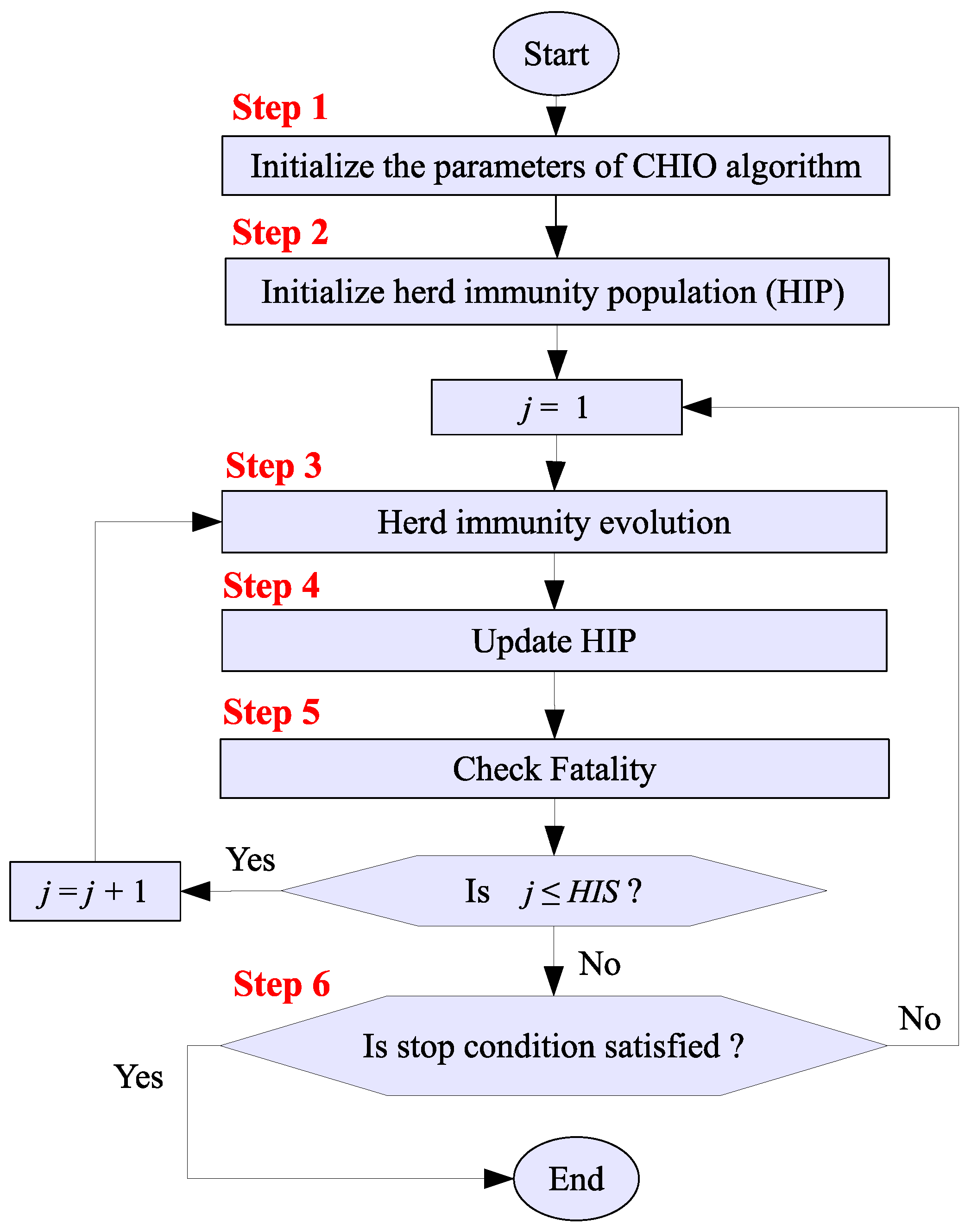
3.2. Optimization Steps of CHIO
| Algorithm 1 CHIO pseudo-code. |
|
- Step 1:
- InitializationInitially, any problem must be modeled as an optimization problem to be addressed by optimization algorithms. In addition, two main parts should be identified, including the solution representation and the objective function. The solution of a constrained optimization problem can be formulated as a vector of d decision variables. Each decision variable has its value range where . where denotes the minimum value range and denotes the maximum value range. Accordingly, the objective function of the solution can be formulated as follows:where is the objective function to measure the fitness of solution x. is the set of equality constraints while is the set of inequality constraints. CHIO has two types of parameters: algorithmic and control. The algorithmic parameters are maximum number of iterations (I), herd immunity population size (), and which is the initial infected cases. CHIO also has two control parameters, including basic reproduction rate () denotes the rate of transmitting the virus from individual to another and max age () which determines the status of infected individual according to its infection age.
- Step 2:
- Initialize herd immunity populationThe herd immunity population (HIP) is a memory matrix of size stored in CHIO individuals. These individuals are initialized normally concerning the equality and inequality constraints. HIP matrix is represented in Equation (24). The objective function values (or immunity rates) are computed for all initialized solutions using Equation (23).To keep tracking the status of HIP individuals, the status vector of size is initialized by zeros as many as and ones as many as . Please note that zeros and ones refer to the susceptible and infected cases, respectively.
- Step 3:
- Herd immunity evolutionIn this step, A new CHIO solution is generated based on three rules, which are discussed below.
- Infected case:
- the decision variable o in the solution y, such as , will be modified based on social distancing calculated based on the difference between the current decision variable and a decision variable taken from any infected case with a probability , such as:wherewhere is selected from infected case whereby the status vector ().
- Susceptible case:
- the decision variable o in the solution y will be modified based on social distancing calculated the difference between the current decision variable and a decision variable taken from any susceptible case with a probability of , such as:wherewhere is selected from any susceptible case based on the status vector ().
- Immune case:
- the decision variable o in the solution y will be modified based on social distancing calculated the difference between the current decision variable and a decision variable from any immune case with a probability of such as:wherewhere is selected from the best immune case with regard to the status vector () such that:
In summary, the operations of the three rules can be formulated as follows: - Step 4:
- Updating HIPThe fitness value (or immunity rate) of each generated solution is computed using fitness function. The generated solution replaces the current one , when . In case the replacement is done, the Age value of such solution is increment by one (i.e., ) if the current solution is infected case ().In addition, CHIO updates the status vector () for generated solution based on the herd immune threshold formulated in Equation (34)Please note that is a binary value set to one if inherited a value from any infected case. The is the fitness mean value of the individuals in HIP, such as .
- Step 5:
- Check FatalityThis step decides whether the infected cases (i.e., ∧ ( == 1)) are dead or immune. This is specified by the parameter . When the infected case’s age exceeds the limit such that ≥ without any improvement, the infected case will be died (or be removed from the HIP) and it is regenerated from scratch. Furthermore, the and are set to zero. This is the main operator for diversification.
- Step 6:
- Stop conditionThe evolution steps (Step 3 to Step 5) are repeated until the HIP is only contained in either susceptible or immune cases but not infected cases. Typically, the maximum number of iterations is used as a stopping criterion.
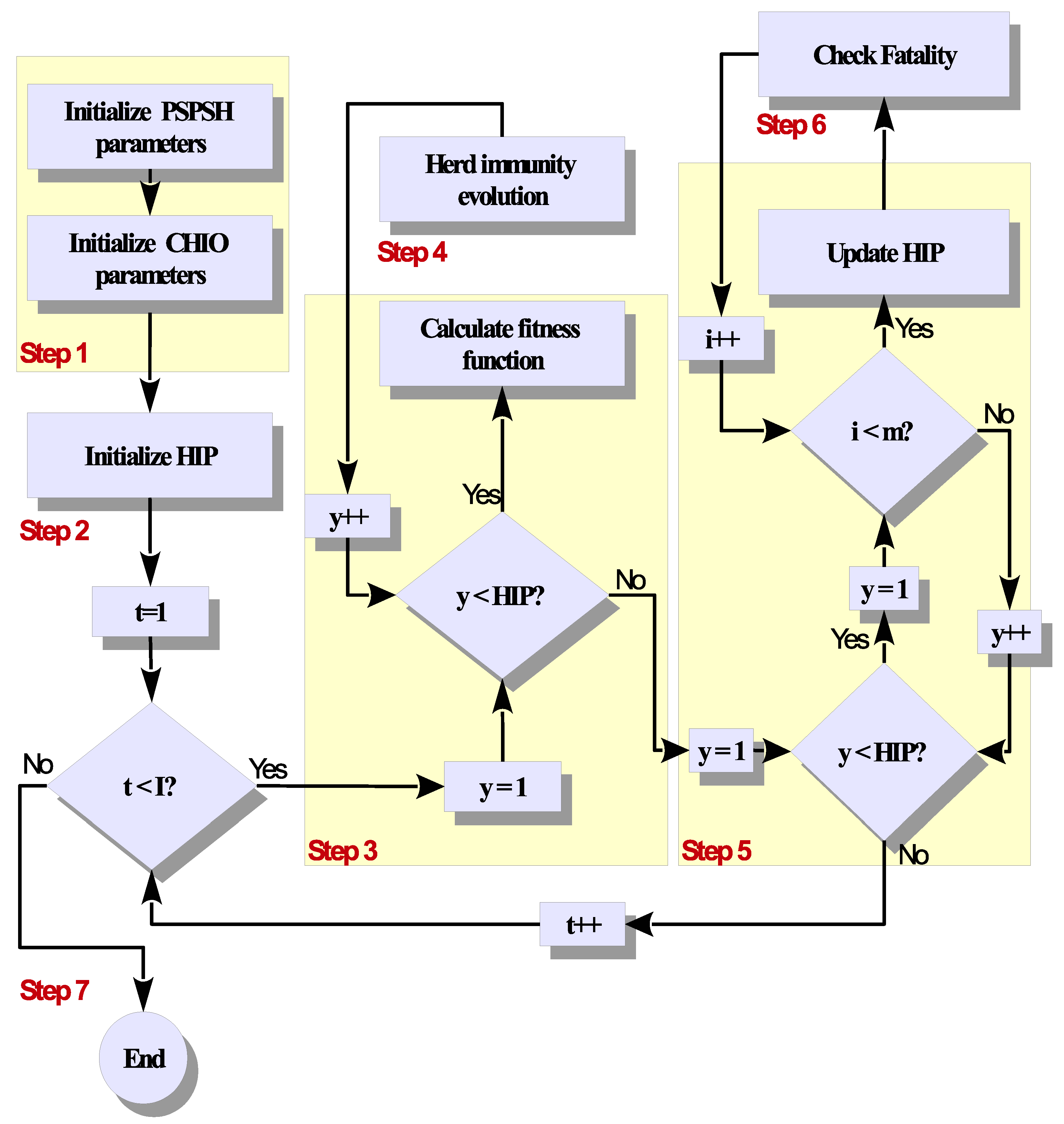
4. The Proposed CHIO-PSPSH
- Step 1:
- Initialize CHIO-PSPSH parametersThe first step of adapting CHIO to handle PSPSH is initializing CHIO and PSPSH parameters. The main parameters of PSPSH that must be initialized are the home appliances and , length of operation cycle , time horizon , power required by appliance and , boundary of operation time periods and , and electricity prices .For the CHIO parameters are the maximum number of iterations (), population size (), Spreading rate (), Max Age (), and number of initial infected ().
- Step 2:
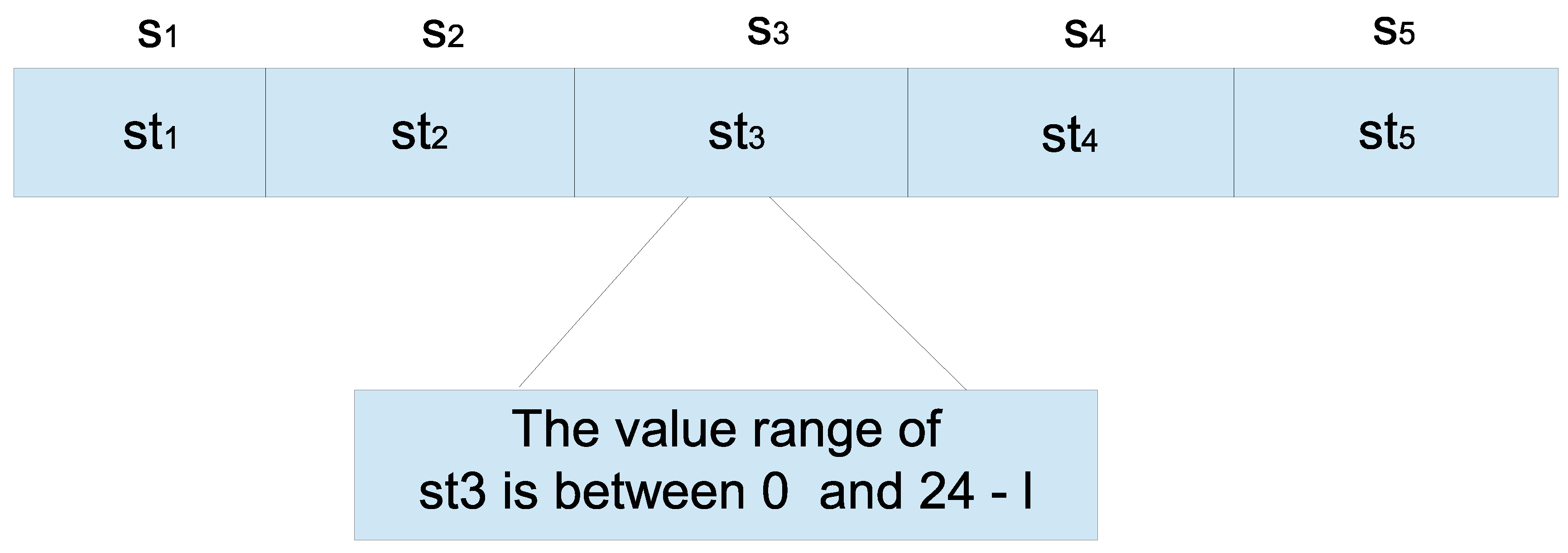
- Initialize CHIO-PSPSH populationPSPSH’s solutions are generated randomly in this step by the CHIO considering the discrete nature of PSPSH. The solutions are presented in a vector of length m containing the SA’s starting time . Figure 4 shows an example of the solution representation. The solution’s length is 5 (m = 5), and each bit in the solution contains of an SA in the range [0, 24 - l].The PSPSH population contains number of solutions, as shown in Equation (33).where denote of SA i in solution y.
- Step 3:
- Calculate fitness functionEach solution is evaluated based on Equation (22) in this step. After the evaluation, the best solution is assigned with the highest immunity rate ().
- Step 4:
- Coronavirus herd immunity evolutionThis step is the primary step of CHIO. The SA i in the solution y may be affected by social distancing or remain the same based on using three rules as follows:
- Step 5:
- Update herd immunity populationIn this step, the fitness value of each PSPSH’s generated solution is calculated and replaced the current solution if achieved a fitter value, such that . The age vector is also increased by one if . In addition, the status vector () is updated for each solution using Equation (31).As mentioned previously, the CHIO is modified to deal with discrete optimization problems. Therefore, in this step, once the PSPSH population is updated, all values in the population will be converted from continuous to discrete values.
- Step 6:
- Fatality casesThis step decides whether the infected solution (i.e., ∧ ( == 1)) is dead or immune. This is specified by the parameter . When the Age of the infected solutions exceed the limit without any improvement, the infected solutions are removed from the population and regenerated. Furthermore, the age and are set to zero.
- Step 7:
- Stop criterion
5. Experimental Results
5.1. Experimental Design
5.2. CHIO Parameters Analyzation
5.3. Illustrative Example
5.4. Experimental Evaluation
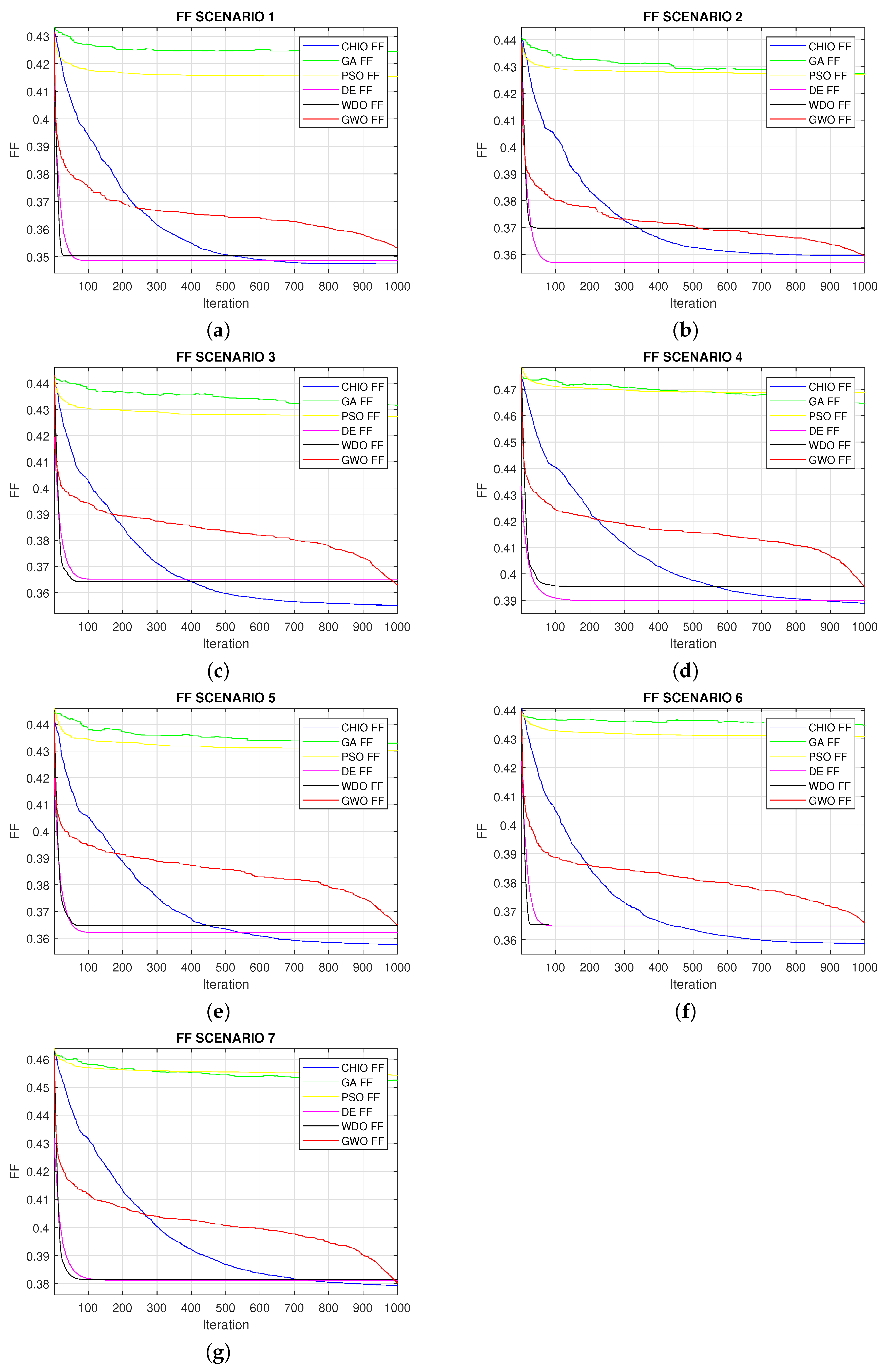
5.4.1. Algorithms Effect on EB
5.4.2. Algorithms Effect on PAR
5.4.3. Algorithms Effect on UC level
5.4.4. Performance and Statistical Evaluation
6. Conclusions and Future Work
- As mentioned previously, CHIO contains two adjustable control parameters, including and , where their values are changing from an optimization problem to another. These parameters are tuned in Section 5.2 based on the recommended values suggested by Al-Betar et al. [43] (, ) to find their best values for PSPSH. However, such parameters best values for PSPSH may not one of the suggested values, for instance, and . Accordingly, new tuning experiments for such control parameters can be conducted to investigate and find better best values. More experiments required a more illustrative presentation approach. Therefore, visualizing the new conducted results in a graph could enhance the presentation of the results.
- Due to the high constraints of the PSPSH that restrict the optimization processes of the algorithms, new power sources, such as storage systems and renewable energy sources, can be integrated with the smart home components to enhance the solutions and schedules of PSPSH.
- Due to the weak performance of CHIO in optimizing EB, CPR, and UC level, the proposed CHIO can be hybridized with components of other efficient methods to enhance its performance and achieve better solutions.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Abbreviations
| CHIO | Coronavirus Herd Immunity Optimizer |
| CPR | Capacity Power Limit Rate |
| ED | Differential Evolution |
| EB | Electricity Bill |
| FF | Fitness Values |
| GA | Genetic Algorithm |
| GWO | Grey Wolf Optimizer |
| HIP | Herd Immunity Population |
| IBR | Inclining Block Rates |
| NSA | Non-Shiftable Appliance |
| PAR | Peak-to-Average Ratio |
| PSO | Particle-Swarm Optimization |
| PSPSH | Power Scheduling Problem in Smart Home |
| RTP | Real-Time Price |
| SA | Shiftable Appliance |
| UC | User Comfort |
| WDO | Wind-Driven Optimization |
| WTR | Waiting Time Rate |
References
- Makhadmeh, S.N.; Khader, A.T.; Al-Betar, M.A.; Naim, S.; Abasi, A.K.; Alyasseri, Z.A.A. Optimization methods for power scheduling problems in smart home: Survey. Renew. Sustain. Energy Rev. 2019, 115, 109362. [Google Scholar] [CrossRef]
- Zhao, Z.; Lee, W.C.; Shin, Y.; Song, K.B. An optimal power scheduling method for demand response in home energy management system. IEEE Trans. Smart Grid 2013, 4, 1391–1400. [Google Scholar] [CrossRef]
- Yan, Y.; Qian, Y.; Sharif, H.; Tipper, D. A survey on smart grid communication infrastructures: Motivations, requirements and challenges. IEEE Commun. Surv. Tutorials 2013, 15, 5–20. [Google Scholar] [CrossRef] [Green Version]
- Khan, A.R.; Mahmood, A.; Safdar, A.; Khan, Z.A.; Khan, N.A. Load forecasting, dynamic pricing and DSM in smart grid: A review. Renew. Sustain. Energy Rev. 2016, 54, 1311–1322. [Google Scholar] [CrossRef]
- Makhadmeh, S.N.; Khader, A.T.; Al-Betar, M.A.; Naim, S. An optimal power scheduling for smart home appliances with smart battery using grey wolf optimizer. In Proceedings of the 2018 8th IEEE International Conference on Control System, Computing and Engineering (ICCSCE), Penang, Malaysia, 23–25 November 2018; pp. 76–81. [Google Scholar]
- Iftikhar, H.; Asif, S.; Maroof, R.; Ambreen, K.; Khan, H.N.; Javaid, N. Biogeography Based Optimization for Home Energy Management in Smart Grid. In Proceedings of the International Conference on Network-Based Information Systems, Toronto, ON, Canada, 24–26 August 2017; pp. 177–190. [Google Scholar]
- Makhadmeh, S.N.; Khader, A.T.; Al-Betar, M.A.; Naim, S.; Abasi, A.K.; Alyasseri, Z.A.A. A novel hybrid grey wolf optimizer with min-conflict algorithm for power scheduling problem in a smart home. Swarm Evol. Comput. 2021, 60, 100793. [Google Scholar] [CrossRef]
- Makhadmeh, S.N.; Khader, A.T.; Al-Betar, M.A.; Naim, S. Multi-objective power scheduling problem in smart homes using grey wolf optimiser. J. Ambient Intell. Humaniz. Comput. 2019, 10, 3643–3667. [Google Scholar] [CrossRef]
- Makhadmeh, S.N.; Al-Betar, M.A.; Alyasseri, Z.A.A.; Abasi, A.K.; Khader, A.T.; Damaševičius, R.; Mohammed, M.A.; Abdulkareem, K.H. Smart Home Battery for the Multi-Objective Power Scheduling Problem in a Smart Home Using Grey Wolf Optimizer. Electronics 2021, 10, 447. [Google Scholar] [CrossRef]
- Makhadmeh, S.N.; Khader, A.T.; Al-Betar, M.A.; Naim, S.; Alyasseri, Z.A.A.; Abasi, A.K. A min-conflict algorithm for power scheduling problem in a smart home using battery. In Proceedings of the 11th National Technical Seminar on Unmanned System Technology, Singapore, 2–3 December 2019; Springer: Singapore, 2020; pp. 489–501. [Google Scholar]
- Khurma, R.A.; Alsawalqah, H.; Aljarah, I.; Elaziz, M.A.; Damaševičius, R. An enhanced evolutionary software defect prediction method using island moth flame optimization. Mathematics 2021, 9, 1722. [Google Scholar] [CrossRef]
- Alyasseri, Z.A.A.; Khader, A.T.; Al-Betar, M.A.; Abasi, A.K.; Makhadmeh, S.N. EEG signals denoising using optimal wavelet transform hybridized with efficient metaheuristic methods. IEEE Access 2019, 8, 10584–10605. [Google Scholar] [CrossRef]
- Alyasseri, Z.A.A.; Khader, A.T.; Al-Betar, M.A.; Papa, J.P.; Alomari, O.A.; Makhadme, S.N. An efficient optimization technique of eeg decomposition for user authentication system. In Proceedings of the 2018 2nd International Conference on BioSignal Analysis, Processing and Systems (ICBAPS), Kuching, Malaysia, 24–26 July 2018; pp. 1–6. [Google Scholar]
- Alyasseri, Z.A.A.; Khadeer, A.T.; Al-Betar, M.A.; Abasi, A.; Makhadmeh, S.; Ali, N.S. The effects of EEG feature extraction using multi-wavelet decomposition for mental tasks classification. In Proceedings of the International Conference on Information and Communication Technology, Singapore, 16–18 August 2019; pp. 139–146. [Google Scholar]
- Xie, Q.; Cheng, G.; Zhang, X.; Lei, P. Feature selection using improved forest optimization algorithm. Inf. Technol. Control 2020, 49, 289–301. [Google Scholar] [CrossRef]
- Alrassas, A.M.; Al-Qaness, M.A.A.; Ewees, A.A.; Ren, S.; Elaziz, M.A.; Damaševičius, R.; Krilavičius, T. Optimized anfis model using aquila optimizer for oil production forecasting. Processes 2021, 9, 1194. [Google Scholar] [CrossRef]
- Alyasseri, Z.A.A.; Khader, A.T.; Al-Betar, M.A.; Papa, J.P.; Alomari, O.A.; Makhadmeh, S.N. Classification of eeg mental tasks using multi-objective flower pollination algorithm for person identification. Int. J. Integr. Eng. 2018, 10. Available online: https://publisher.uthm.edu.my/ojs/index.php/ijie/article/view/3478 (accessed on 26 June 2021). [CrossRef]
- Alyasseri, Z.A.A.; Khader, A.T.; Al-Betar, M.A.; Abasi, A.K.; Makhadmeh, S.N. EEG signal denoising using hybridizing method between wavelet transform with genetic algorithm. In Proceedings of the 11th National Technical Seminar on Unmanned System Technology, Singapore, 2–3 December 2019; Springer: Singapore, 2020; pp. 449–469. [Google Scholar]
- Helmi, A.M.; Al-Qaness, M.A.A.; Dahou, A.; Damaševičius, R.; Krilavičius, T.; Elaziz, M.A. A novel hybrid gradient-based optimizer and grey wolf optimizer feature selection method for human activity recognition using smartphone sensors. Entropy 2021, 23, 1065. [Google Scholar] [CrossRef]
- Altan, A.; Karasu, S.; Zio, E. A new hybrid model for wind speed forecasting combining long short-term memory neural network, decomposition methods and grey wolf optimizer. Appl. Soft Comput. 2021, 100, 106996. [Google Scholar] [CrossRef]
- Abasi, A.K.; Khader, A.T.; Al-Betar, M.A.; Naim, S.; Makhadmeh, S.N.; Alyasseri, Z.A.A. Link-based multi-verse optimizer for text documents clustering. Appl. Soft Comput. 2019, 87, 106002. [Google Scholar] [CrossRef]
- Alrosan, A.; Alomoush, W.; Alswaitti, M.; Alissa, K.; Sahran, S.; Makhadmeh, S.N.; Alieyan, K. Automatic Data Clustering Based Mean Best Artificial Bee Colony Algorithm. Cmc-Comput. Mater. Contin. 2021, 68, 1575–1593. [Google Scholar] [CrossRef]
- Alyasseri, Z.A.A.; Abasi, A.K.; Al-Betar, M.A.; Makhadmeh, S.N.; Papa, J.P.; Abdullah, S.; Khader, A.T. EEG-Based Person Identification Using Multi-Verse Optimizer as Unsupervised Clustering Techniques. In Evolutionary Data Clustering: Algorithms and Applications; Springer: Singapore, 2021; p. 89. Available online: https://www.google.com/books?hl=en&lr=&id=20wfEAAAQBAJ&oi=fnd&pg=PA88&dq=EG-Based+Person+Identification+Using+Multi-Verse+Optimizer+as+++Unsupervised+Clustering+Techniques.&ots=U329jhbpa6&sig=KEDQzcxWM_jcun6McESW5PYF01w (accessed on 1 November 2021).
- Abasi, A.K.; Khader, A.T.; Al-Betar, M.A.; Naim, S.; Makhadmeh, S.N.; Alyasseri, Z.A.A. A Text Feature Selection Technique based on Binary Multi-Verse Optimizer for Text Clustering. In Proceedings of the 2019 IEEE Jordan International Joint Conference on Electrical Engineering and Information Technology (JEEIT), Amman, Jordan, 9–11 April 2019; pp. 1–6. [Google Scholar]
- Abasi, A.K.; Khader, A.T.; Al-Betar, M.A.; Naim, S.; Makhadmeh, S.N.; Alyasseri, Z.A.A. An improved text feature selection for clustering using binary grey wolf optimizer. In Proceedings of the 11th National Technical Seminar on Unmanned System Technology, Singapore, 2–3 December 2019; Springer: Singapore, 2021; pp. 503–516. [Google Scholar]
- Abasi, A.K.; Khader, A.T.; Al-Betar, M.A.; Alyasseri, Z.A.A.; Makhadmeh, S.N.; Al-laham, M.; Naim, S. A Hybrid Salp Swarm Algorithm with β-Hill Climbing Algorithm for Text Documents Clustering. In Evolutionary Data Clustering: Algorithms and Applications; Springer: Singapore, 2021; p. 129. Available online: https://www.google.com/books?hl=en&lr=&id=20wfEAAAQBAJ&oi=fnd&pg=PA129&dq=A+Hybrid+Salp+Swarm+Algorithm+with+%24%5Cbeta%24-Hill+Climbing+Algorithm+++for+Text+Documents+Clustering.&ots=U329jhclec&sig=8XSWNweSeqR0I10YIPIpt4Y75Ic (accessed on 1 November 2021).
- Jouhari, H.; Lei, D.; Al-qaness, M.A.A.; Abd Elaziz, M.; Damaševičius, R.; Korytkowski, M.; Ewees, A.A. Modified Harris Hawks optimizer for solving machine scheduling problems. Symmetry 2020, 12, 1460. [Google Scholar] [CrossRef]
- Ksiazek, K.; Połap, D.; Woźniak, M.; Damaševičius, R. Radiation heat transfer optimization by the use of modified ant lion optimizer. In Proceedings of the 2017 IEEE Symposium Series on Computational Intelligence, SSCI 2017-Proceedings, Honolulu, HI, USA, 27 November–1 December 2017; pp. 1–7. [Google Scholar]
- Khan, D.M.; Aslam, T.; Akhtar, N.; Qadri, S.; Khan, N.A.; Rabbani, I.M.; Aslam, M. Black hole attack prevention in mobile ad hoc network (Manet) using ant colony optimization technique. Inf. Technol. Control 2020, 49, 308–319. [Google Scholar] [CrossRef]
- Abasi, A.K.; Khader, A.T.; Al-Betar, M.A.; Naim, S.; Alyasseri, Z.A.A.; Makhadmeh, S.N. A novel hybrid multi-verse optimizer with K-means for text documents clustering. Neural Comput. Appl. 2020, 32, 17703–17729. [Google Scholar] [CrossRef]
- Abasi, A.K.; Khader, A.T.; Al-Betar, M.A.; Naim, S.; Alyasseri, Z.A.A.; Makhadmeh, S.N. An ensemble topic extraction approach based on optimization clusters using hybrid multi-verse optimizer for scientific publications. J. Ambient. Intell. Humaniz. Comput. 2020, 12, 2765–2801. [Google Scholar] [CrossRef]
- Abasi, A.K.; Khader, A.T.; Al-Betar, M.A.; Naim, S.; Makhadmeh, S.N.; Alyasseri, Z.A.A. A novel ensemble statistical topic extraction method for scientific publications based on optimization clustering. Multimed. Tools Appl. 2021, 80, 37–82. [Google Scholar] [CrossRef]
- Wang, H.; Song, W.; Zio, E.; Kudreyko, A.; Zhang, Y. Remaining useful life prediction for Lithium-ion batteries using fractional Brownian motion and Fruit-fly Optimization Algorithm. Meas. J. Int. Meas. Confed. 2020, 161, 107904. [Google Scholar] [CrossRef]
- Subramaniyan, S.; Perumal, T. Statistical Markov model based natural inspired glowworm swarm multi-objective optimization for energy efficient data delivery in MANET. Inf. Technol. Control 2020, 49, 333–347. [Google Scholar]
- Alrosan, A.; Alomoush, W.; Norwawi, N.; Alswaitti, M.; Makhadmeh, S.N. An improved artificial bee colony algorithm based on mean best-guided approach for continuous optimization problems and real brain MRI images segmentation. Neural Comput. Appl. 2020, 33, 1671–1697. [Google Scholar] [CrossRef]
- Khan, M.A.; Sharif, M.; Akram, T.; Damaševičius, R.; Maskeliūnas, R. Skin lesion segmentation and multiclass classification using deep learning features and improved moth flame optimization. Diagnostics 2021, 11, 811. [Google Scholar] [CrossRef]
- Alomari, O.A.; Makhadmeh, S.N.; Al-Betar, M.A.; Alyasseri, Z.A.A.; Doush, I.A.; Abasi, A.K.; Awadallah, M.A.; Zitar, R.A. Gene selection for microarray data classification based on Gray Wolf Optimizer enhanced with TRIZ-inspired operators. Knowl.-Based Syst. 2021, 223, 107034. [Google Scholar] [CrossRef]
- Alyasseri, Z.A.A.; Al-Betar, M.A.; Awadallah, M.A.; Makhadmeh, S.N.; Abasi, A.K.; Doush, I.A.; Alomari, O.A. A hybrid flower pollination with β-hill climbing algorithm for global optimization. J. King Saud-Univ.-Comput. Inf. Sci. in press. 2021. [Google Scholar] [CrossRef]
- Salehan, A.; Deldari, A. Corona virus optimization (CVO): A novel optimization algorithm inspired from the Corona virus pandemic. J. Supercomput. 2021, 1–32. [Google Scholar] [CrossRef]
- Martínez-Álvarez, F.; Asencio-Cortés, G.; Torres, J.F.; Gutiérrez-Avilés, D.; Melgar-García, L.; Pérez-Chacón, R.; Rubio-Escudero, C.; Riquelme, J.C.; Troncoso, A. Coronavirus optimization algorithm: A bioinspired metaheuristic based on the COVID-19 propagation model. Big Data 2020, 8, 308–322. [Google Scholar] [CrossRef]
- Li, Z.; Tam, V. A novel meta-heuristic optimization algorithm inspired by the spread of viruses. arXiv 2020, arXiv:2006.06282. [Google Scholar]
- Li, M.D.; Zhao, H.; Weng, X.W.; Han, T. A novel nature-inspired algorithm for optimization: Virus colony search. Adv. Eng. Softw. 2016, 92, 65–88. [Google Scholar] [CrossRef]
- Al-Betar, M.A.; Alyasseri, Z.A.A.; Awadallah, M.A.; Doush, I.A. Coronavirus herd immunity optimizer (CHIO). Neural Comput. Appl. 2020, 33, 5011–5042. [Google Scholar] [CrossRef] [PubMed]
- Dalbah, L.M.; Al-Betar, M.A.; Awadallah, M.A.; Zitar, R.A. A modified coronavirus herd immunity optimizer for capacitated vehicle routing problem. J. King Saud-Univ.-Comput. Inf. Sci. 2021; in press. [Google Scholar] [CrossRef]
- Alweshah, M.; Alkhalaileh, S.; Al-Betar, M.A.; Bakar, A.A. Coronavirus herd immunity optimizer with greedy crossover for feature selection in medical diagnosis. Knowl.-Based Syst. 2022, 235, 107629. [Google Scholar] [CrossRef] [PubMed]
- Mahboob, A.S.; Shahhoseini, H.S.; Moghaddam, M.R.O.; Yousefi, S. A Coronavirus Herd Immunity Optimizer For Intrusion Detection System. In Proceedings of the 2021 29th Iranian Conference on Electrical Engineering (ICEE), Tehran, Iran, 18–20 May 2021; pp. 579–585. [Google Scholar]
- Neto, A.S.A. Optimization inspired on herd immunity applied to Non-hierarchical grouping of objects. Rev. Inform. Teór. E Apl. 2021, 28, 50–65. [Google Scholar] [CrossRef]
- Aslam, S.; Iqbal, Z.; Javaid, N.; Khan, Z.A.; Aurangzeb, K.; Haider, S.I. Towards Efficient Energy Management of Smart Buildings Exploiting Heuristic Optimization with Real Time and Critical Peak Pricing Schemes. Energies 2017, 10, 2065. [Google Scholar] [CrossRef] [Green Version]
- Soares, A.; Antunes, C.H.; Oliveira, C.; Gomes, Á. A multi-objective genetic approach to domestic load scheduling in an energy management system. Energy 2014, 77, 144–152. [Google Scholar] [CrossRef]
- Rasheed, M.B.; Javaid, N.; Ahmad, A.; Khan, Z.A.; Qasim, U.; Alrajeh, N. An efficient power scheduling scheme for residential load management in smart homes. Appl. Sci. 2015, 5, 1134–1163. [Google Scholar] [CrossRef] [Green Version]
- Ullah, I.; Hussain, I.; Singh, M. Exploiting grasshopper and cuckoo search bio-inspired optimization algorithms for industrial energy management system: Smart industries. Electronics 2020, 9, 105. [Google Scholar] [CrossRef] [Green Version]
- Rahim, S.; Javaid, N.; Ahmad, A.; Khan, S.A.; Khan, Z.A.; Alrajeh, N.; Qasim, U. Exploiting heuristic algorithms to efficiently utilize energy management controllers with renewable energy sources. Energy Build. 2016, 129, 452–470. [Google Scholar] [CrossRef]
- Muralitharan, K.; Sakthivel, R.; Shi, Y. Multiobjective optimization technique for demand side management with load balancing approach in smart grid. Neurocomputing 2016, 177, 110–119. [Google Scholar] [CrossRef]
- Makhadmeh, S.N.; Khader, A.T.; Al-Betar, M.A.; Naim, S.; Alyasseri, Z.A.A.; Abasi, A.K. Particle swarm optimization algorithm for power scheduling problem using smart battery. In Proceedings of the 2019 IEEE Jordan International Joint Conference on Electrical Engineering and Information Technology (JEEIT), Amman, Jordan, 9–11 April 2019; pp. 672–677. [Google Scholar]
- Khan, H.N.; Iftikhar, H.; Asif, S.; Maroof, R.; Ambreen, K.; Javaid, N. Demand side management using strawberry algorithm and bacterial foraging optimization algorithm in smart grid. In International Conference on Network-Based Information Systems; Springer: Cham, Switzerland, 2017; pp. 191–202. [Google Scholar]
- Farina, M.; Amato, P. A fuzzy definition of “optimality” for many-criteria optimization problems. IEEE Trans. Syst. Man, Cybern.-Part A Syst. Hum. 2004, 34, 315–326. [Google Scholar] [CrossRef]
- López Jaimes, A.; Coello Coello, C.A. Some techniques to deal with many-objective problems. In Proceedings of the 11th Annual Conference Companion on Genetic and Evolutionary Computation Conference: Late Breaking Papers, Montreal, QC, Canada, 8–12 July 2009; pp. 2693–2696. [Google Scholar]
- Farina, M.; Amato, P. Fuzzy optimality and evolutionary multiobjective optimization. In International Conference on Evolutionary Multi-Criterion Optimization; Springer: Berlin/Heidelberg, Germany, 2003; pp. 58–72. [Google Scholar]
- Marler, R.T.; Arora, J.S. Survey of multi-objective optimization methods for engineering. Struct. Multidiscip. Optim. 2004, 26, 369–395. [Google Scholar] [CrossRef]
- Fei, Z.; Li, B.; Yang, S.; Xing, C.; Chen, H.; Hanzo, L. A survey of multi-objective optimization in wireless sensor networks: Metrics, algorithms, and open problems. IEEE Commun. Surv. Tutor. 2017, 19, 550–586. [Google Scholar] [CrossRef] [Green Version]
- Cho, J.H.; Wang, Y.; Chen, R.; Chan, K.S.; Swami, A. A Survey on Modeling and Optimizing Multi-Objective Systems. IEEE Commun. Surv. Tutor. 2017, 19, 1867–1901. [Google Scholar] [CrossRef]
- Simon, D. Evolutionary Optimization Algorithms: Biologically-Inspired and Population-Based Approaches to Computer Intelligence; John Wiley & Sons: Hoboken, NJ, USA, 2013. [Google Scholar]
- Gunantara, N. A review of multi-objective optimization: Methods and its applications. Cogent Eng. 2018, 5, 1502242. [Google Scholar] [CrossRef]
- Lai, C.C.; Shih, T.P.; Ko, W.C.; Tang, H.J.; Hsueh, P.R. Severe acute respiratory syndrome coronavirus 2 (SARS-CoV-2) and corona virus disease-2019 (COVID-19): The epidemic and the challenges. Int. J. Antimicrob. Agents 2020, 55, 105924. [Google Scholar] [CrossRef]
- Kwok, K.O.; Lai, F.; Wei, W.I.; Wong, S.Y.S.; Tang, J.W. Herd immunity–estimating the level required to halt the COVID-19 epidemics in affected countries. J. Infect. 2020, 80, e32–e33. [Google Scholar] [CrossRef]
- Remuzzi, A.; Remuzzi, G. COVID-19 and Italy: What next? Lancet 2020, 395, 1225–1228. [Google Scholar] [CrossRef]
- Ribeiro, G.S.; Hamer, G.L.; Diallo, M.; Kitron, U.; Ko, A.I.; Weaver, S.C. Influence of herd immunity in the cyclical nature of arboviruses. Curr. Opin. Virol. 2020, 40, 1–10. [Google Scholar] [CrossRef]
- Fine, P.E. Herd immunity: History, theory, practice. Epidemiol. Rev. 1993, 15, 265–302. [Google Scholar] [CrossRef]
- Dalbah, L.M.; Al-Betar, M.A.; Awadallah, M.A.; Zitar, R.A. Al-Betar, M.A.; Awadallah, M.A.; Zitar, R.A. A coronavirus herd immunity optimization (chio) for travelling salesman problem. In International Conference on Innovative Computing and Communications; Springer: Singapore, 2022; pp. 717–729. [Google Scholar]
- Kumar, C.; Magdalin Mary, D.; Gunasekar, T. MOCHIO: A novel Multi-Objective Coronavirus Herd Immunity Optimization algorithm for solving brushless direct current wheel motor design optimization problem. Automatika 2021, 63, 149–170. [Google Scholar] [CrossRef]
- Naderipour, A.; Abdullah, A.; Marzbali, M.H.; Nowdeh, S.A. An improved corona-virus herd immunity optimizer algorithm for network reconfiguration based on fuzzy multi-criteria approach. Expert Syst. Appl. 2022, 187, 115914. [Google Scholar] [CrossRef] [PubMed]
- Amini, S.; Ghasemi, S.; Golpira, H.; Anvari-Moghaddam, A. Coronavirus Herd Immunity Optimizer (CHIO) for Transmission Expansion Planning. In Proceedings of the 2021 IEEE International Conference on Environment and Electrical Engineering and 2021 IEEE Industrial and Commercial Power Systems Europe (EEEIC/I&CPS Europe), Bari, Italy, 7–10 September 2021; pp. 1–6. [Google Scholar]
- Central Maine Diesel Inc. Generator Sales; Central Maine Diesel Inc.: Hampden, ME, USA, 2017. [Google Scholar]
- Ogwumike, C.; Short, M.; Abugchem, F. Heuristic optimization of consumer electricity costs using a generic cost model. Energies 2015, 9, 6. [Google Scholar] [CrossRef] [Green Version]
- Forsati, R.; Mahdavi, M.; Shamsfard, M.; Meybodi, M.R. Efficient stochastic algorithms for document clustering. Inf. Sci. 2013, 220, 269–291. [Google Scholar] [CrossRef]
| PSPSH Process | CHIO Process |
|---|---|
| Candidate Solution | Infected, susceptible, and immune cases |
| Social Distancing | Pick a random case and rely on the basic reproduction rate |
| Optimal Solution | immune cases |
| Fitness Value | Immunity rate |
| Fatality Rate | Reach the maximum age |
| Population | HIP |
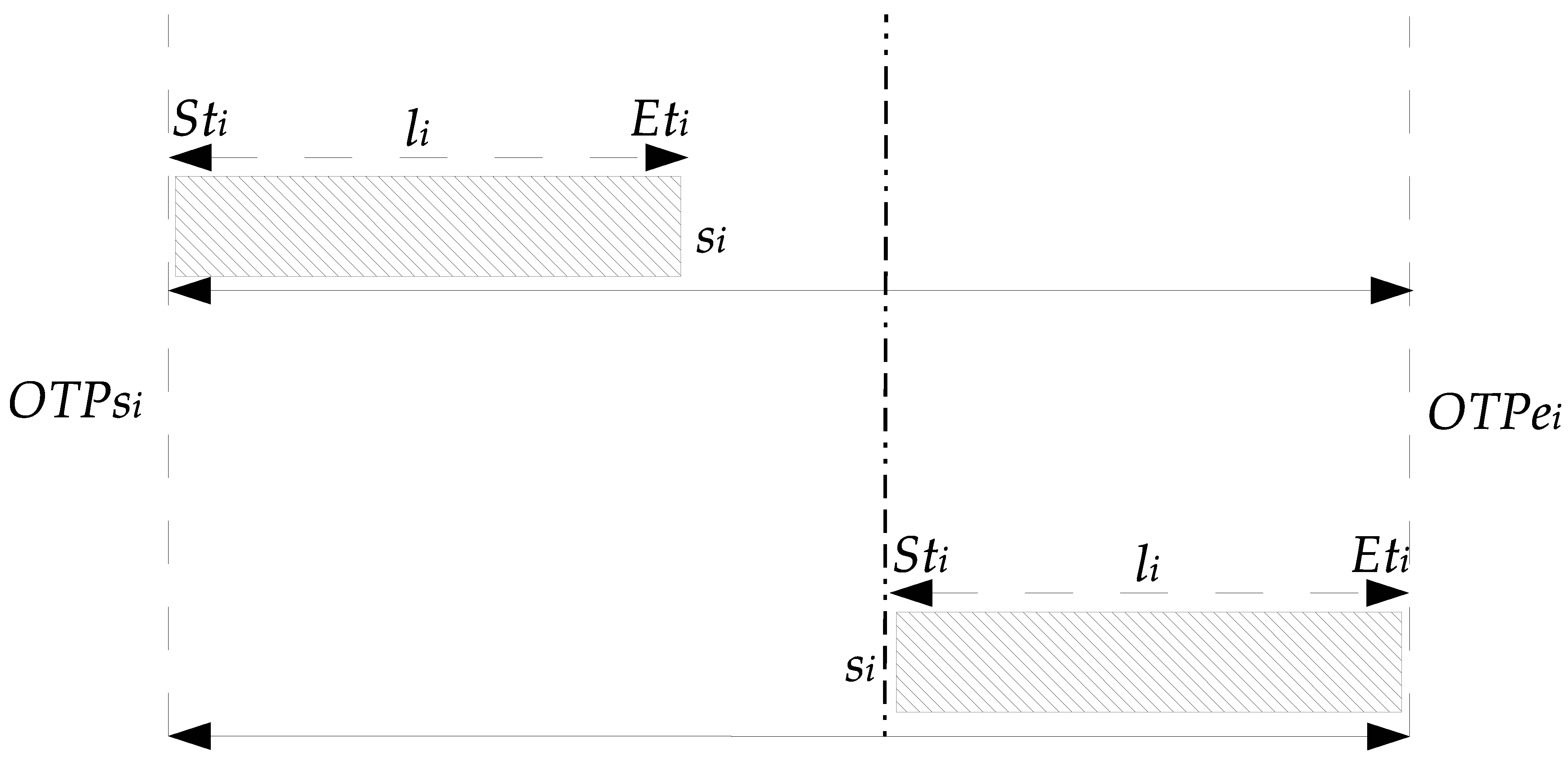
| NO. | Appliances | LOC | OTPs–OTPe | NO. | Appliances | LOC | OTPs–OTPe |
|---|---|---|---|---|---|---|---|
| 1 | Dishwasher | 105 | 540–780 | 19 | Dehumidifier | 30 | 1–120 |
| 2 | Dishwasher | 105 | 840–1080 | 20 | Dehumidifier | 30 | 120–240 |
| 3 | Dishwasher | 105 | 1200–1440 | 21 | Dehumidifier | 30 | 240–360 |
| 4 | Air Conditioner | 30 | 1–120 | 22 | Dehumidifier | 30 | 360–480 |
| 5 | Air Conditioner | 30 | 120–240 | 23 | Dehumidifier | 30 | 480–600 |
| 6 | Air Conditioner | 30 | 240–360 | 24 | Dehumidifier | 30 | 600–720 |
| 7 | Air Conditioner | 30 | 360–480 | 25 | Dehumidifier | 30 | 720–840 |
| 8 | Air Conditioner | 30 | 480–600 | 26 | Dehumidifier | 30 | 840–960 |
| 9 | Air Conditioner | 30 | 600–720 | 27 | Dehumidifier | 30 | 960–1080 |
| 10 | Air Conditioner | 30 | 720–840 | 28 | Dehumidifier | 30 | 1080–1200 |
| 11 | Air Conditioner | 30 | 840–960 | 29 | Dehumidifier | 30 | 1200–1320 |
| 12 | Air Conditioner | 30 | 960–1080 | 30 | Dehumidifier | 30 | 1320–1440 |
| 13 | Air Conditioner | 30 | 1080–1200 | 31 | Electric Water Heater | 35 | 300–420 |
| 14 | Air Conditioner | 30 | 1200–1320 | 32 | Electric Water Heater | 35 | 1100–1440 |
| 15 | Air Conditioner | 30 | 1320–1440 | 33 | Coffee Maker | 10 | 300–450 |
| 16 | Washing Machine | 55 | 60–300 | 34 | Coffee Maker | 10 | 1020–1140 |
| 17 | Clothes Dryer | 60 | 300–480 | 35 | Robotic Pool Filter | 180 | 1–540 |
| 18 | Refrigerator | 1440 | 1–1440 | 36 | Robotic Pool Filter | 180 | 900–1440 |
| No. | Appliances | Power (kW) |
|---|---|---|
| 1 | Light [52] | 0.6 |
| 2 | Attic Fan [73] | 0.3 |
| 3 | Table Fan [73] | 0.8 |
| 4 | Iron [52] | 1.5 |
| 5 | Toaster [73] | 1 |
| 6 | Computer Charger [73] | 1.5 |
| 7 | Cleaner [2] | 1.5 |
| 8 | TV [73] | 0.3 |
| 9 | Hair Dryer [73] | 1.2 |
| 10 | Hand Drill [73] | 0.6 |
| 11 | Water Pump [73] | 2.5 |
| 12 | Blender [73] | 0.3 |
| 13 | Microwave [52] | 1.18 |
| 14 | Electric Vehicle [74] | 1 |
| S # | Appliances |
|---|---|
| S #1 | 1, 3, 4, 5, 6, 7, 15, 18, 19, 20, 21, 22, 23, 24, 25, 26, 27, 28, 29, 30, 31, 33, 35 |
| S #2 | 1, 2, 4, 5, 6, 7, 10, 11, 12, 18, 25, 26, 27, 28, 29, 31, 32, 33, 34, 36 |
| S #3 | 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14, 15, 18, 23, 24, 25, 26, 27, 28, 31, 32, 33, 34, 35 |
| S #4 | 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14, 15, 16, 17, 18, 19, 20, 21, 22, 23, 24, 25, 26, 27, 28, 29, 30, 31, 32, 33, 34, 35, 36 |
| S #5 | 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14, 15, 18, 23, 24, 25, 26, 27, 28, 31, 32, 33, 34, 35 |
| S #6 | 1, 2, 3, 8, 9, 10, 11, 12, 18, 19, 20, 21, 22, 23, 24, 25, 26, 27, 28, 29, 30, 31, 33, 34, 35 |
| S #7 | 1, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14, 15, 16, 17, 18, 19, 20, 21, 22, 23, 24, 25, 26, 27, 28, 29, 30, 31, 33, 34, 35, 36 |
| Parameter | Value |
|---|---|
| Population Size () | 40 |
| Max Iteration (I) | 1000 |
| 0.005 | 0.05 | 0.1 | 0.5 | ||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| S # | EB | PAR | WTR | CPR | EB | PAR | WTR | CPR | EB | PAR | WTR | CPR | EB | PAR | WTR | CPR | |
| 50 | S #1 | 43.4641 | 2.6807 | 0.2242 | 0.3227 | 43.8147 | 2.6044 | 0.0094 | 0.3127 | 43.7384 | 2.6045 | 0.0087 | 0.3129 | 43.5523 | 2.6045 | 0.0458 | 0.3164 |
| S #2 | 64.1402 | 2.6446 | 0.2086 | 0.3462 | 64.6208 | 2.4323 | 0.0124 | 0.3453 | 64.4169 | 2.4254 | 0.0147 | 0.3455 | 64.2613 | 2.4169 | 0.0297 | 0.3460 | |
| S #3 | 65.9196 | 2.3865 | 0.2182 | 0.3934 | 66.4258 | 2.2181 | 0.0150 | 0.3803 | 66.3190 | 2.2117 | 0.0144 | 0.3805 | 66.3121 | 2.2225 | 0.0405 | 0.3832 | |
| S #4 | 63.2499 | 2.5270 | 0.2356 | 0.5101 | 63.3545 | 1.8744 | 0.0431 | 0.5066 | 63.3702 | 1.9665 | 0.0388 | 0.5096 | 62.8679 | 2.0783 | 0.0838 | 0.5135 | |
| S #5 | 46.5781 | 2.4151 | 0.2125 | 0.3929 | 46.7815 | 2.2203 | 0.0157 | 0.3806 | 46.7853 | 2.2160 | 0.0124 | 0.3801 | 46.6086 | 2.2139 | 0.0423 | 0.3843 | |
| S #6 | 52.4087 | 2.5095 | 0.2031 | 0.3570 | 52.6468 | 2.5175 | 0.0095 | 0.3490 | 52.4176 | 2.5040 | 0.0143 | 0.3500 | 52.2710 | 2.5060 | 0.0388 | 0.3521 | |
| S #7 | 63.3368 | 2.3054 | 0.2535 | 0.4800 | 63.0784 | 2.004 | 0.0386 | 0.4661 | 63.2179 | 2.0385 | 0.0337 | 0.4656 | 62.9447 | 2.0086 | 0.0763 | 0.4729 | |
| 100 | S #1 | 43.5971 | 2.7084 | 0.2041 | 0.3220 | 43.8176 | 2.6044 | 0.0076 | 0.3122 | 43.8085 | 2.6045 | 0.0089 | 0.3128 | 43.4891 | 2.6024 | 0.0379 | 0.3164 |
| S #2 | 63.4767 | 2.5924 | 0.2266 | 0.3489 | 64.4900 | 2.4248 | 0.0136 | 0.3454 | 64.290 | 2.4199 | 0.0123 | 0.3456 | 64.5717 | 2.4332 | 0.0304 | 0.3460 | |
| S #3 | 66.4986 | 2.3235 | 0.2269 | 0.3931 | 66.6698 | 2.2246 | 0.0123 | 0.3791 | 66.4452 | 2.216 | 0.0138 | 0.3801 | 66.0401 | 2.2203 | 0.0408 | 0.3844 | |
| S #4 | 62.8937 | 2.4846 | 0.2365 | 0.5113 | 63.3123 | 1.9471 | 0.0373 | 0.5104 | 63.2181 | 1.9723 | 0.0388 | 0.5104 | 62.7356 | 2.0188 | 0.0875 | 0.5157 | |
| S #5 | 46.4773 | 2.4009 | 0.2209 | 0.3931 | 46.7609 | 2.2160 | 0.0154 | 0.3802 | 46.4528 | 2.2117 | 0.0190 | 0.3817 | 46.7672 | 2.2273 | 0.0456 | 0.3841 | |
| S #6 | 51.9756 | 2.5213 | 0.2208 | 0.3608 | 52.5642 | 2.5175 | 0.0116 | 0.3491 | 52.1948 | 2.4944 | 0.0153 | 0.3508 | 52.2699 | 2.5060 | 0.0326 | 0.3515 | |
| S #7 | 63.1163 | 2.3252 | 0.2346 | 0.4784 | 63.3557 | 2.0195 | 0.0297 | 0.4643 | 63.0719 | 2.0152 | 0.0362 | 0.4661 | 62.8943 | 2.0117 | 0.0723 | 0.4724 | |
| 300 | S #1 | 43.5265 | 2.6543 | 0.2239 | 0.3224 | 43.8004 | 2.6044 | 0.0074 | 0.3126 | 43.8163 | 2.6045 | 0.006 | 0.3123 | 43.6746 | 2.6024 | 0.0352 | 0.3156 |
| S #2 | 64.3299 | 2.5915 | 0.2181 | 0.3473 | 64.4096 | 2.4244 | 0.0112 | 0.3454 | 64.2427 | 2.4199 | 0.0129 | 0.3456 | 64.4953 | 2.4341 | 0.026 | 0.3459 | |
| S #3 | 66.0201 | 2.3541 | 0.2266 | 0.3944 | 66.7045 | 2.2267 | 0.0102 | 0.3790 | 66.6802 | 2.2246 | 0.0102 | 0.3791 | 66.3345 | 2.2246 | 0.0425 | 0.3838 | |
| S #4 | 63.1029 | 2.4434 | 0.2352 | 0.5131 | 63.0111 | 1.9239 | 0.0386 | 0.5118 | 63.2983 | 1.9223 | 0.0404 | 0.5112 | 62.5525 | 2.0766 | 0.0785 | 0.5132 | |
| S #5 | 46.3968 | 2.3109 | 0.2172 | 0.3955 | 46.6641 | 2.2117 | 0.0167 | 0.3804 | 46.4139 | 2.2010 | 0.0159 | 0.3816 | 46.4839 | 2.216 | 0.0379 | 0.3847 | |
| S #6 | 52.6838 | 2.5650 | 0.1999 | 0.3565 | 52.4779 | 2.5117 | 0.0102 | 0.3494 | 52.1136 | 2.4887 | 0.0141 | 0.3509 | 52.2548 | 2.506 | 0.0295 | 0.3516 | |
| S #7 | 63.2469 | 2.4141 | 0.2121 | 0.4740 | 63.2371 | 2.0133 | 0.0296 | 0.4647 | 63.1973 | 2.0118 | 0.0325 | 0.4653 | 62.3167 | 2.0149 | 0.081 | 0.4751 | |
| 500 | S #1 | 43.3217 | 2.603 | 0.2088 | 0.3234 | 43.8209 | 2.6044 | 0.0066 | 0.3123 | 43.8142 | 2.6045 | 0.0059 | 0.3124 | 43.6684 | 2.6024 | 0.0251 | 0.315 |
| S #2 | 64.04 | 2.6589 | 0.1998 | 0.3479 | 64.6379 | 2.4359 | 0.0098 | 0.3453 | 64.2235 | 2.4176 | 0.0138 | 0.3456 | 64.5138 | 2.4321 | 0.0284 | 0.346 | |
| S #3 | 65.9527 | 2.3322 | 0.216 | 0.3919 | 66.6666 | 2.2246 | 0.0107 | 0.3791 | 66.642 | 2.2225 | 0.0111 | 0.3795 | 66.2984 | 2.223 | 0.0451 | 0.3843 | |
| S #4 | 63.6569 | 2.5122 | 0.2225 | 0.5076 | 63.3165 | 1.9488 | 0.0350 | 0.5097 | 63.0808 | 1.9197 | 0.0373 | 0.5113 | 62.8417 | 1.9618 | 0.0883 | 0.5173 | |
| S #5 | 46.5366 | 2.3837 | 0.1951 | 0.3933 | 46.5411 | 2.2095 | 0.0143 | 0.3808 | 46.4481 | 2.2031 | 0.0149 | 0.3811 | 46.3428 | 2.2165 | 0.0443 | 0.3855 | |
| S #6 | 52.532 | 2.5412 | 0.1905 | 0.358 | 52.0938 | 2.4944 | 0.0126 | 0.3508 | 52.3337 | 2.5002 | 0.0103 | 0.35 | 52.4137 | 2.5156 | 0.0321 | 0.3517 | |
| S #7 | 62.9267 | 2.2803 | 0.2238 | 0.4807 | 63.2214 | 2.0288 | 0.0304 | 0.4647 | 63.0749 | 2.0071 | 0.0337 | 0.466 | 62.5727 | 2.0133 | 0.0839 | 0.4755 | |
| S # | EB | PAR | WTR | CPR |
|---|---|---|---|---|
| S #1 | 0.005/500 | 0.5/100, 300, 500 | 0.1/500 | 0.05/100 |
| S #2 | 0.005/100 | 0.5/50 | 0.05/500 | 0.05/50, 500 |
| S #3 | 0.005/50 | 0.1/50 | 0.05, 0.1/300 | 0.05/300 |
| S #4 | 0.5/300 | 0.05/50 | 0.05/500 | 0.05/50 |
| S #5 | 0.5/500 | 0.1/300 | 0.1/50 | 0.1/50 |
| S #6 | 0.005/100 | 0.1/300 | 0.05/50 | 0.05/50 |
| S #7 | 0.5/300 | 0.05/50 | 0.05/300 | 0.05/100 |
| Iteration | S1 | S2 | S3 | S4 | S5 | FF | Normal | Infected | Recovered | Decision |
|---|---|---|---|---|---|---|---|---|---|---|
| 1 | 570 | 1218 | 42 | 198 | 275 | 0.4117 | 4 | 1 | 0 | Best solution |
| 2 | 570 | 1218 | 42 | 198 | 275 | 0.4117 | 4 | 1 | 0 | Do not replace best solution |
| 5 | 570 | 1218 | 42 | 198 | 275 | 0.4117 | 4 | 1 | 0 | Do not replace best solution |
| 8 | 557 | 1266 | 12 | 180 | 195 | 0.4100 | 4 | 1 | 0 | Replace best solution |
| 14 | 557 | 1266 | 1 | 180 | 195 | 0.4055 | 4 | 1 | 0 | Replace best solution |
| 33 | 557 | 1266 | 1 | 180 | 195 | 0.4055 | 3 | 2 | 0 | Do not replace best solution |
| 39 | 557 | 1266 | 1 | 180 | 195 | 0.4055 | 3 | 1 | 1 | Do not replace best solution |
| 58 | 576 | 1298 | 6 | 187 | 241 | 0.4049 | 2 | 2 | 1 | Replace best solution |
| 60 | 567 | 1263 | 33 | 137 | 260 | 0.3897 | 2 | 1 | 2 | Replace best solution |
| 77 | 539 | 1213 | 10 | 168 | 260 | 0.3875 | 2 | 1 | 2 | Replace best solution |
| 83 | 541 | 1225 | 38 | 183 | 254 | 0.3813 | 3 | 0 | 2 | Replace best solution |
| 100 | 541 | 1225 | 38 | 183 | 254 | 0.3813 | 3 | 0 | 2 | Replace best solution |
| S # | GA | PSO | WDO | DE | GWO | CHIO |
|---|---|---|---|---|---|---|
| S #1 | 42.8801 | 42.9128 | 43.2542 | 43.8137 | 43.5041 | 43.8147 |
| S #2 | 60.3058 | 62.3731 | 65.1472 | 64.9603 | 64.5597 | 64.6208 |
| S #3 | 65.2185 | 65.1080 | 66.1703 | 67.4365 | 66.1138 | 66.4258 |
| S #4 | 62.2197 | 62.7878 | 64.6019 | 64.2647 | 62.5916 | 63.3545 |
| S #5 | 45.6463 | 45.7852 | 46.4160 | 47.5699 | 46.2879 | 46.7815 |
| S #6 | 51.6958 | 51.9391 | 52.6767 | 52.7780 | 52.2998 | 52.6468 |
| S #7 | 61.5644 | 62.1783 | 64.4241 | 63.3523 | 62.6367 | 63.0784 |
| Average | 55.6472 | 56.1549 | 57.527261 | 57.73940 | 56.85627 | 57.2460 |
| S # | GA | PSO | WDO | DE | GWO | CHIO |
|---|---|---|---|---|---|---|
| S #1 | 2.6074 | 2.5943 | 2.6668 | 2.6044 | 2.6002 | 2.6044 |
| S #2 | 2.4305 | 2.4037 | 2.8451 | 2.4451 | 2.4451 | 2.4323 |
| S #3 | 2.3213 | 2.2409 | 2.2650 | 2.2310 | 2.2267 | 2.2181 |
| S #4 | 2.2516 | 2.3363 | 2.5033 | 2.1096 | 2.2277 | 1.8744 |
| S #5 | 2.2799 | 2.2458 | 2.2310 | 2.2310 | 2.2310 | 2.2203 |
| S #6 | 2.5055 | 2.5055 | 2.6006 | 2.5233 | 2.5233 | 2.5175 |
| S #7 | 2.2604 | 2.2275 | 2.6226 | 2.0071 | 2.0423 | 2.0039 |
| Average | 2.3795 | 2.3649 | 2.5335 | 2.3074 | 2.3280 | 2.2672 |
| S # | GA | PSO | WDO | DE | GWO | CHIO |
|---|---|---|---|---|---|---|
| S #1 | 0.3901 | 0.3523 | 0.0343 | 0.0150 | 0.0302 | 0.0094 |
| S #2 | 0.3709 | 0.3659 | 0.0149 | 0.0046 | 0.0242 | 0.0124 |
| S #3 | 0.3719 | 0.3673 | 0.0438 | 0.0281 | 0.0378 | 0.015 |
| S #4 | 0.3900 | 0.4036 | 0.0200 | 0.0293 | 0.0579 | 0.0431 |
| S #5 | 0.3677 | 0.3596 | 0.0405 | 0.0281 | 0.0396 | 0.0157 |
| S #6 | 0.3890 | 0.3636 | 0.0253 | 0.0136 | 0.0268 | 0.0095 |
| S #7 | 0.3853 | 0.3881 | 0.0092 | 0.0260 | 0.0587 | 0.0386 |
| Average | 0.3807 | 0.3715 | 0.0269 | 0.0207 | 0.0393 | 0.0205 |
| S # | GA | PSO | WDO | DE | GWO | CHIO |
|---|---|---|---|---|---|---|
| S #1 | 0.3248 | 0.3246 | 0.3143 | 0.3122 | 0.3148 | 0.3127 |
| S #2 | 0.3599 | 0.3535 | 0.3429 | 0.3449 | 0.3455 | 0.3453 |
| S #3 | 0.3957 | 0.3959 | 0.3799 | 0.3811 | 0.3815 | 0.3803 |
| S #4 | 0.5200 | 0.5121 | 0.4946 | 0.5044 | 0.5033 | 0.5066 |
| S #5 | 0.3969 | 0.3956 | 0.3801 | 0.3811 | 0.3822 | 0.3806 |
| S #6 | 0.3614 | 0.3594 | 0.3489 | 0.3481 | 0.3504 | 0.349 |
| S #7 | 0.4806 | 0.4797 | 0.4492 | 0.4628 | 0.4688 | 0.4661 |
| Average | 0.4056 | 0.4030 | 0.3871 | 0.3907 | 0.3924 | 0.3915 |
| S # | GA | PSO | WDO | DE | GWO | CHIO |
|---|---|---|---|---|---|---|
| S #1 | 64.2510 | 66.1500 | 82.5642 | 83.6358 | 82.7463 | 83.895 |
| S #2 | 63.4564 | 64.0215 | 82.1037 | 82.5222 | 81.5124 | 82.115 |
| S #3 | 61.6160 | 61.8364 | 78.8101 | 79.5370 | 79.0296 | 80.235 |
| S #4 | 54.4975 | 54.2085 | 74.2622 | 73.3118 | 71.9334 | 72.515 |
| S #5 | 61.7660 | 62.2313 | 78.9602 | 79.5370 | 78.9061 | 80.185 |
| S #6 | 62.4762 | 63.8421 | 81.2855 | 81.9100 | 81.1313 | 82.075 |
| S #7 | 56.6993 | 56.6041 | 77.0780 | 75.5528 | 73.6213 | 74.765 |
| Average | 60.6803 | 61.2705 | 79.2948 | 79.4295 | 78.4115 | 79.3976 |
| S # | GA | PSO | WDO | DE | GWO | CHIO |
|---|---|---|---|---|---|---|
| S #1 | 0.4244 | 0.4153 | 0.3504 | 0.3484 | 0.3531 | 0.3473 |
| S #2 | 0.4274 | 0.4270 | 0.3697 | 0.3569 | 0.3593 | 0.3598 |
| S #3 | 0.4316 | 0.4273 | 0.3641 | 0.3651 | 0.3630 | 0.3551 |
| S #4 | 0.4647 | 0.4686 | 0.3953 | 0.3898 | 0.3952 | 0.3888 |
| S #5 | 0.4329 | 0.4300 | 0.3646 | 0.3620 | 0.3649 | 0.3576 |
| S #6 | 0.4346 | 0.4308 | 0.3651 | 0.3648 | 0.3658 | 0.3586 |
| S #7 | 0.4525 | 0.4542 | 0.3813 | 0.3811 | 0.3803 | 0.3793 |
| S # | GA | PSO | WDO | DE | GWO |
|---|---|---|---|---|---|
| S #1 | 0.2802 | 0.7813 | 0.0333 | ||
| S #2 | 0.0015 | —— | —— | ||
| S #3 | 0.0020 | ||||
| S #4 | 0.0028 | 0.6583 | 0.0050 | ||
| S #5 | 0.0185 | 0.0148 | 0.0026 | ||
| S #6 | 0.0104 | 0.0125 | 0.0021 | ||
| S #7 | 0.4908 | 0.5304 | 0.3743 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Makhadmeh, S.N.; Al-Betar, M.A.; Awadallah, M.A.; Abasi, A.K.; Alyasseri, Z.A.A.; Doush, I.A.; Alomari, O.A.; Damaševičius, R.; Zajančkauskas, A.; Mohammed, M.A. A Modified Coronavirus Herd Immunity Optimizer for the Power Scheduling Problem. Mathematics 2022, 10, 315. https://doi.org/10.3390/math10030315
Makhadmeh SN, Al-Betar MA, Awadallah MA, Abasi AK, Alyasseri ZAA, Doush IA, Alomari OA, Damaševičius R, Zajančkauskas A, Mohammed MA. A Modified Coronavirus Herd Immunity Optimizer for the Power Scheduling Problem. Mathematics. 2022; 10(3):315. https://doi.org/10.3390/math10030315
Chicago/Turabian StyleMakhadmeh, Sharif Naser, Mohammed Azmi Al-Betar, Mohammed A. Awadallah, Ammar Kamal Abasi, Zaid Abdi Alkareem Alyasseri, Iyad Abu Doush, Osama Ahmad Alomari, Robertas Damaševičius, Audrius Zajančkauskas, and Mazin Abed Mohammed. 2022. "A Modified Coronavirus Herd Immunity Optimizer for the Power Scheduling Problem" Mathematics 10, no. 3: 315. https://doi.org/10.3390/math10030315
APA StyleMakhadmeh, S. N., Al-Betar, M. A., Awadallah, M. A., Abasi, A. K., Alyasseri, Z. A. A., Doush, I. A., Alomari, O. A., Damaševičius, R., Zajančkauskas, A., & Mohammed, M. A. (2022). A Modified Coronavirus Herd Immunity Optimizer for the Power Scheduling Problem. Mathematics, 10(3), 315. https://doi.org/10.3390/math10030315








