Interval Fuzzy Type-2 Sliding Mode Control Design of Six-DOF Robotic Manipulator
Abstract
1. Introduction
- -
- Proposing the comprehensive optimal design scheme of interval type-2 fuzzy systems providing the real time slope coefficients of the gains of the switching member of the SMC;
- -
- Presenting an efficient approach for the design of the rule base of interval type-2 fuzzy systems with uncertain scales and lag parameters of lower output membership functions of fuzzy systems to deliver the required parameters of the SMC with optimal tracking performance along with minimum control effort. This approach eliminates the need for expensive computing hardware and expert knowledge as the challenging issue in the fuzzy system design stage, and it prevents the actuators’ saturation due to generating optimal control effort;
- -
- The proposal also offers a vast operating range versus unwanted input disturbances and parametric uncertainties with the ability to reduce the chattering phenomenon.
2. Six-DoF Robot Arm
3. Controller Design
4. General Type-2 Fuzzy Inference Systems
4.1. Fuzzifier Membership
4.2. Fuzzy Rule
4.3. Inference Engine
4.4. Defuzzifier
5. SMC-Based Interval Type-2 Fuzzy System
5.1. T2FSMC Schemes
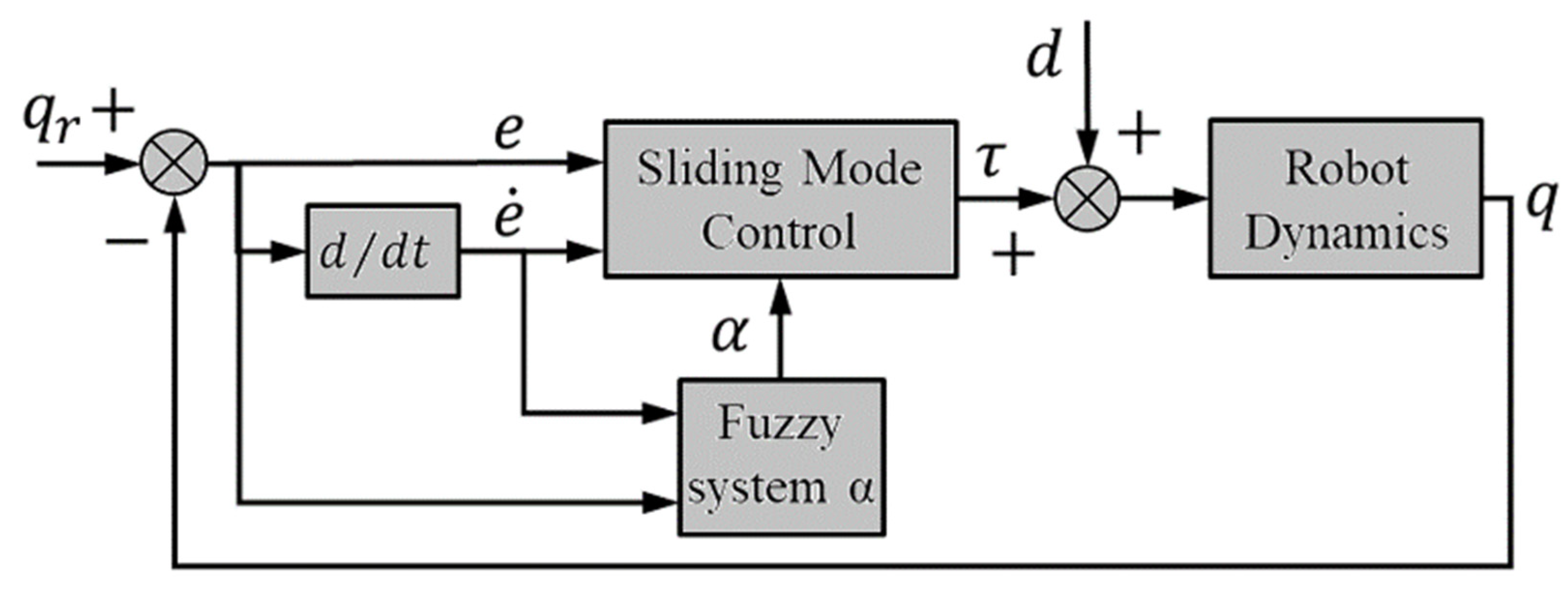
5.2. T2FSMC with Adaptive Gains
5.3. T2FSMC with Tuned α Parameters
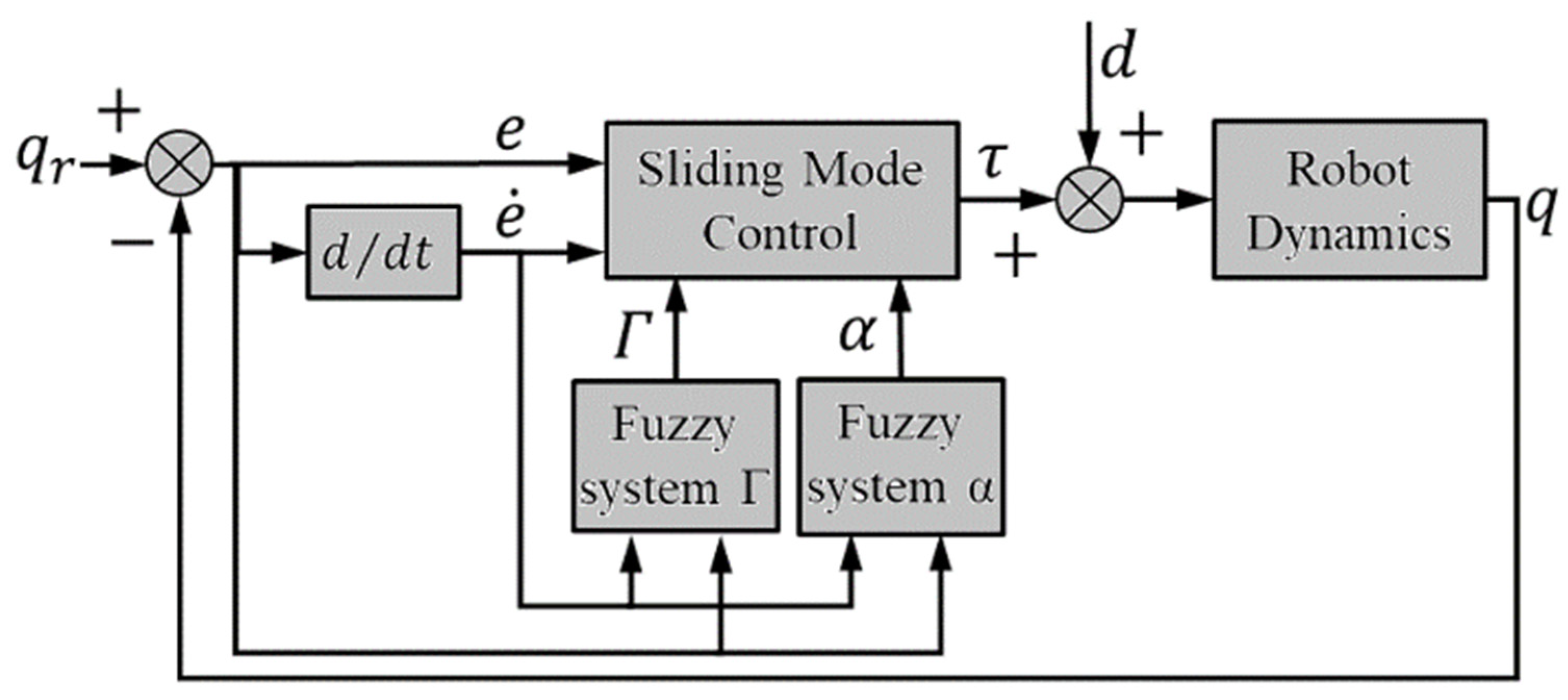
5.4. T2FSMC with Tuned α and Γ Parameters
5.5. Design of Type-2 Fuzzy Systems Assisting SMC
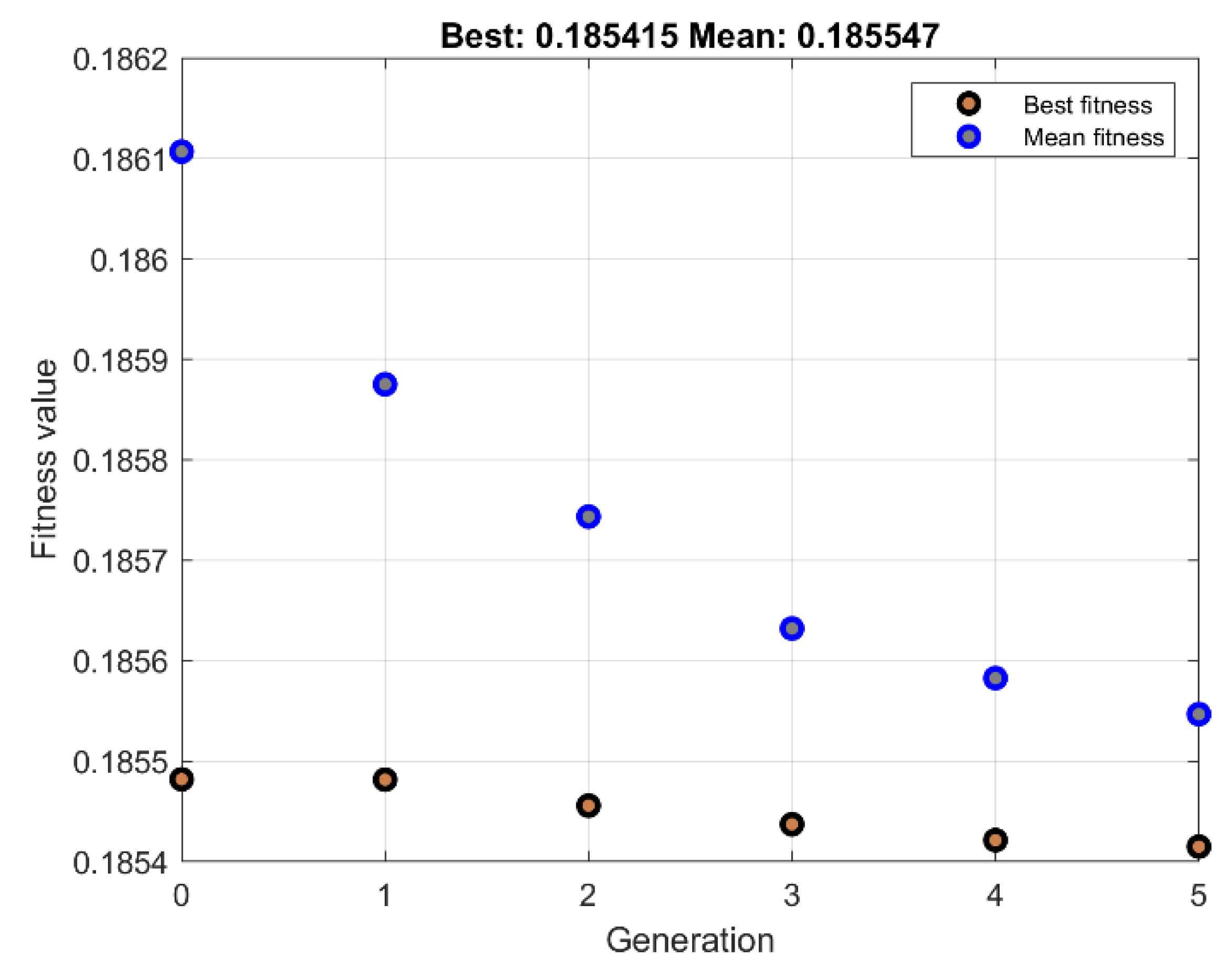
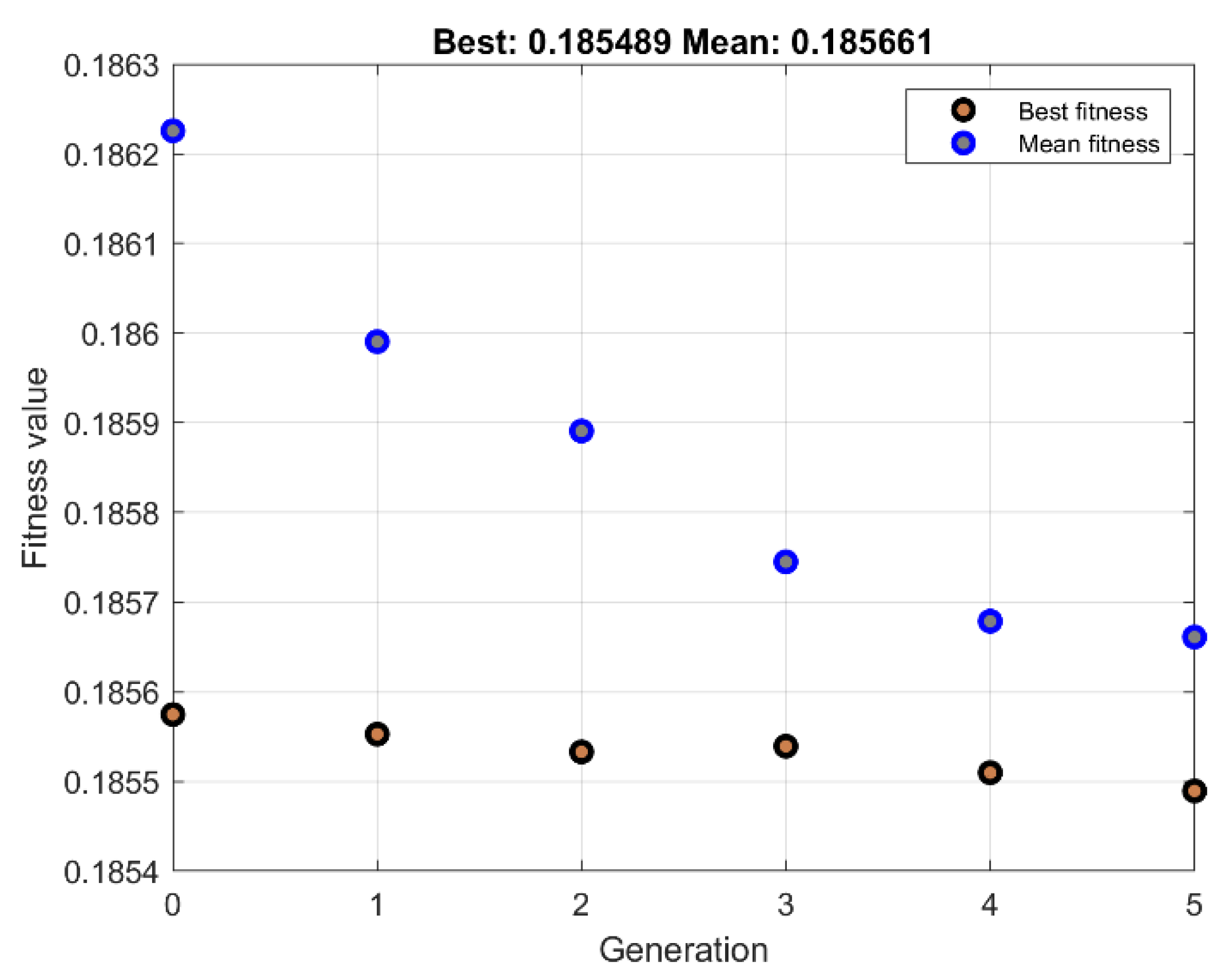
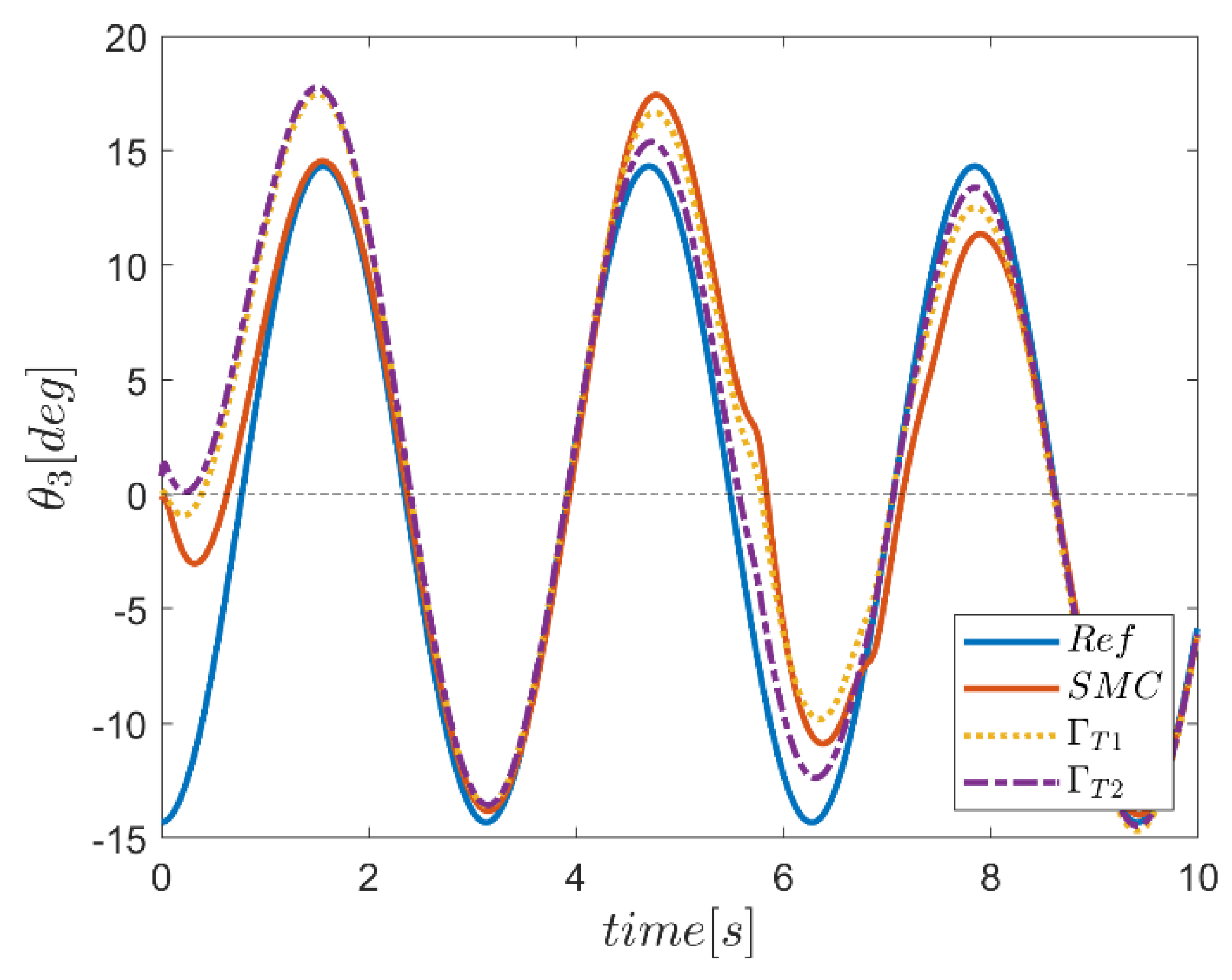
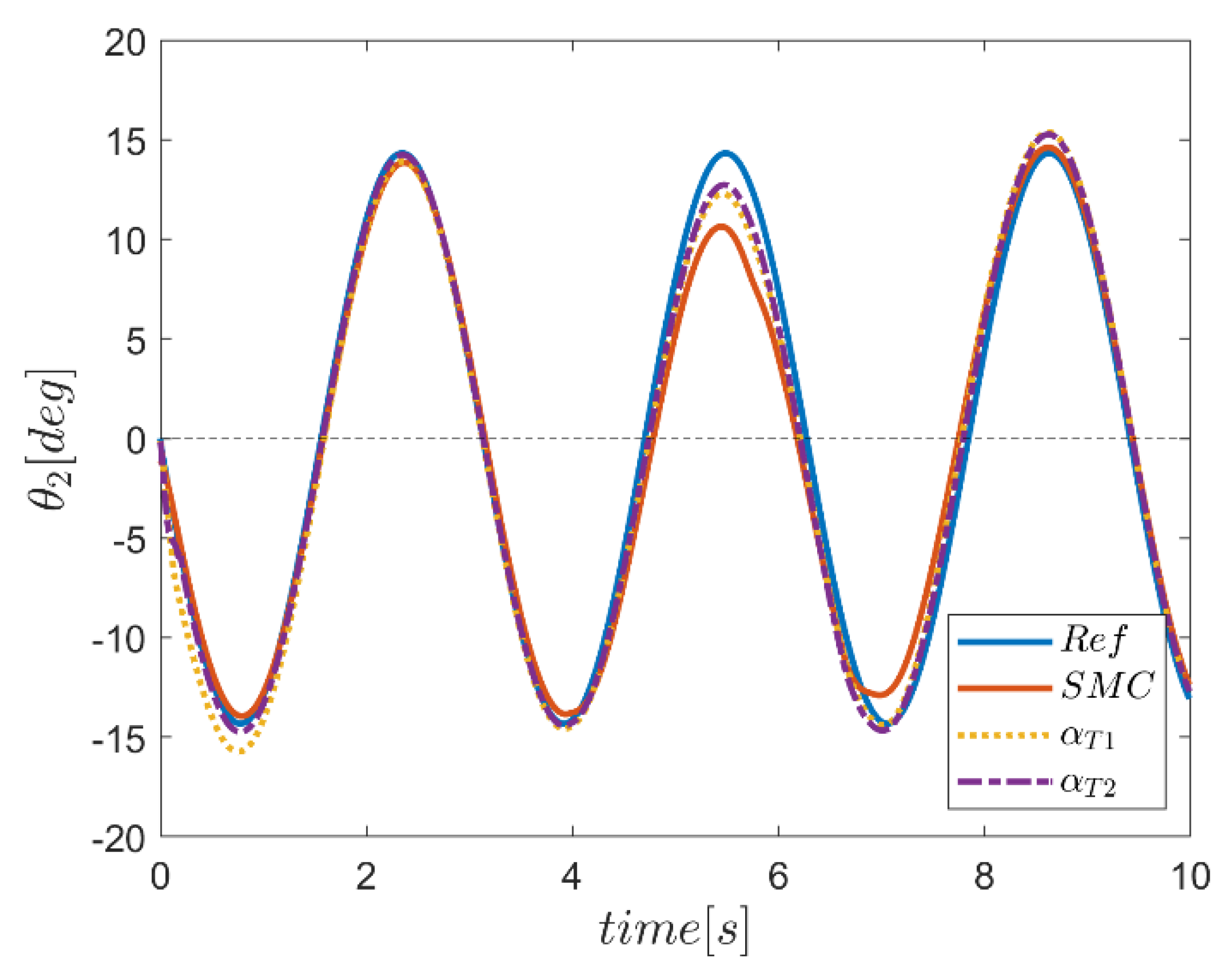
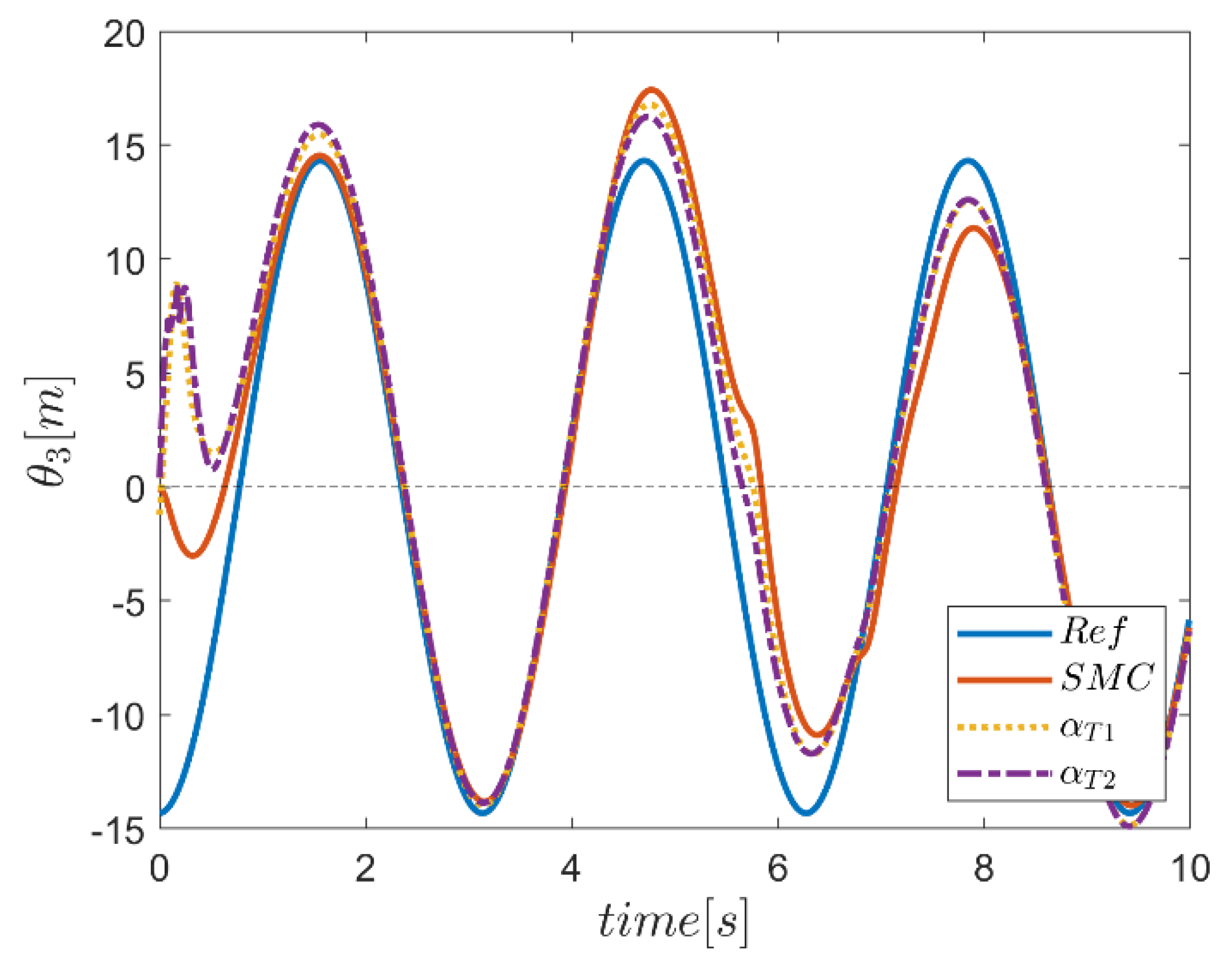
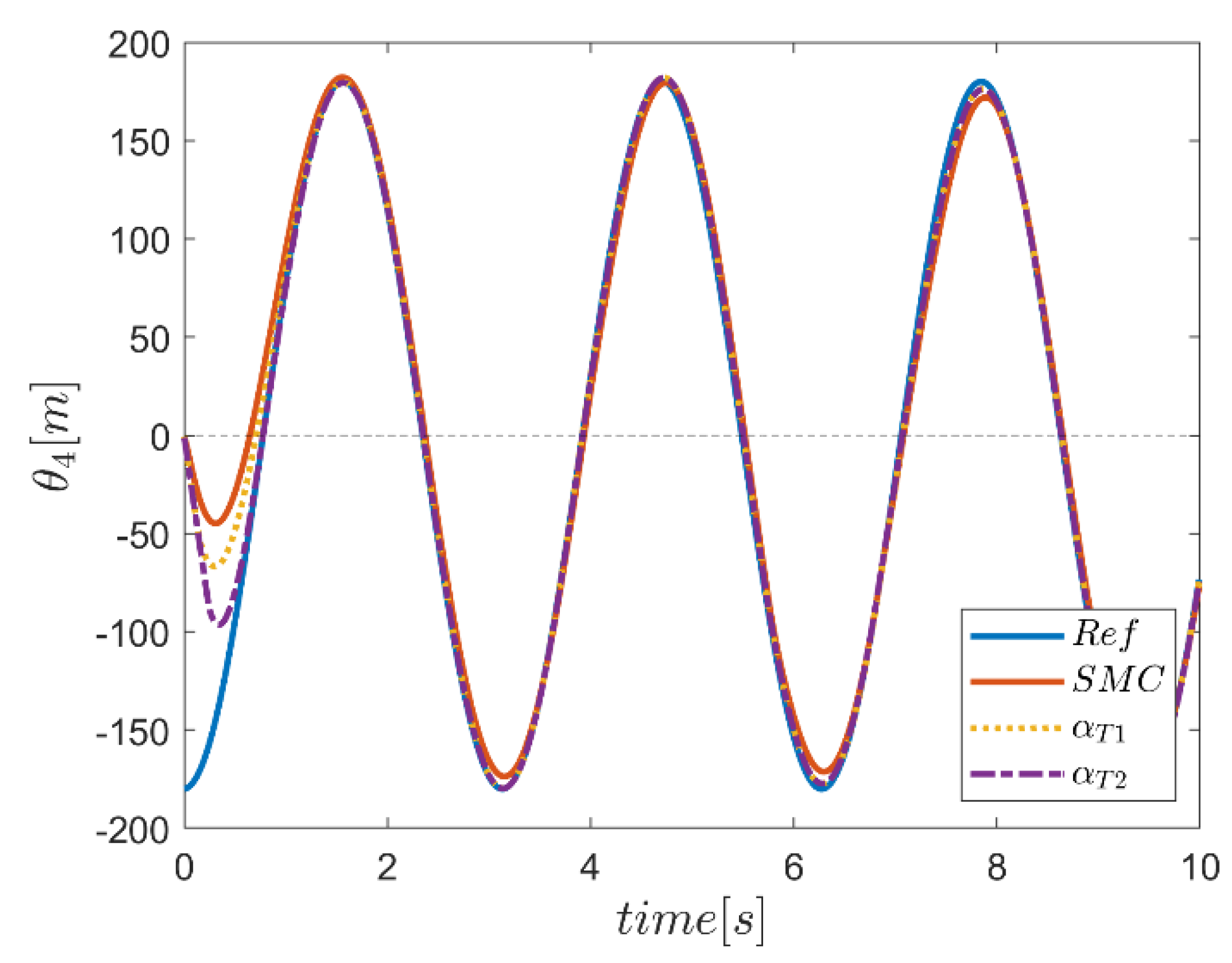
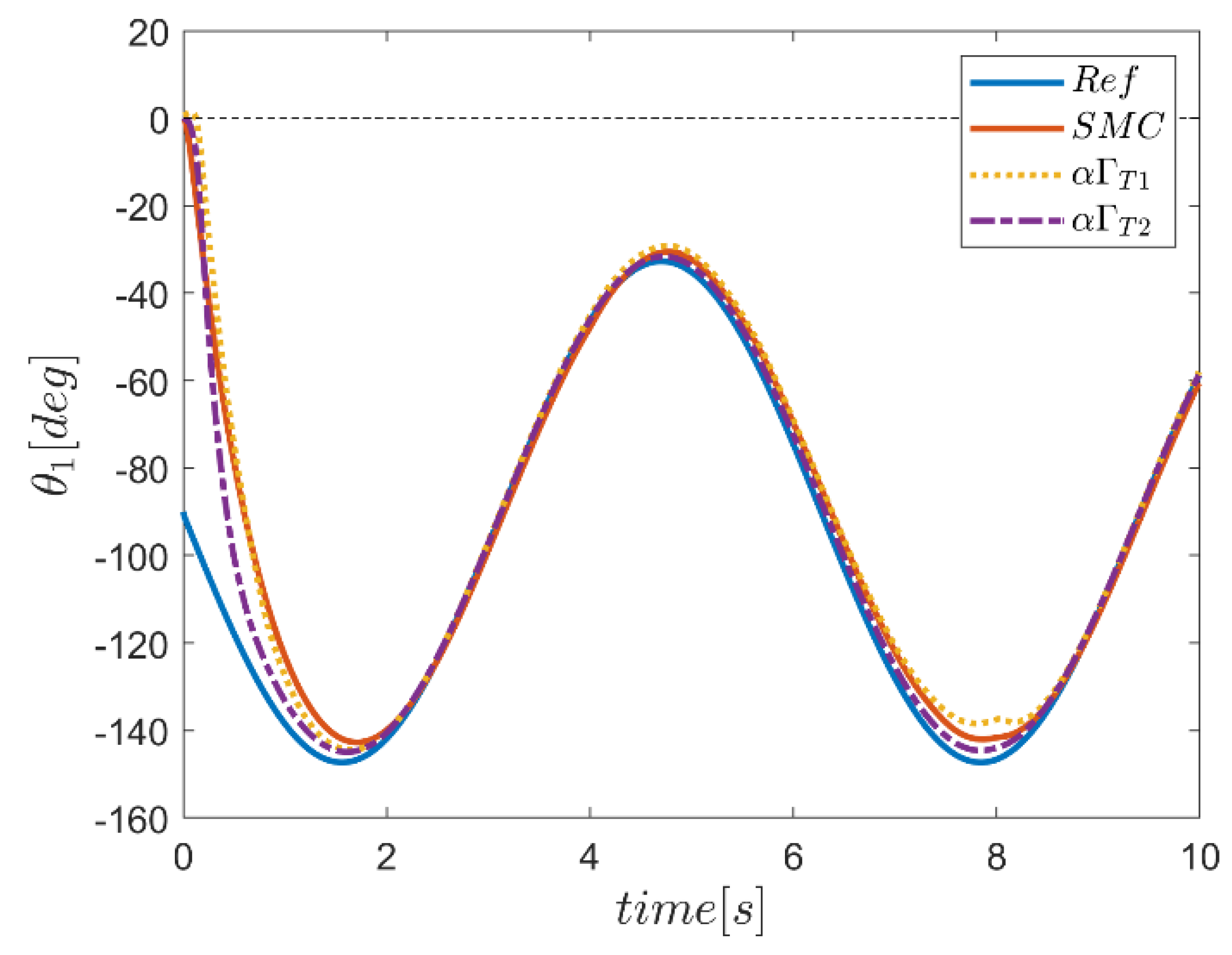
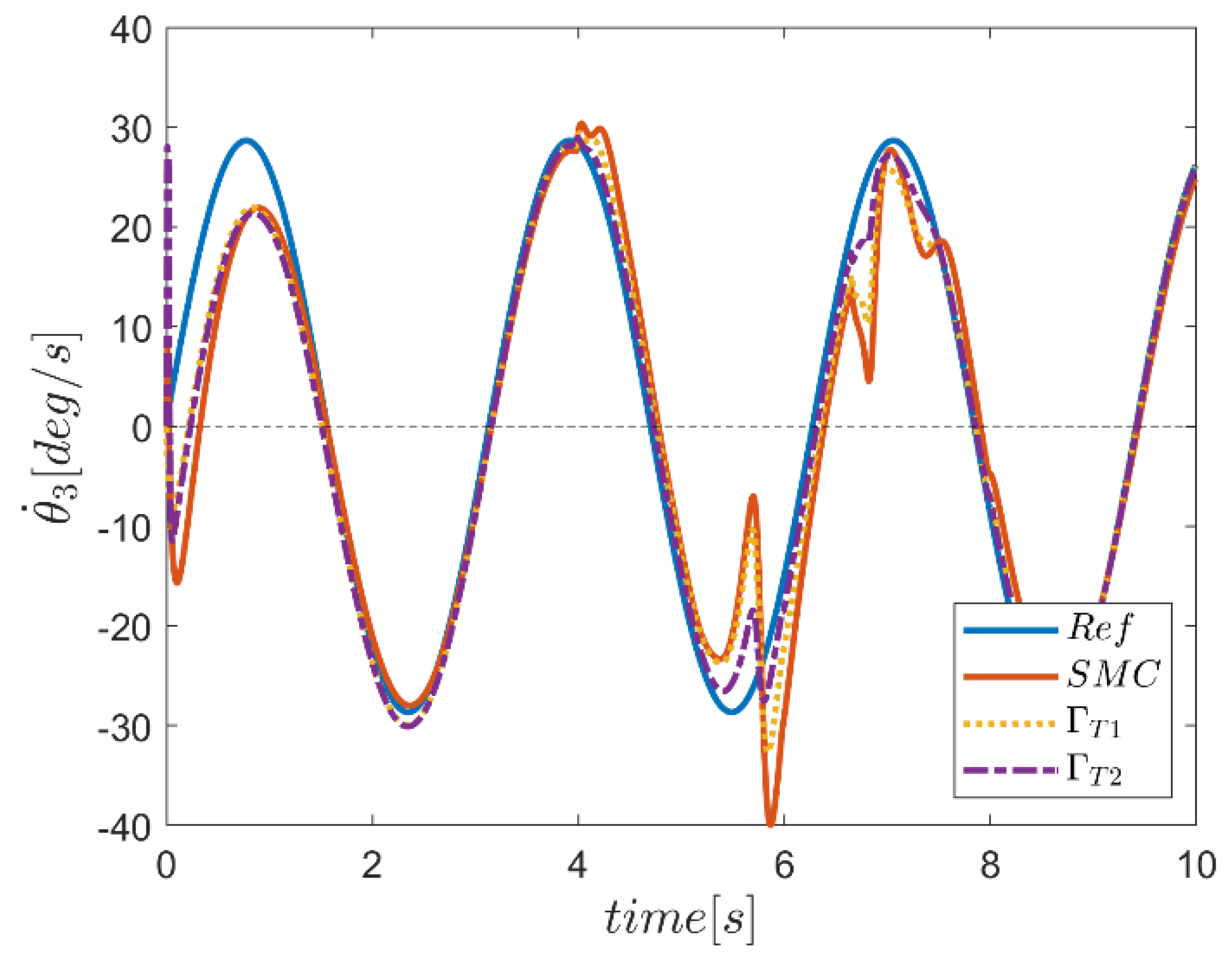
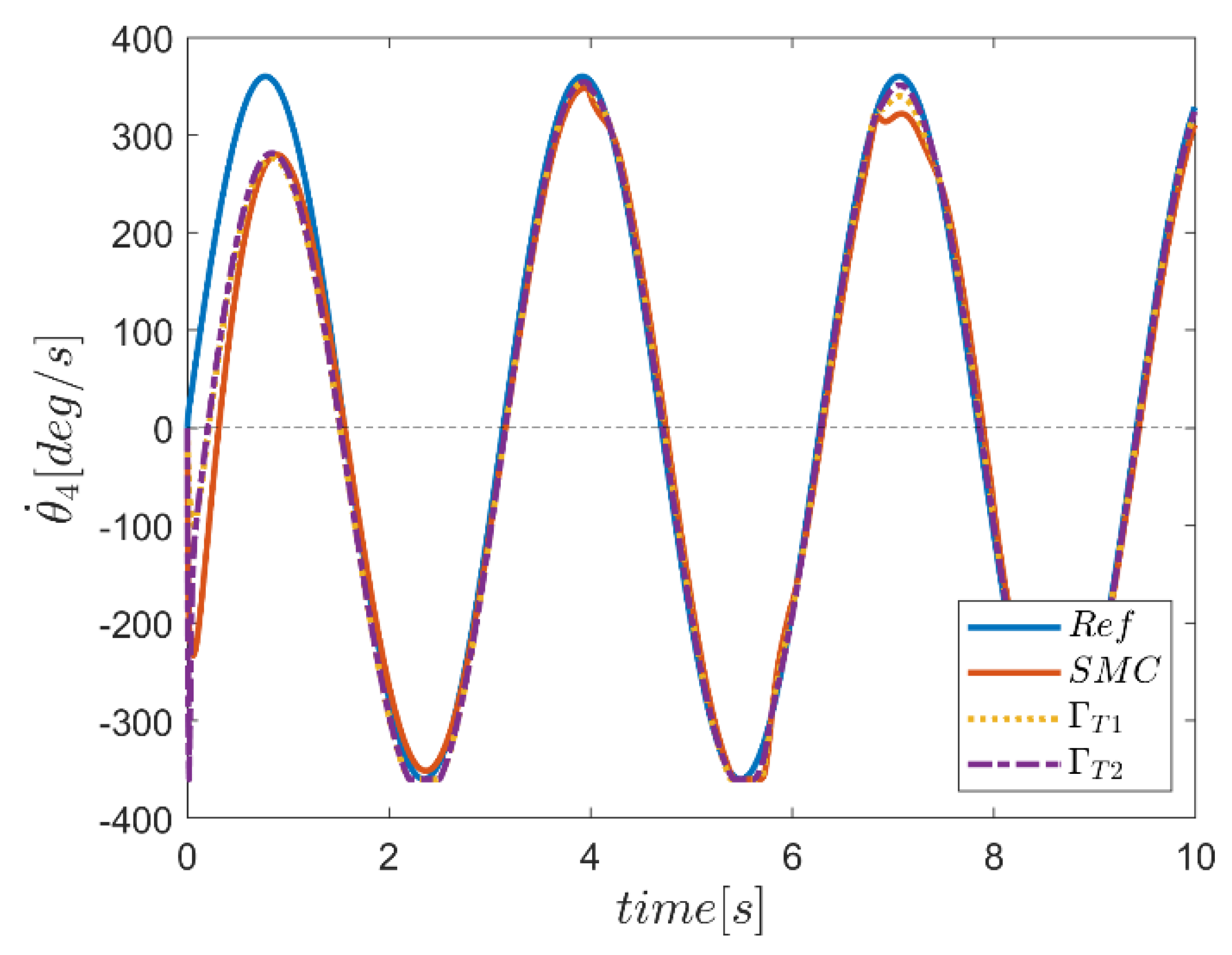
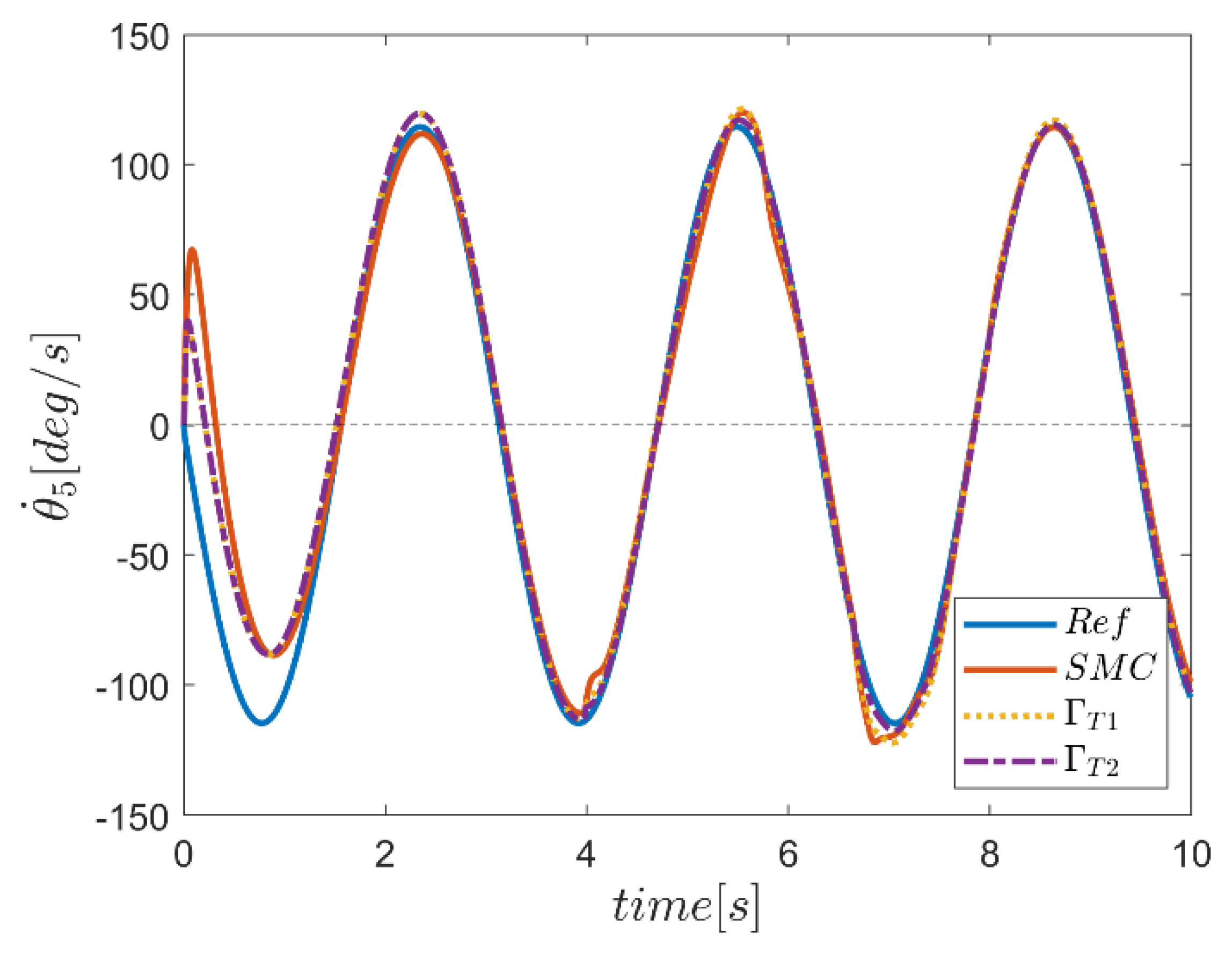
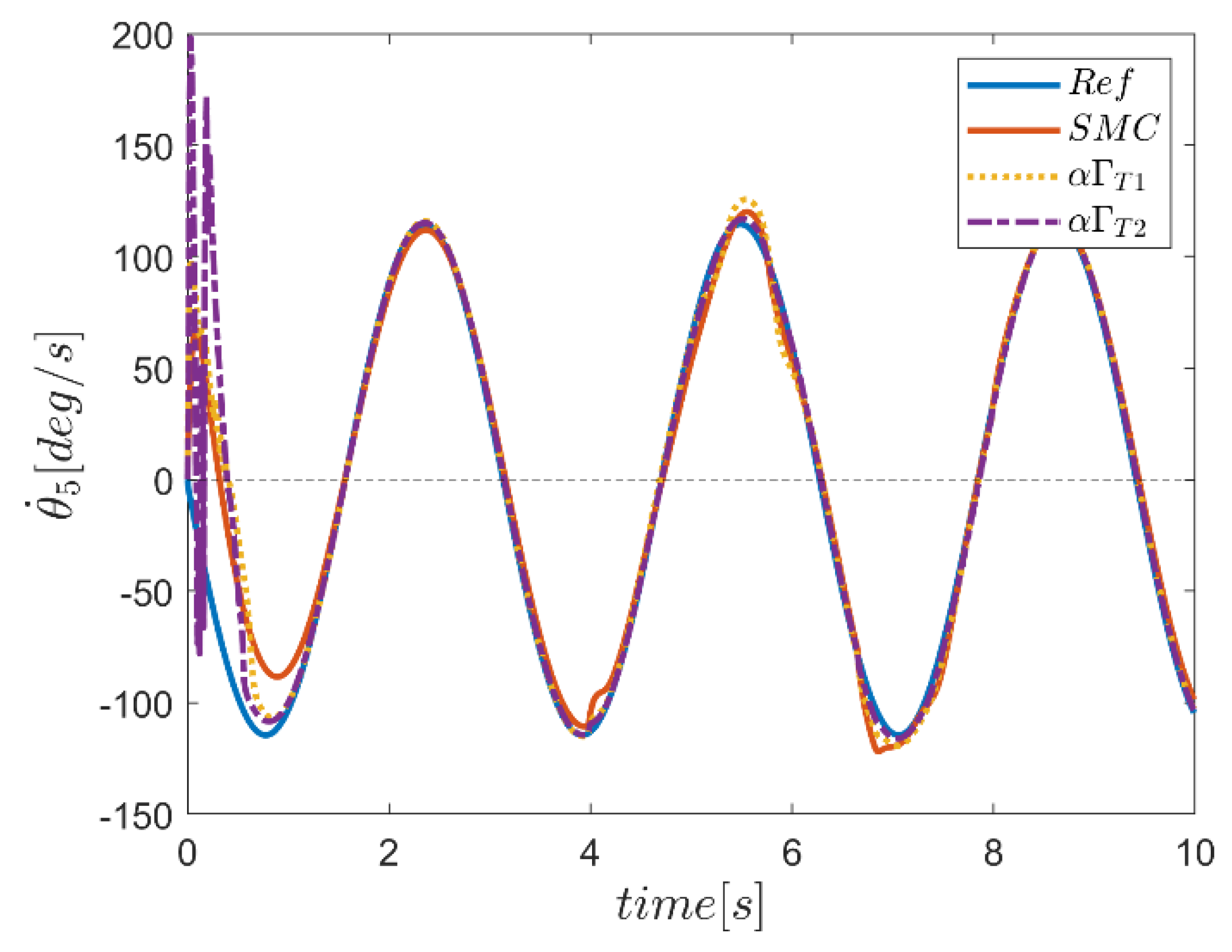
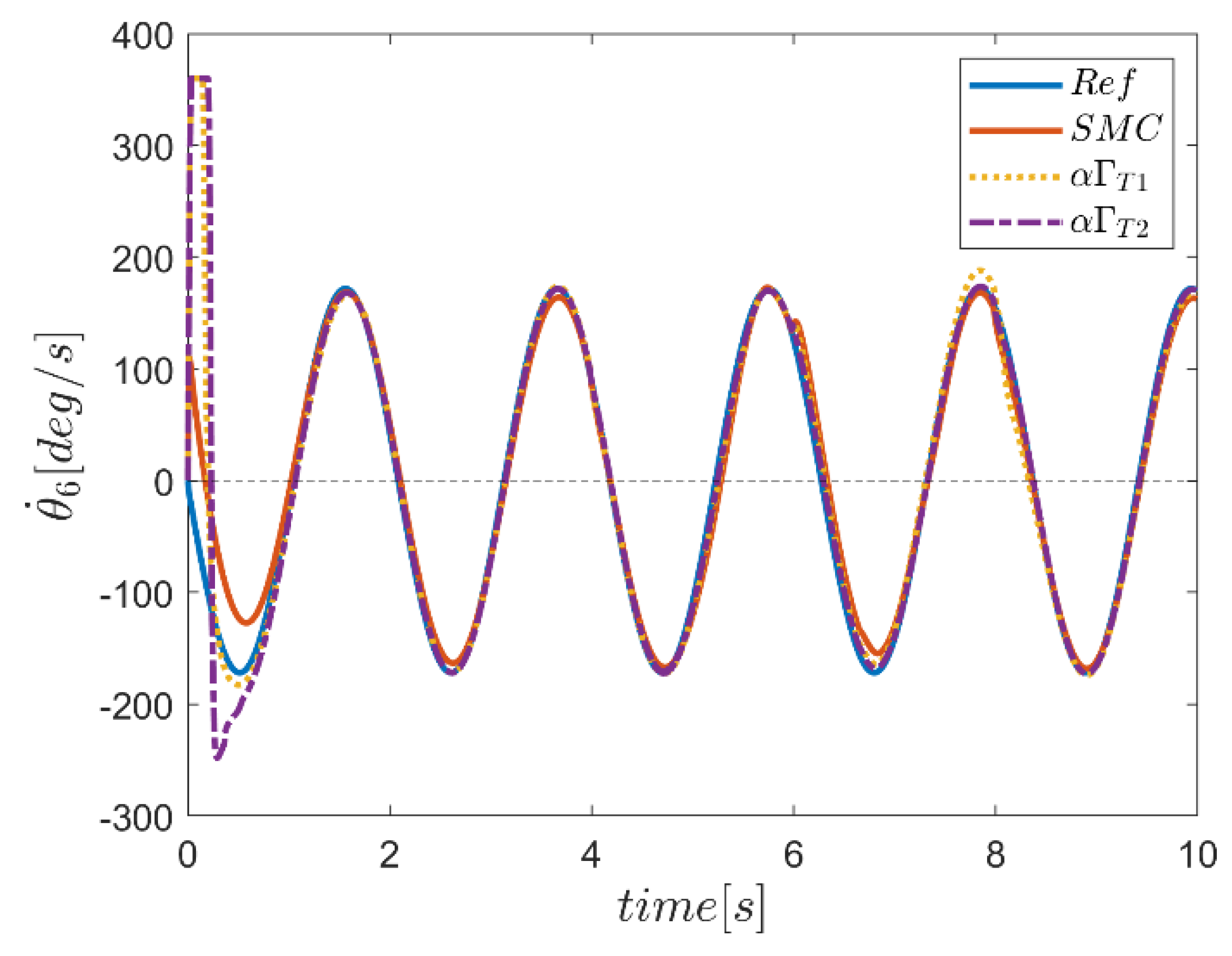
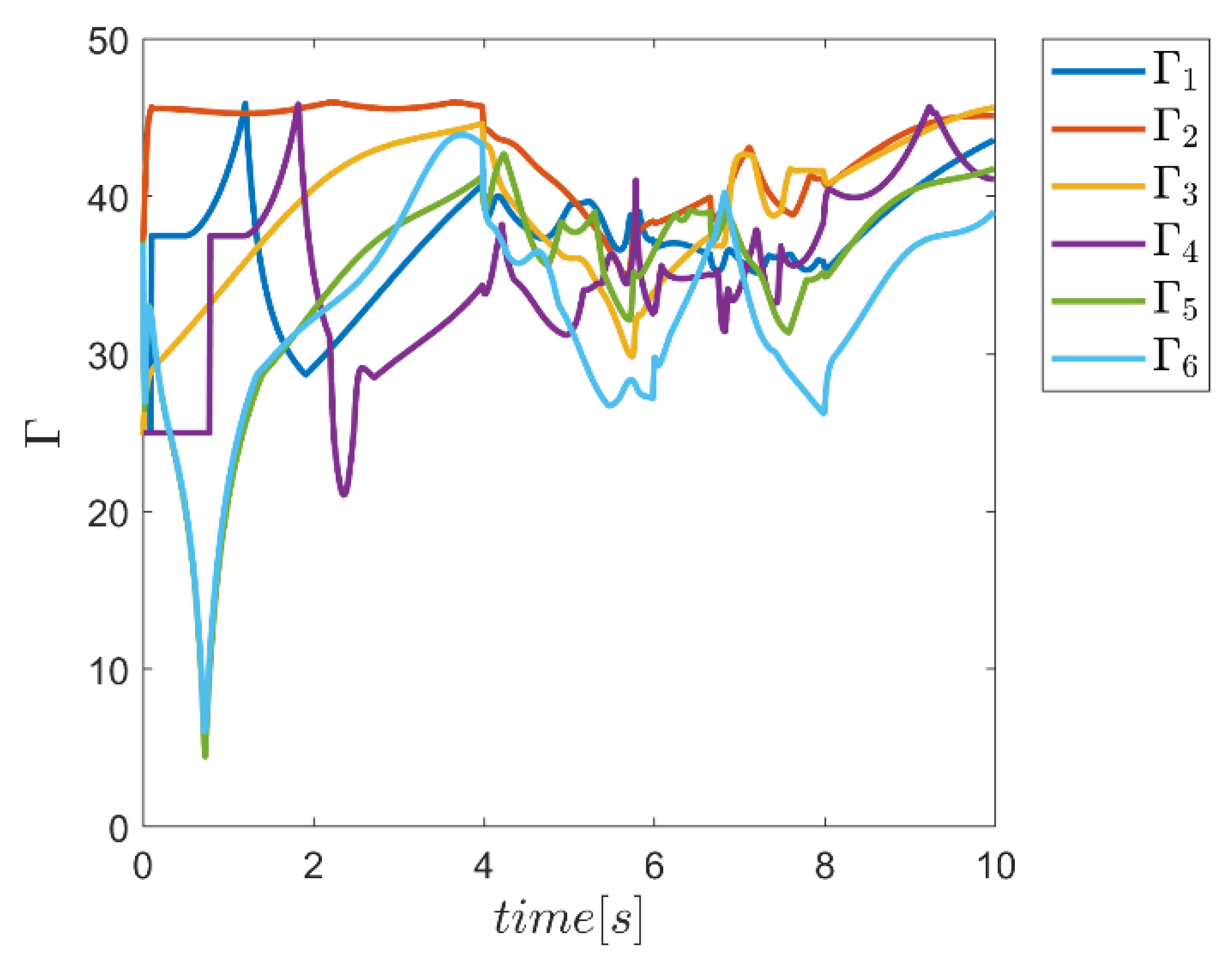
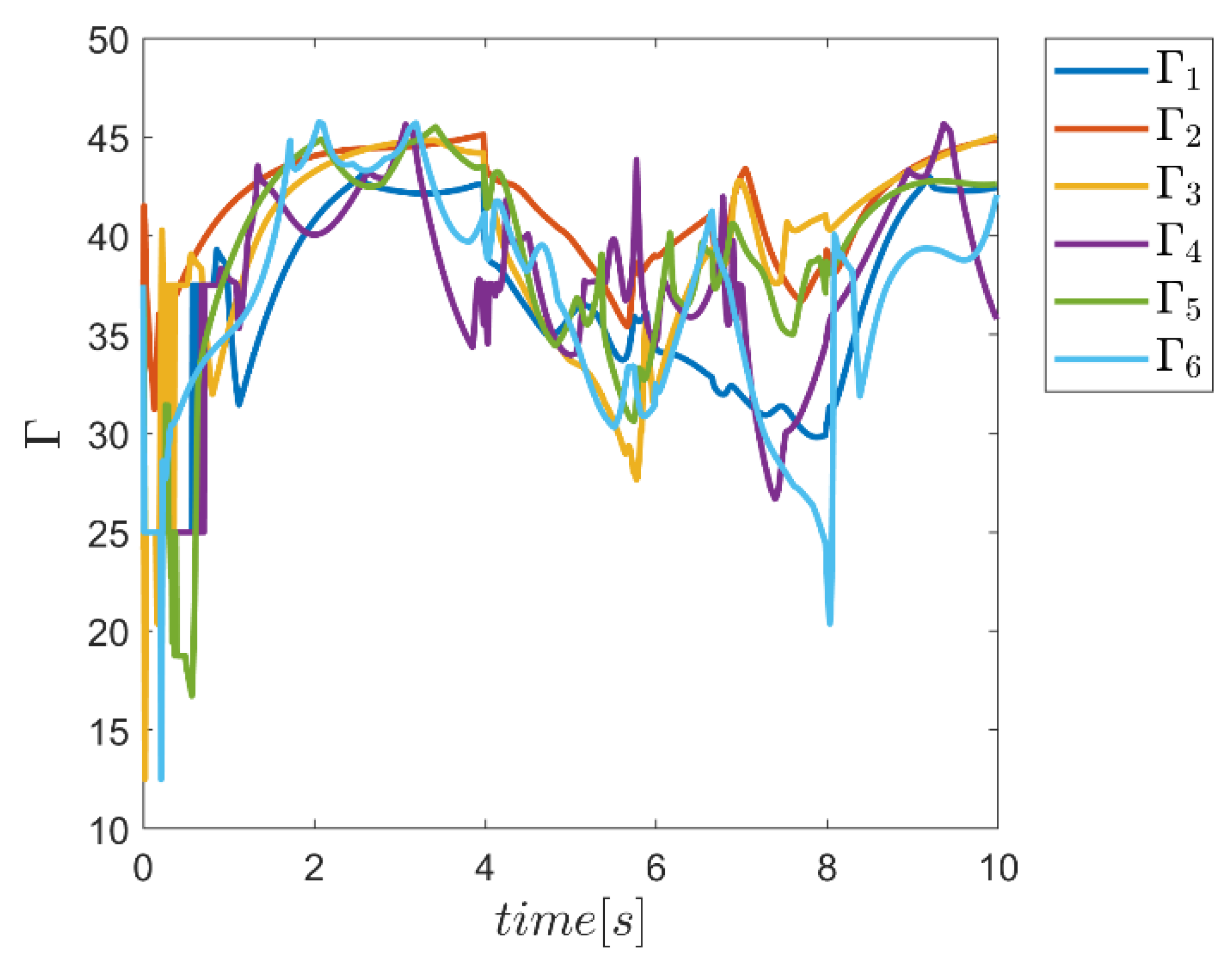
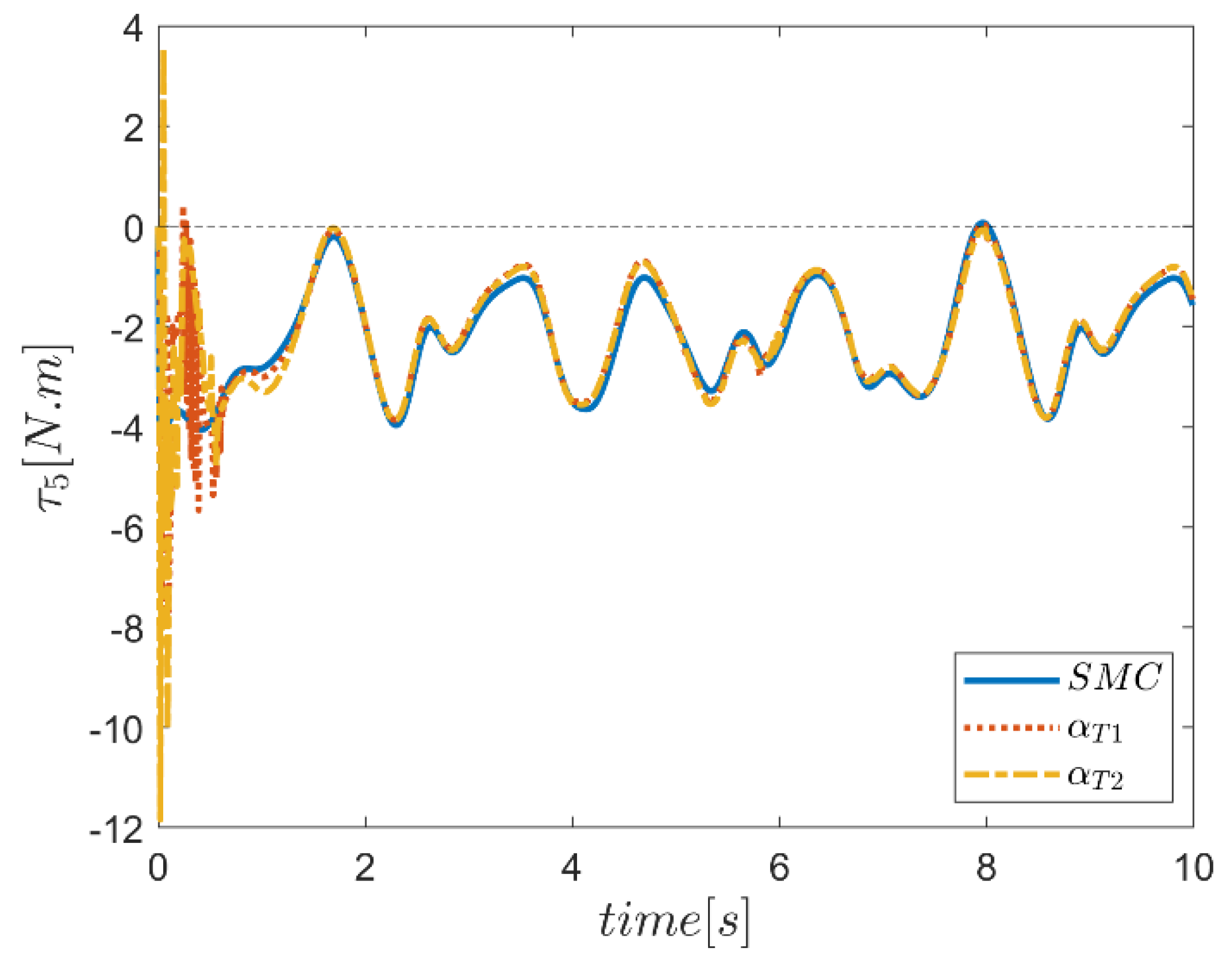
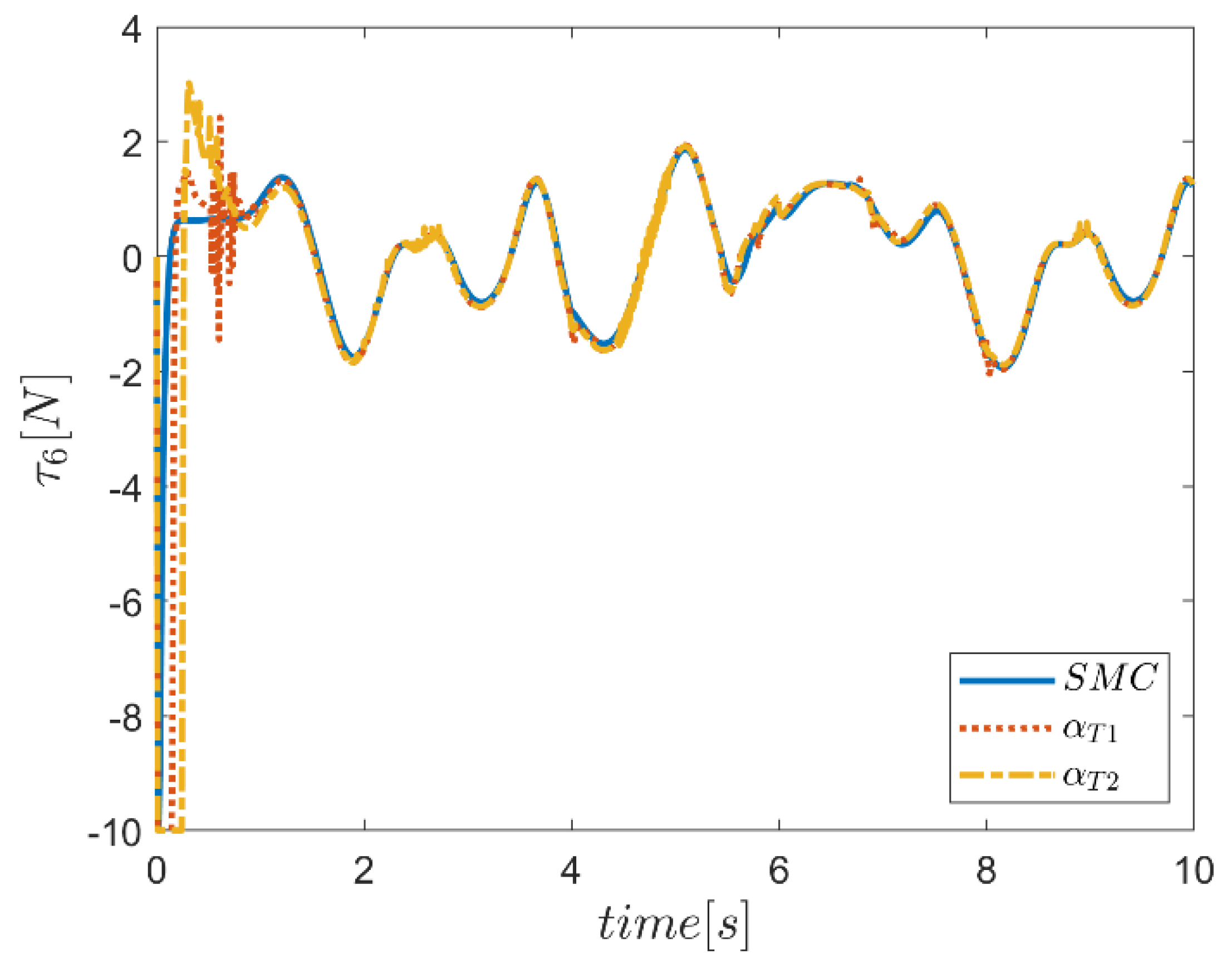
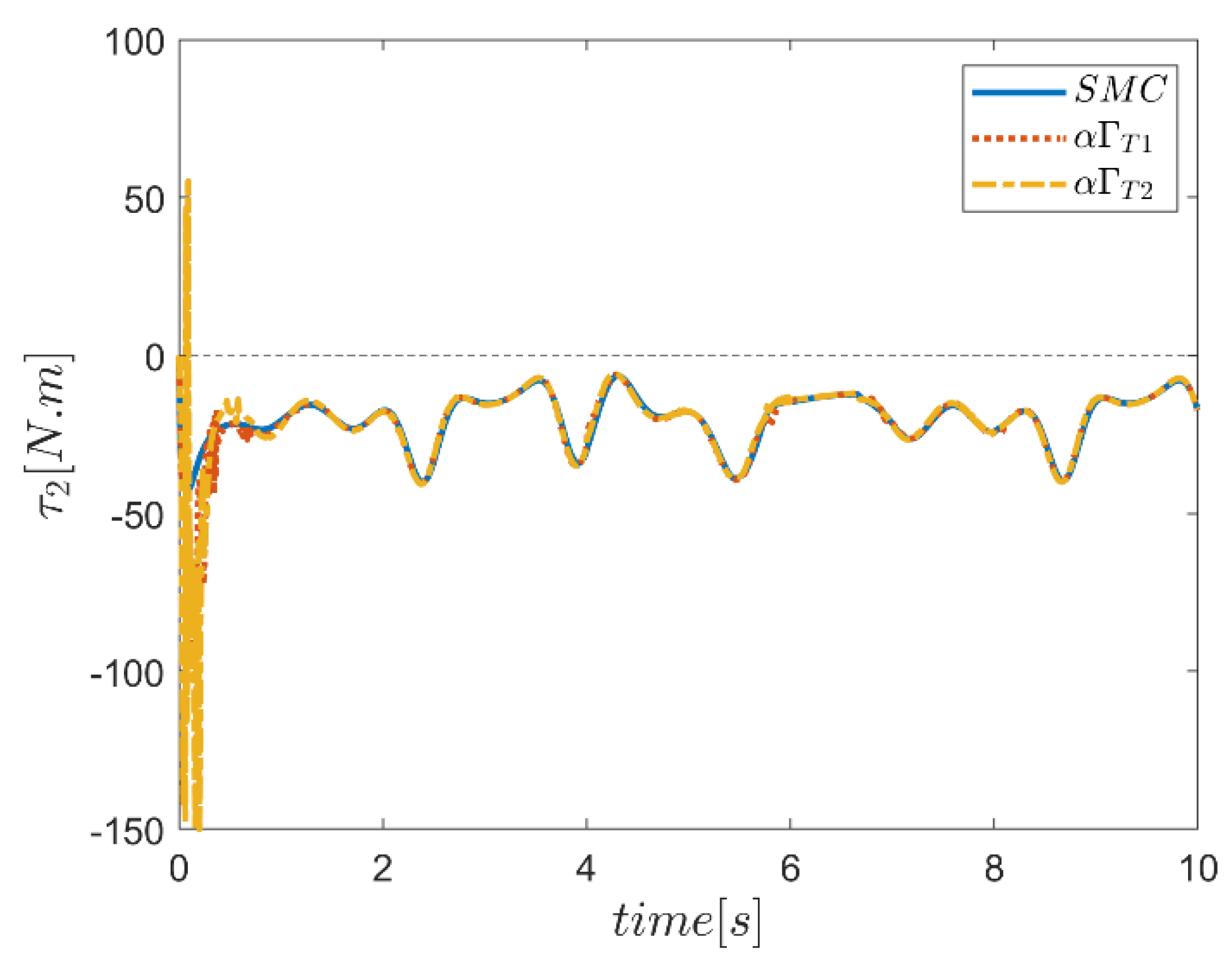
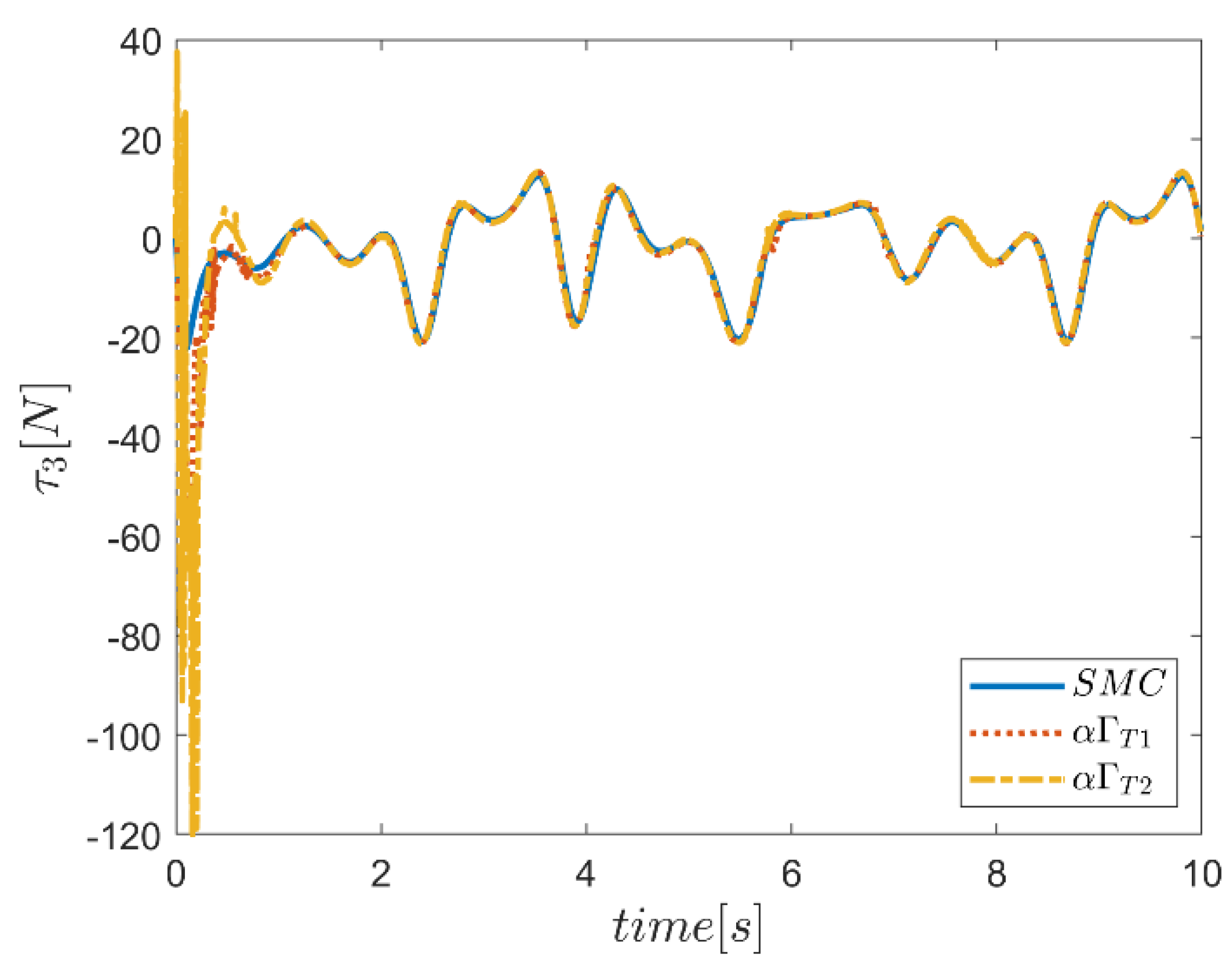
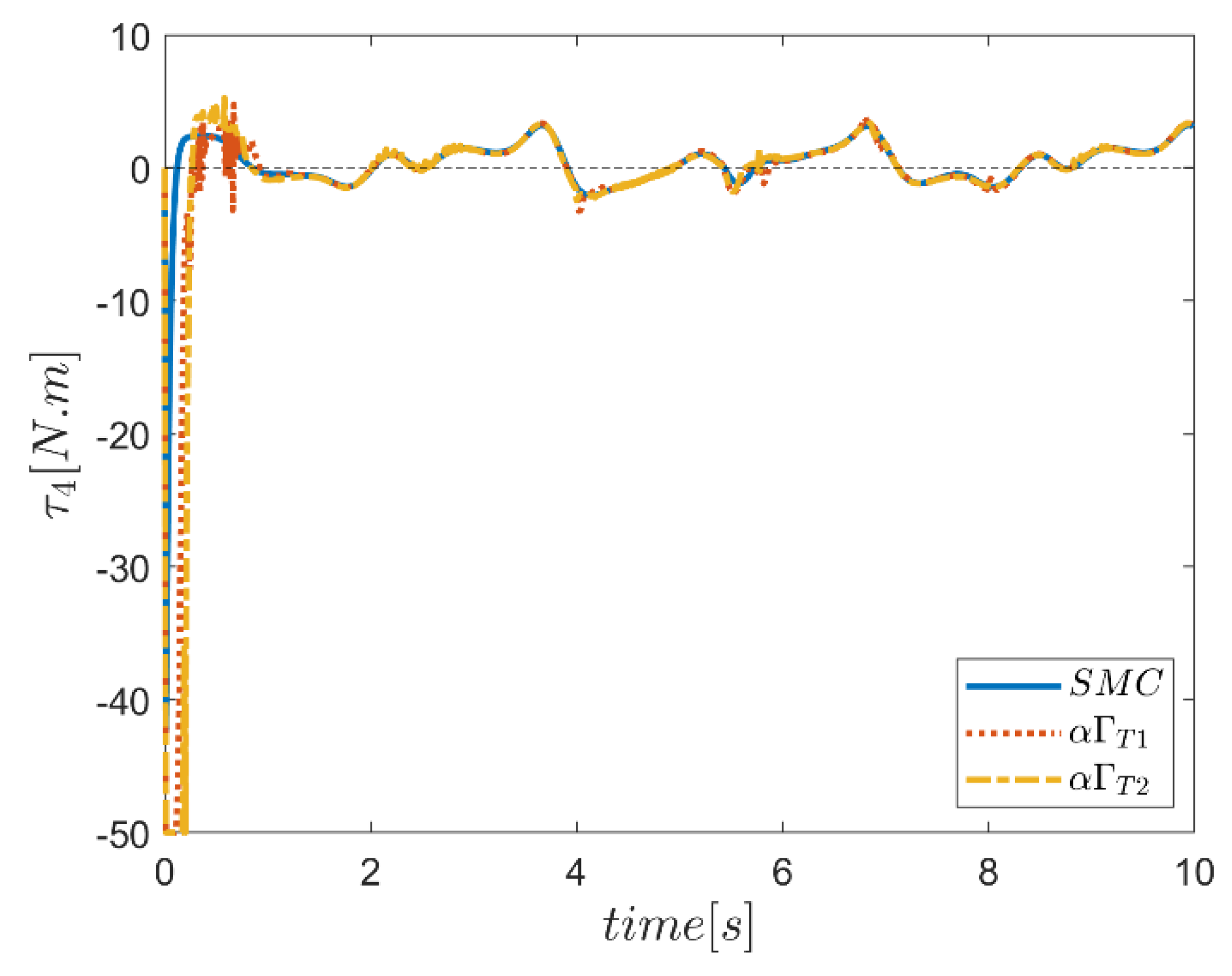
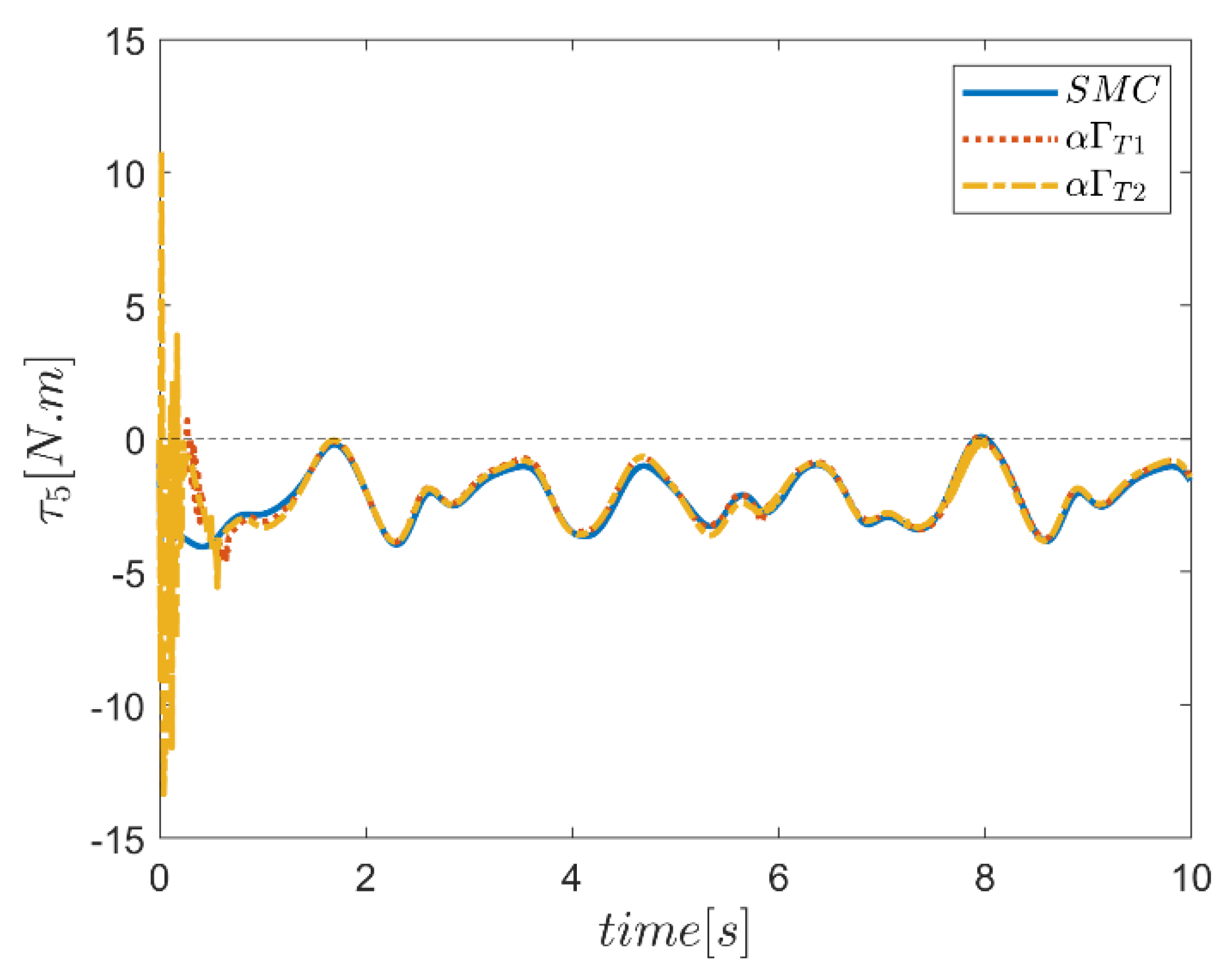
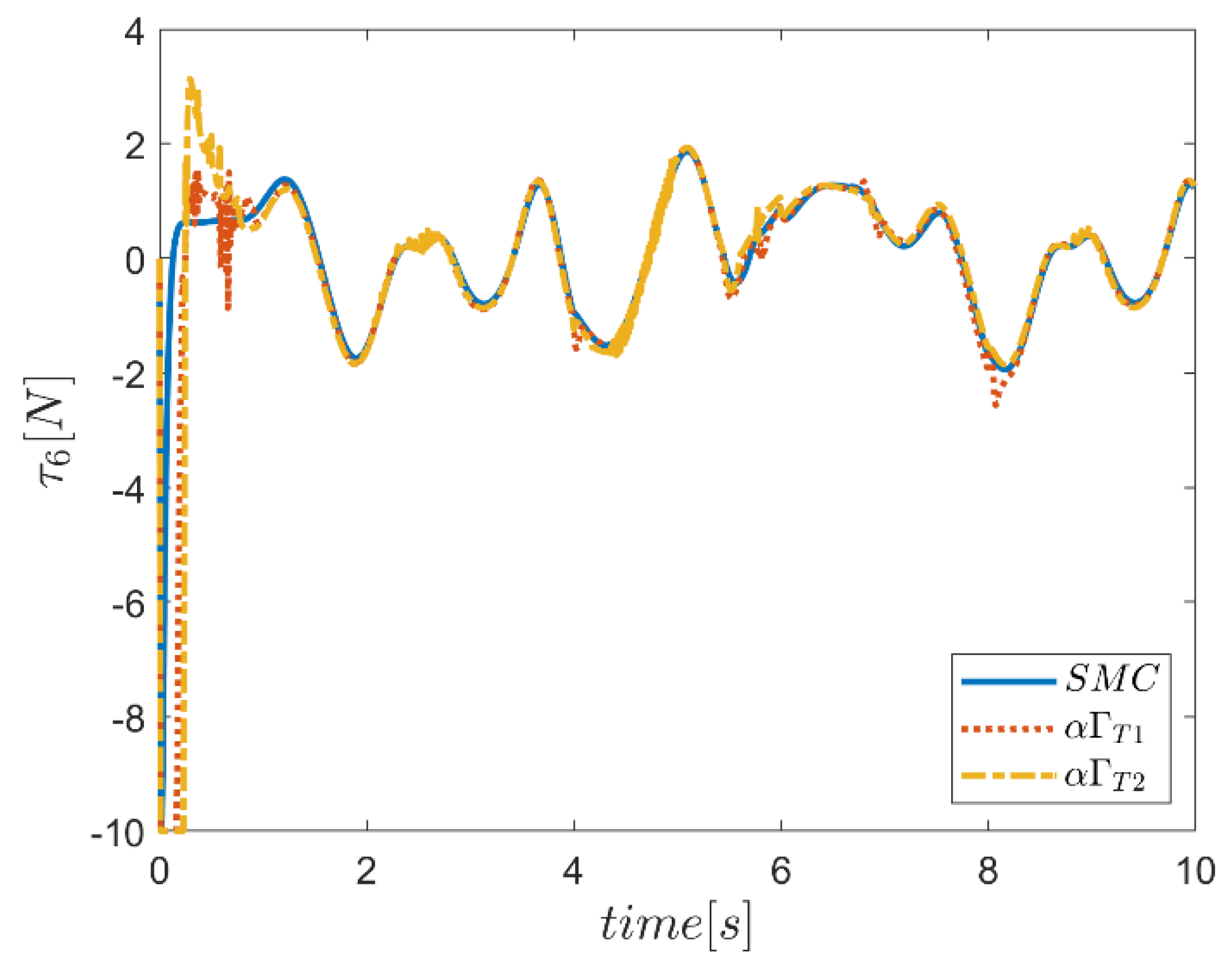
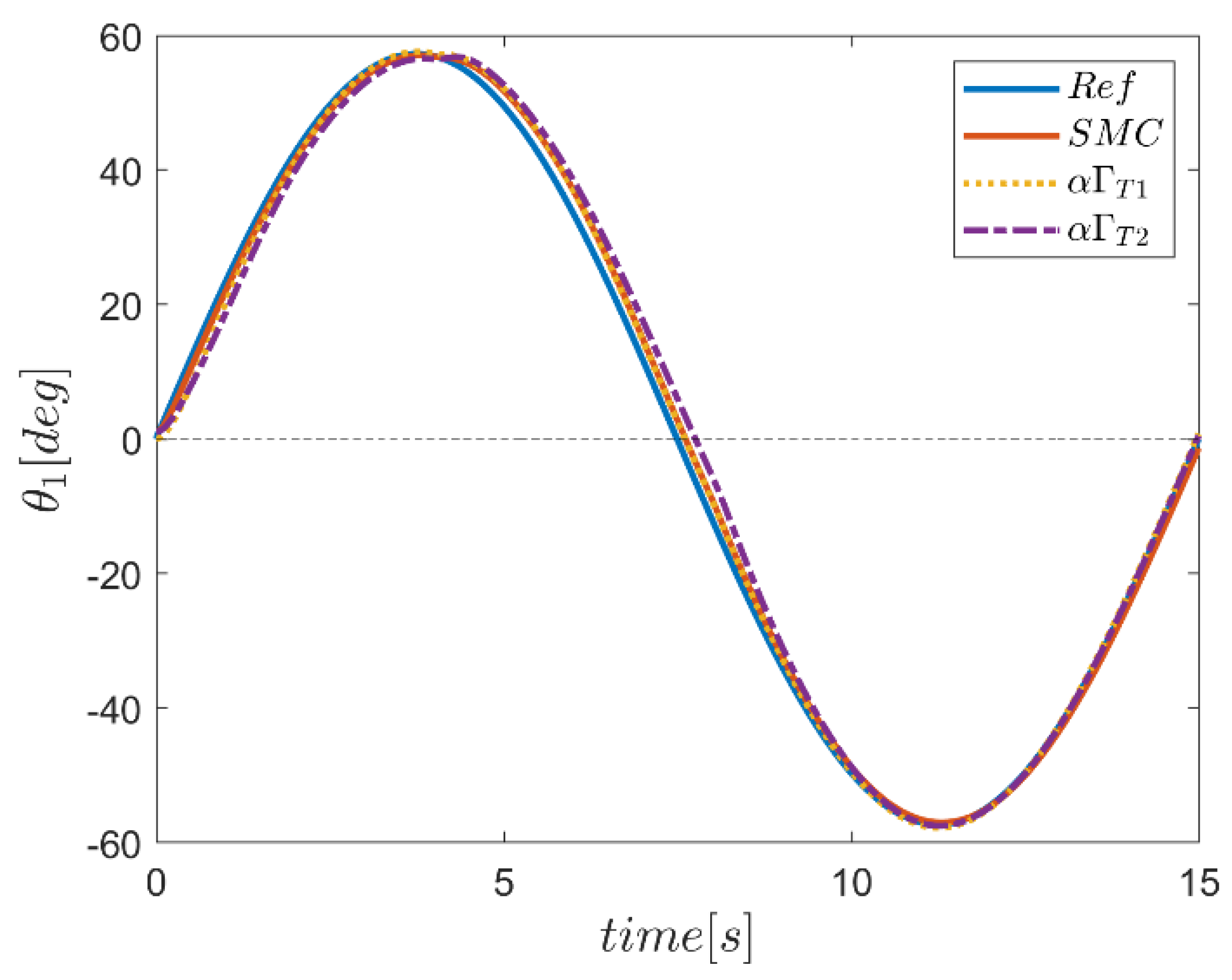
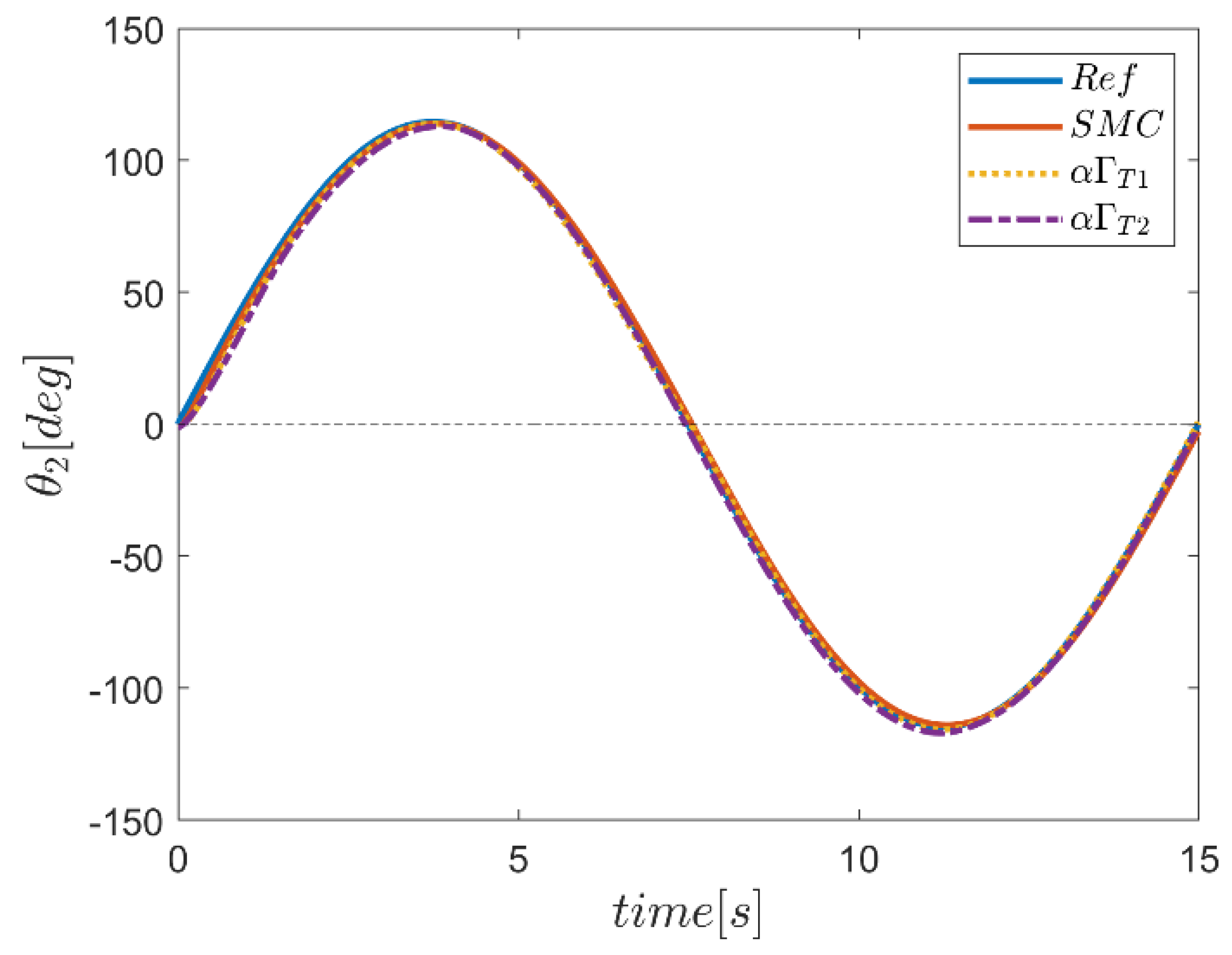
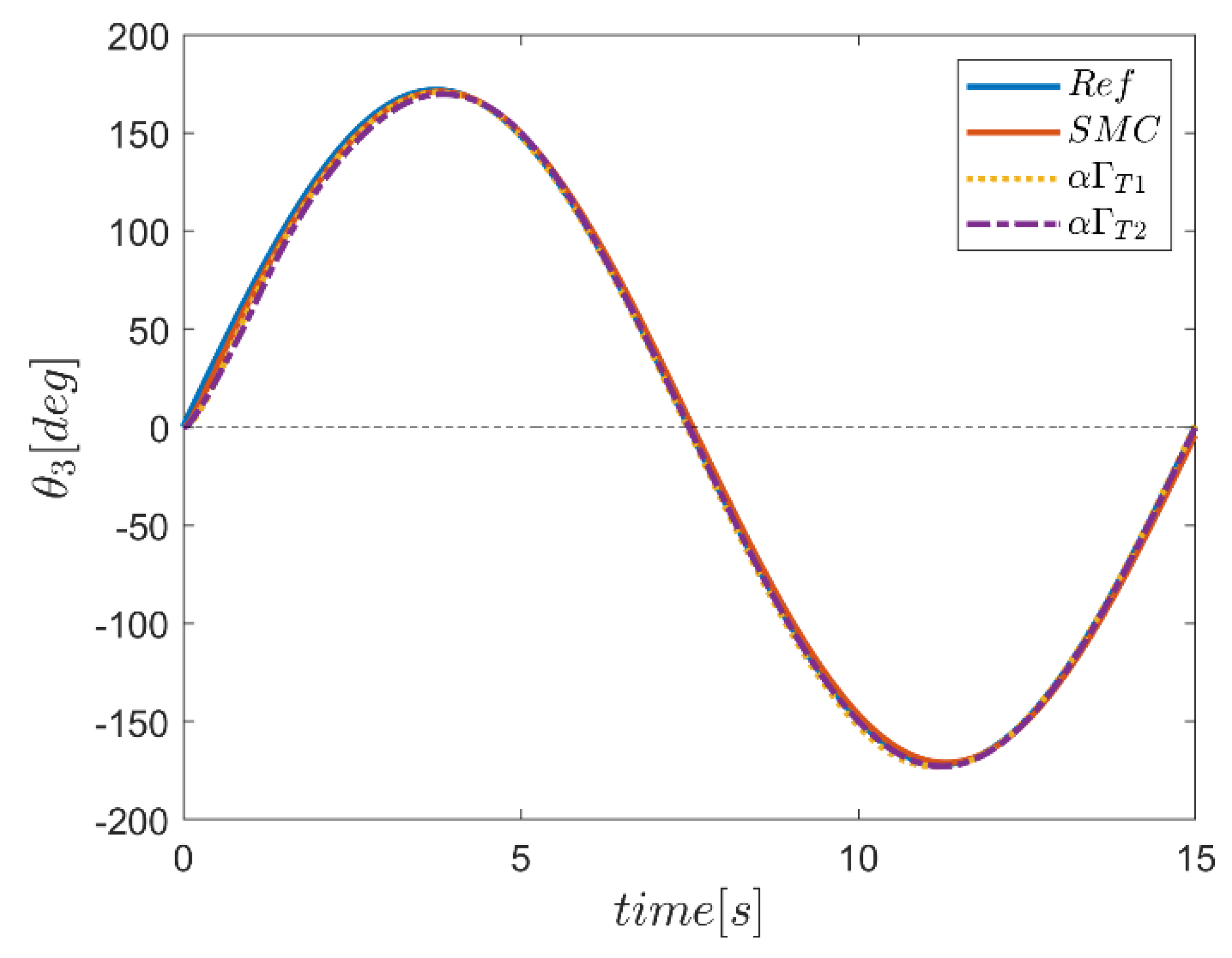
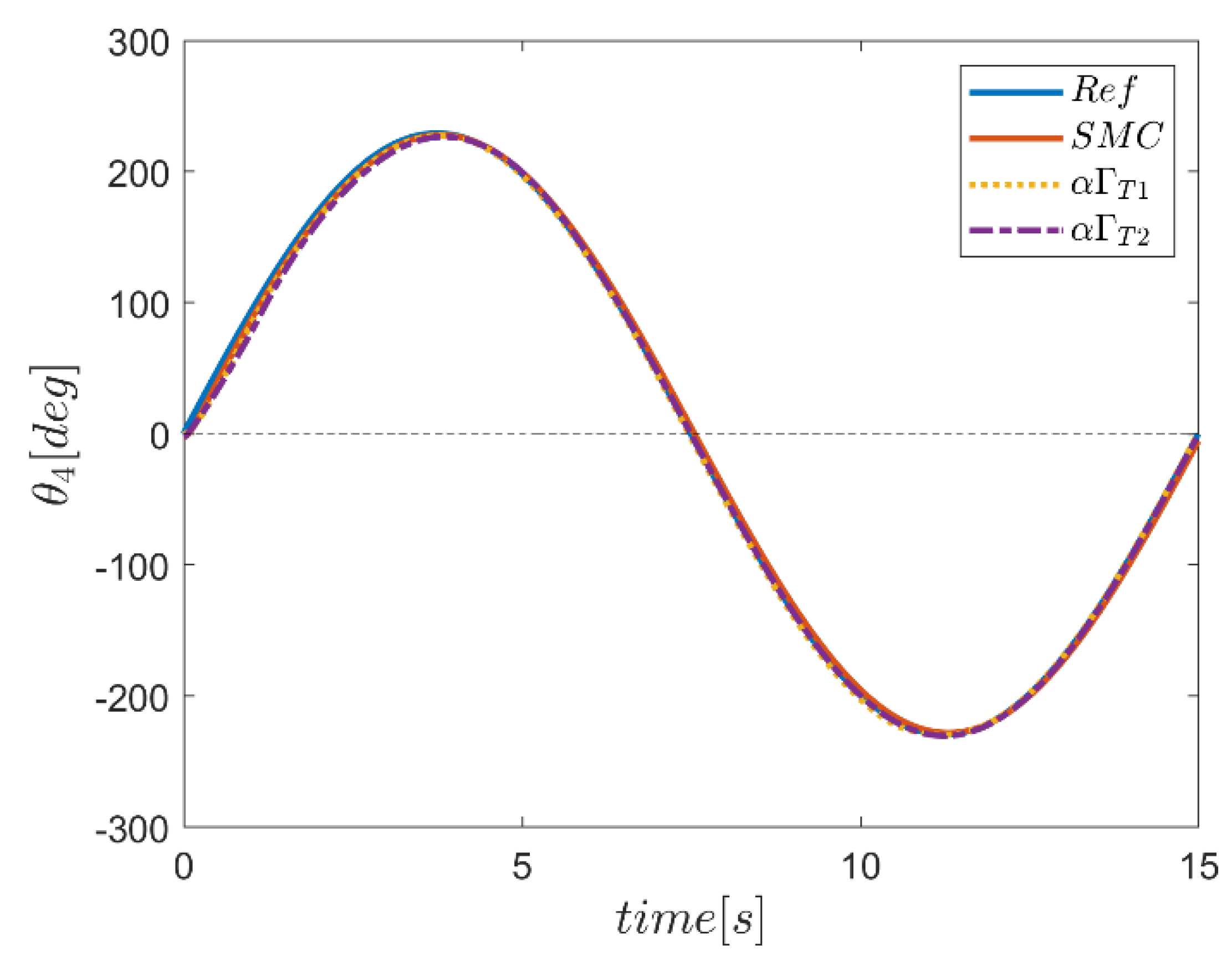
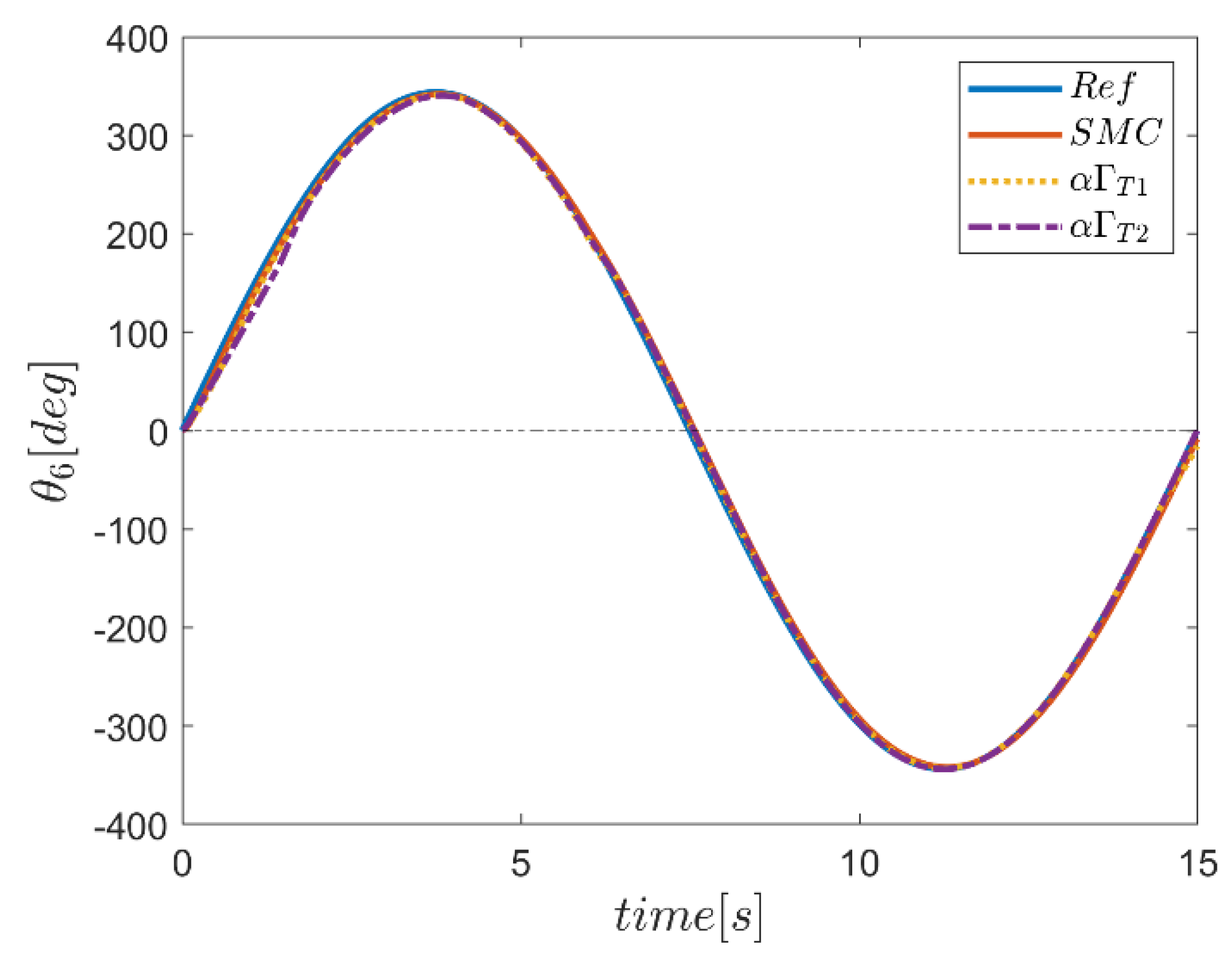
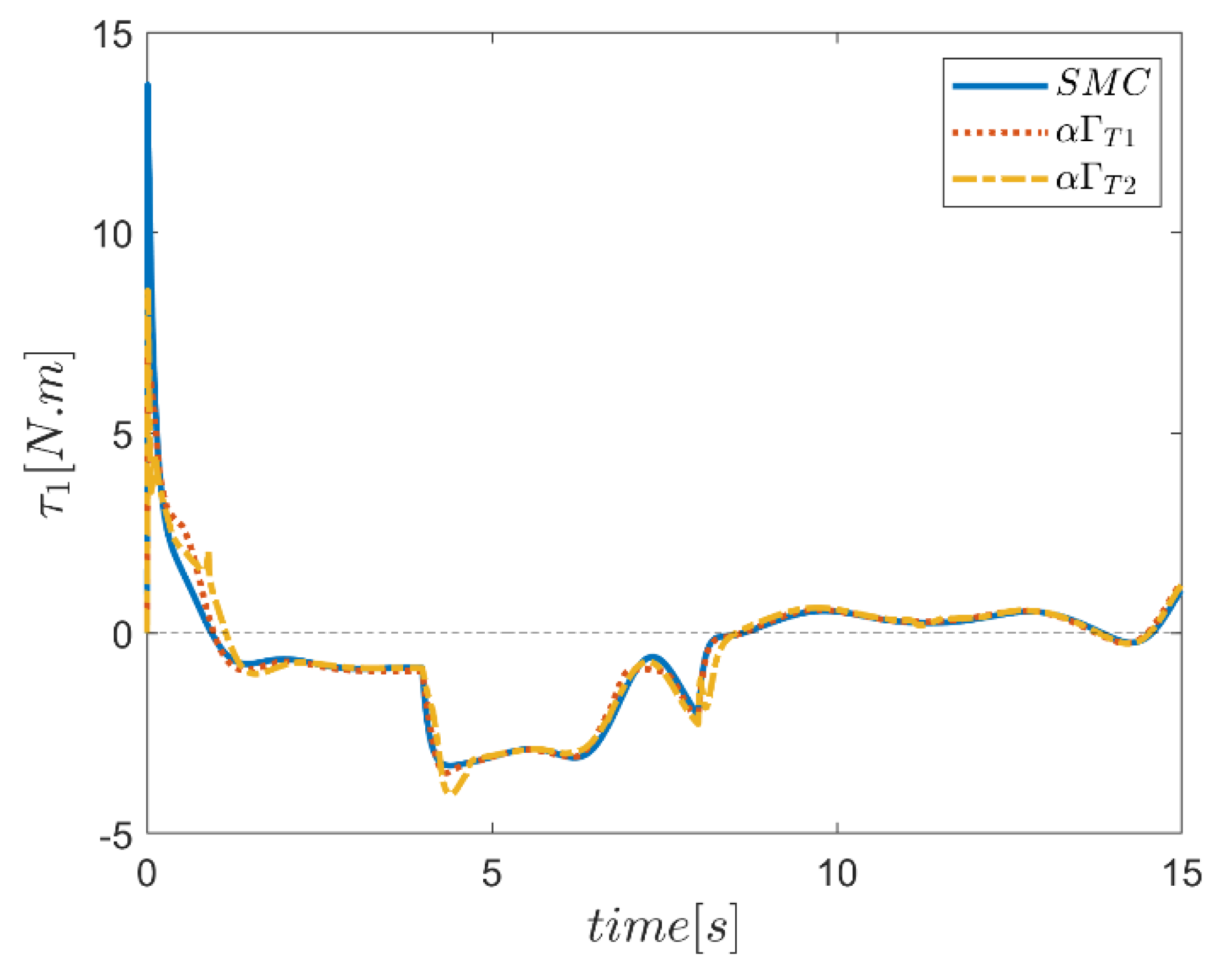
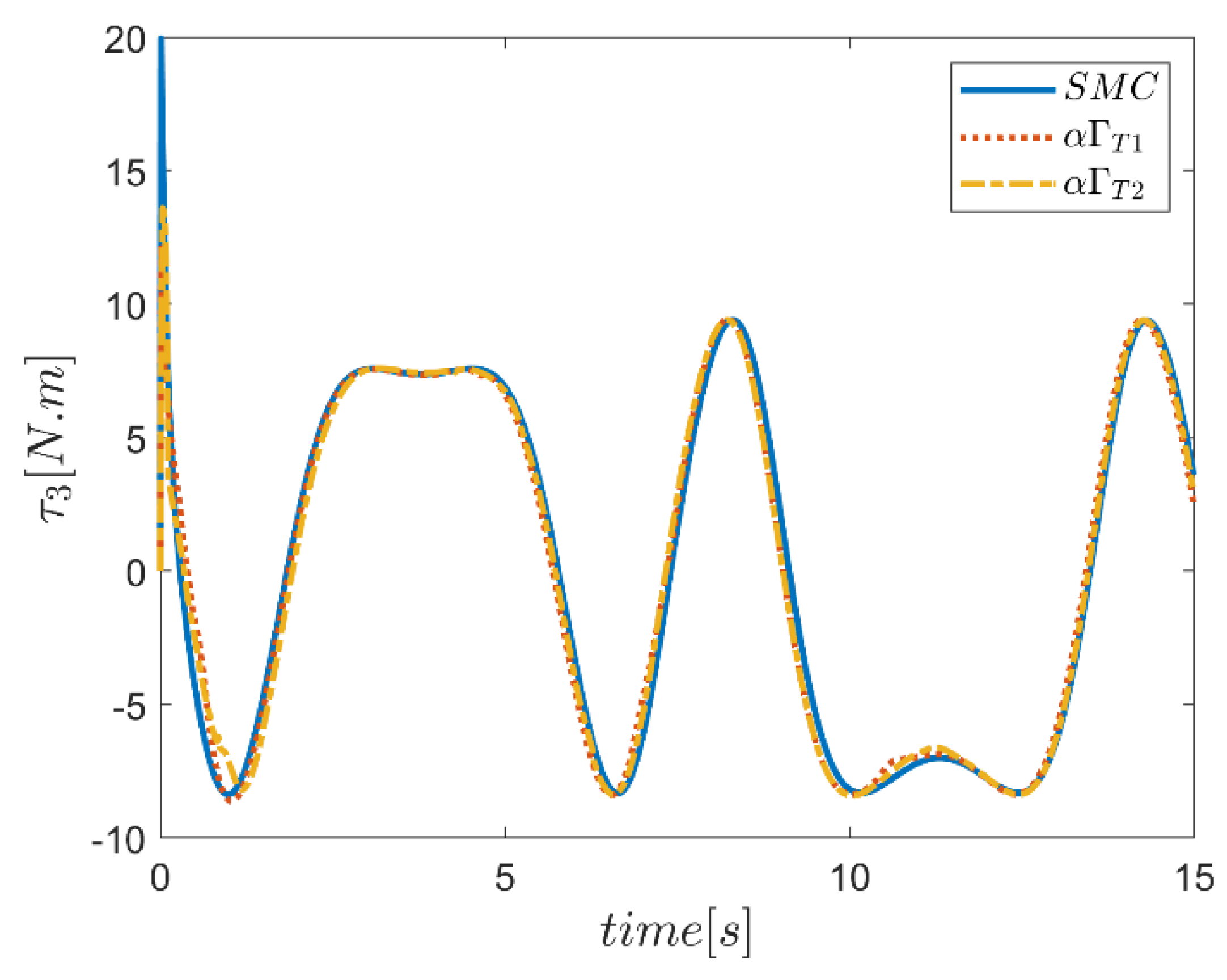
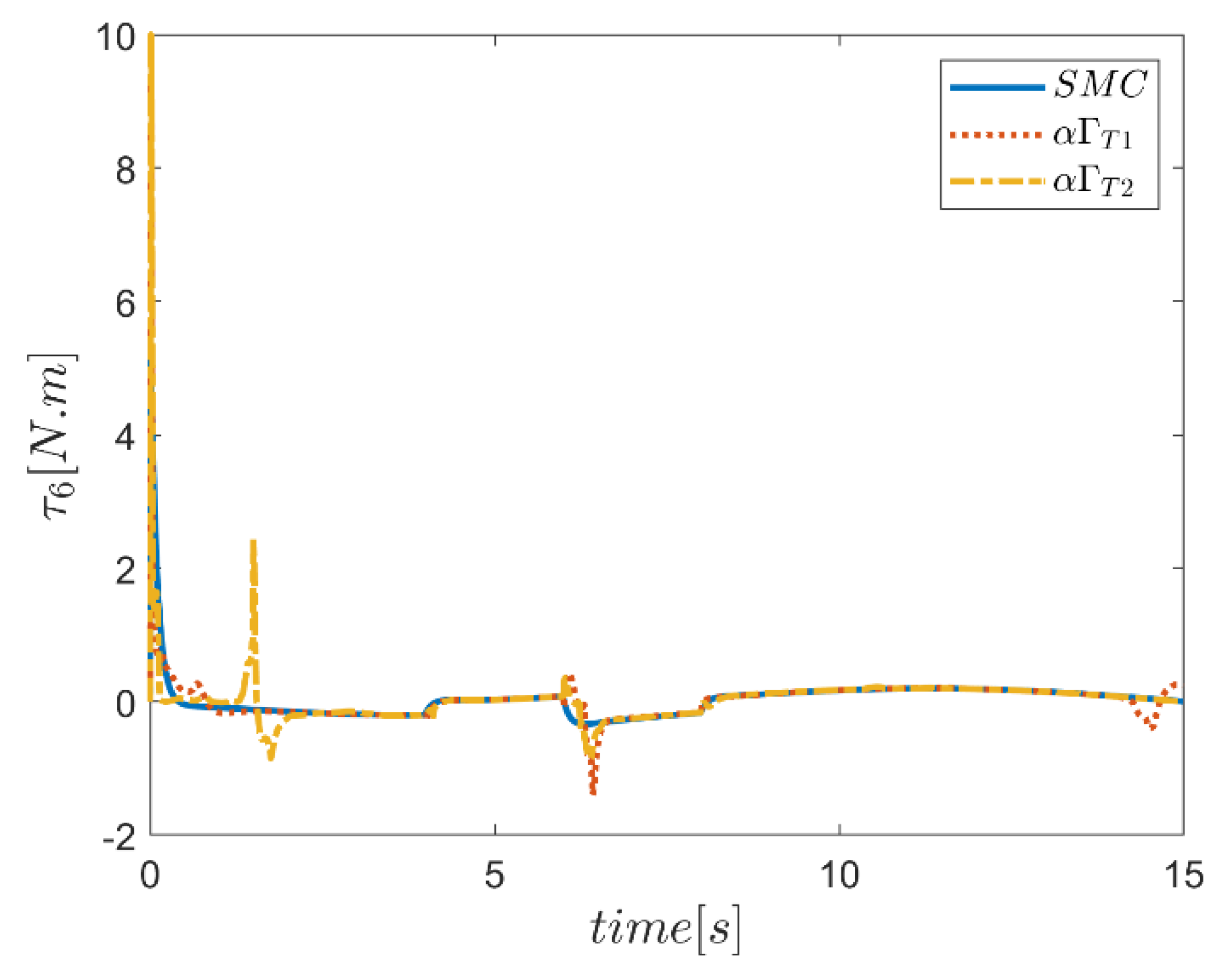
6. Proficiency of the Proposed Hybrid Fuzzy SMCs
7. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Alattas, K.A.; Bouteraa, Y.; Rahmani, R.; Fekih, A.; Mobayen, S.; Assawinchaichote, W. Optimized Fuzzy Enhanced Robust Control Design for a Stewart Parallel Robot. Mathematics 2022, 10, 1917. [Google Scholar]
- Liu, H.; Zhang, T. Fuzzy sliding mode control of robotic manipulators with kinematic and dynamic uncertainties. J. Dyn. Syst. Meas. Control. 2012, 134, 061007. [Google Scholar] [CrossRef]
- Yagiz, N.; Hacioglu, Y. Robust control of a spatial robot using fuzzy sliding modes. Math. Comput. Model. 2009, 49, 114–127. [Google Scholar] [CrossRef]
- Maalej, B.; Medhaffar, H.; Chemori, A.; Derbel, N. A Fuzzy Sliding Mode Controller for Reducing Torques Applied to a Rehabilitation Robot. In Proceedings of the 2020 17th International Multi-Conference on Systems, Signals & Devices (SSD), Sfax, Tunisia, 20–23 July 2020; pp. 740–746. [Google Scholar]
- Zheng, K.; Hu, Y.; Wu, B. Intelligent fuzzy sliding mode control for complex robot system with disturbances. Eur. J. Control. 2020, 51, 95–109. [Google Scholar] [CrossRef]
- Ren, L.-T.; Xie, S.-S.; Miao, Z.-G.; Tian, H.-S.; Peng, J.-B. Fuzzy robust sliding mode control of a class of uncertain systems. J. Cent. South Univ. 2016, 23, 2296–2304. [Google Scholar] [CrossRef]
- Wu, Q.; Wang, X.; Du, F.; Zhu, Q. Fuzzy sliding mode control of an upper limb exoskeleton for robot-assisted rehabilitation. In Proceedings of the 2015 IEEE International Symposium on Medical Measurements and Applications (MeMeA) Proceedings, Torino, Italy, 7–9 May 2015; pp. 451–456. [Google Scholar]
- Razzaghian, A.; Moghaddam, R.K. Fuzzy sliding mode control of 5 DOF upper-limb exoskeleton robot. In Proceedings of the 2015 International Congress on Technology, Communication and Knowledge (ICTCK), Mashhad, Iran, 11–12 November 2015; pp. 25–32. [Google Scholar]
- Qureshi, M.S.; Swarnkar, P.; Gupta, S. A supervisory on-line tuned fuzzy logic based sliding mode control for robotics: An application to surgical robots. Robot. Auton. Syst. 2018, 109, 68–85. [Google Scholar] [CrossRef]
- Soltanpour, M.R.; Khooban, M.H. A particle swarm optimization approach for fuzzy sliding mode control for tracking the robot manipulator. Nonlinear Dyn. 2013, 74, 467–478. [Google Scholar] [CrossRef]
- Taran, B.; Pirmohammadi, A. Designing an optimal fuzzy sliding mode control for a two-link robot. J. Braz. Soc. Mech. Sci. Eng. 2019, 42, 5. [Google Scholar] [CrossRef]
- Xie, Z.; Sun, T.; Kwan, T.; Wu, X. Motion control of a space manipulator using fuzzy sliding mode control with reinforcement learning. Acta Astronaut. 2020, 176, 156–172. [Google Scholar] [CrossRef]
- Vijay, M.; Jena, D. PSO based neuro fuzzy sliding mode control for a robot manipulator. J. Electr. Syst. Inf. Technol. 2017, 4, 243–256. [Google Scholar] [CrossRef]
- Balcazar, R.; Rubio, J.d.J.; Orozco, E.; Andres Cordova, D.; Ochoa, G.; Garcia, E.; Pacheco, J.; Gutierrez, G.J.; Mujica-Vargas, D.; Aguilar-Ibañez, C. The Regulation of an Electric Oven and an Inverted Pendulum. Symmetry 2022, 14, 759. [Google Scholar] [CrossRef]
- Rubio, J.D.J.; Orozco, E.; Cordova, D.A.; Islas, M.A.; Pacheco, J.; Gutierrez, G.J.; Zacarias, A.; Soriano, L.A.; Meda-Campaña, J.A.; Mujica-Vargas, D. Modified linear technique for the controllability and observability of robotic arms. IEEE Access 2022, 10, 3366–3377. [Google Scholar] [CrossRef]
- Meda-Campaña, J.A.; Rodríguez-Manzanarez, R.A.; Ontiveros-Paredes, S.D.; Rubio, J.d.J.; Tapia-Herrera, R.; Hernández-Cortés, T.; Obregón-Pulido, G.; Aguilar-Ibáñez, C. An Algebraic Fuzzy Pole Placement Approach to Stabilize Nonlinear Mechanical Systems. IEEE Trans. Fuzzy Syst. 2022, 30, 3322–3332. [Google Scholar] [CrossRef]
- Lughofer, E.; Skrjanc, I. Evolving Error Feedback Fuzzy Model for Improved Robustness under Measurement Noise. IEEE Trans. Fuzzy Syst. 2022, 1–12. [Google Scholar] [CrossRef]
- Soriano, L.A.; Zamora, E.; Vazquez-Nicolas, J.M.; Hernández, G.; Barraza Madrigal, J.A.; Balderas, D. PD Control Compensation Based on a Cascade Neural Network Applied to a Robot Manipulator. Frontiers in Neurorobotics 2020, 14, 577749. [Google Scholar] [CrossRef]
- Silva-Ortigoza, R.; Hernández-Márquez, E.; Roldán-Caballero, A.; Tavera-Mosqueda, S.; Marciano-Melchor, M.; García-Sánchez, J.R.; Hernández-Guzmán, V.M.; Silva-Ortigoza, G. Sensorless Tracking Control for a “Full-Bridge Buck Inverter–DC Motor” System: Passivity and Flatness-Based Design. IEEE Access 2021, 9, 132191–132204. [Google Scholar] [CrossRef]
- Chin, C.S.; Lin, W.P. Robust genetic algorithm and fuzzy inference mechanism embedded in a sliding-mode controller for an uncertain underwater robot. IEEE/ASME Trans. Mechatron. 2018, 23, 655–666. [Google Scholar] [CrossRef]
- Huaman-Loayza, A.S. Path-Following of a Quadrotor Using Fuzzy Sliding Mode Control. In Proceedings of the 2018 IEEE XXV International Conference on Electronics, Electrical Engineering and Computing (INTERCON), Lima, Peru, 8–10 August 2018; pp. 1–4. [Google Scholar]
- Hu, S.B.; Lu, M.X. Backstepping Fuzzy Sliding Mode Control for a Three-Links Spatial Robot Based on Variable Rate Reaching Law. Appl. Mech. Mater. 2011, 105–107, 2213–2216. [Google Scholar] [CrossRef]
- Khanesar, M.A.; Branson, D. Robust Sliding Mode Fuzzy Control of Industrial Robots Using an Extended Kalman Filter Inverse Kinematic Solver. Energies 2022, 15, 1876. [Google Scholar] [CrossRef]
- Li, F.; Zhang, Z.; Wu, Y.; Chen, Y.; Liu, K.; Yao, J. Improved fuzzy sliding mode control in flexible manipulator actuated by PMAs. Robotica 2022, 40, 2683–2696. [Google Scholar] [CrossRef]
- Bao, L.; Kim, D.; Yi, S.-J.; Lee, J. Design of a Sliding Mode Controller with Fuzzy Rules for a 4-DoF Service Robot. Int. J. Control. Autom. Syst. 2021, 19, 2869–2881. [Google Scholar] [CrossRef]
- Ashagrie, A.; Salau, A.O.; Weldcherkos, T. Modeling and control of a 3-DOF articulated robotic manipulator using self-tuning fuzzy sliding mode controller. Cogent Eng. 2021, 8, 1950105. [Google Scholar] [CrossRef]
- Akhenak, A.; Chadli, M.; Ragot, J.; Maquin, D. Fault detection and isolation using sliding mode observer for uncertain Takagi-Sugeno fuzzy model. In Proceedings of the 2008 16th Mediterranean Conference on Control and automation, Ajaccio, France, 25–27 June 2008; pp. 286–291. [Google Scholar]
- El Hajjaji, A.; Chadli, M.; Oudghiri, M.; Pages, O. Observer-based robust fuzzy control for vehicle lateral dynamics. In Proceedings of the 2006 American Control Conference, Minneapolis, MN, USA, 14–16 June 2006; p. 6. [Google Scholar]
- Mohamed, K.; Chadli, M.; Chaabane, M. Unknown inputs observer for a class of nonlinear uncertain systems: An LMI approach. Int. J. Autom. Comput. 2012, 9, 331–336. [Google Scholar] [CrossRef]
- Castillo, O.; Melin, P.; Kacprzyk, J.; Pedrycz, W. Type-2 Fuzzy Logic: Theory and Applications. In Proceedings of the 2007 IEEE International Conference on Granular Computing (GRC 2007), San Jose, CA, USA, 2–4 November 2007; p. 145. [Google Scholar]
- Mendel, J.; Hagras, H.; Tan, W.-W.; Melek, W.W.; Ying, H. Introduction to Type-2 Fuzzy Logic Control: Theory and Applications; John Wiley & Sons: Hoboken, NJ, USA, 2014. [Google Scholar]
- Castillo, O.; Amador-Angulo, L.; Castro, J.R.; Garcia-Valdez, M. A comparative study of type-1 fuzzy logic systems, interval type-2 fuzzy logic systems and generalized type-2 fuzzy logic systems in control problems. Inf. Sci. 2016, 354, 257–274. [Google Scholar] [CrossRef]
- Sanchez, M.A.; Castillo, O.; Castro, J.R. Generalized type-2 fuzzy systems for controlling a mobile robot and a performance comparison with interval type-2 and type-1 fuzzy systems. Expert Syst. Appl. 2015, 42, 5904–5914. [Google Scholar] [CrossRef]
- Liu, J.; Zhao, T.; Dian, S. General type-2 fuzzy sliding mode control for motion balance adjusting of power-line inspection robot. Soft Comput. 2021, 25, 1033–1047. [Google Scholar] [CrossRef]
- Nafia, N.; El Kari, A.; Ayad, H.; Mjahed, M. Robust interval type-2 fuzzy sliding mode control design for robot manipulators. Robotics 2018, 7, 40. [Google Scholar] [CrossRef]
- Kebria, P.M.; Al-Wais, S.; Abdi, H.; Nahavandi, S. Kinematic and dynamic modelling of UR5 manipulator. In Proceedings of the 2016 IEEE International Conference on Systems, Man, and Cybernetics (SMC), Budapest, Hungary, 9–12 October 2016; pp. 004229–004234. [Google Scholar]
- Universal Robots (UR5). Available online: https://www.universal-robots.com/products/ur5-robot/ (accessed on 20 October 2022).
- Spong, M.W.; Hutchinson, S.; Vidyasagar, M. Robot Modeling and Control; John Wiley & Sons: Hoboken, NJ, USA, 2020. [Google Scholar]
- Mendel, J.M.; John, R.I.; Liu, F. Interval type-2 fuzzy logic systems made simple. IEEE Trans. Fuzzy Syst. 2006, 14, 808–821. [Google Scholar] [CrossRef]
- Alavandar, S.; Nigam, M. Fuzzy PD + I control of a six DOF robot manipulator. Ind. Robot. Int. J. 2008, 35, 125–132. [Google Scholar] [CrossRef]

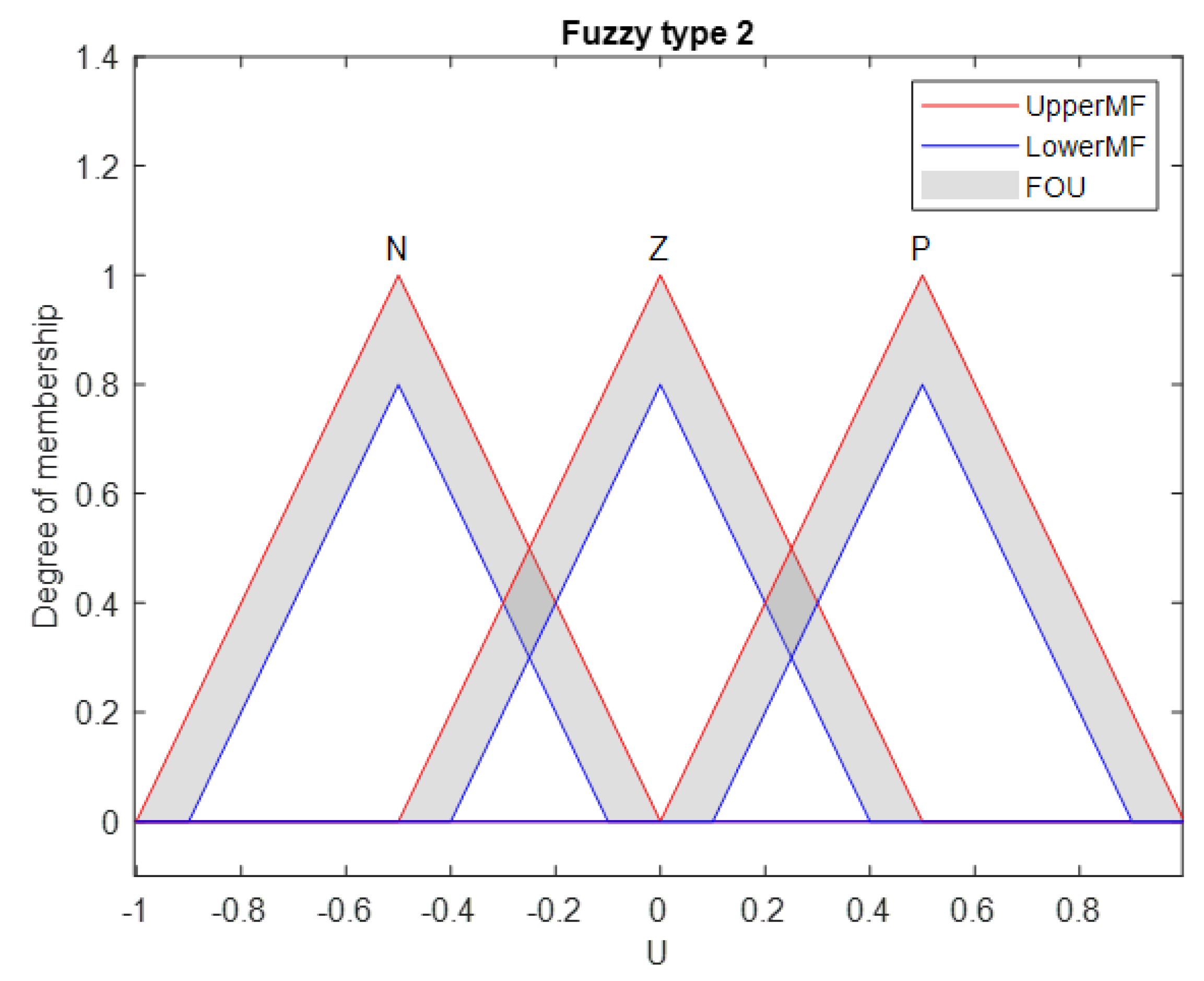



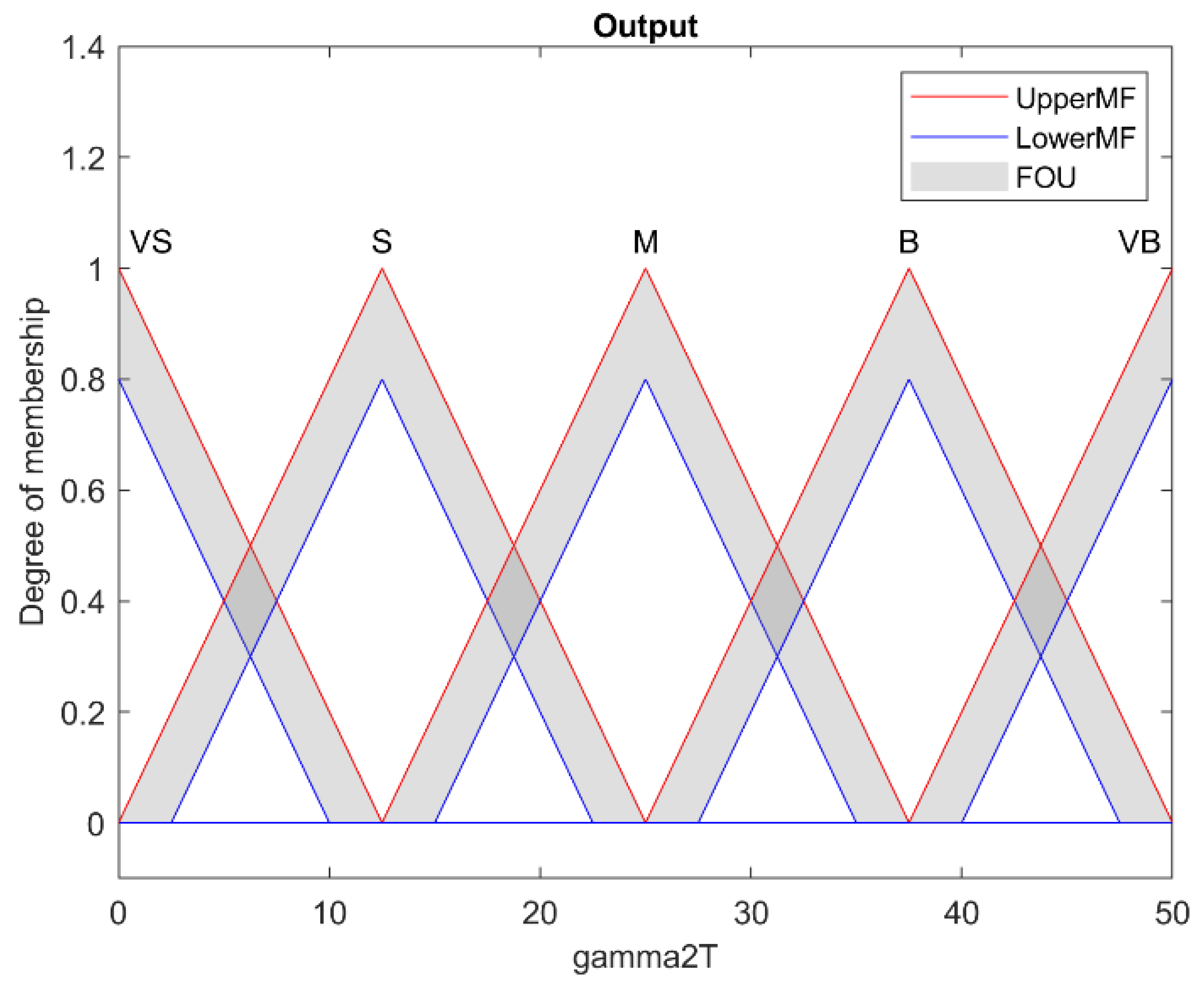

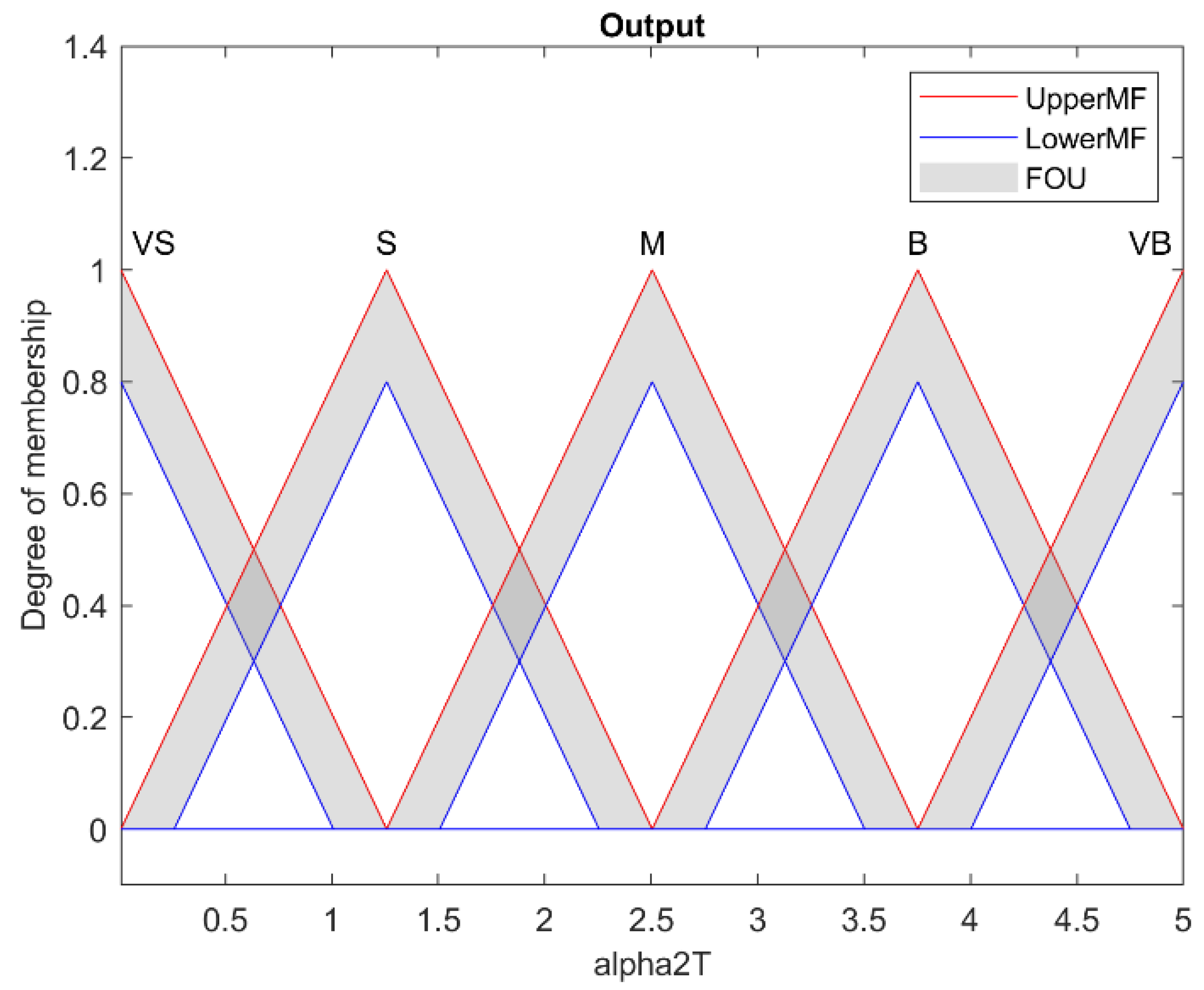
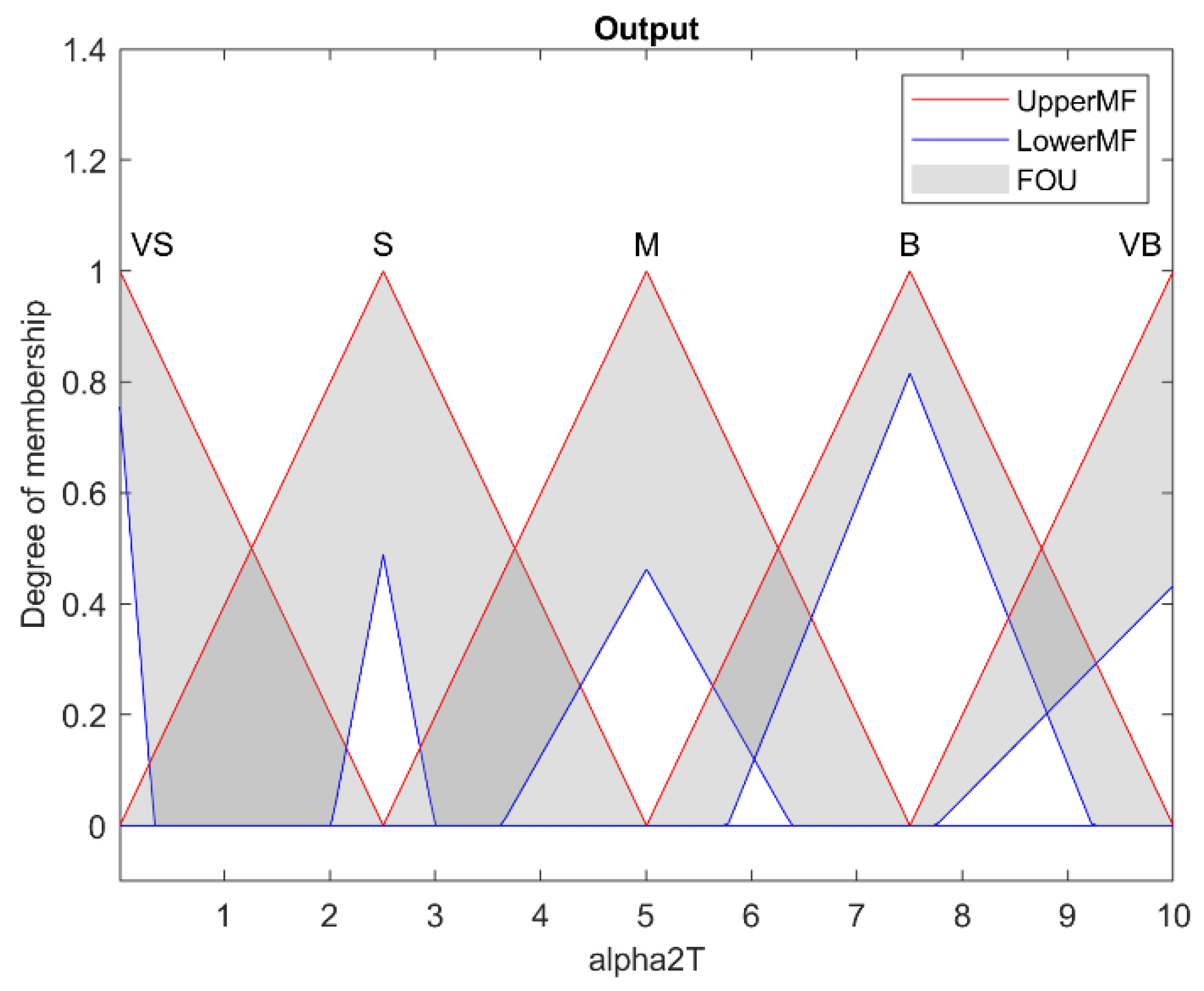
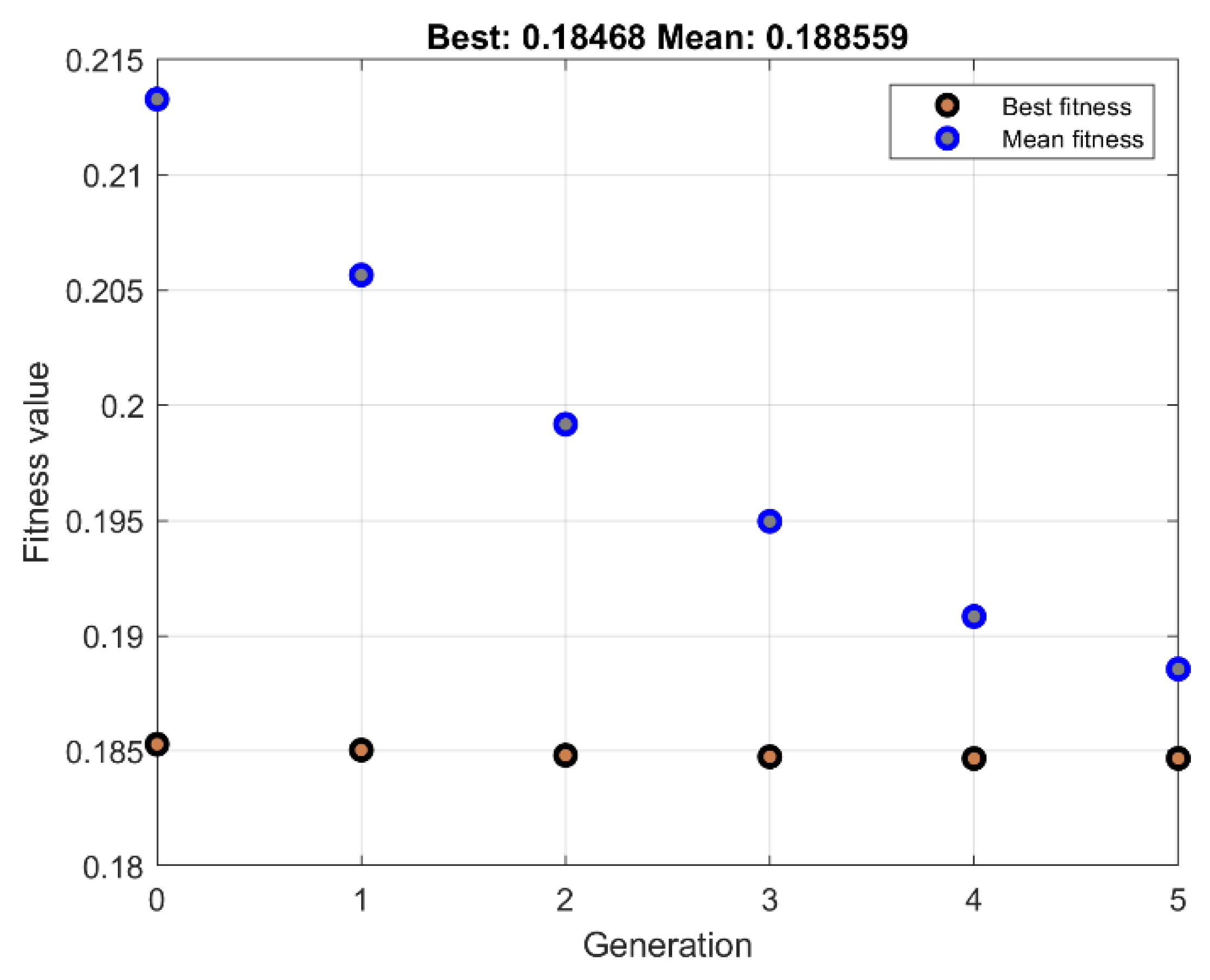




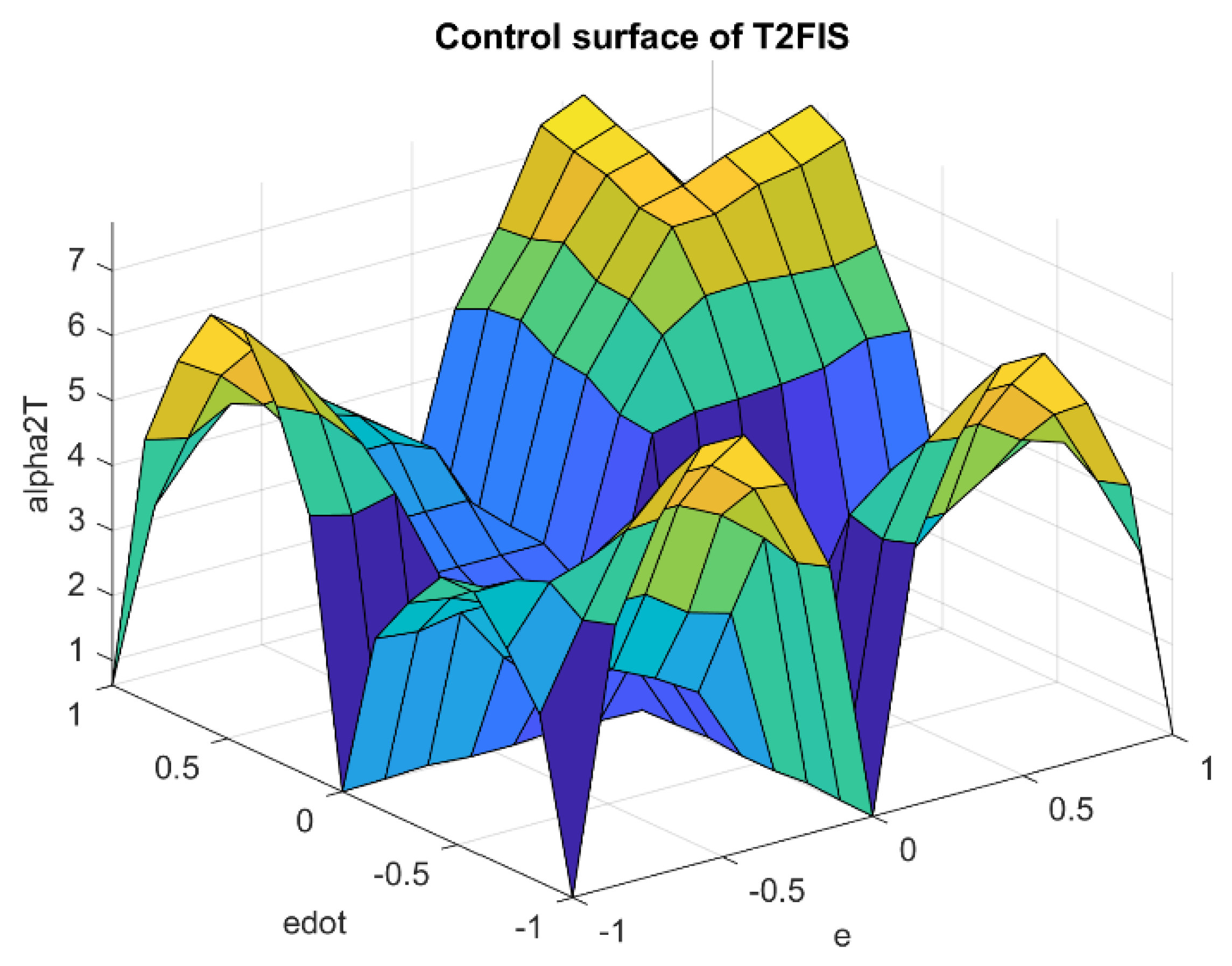

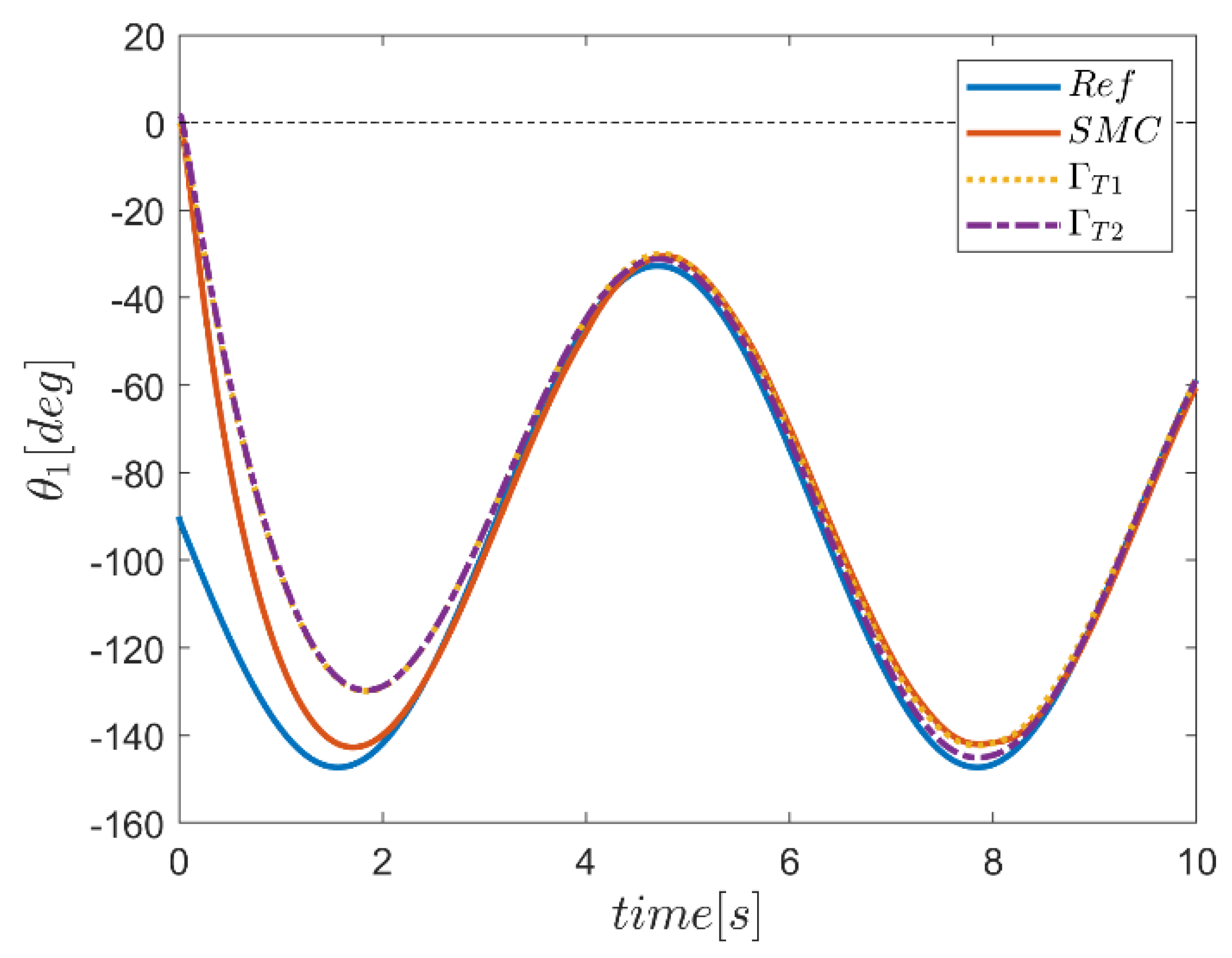
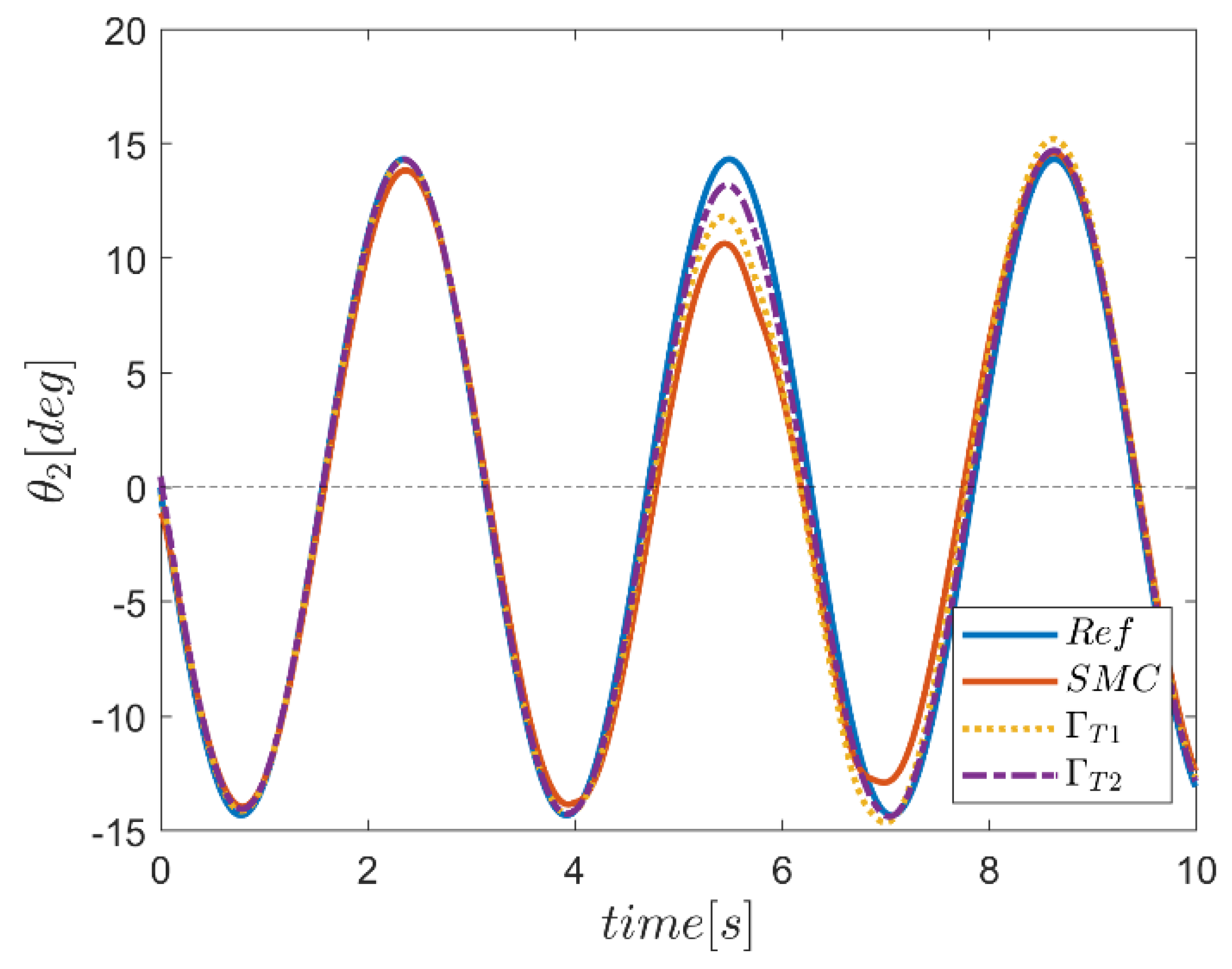













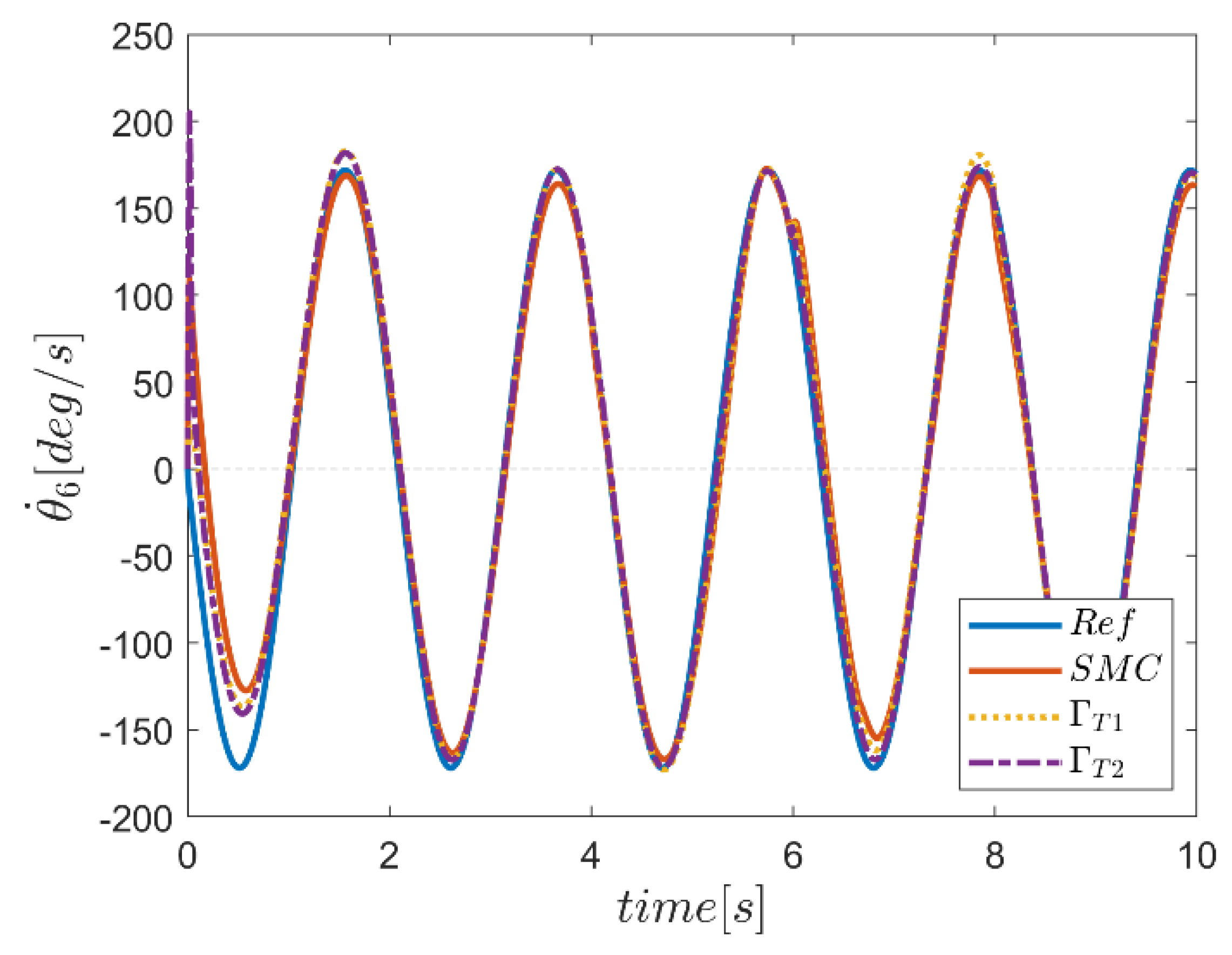
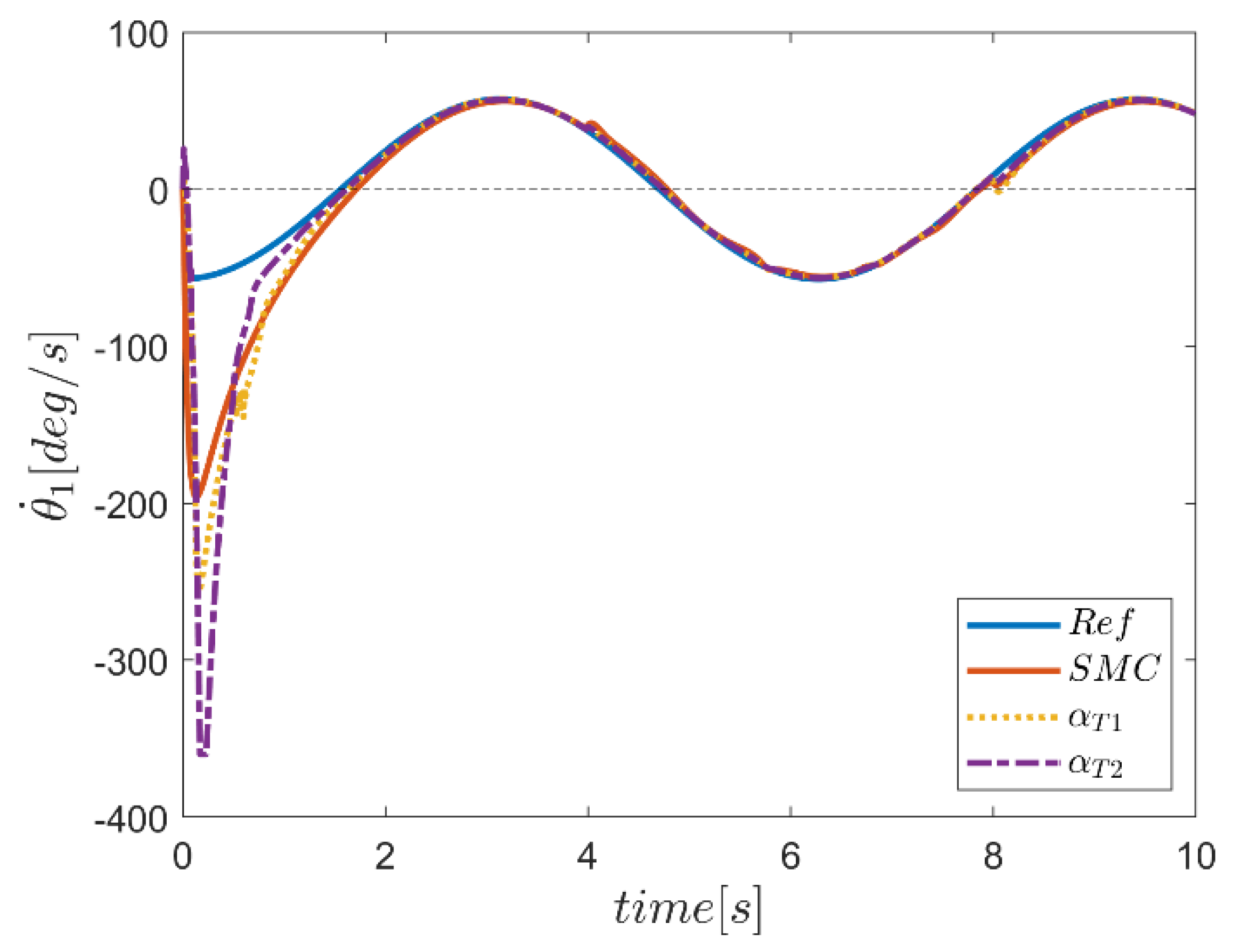
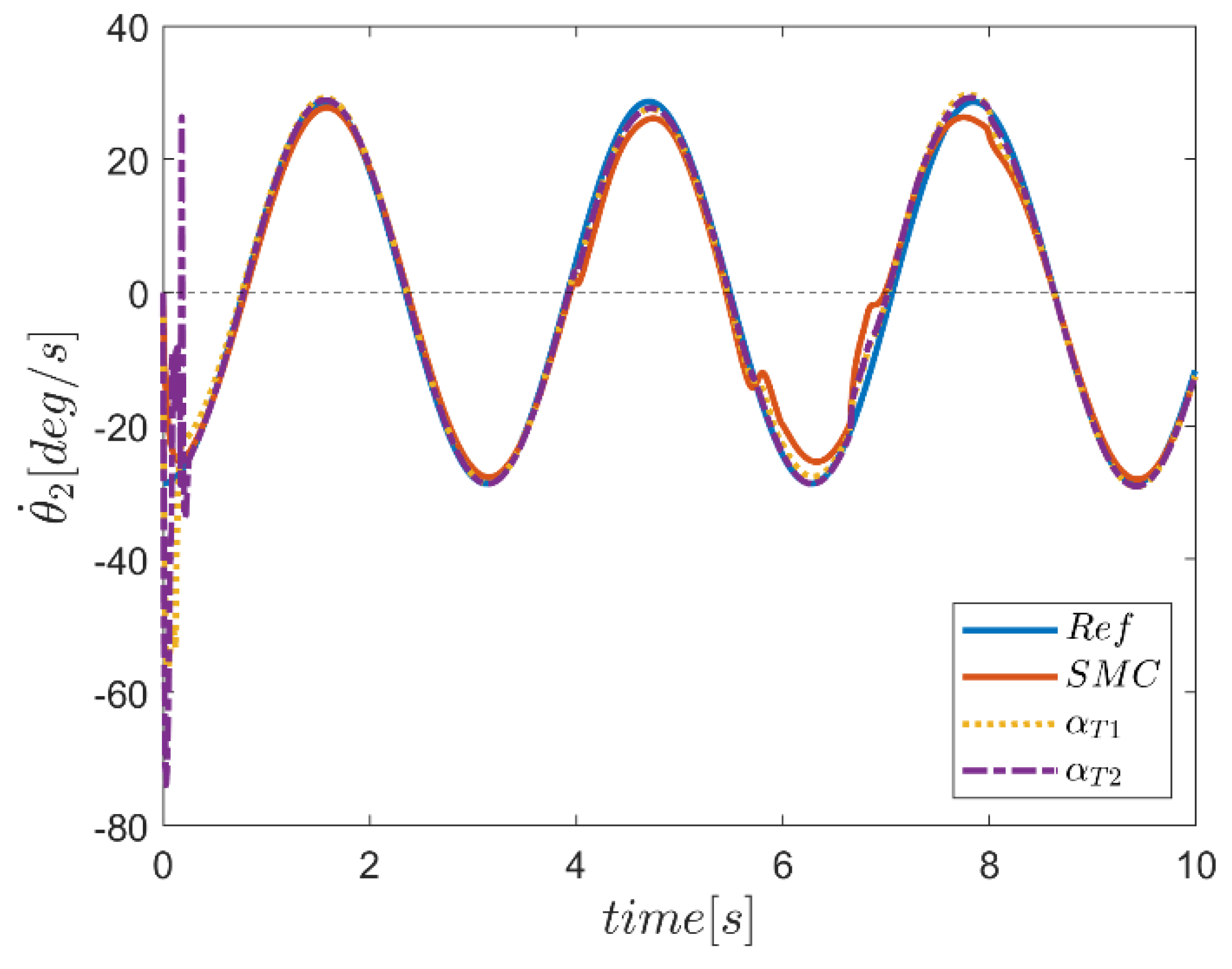
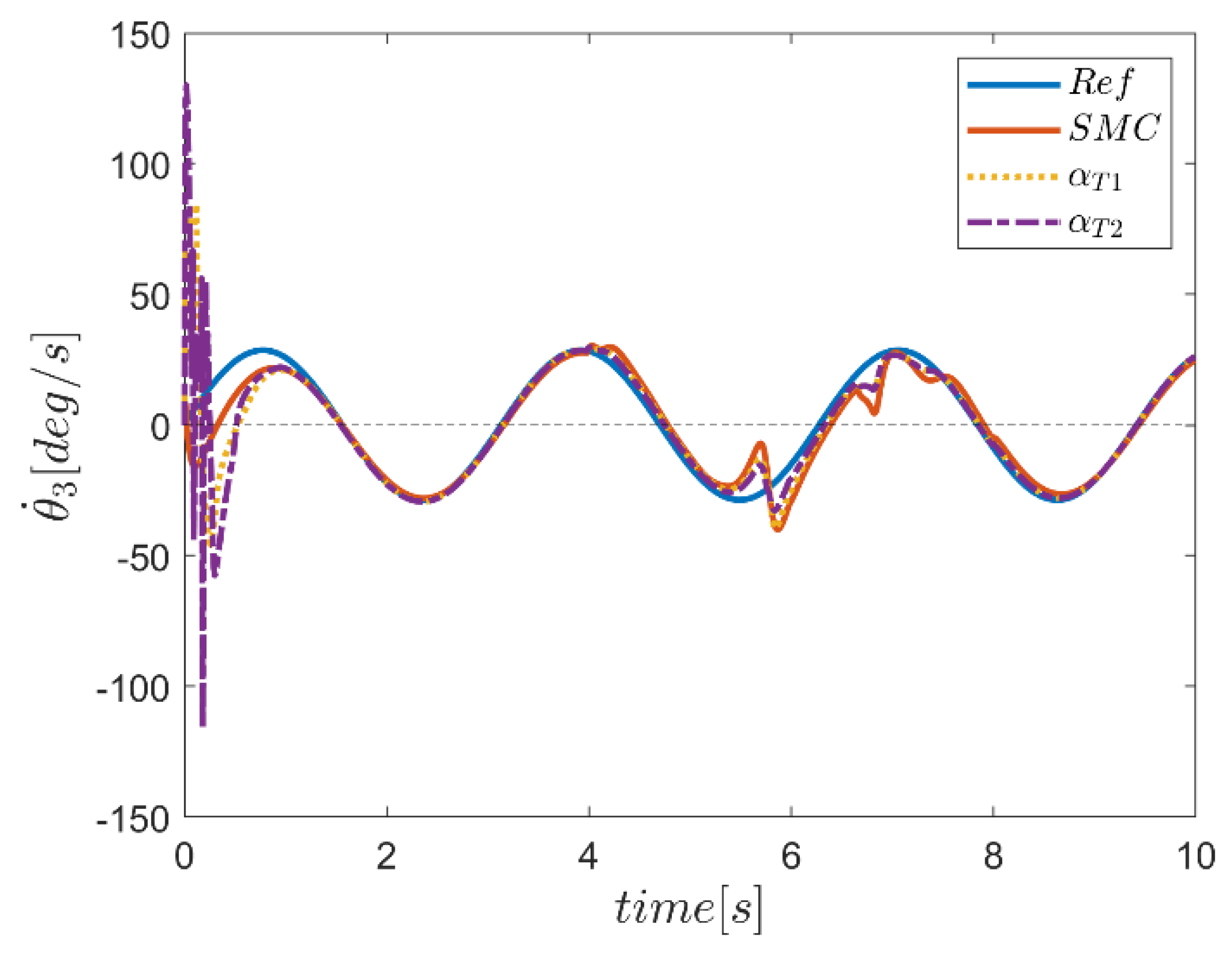
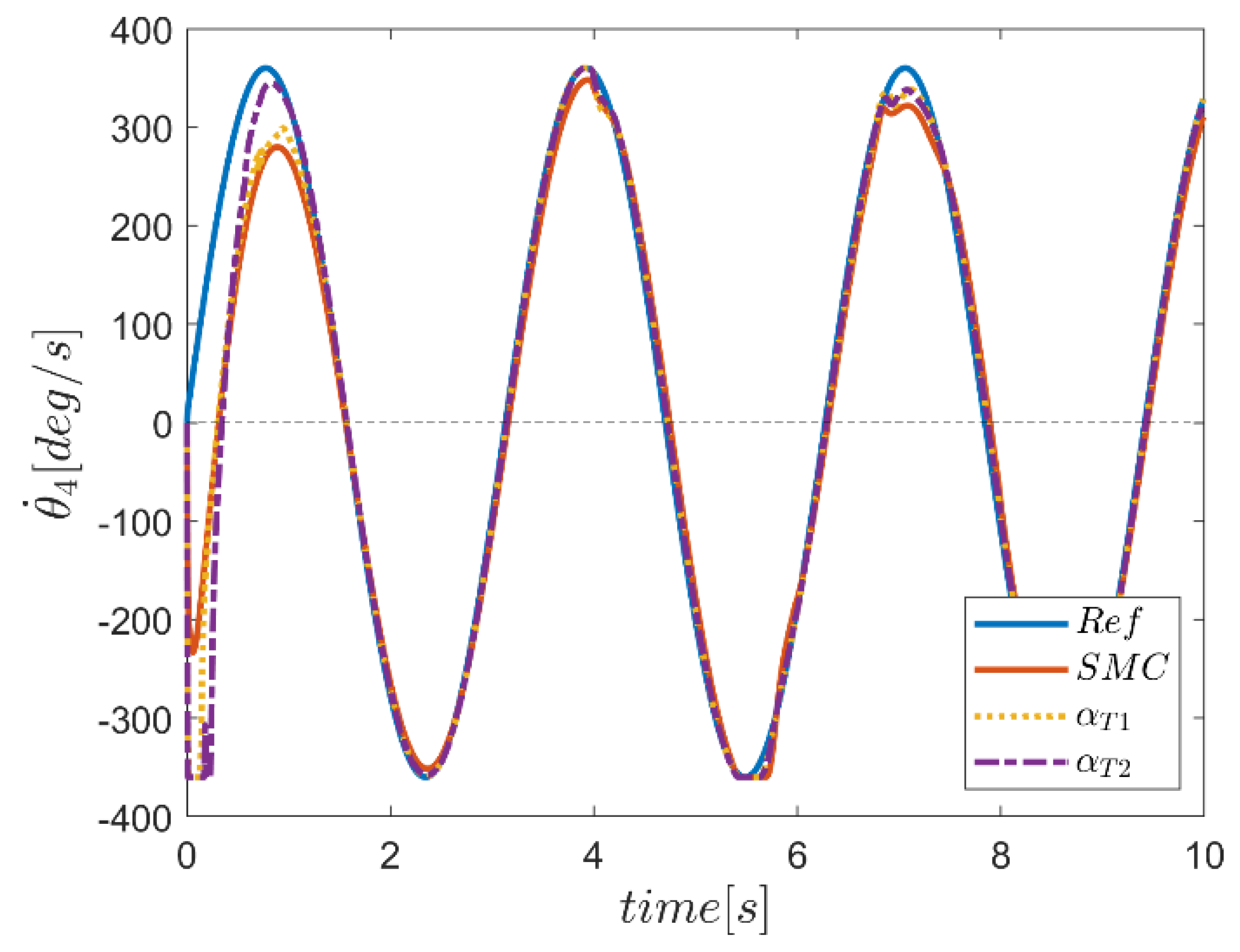


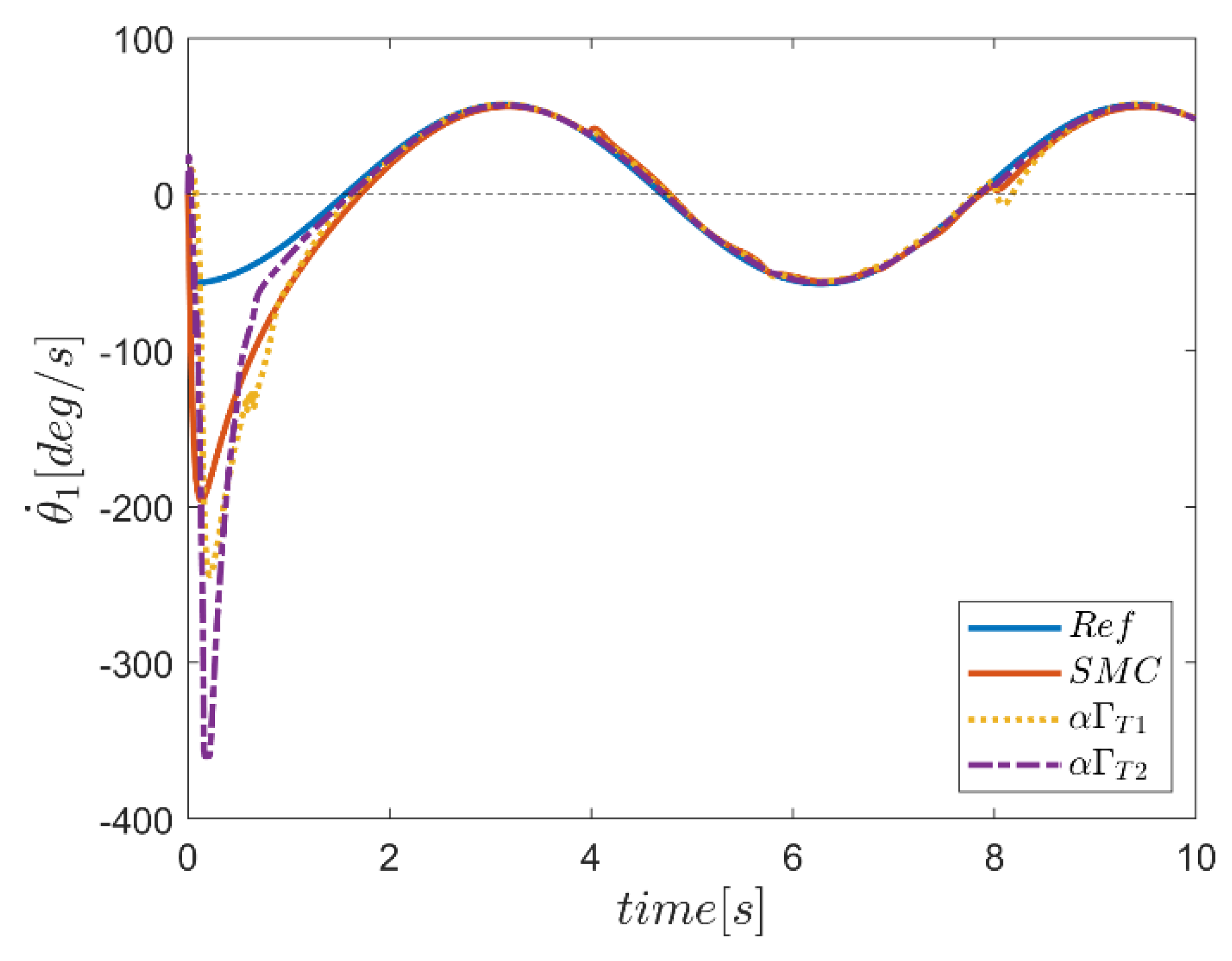
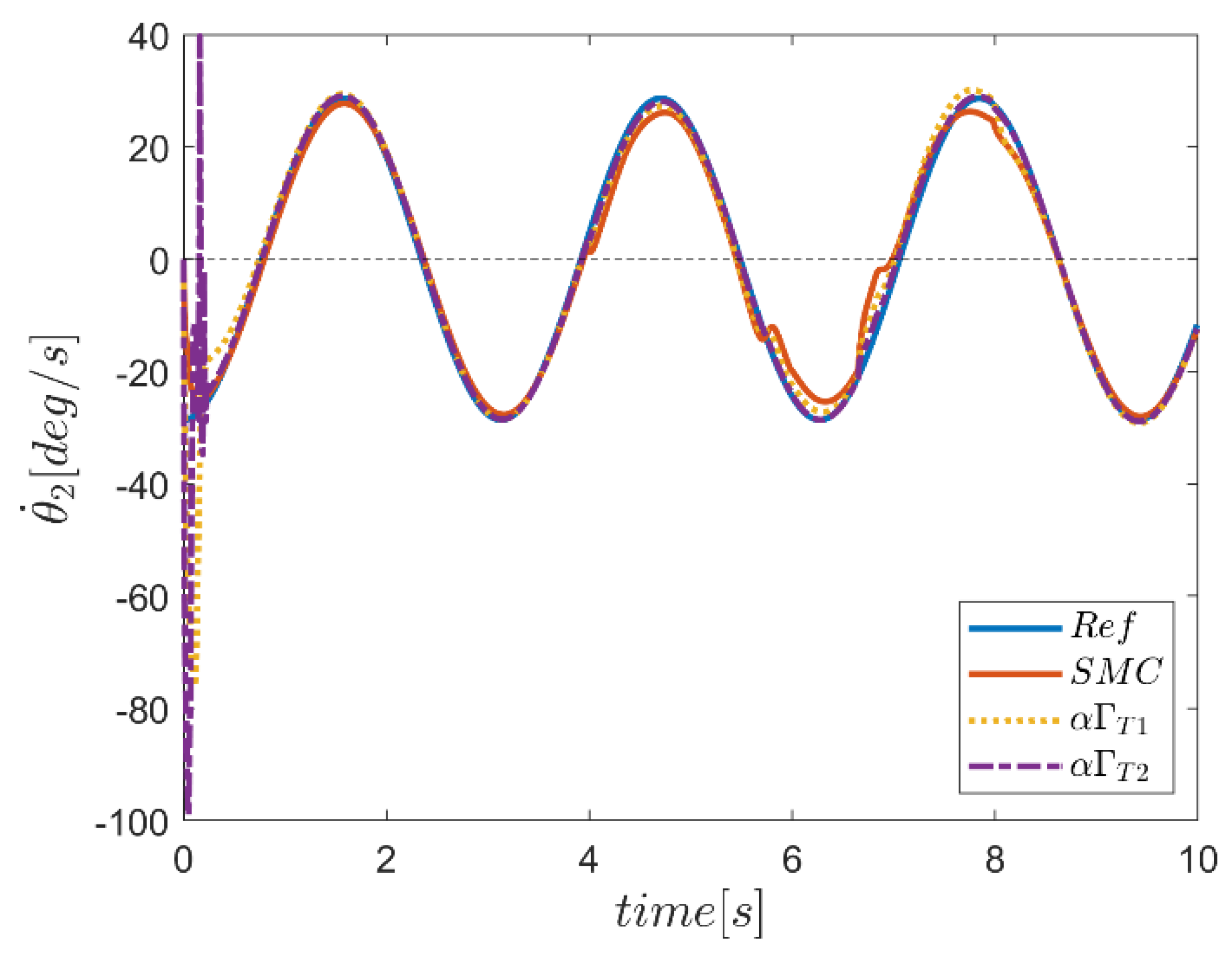

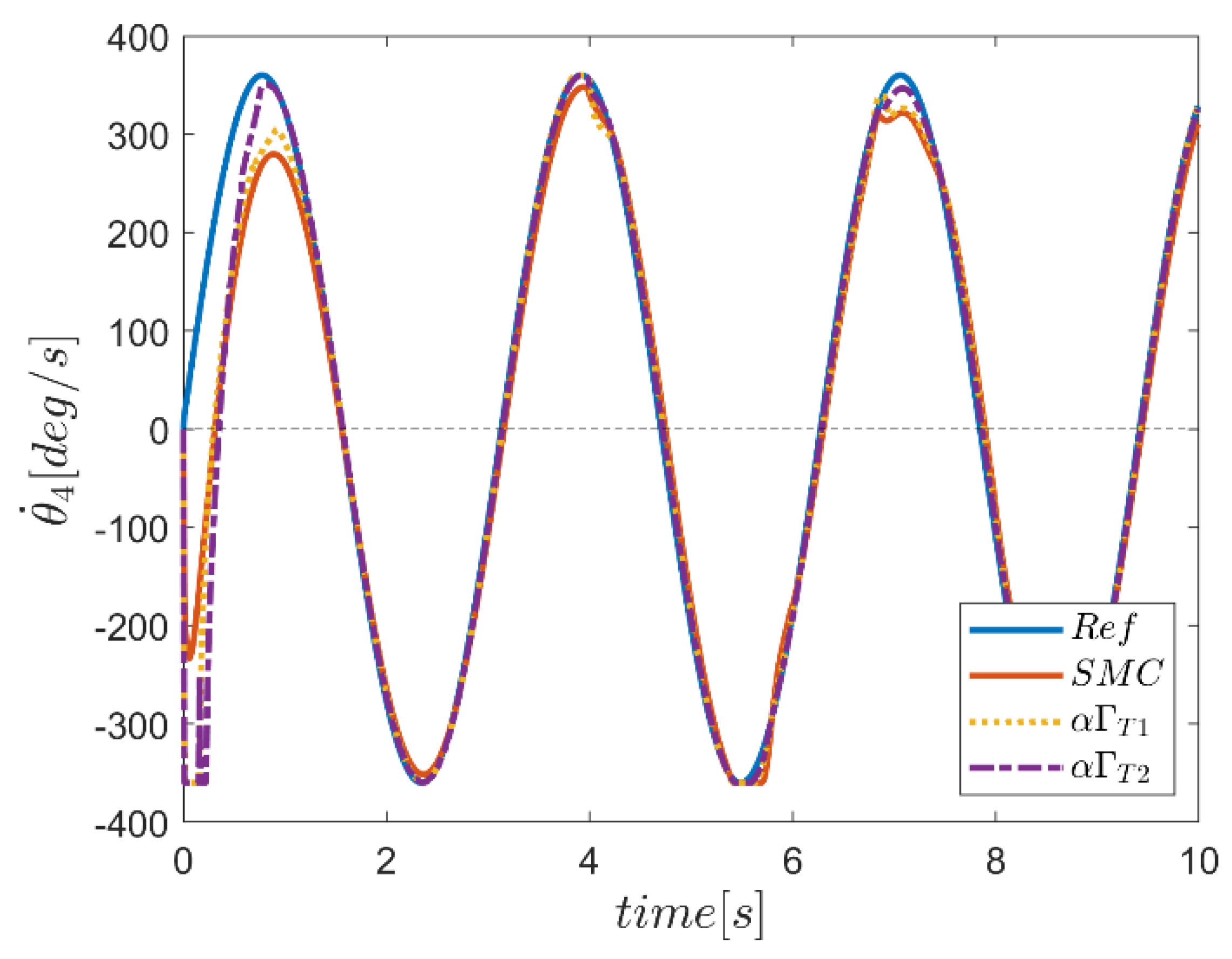




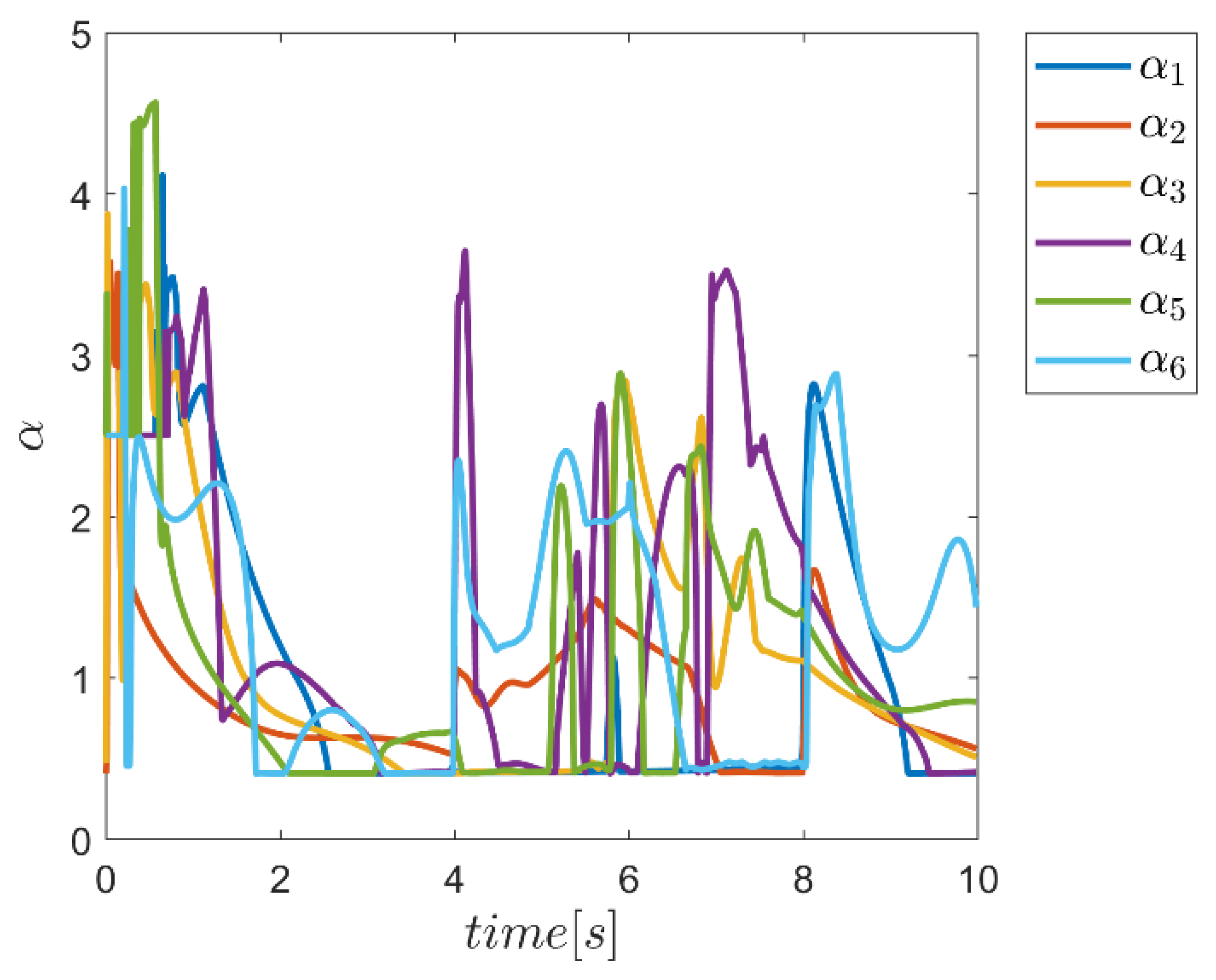
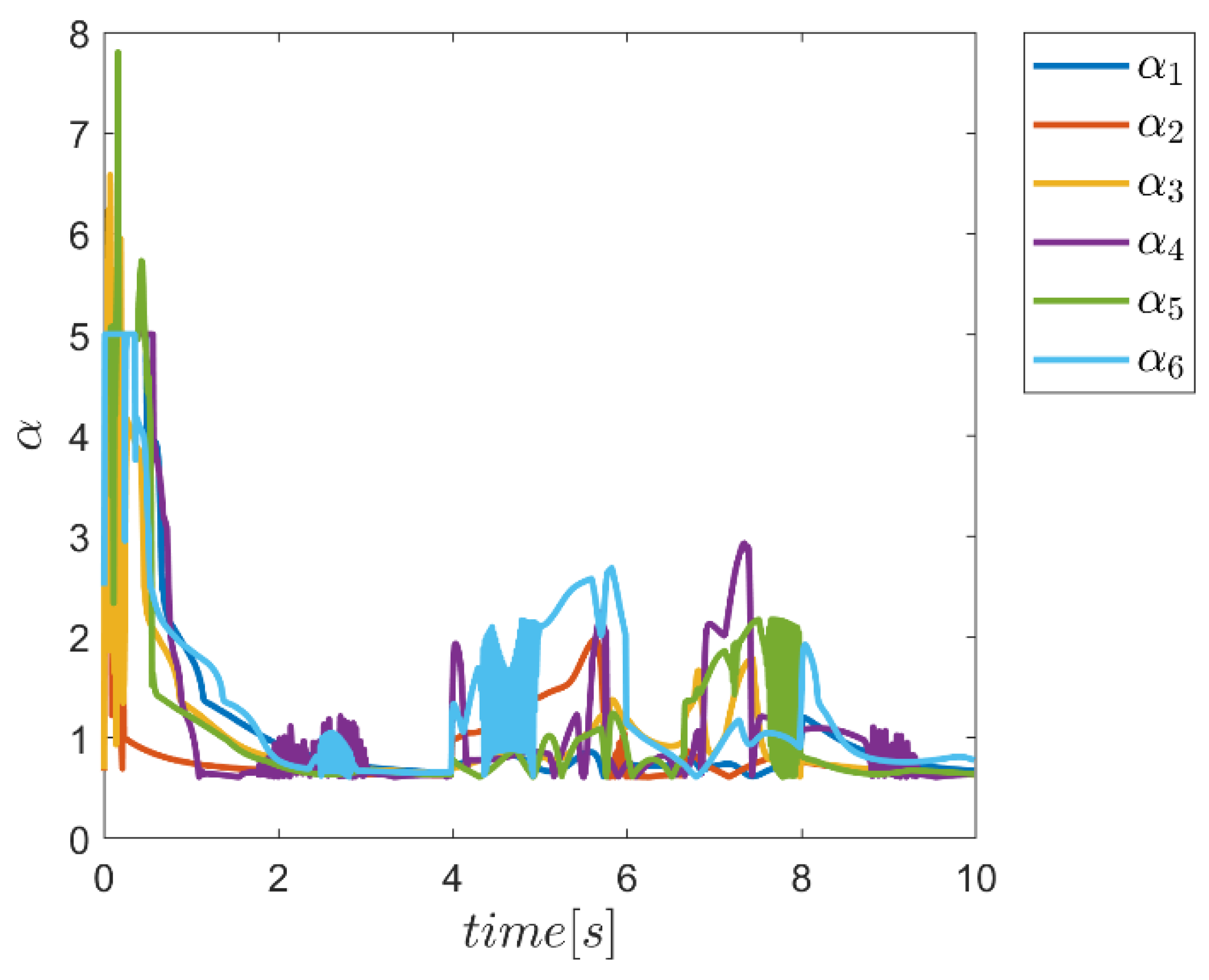

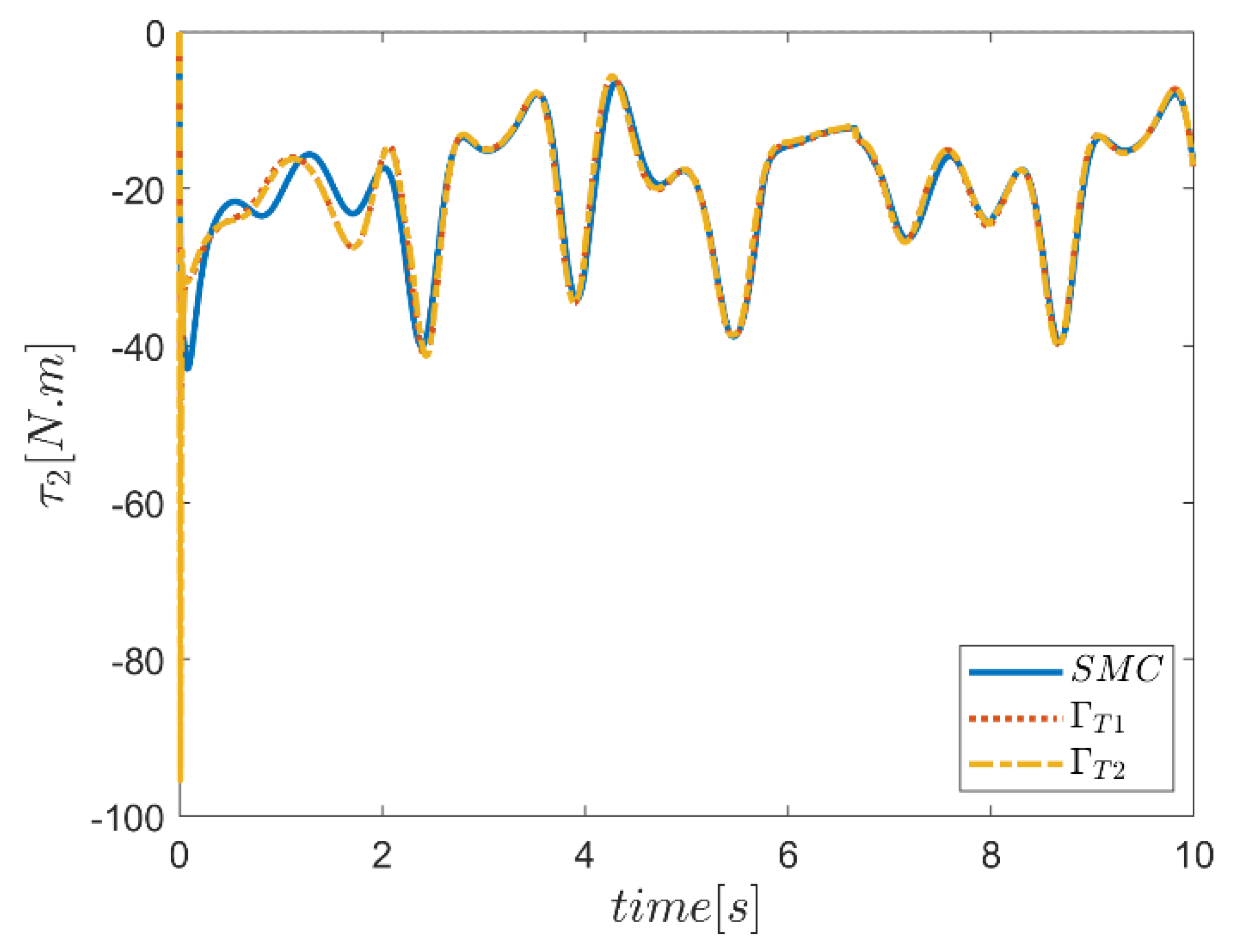


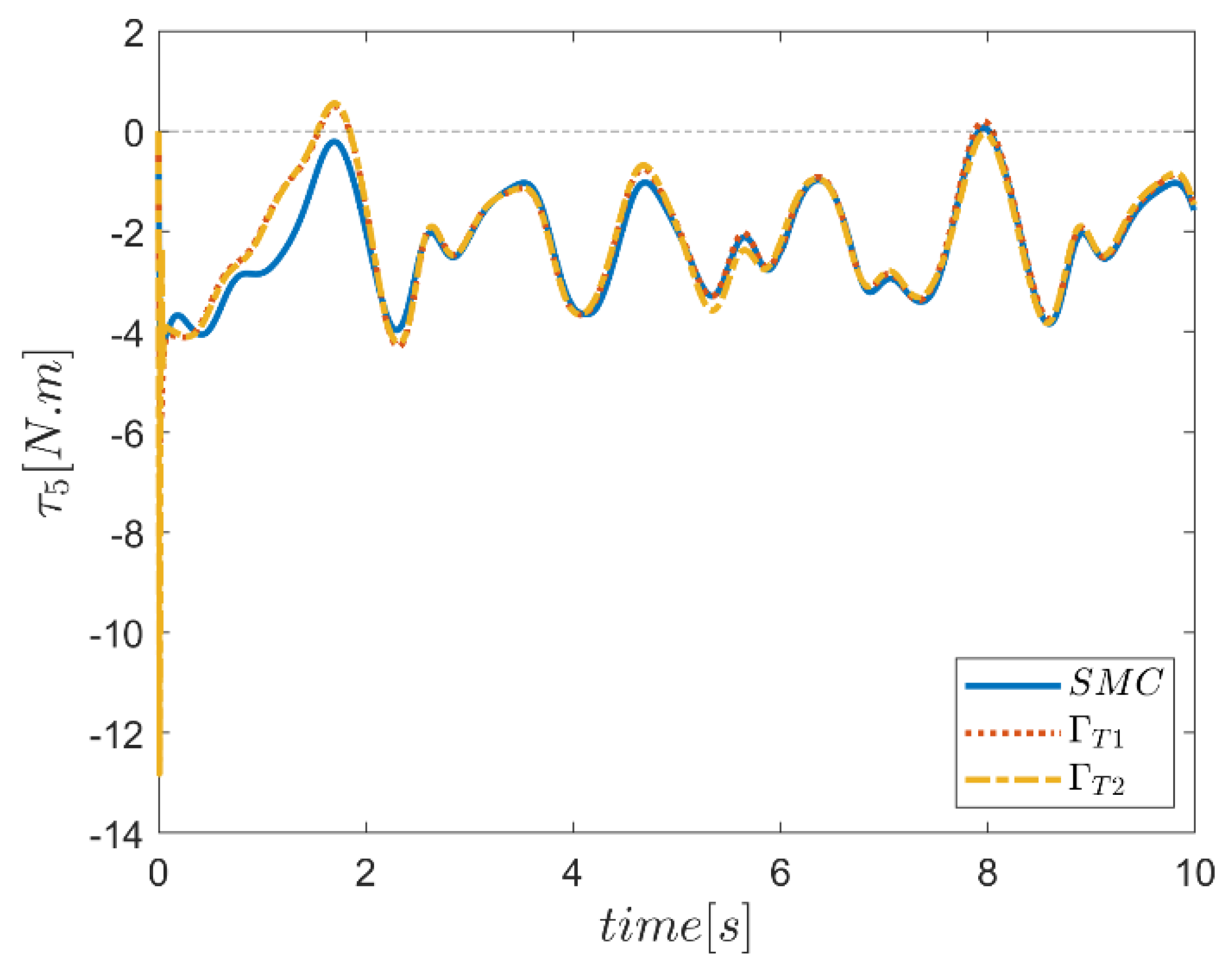
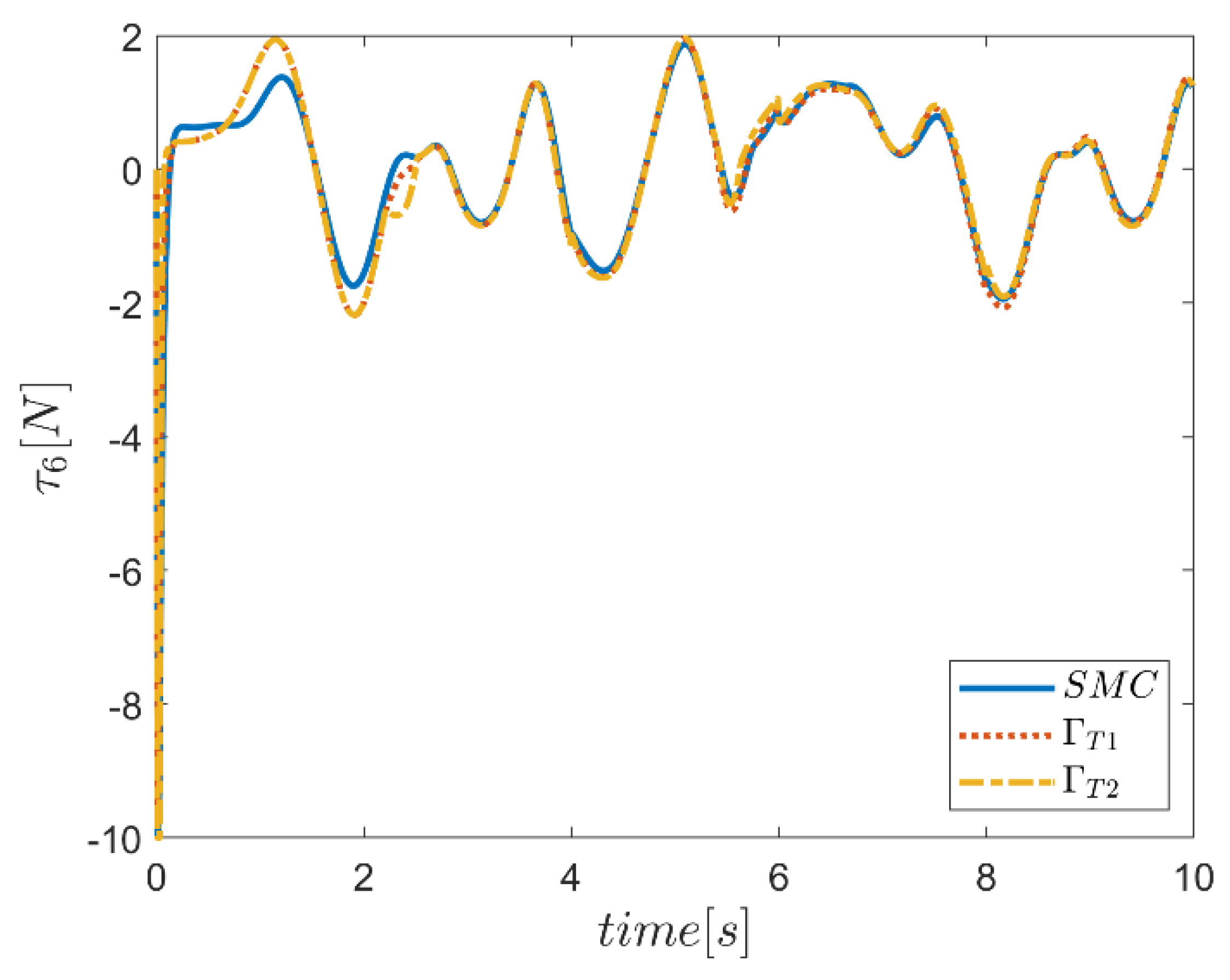
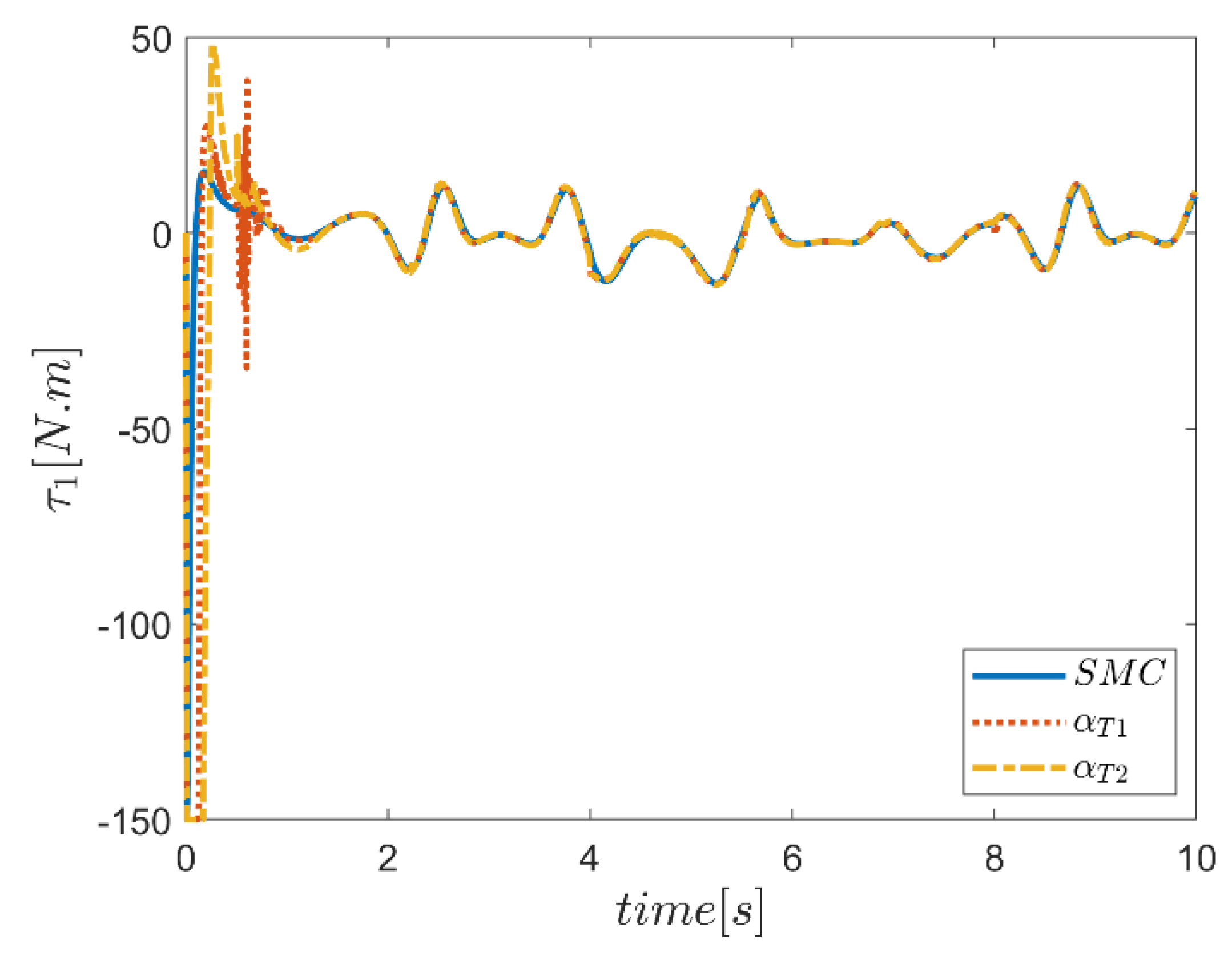
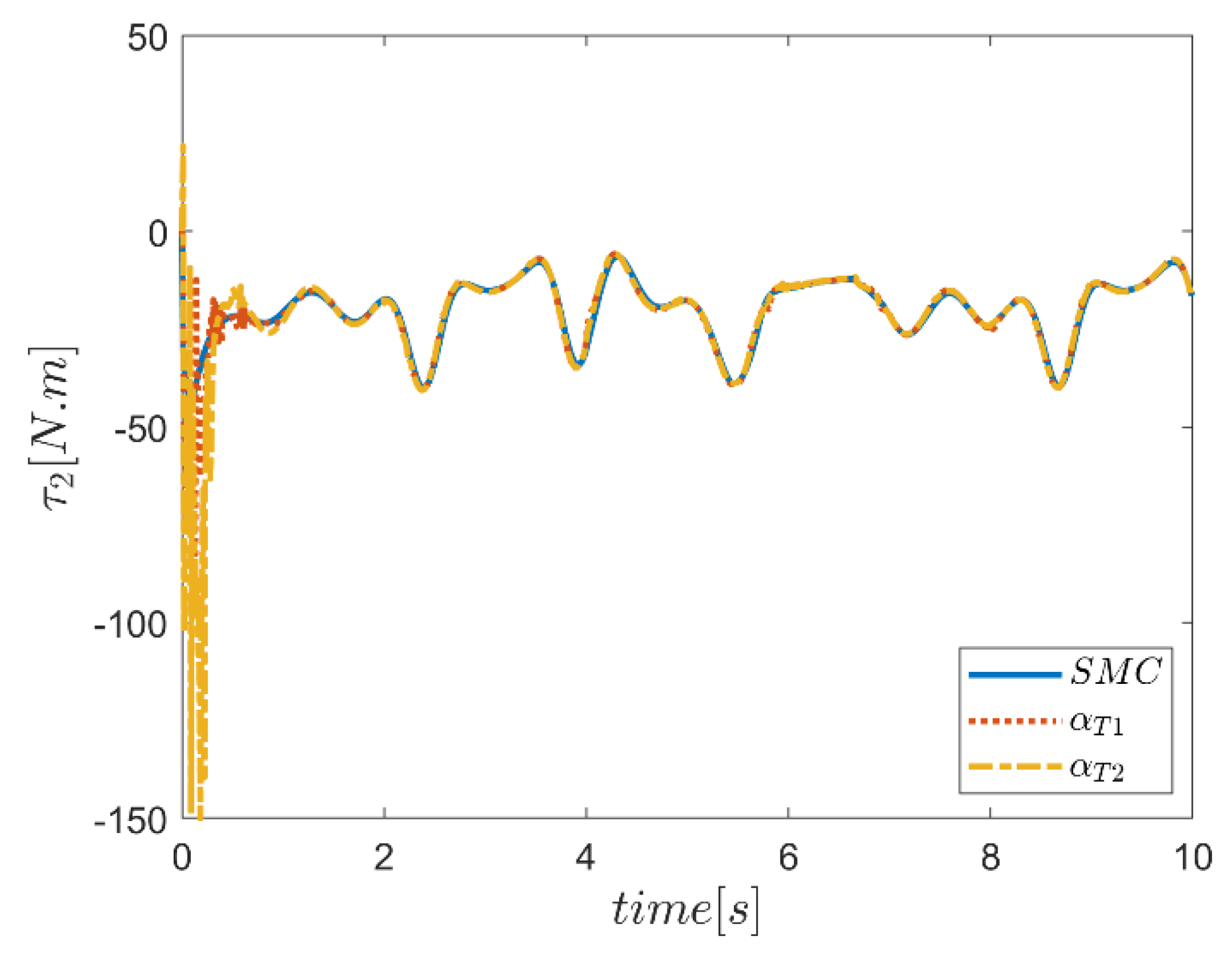

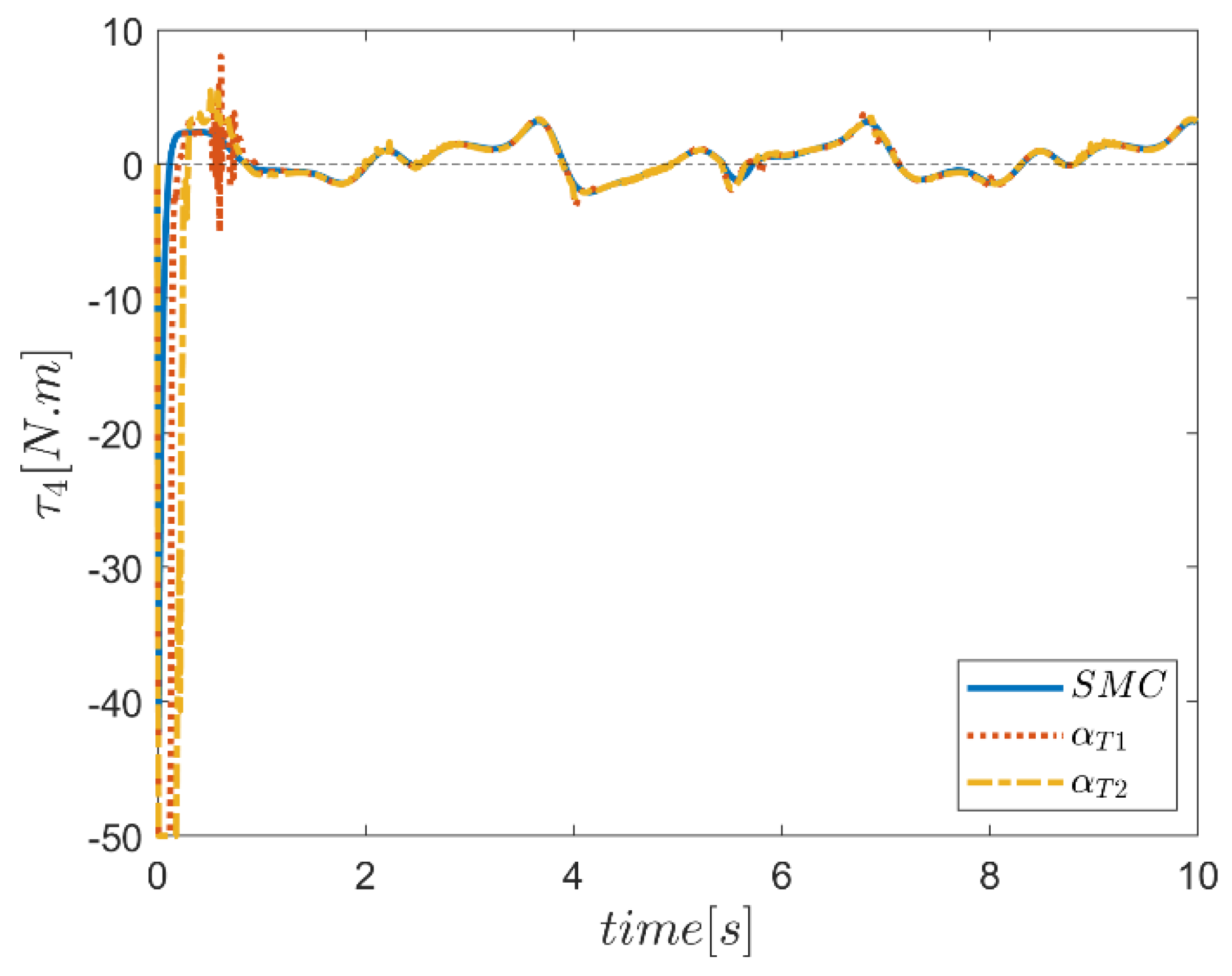




| NB | NS | Z | PS | PB | ||
|---|---|---|---|---|---|---|
| NB | VB | VS | B | B | B | |
| NS | S | M | VS | VB | B | |
| Z | S | B | VB | B | B | |
| PS | M | VS | VS | S | M | |
| PB | VB | M | B | VS | M | |
| NB | NS | Z | PS | PB | ||
|---|---|---|---|---|---|---|
| NB | S | M | VB | S | M | |
| NS | M | M | M | B | B | |
| Z | VS | B | VB | VS | S | |
| PS | B | M | M | B | S | |
| PB | B | B | VB | B | S | |
| NB | NS | Z | PS | PB | ||
|---|---|---|---|---|---|---|
| NB | VS | B | S | S | M | |
| NS | B | VS | S | S | VB | |
| Z | VB | VS | S | B | M | |
| PS | VB | B | B | M | B | |
| PB | B | M | M | VB | M | |
| NB | NS | Z | PS | PB | ||
|---|---|---|---|---|---|---|
| NB | B | S | B | VB | S | |
| NS | M | VS | VS | VS | B | |
| Z | S | M | VS | B | VS | |
| PS | S | B | B | VS | S | |
| PB | S | VB | S | S | M | |
| MF | Scale | Lower Lag | ||
|---|---|---|---|---|
| Initial Value | Tunned Value | Initial Value | Tunned Value | |
| NB | 0.8 | 0.8000 | 0.2 | 0.2399 |
| NS | 0.8 | 0.9133 | 0.2 | 0.2691 |
| Z | 0.8 | 0.4076 | 0.2 | 0.1971 |
| PS | 0.8 | 0.5358 | 0.2 | 0.8950 |
| PB | 0.8 | 0.7689 | 0.2 | 0.1536 |
| MF | Scale | Lower Lag | ||
|---|---|---|---|---|
| Initial Value | Tunned Value | Initial Value | Tunned Value | |
| NB | 0.8 | 0.8003 | 0.2 | 0.9133 |
| NS | 0.8 | 0.0377 | 0.2 | 0.0527 |
| Z | 0.8 | 0.4714 | 0.2 | 0.8419 |
| PS | 0.8 | 0.5737 | 0.2 | 0.3308 |
| PB | 0.8 | 0.3288 | 0.2 | 0.6841 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Bouteraa, Y.; Alattas, K.A.; Alshammari, O.; Aoun, S.B.; Regaieg, M.A.; Mobayen, S. Interval Fuzzy Type-2 Sliding Mode Control Design of Six-DOF Robotic Manipulator. Mathematics 2022, 10, 4835. https://doi.org/10.3390/math10244835
Bouteraa Y, Alattas KA, Alshammari O, Aoun SB, Regaieg MA, Mobayen S. Interval Fuzzy Type-2 Sliding Mode Control Design of Six-DOF Robotic Manipulator. Mathematics. 2022; 10(24):4835. https://doi.org/10.3390/math10244835
Chicago/Turabian StyleBouteraa, Yassine, Khalid A. Alattas, Obaid Alshammari, Sondess Ben Aoun, Mohamed Amin Regaieg, and Saleh Mobayen. 2022. "Interval Fuzzy Type-2 Sliding Mode Control Design of Six-DOF Robotic Manipulator" Mathematics 10, no. 24: 4835. https://doi.org/10.3390/math10244835
APA StyleBouteraa, Y., Alattas, K. A., Alshammari, O., Aoun, S. B., Regaieg, M. A., & Mobayen, S. (2022). Interval Fuzzy Type-2 Sliding Mode Control Design of Six-DOF Robotic Manipulator. Mathematics, 10(24), 4835. https://doi.org/10.3390/math10244835









