Graph Learning for Attributed Graph Clustering
Abstract
1. Introduction
- We develop a similarity graph learning approach for graph clustering. It effectively digs the interplay between the topology and the node features. Meanwhile, it retains the initial high-order relationships;
- A node sampling strategy is applied to choose some important nodes, which makes our method scalable to a large graph;
- Extensive experimental results demonstrate the effectiveness and efficiency of our algorithm with respect to many state-of-the-art methods, including several recent deep models.
2. Related Work
3. Methodology
3.1. Graph Learning
3.2. Scalable Graph Learning
3.3. Anchor Selecting with Graph Mining
| Algorithm 1 GLGC |
Input: The attribute matrix , the affinity matrix A, parameters k, , P and , number of anchors m, cluster number g. Output: g partitions |
4. Experiments
4.1. Datasets
4.2. Comparison Methods
4.3. Evaluation Metric
4.4. Experimental Setup
4.5. Clustering Results
- GLGC outperforms the most recent deep methods GMM-VGAE, DAEGC, DNENC-Att, and DNENC-Con in most cases. Our improvements over DAEGC, DNENC-Att, and DNENC-Con are considerable. For Pubmed, our method and GMM-VGAE produce comparable results. Facing the systematic use of complex deep learning methods, our method is very competitive and attractive;
- With respect to AGC, our method obtains much better performance. Although they both use graph filtering to process the data, our method follows a graph learning approach. This verifies the advantage of automatic graph construction;
- We can see that the methods that only utilize one type of information generate inferior performance. By contrast, the methods that employ both structure and attribute information generally perform better. This verifies the importance of developing methods that incorporate both types of information. Beyond this, it would be crucial to fully explore the interplay of them;
- GLGC consistently outperforms other GCN-based clustering methods: GAE, VGAE, MGAE, ARGE, ARVGE. GLGC’s performance of: ACC and NMI on Cora and Citeseer, NMI on Pubmed, all metrics on Wiki, ACC on Large Cora, all metrics on Coauthor Phy are the best compared with those methods, while other metrics are close to the best one. Other methods learn latent representations and then construct a graph for spectral clustering. The built graph might not be optimal for downstream clustering. By contrast, our method directly outputs a graph for spectral clustering. This is a crucial distinction between our approach and the currently used approaches;
- In most cases, degree sampling performs better than core sampling. Apart from Large Cora, degree sampling has advantages in all the cases on other five datasets. It confirms that the sampling strategy is also data-specific. In particular, it is perhaps related to the size of graph, especially the edge density;
- GLGC produces better performance than FGC in most cases. In fact, FGC is the unsampled version of GLGC. Sampling has the bonus of mitigating some negative effects of noise nodes and edges.
4.6. Time Comparison
4.7. Ablation Study
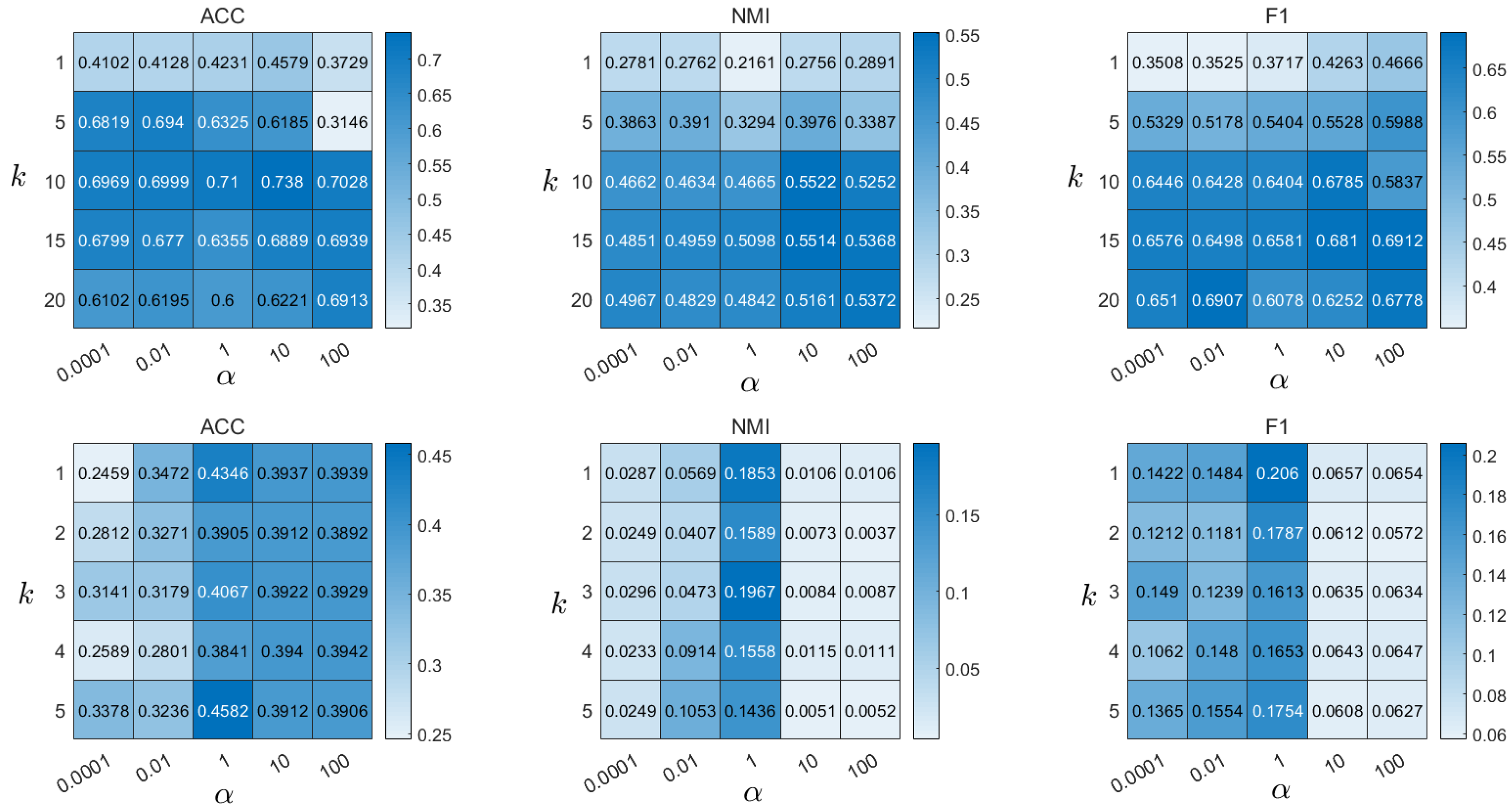
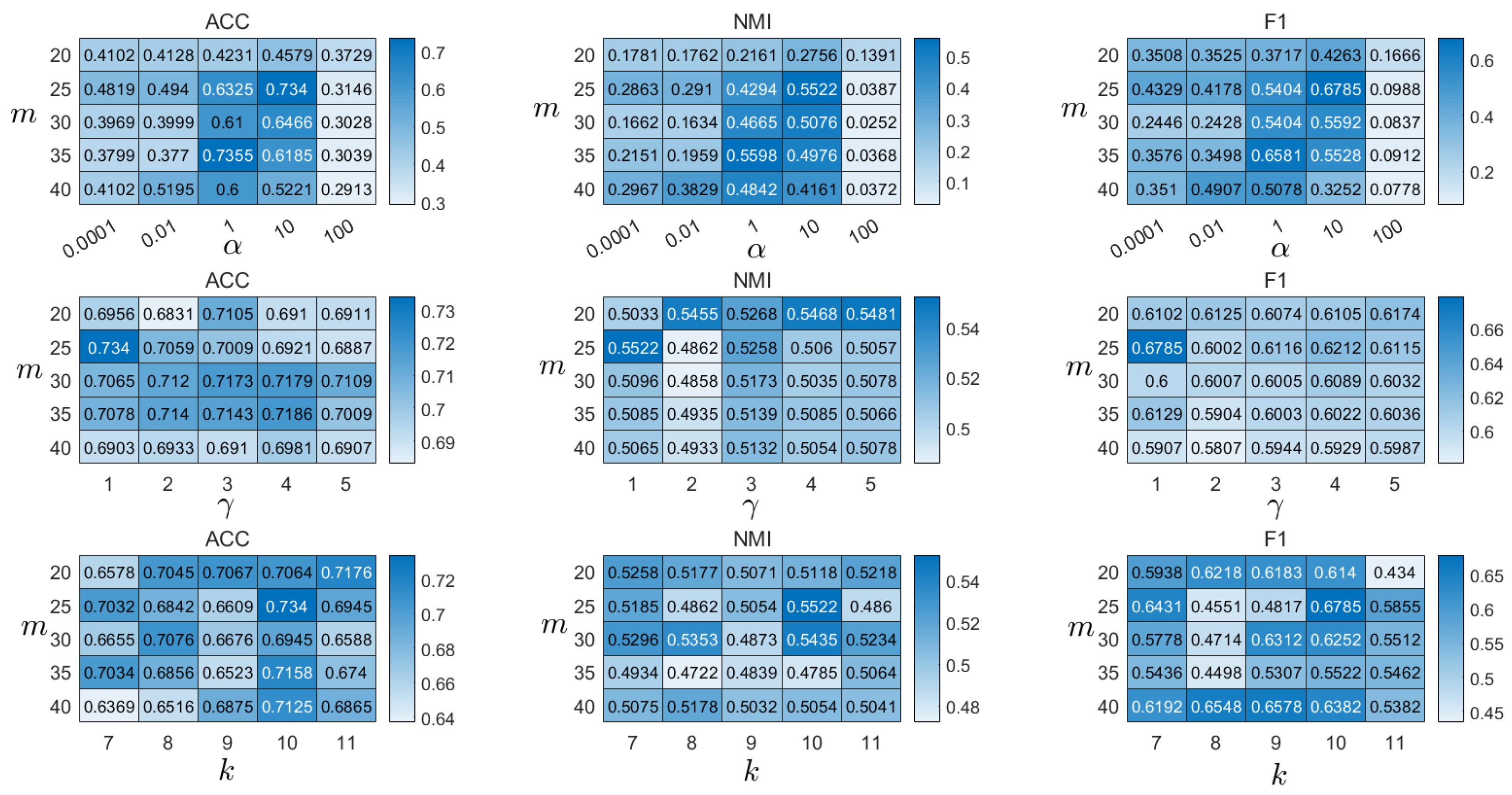
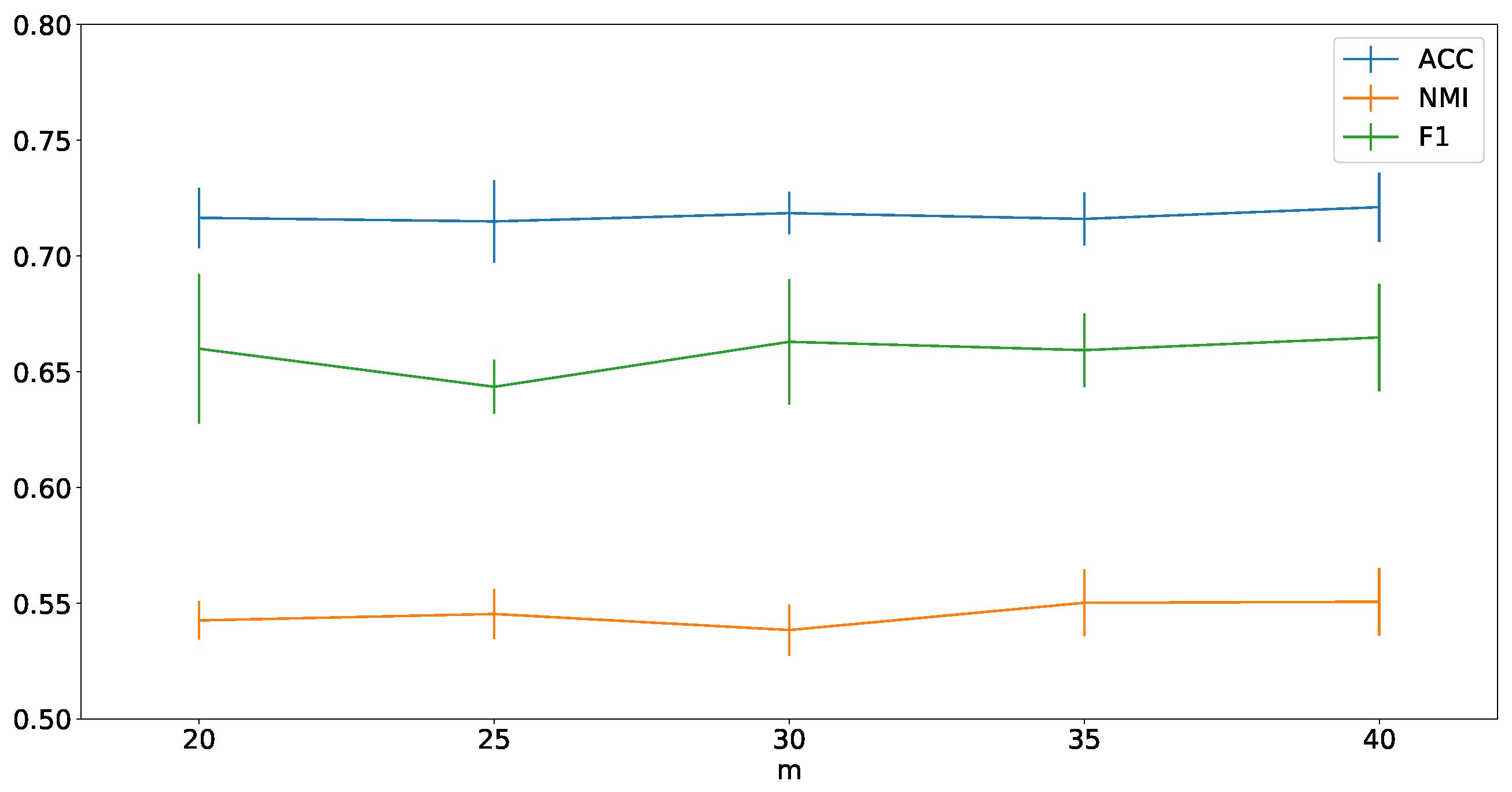
4.8. Parameter Analysis
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Fang, R.; Wen, L.; Kang, Z.; Liu, J. Structure-Preserving Graph Representation Learning. In Proceedings of the IEEE International Conference on Data Mining (ICDM), Orlando, FL, USA, 28 November–1 December 2022. [Google Scholar]
- Cao, S.; Lu, W.; Xu, Q. Deep neural networks for learning graph representations. In Proceedings of the Thirtieth AAAI Conference on Artificial Intelligence, Phoenix, AZ, USA, 12–17 February 2016. [Google Scholar]
- Wang, C.; Pan, S.; Long, G.; Zhu, X.; Jiang, J. Mgae: Marginalized graph autoencoder for graph clustering. In Proceedings of the 2017 ACM on Conference on Information and Knowledge Management, Singapore, 6–10 November 2017; pp. 889–898. [Google Scholar]
- Kang, Z.; Lin, Z.; Zhu, X.; Xu, W. Structured graph learning for scalable subspace clustering: From single view to multiview. IEEE Trans. Cybern. 2022, 52, 8976–8986. [Google Scholar] [CrossRef] [PubMed]
- Liu, L.; Kang, Z.; Ruan, J.; He, X. Multilayer graph contrastive clustering network. Inf. Sci. 2022, 613, 256–267. [Google Scholar] [CrossRef]
- Xu, Z.; Ke, Y.; Wang, Y.; Cheng, H.; Cheng, J. A model-based approach to attributed graph clustering. In Proceedings of the 2012 ACM SIGMOD International Conference on Management of Data, San Diego, CA, USA, 20 May 2012; pp. 505–516. [Google Scholar]
- Huang, S.; Kang, Z.; Xu, Z.; Liu, Q. Robust deep k-means: An effective and simple method for data clustering. Pattern Recognit. 2021, 117, 107996. [Google Scholar] [CrossRef]
- Murtagh, F.; Contreras, P. Algorithms for hierarchical clustering: An overview. Wiley Interdiscip. Rev. Data Min. Knowl. Discov. 2012, 2, 86–97. [Google Scholar] [CrossRef]
- Guo, T.; Pan, S.; Zhu, X.; Zhang, C. CFOND: Consensus factorization for co-clustering networked data. IEEE Trans. Knowl. Data Eng. 2018, 31, 706–719. [Google Scholar] [CrossRef]
- Liu, L.; Xu, L.; Wangy, Z.; Chen, E. Community detection based on structure and content: A content propagation perspective. In Proceedings of the 2015 IEEE International Conference on Data Mining, Atlantic City, NJ, USA, 14 November 2015; pp. 271–280. [Google Scholar]
- Chang, J.; Blei, D. Relational topic models for document networks. In Artificial Intelligence and Statistics; Addison-Wesley: Boston, MA, USA, 2009; pp. 81–88. [Google Scholar]
- Liu, C.; Wen, L.; Kang, Z.; Luo, G.; Tian, L. Self-supervised consensus representation learning for attributed graph. In Proceedings of the 29th ACM International Conference on Multimedia, Chengdu, China, 20 October 2021; pp. 2654–2662. [Google Scholar]
- Kipf, T.N.; Welling, M. Variational graph auto-encoders. arXiv 2016, arXiv:1611.07308. [Google Scholar]
- Pan, S.; Hu, R.; Fung, S.f.; Long, G.; Jiang, J.; Zhang, C. Learning graph embedding with adversarial training methods. IEEE Trans. Cybern. 2019, 50, 2475–2487. [Google Scholar] [CrossRef] [PubMed]
- Tian, F.; Gao, B.; Cui, Q.; Chen, E.; Liu, T.Y. Learning deep representations for graph clustering. In Proceedings of the AAAI Conference on Artificial Intelligence, Quebec City, QC, Canada, 27–30 July 2014; Volume 28. [Google Scholar]
- Hui, B.; Zhu, P.; Hu, Q. Collaborative Graph Convolutional Networks: Unsupervised Learning Meets Semi-Supervised Learning. AAAI Tech. Track Mach. Learn. 2020, 34, 4215–4222. [Google Scholar] [CrossRef]
- Wang, C.; Pan, S.; Hu, R.; Long, G.; Jiang, J.; Zhang, C. Attributed Graph Clustering: A Deep Attentional Embedding Approach. arXiv 2019, arXiv:1906.06532. [Google Scholar]
- Henaff, M.; Bruna, J.; LeCun, Y. Deep convolutional networks on graph-structured data. arXiv 2015, arXiv:1506.05163. [Google Scholar]
- Pan, E.; Kang, Z. Multi-view Contrastive Graph Clustering. Adv. Neural Inf. Process. Syst. 2021, 34, 2148–2159. [Google Scholar]
- Liu, Y.; Gao, Q.; Yang, Z.; Wang, S. Learning with Adaptive Neighbors for Image Clustering. In Proceedings of the Twenty-Seventh International Joint Conference on Artificial Intelligence, Stockholm, Sweden, 13–19 July 2018; pp. 2483–2489. [Google Scholar]
- Mathisen, B.M.; Aamodt, A.; Bach, K.; Langseth, H. Learning similarity measures from data. Prog. Artif. Intell. 2020, 9, 129–143. [Google Scholar] [CrossRef]
- Kang, Z.; Liu, Z.; Pan, S.; Tian, L. Fine-grained Attributed Graph Clustering. In Proceedings of the 2022 SIAM International Conference on Data Mining (SDM), Minneapolis, MN, USA, 27–29 April 2022; pp. 370–378. [Google Scholar]
- Bianchi, F.M.; Grattarola, D.; Alippi, C. Spectral clustering with graph neural networks for graph pooling. In Proceedings of the International Conference on Machine Learning, Seoul, Republic of Korea, 25–28 October 2020; pp. 874–883. [Google Scholar]
- He, D.; Feng, Z.; Jin, D.; Wang, X.; Zhang, W. Joint identification of network communities and semantics via integrative modeling of network topologies and node contents. In Proceedings of the Thirty-First AAAI Conference on Artificial Intelligence, San Francisco, CA, USA, 4–9 February 2017. [Google Scholar]
- Chunaev, P. Community detection in node-attributed social networks: A survey. Comput. Sci. Rev. 2020, 37, 100286. [Google Scholar] [CrossRef]
- Wang, C.; Pan, S.; Celina, P.Y.; Hu, R.; Long, G.; Zhang, C. Deep neighbor-aware embedding for node clustering in attributed graphs. Pattern Recognit. 2022, 122, 108230. [Google Scholar] [CrossRef]
- Zhang, X.; Liu, H.; Li, Q.; Wu, X.M. Attributed Graph Clustering via Adaptive Graph Convolution. In Proceedings of the Twenty-Eighth International Joint Conference on Artificial Intelligence, Macao, China, 10–16 August 2019. [Google Scholar]
- Ma, Z.; Kang, Z.; Luo, G.; Tian, L.; Chen, W. Towards Clustering-friendly Representations: Subspace Clustering via Graph Filtering. In Proceedings of the 28th ACM International Conference on Multimedia, Athlone, Ireland, 26–28 May 2020; pp. 3081–3089. [Google Scholar]
- Chung, F.R.; Graham, F.C. Spectral Graph Theory; Number 92; American Mathematical Soc.: Providence, RI, USA, 1997. [Google Scholar]
- Dong, X.; Thanou, D.; Rabbat, M.; Frossard, P. Learning graphs from data: A signal representation perspective. IEEE Signal Process. Mag. 2019, 36, 44–63. [Google Scholar] [CrossRef]
- Ortega, A.; Frossard, P.; Kovačević, J.; Moura, J.M.; Vandergheynst, P. Graph signal processing: Overview, challenges, and applications. Proc. IEEE 2018, 106, 808–828. [Google Scholar] [CrossRef]
- Kang, Z.; Lu, X.; Liang, J.; Bai, K.; Xu, Z. Relation-Guided Representation Learning. Neural Netw. 2020, 131, 93–102. [Google Scholar] [CrossRef] [PubMed]
- Lin, Z.; Kang, Z.; Zhang, L.; Tian, L. Multi-view Attributed Graph Clustering. IEEE Trans. Knowl. Data Eng. 2021; early access. [Google Scholar] [CrossRef]
- Bo, D.; Wang, X.; Shi, C.; Zhu, M.; Lu, E.; Cui, P. Structural deep clustering network. In Proceedings of the Web Conference 2020, Taipei, Taiwan, 20–24 April 2020; pp. 1400–1410. [Google Scholar]
- Cao, S.; Lu, W.; Xu, Q. Grarep: Learning graph representations with global structural information. In Proceedings of the 24th ACM International on Conference on Information and Knowledge Management, Melbourne, Australia, 19–23 October 2015; pp. 891–900. [Google Scholar]
- Kang, Z.; Zhou, W.; Zhao, Z.; Shao, J.; Han, M.; Xu, Z. Large-Scale Multi-View Subspace Clustering in Linear Time. In Proceedings of the AAAI Conference on Artificial Intelligence, New York, NY, USA, 7–12 February 2020; pp. 4412–4419. [Google Scholar]
- Chen, X.; Cai, D. Large scale spectral clustering with landmark-based representation. In Proceedings of the Twenty-Fifth AAAI Conference on Artificial Intelligence, San Francisco, CA, USA, 7–11 August 2011. [Google Scholar]
- Mikolov, T.; Sutskever, I.; Chen, K.; Corrado, G.S.; Dean, J. Distributed representations of words and phrases and their compositionality. In Advances in Neural Information Processing Systems; Mit Pr: Cambridge, MA, USA, 2013; pp. 3111–3119. [Google Scholar]
- Malliaros, F.D.; Giatsidis, C.; Papadopoulos, A.N.; Vazirgiannis, M. The core decomposition of networks: Theory, algorithms and applications. VLDB J. 2020, 29, 61–92. [Google Scholar] [CrossRef]
- Yang, C.; Liu, Z.; Zhao, D.; Sun, M.; Chang, E. Network representation learning with rich text information. In Proceedings of the Twenty-Fourth International Joint Conference on Artificial Intelligence, Buenos Aires, Argentina, 25–31 July 2015. [Google Scholar]
- Li, Q.; Wu, X.M.; Liu, H.; Zhang, X.; Guan, Z. Label Efficient Semi-Supervised Learning via Graph Filtering. In Proceedings of the Conference on Computer Vision and Pattern Recognition, Long Beach, CA, USA, 15–20 June 2019. [Google Scholar]
- Wang, X.; Cui, P.; Wang, J.; Pei, J.; Zhu, W.; Yang, S. Community preserving network embedding. In Proceedings of the Thirty-First AAAI Conference on Artificial Intelligence, San Francisco, CA, USA, 4–9 February 2017. [Google Scholar]
- Perozzi, B.; Al-Rfou, R.; Skiena, S. Deepwalk: Online learning of social representations. In Proceedings of the 20th ACM SIGKDD International Conference on Knowledge Discovery and Data Mining, New York, NY, USA, 24–27 August 2014; pp. 701–710. [Google Scholar]
- Pan, S.; Hu, R.; Long, G.; Jiang, J.; Yao, L.; Zhang, C. Adversarially regularized graph autoencoder for graph embedding. In Proceedings of the Twenty-Seventh International Joint Conference on Artificial Intelligence, Stockholm, Sweden, 13–19 July 2018. [Google Scholar]
- Zhu, Q.; Du, B.; Yan, P. Multi-hop Convolutions on Weighted Graphs. arXiv 2019, arXiv:1911.04978. [Google Scholar]

| Dataset | Nodes | Edges | Features | Classes |
|---|---|---|---|---|
| Cora | 2708 | 5429 | 1433 | 7 |
| Citeseer | 3327 | 4732 | 3703 | 6 |
| Pubmed | 19,717 | 44,338 | 500 | 3 |
| Wiki | 2405 | 17,981 | 4973 | 17 |
| Large Cora | 11,881 | 64,898 | 3780 | 10 |
| Coauthor Phy | 34,493 | 247,962 | 8415 | 5 |
| Methods | Input | Cora | Citeseer | Pubmed | Wiki | Large Cora | Coauthor Phy | ||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| ACC% | NMI% | F1% | ACC% | NMI% | F1% | ACC% | NMI% | F1% | ACC% | NMI% | F1% | ACC% | NMI% | F1% | ACC% | NMI% | F1% | ||
| Spectral-g | Graph | 34.19 | 19.49 | 30.17 | 25.91 | 11.84 | 29.48 | 39.74 | 3.46 | 51.97 | 23.58 | 19.28 | 17.21 | 39.84 | 8.24 | 10.70 | - | - | - |
| DNGR | Graph | 49.24 | 37.29 | 37.29 | 32.59 | 18.02 | 44.19 | 45.35 | 15.38 | 17.90 | 37.58 | 35.85 | 25.38 | - | - | - | - | - | - |
| DeepWalk | Graph | 46.74 | 31.75 | 38.06 | 36.15 | 9.66 | 26.70 | 61.86 | 16.71 | 47.06 | 38.46 | 32.38 | 25.74 | - | - | - | - | - | - |
| M-NMF | Graph | 42.30 | 25.60 | 32.00 | 33.60 | 9.90 | 25.50 | 47.00 | 8.40 | 44.30 | - | - | - | - | - | - | - | - | - |
| K-means | Feature | 34.65 | 16.73 | 25.42 | 38.49 | 17.02 | 30.47 | 57.32 | 29.12 | 57.35 | 33.37 | 30.20 | 24.51 | 33.09 | 9.36 | 11.31 | 52.79 | 19.84 | 29.01 |
| Spectral-f | Feature | 36.26 | 15.09 | 25.64 | 46.23 | 21.19 | 33.70 | 59.91 | 32.55 | 58.61 | 41.28 | 43.99 | 25.20 | 29.71 | 11.65 | 17.76 | - | - | - |
| ARGE | Both | 64.00 | 44.90 | 61.90 | 57.30 | 35.00 | 54.60 | 59.12 | 23.17 | 58.41 | 41.40 | 39.50 | 38.27 | - | - | - | - | - | - |
| ARVGE | Both | 63.80 | 45.00 | 62.70 | 54.40 | 26.10 | 52.90 | 58.22 | 20.62 | 23.04 | 41.55 | 40.01 | 37.80 | - | - | - | - | - | - |
| GAE | Both | 53.25 | 40.69 | 41.97 | 41.26 | 18.34 | 29.13 | 64.08 | 22.97 | 49.26 | 17.33 | 11.93 | 15.35 | - | - | - | - | - | - |
| VGAE | Both | 55.95 | 38.45 | 41.50 | 44.38 | 22.71 | 31.88 | 65.48 | 25.09 | 50.95 | 28.67 | 30.28 | 20.49 | - | - | - | - | - | - |
| MGAE | Both | 63.43 | 45.57 | 38.01 | 63.56 | 39.75 | 39.49 | 43.88 | 8.16 | 41.98 | 50.14 | 47.97 | 39.20 | 38.04 | 32.43 | 29.02 | - | - | - |
| AGC | Both | 68.92 | 53.68 | 65.61 | 67.00 | 41.13 | 62.48 | 69.78 | 31.59 | 68.72 | 47.65 | 45.28 | 40.36 | 40.54 | 32.46 | 31.84 | 75.21 | 59.10 | 59.81 |
| DAEGC | Both | 70.40 | 52.80 | 68.20 | 67.20 | 39.70 | 63.60 | 67.10 | 26.60 | 65.90 | 38.25 | 37.63 | 23.64 | 39.87 | 32.81 | 19.05 | - | - | - |
| GMM-VGAE | Both | 71.50 | 54.43 | 67.76 | 67.44 | 42.30 | 63.22 | 71.03 | 30.28 | 69.74 | - | - | - | - | - | - | - | - | - |
| DNENC-Att | Both | 70.40 | 52.80 | 68.20 | 67.20 | 39.70 | 63.60 | 67.10 | 26.60 | 65.90 | - | - | - | - | - | - | - | - | - |
| DNENC-Con | Both | 68.30 | 51.20 | 65.90 | 69.20 | 42.60 | 63.90 | 67.70 | 27.50 | 67.50 | - | - | - | - | - | - | - | - | - |
| FGC | Both | 72.90 | 56.12 | 63.27 | 69.01 | 44.02 | 64.43 | 70.01 | 31.56 | 69.10 | 51.10 | 44.12 | 34.79 | 48.25 | 35.24 | 35.52 | - | - | - |
| GLGC (core) | Both | 71.62 | 52.26 | 65.27 | 68.67 | 40.97 | 60.10 | 68.69 | 31.25 | 67.78 | 47.00 | 41.66 | 35.33 | 52.91 | 32.06 | 34.51 | 78.01 | 53.62 | 67.97 |
| GLGC (degree) | Both | 73.40 | 55.22 | 67.85 | 70.38 | 42.92 | 61.12 | 69.88 | 31.87 | 68.88 | 52.78 | 48.62 | 41.56 | 49.40 | 32.27 | 28.48 | 83.15 | 62.83 | 75.12 |
| Method | Cora | Citeseer | Pubmed | Wiki | Large Cora | Coauthor Phy |
|---|---|---|---|---|---|---|
| AGC | 3.42 | 40.36 | 20.77 | 8.21 | 29.18 | 3172.58 |
| DAEGC | 561.69 | 946.89 | 50,854.15 | 562.85 | 9339.67 | - |
| FGC | 4.60 | 9.49 | 268.44 | 8.11 | 58.76 | - |
| GLGC | 2.54 | 17.76 | 297.23 | 1.36 | 165.26 | 2441.03 |
| Method | Cora | Citeseer | Pubmed | Wiki | Large Cora | ||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| ACC% | NMI% | F1% | ACC% | NMI% | F1% | ACC% | NMI% | F1% | ACC% | NMI% | F1% | ACC% | NMI% | F1% | |
| Baseline1 | 67.61 | 53.12 | 56.53 | 67.02 | 41.57 | 62.61 | 69.90 | 32.51 | 68.99 | 53.89 | 51.27 | 46.06 | 48.30 | 26.23 | 13.96 |
| 69.46 | 56.10 | 63.25 | 66.93 | 41.73 | 61.09 | 64.45 | 24.63 | 64.40 | 56.30 | 52.44 | 44.85 | 43.46 | 27.48 | 31.73 | |
| 68.57 | 53.94 | 59.83 | 67.72 | 41.06 | 59.11 | 70.14 | 32.47 | 69.29 | 51.60 | 47.19 | 43.55 | 49.26 | 30.15 | 17.81 | |
| 72.90 | 56.12 | 63.27 | 69.01 | 44.02 | 64.43 | 70.01 | 31.56 | 69.10 | 51.10 | 44.12 | 34.79 | 48.25 | 35.24 | 35.52 | |
| 71.57 | 56.10 | 59.83 | 67.15 | 40.29 | 58.10 | 70.32 | 30.34 | 69.49 | 47.53 | 39.68 | 34.37 | 48.31 | 30.51 | 24.01 | |
| 71.49 | 52.55 | 63.96 | 67.33 | 40.03 | 58.23 | 68.49 | 27.32 | 68.21 | 43.49 | 35.83 | 27.17 | 46.87 | 26.26 | 30.91 | |
| Method | Cora | Citeseer | Pubmed | Wiki | Large Cora | ||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| ACC% | NMI% | F1% | ACC% | NMI% | F1% | ACC% | NMI% | F1% | ACC% | NMI% | F1% | ACC% | NMI% | F1% | |
| Baseline2 | 45.32 | 24.13 | 37.17 | 53.64 | 25.76 | 49.30 | 60.41 | 31.12 | 59.17 | 45.39 | 40.35 | 32.74 | 47.25 | 16.66 | 17.67 |
| 73.40 | 55.22 | 67.85 | 70.38 | 42.92 | 61.12 | 69.88 | 31.87 | 68.88 | 52.78 | 48.62 | 41.56 | 49.40 | 32.27 | 28.48 | |
| 73.42 | 56.17 | 67.96 | 70.56 | 42.97 | 61.22 | 69.91 | 31.93 | 68.91 | 53.67 | 47.74 | 40.26 | 55.11 | 32.55 | 23.32 | |
| 71.12 | 52.66 | 63.93 | 69.56 | 41.61 | 60.34 | 68.96 | 31.57 | 68.03 | 53.05 | 47.14 | 39.81 | 54.32 | 29.27 | 26.14 | |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhang, X.; Xie, X.; Kang, Z. Graph Learning for Attributed Graph Clustering. Mathematics 2022, 10, 4834. https://doi.org/10.3390/math10244834
Zhang X, Xie X, Kang Z. Graph Learning for Attributed Graph Clustering. Mathematics. 2022; 10(24):4834. https://doi.org/10.3390/math10244834
Chicago/Turabian StyleZhang, Xiaoran, Xuanting Xie, and Zhao Kang. 2022. "Graph Learning for Attributed Graph Clustering" Mathematics 10, no. 24: 4834. https://doi.org/10.3390/math10244834
APA StyleZhang, X., Xie, X., & Kang, Z. (2022). Graph Learning for Attributed Graph Clustering. Mathematics, 10(24), 4834. https://doi.org/10.3390/math10244834







