1. Introduction
Since the beginning of the last decade, technological improvements in hardware and software provide new dimensions for the deployment of signal processing techniques in many communication applications. However, the deployment of these signal processing techniques on low-cost wireless sensor nodes still faces the restrictions in terms of low processing power and limited energy resources. In wireless sensor networks, fast processing as well as low energy consumption are prominent requirements for their efficient utilization; therefore, modern engineering techniques try to provide ingenious alternatives, so that one can improve the algorithm having reasonable trade off between the low energy consumption and communication burden overhead [
1,
2]. Distributed network-based architecture provides improved performance for many communication applications, such as channel estimation [
3], system identification [
4,
5], source tracking [
6], and environmental monitoring [
7]. On a distributed adaptive signal processing estimation platform, the processing is distributed over the network where the network nodes are allowed to exchange information among themselves in such a way that the filter parameters converge in much lesser time. In [
8,
9,
10,
11,
12], incremental strategies are introduced in which each node in the distributed network communicates only with the adjacent node. In incremental strategies, the data are transmitted to adjacent nodes cyclically throughout the distributed network. In [
13,
14,
15], diffusion techniques are used to find the unknown filter coefficients for the distributed channel estimation. In these techniques, the parameters of the adaptive algorithm are distributed over the network to improve the estimation of the adaptive algorithm.
Furthermore, in [
16], a Distributed Recursive Least Square (D-RLS) adaptive algorithm is presented. In this technique, the parts of the RLS adaptive algorithm are assigned to different nodes in the network and each respective node waits until information is not collected from the previous node. In [
17], PDASP architecture is introduced which executes the RLS adaptive algorithm in parallel distributed fashion even with the time-non-aligned indexes over the low-cost wireless sensor nodes. The PDASP architecture provides parallelly lesser computational cost and processing time in each node involved as compared to the above-mentioned techniques [
8,
9,
10,
11,
12,
13,
14,
15,
16]. However, it has been never been validated through its implementation on low-cost processing-incapable platforms.
As discussed earlier, the PDASP architecture provides much lesser complexity and processing time than sequentially operated adaptive algorithm on a single unit. However, it has not been validated through implementation. In this manuscript, a communication load-balancing procedure is introduced to validate the PDASP architecture using low-cost wireless sensor nodes, namely NANO, UNO, and MEGA [
18] having diverse memory utilities. Furthermore, for powerful degree of comparisons, we take MIMO channel estimation with the consideration of Line of Sight (LoS) and diffused components as an example application for our research work which helps to perform an in-depth analysis of the PDASP architecture. Using the communication load-balancing procedure, the obtained measurement results show that the PDASP architecture effectively runs the MIMO RLS algorithm on low-cost sensor nodes. On the other hand, the sequentially operated
and
MIMO systems are unable to be run on a single unit. It is also realized that the PDASP architecture using the communication load-balancing procedure provides significant improvement in terms of processing time, computational complexity, and memory utilization as compared to sequentially operated MIMO RLS algorithm. Moreover, the communication burden time is higher than the sequential time of the MIMO RLS algorithm and this time can be reduced by using the transceiver having high data rates as compared to NRF24L01.
The rest of the paper is organized in the following manner. The working procedure of PDASP architecture is described in
Section 2. In
Section 3, the validation of PDASP architecture for MIMO communication system is presented, the complexity analysis is introduced in
Section 4. In
Section 5, measurement results are presented and
Section 6 draws the conclusions.
2. Parallel Distributed Adaptive Signal Processing (PDASP) Architecture
The input signal vector is divided into
N equal-length sub-blocks in a MIMO communication system, each of which is transmitted individually using a different antenna. The block diagram of
MIMO communication system with one diffused component is shown in
Figure 1. At the receiver side, each antenna element receives
signals comprising the effect of
channel coefficients from
transmitting and
L diffused components. The subscript
shows the information of transmitting antenna,
receiving antenna,
and
diffused components.
Therefore, the channel matrix
for the
MIMO communication system at time index
k with
L diffused components [
19] can be expressed as
Each entry of channel coefficient,
, shows a diffused component which exists between
and
receiving antenna elements; however, for
, the channel coefficient shows parallel interference with the line of sight (LoS) only link. Furthermore, the dispersed components have a significant influence on the dimensions of the channel matrix in time-varying channel environments. Likewise, the dimensions of the filter weight matrix for various MIMO communications systems with LoS and dispersed components are therefore displayed in
Table 1.
A well-known RLS algorithm [
20] has been in use for the applications of channel estimation and channel equalization since its advent. In case of the MIMO communication system, the computational complexity of the MIMO RLS algorithm is not only dependent on MIMO antennas but it also depends on multipath components. The step-by-step computational complexity provided by the RLS algorithm is shown in
Table 2, where
N shows the order of the MIMO system. In
Table 2, it can be seen that the
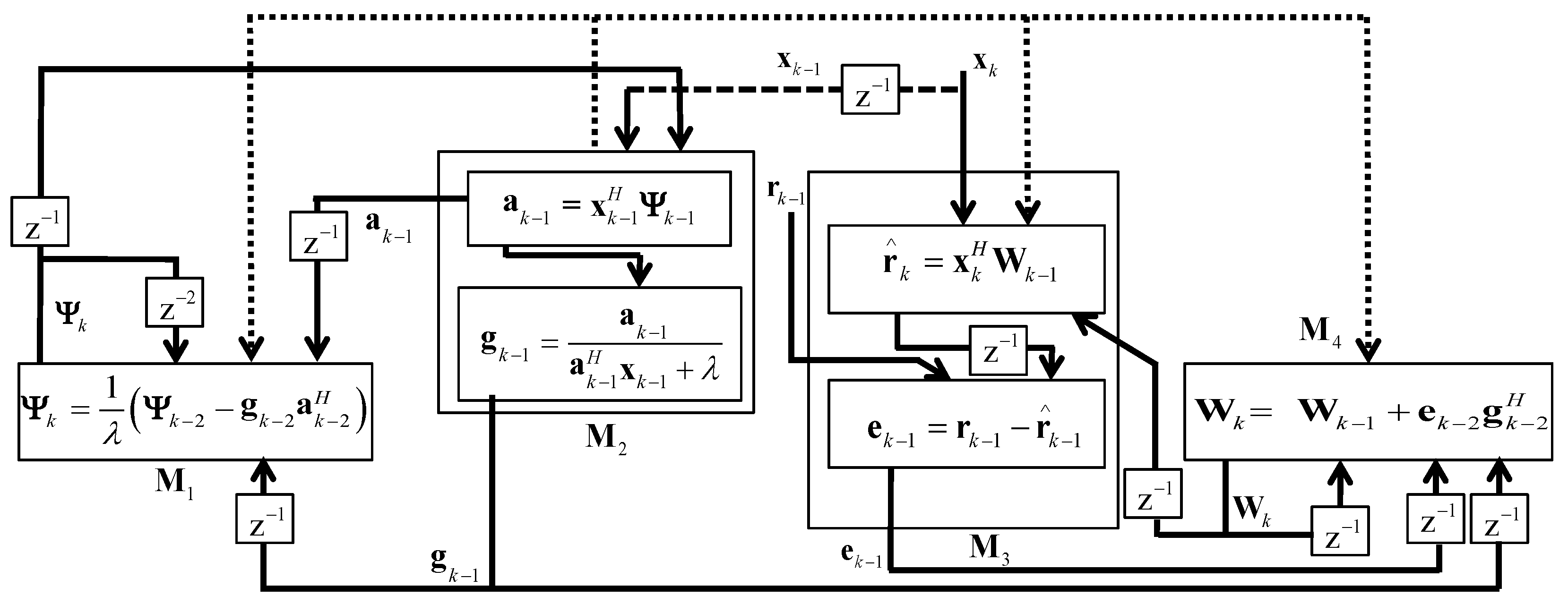
L diffused components in each part of the MIMO RLS algorithm provide critical impact on the computational cost; therefore, the MIMO RLS algorithm cannot be run sequentially on processing-inefficient low-cost platforms. In order to run the MIMO RLS algorithm in parallel fashion, a PDASP architecture with non-aligned time indexes is used. The non-aligned time indexes make run the algorithm parts in parallel fashion. The PDASP architecture with its implementation on the RLS algorithm is shown in
Figure 2; whereas, the selection of four nodes in the PDASP architecture are dependent upon the parts (e.g., Kalman gain, error covariance matrix, etc.) of the RLS algorithm. The RLS method works in parallel with non-aligned time indexes when utilizing the PDASP technique, leading to parallelly low processing times at each processing node. Two considerations must be made in order to run the RLS adaptive filtering method concurrently with various clock systems: first, it should be mentioned that the filter does not behave unstably when used with any application. Second, all of the filter sub-components might be able to operate concurrently. Thus, even with non-aligned time indexes, the sequential structure might be able to operate in parallel.
In
Figure 2, it can be seen that
,
,
, and
are the four processing nodes that make up the distributed RLS filtering. The adaptive filtering algorithm’s parts (e.g., Kalman gain, error covariance matrix, etc.) influence the selection of the four nodes. The processing nodes
and
are interconnected with
and
, respectively, as well as with each other. Similarly,
is linked to
and
, but
is solely linked to
. All of the processing nodes would share data with one another before figuring out the intended process.
In the PDASP architecture, let the processing time taken by filter weight matrix
, estimation error
, Kalman gain
, and error covariance matrix
be
,
,
, and
, respectively. Therefore, the time taken by the MIMO-based sequential RLS algorithm,
, when it executes in cascade fashion [
17], can be written as
The node
requires more computational cost than the other nodes in the distributed network. The time difference which makes the nodes
,
, and
equivalent to node
can be written as
where
shows the
norm operator. The equivalence processing time
can be expressed as
In terms of low processing time, the sufficient and strict condition can thus be written as:
where
, and
are the fetch times for the transmission of data over the PDASP architecture. The working procedure of PDASP using the MIMO RLS algorithm is shown in Algorithm 1, where all the nodes are capable to share the information among themselves after getting the time equivalent to the maximum processing time of node
.
| Algorithm 1: Working procedure of PDASP with Diffused components for MIMO communication system |
| Initialize: |
| parallel procedure for , , and |
for k=0:N
|
| Process node |
| at time : |
| at time : |
at time : wait
|
| Process node |
| at time : |
| at time : |
at time : wait
|
| Process node |
at time :
|
| Process node |
| at time : |
at time : wait
|
| at time : Transmit from to and |
| at time : Transmit from to , from to |
| at time : Transmit from to , from to |
| end for |
3. Communication Load-Balancing Procedure
In this section, the procedure of information interchange over the PDASP architecture is presented. The PDASP architecture consists of four nodes,
,
,
, and
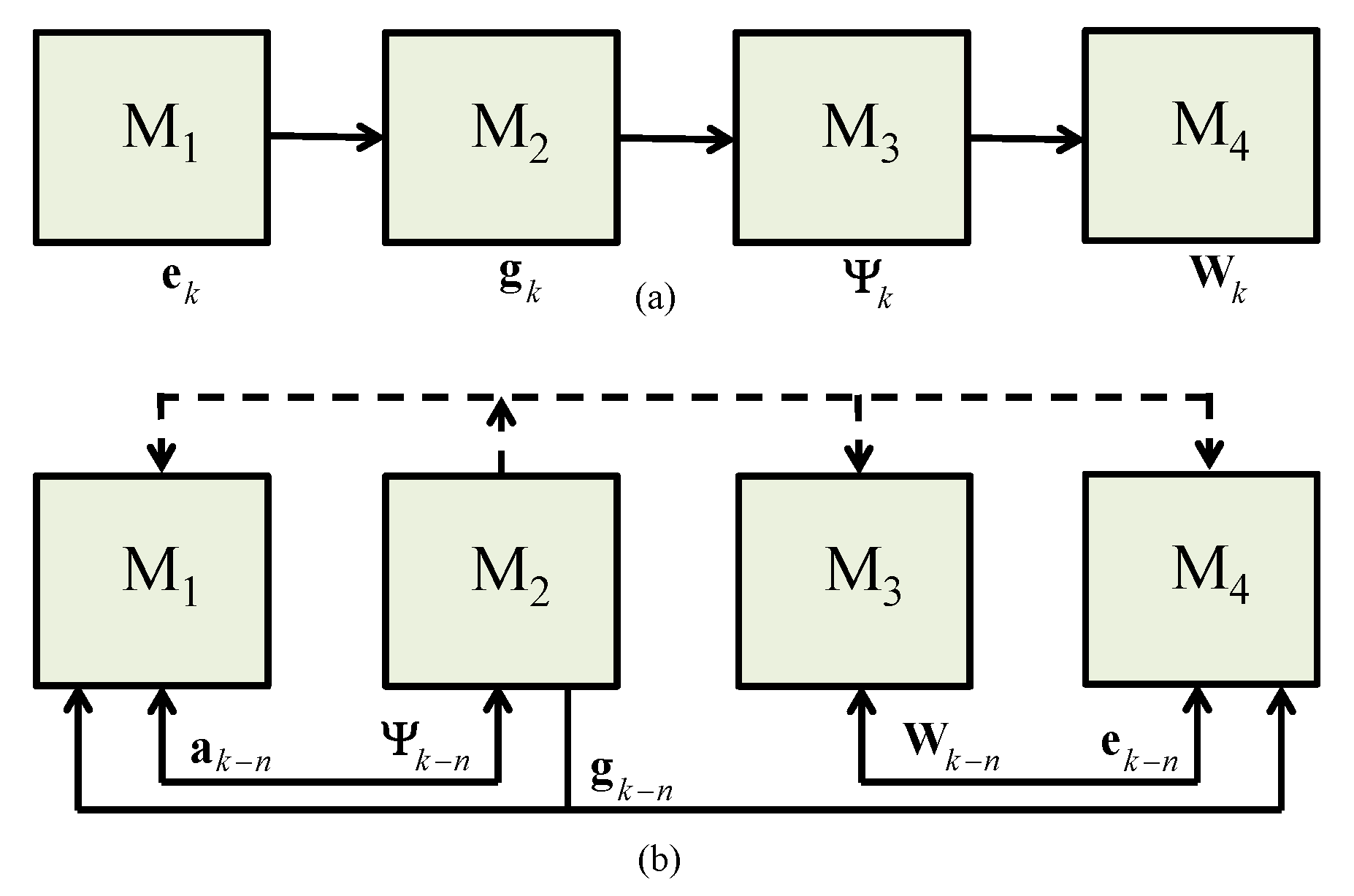
. The block diagrams of the sequentially and parallelly working MIMO RLS algorithm are shown in
Figure 3a,b, respectively.
Before running the expensive procedure parallelly,
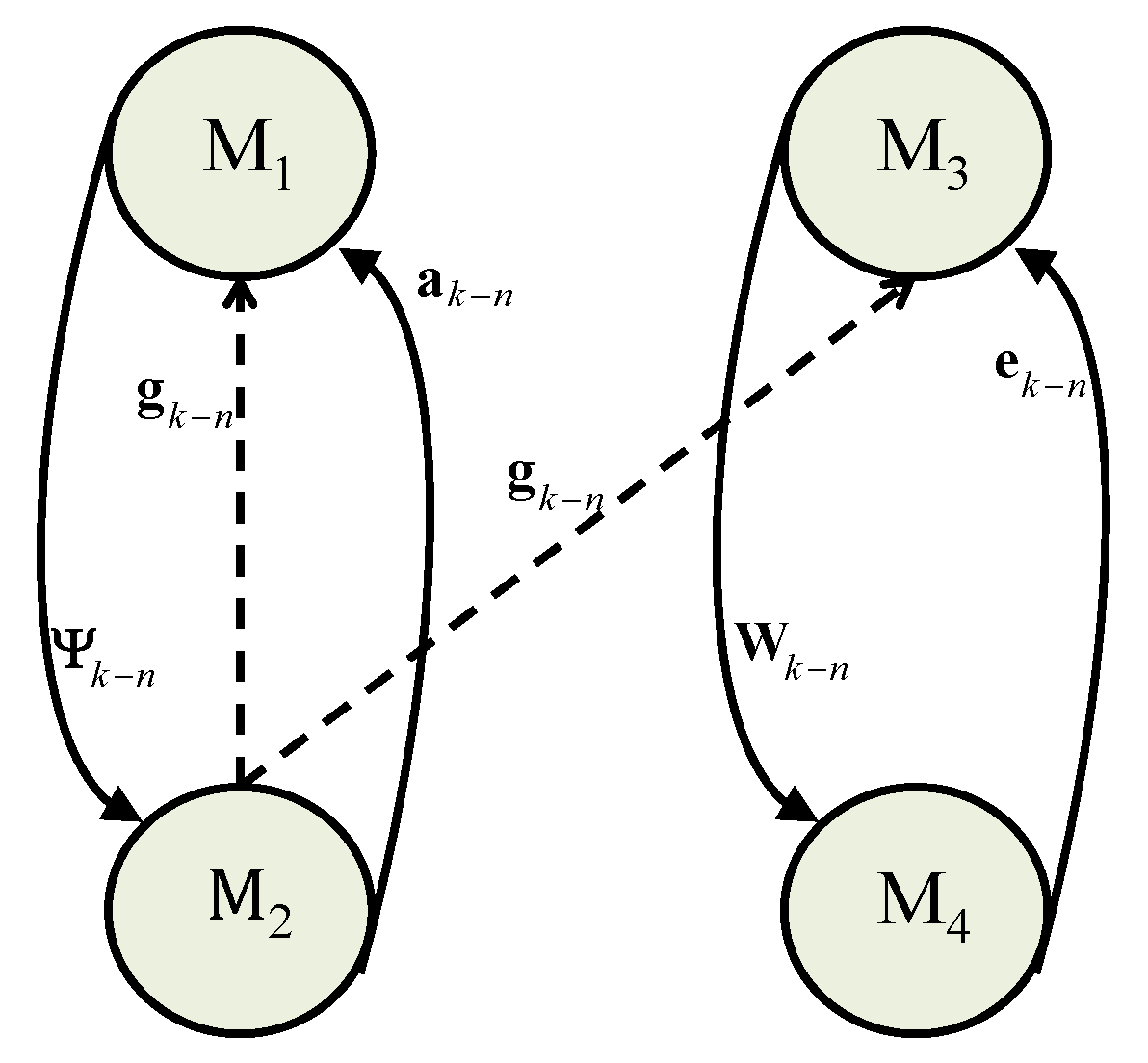
sends a beacon message to all the slave nodes which makes them ready for working on a desired goal. After that, all the four nodes are capable to work on the desired process. The working procedure of information interchange over PDASP architecture is clearly depicted in
Figure 4. In this architecture, first of all,
is transmitted from
towards
and
then
and
become capable to forward information of
and
towards
and
, respectively. Likewise, after getting information of
and
,
and
become capable to share information regarding
and
towards
and
, respectively. In this way, the information interchange is totally balanced over the distributed network.
4. Complexity Analysis
In this section, the complexity of the sequentially operated and distributed adaptive RLS filtering for various MIMO communication systems is discussed. The computational complexity provided by the sequentially operated MIMO RLS algorithm entails multiplications and additions per iteration.
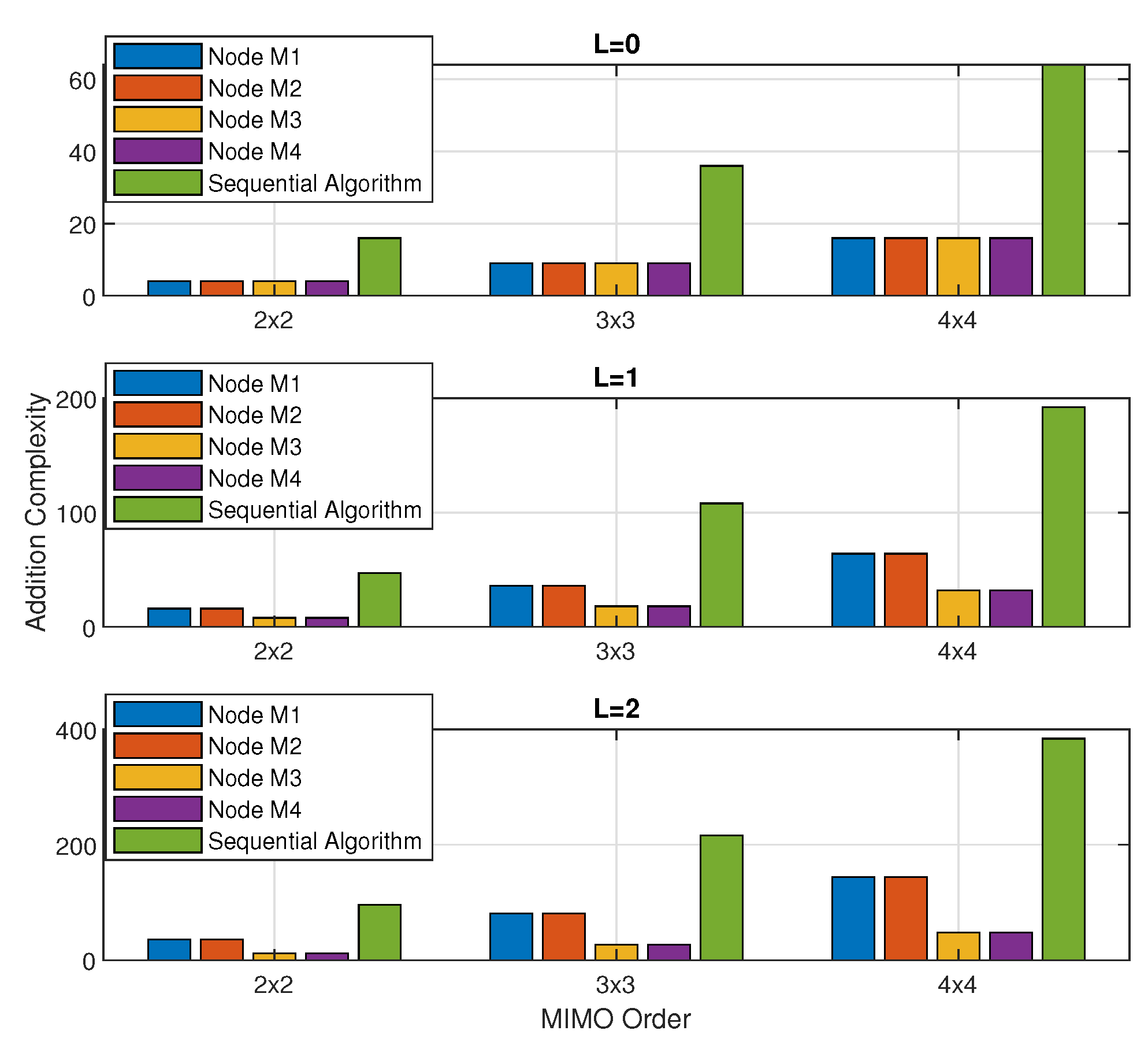
On the other hand, in the PDASP architecture, the node
provides increased computational complexity as compared to the entire nodes in the PDASP architecture; therefore, the node
entails
multiplications and
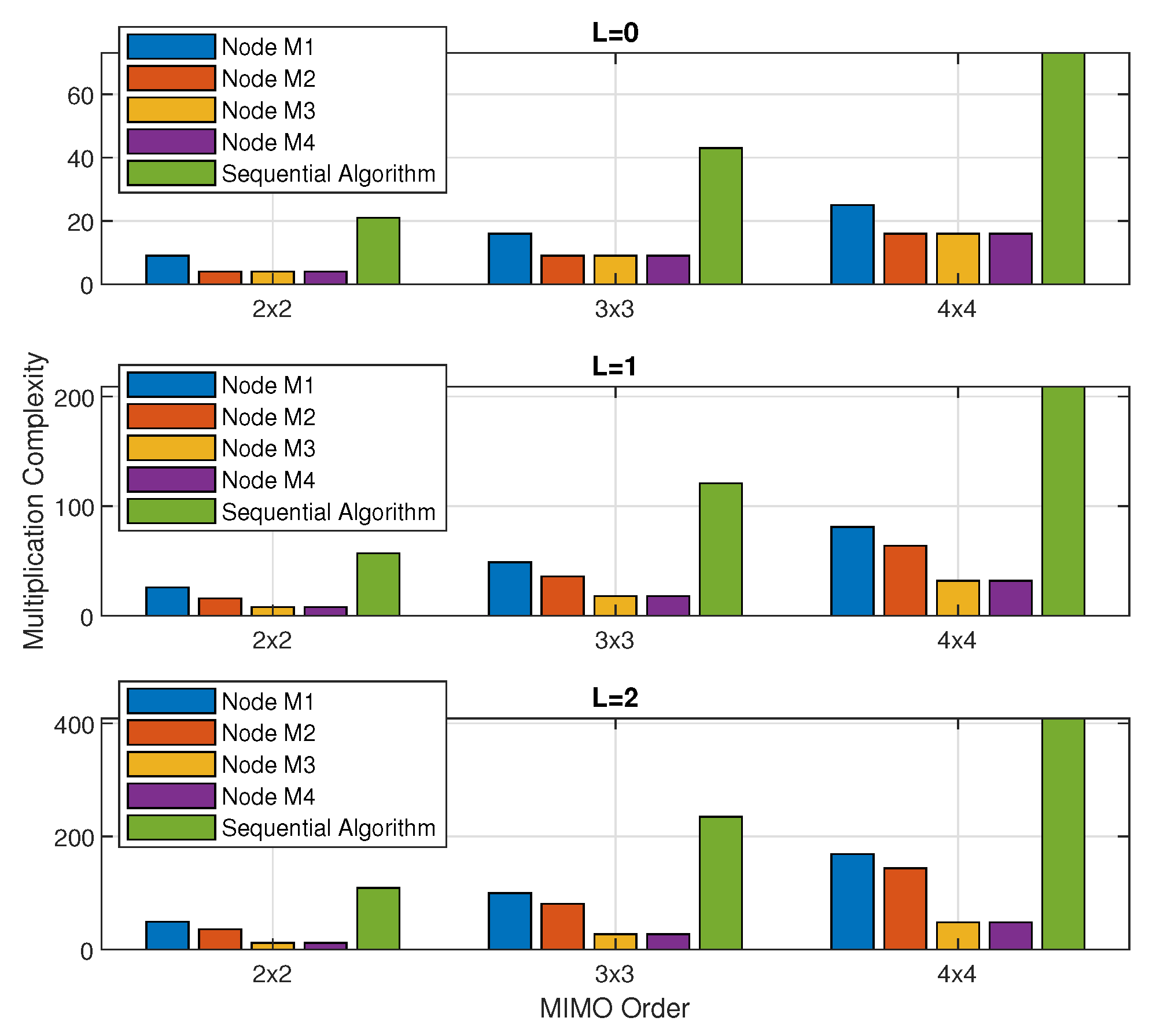
additions at maximum. Likewise, the multiplication and addition complexity with LoS and diffused components for various MIMO systems are shown in
Figure 5 and
Figure 6, respectively. It can be observed that the maximum computational cost provided by the PDASP architecture is much lesser than that of the sequentially operated MIMO RLS algorithm. Furthermore, the percentage improvement in computational complexity provided by the PDASP architecture is shown in
Table 3. It can be visualized that the percentage improvement of more than
in sense of parallelly decreased computational cost shows a superlative enhancement in computational cost of the algorithm as compared to the sequentially operated MIMO RLS algorithm.
5. Measurement Results
In test bed setup, four low-cost wireless sensor nodes from the Arduino platform are used to implement the PDASP architecture. The measurement results are presented by considering various MIMO communication systems with LoS and diffused components. The low-cost wireless sensor nodes, namely NANO, UNO, and MEGA [
18], are used to validate the performance of PDASP architecture. The distance among the four senor nodes is set approximately 24 cm from each apart. All the sensor categories (NANO, UNO, and MEGA) have the same processing speed of 16 MH with diverse static random memory specifications of 1, 2, and 8 KBytes, respectively. The communication is being possible among the network nodes by using NORDIC radio NRF24L01 Module [
21].
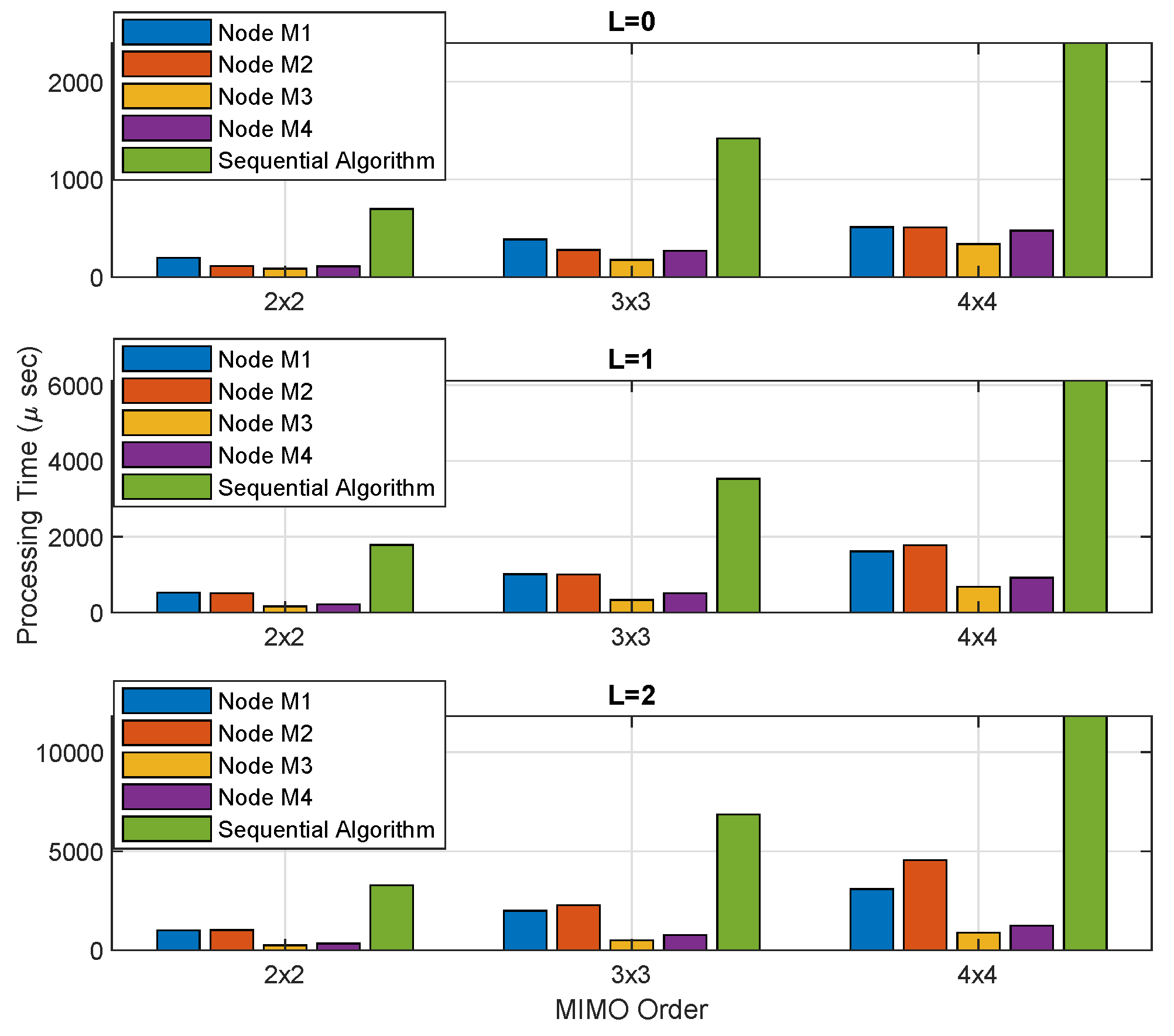
The maximum transmission speed provided by this Module is 2 Mbps at power of 20 dB. The MIMO RLS algorithm is deployed on low-cost wireless sensor nodes to substantiate the validation of the PDASP technique in terms of processing time, computational complexity, and communication burden. The processing time with respect to sequential and PDASP technique relative to each processing node is shown in
Figure 7.
It is realized that the processing time obtained by using the PDASP architecture utilizes parallelly less execution time than the sequential RLS filtering algorithm. Furthermore,
Table 4 displays the reduction in processing time utilizing the PDASP architecture. It can be realized that the PDASP provides significant improvement in decreased processing time parallelly than that of sequential RLS algorithm which makes a critical impact on the efficiency of the processing device as well as on the low power consumption.
Furthermore, the comparison among the working of low-cost devices and their memory limitations for sequential and distributed MIMO systems with multipath components is shown in
Table 5 and
Table 6, respectively. It is observed that the distributive strategy effectively runs the sequential algorithm for various MIMO systems with diffused components without showing any complication of memory error. However, among of all three sensor nodes, NANO is still unable to work for the
and
MIMO system with two diffused components because of lesser memory specification. Moreover, the percentage improvement in memory utilization by using the PDASP architecture is shown in
Table 7. It can be observed that the PDASP architecture while running the sequential algorithm parallelly on low-cost sensor nodes provides lesser memory utilization in the sense of fetching information from the memory which entails proficient impact on the efficiency of the nodes. Furthermore, the time taken by the PDASP architecture for one iteration with a communication burden is presented in
Table 8. It can be realized that the communication time is higher than the MIMO RLS-based sequential processing time, and this communication time can be reduced by using the transceiver with high data rates as compared to NORDIC radio NRF24L01.