On the Optimal Control Problem for Vibrations of the Rod/String Consisting of Two Non-Homogeneous Sections with the Condition at an Intermediate Time
Abstract
1. Introduction
2. Problem Statement
3. Reduction to the Problem with Zero Boundary Conditions
4. Reduction of the Problem with Zero Boundary Conditions to the Problem of Moments
5. Problem Solution
6. Constructing a Solution for
7. The Example with Numerical Experiment
8. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Butkovskii, A.G. Control Methods for Systems with Distributed Parameters; Nauka: Moscow, Russia, 1975. (In Russian) [Google Scholar]
- Barseghyan, V.R. Control Problem of String Vibrations with Inseparable Multipoint Conditions at Intermediate Points in Time. Mech. Solids 2019, 54, 1216–1226. [Google Scholar] [CrossRef]
- Barseghyan, V.R. The problem of optimal control of string vibrations. Intern. Appl. Mech. 2020, 56, 471–480. [Google Scholar] [CrossRef]
- Barseghyan, V.R.; Solodusha, S.V. Optimal Boundary Control of String Vibrations with Given Shape of Deflection at a Certain Moment of Time. Lect. Notes Control Inf. Sci. 2021, 12755, 299–313. [Google Scholar]
- Barseghyan, V.R.; Solodusha, S.V. On One Problem in Optimal Boundary Control for String Vibrations with a Given Velocity of Points at an Intermediate Moment of Time. In Proceedings of the 2021 International Russian Automation Conference (RusAutoCon), Sochi, Russia, 5–11 September 2021; pp. 343–349. [Google Scholar]
- Barseghyan, V.R. Control of Stage by Stage Changing Linear Dynamic Systems. Yugosl. J. Oper. Res. 2012, 22, 31–39. [Google Scholar] [CrossRef]
- Barseghyan, V.R. On the controllability and observability of linear dynamic systems with variable structure. In Proceedings of the 2016 International Conference Stability and Oscillations of Nonlinear Control Systems (Pyatnitskiy’s Conference), Moscow, Russia, 1–3 June 2016; pp. 1–3. [Google Scholar]
- L’vova, N.N. Optimal control of a certain distributed nonhomogeneous oscillatory system. Autom. Remote Control 1973, 34, 1550–1559. [Google Scholar]
- Il’in, V.A. Optimization of the boundary control of the vibrations of a rod consisting of two dissimilar parts. Dokl. Math. 2011, 84, 629–633. [Google Scholar] [CrossRef]
- Il’in, V.A. On the bringing of the oscillations of an initially quiescent rod consisting of two different parts to an arbitrarily given state. Dokl. Math. 2010, 82, 955–958. [Google Scholar] [CrossRef]
- Egorov, A.I.; Znamenskaya, L.N. On the controllability of elastic oscillations of serially connected objects with distributed parameters. Trudy Inst. Mat. i Mekh. UrO RAN 2011, 17, 85–92. (In Russian) [Google Scholar]
- Provotorov, V.V. Construction of boundary controls in the problem of oscillation of a system of strings. Vestn. St. Petersburg University. Appl. Math. Comput. Sci. Control Process. 2012, 1, 62–71. (In Russian) [Google Scholar]
- Ben Amara, J.; Bouzidi, H. Null boundary controllability of a one-dimensional heat equation with an internal point mass and variable coefficients. J. Math. Phys. 2018, 59, 011512. [Google Scholar] [CrossRef]
- Ben Amara, J.; Beldi, E. Boundary controllability of two vibrating strings connected by a point mass with variable coefficients. SIAM J. Control Optim. 2019, 57, 3360–3387. [Google Scholar] [CrossRef]
- Mercier, D.; Regnier, V. Boundary controllability of a chain of serially connected Euler-Bernoulli beams with interior masses. Collectanea Mathematica 2009, 60, 307–334. [Google Scholar] [CrossRef]
- Kuleshov, A.A. Mixed problems for the equation of the longitudinal vibrations of a nonhomogeneous rod and for the equation of the transverse vibrations of a nonhomogeneous string consisting of two segments with different densities and elasticities. Dokl. Math. 2012, 85, 98–101. [Google Scholar] [CrossRef]
- Rogozhnikov, A.M. Investigation of a mixed problem describing the oscillations of a rod consisting of several segments with arbitrary lengths. Dokl. Math. 2012, 85, 399–402. [Google Scholar] [CrossRef]
- Anikonov, D.S.; Konovalova, D.S. Direct and inverse problems for a wave equation with discontinuous coefficients. St. Petersburg State Polytech. Univ. J. Phys. Math. 2018, 11, 61–72. [Google Scholar]
- Zvereva, M.B.; Najdyuk, F.O.; Zalukaeva, Z.O. Modeling vibrations of a singular string. Proc. Voronezh State Univ. Ser. Phys. Math. 2014, 2, 111–119. (In Russian) [Google Scholar]
- Kholodovskii, S.Y.; Chuhrii, P.A. The Problem of Motion of an Unbounded Piecewise Homogeneous String. Sch. Notes Transbaikal State Univ. Ser. Phys. Math. Eng. Technol. 2018, 13, 42–50. (In Russian) [Google Scholar] [CrossRef]
- Krasovsky, N.N. The Theory of Motion Control; Nauka: Moscow, Russia, 1968. (In Russian) [Google Scholar]

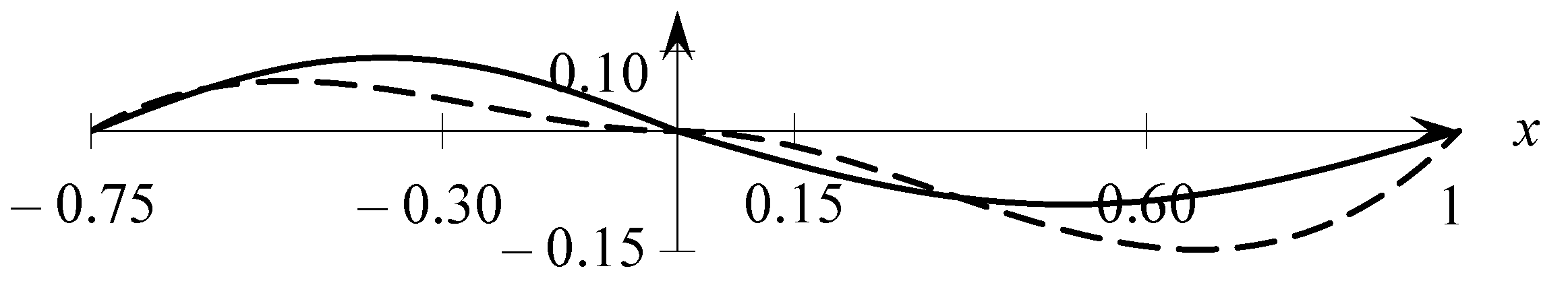
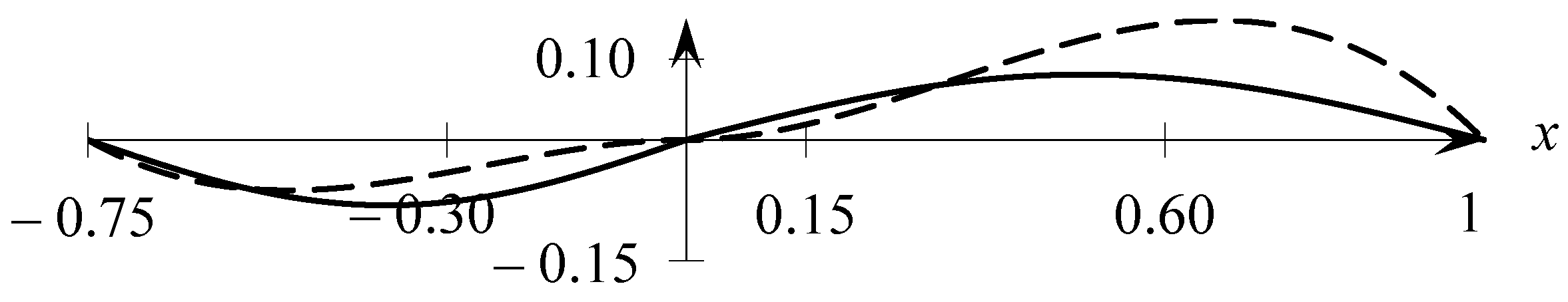

Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Barseghyan, V.; Solodusha, S. On the Optimal Control Problem for Vibrations of the Rod/String Consisting of Two Non-Homogeneous Sections with the Condition at an Intermediate Time. Mathematics 2022, 10, 4444. https://doi.org/10.3390/math10234444
Barseghyan V, Solodusha S. On the Optimal Control Problem for Vibrations of the Rod/String Consisting of Two Non-Homogeneous Sections with the Condition at an Intermediate Time. Mathematics. 2022; 10(23):4444. https://doi.org/10.3390/math10234444
Chicago/Turabian StyleBarseghyan, Vanya, and Svetlana Solodusha. 2022. "On the Optimal Control Problem for Vibrations of the Rod/String Consisting of Two Non-Homogeneous Sections with the Condition at an Intermediate Time" Mathematics 10, no. 23: 4444. https://doi.org/10.3390/math10234444
APA StyleBarseghyan, V., & Solodusha, S. (2022). On the Optimal Control Problem for Vibrations of the Rod/String Consisting of Two Non-Homogeneous Sections with the Condition at an Intermediate Time. Mathematics, 10(23), 4444. https://doi.org/10.3390/math10234444






