Mathematical Properties of a Novel Graph-Theoretic Irregularity Index with Potential Applicability in QSPR Modeling
Abstract
1. Introduction
1.1. Background
1.2. Related Work
1.3. Motivation
- Almost all of the results published on irregularity indices are purely mathematical without discussing their applicability.
- Calculating an irregularity index for graphs on a large number of vertices is rather difficult. No computational technique has been proposed so far to tackle this issue.
- The correlation ability of irregularity indices for predicting physicochemical properties of isomeric octanes, i.e., alkanes, is rather poor.
- No criteria have been published to address the proliferation of newly introduced irregularity indices.
- Mathematical results on composition and product graphs have only been studied for Albertson’s irregularity and the total irregularity indices, which have no practical applicability, except the quantification of the irregularity in a graph.
- There has not been any study published that reflects on how to employ mathematical results on composition and product graphs for practical applications.
1.4. Contributions
- A computational technique is proposed to compute irregularity indices, which efficiently works for large-sized graphs.
- We conduct a comparative testing of commonly occurring irregularity indices for the predicting physicochemical and quantum-theoretic properties of benzenoid hydrocarbons.
- The index outperforms all the irregularity indices by correlating significantly well with the quantum-theoretic and fairly well with the physicochemical properties.
- Having potential applications in QSPR modeling, the index is further studied for various transformation and derived graphs.
- We devise a method of employing mathematical results on transformation and derived graphs in correlating the physicochemical and quantum-theoretic properties of derivative hydrocarbons.
1.5. Organization of the Paper
2. Mathematical Preliminaries
- (i)
- such that in or;
- (ii)
- , , or vice versa, such that in .
- (i)
- such that in or;
- (ii)
- , , or vice versa, such that in .
- (i)
- and .
- (ii)
- .
- (iii)
- and .
- (iv)
- and .
- (v)
- and .
- (i)
- , if and if .
- (ii)
- , , in if and in if .
- (i)
- and .
- (ii)
- and .
- (iii)
- and .
- (iv)
- and .
3. Application of the Index in QSPR Modeling
3.1. Computational Details
- Step 1: Draw in newGraph, and compute its adjacency matrix A.
- Step 2: Input A into our program in MatLab to compute .
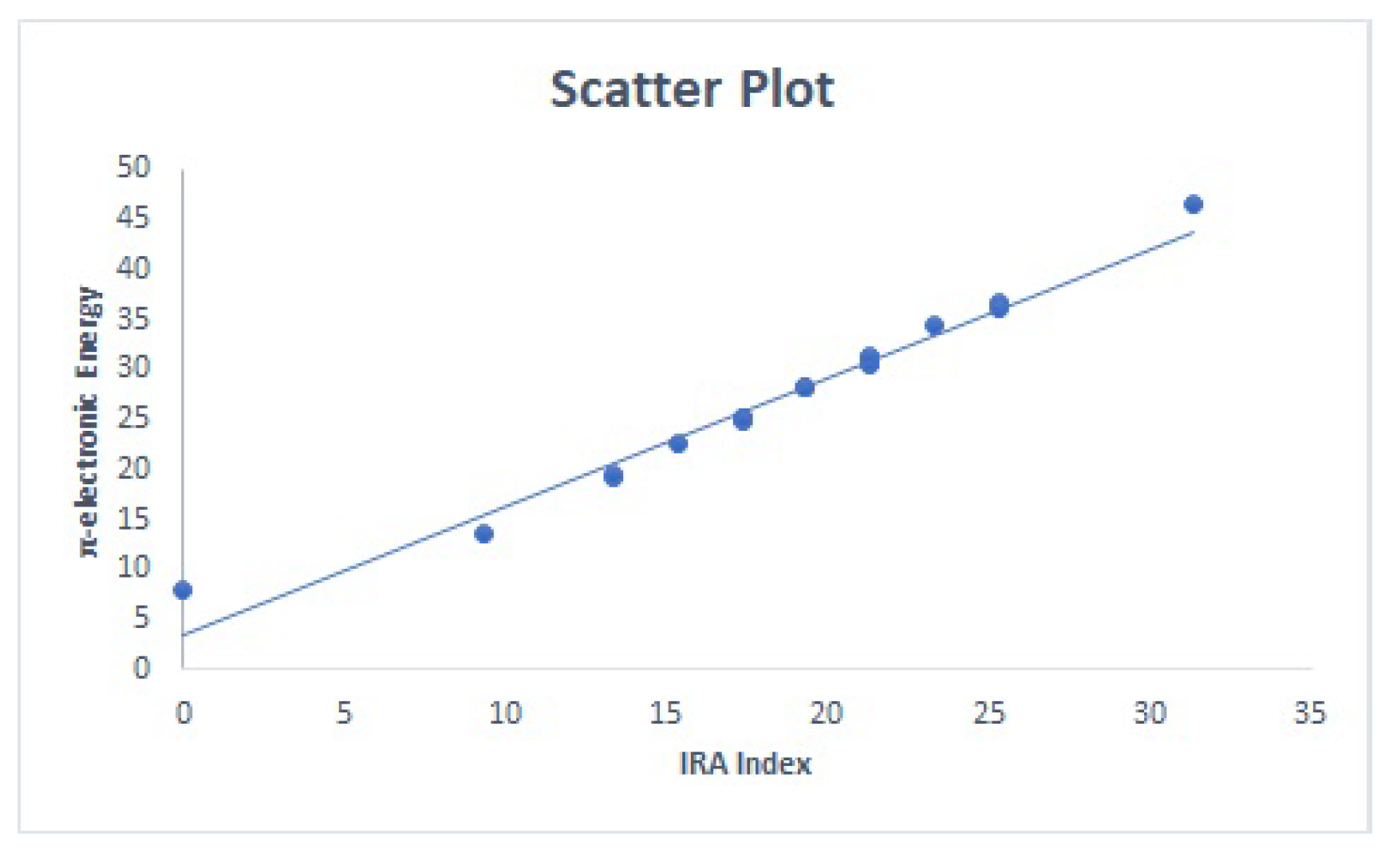
3.2. QSPR Modeling of Physicochemical Properties
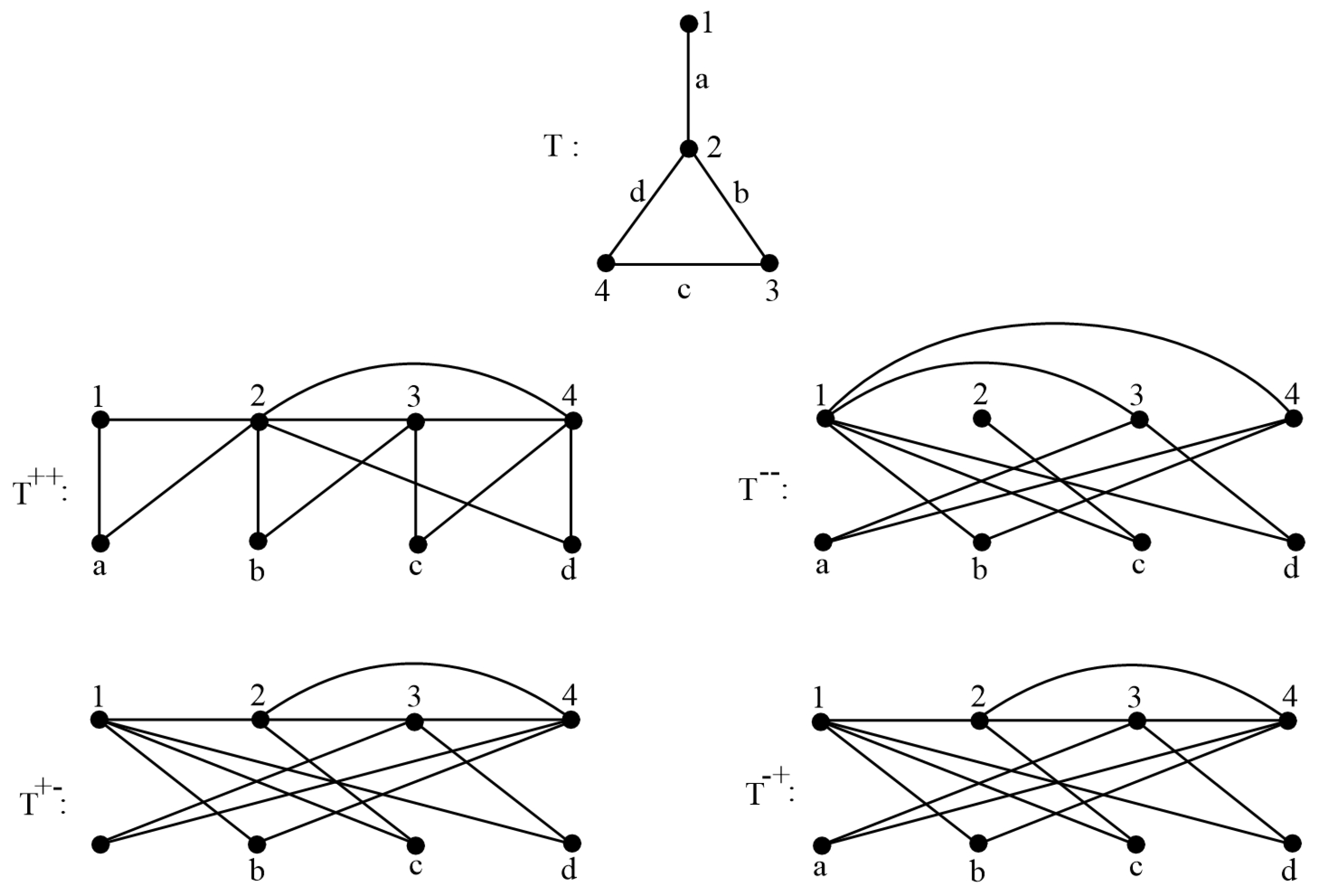
4. The Index of Transformation Graphs
5. The Index of Derived Graphs
6. Applications of Mathematical Results
7. Concluding Remarks
7.1. Conclusions
7.2. Implications
- The strong predictive potential of the index warrants its further usage in the quantitative structure activity/property relationship models.
- The index of all the derived and transformation graphs of a graph can be calculated simply from the information of and .
- The planar version of those operations can be employed to study the physicochemical and quantum-theoretic properties of the derivatives of organic compounds.
7.3. Limitations
7.4. Future Scope
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Roy, K.; Kar, S.; Das, R.N. A Primer on QSAR/QSPR Modeling: Fundamental Concepts; Springer: Berlin/Heidelberg, Germany, 2015. [Google Scholar]
- Allison, T.C.; Burgess, D.R., Jr. First-principles prediction of enthalpies of formation for polycyclic aromatic hydrocarbons and derivatives. J. Phys. Chem. A 2015, 119, 11329–11365. [Google Scholar] [CrossRef]
- Estrada, E.; Torres, L.; Rodríguez, L.; Gutman, I. An atom-bond connectivity index: Modelling the enthalpy of formation of alkanes. Indian J. Chem. 1998, 37A, 849–855. [Google Scholar]
- Redžepović, I.; Marković, S.; Furtula, B. On structural dependence of enthalpy of formation of catacondensed benzenoid hydrocarbons. MATCH Commun. Math. Comput. Chem. 2019, 82, 663–678. [Google Scholar]
- Yu, J.; Sumathi, R.; Green, W.H. Accurate and efficient method for predicting thermochemistry of polycyclic aromatic hydrocarbons-bond-centered group additivity. J. Am. Chem. Soc. 2004, 126, 12685–12700. [Google Scholar] [CrossRef] [PubMed]
- Zavitsas, A.A.; Matsunaga, N.; Rogers, D.W. Enthalpies of formation of hydrocarbons by hydrogen atom counting. Theoretical implications. J. Phys. Chem. A 2008, 112, 5734–5741. [Google Scholar] [CrossRef]
- Teixeira, A.L.; Leal, J.P.; Falcao, A.O. Random forests for feature selection in QSPR models—An application for predicting standard enthalpy of formation of hydrocarbons. J. Cheminf. 2013, 5, 9–24. [Google Scholar] [CrossRef]
- Song, X.; Chai, L.; Zhang, J. Graph signal processing approach to QSAR/QSPR model learning of compounds. IEEE Trans. Pattern Anal. Mach. Intell. 2020; in press. [Google Scholar] [CrossRef]
- Dudek, A.Z.; Arodz, T.; Galvez, J. Computational methods in developing quantitative structure-activity relationships (QSAR): A review. Comb. Chem. High Throughput Screen 2006, 9, 213–228. [Google Scholar] [CrossRef]
- Mauri, A.; Consonni, V.; Todeschini, R. Molecular Descriptors. Handbook of Computational Chemistry; Springer: Cham, Switzerland, 2016. [Google Scholar]
- Todeschini, R.; Consonni, V. Molecular Descriptors for Chemoinformatics; Wiley-VCH: Weinheim, Germany, 2009; Volumes 1 and 2. [Google Scholar]
- Vladimirova, N.; Puchkova, E.; Dar’in, D.; Turanov, A.; Babain, V.; Kirsanov, D. Predicting the potentiometric sensitivity of membrane sensors based on modified diphenylphosphoryl acetamide ionophores with QSPR modeling. Membranes 2022, 12, 953. [Google Scholar] [CrossRef]
- Dearden, J.C. Advances in QSAR Modeling-Applications in Pharmaceutical, Chemical, Food, Agricultural and Environmental Sciences; Roy, K., Ed.; Springer: Cham, Switzerland, 2017. [Google Scholar]
- Devillers, J.; Balaban, A.T. Topological Indices and Related Descriptors in QSAR and QSPR; Gordon & Breach: Amsterdam, The Netherlands, 1999. [Google Scholar]
- Talevi, A.; Bellera, C.L.; Di Ianni, M.; Duchowicz, P.R.; Bruno-Blanch, L.E.; Castro, E.A. An integrated drug development approach applying topological descriptors. Curr. Comput. Aided Drug Des. 2012, 8, 172–181. [Google Scholar] [CrossRef]
- Hayat, S.; Khan, S.; Khan, A.; Imran, M. Distance-based topological descriptors for measuring the π-electronic energy of benzenoid hydrocarbons with applications to carbon nanotubes. Math. Methods Appl. Sci. 2020; Early View. [Google Scholar] [CrossRef]
- Malik, M.Y.H.; Hayat, S.; Khan, S.; Binyamin, M.A. Predictive potential of spectrum-based topological descriptors for measuring the π-electronic energy of benzenoid hydrocarbons with applications to boron triangular and boron α-nanotubes. Math. Methods Appl. Sci. 2021; Early View. [Google Scholar] [CrossRef]
- Azadifar, S.; Rostami, M.; Berahmand, K.; Moradi, P.; Oussalah, M. Graph-based relevancy-redundancy gene selection method for cancer diagnosis. Comput. Biol. Med. 2022, 147, 105766. [Google Scholar] [CrossRef] [PubMed]
- Gutman, I. Degree-based topological indices. Croat. Chem. Acta 2013, 86, 351–361. [Google Scholar] [CrossRef]
- Gutman, I.; Hansen, P.; Mélot, H. Variable neighborhood search for extremal graphs. 10. comparison of irregularity indices for chemical trees. J. Chem. Inf. Model. 2005, 45, 222–230. [Google Scholar] [CrossRef]
- Hansen, P.; Mélot, H. Variable neighborhood search for extremal graphs. 9. bounding the irregularity of a graph. Discret. Math. Theor. Comput. Sci. 2005, 69, 253–264. [Google Scholar]
- Zhou, B.; Luo, W. On irregularity of graphs. Ars Comb. 2008, 88, 55–64. [Google Scholar]
- Luo, W.; Zhou, B. On the irregularity of trees and unicyclic graphs with given matching number. Util. Math. 2010, 83, 141–148. [Google Scholar]
- Mukwembi, S. On maximally irregular graphs. Bull. Malays. Math. Sci. Soc. 2013, 36, 717–721. [Google Scholar]
- Réti, T.; Dimitrov, D. On irregularities of bidegreed graphs. Acta Polytech. Hung. 2013, 10, 117–134. [Google Scholar]
- Dimitrov, D.; Réti, T. Graphs with equal irregularity indices. Acta Polytech. Hung. 2014, 11, 41–57. [Google Scholar]
- Abdo, H.; Dimitrov, D.; Gutman, I. Graph irregularity and its measures. Appl. Math. Comput. 2019, 357, 317–324. [Google Scholar] [CrossRef]
- Réti, T. On some properties of graph irregularity indices with a particular regard to the σ-index. Appl. Math. Comput. 2019, 344–345, 107–115. [Google Scholar] [CrossRef]
- Henning, M.A.; Rautenbach, D. On the irregularity of bipartite graphs. Discret. Math. 2007, 307, 1467–1472. [Google Scholar] [CrossRef]
- Abdo, H.; Brandt, S.; Dimitrov, D. The total irregularity of a graph. Discret. Math. Theor. Comput. Sci. 2014, 16, 201–206. [Google Scholar] [CrossRef]
- Liu, F.; Zhang, Z.; Meng, J. The size of maximally irregular graphs and maximally irregular triangle-free graphs. Graph. Comb. 2014, 30, 699–705. [Google Scholar] [CrossRef]
- Elphick, C.; Wocjan, P. New measures of graph irregularity. arXiv Preprint 2014, arXiv:1305.3570v7. [Google Scholar]
- Abdo, H.; Cohen, N.; Dimitrov, D. Graphs with maximal irregularity. Filomat 2014, 28, 1315–1322. [Google Scholar] [CrossRef]
- Gutman, I.; Togan, M.; Yurttas, A.; Cevik, A.S.; Cangul, I.N. Inverse problem for sigma index. MATCH Commun. Math. Comput. Chem. 2018, 79, 491–508. [Google Scholar]
- Abdo, H.; Dimitrov, D.; Gutman, I. Graphs with maximal σ irregularity. Discret. Appl. Math. 2018, 250, 57–64. [Google Scholar] [CrossRef]
- Chen, X.; Hou, Y.; Lin, F. Some new spectral bounds for graph irregularity. Appl. Math. Comput. 2018, 320, 331–340. [Google Scholar] [CrossRef]
- Abdo, H.; Dimitrov, D. The irregularity of graphs under graph operations. Discuss. Math. Graph Theory 2014, 34, 263–278. [Google Scholar] [CrossRef]
- Abdo, H.; Dimitrov, D. The total irregularity of graphs under graph operations. Miskolc Math. Notes 2014, 15, 3–17. [Google Scholar] [CrossRef]
- Abdo, H.; Dimitrov, D. The total irregularity of some composite graphs. Int. J. Comput. Appl. 2015, 122, 1–9. [Google Scholar] [CrossRef]
- De, N.; Pal, A.; Nayeem, S.M.A. The irregularity of some composite graphs. Int. J. Appl. Comput. Math. 2016, 2, 411–420. [Google Scholar] [CrossRef][Green Version]
- Réti, T.; Sharafdini, R.; Dregelyi-Kiss, A.; Haghbin, H. Graph irregularity indices used as molecular descriptor in QSPR studies. MATCH Commun. Math. Comput. Chem. 2018, 79, 509–524. [Google Scholar]
- Emadi Kouchak, M.M.; Safaei, F.; Reshadi, M. Graph entropies-graph energies indices for quantifying network structural irregularity. J. Supercomput. 2022; Early View. [Google Scholar] [CrossRef]
- Collatz, L.; Sinogowitz, U. Spektren endlicher grafen. Abh. Math. Sem. Univ. Hamburg. 1957, 21, 63–77. [Google Scholar] [CrossRef]
- Bell, F.K. A note on the irregularity of a graph. Linear Algebra Appl. 1992, 161, 45–54. [Google Scholar] [CrossRef]
- Randić, M. On characterization of molecular branching. J. Am. Chem. Soc. 1975, 97, 6609–6615. [Google Scholar] [CrossRef]
- Li, X.; Gutman, I. Mathematical Aspects of Randić-Type Molecular Structure Descriptors; Univ. Kragujevac: Kragujevac, Serbia, 2006. [Google Scholar]
- Gutman, I.; Ruščić, B.; Trinajstić, N.; Wilcox, C.X. Graph theory and molecular orbital. XII. Acyclic polyenes. J. Chem. Phys. 1975, 62, 3399. [Google Scholar] [CrossRef]
- Balaban, A.T.; Motoc, I.; Bonchev, D.; Mekenyan, O. Topological indices for structure-activity correlations. J. Chem. Phys. 1983, 14, 21–55. [Google Scholar]
- Furtula, B.; Gutman, I. A forgotten topological index. J. Math. Chem. 2015, 53, 1184–1190. [Google Scholar] [CrossRef]
- Li, X.; Shi, Y. A survey on the Randić index. MATCH Commun. Math. Comput. Chem. 2008, 59, 127–156. [Google Scholar]
- Estrada, E. Randić index, irregularity and complex biomolecular networks. Acta Chim. Slov. 2010, 57, 597–603. [Google Scholar]
- Estrada, E. Quantifying network heterogeneity. Phys. Rev. E 2010, 82, 066102. [Google Scholar] [CrossRef]
- Gutman, I. Topological indices and irregularity measures. Bull. Int. Math. Virtual Inst. 2018, 8, 469–475. [Google Scholar]
- Kang, S.; Chu, Y.-M.; Virk, A.R.; Nazeer, W.; Jia, J. Computing irregularity indices for probabilistic neural network. Front. Phys. 2020, 8, 359. [Google Scholar] [CrossRef]
- Chu, Y.-M.; Abid, M.; Qureshi, M.I.; Fahad, A.; Aslam, A. Irregular topological indices of certain metal organic frameworks. Main Group Met. Chem. 2021, 44, 73–81. [Google Scholar] [CrossRef]
- Behzad, M. A criterion for the planarity of a total graph. Proc. Camb. Philos. Soc. 1967, 63, 679–681. [Google Scholar] [CrossRef]
- Sampathkumar, E.; Chikkodimath, S.B. The semi-total graphs of a graph-I. J. Karnatak Univ. Sci. 1973, 18, 274–280. [Google Scholar]
- Akiyama, J.; Hamada, T.; Yoshimura, I. Miscellaneous properties of middle graphs. TRU Math. 1974, 10, 41–53. [Google Scholar]
- Alon, N. Eigenvalues and expanders. Combinatorica 1986, 6, 83–89. [Google Scholar] [CrossRef]
- Wu, B.; Meng, J. Basic properties of total transformation graphs. J. Math. Study 2001, 34, 109–116. [Google Scholar]
- Xu, L.; Wu, B. Transformation graph G−+−. Discret. Math. 2008, 308, 5144–5148. [Google Scholar] [CrossRef]
- Yi, L.; Wu, B. The transformation graph G++−. Aust. J. Comb. 2009, 44, 37–42. [Google Scholar]
- Stevanović, D.; Brankov, V.; Cvetković, D.; Simić, S. newGRAPH: A Fully Integrated Environment Used for Research Process in Graph Theory. Available online: http://www.mi.sanu.ac.rs/newgraph/index.html (accessed on 18 November 2022).
- MATLAB 8.0 and Statistics Toolbox 8.1; The MathWorks, Inc.: Natick, MA, USA, 2000.
- Gutman, I.; Tošović, J. Testing the quality of molecular structure descriptors. Vertex-degree-based topological indices. J. Serb. Chem. Soc. 2013, 78, 805–810. [Google Scholar] [CrossRef]
- Gutman, I.; Trinajstić, N. Graph theory and molecular orbitals: Total π-electron energy of alternant hydrocarbons. Chem. Phys. Lett. 1972, 17, 535–538. [Google Scholar] [CrossRef]
- Lučić, B.; Trinajstić, N.; Zhou, B. Comparison between the sum-connectivity index and product-connectivity index for benzenoid hydrocarbons. Chem. Phys. Lett. 2009, 47, 146–148. [Google Scholar] [CrossRef]
- Chen, D. Comparison between two kinds of connectivity indices for measuring the π-electronic energies of benzenoid hydrocarbons. Z. Naturforsch. A 2019, 74, 367–370. [Google Scholar] [CrossRef]
- NIST Standard Reference Database. Available online: http://webbook.nist.gov/chemistry/ (accessed on 18 November 2022).
- Nikolić, S.; Trinajstić, N.; Baučić, I. Comparison between the vertex- and edge-connectivity indices for benzenoid hydrocarbons. J. Chem. Inf. Comput. Sci. 1998, 38, 42–46. [Google Scholar] [CrossRef]
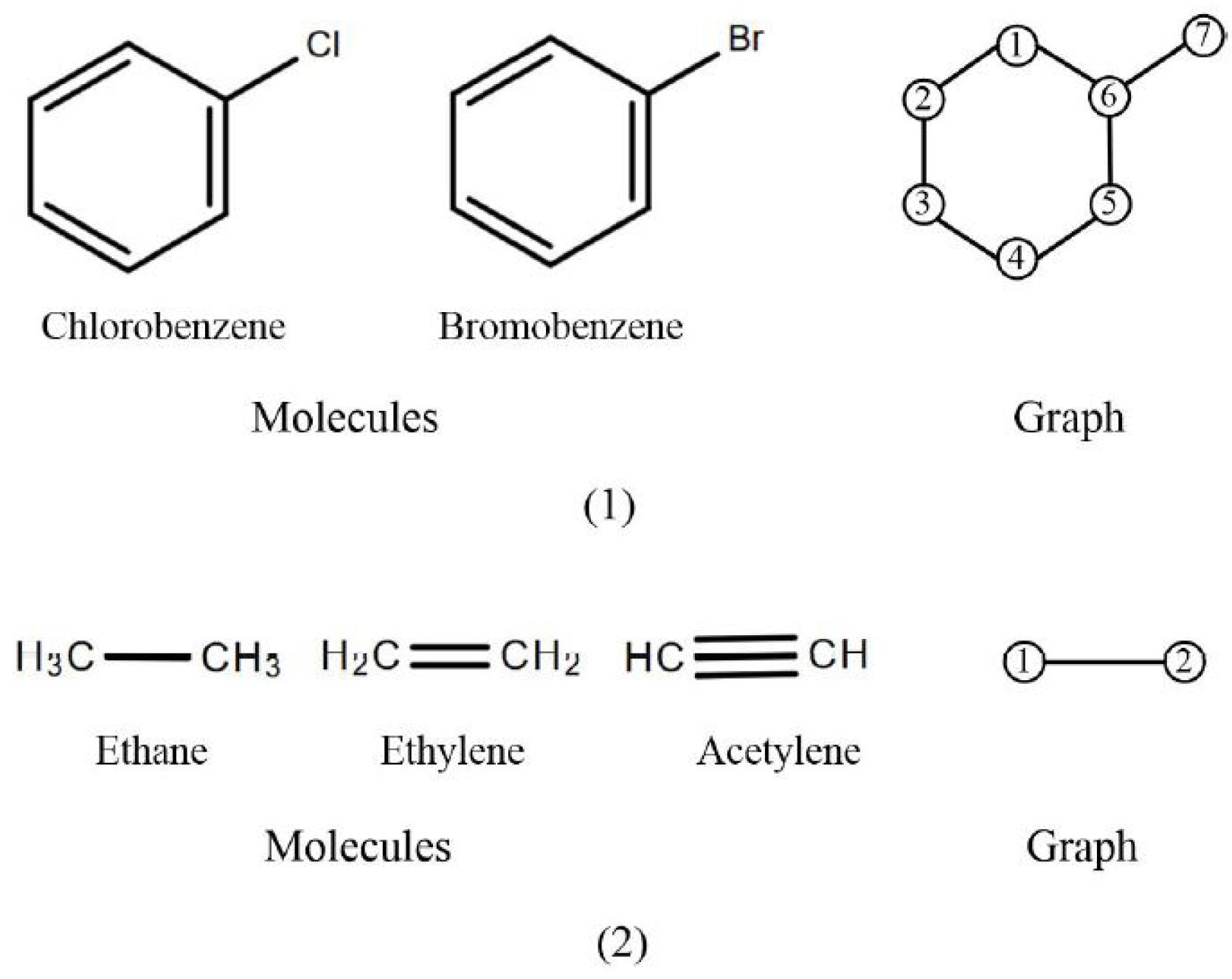
| Method | Description |
|---|---|
| Gutman et al. [20] | Restricted to the class of chemical trees. |
| Hansen and Mélot [21] | Lacks applicability. Restricted to Albertson’s index. |
| Zhou and Luo [22] | Lacks applicability. Restricted to Albertson’s index. |
| Mukwembi in 2013 [24] | Lacks applicability. Restricted to Albertson’s index. |
| Réti and Dimitrov [25] | Lacks applicability. Restricted to bidegreed graphs. |
| Dimitrov and Réti [26] | Lacks applicability. Restricted to Albertson’s index. |
| Abdo et al. [27] | Lacks applicability. |
| Réti [28] | Lacks applicability |
| Abdo and Dimitrov [37] | Applicable to Albertson’s index only. |
| Abdo and Dimitrov [39] | Applicable to Albertson’s index only. |
| De et al. [40] | Applicable to Albertson’s index only. |
| Réti et al. [41] | Chemical applicability restricted to isomeric octanes. |
| Emadi Kouchak et al. [42] | Applications to computer science. |
| Irregularity Index | |||
|---|---|---|---|
| 0.9997 | 0.9976 | 0.9343 | |
| 0.7393 | 0.8091 | 0.7803 | |
| 0.7393 | 0.8091 | 0.7803 | |
| 0.7835 | 0.9021 | 0.7793 | |
| 0.9951 | 0.9964 | 0.9055 | |
| 0.2924 | 0.6989 | 0.6053 | |
| 0.7393 | 0.8091 | 0.7803 | |
| 0.7393 | 0.8091 | 0.7803 | |
| 0.4557 | 0.7955 | 0.6886 | |
| 0.7393 | 0.8091 | 0.7803 | |
| 0.7393 | 0.8091 | 0.7803 | |
| 0.7393 | 0.8091 | 0.7803 | |
| 0.7393 | 0.8091 | 0.7803 | |
| 0.7393 | 0.8091 | 0.7803 | |
| 0.7393 | 0.8091 | 0.7803 | |
| 0.7393 | 0.8092 | 0.7803 | |
| 0.2186 | 0.1072 | 0.1526 | |
| 0.7393 | 0.8091 | 0.7803 |
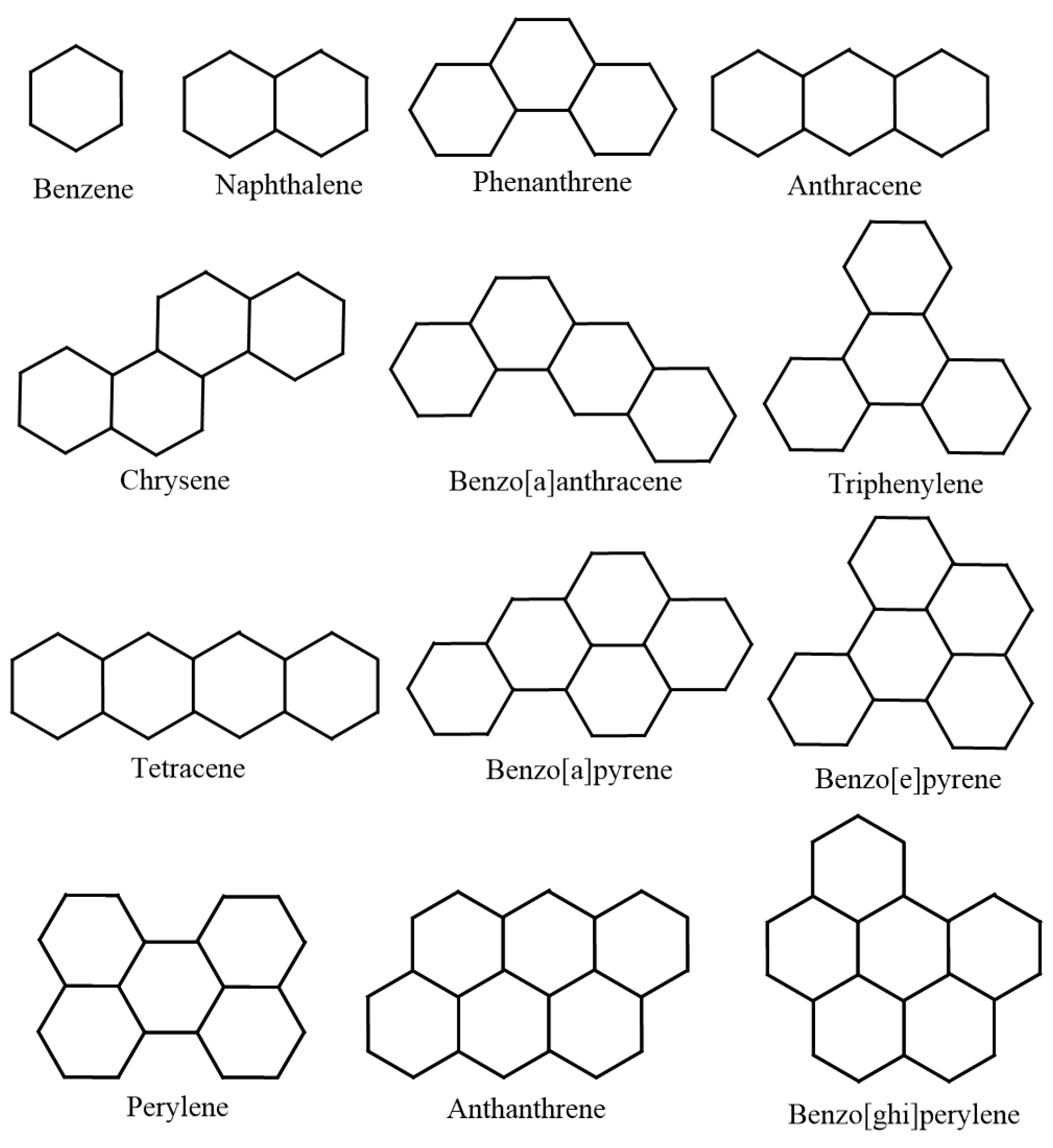
| Molecule | in C | in kJ/mol | |
|---|---|---|---|
| Naphthalene | 218 | 141 | 9.3333 |
| Phenanthrene | 338 | 202.7 | 13.3333 |
| Anthracene | 340 | 222.6 | 13.3333 |
| Chrysene | 431 | 271.1 | 17.3333 |
| Benzo[a]anthracene | 425 | 277.1 | 17.3333 |
| Triphenylene | 429 | 275.1 | 17.3333 |
| Tetracene | 440 | 310.5 | 17.3333 |
| Benzo[a]pyrene | 496 | 296 | 19.3333 |
| Benzo[e]pyrene | 493 | 289.9 | 19.3333 |
| Perylene | 497 | 319.2 | 19.3333 |
| Anthanthrene | 547 | 323 | 21.3333 |
| Benzo[ghi]perylene | 542 | 301.2 | 21.3333 |
| Dibenzo[a,c]anthracene | 535 | 348 | 21.3333 |
| Dibenzo[a,h]anthracene | 535 | 335 | 21.3333 |
| Dibenzo[a,j]anthracene | 531 | 336.3 | 21.3333 |
| Picene | 519 | 336.9 | 21.3333 |
| Coronene | 590 | 296.7 | 23.3333 |
| Dibenzo(a,h)pyrene | 596 | 375.6 | 23.3333 |
| Dibenzo(a,i)pyrene | 594 | 366 | 23.3333 |
| Dibenzo(a,l)pyrene | 595 | 393.3 | 23.3333 |
| Pyrene | 393 | 221.3 | 15.3333 |
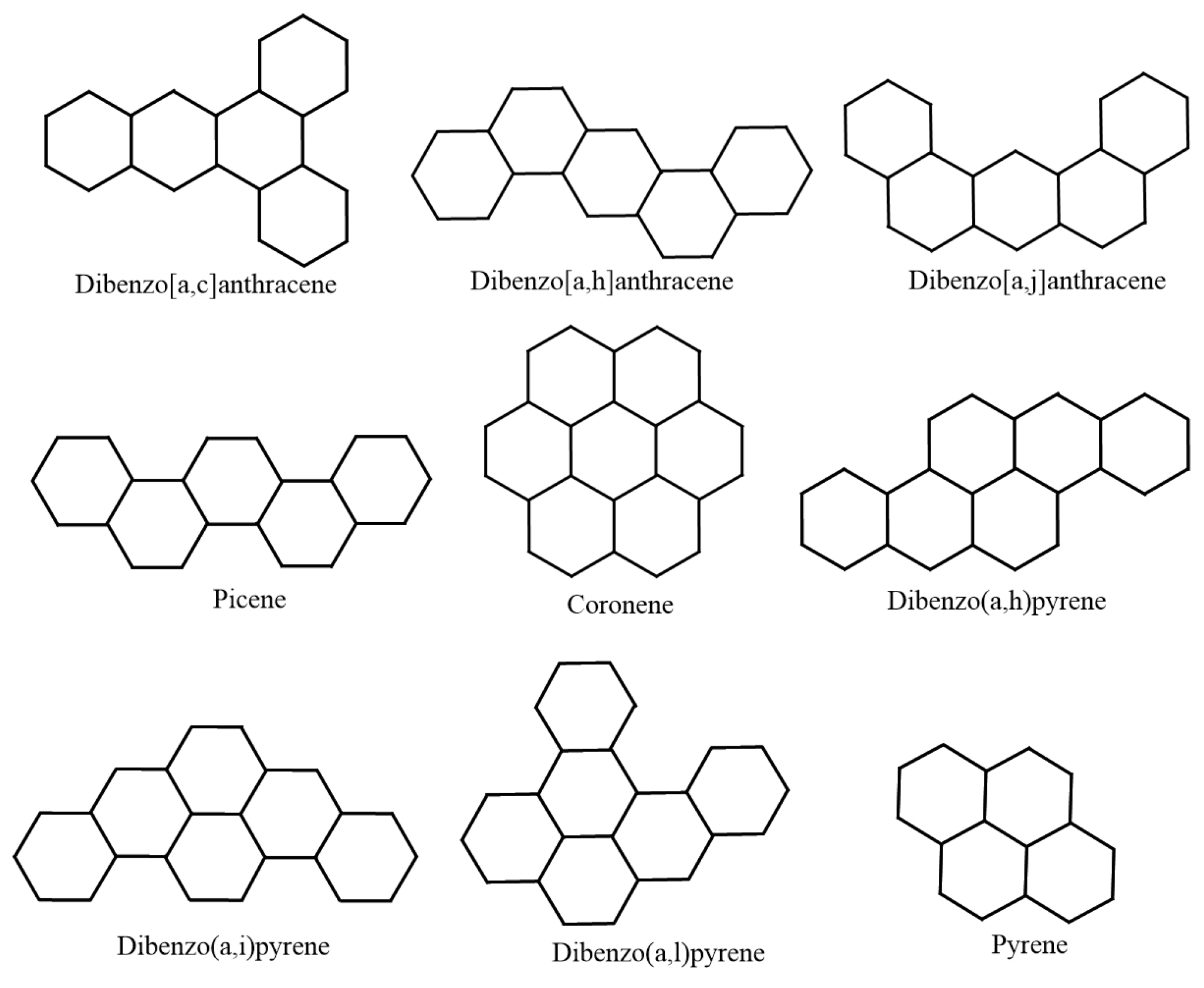
| Molecule | (in Units) | |
|---|---|---|
| Naphthalene | 13.6832 | 9.3333 |
| Anthracene | 19.3137 | 13.3333 |
| Phenanthrene | 19.4483 | 13.3333 |
| Tetracene | 24.9308 | 17.3333 |
| Benzo[c]phenanthrene | 25.1875 | 17.3333 |
| Benzo[a]anthracene | 25.1012 | 17.3333 |
| Chrysene | 25.1922 | 17.3333 |
| Triphenylene | 25.2745 | 17.3333 |
| Pyrene | 22.5055 | 15.3333 |
| Pentacene | 30.544 | 21.3333 |
| Benzo[a]tetracene | 30.7255 | 21.3333 |
| Dibenzo[a,h]anthracene | 30.8805 | 21.3333 |
| Dibenzo[a,j]anthracene | 30.8795 | 21.3333 |
| Pentaphene | 30.7627 | 21.3333 |
| Benzo[g]chrysene | 30.999 | 21.3333 |
| Pentahelicene | 30.9362 | 21.3333 |
| Benzo[c]chrysene | 30.9386 | 21.3333 |
| Picene | 30.9432 | 21.3333 |
| Benzo[b]chrysene | 30.839 | 21.3333 |
| Dibenzo[a,c]anthracene | 30.9418 | 21.3333 |
| Dibenzo[b,g]phenanthrene | 30.8336 | 21.3333 |
| Perylene | 28.2453 | 19.3333 |
| Benzo[e]pyrene | 28.3361 | 19.3333 |
| Benzo[a]pyrene | 28.222 | 19.3333 |
| Hexahelicene | 36.6814 | 25.3333 |
| Benzo[ghi]perylene | 31.4251 | 21.3333 |
| Hexacene | 36.1557 | 25.3333 |
| Coronene | 34.5718 | 23.3333 |
| Ovalene | 46.4974 | 31.3333 |
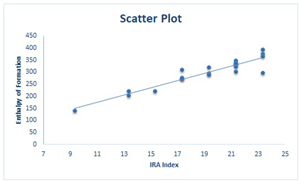
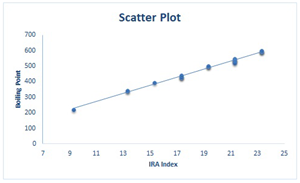 | 
|
|---|---|
| Between and | Between and |
 |  |  |
 |  |  |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Hayat, S.; Arif, A.; Zada, L.; Khan, A.; Zhong, Y. Mathematical Properties of a Novel Graph-Theoretic Irregularity Index with Potential Applicability in QSPR Modeling. Mathematics 2022, 10, 4377. https://doi.org/10.3390/math10224377
Hayat S, Arif A, Zada L, Khan A, Zhong Y. Mathematical Properties of a Novel Graph-Theoretic Irregularity Index with Potential Applicability in QSPR Modeling. Mathematics. 2022; 10(22):4377. https://doi.org/10.3390/math10224377
Chicago/Turabian StyleHayat, Sakander, Amina Arif, Laiq Zada, Asad Khan, and Yubin Zhong. 2022. "Mathematical Properties of a Novel Graph-Theoretic Irregularity Index with Potential Applicability in QSPR Modeling" Mathematics 10, no. 22: 4377. https://doi.org/10.3390/math10224377
APA StyleHayat, S., Arif, A., Zada, L., Khan, A., & Zhong, Y. (2022). Mathematical Properties of a Novel Graph-Theoretic Irregularity Index with Potential Applicability in QSPR Modeling. Mathematics, 10(22), 4377. https://doi.org/10.3390/math10224377







