Abstract
In accordance with the rapid development of smart devices and technology, unmanned aerial vehicles (UAVs) have been developed rapidly. The two-degree-of-freedom helicopter system is a typical UAV that is susceptible to uncertainty, unknown control direction and actuator faults. Hence, a novel adaptive neural network (NN), fault-tolerant control scheme is proposed in this paper. Firstly, to compensate for the uncertainty, a radial-basis NN was developed to approximate the uncertain, unknown continuous function in the controlled system, and a novel weight-adaptive approach is proposed to save on computational cost. Secondly, a class of Nussbaum functions was chosen to solve the unknown-control-direction issue to prevent the effect of an unknown sign for the control coefficient. Subsequently, in response to the actuator faults, an adaptive parameter was designed to compensate for the performance loss of the actuators. Through rigorous Lyapunov analyses, the designed control scheme was proven to enable the states of the closed-loop system to be semi-globally uniformly bounded and the controlled system to be stable. Finally, we conducted a numerical simulation on Matlab to further verify the validity of the proposed scheme.
MSC:
93C40
1. Introduction
Recently, the development of helicopters has attracted remarkable attention. As easy-to-operate and highly maneuverable aircraft, helicopters can take off and land vertically in small areas and can move flexibly in the air [1,2,3]. As a result, helicopters are extensively applied in military, civil and industrial applications, such as reconnaissance patrols, rescue and delivery of supplies [4,5,6]. However, a helicopter is a typical multi-input multi-output system. The complex dynamics model and the coupling between the inputs and outputs bring enormous challenges to the controller design for a helicopter. Moreover, since the model’s parameters are difficult to obtain precisely, there exists a huge uncertainty in the helicopter system. This places a high demand on the control performance of the helicopter controller [7,8]. Hence, there is an extreme requirement for an efficient control strategy to address the uncertainty in helicopter systems.
Thus far, various approaches have reported to address the uncertainty of the 2-degree-of-freedom (2-DOF) helicopters, such as proportional-integral-differential (PID) control, linear quadratic regulator (LQR) control, particle swarm optimization (PSO) and reinforcement Q-learning algorithms. In Raaja et al. [9], to improve the tracking performance of a 2-DOF helicopter system under LQR control, an adaptive law was introduced to compensate for the uncertainty caused by linearized systems. In Nuthi and Subbarao [10], a combination of LQR control and the adaptive augmentation’s robustness was implemented to handle parametric and model uncertainties. In Maiti et al. [11], two independent PID controllers were developed to control each of the two degrees of freedom of the helicopter, and a PSO-based parameter was designed to approximate the system’s uncertainties. In Chun et al. [12], a LQR controller incorporating the Q-learning algorithm was proposed to overcome uncertainties. This algorithm could search for the optimal control law by using the system’s states and input information instead of the system’s modeled knowledge to achieve optimal control. The above schemes have a certain effect on solving the system’s uncertainty; however, designing a linear LQR controller by ignoring the nonlinear part may lead to a controlled system that has poor control performance or even system instability in a real environment. In addition, by introducing complex optimization algorithms, it will cause high computational cost, which causes higher demands for hardware performance [13,14]. Therefore, it is imperative to design a simple and efficient nonlinear controller for a 2-DOF helicopter system.
As neural networks (NNs) have advanced, they have been commonly applied in nonlinear system control engineering to approximate unknown dynamics [15,16], uncertainties [17,18] and unknown external disturbances [19]. Radial basis NN (RBFNN) is a kind of NN with a simple structure and powerful nonlinear approximation ability such that it is often utilized to approximate the uncertain functions in complex systems [20,21,22]. Existing studies have indicated that the RBFNNs perform excellently for approximation of uncertainty in the 2-DOF helicopter systems [23,24,25,26,27]. For example, in Chen et al. [23], an adaptive NN controller with an external disturbance observer scheme was proposed to cope with the system’s uncertainty, nonlinear actuator faults and disturbances. In Ouyang et al. [24], to address the hybrid effects of system uncertainty and input deadzone, the technique of RBFNN was applied in the design of the controller. In addition, to ensure safe system operation, output constraints were taken into account in the control design. In Zhao et al. [25], a reinforcement learning control strategy was presented to enhance the robustness and stability of the 2-DOF helicopter system. In addition, the barrier Lyapunov function was proposed to accelerate the system states’ convergence. In Zhao et al. [26], considering the effects of system uncertainty and unknown backlash-like hysteresis, an adaptive NN controller was introduced to achieve stable tracking of the desired set point and trajectory. Although the aforementioned literature has made good use of NNs to resolve system’s uncertainty, the traditional adaptive law was employed for the updating of NN weights. In addition, the issue of a possible unknown control direction for the 2-DOF helicopter systems has not been considered in the current literature.
In the last few years, the unknown-control-direction issue was widely investigated for nonlinear systems [28,29,30]. The uncertainty in the direction of control is due to the sign of the coefficient of the system controller’s input being indeterminate [31]. To solve the issue of an unknown control direction in nonlinear systems, a kind of controller based on the Nussbaum gain function was proposed [32,33,34,35,36]. In Zhang and Li [33], for the issue of unknown control direction, the Nussbaum function was utilized to design a iterative learning controller for a nonlinear system with unknown time-varying parameters. In Liu and Tong [34], a novel control design was presented with the Nussbaum function technique for a class of nonlinear strict-feedback systems subject to unknown control direction. In addition, the barrier Lyapunov function was adopted to guarantee states within constraints. In Liang et al. [35], a more widely applicable Nussbaum function was introduced, which can be applied in particular to fractional-order interconnected systems. The above literature all strongly suggests that the unknown control direction issue extensively exists in nonlinear systems and the Nussbaum function can be a good solution. A similar issue also exists in the 2-DOF helicopter system. This is because the actuators of the 2-DOF helicopter system are two direct current (DC) motors, and the positive and negative poles of the corresponding electric voltage of the DC motor are generally unknown [37]. Therefore, it is very meaningful to study the controller design for a 2-DOF helicopter system subject to unknown control directions.
In addition, the fault-tolerant control (FTC) of actuator faults should not be neglected in the control design of helicopter systems as well [38,39,40]. Actuator faults during the control process can bring about insufficient drive forces, which will most probably ultimately lead to undesirable movements or even to the destruction of the system [41,42,43]. Thus, to avoid such undesirable results, the FTC must be considered in control design [44,45,46,47]. In Mokhtari et al. [48], the Kalman filter was first incorporated into a helicopter model to estimate faults. Then, based on the signals detected back, an active fault-tolerant controller was developed to compensate for the faults. In Peng et al. [49], the helicopter model was represented firstly using linearly varying parameters. Subsequently, an active fault-tolerant controller was designed based on a linear unknown input observer to reduce the effect of actuator faults. In Chen et al. [50], two auxiliary systems were designed in an adaptive FTC scheme for the unmanned autonomous helicopter system, which can better embody the dynamics of fault signals and solve actuator faults. These literature demonstrated the development of FTC in helicopter systems, but little research has been reported thus far on handling the effects of uncertainty, unknown control direction and actuator faults for the 2-DOF helicopter system, thus inspiring our study.
Based on the above analysis, we developed a novel adaptive neural FTC for a 2-DOF helicopter system subject to unknown control directions and actuator faults. The primary efforts of this study are summarized as follows:
(i) The system’s uncertainty is approximated by the RBFNN. In addition, compared with the conventional adaptive neural control shceme, a novel adaptive law for the RBFNN weights is proposed that can effectively reduce the excessive computational cost.
(ii) The Nussbaum function is adopted to solve the issue of unknown control direction, and the FTC technique is developed to compensate the effects of actuator faults.
(iii) Through theoretical analysis of Lyapunov theorem and numerical simulation verification, the control scheme proposed in this paper is proved to be valid and effective.
The structure of this study is as follows. In Section 2, the problem formulation and preliminaries are provided. In Section 3, we propose a novel adaptive NN fault-tolerant control scheme and present the stability analysis. Section 4 provides the simulation results. Finally, Section 5 concludes the article.
2. Problem Formulation and Preliminaries
2.1. System Description
In this study, the 2-DOF helicopter platform provided by Quanser was used, and its structure was simplified as shown in Figure 1. It can be clearly observed that the 2-DOF helicopter model consists mainly of an airframe and two DC motors. The front motor is used to simulate a propeller, which can generate a lift along the z-axis to control the pitch motion. The back motor is used to simulate a tail rotor, which can generate a thrust along the y-axis to control yaw motion. Therefore, by controlling different lift and thrust, the helicopter can complete flight, landing, hovering and other actions.
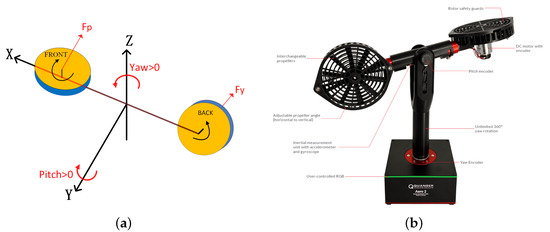
Figure 1.
Schematic diagram of a 2-DOF helicopter. 2-DOF helicopter platform structure (a) schematic diagram (b) physical picture.
Using Lagrange’s equation to analyze the dynamics of the 2-DOF helicopter model, we can obtain the following dynamics equations [27]:
where the detail system parameters are shown in Table 1.

Table 1.
System variables and description of parameters.
Define the states of system and , and the input of system . Then, based on the dynamics Equations (1) and (2), the state-space equations are given by
where
Taking into account the uncertainty of the system, the unknown control direction and actuator faults, the state space Equation (3) can be further given by as follows:
where is an unknown parameter and denotes the FTC input.
For convenience, , , and will be denoted by , , G and below, respectively.
Remark 1.
In [25], we proposed a reinforcement learning control strategy with state constraints for the 2-DOF helicopter system to achieve tracking control. The RBFNNs were used to approximate not only the cost function but also the system’s uncertainty, and the BLF function was used to accelerate the convergence rate of the system. In [27], we proposed a deterministic learning control strategy for the 2-DOF helicopter system to achieve the identification of unknown dynamics and backlash parameters. However, in this paper, our control objective was to solve the system uncertainty, unknown control direction and actuator fault issues of the 2-DOF helicopter system using RBFNNs, Nussbaum functions and adaptive fault-tolerant techniques.
2.2. Preliminaries
According to previous studies on RBFNN, for a continuously bounded unknown function, the RBFNN can approximate such an unknown function with arbitrary accuracy if the nodes are sufficient. This means that if : is continuous, the approximated function can be expressed as [51,52,53]
where denotes the input vector of RBFNN, with q is the input dimension; denotes the weight of RBFNN, with n denoting the number of nodes; stands for the Gaussian function of , which is expressed as
where and represent the center and the width of the RBFNN, respectively.
In addition, the unknown function using the optimal weight vector can be expressed as
with being the optimal weight vector and being the ideal approximation error.
Lemma 1
([54]). Define and as smooth functions. denotes a class of smooth Nussbaum-type function. If the following inequality holds:
where β is a reasonable constant and stands for a moment in time, then the boundedness of , and is guaranteed.
3. Control Design and Stability Analysis
In this section, based on the backstepping design procedure, we design a novel adaptive NN controller to solve the unknown control direction and actuator faults. Additionally, the controller is proved to make the system stable through rigorous Lyapunov analyses.
3.1. Control Design
Considering the actuator faults may occur, the input signal can be expressed as
where represents the actuator bias faults and we assume that is bounded.
Define the tracking error vectors and as follows:
where represents the reference tracking trajectory, and denotes a virtual controller, with being a positive definite diagonal matrix.
Taking the time derivatives of and yields
where is a bounded and continuous function that can be considered as the uncertainty of the system. Hence, we adopt the RBFNN to approximate the unknown function expressed as .
We design the following Lyapunov function as
The derivative of is given by
Subsequently, in order to eliminate , the following Lyapunov function candidate is considered:
Differentiating (14) yields
We designed an adaptive parameter to compensate for the effect of actuator bias faults. The ideal parameter can be expressed as
Remark 2.
Therefore, the desired control law is designed as follows:
where is the designed Nussbaum function, and is the auxiliary controller, which can be expressed as follows:
given and . Additionally, is the approximation error of . is a designed control gain satisfying . In addition, are the input vectors of the RBFNN and is a designed constant.
The adaptive law of is constructed as
where is an adaptive gain constant and is a small constant.
The adaptive law of is defined as
where is a gain diagonal matrix satisfying and is a small constant.
Remark 3.
Compared with the conventional adaptive law , the proposed adaptive law (19) can simplify the design and computational cost of the controller. This is because the weight and its updating law are usually multidimensional vectors, and is an adaptive parameter.
The adaptive law of is designed as
Stability Analysis
The Lyapunov function for stability analysis is chosen as follows:
Combining (15), (18), (19), (20) and (21), the time derivative of V can be derived as
where I denotes the identity matrix.
Subsequently, using the Young’s inequality, we can obtain the following inequality:
Theorem 1.
Consider the helicopter system (4) subject to uncertainty, unknown control direction and actuator faults. The RBFNN is adopted to approximate the system’s uncertainty, a Nussbaum-type function is adopted to handle the issue of unknown control direction and an adaptive parameter is used to handle actuator faults. With the control law (17) and appropriate choice of control parameters, all closed-loop system signals are semi-globally uniformly ultimately bounded if they are bounded initially [55,56]. In other words, the system is eventually stable and the tracking errors are convergent. In addition, the following conclusions hold:
where , ρ and Υ are both positive constants.
Proof.
Multiplying (25) by yields
Then, by integrating (28), we have
According to Lemma 1, we can conclude that , and are bounded. Hence, we can further derive
From the above derivation (28)–(30), it can be found that the signals of , and are bounded. Moreover, based on the control law (17), the control signal u is bounded. Subsequently, it can be obtained from (30) that the signals, , , and , can be made to converge to a small region near zero by adjusting the parameters , , , and to ensure . □
4. Simulations
In this section, in order to verify the effectiveness of the proposed control method, numerical simulations were performed and the expected simulation results were obtained. First, the model of the controlled system for this simulation was described in (4), and the detailed values of the model parameters are presented in Table 2.

Table 2.
System parameters.
Initially, the states of system were set as and . The adaptive NN parameter was set as , and the adaptive parameter of Nussbaum function was set as . The adaptive faults parameter was selected as . In addition, the reference trajectory was chosen as .
For the selection of other parameters, to achieve fast tracking of the reference trajectory, the control gain in the simulation was selected as and . In addition, for further reducing the tracking errors, the parameters and were chosen to minimize the value of . As for the RBFNN, the width and the center of the Gaussian function were set as and 1.2], respectively. In addition, the adaptive gain was selected for the RBFNN and was selected for the adaptive faults parameter . The actuator bias faults was designed as
In order to compare it with the proposed scheme, we designed an LQR controller after linearizing the 2-DOF helicopter system. The simulation results are shown in Figure 2a–e. From Figure 2a,b, owing to ignoring the system’s uncertainty in the control design, the yaw and pitch angles cannot track the reference trajectories with satisfactory tracking errors. In addition, when the actuator faults occur (the time is 5 s), the input voltage signals change significantly, as shown in Figure 2e, and the tracking errors become larger. Therefore, we can conclude that the LQR controller cannot solve the system’s uncertainty and actuator faults of the 2-DOF helicopter system.
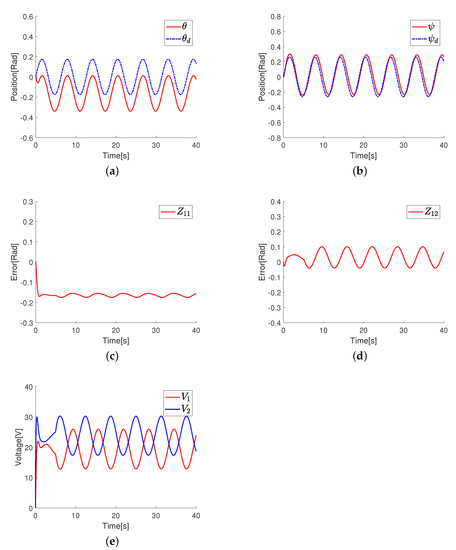
Figure 2.
The control performance under the LQR control. (a) Tracking trajectory diagram of . (b) Tracking trajectory diagram of . (c) Tracking error diagram of . (d) Tracking error diagram of . (e) The input signals of the 2-DOF helicopter system.
The simulation results of the proposed control scheme are displayed in Figure 3 and Figure 4. As can be seen in Figure 3a,b, the pitch angle and the yaw angle successfully tracked the intended trajectories and with few tracking errors. The corresponding error variations can be observed in Figure 3c,d, from which we can see that the tracking errors varied periodically and remained in a small region around zero. Therefore, it is satisfactory in terms of tracking performance. Subsequently, Figure 3e illustrates the input voltage for the 2-DOF helicopter. The input signals rose rapidly at the beginning and stabilized quickly without overlarge voltage shocks. As for the adaptive parameter of the RBFNN, Figure 4a displays its changing trend. It can be seen that the value of rises rapidly at first and then converges to a certain value. In addition, the changes in the adaptive fault tolerance parameter are displayed in Figure 4b. In particular, we can see from the input signals diagram that actuator faults were imposed at 5s and the actuator faults were rapidly compensated.
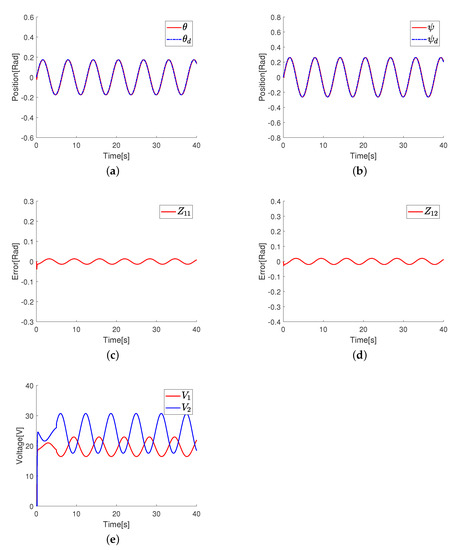
Figure 3.
The control performance under the proposed control. (a) Tracking trajectory diagram of . (b) Tracking trajectory diagram of . (c) Tracking error diagram of . (d) Tracking error diagram of . (e) The input signals of the 2-DOF helicopter system.
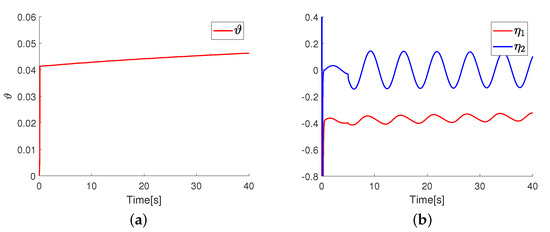
Figure 4.
The variation tendencies of the parameters and . (a) The value of the parameter . (b) The value of the parameter .
By combining above simulation results, we can find that the proposed scheme has a better control performance until 5 s. This suggests that the proposed control strategy can approximate the system’s uncertainty efficiently. Subsequently, when the actuator faults occurr, the tracking errors under the LQR control become larger, while the tracking errors under the proposed strategy remain almost unchanged. Hence, we can conclude that the proposed control scheme effectively solves issue of the uncertainty, unknown direction control and actuator faults for the 2-DOF helicopter system, and achieves quite excellent control performance.
5. Conclusions
This study presented an adaptive NN control scheme for the 2-DOF helicopter system subject to system’s uncertainty, unknown control directions and actuator faults. To approximate the system’s uncertainty, we proposed a novel weight-adaptive law, RBFNN, to approximate the unknown dynamics of the system with low calculation costs. Considering the unknown control direction issue, the Nussbaum function technique was proposed in the control design in order to eliminate the influence of uncertain control coefficients. In addition, we designed the adaptive parameter to compensate for the actuator faults. Finally, the controlled system was demonstrated to be stable under the proposed control scheme, and the simulation results further illustrated that the proposed control scheme was feasible and effective. The limitation of the proposed scheme is that the selection of neural network nodes depends mainly on experience. In addition, there are more control gains to be tuned. In addition, for severe actuator failure, the proposed scheme may not fully compensate for it. Hence, future work will focus on dynamical model identification for the 2-degree-of-freedom helicopter system and the wider application of FTC.
Author Contributions
Conceptualization, B.W. and G.T.; methodology, J.W.; software, J.W.; validation, G.T. and Z.Z.; formal analysis, B.W.; investigation, B.W.; resources, B.W. and W.H.; data curation, W.H.; writing—original draft preparation, B.W. and W.H.; supervision, B.W. and Z.Z.; project administration, G.T.; funding acquisition, B.W. and G.T. All authors have read and agreed to the published version of the manuscript.
Funding
This work was supported by the Scientific Research Projects of Guangzhou Education Bureau under grant 202032793.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
Not applicable.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Jiang, B.; Li, B.; Zhou, W.; Lo, L.Y.; Chen, C.K.; Wen, C.Y. Neural Network Based Model Predictive Control for a Quadrotor UAV. Aerospace 2022, 9, 460. [Google Scholar] [CrossRef]
- Reyhanoglu, M.; Jafari, M.; Rehan, M. Simple Learning-Based Robust Trajectory Tracking Control of a 2-DOF Helicopter System. Electronics 2022, 11, 2075. [Google Scholar] [CrossRef]
- Mu, C.; Zhang, Y. Learning-Based Robust Tracking Control of Quadrotor with Time-Varying and Coupling Uncertainties. IEEE Trans. Neural Netw. Learn. Syst. 2020, 31, 259–273. [Google Scholar] [CrossRef] [PubMed]
- Hernandez-Gonzalez, M.; Alanis, A.Y.; Hernandez-Vargas, E.A. Decentralized discrete-time neural control for a Quanser 2-DOF helicopter. Appl. Soft Comput. 2012, 12, 2462–2469. [Google Scholar] [CrossRef]
- Kim, S.K.; Ahn, C.K. Performance-Boosting Attitude Control for 2-DOF Helicopter Applications via Surface Stabilization Approach. IEEE Trans. Ind. Electron. 2022, 69, 7234–7243. [Google Scholar] [CrossRef]
- Liu, Z.; Liang, J.; Zhao, Z.; Efe, M.O.; Hong, K.S. Adaptive Fault-Tolerant Control of a Probe-and-Drogue Refueling Hose Under Varying Length and Constrained Output. IEEE Trans. Control Syst. Technol. 2022, 30, 869–876. [Google Scholar] [CrossRef]
- Kaletka, J.; Kurscheid, H.; Butter, U. FHS, the new research helicopter: Ready for service. Aerosp. Sci. Technol. 2005, 9, 456–467. [Google Scholar] [CrossRef]
- Verginis, C.K.; Bechlioulis, C.P.; Soldatos, A.G.; Tsipianitis, D. Robust Trajectory Tracking Control for Uncertain 3-DOF Helicopters With Prescribed Performance. IEEE/ASME Trans. Mechatron. 2022, 27, 3559–3569. [Google Scholar] [CrossRef]
- Subramanian, R.G.; Elumalai, V.K. Robust MRAC augmented baseline LQR for tracking control of 2 DoF helicopter. Robot. Auton. Syst. 2016, 86, 70–77. [Google Scholar] [CrossRef]
- Nuthi, P.; Subbarao, K. Experimental Verification of Linear and Adaptive Control Techniques for a Two Degrees-of-Freedom Helicopter. J. Dyn. Syst. Meas. Control 2016, 137, 064501. [Google Scholar] [CrossRef]
- Maiti, R.; Sharma, K.D.; Sarkar, G. PSO based parameter estimation and PID controller tuning for 2-DOF nonlinear twin rotor MIMO system. Int. J. Autom. Control 2018, 12, 582. [Google Scholar] [CrossRef]
- Chun, T.Y.; Park, J.B.; Choi, Y.H. Reinforcement Q-learning based on Multirate Generalized Policy Iteration and Its Application to a 2-DOF Helicopter. Int. J. Control. Autom. Syst. 2018, 16, 377–386. [Google Scholar] [CrossRef]
- Delaram, J.; Houshamand, M.; Ashtiani, F.; Fatahi Valilai, O. A utility-based matching mechanism for stable and optimal resource allocation in cloud manufacturing platforms using deferred acceptance algorithm. J. Manuf. Syst. 2021, 60, 569–584. [Google Scholar] [CrossRef]
- Delaram, J.; Houshamand, M.; Ashtiani, F.; Valilai, O.F. Development of public cloud manufacturing markets: A mechanism design approach. Int. J. Syst. Sci. Oper. Logist. 2022, 1–27. [Google Scholar] [CrossRef]
- Zhang, F.; Wang, C. Deterministic learning from neural control for uncertain nonlinear pure-feedback systems by output feedback. Int. J. Robust Nonlinear Control 2020, 30, 2701–2718. [Google Scholar] [CrossRef]
- Mohamed, I.S.; Rovetta, S.; Do, T.D.; Dragicević, T.; Diab, A.A.Z. A Neural-Network-Based Model Predictive Control of Three-Phase Inverter With an Output LC Filter. IEEE Access 2019, 7, 124737–124749. [Google Scholar] [CrossRef]
- He, W.; Dong, Y.; Sun, C. Adaptive Neural Impedance Control of a Robotic Manipulator With Input Saturation. IEEE Trans. Syst. Man Cybern. Syst. 2016, 46, 334–344. [Google Scholar] [CrossRef]
- Liu, Y.J.; Zhao, W.; Liu, L.; Li, D.; Tong, S.; Chen, C.L.P. Adaptive Neural Network Control for a Class of Nonlinear Systems With Function Constraints on States. IEEE Trans. Neural Netw. Learn. Syst. 2021, 1–10. [Google Scholar] [CrossRef]
- Chen, L.; Cui, R.; Yang, C.; Yan, W. Adaptive Neural Network Control of Underactuated Surface Vessels With Guaranteed Transient Performance: Theory and Experimental Results. IEEE Trans. Ind. Electron. 2020, 67, 4024–4035. [Google Scholar] [CrossRef]
- Zhao, Z.; He, W.; Ge, S.S. Adaptive Neural Network Control of a Fully Actuated Marine Surface Vessel With Multiple Output Constraints. IEEE Trans. Control Syst. Technol. 2014, 22, 1536–1543. [Google Scholar]
- Zhou, Q.; Zhao, S.; Li, H.; Lu, R.; Wu, C. Adaptive Neural Network Tracking Control for Robotic Manipulators With Dead Zone. IEEE Trans. Neural Netw. Learn. Syst. 2019, 30, 3611–3620. [Google Scholar] [CrossRef] [PubMed]
- Chen, Z.; Huang, F.; Sun, W.; Gu, J.; Yao, B. RBF-Neural-Network-Based Adaptive Robust Control for Nonlinear Bilateral Teleoperation Manipulators With Uncertainty and Time Delay. IEEE/ASME Trans. Mechatron. 2020, 25, 906–918. [Google Scholar] [CrossRef]
- Chen, M.; Shi, P.; Lim, C.C. Adaptive Neural Fault-Tolerant Control of a 3-DOF Model Helicopter System. IEEE Trans. Syst. Man Cybern. Syst. 2016, 46, 260–270. [Google Scholar] [CrossRef]
- Ouyang, Y.; Dong, L.; Xue, L.; Sun, C. Adaptive control based on neural networks for an uncertain 2-DOF helicopter system with input deadzone and output constraints. IEEE/CAA J. Autom. Sin. 2019, 6, 807–815. [Google Scholar] [CrossRef]
- Zhao, Z.; He, W.; Mu, C.; Zou, T.; Hong, K.S.; Li, H.X. Reinforcement Learning Control for a 2-DOF Helicopter With State Constraints: Theory and Experiments. IEEE Trans. Autom. Sci. Eng. 2022, 1–11. [Google Scholar] [CrossRef]
- Zhao, Z.; Zhang, J.; Liu, Z.; Mu, C.; Hong, K.S. Adaptive Neural Network Control of an Uncertain 2-DOF Helicopter With Unknown Backlash-Like Hysteresis and Output Constraints. IEEE Trans. Neural Netw. Learn. Syst. 2022, 1–10. https://ieeexplore.ieee.org/abstract/document/9760116. [CrossRef]
- Zhao, Z.; He, W.; Zhang, F.; Wang, C.; Hong, K.S. Deterministic Learning from Adaptive Neural Network Control for a 2-DOF Helicopter System With Unknown Backlash and Model Uncertainty. IEEE Trans. Ind. Electron. 2022, 1–10. [Google Scholar] [CrossRef]
- Oliveira, T.R.; Peixoto, A.J.; Hsu, L. Sliding Mode Control of Uncertain Multivariable Nonlinear Systems With Unknown Control Direction via Switching and Monitoring Function. IEEE Trans. Autom. Control 2010, 55, 1028–1034. [Google Scholar] [CrossRef]
- Wang, C.; Wen, C.; Lin, Y. Adaptive Actuator Failure Compensation for a Class of Nonlinear Systems With Unknown Control Direction. IEEE Trans. Autom. Control 2017, 62, 385–392. [Google Scholar] [CrossRef]
- Choi, Y.H.; Yoo, S.J. Tracking Control Strategy Using Filter-Based Approximation for the Unknown Control Direction Problem of Uncertain Pure-Feedback Nonlinear Systems. Mathematics 2020, 8, 1341. [Google Scholar] [CrossRef]
- Chen, Z. Nussbaum functions in adaptive control with time-varying unknown control coefficients. Automatica 2019, 102, 72–79. [Google Scholar] [CrossRef]
- Chen, W.; Li, X.; Ren, W.; Wen, C. Adaptive Consensus of Multi-Agent Systems with Unknown Identical Control Directions Based on a Novel Nussbaum-Type Function. IEEE Trans. Autom. Control 2014, 59, 1887–1892. [Google Scholar] [CrossRef]
- Zhang, C.L.; Li, J.M. Adaptive iterative learning control of non-uniform trajectory tracking for strict feedback nonlinear time-varying systems with unknown control direction. Appl. Math. Model. 2015, 39, 2942–2950. [Google Scholar] [CrossRef]
- Liu, Y.J.; Tong, S. Barrier Lyapunov functions for Nussbaum gain adaptive control of full state constrained nonlinear systems. Automatica 2017, 76, 143–152. [Google Scholar] [CrossRef]
- Liang, B.; Zheng, S.; Ahn, C.K.; Liu, F. Adaptive Fuzzy Control for Fractional-Order Interconnected Systems With Unknown Control Directions. IEEE Trans. Fuzzy Syst. 2022, 30, 75–87. [Google Scholar] [CrossRef]
- Lv, M.; Yu, W.; Cao, J.; Baldi, S. Consensus in High-Power Multiagent Systems With Mixed Unknown Control Directions via Hybrid Nussbaum-Based Control. IEEE Trans. Cybern. 2022, 52, 5184–5196. [Google Scholar] [CrossRef] [PubMed]
- Xu, Y.; Wang, C.; Wang, G.; Cai, X.; Xu, L.; Jing, C. Connectivity-preserving-based Distributed Synchronized Tracking of Networked Uncertain Underactuated Surface Vessels with Actuator Failures and Unknown Control Directions. Int. J. Control. Autom. Syst. 2021, 19, 3996–4009. [Google Scholar] [CrossRef]
- Shen, Q.; Jiang, B.; Cocquempot, V. Fault-Tolerant Control for T–S Fuzzy Systems With Application to Near-Space Hypersonic Vehicle with Actuator Faults. IEEE Trans. Fuzzy Syst. 2012, 20, 652–665. [Google Scholar] [CrossRef]
- Jin, X.; Lü, S.; Qin, J.; Zheng, W.X. Auxiliary Constrained Control of a Class of Fault-Tolerant Systems. IEEE Trans. Syst. Man Cybern. Syst. 2021, 51, 2272–2283. [Google Scholar] [CrossRef]
- Zhao, Z.; Liu, Z.; He, W.; Hong, K.S.; Li, H.X. Boundary adaptive fault-tolerant control for a flexible Timoshenko arm with backlash-like hysteresis. Automatica 2021, 130, 109690. [Google Scholar] [CrossRef]
- Guan, X.; Fan, F.; Zhu, Y.; Song, W.; Guirao, J.; Gao, W. Application of RBF neural network optimized globally by genetic algorithm in intelligent color matching of wood dyeing. J. Intell. Fuzzy Syst. 2017, 33, 2895–2901. [Google Scholar] [CrossRef]
- Ma, L.; Xu, N.; Zhao, X.; Zong, G.; Huo, X. Small-Gain Technique-Based Adaptive Neural Output-Feedback Fault-Tolerant Control of Switched Nonlinear Systems With Unmodeled Dynamics. IEEE Trans. Syst. Man Cybern. Syst. 2021, 51, 7051–7062. [Google Scholar] [CrossRef]
- Zhao, Z.; Liu, Y.; Zou, T.; Hong, K.S.; Li, H.X. Robust Adaptive Fault-Tolerant Control for a Riser-Vessel System With Input Hysteresis and Time-Varying Output Constraints. IEEE Trans. Cybern. 2022, 1–12. [Google Scholar] [CrossRef] [PubMed]
- Yin, S.; Wang, G.; Gao, H. Data-Driven Process Monitoring Based on Modified Orthogonal Projections to Latent Structures. IEEE Trans. Control Syst. Technol. 2016, 24, 1480–1487. [Google Scholar] [CrossRef]
- Liu, Z.; Shi, J.; Zhao, X.; Zhao, Z.; Li, H.X. Adaptive Fuzzy Event-Triggered Control of Aerial Refueling Hose System with Actuator Failures. IEEE Trans. Fuzzy Syst. 2022, 30, 2981–2992. [Google Scholar] [CrossRef]
- Mu, C.; Zhang, Y.; Sun, C. Data-Based Feedback Relearning Control for Uncertain Nonlinear Systems with Actuator Faults. IEEE Trans. Cybern. 2022, 1–14. [Google Scholar] [CrossRef]
- Wang, T.; Lu, M.; Zhu, X.; Patton, R.J. Aggressive Maneuver Oriented Robust Actuator Fault Estimation of a 3-DOF Helicopter Prototype Considering Measurement Noises. IEEE/ASME Trans. Mechatron. 2022, 27, 1672–1682. [Google Scholar] [CrossRef]
- Mokhtari, S.; Abbaspour, A.; Kang, K.Y.; Sargolzaei, A. Neural Network-Based Active Fault-Tolerant Control Design for Unmanned Helicopter with Additive Faults. Remote Sens. 2021, 13, 2396. [Google Scholar] [CrossRef]
- Peng, H.; Wei, L.; Zhu, X.; Xu, W.; Zhang, S. Aggressive maneuver oriented integrated fault-tolerant control of a 3-DOF helicopter with experimental validation. Aerosp. Sci. Technol. 2022, 120, 107265. [Google Scholar] [CrossRef]
- Chen, M.; Yan, K.; Wu, Q. Multiapproximator-Based Fault-Tolerant Tracking Control for Unmanned Autonomous Helicopter With Input Saturation. IEEE Trans. Syst. Man Cybern. Syst. 2022, 52, 5710–5722. [Google Scholar] [CrossRef]
- Zhang, F.; Wang, C.; Yang, F. Pattern-based NN control for uncertain pure-feedback nonlinear systems. J. Frankl. Inst. 2019, 356, 2530–2558. [Google Scholar] [CrossRef]
- Zhao, Z.; Ren, Y.; Mu, C.; Zou, T.; Hong, K.S. Adaptive Neural-Network-Based Fault-Tolerant Control for a Flexible String With Composite Disturbance Observer and Input Constraints. IEEE Trans. Cybern. 2021, 1–11. [Google Scholar] [CrossRef] [PubMed]
- Zhang, F.; Wu, W.; Hu, J.; Wang, C. Deterministic learning from neural control for a class of sampled-data nonlinear systems. Inf. Sci. 2022, 595, 159–178. [Google Scholar] [CrossRef]
- Ye, X.; Jiang, J. Adaptive nonlinear design without a priori knowledge of control directions. IEEE Trans. Autom. Control 1998, 43, 1617–1621. [Google Scholar]
- Chen, H.; Haus, B.; Mercorelli, P. Extension of SEIR Compartmental Models for Constructive Lyapunov Control of COVID-19 and Analysis in Terms of Practical Stability. Mathematics 2021, 9, 2076. [Google Scholar] [CrossRef]
- Mu, C.; Wang, K.; Ni, Z. Adaptive Learning and Sampled-Control for Nonlinear Game Systems Using Dynamic Event-Triggering Strategy. IEEE Trans. Neural Netw. Learn. Syst. 2022, 33, 4437–4450. [Google Scholar] [CrossRef]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).