A Differential Privacy Budget Allocation Algorithm Based on Out-of-Bag Estimation in Random Forest
Abstract
1. Introduction
- 1.
- We propose a differential privacy budget allocation algorithm based on out-of-bag estimation in random forest.
- 2.
- We improve the algorithm for differential privacy out-of-bag estimation to obtain more accurate decision tree weights in out-of-bag forests. We introduce decision tree weights when using the VIM variable importance measure to obtain a more accurate set of feature weights and use statistical methods for classification.
- 3.
- We creatively give computational methods to allocate the overall privacy protection budget to each tree in the random forest and to each layer of each tree to achieve a more targeted privacy budget allocation.
- 4.
- We conduct a series of experiments on Adult and Mushroom datasets to demonstrate the advantages of the algorithm in this paper.
2. Differential Privacy Background Knowledge
- 1.
- Laplace mechanism [29,30,31]. This mechanism is implemented by adding noise satisfying the Laplace distribution to the output result. Given any function , if the meets Formula (3), it means that it satisfies ϵ-differential privacy.where , beying the Laplace distribution with scale parameter .
- 2.
- Exponential mechanism [30,31]. Let the input of the randomized algorithm M be a dataset D and the output be an entity object , is the availability function, is the sensitivity of the function . If algorithm M selects and outputs r from with probability proportional to , then algorithm M provides ϵ-differential privacy.
- 1.
- Sequential composition [32]. Assuming that in a set of mechanisms provide -differential privacy protection respectively, for a same data set D, algorithms has -differential privacy.
- 2.
- Parallel composition [32]. Assuming that in a set of mechanisms provide -differential privacy protection respectively, for the disjoint dataset D, algorithms constitute the combination with -differential privacy.
3. Proposed Method
3.1. Solving Decision Tree Weights
3.2. Feature Weight Calculation and Feature Selection
3.2.1. Feature Weight Calculation
3.2.2. Feature Selection
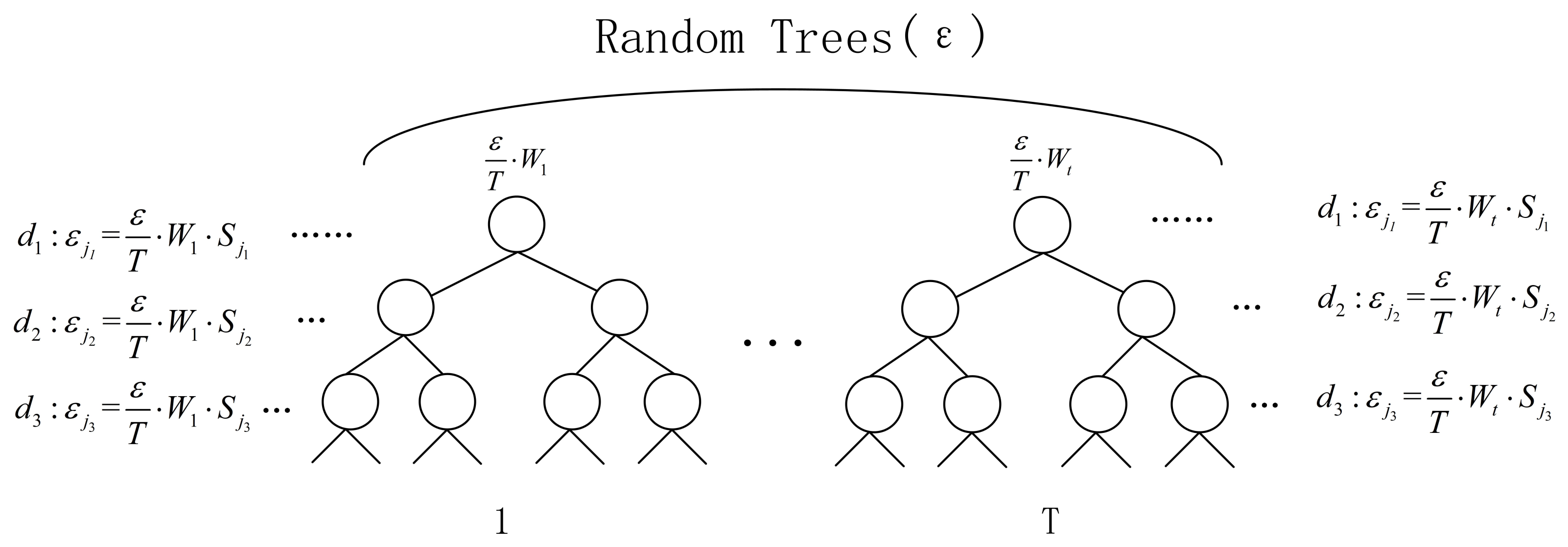
3.3. Method for Allocating Privacy Protection Budgets Based on Weights
3.4. Pruning Based on the Divided Set of Attributes
3.5. Algorithm Flow
3.6. Description
| Algorithm 1 Extract Out-of-Bag Data Algorithm |
Input: Training set D, feature set , number of decision trees t, maximum depth of the decision trees d, number of randomly selected features at splitting a. Output: Random forest , Out-of-bag datasets . Stopping condition: All samples on a decision tree node are consistently classified, or the maximum depth of the decision tree is reached d, or the number of features set features less than a. Step 1. Take out m samples from the training set D with put-back as , and randomly select n features from J. Step 2. Calculate the Gini coefficient of each feature, and select the best splitting feature as the splitting feature. Step 3. According to the different values of feature , the samples on the node are divided into different child nodes, and a decision tree is generated. Step 4. Repeat steps 1–3 t times to get t decision trees. Step 5. Put the data in the training set D that was not used to build the decision tree into . Step 6. Get random forest , out-of-bag datasets . |
| Algorithm 2 Solving Feature Weights and Selecting Algorithms Using Out-of-Bag Estimation |
Input: Out-of-bag datasets , random forest , privacy protection budget , feature set . Output: Selected feature weight set , selected feature set , pruned feature set (PFS), best feature set (BFS). Stopping condition: All features are calculated and screened. Step 1. For decision tree t, select data containing tree features from out-of-bag data set , test and count. Step 2. Add Laplacian noise to all categorical counts for each tree in a random forests, the size of the privacy protection budget for each tree is . Step 3. Get the differential privacy out-of-package estimation using the Formula (4). Step 4. Calculate the decision tree weight using the Formula (5). Step 5. Repeat steps 1–4 to calculate the weight of each tree in the random forests in turn, and get the weight set of the tree. Step 7. Calculate the feature weight of this feature in the whole random forest using Formula (9). Step 8. Repeat steps 6–7 to obtain the feature weight set R of all features. Step 9. If feature weight set R satisfies Formula (11), put corresponding feature into the removable feature set RFS; if it satisfies Formula (12), put corresponding feature into the pruned feature set (PFS); the remaining features are best feature set (BFS). Step 10. Delete the features and feature weights in the removable feature set RFS in turn from the initial feature set and feature weight set R. Step 11. Get the selected feature weight set , selected feature set , pruned feature set (PFS), best feature set (BFS). |
| Algorithm 3 Differential Privacy Budget Algorithm Based on Tree Weight and Feature Weight |
Input: Training set D, selected feature set , selected feature weight set , number of decision trees T, maximum depth of the decision trees d, number of features b randomly selected when splitting, privacy protection budget , pruned feature set (PFS), best feature set (BFS). Output: Random forests satisfying -differential privacy protection. Stopping condition: All samples on a decision tree node are consistently classified, or the maximum depth of the decision tree is reached d, or the feature number of the filtered feature set is less than b, or the privacy protection budget is exhausted. Step 1. For decision tree t, b features are randomly selected, the feature set is , and the corresponding feature weight set calculated by Formula (10) is . Step 2. If the feature set has features belonging to the pruned feature set (PFS), the corresponding feature weight set removes these feature weights to obtain the feature set . if the feature set belongs to the best feature set (BFS), the corresponding feature weight set does not change. Step 3. For the feature set , the weight of the decision tree is obtained according to Formula (13). Step 4. The privacy budget of the tree is obtained from the weights of the tree as . Step 5. In the feature weight set , the feature weight ratio of the feature is calculated according to Formula (14). Step 6. In the tree t, according to the size of the feature weight set , the features are sequentially selected from the corresponding feature set as the best splitting feature. Step 7. The privacy protection budget allocated by the optimal splitting feature is Step 8. Repeat T times to calculate the privacy protection budget required for each feature split on each tree. Step 9. When constructing the tree to select features, if the best split feature is a continuous feature, an exponential mechanism is invoked to select the best point for splitting: Step 10. If stopping condition is met, the creation of node is stopped, and the node is set as a leaf node. Step 11. Noise is added to the count value of the leaf nodes of each tree, and the classification with the most samples is selected as the label of the leaf node. |
4. Experimental Results and Analysis
4.1. Privacy Analysis
4.2. Experimental Design
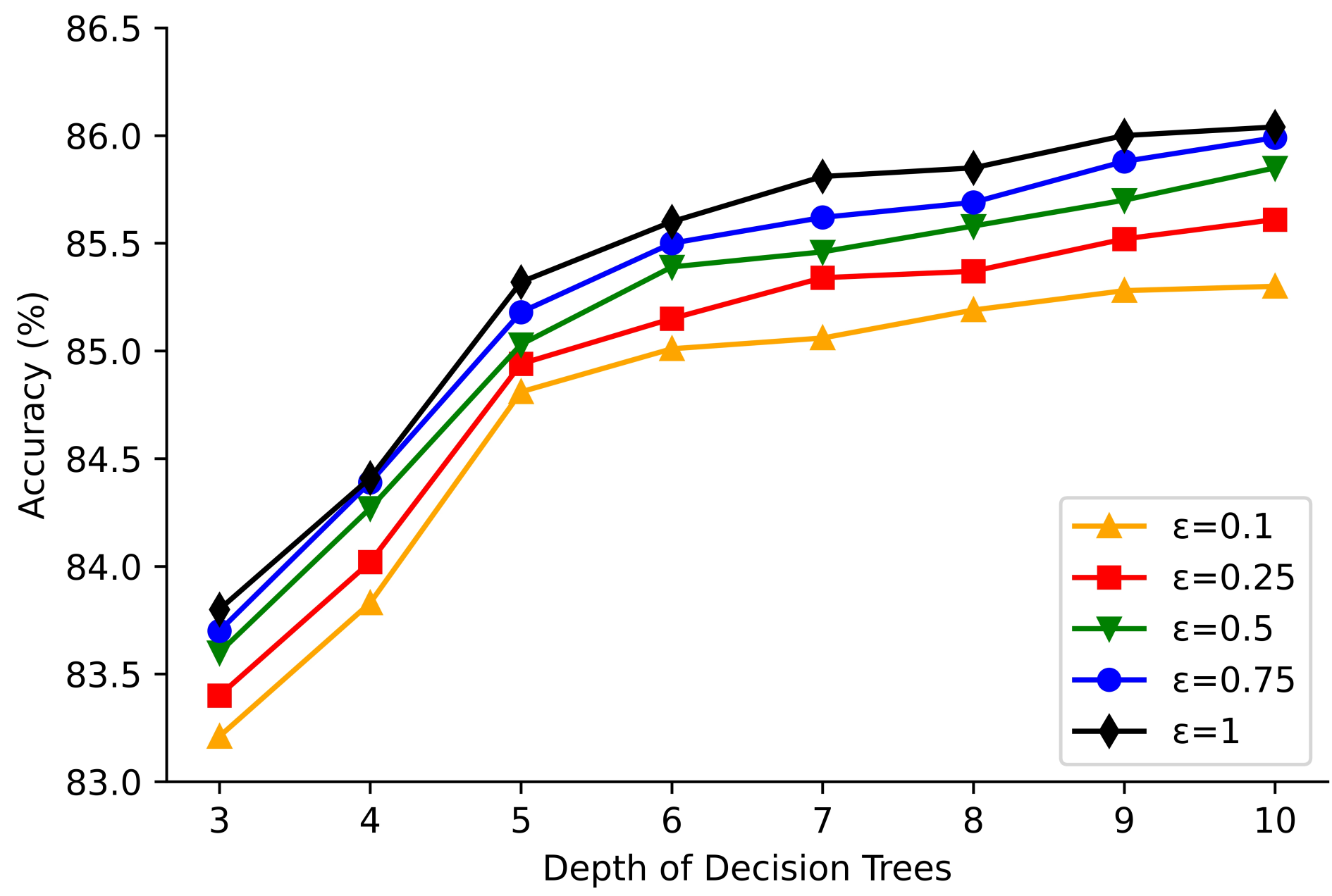
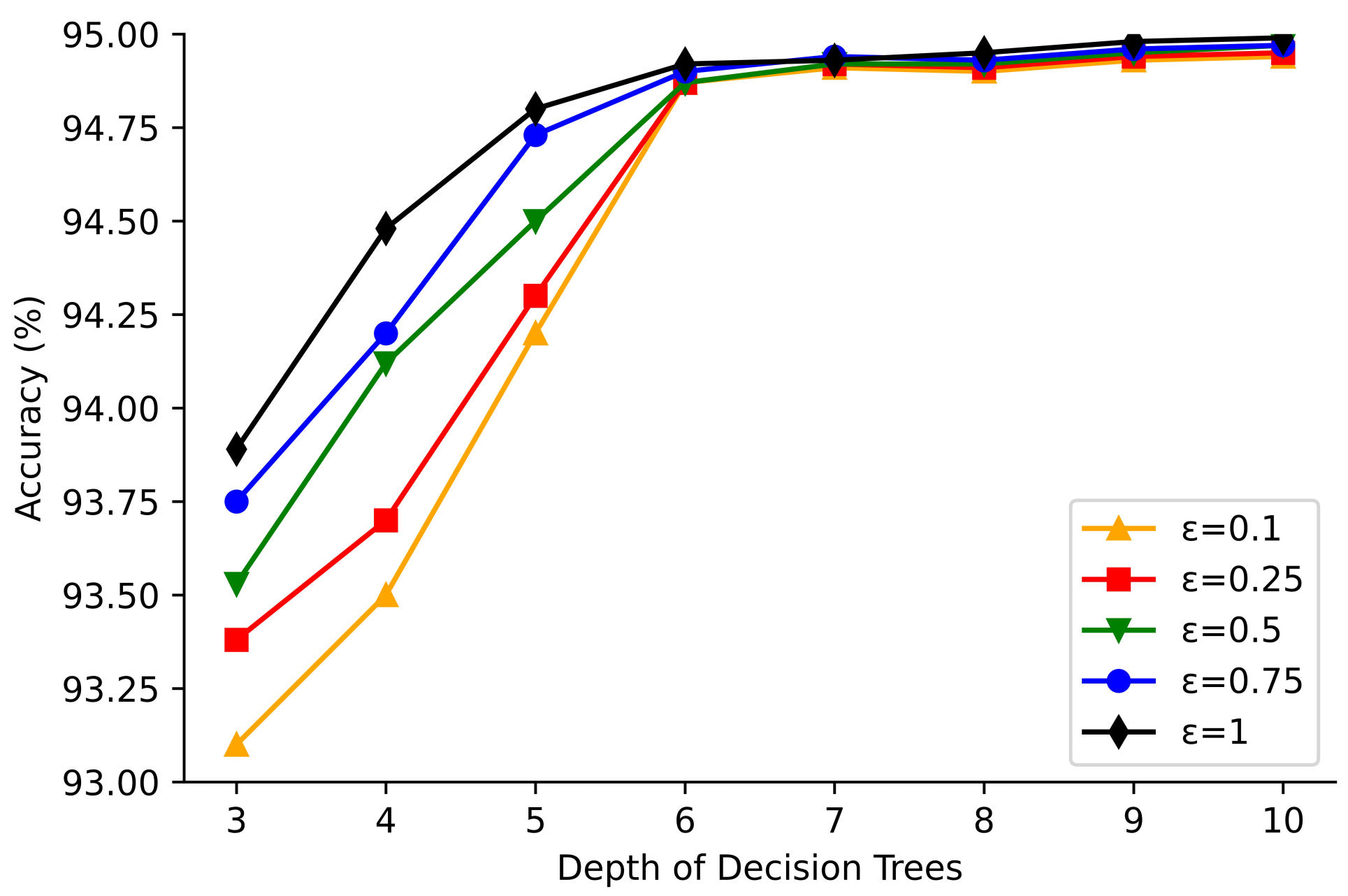
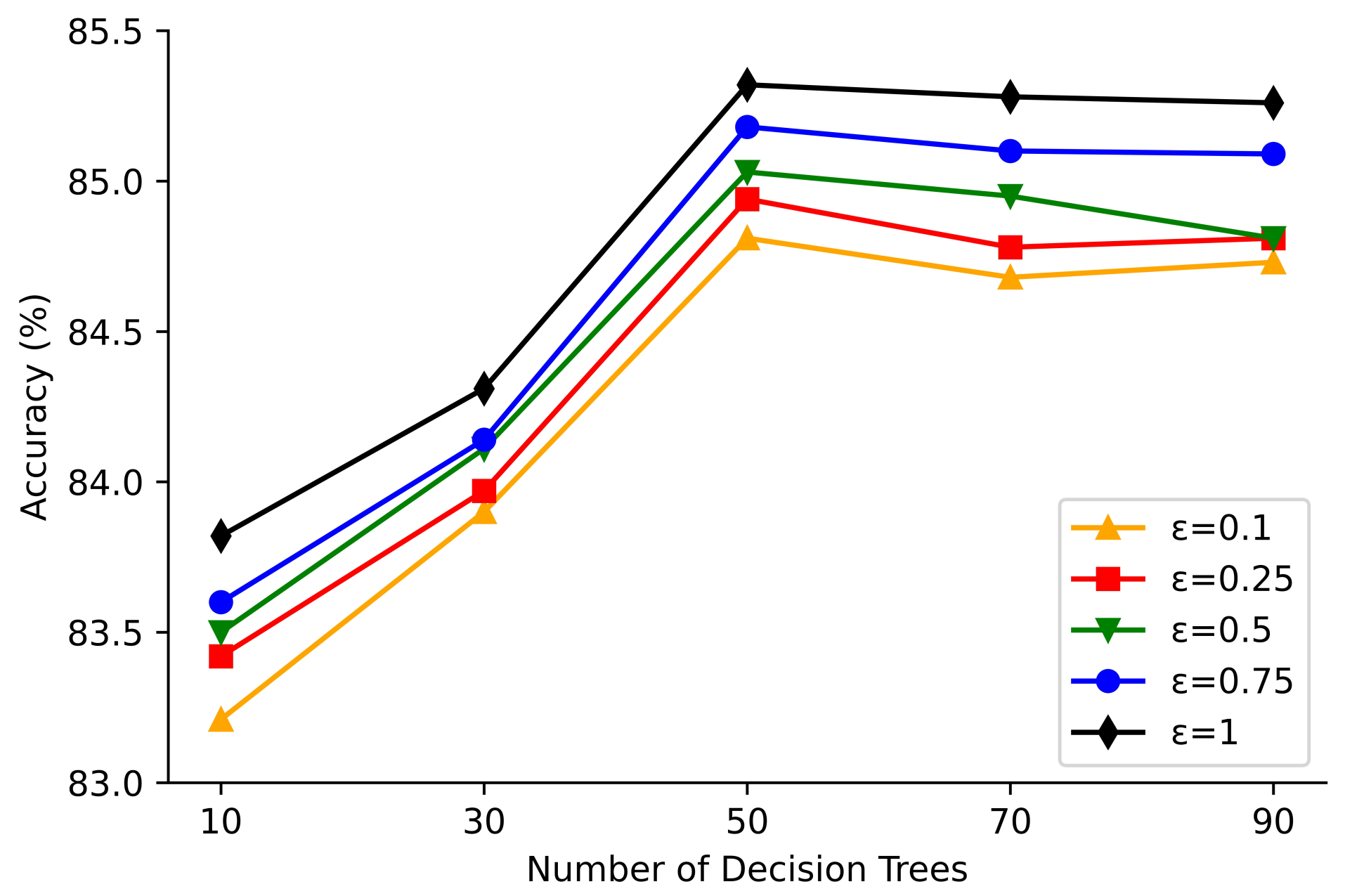
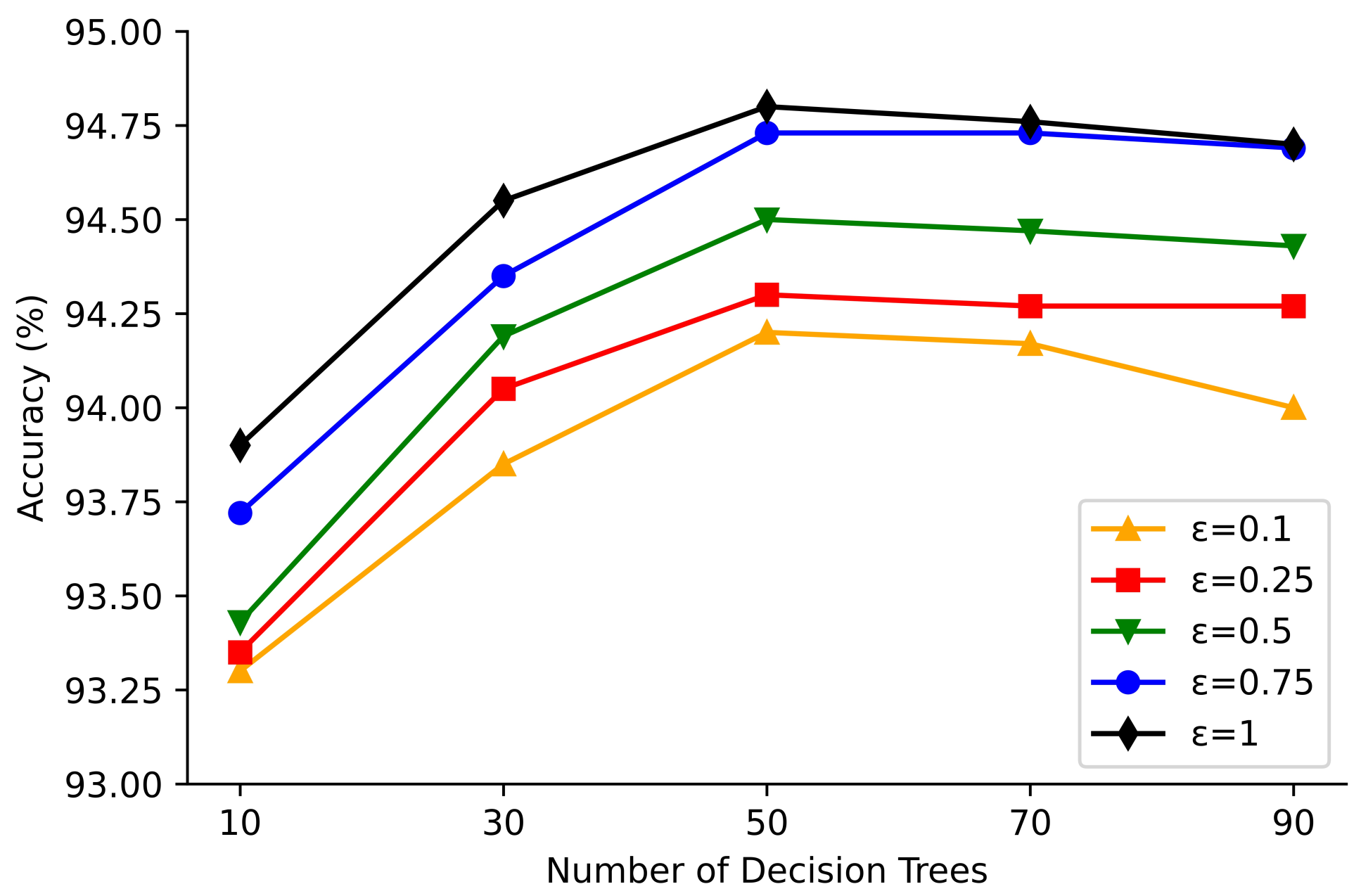
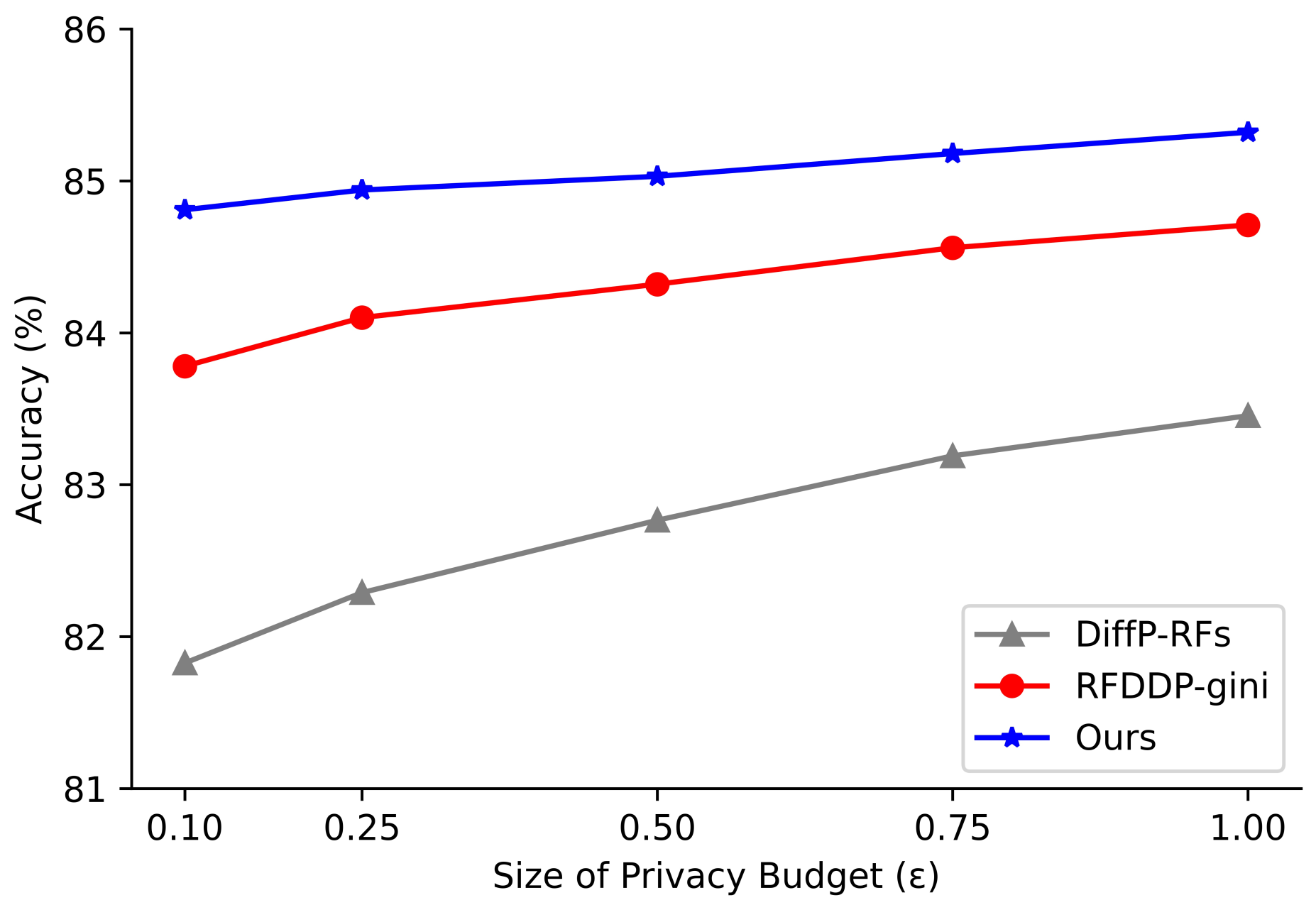
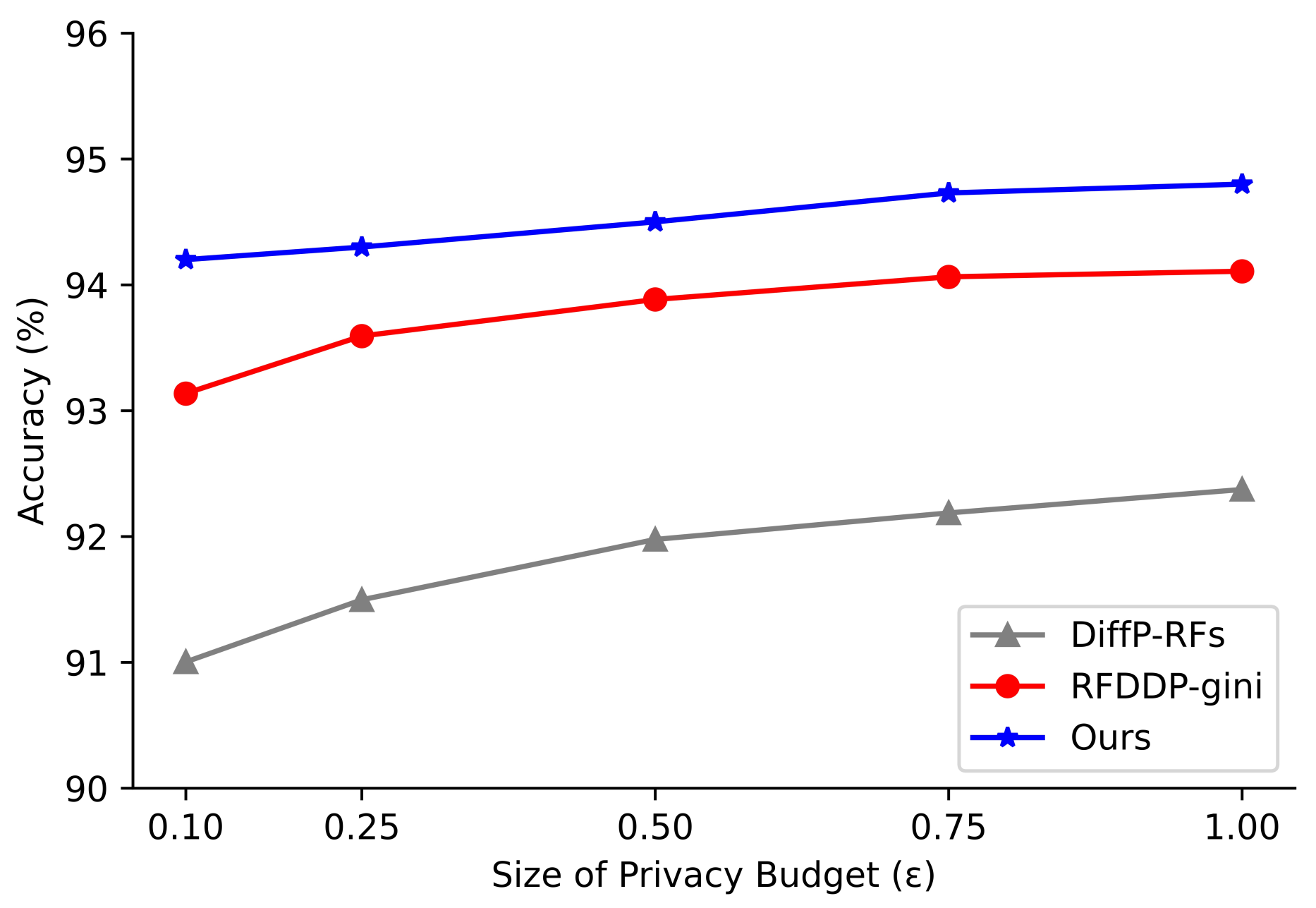
4.3. Experimental Results
4.4. Comparisons
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Marina, S.; Stan, M. Challenges in Computational Statistics and Data Mining; Springer: Cham, Switzerland, 2016; pp. 365–380. [Google Scholar]
- Hu, X.Y.; Yuan, M.X.; Yao, J.G.; Deng, Y.; Chen, L.; Yang, Q.; Guan, H.B.; Zeng, J. Differential privacy in telco big data platform. Proc. VLDB Endow. 2015, 24, 1692–1703. [Google Scholar] [CrossRef]
- Abid, M.; Iynkaran, N.; Yong, X.; Guang, H.; Song, G. Protection of big data privacy. IEEE Access 2016, 4, 1821–1834. [Google Scholar]
- Qi, X.J.; Zong, M.K. An overview of privacy preserving data mining. Procedia Environ. Sci. 2012, 12, 1341–1347. [Google Scholar] [CrossRef]
- Dwork, C. Differential privacy. Lect. Notes Comput. Sci. 2006, 10, 4052. [Google Scholar]
- Liu, H.Y.; Chen, J.; Chen, G.Q. A review of data classification algorithms in data mining. J. Tsinghua Univ. (Nat. Sci. Ed.) 2002, 12, 727–730. [Google Scholar]
- Kotsiantis, S.B. Decision trees: A recent overview. Artif. Intell. Rev. 2013, 39, 261–283. [Google Scholar] [CrossRef]
- Peter, A.; Yaw, M.M.; Ussiph, N. Predicting bank operational efficiency using machine learning algorithm: Comparative study of decision tree, random Forest, and neural networks. Adv. Fuzzy Syst. 2020, 2020, 8581202. [Google Scholar]
- Izonin, I.; Tkachenko, R.; Shakhovska, N.; Ilchyshyn, B.; Singh, K.K. A Two-Step Data Normalization Approach for Improving Classification Accuracy in the Medical Diagnosis Domain. Mathematics 2022, 10, 1942. [Google Scholar] [CrossRef]
- Huang, B.; Huang, D.R.; Mi, B. Research on E-Commerce Transaction Payment System Basedf on C4.5 Decision Tree Data Mining Algorithm. Comput. Syst. Sci. Eng. 2020, 35, 113–121. [Google Scholar]
- Sembiring, N.S.B.; Sinaga, M.D.; Ginting, E.; Tahel, F.; Fauzi, M.Y. Predict the Timeliness of Customer Credit Payments at Finance Companies Using a Decision Tree Algorithm. In Proceedings of the 2021 9th International Conference on Cyber and IT Service Management (CITSM), Bengkulu, Indonesia, 22–23 September 2021; pp. 1–4. [Google Scholar]
- Zhang, Y.L.; Feng, P.F.; Ning, Y. Random forest algorithm based on differential privacy protection. In Proceedings of the 20th IEEE International Conference on Trust, Security and Privacy in Computing and Communications (TrustCom 2021), Shenyang, China, 20–22 October 2021; pp. 1259–1264. [Google Scholar]
- Lv, C.X.; Li, Q.L.; Long, H.Q.; Ren, Y.M.; Ling, F. A differential privacy random forest method of privacy protection in cloud. In Proceedings of the 2019 IEEE International Conference on Computational Science and Engineering (CSE) and IEEE International Conference on Embedded and Ubiquitous Computing (EUC), New York, NY, USA, 1–3 August 2019; pp. 470–475. [Google Scholar]
- Mu, H.R.; Ding, L.P.; Song, Y.N.; Lu, G.Q. DiffPRFs: Random forest under differential privacy. J. Commun. 2016, 37, 175–182. [Google Scholar]
- Wang, M.S.; Yao, L.; Gao, F.X.; Xu, J.C. Study on differential privacy protection for medical set-valued data. Comput. Sci. 2022, 49, 362–368. [Google Scholar]
- Fu, J.B.; Zhang, X.J.; Ding, L.P. MAXGDDP: Decision data release with differential privacy. J. Commun. 2018, 39, 136–146. [Google Scholar]
- Zhang, S.Q.; Li, X.H.; Jiang, X.Y.; Li, B. Aur-tree differential privacy data publishing algorithm for medical data. Appl. Res. Comput. 2022, 39, 2162–2166. [Google Scholar]
- Blum, A.; Dwork, C.; McSherry, F.; Nissim, K. Practical privacy: The SuLQ framrk. In Proceedings of the Twenty-Fourth ACM SIGMOD-SIGACT-SIGART Symposium on Principles of Database Systems (PODS’05), Baltimore, MD, USA, 13–15 June 2005; Association for Computing Machinery: New York, NY, USA, 2005; pp. 128–138. [Google Scholar]
- McSherry, F.D. Privacy integrated queries: An extensible platform for privacy-preserving data analysis. In Proceedings of the 2009 ACM SIGMOD International Conference on Management of Data (SIGMOD’09), Providence, RI, USA, 29 June–2 July 2009; Association for Computing Machinery: New York, NY, USA, 2009; pp. 19–30. [Google Scholar]
- Friedman, A.; Schuster, A. Data mining with differential privacy. In Proceedings of the 16th ACM SIGKDD International Conference on Knowledge Discovery and Data Mining (KDD’10), Washington, DC, USA, 25–28 July 2010; Association for Computing Machinery: New York, NY, USA, 2010; pp. 493–502. [Google Scholar]
- Mohammed, N.; Chen, R.; Fung, B.C.M.; Yu, P.S. Data mining with differential privacy. In Proceedings of the 17th ACM SIGKDD International Conference on Knowledge Discovery and Data Mining (KDD’11), San Diego, CA, USA, 21–24 August 2011; Association for Computing Machinery: New York, NY, USA, 2011; pp. 493–501. [Google Scholar]
- Zhu, T.Q.; Xiong, P.; Xiang, Y.; Zhou, W.L. An Effective Deferentially Private Data Releasing Algorithm for Decision Tree. In Proceedings of the 2013 12th IEEE International Conference on Trust, Security and Privacy in Computing and Communications, Melbourne, Australia, 16–18 July 2013; pp. 388–395. [Google Scholar]
- Patil, A.; Singh, S. Differential private random forest. In Proceedings of the 2014 International Conference on Advances in Computing, Communications and Informatics (ICACCI), Delhi, India, 24–27 September 2014; pp. 2623–2630. [Google Scholar]
- Li, Y.H.; Chen, X.L.; Liu, L. Random forest algorithm for differential privacy protection. Comput. Eng. 2020, 46, 93–101. [Google Scholar]
- Paul, A.; Mukherjee, D.P.; Das, P.; Gangopadhyay, A.; Chintha, A.R.; Kundu, S. Improved random forest for classification. IEEE Trans. Image Process. 2018, 27, 4012–4024. [Google Scholar] [CrossRef] [PubMed]
- Truex, S.; Liu, L.; Gursoy, M.E.; Yu, L. Privacy-preserving inductive learning with decision trees. In Proceedings of the 2017 IEEE International Congress on Big Data (BigData Congress), Honolulu, HI, USA, 25–30 June 2017; pp. 57–64. [Google Scholar]
- Li, Y.Q.; Chen, Y.H.; Li, Q.; Liu, A.H. Random forest algorithm under differential privacy based on out-of-bag estimate. J. Harbin Inst. Technol. 2021, 53, 146–154. [Google Scholar]
- Dwork, C. A firm foundation for private data analysis. Commun. ACM 2011, 54, 86–95. [Google Scholar] [CrossRef]
- Dwork, C.; McSherry, F.; Nissim, K.; Smith, A. Theory of Cryptography Conference; Halevi, S., Rabin, T., Eds.; Springer: Berlin/Heidelberg, Germany, 2006; Volume 3876. [Google Scholar]
- Geng, Q.; Viswanath, P. The optimal noise-adding mechanism in differential privacy. IEEE Trans. Inf. Theory 2015, 62, 925–951. [Google Scholar] [CrossRef]
- Mironov, I. Rényi Differential Privacy. In Proceedings of the 2017 IEEE 30th Computer Security Foundations Symposium (CSF), Santa Barbara, CA, USA, 21–25 August 2017; pp. 263–275. [Google Scholar]
- Xiong, P.; Zhu, T.Q.; Wang, X.F. Differential privacy protection and its application. J. Comput. Sci. 2014, 37, 101–122. [Google Scholar]
| Dataset | Characteristic Number (Discrete/Continuous) | Size | Class Attribute |
|---|---|---|---|
| Adult | 14 (8/6) | 32,561 | 1 |
| Mushroom | 22 (22/0) | 8124 | 1 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Li, X.; Qin, B.; Luo, Y.; Zheng, D. A Differential Privacy Budget Allocation Algorithm Based on Out-of-Bag Estimation in Random Forest. Mathematics 2022, 10, 4338. https://doi.org/10.3390/math10224338
Li X, Qin B, Luo Y, Zheng D. A Differential Privacy Budget Allocation Algorithm Based on Out-of-Bag Estimation in Random Forest. Mathematics. 2022; 10(22):4338. https://doi.org/10.3390/math10224338
Chicago/Turabian StyleLi, Xin, Baodong Qin, Yiyuan Luo, and Dong Zheng. 2022. "A Differential Privacy Budget Allocation Algorithm Based on Out-of-Bag Estimation in Random Forest" Mathematics 10, no. 22: 4338. https://doi.org/10.3390/math10224338
APA StyleLi, X., Qin, B., Luo, Y., & Zheng, D. (2022). A Differential Privacy Budget Allocation Algorithm Based on Out-of-Bag Estimation in Random Forest. Mathematics, 10(22), 4338. https://doi.org/10.3390/math10224338





