A VNS-Based Matheuristic to Solve the Districting Problem in Bicycle-Sharing Systems

Abstract

A matheuristic approach that combines a reduced variable neighbourhood search (rVNS) algorithm and a mathematical programming (MP) solver to solve a novel model for the districting problem in a public bicycle-sharing system is presented. The problem is modelled as an integer programming problem. While the rVNS algorithm aims to find a high-quality set of centres for the repositioning zones, the MP solver computes the optimal allocation network of the stations to the centres of the repositioning zones. We use a predefined grid to reduce the search space the rVNS needs to explore. The proposed approach obtains promising results for small and medium-sized instances, and is also able to handle large-sized models.

1. Introduction

Bicycle-sharing systems (BSSs) involve the provision of a pool of bicycles across a network of strategically positioned stations. Bicycles are typically distributed in an urban area, which can be accessed by different types of users (i.e., registered members or occasional/casual users) for short-term rentals allowing point-to-point journeys [1]. BSSs have existed for almost fifty years, but only in the last decade have they been positioned as a sustainable alternative for urban mobility. One of the first papers regarding BSSs in the literature is the one in [2].

Recently, the COVID-19 pandemic has influenced the use of public transport, favouring BSSs [3]. It is important to point out that similar shared systems are also deployed in many cities with scooters and electric cars, where similar problems occur at different scales.

One of the factors with a more significant impact on the service level of a BSS is its demand pattern. BSSs have unpredictable, asymmetric, and spatial-time dependant demand that is also affected by factors such as weather and topographical conditions [4]. This demand pattern generates that the number of bicycles increases in some stations (which makes it difficult for users to return bikes) while other stations do not have available bicycles to satisfy new users’ service demands.

The repositioning of bicycles is the most used strategy to deal with the unbalance generated by the specific demand process of BSSs. In the repositioning strategy, external vehicles (trucks with a capacity for several bicycles) transport units from crowded stations to empty stations for which a demand peak is foreseen. Laporte et al. [5] and Dell’Amico et al. [6] classify repositioning into two categories, namely static and dynamic repositioning, depending on the operational condition in which it is performed. On the one hand, static repositioning occurs during the night, during the system’s idle time, or in periods of low demand. Its main goal is either to prepare the system for the beginning of the operation or to face upcoming peak demand periods. On the other hand, dynamic repositioning is performed during the operation, responding to the immediate needs of the system, and its primary goal is to keep the balance of the BSS system.

Some operators address the balancing of the system, particularly repositioning bicycles, by dividing the system into zones. Generally, the number of zones depends on the size and type of the fleet of repositioning vehicles. The definition of zones aims at distributing the fleet’s repositioning workload among the vehicles while facilitating the fleet’s routing, particularly under heavily congested conditions. Dividing the system into zones leads to a districting problem in the BSS. Maya-Duque et al. [7] propose a mathematical model to tackle the districting problem in BSSs that takes into account not only distance and connectivity when defining the districts of the BSS but also criteria such as demand patterns and station hierarchy. However, the authors pointed out the need to consider different solution strategies, such as approximated methods, that not only solve larger instances within acceptable computational time but also incorporate additional features to the districting model, such as those described in [8].

This paper proposes a matheuristic approach that combines an algorithm based on a variable neighbourhood search (VNS) and a mathematical programming solver to tackle the districting problem faced by BSS operators when they have to divide the operation area of the system into a set of zones to be covered by each of the repositioning vehicles. The main contributions of this work are:

• A matheuristic algorithm that combines an rVNS strategy and mathematical programming is proposed to solve the districting problem in BSS systems, taking into account geographical information and data about demand patterns and station criticality.
• A strategy to reduce the complexity of the sub-problems speeding up the algorithm’s convergence is proposed. This strategy relies on the idea that repositioning zone’s centres are uniformly distributed along the area covered by the BSS.
• The proposed strategy can solve large instances within acceptable time frames, providing operators with a suitable tool to support decision-making processes in BSS.

Problem Definition

The districting problem for the BBS problem is described by [7] as follows:

Let $\mathcal{E}$ be the set of stations and $\mathcal{C}$ a subset of $\mathcal{E}$ that contains the candidate stations to be the centre of a repositioning zone. Let $\mathcal{P}$ be a set of importance levels that defines the priority that each station is granted for the repositioning strategy. We define $r_i^{+}$ and $r_i^{-}$ as the number of bicycles and parking docks required by station i at peak hours. We also say that $d_{ij}$ is the distance between stations i and j, $c_{ij}$ is the binary indicator of the connectivity between stations i and j, $p_{il}$ is the binary parameter that indicates whether the station i is assigned priority l, and parameter k is the number of repositioning zones to be defined. The model considers two decision variables, x and y. The binary variable $y_j$ indicates whether the j-th candidate station in $\mathcal{C}$ is designated as the centre of a repositioning zone. Variable $x_{ij}$ indicates whether the i-th station in $\mathcal{E}$ is assigned to the zone centred in j. Then, the optimisation model of the districting problem for BSS we address in this paper is as follows:

$$\begin{array}{cc}\hfill \mathbf{BSS}(\mathbf{x},\mathbf{y}):min& {max}_{i,k\in \mathcal{E},j\in \mathcal{C}}\left\{d_{ik}{x}_{ij}{x}_{kj}\right\}\end{array}$$

(1)

$$\begin{array}{ccc}\hfill \mathrm{s}.\mathrm{t}.& {\sum }_{j\in \mathcal{C}}{x}_{ij}=1& \forall i\in \mathcal{E}\hfill \end{array}$$

(2)

$$\begin{array}{ccc}& x_{ij}\le c_{ij}{y}_j& \forall i\in \mathcal{E}\forall j\in \mathcal{C}\hfill \end{array}$$

(3)

$$\begin{array}{cc}& {\sum }_{j\in \mathcal{C}}{y}_j=k\end{array}$$

(4)

$$\begin{array}{ccc}& \left|{\displaystyle \frac{{\sum }_{i\in \mathcal{E}}{r}_i^{+}{x}_{ij}-{\sum }_{i\in \mathcal{E}}{r}_i^{-}{x}_{ij}}{{\sum }_{i\in \mathcal{E}}{r}_i^{+}{x}_{ij}+{\sum }_{i\in \mathcal{E}}{r}_i^{-}{x}_{ij}}}\right|\le \alpha & \forall j\in \mathcal{C}\hfill \end{array}$$

(5)

$$\begin{array}{ccc}& \left|{\sum }_{i\in \mathcal{E}}{p}_{il}{x}_{ij}-⌊{\displaystyle \frac{{\sum }_{i\in \mathcal{E}}{p}_{il}}{k}}⌋\right|\le \beta & \forall l\in \mathcal{P},\forall j\in \mathcal{C}\hfill \end{array}$$

(6)

$$\begin{array}{ccc}& x_{ij},y_j\in \{0,1\}& \forall i\in \mathcal{E}\forall j\in \mathcal{C}\hfill \end{array}$$

(7)

The objective function (1) aims to minimise the sum of the distances between each station and its assigned centre. Minimising this summation of distances will lead to more compact repositioning zones. It is important to note that, from a theoretical point of view, it would have been preferable to consider a function that minimises the maximum distance between the centre of each repositioning zone and its stations. However, to keep the model computationally tractable, we chose to use the objective function in (1) and include a maximum coverage distance in the definition of the connectivity parameter $c_{ij}$. Constraints (2) to (4) establish the number of repositioning zones and ensure that each station is assigned to only one of the considered repositioning zones. Constraint (5) aims to balance both the bicycle and parking dock demands within each zone such that, at peak hours, not all the stations in the same zone demand either bikes or only parking docks. Parameter $\alpha$ is the maximum tolerable percentage of unbalance. The smaller the parameter $\alpha$ is, the higher the required balance between bicycles and docks. Similarly, constraint (6) aims to distribute the stations among the repositioning zones homogeneously with respect to their priority levels. That is, the most critical stations (higher priority values) should not be concentrated in a reduced set of repositioning zones. Parameter $\beta$ is the maximum allowed difference between the number of stations of a given priority level and the ideal value within each zone. A different value of $\beta$ might be used for each priority level. Finally, constraint (7) defines the variables to be binary.

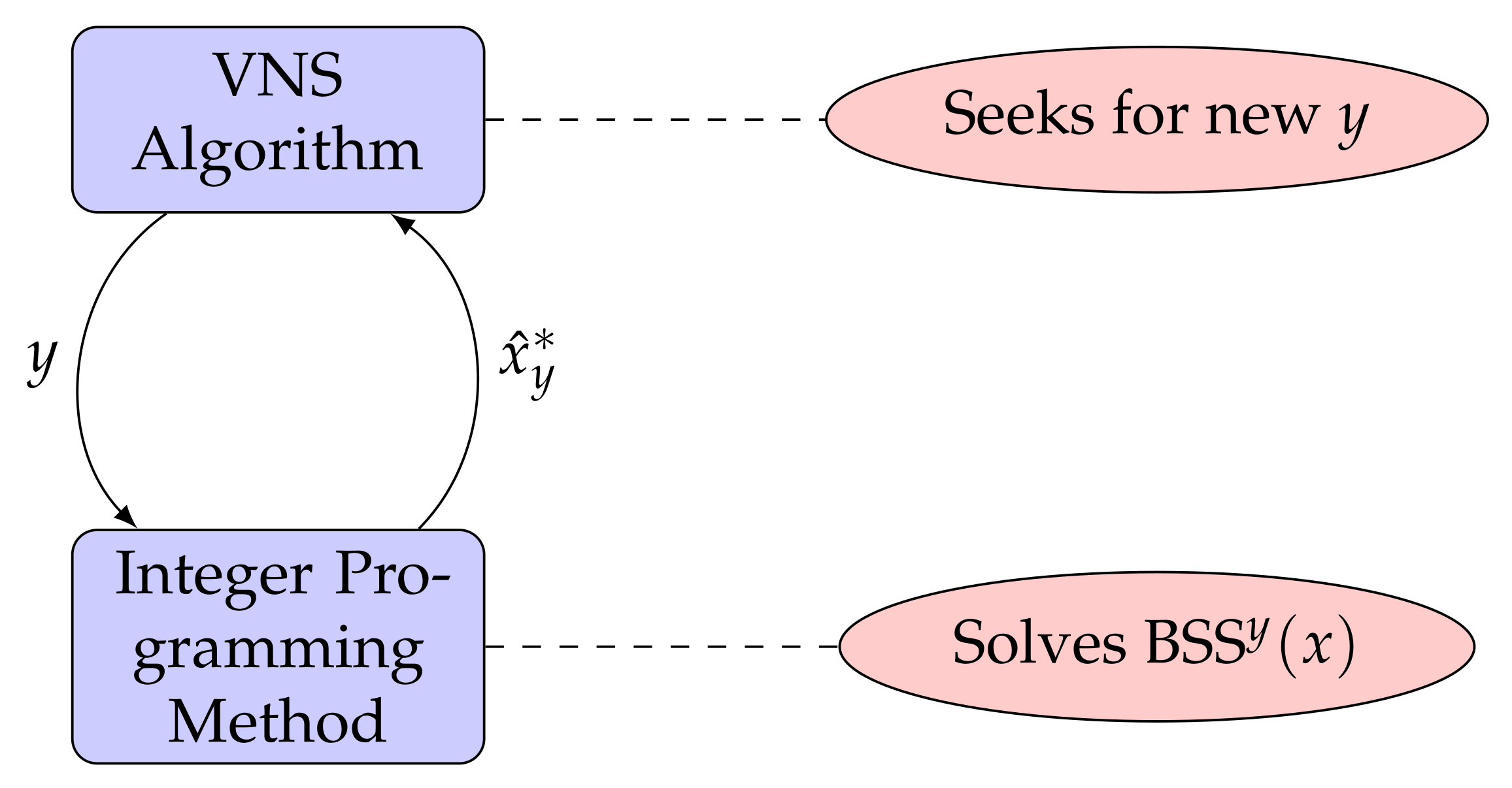
The BSS problem described above is an integer (binary) problem. It is interesting to note that we can split this problem into two sequential problems: the location of the repositioning centres and the allocation network for such repositioning centres. Thus, if we set vector y to some value that satisfies the constraints in Equation (4), we then have a simpler IP problem where the objective function is as in Equation (1), constraints (2), (3), (5) and (6) are as in the original BSS($x,y$) problem and constraint (7) is replaced by $x_{ij}\in \{0,1\}\forall i\in \mathcal{E}\forall j\in \mathcal{C}$. We call this sub-problem BSS${}^y\left(x\right)$.

The BSS${}^y\left(x\right)$ sub-problem is simpler than the original BSS($x,y$). In fact, keeping the number of stations within a reasonable range, we have that well-known IP exact methods can find an optimal solution for the BSS${}^y\left(x\right)$ sub-problem. However, such solvers cannot find an optimal solution for the main BSS($x,y$) problem. Thus, it might make sense to consider incomplete techniques that provide good quality y vectors to iteratively solve the sub-problem BSS${}^y\left(x\right)$. In this paper, we propose to use an rVNS algorithm to produce y vectors that, in turn, are passed on to the MP solver. The algorithm will iteratively evaluate the optimal solutions obtained for the BSS${}^y\left(x\right)$ sub-problem that are also feasible solutions of the original BSS($x,y$) problem.

The rest of this paper is organised as follows. Section 2 briefly reviews the state of the art for the districting problem in the context of the repositioning operations. Section 3 describes a solution strategy that combines variable neighbourhood search metaheuristic (rVNS) and mathematical programming (MP). The computational experiments to test the solution strategy are described in Section 4. Finally, Section 5 draws the main conclusions and highlights areas for future work.

2. State of the Art

The repositioning problem for BSSs has been a topic largely studied during the last years [5]. Two main sets of operational decisions have been considered in those studies, namely, routing decisions (concerning the vehicles) and inventory decisions (concerning bicycles in the stations). However, operators recognise the need to involve not only operational decisions, such as the routing, but also tactical and strategic decisions when planning the repositioning of bicycles [9]. In particular, the definition of the zones or districts where the repositioning vehicles operate seems to have a significant impact on the performance of the operation. Grouping small geographic areas or units into larger geographic clusters, called districts, is usually known as the districting problem (DP) [10].

One of the first studies on the districting problem was made in [11]. In their work, the authors divided a governmental area, such as a city or a state, into constituencies from which political candidates are elected. After that, the DP applications spanned a diverse set of domains. Kalcsics [8] identifies four major application areas for districting problems: political districting, sales territory design, service districts and distribution districts. The districting problem for the BSSs falls within the intersection of the last two categories (service and distribution districting). The service districting applications focus on social facilities, such as hospitals and public utilities, for which districts need to be defined so each inhabitant knows which facility should visit to obtain the required service. Distribution districting involves the design of pickup and delivery districts in logistics. Although such problems are usually modelled and solved as vehicle routing, in the presence of considerable uncertainty in customers’ demand, several authors have proposed two-phase approaches that first build the pickup and delivery districts and then do the routing on a day-to-day basis. In that case, basic units correspond to potential customers to be partitioned into districts that satisfy specific planning criteria.

Several authors address the repositioning problem in BSSs as a variant of the vehicle routing problem (VRP) in which a fleet of capacitated vehicles is employed to re-distribute the bikes to minimise total cost. Dell’Amico et al. [6] summarises four mixed integer linear programming formulations where the problem is modelled as a special one-commodity pickup-and-delivery capacitated vehicle routing problem. As pointed out by de Chardon et al. [12], based on the analysis of rebalancing operations of nine BSSs, the system obeys very consistent patterns during the operation (unless weather or exceptional circumstances), which generates a predictable rebalancing operation during the peak periods. Additionally, rather than rebalancing at the system scale, BSSs, such as in NYC and Washington, delineate smaller control zones to rebalance within. Song et al. [13] highlights that the partition of subzones is essential to achieve high service levels and that such partition could be found through the scenario-based optimisation process. Schuijbroek et al. [14] and Raviv et al. [15] used cluster-first route-second heuristics to solve the static repositioning problem evidencing the importance of the clustering phase on the efficiency of the rebalancing operation.

Therefore, we decouple the districting problem (which creates the zones for each vehicle) from the routing problem (which defines the scheduling and sequence of the route within each district) and focus on the former while recognising that the two problems are faced at different decision-making horizons. According to Lin et al. [9], the problem of scheduling area division in BSSs is solved mainly using clustering algorithms. We then summarise the most recent works that consider the specific dynamics of BSS alongside the traditional clustering algorithms to facilitate balancing operations.

Lin et al. [16] proposes a model to define an effective scheduling region partition that uses as clustering criteria not only the geographical position of the station but also the lease/return relationship between them. The authors propose a solution approach based on the affinity propagation clustering algorithm and compare their results to the existing administrative division method and the k-means algorithm using data from the Hangzhou BSS. Experimental results show that the proposed model’s correlation degree between scheduling regions is lower than that achieved by other methods. Additionally, the authors note that the partition results are reasonable, and the scheduling workload is mainly concentrated in each region. Similarly, Lin et al. [9] proposes a community discovery algorithm based on multi-objective optimisation (CDoMO) to solve the problem of regional division of public bicycles. In their paper, the authors consider the lease/return dynamics to balance the scheduling workload between areas while minimising the variance between the estimated dispatch distances and the number of sites in each area.

Based on the fact that public bicycles are mainly used as a last kilometre connection, and therefore, the trip distances between origin and destination are usually short, Liu et al. [17] propose a model to identify closed areas within the public bicycles’ typical flow. The proposed model is based on the ordering points to identify the clustering structure (OPTICS) and classify the public bicycle stations into related closed regions using the loan-return data between stations instead of station scalar data.

3. VNS-Based Matheuristic

As mentioned in previous sections, in this paper, we implement a hybrid algorithm that combines a reduced variable neighbourhood search (rVNS) metaheuristic strategy and mathematical programming (MP). Since the problem can be divided into two sequential sub-problems, we propose to combine rVNS and MP to better address these sub-problems. Thus, we let the rVNS algorithm seek a set of promising repositioning centres and then apply the MP integer programming solver to find the corresponding optimal allocation network. Figure 1 shows the general architecture of the proposed VNS-based matheuristic strategy.

It is important to note that efforts in combining both heuristic and exact methods have been made during the last two decades. In fact, the term matheuristic was coined just in 2010 [18]. In particular, several works have focused on solving IP and MIP problems using the less-is-more approach combining VNS-based algorithms and exact methods [19,20,21,22,23]. Moreover, similar approaches have been successfully applied to mixed integer linear and non-linear optimisation problems in the literature [24,25,26].

We briefly explain the main features of the proposed rVNS and the neighbourhood movements implemented in this study. It is interesting to note that the algorithm implemented here differs from the ones mentioned above in that the sub-problem solved by the exact method is a purely IP sub-problem rather than a continuous one. In our experience, however, this does not have an impact on the performance of the algorithm.

3.1. Variable Neighbourhood Search: Overview

In this paper, we use the less-is-more approach proposed in [27]. This means we avoid implementing complex transition rules and neighbourhood definitions and, instead, implement a basic rVNS algorithm that considers only one neighbourhood definition and three different step sizes. The neighbourhood definition implemented in this work involves selecting k centres to be open and other k open centres to be closed. Mathematically, we can define the neighbourhood used here as

$${\mathcal{N}}_k\left(y\right)=\{\widehat{y}\in \mathcal{Y}:\sum _{i=1}^{\left|\mathcal{C}\right|}\mathit{equal}(y_i,{\widehat{y}}_i)=\left|\mathcal{C}\right|-k\}$$

(8)

where

$$\begin{array}{cc}\hfill & \mathit{equal}=\left\{\begin{array}{cc}1,\hfill & \mathrm{if}{y}_i={\widehat{y}}_i,\hfill \\ 0\hfill & \mathrm{otherwise}.\hfill \end{array}\right.\end{array}$$

(9)

From Equation (8), we have that different neighbourhoods can be used by varying the step size, $k\in \mathcal{K}$. We need to note that the larger the value of k, the larger the change in the structure of the current solution. In Section 3.3 we discuss which values of k were finally considered in our experiments.

The rVNS approach implemented in this paper to address the BSS($x,y$) problem is described in Algorithm 1.

Algorithm 1: Algorithm rVNS + MILP

The rVNS algorithm starts by generating an initial vector y of repositioning zones’ centres. To this end, the algorithm randomly selects $\left|C\right|$ stations to be zones’ centres (line 2 in Algorithm 1). Then, we solve the sub-problem BSS${}^y\left(x\right)$ for the computed vector y and obtain the optimal allocation matrix $x_y$ for vector y (line 3 in Algorithm 1). As the tuple $(y,x_y)$ is the very first solution we found for our problem, we set it as the best solution found so far by the algorithm, $(y^{*},x_{y^{*}})$ (line 4 in Algorithm 1). Once we have our initial solution, we generate its neighbourhood by computing s neighbours for each neighbourhood step size, k. All the computed neighbours are added to the neighbourhood set of vector y, $\mathcal{N}\left(y\right)$ (lines 7 to 9 in Algorithm 1). Then, the best neighbour solution is obtained and compared to the best solution found so far by the algorithm. If the best neighbour is better than the best solution found so far, we update the best solution and reset the no improvement counter. Otherwise, we increase by one the no improvement counter. The algorithm stops either when it reaches the maximum number of iterations $I_{max}$ or the no improvement counter reaches its threshold $I_{max}^{-}$.

3.2. Grid Cells

Ideally, repositioning zones must be compact and cover the entire operational area of the system. To this end, the selected centres should be uniformly distributed throughout that area. Additionally, although we largely reduce the search space of the problem when setting variable y, the resulting allocation sub-problem, BSS${}^y\left(x\right)$, is still hard to solve, and the number of iterations the $rVNS$ algorithm can perform before reaching some time limit is heavily reduced. To tackle these two issues, we propose grouping the stations based on their geographical location rather than randomly opening and closing the repositioning zone centres. That is, we superpose a grid over the map, with the number of grid cells equal to the number of repositioning zones we need to create. Figure 2a shows the distribution of all centres that must be allocated, and Figure 2b shows the grid pattern we use in the case study of this paper.

Using the grid cells idea, we can define neighbour cells as any pair of cells that share one side (or part of it) of the grid. As Figure 2c shows, grid cells in grey share one side of the grid cell in black. Then, centres within the black grid cell might be allocated to repositioning zones belonging to the same grid cell (black) or those in grey. It is important to note that both the grid cells pattern and the neighbour cells definition might be modified to better fit the instance problem we need to solve. We further discuss this in Section 5.

With the neighbour cells concept already defined, we now need to slightly modify the neighbourhood movements explained in the previous section. The idea is to restrict the swap movement of centres to those stations that belong to either the same grid cell or some neighbour grid cell. In the same way, we restrict the allocation of stations to those centres that belong to either the same grid cell or some neighbour grid cell. Depending on the grid cell pattern we are using, this change can reduce the search space of the sub-problem BSS${}^y\left(x\right)$ and, thus, the time the solver needs to solve it. Thus, finding a high-quality grid pattern is critical for the algorithm’s performance, as some grid patterns might even make the sub-problem unfeasible. We found that a grid cell similar to the one in Figure 2b works well for our problem. Furthermore, obtained results demonstrate that including the set of constraints associated with the proposed grid cell leads to better objective function values and shorter running times. Hereafter, the results reported in this paper correspond to those obtained by our rVNS-based matheuristic algorithm, including the constraints associated with the grid cells idea. In Section 5 we discuss some strategies to generate good quality patterns and some ideas on including more than one pattern during the search.

3.3. Neighbourhood Step Size

The neighbourhood step size k is a key element of our rVNS algorithm as it determines the compromise between the exploration and the exploitation features of the algorithm.

Thus, we performed some initial experiments to determine the best values we should include in set $\mathcal{K}$. We initially tried five different step sizes, i.e., $\mathcal{K}=\{1,2,3,4,5\}$. We ran our algorithm seven times using these values with 224 iterations (32 iterations per run on average). We then determined which step sizes consistently generated better solutions at each iteration.

Table 1. Number of times solutions generated using neighbourhood size k were selected as the best neighbour.

k Value	Frequency (Total)	Frequency (Avg Per Run)	Percentage
1	169	24.14	75.45%
2	27	3.85	12.05%
3	26	3.71	11.61%
4	1	0.14	0.45%
5	1	0.14	0.45%

shows the number of times a solution generated by a step size k was selected as the best of one from neighbourhood $\mathcal{N}\left(y\right)$ at each iteration.

As we can see, almost all best neighbours were generated using $k=\{1,2,3\}$ values. Further, we can note that most of the improvements were produced using $k=1$ while the performance of $k=2$ and $k=3$ are very similar. We then considered $k=\{1,2,3\}$ for all the experiments performed hereafter.

3.4. Parallel Threads Strategy

In our approach, the BSS integer programming problem is split into two sequential problems, namely, the location of the repositioning centres and the allocation network for such repositioning centres. The former was denoted as BSS${}^y\left(x\right)$. Solving the BSS${}^y\left(x\right)$ sub-problem for a given y is time-consuming, even more so if several neighbours are considered at each iteration ($s\ge 2$). Therefore, a version of the rVNS that involves a parallel threads strategy was implemented. This strategy assigns the solution of the BSS${}^y\left(x\right)$ associated with each neighbour to an independent execution thread (line 8 in Algorithm 1). Once all the needed neighbour solutions are evaluated, the algorithm returns to the main thread and chooses the best feasible neighbour. This strategy allows us to heavily reduce the execution time of our approach, although (as expected) it has no significant impact on the quality of the obtained results. We need to point out that we ran a single rVNS instance and that the parallel strategy is only applied to the sub-problem’s solving step, allowing Gurobi to use the maximal number of threads for the sub-problems.

4. Computational Experiments

To test the solution strategy for the BSS districting problem proposed in Section 3, we use the set of instances described in [7], which are based on the bicycle sharing system ECOBICI that operates in Mexico City. The system has a policy of open data that allows access to the operational data through an API (https://www.ecobici.cdmx.gob.mx/en/) (accessed on 3 September 2020). Therefore, transactional records of loans between September and November of 2016 (2,353,389 travel records) were used to build three instances: a large instance that involves 452 stations (instance 1) and two medium size instances that consider 224 stations (instance 2) and 228 stations (instance 3). The sizes of the instances considered in this analysis are similar to those of real systems in Latin America. For instance, the public system in Mexico City has 452 stations, while the system in Buenos Aires has 318 stations. There are, of course, larger systems such as the one in Grater Paris with 1400 stations. For instance 1, the stations must be partitioned into 15 repositioning zones, while instances 2 and 3 consider only 7 zones. This section describes the experiments designed to test the rVNS algorithm, the obtained results and the insights they provide. All results were analysed using the statistical software R [28].

4.1. Design of Experiments

Considering the three instances mentioned above, three parameters define the specific BBS districting problem to be solved, summarised in

Table 2. Parameters to define the experimental units.

Factor	Level	Units
Parameters of the instance
$dmax$	2500	meters
$\alpha$	0.2, 0.5	deviation from the ideal (%)
$\beta$	5, 10	deviation from ideal (# of stations)
Total feasible instances: 10

. The maximum distance, $dmax$, is used to establish the connectivity $c_{ij}$ of each pair of stations and works as an upper bound of the diameter of the repositioning zones. Parameter $\alpha$, from Equation (5) in the mathematical model, represents the maximum allowed percentage of unbalance between the demand for bicycles and the demand for parking docks within any repositioning zone at the peak hour. Finally, the parameter $\beta$, from Equation (6) in the mathematical model, represents the maximum allowed difference between the number of stations of a given priority level and the ideal value within each zone. Based on the results described by Maya-Duque et al. [7], we set $dmax=2500$ and consider values for $\alpha =\{0.2,0.5\}$ and $\beta =\{5,10\}$ generating a set of 12 possible experiments. We need to point out that, depending on the grid cell we choose, some instances might not have a feasible solution for such a grid. This situation might occur when there is no combination of repositioning zones that fulfil the distribution of the prioritised stations among the defined grids while observing the fixed minimum distance. In order to make the experiments comparable, we stick to the grid described in Section 3.2, for which 10 instances remain feasible. Therefore, those are the experimental units to be solved to analyse the parameter setting and performance of the proposed algorithm.

The rVNS algorithm has three parameters that need to be set: the number of total iterations N, the set of step sizes $k\in \mathcal{K}$ and the number of neighbours considered within each neighbourhood, s.

Table 3. Experimental factors and levels.

Parameters of the Algorithm
N	300, 600	iterations
K	{1}, {2}, {3}, {1,2,3}	set $\mathcal{K}$ of step sizes
s	3, 9	Number of neighbours

summarises the values considered for each parameter.

For the set $\mathcal{K}$, we first analyse each step size k individually. In this case, the rVNS reduces to a basic restricted local search (rLS). We also consider the three step sizes simultaneously as was described for the rVNS in Section 3.1. The analysis of this parameter would provide information about how significant should be the perturbation in the vector of centres of the repositioning zones to keep a balance between diversification and intensification. Additionally, it would generate insights on the effect of considering several neighbourhoods (i.e., step sizes) simultaneously. To perform these experiments, the parameter s (number of explored neighbours) is set to 3 and 9 for the rLS. We then compare the results obtained by the rLS to those obtained by the rVNS considering all three step sizes simultaneously, with three neighbours per each step size. We do this so that the number of neighbours generated by the rVNS with three neighbours for each step size $\{1,2,3\}$ would equal the number of neighbours generated by the rLS for each step size, separately. Additionally, to test the parallel threads strategy used in the rVNS, we run a set of experiments for both instances (2 and 3) with and without the parallel threads strategy. The results obtained for these experiments are reported in Section 4.2

The rVNS algorithm was implemented in Julia v1.2 [29] while the mathematical model was implemented using the JuMP interface [30] that, in turn, is called Gurobi 7.5. The MIP model was run for each experiment either for 10,000 s or until it reached a $2.0\%$ of optimality gap. The rVNS stops either because the maximum number of iterations N or the maximum iterations without improvement is reached. The latter was set to $\frac{N}{4}$. All the experiments were run on Ubuntu 20.02 using an Intel(R) Core(TM) i7-10700 CPU @ 2.9 GHz processor with 8 cores and 16 GB RAM.

We solve ten instances with the exact model and run 140 experiments with our proposed solution strategy. For each of them, we compute four indicators to evaluate the algorithm’s performance.

• $gap$: the percentage difference to the optimal solution (or the best know solution) obtained by the mathematical model. The $gap$ can be positive or negative. The latter would mean that the rVNS algorithm provides a better solution than the one provided by the mathematical model. This is because we allow a tolerance of $2.0\%$ for the exact optimiser
• $AvgDiameter$: Average of the diameters of the repositioning zones.
• $MaxDiameter$: Maximum diameter of the repositioning zones.
• $cpuTime$: Computational time to solve the experiment.

4.2. Experimental Results

The analysis of the experimental results was divided into four main parts. First, we analyse the effect of the different parameters of the algorithm on the solution quality based on the obtained gap values. Second, we consider the computational time concerning the parameter setting. Then, the parallel threads strategy is analysed. Finally, the solutions obtained by the best algorithm’s configuration are compared in terms of quality with those provided by the MIP model.

4.2.1. Gap vs. Parameters Settting

First, we graphically explore how the gap changes given specific levels of the factors considered by plotting the univariate effects. Figure 3 shows that the set of step sizes $\mathcal{K}$ has the largest effect. The rVNS that considers the three step sizes simultaneously provides, on average, smaller gaps. In contrast, for the rLS, increasing the step size seems to have no positive impact on the quality of the solutions. The number of neighbours considered at each iteration (s) and the number of iterations (N) have a moderate effect on the obtained gap values. We can also note that the greater the number of iterations, the lower the gap value, while for the number of neighbours, generating only three neighbours works better, on average, than generating nine neighbours.

Table 4. ANOVA: gap vs. experimental factors.

Factor	Df	Sum Sq	Mean Sq	F Value	Pr (>F)
instance	2	323	161.36	2.132	0.1227
balance $\alpha$	1	21	20.74	0.274	0.6015
priority $\beta$	1	148	147.85	1.954	0.1646
iterations N	1	153	153.45	2.028	0.1569
neigStruc $\mathcal{K}$	3	742	247.42	3.269	0.0234
neigLen s	1	9	8.75	0.116	0.7344
Residuals	130	9838	75.68

summarises the analysis of variance (ANOVA) considering both the parameters that define the experimental units (i.e., $\alpha$ and $\beta$) and the parameters of the algorithm (i.e., N, $\mathcal{K}$, s). It confirms that the structure of the neighbourhoods, that is, the set of step sizes $\mathcal{K}$, has the largest effect. Similar results were obtained with the analysis that only considers the algorithm’s parameters and interactions.

Figure 4 gives a more detailed glance at how the gap changes for the different step sizes and the number of neighbours considered in each movement. It shows that as the step size increases from 1 to 3, the gap to the optimal solution also increases. That is, the movement of changing one district centre is more effective than changing two or three simultaneously. However, mixing these three individual movements into the rVNS produces good results as it generates solutions with smaller gaps and the variability of these measures is also significantly lower. The plot also shows that there is no significant difference in the gap when exploring three or nine neighbours at each iteration.

The analysis of the interaction between the factor k and s indicates that no coupled effect between these two parameters is observed. Moreover,

Table 5. Percentage of improvement movements.

	Number of Neighb (s)
Factor	3	9
$\left\{1\right\}$	9.52	11.0
$\left\{2\right\}$	6.46	6.75
$\left\{3\right\}$	5.18	6.54
$\{1,2,3\}$	8.98

shows the percentage of movements that generate and improvement on the solution for each combination of k and s (i.e., $\frac{improvementMov}{totalIntentedMov}$). It shows that the step size $k=\left\{1\right\}$ is the most efficient movement while simultaneously changing three zone centres produces fewer improvement moves. The strategy of the rVNS that combines the tree step sizes aims at capturing both the good intensification of changing a single centre and the diversification of changing more than one centre.

4.2.2. Running Time vs. Parameter Settings

Regarding the running time, Figure 5 shows the effect of the different parameters of the algorithm. The step size parameter has the largest impact. The rVNS that considers the three steps simultaneously generates larger computational times. However, it also obtains the best objective function values. The number of iterations and the number of neighbours considered at each iteration have a moderate effect: the larger the number of iterations or the neighbourhood size, the larger the computing time. However, it is important to note that the computing time depends mainly on the number of generated neighbours. This is, however, attenuated by the parallel thread strategy.

Table 6. ANOVA: gap vs. running time vs. experimental factors.

Factor	Df	Sum Sq	Mean Sq	F Value	Pr (>F)
instance	2	$1.982\times {10}^9$	990,852,745	35.564	$4.79\times {10}^{-13}$
balance $\alpha$	1	$8.725\times {10}^8$	872,540,291	31.317	$1.24\times {10}^{-7}$
priority $\beta$	1	$6.069\times {10}^6$	6,068,963	0.218	0.64148
iterations N	1	$1.903\times {10}^8$	190,263,767	6.829	0.01003
neigStruc $\mathcal{K}$	3	$1.895\times {10}^8$	63,177,058	2.268	0.08371
neigLen s	1	$2.877\times {10}^8$	287,652,165	10.324	0.00166
Residuals	130	$3.622\times {10}^9$	27,861,365

summarises the analysis of variance (ANOVA) considering both the parameters that define the experimental units (i.e., $\alpha$ and $\beta$) and the parameters of the algorithm (i.e., N, k, s). As we can see, the parameters that define the instances account for the largest portion of the variability on the computing time, which is consistent with what was pointed out by Maya-Duque et al. [7] regarding the importance of the parameter $\alpha$ (i.e., balance) on the instance’s difficulty. Regarding the algorithm’s parameters (i.e., N, k and s), although all of them are significant in the computing time variability, the number of generated neighbours is the one that accounts for the largest portion of the variability.

Figure 6 presents the box plots that describe the computing time with respect to parameters of the algorithm without considering 15 instances in which computing time exceeds 10,000 s. It shows that most of the computing times are concentrated below 2500 s. However, there are a few difficult instances in which the computing time is larger, including the 15 excluded for visualisation purposes.

4.2.3. Parallel Threads Strategy

To evaluate the parallel threads strategy described in Section 3.4, a set of 24 experiments was run with the proposed rVNS and a restricted version that does not use parallel threads. For each of the paired experiments, we compute the running time difference with and without parallelism denoted as $\Delta runTime$ and the percentage of time change between the rVNS and its restricted version. Using parallel threads reduces the average computing time by $35.6\%$. Additionally, the parametric (i.e., paired sample t-test) test and the non-parametric (i.e., Wilcoxon signed rank test) test for paired samples were applied to $\Delta runTime$. Both indicate that the observed difference is statistically significant.

5. Conclusions and Future Work

This paper implements a matheuristic approach that combines an rVNS heuristic and the Gurobi solver to solve the districting problem arising in BSSs. The problem is divided into two sequential problems, namely repositioning zone selection and the centre allocation. While the first one is solved using the rVNS algorithm, the second is solved using the Gurobi solver. Furthermore, in order to reduce the search space of the allocation problem, a grid cell strategy is proposed.

Although the proposed rVNS matheuristic is quite competitive in terms of solution quality, it is still slower than the Gurobi solver. This is especially true for those small-size instances where the Gurobi solver is several times faster than our approach. However, as the instance size increases, our approach becomes more competitive in terms of time. The scalability of the proposed approach is mainly due to three factors. First, after the repositioning centres are defined, the associated sub-problem is an allocation problem usually tackled efficiently by the optimiser. Second, the grid cell strategy attenuates the effect of increasing the number of decision variables as, generally, the number of adjacent cells remains the same. Finally, the parallel thread strategy has been designed to accelerate the solution of multiple allocation problems simultaneously.

It is important to note that, although the grid cells strategy allows us to reduce the search space, this reduction might lead to the unfeasibility of the sub-problem BSS${}^y\left(x\right)$. This is mainly because the solver cannot find a feasible solution using only the stations belonging to adjacent cells. For this reason, although appealing, using the grid cell strategy must be done carefully. First, a meaningful strategy to create the grid must be considered. In this work, we try clustering strategies to generate our grid. Secondly, since using only one grid for all instances will probably lead to the unfeasibility of some of them (usually the most restrictive ones), using different grids would help the algorithm to find feasible solutions for those more complicated instances. How different grids are generated and applied to the proposed rVNS strategy is worth further studying.

As future work, we aim to extend the current BSS model to a bi-objective one, where the model should also maximise the network’s balance. Additionally, making the grid cells more self-adaptive might contribute to the exploration–exploitation compromise of our algorithm. Further, other (meta)heuristic methods can also be included within the proposed matheuristic framework to solve the BSS problem. Finally, as mentioned in the previous paragraph, generating and applying different grids during the algorithm execution might also be an interesting research line.