The Effects of Variable Thermal Conductivity in Thermoelastic Interactions in an Infinite Material with and without Kirchhoff’s Transformation
Abstract
1. Introduction
2. Basic Equations
3. Application
4. Numerical Scheme
5. Linear Case (with Kirchhoff’s Transformation)
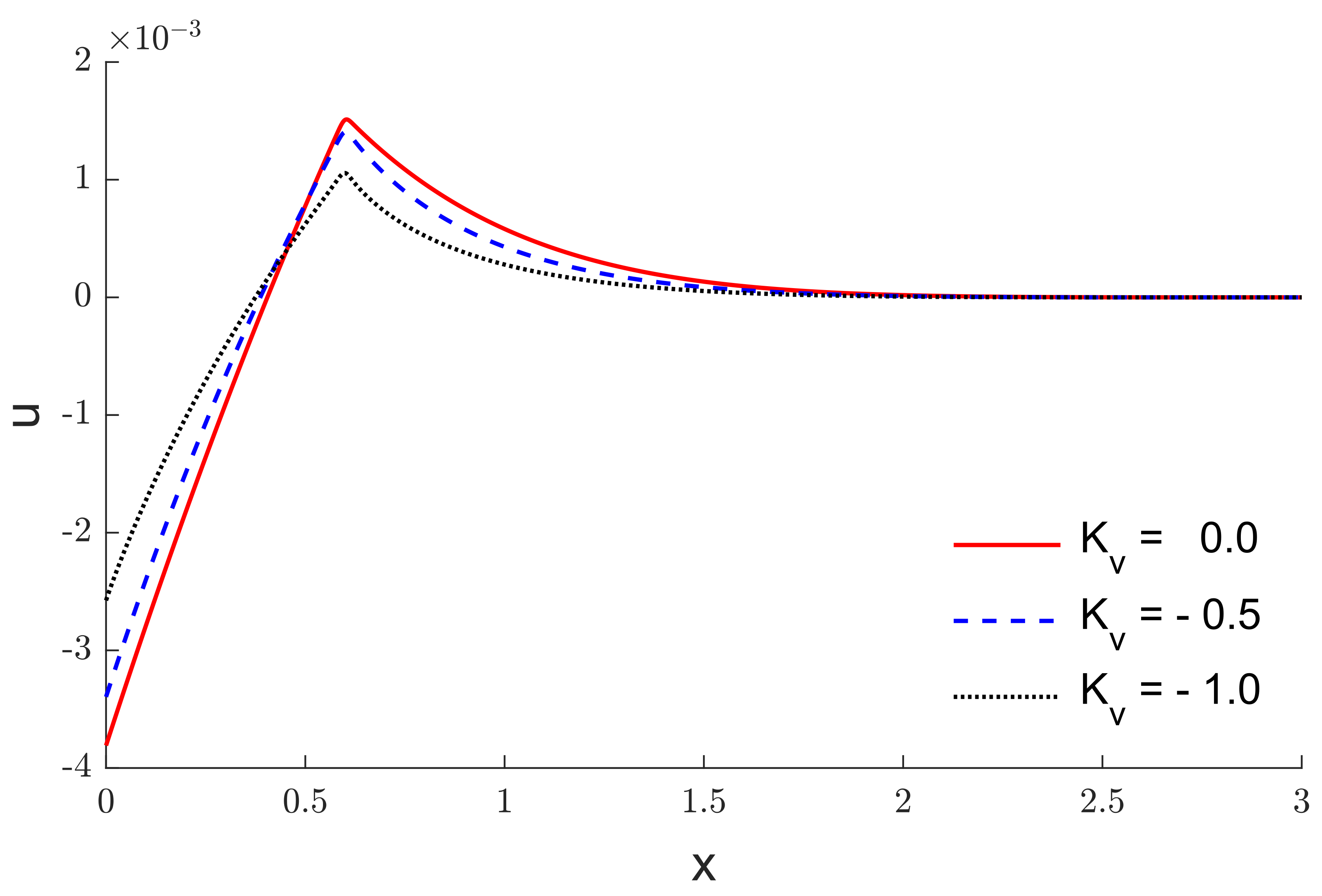
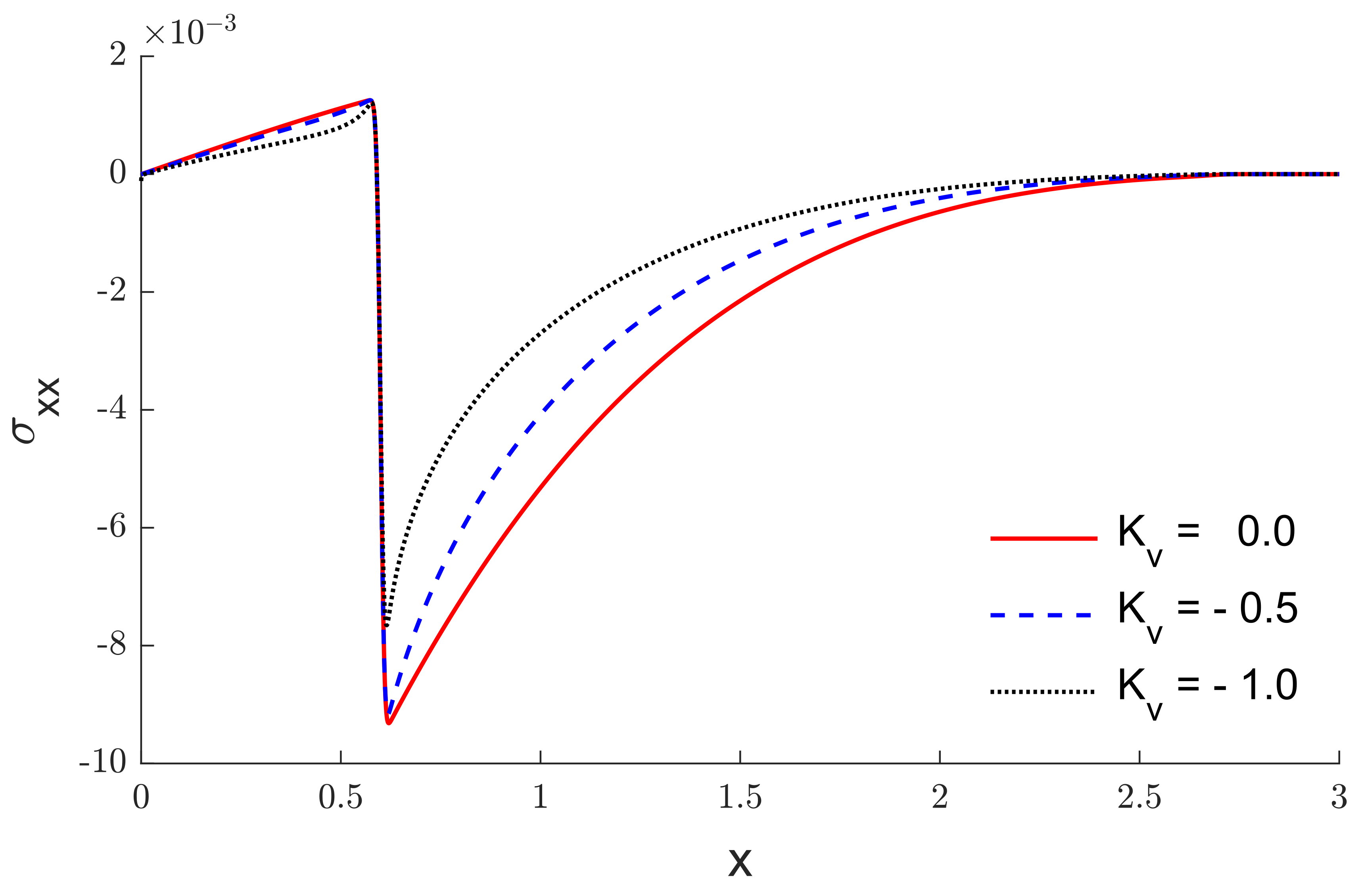
6. Results and Discussion

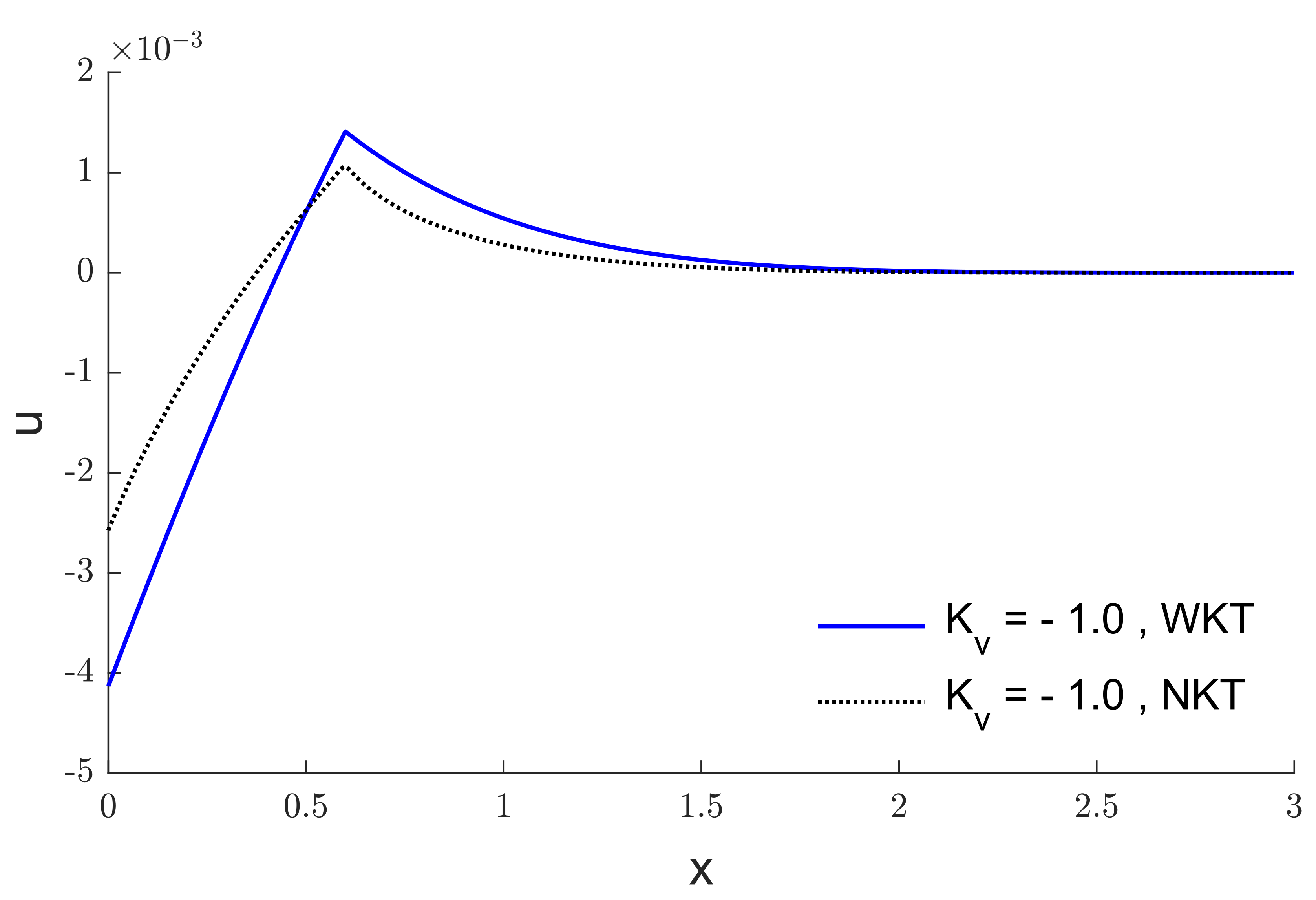
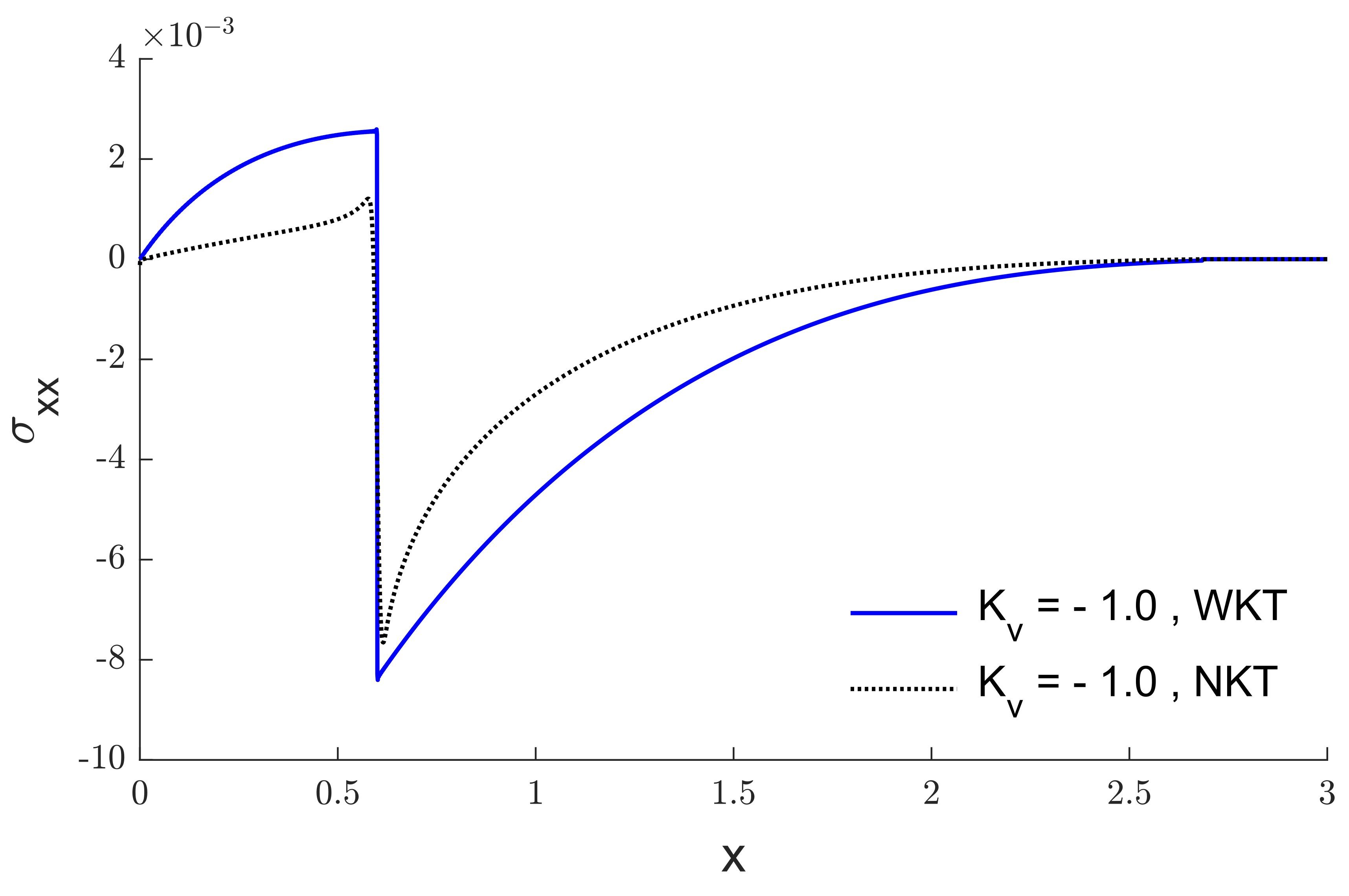
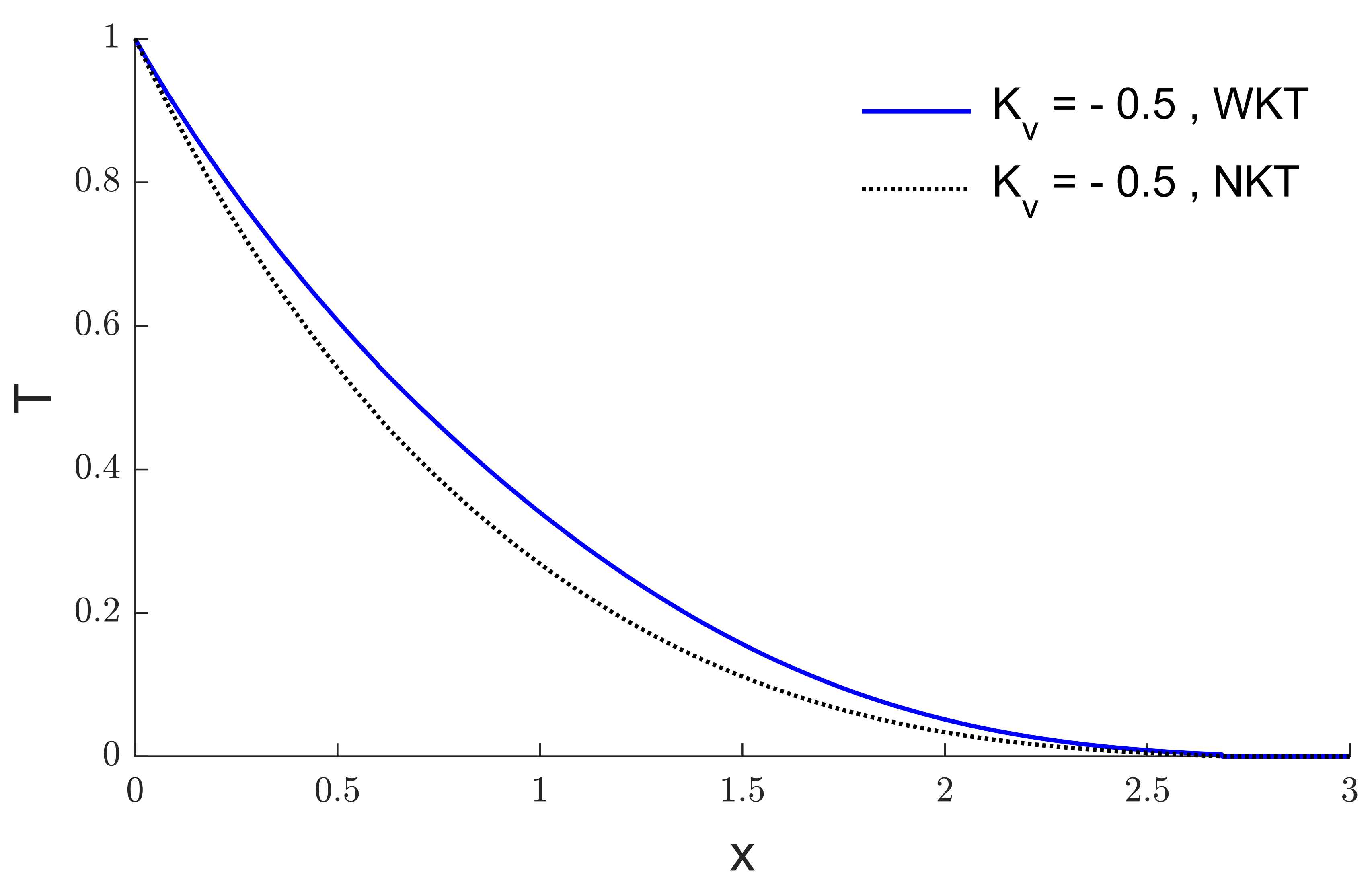

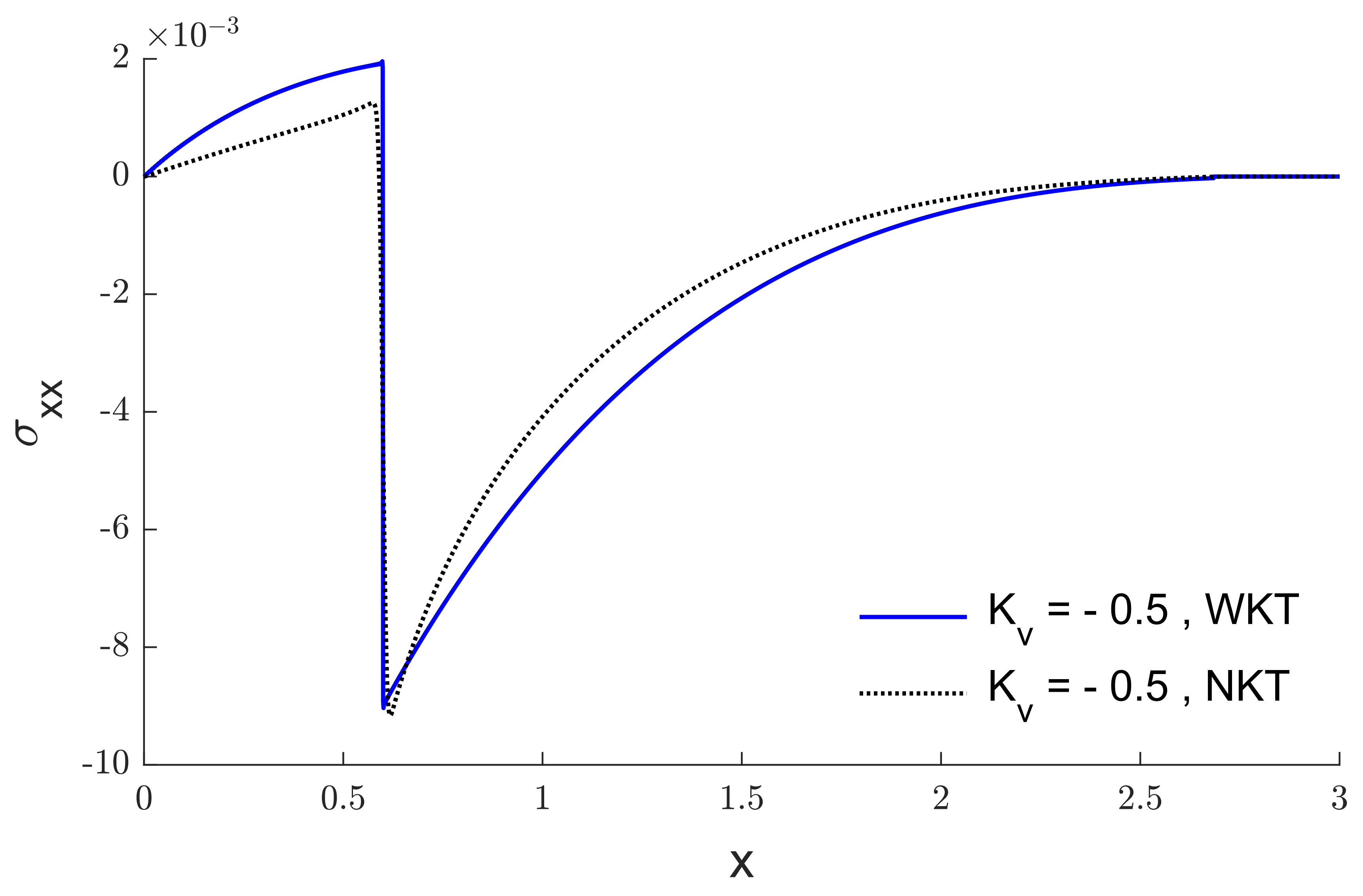
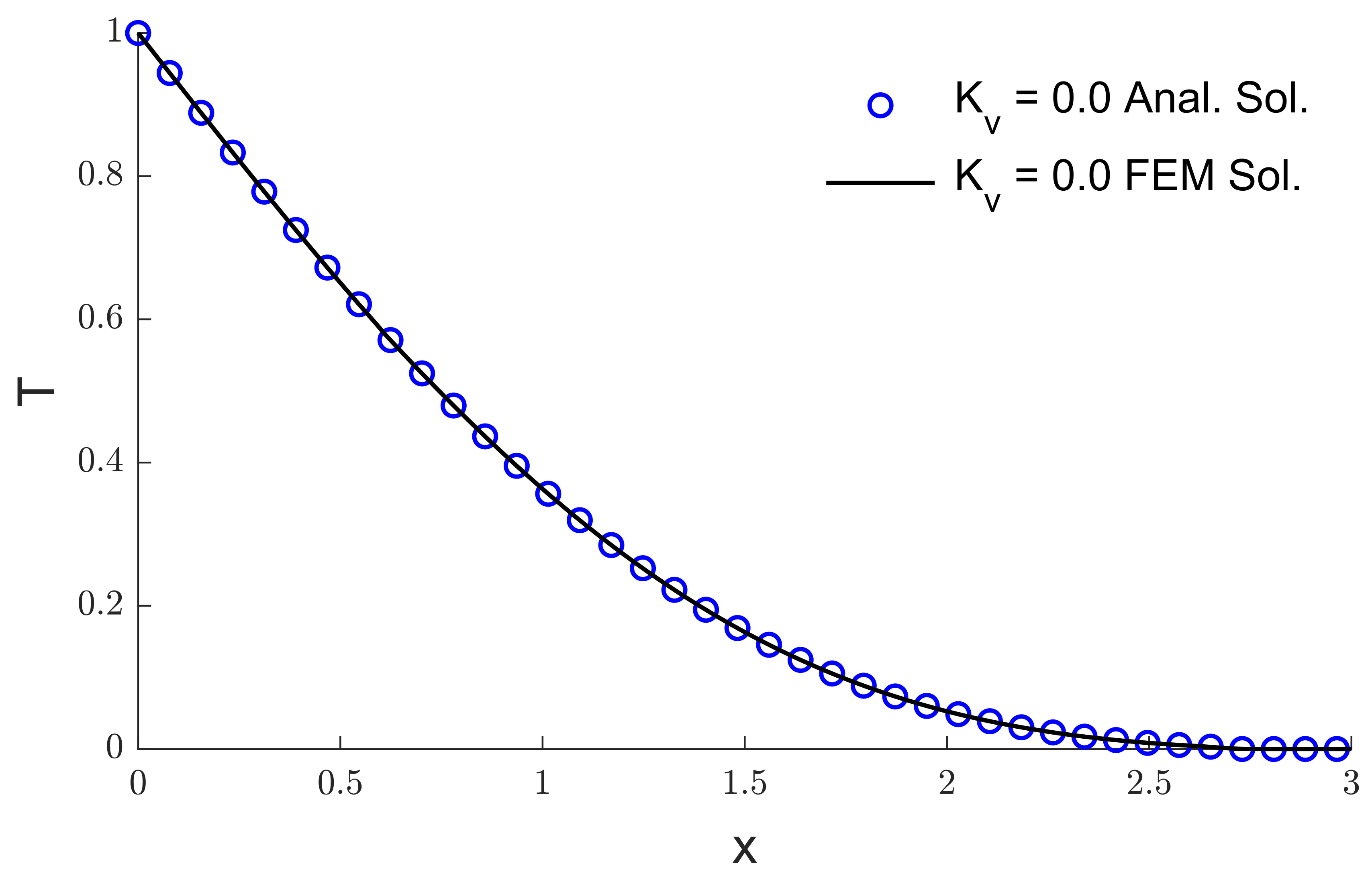
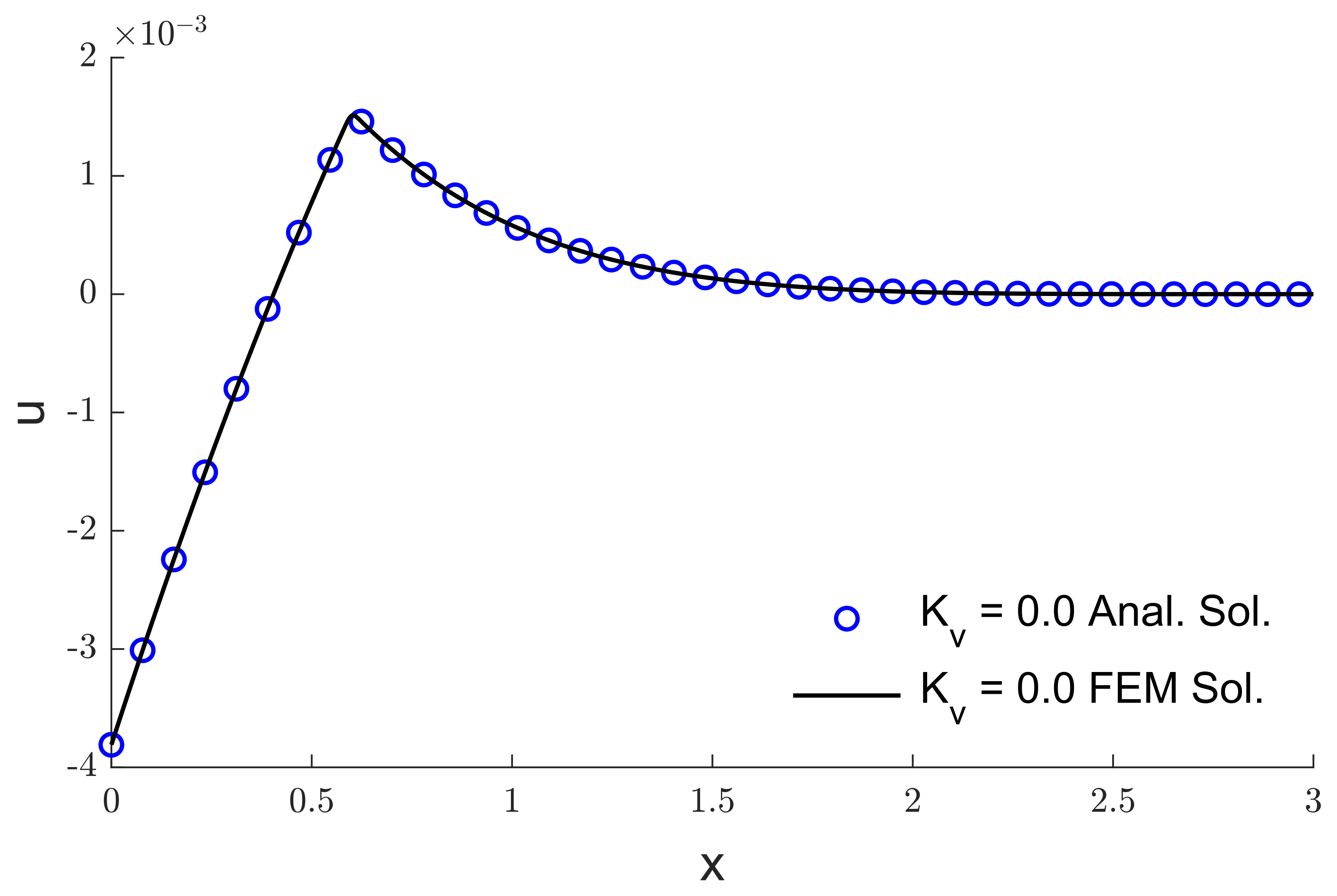
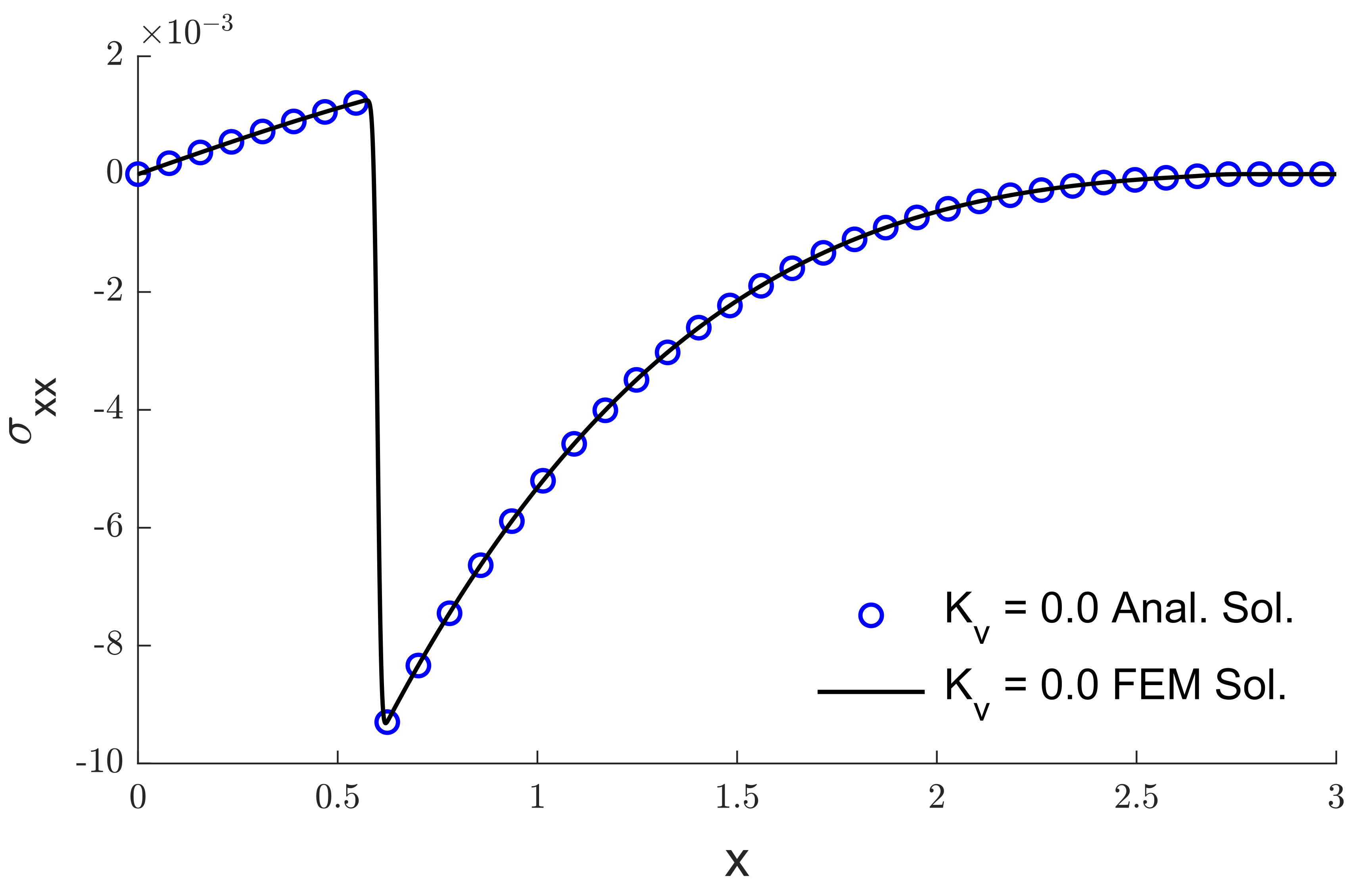
7. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Noda, N. Thermal stresses in materials with temperature-dependent properties. Appl. Mech. Rev. 1991, 44, 383–397. [Google Scholar]
- Lord, H.W.; Shulman, Y. A generalized dynamical theory of thermoelasticity. J. Mech. Phys. Solids 1967, 15, 299–309. [Google Scholar] [CrossRef]
- Youssef, H.M.; Abbas, I.A. Thermal shock problem of generalized thermoelasticity for an infinitely long annular cylinder with variable thermal conductivity. Comput. Methods Sci. Technol. 2007, 13, 95–100. [Google Scholar]
- Sherief, H.H.; Hamza, F.A. Modeling of variable thermal conductivity in a generalized thermoelastic infinitely long hollow cylinder. Meccanica 2016, 51, 551–558. [Google Scholar] [CrossRef]
- Othman, M.I. Lord-Shulman theory under the dependence of the modulus of elasticity on the reference temperature in two-dimensional generalized thermoelasticity. J. Therm. Stress. 2002, 25, 1027–1045. [Google Scholar] [CrossRef]
- Zenkour, A.M.; Abbas, I.A. A generalized thermoelasticity problem of an annular cylinder with temperature-dependent density and material properties. Int. J. Mech. Sci. 2014, 84, 54–60. [Google Scholar] [CrossRef]
- Abbas, I.A. Generalized magneto-thermoelasticity in a nonhomogeneous isotropic hollow cylinder using the finite element method. Arch. Appl. Mech. 2009, 79, 41–50. [Google Scholar] [CrossRef]
- Aboueregal, A.E.; Sedighi, H.M. The effect of variable properties and rotation in a visco-thermoelastic orthotropic annular cylinder under the Moore–Gibson–Thompson heat conduction model. Proc. Inst. Mech. Eng. Part L J. Mat. Des. Appl. 2021, 235, 1004–1020. [Google Scholar] [CrossRef]
- Xiong, C.; Guo, Y. Effect of Variable Properties and Moving Heat Source on Magnetothermoelastic Problem under Fractional Order Thermoelasticity. Adv. Mater. Sci. Eng. 2016, 2016, 5341569. [Google Scholar] [CrossRef]
- Singh, S.; Kumar, D.; Rai, K. Convective-radiative fin with temperature dependent thermal conductivity, heat transfer coefficient and wavelength dependent surface emissivity. Propuls. Power Res. 2014, 3, 207–221. [Google Scholar] [CrossRef]
- Zhang, H.; Shang, C.; Tang, G. Measurement and identification of temperature-dependent thermal conductivity for thermal insulation materials under large temperature difference. Int. J. Therm. Sci. 2022, 171, 107261. [Google Scholar] [CrossRef]
- Pan, W.; Yi, F.; Zhu, Y.; Meng, S. Identification of temperature-dependent thermal conductivity and experimental verification. Meas. Sci. Technol. 2016, 27, 075005. [Google Scholar] [CrossRef]
- Wang, Y.Z.; Zan, C.; Liu, D.; Zhou, J.Z. Generalized solution of the thermoelastic problem for the axisymmetric structure with temperature-dependent properties. Eur. J. Mech. A/Solids 2019, 76, 346–354. [Google Scholar] [CrossRef]
- Liang, W.; Huang, S.; Tan, W.S.; Wang, Y.Z. Asymptotic approach to transient thermal shock problem with variable material properties. Mech. Adv. Mater. Struct. 2019, 26, 350–358. [Google Scholar] [CrossRef]
- Wang, Y.Z.; Liu, D.; Wang, Q.; Zhou, J.Z. Thermoelastic interaction in functionally graded thick hollow cylinder with temperature-dependent properties. J. Therm. Stress. 2018, 41, 399–417. [Google Scholar] [CrossRef]
- Wang, Y.; Liu, D.; Wang, Q.; Zhou, J. Asymptotic solutions for generalized thermoelasticity with variable thermal material properties. Arch. Mech. 2016, 68, 181–202. [Google Scholar]
- Wang, Y.; Liu, D.; Wang, Q.; Zhou, J. Problem of axisymmetric plane strain of generalized thermoelastic materials with variable thermal properties. Eur. J. Mech. A/Solids 2016, 60, 28–38. [Google Scholar] [CrossRef]
- Wang, Y.; Liu, D.; Wang, Q.; Zhou, J. Effect of fractional order parameter on thermoelastic behaviors of elastic medium with variable properties. Acta Mech. Solida Sin. 2015, 28, 682–692. [Google Scholar] [CrossRef]
- Ezzat, M.A.; El-Bary, A.A. On thermo-viscoelastic infinitely long hollow cylinder with variable thermal conductivity. Microsyst. Technol. 2017, 23, 3263–3270. [Google Scholar] [CrossRef]
- Othman, M.I.A.; Abouelregal, A.E.; Said, S.M. The effect of variable thermal conductivity on an infinite fiber-reinforced thick plate under initial stress. J. Mech. Mater. Struct. 2019, 14, 277–293. [Google Scholar] [CrossRef]
- Xiong, C.B.; Yu, L.N.; Niu, Y.B. Effect of Variable Thermal Conductivity on the Generalized Thermoelasticity Problems in a Fiber-Reinforced Anisotropic Half-Space. Adv. Mater. Sci. Eng. 2019, 2019, 8625371. [Google Scholar] [CrossRef]
- Abbas, I.; Hobiny, A.; Marin, M. Photo-thermal interactions in a semi-conductor material with cylindrical cavities and variable thermal conductivity. J. Taibah Univ. Sci. 2020, 14, 1369–1376. [Google Scholar] [CrossRef]
- Alzahrani, F. The Effects of Variable Thermal Conductivity in Semiconductor Materials Photogenerated by a Focused Thermal Shock. Mathematics 2020, 8, 1230. [Google Scholar]
- Ghasemi, S.E.; Hatami, M.; Ganji, D.D. Thermal analysis of convective fin with temperature-dependent thermal conductivity and heat generation. Case Stud. Therm. Eng. 2014, 4, 1–8. [Google Scholar] [CrossRef]
- Khoukhi, M.; Abdelbaqi, S.; Hassan, A. Transient temperature change within a wall embedded insulation with variable thermal conductivity. Case Stud. Therm. Eng. 2020, 20, 100645. [Google Scholar] [CrossRef]
- Othman, M.I.A.; Tantawi, R.S.; Eraki, E.E.M. Effect of initial stress on a semiconductor material with temperature dependent properties under DPL model. Microsyst. Technol. 2017, 23, 5587–5598. [Google Scholar] [CrossRef]
- Hobiny, A.; Alzahrani, F.; Abbas, I.; Marin, M. The effect of fractional time derivative of bioheat model in skin tissue induced to laser irradiation. Symmetry 2020, 12, 602. [Google Scholar] [CrossRef]
- Abbas, I.A. A GN model for thermoelastic interaction in an unbounded fiber-reinforced anisotropic medium with a circular hole. Appl. Math. Lett. 2013, 26, 232–239. [Google Scholar] [CrossRef]
- Li, C.; Guo, H.; Tian, X.; Tian, X. Transient response for a half-space with variable thermal conductivity and diffusivity under thermal and chemical shock. J. Therm. Stress. 2017, 40, 389–401. [Google Scholar] [CrossRef]
- Marin, M.; Florea, O. On temporal behaviour of solutions in thermoelasticity of porous micropolar bodies. An. Stiint. Univ. Ovidius Constanta Ser. Mat. 2014, 22, 169–188. [Google Scholar] [CrossRef]
- Bhatti, M.M.; Marin, M.; Zeeshan, A.; Abdelsalam, S.I. Editorial: Recent Trends in Computational Fluid Dynamics. Front. Phys. 2020, 8, 593111. [Google Scholar] [CrossRef]
- Abouelregal, A.E.; Marin, M. The Size-Dependent Thermoelastic Vibrations of Nanobeams Subjected to Harmonic Excitation and Rectified Sine Wave Heating. Mathematics 2020, 8, 1128. [Google Scholar] [CrossRef]
- Moradnouri, A.; Vakilian, M.; Hekmati, A.; Fardmanesh, M. Multi-segment Winding Application for Axial Short Circuit Force Reduction Under Tap Changer Operation in HTS Transformers. J. Supercond. Nov. Magn. 2019, 32, 3171–3182. [Google Scholar] [CrossRef]
- Youssef, H. State-space approach on generalized thermoelasticity for an infinite material with a spherical cavity and variable thermal conductivity subjected to ramp-type heating. Can. Appl. Math. Quaterly 2005, 13, 369–390. [Google Scholar]
- Abbas, I.A.; Kumar, R. Deformation due to thermal source in micropolar generalized thermoelastic half-space by finite element method. J. Comput. Theor. Nanosci. 2014, 11, 185–190. [Google Scholar]
- Abbas, I.A. Eigenvalue approach on fractional order theory of thermoelastic diffusion problem for an infinite elastic medium with a spherical cavity. Appl. Math. Model. 2015, 39, 6196–6206. [Google Scholar] [CrossRef]
- Othman, M.I.A.; Abbas, I.A. Eigenvalue approach for generalized thermoelastic porous medium under the effect of thermal loading due to a laser pulse in DPL model. Indian J. Phys. 2019, 93, 1567–1578. [Google Scholar] [CrossRef]
- Kumar, R.; Miglani, A.; Rani, R. Eigenvalue formulation to micropolar porous thermoelastic circular plate using dual phase lag model. Multidiscip. Model. Mater. Struct. 2017, 13, 347–362. [Google Scholar] [CrossRef]
- Kumar, R.; Miglani, A.; Rani, R. Analysis of micropolar porous thermoelastic circular plate by eigenvalue approach. Arch. Mech. 2016, 68, 423–439. [Google Scholar]
- Gupta, N.D.; Das, N.C. Eigenvalue approach to fractional order generalized thermoelasticity with line heat source in an infinite medium. J. Therm. Stress. 2016, 39, 977–990. [Google Scholar] [CrossRef]
- Santra, S.; Lahiri, A.; Das, N.C. Eigenvalue Approach on Thermoelastic Interactions in an Infinite Elastic Solid with Voids. J. Therm. Stress. 2014, 37, 440–454. [Google Scholar] [CrossRef]
- Baksi, A.; Roy, B.K.; Bera, R.K. Eigenvalue approach to study the effect of rotation and relaxation time in generalized magneto-thermo-viscoelastic medium in one dimension. Math. Comput. Model. 2006, 44, 1069–1079. [Google Scholar] [CrossRef]
- Das, N.C.; Lahiri, A.; Giri, R.R. Eigenvalue approach to generalized thermoelasticity. Indian J. Pure Appl. Math. 1997, 28, 1573–1594. [Google Scholar]
- Stehfest, H. Algorithm 368: Numerical inversion of Laplace transforms [D5]. Commun. ACM 1970, 13, 47–49. [Google Scholar] [CrossRef]
- Abbas, I.A.; Abdalla, A.E.N.N.; Alzahrani, F.S.; Spagnuolo, M. Wave propagation in a generalized thermoelastic plate using eigenvalue approach. J. Therm. Stresses 2016, 39, 1367–1377. [Google Scholar] [CrossRef]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Hobiny, A.; Abbas, I. The Effects of Variable Thermal Conductivity in Thermoelastic Interactions in an Infinite Material with and without Kirchhoff’s Transformation. Mathematics 2022, 10, 4176. https://doi.org/10.3390/math10224176
Hobiny A, Abbas I. The Effects of Variable Thermal Conductivity in Thermoelastic Interactions in an Infinite Material with and without Kirchhoff’s Transformation. Mathematics. 2022; 10(22):4176. https://doi.org/10.3390/math10224176
Chicago/Turabian StyleHobiny, Aatef, and Ibrahim Abbas. 2022. "The Effects of Variable Thermal Conductivity in Thermoelastic Interactions in an Infinite Material with and without Kirchhoff’s Transformation" Mathematics 10, no. 22: 4176. https://doi.org/10.3390/math10224176
APA StyleHobiny, A., & Abbas, I. (2022). The Effects of Variable Thermal Conductivity in Thermoelastic Interactions in an Infinite Material with and without Kirchhoff’s Transformation. Mathematics, 10(22), 4176. https://doi.org/10.3390/math10224176






