1. Introduction
Vector-borne infectious diseases are among the serious health problems faced by many tropical countries. An example is the dengue disease, which is transmitted by mosquitoes that may lead to fatality in some cases. Four identified strains of flavivirus, namely DEN-1, DEN-2, DEN-3, and DEN-4, are responsible for the disease. Although it is reported that some mosquitoes, such as
Aedes albopictus, are able to transmit the disease, but the main vector which is responsible for the transmission is the female of
Aedes aegypti. Due to frequent, large outbreaks of the disease in many countries, some attempts are continuously undertaken to eliminate the disease, such as fogging the adult-class of the mosquitoes using an insecticide and introducing predators to the larvae-class of the mosquitoes [
1,
2]. Beside those attempts, several efforts, such as developing a safe vaccine that can protect humans from all known strains of dengue viruses are being developed, and some other means have already become available as common practices [
3,
4].
Mathematical models have been known among the tools to understand the phenomena of the transmission of infectious diseases for a long time [
5,
6]. Many studies have been devoted to dengue dynamic modeling [
7,
8,
9,
10]. Various complexities considering many important factors, such as physiological- and age-structures, have been added to existing models to increase the realism of the models. Many scientists believe that these are important factors that should be included in population dynamic modeling in general [
11,
12,
13,
14,
15,
16]. The authors in [
17] have shown the contribution of age structure in some important biological processes, such as therapeutic consequences in a disease cure. The theory of age structure in the general population model is well presented in a seminal book [
18]. In disease dynamic modeling with direct transmission or with non-transmitted disease, examples that incorporate age structure in the models are abundant [
19,
20,
21,
22,
23]. However, although many mathematical models have been devoted to address issues in dengue disease transmission, most of the authors have ignored age structure, with few exceptions, such as [
24,
25,
26]. Some authors have studied age structure less explicitly, for example, by only looking at the effects of age on a certain population parameter, such as survival rates [
19,
27].
In this paper we discuss an SIR dengue transmission model with age-dependent survival rates by generalizing the model in [
19] to include host-vector interactions, assuming that the survival rate of individuals varies as their age goes up by following a certain function. Here we assume that the function is monotonically non-increasing with respect to age. The underlying model is closely related to the works in [
28,
29], but here we perform a more rigorous and complete analysis. The former work [
28] applied the model without examining the mathematical properties of the model, while the latter [
29] discussed some preliminary properties of the model. The existence of a solution to a system of equations and its stability to a small perturbation is vital in providing a sound recommendation to confine the spread of disease represented by the system of those equations. The works in [
28,
29] have claimed the existence and stability of the non-trivial solution for a certain threshold value without giving the proof of it analytically. In this paper, we show the proof of the existence of the trivial and non-trivial solutions of the model and discuss the stability properties of the solutions. We also show that there is an endemic threshold in which the disease disappears whenever the threshold value is below one and the disease will stay endemic whenever the threshold value is above one. Furthermore, it will be shown that the critical level of vaccination rule generalizes to the age-structured host-vector transmission model. This work is regarded as necessary to support the application discussed in [
28], where otherwise the validity of the recommendation based on the model therein is questionable.
Following [
28], the model is then applied to assess the presence of the wolbachia infected mosquito population to control the natural mosquito population. Recently, many scientists have pointed out that an introduction of bacteria from the genus wolbachia into the vector mosquitoes may reduce the transmission of dengue disease [
30,
31]. Wolbachia infection reduces the biting rate of the dengue fever mosquito,
Aedes aegypti, by destroying the mosquito’s proboscis so that it is difficult to penetrate human skin. The infection also reduces the life span of the mosquitoes [
32]. It is reported that the use of wolbachia infection in mosquitoes seems prospective in controlling dengue disease. However, a study regarding its effect compared to other control strategies, such as doing nothing and vaccination, from different analogous/counterpart models is still needed to show the robustness of this kind of attempt in controlling dengue disease. This paper aims to fill this gap via mathematical modeling by first developing a different kind of dengue transmission model, i.e., by constructing a system of integral equations, followed by its application in comparing the transmission between the cases of absence and presence of wolbachia in the system. In this model (in the presence of a wolbachia infected population) we assume that the mosquito’s life expectancy and biting rate decrease due to the presence of wolbachia bacterial infection in the mosquito population.
2. Materials and Methods
Brauer in [
19] discussed a mathematical model for an epidemic of
S and
I compartments in which he assumed a permanent infection in the form of a system of integral equations. Later on, this model was generalized into an SIR case in [
29]. The model is closely related to the SIR model in [
33]. Like the authors in [
19,
29], the authors in [
33] consider generational recruitment as one of the vital dynamics in their model. However, other complexities, such as the dependency of survival on age, are not considered in [
33] but are taken into account in [
19,
29]. In [
19,
29], the authors assume a direct transmission of infection occurs to a susceptible individual from an infective individual. In the present paper we generalize their models to include vector-born transmitted disease by assuming indirect transmission of the disease, such as in dengue disease transmission, in which human infection is caused by infective mosquitoes (not an infective human). We also include recovery in the model; hence the disease is not permanent.
To formulate the model, we assume that the host population
is divided into three compartments, namely susceptibles
infectives
, and recovered individuals
and hence
We assume that recovered host individuals are immune to the disease. However, we assume that infective vectors remain infective for life. This is because the duration of the disease is relatively long compared to the short life period of the mosquitoes. Hence, the vector population only has two compartments, namely susceptibles
and infectives
to form
Recruitment rates for the host and the vector are
and
with death rates
and
respectively. The disease transmission probability from vector to host and from host to vector are given by
and
respectively. Furthermore, it is assumed that there exist the functions
and
which describe the fractions of the host and vector populations that survive to the age of
or more. These functions are non-negative monotonically decreasing with respect to age, satisfying
and
. These functions are introduced to mimic the age structure effect on the survival rates. The functions are closely related to the probability of being alive at time
t0 +
t, provided an individual is alive at time
t0 as suggested by [
33]. The difference is that in this paper we use a decreasing function with respect to age, while in [
33] the authors assume a decreasing function independent of age (see
Section 4 as an example).
Here we assume that the life expectancy of the host is finite,
so that
The notations
and
will be used to indicate the portion of offspring that survive to the age
or more. The number of susceptibles at time
is given by
with
and
, since
is the per capita rate of infection in the host population at time
. Here,
is the fraction of susceptibles of the age
that survive to time
or more and are still free from dengue. Furthermore, the number of infective hosts at time
is given by
if we assume that the rate of recovery is given by
, with
Here
is the fraction of the infective host of the age
that are alive at least up until time
and still have not recovered yet. Furthermore, since
, then we have
with
and
as the fraction of the recovered host of the age
that survive at least up to time
. Note that, throughout the paper, we simplify some notations using an over line symbol which is defined similarly to the symbol that was just described for the
notation. Note that the transmission dynamics in the host population are given by Equations (4)–(6).
Similarly, since
with
, the transmission dynamics in the vector population are given by
with
, and
, and
with
Hence, Equations (4)–(6), (8) and (9) govern the complete model for the SIR-SI host-vector dengue transmission model. In the next section we analyze these equations and look for the equilibria of the model. We also look for a threshold epidemic
which determines the existence of the non-trivial equilibrium. In the subsequent section we also show that the stability of the non-trivial equilibrium point is indeed determined by this threshold.
3. Results
3.1. The Boundedness of the Solution
The boundedness of the solution for the human compartment is readily given from the fact that for all we have , so that and for all Analogously, we also have the boundedness of the solution for the vector compartment, i.e., and for all
3.2. The Positivity of the Solution
First, let us see the solutions for the human compartment. It is clear from (3) that for all we have . Considering for all , then we have the number of susceptibles from (4), since and . The number of infectives is given by (5) to be since we have also . Moreover, from (6), the recovery number is since and . This proves that and for all Finally, the positivity of the solutions for the vector compartment, i.e., and for all , can be similarly proven.
3.3. The Existence of a Non-Trivial (Endemic) Equilibrium Point
In the epidemic modeling literature, the existence of a non-trivial or endemic equilibrium point is very important. This existence depends critically on a threshold number, which is often called the basic reproduction number [
34,
35]. In this section, we will formulate the basic reproduction number for the model discussed here. The basic reproduction number (
) is defined as “the expected number of secondary cases produced, in a completely susceptible population, by a typical infective individual” [
34]. In general, it can determine the stability of the non-endemic and endemic equilibria, in the sense that if
then the non-endemic equilibrium is asymptotically stable, but unstable otherwise. Moreover, if
then the endemic equilibrium is asymptotically stable [
36] In our model, we also show that when
, then the non-trivial equilibrium point is unique.
Since we are interested in the long-term behavior of the model, let us consider the limiting condition of (3) to (9), as in [
19]. It is clear that
since
is a decreasing function. Hence, whenever
the system consisting of these equations has the same behavior as the system of equations
Here, we have (10) to (14) as a representation of the dynamics of an SIR-SI age-structured host-vector model.
The equilibria of the system, if they exist, are given by
with
and
satisfying
Note that (15) can be written as
with
and
It is easy to see that
is a trivial or disease-free equilibrium. To find a non-trivial endemic equilibrium, we could observe that
is bounded and
This means that the function
(
) is concave downward. In order for the equation
to have a solution, we need
. By considering this condition, together with the differentiation of Equation (17) with respect to
it will result in
. Next, by letting
and
, a unique non-trivial value of
exists whenever
is greater than 1. The existence of the corresponding non-trivial value of
follows immediately. The left-hand side of (19) is called the threshold number or the basic reproduction number of dengue transmission. We conclude that an endemic equilibrium
with
and
occurs whenever
.
3.4. The Stability of the Equilibria
To investigate the stability of the equilibria, we use the method in [
19] and the Gronwall-like inequality lemma therein.
Lemma 1 [19].Let be a bounded non-negative continuous function satisfyingwhereis a non-negative continuous function withandis a non-negative continuous function with.
Then.
It is also shown in [
19] that the lemma is still true if the inequality in the lemma is replaced by
Further, we generalize Lemma 1 as follows.
Lemma 2. Let be bounded non-negative continuous functions satisfyingwhere is non-negative continuous with and is non-negative continuous with .
Then.
Proof. A direct proof is given in [
37]. The following is an alternative proof as a consequence of Lemma 1.
and hence
with
and
Lemma 1 gives
and this is sufficient to conclude that
. □
3.4.1. The Stability of the Trivial (Disease-Free) Equilibrium
To investigate the stability of the equilibrium we will assume that
. Consider the equilibrium infective class
and the following inequalities
Hence, from (5) and (9) we have
If we further assume that and then using Lemma 2 we conclude that and . This shows that the disease-free (trivial) equilibrium is globally stable irrespective of the initial values and .
3.4.2. The Stability of the Non-Trivial (Endemic) Equilibrium
The endemic equilibrium, i.e.,
with
and
, occurs if and only if
. Let us see the perturbations of
and
respectively, by
and
Define
and
and substitute these quantities into Equation (5) to obtain
or alternatively
with
and
Since
is the equilibrium point, then we have
which is equivalent to
and can be simplified into
with
satisfying
and hence we have
By defining
and
we have an equation in the form of
in Lemma 2. Similarly, we can obtain
Next, if
and
then we have an equation in the form of
in Lemma 2. It is shown in
Appendix A that
. Furthermore,
Appendix B shows that Lemma 2 is still true if we replace the condition
with a weaker condition
. Hence, we conclude that
and
meaning that the endemic equilibrium is globally stable irrespective of the initial values
and
.
Remark 1. Note that in Section 3.4.1, we have shown that the disease-free equilibrium is globally stable, irrespective of the initial valuesand, whenever.
Meanwhile, inSection 3.4.2, we have shown that the endemic equilibrium is stable, irrespective of the initial valuesand, whenever.
As pointed out by one of the reviewers, it is usually tough to prove results concerning the global stability of endemic equilibrium. Fortunately, by following the idea in [
19],
we have a result for a priori estimate of a bounded non-negative function satisfying the condition in Lemma 2 which we use to show that every solution of the limit system (11) and (14) approaches and , respectively, for any initial values and , whenever .
This leads to the global stability of the endemic equilibrium .
Remark 2. In the previous remark, constitutes a sufficient condition for the global stability of the endemic equilibrium .
It also serves as a necessary condition for the permanence of the system. In biology, permanence is a concept that studies the long-term survival of each species in a set of populations [
38].
There are many criteria that have been proposed to express the notion of this long-term survival, such as permanence and persistence. Initially, the idea of permanence goes back at least to Lewontin [
39],
who asserted that sometimes it is important to know the presence or absence of species, regardless of some variation in their abundance from time to time. In an epidemiological context, the presence of infective species or the long-term survival of infective species is an unwanted situation, while its absence from the system is the most wanted situation and is the target of any man-made intervention. There are a lot of slightly different definitions of permanence in literature [
40].
By referring to [
38],
the system (4)–(6), (8) and (9) is said to be permanent if there are numbers with such that, given any initial value , there is such that Considering the boundedness of the solution, this condition is met by choosing, regardless of the value of the basic reproduction number. Meanwhile, by considering the positivity of the solution, we may chooseprovided that the basic reproduction numberand all of the infima are not zero. Hence, in an epidemiological context, there is a strong relationship between the basic reproduction number and the permanence of the system. In this context, permanence is interpreted as an endemic or long-term circulation of the disease. Here, we do not attempt to prove the permanence of the system, instead we prove the stability of the disease-free equilibrium whenever the basic reproduction numberand the stability of the endemic equilibrium whenever the basic reproduction number. A more detailed relationship between the notions of the basic reproduction number and the permanence of an epidemic model is currently under investigation.
4. Numerical Examples and Discussions
The Equations (4)–(6), (8) and (9) are a system of Volterra integral equations of the second kind. Numerical treatise on how to solve this system can be found in [
41,
42,
43,
44,
45] in which some numerical schemes are presented therein. We use Maple 18 from Maplesoft to implement the scheme discussed in [
45]. For these numerical examples we use the exponential survival rate given by
and
for human and mosquito populations, respectively. The parameters used in the numerical examples are shown in
Table 1, composing several data sets. The values are chosen as close as possible to known parameters in literature [
28,
46,
47,
48,
49], while the initial values are chosen to be the same for all data sets. The data sets reflect different degrees of basic reproduction numbers, i.e., very large, large, medium, small, and very small basic reproduction numbers.
Table 1 also presents the basic reproduction number by computing the formula in Equation (19) for each data set. We deliberately chose such a combination of data sets to illustrate different values of the basic reproduction number to the dynamics of the disease transmission. For the first example, we will discuss the dynamic of the system which has a very large value of the basic reproduction number, i.e.,
166.321.
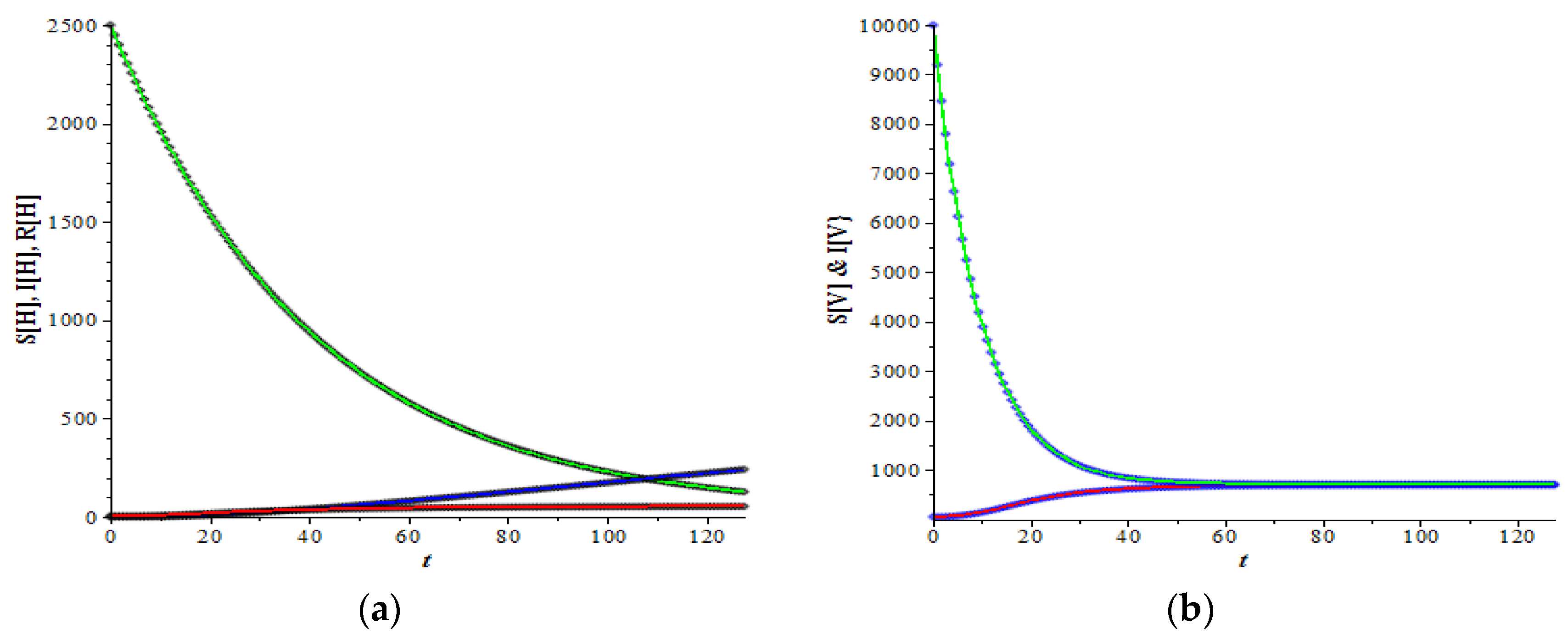
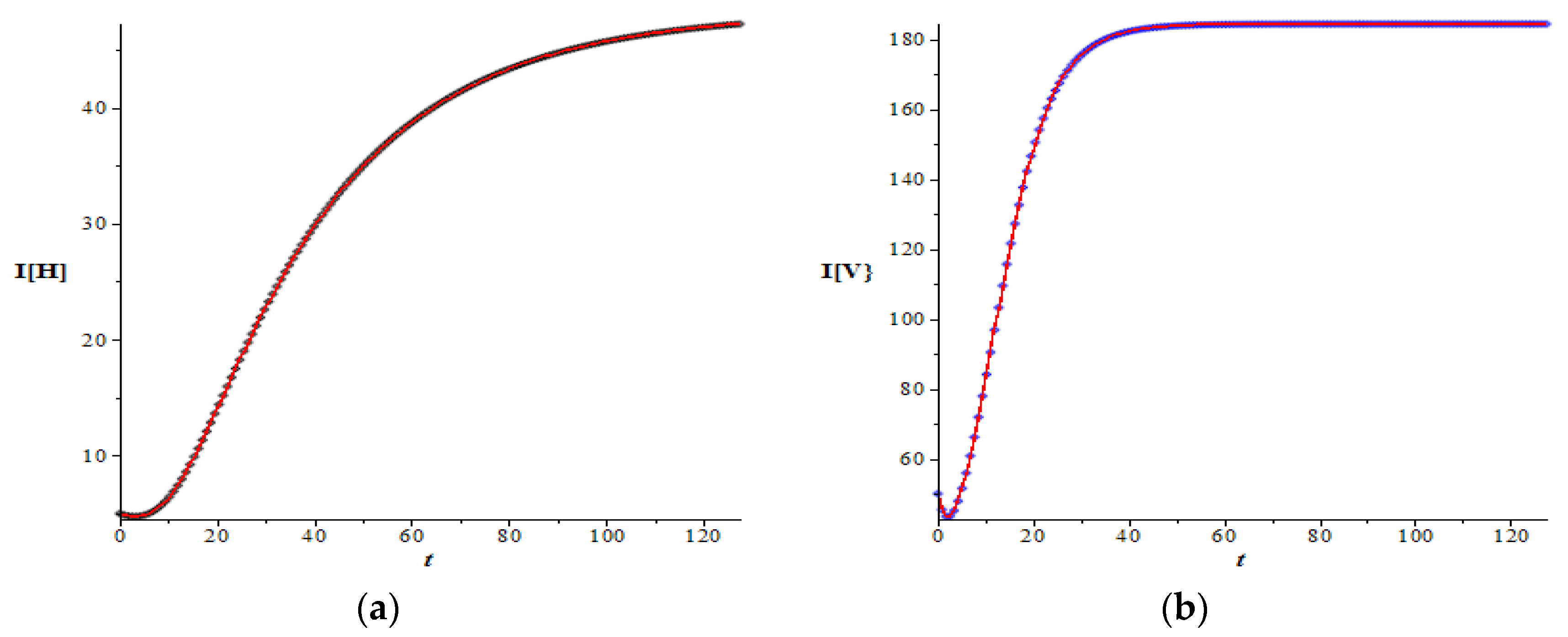
Figure 1 and
Figure 2 show the graphs of host and vector dynamics for various combinations of plots resulting from a data set which has an very large basic reproduction number, i.e.,
166.321. As expected by the theory in the previous section, for this large basic reproduction number, both the number of infected hosts and infected mosquitoes increase as time increases (
Figure 1a,b). The increase is more apparent when the figures are zoomed in (
Figure 1c,d). Both infected populations approach their non-trivial equilibrium, respectively.
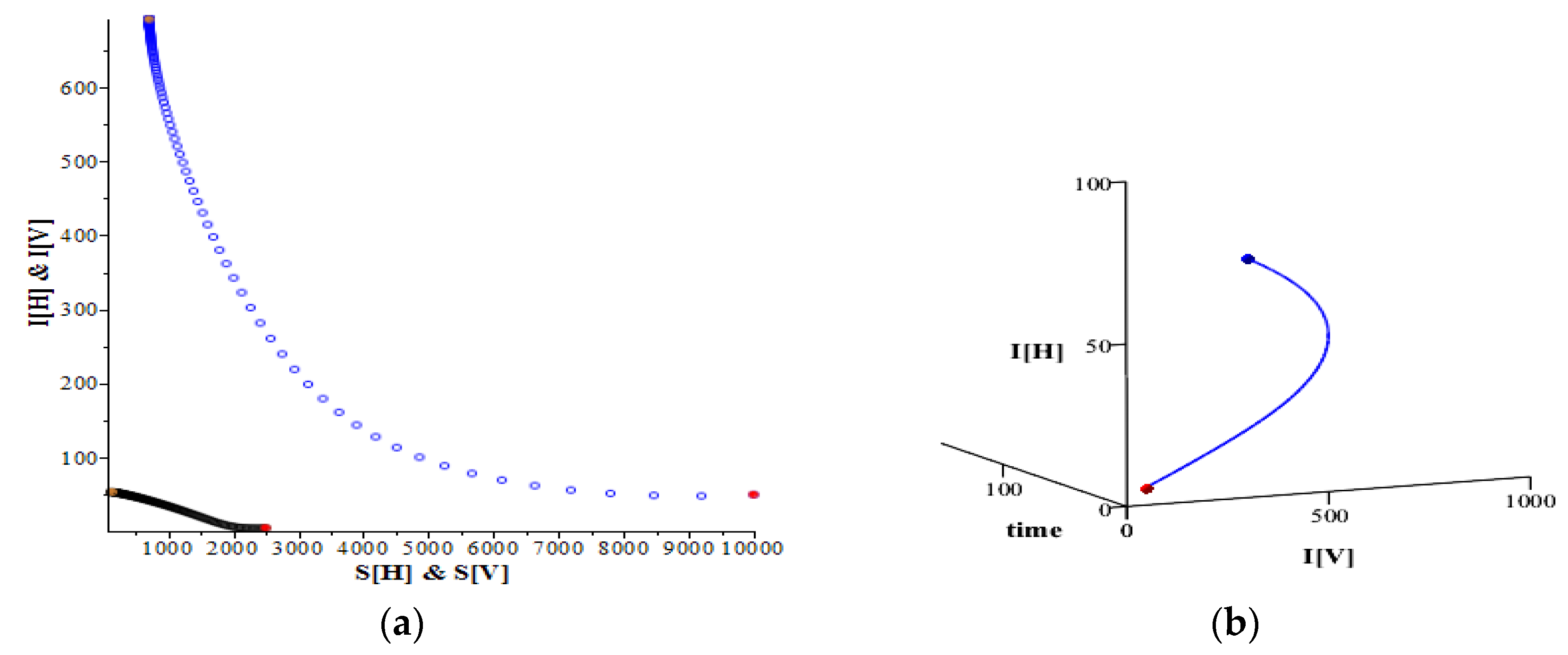
Figure 2a shows that the trajectory of these two infective populations travel to approach the equilibrium (
= (53.7291…, 708.6784…).
Figure 2b reveals the same case by showing the trajectory of these two infective populations in a 3D graph.
For the second example, we present the dynamics of the dengue transmission system with a medium value of the basic reproduction number, i.e.,
2.772. The results can be seen in
Figure 3 and
Figure 4.
Figure 3 and
Figure 4 show the graphs of the host and vector dynamics for various combinations of plots resulting from a data set which has a medium basic reproduction number, i.e.,
2.772. Compared to the similar graphs in
Figure 1 and
Figure 2, where both the infective host and infective vector increase as time increases, here only the infective host increases (
Figure 3c), while the vector decreases from a relatively high number initial value to a lower value (
Figure 3d).
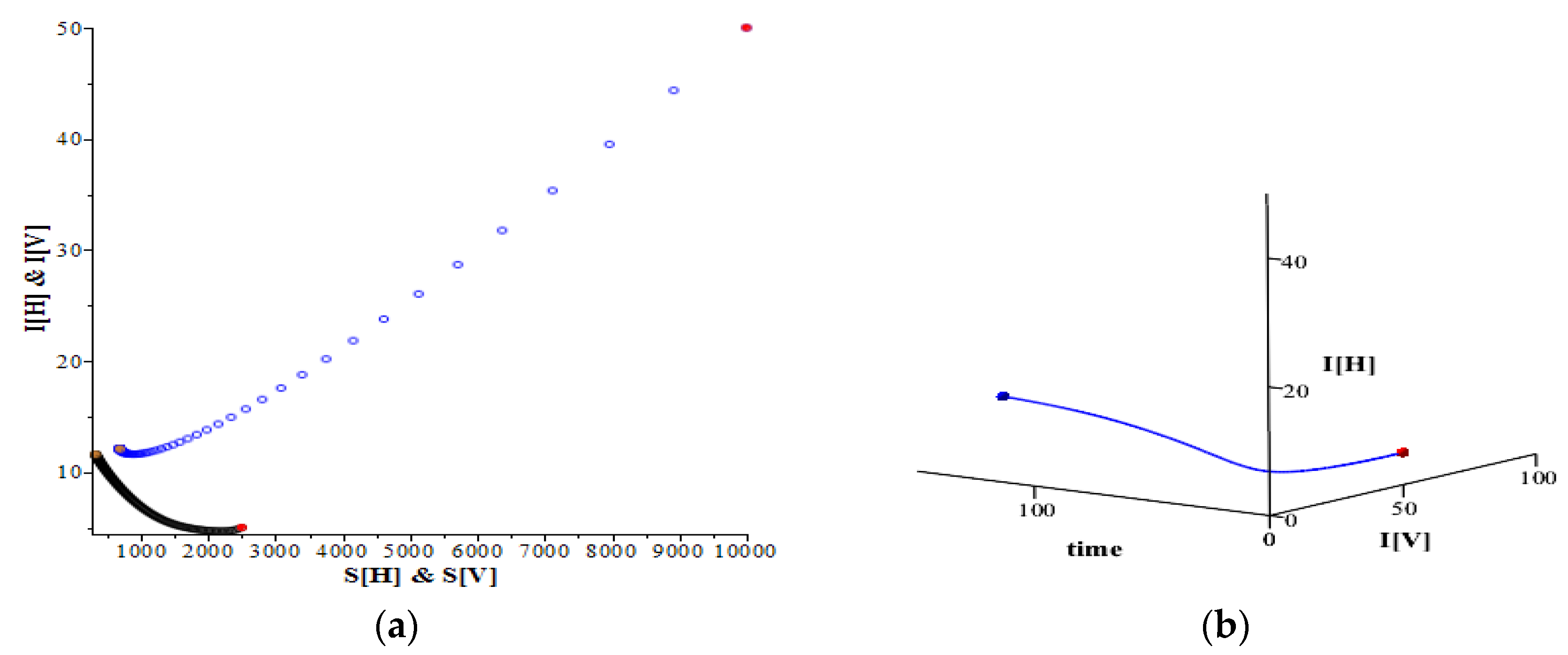
Figure 4a shows that the trajectory of these two infective populations travel to approach the equilibrium (
= (11.5844…, 12.0701…). Clearly the number of infective hosts only increase a relatively small amount from 5 to 11, while the infective mosquito number goes down from 50 to 12. This is due to the small rate of infection for the mosquitoes (
0.0005) compared to that in the previous example (
0.0075), together with the increase in the mortality rate (
1/7) compared to that in the previous example (
1/14). This result is expected by the theory in the previous section.
Figure 4b reveals the same case by showing the trajectory of these two infective populations in a 3D graph.
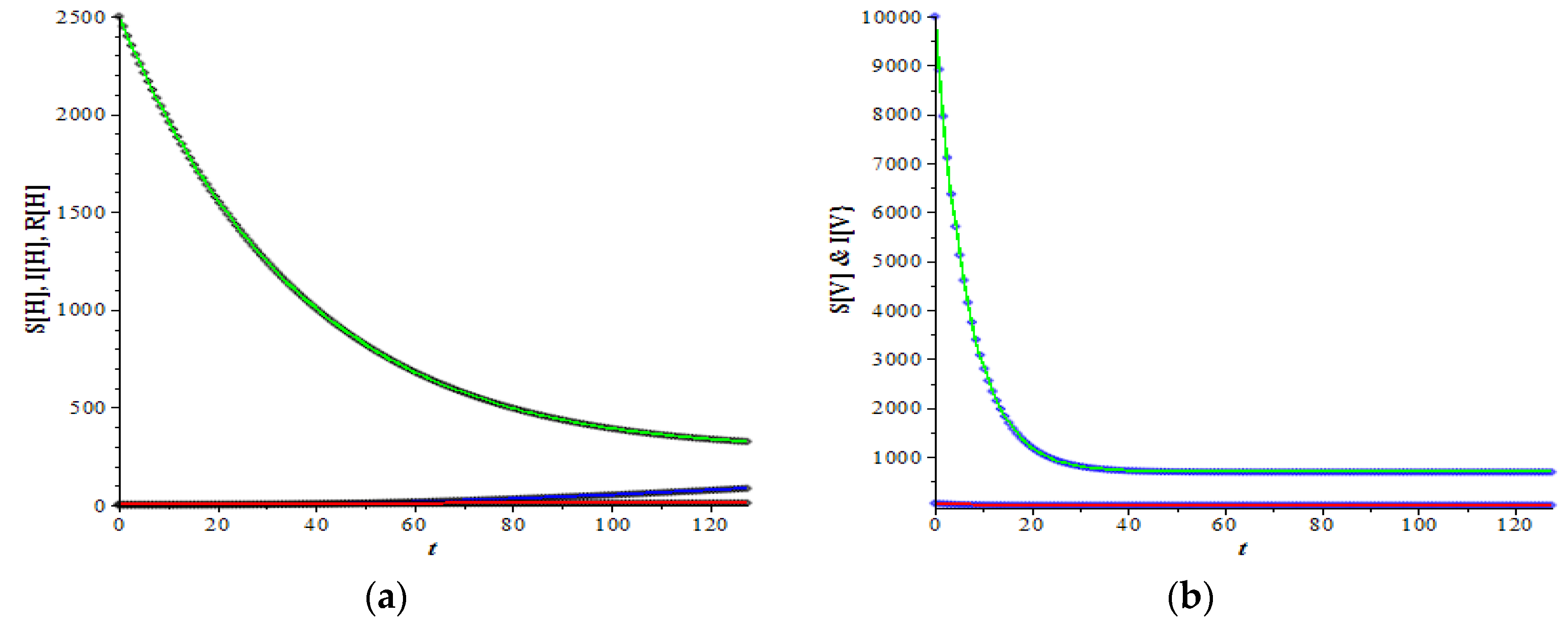
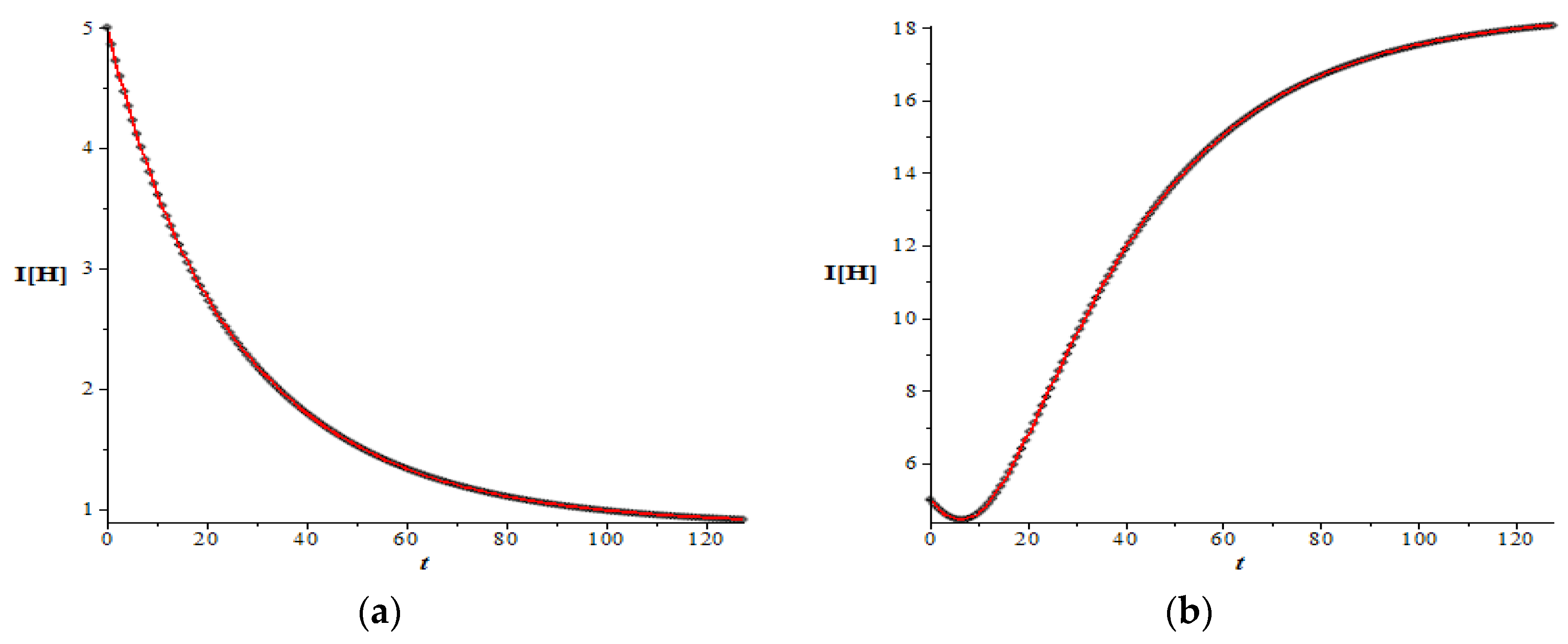
The next example is the dynamic of dengue transmission in which the basic reproduction number is very small, given by the last data set in
Table 1. In this case, the basic reproduction number is
0.042. In line with the theory presented in the previous section, in this case both of the infective populations do not increase at all (
Figure 5).
Figure 6 also reveals the same results for this very small basic reproduction number.
4.1. The Effect of Vaccination
In this section, we take into account vaccination and the introduction of wolbachia infection into the previous model. Here, it is assumed that, in the host population, a portion
of them is vaccinated at birth, then the number of the susceptible host population at time
in (4) changes into
Assuming that vaccination is perfect, then all vaccinated individuals will be immune and are removed to the vaccination compartment, which has dynamics
The number of infected humans is
and hence, the number of those who are still infectious is given by
The number of individuals in the recovered class can be obtained from
that is,
The equations for the mosquitoes are the same as in the case of no vaccination, hence the full system of the age-structured host-vector dengue model is given by Equations (26)–(29), (8) and (9). Using the same argument as before, it can be shown that the effective reproduction number is given by
where
represents the basic reproduction number. The expression in (30) is often called the effective reproduction number. From the last expression of the effective reproduction number, we conclude that the endemic equilibrium disappears whenever
The quantity
can be defined as the critical vaccination level. The value of the critical vaccination level certainly depends on the value of the basic reproduction number. It is well known in many studies that for the case of the direct transmission disease model, we could estimate the threshold number
by using the ratio of life expectancy and mean age at infection. If we choose the survival function to be a negative exponential function, then this estimation is still valid for the indirect transmission model discussed in the previous section [
28].
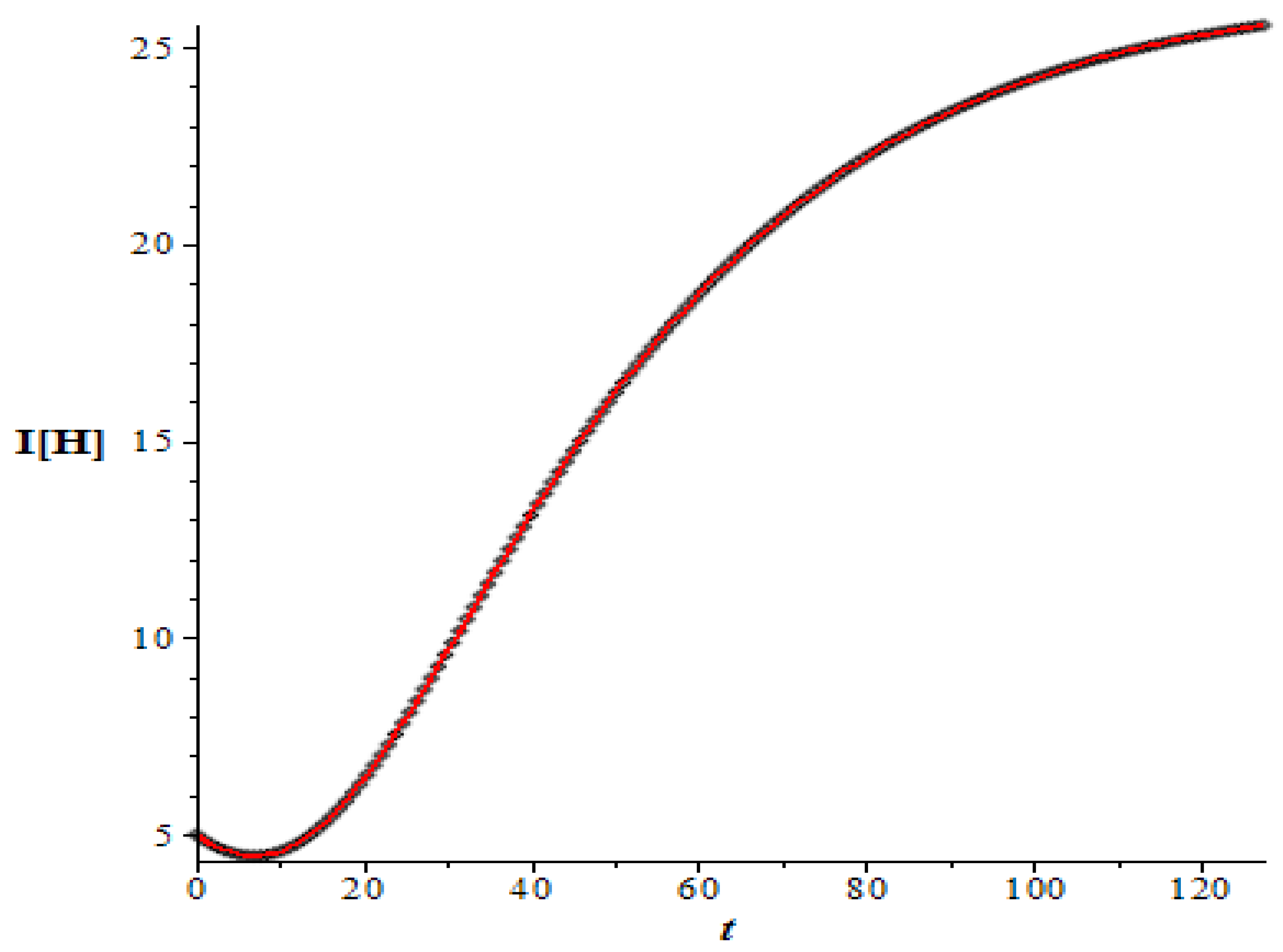
To illustrate the result, let us consider the second data set in
Table 1 with the visual solution for the infective populations shown in
Figure 7. This data set gives rise to a large basic reproduction number, i.e.,
41.580. Suppose that we would like to undertake the vaccination of the susceptible population, then according to Equation (31), we need to vaccinate no less than
or 97.595% of the susceptibles.
Figure 8a shows the graph of
if we vaccinate 98% of the susceptibles, resulting in the elimination of the infective population, and
Figure 8b shows the graph of
if we vaccinate only 60% of the susceptibles (less than 97.595%), resulting in only a partial decrease in the infective population. These figures agree with the theory discuss above.
4.2. Decaying Effect of Vaccination
In this section, we consider a vaccination with a decaying effect. As before, it is assumed that the host population is vaccinated at birth, as much as
portion, and is removed to the immune class
However, it is also assumed that the vaccination has a decaying effect where
is the survival from losing immunity of an individual of age
. Hence, the number of immune individuals at time
is given by
Individuals that lose immunity go back to the susceptible class, which now has dynamics
The number of infected humans can be computed either from the relation
or straight forward by looking at the number of susceptibles who are infected, no longer in the susceptible class (33), and still infectious, that is
The equation for the infected mosquitoes,
remains as in (9). Using the same argument as before, it can be shown that the equilibrium points
and
are given by
Which, by considering
, will give the effective reproduction number
where
is the basic reproduction number and
.
Let us see two extreme conditions in the last expression, i.e., when the rate of losing immunity is relatively low and relatively high. Note that if
then we can ignore the presence of decaying immunity, since the minimum level of vaccination
remains the same as before, that is,
. However, if
(the rate of losing immunity is sufficiently high), then the reduction in the value of the basic reproduction number
could be negligible, no matter how large the vaccination rate
is. However, in general, the value of the waning immunity lies in between those two extreme values. In this case, to eliminate the disease, we need
or equivalently
in which the inequality
holds. This indicates that we may underestimate the critical vaccination level
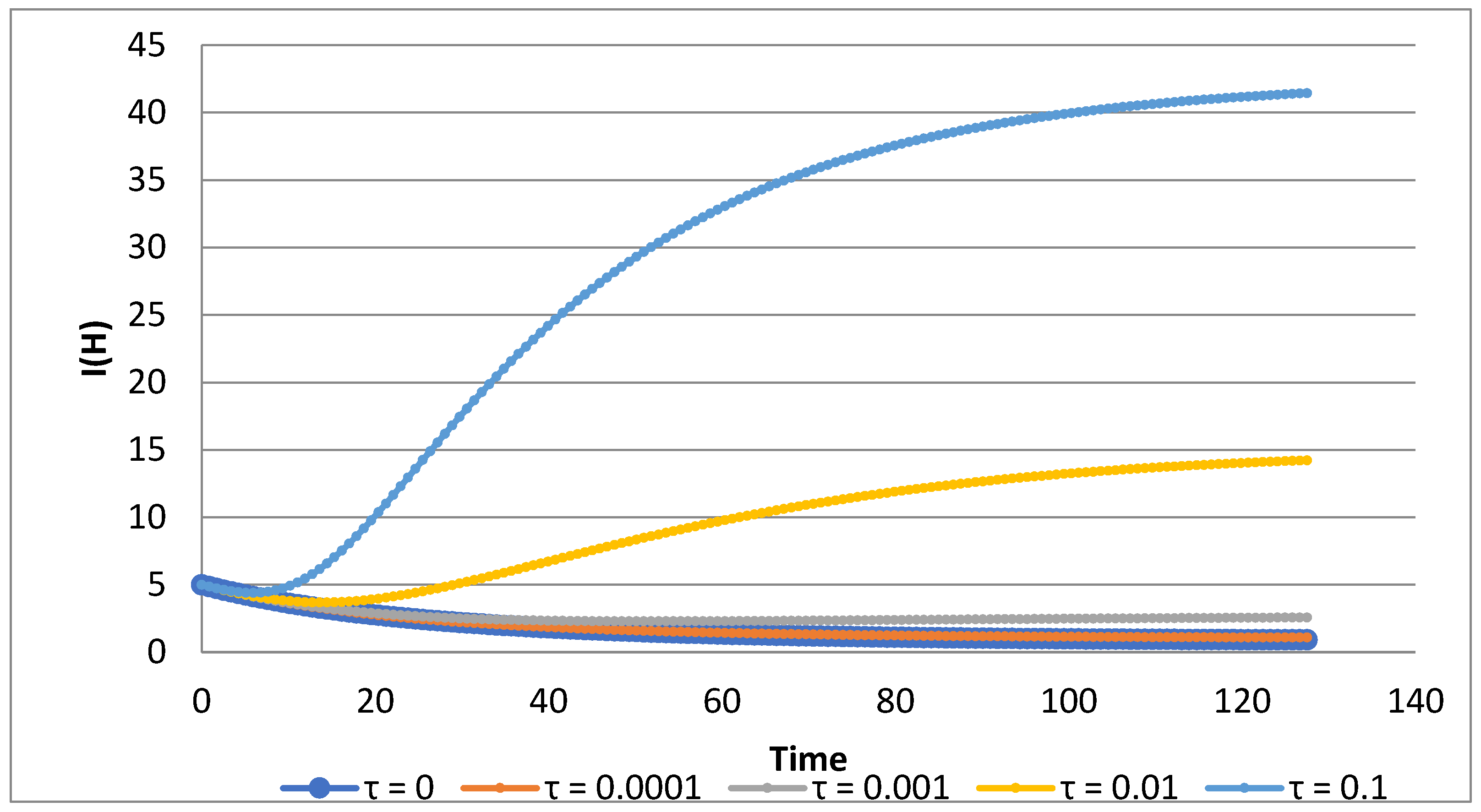
if we ignore the presence of decaying immunity, which may consequently result in failing to eliminate the disease. As an illustration we plot the graphs of human infected population for various decaying rates of vaccination (
Figure 9). The figure shows the effect of the decaying vaccination for different decay rates for the graphs of human infective population I_H (t) if 98% of the susceptibles are vaccinated. In the absence of decaying effects, this rate of vaccination could drive the infective population to extinction (
Figure 8a). However, in the presence of 10% of decaying effects, vaccination has almost no effect in reducing the infective human population.
4.3. The Effect of Wolbachia Infection in the Basic Reproduction Number
In the previous sections we have assumed that there is a natural population of mosquitoes, i.e., there is no wolbachia infection in the mosquitoes. We have assumed that the recruitment rate for the mosquitoes is with a natural death rate . Let us also assume that and are the disease transmission probabilities from vector to host and from host to vector, respectively.
Now we assume that the life span of mosquitoes is reduced by wolbachia infection. This is equivalent to saying that wolbachia infection makes the death rate of the mosquitoes increase. Hence, in the presence of wolbachia infection, the natural death rate changes into a larger rate , say with . The constant can be interpreted as a magnification factor of the natural mortality rates . Here, (and so ) is the parameter of the survival function Recall that the basic reproduction number is given by , or if we write down the parameter explicitly, we have in the absence of wolbachia and by following the same calculation in the derivation of Equation (19), in the presence of wolbachia we have . Note that the ratio of is given by .
Next, we assume that the transmission probability is reduced by wolbachia infection. Hence, in the presence of wolbachia infection, the natural transmission rates and change into smaller rates and , say and with . The constant can be interpreted as a reduction factor of the natural transmission rates and . As before, recall that for the basic reproduction number if we write down the parameter and explicitly we have in the absence of wolbachia and by following the same calculation in the derivation of Equation (19), in the presence of wolbachia we have . Note that the ratio of is given by .
Now we look at specific survival functions, namely
and
, which mimic the survival rates for humans and mosquitoes, respectively. Consequently, the reproduction number is given by
in the absence of wolbachia and
in the presence of wolbachia, so that
which shows that there is a significant reduction of the basic reproduction number when the wolbachia infected mosquito presence replaces the natural mosquitoes.
An example can be seen in [
29], which agrees with the belief in the effectiveness of wolbachia introduction in controlling the disease. Now, let us consider another example by considering the first data set in
Table 1, which has
and
. Suppose that the presence of wolbachia could force an increase in the mortality rate to
, then in this case
. Moreover, let us assume that the presence of wolbachia also decreases the mosquito infection rate due to proboscis damage to half of the current infection rate, i.e.,
and
, or equivalently
. Then, we have the resulting graph for the human infective population, as presented in
Figure 10, with the effective reproduction number 10.395. The number of human infective is almost half of the original number in the absence of wolbachia (
Figure 1c). The original basic reproduction number is 166.321. Hence the ratio between the original basic reproduction number and the effective reproduction number in the presence of wolbachia is 16.0000962, which is almost exactly the same as
=16. The error is due to the rounding off during the computation. As another example, if we know that the natural basic reproduction number is eight as in [
28], then the introduction of wolbachia infection to the mosquitoes could reduce the biting rate by half and increase the mosquito death rate by half of its current level, and theoretically this will make the disease die out. From Equation (31), in the absence of waning immunity, we need to vaccinate at least
of the total human population. However, in the presence of waning immunity, then from Equation (36) the vaccination coverage should be much larger than
.