1. Introduction
Mechanical systems, which are elastic structures that interact with a fluid, are currently actively used in mechanical engineering and aircraft-building. Such structures can be systems of rigid bodies on an elastic suspension [
1,
2] or linear, or nonlinear, plates and shells, with or without geometrical irregularity [
3,
4,
5]. In particular, Indeitsev et al. [
1] studied the interaction of a vibrating stamp supported by a spring and an ideal fluid with a free surface located in a plane of an infinitely long channel of small depth. A study of the longitudinal oscillations of the plate excited by an oncoming flow of a viscous fluid in a channel with parallel walls was carried out by Kurzin et al. [
2] Kurzin et al. considered the case when the plate’s end is fixed on a spring and the plate itself performs forced transverse oscillations. The influence of a liquid’s viscosity leads to the complete damping of the free vibrations of such elastic structural elements over time, which allows us to consider only the forced vibrations arising from various causes.
There are a fair number of publications devoted to studying the interaction of fluid and elastic elements. For example, in [
6], Bochkarev et al. carried out experimental studies to determine the natural frequencies of the oscillations of rectangular plates that interact with the free surface of water. For this, various types of supports at the ends of the plates were considered. Amabile et al. [
7,
8] engaged in research on the state of shells that contained a flow of an inviscid and incompressible fluid. For example, the response of such shells to harmonic excitation in the spectral vicinity of one of the lowest natural frequencies was studied in [
7], and the stability of a circular, cross-sectional cylindrical shell with hinged ends was studied in [
8] using the Galerkin method. The effect of viscous structural damping was introduced in [
8] to account for energy dissipation.
Numerical modeling of the stability of the gap between two shells was carried out in [
9,
10] using the finite element method for different values of the stiffness of the outer shell and the fluid flow parameters. A mathematical model was considered to predict the hydroelastic response of a mechanical system consisting of a multilayer, circular plate that forms the wall of a narrow channel filled with viscous fluid [
11]. Kondratov et al. [
12] constructed a mathematical model for the two-dimensional problem of the hydroelastic interaction between the channel wall and the end seal through a pulsating layer of a viscous fluid. The end seal was considered as a linear elastic suspension.
Kheiri et al. [
13] studied the dynamics and stability of a pipe conveying fluid in the case when the restrained end supports of the pipe are flexible. Barman et al. [
14] studied the effect of an elastic bottom in the interaction of a two-layer fluid with a caisson-type, multi-chamber, porous breakwater fitted with a perforated frontwall. In addition, Barman et al. [
14] showed that shear force and bottom deflection, and accordingly the elastic parameters of the seafloor, affect wave scattering.
The evaluation of the Duffing equation parameters is one of the most important tasks that should be resolved for solving the above problems. There are a number of works that are devoted to the experimental determination of the parameters of the Duffing equation, for example [
15,
16]. However, the experimental data must be processed by numerical methods, and this introduces an additional error in determining the values of the parameters.
In the model proposed in this work, the damping coefficient is determined analytically from the solution of the coupled hydroelasticity problem. This coefficient is determined by the physical parameters of the liquid and the geometric dimensions of the channel. However, there are no studies of the hydroelastic response of the channel endwall suspended on a nonlinear spring due to the interaction of the endwall with the vibrating wall of the channel through the viscous fluid that fills it. At the same time, the solution to this theoretical problem is required to solve such practical problems as studying the vibrations of bellows made of nonlinear materials or located on a nonlinear foundation; studying the oscillations of sensitive elements of pressure sensors (piezoelectric elements) mounted on a non-linear substrate; the study and control of the state of the channel with liquid according to the parameters of the vibration of its mechanical seal; etc. For example, the results of the proposed theoretical study can be useful for such problems as the hydroelastic analysis of a moored, floating, and submerged flexible, porous plate [
17], the investigation of the effect of a flexible, floating plate on the dynamics of fluid flow over a mild slope [
18], the analysis of the hydroelastic response of a moored, floating, flexible plate [
19], etc. [
20,
21,
22,
23]. The future perspective is the application of the presented solution to the mathematical modeling of nano- and micro-spacecraft systems with fluids. Such an application is related to space sustainability, which is a new topic that involves knowledge in different fields aimed at the conscious use of space and its transportations and facilities for future life in space and on new planets [
24].
Thus, it can be noted that the problem that is proposed in the paper for a solution is relevant to modern practical problems of technology and therefore requires a solution. This fact determines the scientific novelty and relevance of this study.
2. Problem Statement
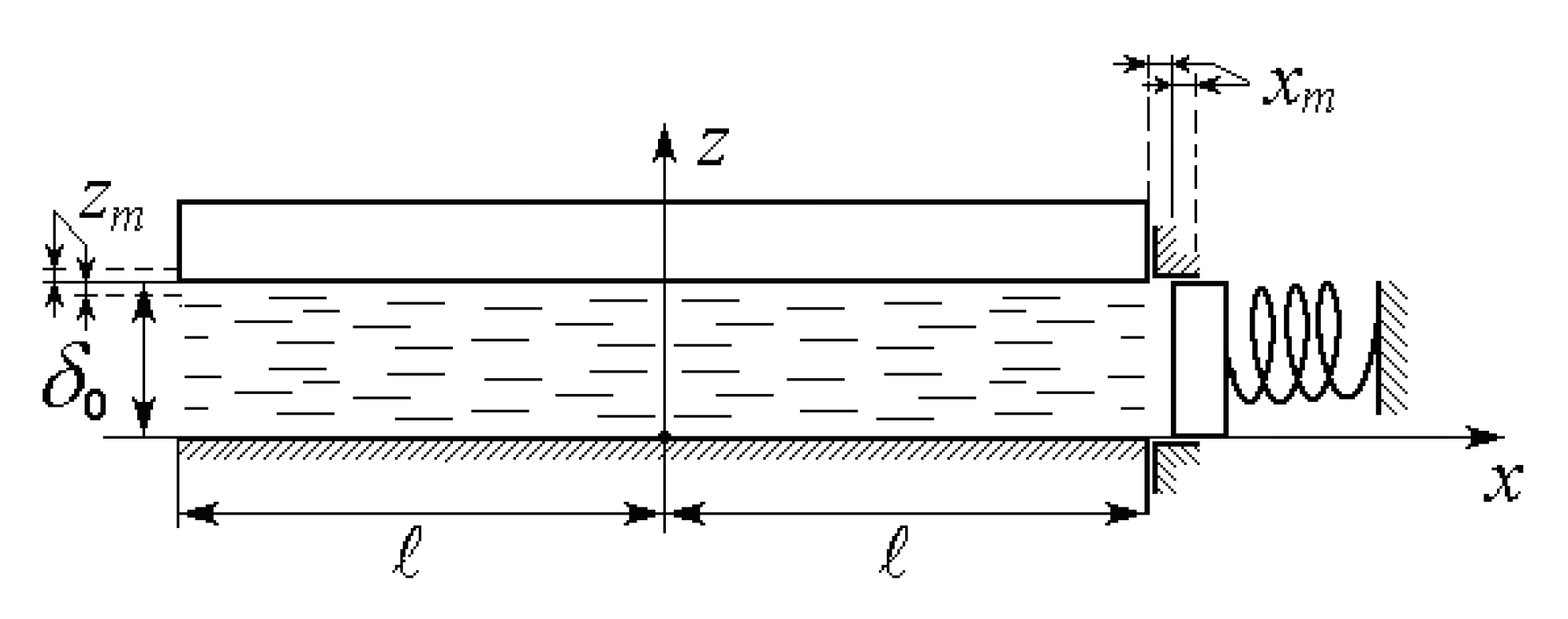
Consider a narrow channel formed by two parallel, rigid walls (
Figure 1). The channel-wall dimensions in the plan are 2
ℓ ×
b. The center of the Cartesian coordinate system
xyz is located at the center of the inner surface of the lower fixed wall. We are studying a two-dimensional problem, so the change in the hydrodynamic parameters of the fluid along the
y axis is neglected, which is equivalent to condition 2
ℓ <<
b.
The upper-channel wall oscillates in the direction of the
z-axis according to a given harmonic law. The initial distance between the upper and lower walls is
δ0, and, since the channel is narrow, 2
ℓ >>
δ0. The channel is completely filled with a viscous fluid, the compressibility of which is neglected. The amplitude of the oscillations of the upper wall is
zm <<
δ0. At the left end of the channel, it is assumed that the pressure
p0 is constant, which is equivalent to the free outflow of fluid into a large cavity. Starting at this point in time, the value of this pressure is taken as the reference value and set equal to zero. The right channel-end is a mechanical seal in the form of a rigid wall supported by a spring with rigid cubic nonlinearity. That means the spring has the nonlinear characteristic of the restoring force, which changes symmetrically depending on its tension–compression, and the spring stiffness increases during compression. The rigid wall at the end of the right channel can move in the direction of the axis with the amplitude
xm <<
ℓ. At the right end, we assume that the fluid flow rate coincides with the flow rate due to its displacement by the endwall, so no leaks are present. Moreover, we take into account that the transient processes decay due to the viscosity of the liquid. So, we study the steady, nonlinear, forced vibrations of the endwall of the channel, i.e., the anharmonic vibrations [
25,
26].
It should be noted that, since the problem is symmetrical about the Oy axis, it is sufficient to consider this problem in the two-dimensional case. This approach is widely used in solving practical problems.
Let the law of motion of the upper wall be harmonic, and it can be expressed in the following form:
where
ω is the frequency of harmonic oscillations, and
t is the time.
The equations of motion for a viscous fluid in the narrow channel are the Navier–Stokes equations and the continuity equation, written for a plane problem of hydromechanics [
27,
28]:
where
ux, uz are the projections of the fluid velocity vector on the coordinate axes,
p is the pressure,
ρ is the density, and
ν is the fluid kinematic viscosity.
The boundary conditions of Equation (2) are the non-slip conditions for the liquid at the upper and lower walls of the channel. They are expressed in the coincidence of the velocities of the fluid and the channel walls:
For the right and left channels, two different types of conditions should be formulated. The first one is the condition that the pressure at the left end coincides with the reference value of pressure. The second is the condition that the fluid flow rate at the channel end coincides with the flow rate because of its displacement by the endwall. These conditions can be written as follow:
where
is the motion predetermined law of the upper channel wall,
is the motion law of the channel endwall, and
p0 is the reference pressure value.
Note that the wall displacements in the x and z directions are represented as and in expressions (3) and (4). Additionally, η is the characteristic frequency of the nonlinear oscillations of the endwall.
The equation of motion for the endwall as a nonlinear spring-mass system has the following form:
where
m is the endwall mass,
n1 is the coefficient of rigidity of the support spring attached to the linear term, and
n3 > 0 is the stiffness coefficient of the support spring attached to the nonlinear cubic term.
3. Determination of Endwall Response
Let us introduce the dimensionless variables and small parameters of the problem:
where
ψ, λ are the small parameters that characterize the problem; also, we will consider that, in the formulation under consideration,
and
Studying the equations of fluid dynamics, we take into account those for narrow gaps; as follows from the theory of hydrodynamic lubrication [
27,
28], the motion of the fluid can be considered as creeping; that is, the inertial terms in these equations can be neglected. Then, taking into account the variables (6), Equation (2) has the form
The boundary conditions for Equation (7) in dimensionless variables (5), according to Equations (3) and (4), are written as follows:
Note that there are regular perturbations in the proposed formulation of the problem. This means that each subsequent term of the asymptotic decomposition in a small parameter will be significantly lesser than the previous ones. Additionally, that will be true in the entire range of changes in the problem’s independent variables and physical parameters. Using this approach, we have, in Equation (7) and the boundary conditions (8),
,
,
, and the terms at
,
,
, and
can be omitted [
29]. As a result, for the case of creeping fluid motion in a narrow channel, we obtain the following equations for its dynamics:
Taking into account the above remarks, the boundary conditions (8) have the following form:
According to the second equation in Equation (9), the pressure does not depend on the coordinate
ζ. Therefore, Equation (5), taking into account Equation (6), is written as
Solving Equation (9) with boundary conditions (10), we find that
Then, the pressure in the channel cross-section at its right end is equal to
Taking into account Equation (13), we write Equation (11) as
and taking into account the predetermined law of the movement of the upper wall (1), this equation can be written in the following form:
where
and
are the damping coefficients due to the viscous fluid influence.
The multiplier
represents the amplitude of the vibration velocity of the upper channel wall. The right side of Equation (15) is the driving force, which varies according to the harmonic law with amplitude
. Therefore, Equation (15) is the Duffing oscillator equation. Furthermore, we assume that the vibration velocity amplitude
is set on the basis of a velocity of 1 m/s, i.e.,
∙1 (m/s), where
k is the coefficient determining vibration overload by speed. It is known [
25,
26] that the solution of the Duffing equation for small oscillation amplitudes and damping coefficients is an anharmonic oscillation.
As is known [
25,
26], the Duffing equation (Equation (15)) can be solved using the harmonic balance method. Further study is limited by the research of the main hydroelastic response of the channel endwall at a frequency close to the driving force frequency. The frequency of the forced vibrations of the endwall is assumed to be equal to the frequency of the driving force in this method, and the desired solution is represented as a harmonic one, that is
η ≈
ω and
x =
xmcos(
ωt −
φ). When we perform the linearization procedure for Equation (15) by the harmonic balance method [
25,
26], we obtain the following algebraic system:
Squaring the right and left parts of these equations and then adding them, we obtain an equation for determining the primary hydroelastic response of the endwall:
From Equation (17), taking into account our previous remarks, we can write the primary hydroelastic response of the channel endwall, which is supported on the spring with cubic nonlinearity and performs nonlinear oscillations with the frequency of the driving force, i.e., its nonlinear amplitude-frequency response:
which, by solving it for ω, can be reduced to the form:
The first term ω∗ in Equation (19) defines the so-called skeletal curve, which corresponds to the Duffing equation, from which the damping term and driving force are excluded, i.e., for the problem under consideration, in Equation (15) (or in Equation (19)) is set. In other words, the skeletal curve is the curve of the natural undamped oscillations of a nonlinear conservative system with cubic nonlinearity.
In addition, from Equation (16), the phase characteristic of the considered channel wall can be obtained:
The right and left parts of expression (18) include the amplitude of the endwall vibrations, making it difficult to use this expression directly. However, the nonlinear hydroelastic response can be constructed numerically using expression (19). Note that we have the case of supporting the endwall of the channel on a linear spring for which n3 = 0. In this case, the endwall will undergo harmonic oscillations excited by the vibration of the upper wall of the channel, and expression (18) will be a linear amplitude characteristic that unambiguously connects the amplitude and frequency of the oscillations of the endwall.
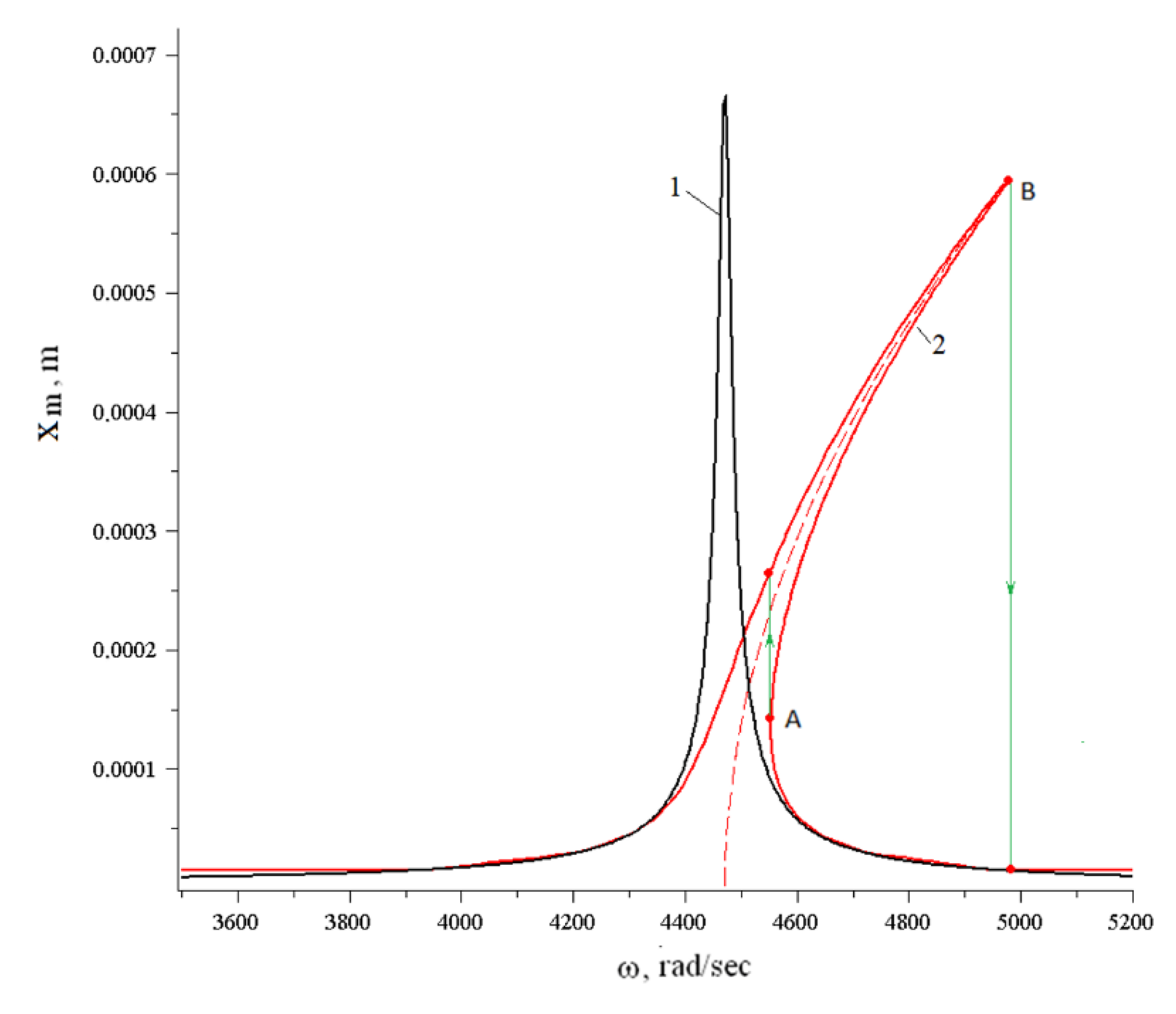
Some numerical experiments were conducted to illustrate the results obtained. The nonlinear and linear hydroelastic responses of the channel endwall were calculated according to (19) and (18) for
zmω = 1 m/s,
k = 1.5 with the following geometric and physical–mechanical parameters:
ℓ = 0.1 m,
δ0 = 0.05 m,
b = 0.5 m,
m = 0.5 kg,
n1 = 10
7 kg/s
2,
n3 = 9 × 10
12 kg/(m
2s
2),
ρ = 1.84 × 10
3 kg/m
3, and
ν = 2.53 × 10
−4 m
2/s. The calculated curves of the hydroelastic response of the channel wall are shown in
Figure 2.
4. Discussion
As can be seen from the presented calculations, the curvature of the amplitude characteristic at the primary resonance is observed when the cubic nonlinearity of the end-support spring is considered. Moreover, the constructed mathematical model makes it possible to determine the frequencies at which the amplitudes of nonlinear oscillations can change abruptly. As shown in
Figure 2, these frequencies are in the range between points A and B. A jump change in the oscillations’ amplitude of the endwall is observed at these points when the frequency of oscillations of the upper wall changes. It is known [
25,
26] that the lower part of the nonlinear hydroelastic response curve between points A and B is unstable. Arrows indicate the directions of the jumps in amplitude. An increase in the amplitude of the vibration velocity of the upper wall will lead to a rise in the range of these frequencies.
To verify the constructed mathematical model, the experimental results obtained by Jiao et al. [
23] can be used. Jiao et al. studied the longitudinal vibrations of the bellows, considering the damping properties of a viscous fluid in a linear formulation using the following parameters:
The calculated theoretical value of the damping factor in the longitudinal direction is equal to Kx = 2 Ns/m (see Formula (15)) for a system with the parameters presented above. The experimentally determined damping coefficient in the longitudinal direction was 3.547 Ns/m.
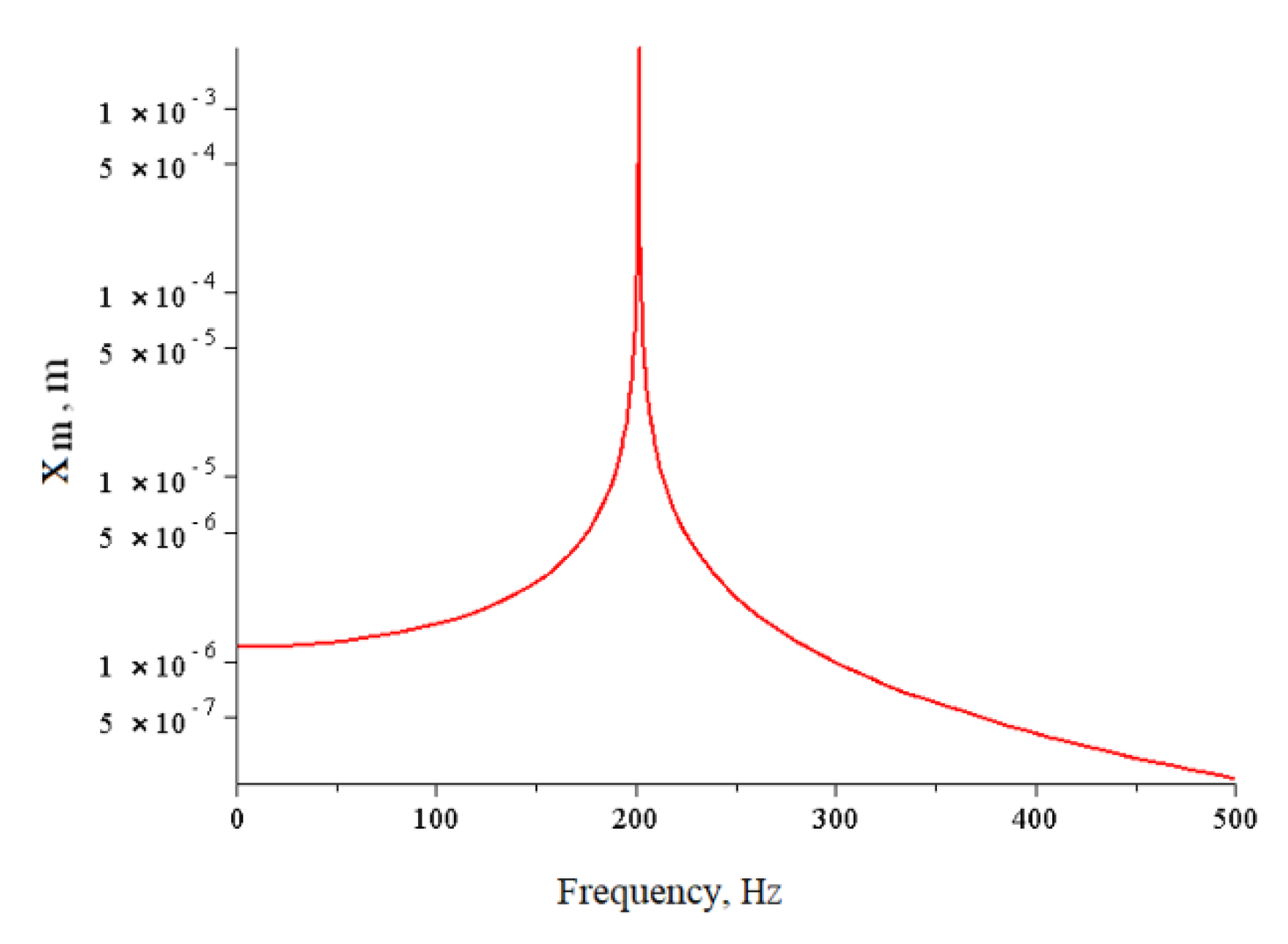
Furthermore, the linear hydroelastic response of the bellows was calculated using Formula (18), assuming
n3 = 0, to reduce the proposed model to a linear one. The calculation result is shown in
Figure 3.
The experimental data presented above were obtained at a resonance frequency of 200 Hz, as stated in [
23]. The resonant frequency calculated according to the proposed model is equal to 201.3 Hz. So, theoretical and experimental results are in good agreement for the linear case.
The above comparison shows that the proposed model is quite adequate for the process under study and expands the possibility of its use in the case when taking into account the nonlinear properties of the bellows material.
Thus, the proposed model can evaluate vibrations of sensitive elements mounted on nonlinear elastic foundations and those in contact with a layer of viscous fluid, as used, for example, in pressure sensors.
5. Conclusions
Since the developed mathematical model is fundamental in nature, it can be used in modeling various devices and systems which have narrow channels filled with a viscous fluid and which are subjected to vibrations on one side of the channel.
For example, the mathematical model developed can be used in the aerospace field to model the dynamics of fluid-based angular rate sensors [
30], for instance, for the rate-integrating gyroscope, when we are considering the nonlinearity of the end seal (bellows) of the sensor cavity where the float is located.
Another example would be coolant pipes that are subjected to vibration from the engine. Of particular interest is the application of the presented solution to the mathematical modeling of nano- and micro-spacecraft systems with fluids since the proposed model allows the consideration of some boundary effects, which is important for nano- and micro-spacecraft due to their small size.
Thus, in this paper, a new mathematical model for studying nonlinear hydroelastic oscillations of a channel endwall supported by a spring with strong cubic nonlinearity is proposed. It is shown that, for a narrow channel filled with a viscous incompressible fluid, the equation of motion for its endwall is reduced to the Duffing equation, with the damping coefficient determined by the viscosity of the fluid and the geometric dimensions of the channel.