Recovering Heat Source from Fourth-Order Inverse Problems by Weighted Gradient Collocation

Abstract

The weighted gradient reproducing kernel collocation method is introduced to recover the heat source described by Poisson’s equation. As it is commonly known that there is no unique solution to the inverse heat source problem, the weak solution based on a priori assumptions is considered herein. In view of the fourth-order partial differential equation (PDE) in the mathematical model, the high-order gradient reproducing kernel approximation is introduced to efficiently untangle the problem without calculating the high-order derivatives of reproducing kernel shape functions. The weights of the weighted collocation method for high-order inverse analysis are first determined. In the benchmark analysis, the unclear illustration in the literature is clarified, and the correct interpretation of numerical results is given particularly. Two mathematical formulations with four examples are provided to demonstrate the viability of the method, including the extreme cases of the limited accessible boundary.

1. Introduction

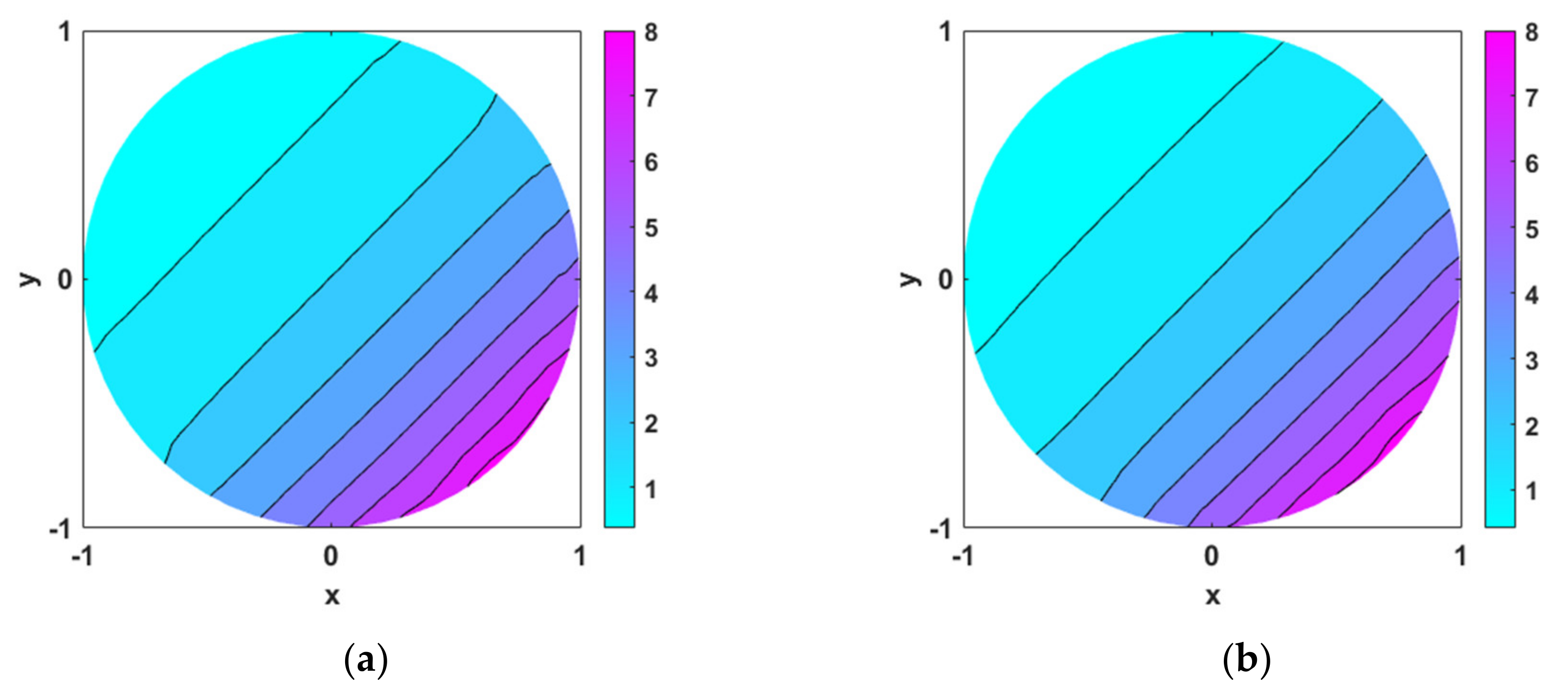
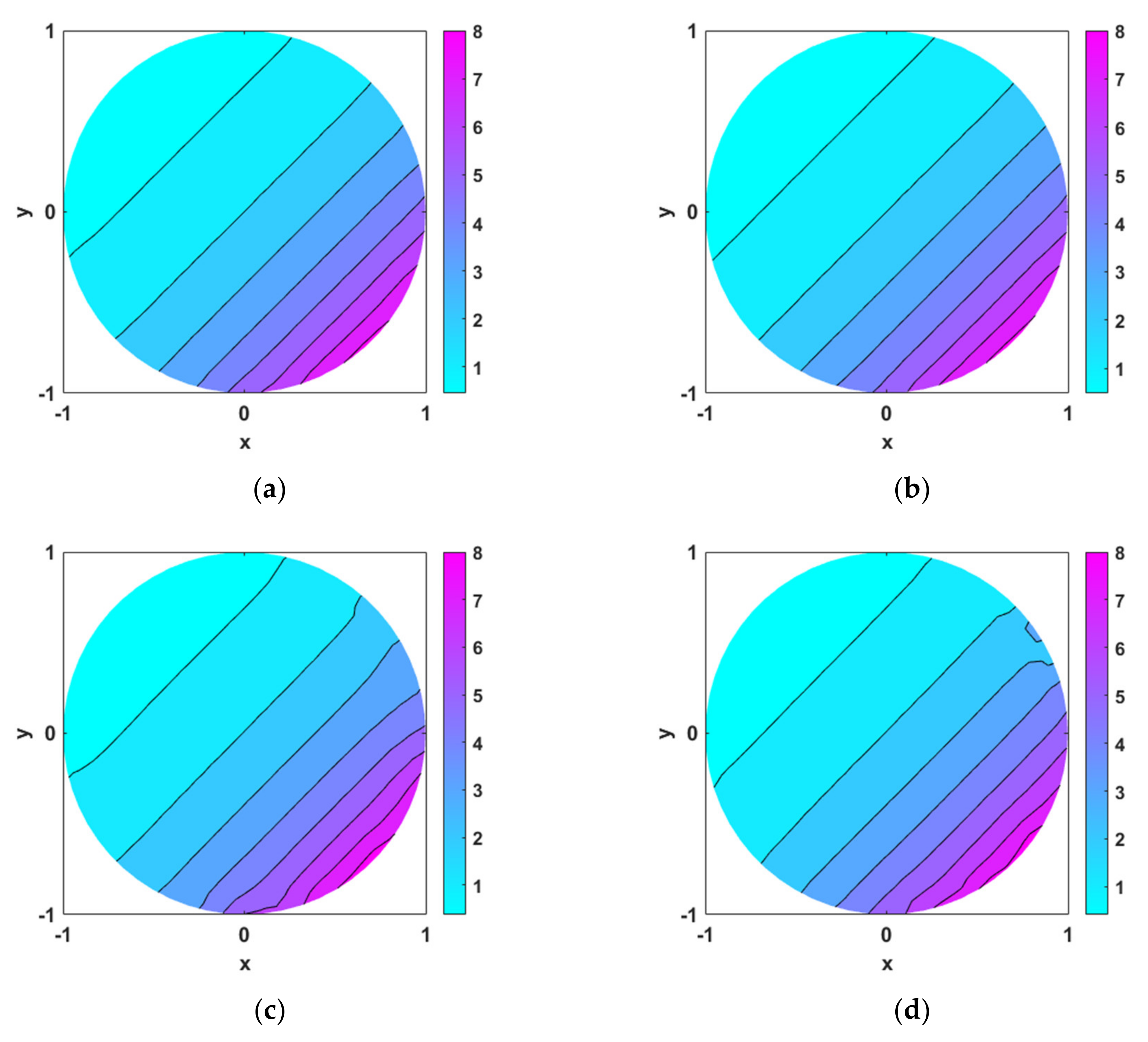
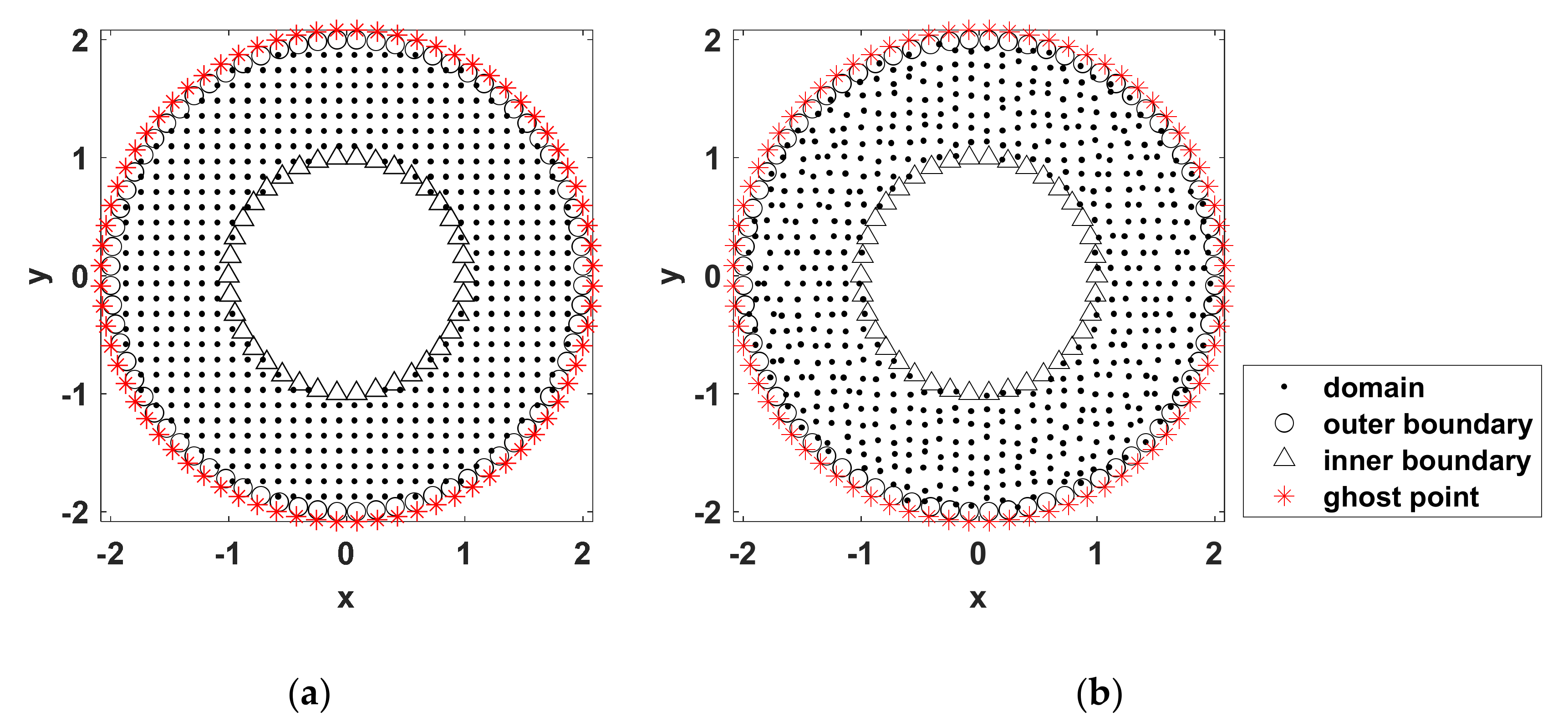
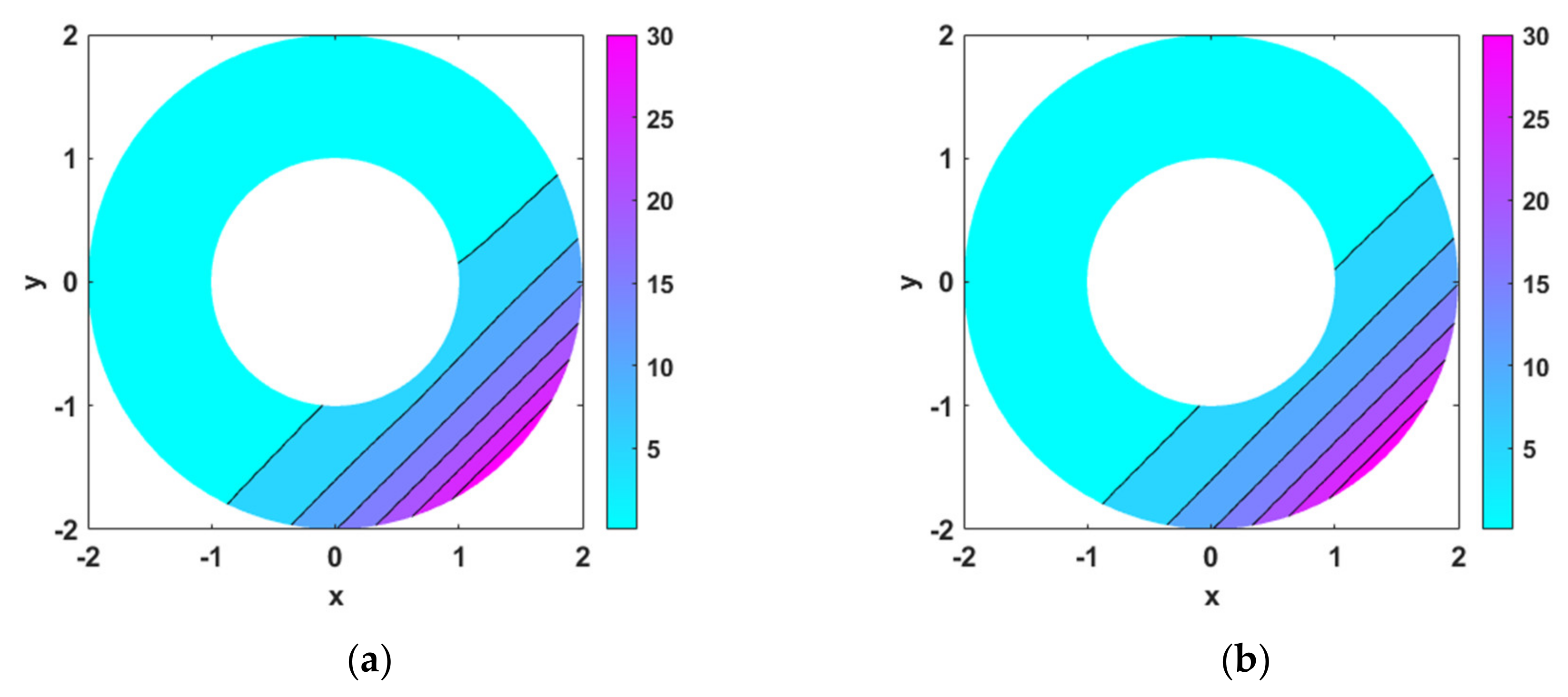
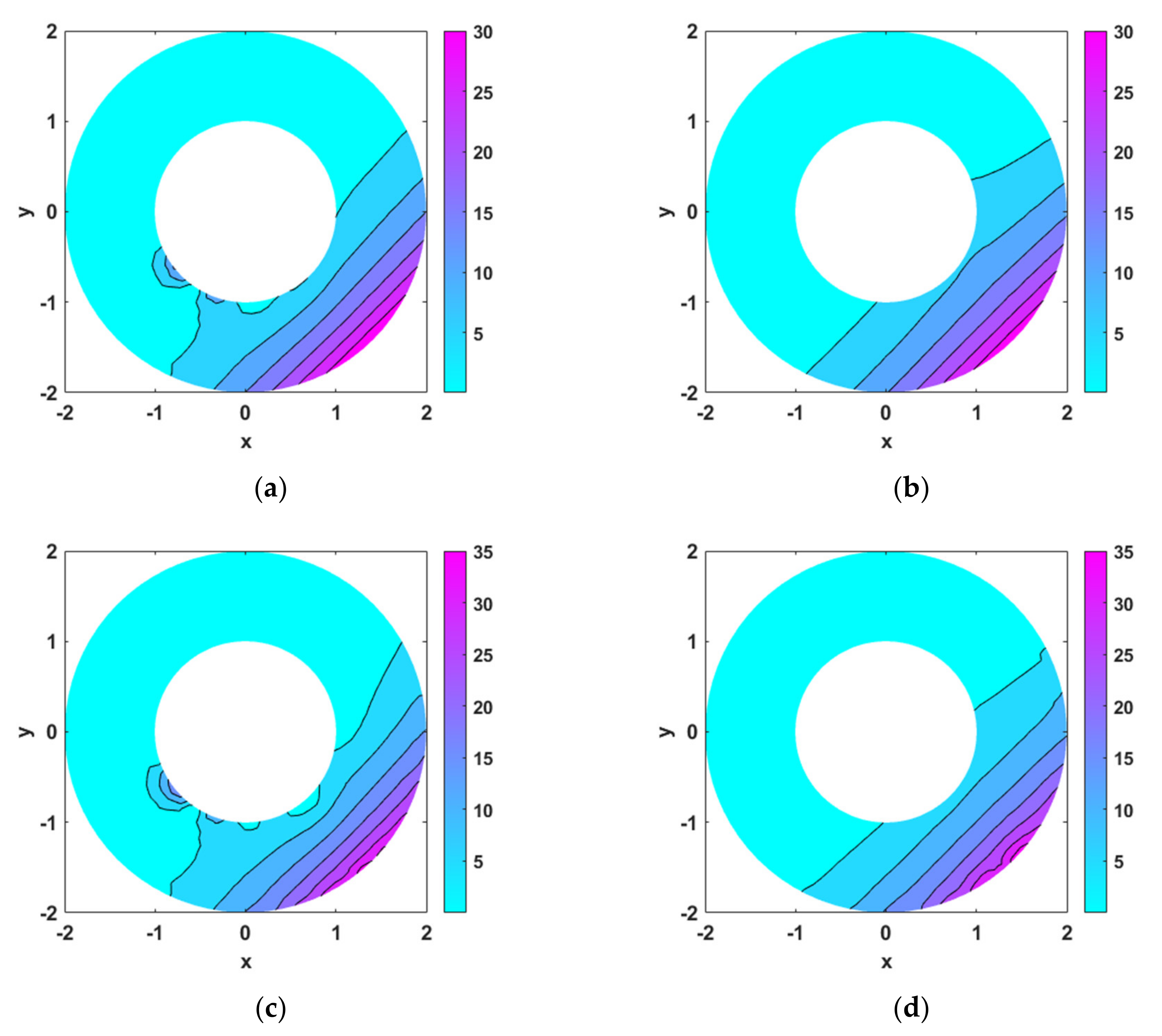
Among the inverse heat source problems are the cylindrical source problems, point source problems, and problems with specified source functions. In the inverse analyses of the aforementioned problems, it is commonly known that there is strong non-uniqueness of the solutions [1]. In other words, it is hard to determine the heat source uniquely via measured data on the boundary. From a practical point of view, seeking weak solutions might be an option. To this end, some weak assumptions have been proposed accordingly in order to find the so-called weak solutions to inverse source problems. This turns out to be a priori knowledge, which makes the inverse source problems solvable [2]. For example, if one variable of the product is known when using the separation of variables, the bottom area is known for the source to be sought in a cylinder, while the source to be sought is described by a characteristic function. According to the principle of parsimony [3], a minimum-norm solution to the inverse problem can be regarded as the approximate solution to this problem, provided that the minimum-norm solution is the simple one revealing the minimum detail. By relating the inverse source problem to Poisson’s equation, it was shown that the minimum-norm solution satisfies Laplace’s equation [1]. On the other hand, there are limited numerical methods proposed to solve inverse heat source problems effectively so far [4]. Farcas et al. used the Tikhonov regularization method to recover the minimum-norm solution [1]. Gu et al. introduced the generalized finite difference method to solve the inverse heat source problems [4]. The weighted collocation method with reproducing kernel approximation and/or gradient reproducing kernel approximation has been applied to inverse analysis with great success to, for example, elasticity problems [5], Cauchy problems with complex geometry such as singularity [6], and multiply connected problems [7]. Nevertheless, the aforementioned problems are of second order while the inverse source problems are analyzed by solving the fourth-order PDEs in strong form, which indicates that the computation of the fourth-order derivatives of reproducing kernel shape functions is required. Due to the complicated composition of reproducing kernel shape functions, constructing the direct derivatives of reproducing kernel shape functions involves the calculation of derivatives of inverse matrix and other functions. In view of this, the present study further introduces the weighted high-order gradient reproducing kernel collocation method (G-RKCM) to compute derivatives implicitly and solve inverse heat source problems efficiently and effectively. Other advanced versions of smooth or gradient reproducing kernel collocation methods have shown the efficacy of solving both the second-order and fourth-order partial differential equations with superconvergent rates recently [8,9,10]. With the aid of high-order gradient approximation [11], the direct differentiation of reproducing kernel (RK) shape functions is avoided. It should be noted that the weighted collocation method is established on the basis of the least-squares minimization [12,13]. The weights imposed on the boundary collocation equations can be treated as one kind of regularization techniques of the system equations. Under the framework of a weighted least-squares functional, the weights on the boundary conditions act to keep balance of errors arising from the domain and boundary. As such, the minimum-norm solution to the inverse source problem can be obtained numerically.

It should be particularly noticed that the weights are different for direct problems and inverse problems in general. Hence, the proper weights are determined uniquely on the basis of theoretical error estimates derived from the inverse analysis. Then, several benchmark problems are provided to demonstrate the viability of the proposed weighted high-order G-RKCM in solving the fourth-order partial differential equations. Especially, a conscientious comparison is made, and the unlikely results in the literature are pointed out with correct presentation instead. The present study is arranged in the following way: The two mathematical formulations of inverse source problems are given in Section 2. The weighted high-order G-RKCM for solving the fourth-order partial differential equations is introduced in Section 3. The numerical examples are provided in Section 4. Section 5 concludes this paper.

2. Mathematical Formulation

Assuming that the medium of a heat conduction problem is isotropic and in the steady-state condition, the corresponding governing equation can be described by the following Poisson’s equation [2]:

$${\nabla }^{2}u\left(x,y\right)=f\left(x,y\right) \mathrm{in} \Omega$$

(1)

where $u\left(x,y\right)$ is the potential field and $f\left(x,y\right)$ is the heat source in the domain $\Omega$. The domain is enclosed by the boundary $\partial \Omega$, where the heat flux $q\left(x,y\right)$ flowing across the boundary is expressed as:

$$q\left(x,y\right)=u_n \mathrm{on} \partial \Omega$$

(2)

where $u_n=\nabla u\cdot n$ and $n$ denotes the unit outward normal on the boundary.

The heat source is assumed to be unknown. Let $\partial {\Omega }_1\in \partial \Omega$ denote the accessible boundary with measured data, and $\partial {\Omega }_2\in \partial \Omega$ denote the inaccessible part of the boundary, i.e., $\partial \Omega =\partial {\Omega }_1\cup \partial {\Omega }_2$. The governing equation is as follows:

$${\nabla }^{2}u\left(x,y\right)=f\left(x,y\right) \mathrm{in} \Omega \cup \partial {\Omega }_2$$

(3)

The boundary conditions are as follows:

$$u\left(x,y\right)=\overline{u}\left(x,y\right) \mathrm{on} \partial {\Omega }_1$$

(4)

$$q\left(x,y\right)=\overline{q}\left(x,y\right) \mathrm{on} \partial {\Omega }_1$$

(5)

From Equations (1), (4), and (5), it is obvious that this problem is mathematically under-determined due to the unknown heat source and inaccessible boundary. For the current purpose of numerical investigation on the methodology, two mathematical formulations including Laplace’s and modified Helmholtz equations as a priori assumptions will be provided in Section 2.1 and Section 2.2 in order to seek the weak solutions to the fourth-order inverse problems, while it is assumed that the heat source satisfies the second-order PDE. Nevertheless, other formulations might be possible for this problem. As it is outside the scope of the present study, only the heat conduction described by Poisson’s equation is considered in this regard. Once $u\left(x,y\right)$ is found by solving the fourth-order inverse problems, the heat source can be inversely computed by using Equation (3) as $f\left(x,y\right)={\partial }^{2}u/\partial x^2+{\partial }^{2}u/\partial y^2$.

2.1. Mathematical Formulation I

The heat source $f\left(x,y\right)$ is assumed to be a harmonic function varying in the domain, which satisfies the following Laplace’s equation:

$${\nabla }^{2}f\left(x,y\right)=0 \mathrm{in} \Omega \cup \partial {\Omega }_2$$

(6)

Applying the Laplace operator ${\nabla }^2$ to both sides of Equation (1) leads to:

$${\nabla }^2\left({\nabla }^{2}u\right)={\nabla }^{2}f=0 \mathrm{in} \Omega \cup \partial {\Omega }_2$$

(7)

Combining the boundary conditions yields the following fourth-order inverse source problem:

$$\frac{{\partial }^{4}u}{\partial x^4}+2\frac{{\partial }^{4}u}{\partial x^2\partial y^2}+\frac{{\partial }^{4}u}{\partial y^4}=0 \mathrm{in} \Omega \cup \partial {\Omega }_2$$

(8)

$$q\left(x,y\right)=\overline{q}\left(x,y\right) \mathrm{on} \partial {\Omega }_1$$

(9)

$$u\left(x,y\right)=\overline{u}\left(x,y\right) \mathrm{on} \partial {\Omega }_1$$

(10)

2.2. Mathematical Formulation II

The heat source $f\left(x,y\right)$ is assumed to satisfy the following homogeneous modified Helmholtz equation:

$$\left({\nabla }^2-{\lambda }^2\right)f\left(x,y\right)=0 \mathrm{in} \Omega \cup \partial {\Omega }_2$$

(11)

where $\lambda$ is the wave number of a known value. Applying the operator $\left({\nabla }^2-{\lambda }^2\right)$ to both sides of Equation (1) leads to:

$${\nabla }^{4}u-{\lambda }^2{\nabla }^{2}u=0 \mathrm{in} \Omega \cup \partial {\Omega }_2$$

(12)

Similarly, combining the boundary conditions yields the following fourth-order inverse source problem:

$$\frac{{\partial }^{4}u}{\partial x^4}+2\frac{{\partial }^{4}u}{\partial x^2\partial y^2}+\frac{{\partial }^{4}u}{\partial y^4}-{\lambda }^2\frac{{\partial }^{2}u}{\partial x^2}-{\lambda }^2\frac{{\partial }^{2}u}{\partial y^2}=0 \mathrm{in} \Omega \cup \partial {\Omega }_2$$

(13)

$$q\left(x,y\right)=\overline{q}\left(x,y\right) \mathrm{on} \partial {\Omega }_1$$

(14)

$$u\left(x,y\right)=\overline{u}\left(x,y\right) \mathrm{on} \partial {\Omega }_1$$

(15)

3. Weighted High-Order Gradient Reproducing Kernel Collocation Method

3.1. Review of High-Order Gradient Reproducing Kernel Approximation

In the collocation method, the unknown $u$ can be approximated by reproducing kernel (RK) shape function through $N_s$ source points as follows:

$$u\left(x\right)\approx v\left(x\right)={\displaystyle \sum _{I=1}^{N_s}{\Psi }_I\left(x\right)} a_I$$

(16)

where $a_I$ is the generalized coefficient. The RK shape function ${\Psi }_I\left(x\right)$, consisting of a monomial basis $H\left(x-x_I\right)$, coefficient vector $b\left(x\right)$, and kernel function ${\phi }_a\left(x-x_I\right)$, takes the following form:

$${\Psi }_I\left(x\right)=H^{\mathrm{T}}\left(x-x_I\right)b\left(x\right){\phi }_a\left(x-x_I\right)$$

(17)

where $b\left(x\right)$ is found by the reproducing conditions listed below:

$${\displaystyle \sum _{I=1}^{N_s}{\Psi }_I\left(x\right)x_I^{\alpha }}=x^{\alpha }, 0\le \left|\alpha \right|\le p$$

(18)

where $\alpha$ is the multi-index defined as $\left|\alpha \right|={\alpha }_1+{\alpha }_2$ in two dimensions and $p$ is the order of $H\left(x-x_I\right)$. The details of deriving RK shape functions are described in a previous study [13]. The explicit form of RK shape functions is as follows:

$${\Psi }_I\left(x\right)=H^{\mathrm{T}}\left(0\right)M^{-1}\left(x\right)H\left(x-x_I\right){\phi }_a\left(x-x_I\right)$$

(19)

with the moment matrix $M\left(x\right)$ defined as:

$$M\left(x\right)={\displaystyle \sum _{I=1}^{N_s}H\left(x-x_I\right)H^{\mathrm{T}}\left(x-x_I\right){\phi }_a\left(x-x_I\right)}$$

(20)

For the fourth-order differential equations considered in this paper, the high-order gradient reproducing kernel approximation is introduced to reduce the complexity of constructing the derivatives of RK shape functions directly. The mathematical proof of reduced complexity in comparison with reproducing kernel approximation is described in a previous study [13]. For direct problems solved by using high-order implicit gradient reproducing kernel approximation, the details are described in a recent study [11]. In the present study, the fourth-order gradient reproducing kernel approximation is adopted, and the corresponding implicit RK shape functions to the first-, second-, third-, and fourth-order are expressed explicitly as follows:

$$\begin{array}{l}{\Psi }_I^x\left(x\right)=-H_{,x}^{\mathrm{T}}\left(0\right)M^{-1}\left(x\right)H\left(x-x_I\right){\phi }_a\left(x-x_I\right)\\ {\Psi }_I^y\left(x\right)=-H_{,y}^{\mathrm{T}}\left(0\right)M^{-1}\left(x\right)H\left(x-x_I\right){\phi }_a\left(x-x_I\right)\end{array}$$

(21)

$$\begin{array}{l}{\Psi }_I^{xx}\left(x\right)=H_{,xx}^{\mathrm{T}}\left(0\right)M^{-1}\left(x\right)H\left(x-x_I\right){\phi }_a\left(x-x_I\right)\\ {\Psi }_I^{yy}\left(x\right)=H_{,yy}^{\mathrm{T}}\left(0\right)M^{-1}\left(x\right)H\left(x-x_I\right){\phi }_a\left(x-x_I\right)\end{array}$$

(22)

$$\begin{array}{l}{\Psi }_I^{xxx}\left(x\right)=-H_{,xxx}^{\mathrm{T}}\left(0\right)M^{-1}\left(x\right)H\left(x-x_I\right){\phi }_a\left(x-x_I\right)\\ {\Psi }_I^{yyy}\left(x\right)=-H_{,yyy}^{\mathrm{T}}\left(0\right)M^{-1}\left(x\right)H\left(x-x_I\right){\phi }_a\left(x-x_I\right)\end{array}$$

(23)

$$\begin{array}{l}{\Psi }_I^{xxxx}\left(x\right)=H_{,xxxx}^{\mathrm{T}}\left(0\right)M^{-1}\left(x\right)H\left(x-x_I\right){\phi }_a\left(x-x_I\right)\\ {\Psi }_I^{yyyy}\left(x\right)=H_{,yyyy}^{\mathrm{T}}\left(0\right)M^{-1}\left(x\right)H\left(x-x_I\right){\phi }_a\left(x-x_I\right)\end{array}$$

(24)

From Equations (21)–(24), it is obvious that the major difference lies in the derivatives of monomial basis $H\left(x-x_I\right)$ and the sign. To ensure continuity, higher order B-spline kernel function is particularly needed in strong form collocation methods. The common B-spline kernel functions such as quintic and sextic B-spline kernel functions are given by:

$${\phi }_a\left(s\right)=\left\{\begin{array}{cc}\frac{11}{20}-\frac{9s^2}{2}+\frac{81s^4}{4}-\frac{81s^5}{4},\hfill & 0\le s<\frac{1}{3}\\ \frac{17}{40}+\frac{15s}{8}-\frac{63s^2}{4}+\frac{135s^3}{4}-\frac{243s^4}{8}+\frac{81s^5}{8},\hfill & \frac{1}{3}\le s<\frac{2}{3}\\ \frac{81}{40}-\frac{81s}{8}+\frac{81s^2}{4}-\frac{81s^3}{4}+\frac{81s^4}{8}-\frac{81s^5}{40},\hfill & \frac{2}{3}\le s<1\\ 0,\hfill & s\ge 1\end{array}\right.$$

(25)

and

$${\phi }_a\left(s\right)=\left\{\begin{array}{cc}\frac{5887}{1920}-\frac{3773s^2}{128}+\frac{\mathrm{16,807}{s}^4}{128}-\frac{\mathrm{117,649}{s}^6}{384},\hfill & 0\le s<\frac{1}{7}\\ \frac{7861}{2560}-\frac{49s}{256}-\frac{\mathrm{13,377}{s}^2}{512}-\frac{\mathrm{12,005}{s}^3}{384}+\frac{\mathrm{151,263}{s}^4}{512}-\frac{\mathrm{117,649}{s}^5}{256}+\frac{\mathrm{117,649}{s}^6}{512},\hfill & \frac{1}{7}\le s<\frac{3}{7}\\ \frac{1379}{1280}+\frac{8869s}{320}-\frac{\mathrm{48,363}{s}^2}{256}+\frac{\mathrm{45,619}{s}^3}{96}-\frac{\mathrm{151,263}{s}^4}{256}+\frac{\mathrm{117,649}{s}^5}{320}-\frac{\mathrm{117,649}{s}^6}{1280},\hfill & \frac{3}{7}\le s<\frac{5}{7}\\ \frac{\mathrm{117,649}}{7680}-\frac{\mathrm{117,649}s}{1280}+\frac{\mathrm{117,649}{s}^2}{512}-\frac{\mathrm{117,649}{s}^3}{384}+\frac{\mathrm{117,649}{s}^4}{512}-\frac{\mathrm{117,649}{s}^5}{1280}+\frac{\mathrm{117,649}{s}^6}{7680},\hfill & \frac{5}{7}\le s<1\\ 0,\hfill & s\ge 1\end{array}\right.$$

(26)

where the nodal distance is normalized by RK support size $a$, namely $s=‖x-x_I‖/a$. For the $p$th order monomial basis, the RK support size is chosen as $a=\left(p+\delta \right)h$ with $\delta >0$ and $h$ the average nodal distance.

3.2. Weighted Collocation Method with High-Order Gradient Approximation

According to Section 2, the general strong form of the fourth-order PDEs can be written as:

$$L^a{u}_{,xxxx}+L^b{u}_{,xxyy}+L^c{u}_{,yyyy}+L^d{u}_{,xx}+L^e{u}_{,yy}=m \mathrm{in} \Omega \cup \partial {\Omega }_2$$

(27)

$$B_h{u}_{,n}=\overline{q} \mathrm{on} \partial {\Omega }_1$$

(28)

$$B_{g}u=\overline{u} \mathrm{on} \partial {\Omega }_1$$

(29)

where $L^a$, $L^b$, $L^c$, $L^d$, and $L^e$ are the differential operators in the domain, $B_h$ is the Neumann boundary operator, $B_g$ is the Dirichlet boundary operator, and $m=m\left(x\right)$ is a given function. For illustration purposes, take the problem described in Section 2.2 as an example; the operators are explicitly derived by using the implicit approximation: $L^a=L^c=1$, $L^b=2$, $L^d=L^e=-{\lambda }^2$, $B_h=n$, $B_g=1$, and $m=0$. As $\partial {\Omega }_2$ denotes the inaccessible boundary, it is numerically enforced to satisfy the governing equation, which is commonly done in solving inverse problems [5]. Without loss of generality, the same discretization of collocation points $N_c$ and source points $N_s$ is adopted in this study. In other words, an over-determined system of collocation equations is established. Thus, according to Equations (27)–(29) and introducing the approximation, a weighted version of least-squares functional is constructed as follows:

$$\begin{array}{lll}E\left(v\right)& =\frac{1}{2}{\int }_{\Omega \cup \partial {\Omega }_2}& {\left(L^a{v}_{xxxx}+L^b{v}_{xxyy}+L^c{v}_{yyyy}+L^d{v}_{xx}+L^e{v}_{yy}-m\right)}^{\mathrm{T}}\\ & & \left(L^a{v}_{xxxx}+L^b{v}_{xxyy}+L^c{v}_{yyyy}+L^d{v}_{xx}+L^e{v}_{yy}-m\right)d\Omega \\ & +\frac{w_h^2}{2}{\int }_{\partial {\Omega }_1}& {\left(B_h{v}_n-\overline{q}\right)}^{\mathrm{T}}\left(B_h{v}_n-\overline{q}\right)d{\Omega }_1+\frac{w_g^2}{2}{\displaystyle {\int }_{\partial {\Omega }_1}{\left(B_{g}v-\overline{u}\right)}^{\mathrm{T}}\left(B_{g}v-\overline{u}\right)d{\Omega }_1}\end{array}$$

(30)

where $w_h^2$ and $w_g^2$ are the weights introduced in order to balance the errors in the domain and on the boundary.

With reference to our previous study [5], the discrete weighted collocation system can be derived by using the equivalent quadrature rule, i.e., performing the integration at collocation points, and by minimizing the functional, i.e., utilizing the stationary condition. As such, the following collocation equation can be reached:

$$\left(\begin{array}{c}A\\ w_h{A}_h\\ w_g{A}_g\end{array}\right)a=\left(\begin{array}{c}b\\ w_h{b}_h\\ w_g{b}_g\end{array}\right)$$

(31)

where $a$ contains the generalized coefficients $a_I\left(I=1,2,\dots ,N_s\right)$ as introduced in Equation (16). Three sets, $x_p$, $x_q$, and $x_r$, containing $N_p$, $N_q$, and $N_r$ collocation points, are defined as follows:

$$\begin{array}{l}{x}_p=\left[x_{p1},x_{p2},\cdots ,x_{p{N}_p}\right] \subseteq \Omega \cup \partial {\Omega }_2\\ x_q=\left[x_{q1},x_{q2},\cdots ,x_{q{N}_q}\right] \subseteq \partial {\Omega }_1\\ x_r=\left[x_{r1},x_{r2},\cdots ,x_{r{N}_r}\right] \subseteq \partial {\Omega }_1\end{array}$$

(32)

where the domain $\Omega$ is partially enclosed by $\partial {\Omega }_1$ in a simply connected domain with the inaccessible boundary denoted by $\partial {\Omega }_2$. It should be noticed that $x_q$ may not be the same as $x_r$ in a multiply connected domain. Then, the submatrices in Equation (31) are given explicitly as:

$$\mathbf{A}=\left(\begin{array}{c}{L}^a\left({\Psi }^{xxx{x}^{\mathrm{T}}}\left(x_{p1}\right)\right)+L^b\left({\Psi }^{xxy{y}^{\mathrm{T}}}\left(x_{p1}\right)\right)+L^c\left({\Psi }^{yyy{y}^{\mathrm{T}}}\left(x_{p1}\right)\right)+L^d\left({\Psi }^{x{x}^{\mathrm{T}}}\left(x_{p1}\right)\right)+L^e\left({\Psi }^{y{y}^{\mathrm{T}}}\left(x_{p1}\right)\right)\\ L^a\left({\Psi }^{xxx{x}^{\mathrm{T}}}\left(x_{p2}\right)\right)+L^b\left({\Psi }^{xxy{y}^{\mathrm{T}}}\left(x_{p2}\right)\right)+L^c\left({\Psi }^{yyy{y}^{\mathrm{T}}}\left(x_{p2}\right)\right)+L^d\left({\Psi }^{x{x}^{\mathrm{T}}}\left(x_{p2}\right)\right)+L^e\left({\Psi }^{y{y}^{\mathrm{T}}}\left(x_{p2}\right)\right)\\ ⋮\\ L^a\left({\Psi }^{xxx{x}^{\mathrm{T}}}\left(x_{p{N}_p}\right)\right)+L^b\left({\Psi }^{xxy{y}^{\mathrm{T}}}\left(x_{p{N}_p}\right)\right)+L^c\left({\Psi }^{yyy{y}^{\mathrm{T}}}\left(x_{p{N}_p}\right)\right)+L^d\left({\Psi }^{x{x}^{\mathrm{T}}}\left(x_{p{N}_p}\right)\right)+L^e\left({\Psi }^{y{y}^{\mathrm{T}}}\left(x_{p{N}_p}\right)\right)\end{array}\right)$$

(33)

$$A_h=\left(\begin{array}{c}{B}_h\left({\Psi }^{n^{\mathrm{T}}}\left(x_{q1}\right)\right)\\ B_h\left({\Psi }^{n^{\mathrm{T}}}\left(x_{q2}\right)\right)\\ ⋮\\ B_h\left({\Psi }^{n^{\mathrm{T}}}\left(x_{q{N}_q}\right)\right)\end{array}\right)$$

(34)

$$A_g=\left(\begin{array}{c}{B}_g\left({\Psi }^{\mathrm{T}}\left(x_{r1}\right)\right)\\ B_g\left({\Psi }^{\mathrm{T}}\left(x_{r2}\right)\right)\\ ⋮\\ B_g\left({\Psi }^{\mathrm{T}}\left(x_{r{N}_r}\right)\right)\end{array}\right)$$

(35)

$$b=\left(\begin{array}{c}m\left(x_{p1}\right)\\ m\left(x_{p2}\right)\\ ⋮\\ m\left(x_{p{N}_p}\right)\end{array}\right), b_h=\left(\begin{array}{c}\overline{q}\left(x_{q1}\right)\\ \overline{q}\left(x_{q2}\right)\\ ⋮\\ \overline{q}\left(x_{q{N}_q}\right)\end{array}\right), b_g=\left(\begin{array}{c}\overline{u}\left(x_{r1}\right)\\ \overline{u}\left(x_{r2}\right)\\ ⋮\\ \overline{u}\left(x_{r{N}_r}\right)\end{array}\right)$$

(36)

For the problem described in Section 2.2, the components in the submatrices $A$, $A_h$, and $A_g$ and the sub-vectors $b$, $b_h$, and $b_g$ are derived as:

$$\begin{array}{l}{A}_{IJ}=\left[{\Psi }_J^{xxxx}\left(x_{pI}\right)+2{\Psi }_J^{xxyy}\left(x_{pI}\right)+{\Psi }_J^{yyyy}\left(x_{pI}\right)-{\lambda }^2{\Psi }_J^{xx}\left(x_{pI}\right)-{\lambda }^2{\Psi }_J^{yy}\left(x_{pI}\right)\right]\\ A_{hIJ}=\left[n{\Psi }_J^n\left(x_{qI}\right)\right]\\ A_{gIJ}=\left[{\Psi }_J\left(x_{rI}\right)\right]\end{array}$$

(37)

$$\begin{array}{l}{b}_{IJ}=0 \forall x_{pI}\\ b_{hIJ}=\overline{q} \forall x_{qI}\\ b_{gIJ}=\overline{u} \forall x_{rI}\end{array}$$

(38)

As for the values of weights $w_h$ and $w_g$, they are determined both theoretically and numerically according to the error estimate and computational results. Referring to a previous study [13], it was shown that the weights in the gradient reproducing kernel collocation method for solving second-order direct Cauchy problems are given by:

$$w_h\approx O\left(1\right),w_g\approx O\left(a^{q-p-1}\right)\approx O\left(\frac{1}{a}\right)$$

(39)

where $p$ and $q$ denote the order of basis for RK shape functions and gradient RK shape functions, respectively, and $a$ denotes the support size of RK and gradient RK shape functions. It was reported that the equal-order basis $p=q=2$ can reach synchronized convergence rates of $u$ and its derivatives. For the fourth-order PDEs in consideration, $p=q=4$ is adopted herein. On the other hand, referring to another previous study [11], the weights in the high-order gradient RKCM for solving fourth-order Kirchhoff plate problems are given by:

$$w_h\approx O\left(\frac{G}{a^2}\right),w_g\approx O\left(\frac{G}{a^3}\right)$$

(40)

where $G$ is the constant related to Young’s modulus, Poisson’s ratio, and the plate’s thickness. As the fourth-order PDEs described in Section 2 do not contain the elasticity problem, the normalized version of Equation (40) should be used instead, which is given by:

$$w_h\approx O\left(\frac{1}{a^2}\right),w_g\approx O\left(\frac{1}{a^3}\right)$$

(41)

As the fourth-order inverse source problem is of major interest in the present study, either Equation (39) or Equation (41) might be a good candidate to meet our need. To this end, the proper weights will be determined numerically in the next section.

4. Numerical Examples

In this section, four examples are provided to demonstrate the viability of the weighted high-order G-RKCM in solving the fourth-order PDEs with two mathematical formulations. As mentioned in Section 3, the proper weights will be investigated numerically on the basis of the theoretical derivation, as described in Equations (39) and (41). Furthermore, the RK and high-order gradient RK shape functions are constructed by using the equal-order basis function of quartic order to ensure consistency. Both quintic and sextic B-spline kernel functions are adopted to assure smoothness in the approximation. Without loss of generality, the RK support size is $a=5h$. To compare the approximate solutions with reference solutions in the literature, the following error norm is defined [2,4]:

$$\mathrm{relative} \mathrm{error} \mathrm{norm}=\frac{\sqrt{{\displaystyle {\sum }_{i=1}^{N_c}{\left(f_{numerical}^i-f_{analytical}^i\right)}^2}}}{\sqrt{{\displaystyle {\sum }_{i=1}^{N_c}{f}_{analytical}^i{}^2}}}$$

(42)

The presentation of contour plot is expressed in terms of the maximum relative error defined as:

$$\mathrm{maximum} \mathrm{relative} \mathrm{error}=\frac{\left|f_{numerical}^i-f_{analytical}^i\right|}{\left|f_{analytical}^i\right|}$$

(43)

for $i=1,2,\dots ,N_c$.

4.1. Mathematical Formulation I in a Square Domain

The governing equation together with boundary conditions in a square domain are described as follows:

$$\frac{{\partial }^{4}u}{\partial x^4}+2\frac{{\partial }^{4}u}{\partial x^2\partial y^2}+\frac{{\partial }^{4}u}{\partial y^4}=0 \mathrm{in} \Omega =\left\{\left.\left(x,y\right)\right|0<x,y<6\right\}$$

(44)

$$\begin{array}{ccc}u=\frac{1}{4}{y}^2\left(1+\frac{s}{100}\times rand\right)& \mathrm{on}& x=0\\ u=\frac{1}{4}\left(36+y^2\right)\left(1+\frac{s}{100}\times rand\right)& \mathrm{on}& x=6\\ u=\frac{1}{4}{x}^2\left(1+\frac{s}{100}\times rand\right)& \mathrm{on}& y=0\\ u=\frac{1}{4}\left(x^2+36\right)\left(1+\frac{s}{100}\times rand\right)& \mathrm{on}& y=6\end{array}$$

(45)

$$\begin{array}{ccc}{u}_{,x}=\frac{s}{100}\times rand& \mathrm{on}& x=0\\ u_{,x}=3\left(1+\frac{s}{100}\times rand\right)& \mathrm{on}& x=6\\ u_{,y}=\frac{s}{100}\times rand& \mathrm{on}& y=0\\ u_{,y}=3\left(1+\frac{s}{100}\times rand\right)& \mathrm{on}& y=6\end{array}$$

(46)

where $rand$ denotes the Matlab built-in function of a random number in the interval 0~1. Referring to Ref. [4], the accessible boundary $\partial {\Omega }_1$ is taken as the $\partial \Omega$. For $s=0$, the analytical solutions to this problem are given by:

$$u\left(x,y\right)=\frac{1}{4}\left(x^2+y^2\right)$$

(47)

$$f\left(x,y\right)=1$$

(48)

To determine the weights in the proposed method for solving the fourth-order PDEs in consideration, two sets of weights introduced in Section 3.2 are investigated through the $L_2$ norms of $u$ and $u_{,\alpha }$. The uniform discretization is schematically shown in Figure 1a. In Figure 2, both sets of weights exhibit similar convergence rates for $L_2$ norms of $u$ and $u_{,\alpha }$ with respect to the quintic kernel function ($a=4.95h$) and sextic kernel function ($a=5.25h$), except the $L_2$ norm of $u_{,\alpha }$ for the quintic kernel function. Furthermore, some negative slopes are observed as high-order gradient approximation, which might cause numerical instability for certain discretization. Reaching an acceptable convergence rate with high accuracy becomes critical for high-order G-RKCM in approximating high order derivatives by high order basis functions. In general, the sextic kernel function shows higher convergence and accuracy in the approximation. The reason for similar convergence rates might be explained as follows: for RK support size $a=6h$ with $N_s={30}^2$, the two sets of weights are $O\left(1\right)=1$ and $O\left(1/a\right)\approx \frac{1}{6h}=\frac{1}{6\times \left(6/29\right)}=0.8$, and $O\left(1/a^2\right)\approx 1/a^2=0.64$ and $O\left(1/a^3\right)\approx 1/a^3=0.51$, respectively. The ratios of weights in each set are equal to each other, i.e., $\frac{O\left(1\right)/O\left(1/a\right)}{O\left(1/a^2\right)/O\left(1/a^3\right)}=1.25$. As the set of weights given in Equation (41) can be more sensitive to the discretization, it is adopted in the following study.

The results obtained by the weighted high-order G-RKCM are first verified with the results obtained by the method of fundamental solutions (MFS) [2] and the generalized finite difference method (GFDM) [4] in the literature. Referring to

Table 1. Comparison of relative error norms of $f$ by different methods and influence of RK support size in G-RKCM with $N_s={25}^2$.

Method	Relative Error Norm
MFS with $N_s=40$ [2]	$2.13\times {10}^{-7}$
GFDM with $N_s={25}^2$ [4]	$8.26\times {10}^{-8}$
G-RKCM (quintic) $a=4.5h$	$1.63\times {10}^{-10}$
G-RKCM (sextic) $a=4.5h$	$7.30\times {10}^{-10}$
G-RKCM (quintic) $a=5h$	$4.32\times {10}^{-11}$
G-RKCM (sextic) $a=5h$	$7.89\times {10}^{-11}$
G-RKCM (quintic) $a=5.5h$	$4.08\times {10}^{-11}$
G-RKCM (sextic) $a=5.5h$	$5.07\times {10}^{-11}$
G-RKCM (quintic) $a=6h$	$2.44\times {10}^{-11}$
G-RKCM (sextic) $a=6h$	$2.90\times {10}^{-11}$

, the present method yields the best results with high accuracy among the three methods, regardless of the RK support size used in the approximation. The selected contour plots of maximum relative error of $f$ obtained by $a=5h$ are depicted in Figure 3; it is confirmed that high accuracy for recovering source $f$ is assured. Next, the boundary equations in Equations (45) and (46) are disturbed by some percentage of noise $s$, and the results obtained by using $N_s=N_c={25}^2$ are summarized in

Table 2. Comparison of relative error norms of $f$ by various $s$ on boundary conditions in Section 4.1.

$s$		1	2	3
GFDM [4]		0.025	-	-
G-RKCM (quintic)	Neumann BC	0.0198	0.0480	0.0614
	Dirichlet BC	0.0464	0.1062	0.1387
	both BCs	0.0432	0.1203	0.1613
G-RKCM (sextic)	Neumann BC	0.0144	0.0295	0.0432
	Dirichlet BC	0.0189	0.0388	0.0824
	both BCs	0.0184	0.0417	0.0661

. As the reference result was obtained by adding noise into the input data as described ambiguously in [4], three possible scenarios with disturbance adding on various kinds of boundary conditions (BCs) are investigated herein. Still, the present method yields better accuracy than the reference method in general, although G-RKCM with the quintic kernel function shows larger errors when Dirichlet boundary condition or both boundary conditions are disturbed. Nevertheless, the present method is quite stable up to the noise level $s=3$. As shown in Figure 1b, the non-uniform discretization for $N_s=N_c={25}^2$ obtained by 5% disturbance of domain points is considered. The contour plots of maximum relative error of $f$ are depicted in Figure 4; furthermore, the corresponding relative error norms of $f$ obtained by various kinds of disturbance of boundary conditions are summarized in

Table 3. Comparison of relative error norms of $f$ obtained by non-uniform discretization with various $s$ added to the boundary conditions in Section 4.1.

$s$		1	2	3
G-RKCM (quintic)	Neumann BC	0.0285	0.0578	0.0834
	Dirichlet BC	0.1189	0.1531	0.2297
	both BCs	0.0940	0.1462	0.2069
G-RKCM (sextic)	Neumann BC	0.0263	0.0562	0.1114
	Dirichlet BC	0.0868	0.1411	0.1900
	both BCs	0.0926	0.1745	0.1925

. From Table 2 and Table 3, it is observed that the disturbance adding on the Neumann boundary condition produces minimal error, while the other two kinds of boundary disturbances produce a similar amount of error. Even subjected to double disturbance of discretization and boundary condition, the robustness of the method is apparently demonstrated.

4.2. Mathematical Formulation I in an Annular Domain

The governing equation and boundary conditions in an annular domain are described as follows:

$$\frac{{\partial }^{4}u}{\partial x^4}+2\frac{{\partial }^{4}u}{\partial x^2\partial y^2}+\frac{{\partial }^{4}u}{\partial y^4}=0 \mathrm{in} \Omega =\left\{\left.\left(x,y\right)\right|R_i=1<r=\sqrt{x^2+y^2}<R_o=2\right\}$$

(49)

$$u\left(R_o,\theta \right)=-\frac{1}{6}\left[{\left(R_o\cos \theta -6\right)}^3+{\left(R_o\sin \theta -6\right)}^3\right],0\le \theta \le {\beta }_o$$

(50)

$$u_n\left(R_o,\theta \right)=-\frac{1}{2}\left[{\left(R_o\cos \theta -6\right)}^2\cos \theta +{\left(R_o\sin \theta -6\right)}^2\sin \theta \right],0\le \theta \le {\beta }_o$$

(51)

with the inner boundary condition:

$$u\left(R_i,\theta \right)=-\frac{1}{6}\left[{\left(R_i\cos \theta -6\right)}^3+{\left(R_i\sin \theta -6\right)}^3\right],0\le \theta \le 2\pi$$

(52)

In Equations (50) and (51), ${\beta }_o$ denotes the angle along the outer boundary, measured from positive $x$ axis in the counterclockwise direction, in which the portion of outer boundary is imposed with both Dirichlet and Neumann boundary conditions. The analytical solutions to this problem are as follows:

$$u\left(x,y\right)=-\frac{1}{6}\left[{\left(x-6\right)}^3+{\left(y-6\right)}^3\right]$$

(53)

$$f\left(x,y\right)=12-x-y$$

(54)

The discretization of the problem using $N_s=386$ is depicted in Figure 5, and the corresponding contour plots of maximum relative error of $f$ obtained by quintic and sextic kernel functions are shown in Figure 6. The relative error norms obtained by various RK support size are summarized in

Table 4. Comparison of the relative error norms of $f$ by different methods and influence of RK support size in G-RKCM with $N_s=386$.

Method	Relative Error Norm
GFDM with $N_s=386$ [4]	$8.00\times {10}^{-8}$
G-RKCM (quintic) $a=4.5h$	4.34 $\times {10}^{-10}$
G-RKCM (sextic) $a=4.5h$	3.44 $\times {10}^{-9}$
G-RKCM (quintic) $a=5h$	2.99 $\times {10}^{-10}$
G-RKCM (sextic) $a=5h$	1.75 $\times {10}^{-10}$
G-RKCM (quintic) $a=5.5h$	4.12 $\times {10}^{-10}$
G-RKCM (sextic) $a=5.5h$	4.57 $\times {10}^{-10}$
G-RKCM (quintic) $a=6h$	5.23 $\times {10}^{-10}$
G-RKCM (sextic) $a=6h$	5.02 $\times {10}^{-10}$

. Obviously, the present method with both kernel functions exhibits higher accuracy in retrieving the heat source $f$ regardless of the RK support size in comparison with the reference solution by GFDM given in [4]. Concerning the disturbance with various $s$ added to the outer boundary, the comparison of relative error norms of $f$ is made in

Table 5. Comparison of the relative error norms of $f$ by various $s$ on boundary conditions in Section 4.2.

$s$		1	2	3
GFDM [4]		0.06	-	-
G-RKCM (quintic)	Neumann BC	0.0348	0.0701	0.1147
	Dirichlet BC	0.1694	0.4567	0.6620
	both BCs	0.1815	0.4380	0.7094
G-RKCM (sextic)	Neumann BC	0.0465	0.0942	0.1488
	Dirichlet BC	0.3731	0.6007	0.9965
	both BCs	0.2897	0.6417	1.2433

. It is observed that the disturbance added to the Neumann boundary conditions has the smallest error among three scenarios of boundary conditions. The selected contour plots of maximum relative error of $f$ obtained by adding $s=1$ to the Neumann boundary condition are shown in Figure 7. Still, the present method is stable under various kinds of boundary disturbance. To further investigate the limitation of the method in retrieving the heat source, the relative error norms obtained by accessible outer boundary with different angles ${\beta }_o$ without considering disturbance on the outer boundary are shown in Figure 8. It is observed that both kernel functions yield similar accuracy when ${\beta }_o\ge \pi$, while the quintic kernel function maintains accuracy for ${\beta }_o< \pi$. As discussed in [11], reaching acceptable accuracy becomes critical for high-order G-RKCM in approximating high order derivatives by high-order basis functions in direct problems. Although a similar situation is observed for the inverse problem in consideration, the present method is able to retrieve heat source with high accuracy within limited accessible boundary ${\beta }_o/2\pi =0.1$, which is much better than ${\beta }_o/2\pi =0.4$, as reported in the literature [4].

4.3. Mathematical Formulation II in a Circular Domain

The governing equation together with boundary conditions in a circular domain are described as follows:

$$\frac{{\partial }^{4}u}{\partial x^4}+2\frac{{\partial }^{4}u}{\partial x^2\partial y^2}+\frac{{\partial }^{4}u}{\partial y^4}-{\lambda }^2\frac{{\partial }^{2}u}{\partial x^2}-{\lambda }^2\frac{{\partial }^{2}u}{\partial y^2}=0 \mathrm{in} \Omega =\left\{\left.\left(x,y\right)\right|r=\sqrt{x^2+y^2}<1\right\}$$

(55)

$$u\left(r,\theta \right)=\left[e^{\cos \theta }\sin \left(\sin \theta \right)+e^{\cos \theta -\sin \theta }\right]\left(1+\frac{s}{100}\times rand\right), 0\le \theta <2\pi$$

(56)

$$\begin{array}{ll}{u}_n\left(r,\theta \right)& =\left\{e^{\cos \theta }\left[\sin \left(\sin \theta \right)+e^{-\sin \theta }\right]\cos \theta \right.\\ & \left.+e^{\cos \theta }\left[\cos \left(\sin \theta \right)-e^{-\sin \theta }\right]\sin \theta \right\}\left(1+\frac{s}{100}\times rand\right), 0\le \theta <2\pi \end{array}$$

(57)

where the wave number is $\lambda =\sqrt{2}$. The analytical solutions to this problem are given by:

$$u\left(x,y\right)=e^x\sin y+e^{x-y}$$

(58)

$$f\left(x,y\right)=2e^{x-y}$$

(59)

The discretizations of the domain by uniform and non-uniform points $N_s=N_c=468$ are shown in Figure 9a,b, respectively. As the reference solution in the literature is given with disturbed noise, to verify the results obtained by the present method, different levels of noise $s$ on various kinds of boundary conditions is considered.

Table 6. Comparison of the relative error norms of $f$ by various $s$ on boundary conditions in Section 4.3.

$s$		2	3
MFS [2]		0.0175	-
G-RKCM (quintic) $a=4.5h$	Neumann BC	0.0157	0.0391
	Dirichlet BC	0.0343	0.0718
	both BCs	0.0468	0.0749
G-RKCM (sextic) $a=4.5h$	Neumann BC	0.0166	0.0392
	Dirichlet BC	0.0410	0.0651
	both BCs	0.0409	0.0747
G-RKCM (quintic) $a=5h$	Neumann BC	0.0237	0.0427
	Dirichlet BC	0.0512	0.0549
	both BCs	0.0411	0.0735
G-RKCM (sextic) $a=5h$	Neumann BC	0.0243	0.0399
	Dirichlet BC	0.0397	0.0457
	both BCs	0.0428	0.0675

summarizes the relative error norms of $f$ obtained by the method of fundamental solutions (MFS) [2] and the present G-RKCM, in which smaller errors can be obtained when a smaller RK support size $a=4.5h$ is adopted as compared with reference solution. The flexibility of reproducing kernel approximation in adjusting the support size is observed. Additionally, G-RKCM with the sextic kernel function yields higher accuracy than the quintic kernel function. The contour plots of $f$ obtained by adding $s=2$ to the Neumann boundary condition are depicted in Figure 10; the distribution of magnitude of $f$ agrees well with the reference solution [2]. Nevertheless, by checking $x=y$ in the analytical solution given in Equation (59), it is easily found that $f\left(x,y\right)=2$ along the diagonal direction with ${45}^{\circ }$. Therefore, the trend or orientation of the contour in the reference [2] is not correct, and the correct contours of $f$ are provided in Figure 10 and Figure 11. Particularly, Figure 11 presents the corresponding contours obtained by non-uniform discretization (5% noise added to uniform discretization) with various $s$ added to the Neumann boundary condition. The relative error norms of $f$ obtained by non-uniform discretization with various $s$ added to the boundary conditions are summarized in

Table 7. Comparison of relative error norms of $f$ obtained by non-uniform discretization with various $s$ added to the boundary conditions in Section 4.3.

$s$		1	2	3
G-RKCM (quintic) $a=4.5h$	Neumann BC	0.0149	0.0278	0.0413
	Dirichlet BC	0.0298	0.0531	0.0850
	both BCs	0.0279	0.0528	0.0784
G-RKCM (sextic) $a=4.5h$	Neumann BC	0.0128	0.0263	0.0428
	Dirichlet BC	0.0250	0.0526	0.0715
	both BCs	0.0284	0.0572	0.0613
G-RKCM (quintic) $a=5h$	Neumann BC	0.0156	0.0287	0.0494
	Dirichlet BC	0.0379	0.0425	0.0752
	both BCs	0.0273	0.0517	0.0878
G-RKCM (sextic) $a=5h$	Neumann BC	0.0166	0.0314	0.0579
	Dirichlet BC	0.0393	0.0488	0.0702
	both BCs	0.0320	0.0479	0.0743

; again, $a=4.5h$ yields better accuracy than $a=5h$, and the sextic kernel function is more accurate than the quintic kernel function. From above results, it is found that the present method is stable no matter what kinds of disturbance and levels of noise are imposed on.

4.4. Mathematical Formulation II in an Annular Domain

The governing equation with boundary conditions in an annular domain are described as follows:

$$\begin{array}{ccc}\hfill \frac{{\partial }^{4}u}{\partial x^4}+2\frac{{\partial }^{4}u}{\partial x^2\partial y^2}+\frac{{\partial }^{4}u}{\partial y^4}-{\lambda }^2\frac{{\partial }^{2}u}{\partial x^2}-{\lambda }^2\frac{{\partial }^{2}u}{\partial y^2}& =& 0\hfill \\ \hfill \mathrm{in} \Omega =\{\left.\left(x,y\right)\right|R_i& =& 1<r=\sqrt{x^2+y^2}<R_o=2\}\end{array}$$

(60)

$$u\left(R_o,\theta \right)=e^{R_o\cos \theta }\sin \left(R_o\sin \theta \right)+e^{R_o\left(\cos \theta -\sin \theta \right)},0\le \theta \le {\beta }_o$$

(61)

$$\begin{array}{ll}{u}_n\left(R_o,\theta \right)& =e^{R_o\cos \theta }\left[\sin \left(R_o\sin \theta \right)+e^{-R_o\sin \theta }\right]\cos \theta \\ & +e^{R_o\cos \theta }\left[\cos \left(R_o\sin \theta \right)-e^{-R_o\sin \theta }\right]\sin \theta ,0\le \theta \le {\beta }_o\end{array}$$

(62)

with the inner boundary condition:

$$u\left(R_i,\theta \right)=e^{R_i\cos \theta }\sin \left(R_i\sin \theta \right)+e^{R_i\left(\cos \theta -\sin \theta \right)},0\le \theta \le 2\pi$$

(63)

where the wave number is $\lambda =\sqrt{2}$. The same analytical solutions are described in Section 4.3.

The uniform discretization and non-uniform discretization (5% noise added to uniform discretization) of the annular domain by $N_s=N_c=666$ are depicted in Figure 12a,b, respectively. To reach the desired accuracy, a layer of ghost points is arranged along the radial direction with a distance of $0.65h$ from the outer boundary of the domain, i.e., total points $N_{sg}=742$. For quintic and sextic kernel functions, the RK support size is chosen as $a=4.75h$ and $a=4.35h$, respectively. The corresponding contour plots of $f$ obtained by uniform discretization are shown in Figure 13; both kernel functions generate consistent contour plots. Next, different levels of noise $s$ are added to various boundary conditions, and the results are summarized in

Table 8. Comparison of relative error norms of $f$ obtained by uniform discretization with various $s$ added to the boundary conditions in Section 4.4.

$s$		0	1	2
G-RKCM (quintic)	Neumann BC	0.0095	0.0219	0.0385
	Dirichlet BC	0.0095	0.3180	0.5597
	both BCs	0.0095	0.3577	0.6664
G-RKCM (sextic)	Neumann BC	0.0040	0.0135	0.0299
	Dirichlet BC	0.0040	0.1553	0.2972
	both BCs	0.0040	0.1610	0.2389

. It is observed that more accurate results are reached by G-RKCM with the sextic kernel function than those by the quintic kernel function, and the case with noise added to the Neumann boundary condition has the smallest error for G-RKCM with both kernel functions. For non-uniform discretization disturbed by various $s$ added to the Neumann boundary condition, the contour plots of $f$ are given in Figure 14. Especially, Figure 14c,d are the contours obtained by quintic kernel function with $s=1$ and sextic kernel function with $s=2$. By observation, the contours of $f$ obtained by G-RKCM with the sextic kernel function are more stable than those obtained by quintic kernel function, even under disturbance on both discretization and boundary condition. The corresponding relative error norms of $f$ obtained by various $s$ on different boundary conditions are summarized in

Table 9. Comparison of relative error norms of $f$ obtained by non-uniform discretization with various $s$ added to the boundary conditions in Section 4.4.

$s$		0	1	2
G-RKCM (quintic)	Neumann BC	0.1804	0.2349	0.3903
	Dirichlet BC	0.1804	0.4305	1.3475
	both BCs	0.1804	0.7970	1.8118
G-RKCM (sextic)	Neumann BC	0.0535	0.0599	0.0606
	Dirichlet BC	0.0535	0.2250	0.3218
	both BCs	0.0535	0.2971	0.3126

. Again, higher accuracy of G-RKCM with the sextic kernel function is observed. For an accessible outer boundary in the range $0\le {\beta }_o\le 2\pi$, the relative error norms are depicted in Figure 15. Obviously, both kernel functions exhibit similar accuracy, and the error increases with reducing accessible outer boundary while the approximation retains acceptable accuracy for ${\beta }_o\ge \pi$.

5. Conclusions

The high-order gradient reproducing kernel approximation is introduced to solve fourth-order PDEs with weak solutions to inverse source problems. With the aid of gradient approximation, tedious computation is avoided. For the present study concerning the fourth-order PDEs, it is efficacious to use equal-order bases of quartic order. The numerical results have shown that the sextic kernel function exhibits higher accuracy and convergence rate than the quintic kernel function; nevertheless, to retrieve the heat source with a reducing accessible boundary, the quintic kernel function might be a better choice.

Theoretically, the convergence rates of unknown variable $u$ and its derivatives are directly related to the bases adopted in constructing RK and high-order gradient RK shape functions. As the heat source $f$ is recovered from $u$ by using the second-order gradient RK approximation, the fluctuation of $f$ is determined by the order of $u$. From the example in Section 4.3, it was found that the equal quartic-order bases are able to reproduce the infinite-order polynomial function with desired accuracy in the inverse analysis, except for the example in Section 4.4 needing additional ghost points due to more complex geometry.

Concerning the disturbance on discretization and boundary conditions, the present method has shown the robustness in sight of non-uniform discretization and various noise levels on boundary conditions. Especially the reproducing kernel approximation offers flexibility in adjusting the support size if need be. From the investigation of benchmark problems, it is demonstrated that the weighted high-order G-RKCM is able to retrieve a heat source from the fourth-order PDEs with desired accuracy, even with limited accessible boundary.