Abstract
After the research on naBL-algebras gained by the non-associative t-norms and overlap functions, inflationary BL-algebras were also studied as a recent kind of non-associative generalization of BL-algebras, which can be obtained by general overlap functions. In this paper, we show that not every inflationary general overlap function can induce an inflationary BL-algebra by a counterexample and thus propose the new concept of weak inflationary BL-algebras. We prove that each inflationary general overlap function corresponds to a weak inflationary BL-algebra; therefore, two mistaken results in the previous paper are revised. In addition, some properties satisfied by weak inflationary BL-algebras are discussed, and the relationships among some non-classical logic algebras are analyzed. Finally, we establish the theory of filters and quotient algebras of inflationary general residuated lattice (IGRL) and inflationary pseudo-general residuated lattice (IPGRL), and characterize the properties of some kinds of IGRLs and IPGRLs by naBL-filters, (weak) inflationary BL-filters, and weak inflationary pseudo-BL-filters.
Keywords:
fuzzy logic; overlap function; weak inflationary BL-algebra; filter; inflationary pseudo-general residuated lattice MSC:
06B10; 06D72; 08A72
1. Introduction
The notions of t-norm and residuated lattice are significant parts of fuzzy logic. Residuated lattices can be used as a special unsupervised learning method in formal concept analysis. BL-algebras are algebraic structures, proposed in [1,2], based on the residuated lattice theory [3], which correspond to the continuous t-norms [4,5] on the interval [0, 1]. As a kind of aggregation function [6], the associativity of t-norms brings great restrictions to them. On the contrary, other operators such as copulas [7] do not require associativity. A non-associative fuzzy logic , which can be regarded as a commutative basic algebra, is also studied in [8]. This has led many scholars to explore the reasonable non-associative extension of fuzzy logic. For instance, M. Botur introduced naBL-algebras corresponding to non-associative t-norms and their residuated implications [9]. However, the t-norms still have 1 as the unit element, which makes us consider a wider range of algebraic structure corresponding to operators without a unit element.
As a special class of aggregation operators, overlap functions [10] play an important role in many practical applications, such as classification problems, image processing, and so on (see [11,12,13,14]). They also do not need associativity, and a continuous t-norm without nontrivial zero factors can be seen as a special overlap function, which has attracted many scholars to study them. This includes the subclass of naBL-algebras constructed based on overlap functions shown in [15]. In addition, the general overlap functions [16] obtained on the basis of relaxing the boundary conditions of overlap functions have been proven to have a better application effect in fuzzy-rule-based classification systems, which leads scholars to replace the t-norms with the general overlap functions, so as to study a new kind of non-associative spread for BL-algebras, that is, the inflationary BL-algebras (briefly, IBL-algebra) [17].
Our research is based on the paper [17]. We give two counterexamples to show that not every inflationary general overlap function and its residuated implication can construct an inflationary BL-algebra. Therefore, we further generalize it, provide the new concept of weak inflationary BL-algebras (briefly weak IBL-algebra), and elaborate the one-to-one correspondence between inflationary general overlap functions and weak IBL-algebras. Then, some properties of weak IBL-algebra and some filters of inflationary (pseudo-) general residuated lattices are discussed (some of the latest studies on overlap functions, pseudo overlap functions, and residuated lattices that we refer to are contained in [18,19,20,21,22,23]).
The structure of this article is as follows. In the second part, we provide some specific definitions of concepts that will be involved in the article. In Section 3, two specific counterexamples are given to illustrate the omission in [17], then the concept of weak IBL-algebras is introduced, and we analyze the relationship between some algebras mentioned in the paper, discuss some properties that weak IBL-algebras satisfy, and finally prove that every inflationary general overlap function and its residuated implication can induce a weak IBL-algebra. As for Section 4, we describe the definition of some special filters of inflationary general residuated lattices, and declare the necessary and sufficient conditions for inflationary general residuated lattices to form naBL-algebras and weak IBL-algebras. Then, the definition of filters of inflationary pseudo-general residuated lattices and the construction of quotient algebras are presented, and the concept of weak inflationary pseudo BL-filters is provided so as to characterize the requirements for an inflationary pseudo-general residuated lattice to become a weak inflationary pseudo BL-algebra in Section 5. The last part is the conclusions and references.
2. Preliminaries
Some related concepts of general overlap functions are reviewed first.
Definition 1
([16,17]). Given a mapping GO: , if for any , GO meets the requirements below, then GO is called a general overlap function (briefly, ):
(GO1) GO is commutative;
(GO2) when or ;
(GO3) ;
(GO4) GO has a monotonically increasing nature;
(GO5) It meets continuity.
Definition 2
([17]). Given a on denoted as GO, if for arbitrary it satisfies , then it is called inflationary.
Definition 3
([17]). Given an inflationary on denoted as GO, the binary mapping on is defined as
for any , it is called the residuated implication induced by GO.
In fuzzy logic, the commonly used aggregation operator is the t-norm, which is defined below.
Definition 4
([4,5]). Given a binary mapping T on , when for any , T meets the requirements below, it is called a t-norm:
(T1) T is commutative;
(T2) T meets associativity;
(T3) T is a monotonically increasing property, that is, when ;
(T4) T has 1 as the unit element, that is, .
Evidently, a continuous t-norm is a GOF by definition. Next, we present some notions of existing algebraic structures for analysis later.
Definition 5
([3,24]). Given an algebra , if it meets the requirements below, then it is called a residuated lattice:
(L1) is a bounded lattice;
(L2) is a commutative monoid;
(L3) The pair meets the residuation principle, that is, for arbitrary , when and only when .
Definition 6
([1,2,25]). Given a residuated lattice , when for arbitrary , it meets the requirements below, it is called a BL-algebra:
(BL1) (divisibility);
(BL2) (prelinearity).
Definition 7
([9]). Given an algebra , when for arbitrary , it meets the requirements below, it is called a non-associative residuated lattice:
(naL1) is a lattice with 0 as the lower bound and 1 as the upper bound;
(naL2) is a commutative groupoid with 1 as unit element, that is, L is a nonempty set, ∗ is a commutative binary operator with unit element 1 on L;
(naL3) satisfies the residuation principle.
Definition 8
([9]). Given a non-associative residuated lattice , it is called a naBL-algebra when for arbitrary , it meets the following requirements:
(naBL1) ;
(naBL2) (α-prelinearity)
(naBL3) (β-prelinearity)
The filter is a vital portion in logical algebra, especially in constructing a quotient algebra. Here, we state the definition of filters of non-associative residuated lattices.
Definition 9
([9]). Given a non-associative residuated lattice , and a nonempty set , F is called a filter of L if it satisfies the following:
(1) For arbitrary , if and , then ;
(2) For arbitrary , ;
(3) For arbitrary and , , where
At the end of this part, we look back at the conception of inflationary pseudo-general residuated lattices proposed in [23], as well as a few properties they satisfy and the definition of a special class of weak inflationary pseudo-BL-algebras they contain.
Definition 10
([23]). An algebra of type (2, 2, 2, 2, 2, 0, 0), where ∗ is an inflationary binary operator, that is, the result of operation ∗ between any element on L and 1 is greater than or equal to the element, is known as an inflationary pseudo-general residuated lattice (for short, named ) when it satisfies the following conditions:
(PL1) is a bounded lattice;
(PL2) is a groupoid, that is, a binary operator ∗ defined on a nonempty set L;
(PL3) when and only when , when and only when , for arbitrary .
Proposition 1
([23]). Given an , for arbitrary , it meets the requirements below:
(PL4) , ;
(PL5) If , then and ;
(PL6) , ;
(PL7) , ;
(PL8) , ;
(PL9) ;
(PL10) when or ;
(PL11) and .
Definition 11
([23]). An is known as a weak inflationary pseudo-BL-algebra (briefly, weak inflationary PBL-algebra) when for arbitrary , it meets the requirements below:
(WIPBL1) If , ;
(WIPBL2) .
3. Inflationary BL-Algebras and Weak Inflationary BL-Algebras
In this part, we introduce the definition of weak inflationary BL-algebras and explore their properties. Let us first review the definition of inflationary BL-algebra (see [17]).
Definition 12
([17]). Given an algebra , where the operator ∗ is inflationary, it is an inflationary general residuated lattice (briefly ) when it holds that:
(A1) is a lattice with 0 as the lower bound and 1 as the upper bound;
(A2) The commutative binary operator ∗ is defined on the nonempty set L;
(A3) satisfies the residuation principle.
Proposition 2.
Given an , for arbitrary , it meets the requirements below:
(A4) when ;
(A5) when ;
(A6) when ;
(A7) ;
(A8) ;
(A9) ;
(A10) ;
(A11) ;
(A12) ;
(A13) ;
(A14) if and only if for each ;
(A15) If , then ;
(A16) are comparable and ;
(A17) when .
Proof.
The above certificates of (A4)–(A6) and (A9)–(A16) are detailed in [17]. With regard to (A7) and (A8), because an IGRL is also an IPGRL, it meets (PL6) and (PL7) according to Proposition 2.11, and at this time, . As for (A17), if , then by the residuation principle. By (A16), we can obtain . □
Definition 13
([17]). Given an , it is an inflationary BL-algebra (briefly IBL-algebra) when it meets the followng conditions:
(IBL1) ;
(IBL2) (general prelinearity).
In Lemma 5.1 of [17], it is considered that the inflationary GOF meets (BL1). In fact, this is not true. We provide two examples below.
Example 1.(1) Given the operator GO: defined as , it satisfies (GO1)∼(GO5), that is, the function GO is a . Moreover, since , GO is inflationary. Then, we can obtain its residuated implication as follows:
It is clear that when , , there is and , but , that is, it does not satisfy divisibility.
(2) Given the operator GO: defined as , it is a . Since , it is inflationary. The residuated implication induced by it is formulated as:
When , , there is and , but , that is, it does not satisfy divisibility.
Therefore, we can know that the algebra composed of the minimization operator ∧, maximization operator ∨, inflationary GOF ∗, and its residue → of Proposition 5.2 of [17] is not necessarily an inflationary BL-algebra. Therefore, we consider a broader inflationary BL-algebra, which we call weak inflationary BL-algebra.
Next, we provide the definition of weak inflationary BL-algebra.
Definition 14.
Given an , it is a weak inflationary BL-algebra (briefly weak IBL-algebra) when for arbitrary , it satisfies the conditions below:
(W1) If , then (general divisibility);
(W2) .
Example 2.
We take the mapping GO in Example 1 (1) as the operator ∗ and the residuated implication induced by it as the operator →, for arbitrary , , , thereby the lattice satisfies (A1)∼(A3), that is, it is an . By definition, we obtain that when , thereby , that is, L satisfies general divisibility. Since it is clear that
L satisfies general prelinearity. Thus, is a weak IBL-algebra.
Evidently, every IBL-algebra is a weak IBL-algebra. In addition, we find that the inflationary general overlap functions satisfying divisibility actually have 1 as the unit element, and the derivation process is as follows.
Proposition 3.
Given an inflationary , if it satisfies divisibility, then it has 1 as the unit element.
Proof.
Suppose that the operator ∗ is an inflationary GOF satisfying divisibility. Since , that is, , and by divisibility. Because , according to residuation principle, there is , that is, . Therefore, , that is, the operator ∗ has 1 as the unit element. □
Therefore, the general prelinearity satisfied by the inflationary general overlap functions satisfying divisibility amounts to prelinearity. We know that the non-associative t-norms that can form naBL-algebra are included in the general overlap functions with unit element 1. In addition, there exist residuated lattices satisfying divisibility and prelinearity but not a naBL-algebra under non-total order. Examples are as follows.
Example 3.
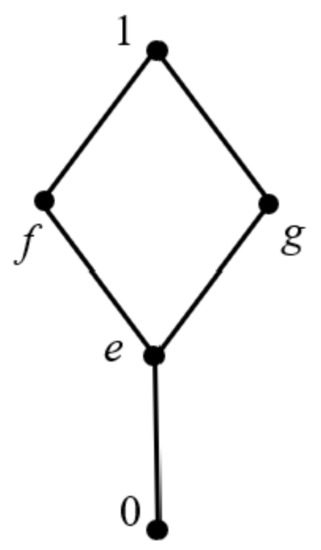
(1) Given a lattice L, the structure is as shown in Figure 1. Two operations, ∗ and →, of it are shown below:

Figure 1.
Lattice structure of (1) in Example 3.
Then, is an IBL-algebra but not a naBL-algebra, where .
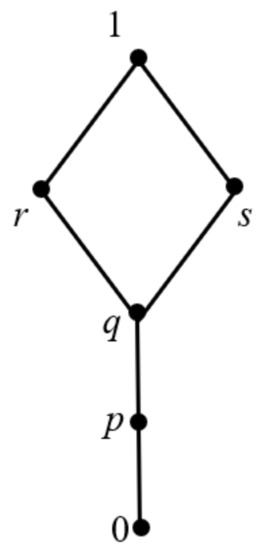
(2) Given a lattice L, the structure is as shown in Figure 2. Two operations, ∗ and →, are shown below:

Figure 2.
Lattice structure of (2) in Example 3.
Then, is an IBL-algebra but not a naBL-algebra, where .
Thus, we can obtain the diagram shown in Figure 3. Among them, naBL-algebras can be obtained from non-associative t-norms. The operators corresponding to IBL-algebras are inflationary general overlap functions with unit element 1, while weak IBL-algebras no longer require the corresponding operators to have a unit element.
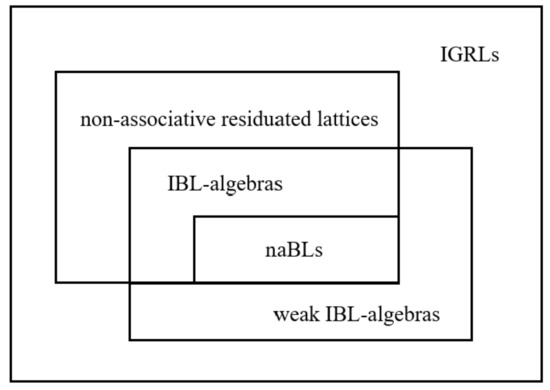
Figure 3.
Relationship between several algebraic structures.
In Figure 3, specific examples corresponding to several types of algebra are as follows: I The two algebraic structures in Example 3 are IBL-algebras, but not naBLs. II The algebraic structure in Example 2 is a weak IBL-algebra, but not an IBL-algebra. III The algebraic structure in (1) of Example 4 is a non-associative residuated lattice, but not an IBL-algebra. IV The algebraic structure in (2) of Example 4 is an IGRL, but it is neither a non-associative residuated lattice nor a weak IBL-algebra.
Example 4.
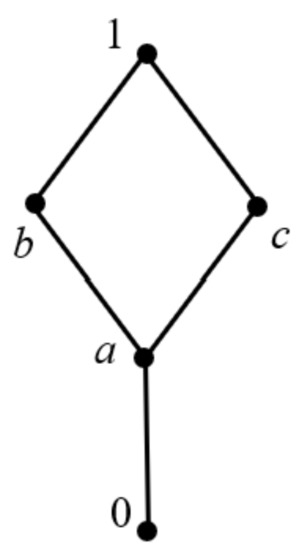
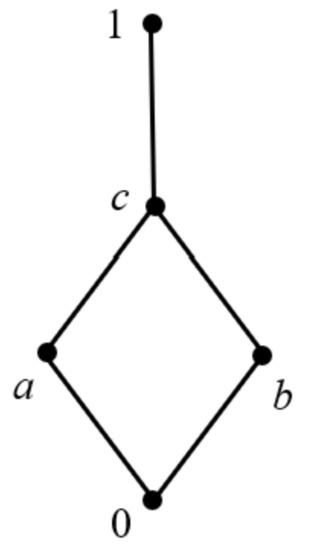
(1) Given a lattice L, the structure is as shown in Figure 4. Two operations, ∗ and →, of it are shown below:

Figure 4.
Lattice structure of (1) in Example 4.
(2) Given a lattice L, the structure is as shown in Figure 5. Two operations, ∗ and →, are shown below:

Figure 5.
Lattice structure of (2) in Example 4.
Next, we discuss some properties of weak IBL-algebras. Because the weak IBL-algebras are a class of IGRL, they satisfy the properties that are satisfied by IGRL, which will not be repeated here.
Proposition 4.
Let be a weak IBL-algebra; then, for arbitrary , it meets the requirements below:
(W3) If , then ;
(W4) ;
(W5) when ;
(W6) ;
(W7) when and only when .
Proof.
(1) If , then , and by the residuation principle, we have that . Since the operator ∗ is inflationary, . Thus, by general divisibility, .
(2) By (A10) and (A11), .
(3) By (A10) and (A11), it is evident.
(4) By (A10), it is clear that . Since , it is obvious that .
(5) Suppose that the operator ∗ has 1 as the unit element. It is clear that , and thereby, according to the residuation principle, . Because for arbitrary , . Conversely, assume , in that way . By the residuation principle, . Since operator ∗ is inflationary, we have , that is, the operator ∗ has 1 as the unit element. □
Remark 1.
If the operator ∗ of an , which is total order and has 1 as unit element, then the general divisibility it satisfies is divisibility, and the general prelinearity it satisfies is actually prelinearity. Because (by A16) when ∗ with unit element 1; then, it meets (BL1) when , and when also holds by general divisibility. In addition, if , then , that is, operator ∗ satisfies prelinearity.
Lemma 1.
Given an inflationary on , it meets general divisibility.
Proof.
Assume that the operator ∗ is an inflationary GOF. If , then we have that . Since ∗ is continuous, there is meets , then . Hence, by the residuation principle, . Since by (A4), , and by (A11), , . Thus, the inflationary GOF meets general divisibility. □
The following proposition shows that every inflationary GOF and its residuated implication can induce a weak IBL-algebra.
Proposition 5.
Given that the operator ∗ is an inflationary on , → is the residue of ∗, taking ∧ as the minimization operation and ∨ as maximization operation. Therefore, the algebra is a weak IBL-algebra.
Proof.
It is clear that the algebra L has 0 as the lower bound and 1 as the upper bound; the operator ∗ is inflationary and commutative on . By the definition of the residuated implication and continuity of ∗, the operators ∗ and → satisfy (A3), that is, the algebra L is an IGRL. Then, according to Lemma 1 and Lemma 5.2 of [17], the algebra L satisfies general divisibility and general prelinearity. Thus, the algebra is a weak IBL-algebra. □
4. The naBL-Filters, Weak Inflationary BL-Filters, and Quasi-IBL-Filters of IGRL
In this section, we discuss the filters of IGRL, including the particularity of naBL-filters, weak inflationary BL-filters, and quasi-IBL-filters.
The definition of filters of IGRL in [17] is given first below.
Definition 15.
Given an , F is a set of at least one element on L and . F is called a filter of L when it meets:
(F1) If are taken to meet as well as , and it holds that ;
(F2) If , then ;
(F3) If , then ;
(F4) for arbitrary ;
(F5) For any , as well as , , .
Remark 2.
It is clear that the filter F of an also meets the properties below:
(F6) ;
(F7) When we take an arbitrary satisfying , there is .
In fact, (F5) of Definition 15 can be replaced by another equivalent expression. We give the following proposition.
Proposition 6.
Given an L and a filter F of L, the two conditions below are equal in value:
(1) For arbitrary , , it holds that , where , ;
(2) For any , it holds that , that is, , meets as well as , such that ( and , and are not necessarily equal).
Proof.
(1) ⇒ (2) Assume that for any and , and . Taking , and , and by the residuation principle it holds that . Taking , . Hence, by the residuation principle, , as well as .
(2) ⇒ (1) Assume that for any and , satisfying . Then, it is obvious that according to (A6), and by (A10) it holds that . Therefore, according to (F1). On the other side, because satisfying , according to (A6) and (A10). Thus, by (F1) we have that . □
Next, the naBL-filter of IGRL is studied. We first provide a definition below.
Definition 16.
Given an , and a filter F of it, for arbitrary , when F meets the requirements below, it is known as an naBL-filter:
(F8) ;
(F9) , , where , .
Example 5.
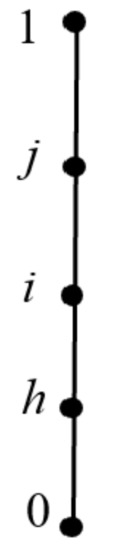
Given the lattice L, as shown in Figure 6, two operations, ∗ and →, are shown below:
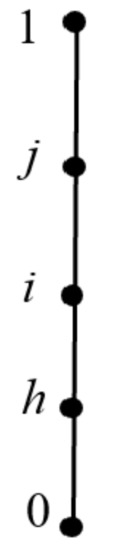
Figure 6.
Lattice structure of Example 5.
Then, is obviously an . It satisfies divisibility, α-prelinearity, and β-prelinearity, that is, it is also an naBL-algebra (). After verification, satisfies (F1)∼(F5), and further, it satisfies (F8) and (F9), so it is an naBL-filter. However, are not naBL-filters of L.
Some properties of the naBL-filters are as follows.
Proposition 7.
Given an , and a naBL-filter F of it, then for arbitrary , it holds that:
(1) ;
(2) If , then ;
(3) ;
(4) If , then , ;
(5) If , then ;
(6) If , then ;
(7) when L is distributive.
Proof.
(1) By (A6) and (A11), we obtain that . Therefore, since by (F8), it is clear that according to (F1).
(2) If , according to (A5) and (A14), . Then, according to (1) and (F1), it holds that .
(3) By (F2) and (F9), it is evident.
(4) According to Lemma 4.3 of [16], for arbitrary , . Then, by (A9) we have that . Since , by (F2) and (F9). Therefore, by (F1), it is clear that . Similarly, .
(5) If , by (A14), we have that . Then, by (A6). Therefore, by (F1) and (F8), . (On the other side, if , by (A4), thus according to (A6), (F8), and (F1).
(6) If , then for arbitrary , by (5). Since by (A8), it is clear that according to (A5). Therefore, by (F1) .
(7) Since by (F1) and (F5), and . Thus, by (F3), . □
Proposition 8.
Given an L and an naBL-filter F of L, if G is a filter of L such that , then G is also an naBL-filter.
Proof.
Since F is an naBL-filter of L, F meets (F8) and (F9). Because , we can obtain and , for arbitrary , that is, G satisfies (F8) and (F9). Therefore, G is also an naBL-filter of L. □
Next, we discuss the role of naBL-filters of IGRL in generating naBL-algebras.
Theorem 1.
Given an , and a filter F of it, then the conditions below are equal in value:
(1) L is an naBL-algebra;
(2) {1} is an naBL-filter of L, and the operator ∗ has 1 as the unit element.
Proof.
(1) ⇒ (2) Assume that L meets (naBL1)–(naBL3), that is, when taking an arbitrary , and , . Obviously, {1} is a filter on IGRL, because by (F4), , that is, {1} satisfies (F8). Because as well as , {1} satisfies (F9). Thus, {1} is an naBL-filter of L. Since the operation ∗ meets , according to divisibility, . On the other hand, it holds that by the residuation principle, and ; hence, . Consequently, we can get , that is, the operator ∗ has 1 as the unit element.
(2) ⇒ (1) Assume that {1} satisfies (F8) and (F9), that is, it is an naBL-filter. Then, and for arbitrary , that is, L satisfies -prelinearity and -prelinearity. Moreover, . By (A15), . If operator ∗ has 1 as the unit element, then by (A4), we obtain , and according to (A11), . Therefore, for arbitrary , that is, L satisfies divisibility. Hence, L is an naBL-algebra. □
Corollary 1.
Given an , each filter of it is an naBL-filter and ∗ has 1 as unit element when and only when it is an naBL-algebra.
Proof.
It is obvious that {1} is a naBL-filter of L when all filters on IGRL are naBL-filters. By Proposition 8, it holds that all filters on IGRL are naBL-filters when {1} is an naBL-filter, so all filters of L being naBL-filters is equivalent to {1} being an naBL-filter on IGRL. Thus, each filter of L is an naBL-filter, and when and only when L is an naBL-algebra according to Theorem 1. □
In addition, the quotient structure of IGRL is also important content. The definition of quotient algebra constructed by a filter of IGRL has been given in [17], as follows.
Definition 17.
Given an and a filter F of L, the relation is defined as: and ; then, is a relation satisfying congruence on L (see [17] for details).
For an IGRL L, the equivalent class of is written as , the quotient set is an IGRL, and is formulated as , is formulated as , is formulated as , and is formulated as ; the partial order is written as iff (see [16] for details).
After that, we have the following theorem.
Theorem 2.
Given an , all filters of L are naBL-filters and the operator ∗ has 1 as the unit element when and only when the quotient structure meets (naBL1)∼(naBL3).
Proof.
(⇒) Assume all filters of L are naBL-filters and the operator ∗ has 1 as unit element; by Corollary 1, we have that L meets (naBL1)∼(naBL3). Thereby, when we take arbitrary , , and . Since , , it holds that , that is, the quotient set meets divisibility. Similarly, we have that meets -prelinearity and -prelinearity. Therefore, satisfies (naBL1)∼(naBL3).
(⇐) If meets (naBL1)∼(naBL3), then , , . Therefore, by definition we have that , and on L, that is, L is an naBL-algebra. It is clear that {1} is an naBL-filter of L, and the operator ∗ has 1 as the unit element according to Theorem 1. Since for arbitrary filter F of L, , F is an naBL-filter of L by Proposition 8. □
Corollary 2.
Given an , {1} is an naBL-filter of L, and the operator ∗ has 1 as the unit element when and only when the quotient structure meets (naBL1)∼(naBL3).
Example 6.
Given the lattice L and operators on it provided in Example 5, L is an . It is clear that the operator ∗ has 1 as the unit element, and {1}, {j, 1}, {0, h, i, j, 1} are filters of L. Since {1} meets (F8) and (F9) for arbitrary , {1}, {j, 1}, {0, h, i, j, 1} are naBL-filters of L. We take , and obtain the quotient set . The operators ⊛ and → of are defined as below:
Then, the algebra is an . Since it meets (naBL1)∼(naBL3), is an naBL-algebra.
Then, we can give the concept of weak inflationary BL-filters similar to naBL-filters of IGRL.
Definition 18.
Given an , and a filter F of it, for arbitrary , F is called a weak inflationary BL-filter (briefly weak IBL-filter) if it meets the conditions below:
(F10) If , then ;
(F11) .
Example 7.
Given the L as in Example 5, is evidently a filter of L. Since it meets (F10) and (F11), it is a weak IBL-filter of L.
Obviously, when F is a weak IBL-filter of IGRL L, and G is a filter of L satisfying , G also meets (F10) and (F11). Then, we obtain the theorem below.
Theorem 3.
Given an , and a filter F of L, the requirements below are equal in value:
(1) L is a weak IBL-algebra;
(2) Each filter of L is a weak IBL-filter;
(3) {1} meets (F10) and (F11).
Proof.
(1) ⇒ (2) Assume that L meets (W1) and (W2); then, for arbitrary , when , as well as . If , by (F4), . By (F6), , so F meets (F10) and (F11), that is, F is a weak IBL-filter of L.
(2) ⇒ (3) Since {1} is a filter on IGRL, by (2) we can get that {1} is a weak IBL-filter on IGRL.
(3) ⇒ (1) Assume that {1} is a weak IBL-filter of L, then when , and . Therefore, we have that when , , and it is clear that L satisfies general prelinearity. On the other side, by (A15) we can obtain when . Since by (A11), we have that , when . Thus, L satisfies general divisibility. Therefore, L is a weak IBL-algebra. □
The relationship between the naBL-filters and the weak IBL-filters of IGRLs is analyzed as follows.
Proposition 9.
Given an . If all filters of L are naBL-filters, and ∗ has a unit element of 1, then all filters of L are weak IBL-filters.
Proof.
It is clear by Corollary 1 and Theorem 3. □
The inverse of the above proposition does not necessarily hold. We give the following example.
Example 8.
We take the lattice in Example 3 (1) as L. It is clear that L is an , and {1} is a weak IBL-filter of it, that is, all filters of L are weak IBL-filters. However, is not an naBL-filter because it does not satisfy (F9), for instance, .
Finally, a new class of filters is also studied in this part. The quasi IBL-filter of IGRL is defined as follows.
Definition 19.
Given an L and a filter F on it, F is called a quasi IBL-filter when F meets (F10).
Example 9.
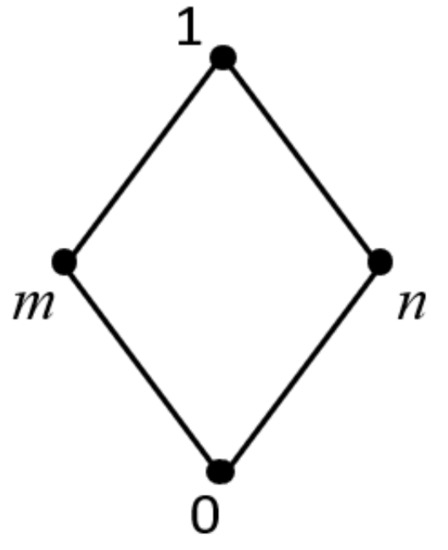
Given the lattice shown in Figure 7, two operations, ∗ and →, are as detailed below:

Figure 7.
Lattice structure of Example 9.
Then, L is an , and it is clear that is a quasi IBL-filter of L.
It is obvious that every weak IBL-filter and naBL-filter of IGRL is a quasi IBL-filter. Some of the properties they satisfy are given below.
Proposition 10.
Given an , and a quasi IBL-filter F of it, for arbitrary satisfying , the requirements below are true:
(1) ;
(2) ;
(3) if ∗ is associative;
(4) ;
(5) ;
(6) if .
Proof.
(1) There is when by (A6). Thus, by (F1).
(2) When , there is . Then, by (A4) and (A6), we have that . Therefore, by (F1).
(3) By (A10), ; then, . If , that is, the operator ∗ is associative, then . By (A11), , thereby . By the residuation principle, it is clear that . Therefore, , and by (F1).
(4) Because the operator ∗ is inflationary, that is, , by (A6), (2), and (F1), .
(5) Similar to the above, we can get according to (1).
(6) If , by (A14) we have that . Then, by (A6), . Therefore, by (F1) and (F10), . □
It is clear that for an IGRL, {1} is a quasi IBL-filter of L when and only when all filters of L are quasi IBL-filters. The proof will not be repeated. The equivalent conditions for an IGRL to form a weak IBL-algebra through quasi IBL-filters are as follows.
Proposition 11.
Given an , which is total order, every filter of L is a quasi IBL-filter when and only when L is a weak IBL-algebra.
Proof.
(1) In total order, there is or for arbitrary . Then, according to (A16), we have that or , that is, , so L satisfies general prelinearity under total order. If all filters of L are quasi IBL-filters, then when . According to (A15), it is clear that . Since, by (A11), we have , it is clear that , that is, L satisfies general divisibility. Therefore, L is a weak IBL-algebra. (2) Suppose that L is a weak IBL-algebra; by Theorem 3, we have that all filters of L are weak IBL-filters. It then holds that all filters of L are quasi IBL-filters. □
5. Filters and Weak Inflationary Pseudo BL-Filters of IPGRL
In this section, we mainly study filters of IPGRLs. The exact definition of filters is given as follows.
Definition 20.
Let be an . A nonempty set is called a filter of L when it meets the following conditions:
(F1) when , satisfying ;
(F2) When we take , there is ;
(F3) If , then ;
(F4) For all , ;
(F5’) If , , then and , where , , , ;
(F6’) If , for arbitrary , , ; if , for arbitrary , , such that , .
Additionally, G is called the normal filter when it meets:
(F7’) iff for arbitrary .
Example 10.
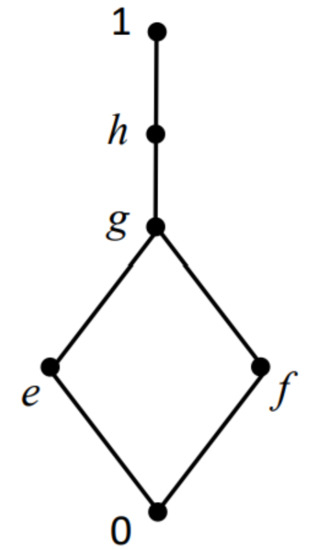
Given the lattice , as shown in Figure 8, the operators ∗, →, and ⇝ are defined as below, respectively:

Figure 8.
Lattice structure of Example 10.
L is an . It is clear that and are filters of L. However, is also a normal filter, and is not. In addition, , are not filters of L.
Some properties of filters are revealed as follows.
Proposition 12.
Given an L and a filter F of L, it meets requirements below:
(F8’) .
(F9’) , for any .
(F10’) For arbitrary , (i) , , such that and , , such that (ii) , , which meets and , , such that .
Proof.
(1) Since the filter F is a nonempty set, at least one element belongs to it. We suppose that there is such that . Due to and , by (F1) it holds that . Therefore, F satisfies (F8’).
(2) According to (PL9), . By (F8’), it is clear that and ; thus, F satisfies (F9’).
(3) We prove that (F10’) is equivalent to (F5’). (F10’) ⇒ (F5’) If , , , such that by (i), (PL5) and (PL8), then by (F1) we have that . It is clear that , satisfying , so . Analogously, we have and . (F5’) ⇒ (F10’). For arbitrary , , we take and , then by (PL3). Taking , obviously there is iff iff . Similarly, we can get (). □
Proposition 13.
Let be an . Given a filter , it meets statements below:
(1) when s, ;
(2) when s, .
Proof.
(1) By (F2), if s, . Since satisfies (PL4), , and according to (F1).
(2) Similarly, since according to (PL4), it is clear that s, (by F2) (by F1). □
Lemma 2.
Let be an . Then, for arbitrary , it holds that:
(1) , ;
(2) , .
Proof.
(1) By (PL4), it holds that . Thereby, . Similarly, .
(2) By (PL4), it holds that . Similarly, it is clear that . □
Corollary 3.
Let be an . Given a filter , for arbitrary , when and only when , when and only when .
Proof.
(1) We verify that . (i) Assume that . We take . Then, according to (PL3). By Lemma 2, , where according to (F5’). Since according to (PL3), we have by (F1). () Assume that , . According to (PL3), it holds that iff iff . Since by Lemma 2, and according to (PL3), where , so by (F1) .
(2) Analogously, . □
The quotient algebras obtained by filters of IPGRLs are discussed below.
Proposition 14.
Given an and a normal filter F of it, and given defined as iff , , the relation is a congruence relation.
Proof.
(i) We first verify that is an equivalent relation of IPGRL. (1) By (F3), , so it satisfies reflexivity. (2) It is clear that it satisfies symmetry according to the definition. (3) Suppose and ; by definition, it holds that , and , . According to (F2) and (F5’), ; thus, it is clear that according to Lemma 2. Then, by (PL3), we have that , that is, by (F1). Similarly, it holds that . Therefore, it satisfies transitivity.
() We verify that is congruent regarding five operations on L. Suppose that , . (1) It is obvious that and . Then, by Lemma 2 we have (by PL4) (by PL4). Since the existence of makes according to (F6’), it holds that , by (PL3), , thus by (F7’). Analogously, we have . Thus, . (2) According to (F3), it holds that . Since (by PL5) (by PL6), and by (F1), . Analogously, . Therefore, . (3) Since , analogously, . Hence, . (4) Since , by (F6’), there exists , such that , then by (PL3), we have , that is, according to (F1). Analogously, we can obtain ; thus, . In addition, , because by Lemma 2, and it holds that according to (PL3). Therefore, by (F1) , and similarly, , that is, . At last, we can get according to transitivity. (5) Suppose , , because , , by (F6’), , it holds that . Then, by (PL3) we obtain , that is, according to (F1). Similarly, . Thus, . On the other hand, it is clear that , according to Lemma 2, , so by (PL3), ; then, by (F1) . Analogously, . Hence, . Afterwards, it is clear that according to transitivity. Therefore, is congruent with respect to operations ∗, ∨, ∧, →, and ⇝. □
Definition 21.
Given an , a normal filter I of L, and the congruence relation , when and only when , . When taking an arbitrary , we define as the equivalent classes of x concerning , and the quotient structure as , and we define some operations of as follows: is formulated as , is formaluted as , is formulated as , is formulated as , is formulated as , and .
Proposition 15.
Let be an . G is a normal filter of L. The congruence relation iff , . Then, the quotient structure meets (PL1)∼(PL3).
Proof.
It is clear that is the lower bound and is the upper bound of . For arbitrary , by (F3) , and , that is, . Assume that , . Then, we verify that . Since , according to (F6’) there exists that meets ; then, by (PL5). Since by (F2) and on the basis of (PL3), by (F1). Therefore, by (PL4), it is obvious that , i.e., . By (PL11), , so according to (F8’). Then, by definition; thus, ⊛ is inflationary. Since (by Corollary 3) and (by Corollary 3) , it satisfies (PL3). Therefore, the quotient set meets (PL1)∼(PL3). □
At the end of this part, we describe the concept of weak inflationary pseudo BL-filters of IPGRLs and characterize the sufficient and necessary conditions for an IPGRL to form a weak inflationary pseudo-BL-algebra.
Definition 22.
Given the lattice is an , and a filter F, if F meets the requirements below for arbitrary , then it is called a weak inflationary pseudo-BL-filter (briefly WIPBL-filter):
(F11’) If , and ;
(F12’) and .
Remark 3.
If H is a WIPBL-filter of an L, and G is a filter on satisfying , then G also meets (F11’) and (F12’).
Example 11.
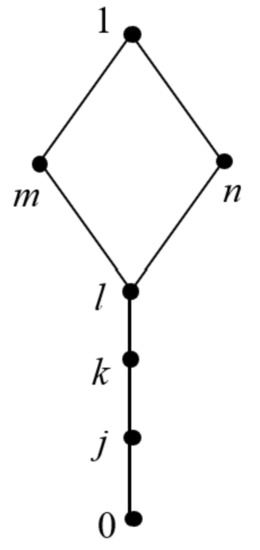
Given a lattice L, as shown in Figure 9, the three operators ∗, →, and ⇝ are defined as follows, respectively:

Figure 9.
Lattice structure of Example 11.
Then, L is an . It is clear that is a normal filter on . Since for arbitrary , and when , and , {1} satisfies (F11’) and (F12’). Therefore, {n, 1} is a WIPBL-filter. In addition, {m, 1} and {l, m, n, 1} are also WIPBL-filters of L.
Theorem 4.
Given the lattice is an , the requirements below are equal in value:
(1) L is a weak inflationary PBL-algebra;
(2) Each filter of L is a WIPBL-filter;
(3) {1} is a WIPBL-filter of L.
Proof.
(1) ⇒ (2) Assume that L is a weak inflationary PBL-algebra; then, for arbitrary , it meets (WIPBL1) and (WIPBL2). Suppose F is a filter on the lattice; then, . By (F4), and if . Therefore, F satisfies (F11’), since , F satisfies (F12’). Thus, all filters of L are WIPBL-filters.
(2) ⇒ (3) Evidently, {1} is a filter on the lattice, so {1} is a WIPBL-filter of L by (2).
(3) ⇒ (1) Assume that {1} is a WIPBL-filter of L; then, it meets (F11’) and (F12’). By (PL10), , if . Since , by (PL4), for arbitrary when , that is, L satisfies general 2-divisibility. On the other hand, it is clear that L satisfies general 2-prelinearity. Thus, L is a weak inflationary PBL-algebra. □
Proposition 16.
Given the lattice is an , and G is a normal filter on . Suppose that {1} is a WIPBL-filter of L; then, it holds that the quotient algebra meets (WIPBL1) and (WIPBL2).
Proof.
It holds that L is a weak inflationary pseudo-BL-algebra according to Theorem 4. Moreover, G is also a WIPBL-filter by Remark 3. It is clear that the quotient set is an IPGRL by Proposition 15. Since if , , then , and for arbitrary , , the IPGRL satisfies (WIPBL1) and (WIPBL2). Hence, the quotient structure is a weak inflationary pseudo-BL-algebra. □
Example 12.
Given the lattice L and the operators in Example 11, L is an , and is a normal filter of L. Since {1} is a WIPBL-filter of L, we can obtain that the following binary operators on quotient algebra :
It is clear that is a weak inflationary pseudo-BL-algebra.
6. Conclusions
In this article, we first propose the concept of weak IBL-algebras, verify that they can be obtained from inflationary general overlap functions, and illustrate the relationship between them and naBL-algebras and inflationary BL-algebras through some examples. Then, we give the properties they satisfy. Second, we elaborate the equivalent characterization of filters of IGRL by describing a new condition, and study special naBL-filters and weak IBL-filters of IGRL, by which IGRL can form naBL-algebras and weak IBL-algebras. In addition, a new class of quasi IBL-filters of IGRL is researched, as well as each filter of IGRL, under a totally ordered structure is a quasi-IBL-filter, which is equivalent to IGRL being a weak IBL-algebra. Finally, the definitions of filters of IPGRL are presented, some of their properties are shown, and on this basis, the quotient structure is obtained. In addition, a special class of WIPBL-filter is proposed to prove that an IPGRL becomes a weak inflationary pseudo-BL-algebra if and only if {1} is its WIPBL-filter.
As further research, we can refer to [24] to discuss other new subclasses of filters of the inflationary (pseudo-) general residuated lattices and explore the relationship between them. In addition, considering non-commutative fuzzy logic, the non-commutative generalization of weak IBL-algebras is also worth studying, which is what we are doing. Moreover, as an interesting research topic, we can consider a new model of fuzzy rough sets (see [26,27,28]) based on inflationary (pseudo-) general residuated lattices.
Author Contributions
Writing—original draft preparation, R.L.; writing—review and editing, X.Z. and B.B. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by National Science Foundation of China, grant numbers 12271319 and 62081240416.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
Not applicable.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Hájek, P. Basic fuzzy logic and BL-algebras. Soft Comput. 1998, 2, 124–128. [Google Scholar] [CrossRef]
- Hájek, P. Metamathematics of Fuzzy Logic; Springer Science & Business Media: Berlin/Heidelberg, Germany, 2013. [Google Scholar]
- Ward, M.; Dilworth, R.P. Residuated lattices. Trans. Am. Math. Soc. 1939, 45, 335–354. [Google Scholar] [CrossRef]
- Klir, G.; Yuan, B. Fuzzy Sets and Fuzzy Logic; Prentice Hall: Hoboken, NJ, USA, 1995. [Google Scholar]
- Klement, E.P.; Mesiar, R.; Pap, E. Triangular Norms; Kluwer Academic Publishers: Dordrecht, The Netherlands, 2000. [Google Scholar]
- Dimuro, G.P.; Fernández, J.; Bedregal, B.; Mesiar, R.; Sanz, J.A.; Lucca, G.; Bustince, H. The state-of-art of the generalizations of the Choquet integral: From aggregation and pre-aggregation to ordered directionally monotone functions. Inf. Fusion 2020, 57, 27–43. [Google Scholar] [CrossRef]
- Mesiar, R.; Kolesárová, A. Copulas and fuzzy implications. Int. J. Approx. Reason. 2020, 117, 52–59. [Google Scholar] [CrossRef]
- Botur, M.; Halaš, R. Commutative basic algebras and non-associative fuzzy logics. Arch. Math. Log. 2009, 48, 243–255. [Google Scholar] [CrossRef]
- Botur, M. A non-associative generalization of Hájek’s BL-algebras. Fuzzy Sets Syst. 2011, 178, 24–37. [Google Scholar] [CrossRef]
- Bustince, H.; Fernandez, J.; Mesiar, R.; Montero, J.; Orduna, R. Overlap functions. Nonlinear Anal. 2010, 72, 1488–1499. [Google Scholar] [CrossRef]
- Bustince, H.; Pagola, M.; Mesiar, R.; Hullermeier, E.; Herrera, F. Grouping, overlap, and generalized bientropic functions for fuzzy modeling of pairwise comparisons. IEEE Trans. Fuzzy Syst. 2011, 20, 405–415. [Google Scholar] [CrossRef]
- Jurio, A.; Bustince, H.; Pagola, M.; Pradera, A.; Yager, R.R. Some properties of overlap and grouping functions and their application to image thresholding. Fuzzy Sets Syst. 2013, 229, 69–90. [Google Scholar] [CrossRef]
- Garcia-Jimenez, S.; Bustince, H.; Hullermeier, E.; Mesiar, R.; Pal, N.R.; Pradera, A. Overlap indices: Construction of and application to interpolative fuzzy systems. IEEE Trans. Fuzzy Syst. 2014, 23, 1259–1273. [Google Scholar] [CrossRef]
- Elkano, M.; Galar, M.; Sanz, J.; Bustince, H. Fuzzy rule-based classification systems for multi-class problems using binary decomposition strategies: On the influence of n-dimensional overlap functions in the fuzzy reasoning method. Inf. Sci. 2016, 332, 94–114. [Google Scholar] [CrossRef]
- Paiva, R.; Santiago, R.; Bedregal, B.; Rivieccio, U. naBL-algebras based on overlaps and their conjugates. In Proceedings of the 2018 IEEE International Conference on Fuzzy Systems (FUZZ-IEEE), Rio de Janeiro, Brazil, 8–13 July 2018. [Google Scholar]
- De Miguel, L.; Gomez, D.; Rodriguez, J.T.; Montero, J.; Bustince, H.; Dimuroand, G.P.; Sanz, J.A. General overlap functions. Fuzzy Sets Syst. 2019, 372, 81–96. [Google Scholar] [CrossRef]
- Paiva, R.; Santiago, R.; Bedregal, B.; Rivieccio, U. Inflationary BL-algebras obtained from 2-dimensional general overlap functions. Fuzzy Sets Syst. 2021, 418, 64–83. [Google Scholar] [CrossRef]
- Qiao, J. Overlap and grouping functions on complete lattices. Inf. Sci. 2021, 542, 406–424. [Google Scholar] [CrossRef]
- Wang, Y.; Hu, B. On interval-valued pre-(quasi-) overlap functions. Inf. Sci. 2022, 606, 945–967. [Google Scholar] [CrossRef]
- Qiao, J. On discrete quasi-overlap functions. Inf. Sci. 2022, 584, 603–617. [Google Scholar] [CrossRef]
- Liang, R.; Zhang, X.H. Interval-valued pseudo overlap functions and application. Axioms 2022, 11, 216. [Google Scholar] [CrossRef]
- Sheng, N.; Zhang, X. Regular partial residuated lattices and their filters. Mathematics 2022, 10, 2429. [Google Scholar] [CrossRef]
- Liang, R.; Zhang, X. Pseudo general overlap functions and weak inflationary pseudo BL-algebras. Mathematics 2022, 10, 3007. [Google Scholar] [CrossRef]
- Ma, Z.; Hu, B. Characterizations and new subclasses of I-filters in residuated lattices. Fuzzy Sets Syst. 2014, 247, 92–107. [Google Scholar] [CrossRef]
- Haveshki, M.; Saeid, A.B.; Eslami, E. Some types of filters in BL algebras. Soft Comput. 2006, 10, 657–664. [Google Scholar] [CrossRef]
- Zhang, X.; Wang, J.; Zhan, J.; Dai, J. Fuzzy measures and Choquet integrals based on fuzzy covering rough sets. IEEE Trans. Fuzzy Syst. 2022, 30, 2360–2374. [Google Scholar] [CrossRef]
- Wang, J.; Zhang, X. A novel multi-criteria decision-making method based on rough sets and fuzzy measures. Axioms 2022, 11, 275. [Google Scholar] [CrossRef]
- Wang, J.; Zhang, X.; Hu, Q. Three-way fuzzy sets and their applications (II). Axioms 2022. under review of the second version. [Google Scholar]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).