Parameter Uniform Numerical Method for Singularly Perturbed 2D Parabolic PDE with Shift in Space

Abstract

Singularly perturbed 2D parabolic delay differential equations with the discontinuous source term and convection coefficient are taken into consideration in this paper. For the time derivative, we use the fractional implicit Euler method, followed by the fitted finite difference method with bilinear interpolation for locally one-dimensional problems. The proposed method is shown to be almost first-order convergent in the spatial direction and first-order convergent in the temporal direction. Theoretical results are illustrated with numerical examples.

1. Introduction

Differential equations with small or large parameters can be used to describe a variety of applied practical problems, including the theory of boundary layers. For example, the shock waves occurring in gas motions, edge effects when elastic plates deform, etc. These mathematical problems are very difficult (or even impossible) to solve exactly, so approximate solutions are necessary. It is possible to obtain an approximation of the solution through perturbation methods. Basically, these methods aim to solve a simpler problem (as a first approximation) and systematically improve the approximate solution.

When using finite difference or finite element methods on equally spaced grids and allowing the perturbation parameter tend to zero, boundary layers produce inaccurate numerical solutions. The most popular method for overcoming this difficulty is to construct uniformly valid numerical methods on layers adapted to the mesh. There are several uniformly valid methods available in the literature, for instance, to cite a few (see Refs. [1,2] and the references therein). As pointed out in Ref. [3], the direct discretization of the singularly perturbed 2D parabolic differential equations leads to a pentadiagonal linear system of equations. This problem is exceedingly complex to solve computationally. We use the fractional step method in order to reduce the computation cost. At each time level, the fractional step method leads to the tridiagonal system of algebraic equations. Several types of research have been conducted recently on the fractional step method, such as Refs. [4,5,6] and the references therein.

Singularly perturbed delay differential equations (SPDDEs) are a class of perturbation problems with at least one delay or deviating argument. This type of problem occurs frequently in the modelling of various types of physical and biological problems. For example, the neuronal variability and its theoretical analysis have been modelled as delay parabolic equations [7,8]. Asymptotic analyses for 1D stationery SPDDEs have been well studied by Lange and Miura [9]. Several numerical methods for SPDDEs of 1D stationery problems have been reported in the literature, such as Refs. [10,11,12,13] and the reference therein. The numerical method for 1D parabolic equations was initiated by Ref. [14] and it gained the interest of many researchers. Das and Natesan [15] presented computing techniques for solving 2D time SPDDEs. Ref. [16] presented some applications and existence results for partial delay differential equations. The modelling of option pricing, to generalize the celebrated Black–Scholes equation with suitable weight, led to the 2D parabolic differential equations with space shift [17]. We consider discontinuous convection and source terms in 2D parabolic SPDDEs in this article, as mentioned in the abstract. This problem exhibits interior layers at $x=d_x$ and $y=d_y$ and, due to the presents of the shift in space, the boundary layers occurs at $x=1$ and $y=1$. The existence results pertaining to the parabolic equation with discontinuous coefficients are addressed in Ref. [18]. The method presented in this article is a combination of the layers adopted technique and linear interpolations. The interpolation term takes care of the delay arguments. The proposed method is validated theoretically and numerically to be uniformly convergent in both space and time by considering some numerical examples.

The constant C is generic positive, that is, it is independent of the perturbation parameter as well as the discretization parameters N and M throughout the paper. For convenience, it is assumed that the number of mesh points in the spatial domains ${\mathrm{\Omega }}_x$ and ${\mathrm{\Omega }}_y$ are same, that is, N and the index set ${\mathcal{I}}_{N_0}=\{1,2,3,\cdots ,N_0\}$ for any positive integer $N_0.$ It is conventional to assume for the convection coefficient problem that $\epsilon \le C{N}^{-1}$ for practical purposes. Further, to measure the error bounds and derivative bounds, we use the following norm ${\parallel \psi \parallel }_D={sup}_{\mathbf{x}\in D}\parallel \psi \left(\mathbf{x}\right)\parallel ,$$\mathbf{x}=(x,y).$

The article is organized as follows: the problem is considered in Section 2. The fractional implicit Euler method for time derivative and locally 1D problems are presented in Section 3. In the same section, the stability results and derivative estimates of the locally one-dimensional problems are presented. Section 4 presents the numerical method for the considered problem. The discretizations incurred by the errors are estimated in Section 5. Numerical validations through some test example problems are done in Section 6. Finally, in Section 7, some concluding remarks are made.

2. Statement of Continuous Problem

Motivated by the works of Refs. [7,17], we consider the following two-dimensional singularly perturbed parabolic differential equations: We find u such that

$$\begin{array}{cc}\hfill \mathfrak{L}u:=& u_t-\epsilon \mathrm{\Delta }u+\nabla u·\overline{p}\left(\mathbf{x}\right)+q\left(\mathbf{x}\right)u(\mathbf{x}-\mathbf{d},t)=g(\mathbf{x},t),(\mathbf{x},t)\in {\mathfrak{D}}^{*}\times (0,T],\hfill \end{array}$$

(1)

$$\begin{array}{cc}\hfill & u(\mathbf{x},0)=u_0\left(\mathbf{x}\right),\mathbf{x}\in \mathfrak{D},\hfill \end{array}$$

(2)

$$\begin{array}{cc}\hfill & u(\mathbf{x},t)=0,\mathrm{on}\partial \mathfrak{D}\times [0,T],\hfill \end{array}$$

(3)

$$\begin{array}{cc}\hfill & u(\mathbf{x},t)=0,\mathrm{on}[-d_x,0]\times [-d_y,1]\times [0,T]\cup [-d_x,1]\times [-d_y,0]\times [0,T],\hfill \end{array}$$

(4)

where $\mathbf{x}=(x,y),$$\mathbf{d}=(d_x,d_y)$, ${\mathrm{\Omega }}_x=(0,1)={\mathrm{\Omega }}_y,$ $\mathfrak{D}={\mathrm{\Omega }}_x\times {\mathrm{\Omega }}_y,$${\mathfrak{D}}^{*}={\mathrm{\Omega }}_x^{*}\times {\mathrm{\Omega }}_y^{*}$, ${\mathrm{\Omega }}_{\nu }^{*}={\mathrm{\Omega }}_{\nu }^{-}\cup {\mathrm{\Omega }}_{\nu }^{+},$ ${\mathrm{\Omega }}_{\nu }^{-}=(0,d_{\nu }),$${\mathrm{\Omega }}_{\nu }^{+}=(d_{\nu },1),\nu =x,y,$ the functions $u_0,q$ are sufficiently differentiable and bonded on $\overline{\mathfrak{D}}$, $p_1,p_2,$$g_1,g_2$ are sufficiently differentiable and bounded on their respective domains ${\mathfrak{D}}^{*},{\mathfrak{D}}^{*}\times [0,T]$. In addition, we assume that,

$$\begin{array}{cc}\hfill & u_x(d_x^{-},y,t)=u_x(d_x^{+},y,t),u_y(x,d_y^{-},t)=u_y(x,d_y^{+},t),\hfill \\ \hfill & \overline{p}\left(\mathbf{x}\right)={(p_1\left(\mathbf{x}\right),p_2\left(\mathbf{x}\right))}^T,\nabla u=(u_x,u_y),\hfill \\ \hfill & p_1^{+}\ge p_1\left(\mathbf{x}\right)\ge p_1^{-}>0,\mathbf{x}\in {\mathrm{\Omega }}_x^{-}\times {\mathrm{\Omega }}_y^{*},p_1^{+}\ge -p_1\left(\mathbf{x}\right)\ge p_1^{-}>0,\mathbf{x}\in {\mathrm{\Omega }}_x^{+}\times {\mathrm{\Omega }}_y^{*},\hfill \\ \hfill & p_2^{+}\ge p_2\left(\mathbf{x}\right)\ge p_2^{-}>0,\mathbf{x}\in {\mathrm{\Omega }}_x^{*}\times {\mathrm{\Omega }}_y^{-},p_2^{+}\ge -p_2\left(\mathbf{x}\right)\ge p_2^{-}>0,\mathbf{x}\in {\mathrm{\Omega }}_x^{*}\times {\mathrm{\Omega }}_y^{+},\hfill \\ \hfill & |p_1(d_x^{-},y)-p_1(d_x^{+},y)|<\infty ,|p_2(x,d_y^{-})-p_2(x,d_y^{+})|<\infty ,\hfill \\ \hfill & q\left(\mathbf{x}\right)=q_1\left(\mathbf{x}\right)+q_2\left(\mathbf{x}\right),0\ge q_1,q_2\ge \beta ,g(\mathbf{x},t)=g_1(\mathbf{x},t)+g_2(\mathbf{x},t).\hfill \end{array}$$

Let ${\mathfrak{L}}_x:=-\epsilon \frac{{\partial }^2}{\partial x^2}+p_1\left(\mathbf{x}\right)\frac{\partial }{\partial x}+q_1\left(\mathbf{x}\right)I_{\mathbf{d}}$ and ${\mathfrak{L}}_y:=-\epsilon \frac{{\partial }^2}{\partial y^2}+p_2\left(\mathbf{x}\right)\frac{\partial }{\partial y}+q_2\left(\mathbf{x}\right)I_{\mathbf{d}}$ be two differential operators, $I_{\mathbf{d}}u(\mathbf{x},t)=u(\mathbf{x}-\mathbf{d},t)$, then the differential operator $\mathfrak{L}$ defined in (1) can be written as $\mathfrak{L}:=\frac{\partial }{\partial t}+{\mathfrak{L}}_x+{\mathfrak{L}}_y$.

3. Time Domain Discretization and Stability Analysis

3.1. Discretization of Time Domain

The time domain $[0,T]$ is discretized uniformly with step length $h_t=T/M$, where M is a positive integer. Then we have the uniform mesh in the temporal direction ${\overline{\mathrm{\Omega }}}_t^M={\{t_k=k\times h_t\}}_{k=0}^M.$

3.2. An Alternating Direction Implicit Method

Let us assume that ${\widehat{u}}^0\left(\mathbf{x}\right)=u_0\left(\mathbf{x}\right),\mathbf{x}\in \overline{\mathfrak{D}}.$ Now, we discretize the IBVP (1)–(3) using the fractional implicit Euler method and obtain the following semidiscrete scheme on the time levels $n=0,1,\cdots ,M-1$:

let $y\in {\mathrm{\Omega }}_y$, then

$$\begin{array}{c}\hfill \left\{\begin{array}{c}{\mathfrak{D}}_x{\widehat{u}}^{n+\frac{1}{2}}={\widehat{u}}^n+h_t{g}_1(x,y,t_{n+1}),x\in {\mathrm{\Omega }}_x^{*},\hfill \\ {\widehat{u}}^{n+\frac{1}{2}}(0,y)=0={\widehat{u}}^{n+\frac{1}{2}}(1,y),\hfill \\ {\widehat{u}}_x^{n+\frac{1}{2}}(d_x^{-},y)={\widehat{u}}_x^{n+\frac{1}{2}}(d_x^{+},y),\hfill \end{array}\right.\end{array}$$

(5)

let $x\in {\mathrm{\Omega }}_x$, then

$$\begin{array}{c}\hfill \left\{\begin{array}{c}{\mathfrak{D}}_y{\widehat{u}}^{n+1}={\widehat{u}}^{n+\frac{1}{2}}+h_t{g}_2(x,y,t_{n+1}),y\in {\mathrm{\Omega }}_y^{*}\hfill \\ {\widehat{u}}^{n+1}(x,0)=0={\widehat{u}}^{n+1}(x,1),\hfill \\ {\widehat{u}}_y^{n+1}(x,d_y^{-})={\widehat{u}}_y^{n+1}(x,d_y^{+}),\hfill \end{array}\right.\end{array}$$

(6)

where ${\widehat{u}}^n(x,y)$ is the exact solution of u at the time level $t=t_n$, ${\mathfrak{D}}_x:=I+h_t{\mathfrak{L}}_x$ and ${\mathfrak{D}}_y:=I+h_t{\mathfrak{L}}_y$.

If the exact solution of the problem (1) is known at $t=t_n$, then we have the following semi-discrete scheme: let $y\in {\mathrm{\Omega }}_y$, then

$$\begin{array}{c}\hfill \left\{\begin{array}{c}{\mathfrak{D}}_x{\overline{u}}^{n+\frac{1}{2}}=u(x,y,t_n)+h_t{g}_1(x,y,t_{n+1}),x\in {\mathrm{\Omega }}_x^{*},\hfill \\ {\overline{u}}^{n+\frac{1}{2}}(0,y)={\overline{u}}^{n+\frac{1}{2}}(1,y)=0,\hfill \\ {\overline{u}}_x^{n+\frac{1}{2}}(d_x^{-},y)={\overline{u}}_x^{n+\frac{1}{2}}(d_x^{+},y),\hfill \end{array}\right.\end{array}$$

(7)

let $x\in {\mathrm{\Omega }}_x$, then

$$\begin{array}{c}\hfill \left\{\begin{array}{c}{\mathfrak{D}}_y{\overline{u}}^{n+1}={\overline{u}}^{n+\frac{1}{2}}+h_t{g}_2(x,y,t_{n+1}),y\in {\mathrm{\Omega }}_y^{*},\hfill \\ {\overline{u}}^{n+1}(x,0)={\overline{u}}^{n+1}(x,1)=0,\hfill \\ {\overline{u}}_y^{n+1}(x,d_y^{-})={\overline{u}}_y^{n+1}(x,d_y^{+}).\hfill \end{array}\right.\end{array}$$

(8)

Solving the problem (1)–(4) is more computationally expensive than solving lower-dimensional problems. As a result, we used the ADI scheme to divide the two-dimensional problem into two sets of one-dimensional problems in order to decrease the computing cost and to have an efficient numerical solution.

3.3. Stability Results and Derivative Estimates

This section presents the maximum principles for the above-mentioned locally one dimensional problems. Further, with regard to the applications of the maximum principle, we estimate the solution derivative bounds and local and global truncation errors in the temporal direction.

The test functions

$$s\left(x\right)=\left\{\begin{array}{c}x+1,x\in [x,d_x],\hfill \\ d_x{\displaystyle \frac{d_x-x}{1-d_x}}+d_x+1,x\in [d_x,1]\hfill \end{array}\right.ands\left(y\right)=\left\{\begin{array}{c}y+1,y\in [0,d_y],\hfill \\ d_y{\displaystyle \frac{d_y-y}{1-d_y}}+d_y+1,y\in [d_y,1]\hfill \end{array}\right.$$

are used in the following lemmas and sections.

Lemma 1.

Let $\psi \in C^0\left({\overline{\mathrm{\Omega }}}_x\right)\cap C^2\left({\mathrm{\Omega }}_x^{*}\right)$ be a function satisfying $\psi \left(x\right)\ge 0,x=0,1,$${\mathfrak{D}}_x\psi \left(x\right)\ge 0,x\in {\mathrm{\Omega }}_x^{*}$ and ${\psi }^{\prime }(d_x-)-{\psi }^{\prime }(d_x+)\ge 0,$ then $\psi \left(x\right)\ge 0,x\in {\overline{\mathrm{\Omega }}}_x.$

Proof. 

The proof is by construction and similar to Refs. [12,13]. It is shown that ${\mathfrak{D}}_{x}s\left(x\right)>0,x\ne d_x$ and $s^{\prime }\left(d_x^{-}\right)-s^{\prime }\left(d_x^{+}\right)\ge 0$. By using the argument given by Ref. [12], Theorem 3.1, one can prove this lemma. □

Similar to the above lemma and using the test function $s\left(y\right)$, we can prove the following lemma.

Lemma 2.

Let $\psi \in C^0\left({\overline{\mathrm{\Omega }}}_y\right)\cap C^2\left({\mathrm{\Omega }}_y^{*}\right)$ be a function satisfies $\psi \left(y\right)\ge 0,y=0,1,$${\mathfrak{D}}_y\psi \left(y\right)\ge 0,y\in {\mathrm{\Omega }}_y^{*}$ and ${\psi }^{\prime }(d_y-)-{\psi }^{\prime }(d_y+)\ge 0,$ then $\psi \left(y\right)\ge 0,x\in {\overline{\mathrm{\Omega }}}_y.$

One can prove that the solutions of (5) and (6) are stable and unique if they exist. Further, they are bounded from Lemmas 1 and 2.

Lemma 3.

Assume that $\left|{\displaystyle \frac{{\partial }^{i}u}{\partial t^i}}\right|\le C,0\le i\le 3.$ Then $\Vert e_n\Vert \le C{h}_t^2$ where $u\left(t_n\right)={\overline{u}}^n(x,y)+e_n$, $u\left(t_n\right)=u(x,y,t_n).$ In addition, ${sup}_{n\le T/h_t}{\parallel E_n\parallel }_{\infty }\le C{h}_t,$ where the global error $E_n=u\left(t_n\right)-{\widehat{u}}^n.$

Proof. 

The proof is similar to that of Refs. [4,6]. For that, one can express

$$\begin{array}{cc}\hfill & u\left(t_{n-1}\right)={\mathfrak{D}}_x[{\mathfrak{D}}_{y}u\left(t_n\right)-h_t{g}_2(x,y,t_n)]-h_t{g}_1(x,y,t_n)+O\left(h_t^2\right)\hfill \\ \hfill & u\left(t_{n-1}\right)={\mathfrak{D}}_x[{\mathfrak{D}}_y\overline{u}\left(t_n\right)-h_t{g}_2(x,y,t_n)]-h_t{g}_1(x,y,t_n),\hfill \\ & {\mathfrak{D}}_x{\mathfrak{D}}_y{e}_n=O\left(h_t^2\right).\hfill \end{array}$$

First by the application of Lemma 1 then by Lemma 2, we have $|e_n|\le C{h}_t^2.$ To prove the second part, consider

$$\begin{array}{cc}\hfill & E_n=e_n+{\overline{u}}^n-{\widehat{u}}^n,\hfill \\ \hfill & {\mathfrak{D}}_y({\overline{u}}^n-{\widehat{u}}^n)={\overline{u}}^{(n-1)+\frac{1}{2}}-{\widehat{u}}^{(n-1)+\frac{1}{2}},{\mathfrak{D}}_x({\overline{u}}^{(n-1)+\frac{1}{2}}-{\widehat{u}}^{(n-1)+\frac{1}{2}})=E_{n-1},\hfill \\ \hfill & {\overline{u}}^n-{\widehat{u}}^n={\mathfrak{D}}_y^{-1}{\mathfrak{D}}_x^{-1}{E}_{n-1},\hfill \end{array}$$

making use of the arguments given in Ref. [4], we have $|E_n|\le C{h}_t$, which concludes the proof. □

From the above lemma, we can conclude that the semidiscretization process is uniformly convergent of order $O\left(h_t\right).$ In the rest of the sections it is assumed that, $d_x=0.5=d_y.$

Let the solution ${\widehat{u}}^{n+\frac{1}{2}}$ be decomposed as ${\widehat{u}}^{n+\frac{1}{2}}=v^{n+\frac{1}{2}}+w^{n+\frac{1}{2}}$ for obtaining the sharp bounds on the derivatives. Further, let the decomposition of the regular component be $v^{n+\frac{1}{2}}={\sum }_{k=0}^2{\epsilon }^k{v}_k^{n+\frac{1}{2}}$, leading the desired bounds on the derivatives. The functions $v_k^{n+\frac{1}{2}},k=0,1,2,w^{n+\frac{1}{2}}$ satisfy the following problems:

$$\begin{array}{c}\hfill \left\{\begin{array}{c}{v}_0^{n+\frac{1}{2}}+h_t\left(p_1\left(\mathbf{x}\right)\frac{d}{dx}{v}_0^{n+\frac{1}{2}}+q_1\left(\mathbf{x}\right)I_{\mathbf{d}}{v}_0^{n+\frac{1}{2}}\right)=v_0^n+h_t{g}_1\left(t_{n+1}\right),x\in {\mathrm{\Omega }}_x^{*},\hfill \\ v_0^{n+\frac{1}{2}}\left(x\right)={\widehat{u}}^{n+\frac{1}{2}}\left(x\right),x\in [-d_x,0],v_0^{n+\frac{1}{2}}\left(1\right)={\widehat{u}}^{n+\frac{1}{2}}\left(1\right),\hfill \end{array}\right.\end{array}$$

(9)

$$\begin{array}{c}\hfill \left\{\begin{array}{c}{v}_1^{n+\frac{1}{2}}+h_t\left(p_1\left(\mathbf{x}\right)\frac{d}{dx}{v}_1^{n+\frac{1}{2}}+q_1\left(\mathbf{x}\right)I_{\mathbf{d}}{v}_1^{n+\frac{1}{2}}\right)=v_1^n+h_t{\displaystyle \frac{d^2}{d{x}^2}}\left(v_0^{n+\frac{1}{2}}\right),x\in {\mathrm{\Omega }}_x^{*},\hfill \\ v_1^{n+\frac{1}{2}}\left(x\right)=0,x\in [-d_x,0],v_1^{n+\frac{1}{2}}\left(1\right)=0,\hfill \end{array}\right.\end{array}$$

(10)

$$\begin{array}{c}\hfill \left\{\begin{array}{c}{\mathfrak{D}}_x{v}_2^{n+\frac{1}{2}}=v_2^n+h_t{\displaystyle \frac{d^2}{d{x}^2}}\left(v_1^{n+\frac{1}{2}}\right),x\in {\mathrm{\Omega }}_x^{*},\hfill \\ v_2^{n+\frac{1}{2}}\left(x\right)=0,x\in [-d_x,0],v_2^{n+\frac{1}{2}}\left(1\right)=0,\hfill \\ \frac{d}{dx}{v}_2^{n+\frac{1}{2}}\left(d_x^{-}\right)=\frac{d}{dx}{v}_2^{n+\frac{1}{2}}\left(d_x^{+}\right),\hfill \end{array}\right.\end{array}$$

(11)

and the functions $v^{n+\frac{1}{2}}$ and $w^{n+\frac{1}{2}}$ satisfy the following boundary-value problems (BVPs):

$$\begin{array}{c}\hfill \left\{\begin{array}{c}{\mathfrak{D}}_x{v}^{n+\frac{1}{2}}=v^n+h_t{g}_1\left(t_{n+1}\right),x\in {\mathrm{\Omega }}_x^{*},\hfill \\ v^{n+\frac{1}{2}}\left(x\right)={\widehat{u}}^{n+\frac{1}{2}}\left(x\right),x\in [-d_x,0],v^{n+\frac{1}{2}}\left(1\right)={\widehat{u}}^{n+\frac{1}{2}}\left(1\right),\hfill \\ \left[v^{n+\frac{1}{2}}\left(d_x\right)\right]=\sum _{k=0}^2\left[v_k^{n+\frac{1}{2}}\left(d_x\right)\right],\left[\frac{d}{dx}{v}^{n+\frac{1}{2}}\left(d_x\right)\right]=\sum _{k=0}^1{\epsilon }^k\left[\frac{d}{dx}{v}_k^{n+\frac{1}{2}}\left(d_x\right)\right],\hfill \end{array}\right.\end{array}$$

(12)

and

$$\begin{array}{c}\hfill \left\{\begin{array}{c}{\mathfrak{D}}_x{w}^{n+\frac{1}{2}}=w^n,x\in {\mathrm{\Omega }}_x^{*},\hfill \\ w^{n+\frac{1}{2}}\left(x\right)=0,x\in [-d_x,0],w^{n+\frac{1}{2}}\left(1\right)=0,\hfill \\ \left[w^{n+\frac{1}{2}}\left(d_x\right)\right]=-\left[v^{n+\frac{1}{2}}\left(d_x\right)\right],\left[\frac{d}{dx}{w}^{n+\frac{1}{2}}\left(d_x\right)\right]=-\left[\frac{d}{dx}{v}^{n+\frac{1}{2}}\left(d_x\right)\right],\hfill \end{array}\right.\end{array}$$

(13)

where the square bracket operation denotes the jump discontinuity $\left[\alpha \left(\zeta \right)\right]=\alpha \left({\zeta }^{+}\right)-\alpha \left({\zeta }^{-}\right).$ It is assumed that $v^0={\widehat{u}}^0,w^0=0.$

Theorem 1.

Let ${\widehat{u}}^{n+\frac{1}{2}}$ be the solution of the problem (5) and let k be a nonnegative integer, then the regular and singular components satisfy the following bounds on the derivatives

$$\begin{array}{cc}\hfill & {∥{\displaystyle \frac{d^k{v}^{n+\frac{1}{2}}}{d{x}^k}}∥}_{{\mathrm{\Omega }}^{*}}\le C({\epsilon }^{-k+2}+1),0\le k\le 3,\hfill \\ \hfill & \left|{\displaystyle \frac{d^k{w}^{n+\frac{1}{2}}\left(x\right)}{d{x}^k}}\right|\le C{\epsilon }^{-k}\left\{\begin{array}{c}exp\left({\displaystyle \frac{p_1^{-}(x-d_x)}{\epsilon }}\right),x\in {\mathrm{\Omega }}_x^{-},0\le k\le 3,\hfill \\ exp\left({\displaystyle \frac{p_1^{-}(d_x-x)}{\epsilon }}\right)+\epsilon exp\left({\displaystyle \frac{p_1^{-}(x-1)}{\epsilon }}\right),x\in {\mathrm{\Omega }}_x^{+}.\hfill \end{array}\right.\hfill \end{array}$$

Proof. 

We show that by integrating the differential Equations (9)–(11), and using the argument presented in Refs. [13,19], and Lemma 1, we have $\parallel v^{n+\frac{1}{2}}\parallel \le C.$ Successive differentiation of Equations (9)–(11), we have $\parallel \frac{d^k}{d{x}^k}{v}^{n+\frac{1}{2}}\parallel \le C({\epsilon }^{2-k}+1)$. From the Lemma 1, we see that ${\widehat{u}}^{n+\frac{1}{2}}$ and $v^{n+\frac{1}{2}}$ are bounded, hence $w^{n+\frac{1}{2}}$. Let us assume that $|w^{n+\frac{1}{2}}\left(d_x\right)|\le \gamma .$ Now define the barrier functions

$${\varphi }^{\pm }\left(x\right)=C\gamma exp\left({\displaystyle \frac{p_1^{-}(x-d_x)}{\epsilon }}\right)\pm w^{n+\frac{1}{2}},x\in {\mathrm{\Omega }}_x^{-}.$$

It is easy to show that ${\varphi }^{\pm }\left(0\right)\ge 0,$${\varphi }^{\pm }\left(d_x\right)\ge 0$ and ${\mathfrak{D}}_x{\varphi }^{\pm }\left(x\right)\ge 0$ on ${\mathrm{\Omega }}_x^{-}.$ From the results of Ref. [19], we have $|w^{n+\frac{1}{2}}\left(x\right)|\le Cexp\left({\displaystyle \frac{p_1^{-}(x-d_x)}{\epsilon }}\right),x\in {\mathrm{\Omega }}_x^{-}.$ Using the following barrier functions

$$\begin{array}{c}\hfill {\psi }^{\pm }=C\gamma (\epsilon +exp\left({\displaystyle \frac{p_1^{-}(d_x-x)}{\epsilon }}\right)-\epsilon exp\left({\displaystyle \frac{p_1^{-}(x-1)}{\epsilon }}\right))\pm w^{n+\frac{1}{2}},x\in {\mathrm{\Omega }}_x^{+}\end{array}$$

we prove that $|w^{n+\frac{1}{2}}\left(x\right)|\le C\left(exp\left({\displaystyle \frac{p_1^{-}(d_x-x)}{\epsilon }}\right)+\epsilon exp\left({\displaystyle \frac{p_1^{-}(x-1)}{\epsilon }}\right)\right),x\in {\mathrm{\Omega }}_x^{+}.$ Further the successive differentiation’s leads the desired results. □

In a similar manner, one can decompose ${\widehat{u}}^{n+1}$ as $v^{n+1}+w^{n+1}={\widehat{u}}^{n+1}$ and $v^{n+1}$, $w^{n+1}$ satisfy the following BVPs:

$$\begin{array}{c}\hfill \left\{\begin{array}{c}{\mathfrak{D}}_y{v}^{n+1}=v^{n+\frac{1}{2}}+h_t{g}_2\left(t_{n+1}\right),y\in {\mathrm{\Omega }}_y^{*},\hfill \\ v^{n+1}\left(y\right)={\widehat{u}}^{n+1}\left(y\right),y\in [-d_y,0],v^{n+1}\left(1\right)={\widehat{u}}^{n+1}\left(1\right),\hfill \\ \left[v^{n+1}\left(d_y\right)\right]=\sum _{k=0}^1{\epsilon }^k\left[v_k^{n+1}\left(d_y\right)\right],\left[\frac{d}{dy}{v}^{n+1}\left(d_y\right)\right]=\sum _{k=0}^1{\epsilon }^k\left[\frac{d}{dy}{v}_k^{n+1}\left(d_y\right)\right],\hfill \end{array}\right.\end{array}$$

(14)

$$\begin{array}{c}\hfill \left\{\begin{array}{c}{\mathfrak{D}}_y{w}^{n+1}=w^{n+\frac{1}{2}},y\in {\mathrm{\Omega }}_y^{*},\hfill \\ w^{n+1}\left(y\right)=0,y\in [-d_y,0],w^{n+1}\left(1\right)=0,\hfill \\ \left[w^{n+1}\left(d_y\right)\right]=-\left[v^{n+1}\left(d_y\right)\right],\left[\frac{d}{dy}{w}^{n+1}\left(d_y\right)\right]=-\left[\frac{d}{dy}{v}^{n+1}\left(d_y\right)\right]\hfill \end{array}\right.\end{array}$$

(15)

and we have the following result.

Theorem 2.

Let ${\widehat{u}}^{n+1}$ be the solution to the problem (6), then its regular and singular components satisfy the following bounds on the derivatives

$$\begin{array}{cc}\hfill & {∥{\displaystyle \frac{d^k{v}^{n+1}}{d{y}^k}}∥}_{{\mathrm{\Omega }}^{*}}\le C(1+{\epsilon }^{2-k}),k=0,1,2,3,\hfill \\ \hfill & \left|{\displaystyle \frac{d^k{w}^{n+1}\left(x\right)}{d{y}^k}}\right|\le C\left\{\begin{array}{c}{\epsilon }^{-k}exp\left({\displaystyle \frac{p_2^{-}(y-d_y)}{\epsilon }}\right),y\in {\mathrm{\Omega }}_y^{-},k=0,1,2,3,\hfill \\ {\epsilon }^{-k}exp\left({\displaystyle \frac{p_2^{-}(d_y-y)}{\epsilon }}\right)+{\epsilon }^{-k+1}exp\left({\displaystyle \frac{p_2^{-}(y-1)}{\epsilon }}\right),y\in {\mathrm{\Omega }}_y^{+}.\hfill \end{array}\right.\hfill \end{array}$$

4. Discrete Problem

4.1. Spatial Domain Discretization

From Theorems 1 and 2, we observe that the IBVP (1)–(3) exhibits twin interior layers along the lines $(d_x,y),y\in {\mathrm{\Omega }}_y$ and $(x,d_y),x\in {\mathrm{\Omega }}_x$ and weak boundary layers along $x=1$ and $y=1$. Let N be the number of mesh points in both spatial x and y directions. As the mesh defined in Ref. [13], we define the mesh points in both x and y directions, which is given in the following: let ${\tau }_{1,x}=min\{\frac{d_x}{2},\frac{2}{p_1^{-}}\epsilon lnN\}$, ${\tau }_{2,x}=min\{\frac{1-d_x}{4},\frac{2}{p_1^{-}}\epsilon lnN\}$, ${\tau }_{1,y}=min\{\frac{d_y}{2},\frac{2}{p_2^{-}}\epsilon lnN\}$ and ${\tau }_{2,y}=min\{\frac{1-d_y}{4},\frac{2}{p_2^{-}}\epsilon lnN\}$. Using the transition parameters ${\tau }_{i,\nu },i=1,2,\nu =x,y$, we partitioned the domains ${\overline{\mathrm{\Omega }}}_x$ and ${\overline{\mathrm{\Omega }}}_y$ as follows:

$$\begin{array}{cc}\hfill & {\displaystyle {\overline{\mathrm{\Omega }}}_x={\cup }_{i=1}^5{\mathrm{\Omega }}_{i,x},{\mathrm{\Omega }}_{1,x}=[0,d_x-{\tau }_{1,x}],{\mathrm{\Omega }}_{2,x}=[d_x-{\tau }_{1,x},d_x],{\mathrm{\Omega }}_{3,x}=[d_x,d_x+{\tau }_{2,x}],}\hfill \\ \hfill & {\mathrm{\Omega }}_{4,x}=[d_x+{\tau }_{2,x},1-{\tau }_{2,x}],{\mathrm{\Omega }}_{5,x}=[1-{\tau }_{2,x},1],\hfill \\ \hfill & {\overline{\mathrm{\Omega }}}_y={\cup }_{i=1}^5{\mathrm{\Omega }}_{i,y},{\mathrm{\Omega }}_{1,y}=[0,d_y-{\tau }_{1,y}],{\mathrm{\Omega }}_{2,y}=[d_y-{\tau }_{1,y},d_y],{\mathrm{\Omega }}_{3,y}=[d_y,d_y+{\tau }_{2,y}],\hfill \\ \hfill & {\mathrm{\Omega }}_{4,y}=[d_y+{\tau }_{2,y},1-{\tau }_{2,y}],{\mathrm{\Omega }}_{5,y}=[1-{\tau }_{2,y},1].\hfill \end{array}$$

On each sub-domains ${\mathrm{\Omega }}_{i,x},i=1,2,3,4,5$, respectively, we place $\frac{N}{4},\frac{N}{4},\frac{N}{8},\frac{N}{4},\frac{N}{8}$ mesh points with mesh sizes $\frac{4(d_x-{\tau }_{1,x})}{N}$, $\frac{4{\tau }_{1,x}}{N}$, $\frac{8{\tau }_{2,x}}{N}$, $\frac{4(1-2{\tau }_{2,x}-d_x)}{N}$, $\frac{8{\tau }_{2,x}}{N}$. In the same manner the mesh points in ${\mathrm{\Omega }}_{i,y},i=1,2,3,4,5$ are defined. Now let us denote the mesh sizes to be $h_x\left(i\right)=x_i-x_{i-1},i\in {\mathcal{I}}_N$ and $h_y\left(i\right)=y_i-y_{i-1},i\in {\mathcal{I}}_N$ and define the mesh ${\overline{\mathrm{\Omega }}}_x^N={\left\{x_i\right\}}_{i=0}^{i=N}$, $x_0=0,$$x_i=x_{i-1}+h_x\left(i\right),i\in {\mathcal{I}}_N$ and ${\overline{\mathrm{\Omega }}}_y^N={\left\{y_i\right\}}_{i=0}^{i=N}$, $y_0=0,$$y_i=y_{i-1}+h_y\left(i\right),i\in {\mathcal{I}}_N.$ The mesh distribution is depicted in the Figure 1.

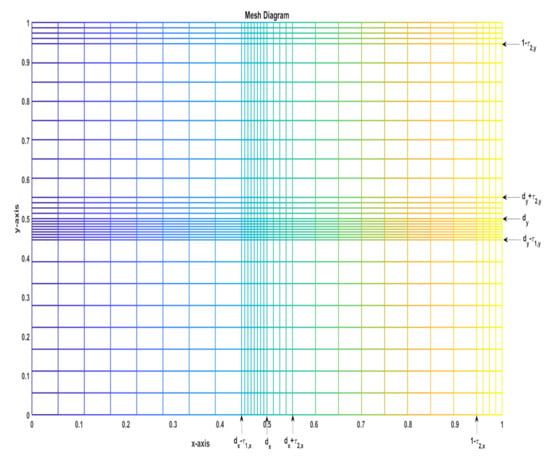
Figure 1. Mesh points distribution.

4.2. The Finite Difference Schemes

On the meshes ${\overline{\mathrm{\Omega }}}_x^N$ and ${\overline{\mathrm{\Omega }}}_y^N$, we define the following finite difference schemes.

fix $y=y_j$,

$$\begin{array}{cc}\hfill & {\mathfrak{D}}_x^N{U}_{i,j}^{n+\frac{1}{2}}:=\left\{\begin{array}{c}{U}_{i,j}^{n+\frac{1}{2}}+(-\epsilon {\delta }_x^2{U}_{i,j}^{n+\frac{1}{2}}+p_{1_{i,j}}{D}_x^{-}{U}_{i,j}^{n+\frac{1}{2}}+q_{1_{i,j}}{I}_{\mathbf{d}}^N{U}_{i,j}^{n+\frac{1}{2}})h_t=U_{i,j}^n\hfill \\ \hfill +h_t{g}_1(x_i,y_j,t_{n+1}),i\in {\mathcal{I}}_{\frac{N}{2}-1},\\ D_x^{-}{U}_{N/2,j}^{n+\frac{1}{2}}=D_x^{+}{U}_{N/2,j}^{n+\frac{1}{2}},i=\frac{N}{2},\hfill \\ U_{i,j}^{n+\frac{1}{2}}+(-\epsilon {\delta }_x^2{U}_{i,j}^{n+\frac{1}{2}}+p_{1_{i,j}}{D}_x^{+}{U}_{i,j}^{n+\frac{1}{2}}+q_{1_{i,j}}{I}_{\mathbf{d}}^N{U}_{i,j}^{n+\frac{1}{2}})h_t=U_{i,j}^n\hfill \\ \hfill +h_t{g}_1(x_i,y_j,t_{n+1}),i\in {\mathcal{I}}_{N-1}\setminus {\mathcal{I}}_{\frac{N}{2}},\end{array}\right.\hfill \\ \hfill & U_{0,j}^{n+\frac{1}{2}}={\widehat{u}}^{n+\frac{1}{2}}(0,y_j);U_{N,j}^{n+\frac{1}{2}}={\widehat{u}}^{n+\frac{1}{2}}(1,y_j),\hfill \end{array}$$

(16)

fix $x=x_i$,

$$\begin{array}{cc}\hfill & {\mathfrak{D}}_y^N{U}_{i,j}^{n+1}:=\left\{\begin{array}{c}{U}_{i,j}^{n+1}+(-\epsilon {\delta }_y^2{U}_{i,j}^{n+1}+p_{2_{i,j}}{D}_y^{-}{U}_{i,j}^{n+1}+q_{2_{i,j}}{I}_{\mathbf{d}}^N{U}_{i,j}^{n+1})h_t=U_{i,j}^{n+\frac{1}{2}}\hfill \\ \hfill +h_t{g}_2(x_i,y_j,t_{n+1}),j\in {\mathcal{I}}_{\frac{N}{2}-1}\\ D_y^{-}{U}_{i,N/2}^{n+1}=D_y^{+}{U}_{i,N/2}^{n+1},j=\frac{N}{2},\hfill \\ U_{i,j}^{n+1}+(-\epsilon {\delta }_y^2{U}_{i,j}^{n+1}+p_{2_{i,j}}{D}_y^{+}{U}_{i,j}^{n+1}+q_{2_{i,j}}{I}_{\mathbf{d}}^N{U}_{i,j}^{n+1})h_t=U_{i,j}^{n+\frac{1}{2}}\hfill \\ \hfill +h_t{g}_2(x_i,y_j,t_{n+1}),j\in {\mathcal{I}}_{N-1}\setminus {\mathcal{I}}_{\frac{N}{2}},\end{array}\right.\hfill \\ \hfill & U_{0,j}^{n+1}={\widehat{u}}^{n+1}(x_i,0);U_{i,N}^{n+1}={\widehat{u}}^{n+1}(x_i,1),\hfill \end{array}$$

(17)

where ${\delta }_{\zeta }^2,$$D_{\zeta }^{-}$ and $D_{\zeta }^{+},\zeta =x,y$ are the standard finite difference operators,

$$\begin{array}{c}\hfill I_{\mathbf{d}}^N{U}_{i,j}^{n+\frac{1}{2}}=\left\{\begin{array}{c}0,i\in {\mathcal{I}}_{\frac{N}{2}-1},\hfill \\ U_{\eta ,\xi }^{n+\frac{1}{2}}{l}_{\eta ,x}(x_i-d_x)l_{\xi ,y}(y_j-d_y)+U_{\eta +1,\xi }^{n+\frac{1}{2}}{l}_{\eta +1,x}(x_i-d_x)l_{\xi ,y}(y_j-d_y)\hfill \\ +U_{\eta ,\xi +1}^{n+\frac{1}{2}}{l}_{\eta ,x}(x_i-d_x)l_{\xi +1,y}(y_j-d_y)\hfill \\ +U_{\eta +1,\xi +1}^{n+\frac{1}{2}}{l}_{\eta +1,x}(x_i-d_x)l_{\xi +1,y}(y_j-d_y),i\in {\mathcal{I}}_{N-1}\setminus {\mathcal{I}}_{\frac{N}{2}}\hfill \end{array}\right.\\ \hfill I_{\mathbf{d}}^N{U}_{i,j}^{n+1}=\left\{\begin{array}{c}0,j\in {\mathcal{I}}_{\frac{N}{2}-1},\hfill \\ U_{\eta ,\xi }^{n+1}{l}_{\eta ,x}(x_i-d_x)l_{\xi ,y}(y_j-d_y)+U_{\eta +1,\xi }^{n+1}{l}_{\eta +1,x}(x_i-d_x)l_{\xi ,y}(y_j-d_y)\hfill \\ +U_{\eta ,\xi +1}^{n+1}{l}_{\eta ,x}(x_i-d_x)l_{\xi +1,y}(y_j-d_y)\hfill \\ +U_{\eta +1,\xi +1}^{n+1}{l}_{\eta +1,x}(x_i-d_x)l_{\xi +1,y}(y_j-d_y),j\in {\mathcal{I}}_{N-1}\setminus {\mathcal{I}}_{\frac{N}{2}},\hfill \end{array}\right.\end{array}$$

$l_{\eta ,x}(x_i-d_x)={\displaystyle \frac{x_{\eta +1}-(x_i-d_x)}{h_x(\eta +1)}}$, $l_{\eta +1,x}(x_i-d_x)={\displaystyle \frac{(x_i-d_x)-x_{\eta }}{h_x(\eta +1)}}$,

$l_{\xi ,y}(y_j-d_y)={\displaystyle \frac{y_{\xi +1}-(y_j-d_y)}{h_y(\xi +1)}}$, $l_{\xi +1,y}(y_j-d_y)={\displaystyle \frac{(y_j-d_y)-y_{\xi }}{h_y(\xi +1)}}$, $x_{\eta },x_{\eta +1},y_{\xi },y_{\xi +1}$ are the nodal points such that $x_i-d_x\in [x_{\eta },x_{\eta +1}]$ and $y_j-d_y\in [y_{\xi },y_{\xi +1}].$ The above two difference operators ${\mathfrak{D}}_x^N$ and ${\mathfrak{D}}_y^N$ satisfy the following discrete maximum principles.

Note: Let us denote the difference operators $D_x^{*}=\left\{\begin{array}{c}{D}_x^{-},i<\frac{N}{2},\hfill \\ D_x^{+},i>\frac{N}{2},\hfill \end{array}\right.$ and $D_y^{*}=\left\{\begin{array}{c}{D}_y^{-},j<\frac{N}{2},\hfill \\ D_y^{+},j>\frac{N}{2}.\hfill \end{array}\right.$ In the following we use the above difference operators. Further, the test functions $s\left(x_i\right)=\left\{\begin{array}{c}{x}_i+1,i\le N/2,\hfill \\ d_x{\displaystyle \frac{d_x-x_i}{1-d_x}}+d_x+1,i>N/2,\hfill \end{array}\right.$ and $s\left(y_j\right)=\left\{\begin{array}{c}{y}_j+1,j\le N/2,\hfill \\ d_y{\displaystyle \frac{d_y-y_j}{1-d_y}}+d_y+1,j>N/2,\hfill \end{array}\right.$ are also used.

4.3. Discrete Stability Results

Lemma 4.

Let the mesh function be ${\mathrm{\Psi }}_{i,j}$, satisfies ${\mathrm{\Psi }}_{0,j}\ge 0,{\mathrm{\Psi }}_{N,j}\ge 0$, ${\mathfrak{D}}_x^N{\mathrm{\Psi }}_{i,j}\ge 0$ and $[D_x^{+}-D_x^{-}]{\mathrm{\Psi }}_{N/2,j}\le 0$, then ${\mathrm{\Psi }}_{i,j}\ge 0$ for all $i.$

Proof. 

Making use of the test mesh function $s\left(x_i\right)$ and the arguments given in Ref. [13], Lemma 6.1, the lemma can be proved. □

Lemma 5.

Let the mesh function be ${\mathrm{\Psi }}_{i,j}$, satisfies ${\mathrm{\Psi }}_{i,0}\ge 0,{\mathrm{\Psi }}_{i,N}\ge 0$, ${\mathfrak{D}}_y^N{\mathrm{\Psi }}_{i,j}\ge 0$ and $[D_y^{+}-D_y^{-}]{\mathrm{\Psi }}_{i,N/2}\le 0$, then ${\mathrm{\Psi }}_{i,j}\ge 0$ for all $j.$

Using the above two Lemmas 4 and 5, we can have the following discrete stability results.

Lemma 6.

Let $U_{i,j}^{n+\frac{1}{2}}$ be a numerical solution defined by (16), then

$$|U_{i,j}^{n+\frac{1}{2}}|\le Cmax\left\{|U_{0,j}^{n+\frac{1}{2}}|,|U_{N,j}^{n+\frac{1}{2}}|,\underset{i}{sup}|{\mathfrak{D}}_x^N{U}_{i,j}^{n+\frac{1}{2}}|\right\},\mathit{for}\mathit{all}i.$$

Lemma 7.

Let $U_{i,j}^{n+1}$ be a numerical solution defined by (17), then

$$|U_{i,j}^{n+1}|\le Cmax\left\{|U_{i,0}^{n+1}|,|U_{i,N}^{n+1}|,\underset{j}{sup}|{\mathfrak{D}}_y^N{U}_{i,j}^{n+1}|\right\},\mathit{for}\mathit{all}j.$$

Remark 1.

From Lemmas 6 and 7, we can see that, the numerical solutions defined in (16) and (17) are stable. Further, by the results of Ref. [20], the matrices associated with the difference schemes (16) and (17) are M-matrices.

5. Error Computation

Analogous to the continuous solution, the numerical solution is decomposed into smooth and singular components. The solution $U^{n+\frac{1}{2}}$ is decomposed as $U^{n+\frac{1}{2}}=V^{n+\frac{1}{2}}+W^{n+\frac{1}{2}}$ satisfy the following difference equations:

$$\begin{array}{c}\hfill \left\{\begin{array}{c}{\mathfrak{D}}_x^N{V}_{i,j}^{n+\frac{1}{2}}=V_{i,j}^n+h_t{g}_1(x_i,y_j,t_{n+1}),i\in {\mathcal{I}}_N\setminus \{N,\frac{N}{2},0\},\hfill \\ D_x^{+}{V}_{N/2,j}^{n+\frac{1}{2}}-D_x^{-}{V}_{N/2,j}^{n+\frac{1}{2}}=\left[v^{n+{\frac{1}{2}}^{\prime }}\left(d_x\right)\right],V_{0,j}^{n+\frac{1}{2}}=0,V_{N,j}^{n+\frac{1}{2}}=0,\hfill \end{array}\right.\end{array}$$

(18)

$$\begin{array}{c}\hfill \left\{\begin{array}{c}{\mathfrak{D}}_x^N{W}_{i,j}^{n+\frac{1}{2}}=W_{i,j}^n,i\in {\mathcal{I}}_N\setminus \{N,\frac{N}{2},0\},\hfill \\ D_x^{+}{W}_{N/2,j}^{n+\frac{1}{2}}-D_x^{-}{W}_{N/2,j}^{n+\frac{1}{2}}=-\left[v^{n+{\frac{1}{2}}^{\prime }}\left(d_x\right)\right],W_{0,j}^{n+\frac{1}{2}}=0,W_{N,j}^{n+\frac{1}{2}}=0.\hfill \end{array}\right.\end{array}$$

(19)

Similarly, the solution $U^{n+1}$ is decomposed as $U^{n+1}=V^{n+1}+W^{n+1}$ and they satisfy the following difference equations:

$$\begin{array}{c}\hfill \left\{\begin{array}{c}{\mathfrak{D}}_y^N{V}_{i,j}^{n+1}=V_{i,j}^{n+\frac{1}{2}}+h_t{g}_2(x_i,y_j,t_{n+1}),j\in {\mathcal{I}}_N\setminus \{N,\frac{N}{2},0\},\hfill \\ D_y^{+}{V}_{i,N/2}^{n+1}-D_y^{-}{V}_{i,N/2}^{n+1}=\left[v^{n+1^{\prime }}\left(d_y\right)\right],V_{i,0}^{n+1}=0,V_{i,N}^{n+1}=0,\hfill \end{array}\right.\end{array}$$

(20)

$$\begin{array}{c}\hfill \left\{\begin{array}{c}{\mathfrak{D}}_y^N{W}_{i,j}^{n+1}=W_{i,j}^{n+\frac{1}{2}},j\in {\mathcal{I}}_N\setminus \{N,\frac{N}{2},0\},\hfill \\ D_y^{+}{W}_{i,N/2}^{n+1}-D_y^{-}{W}_{i,N/2}^{n+1}=-\left[v^{n+1^{\prime }}\left(d_y\right)\right],W_{i,0}^{n+1}=0,W_{i,N}^{n+1}=0.\hfill \end{array}\right.\end{array}$$

(21)

Note: The error estimate in each time level is proved in the following way:

• Step 1 :  First we estimate the absolute difference of U and V;
• Step 2 :  We estimate the error bound of the regular component, that is $|v-V|$;
• Step 3 :  To estimate the error bound of the singular component $|w-W|$ in the entire domain, first we estimate in the outer region and then using the estimate of $|U-V|$, we estimate $|w-W|$ in the inner layer region;
• Step 4 :  Using the triangle inequality, we estimate the error bound of the numerical solution in each time level.

Lemma 8.

Let $U_{i,j}^{\frac{1}{2}}$ and $V_{i,j}^{\frac{1}{2}}$ be numerical solutions of (16) and (18), respectively, when $n=0$, then

$$|U_{i,j}^{\frac{1}{2}}-V_{i,j}^{\frac{1}{2}}|\le C\left\{\begin{array}{c}{N}^{-1},i\in {\mathcal{I}}_{\frac{N}{4}},\hfill \\ \zeta +N^{-1},i\in {\mathcal{I}}_{\frac{5N}{8}}\setminus {\mathcal{I}}_{\frac{N}{4}},\hfill \\ N^{-1},i\in {\mathcal{I}}_{N-1}\setminus {\mathcal{I}}_{\frac{5N}{8}},\hfill \end{array}\right.$$

ζ is constant.

Proof. 

Fix j. Let us consider the mesh function

$${\mathrm{\Psi }}^{\pm }\left(x_i\right)=C[N^{-1}s\left(x_i\right)+\psi \left(x_i\right)]\pm [U_{i,j}^{\frac{1}{2}}-V_{i,j}^{\frac{1}{2}}],\forall i,$$

where $\zeta ={max}_{\frac{N}{4}+1\le i,j\le \frac{5N}{8}-1}|U_{i,j}^{\frac{1}{2}}-V_{i,j}^{\frac{1}{2}}|$, and

$\psi \left(x_i\right)=\left\{\begin{array}{c}\left({\displaystyle \frac{x_i-(d_x-{\tau }_{1,x})}{{\tau }_{1,x}}}\right)\zeta ,i\in {\mathcal{I}}_{\frac{N}{2}}\setminus {\mathcal{I}}_{\frac{N}{4}}\hfill \\ \left(1+{\displaystyle \frac{d_x-x_i}{{\tau }_{2,x}}}\right)\zeta ,i\in {\mathcal{I}}_{\frac{5N}{8}-1}\setminus {\mathcal{I}}_{\frac{N}{2}}\hfill \\ 0, \mathrm{otherwise}.\hfill \end{array}\right.$

It is easy to show that ${\mathrm{\Psi }}^{\pm }\left(x_i\right)\ge 0,i=0,N,$ and by the arguments of [13], we have

$$\begin{array}{cc}\hfill & {\mathfrak{D}}_x^N{\mathrm{\Psi }}^{\pm }\left(x_i\right)={\mathfrak{D}}_x^N(C{N}^{-1}s\left(x_i\right)+\psi \left(x_i\right))\pm {\mathfrak{D}}_x^N(U_{i,j}^{\frac{1}{2}}-V_{i,j}^{\frac{1}{2}})\ge 0,i\ne \frac{N}{2},\hfill \\ \hfill & (D_x^{+}-D_x^{-}){\mathrm{\Psi }}^{\pm }\left(x_{\frac{N}{2}}\right)\le 0,i=\frac{N}{2}.\hfill \end{array}$$

By the Lemma 4, we have ${\mathrm{\Psi }}^{\pm }\left(x_i\right)\ge 0.$ Hence the proof of the lemma. □

Lemma 9.

Let $v^{\frac{1}{2}}$ and $V^{\frac{1}{2}}$ be two solutions of (12) and (18), respectively, the $|v^{\frac{1}{2}}(x_i,y)-V_{i,y}^{\frac{1}{2}}|\le C{N}^{-1},\forall i.$

Proof. 

Now, we see that

$$\begin{array}{cc}\hfill {\mathfrak{D}}_x^N(v^{\frac{1}{2}}(x_i,y)-V_{i,y}^{\frac{1}{2}})& ={\mathfrak{D}}_x^N{v}^{\frac{1}{2}}(x_i,y)-{\mathfrak{D}}_x^N{V}_{i,y}^{\frac{1}{2}}={\mathfrak{D}}_x^N{v}^{\frac{1}{2}}(x_i,y)-{\mathfrak{D}}_x{v}^{\frac{1}{2}}(x_i,y)\hfill \\ \hfill & =h_t\left[-\epsilon \left({\delta }_x^2-\frac{d^2}{d{x}^2}\right)+p_{1_{i,j}}\left(D_x^{*}-\frac{d}{dx}\right)+q_{1_{i,j}}[I_{\mathbf{d}}^N-I_{\mathbf{d}}]\right]v^{\frac{1}{2}}(x_i,y),\hfill \end{array}$$

from the results given in Refs. [2,21,22], we have $|{\mathfrak{D}}_x^N(v^{\frac{1}{2}}(x_i,y)-V_{i,y}^{\frac{1}{2}})|\le C{h}_t{N}^{-1}.$ Using the following barrier function

$${\psi }^{\pm }(x_i)=C{N}^{-1}s(x_i)\pm (v^{\frac{1}{2}}(x_i,y)-V_{i,y}^{\frac{1}{2}}),$$

we can see that ${\psi }^{\pm }\left(x_i\right)\ge 0,i=0,N$, ${\mathfrak{D}}_x^N{\psi }^{\pm }(x_i)\ge 0$ and $(D_x^{+}-D_x^{-}){\psi }^{\pm }(x_{\frac{N}{2}})\le 0.$ From the Lemma 4, we have the desired result. □

Lemma 10.

Let $w^{\frac{1}{2}}$ and $W^{\frac{1}{2}}$ be the solutions of (13) and (19), respectively, then $|w^{\frac{1}{2}}(x_i,y)-W_{i,y}^{\frac{1}{2}}|\le C{N}^{-1}lnN,\forall i.$

Proof. 

By the triangle inequality, Theorem 1, Lemmas 8 and 9, we have

$$\begin{array}{cc}\hfill & |{\widehat{u}}^{\frac{1}{2}}(x_i,y)-U_{i,y}^{\frac{1}{2}}|\le |U_{i,y}^{\frac{1}{2}}-V_{i,y}^{\frac{1}{2}}|+|v^{\frac{1}{2}}(x_i,y)-V_{i,y}^{\frac{1}{2}}|+|{\widehat{u}}^{\frac{1}{2}}(x_i,y)-v^{\frac{1}{2}}(x_i,y)|\hfill \\ \hfill & \le C{N}^{-1}+C\left\{\begin{array}{c}exp\left({\displaystyle \frac{p_1^{-}(x_i-d_x)}{\epsilon }}\right),i\in {\mathcal{I}}_{\frac{N}{2}},\hfill \\ \epsilon exp\left({\displaystyle \frac{p_1^{-}(x_i-1)}{\epsilon }}\right)+exp\left({\displaystyle \frac{p_1^{-}(d_x-x_i)}{\epsilon }}\right),i\in {\mathcal{I}}_N-{\mathcal{I}}_{\frac{N}{2}},\hfill \end{array}\right.\hfill \\ \hfill & +C\left\{\begin{array}{c}{N}^{-1},i\in {\mathcal{I}}_{\frac{N}{4}},\hfill \\ \zeta +N^{-1},i\in {\mathcal{I}}_{\frac{5N}{8}-1}\setminus {\mathcal{I}}_{\frac{N}{4}},\hfill \\ N^{-1},i\in {\mathcal{I}}_N\setminus {\mathcal{I}}_{\frac{5N}{8}-1}\hfill \end{array}\right.\hfill \\ \hfill & \le C\left\{\begin{array}{c}{N}^{-1},i\in {\mathcal{I}}_{\frac{N}{4}},\hfill \\ \zeta +N^{-1}+exp\left({\displaystyle \frac{p_1^{-}(x_i-d_x)}{\epsilon }}\right),i\in {\mathcal{I}}_{\frac{N}{2}}\setminus {\mathcal{I}}_{\frac{N}{4}},\hfill \\ \zeta +N^{-1}+exp\left({\displaystyle \frac{p_1^{-}(d_x-x_i)}{\epsilon }}\right),i\in {\mathcal{I}}_{\frac{5N}{8}-1}\setminus {\mathcal{I}}_{\frac{N}{2}},\hfill \\ N^{-1},i\in {\mathcal{I}}_N\setminus {\mathcal{I}}_{\frac{5N}{8}-1},\hfill \end{array}\right.\hfill \end{array}$$

where $\zeta ={max}_{\frac{N}{4}+1\le i,j\le \frac{5N}{8}-1}|U_{i,j}^{\frac{1}{2}}-V_{i,j}^{\frac{1}{2}}|$. Hence $|{\widehat{u}}^{\frac{1}{2}}(x_i,y)-U_{i,y}^{\frac{1}{2}}|\le C{N}^{-1},i=0,1,\cdots ,\frac{N}{4},$$\frac{5N}{8},\cdots ,N.$ Therefore $|w^{\frac{1}{2}}(x_i,y)-W_{i,y}^{\frac{1}{2}}|\le C{N}^{-1},i=0,1,\cdots ,\frac{N}{4},\frac{5N}{8},\cdots ,N.$ To prove the result inside the inner region, we consider the following mesh function

$${\psi }^{\pm }\left(x_i\right)=C{N}^{-1}\varphi \left(x_i\right)\pm (w^{\frac{1}{2}}-W^{\frac{1}{2}}),x_i\in (d_x-{\tau }_{1,x},d_x)\cup (d_x,d_x+{\tau }_{2,x})\cap {\overline{\mathrm{\Omega }}}_x^N,$$

where $\varphi \left(x_i\right)=\left\{\begin{array}{c}\left(1+x_i\right)+\frac{{\tau }_x}{{\epsilon }^2}(x_i-(d_x-{\tau }_{1,x})),x_i\in [d_x-{\tau }_{1,x},d_x)\cap {\overline{\mathrm{\Omega }}}_x^N,\hfill \\ \left(1+d_x+d_x{\displaystyle \frac{d_x-x_i}{1-d_x}}\right)+\frac{{\tau }_x}{{\epsilon }^2}(d_x+{\tau }_{2,x}-x_i),x_i\in [d_x,d_x+{\tau }_{2,x}]\cap {\overline{\mathrm{\Omega }}}_x^N,\hfill \end{array}\right.$, ${\tau }_x=min\{{\tau }_{1,x},{\tau }_{2,x}\}.$ Then we have, ${\psi }^{\pm }\left(x_i\right)\ge 0,i=\frac{N}{4},\frac{5N}{8}.$ Further $|{\mathfrak{D}}_x^N(w^{\frac{1}{2}}-W^{\frac{1}{2}})|\le C_1{h}_t{\epsilon }^{-2}{N}^{-1},$$i=\frac{N}{4}+1,\cdots ,\frac{N}{2}-1,$$\frac{N}{2}+1,\cdots ,\frac{5N}{8}.$ Now,

$$\begin{array}{cc}\hfill {\mathfrak{D}}_x^N{\psi }^{\pm }\left(x_i\right)& =C{N}^{-1}{\mathfrak{D}}_x^N\varphi \left(x_i\right)\pm {\mathfrak{D}}_x^N(w^{\frac{1}{2}}-W^{\frac{1}{2}}),x_i\in (d_x-{\tau }_{1,x},d_x)\cup (d_x,d_x+{\tau }_{2,x})\cap {\overline{\mathrm{\Omega }}}_x^N\hfill \\ \hfill & \ge C{N}^{-1}\left\{\begin{array}{c}1+h_t{p}_1^{-}+\frac{{\tau }_x}{{\epsilon }^2}{h}_t{p}_1^{-},x_i\in (d_x-{\tau }_{1,x},d_x)\cap {\overline{\mathrm{\Omega }}}_x^N\hfill \\ 1+h_t(p_1^{-}\frac{d_x}{1-d_x}+{\beta }_1)+\frac{{\tau }_x}{{\epsilon }^2}{h}_t(p_1^{-}+{\beta }_1),x_i\in (d_x,d_x+{\tau }_{2,x})\cap {\overline{\mathrm{\Omega }}}_x^N\hfill \end{array}\right.\hfill \\ \hfill & \mp C_1{h}_t{\epsilon }^{-2}{N}^{-1}\ge 0\hfill \end{array}$$

for a suitable choice of $C>0.$ At the point $x_{N/2}$, we have $(D_x^{+}-D_x^{-}){\psi }^{\pm }\left(x_{N/2}\right)\le 0.$ From the Lemma 4, we have $|w^{\frac{1}{2}}-W^{\frac{1}{2}}|\le C{N}^{-1}lnN$, $i=\frac{N}{4},\cdots ,\frac{5N}{8}$. Therefore $|w^{\frac{1}{2}}(x_i,y)-W_{i,y}^{\frac{1}{2}}|\le C{N}^{-1}lnN,\forall i.$ □

Lemma 11.

Let ${\widehat{u}}^{\frac{1}{2}}$ and $U^{\frac{1}{2}}$ be the solution of (5) and (16), respectively, then $\parallel {\widehat{u}}^{\frac{1}{2}}-U^{\frac{1}{2}}\parallel \le C{N}^{-1}lnN.$

Proof. 

The proof follows from the above two lemmas. □

Lemma 12.

Let $v^1$, $w^1$, ${\widehat{u}}^1$, $V^1$, $W^1$, and $U^1$ be the solutions of (14), (15), (6), (20), (21), and (17), respectively, then

$$\begin{array}{cc}\hfill & \parallel v^1-V^1\parallel \le C{N}^{-1},\parallel w^1-W^1\parallel \le C{N}^{-1}lnN,\hfill \\ \hfill & \parallel {\widehat{u}}^1-U^1\parallel \le C{N}^{-1}lnN.\hfill \end{array}$$

Proof. 

We see that, ${\widehat{u}}^1(x,0)=U_{x,0}^1$ and ${\widehat{u}}^1(x,1)=U_{x,N}^1$.

Similar to the proof of Lemma 8, we can prove the following,

$$\begin{array}{c}\hfill |U^1-V^1|\le C\left\{\begin{array}{c}{N}^{-1},i,j\in {\mathcal{I}}_{\frac{N}{4}},\hfill \\ \zeta +N^{-1},i,j\in {\mathcal{I}}_{\frac{5N}{8}}\setminus {\mathcal{I}}_{\frac{N}{4}},\hfill \\ N^{-1},i,j\in {\mathcal{I}}_{N-1}\setminus {\mathcal{I}}_{\frac{5N}{8}}\hfill \end{array}\right.\zeta =\underset{\frac{N}{4}+1\le i,j\le \frac{5N}{8}-1}{max}|U_{i,j}^1-V_{i,j}^1|.\end{array}$$

Let $v^1$ and $V^1$ be the solutions of (14) and (20), then similar to Lemma 9, we have

$$\begin{array}{cc}\hfill {\mathfrak{D}}_y^N(v^1(x,y_j)-V_{x,j}^1)& ={\mathfrak{D}}_y^N{v}^1(x,y_j)-{\mathfrak{D}}_y^N{V}_{x,j}^1={\mathfrak{D}}_y^N{v}^1(x,y_j)-{\mathfrak{D}}_y{v}^1(x,y_j)\hfill \\ \hfill & =h_t\left[-\epsilon \left({\delta }_y^2-\frac{d^2}{d{y}^2}\right)+p_{2_{i,j}}\left(D_y^{*}-\frac{d}{dy}\right)+q_{2_{i,j}}[I_{\mathbf{d}}^N-I_{\mathbf{d}}]\right]v^1(x,y_j),\hfill \end{array}$$

and $|{\mathfrak{D}}_y^N(v^1(x,y_j)-V_{x,j}^1)|\le C{h}_t{N}^{-1}.$ Then by a suitable barrier function one can prove that $\parallel v^1-V^1\parallel \le C{N}^{-1}.$ Similar to the Lemma 11, we estimate $\parallel w^1-W^1\parallel ,$

$$\begin{array}{cc}\hfill & |{\widehat{u}}^1(x,y_j)-U_{x,j}^1|\le |U_{x,j}^1-V_{x,j}^1|+|v^1(x,y_j)-V_{x,j}^1|+|{\widehat{u}}^1(x,y_j)-v^{}(x,y_j)|\hfill \\ \hfill & \le C\left\{\begin{array}{c}{N}^{-1},i,j\in {\mathcal{I}}_{\frac{N}{4}},\hfill \\ \zeta +N^{-1}+exp\left({\displaystyle \frac{p_2^{-}(y_j-d_y)}{\epsilon }}\right),i,j\in {\mathcal{I}}_{\frac{N}{2}}\setminus {\mathcal{I}}_{\frac{N}{4}},\hfill \\ \zeta +N^{-1}+exp\left({\displaystyle \frac{p_2^{-}(d_y-y_j)}{\epsilon }}\right),i,j\in {\mathcal{I}}_{\frac{5N}{8}}\setminus {\mathcal{I}}_{\frac{N}{2}},\hfill \\ N^{-1},i,j\in {\mathcal{I}}_N\setminus {\mathcal{I}}_{\frac{5N}{8}}.\hfill \end{array}\right.\hfill \end{array}$$

Hence $|{\widehat{u}}^1(x,y_j)-U_{x,j}^1|\le C{N}^{-1},j=0,1,\cdots ,\frac{N}{4},\frac{5N}{8},\cdots ,N$ and $|w^1(x,y_j)-W_{x,j}^1|\le C{N}^{-1},j=0,1,\cdots ,\frac{N}{4},\frac{5N}{8},\cdots ,N.$ Using the barrier function

$${\psi }^{\pm }\left(y_j\right)=C{N}^{-1}\varphi \left(y_j\right)\pm (w^1-W^1),y_j\in (d_y-{\tau }_{1,y},d_y)\cup (d_y,d_y+{\tau }_{2,y})\cap {\overline{\mathrm{\Omega }}}_y^N,$$

where $\varphi \left(y_j\right)=\left\{\begin{array}{c}\left(1+y_j\right)+\frac{{\tau }_y}{{\epsilon }^2}(y_j-(d_y-{\tau }_{1,y})),y_j\in [d_y-{\tau }_{1,y},d_y)\cap {\overline{\mathrm{\Omega }}}_y^N,\hfill \\ \left(1+d_y+d_y{\displaystyle \frac{d_y-y_j}{1-d_y}}\right)+\frac{{\tau }_y}{{\epsilon }^2}(d_y+{\tau }_{2,y}-y_j),y_j\in [d_y,d_y+{\tau }_{2,y}]\cap {\overline{\mathrm{\Omega }}}_y^N,\hfill \end{array}\right.$, ${\tau }_y=min\{{\tau }_{1,y},{\tau }_{2,y}\}$ we prove that $\parallel w^1-W^1\parallel \le C{N}^{-1}lnN,$$j=\frac{N}{4}+1,\cdots ,\frac{5N}{8}-1.$ Hence the proof. □

Theorem 3.

Let ${\widehat{u}}^{n+\frac{1}{2}}$, ${\widehat{u}}^{n+1}$, $U_{i,j}^{n+\frac{1}{2}}$ and $U_{i,j}^{n+1}$ be the solutions of (5), (6), (16), and (17), respectively, then

$$\begin{array}{c}\hfill \parallel {\widehat{u}}^{n+\frac{1}{2}}-U^{n+\frac{1}{2}}\parallel \le C{N}^{-1}lnN,and\parallel {\widehat{u}}^{n+1}-U^{n+1}\parallel \le C{N}^{-1}lnN.\end{array}$$

Proof. 

We prove the theorem on each time level $t=t_n$. We know that ${\widehat{u}}^{n+\frac{1}{2}}(0,y)-U_{0,y}^{n+\frac{1}{2}}=0$, ${\widehat{u}}^{n+\frac{1}{2}}(1,y)-U_{N,y}^{n+\frac{1}{2}}=0$, ${\widehat{u}}^{n+1}(x,0)-U_{x,0}^{n+1}=0$ and ${\widehat{u}}^{n+1}(x,1)-U_{x,N}^{n+1}=0$.

$$\begin{array}{cc}\hfill & {\mathfrak{D}}_x^N(U^{n+\frac{1}{2}}-V^{n+\frac{1}{2}})={\mathfrak{D}}_x^N{U}^{n+\frac{1}{2}}-{\mathfrak{D}}_x^N{V}^{n+\frac{1}{2}}=U^n-V^n,\hfill \\ \hfill & \parallel {\mathfrak{D}}_x^N(U^{n+\frac{1}{2}}-V^{n+\frac{1}{2}})\parallel \le C\left\{\begin{array}{c}{N}^{-1},i,j\in {\mathcal{I}}_{\frac{N}{4}},\hfill \\ \zeta +N^{-1},i,j\in {\mathcal{I}}_{\frac{5N}{8}}\setminus {\mathcal{I}}_{\frac{N}{4}},\hfill \\ N^{-1},i,j\in {\mathcal{I}}_{N-1}\setminus {\mathcal{I}}_{\frac{5N}{8}},\hfill \end{array}\right.\hfill \\ \hfill & {\mathfrak{D}}_y^N(U^{n+1}-V^{n+1})={\mathfrak{D}}_y^N{U}^{n+1}-{\mathfrak{D}}_y^N{V}^{n+1}=U^{n+\frac{1}{2}}-V^{n+\frac{1}{2}},\hfill \\ \hfill & \parallel {\mathfrak{D}}_x^N(U^{n+1}-V^{n+1})\parallel \le C\left\{\begin{array}{c}{N}^{-1},i,j\in {\mathcal{I}}_{\frac{N}{4}},\hfill \\ \zeta +N^{-1},i,j\in {\mathcal{I}}_{\frac{5N}{8}}\setminus {\mathcal{I}}_{\frac{N}{4}},\hfill \\ N^{-1},i,j\in {\mathcal{I}}_{N-1}\setminus {\mathcal{I}}_{\frac{5N}{8}},\hfill \end{array}\right.\hfill \\ \hfill & \zeta =\underset{n}{max}\underset{\frac{N}{4}+1\le i,j\le \frac{5N}{8}-1}{max}|U_{i,j}^n-V_{i,j}^n|,\hfill \end{array}$$

with the successive applications of Lemmas 6 and 7 and the iteration in n, we prove that

$$\parallel U^{\mu }-V^{\mu }\parallel \le C\left\{\begin{array}{c}{N}^{-1},i,j\in {\mathcal{I}}_{\frac{N}{4}},\hfill \\ \zeta +N^{-1},i,j\in {\mathcal{I}}_{\frac{5N}{8}}\setminus {\mathcal{I}}_{\frac{N}{4}},\hfill \\ N^{-1},i,j\in {\mathcal{I}}_{N-1}\setminus {\mathcal{I}}_{\frac{5N}{8}},\hfill \end{array}\right.\mu =n+1\&\mu =n+\frac{1}{2}.$$

Using the following barrier functions

$$\begin{array}{c}\hfill {\mathrm{\Psi }}_1^{\pm }\left(x_i\right)=C{N}^{-1}s\left(x_i\right)\pm [v^{n+\frac{1}{2}}(x_i,y_j)-V_{i,j}^{n+\frac{1}{2}}],\forall i,\\ \hfill {\mathrm{\Psi }}_2^{\pm }\left(y_j\right)=C{N}^{-1}s\left(y_j\right)\pm [v^{n+1}(x_i,y_j)-V_{i,j}^{n+1}],\forall j,\end{array}$$

and from Lemmas 6 and 7, we can prove that

$$\parallel v^{n+\frac{1}{2}}-V^{n+\frac{1}{2}}\parallel \le C{N}^{-1},\parallel v^{n+1}-V^{n+1}\parallel \le C{N}^{-1}.$$

It is observed that $|w^{\mu }(x_i,y_j)-W_{i,j}^{\mu }|\le C{N}^{-1},$$\mu =n+\frac{1}{2},n+1,$$i,j=0,1,\cdots ,\frac{N}{4},$$\frac{5N}{8},\cdots ,N$. Using the following barrier functions

$$\begin{array}{cc}\hfill & {\mathrm{\Phi }}_1^{\pm }\left(x_i\right)=C{N}^{-1}{\varphi }_1\left(x_i\right)\pm (w^{n+\frac{1}{2}}-W^{n+\frac{1}{2}}),x_i\in [{\mathrm{\Omega }}_{2,x}\cup {\mathrm{\Omega }}_{3,x}]\cap {\overline{\mathrm{\Omega }}}_x^N,\hfill \\ \hfill & {\mathrm{\Phi }}_2^{\pm }\left(y_j\right)=C{N}^{-1}{\varphi }_2\left(y_j\right)\pm (w^{n+1}-W^{n+1}),y_j\in [{\mathrm{\Omega }}_{2,y}\cup {\mathrm{\Omega }}_{3,y}]\cap {\overline{\mathrm{\Omega }}}_y^N,\hfill \end{array}$$

where ${\varphi }_1\left(x_i\right)=\left\{\begin{array}{c}\left(1+x_i\right)+\frac{{\tau }_x}{{\epsilon }^2}(x_i-(d_x-{\tau }_{1,x})),x_i\in {\mathrm{\Omega }}_{2,x}\cap {\overline{\mathrm{\Omega }}}_x^N,\hfill \\ \left(1+d_x+d_x{\displaystyle \frac{d_x-x_i}{1-d_x}}\right)+\frac{{\tau }_x}{{\epsilon }^2}(d_x+{\tau }_{2,x}-x_i),x_i\in {\mathrm{\Omega }}_{3,x}\cap {\overline{\mathrm{\Omega }}}_x^N,\hfill \end{array}\right.$

${\varphi }_2\left(y_j\right)=\left\{\begin{array}{c}\left(1+y_j\right)+\frac{{\tau }_y}{{\epsilon }^2}(y_j-(d_y-{\tau }_{1,y})),y_j\in {\mathrm{\Omega }}_{2,y}\cap {\overline{\mathrm{\Omega }}}_y^N,\hfill \\ \left(1+d_y+d_y{\displaystyle \frac{d_y-y_j}{1-d_y}}\right)+\frac{{\tau }_y}{{\epsilon }^2}(d_y+{\tau }_{2,y}-y_j),y_j\in {\mathrm{\Omega }}_{3,y}\cap {\overline{\mathrm{\Omega }}}_y^N,\hfill \end{array}\right.$

${\tau }_{\mu }=min\{{\tau }_{1,\mu },{\tau }_{2,\mu }\}$, $\mu =x,y$ we prove that $|w^{\mu }(x_i,y_j)-W_{i,j}^{\mu }|\le C{N}^{-1},\mu =n+\frac{1}{2},n+1,$ and $i,j=\frac{N}{4}+1,\cdots ,\frac{5N}{8}-1$. By the triangle inequality, we have the desired results. □

Theorem 4.

Let $u(x_i,y_j,t_n)$ and $U_{i,j}^n$ be the solutions of (1) and (17), then

$$\parallel u-U\parallel \le C(h_t+N^{-1}lnN).$$

Proof. 

The error can be obtained from the following

$$\begin{array}{cc}\hfill u(x_i,y_j,t_n)-U_{i,j}^n& ={\widehat{u}}^n(x_i,y_j)-U_{i,j}^n+u(x_i,y_j,t_n)-{\overline{u}}^n(x_i,y_j)+{\overline{u}}^n(x_i,y_j)-{\widehat{u}}^n(x_i,y_j)\hfill \\ \hfill \parallel u\left(t_n\right)-U^n\parallel & \le \parallel {\overline{u}}^n-{\widehat{u}}^n\parallel +\parallel {\widehat{u}}^n-U^n\parallel +\parallel u\left(t_n\right)-{\overline{u}}^n\parallel .\hfill \end{array}$$

From Lemma 3, Theorem 3 and Ref. [6], Theorem 1, we have

$$\begin{array}{c}\hfill \parallel u\left(t_n\right)-U^n\parallel \le \parallel u\left(t_n\right)-{\overline{u}}^n\parallel +\parallel {\overline{u}}^n-{\widehat{u}}^n\parallel +\parallel {\widehat{u}}^n-U^n\parallel \le C{h}_t+C{N}^{-1}lnN,\end{array}$$

which completes the proof. □

6. Numerical Validation

Two examples are presented in this section to validate the theoretical results presented in this article. The exact analytical solutions to the test problems are unknown, therefore we use the double mesh principle to calculate the maximum point-wise error and computational order of convergence. For fixed M, we define

$$\begin{array}{cc}\hfill & E_{\epsilon }^N=\underset{i,j}{max}\mid U_{i,j}^N(h_x,h_y,h_t)-U_{i,j}^N(\frac{h_x}{2},\frac{h_y}{2},\frac{h_t}{2})\mid ,0\le i,j\le N\hfill \\ \hfill & D_{x,y}^N=\underset{\epsilon }{max}{E}_{\epsilon }^N,{\rho }^N={log}_2\left(\frac{D_{x,y}^N}{D_{x,y}^{2N}}\right),\hfill \end{array}$$

where $U_{i,j}^N(h_x,h_y,h_t)$ and $U_{i,j}^N(\frac{h_x}{2},\frac{h_y}{2},\frac{h_t}{2})$ are the numerical solutions at the node $(x_i,y_j,t_n)$ with mesh sizes $(h_x,h_y,h_t)$ and $(\frac{h_x}{2},\frac{h_y}{2},\frac{h_t}{2})$, respectively, $D_{x,y}^N$ is maximum over $\epsilon$ for fixed N.

Example 1.

Consider the 2D parabolic PDE (1) with discontinuous source and convection coefficients with the following data:

$$\begin{array}{cc}\hfill & \frac{\partial u}{\partial t}-\epsilon \mathrm{\Delta }u+\overline{p}\left(\mathbf{x}\right)·\nabla u+q\left(\mathbf{x}\right)u(\mathbf{x}-\mathbf{d},t)=g(\mathbf{x},t),(\mathbf{x},t)\in {\mathfrak{D}}^{*}\times (0,T]\hfill \\ \hfill & p_1\left(\mathbf{x}\right)=\left\{\begin{array}{c}1+x(1-x),x\in (0,d_x),\forall y,\hfill \\ -(1+x(1-x)),x\in (d_x,1),\hfill \end{array}\right.p_2\left(\mathbf{x}\right)=\left\{\begin{array}{c}1+y(1-y),y\in (0,d_y),\forall x,\hfill \\ -(1+x(1-x)),y\in (d_y,1),\hfill \end{array}\right.,\hfill \\ \hfill & q_1\left(\mathbf{x}\right)=-0.5-x(1-x),q_2\left(\mathbf{x}\right)=-0.5-y(1-y),d_x=0.5=d_y,\hfill \\ \hfill & g_1(\mathbf{x},t)=\left\{\begin{array}{c}-x^{2}y(1-x){(1-y)}^{2}exp\left(t^2-{\displaystyle \frac{xy}{1+x^2+y^2}}\right),x\in (0,d_x),\hfill \\ xy{(1-x)}^2(1-y)exp\left(t^2-{\displaystyle \frac{x^2{y}^2}{1+x^2-y^2}}\right),x\in (d_x,1),\hfill \end{array}\right.\hfill \\ \hfill & g_2(\mathbf{x},t)=\left\{\begin{array}{c}-x^3{y}^2,y\in (0,d_y),\hfill \\ {(1-x)}^5\sqrt{1-y},y\in (d_y,1),\hfill \end{array}\right.u_0={\displaystyle \frac{xy(1-x)(1-y)}{1+x^2+y^2}}.\hfill \end{array}$$

Table 1 presents the maximum pointwise error and the order of convergence corresponding to Example 1. Figure 2 and Figure 3 depict the numerical solution and pointwise maximum error of the problem studied in Example 1, respectively.

Table 1. Maximum error and order of convergence for the Example 1 with $M=2^7$.

	N Number of Mesh Points in Space Directions
$\mathbf{\epsilon }$↓	16	32	64	128	256
${10}^{-1}$	5.5196 × 10${}^{-3}$	3.0933 × 10${}^{-3}$	1.6543 × 10${}^{-3}$	8.5850 × 10${}^{-4}$	4.3790 × 10${}^{-4}$
	$\mathbf{0}.\mathbf{83544}$	$\mathbf{0}.\mathbf{90292}$	$\mathbf{0}.\mathbf{94632}$	$\mathbf{0}.\mathbf{97123}$	-
${10}^{-3}$	2.1762 × 10${}^{-2}$	1.5092 × 10${}^{-2}$	1.0563 × 10${}^{-2}$	7.6976 × 10${}^{-3}$	5.4021 × 10${}^{-3}$
	$\mathbf{0}.\mathbf{52801}$	$\mathbf{0}.\mathbf{51484}$	$\mathbf{0}.\mathbf{45650}$	$\mathbf{0}.\mathbf{51089}$	-
${10}^{-5}$	2.2373 × 10${}^{-2}$	1.5657 × 10${}^{-2}$	1.0944 × 10${}^{-2}$	8.0343 × 10${}^{-3}$	5.6554 × 10${}^{-3}$
	$\mathbf{0}.\mathbf{51496}$	$\mathbf{0}.\mathbf{51669}$	$\mathbf{0}.\mathbf{44586}$	$\mathbf{0}.\mathbf{50655}$	-
${10}^{-7}$	2.2379 × 10${}^{-2}$	1.5663 × 10${}^{-2}$	1.0948× 10${}^{-2}$	8.0378 × 10${}^{-3}$	5.6580 × 10${}^{-3}$
	$\mathbf{0}.\mathbf{51482}$	$\mathbf{0}.\mathbf{51668}$	$\mathbf{0}.\mathbf{44577}$	$\mathbf{0}.\mathbf{50650}$	-
${10}^{-9}$	2.2379 × 10${}^{-2}$	1.5663 × 10${}^{-2}$	1.0948 × 10${}^{-2}$	8.0378 × 10${}^{-3}$	5.6580 × 10${}^{-3}$
	$\mathbf{0}.\mathbf{51482}$	$\mathbf{0}.\mathbf{51668}$	$\mathbf{0}.\mathbf{44577}$	$\mathbf{0}.\mathbf{50650}$	-
${\mathbf{D}}_{\mathbf{x},\mathbf{y}}^{\mathbf{N}}$	2.2379×10${}^{-\mathbf{2}}$	1.5663×10${}^{-\mathbf{2}}$	1.0948×10${}^{-\mathbf{2}}$	8.0378×10${}^{-\mathbf{3}}$	5.6580×10${}^{-\mathbf{3}}$
${\rho }^N$	$\mathbf{0}.\mathbf{51482}$	$\mathbf{0}.\mathbf{51668}$	$\mathbf{0}.\mathbf{44577}$	$\mathbf{0}.\mathbf{50650}$	-

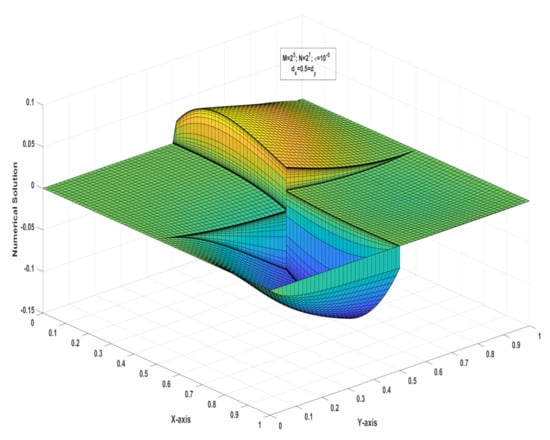
Figure 2. Numerical solution of Example 1 for fixed $M=2^5,N=2^7,\epsilon ={10}^{-5}$.

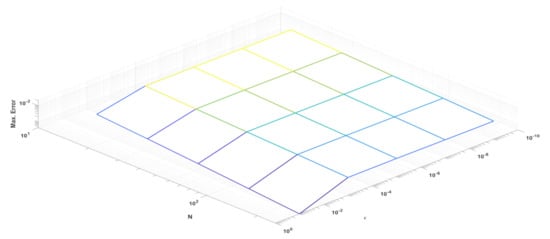
Figure 3. Maximum error of Example 1.

Example 2.

Consider the 2D parabolic PDE (1) with discontinuous source and convection coefficients with the following data:

$$\begin{array}{cc}\hfill & p_1\left(\mathbf{x}\right)=\left\{\begin{array}{c}1+x(1-x)+y^2,x\in (0,d_x),\forall y,\hfill \\ -(1+x(1-x)+exp(-y)),x\in (d_x,1),\hfill \end{array}\right.d_x=0.5,d_y=0.25\hfill \\ \hfill & p_2\left(\mathbf{x}\right)=\left\{\begin{array}{c}1+y(1-y)+\sqrt{x},y\in (0,d_y),\forall x,\hfill \\ -(1+y(1-y)+x^2),y\in (d_y,1),\hfill \end{array}\right.,\hfill \\ \hfill & c_1\left(\mathbf{x}\right)=-0.5-x(1-x),c_2\left(\mathbf{x}\right)=-0.5-y^2(1-y),\hfill \\ \hfill & g_1(\mathbf{x},t)=\left\{\begin{array}{c}4txyexp\left(x^2+y^2\right),x\in (0,d_x),\hfill \\ 4t(1-x)(1-y),x\in (d_x,1),\hfill \end{array}\right.g_2(\mathbf{x},t)=\left\{\begin{array}{c}4xyexp(x^2+y^2),y\in (0,d_y),\hfill \\ 4t(1-x)(1-y),y\in (d_y,1),\hfill \end{array}\right.\hfill \\ \hfill & u_0={\displaystyle \frac{xy(1-x)(1-y)}{1+x^2+y^2}}.\hfill \end{array}$$

The maximum pointwise error and the order of convergence corresponding to Example 2 are given in Table 2. Figure 4 and Figure 5 display the numerical solution and pointwise maximum error of Example 2, respectively.

Table 2. Maximum error and order of convergence for the Example 2 with $M=2^7$.

	N Number of Mesh Points in Space Directions
$\mathbf{\epsilon }$↓	16	32	64	128	256
${10}^{-1}$	4.6432 × 10${}^{-2}$	2.4055 × 10${}^{-2}$	1.2254 × 10${}^{-2}$	6.1910 × 10${}^{-3}$	3.1182 × 10${}^{-3}$
	$\mathbf{0}.\mathbf{94879}$	$\mathbf{0}.\mathbf{97310}$	$\mathbf{0}.\mathbf{98498}$	$\mathbf{0}.\mathbf{98946}$	-
${10}^{-3}$	4.3139 × 10${}^{-2}$	2.9874 × 10${}^{-2}$	2.3658 × 10${}^{-2}$	1.8574 × 10${}^{-2}$	1.5132 × 10${}^{-2}$
	$\mathbf{0}.\mathbf{53011}$	$\mathbf{0}.\mathbf{33654}$	$\mathbf{0}.\mathbf{34909}$	$\mathbf{0}.\mathbf{29568}$	-
${10}^{-5}$	4.4807 × 10${}^{-2}$	3.1372 × 10${}^{-2}$	2.3990 × 10${}^{-2}$	1.8528 × 10${}^{-2}$	1.5113 × 10${}^{-2}$
	$\mathbf{0}.\mathbf{51422}$	$\mathbf{0}.\mathbf{38706}$	$\mathbf{0}.\mathbf{37270}$	$\mathbf{0}.\mathbf{29390}$	-
${10}^{-7}$	4.4821 × 10${}^{-2}$	3.1389 × 10${}^{-2}$	2.3995 × 10${}^{-2}$	1.8528 × 10${}^{-2}$	1.5113 × 10${}^{-2}$
	$\mathbf{0}.\mathbf{51390}$	$\mathbf{0}.\mathbf{38755}$	$\mathbf{0}.\mathbf{37302}$	$\mathbf{0}.\mathbf{29389}$	-
${10}^{-9}$	4.4821 × 10${}^{-2}$	3.1389 × 10${}^{-2}$	2.3995 × 10${}^{-2}$	1.8528 × 10${}^{-2}$	1.5113 × 10${}^{-2}$
	$\mathbf{0}.\mathbf{51390}$	$\mathbf{0}.\mathbf{38756}$	$\mathbf{0}.\mathbf{37302}$	$\mathbf{0}.\mathbf{29389}$	-
${\mathbf{D}}_{\mathbf{x},\mathbf{y}}^{\mathbf{N}}$	4.6432 × 10${}^{-\mathbf{2}}$	3.1389 × 10${}^{-\mathbf{2}}$	2.3995 × 10${}^{-\mathbf{2}}$	1.8574 × 10${}^{-\mathbf{2}}$	1.5132 × 10${}^{-\mathbf{2}}$
${\rho }^N$	$\mathbf{0}.\mathbf{56483}$	$\mathbf{0}.\mathbf{38756}$	$\mathbf{0}.\mathbf{36945}$	$\mathbf{0}.\mathbf{29568}$	-

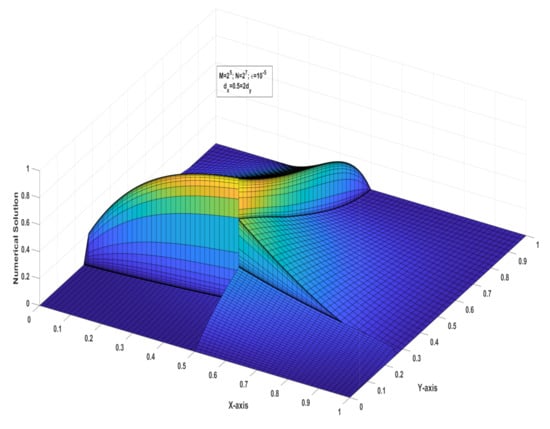
Figure 4. Numerical solution of Example 2 for fixed $M=2^5,N=2^7,\epsilon ={10}^{-5}$.

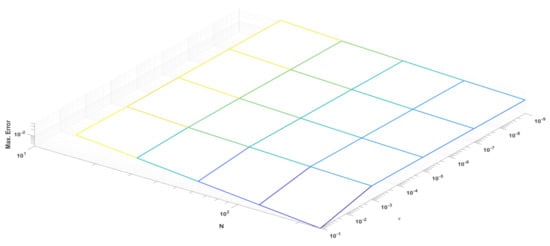
Figure 5. Maximum error of Example 2.

7. Concluding Remarks

This article discusses singularly perturbed 2D parabolic delay differential equations with discontinuous convection coefficients and source terms. As pointed out in Ref. [3], the fractional step method results in low-cost computation for 2D problems. Therefore, we first apply the fractional implicit Euler method for the time derivative. Then the higher dimensional problem is reduced to lower dimensional problems. In fact, we get $2N$ system of uncoupled equations. Each equation is a singularly perturbed differential equation with a discontinuous convection coefficient and source term. As discussed in Ref. [13], we discretized the spatial domains ${\mathrm{\Omega }}_{\mu },\mu =x,y$ in the same manner, such as ${\overline{\mathrm{\Omega }}}_{\mu }^N,\mu =x,y$. On each mesh we apply the difference scheme ${\mathfrak{D}}_{\mu }^N{U}_{i,j},\mu =x,y.$ It is proved that the present method is of almost first-order convergence in space and time. Figure 2 and Figure 4 represent the test problems solutions stated in Examples 1 and 2, respectively, we see that, the layers occurs at the points $d_x$ and $d_y$. Table 1 and Table 2 present the maximum pointwise errors of the test example problems. It is also worth noting that when the parameter $\epsilon$ drops, the maximum pointwise error grows and stabilizes. It is assumed that the number of mesh points in the time direction is $M=128$. From Figure 3 and Figure 5 we see that the maximum pointwise error decreases as N increases. The present method works for the problems with any delay arguments of size $0<<d_{\mu }\le 1,\mu =x,y.$ In Example 1 we assumed that $d_x=0.5=d_y,$, whereas in Example 2 we assumed that $d_x=0.5,d_y=0.25.$