Advanced Analytic Self-Similar Solutions of Regular and Irregular Diffusion Equations

Abstract

We study the diffusion equation with an appropriate change of variables. This equation is, in general, a partial differential equation (PDE). With the self-similar and related Ansatz, we transform the PDE of diffusion to an ordinary differential equation. The solutions of the PDE belong to a family of functions which are presented for the case of infinite horizon. In the presentation, we accentuate the physically reasonable solutions. We also study time-dependent diffusion phenomena, where the spreading may vary in time. To describe the process, we consider time-dependent diffusion coefficients. The obtained analytic solutions all can be expressed with Kummer’s functions.

1. Introduction

The study of classical transport processes are crucial both from scientific and from engineering points. One of such process is diffusion, which is a quite general phenomena. It can be formulated for particles, which are the mass diffusion, or to energy transport, which is related to thermal conduction. This manuscript is an extension of certain studies, in which we present additional analytic solutions for the regular diffusion equation from symmetry considerations. In our last paper [1], after a historical overview, we presented a new class of analytic solutions derived with the help of the reduction mechanism provides a more detailed analysis of various self-similar and generalized self-similar solutions. Here, we show how the original self-similar trial function can be generalized in a kind of power law expansion. All the presented solutions are new and cannot be found elsewhere in the literature.

The whole diffusion phenomena is, in general, well introduced—with cases and studies—by the monograph of Ghez [2]. Embedding into the larger field of transport processes diffusion is discussed by John Newman and Vincent Battaglia in their series of lectures [3]. Gillespie and Seitariodu provided an introduction to the standard theoretical models for simple Brownian type diffusion [4] in 2013. The diffusion equation can be also related to the Wiener process [5]. The anomalous diffusion was analyzed with statistical methods by Weihua and co-workers [6]. Uchaikin investigated self-similar anomalous diffusion [7]. Ari Arapostathis et al. studied the ergodic control of diffusion processes in a monograph [8]. One may find applications in solid state physics, binary alloys, thin films, etc., in [9,10,11,12,13,14,15]. Defects and diffusion in nanotubes was summarized by Fisher [16]. Diffusion processes a peculiar material in ceramics was analyzed in the monograph by Pelleg [17]. Atomic diffusion processes is a scientific field which was presented in a monograph as well [18]. Diffusion processes are the starting points for reaction diffusion processes [19] or diffusion in porous media [20]. A vitally important application of such mathematical equations is the mathematical modeling of aircraft cabin fires [21,22]. The two dimensional diffusion equation, completed with certain reaction terms may lead to pattern formation, for instance the Turing patterns derived from Schnakenberg equations [23] or Brusselator model [24]. If the diffusion equation is completed with the simplest nonlinear term, the gradient of the variable on the second power we arrive to the Kardar–Parizi–Zwang (KPZ) equation which is the simplest successful model for surface growth phenomena. In two of our former studies we investigated the KPZ equation (with additional noise terms) with the self-similar [25] and the traveling waves Ansatz [26]. Interesting results have been obtained in the study of irregular diffusion [27,28]. Now, in the following we deepen this analysis and present additional analytic solutions with detailed parameter study. We present a series of solutions which are defined on the whole real axis having a decaying and spreading property with additional oscillations. Our main investigation tool, the self-similar Ansatz, helps us to build a link from the regular to irregular diffusion processes, which makes up the second part of the study.

Although the diffusion process can be studied in different dimensions, here, we consider only one Cartesian coordinate therefore the equation reads

$$\begin{array}{c}\hfill \frac{\partial C(x,t)}{\partial t}=D\frac{{\partial }^{2}C(x,t)}{\partial x^2},\end{array}$$

(1)

where $C(x,t)$ is the distributions of the particle concentration in space and time and D is the diffusion coefficient. $C(x,t)$ in the equation above is considered up to a constant, which means, that $C(x,t)+C_0$ may be also a solution, depending on the initial conditions. The function $C(x,t)$ fulfills the necessary smoothness conditions with existing continuous first and second derivatives in respect to time and and space. From causality, the diffusion coefficient should be a positive real number $(D>0)$. Numerous physics textbooks gives us the derivation how the fundamental (the Gaussian) solutions can be obtained, e.g., [29,30].

The derivation and analysis of various analytic solutions of physical processes described by various mathematical equations, (e.g., algebraic, differential or partial differential) have crucial importance. As it was shown in our former paper [1] and as it will be shown here, there are far more solutions known for diffusion than the Gaussian and the error functions. We presented some relatively simple solutions (e.g., $Dt+x^2/2$), other solutions which can derived with the general symmetry analysis method by Clarkson and Kruskal [31], the traveling profile method of Benhamidouche [32] or the self-similar Ansatz of Sedov [33]. Beyond the Gaussian and error functionsm most of our results are expressible with the Kummer special functions. In the following, we try additional two trial functions and enlarge the number of solutions known from the self-similar Ansatz. In the last part of the study, we investigate less regular diffusion processes where the diffusion coefficients gain temporal dependencies. The diffusion equation stands at the basis of more complex equations: in case on the r.h.s. beyond the second derivative, there is a function $F\left(C\right)$ with certain properties, we can talk about the Kolmogorov–Petrovskii–Piskunov equation [34]. Explicitly, on the r.h.s., the term $C(1-C)$ yields the Fisher equation [35,36]. Environmental aspects can be found in [37]. The term $pC+r{C}^q$ in general means the Newel–Whitehead–Segel (NWS) equation [38,39] and the term $C(1-C)(C-\alpha )$ where $0<\alpha <1$ defines the general Zeldovich equation (or Huxley equation) which arises in combustion theory [40]. For certain non-trivial values of $p,r$ and q, one may find exact solutions of the NWS equation [41,42]. Frank–Kamenetzkii used the $exp(a·e^{-\frac{b}{C}})$ term [43] to explain thermal explosion.

Burgers used the $C·C_x$ (where the subscript stands for partial derivation) term to study turbulence [44]. Nariboli and Lin introduced the quadratic Burgers equation with the term of $C^2·C_x$ [45]. Sachdev [46] modified the original Burgers equation and used a third order term of $C^3·C_x$. Later numerous generalization saw the light of sun by various authors, and the originality of the models are hard to identify. The generalized Huxley equation [47] has the source term of $\beta C(1-C^{\delta })(C^{\delta }-\gamma )$ where $\beta , \delta ,\gamma$ are free real parameters. Lastly, we mention the the Burgers–Huxley and the Burgers–Fisher equations [48]. The first has the source term of $-\gamma C_x+\beta C(1-C^{\delta })(C^{\delta }-\gamma )$ and the second of $-\gamma C_x+\beta C(1-C)$. Our presented list is of course far from being complete.

Applications in different fields—for instance, plasma physics or condensed matter—one may find in [49,50,51].

We hope that this work may bring deeper understanding in the study of vapor diffusion [52,53], of the one dimensional convection- diffusion-reaction problem [54,55,56], and of diffusive aspects in different flows [57].

Diffusion processes can be coupled to fluid dynamics phenomenon to describe the double (or multiple) diffusive convection phenomena [58] where a convection is driven by two (or more) different density gradients described with different rates of diffusions.

Another way of generalization of diffusion is the application of fractional derivatives. First, consider when the time derivative is fractional. Such a study was conducted in the work of Wyss [59]. The solutions were exactly given and could be expressed with the Fox functions. For the mathematical details of Fox functions, see [60]. Regarding the space fractional diffusion equation, one may find studies in [61]. Comparison of our results to such functions could be the subject of future study.

The analysis and control of coupled neural networks can be conducted with the reaction diffusion term, as was given in the monograph of Wang et al. [62]. It is obvious, but we mention that the diffusion equation has the same form as the heat conduction equation. This field has a wealth of literature as well, from which we mention only two monographs [63,64]. Lastly, not to forget the field of continuously developing numerical methods of PDEs, it is worthwhile to mention the new results obtained by [65,66].

2. Theory and Results

2.1. Self-Similar Ansatz

We start the analysis with the self-similar Ansatz

$$\begin{array}{c}\hfill C(x,t)=t^{-\alpha }f\left(\frac{x}{t^{\beta }}\right)=t^{-\alpha }f\left(\eta \right),\end{array}$$

(2)

where $\alpha$ and $\beta$ are the self-similar exponents being real numbers describing the decay and the spreading of the solution in time and space. These properties makes this Ansatz physically extraordinarily relevant; it was first introduced by Sedov [33]. Together with dimension-analysis method He applied it to various fluid mechanical problems such as incompressible heavy fluids or gas dynamics. Later Zeldovich [67] exhaustively investigated high temperature gas dynamical problems. The most recent and modern literature where the reader can learn the method and the possible connections to dimension-analysis was written by Barenblatt [68] in 2003. He addressed problems such as very intense concentrated flooding or flow in porous media.

For the present diffusion equation, after some trivial algebra (which can be found in our previous paper [1]) we get:

$$\alpha =\mathrm{arbitrary}\mathrm{real}\mathrm{number},\beta =1/2,$$

(3)

and there is a clear-cut time-independent ordinary differential equation (ODE) of

$$-\alpha f-\frac{1}{2}\eta f^{\prime }=D{f}^{″}.$$

(4)

with the choice of $\alpha =1/2$ and setting the first integration constant to zero $c_1=0$ we obtain back the well-known Gaussian solution.

This is the so-called fundamental solution and sometimes referred to as source type solution—by mathematicians—because for $t\to 0$ the $C(x,0)\to \delta \left(x\right)$.

The main goal of the present study is to evaluate and analyze the solutions for general $(\alpha \ne 1/2)$ real parameter values. All the subsequent results are completely new and cannot be found elsewhere in the scientific literature. Luckily, the ODE Equation (4) has closed-form analytic values, which are

$$f\left(\eta \right)=\eta ·e^{-\frac{{\eta }^2}{4D}}\left(c_{1}M\left[1-\alpha ,\frac{3}{2},\frac{{\eta }^2}{4D}\right]+c_{2}U\left[1-\alpha ,\frac{3}{2},\frac{{\eta }^2}{4D}\right]\right),$$

(5)

where $M(·,·,·)$ and $U(·,·,·)$ are the Kummer functions. As definition consider the series expansion of M

$$M(a,b,z)=1+\frac{az}{b}+\frac{{\left(a\right)}_2{z}^2}{{\left(b\right)}_{2}2!}+\dots +\frac{{\left(a\right)}_n{z}^n}{{\left(b\right)}_{n}n!},$$

(6)

with the ${\left(a\right)}_n=a(a+1)(a+2)\dots (a+n-1),{\left(a\right)}_0=1$ which is the so-called rising factorial or Pochhammer’s Symbol [60]. In our present case, b has a fix non-negative integer value, so none of the solutions have poles at $b=-n$. For the Kummer function M, when the parameter a has negative integer numerical values ($a=-m$), the solution is reduced to a polynomial of degree m for the variable z. In other cases, $a\ne -m$, we obtain a convergent infinite series for all values of $a,b$ and z. There is a connecting formula between the two Kummer’s functions, U is defined from M via

$$U(a,b,z)=\frac{\pi }{sin\left(\pi b\right)}\left(\frac{M[a,b,z]}{\Gamma [1+a-b]\Gamma \left[b\right]}-z^{1-b}\frac{M[1+a-b,2-b,z]}{\Gamma \left[a\right]\Gamma [2-b]}\right),$$

(7)

where $\Gamma \left(a\right)$ is the Gamma function [60]. For exhaustive details (e.g., integral representation, recursion formula), see the NIST Handbook [60]. For non-negative integer $\alpha$s, an alternative formulations of the result is possible in the form of

$$f\left(\eta \right)=e^{-\frac{{\eta }^2}{4D}}\left({\tilde{c}}_1{H}_{2\alpha -1}\left[\frac{\eta }{2\sqrt{D}}\right]+{\tilde{c}}_2·{}_1{F}_1\left[\frac{1-2\alpha }{2},\frac{1}{2};\frac{{\eta }^2}{4D}\right]\right),$$

(8)

where $H_a\left(\eta \right)$ is the Hermite polynomial and ${}_1{F}_1(·,·;·)$ is the hypergeometric function. The first part of the solution, the Hermite polynomials, form a complete orthonormal basis set on the $-\infty \cdots +\infty$ range with the Gaussian weight function and defines a Hilbert space (note that Hermite polynomials play an extraordinary role in quantum mechanics as the solution of the harmonic oscillator problem [69] which pioneered the way to second quantization or field theory). Unfortunately, the second term in Equation (8) if $c_2\ne 0$ destroys the orthogonality causing over-completeness, which is an interesting feature, taking out the scope that the functional analysis might have far-reaching consequences, needing further in-depth investigation. We have an intuition that such a property could also help us say something new about turbulence. However, that is out of the scope of the present study, but is in line with our long-range scientific interest.

It is important to emphasize that there are four parameter ranges where the derived solutions behave qualitatively differently:

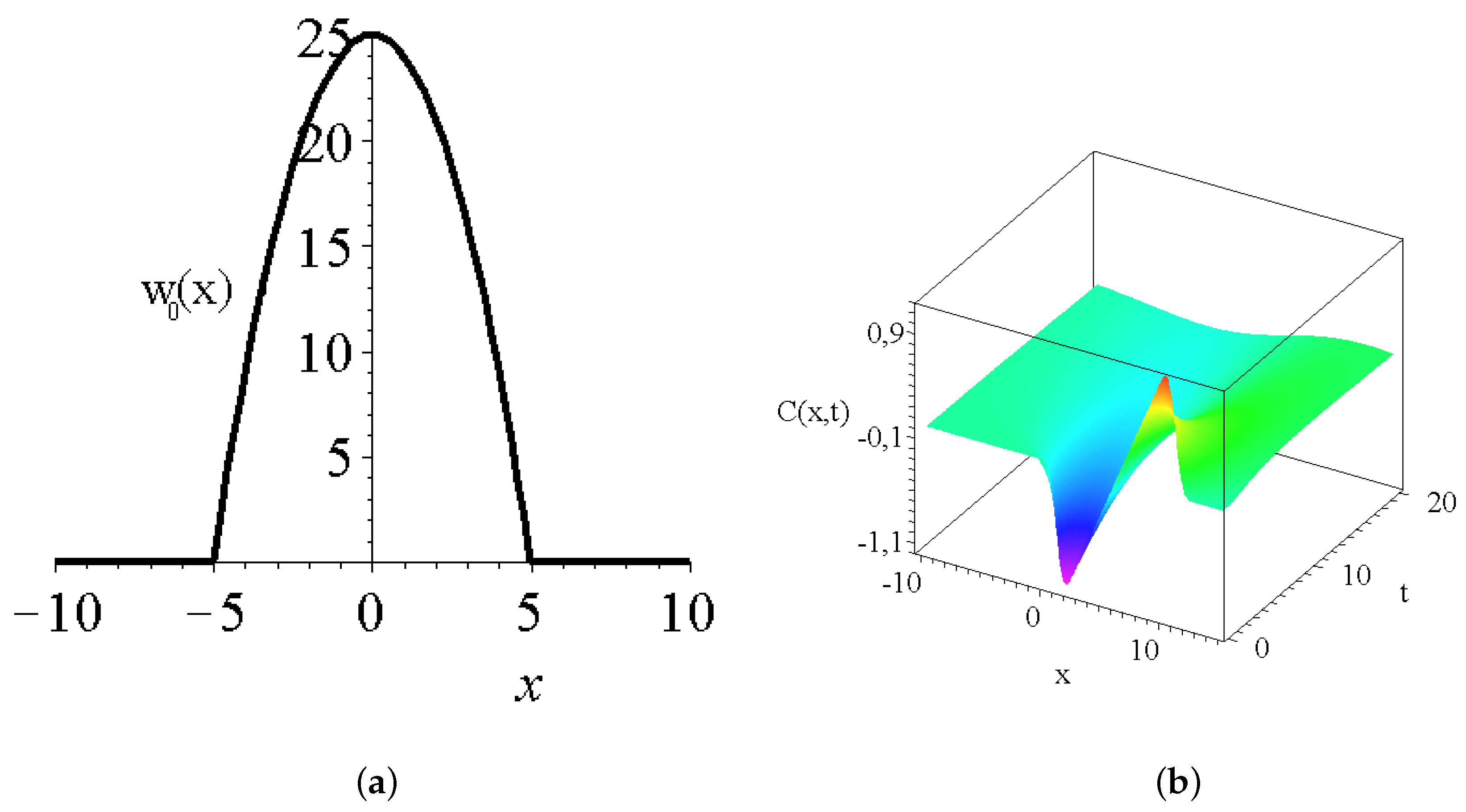
• $\alpha <0,$ where the derived solutions are divergent for large $\eta$s, such solutions are nonphysical and out of the scope of our present analysis
• $\alpha =0,$ the solution is zero in the origin and has an asymptotic positive finite value at asymptotic large $\eta$
• $0<\alpha <1,$ the solution is zero in the origin has a local maxima and a decay to zero as $\eta$ goes to infinity
• $1<\alpha ,$ the solutions are again zero in the origin then have a local maxima and a quick oscillatory decay to zero, larger $\alpha$ values mean more oscillations with more and more zero transitions.

We present here the form of f for the cases of $\alpha =0,1,2,3,4$; the last two cases are evaluated for the first time:

$$\begin{array}{ccc}\hfill f\left(\eta \right)& =& erf\left(\frac{\eta }{2\sqrt{D}}\right),\hfill \\ \hfill f\left(\eta \right)& =& {\kappa }_0·\eta ·e^{-\frac{{\eta }^2}{4D}},\hfill \\ \hfill f\left(\eta \right)& =& {\kappa }_0·\eta ·e^{-\frac{{\eta }^2}{4D}}·\left(1-\frac{1}{6D}{\eta }^2\right),\hfill \\ \hfill f\left(\eta \right)& =& {\kappa }_0·\eta ·e^{-\frac{{\eta }^2}{4D}}·\left(1-\frac{1}{3D}{\eta }^2+\frac{1}{60}\frac{1}{D^2}{\eta }^4\right),\hfill \\ \hfill f\left(\eta \right)& =& {\kappa }_0·\eta ·e^{-\frac{{\eta }^2}{4D}}·\left(1-\frac{1}{2D}{\eta }^2+\frac{1}{20}\frac{1}{D^2}{\eta }^4-\frac{1}{840}\frac{1}{D^3}{\eta }^6\right),\hfill \end{array}$$

(9)

the ${\kappa }_0$ is an arbitrary normalization constant and will be given later on. For completeness, the final concentration distributions are also provided; by inserting $\eta =x/t^{1/2}$ and the actual value of $\alpha$, we obtain:

$$\begin{array}{ccc}\hfill C(x,t)& =& erf\left(\frac{x}{2\sqrt{Dt}}\right),\hfill \\ \hfill C(x,t)& =& \left(\frac{{\kappa }_{1}x}{t^{\frac{3}{2}}}\right)e^{-\frac{x^2}{4Dt}},\hfill \\ \hfill C(x,t)& =& \left(\frac{{\kappa }_{1}x}{t^{\frac{5}{2}}}\right)e^{-\frac{x^2}{4Dt}}\left(1-\frac{x^2}{6Dt}\right),\hfill \\ \hfill C(x,t)& =& \left(\frac{{\kappa }_{1}x}{t^{\frac{7}{2}}}\right)e^{-\frac{x^2}{4Dt}}\left(1-\frac{x^2}{3Dt}+\frac{x^4}{60{\left(Dt\right)}^2}\right),\hfill \\ \hfill C(x,t)& =& \left(\frac{{\kappa }_{1}x}{t^{\frac{9}{2}}}\right)e^{-\frac{x^2}{4Dt}}\left(1-\frac{x^2}{2Dt}+\frac{x^4}{20{\left(Dt\right)}^2}-\frac{x^6}{840{\left(Dt\right)}^3}\right).\hfill \end{array}$$

(10)

Figure 1 shows the given five shape functions. Functions with $\alpha >0$ clearly show a decaying and oscillatory behavior in terms of $\eta$. Figure 2 shows six $C(x,t)$s for different $\alpha$s; for generality, we also show two solutions for half-integer $\alpha$s. The quick decay and the slight oscillations are clear to see in all cases. Due to the linearity of the diffusion equation, any linear combination of Equation (5) is automatically a solution, also enriching the possible mathematical structure of the diffusion process.

To complete our investigation, we have to analyse which kind of initial and boundary value problems can be satisfied by these solutions. Our answer is twofold: Firstly, if one of the above solutions (10) is explicitly given, with a fixed numerical value of $c_1, c_2, D$ and ${\kappa }_i$, then we may fix an arbitrary time point as $t_0=t$, and the corresponding $C\left(x\right)$ curve can be defined as the initial problem. This curve is presented in Figure 2 for $\alpha =1$. We focus on physically relevant boundary values, which mean, asymptotically for $x\to \pm \infty$, the solutions $C\left(\right)\to 0$, to which one may arrive if $\alpha >0$.

Secondly, even the general initial value problem can be handled with the help of the Green’s functions formalism. According to the standard theory of Green’s functions the solution of the diffusion Equation (1) can be obtained via the following convolution integral

$$C(x,t)=\frac{1}{\sqrt{\pi t}}{\int }_{-\infty }^{+\infty }w\left(x_0\right)G(x-x_0)d{x}_0$$

(11)

where $\left(x_0\right)$ contains the initial condition of the problem, ${C|}_{t=0}=w\left(x_0\right)$.

The Green function for diffusion is well-known and can be found in numerous mathematical textbooks, such as [70,71,72,73],

$$G(x-x_0)=exp\left[-\frac{{(x-x_0)}^2}{4tD}\right],$$

(12)

which is the fundamental solution of diffusion.

It is now straightforward to use our new functions (10) in the convolution integral as a Green’s function to derive solutions for arbitrary initial conditions ${C|}_{t=0}=w\left(x_0\right)$. So, in this sense, we can give the most general Green’s functions

$$\begin{array}{cc}\hfill C(x,t)=& \frac{{\kappa }_n}{t^{\alpha }}{\int }_{-\infty }^{+\infty }w\left(x_0\right)·\frac{(x-x_0)}{t^{1/2}}·e^{-\frac{{(x-x_0)}^2}{4Dt}}\left(c_{1}M\left[1-\alpha ,\frac{3}{2},\frac{{(x-x_0)}^2}{4Dt}\right]+\right.\\ & \left.c_{2}U\left[1-\alpha ,\frac{3}{2},\frac{{(x-x_0)}^2}{4Dt}\right]\right)d{x}_0\end{array}$$

(13)

where ${\kappa }_n$ stands for the proper normalization. We see in the following that for some special forms of the initial conditions, such as polynomials, Gaussian, Sinus, or Cosines, the convolution integral can be conducted analytically. It is clear that, for $\alpha =1/2$, we automatically obtain back the Gaussian Green’s function of (12).

Note that for positive integer values of $\alpha$ both Kummer’s U and Kummer’s M functions contain the same polynomials the only difference is just an overall normalization constant. It can be shown, as it was visualized in our last study [1], that for negative $\alpha$s the shape functions $f\left(\eta \right)$ are divergent for large $\eta$s. In the regime of $0\le \alpha \le 1$ the solutions are similar to the “usual Gaussian” solutions, positive on the whole axis and goes to zero at infinite $\eta$. These solutions can be understood as different probability distribution functions and the corresponding expectation values, variance, higher moments, skewness, kurtosis, and other probabilities can be evaluated.

For $\alpha >1$, the shape functions show some oscillations have finite negative values at some arguments and have a quick decay at large arguments $\eta$. The norm of the functions are still finite but, due to the oscillations such functions, cannot be interpreted as probability distributions.

To present a solution for a given initial value $w\left(x_0\right)$, the numerical values of the normalization constants ${\kappa }_{\alpha }$ have to be given. We apply the $L^1$ normalization with the definition of

$$1={\kappa }_{\alpha }{\int }_0^{\infty }\eta ·e^{-\frac{{\eta }^2}{4D}}M\left[1-\alpha ,\frac{3}{2},\frac{{\eta }^2}{4D}\right]d\eta .$$

(14)

arriving to the numerical values of: ${\kappa }_{1,2,3,4}=(\frac{1}{2},\frac{3}{2},\frac{5}{2},\frac{7}{2})$. In some cases, the $L^2$ normalizations have to be used with the coefficients of ${\kappa }_{1,2,3,4}=\left(\frac{\sqrt{2}}{\sqrt[4]{2\pi }},\frac{1}{5}\frac{\sqrt{120}}{\sqrt[4]{2\pi }},\frac{1}{21}\frac{\sqrt{21·160}}{\sqrt[4]{2\pi }},\frac{1}{429}\frac{\sqrt{429·4480}}{\sqrt[4]{2\pi }}\right)$

As a rather physical example, we study the $\alpha =1, c_1=1, c_2=0$ case for the initial condition of

$$w\left(x_0\right)=\frac{\mathrm{Heaviside}(x_0-1)·\mathrm{Heaviside}(11-x_0)·(-{[x_0-6]}^2+25)}{25}$$

(15)

which is an up-shifted upside down parabola cut at the $x_0=+1,+11$ visualized in Figure 3. Note that the $w(x_0\to -\infty )=0$ and the $w(x_0=+\infty )=0$ boundary conditions are fulfilled. The solution obtained with the convolution integral of (13)

$$\begin{array}{c}\hfill C(x,t)=\frac{1}{t}·\left(\frac{2t}{25}\sqrt{\pi }(x-6)\left[erf\left\{\frac{x-1}{2\sqrt{t}}\right\}-erf\left\{\frac{x-11}{2\sqrt{t}}\right\}\right]+\right.\\ \hfill \left.\frac{4}{25}{t}^{\frac{3}{2}}\left[e^{-\frac{1}{4t}{\left\{x-1\right\}}^2}-e^{-\frac{1}{4t}{\left\{x-11\right\}}^2}\right]\right)\end{array}$$

(16)

For a better understanding, this result is presented in Figure 3. Note that the solution function $C(x,t)$ fulfills the $C(x_0\to -\infty )=0$ condition and the $C(x_0\to +\infty )=0$ asymptotic condition as well. The convolution integral of (13) results a single-valued function of (16) therefore the derived solution is unique.

2.2. An Interesting Ansatz

To have a mathematically complete analysis of the possible Ansatz we have to investigate the “inverse self-similar Ansatz” in the form of:

$$C(x,t)=x^{-\alpha }g\left(\frac{t}{x^{\beta }}\right)=x^{-\alpha }g\left(\omega \right).$$

(17)

Now, the role of the temporal and spatial variables is interchanged. The physical interpretation of this new trial function is hard to see; until now, we cannot find any kind of reasonable physical explanation of this new Ansatz Equation (17). (To avoid confusion with the original Ansatz, we use the $g\left(\omega \right)$ notation for this case.) After having conducted the usual derivation and algebraic steps, we arrive at the relations of

$$\alpha =\mathrm{arbitrary}\mathrm{real}\mathrm{number},\beta =2.$$

(18)

The obtained ODE looks similar but obviously contains more terms then the previous ones

$$4D{\omega }^2{g}^{″}+\omega g^{\prime }[-2\alpha D-4D+2(\alpha -1)D]-g^{\prime }+D\alpha (\alpha -1)g=0.$$

(19)

The solutions for the shape functions can be evaluated with the help of the usual Kummer’s and exponential functions in the form of

$$\begin{array}{ll}g=& c_1{e}^{-\frac{1}{4D\omega }}{\omega }^{\left(\frac{5}{4}-\frac{\sqrt{25-4{\alpha }^2+4\alpha }}{4}\right)}M\left(\frac{9}{4}+\frac{\sqrt{25-4{\alpha }^2+4\alpha }}{4},\frac{\sqrt{25-4{\alpha }^2+4\alpha }}{2},\frac{1}{4D\omega }\right)+\\ & c_2{e}^{-\frac{1}{4D\omega }}{\omega }^{\left(\frac{5}{4}-\frac{\sqrt{25-4{\alpha }^2+4\alpha }}{4}\right)}U\left(\frac{9}{4}+\frac{\sqrt{25-4{\alpha }^2+4\alpha }}{4},\frac{\sqrt{25-4{\alpha }^2+4\alpha }}{2},\frac{1}{4D\omega }\right).\end{array}$$

(20)

The two parameters of the Kummer functions should be real therefore $\alpha$ must lie in the interval of $[\frac{1}{2}-\frac{\sqrt{26}}{2},\frac{1}{2}-\frac{\sqrt{26}}{2}]$ which is approximately $-2.1<\alpha <3.1$. Our experience showed, that basically for any numerical $\alpha$ values the shape functions have a power-law dependence such as $f\left(\eta \right)\propto {\eta }^n$ where $0<n<1$ and the $C(x,t)$s are divergent at large x arguments. Therefore, we found no physically reasonable solutions, therefore present no figures for Equation (20).

2.3. A Generalization

At this point, it is straightforward to try the generalized form of the self-similar Ansatz

$$C(x,t)=a\left(t\right)·h\left(\frac{x}{b\left(t\right)}\right)=a\left(t\right)·h\left(\omega \right),$$

(21)

where all $a,b$ and h are continuous real functions with existing continuous first temporal and second spatial derivatives and $\omega$ is the new reduced independent variable. Note that now the functions which are responsible for the time decay and spreading have a general form. Instead of the power law dependencies $t^{-\alpha }$ and $t^{\beta }$, we apply $a\left(t\right)$ and $b\left(t\right)$. By calculating the needed temporal and spatial derivatives and plugging back to the original diffusion equation, we arrive to the ODE of

$$a_{t}h-\left(\frac{a{b}_t}{b}\right)\omega h^{\prime }=\frac{Da}{b^2}{h}^{″},$$

(22)

where prime means derivation in respect to $\omega$ and subscript t in respect to time. This equation should be an ODE for $h\left(\omega \right)$; therefore, the coefficients of h and $h^{\prime }$ should be independent of time therefore should be equal to constants, so Equation (22) become:

$$h-\omega h^{\prime }=D{h}^{″},$$

(23)

It has the solution of

$$h\left(\omega \right)=C_1\omega +C_2\left(2D{e}^{-\frac{{\omega }^2}{2D}}+\sqrt{2\pi D}\omega ·erf\left[\frac{\sqrt{2}\omega }{2\sqrt{D}}\right]\right).$$

(24)

The equations of constraints have to be fulfilled as well:

$$b^2{a}_t=a·b·b_t=a,b^2\ne 0.$$

(25)

The corresponding solutions can be easily obtained by direct integration and read:

$$a\left(t\right)=\pm \sqrt{2t+c_1},b\left(t\right)=c_2·\sqrt{2t+c_1}.$$

(26)

Using the original definitions of the Ansatz (21) we can obtain the final solution in the form of:

$$\begin{array}{c}\hfill C(x,t)=(\pm \sqrt{2t+c_1})·\left(\frac{C_{1}x}{c_2·\sqrt{2t+c_1}}+C_2\left[2D{e}^{-\frac{x^2}{2D{c}_2^2(2Dt+c_1)}}+\right.\right.\\ \hfill \left.\left.\sqrt{2\pi D}·\frac{x}{c_2·\sqrt{2t+c_1}}·erf\left\{\frac{\sqrt{2}x}{2c_2\sqrt{D(2t+c_1)}}\right\}\right]\right).\end{array}$$

(27)

where $c_1, c_2, C_1, C_2$ are integration constants. Choosing $C_1=c_1=0$, we obtain back the usual solution which is a sum of a Gaussian and and error function. Note that this is equivalent to the self-similar solution where $\alpha =\beta =1/2$. It is instructive to see that a more general form of the Ansatz does not necessarily lead to a larger class of solutions. The functions $a\left(t\right)$ and $b\left(t\right)$ do not have additional freedom, the power laws however have two free parameters—$\alpha$ and $\beta$ two real numbers—which expand the class of possible solutions. To the best of our best knowledge, this relatively simple derivation is not yet published or widely known in the scientific community. At this point, we have to note that, in our former study [1], we investigated the traveling-profile Ansatz from [32], which interpolates between the traveling wave and the self-similar trial functions in the form of $C(x,t)=a\left(t\right)·h\left(\right[x-b\left(t\right)/c\left(t\right)]=a(f\left)h\right(\omega )$, where $a\left(t\right),b\left(t\right)$ and $c\left(t\right)$ are arbitrary continuous functions, with existing first derivatives. The derived results were very similar to the Equation (5).

2.4. A Redefinition of Variables

In the following, we use the conjecture that the f function can be written as:

$$f\left(\eta \right)=\eta e^{-\frac{{\eta }^2}{4D}}g\left(\eta \right).$$

(28)

It is worth checking this form to derive possible new results. The derivative of the function $f\left(\eta \right)$ is:

$$f^{\prime }\left(\eta \right)=e^{-\frac{{\eta }^2}{4D}}g\left(\eta \right)-\eta \frac{\eta }{2D}{e}^{-\frac{{\eta }^2}{4D}}+\eta e^{-\frac{{\eta }^2}{4D}}{g}^{\prime }\left(\eta \right).$$

(29)

The second derivative of function f reads as follows:

$$\begin{array}{cc}& f^{″}\left(\eta \right)=\\ & e^{-\frac{{\eta }^2}{4D}}\left[-\frac{-\eta }{2D}g\left(\eta \right)+g^{\prime }\left(\eta \right)-\frac{-\eta }{D}g\left(\eta \right)+\eta \frac{{\eta }^2}{4D^2}g\left(\eta \right)-\frac{{\eta }^2}{2D}{g}^{\prime }\left(\eta \right)+g^{\prime }\left(\eta \right)\right.\\ & \left.-\frac{{\eta }^2}{2D}{g}^{\prime }\left(\eta \right)+\eta g^{″}\left(\eta \right)\right].\end{array}$$

(30)

Inserting these functions into the equation, while keeping in mind that $\beta =\frac{1}{2}$

$$-\alpha f-\frac{1}{2}\eta f^{\prime }=D{f}^{″},$$

(31)

we obtain for $g=g\left(\eta \right)$

$$-\alpha \eta g=2D{g}^{\prime }\left(\eta \right)-\eta g-\frac{{\eta }^2}{2}{g}^{\prime }+\eta g^{″}D.$$

(32)

Reordering the terms leads to

$$\eta g^{″}+2g^{\prime }-\frac{{\eta }^2}{2D}{g}^{\prime }+(\alpha -1)\frac{\eta }{D}g=0.$$

(33)

The solutions read

$$g\left(\eta \right)=c_{1}M\left[1-\alpha ,\frac{3}{2},\frac{{\eta }^2}{4D}\right]+c_{2}U\left[1-\alpha ,\frac{3}{2},\frac{{\eta }^2}{4D}\right],$$

(34)

note that these are the same solutions as for the self-similar Ansatz, only in a separated form. These two examples clearly show that there is a relatively large freedom to define an Ansatz, but only few of them lead to reasonable new solutions.

2.5. Using Various Series Expansions of $f\left(\eta \right)$

As a possible generalization of the self-similar Ansatz, we may define the following infinite power series of

$$C(x,t)=\sum _{i=1}^{\infty }{a}_i·t^{-{\alpha }_i}·{\left(f\left[\eta \right]\right)}^i,$$

(35)

where $a_i$s and ${\alpha }_i$s are arbitrary real numbers. As first (and most logical case) just take the following two terms of:

$$\begin{array}{c}\hfill C(x,t)=a{t}^{-\alpha }f\left(\frac{x}{t^{\beta }}\right)+b{t}^{-\alpha }f{\left(\frac{x}{t^{\beta }}\right)}^2=a{t}^{-\alpha }f\left(\eta \right)+b{t}^{-\alpha }f{\left(\eta \right)}^2,\end{array}$$

(36)

the role of $\alpha$ and $\beta$ is still the same, and the role of a and b are to fix the ratio of the two components or—more importantly—to turn-on or turn-off one of them. It is clear that if we want to derive an ODE for the shape function the argument $\eta$ should remain on the same first power.

After some relatively simple algebraic steps we got the usual constraints for the two exponents

$$\alpha =\mathrm{arbitrary}\mathrm{real}\mathrm{number},\beta =1/2.$$

(37)

The derived ODE is

$$-a\alpha f-\frac{a}{2}\eta f^{\prime }-b(\alpha f^2-\eta f{f}^{\prime })=D(a{f}^{″}+2b[f^{\prime 2}+f{f}^{″}]),$$

(38)

for general $\alpha$, the solution is cumbersome containing large number of Kummer’s M and Kummer’s U functions and given in the Appendix A at the end of the paper. However, for some given small values $\alpha =1, \pm 1/2, \pm 1, 3/2, 5/2$, the results can be expressed with the help of Gaussians and with the error function. The overall and complete function test of the solutions of Equation (38) is a hard question due to the five parameters of $\{D,a,b,c_1,c_2\}$ ($c_1$ and $c_2$ stand for the integration constants).

For $\alpha =1/2$ and for arbitrary other real parameters the result reads the follows:

$$\begin{array}{cc}& f=\\ & -\frac{a{e}^{\frac{{\eta }^2}{4D}}\sqrt{-\frac{1}{D}}\pm \sqrt{-e^{\frac{{\eta }^2}{4D}}\left[a^2{e}^{\frac{{\eta }^2}{4D}}-4b{c}_{1}D\sqrt{-\frac{\pi }{D}}+4Db{c}_2\sqrt{-\frac{\pi }{D}}erf\left\{\frac{1}{2}\sqrt{\frac{-1}{D}}\eta \right\}\right]/D}}{2b{e}^{\frac{{\eta }^2}{4D}}\sqrt{-\frac{1}{D}}},\end{array}$$

(39)

where erf is the usual error function. Note that this solution let $(a=0\&bϵ\mathbb{R})$, but not the opposite case. Therefore, it is impossible to obtain back the fundamental or Gaussian solution.

Figure 4 shows the shape functions of Equation (39) for $a=2, b=1$ and for $a=0, b=1$ and the corresponding final $C(x,t)$s as well. Note the remarkable new feature when the $f^2\left(\eta \right)$ term is considered alone; the solutions have a compact support. In this sense, a linear PDE is reduced with a non-linear Ansatz to a non-linear ODE having non-linear properties. This solution is definitely unknown in the scientific community. We might begin to speculate about that even the regular diffusion equation could describe non-regular diffusion phenomena such as the porous media equation [20].

If we consider the quadratic term in (36) alone, we obtain a solution which is just a little more simplified than the one provided in the Appendix A. Therefore, we skip to presenting it.

After this idea, we may go a bit further, considering additional generalized forms such as

$$C(x,t)=t^{-\alpha }f\left(\frac{x}{t^{\beta }}\right)+\sum _{i=1}^{\infty }{a}_i·t^{-{\alpha }_i}·{\eta }^i·{\left(f\left[\eta \right]\right)}^i,$$

(40)

Keeping only the first two terms, we arrive to

$$C(x,t)=t^{-\alpha }f\left(\frac{x}{t^{\beta }}\right)+a{t}^{-\alpha }\eta f\left(\frac{x}{t^{\beta }}\right)=t^{-\alpha }f\left(\eta \right)+a{t}^{-\alpha }\eta f\left(\eta \right),$$

(41)

which has the solutions of

$$f\left(\eta \right)=\frac{\left(e^{-\frac{{\eta }^2}{4D}}\left[c_{1}M\left\{1-\alpha ,\frac{3}{2},\frac{{\eta }^2}{4D}\right\}\eta +c_{2}U\left\{1-\alpha ,\frac{3}{2},\frac{{\eta }^2}{4D}\right\}\eta \right]\right)}{a+b\eta }.$$

(42)

Note that, for $a,b>0$, the only change is only a little different in terms of the scaling of the results. However, if the $a·b<0$, the solution has an obvious singularity, which makes it interesting, but nonphysical; therefore, for now, we ignore this. Last along this line of thought, we may try an Ansatz with the shape of:

$$C(x,t)=a{t}^{-\alpha }f\left(\frac{x}{t^{\beta }}\right)+b{t}^{-\alpha }f{\left(\frac{x}{t^{\beta }}\right)}^{1/2},$$

(43)

which, unfortunately, provides no analytic solutions. Generally, higher order terms in power expansions provide higher degree non-linear second-oder ODEs, which rarely have analytic solutions.

2.6. Arbitrary Self-Similar Exponents

Lastly, we arrived at a question which leads us out of the problem of regular diffusion. We might ask (if nothing else, only for the sake of completeness): what does it mean when both $\alpha$, $\beta$ are arbitrary real numbers dictating the ODE of

$$-\alpha f-\beta \eta f^{\prime }=D{f}^{″}.$$

(44)

where D is still the usual diffusion coefficient. The solutions remain similar

$$f\left(\eta \right)=\eta e^{-\frac{\beta {\eta }^2}{2D}}\left(c_{1}M\left[\frac{2\beta -\alpha }{2\beta },\frac{3}{2},\frac{\beta {\eta }^2}{2D}\right]+c_{2}U\left[\frac{2\beta -\alpha }{2\beta },\frac{3}{2},\frac{\beta {\eta }^2}{2D}\right]\right).$$

(45)

With some easy reasoning, we can find out the the original form of PDE. An additional $t^{2\beta -1}$ time dependence has to be included to cancel the usual $\beta =1/2$ constraint. Therefore, the starting PDE reads

$$\frac{\partial C(x,t)}{\partial t}=D·t^{2\beta -1}·\frac{{\partial }^{2}C(x,t)}{\partial x^2}.$$

(46)

The role of the $\alpha$ parameter—which is responsible for the temporal decay—could be easily investigated, as we saw above; however, now the role of the $\beta$—which is responsible for the spreading—was hidden until now. The solution functions are even functions; therefore, we only concentrate on positive arguments and investigate the Kummer M function only. From the formula of (45) two conditions are easy to notice. The first one is that $\beta \ne 0$ this is due to the denominator of the first parameter in the Kummer function, and the second one is that for $\beta <0$ the exponential multiplier function goes to infinity at large arguments. We ignore such nonphysical solutions.

The next figure, Figure 5a, presents various $f\left(\eta \right)$ shape functions for $\alpha =1$. Three cases can be distinguished:

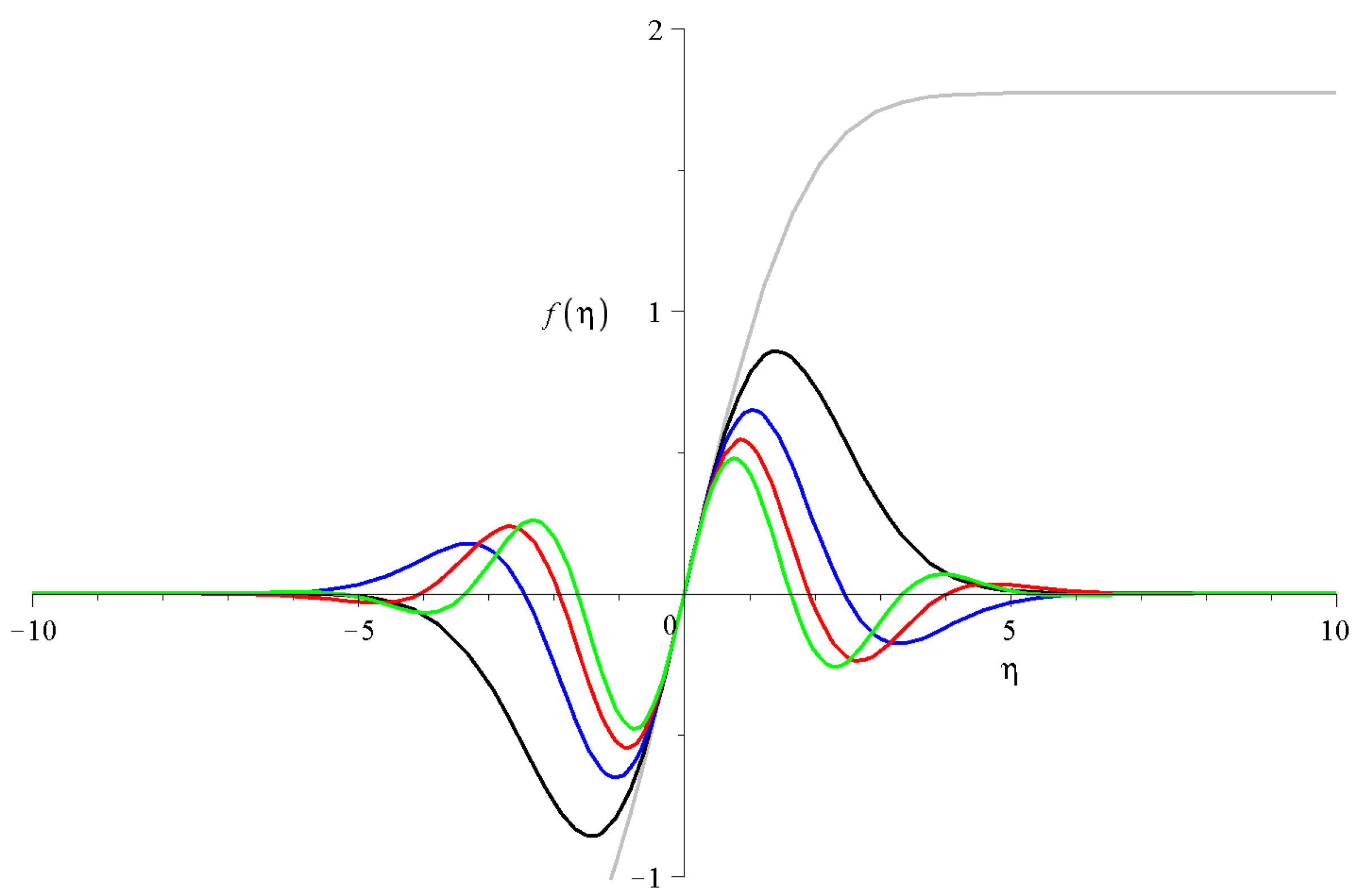
• When $2\beta <\alpha$, the functions have zero transitions and show oscillatory behavior.
• When $2\beta =\alpha$, Kummer’s functions are equal to unity; hence, the solution is purely Gaussian, with the quickest possible decay to zero.
• When $2\beta >\alpha$, the larger the beta the lower the global maximum and the slower the decay at large argument. The numerical value of $\alpha$ is irrelevant if it is positive. It is interesting that for negative $\alpha$s and for positive $\beta$s the total solution is again divergent at large arguments. For completeness, we show the $C(x,t)$ for $\alpha =1$ and $\beta =1$ on Figure 5b.

One can see, that for sufficiently large values of $\beta$, the shape function f has a maximum, which is followed by a relatively slow decay. For $\beta =1/4$, there is one root of the shape function $f\left(\eta \right)$, and correspondingly of the function $C(x,t)$. This shows that for values $\beta$ smaller than $1/2$, the existence of nontrivial fluctuations in the value of $C(x,t)$ is possible, which means that it may become smaller than the average of the background. If $\beta$ is smaller than $1/4$, more roots of the shape function $f\left(\eta \right)$ are possible, on Figure 6. These values of $\beta$ shows a special behavior of the system, where the nontrivial diffusive effects may lead to temporal mass concentrations in case of mass diffusion.

3. Summary and Outlook

We investigated the regular diffusion equation with the usual self-similar Ansatz and discussed all the solutions which are achievable beyond the Gaussian one. Most of the solutions can be described with the help of Kummer’s M and Kummer’s U functions. In certain cases, the linear combination of these functions, which lead to solutions, are explicitly evaluated. For some special parameters, the solutions go over the Hermite polynomials. In the second part of the study, we presented additional solutions which all can be derived from different modifications of the original self-similar Ansatz. Such solutions are again far from being well-known among the scientific community and therefore have to be published and discussed in detail. At the end of our manuscript, we investigated a special diffusion process which has time-dependent diffusion coefficient. This time dependence may be associated to the parameter of spreading, and certain analytic forms can be obtained. Work is in progress to analyze spatial and temporal dependent diffusion equations, which will be the topic of out next study. In the long run, we would like to also investigate reaction–diffusion equations (even with non-constant diffusion coefficients). Our experience so far suggests that numerous existing models can have new solutions with interesting features.