Non-Relativistic Treatment of the 2D Electron System Interacting via Varshni–Shukla Potential Using the Asymptotic Iteration Method
Abstract
:1. Introduction
2. Theory and Solutions
3. Magnetotransport and Thermal Properties of Varshni–Shukla Potential (V–SP)
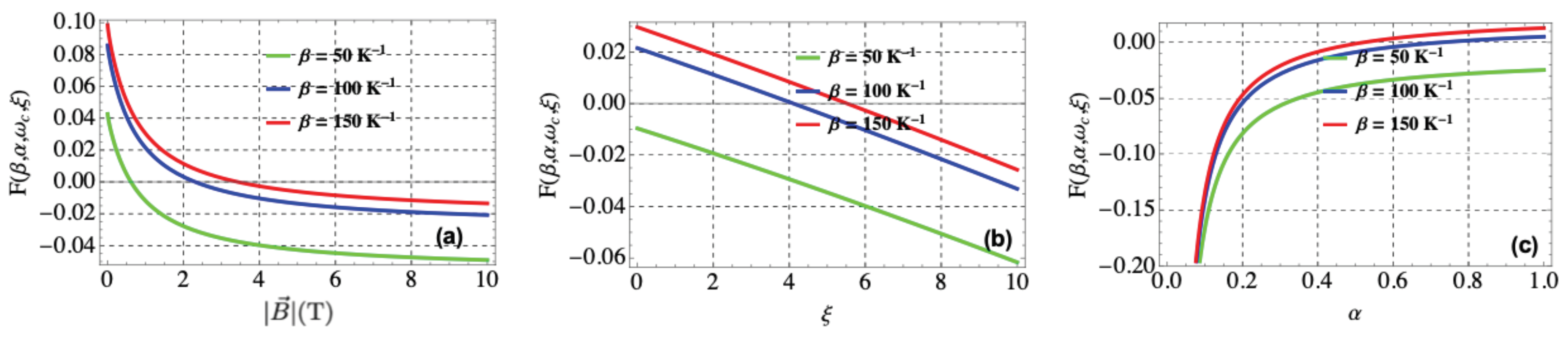
3.1. Free Energy
3.2. Entropy
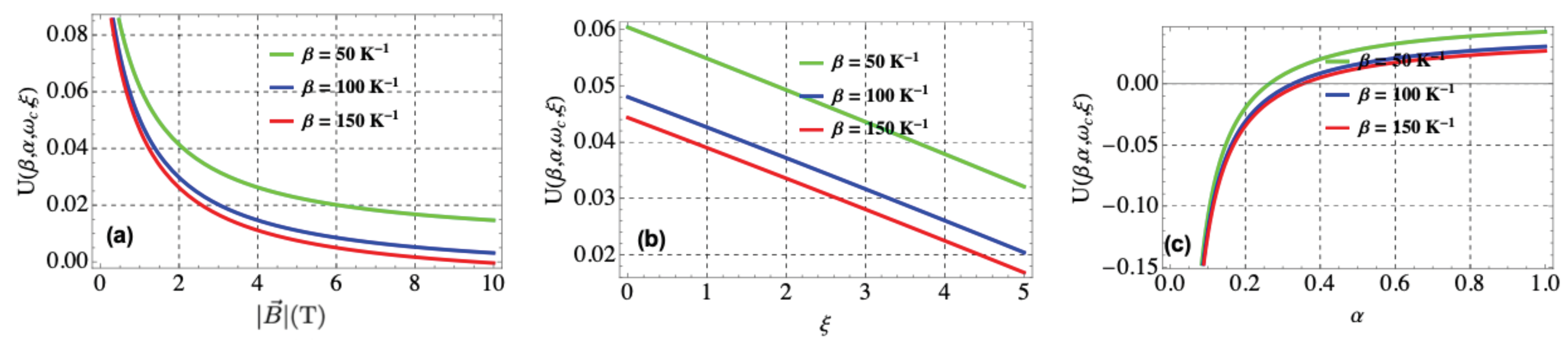
3.3. Internal or Mean Energy
3.4. Heat Capacity
3.5. Magnetotransport Properties
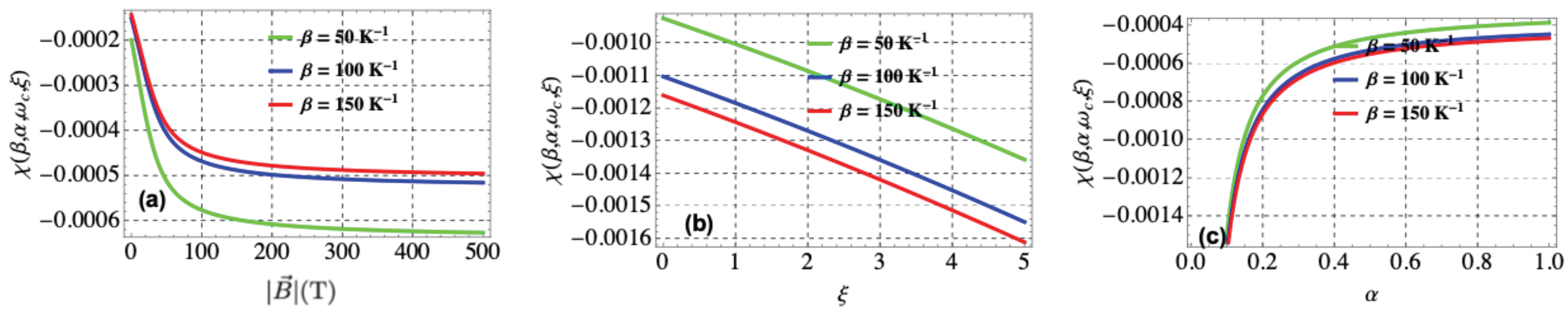
3.5.1. Magnetic Susceptibility
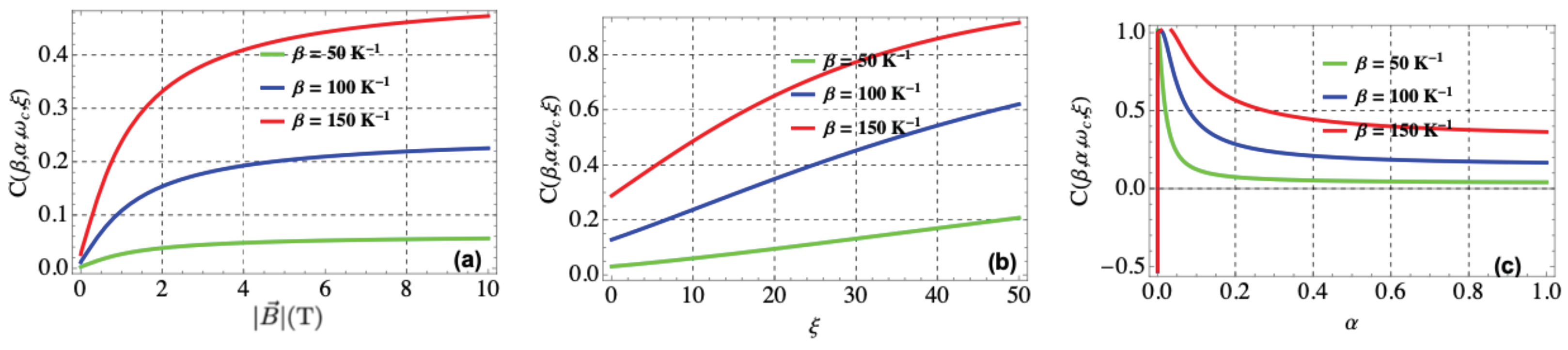
3.5.2. Persistent Current
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Marques, G.D.A.; Bezerra, V.B. Hydrogen atom in the gravitational fields of topological defects. Phys. Rev. D 2002, 66, 105011. [Google Scholar] [CrossRef] [Green Version]
- Bakke, K.; Furtado, C. On the interaction of the Dirac oscillator with the Aharonov–Casher system in topological defect backgrounds. Ann. Phys. 2013, 336, 489–504. [Google Scholar] [CrossRef] [Green Version]
- Bakke, K.; Ribeiro, L.R.; Furtado, C.; Nascimento, J.R. Landau quantization for a neutral particle in the presence of topological defects. Phys. Rev. D 2009, 79, 024008. [Google Scholar] [CrossRef] [Green Version]
- Carvalho, J.; Furtado, C.; Moraes, F. Dirac oscillator interacting with a topological defect. Phys. Rev. A 2011, 84, 032109. [Google Scholar] [CrossRef]
- Marques, G.D.A.; Bezerra, V.B. Non-relativistic quantum systems on topological defects spacetimes. Class. Quantum Gravity 2002, 19, 985. [Google Scholar] [CrossRef]
- Hassanabadi, H.; Hosseinpour, M. Thermodynamic properties of neutral particle in the presence of topological defects in magnetic cosmic string background. Eur. Phys. J. C 2016, 76, 1–7. [Google Scholar] [CrossRef] [Green Version]
- Castano-Yepes, J.D.; Amor-Quiroz, D.A.; Ramirez-Gutierrez, C.F.; Gómez, E.A. Impact of a topological defect and Rashba spin–orbit interaction on the thermo-magnetic and optical properties of a 2D semiconductor quantum dot with Gaussian confinement. Phys. E Low-Dimens. Syst. Nanostruct. 2019, 109, 59–66. [Google Scholar] [CrossRef] [Green Version]
- Hosseinpour, M.; Andrade, F.M.; Silva, E.O.; Hassanabadi, H. Scattering and bound states for the Hulthén potential in a cosmic string background. Eur. Phys. J. C 2017, 77, 1–6. [Google Scholar]
- Nwabuzor, P.; Edet, C.; Ikot, A.N.; Okorie, U.; Ramantswana, M.; Horchani, R.; Abdel-Aty, A.-H.; Rampho, G. Analyzing the Effects of Topological Defect (TD) on the Energy Spectra and Thermal Properties of LiH, TiC and I2 Diatomic Molecules. Entropy 2021, 23, 1060. [Google Scholar] [CrossRef]
- Edet, C.O.; Ikot, A.N. Effects of Topological Defect on the Energy Spectra and Thermo-magnetic Properties of CO Diatomic Molecule. J. Low Temp. Phys. 2021, 203, 84–111. [Google Scholar] [CrossRef]
- Aharonov, Y.; Bohm, D. Significance of Electromagnetic Potentials in the Quantum Theory. Phys. Rev. (Ser. I) 1959, 115, 485–491. [Google Scholar] [CrossRef]
- Edet, C.; Nwbabuzor, P.; Ettah, E.; Duque, C.; Ali, N.; Ikot, A.; Mahmoud, S.; Asjad, M. Magneto-transport and thermal properties of the Yukawa potential in cosmic string space-time. Results Phys. 2022, 39, 105749. [Google Scholar] [CrossRef]
- Edet, C.O.; Amadi, P.O.; Ettah, E.B.; Ali, N.; Asjad, M.; Ikot, A.N. The magnetocaloric effect, thermo-magnetic and transport properties of LiH diatomic molecule. Mol. Phys. 2022, 120, e2059025. [Google Scholar] [CrossRef]
- Abu-Shady, M.; Edet, C.; Ikot, A. Non-relativistic quark model under external magnetic and Aharanov–Bohm (AB) fields in the presence of temperature-dependent confined Cornell potential. Can. J. Phys. 2021, 99, 1024–1031. [Google Scholar] [CrossRef]
- Khordad, R. Effect of magnetic field on linear and nonlinear optical properties in a parabolic cylindrical quantum dot. J. Opt. 2013, 42, 83–91. [Google Scholar] [CrossRef]
- Al, E.B.; Kasapoglu, E.; Sari, H.; Sökmen, I. Zeeman splitting, Zeeman transitions and optical absorption of an electron confined in spherical quantum dots under the magnetic field. Philos. Mag. 2020, 101, 117–128. [Google Scholar] [CrossRef]
- Ikhdair, S.M.; Falaye, B.J.; Hamzavi, M. Nonrelativistic molecular models under external magnetic and AB flux fields. Ann. Phys. 2015, 353, 282–298. [Google Scholar] [CrossRef] [Green Version]
- Ikot, A.N.; Edet, C.; Amadi, P.O.; Okorie, U.S.; Rampho, G.J.; Abdullah, H.Y. Thermodynamic properties of Aharanov–Bohm (AB) and magnetic fields with screened Kratzer potential. Eur. Phys. J. D 2020, 74, 1–13. [Google Scholar] [CrossRef]
- M’Zerd, S.; El Haouari, M.; Talbi, A.; Feddi, E.; Mora-Ramos, M. Impact of electron-LO-phonon correction and donor impurity localization on the linear and nonlinear optical properties in spherical core/shell semiconductor quantum dots. J. Alloys Compd. 2018, 753, 68–78. [Google Scholar] [CrossRef]
- Edet, C.O.; Ettah, E.B.; Aljunid, S.A.; Endut, R.; Ali, N.; Ikot, A.N.; Asjad, M. Global Quantum Information-Theoretic Measures in the Presence of Magnetic and Aharanov-Bohm (AB) Fields. Symmetry 2022, 14, 976. [Google Scholar] [CrossRef]
- Edet, C.O.; Lima, F.C.E.; Almeida, C.A.S.; Ali, N.; Asjad, M. Quantum Information of the Aharanov–Bohm Ring with Yukawa Interaction in the Presence of Disclination. Entropy 2022, 24, 1059. [Google Scholar] [CrossRef]
- Tavares, C.; Oliveira, S.; Fernandes, V.; Postnikov, A.; Vasilevskiy, M.I. Quantum simulation of the ground-state Stark effect in small molecules: A case study using IBM Q. Soft Comput. 2021, 25, 6807–6830. [Google Scholar] [CrossRef]
- Rastegar-Sedehi, H.R. Magnetocaloric effect in Rashba spin–orbit coupling and Zeeman splitting of a narrow nanowire quantum dot. Eur. Phys. J. Plus 2021, 136, 1–8. [Google Scholar] [CrossRef]
- Rampho, G.J.; Ikot, A.N.; Edet, C.O.; Okorie, U.S. Energy spectra and thermal properties of diatomic molecules in the presence of magnetic and AB fields with improved Kratzer potential. Mol. Phys. 2020, 119, e1821922. [Google Scholar] [CrossRef]
- Edet, C.O.; Amadi, P.O.; Onyeaju, M.C.; Okorie, U.S.; Sever, R.; Rampho, G.J.; Abdullah, H.Y.; Salih, I.H.; Ikot, A.N. Thermal Properties and Magnetic Susceptibility of Hellmann Potential in Aharonov–Bohm (AB) Flux and Magnetic Fields at Zero and Finite Temperatures. J. Low Temp. Phys. 2020, 202, 83–105. [Google Scholar] [CrossRef]
- Karayer, H. Study of the radial Schrödinger equation with external magnetic and AB flux fields by the extended Nikiforov–Uvarov method. Eur. Phys. J. Plus 2020, 135, 1–10. [Google Scholar] [CrossRef]
- Edet, C.O.; Ikot, A.N. Shannon information entropy in the presence of magnetic and Aharanov–Bohm (AB) fields. Eur. Phys. J. Plus 2021, 136, 1–11. [Google Scholar] [CrossRef]
- Oluwadare, O.J.; Oyewumi, K.J. Scattering state solutions of the Duffin-Kemmer-Petiau equation with the Varshni potential model. Eur. Phys. J. A 2017, 53, 1–6. [Google Scholar] [CrossRef]
- Oluwadare, O.J.; Oyewumi, K.J. The semi-relativistic scattering states of the two-body spinless Salpeter equation with the Varshni potential model. Eur. Phys. J. Plus 2017, 132, 277. [Google Scholar] [CrossRef] [Green Version]
- Oluwadare, O.; Oyewumi, K.J. Scattering states solutions of Klein–Gordon equation with three physically solvable potential models. Chin. J. Phys. 2017, 55, 2422–2435. [Google Scholar] [CrossRef] [Green Version]
- Varshni, Y.P. Comparative study of potential energy functions for diatomic molecules. Rev. Mod. Phys. 1957, 29, 664. [Google Scholar] [CrossRef] [Green Version]
- Inyang, E.P.; Inyang, E.P.; William, E.S.; Ibekwe, E.E. Study on the applicability of Varshni potential to predict the mass-spectra of the Quark-antiquark systems in a non-relativistic framework. Jordan J. Phys. 2021, 14, 337–345. [Google Scholar]
- Bayrak, O.; Boztosun, I. Bound state solutions of the Hulthon potential by using the asymptotic iteration method. Phys. Scr. 2007, 76, 92. [Google Scholar] [CrossRef]
- Greene, R.L.; Aldrich, C. Variational wave functions for a screened Coulomb potential. Phys. Rev. A 1976, 14, 2363–2366. [Google Scholar] [CrossRef]
- Ciftci, H.; Hall, R.; Saad, N. Asymptotic iteration method for eigenvalue problems. J. Phys. A Math. Gen. 2003, 36, 11807–11816. [Google Scholar] [CrossRef] [Green Version]
- Falaye, B.J. Any l-state solutions of the Eckart potential via asymptotic iteration method. Cent. Eur. J. Phys. 2012, 10, 960–965. [Google Scholar] [CrossRef] [Green Version]
- Jia, C.-S.; Wang, C.-W.; Zhang, L.-H.; Peng, X.-L.; Zeng, R.; You, X.-T. Partition function of improved Tietz oscillators. Chem. Phys. Lett. 2017, 676, 150–153. [Google Scholar] [CrossRef]
- Jia, C.-S.; Zhang, L.-H.; Peng, X.-L.; Luo, J.-X.; Zhao, Y.-L.; Liu, J.-Y.; Guo, J.-J.; Tang, L.-D. Prediction of entropy and Gibbs free energy for nitrogen. Chem. Eng. Sci. 2019, 202, 70–74. [Google Scholar] [CrossRef]
- Wang, J.; Jia, C.-S.; Li, C.-J.; Peng, X.-L.; Zhang, L.-H.; Liu, J.-Y. Thermodynamic Properties for Carbon Dioxide. ACS Omega 2019, 4, 19193–19198. [Google Scholar] [CrossRef] [Green Version]
- Edet, C.O.; Okorie, U.S.; Osobonye, G.; Ikot, A.N.; Rampho, G.J.; Sever, R. Thermal properties of Deng–Fan–Eckart potential model using Poisson summation approach. J. Math. Chem. 2020, 58, 989–1013. [Google Scholar] [CrossRef]
- Kria, M.; Feddi, K.; Aghoutane, N.; El-Yadri, M.; Pérez, L.M.; Laroze, D.; Dujardin, F.; Feddi, E. Thermodynamic properties of SnO2/GaAs core/shell nanofiber. Phys. A Stat. Mech. Its Appl. 2020, 560, 125104. [Google Scholar] [CrossRef]
- Lakaal, K.; Kria, M.; El Hamdaoui, J.; Varsha; Prasad, V.; Nautiyal, V.V.; El-Yadri, M.; Pérez, L.; Laroze, D.; Feddi, E. Polaronic corrections on magnetization and thermodynamic properties of electron–electron in 2D systems with Rashba spin–orbit coupling. J. Magn. Magn. Mater. 2022, 551, 169042. [Google Scholar] [CrossRef]
- Servatkhah, M.; Khordad, R.; Firoozi, A.; Sedehi, H.R.R.; Mohammadi, A. Low temperature behavior of entropy and specific heat of a three dimensional quantum wire: Shannon and Tsallis entropies. Eur. Phys. J. B 2020, 93, 1–7. [Google Scholar] [CrossRef]
- Castaño-Yepes, J.; Ramirez-Gutierrez, C.; Correa-Gallego, H.; Gómez, E.A. A comparative study on heat capacity, magnetization and magnetic susceptibility for a GaAs quantum dot with asymmetric confinement. Phys. E Low-Dimens. Syst. Nanostruct. 2018, 103, 464–470. [Google Scholar] [CrossRef] [Green Version]
- Adhikari, R.B.; Shen, P.; Kunwar, D.L.; Jeon, I.; Maple, M.B.; Dzero, M.; Almasan, C.C. Magnetic field dependence of the Schottky anomaly in filled skutterudites Pr1−xEuxPt4Ge12. Phys. Rev. B 2019, 100, 174509. [Google Scholar] [CrossRef] [Green Version]




Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Edet, C.O.; Mahmoud, S.; Inyang, E.P.; Ali, N.; Aljunid, S.A.; Endut, R.; Ikot, A.N.; Asjad, M. Non-Relativistic Treatment of the 2D Electron System Interacting via Varshni–Shukla Potential Using the Asymptotic Iteration Method. Mathematics 2022, 10, 2824. https://doi.org/10.3390/math10152824
Edet CO, Mahmoud S, Inyang EP, Ali N, Aljunid SA, Endut R, Ikot AN, Asjad M. Non-Relativistic Treatment of the 2D Electron System Interacting via Varshni–Shukla Potential Using the Asymptotic Iteration Method. Mathematics. 2022; 10(15):2824. https://doi.org/10.3390/math10152824
Chicago/Turabian StyleEdet, Collins Okon, Salman Mahmoud, Etido P. Inyang, Norshamsuri Ali, Syed Alwee Aljunid, Rosdisham Endut, Akpan Ndem Ikot, and Muhammad Asjad. 2022. "Non-Relativistic Treatment of the 2D Electron System Interacting via Varshni–Shukla Potential Using the Asymptotic Iteration Method" Mathematics 10, no. 15: 2824. https://doi.org/10.3390/math10152824
APA StyleEdet, C. O., Mahmoud, S., Inyang, E. P., Ali, N., Aljunid, S. A., Endut, R., Ikot, A. N., & Asjad, M. (2022). Non-Relativistic Treatment of the 2D Electron System Interacting via Varshni–Shukla Potential Using the Asymptotic Iteration Method. Mathematics, 10(15), 2824. https://doi.org/10.3390/math10152824








