Activation Energy Performance through Magnetized Hybrid Fe3O4–PP Nanofluids Flow with Impact of the Cluster Interfacial Nanolayer
Abstract
:1. Introduction
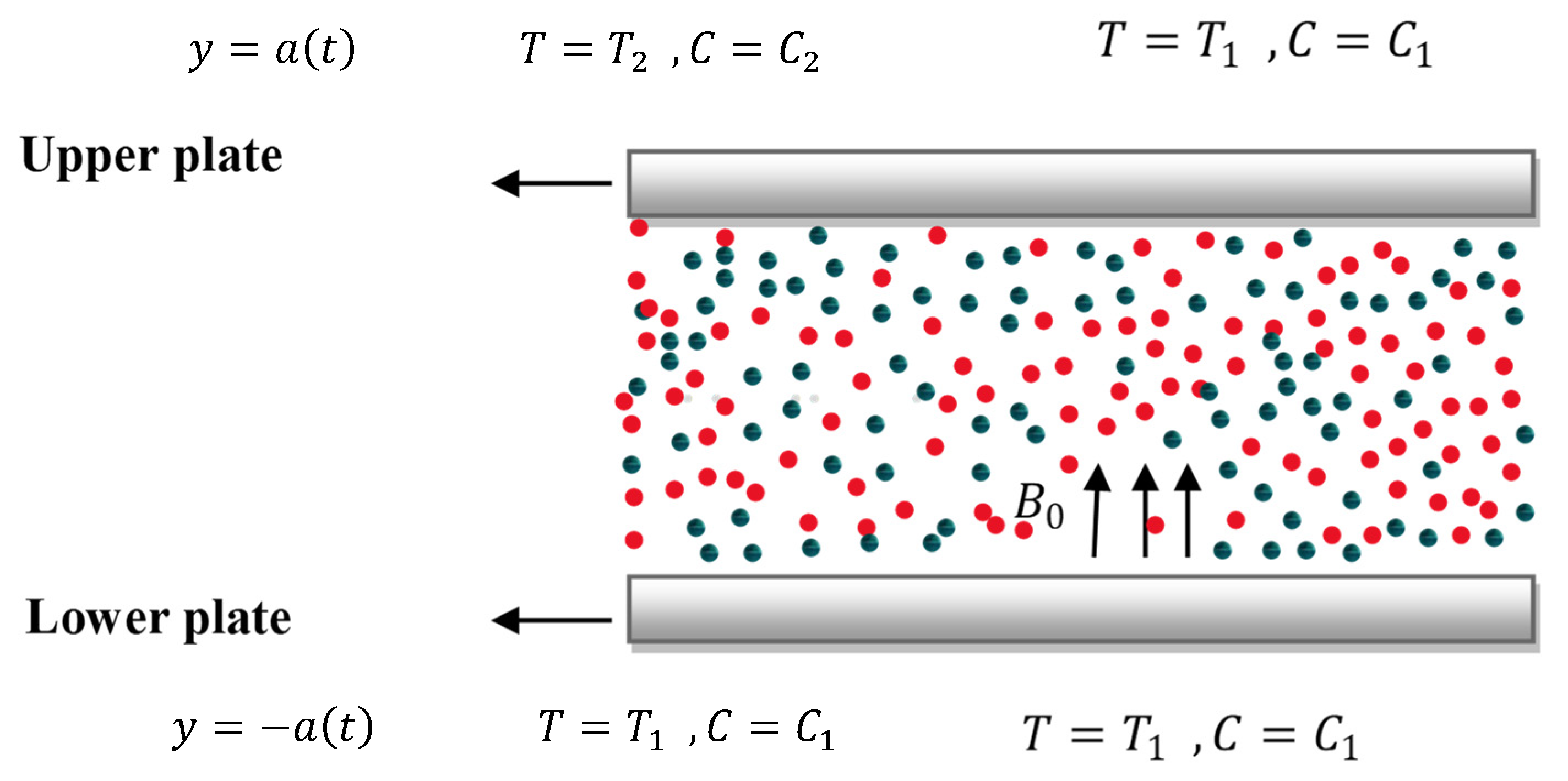
2. Formulation of Governing Equations
3. Numerical Procedure
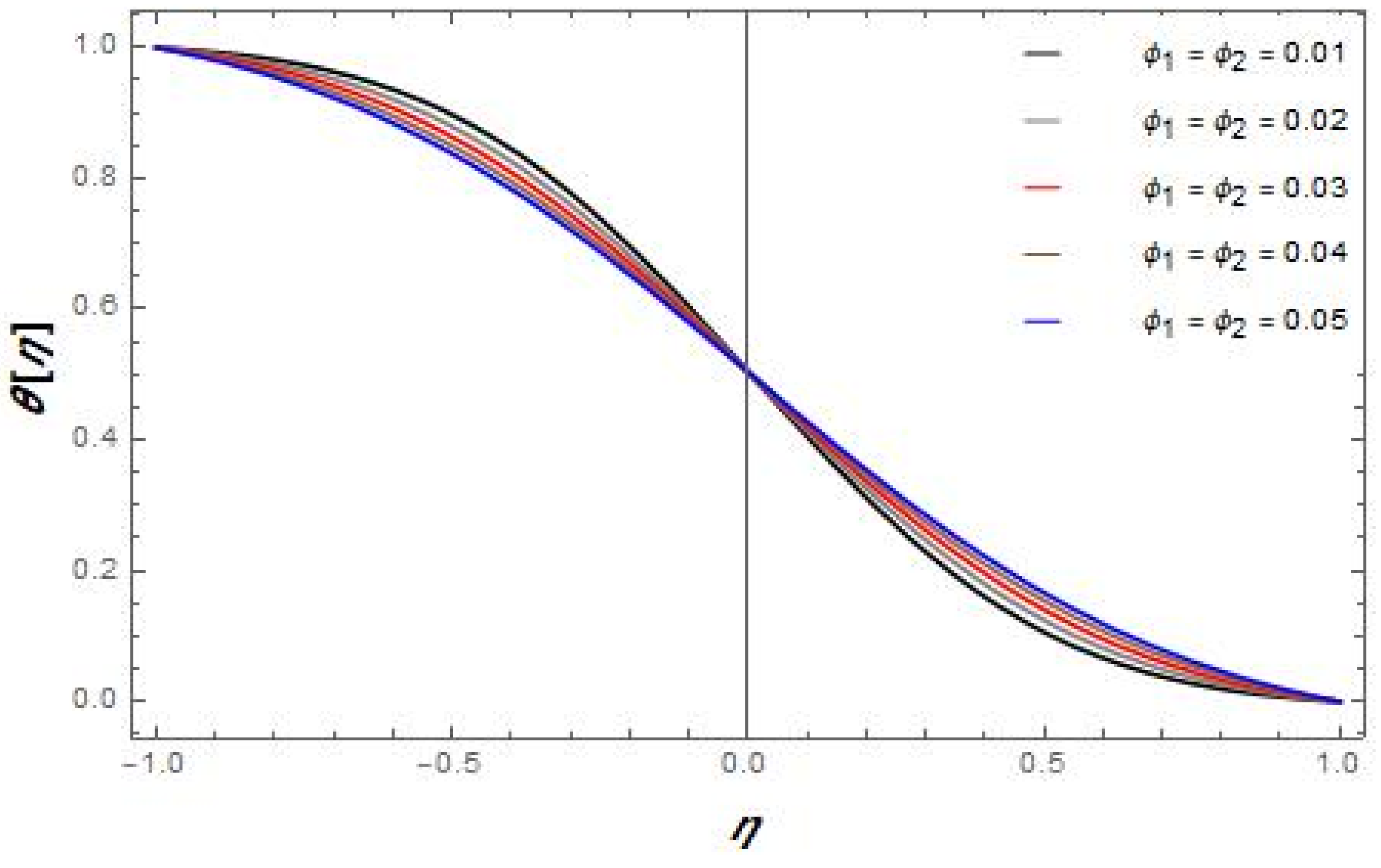
4. Results and Discussion
5. Conclusions
- Effective nanolayer thermal conductivity indicates better results as compared to noneffective nanolayer thermal conductivity.
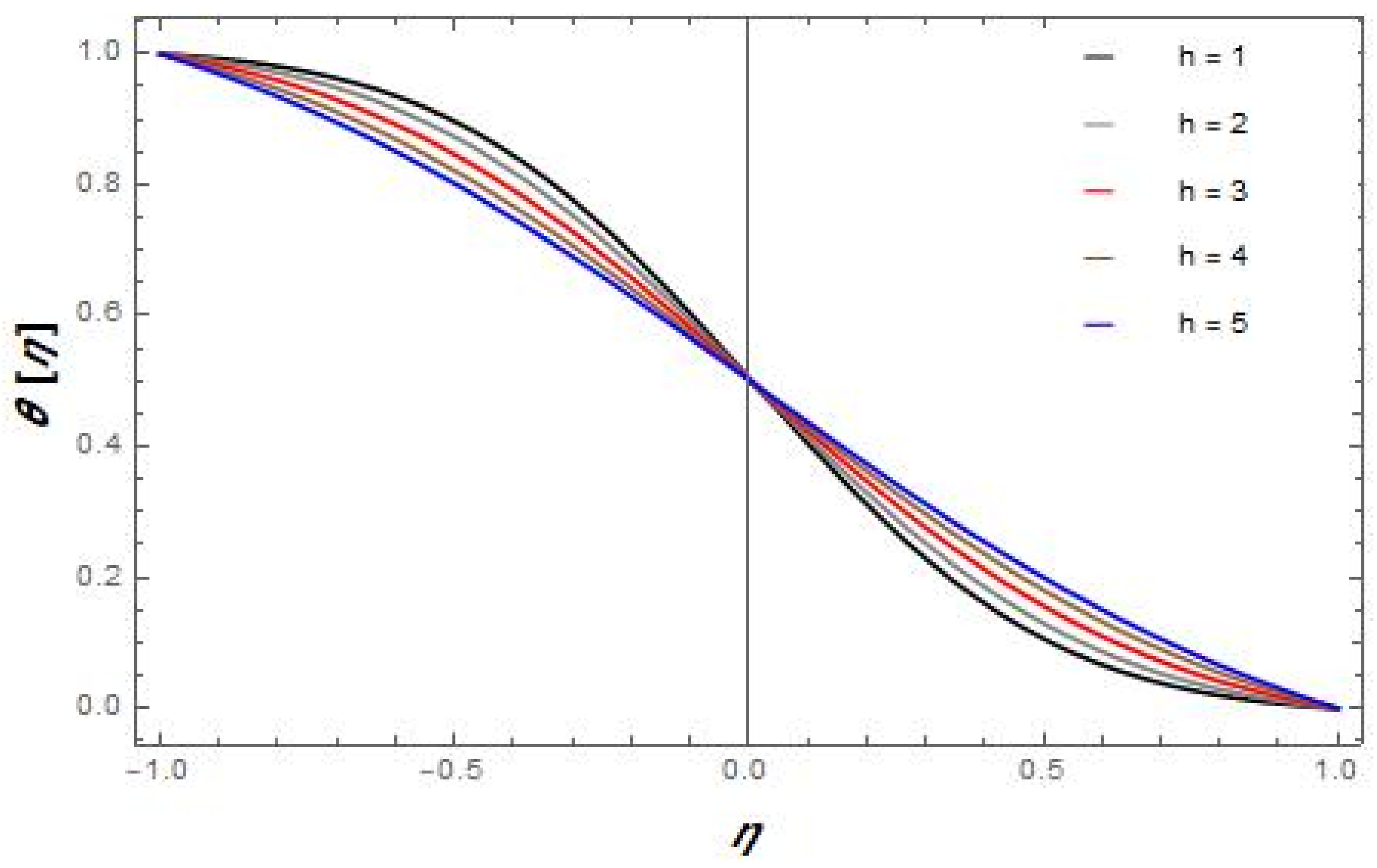
- Interfacial nanolayer thickness has a significant effect on the effective thermal conductivity and heat transfer rate of hybrid nanofluids.
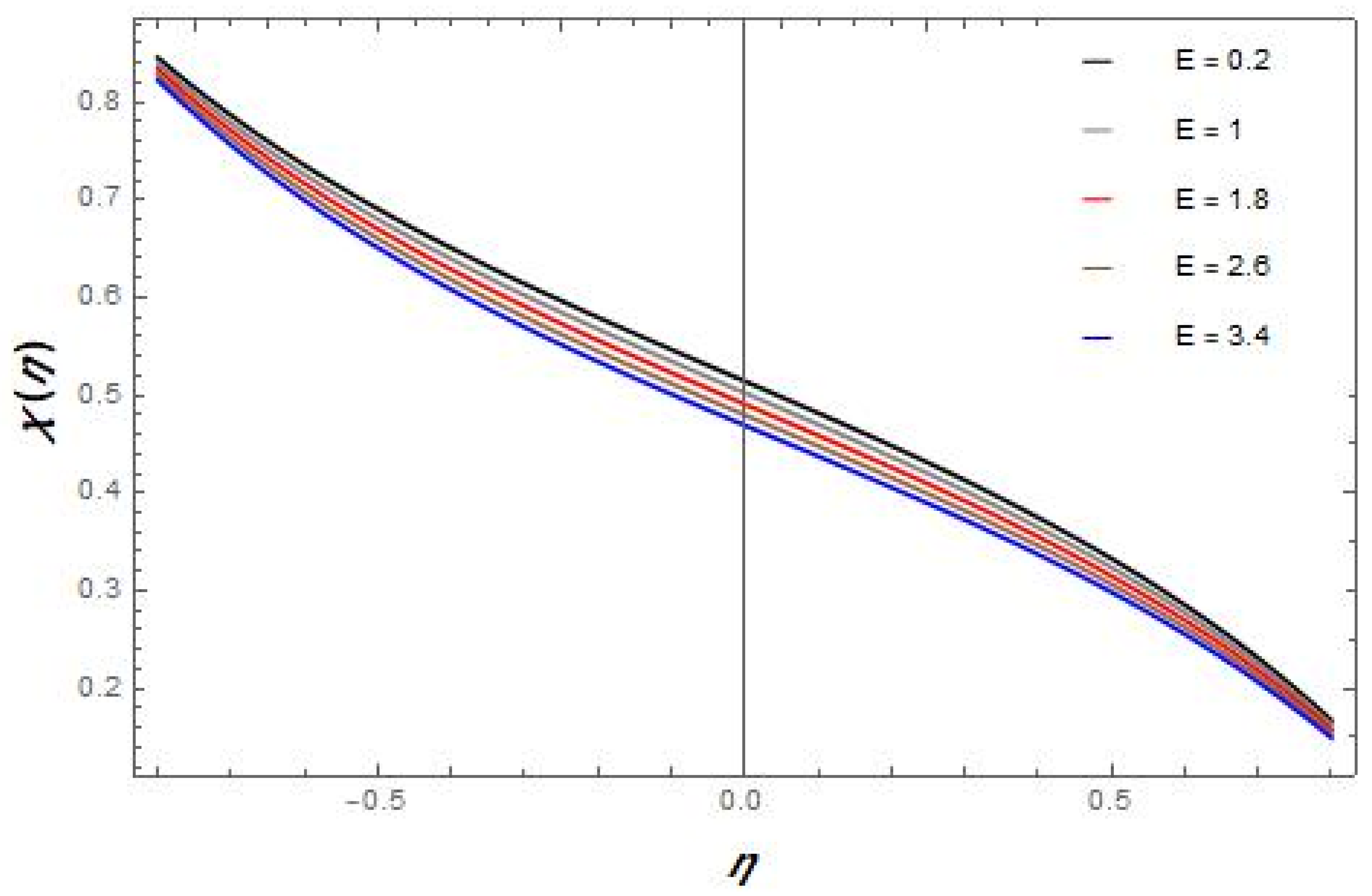
- The heat and mass transfer rate increases with the increment in values of the interfacial nanolayer thickness and the activation energy parameter but decreases with the increase in values of particles , and for the suction case.
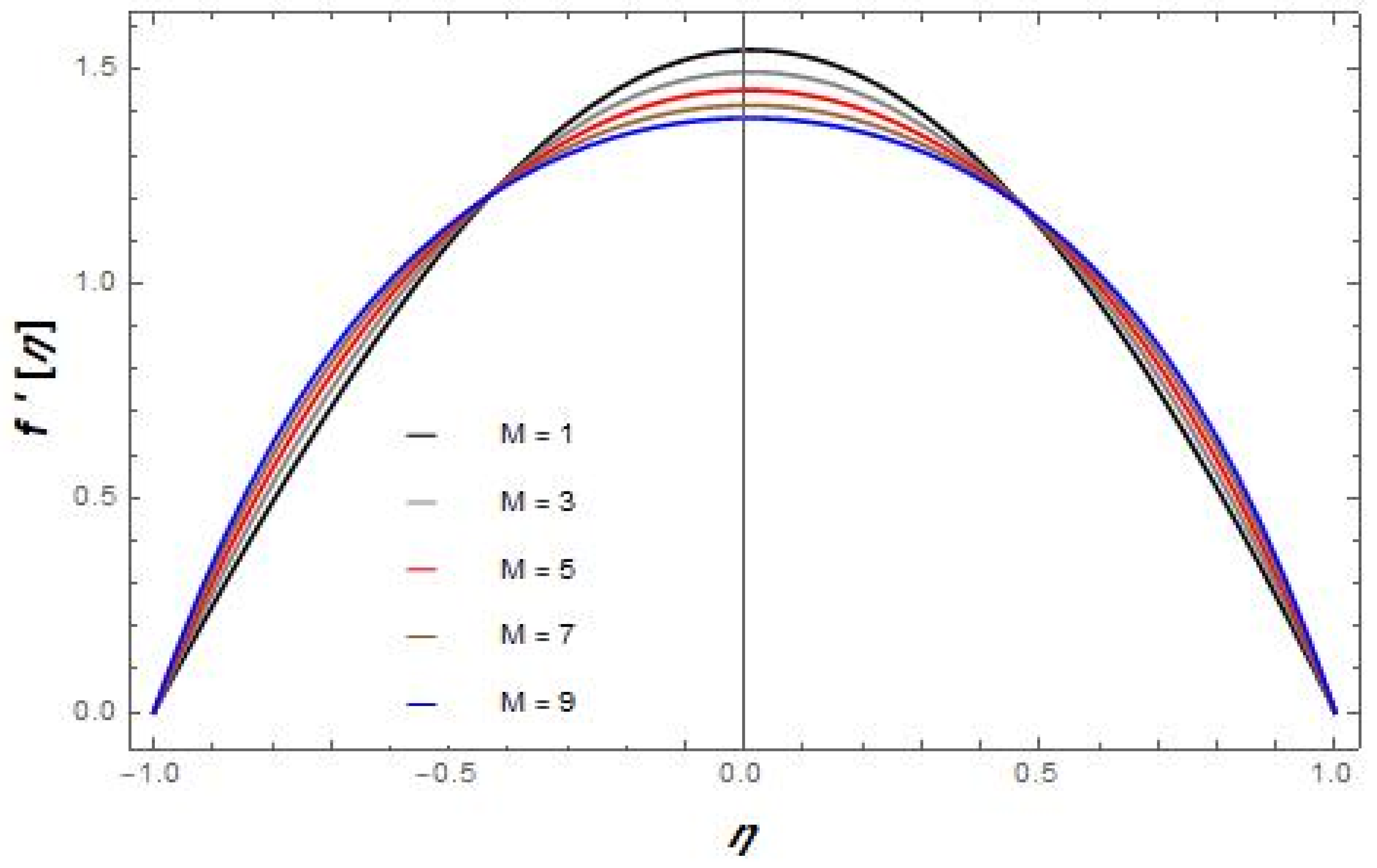
- Shear stress is reduced with the increase in volume fraction and the value of for both cases of suction/injection.
- Mass transfer rate increase with the increment in values of the activation energy parameter.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Nomenclature
| Uniform magnetic field | |
| Specific heat capacity | |
| C | Fluid concentration |
| Upper plate temperature | |
| Lower plate temperature | |
| Upper plate concentration | |
| Lower plate concentration | |
| K | Dimensionless parameter |
| M | Magnetic parameter |
| Prandtl number | |
| Re | Reynolds number |
| D | Diffusion coefficient |
| Specific heat capacity | |
| Chemical reaction rate constant | |
| Activation energy | |
| Dimensionless reaction rate | |
| h | Nanolayer parameter |
| Temperature difference parameter | |
| Exothermic/endothermic coefficient | |
| Density for the | |
| Thermal conductivity for the base fluid | |
| NPs | Nanoparticles |
| Shear stress | |
| Mass transfer | |
| Viscosity for the base fluid | |
| Kinematic viscosity for the hybrid nanofluid | |
| Dimensionless constant | |
| Dimensionless radial velocity profile | |
| Dimensionless temperature profile | |
| Thermal conductivity | |
| V | Kinematic viscosity |
| Dynamic viscosity | |
| Density (kg/m3) | |
| Specific heat capacity | |
| T | Temperature (K) |
| Sc | Schmidt number |
| Specific heat capacity for the hybrid nanofluid | |
| Thermal conductivity for the hybrid nanofluid | |
| p | Pressure |
| Viscosity for the |
References
- Buongiorno, J.; Venerus, D.C.; Prabhat, N.; McKrell, T.J.; Townsend, J.; Christianson, R.J.; Tolmachev, Y.V.; Keblinski, P.; Hu, L.-W.; Alvarado, J.L.; et al. A benchmark study on the thermal conductivity of nanofluids. J. Appl. Phys. 2009, 106, 094312. [Google Scholar] [CrossRef]
- GÜREL, B. A numerical investigation of the melting heat transfer characteristics of phase change materials in different plate heat exchanger (latent heat thermal energy storage) systems. Int. J. Heat Mass Transf. 2020, 148, 119117. [Google Scholar] [CrossRef]
- Dhlamini, M.; Kameswaran, P.K.; Sibanda, P.; Motsa, S.; Mondal, H. Activation energy and binary chemical reaction effects in mixed convective nanofluid flow with convective boundary conditions. J. Comput. Des. Eng. 2018, 6, 149–158. [Google Scholar] [CrossRef]
- Zhu, C.; Zhu, W.; Xu, L.; Zhou, X. A label-free electrochemical aptasensor based on magnetic biocomposites with Pb2+-dependent DNAzyme for the detection of thrombin. Anal. Chim. Acta 2018, 1047, 21–27. [Google Scholar] [CrossRef] [PubMed]
- Wakif, A.; Animasaun, I.L.; Khan, U.; Shah, N.A.; Thumma, T. Dynamics of radiative-reactive Walters-b fluid due to mixed convection conveying gyrotactic microorganisms, tiny particles experience haphazard motion, thermo-migration, and Lorentz force Phys. Scripta 2021, 96, 125239. [Google Scholar] [CrossRef]
- Sreenivasulu, M.; Vijaya, R.B. Influence of Activation Energy on the Hybrid Nanofluid Flow over a Flat Plate with Quadratic Thermal Radiation: An Irreversibility Analysis. Int. J. Ambient. Energy 2022, 1–29. [Google Scholar] [CrossRef]
- Ramesh, G.; Madhukesh, J. Activation energy process in hybrid CNTs and induced magnetic slip flow with heat source/sink. Chin. J. Phys. 2021, 73, 375–390. [Google Scholar] [CrossRef]
- Wasif, M.; Mishal, K.A.; Haque, M.R.; Haque, M.M.; Rahman, F. Investigation of fluid flow and heat transfer for an optimized lid driven cavity shape under the condition of inclined magnetic field. Energy Eng. 2021, 1, 47–57. [Google Scholar]
- Kumar, K.G.; Baslem, A.; Prasannakumara, B.C.; Majdoubi, J.; Rahimi-Gorji, M.; Nadeem, S. Significance of Arrhenius activation energy in flow and heat transfer of tangent hyperbolic fluid with zero mass flux condition. Microsyst. Technol. 2020, 26, 2517–2526. [Google Scholar] [CrossRef]
- Awad, F.G.; Motsa, S.; Khumalo, M. Heat and Mass Transfer in Unsteady Rotating Fluid Flow with Binary Chemical Reaction and Activation Energy. PLoS ONE 2014, 9, e107622. [Google Scholar] [CrossRef]
- Rekha, M.B.; Sarris, I.E.; Madhukesh, J.K.; Raghunatha, K.R.; Prasannakumara, B.C. Activation energy impact on flow of AA7072-AA7075/Water-Based hybrid nanofluid through a cone, wedge and plate. Micromachines 2022, 13, 302. [Google Scholar] [CrossRef] [PubMed]
- Tang, S.; Lan, Q.; Liang, J.; Chen, S.; Liu, C.; Zhao, J.; Cheng, Q.; Cao, Y.-C.; Liu, J. Facile synthesis of Fe3O4 @PPy core-shell magnetic nanoparticles and their enhanced dispersity and acid stability. Mater. Des. 2017, 121, 47–50. [Google Scholar] [CrossRef]
- Rehman, S.U.; Fatima, N.; Ali, B.; Imran, M.; Ali, L.; Shah, N.A.; Chung, J.D. The Casson Dusty Nanofluid: Significance of Darcy–Forchheimer Law, Magnetic Field, and Non-Fourier Heat Flux Model Subject to Stretch Surface. Mathematics 2022, 10, 2877. [Google Scholar] [CrossRef]
- Suri, K.; Annapoorni, S.; Sarkar, A.; Tandon, R. Gas and humidity sensors based on iron oxide–polypyrrole nanocomposites. Sensors Actuators B Chem. 2002, 81, 277–282. [Google Scholar] [CrossRef]
- Sun, Y.; Xiao, F.; Liu, X.; Feng, C.; Jin, C. Preparation and electromagnetic wave absorption properties of core–shell structured Fe3O4–polyaniline nanoparticles. RSC Adv. 2013, 3, 22554–22559. [Google Scholar] [CrossRef]
- Zhao, H.; Huang, M.; Wu, J.; Wang, L.; He, H. Preparation of Fe3O4@PPy magnetic nanoparticles as solid-phase extraction sorbents for preconcentration and separation of phthalic acid esters in water by gas chromatography–mass spectrometry. J. Chromatogr. B 2016, 1011, 33–44. [Google Scholar] [CrossRef]
- Salmi, A.; Madkhali, H.A.; Ali, B.; Nawaz, M.; Alharbi, S.O.; Alqahtani, A. Numerical study of heat and mass transfer enhancement in Prandtl fluid MHD flow using Cattaneo-Christov heat flux theory. Case Stud. Therm. Eng. 2022, 33, 101949. [Google Scholar] [CrossRef]
- Roy, N.C.; Pop, I. Heat and mass transfer of a hybrid nanofluid flow with binary chemical reaction over a permeable shrinking surface. Chin. J. Phys. 2021, 76, 283–298. [Google Scholar] [CrossRef]
- Oke, A.S. Heat and Mass Transfer in 3D MHD Flow of EG-Based Ternary Hybrid Nanofluid Over a Rotating Surface. Arab. J. Sci. Eng. 2022, 1–17. [Google Scholar] [CrossRef]
- Babu, B.H.; Rao, P.S.; Varma, S.V.K. Heat and Mass Transfer on Unsteady Magnetohydrodynamics (MHD) Convective Flow of Casson Hybrid Nanofluid Over a Permeable Media with Ramped Wall Temperature. J. Nanofluids 2022, 11, 552–562. [Google Scholar] [CrossRef]
- Kakaç, S.; Pramuanjaroenkij, A. Review of convective heat transfer enhancement with nanofluids. Int. J. Heat Mass Transf. 2009, 52, 3187–3196. [Google Scholar] [CrossRef]
- Demir, H.; Dalkilic, A.; Kürekci, N.; Duangthongsuk, W.; Wongwises, S. Numerical investigation on the single phase forced convection heat transfer characteristics of TiO2 nanofluids in a double-tube counter flow heat exchanger. Int. Commun. Heat Mass Transf. 2011, 38, 218–228. [Google Scholar] [CrossRef]
- Fetecau, C.; Shah, N.A.; Vieru, d. General Solutions for Hydromagnetic Free Convection Flow over an Infinite Plate with Newtonian Heating, Mass Diffusion and Chemical Reaction. Commun. Theor. Phys. 2017, 68, 768–782. [Google Scholar]
- Ashraf, M.Z.; Rehman, S.U.; Farid, S.; Hussein, A.K.; Ali, B.; Shah, N.A.; Weera, W. Insight into Significance of Bioconvection on MHD Tangent Hyperbolic Nanofluid Flow of Irregular Thickness across a Slender Elastic Surface. Mathematics 2022, 10, 2592. [Google Scholar] [CrossRef]
- Lou, Q.; Ali, B.; Rehman, S.U.; Habib, D.; Abdal, S.; Shah, N.A.; Chung, J.D. Micropolar Dusty Fluid: Coriolis Force Effects on Dynamics of MHD Rotating Fluid When Lorentz Force Is Significant. Mathematics 2022, 10, 2630. [Google Scholar] [CrossRef]
- Sreedevi, P.; Reddy, P.S. Impact of Convective Boundary Condition on Heat and Mass Transfer of Nanofluid Flow Over a Thin Needle Filled with Carbon Nanotubes. J. Nanofluids 2020, 9, 282–292. [Google Scholar] [CrossRef]
- Salmi, A.; Madkhali, H.A.; Nawaz, M.; Alharbi, S.O.; Alqahtani, A. Numerical study on non-Fourier heat and mass transfer in partially ionized MHD Williamson hybrid nanofluid. Int. Commun. Heat Mass Transf. 2022, 133, 105967. [Google Scholar] [CrossRef]
- Santhi, M.; Rao, K.V.S.; Reddy, P.S.; Sreedevi, P. Heat and mass transfer characteristics of radiative hybrid nanofluid flow over a stretching sheet with chemical reaction. Heat Transf. 2020, 50, 2929–2949. [Google Scholar] [CrossRef]
- Raja, M.A.Z.; Shoaib, M.; Khan, Z.; Zuhra, S.; Saleel, C.A.; Nisar, K.S.; Islam, S.; Khan, I. Supervised neural networks learning algorithm for three dimensional hybrid nanofluid flow with radiative heat and mass fluxes. Ain Shams Eng. J. 2021, 13, 101573. [Google Scholar] [CrossRef]
- Shah, N.A.; Wakif, A.; El-Zahar, E.R.; Ahmad, S.; Yook, S.-J. Numerical simulation of a thermally enhanced EMHD flow of a heterogeneous micropolar mixture comprising (60%)-ethylene glycol (EG), (40%)-water (W), and copper oxide nanomaterials (CuO). Case Stud. Therm. Eng. 2022, 35, 102046. [Google Scholar]
- Kumbhakar, B.; Nandi, S.; Chamkha, A.J. Unsteady hybrid nanofluid flow over a convectively heated cylinder with inclined magnetic field and viscous dissipation: A multiple regression analysis. Chin. J. Phys. 2022, 79, 38–56. [Google Scholar]
- Farooq, U.; Lu, D.; Munir, S.; Ramzan, M.; Suleman, M.; Hussain, S. MHD flow of Maxwell fluid with nanomaterials due to an exponentially stretching surface. Sci. Rep. 2019, 9, 7312. [Google Scholar] [CrossRef] [PubMed]
- Oke, A.S. Combined effects of Coriolis force and nanoparticle properties on the dynamics of gold–water nanofluid across nonuniform surface. Z. Angew. Math. Mech. 2022, e202100113. [Google Scholar] [CrossRef]
- Kigio, J.K.; Nduku, M.W.; Samuel, O.A. Analysis of Volume Fraction and Convective Heat Transfer on MHD Casson Nanofluid over a Vertical Plate. Fluid Mech. 2021, 7, 1–8. [Google Scholar] [CrossRef]
- Tso, C.; Fu, S.; Chao, C.Y. A semi-analytical model for the thermal conductivity of nanofluids and determination of the nanolayer thickness. Int. J. Heat Mass Transf. 2014, 70, 202–214. [Google Scholar] [CrossRef]
- Murshed, S.; Leong, K.; Yang, C. Thermophysical and electrokinetic properties of nanofluids–A critical review. Appl. Therm. Eng. 2008, 28, 2109–2125. [Google Scholar] [CrossRef]
- Acharya, N.; Mabood, F.; Shahzad, S.; Badruddin, I. Hydrothermal variations of radiative nanofluid flow by the influence of nanoparticles diameter and nanolayer. Int. Commun. Heat Mass Transf. 2021, 130, 105781. [Google Scholar] [CrossRef]
- Zhao, C.; Tao, Y.; Yu, Y. Molecular dynamics simulation of thermal and phonon transport characteristics of nanocomposite phase change material. J. Mol. Liq. 2021, 329, 115448. [Google Scholar] [CrossRef]
- Ahmad, S.; Farooq, M.; Mir, N.A.; Anjum, A.; Javed, M. Magneto-hydrodynamic flow of squeezed fluid with binary chemical reaction and activation energy. J. Central South Univ. 2019, 26, 1362–1373. [Google Scholar] [CrossRef]
- Majdalani, J.; Zhou, C.; Dawson, C.A. Two-dimensional viscous flow between slowly expanding or contracting walls with weak permeability. J. Biomech. 2002, 35, 1399–1403. [Google Scholar] [CrossRef]
- Saba, F.; Ahmed, N.; Khan, U.; Waheed, A.; Rafiq, M.; Mohyud-Din, S.T. Thermophysical Analysis of Water Based (Cu–Al2O3) Hybrid Nanofluid in an Asymmetric Channel with Dilating/Squeezing Walls Considering Different Shapes of Nanoparticles. Appl. Sci. 2018, 8, 1549. [Google Scholar] [CrossRef]
- Murshed, S.M.S.; Leong, K.; Yang, C. Investigations of thermal conductivity and viscosity of nanofluids. Int. J. Therm. Sci. 2008, 47, 560–568. [Google Scholar] [CrossRef]
- Raza, Q.; Qureshi, M.Z.A.; Khan, B.A.; Kadhim Hussein, A.; Ali, B.; Shah, N.A.; Chung, J.D. Insight into Dynamic of Mono and Hybrid Nanofluids Subject to Binary Chemical Reaction, Activation Energy, and Magnetic Field through the Porous Surfaces. Mathematics 2022, 10, 3013. [Google Scholar] [CrossRef]

| Physical Properties | PPy | ||
|---|---|---|---|
| 997.0 | 5180 | 1.32 | |
| 4180 | 670 | 800 | |
| 0.6071 | 9.7 | 0.24 |
| For a Nanofluid | For a Hybrid Nanofluid |
|---|---|
, = = | = + − (1 − − ()() = where = = |
| for the Suction Case | for the Suction Case | for the Suction Case | for the Injection Case | for the Injection Case | for the Injection Case | ||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| −1.5 | 0.01 | 0.01 | 4.21559 | 1.80925 | 0.84674 | 4.87378 | 4.40691 | 1.52166 | |||||
| −1 | 3.77813 | 0.94617 | 0.62276 | 4.40357 | 3.20740 | 1.20431 | |||||||
| 0 | 2.94105 | 0.16084 | 0.31088 | 3.49395 | 1.18698 | 0.69946 | |||||||
| 1 | 2.16279 | 0.01814 | 0.14104 | 2.63460 | 0.24412 | 0.36152 | |||||||
| 1.5 | 1.79889 | 0.00558 | 0.09193 | 2.22761 | 0.09233 | 0.25207 | |||||||
| 0.2 | 2.54393 | 0.05592 | 0.21175 | 3.05725 | 0.57754 | 0.50711 | |||||||
| 1 | 2.54393 | 0.56180 | 0.22352 | 3.05725 | 0.57851 | 0.55284 | |||||||
| 1.8 | 2.54393 | 0.05643 | 0.23519 | 3.05725 | 0.57945 | 0.54940 | |||||||
| 2.6 | 2.54393 | 0.05667 | 0.24678 | 3.05725 | 0.58037 | 0.57001 | |||||||
| 3.4 | 2.54393 | 0.05693 | 0.25827 | 3.05726 | 0.58128 | 0.59025 | |||||||
| 1 | 2.54393 | 0.05593 | 0.21175 | 3.05725 | 0.57754 | 0.50711 | |||||||
| 2 | 2.54393 | 0.09414 | 0.21175 | 3.05725 | 0.56028 | 0.50711 | |||||||
| 3 | 2.54393 | 0.15128 | 0.21775 | 3.05725 | 0.54416 | 0.50711 | |||||||
| 4 | 2.54393 | 0.21969 | 0.21175 | 3.05725 | 0.53125 | 0.50711 | |||||||
| 5 | 2.54393 | 0.28211 | 0.21175 | 3.05725 | 0.52190 | 0.50711 | |||||||
| 4.5 | 2.54393 | 0.1072 | 0.21176 | 3.05725 | 0.55586 | 0.50716 | |||||||
| 5.2 | 2.54393 | 0.08231 | 0.21176 | 3.0572 | 0.56589 | 0.50711 | |||||||
| 5.5 | 2.54393 | 0.07337 | 0.21175 | 3.05725 | 0.56846 | 0.50711 | |||||||
| 6.1 | 254393 | 0.05593 | 0.21175 | 305725 | 0.57754 | 0.50711 | |||||||
| 6.2 | 2.54393 | 0.05252 | 0.21175 | 3.05725 | 0.57754 | 0.50711 | |||||||
| 1.2 | 2.54393 | 0.05252 | 0.21175 | 3.05725 | 0.56490 | 0.50711 | |||||||
| 1.3 | 2.54393 | 0.05138 | 0.21175 | 3.05725 | 0.56489 | 0.50711 | |||||||
| 1.7 | 2.54393 | 0.05138 | 0.21175 | 3.05725 | 0.56068 | 0.50711 | |||||||
| 1.9 | 2.54393 | 0.05082 | 0.21175 | 3.0575 | 0.55857 | 0.50711 | |||||||
| 2.1 | 2.54393 | 0.05025 | 0.21175 | 3.05725 | 0.55646 | 0.50711 | |||||||
| 0.2 | 2.54393 | 0.05593 | 0.21175 | 3.05725 | 0.57754 | 0.50711 | |||||||
| 0.3 | 2.54393 | 0.05593 | 0.21161 | 3.05725 | 0.57754 | 0.50694 | |||||||
| 0.4 | 2.54393 | 0.05592 | 0.21152 | 3.05725 | 0.57757 | 0.50676 | |||||||
| 0.5 | 2.54393 | 0.05592 | 0.21175 | 3.05725 | 0.57752 | 0.50659 | |||||||
| 0.6 | 2.54393 | 0.05592 | 0.21175 | 3.05725 | 0.57751 | 0.50643 | |||||||
| 0.02 | 2.05612 | 0.05014 | 0.23003 | 3.14578 | 0.08917 | 0.28112 | |||||||
| 0.03 | 1.87661 | 0.04852 | 0.22816 | 2.89971 | 0.08710 | 0.25715 | |||||||
| 0.04 | 1.73051 | 0.04646 | 0.22648 | 2.65364 | 0.08571 | 0.23846 | |||||||
| 0.05 | 1.55101 | 0.04462 | 0.22419 | 1.30494 | 0.08325 | 0.21019 | |||||||
| 0.02 | 1.99860 | 0.04822 | 0.22941 | 2.87560 | 0.10870 | 0.25989 | |||||||
| 0.03 | 1.93061 | 0.04445 | 0.22871 | 2.62953 | 0.09875 | 0.24845 | |||||||
| 0.04 | 1.88152 | 0.03947 | 0.22821 | 2.38082 | 0.09650 | 0.23587 | |||||||
| 0.05 | 1.81351 | 0.03442 | 0.22751 | 1.88343 | 0.09430 | 0.22761 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Qureshi, M.Z.A.; Raza, Q.; Ramzan, A.; Faisal, M.; Ali, B.; Shah, N.A.; Weera, W. Activation Energy Performance through Magnetized Hybrid Fe3O4–PP Nanofluids Flow with Impact of the Cluster Interfacial Nanolayer. Mathematics 2022, 10, 3277. https://doi.org/10.3390/math10183277
Qureshi MZA, Raza Q, Ramzan A, Faisal M, Ali B, Shah NA, Weera W. Activation Energy Performance through Magnetized Hybrid Fe3O4–PP Nanofluids Flow with Impact of the Cluster Interfacial Nanolayer. Mathematics. 2022; 10(18):3277. https://doi.org/10.3390/math10183277
Chicago/Turabian StyleQureshi, M. Zubair Akbar, Qadeer Raza, Aroosa Ramzan, M. Faisal, Bagh Ali, Nehad Ali Shah, and Wajaree Weera. 2022. "Activation Energy Performance through Magnetized Hybrid Fe3O4–PP Nanofluids Flow with Impact of the Cluster Interfacial Nanolayer" Mathematics 10, no. 18: 3277. https://doi.org/10.3390/math10183277
APA StyleQureshi, M. Z. A., Raza, Q., Ramzan, A., Faisal, M., Ali, B., Shah, N. A., & Weera, W. (2022). Activation Energy Performance through Magnetized Hybrid Fe3O4–PP Nanofluids Flow with Impact of the Cluster Interfacial Nanolayer. Mathematics, 10(18), 3277. https://doi.org/10.3390/math10183277







