Abstract
Precise streamflow estimation plays a key role in optimal water resource use, reservoirs operations, and designing and planning future hydropower projects. Machine learning models were successfully utilized to estimate streamflow in recent years In this study, a new approach, covariance matrix adaptation evolution strategy (CMAES), was utilized to improve the accuracy of seven machine learning models, namely extreme learning machine (ELM), elastic net (EN), Gaussian processes regression (GPR), support vector regression (SVR), least square SVR (LSSVR), extreme gradient boosting (XGB), and radial basis function neural network (RBFNN), in predicting streamflow. The CMAES was used for proper tuning of control parameters of these selected machine learning models. Seven input combinations were decided to estimate streamflow based on previous lagged temperature and streamflow data values. For numerical prediction accuracy comparison of these machine learning models, six statistical indexes are used, i.e., relative root mean squared error (RRMSE), mean absolute error (MAE), mean absolute percentage error (MAPE), Nash–Sutcliffe efficiency (NSE), and the Kling–Gupta efficiency agreement index (KGE). In contrast, this study uses scatter plots, radar charts, and Taylor diagrams for graphically predicted accuracy comparison. Results show that SVR provided more accurate results than the other methods, especially for the temperature input cases. In contrast, in some streamflow input cases, the LSSVR and GPR were better than the SVR. The SVR tuned by CMAES with temperature and streamflow inputs produced the least RRMSE (0.266), MAE (263.44), and MAPE (12.44) in streamflow estimation. The EN method was found to be the worst model in streamflow prediction. Uncertainty analysis also endorsed the superiority of the SVR over other machine learning methods by having low uncertainty values. Overall, the SVR model based on either temperature or streamflow as inputs, tuned by CMAES, is highly recommended for streamflow estimation.
Keywords:
streamflow prediction; extreme learning machine; support vector regression; elastic net; covariance matrix adaptation evolution strategy MSC:
68T20
1. Introduction
Reliable streamflow prediction is vital for many hydrological and environmental studies, such as flood risk assessment, hydroelectric power, water allocations, irrigation scheduling, and water protection [1,2]. Many factors, such as temperature, precipitation, evapotranspiration, soil types, and urbanization affect the reliability of prediction [3,4,5]. In recent years, due to climate change in the whole world, water resources faced much change, which resulted in extreme events such as frequent floods and drought. These extreme events not only cause the loss of many human lives but also create economic instability [6,7]. Therefore, precise estimation of streamflow is necessary to avoid and mitigate this loss by extreme events. The basic characteristic of the whole process is a nonlinear connection between these factors and streamflow.
There are two groups of streamflow prediction techniques: (1) physically based models and (2) data-driven techniques. Numerous previous studies concluded that nonlinear data-driven approaches often outperform physically based models and linear data-driven techniques [8,9,10,11]. Among the data-driven techniques, a series of existing studies indicated the potential of machine learning methods (MLMs) in streamflow prediction [12,13,14]. Kagoda et al. [15] successfully applied RBFNN to predict monthly streamflow in South Africa. Sun et al. [16] introduced the GPR model to predict monthly streamflow using the US MOPEX database. GPR produced more accurate predictions than artificial neural networks (ANN) and linear regression (LR). Mehr et al. [17] compared three ANN techniques. They concluded that RBFNN yielded the best results in monthly streamflow prediction in the Coruh Basin (Turkey). Kisi [18] reported that the LSSVR models outperformed the adaptive neuro-fuzzy embedded fuzzy c-means clustering (ANFIS-FCM) and autoregressive moving average (ARMA) models in monthly streamflow prediction in the Dicle Watershed (Turkey). Yaseen et al. [19] found that LSSVR yielded superior results to the M5 Tree and MARS models in predicting streamflow from observed precipitation.
Modaresi et al. [20] found that LSSVR performed better than the ANN model for monthly streamflow prediction nonlinear conditions in Iran. Worland et al. [21] compared EN, support vector machines (SVM), and the gradient boosting machine (GBM) with the null physically based model for weekly streamflow prediction. The results show that MLMs made more reliable predictions than physically based models. Hadi et al. [22] employed a hybrid XGB-ELM model. XGB was applied as an input selection technique, and ELM as a predicting technique. Climatic data predicted monthly streamflow, including temperature, precipitation, and evapotranspiration from the Goksu-Himmeti basin (Turkey). Overall results prove that the XGB-ELM model improved the streamflow prediction. The authors concluded that reliable streamflow prediction is possible using only temperature data; however, other meteorological variables enhance the model’s capability. Li et al. [23] investigated EN, XGB, and SVR in monthly streamflow prediction using data from China. XGB outperformed EN, and SVR approaches. The authors concluded that MLMs could be used for monthly prediction.
Ni et al. [24] successfully predicted monthly streamflows by using a new hybrid technique based on XGB coupled with the Gaussian mixture model. The new technique performed better compared to SVM. Adnan et al. [25] applied multivariate adaptive regression splines (MARS), least square SVM (LSSVM), M5 model tree (M5 Tree), optimally pruned extreme learning machines (OP-ELM), and the seasonal autoregressive moving average (SARIMA) for predicting river flow using the temperature and precipitation data of two mountainous stations of Pakistan. The LSSVM and MARS models yielded the best results in Kalam station and Chakdara station, respectively. Only temperature data from Kalam station provided a successful streamflow prediction. LSSVM, OP-ELM, and MARS performed better than the SARIMA model. Thapa et al. [26] used SVR and GPR models for predicting snowmelt streamflow in the Langtang basin (Nepal). Jiang et al. [27] implemented the new ELM model with enhanced particle swarm optimization (ELM-IPSO) for simulating discharge from the Chaohe River basin (China). The ELM-IPSO made more reliable monthly streamflow predictions than ANN, the auto-regression method (AR), ELM with PSO algorithm (ELM-PSO), and ELM with genetic algorithm (ELM-GA). Malik et al. [28] applied SVR models to predict daily river flow in the Naula basin (India). They employed six meta-heuristic algorithms for optimizing SVR models. Authors reported that Harris hawks optimization (HHO) provided the best performance to the hybrid SVR-HHO model. Parisouj et al. [29] investigated ANN, ELM, and SVR in daily and monthly streamflow prediction using temperature and precipitation input data from four basins in the western USA. The results show that SVR made more reliable daily and monthly predictions than ELM and ANN models. Niu and Feng [30] applied ANFIS, ANN, SVM, ELM, and GPR for daily streamflow prediction using data from south China. Obtained results show that ELM, GPR, and SVM models outperformed ANN and ANFIS models.
In recent years, hybrid machine learning models (MLMs) became preferred over standalone models and are successfully applied in the difference fields to model different variables; e.g., for load forecasting [31], to estimate the international airport freight volumes [32], to predict electricity prices [33], and for modeling of the tensile strength of the concrete [34]. Due to the nonlinear nature of hydrological variables’ time series, researchers found more precise and accurate results by utilizing hybrid MLMs than standalone MLMs. Numerous meta-heuristic algorithms, such as Harris Hawks optimization (HHO), Particle Swarm Optimization (PSO), Ant Lion Optimization (ALO), Grey Wolf Optimizer (GWO), and the Fruit Fly Algorithm (FFA) were integrated with MLMs for streamflow prediction in recent studies [28,35,36]. However, in addition to the precision of meta-heuristics algorithms, the robustness and simplicity of meta-heuristic algorithms are also considered. Therefore, in this study, instead of complex metaheuristic algorithms, a simple robust meta-heuristic algorithm, the covariance matrix adaptation evolution strategy (CMAES), is introduced to build hybrid machine learning methods [37]. CMAES was successfully applied to solve many engineering problems [38,39,40,41]. However, CMAES was so far never used to predict streamflow. That fact was the key motivation for this study. This study demonstrates that CMAES is an alternative to perform the selection of different machine learning models in flow prediction. In this research, the hybrid explores the CMAES algorithm’s search potential to generate benefits for machine learning models through the suitable selection of internal parameters. Furthermore, this study also performs an uncertainty analysis of the developed models, contributing to ensuring the robustness of the generated models and assisting in faster decision making. The computational framework is flexible and has the potential to embed different machine learning models that were not addressed in this study. The proposed strategy can be used by environmental monitoring and water management agencies, delivered as a web service and serving to issue short-term alerts, mitigating the effect of flash floods and assisting in managing water resources along the river studied in this research.
The objectives of this study are: (1) to predict monthly streamflow using antecedent streamflow observations and/or temperatures by different hybrid machine learning methods (MLMs), such as elastic net (EN), extreme learning machine (ELM), least squares support vector regression (LSSVR), support vector regression (SVR), radial basis function neural network (RBFNN), extreme gradient boosting (XGB) and Gaussian processes regression (GPR) (2) to implement CMAES as an optimization algorithm for these MLMs and (3) to evaluate the results of the applied hybrid machine learning methods.
2. Materials and Methods
2.1. Study Region and Datasets
The Upper Indus basin is selected as a case study in this study. The Upper Indus basin (UIB) is part of the world’s largest transboundary river basin, i.e., the Indus Basin, with a catchment area of 289,000 km2, almost covering 56% of the main Indus basin. UIB is located in the western area of Pakistan with a catchment elevation variation of 200 m to 8500 m. UIB is chosen due to the backbone role of this basin in the country’s agriculture sector. UIB fulfills the 90% irrigation requirements of the agriculture sector of Pakistan. However, the agriculture sector was affected in recent years due to insufficient water supplies. Therefore, precise measurement in this key basin is important for proper water supply management. For streamflow estimation, the Bunji sub-basin in this key basin is selected in this study (Figure 1). Monthly streamflow data of the Bunji hydraulic station (latitude: 35.4, longitude: 74.4) and temperature data of the Bunji meteorological station from 1977 to 2008 is obtained from WAPDA. Thirty-two years of monthly data are partitioned into calibration and testing parts for streamflow analysis with training and testing proportions of 75% and 25% training and testing proportions, respectively. Table 1 shows the statistical parameters of the streamflow and temperature data. Bunji basin is located at the confluence of the three biggest mountain ranges in the world, i.e., Hindu Kush, the Karakoram, and the Himalaya (HKH) mountains. This basin is selected as it directly drains to UIB. A key hydropower project is planned in this basin, i.e., Bunji Hydropower with 7100 MW generation capacity. Therefore, precise discharge simulation in this key basin can help the water manager optimize the scheduling of planned hydropower projects. Figure 2 shows the training (blue) and test set (orange) used in this study.
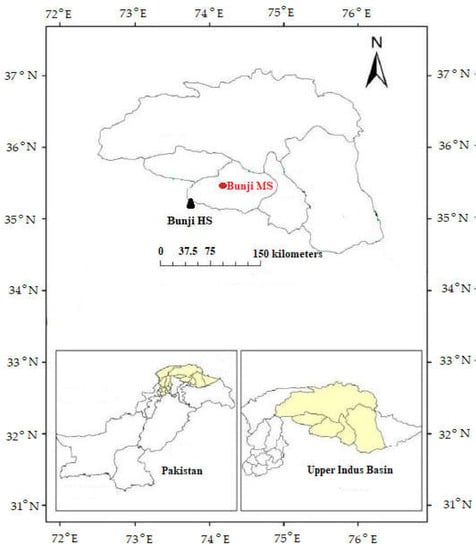
Figure 1.
Location map of selected stations.

Table 1.
The statistical parameters of the streamflow and temperature data.
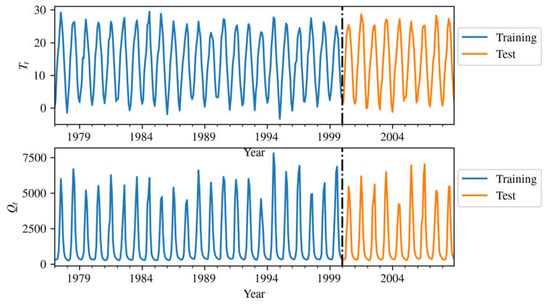
Figure 2.
Training set and test set.
2.2. Streamflow Estimation Models
The prediction model considers the present streamflow as a function of antecedent streamflow and/or temperatures. The predictive model has the following form:
where represent streamflow at month , is the temperature measured at month , and is an estimation function. Table 2 shows the input combinations to the model presented in Equation (1). Each input combination represents a case shown in the first column. The databases in the input and output nodes were normalized between −1 and 1 as below:
where XtN = normalized data of Q and T, whereas i = t, t − 1, t − 2, t − 3, and t − 4.

Table 2.
Input features associated with models tested in this paper.
2.2.1. Elastic Net (EN)
The EN uses a generalized linear regression [42] to best fit the coefficients by minimizing the residual of the fitted model. The optimization problem of EN can be stated as,
where represents sample size, is the dataset, is the outputs, , and represent the - and -norm of the parameter vector, respectively, and represents the -ratio parameter. EN model is trained with and for learning a sparse model with few non-zero weights while maintaining regularization properties. This trade-off is controlled using the parameter , and the so-called -ratio parameter. EN is suitable for developing a model with multiple inter-correlated inputs [43].
2.2.2. Extreme Learning Machine (ELM)
ELM is a kind of a feedforward ANN consisting of a single hidden layer. It can learn fast and is generalized efficiently, and therefore, suitability for modeling [44]. ELMs have three stages of randomness: (1) completely connected hidden node parameters are created randomly; (2) inputs to hidden node connections are produced randomly; and (3) a hidden node acts as a subnetwork consisting of several nodes. ELM can be mathematically presented as [45],
where represents the output for the input , denotes the th hidden node’s weight, denotes the hidden node’s biases of the neurons in the hidden layer, represents the output weight, represents the activation function, and denotes the hidden node number. The parameters are random numbers, having a normal distribution, while is decided logically. Table 3 provides the for .

Table 3.
Activation functions used in ELM.
The values of are estimated by minimizing [46],
where represents the hidden layer output matrix. The optimal weight () can be estimated as,
where is the pseudoinverse of .
2.2.3. Least Squares Support Vector Regression (LSSVR)
The LSSVR method [47] assumes that a nonlinear function () represents a dataset as,
where , represents weight, and denotes bias. The unknown parameters can be estimated by minimizing a residual function R(w, e, b)
where is the regularization constant, and represents error. The objective function R(w, e, b) consists of a loss and a regularization term, such as a feedforward ANN. However, R(w, e, b) is hard to solve for larger . The Lagrange multiplier optimal programming method is generally employed for its solution,
where is a Lagrange multiplier. It is solved by optimizing the following criteria:
Eliminating and , the optimization problem can be presented as below:
where y = [ ], and , as well as the kernel function are defined as
where
is the radial basis function (RBF) kernel. The LSSVR model output can be written as,
where and are the solutions to the linear system, and represents the kernel function parameter. The tuning parameters are generally defined by the user.
2.2.4. Support Vector Regression (SVR)
SVR is a classical algorithm [48] applied to solve regression problems [49]. It can be presented as,
where represents kernel function, represent weights, and denote bias and sample size, respectively. RBF is used in this study, which can be presented as,
where is the bandwidth parameter; and is determined by minimizing
where presents the output for inputs denotes the -insensitive loss function, and C denotes the regularization parameter [50]. In the SVR model presented in this paper, the parameters C and are to be adjusted to improve the SVR ability to model the regression problem [51].
2.2.5. Radial Basis Function Neural Network (RBFNN)
RBFNN [52] is a three-layer ANN commonly used for function interpolation problems. RBFNN is different from other ANN types in its universal approximation and rapid learning ability. The first and the last layers of RBFNN are used for attaining inputs and providing output, respectively. The hidden layer is composed of several radial basis nonlinear activation units. Compared to multilayer neural networks, RBFNN presents some differences: (1) the RBF network has only one hidden layer, (2) the activation function is according to distances instead of an inner product in multilayer networks; and (3) the approximation for an RBFNN network is a local one, while multilayer networks realize global approximation for the entire space.
For an array of points and their respective functional values, , where is a functional input/output relationship, the RBFNN constructs an approximation to in the form
where
is the th hidden layer’s activation function, id denotes the th data point, and is the width of the activation function. Inserting the condition displayed in the previous equations gives the following set of linear equations where, , , and . The training procedure for the RBFNN includes calculating the widths and weights. The adjustment of weights is performed using least squares, adding a smoothing parameter
where l is the smooth parameter. The smoothness of the approximation is increased when l > 0 and l = 0 is for interpolation. As a result, the function will always go through the nodal points in this case. The activation function in the RBFNN formulation is crucial to its performance. Table 4 shows a set of radial basis activation functions used in this study. The smooth parameter ε is only used in multiquadric, inverse multiquadric, and Gaussian activation functions.

Table 4.
Activation functions used in RBFNN.
2.2.6. eXtreme Gradient Boosting (XGB)
XGB [53] is an ensemble algorithm that combines several weak learners to predict better. In XGB, weak learners are regularized decision trees [54]. The XGB can mathematically be presented as,
where is the number of estimators, represents weak learners (decision trees) with depth defined by parameter . XGB is developed greedily,
where is a learning rate and the newly added tree is fitted to minimize a sum of losses and is given by
In the XGB formulation, the loss function is written as
where is the number of samples and
is the regularization term, where T represents the number of leaves, w denotes leaf weights, and is the regularization term on weights.
2.2.7. Gaussian Processes Regression (GPR)
The GPR predicts output based on the distribution over function instead of considering the function’s parameter distribution [55]. A Gaussian process model is represented as:
where is a nonlinear function that is used to infer output, y from inputs, x, is Gaussian noise with zero means (i.e., ). The prior for is a Gaussian process, and and represent the covariance matrix.
The predictive distribution of the output parameter , given its input , is formulated as [56],
where y = [y1, y2, …, yN]T is the vector of training data, k = [K(x, x1), K(x, x2), …, K(x, xN)]T, and K represents the function of covariance matrix, and a refers to regularization parameter. Equation (28) gives the covariance between xi and xj [57] as,
where and are positive parameters, and are the gamma and the modified Bessel function [58].
2.3. Parameter Tuning Guided by a CMAES
CMAES as an evolutionary algorithm [59] applies iterative optimization by sampling population involving solutions obtained from multi-dimensional normal distribution. CMAES is dependent on a means vector m and a covariance matrix C using a step size [60]. The pseudocode of CMAES is shown in Algorithm 1. Details of CMAES are provided in [61]. In CMAES, each candidate solution encodes the internal parameters of the machine learning model in the form , where is the hyperparameter number of the machine learning model. Table 5 shows the internal parameters and their respective description and range.
| Algorithm 1. Pseudocode of the CMAES searches the internal parameters of the machine learning models. |
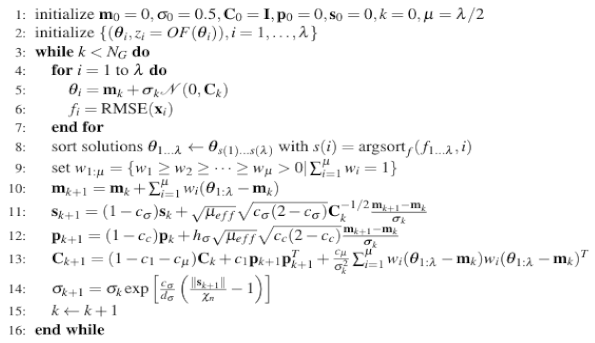 |

Table 5.
Encoding of candidate solutions. The column IP indicates the internal parameter in the CMAES encoding.
Root mean squared error (RMSE) between simulated and actual values is used as the objective function in CMAES to evaluate the solutions. For assessing an individual’s fitness, 5-fold was set and cross validation was employed. In this method, data are randomly split into 5 subsets. The machine learning model using the internal parameter vector is trained using 4 subsets, and the remaining subset is used for RMSE calculation. The process is iterated 5 times and the average RMSE is computed. According to the RMSE, the population is evolved over generations. The objective is the estimate of the optimal parameter with the least RMSE. At each iteration , the parameters , , and are updated considering the evaluated population based on the algorithm (see Algorithm 1). Figure 3 shows the architecture of the proposed approach and the integration of CMAES with machine learning models. The training modeling phase involves fine tuning the internal estimator parameters using the CMAES. The model decoded from the best individual is employed for predictions during testing.
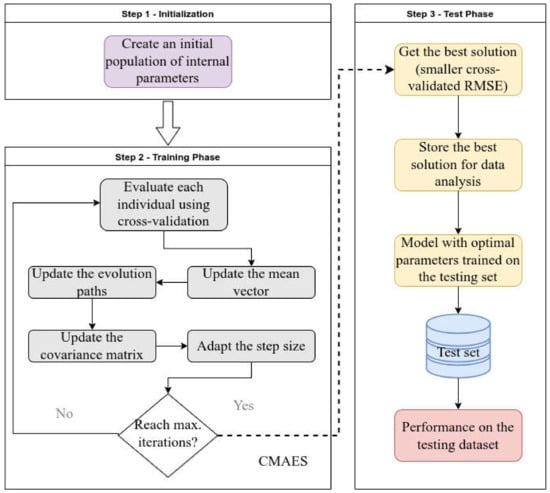
Figure 3.
Framework used in this paper showing the combination of the CMAES evolutionary algorithm and the machine learning models.
2.4. Performance Metrics
Six metrics are used in this paper to assess the model’s performance. Table 6 represents the metrics applied and their expressions. In Table 6, MAE, RRMSE, and WI represent the mean absolute error, relative root mean squared error, and agreement index, respectively [62]. MAPE and NSE refer to the mean absolute percentage error and Nash–Sutcliffe efficiency [63]. KGE represents the Kling–Gupta efficiency between simulated and observed values [64]. The metrics used in this study were commonly and successfully used in recent years to model streamflow and hydrological variables [65,66,67]. The purpose of using multiple metrics was to show that the optimized models present good performance in many aspects. KGE and NSE metrics were explicitly developed for hydrological modeling and are used by hydrologists for decision making regarding the accuracy and consistency of models. MAE and MAPE metrics are widely used in machine learning research. RRMSE allows for evaluating the performance of models in rivers with flows of different magnitudes and is helpful in cases where it is desired to assess the performance of the same model and rivers with wide channels (higher flows) or narrow ones (smaller flows). The WI index represents the ratio between the mean square error and the potential error and brings relevant information to specialists/hydrologists in the analysis of the calibration of forecast models. In Table 6, Oi and Pi represent observation and prediction, respectively. O represents observation mean, r represents Pearson product–moment correlation coefficient, a is the standard deviation (SD) of the predictions, and the SD of observation. B is the ratio of the prediction and observation means.

Table 6.
Performance metrics used in the study.
3. Results and Discussion
3.1. Results
This section presents the results and compares the performances of seven machine learning methods tuned by CMAES: ELM, EN, GPR, LSSVR, RBFNN, SVR, and XGB for predicting monthly streamflow. Methods were assessed considering the metrics given in Table 6. Various internal parameters were attempted in order to reach the optimal models for each method and input case. Table 5 sums up the considered ranges of the internal parameters.
Figure 4 displays the SVR internal parameters C, g, and e. C refers to the penalization parameter, e defines the penalization related to training loss function, and g refers to the kernel coefficient. Analyzing the boxplots, the distributions of the parameters g and e are similar in both cases. In addition, the parameter values of C are higher for Case 1 compared to other cases. C as a regularization parameter has an important role in support vector machines. The strength of regularization is directly proportional to 1/C. Thus, the estimations are smoother for Case 0 compared to Case 1. The lower RMSE for Case 1 illustrated in the bar plots in Figure 4 (averaged in 50 runs) supports this interpretation.
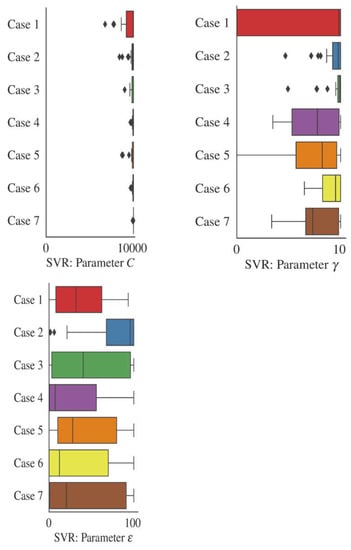
Figure 4.
Distribution of the internal parameters for the SVR models over 50 independent runs. Each color represents a case study in Table 2. Black diamond shapes represent outliers.
Test outcomes of the optimal hybrid ELM, EN, GPR, LSSVR, RBFNN, SVR, and XGB models calibrated by CMAES are shown in Table 7, Table 8, Table 9, Table 10, Table 11, Table 12 and Table 13 for seven input cases. For input Case 1 (Table 7), SVR showed the best accuracy with the lowest RRMSE (0.375), MAE (412.98), and MAPE (25.91), and the highest WI (0.970), NSE (0.876), and KGE (0.915) in streamflow prediction, and the GPR follows it. At the same time, the EN acts worse than the other models. In other temperature-based input cases, the SVR offers the best accuracy, generally having the lowest SD (values within brackets). The models’ efficiency decreases by adding more temperature inputs (from input Case 1 to 3), whereas the Tt−12 input decreases the prediction results. The third input case provides the highest accuracy for all models among the temperature inputs. The temperature-based SVR model (input Case 3 with Tt−11, Tt−1, and Tt) has the lowest RRMSE (0.290), MAE (289.21), and the highest WI (0.981), NSE (0.925), and KGE (0.962), and EN provides the worst efficiency. From input Case 1 to Case 3, improvements in the RRMSE (NSE) accuracy of the ELM, EN, GPR, LSSVR, RBFNN, SVR, and XGB are 22.1 (6.8), 0.5 (0.6), 21.3 (5.8), 19.5 (5.3), 18.9 (5.3), 22.7 (5.6), and 14% (4%) in streamflow prediction, respectively. The best SVR model utilizing the input Case 3 improves the prediction accuracy (concerning RRMSE) by 7.3, 50, 4.3, 6.5, 7.6, and 12.9% compared to ELM, EN, GPR, LSSVR, RBFNN, and XGB, respectively.

Table 7.
Model results for Case 1.

Table 8.
Model results for Case 2.

Table 9.
Model results for Case 3.

Table 10.
Model results for Case 4.

Table 11.
Model results for Case 5.

Table 12.
Model results for Case 6.

Table 13.
Model results for Case 7.
Table 11, Table 12 and Table 13 sum up the testing outcomes of the implemented hybrid models for the discharge inputs (input Cases 5 to 7). The tables clearly show that only discharge (streamflow) of one previous month (Qt−1) is insufficient in modeling streamflow. However, inclusion of Qt−11 and Qt−12 considering correlation analysis considerably increases the models’ accuracies; increase (decrease) in RRMSE (NSE) of the ELM, EN, GPR, LSSVR, RBFNN, SVR, and XGB is 62 (68), 52 (64), 66 (94), 60 (50), 61 (96), 63 (73), and 55% (64%) from input Case 5 (Table 11) to input Case 7 (Table 13), respectively. The best discharge-based LSSVR model (input Case 7 with Qt−12, Qt−11, and Qt−1) has the lowest RRMSE (0.256) and MAE (255.54) and the highest WI (0.985) and NSE (0.942), while the GPR has the lowest MAPE (11.69) and the highest WI (0.985) and KGE (0.967). The LSSVR performs slightly better than the GPR. SVR also has good accuracy and closely follows the LSSVR and GPR in streamflow prediction, using only previous values as inputs.
Comparison of the outcomes provided by the temperature-based and discharge-based models reveals that the discharge-based models have higher accuracy than the temperature-based models; decrease in RRMSE from 0.290 (SVR) to 0.256 (LSSVR), in MAE from 289.21 (SVR) to 255.54 (LSSVR), in MAPE from 16.12 (SVR) to 11.69 (GPR) and increase in WI from 0.981 (SVR) to 0.985 (GPR), in NSE from 0.925 (SVR) to 0.942 (LSSVR), and in KGE from 0.962 (SVR) to 0.967 (GPR). However, TB models also provide good accuracy.
For Cases 1 to 7, Figure 5 depicts the scatterplots of the observed and best model (SVR)-predicted streamflow in the test stage. As clearly observed from the graphs, temperature-based models also provide good predictions, especially with input Case 3. Considerable improvement in prediction efficiency by including Qt−11 and Qt−12 inputs (Case 6 and 7) is observed. Figure 6 illustrates the radar charts of the metrics used for model assessments. They were obtained, averaging over 50 runs for each method. These graphs were provided for visually justifying the statistics given in Table 7, Table 8, Table 9, Table 10, Table 11, Table 12 and Table 13.
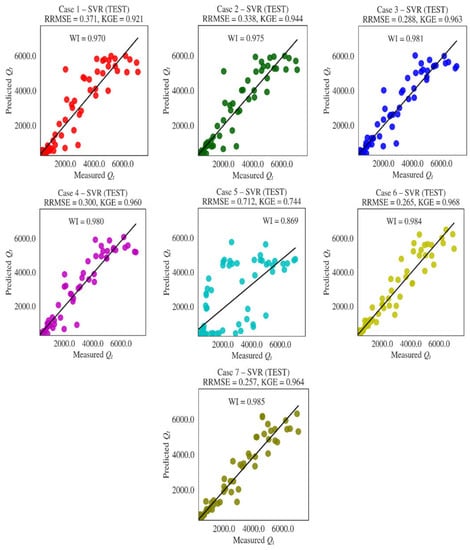
Figure 5.
Scatterplots of the observed and predicted streamflow by the best models in the test stage.
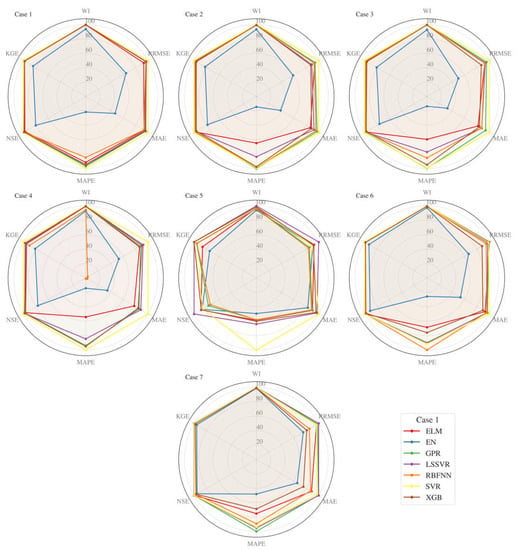
Figure 6.
Radar charts for all metrics (averaged over 50 runs).
The lowest accuracy of EN is observed from the charts, while the SVR generally provides superior accuracy. In some cases (Case 6 and 7), the LSSVR and XGB may perform better than the SVR. Taylor diagrams of the optimal models for all cases (averaged over 50 runs) are given in Figure 7. The diagrams show that the SVR generally has the lowest square error, highest association, and similar SD to observation than the other models. The inferior output of EN is depicted in the diagrams.
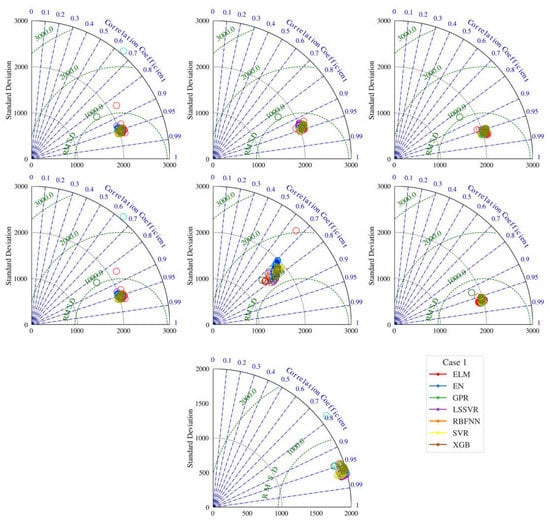
Figure 7.
Taylor diagrams of the optimal models for all cases (averaged over 50 runs).
3.2. Uncertainty Analysis
The uncertainty analysis is based on the logarithm of the prediction errors for the test dataset that are used to calculate the mean and standard deviation of the prediction errors given by:
and
where and are the mean and standard deviation of the logarithm errors, is the measured streamflow and is the predicted streamflow for the th sample. Using the error above, an approximately 95% confidence band around the predicted value is defined by .
The uncertainty analysis allows for comparing the proposed models and the input cases in this study. Table 14 presents a quantitative evaluation of uncertainties in river flow forecasting for each machine learning model and each input case to see the effects of the uncertainty study, the models’ mean prediction errors, the width of the uncertainty band, and the 95% prediction interval error. Negative mean prediction error averages indicate that the prediction models underestimated the observed values. On the other hand, positive values indicate that they overestimated the outcomes. Smaller mean predicted errors represent the ability to model the streamflow. The SVR model leads to smaller overall mean prediction errors for all input cases. The uncertainty bands for both models ranged from 0.071 to 0.320, with SVR, XGB, LSSVR, and RBFNN models having smaller uncertainty bands.

Table 14.
Uncertainty estimates for machine learning models.
In the experiments conducted for this research, the variations of the input parameters were modeled using the uniform distribution with the lower and upper bounds given by the minimum and maximum values for each parameter, as shown in Table 1. The deterministic outcome is calculated for each model developed in this paper for each MCS run. A total of 250,000 outcomes were calculated. The mean absolute deviation (MAD) around the median of the output distribution is written as
while the uncertainty of the model output can be given by
where Qtpi is the predicted streamflow for the ith sample. A detailed description of the MCS method can be found in [68]. Uncertainty analysis results for the Qt using the developed models are presented in Table 14. The uncertainty analysis shows that the SVR generally has lower uncertainty than other machine learning methods in streamflow prediction, except for the EN. Even though EN has the lowest uncertainty, its prediction efficiency is very low in all cases. It is clear from the figure that the SVR generally has lower uncertainty compared to other methods. Additionally, increasing input parameters increases the methods’ prediction efficiency (decrease in RMSE).
Table 15 shows the uncertainty analysis using the Monte Carlo simulation. The uncertainty analysis shows that SVR, LSSVR, GPR, and XGB produced lower uncertainty than other machine learning methods in streamflow prediction. Figure 8 shows the scatterplot of uncertainty (%) and relative root mean squared error for all models. Each pair (x,y) represents a particular model, depicted differently. The size of the point represents the number of features in the model. To facilitate the visualization, Cases 1–7 are shrunk to C1–C7. The scatter plots presented in Figure 8 show that the machine learning models using the input Cases 6 and 7 are near the left bottom corner of the figure, indicating that the input of these cases produced models with smaller uncertainty and smaller RRMSE. Cases C2 and C3 lead to models with higher uncertainties and moderate RRMSE. In contrast, input Case 5, although producing models with small uncertainties, leads to higher RRMSE values.

Table 15.
Uncertainty analysis for the test set using Monte Carlo simulation (MCS).
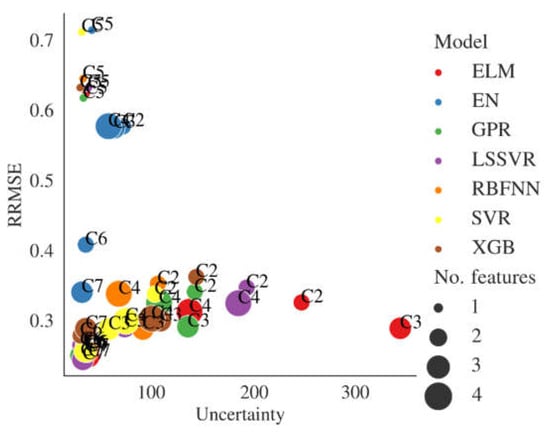
Figure 8.
Scatter plots comparing the uncertainty and root mean squared error for all models.
3.3. Discussion
By the presented study, the accuracy of seven machine learning methods, ELM, EN, GPR, SVR, LSSVR, XGB, and RBFNN, tuned with covariance matrix adaptation evolution strategy, was assessed and compared in streamflow prediction considering different input combinations involving temperature and previous discharge values. The inputs of the models were decided using correlation analysis and it was observed that this method is very useful in the determination of the most suitable inputs for the machine learning methods. This finding is consistent with the previous research [25,69,70,71,72], which reported the necessity of correlation analysis in defining optimal inputs. It is clearly observed from quantitative and graphical assessments that the EN method provides inferior predictions. The low accuracy of the EN method may be explained by its linear structure, which prevents it from adequately mapping the streamflow phenomenon. It is observed from statistical and graphical comparison that the temperature-based models also provide good accuracy in streamflow prediction. They can be considered better alternatives to the discharge-based models, especially in case of unavailability of discharge (streamflow) data. Measuring streamflow is a very difficult task, especially in developing countries, for technical reasons. In such cases, temperature-based models can be successfully implemented. The results align with the earlier studies [25,72]. Adnan et al. [25] employed LSSVR, MARS, and optimally pruned ELM and M5 model trees in streamflow prediction and found good accuracies from the temperature-based models. In the study by Adnan et al. [72], they implemented the group method of data handling neural networks, dynamic evolving neural fuzzy system, and MARS methods in monthly streamflow prediction. They obtained promising accuracies from the temperature-based models. An advantage of using the machine learning model is the accurate streamflow prediction commonly reported in the literature. On the other hand, the machine learning model’s performance mainly depends on the proper choice of internal parameters, which is a challenge for data modelers. Moreover, parameters can vary across different data sets and result in performance disparities. In this context, an advantage of the proposed approach is the automatic adjustment of models’ parameters through the CMAES algorithm, allowing for the exploitation of the models’ capabilities, considering the data’s specificities. Furthermore, the proposed strategy employs a cross-validation strategy to avoid data leakage, providing a realistic forecast of monthly flow data. However, the lack of interpretability is an intrinsic aspect of machine learning models. Although they produce accurate predictions, the relationships between input and output variables are challenging for humans to interpret. Although they have a rigid and concise mathematical formulation, machine learning models can be built with several data processing procedures, which makes a posteriori analysis difficult.
Adnan et al. [5] compared the accuracy of optimally pruned ELM, MARS, ANN, M5 model tree, and neuro-fuzzy tuned with particle swarm optimization in streamflow prediction, and the best ELM gave the NSE of 0.761 and 0.711 for the Fujiangqiao and Shehang stations in China. Adnan et al. [27] compared the abovementioned machine learning methods and they obtained an NSE of 0.886 from the best MARS model, which uses precipitation, temperature, and streamflow inputs in prediction streamflow. Adnan et al. [72] assessed the abovementioned three machine learning methods in streamflow prediction and they found that the dynamic evolving neural fuzzy system performed the best with the NSE of 0.915. Compared to the abovementioned studies, the accuracy of the best SVR-CMAES model developed in this study seems promising, with the NSE of 0.937.
4. Conclusions
- -
- This research evaluated the feasibility of seven hybrid machine learning methods in monthly streamflow forecasting. In the hybridization process, the metaheuristic covariance matrix adaptation evolution strategy assisted in adjusting the internal parameters of the models. In addition, an uncertainty analysis was performed on the resulting models. Methods were compared to each other considering the several metrics (e.g., WI, RRMSE, MAE, MAPE, NSE, and KGE together with standard deviation) and visual methods, such as radar chart, scatter, and Taylor diagrams. Seven input cases were taken into account, including temperature and discharge data. All the implemented methods provided better efficiency for discharge input cases, while temperature input cases also produced promising predictions. Among the implemented methods, the SVR generally performed superior to the other methods, especially for the temperature input cases. In contrast, the LSSVR and GPR were found to do better than the SVR in some discharge input cases. The EN method provided the worst streamflow predictions, according to all evaluation statistics and visual comparison. Uncertainty analysis revealed that the SVR generally has low uncertainty compared to other machine learning methods and the EN has the lowest uncertainty. Overall, temperature-based SVR models are highly recommended in monthly streamflow prediction. These outcomes are very useful in practical applications, especially in developing countries. Temperature data are easily measured, and the models that only use such data will be very beneficial for streamflow predictions in the basins where streamflow data are missing because of technical/economic reasons. The main limitation of this study is the use of limited data from one location. More data from different climatic regions are required to justify the accuracy of the proposed models. The covariance matrix adaptation evolution strategy was successfully applied for improving the accuracy of the ELM, EN, GPR, LSSVR, RBFNN, SVR, and XGB methods. This strategy can also be employed for other machine learning methods, such as ANN, ANFIS, and deep learning in future studies.
Author Contributions
Conceptualization: R.M.A.I., O.K. and L.G.; formal analysis: L.G., S.S. and O.K.; validation: O.K., L.G. and R.M.A.I.; supervision: O.K. and S.T.; writing—original draft: O.K., L.G. and R.M.A.I.; visualization: R.M.A.I. and S.T.; investigation: O.K., S.S. and S.T. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
The data presented in this study will be available on an interesting request from the corresponding author.
Conflicts of Interest
There is no conflict of interest in this study.
References
- Erdal, H.I.; Karakurt, O. Advancing monthly streamflow prediction accuracy of CART models using ensemble learning paradigms. J. Hydrol. 2013, 477, 119–128. [Google Scholar] [CrossRef]
- Yaseen, Z.M.; El-Shafie, A.; Jaafar, O.; Afan, H.A.; Sayl, K.N. Artificial intelligence based models for stream-flow forecasting: 2000–2015. J. Hydrol. 2015, 530, 829–844. [Google Scholar] [CrossRef]
- Rasouli, K.; Hsieh, W.W.; Cannon, A.J. Daily streamflow forecasting by machine learning methods with weather and climate inputs. J. Hydrol. 2012, 414–415, 284–293. [Google Scholar] [CrossRef]
- Liu, Z.; Zhou, P.; Zhang, Y. A Probabilistic Wavelet–Support Vector Regression Model for Streamflow Forecasting with Rainfall and Climate Information Input. J. Hydrometeorol. 2015, 16, 2209–2229. [Google Scholar] [CrossRef]
- Adnan, R.M.; Liang, Z.; Trajkovic, S.; Zounemat-Kermani, M.; Li, B.; Kisi, O. Daily streamflow prediction using optimally pruned extreme learning machine. J. Hydrol. 2019, 577, 123981. [Google Scholar] [CrossRef]
- Kisi, O.; Heddam, S.; Keshtegar, B.; Piri, J.; Adnan, R.M. Predicting Daily Streamflow in a Cold Climate Using a Novel Data Mining Technique: Radial M5 Model Tree. Water 2022, 14, 1449. [Google Scholar] [CrossRef]
- Faye, C. Comparative Analysis of Meteorological Drought Based on the SPI and SPEI Indices; Ziguinchor University: Ziguinchor, Senegal, 2022. [Google Scholar]
- Dawson, C.; Wilby, R. An artificial neural network approach to rainfall-runoff modelling. Hydrol. Sci. J. 1998, 43, 47–66. [Google Scholar] [CrossRef]
- Demirel, M.C.; Venancio, A.; Kahya, E. Flow forecast by SWAT model and ANN in Pracana basin, Portugal. Adv. Eng. Softw. 2009, 40, 467–473. [Google Scholar] [CrossRef]
- Bhadra, A.; Bandyopadhyay, A.; Singh, R.; Raghuwanshi, N.S. Rainfall-Runoff Modeling: Comparison of Two Approaches with Different Data Requirements. Water Resour. Manag. 2010, 24, 37–62. [Google Scholar] [CrossRef]
- Sudheer, C.; Maheswaran, R.; Panigrahi, B.K.; Mathur, S. A hybrid SVM-PSO model for forecasting monthly streamflow. Neural Comput. Appl. 2014, 24, 1381–1389. [Google Scholar] [CrossRef]
- Raghavendra, N.S.; Deka, P.C. Support vector machine applications in the field of hydrology: A review. Appl. Soft Comput. 2014, 19, 372–386. [Google Scholar] [CrossRef]
- Nourani, V.; Baghanam, A.H.; Adamowski, J.; Kisi, O. Applications of hybrid wavelet–Artificial Intelligence models in hydrology: A review. J. Hydrol. 2014, 514, 358–377. [Google Scholar] [CrossRef]
- Ibrahim, K.S.M.H.; Huang, Y.F.; Ahmed, A.N.; Koo, C.H.; El-Shafie, A. A review of the hybrid artificial intelligence and optimization modelling of hydrological streamflow forecasting. Alex. Eng. J. 2021, 61, 279–303. [Google Scholar] [CrossRef]
- Kagoda, P.A.; Ndiritu, J.; Ntuli, C.; Mwaka, B. Application of radial basis function neural networks to short-term streamflow forecasting. Phys. Chem. Earth Parts A/B/C 2010, 35, 571–581. [Google Scholar] [CrossRef]
- Sun, A.Y.; Wang, D.; Xu, X. Monthly streamflow forecasting using Gaussian Process Regression. J. Hydrol. 2014, 511, 72–81. [Google Scholar] [CrossRef]
- Mehr, A.D.; Kahya, E.; Şahin, A.; Nazemosadat, M.J. Successive-station monthly streamflow prediction using different artificial neural network algorithms. Int. J. Environ. Sci. Technol. 2015, 12, 2191–2200. [Google Scholar] [CrossRef]
- Kisi, O. Streamflow Forecasting and Estimation Using Least Square Support Vector Regression and Adaptive Neuro-Fuzzy Embedded Fuzzy c-means Clustering. Water Resour. Manag. 2015, 29, 5109–5127. [Google Scholar] [CrossRef]
- Yaseen, Z.M.; Kisi, O.; Demir, V. Enhancing Long-Term Streamflow Forecasting and Predicting using Periodicity Data Component: Application of Artificial Intelligence. Water Resour. Manag. 2016, 30, 4125–4151. [Google Scholar] [CrossRef]
- Modaresi, F.; Araghinejad, S.; Ebrahimi, K. A Comparative Assessment of Artificial Neural Network, Generalized Regression Neural Network, Least-Square Support Vector Regression, and K-Nearest Neighbor Regression for Monthly Streamflow Forecasting in Linear and Nonlinear Conditions. Water Resour. Manag. 2018, 32, 243–258. [Google Scholar] [CrossRef]
- Worland, S.C.; Farmer, W.; Kiang, J.E. Improving predictions of hydrological low-flow indices in ungaged basins using machine learning. Environ. Model. Softw. 2018, 101, 169–182. [Google Scholar] [CrossRef]
- Hadi, S.J.; Abba, S.I.; Sammen, S.S.; Salih, S.Q.; Al-Ansari, N.; Yaseen, Z.M. Non-Linear Input Variable Selection Approach Integrated With Non-Tuned Data Intelligence Model for Streamflow Pattern Simulation. IEEE Access 2019, 7, 141533–141548. [Google Scholar] [CrossRef]
- Li, Y.; Liang, Z.; Hu, Y.; Li, B.; Xu, B.; Wang, D. A multi-model integration method for monthly streamflow prediction: Modified stacking ensemble strategy. J. Hydroinform. 2020, 22, 310–326. [Google Scholar] [CrossRef]
- Ni, L.; Wang, D.; Wu, J.; Wang, Y.; Tao, Y.; Zhang, J.; Liu, J. Streamflow forecasting using extreme gradient boosting model coupled with Gaussian mixture model. J. Hydrol. 2020, 586, 124901. [Google Scholar] [CrossRef]
- Adnan, R.M.; Liang, Z.; Heddam, S.; Zounemat-Kermani, M.; Kisi, O.; Li, B. Least square support vector machine and multivariate adaptive regression splines for streamflow prediction in mountainous basin using hydro-meteorological data as inputs. J. Hydrol. 2020, 586, 124371. [Google Scholar] [CrossRef]
- Thapa, S.; Zhao, Z.; Li, B.; Lu, L.; Fu, D.; Shi, X.; Tang, B.; Qi, H. Snowmelt-Driven Streamflow Prediction Using Machine Learning Techniques (LSTM, NARX, GPR, and SVR). Water 2020, 12, 1734. [Google Scholar] [CrossRef]
- Jiang, Y.; Bao, X.; Hao, S.; Zhao, H.; Li, X.; Wu, X. Monthly Streamflow Forecasting Using ELM-IPSO Based on Phase Space Reconstruction. Water Resour. Manag. 2020, 34, 3515–3531. [Google Scholar] [CrossRef]
- Malik, A.; Tikhamarine, Y.; Souag-Gamane, D.; Kisi, O.; Pham, Q.B. Support vector regression optimized by meta-heuristic algorithms for daily streamflow prediction. Stoch. Hydrol. Hydraul. 2020, 34, 1755–1773. [Google Scholar] [CrossRef]
- Parisouj, P.; Mohebzadeh, H.; Lee, T. Employing Machine Learning Algorithms for Streamflow Prediction: A Case Study of Four River Basins with Different Climatic Zones in the United States. Water Resour. Manag. 2020, 34, 4113–4131. [Google Scholar] [CrossRef]
- Niu, W.-J.; Feng, Z.-K. Evaluating the performances of several artificial intelligence methods in forecasting daily streamflow time series for sustainable water resources management. Sustain. Cities Soc. 2021, 64, 102562. [Google Scholar] [CrossRef]
- Jiang, Q.; Cheng, Y.; Le, H.; Li, C.; Liu, P.X. A Stacking Learning Model Based on Multiple Similar Days for Short-Term Load Forecasting. Mathematics 2022, 10, 2446. [Google Scholar] [CrossRef]
- Yang, C.-H.; Shao, J.-C.; Liu, Y.-H.; Jou, P.-H.; Lin, Y.-D. Application of Fuzzy-Based Support Vector Regression to Forecast of International Airport Freight Volumes. Mathematics 2022, 10, 2399. [Google Scholar] [CrossRef]
- Su, H.; Peng, X.; Liu, H.; Quan, H.; Wu, K.; Chen, Z. Multi-Step-Ahead Electricity Price Forecasting Based on Temporal Graph Convolutional Network. Mathematics 2022, 10, 2366. [Google Scholar] [CrossRef]
- De-Prado-Gil, J.; Zaid, O.; Palencia, C.; Martínez-García, R. Prediction of Splitting Tensile Strength of Self-Compacting Recycled Aggregate Concrete Using Novel Deep Learning Methods. Mathematics 2022, 10, 2245. [Google Scholar] [CrossRef]
- Samadianfard, S.; Jarhan, S.; Salwana, E.; Mosavi, A.; Shamshirband, S.; Akib, S. Support Vector Regression Integrated with Fruit Fly Optimization Algorithm for River Flow Forecasting in Lake Urmia Basin. Water 2019, 11, 1934. [Google Scholar] [CrossRef]
- Tikhamarine, Y.; Souag-Gamane, D.; Kisi, O. A new intelligent method for monthly streamflow prediction: Hybrid wavelet support vector regression based on grey wolf optimizer (WSVR–GWO). Arab. J. Geosci. 2019, 12, 540. [Google Scholar] [CrossRef]
- Hansen, N.; Müller, S.D.; Koumoutsakos, P. Reducing the Time Complexity of the Derandomized Evolution Strategy with Covariance Matrix Adaptation (CMA-ES). Evol. Comput. 2003, 11, 1–18. [Google Scholar] [CrossRef]
- Rouchier, S.; Woloszyn, M.; Kedowide, Y.; Bejat, T. Identification of the hygrothermal properties of a building envelope material by the covariance matrix adaptation evolution strategy. J. Build. Perform. Simul. 2016, 9, 101–114. [Google Scholar] [CrossRef]
- Liang, Y.; Wang, X.; Zhao, H.; Han, T.; Wei, Z.; Li, Y. A covariance matrix adaptation evolution strategy variant and its engineering application. Appl. Soft Comput. 2019, 83, 105680. [Google Scholar] [CrossRef]
- Chen, G.; Li, S.; Wang, X. Source mask optimization using the covariance matrix adaptation evolution strategy. Opt. Express 2020, 28, 33371–33389. [Google Scholar] [CrossRef]
- Kaveh, A.; Javadi, S.M.; Moghanni, R.M. Reliability Analysis via an Optimal Covariance Matrix Adaptation Evolution Strategy: Emphasis on Applications in Civil Engineering. Period. Polytech. Civ. Eng. 2020, 64, 579–588. [Google Scholar] [CrossRef]
- Hastie, T.; Tibshirani, R.; Friedman, J.H.; Friedman, J.H. The Elements of Statistical Learning-Data Mining, Inference, and Prediction, 2nd ed.; Springer: New York, NY, USA, 2009. [Google Scholar]
- Zou, H.; Hastie, T. Regularization and Variable Selection via the Elastic Net. J. R. Stat. Soc. 2005, 67, 301–320. [Google Scholar] [CrossRef]
- Guo, P.; Cheng, W.; Wang, Y. Hybrid evolutionary algorithm with extreme machine learning fitness function evaluation for two-stage capacitated facility location problems. Expert Syst. Appl. 2017, 71, 57–68. [Google Scholar] [CrossRef]
- Saporetti, C.M.; Duarte, G.R.; Fonseca, T.L.; Da Fonseca, L.G.; Pereira, E. Extreme Learning Machine combined with a Differential Evolution algorithm for lithology identification. RITA 2018, 25, 43–56. [Google Scholar] [CrossRef]
- Huang, G.; Huang, G.-B.; Song, S.; You, K. Trends in extreme learning machines: A review. Neural Netw. 2015, 61 (Suppl. C), 32–48. [Google Scholar] [CrossRef]
- Suykens, J.A.K.; Vandewalle, J. Least Squares Support Vector Machine Classifiers. Neural Process. Lett. 1999, 9, 293–300. [Google Scholar] [CrossRef]
- Chang, C.C.; Lin, C.J. LIBSVM: A Library for Support Vector Machines. ACM Trans. Intell. Syst. Technol. 2011, 2, 1–27. [Google Scholar] [CrossRef]
- Karthikeyan, M.; Vyas, R. Machine learning methods in chemoinformatics for drug discovery. In Practical Chemoinformatics; Springer: Berlin/Heidelberg, Germany, 2014; pp. 133–194. [Google Scholar] [CrossRef]
- Gunn, S.R. Support Vector Machines for Classification and Regression. ISIS Tech. Rep. 1998, 14, 5–16. [Google Scholar]
- Kargar, K.; Samadianfard, S.; Parsa, J.; Nabipour, N.; Shamshirband, S.; Mosavi, A.; Chau, K.-W. Estimating longitudinal dispersion coefficient in natural streams using empirical models and machine learning algorithms. Eng. Appl. Comput. Fluid Mech. 2020, 14, 311–322. [Google Scholar] [CrossRef]
- Broomhead, D.S.; Lowe, D. Radial basis functions, multi-variable functional interpolation and adaptive networks. In Royal Signals; Radar Establishment Malvern: Malvern, UK, 1988. [Google Scholar]
- Chen, T.; Guestrin, C. XGBoost: A Scalable Tree Boosting System. In Proceedings of the 22nd ACM Sigkdd International Conference on Knowledge Discovery and Data Mining, San Francisco, CA, USA, 13–17 August 2016; KDD’16. ACM: New York, NY, USA, 2016; pp. 785–794. [Google Scholar]
- Chen, T.; He, T. Higgs boson discovery with boosted trees. In NIPS 2014 Workshop on High-Energy Physics and Machine Learning; PMLR: London, UK, 2015; pp. 69–80. [Google Scholar]
- Ou, X.; Morris, J.; Martin, E. Gaussian Process Regression for Batch Process Modelling. IFAC Proc. Vol. 2004, 37, 817–822. [Google Scholar] [CrossRef]
- Wang, B.; Chen, T. Gaussian process regression with multiple response variables. Chemom. Intell. Lab. Syst. 2015, 142, 159–165. [Google Scholar] [CrossRef]
- Schulz, E.; Speekenbrink, M.; Krause, A. A Tutorial on Gaussian Process Regression: Modelling, Exploring, and Exploiting Functions. J. Math. Psychol. 2018, 85, 1–16. [Google Scholar] [CrossRef]
- Kumar, R. The generalized modified Bessel function and its connection with Voigt line profile and Humbert functions. Adv. Appl. Math. 2020, 114, 101986. [Google Scholar] [CrossRef]
- Hansen, N.; Ostermeier, A. Completely Derandomized Self-Adaptation in Evolution Strategies. Evol. Comput. 2001, 9, 159–195. [Google Scholar] [CrossRef] [PubMed]
- Beyer, H.G.; Schwefel, H.P. Evolution Strategies–a Comprehensive Introduction. Nat. Comput. 2002, 1, 3–52. [Google Scholar] [CrossRef]
- Li, Z.; Zhang, Q.; Lin, X.; Zhen, H.-L. Fast Covariance Matrix Adaptation for Large-Scale Black-Box Optimization. IEEE Trans. Cybern. 2018, 50, 2073–2083. [Google Scholar] [CrossRef]
- Willmott, C.J. ON the Validation of Models. Phys. Geogr. 1981, 2, 184–194. [Google Scholar] [CrossRef]
- Nash, J.E.; Sutcliffe, J.V. River flow forecasting through conceptual models part I—A discussion of principles. J. Hydrol. 1970, 10, 282–290. [Google Scholar] [CrossRef]
- Gupta, H.V.; Kling, H.; Yilmaz, K.K.; Martinez, G.F. Decomposition of the mean squared error and NSE performance criteria: Implications for improving hydrological modelling. J. Hydrol. 2009, 377, 80–91. [Google Scholar] [CrossRef]
- Kisi, O.; Shiri, J.; Karimi, S.; Adnan, R.M. Three different adaptive neuro fuzzy computing techniques for forecasting long-period daily streamflows. In Big Data in Engineering Applications; Springer: Singapore, 2018; pp. 303–321. [Google Scholar] [CrossRef]
- Alizamir, M.; Kisi, O.; Adnan, R.M.; Kuriqi, A. Modelling reference evapotranspiration by combining neuro-fuzzy and evolutionary strategies. Acta Geophys. 2020, 68, 1113–1126. [Google Scholar] [CrossRef]
- Yuan, X.; Chen, C.; Lei, X.; Yuan, Y.; Muhammad Adnan, R. Monthly runoff forecasting based on LSTM–ALO model. Stoch. Environ. Res. Risk Assess. 2018, 32, 2199–2212. [Google Scholar] [CrossRef]
- Sattar, A.M.; Gharabaghi, B. Gene expression models for prediction of longitudinal dispersion coefficient in streams. J. Hydrol. 2015, 524, 587–596. [Google Scholar] [CrossRef]
- Sudheer, K.P.; Gosain, A.K.; Ramasastri, K.S. A data-driven algorithm for constructing artificial neural network rainfall-runoff models. Hydrol. Process. 2002, 16, 1325–1330. [Google Scholar] [CrossRef]
- Kisi, O. Constructing neural network sediment estimation models using a data-driven algorithm. Math. Comput. Simul. 2008, 79, 94–103. [Google Scholar] [CrossRef]
- Wu, C.; Chau, K. Prediction of rainfall time series using modular soft computingmethods. Eng. Appl. Artif. Intell. 2013, 26, 997–1007. [Google Scholar] [CrossRef]
- Adnan, R.M.; Liang, Z.; Parmar, K.S.; Soni, K.; Kisi, O. Modeling monthly streamflow in mountainous basin by MARS, GMDH-NN and DENFIS using hydroclimatic data. Neural Comput. Appl. 2021, 33, 2853–2871. [Google Scholar] [CrossRef]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).