Abstract
Vaccinations are one of the most important steps in combat against viral diseases such as COVID-19. Determining the influence of the number of vaccinated patients on the infected population represents a complex problem. For this reason, the aim of this research is to model the influence of the total number of vaccinated or fully vaccinated patients on the number of infected and deceased patients. Five separate modeling algorithms are used: Linear Regression (LR), Logistic Regression (LogR), Least Absolute Shrinkage and Selection Operator (LASSO), Multilayer Perceptron (MLP), and Support Vector Regression (SVR). Cross-correlation analysis is performed to determine the optimal lags in data to assist in obtaining better scores. The cross-validation of models is performed, and the models are evaluated using Mean Absolute Percentage Error (MAPE). The modeling is performed for four different countries: Germany, India, the United Kingdom (UK), and the United States of America (USA). Models with an error below 1% are found for all the modeled cases, with the best models being achieved either by LR or MLP methods. The obtained results indicate that the influence of vaccination rates on the number of confirmed and deceased patients exists and can be modeled using ML methods with relatively high precision.
Keywords:
COVID-19; cross-correlation analysis; machine learning; regression modeling; vaccination rates MSC:
68T01
1. Introduction
COVID-19 is a viral disease caused by the SARS-COV-2 virus [1]. It first appeared in China in December of 2019, soon spreading to other countries [2]. World Health Organization (WHO) pronounced COVID-19 a global pandemic in March of 2020 [3]. Many measures have been taken to combat the spread of COVID-19 since the beginning of the pandemic, including the introduction of mandatory personal hygienic measures [4], mask-wearing [5], internal and external travel restrictions [6] and lockdowns [7]. An important step in the development of measures combating COVID-19 is the development and introduction of vaccines for the disease [8]. Various vaccines were developed, and the vaccination efforts started at the end of 2020 [9]. It is hard to determine the influence of vaccination rates on the spread of viral diseases such as COVID-19 [9,10]. The creation of predictive models for such a problem is a complex issue due to many interacting factors [11,12]. The development of such models is a goal of this paper. The main motivation is to create models that will enable the prediction of the future rates of infection and patient deaths based on the vaccination rates in the given country. This would enable further strategic planning regarding the hospital systems in the given countries because a high number of patients represents one of the biggest healthcare challenges related to the COVID-19 pandemic. Various regressive techniques have been utilized in the past to model the spread and influence of COVID-19. The regression methods, especially AI-based, have shown good results in modeling the COVID-19 spread. One of the earliest papers modeling the COVID-19 spread with AI-based algorithms is that of Car et al. [13]. The paper demonstrates the use of MLP for the modeling of confirmed, recovered, and deceased patients in various countries, with high accuracy. Rustam et al. [14] demonstrate the use of various techniques, including LR, LASSO, and SVR, to model the spread of COVID-19 in Iran. Mollalo et al. [15] apply the artificial neural network and LogR to model the incidence rates of COVID-19 in the USA, achieving high accuracy. Gupta and Gharehgozli [16] show the use of LR and SVR in modeling the spread of COVID-19 in the USA based on the population and weather variables, determining the existing correlation and presenting high-fidelity models. Onovo et al. [17] demonstrate the use of LASSO for statistical inference, using data provided by John Hopkins University for sub-Saharan Africa. The wealth of research in using machine learning techniques for the prediction of COVID-19 spread shows their value in modeling complex relations connected to COVID-19. Bagabir et al. [18] discuss many applications of AI regarding COVID-19, including genome sequencing and drug/vaccination development, noting it to be an indispensable tool. The comparisons between the goals of the aforementioned papers, results, and drawbacks are given in Table 1.

Table 1.
Comparison of goals, results, and drawbacks for discussed papers.
While some authors, namely Bharadwaj et al. [19], Ong [20] and Keshavarzi et al. [21], have suggested the use of computational and AI-based techniques to assist in vaccine development and adjustment, there is a distinct lack of papers exploring the use of AI to determine the influence of vaccination numbers on the infected population. Despite ML being a commonly referenced tool in the scope of COVID-19, as can be seen from Mariappan et al. [22], where the shipment times of vaccines are modeled using it, or Tong et al. [23], who use AI-assisted techniques to determine the antibody flow and quantitative detection, the direct modeling of the influence of vaccination rates on the number of patients is currently an unexplored area. Another area of AI use in relation to COVID-19 was the identification of misinformation shared on social media [24]. The spread of misinformation is an important factor that can have a high influence on the success of different governmental decisions, as it can influence the likelihood of people following the recommendations—such as vaccinations [25]. In this paper, the researchers propose the use of various regressive techniques to determine the models predicting the influence between the number of vaccinated or fully-vaccinated patients to the number of deceased and infected patients.
This paper poses the following research questions:
- Is there a correlation between the number of vaccinated, fully vaccinated, and boosted patients and the number of new confirmed and deceased cases?
- Can the above be modeled using AI-based regression methods?
- Does the use of cross-correlation determined lags (the time-shifts of discrete data points between the input and output datasets) enable better performance when regressing with AI-based regression methods?
The paper will first present the dataset used and the preprocessing performed on the data. Then, the used techniques and correlation analysis will be presented, followed by the presentation of the best-achieved results for each of the countries observed in the research—Germany, India, the United Kingdom, and the United States of America.
2. Materials and Methods
In this section, the used dataset is presented as well as used regression methods, cross-validation, and evaluation metrics.
2.1. Dataset
The dataset used in this research was made publicly available by Our World in Data website [26]. The dataset consists of various COVID-19-related metrics, such as the number of confirmed, deceased, and recovered cases, and other metrics, such as the population numbers, and the number of individuals in various age groups. Most importantly, for the presented research, the dataset contains the total numbers of partially vaccinated and fully vaccinated patients and boosted per country. The data in the dataset are updated daily.
For the regression modeling, the data were extracted for each of the countries of interest for this paper—USA, Germany, UK, and India. The countries were selected based on the differing vaccination approaches and geographical regions in an attempt to provide a wider image. The data of interest in the presented research are the total numbers of infected patients, deceased patients, vaccinated patients, fully vaccinated patients, and boosted patients. Fully vaccinated patients refer to those patients who have received both doses of the vaccines, which are administered in two doses and one dose of the Janssen COVID-19 vaccine [26,27]. Boosted patients refer to those patients who have received additional booster doses after the full vaccination [28]. The last date selected for the data used inside the models is 12 July 2022. Due to the different starting dates of vaccinations, this results in different amounts of data for each of the used countries. The exact length of data vectors for each country is given in Table 2.

Table 2.
The starting date of vaccination data in the dataset and the number of used data points per country.
The data from the dataset is shown in Figure 1 for each of the countries used. Each of the subfigures shows the number of vaccinated patients, fully vaccinated patients, and patients confirmed as infected and deceased patients. The trends for vaccinated patients (single vaccinations, full vaccinations and boosters) differ noticeably across all the analyzed countries. This indicates a difference in vaccination strategies and acceptance of vaccinations among the populace for each of the analyzed countries. Taking the difference in vaccination rates in comparison to the number of infected and deceased patients, it is clear that differences exist between analyzed countries in that area as well. This illustrates the differences between analyzed countries, in both the vaccination rates and infection rates, showing why they have been selected for modeling and analysis.
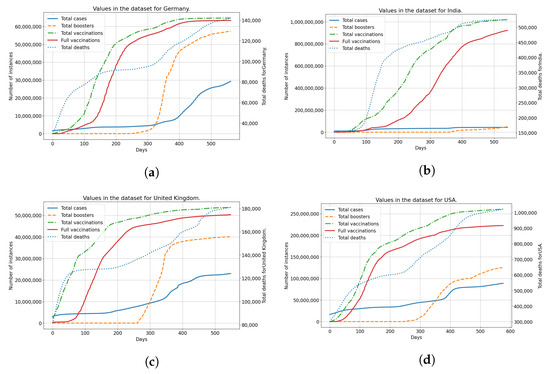
Figure 1.
The display of the data contained within the dataset for all used countries, including confirmed cases, deceased patients, vaccinated and fully vaccinated patients. (a) Data for Germany; (b) Data for India; (c) Data for United Kingdom; (d) Data for United States.
Cross-Correlation Analysis
To determine the lag between the two time-series (for example, confirmed patients and vaccinated patients in Germany) at which correlation is highest. If the is the first time series, and the is the second time series, cross-correlation can be calculated using [29]:
where the N is equal to the number of elements in a time series. The “full” cross-correlation is used, in which zero padding is applied to elements to calculate the cross-correlation values for each overlap of the two time-series. To obtain the correlation coefficient, normalized cross-correlation with time shift can be used, defined as the discrete normalized temporal cross-correlation, per [30]:
where M signifies the number of elements of and used to evaluate the correlation coefficient.
The modeling using AI-based regression methods will be performed for the delay calculated using the above-described method.
2.2. Regression Methods
This subsection will present a short description of the five used regression methods—LR, LogR, LASSO, MLP, and SVR. All the used algorithms have certain hyperparameters, which must be adjusted due to their high influence on the model quality [31]. This adjustment is performed in the same manner for all the algorithms, using the Grid Search (GS) procedure. GS takes the discrete vectors of possible hyperparameter values and creates the n-dimensional discrete hyperspace, where n is the number of adjusted hyperparameters [32]. Every possible hyperparameter combination, presented as a point in the hyperparameter space, is then used to create a model [33]. This approach allows for a quick test of various hyperparameters and is especially appropriate when most hyperparameters are defined discretely [34]. The individual values of each adjusted hyperparameter are given for each algorithm in the appropriate subsection.
2.2.1. Linear Regression
LR is a statistical or ML method that allows the determination of the linear regression model between two sets of data. The type of LR used in the presented work is the so-called Ordinary Least Squares LR. This means that the shape of the achieved model will be provided as [35]:
where and are model coefficients, is the predicted output vector, while the X is the input vector. Finally, represents the error vector, where each element corresponds to the error in the predicted element of the vector . The goal of the linear optimization may be defined as the minimization of the error terms for coefficients and in regards to , according to [36]:
and
This minimization allows the determination of the linear model with the lowest error for the given sets X and Y.
The hyperparameters of the LR that are adjusted are: fit intercept, which adjusts the intercept point of the model for X and Y; normalize, which normalizes the regressors by subtracting the mean and dividing by L2-norm; positive, which forces the coefficients of the LR to remain positive [37].
The possible values of adjusted hyperparameters for LR are given in Table 3.

Table 3.
Adjusted hyperparameters and their possible values for LR.
2.2.2. LASSO
LASSO is a linear regression model with an implementation of shrinkage, where data points are transformed towards the convergent central point, such as the data mean [38]. This allows the development of sparse models [39]. The model shape is given as:
The training of LASSO is performed similarly to the training of linear regression, the goal being the minimization of error , expressed as [40]:
The main visible difference is the addition of , the tuning parameter for regularization, which adds a penalty equal to the magnitude of coefficients. This parameter can assist with the elimination of unnecessary coefficients, resulting in sparser models [41].
Regarding the adjusted hyperparameters, they are equal to the LR, with the addition of the regularization parameter [37].
Table 4 provides the values of hyperparameters used in the presented research.

Table 4.
Adjusted hyperparameters and their possible values for LASSO.
2.2.3. Logistic Regression
LogR similarly fits the data to LR, with the difference that it uses a logistic function to fit the data [42]. LogR can show high performance for the prediction of probabilities [43]. The model shape of the LogR estimates the data through a multiple linear regression function as:
The hyperparameter values of LogR are similar to the LR and LASSO with the addition of two values: the parameter C and the Solver. The Solver represents the algorithm that is used to minimize and determine the models, while C is the regularization parameter [37].
The values of hyperparameters used in GS for LogR are given in Table 5.

Table 5.
Adjusted hyperparameters and their possible values for LogR.
2.2.4. Multilayer Perceptron
MLP is a feed-forward neural network consisting of input neurons, the number of which corresponds to the number of the inputs, one or more hidden layers, and an output layer with a single neuron, the value of which is the output of the network [44]. All the neurons in one layer are connected to all other neurons in the subsequent layer with weighted connections W. As such, the value of the neuron is the activated weighted sum of the neurons in the previous layer , written as [45]:
with being the number of the neurons in -th layer, and being the activation function of the neuron that adjusts or transforms its value into a selected domain [46]. The calculation process is repeated from the input layer to the output neuron, the process of which is referred to as the forward propagation. The process of training consists of the minimization of the error [47]. This error is backpropagated from the output layer to the input, with weights of connections W in layer k being adjusted according to [48,49]:
The hyperparameters of the MLP regressor are hidden layer sizes, which are the tuple representing the number of neurons in hidden layers, activation function, solver—the algorithm used for backpropagation, the initial learning rate , which adjusts the speed of adjustment during the process of backpropagation, learning rate type, which describes how the value of the changes through the training iterations, and the L2 regularization parameter [37].
The values of MLP hyperparameters used in the GS procedure are given in Table 6.

Table 6.
Adjusted hyperparameters and their possible values for MLP.
2.2.5. Support Vector Regression
While Support Vector Machines are commonly used in classification issues, they can be utilized in regression problems to generate models. SVR will generate a hyperplane as a model [50]. Such a hyperplane will have margins that contain the data, with the goal of the optimization being the minimization of distances from the hyperplane margins defined as and for positive and negative directions. If the wanted hyperplane is defined as , then the optimization problem can be defined as [50]:
for the constraints
SVR also allows for non-linear hyperplane models through the utilization of kernels, which transform the data relation shape into a linear one [51]. This is one of the hyperparameters of the SVR. The other hyperparameters are connected to the individual kernel, such as the degree hyperparameter stating the degree of the polynomial in the appropriate kernel, gamma being the parameter of radial basis function (RBF), polynomial and sigmoid kernels, and coef0 being the independent term in polynomial and sigmoid kernels. The hyperparameter C is the regularization parameter, similar to in the case of the LogR method [37].
As with previous methods, the hyperparameter values for SVR are given in Table 7.

Table 7.
Adjusted hyperparameters and their possible values for SVR.
2.3. Evaluation
The metric used for the evaluation of the achieved results is the Mean Average Percentage Error (MAPE). If the real value is defined as , and the predicted value of the model is defined by , then the MAPE can be defined using [52]:
Using MAPE expresses the error as a percentage, allowing easy comparison of models for various goals that may have differently bounded values [33]. This is the reason why it has been selected for this research—as the values of confirmed and deceased patients will vary between countries. Using an error metric that provides an error in the same dimension instead of the percentage would make it hard to compare the model results between countries.
Cross-Validation
Due to the low amount of data points in the dataset, a 5-fold cross-validation was performed. Five-fold cross-validation is a process that splits the dataset into 5 equal parts (folds) through a uniform random selection without repetition. Then, the training and testing procedure is repeated 5 times. In each of these iterations, a different fold of the dataset is used for testing, while the remaining four folds are combined and used as the training dataset [53,54].
This process is illustrated in Figure 2. For simplicity, only 10 datapoints have been used. As it can be seen, the full dataset is split into five different folds randomly across its length. Each data point can belong to only one data fold, and it has the same chance of becoming part of each fold. Then, a single data point is selected to be the training set, while the remaining four are to be used as a testing set. Note that, while the figure shows data points to be held together as folds in this process—this is conducted only for a simpler understanding of the illustration, and the data points are actually shuffled. This process is then repeated, with a different fold being taken as a training set each time, until all of the folds have been used.
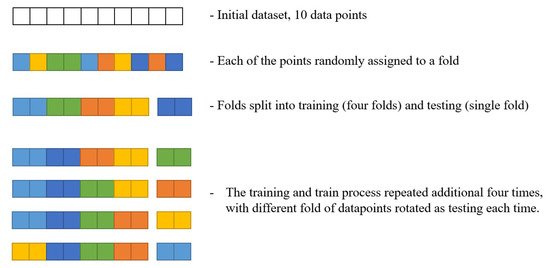
Figure 2.
The illustration of the cross-validation procedure.
This allows the evaluation of the model to be performed on the entirety of the dataset, guaranteeing the good generalization of the model. Without cross-validation, a model may perform well on the selected testing set but may show significantly poorer performance on the rest of the data. The performance with cross-validation is evaluated as the average of the scores on each fold, along with the standard error across the folds [55].
3. Results and Discussion
The results of the described methodology are presented and discussed in this section. The results and discussion are separated per each of the countries used in the research, with two subsections. The first subsection refers to the correlation analysis, presenting the obtained cross-correlation results for each data pair. The second subsection graphically presents the best results achieved by each of the five used methods for each of the goals to allow for the performance comparison, followed by the presentation of the best-achieved model per goal, with the hyperparameters of the used method. Abbreviations of the goals (data pairs) used in the presentation of the results are:
- Vaccinated Patients and Confirmed Patients (VC),
- Vaccinated Patients and Deceased Patients (VD),
- Fully Vaccinated Patients and Confirmed Patients (FVC),
- Fully Vaccinated Patients and Deceased Patients (FVD),
- Boosted Patients and Confirmed Patients (BC), and
- Boosted Patients and Deceased Patients (BD).
It should be noted that, in cases where the same model was achieved (same results in terms of MAPE and standard error), the method that generates a simpler model has been selected. This was chosen because simpler models tend to offer better generalization and simpler implementation [31].
3.1. USA
In this subsection, the results of the research performed on the data for the United States of America are presented. The following subsections present the values of correlation analysis and regression results. The obtained results are presented graphically and tabularly with a discussion of the results given.
3.1.1. Correlation Analysis Results
The cross-correlation analysis shows that the highest correlation is achieved for the lag equal to the length of the series, meaning that the highest correlation is achieved when both series fully overlap. Analyzing the values of the correlation for the given lag shows us that the correlation between the total cases equals for vaccinations, for full vaccination and for boosters. This also holds true for the correlations with deceased patients, which have values of for vaccinations, for full vaccinations and for boosters. The data shows somewhat high positive correlations between the tested values, with the highest shown between the number of confirmed cases and boosters. The described results are presented with cross-correlated signals in Figure 3.
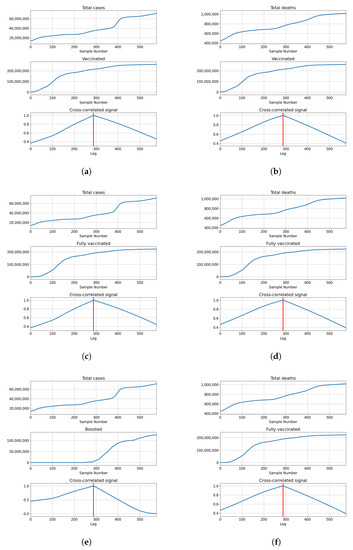
Figure 3.
Cross-correlation data for USA. (a) Cross-correlation results, data for confirmed cases and vaccinations in the United States; (b) cross-correlation results, data for deceased patients and vaccinations in the United States; (c) cross-correlation results, data for confirmed cases and full vaccinations in the United States; (d) cross-correlation results, data for deceased patients and full vaccinations in the United States; (e) cross-correlation results, data for confirmed cases and boosted patients in the United States; (f) cross-correlation results, data for deceased patients and boosted patients in the United States.
3.1.2. Regression Results
The results obtained in this part of the research are shown in Figure 4. As can be seen from Figure 4, the best results were given by LR/Lasso or MLP, with MLP achieving the best possible results for the BC model. As for the MAPE results, some algorithms give satisfactory results, and it is important to note that the best results obtained with this training amount to less than , which adds to the validation of the used algorithms. The final models obtained for confirmed cases give a smaller error in relation to related elements, i.e., the number of deceased patients, which is quite expected considering the dizzying circumstances of real deaths.
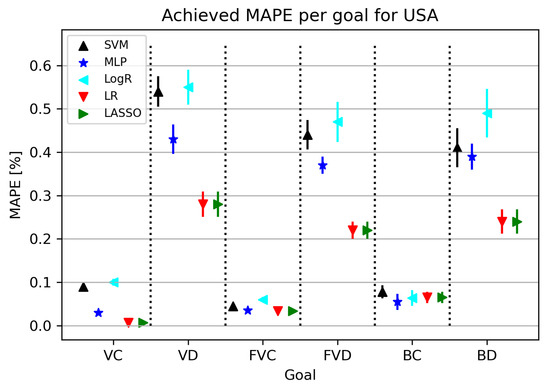
Figure 4.
The results of ML methods per goal for USA (VC—vaccinated-confirmed, VD—vaccinated-deceased, FVC—fully vaccinated-confirmed, FVD—fully vaccinated-deceased, BC—boosted-confirmed, BD—boosted-deceased; lower is better).
Furthermore, in Table 8, all obtained results for each individual target value are presented. MAPE values range from 0.007 to 0.23, with the best model obtained using LR using the fit intercept parameters and the positive hyperplane set to false.

Table 8.
Best achieved results for the USA.
3.2. United Kingdom
In this subsection, the results of the research related to the United Kingdom are presented. The United Kingdom showed a rapid acceptance and distribution of vaccinations. This is paired with a relatively stable increase in infection rates, which differs it from other analyzed countries. The following subsections present the values of correlation analysis and regression results. The obtained results are presented graphically and tabularly with the explanation of the results following.
3.2.1. Correlation Analysis Results
The highest correlations are shown with the booster doses with for deceased patients, and for confirmed cases. The values show that the confirmed cases have a higher correlation value compared to the deceased. This is not the case with vaccinated and fully vaccinated correlations, with the number of deceased patients equaling and . In comparison, the same series compared to the number of deceased patients equals and , respectively. The described results are presented with cross-correlated signals in Figure 5.
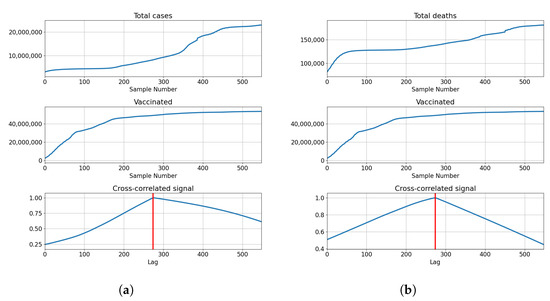
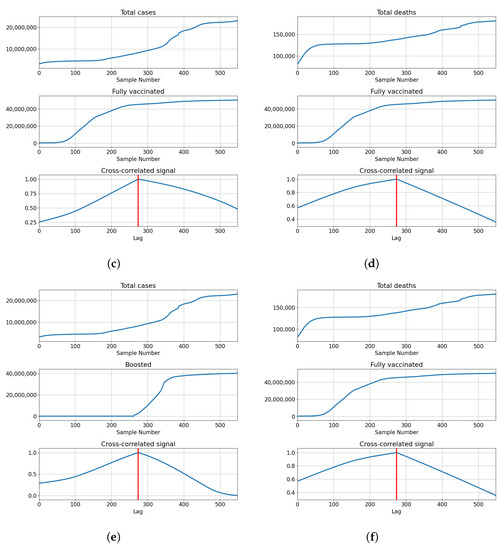
Figure 5.
Cross-correlation data for the UK. (a) Cross-correlation results, data for confirmed cases and vaccinations in the United Kingdom; (b) cross-correlation results, data for deceased patients and vaccinations in the United Kingdom; (c) cross-correlation results, data for confirmed cases and full vaccinations in the United Kingdom; (d) cross-correlation results, data for deceased patients and full vaccinations in the United Kingdom; (e) cross-correlation results, data for confirmed cases and boosted patients in the United Kingdom; (f) cross-correlation results, data for deceased patients and boosted patients in the United Kingdom.
3.2.2. Regression Results
The results related to individual target values are shown in Figure 6. By observing the results shown in Figure 6, it is possible to notice that the errors obtained for VC and FVC are much lower compared to the results obtained for VD and FVD. It is interesting to note that the obtained trend does not follow the BC and BD models, which show some similarities to each other.
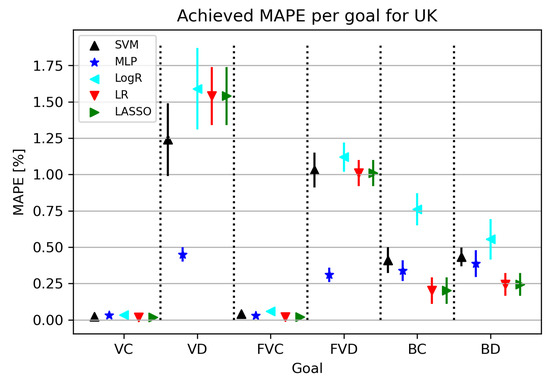
Figure 6.
The results of ML methods per goal for the UK (VC—vaccinated-confirmed, VD—vaccinated-deceased, FVC—fully vaccinated-confirmed, FVD—fully vaccinated-deceased, BC—boosted-confirmed, BD—boosted-deceased; lower is better).
Table 9 shows individual results for each target value. The model for deceased cases was obtained by thoroughly training the MLP algorithm using the vaccinated and fully vaccinated variables. As for the other models, they were obtained by re-using the LR algorithm, in which the parameters were adjusted in the manner of regulating the fit intercept hyperparameter and setting the positive hyperparameter set to true. Future trends cannot be observed in this case.

Table 9.
Best achieved results for the UK.
3.3. Germany
In this subsection, the results of the research related to Germany are presented and discussed. Germany, similarly to most EU countries, shows high vaccination rates with relatively high but stable infection rates, which continue to grow slightly even after the introduction of vaccines. As with previous countries, the following subsections will present the cross-correlation analysis both numerically and graphically, with the same for the regression analysis.
3.3.1. Correlation Analysis Results
Correlations for Germany are also the highest at the full overlap of the series. The lowest correlations are shown with for number of vaccinations and full vaccinations at and , respectively. The number of booster doses shows a higher correlation with . The correlation is higher with the number of deceased patients for vaccinations and full vaccinations at and , but lower in the case of boosted patients . The described results are presented with cross-correlated signals in Figure 7.
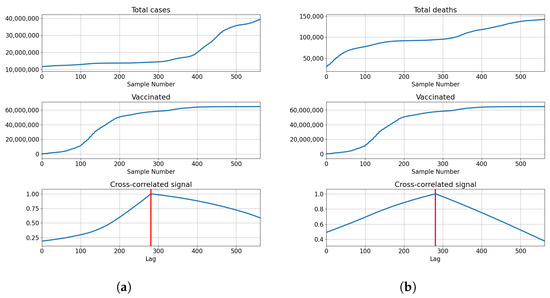
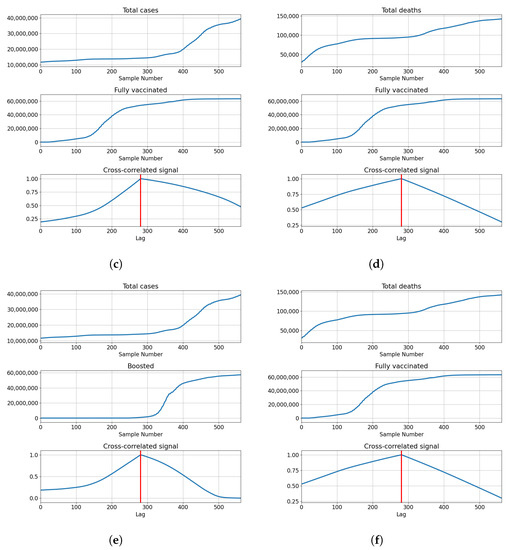
Figure 7.
Cross-correlation data for Germany. (a) Cross-correlation results, data for confirmed cases and vaccinations in Germany; (b) cross-correlation results, data for deceased patients and vaccinations in Germany; (c) cross-correlation results, data for confirmed cases and full vaccinations in Germany; (d) cross-correlation results, data for deceased patients and full vaccinations in Germany; (e) cross-correlation results, data for confirmed cases and boosted patients in Germany; (f) cross-correlation results, data for deceased patients and boosted patients in Germany.
3.3.2. Regression Results
Figure 8 shows that models for confirmed cases achieve better results than the ones targeting deceased patients. Models for deceased patients show MLP as the best modeling algorithm.
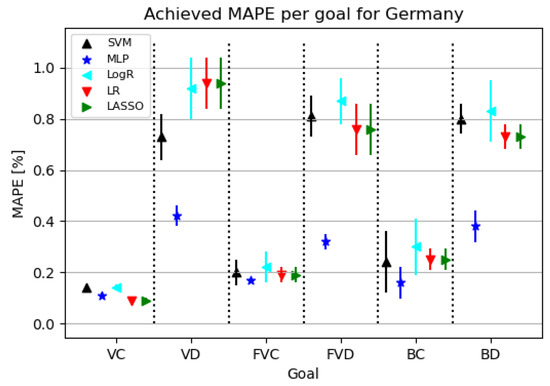
Figure 8.
The results of ML methods per goal for Germany (VC—vaccinated-confirmed, VD—vaccinated-deceased, FVC—fully vaccinated-confirmed, FVD—fully vaccinated-deceased, BC—boosted-confirmed, BD—boosted-deceased; lower is better).
Table 10 shows that using the MLP algorithm, the best results are obtained for almost all target values except VC. Looking at the configured network for the given challenge, it is evident that a relatively small neural network was used to achieve the given results. In addition, the learning rate tended to increase, resulting in a faster convergence of the obtained end result.

Table 10.
Best achieved results for Germany.
3.4. India
India is one of the most populous countries in the world, so it is of great importance to predict the potential increase in the number of patients, deaths and the impact of vaccination itself. As defined in the previous subsections, in this subsection, the results of the research related to India are presented. The following subsections present the values of correlation analysis and regression results. The obtained results are presented graphically and tabularly with the explanation of the results in the following sections.
3.4.1. Correlation Analysis Results
India also shows the highest correlation for full overlap, indicating that cross-correlation of series is not necessary to determine the best lag for modeling. The correlations of total vaccinations are relatively high at and . Full vaccinations show a somewhat lower correlation in both cases with for confirmed patients and for deceased patients. The number of boosted patients shows relatively low correlations at and . The described results are presented with cross-correlated signals in Figure 9.
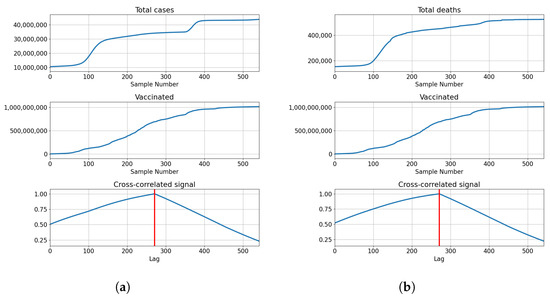
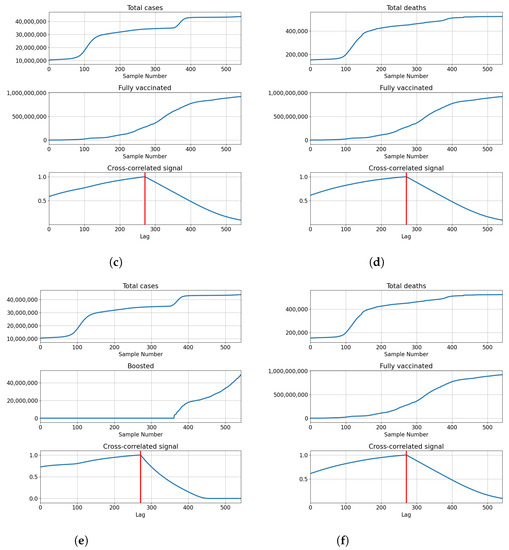
Figure 9.
Cross-correlation data for India. (a) Cross-correlation results, data for confirmed cases and vaccinations in India; (b) cross-correlation results, data for deceased patients and vaccinations in India; (c) cross-correlation results, data for confirmed cases and full vaccinations in India; (d) cross-correlation results, data for deceased patients and full vaccinations in India; (e) cross-correlation results, data for confirmed cases and boosted patients in India; (f) cross-correlation results, data for deceased patients and boosted patients in India.
3.4.2. Regression Results
India is one of the most populous countries in the world, so obtaining a model with a low error rate greatly contributes to research development. The ML algorithms used in this part of the research are shown in Figure 10. An interesting fact is that the MLP algorithm shows a high rate of standard deviation for all folds at all target values except for VC. MAPE metrics related to India range between 0.05 and 0.31 for certain research elements. LR obtains the best results in relation to “rival” algorithms for VC and FVC target values, while other acceptable results are given by MLP, which is visible and shown in Table 11.
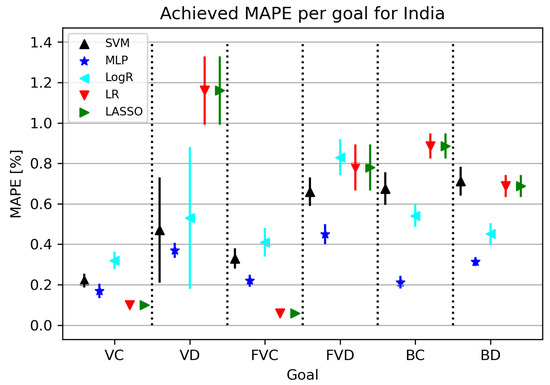
Figure 10.
The results of ML methods per goal for India (VC—vaccinated-confirmed, VD—vaccinated-deceased, FVC—fully vaccinated-confirmed, FVD—fully vaccinated-deceased, BC—boosted-confirmed, BD—boosted-deceased; lower is better).

Table 11.
Best achieved results per goal for India.
4. Conclusions
In this paper, AI-based regression modeling of confirmed and deceased patient rates through the number of vaccinated individuals was demonstrated. Five different regression methods were applied: LR, LASSO, LogR, MLP, and SVR. Cross-correlation analysis was performed on the used time series to determine the lags that can be between the data series before modeling in order to improve the performance. All the regression goals have achieved satisfactory results when evaluated using MAPE, with errors below 1%—with the five-fold cross-validation applied. It can be seen that the most successful techniques are MLP and LR/LASSO, with all the best models per goal consisting of the ones achieved with these methods. It has to be noted that LR and LASSO achieved the same error, suggesting that they produced the same model. This points towards the conclusion that there may be no need to use LASSO in comparatively simple (low number of variables) regression tasks such as the ones presented. Cross-correlation testing was performed to determine if there is a correlation between the numbers of confirmed or deceased patients with the numbers of vaccinated, fully vaccinated or boosted patients. The results show that the highest correlation for all of the analyzed countries (USA, UK, Germany and India), and all data pairs used, is equal to the length of the data series. This suggests that the best correlation is achieved when the time series overlap completely—in other words, when no delays are introduced. The cross-correlation results achieved show that the correlation coefficients are relatively high around the maximum cross-correlation lag, suggesting that smaller delays be used between the data series for predictive modeling. The analyzed results demonstrate that the highest correlation is shown when the lag is zero, or in other words, when the data series fully overlap. Observing the achieved cross-correlation values and methods used to model the data-pair regression models, a conclusion can be drawn that the models of those data pairs that had lower correlation tended to achieve lower errors when modeled with MLP. In cases where the correlation coefficient was higher, the models tended to be achieved by LR. As MLP is a more complex method, generating complex models in comparison to LR, it can be concluded that such a method was necessary to make up for the deficiencies in correlation present in the data. Future work in regressive modeling may include the testing of the findings on the vaccination rates of other viral diseases, seeing if the applied methods may demonstrate similar results.
Author Contributions
Conceptualization, S.B.Š., I.L., S.V. and Z.C.; methodology, S.B.Š., J.M. and D.Š.; software, S.B.Š. and M.G.; validation, I.L., N.A., S.V. and Z.C.; formal analysis, S.V. and Z.C.; investigation, S.B.Š., I.L., N.A. and M.G.; resources, J.M., D.Š. and M.G.; data curation, I.L. and N.A.; writing—original draft preparation, S.B.Š., I.L., N.A., J.M. and D.Š.; writing—review and editing, S.V., M.G. and Z.C.; visualization, S.B.Š.; supervision, S.V. and Z.C.; project administration, S.V. and Z.C.; funding acquisition, S.V. and Z.C. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
The data used in this paper were obtained from a publicly available repository located at https://ourworldindata.org/coronavirus.
Acknowledgments
This research was (partly) supported by the CEEPUS network CIII-HR-0108, European Regional Development Fund under the grant KK.01.1.1.01.0009 (DATACROSS), project CEKOM under the grant KK.01.2.2.03.0004, CEI project “COVIDAi” (305.6019-20) and University of Rijeka scientific grants uniri-tehnic-18-275-1447 and “Development of intelligent systems for the prediction of medical and economical effect of COVID-19”.
Conflicts of Interest
The authors declare no conflict of interest.
Abbreviations
The following abbreviations are used in this manuscript:
| MLP | Multilayer Perceptron |
| SVR | Support Vector Regressor |
| FVC | Fully Vaccinated Patients—Confirmed Patients Data Pair |
| FVD | Fully Vaccinated Patients—Deceased Patients Data Pair |
| GER | Germany |
| IND | India |
| LASSO | Least Absolute Shrinkage and Selection Operator |
| LogR | Logistic Regression |
| LR | Linear Regression |
| MAPE | Mean Average Percentage Error |
| OWID | Our World in Data |
| UK | United Kingdom |
| USA | United States of America |
| VC | Vaccinated Patients—Confirmed Patients Data Pair |
| VD | Vaccinated Patients—Deceased Patients Data Pair |
| BC | Boosted Patients—Confirmed Patients Data Pair |
| BD | Boosted patients—Deceased patients Data Pair |
References
- Fauci, A.S.; Lane, H.C.; Redfield, R.R. COVID-19—Navigating the uncharted. N. Engl. J. Med. 2020, 382, 1268–1269. [Google Scholar] [CrossRef] [PubMed]
- Velavan, T.P.; Meyer, C.G. The COVID-19 epidemic. Trop. Med. Int. Health 2020, 25, 278. [Google Scholar] [CrossRef] [PubMed]
- Jebril, N. World Health Organization declared a pandemic public health menace: A systematic review of the coronavirus disease 2019 “COVID-19”. SSRN Electron. J. 2020, 3566298. [Google Scholar] [CrossRef]
- Cavanagh, G.; Wambier, C.G. Rational hand hygiene during the coronavirus 2019 (COVID-19) pandemic. J. Am. Acad. Dermatol. 2020, 82, e211. [Google Scholar] [CrossRef]
- Zhang, K.; Vilches, T.N.; Tariq, M.; Galvani, A.P.; Moghadas, S.M. The impact of mask-wearing and shelter-in-place on COVID-19 outbreaks in the United States. Int. J. Infect. Dis. 2020, 101, 334–341. [Google Scholar] [CrossRef]
- Chinazzi, M.; Davis, J.T.; Ajelli, M.; Gioannini, C.; Litvinova, M.; Merler, S.; Y Piontti, A.P.; Mu, K.; Rossi, L.; Sun, K.; et al. The effect of travel restrictions on the spread of the 2019 novel coronavirus (COVID-19) outbreak. Science 2020, 368, 395–400. [Google Scholar] [CrossRef]
- Lau, H.; Khosrawipour, V.; Kocbach, P.; Mikolajczyk, A.; Schubert, J.; Bania, J.; Khosrawipour, T. The positive impact of lockdown in Wuhan on containing the COVID-19 outbreak in China. J. Travel Med. 2020, 27, taaa037. [Google Scholar] [CrossRef]
- Tregoning, J.S.; Brown, E.S.; Cheeseman, H.M.; Flight, K.E.; Higham, S.L.; Lemm, N.M.; Pierce, B.F.; Stirling, D.C.; Wang, Z.; Pollock, K.M. Vaccines for COVID-19. Clin. Exp. Immunol. 2020, 202, 162–192. [Google Scholar] [CrossRef]
- Forni, G.; Mantovani, A. COVID-19 vaccines: Where we stand and challenges ahead. Cell Death Differ. 2021, 28, 626–639. [Google Scholar] [CrossRef]
- Yamey, G.; Schäferhoff, M.; Hatchett, R.; Pate, M.; Zhao, F.; McDade, K.K. Ensuring global access to COVID-19 vaccines. Lancet 2020, 395, 1405–1406. [Google Scholar] [CrossRef]
- Lurie, N.; Saville, M.; Hatchett, R.; Halton, J. Developing Covid-19 vaccines at pandemic speed. N. Engl. J. Med. 2020, 382, 1969–1973. [Google Scholar] [CrossRef] [PubMed]
- Wedlund, L.; Kvedar, J. New machine learning model predicts who may benefit most from COVID-19 vaccination. PJ Digit. Med. 2021, 4, 1. [Google Scholar] [CrossRef] [PubMed]
- Car, Z.; Baressi Šegota, S.; Andelić, N.; Lorencin, I.; Mrzljak, V. Modeling the spread of COVID-19 infection using a multilayer perceptron. Comput. Math. Methods Med. 2020, 2020, 5714714. [Google Scholar] [CrossRef] [PubMed]
- Rustam, F.; Reshi, A.A.; Mehmood, A.; Ullah, S.; On, B.W.; Aslam, W.; Choi, G.S. COVID-19 future forecasting using supervised machine learning models. IEEE Access 2020, 8, 101489–101499. [Google Scholar] [CrossRef]
- Mollalo, A.; Rivera, K.M.; Vahedi, B. Artificial neural network modeling of novel coronavirus (COVID-19) incidence rates across the continental United States. Int. J. Environ. Res. Public Health 2020, 17, 4204. [Google Scholar] [CrossRef]
- Gupta, A.; Gharehgozli, A. Developing a machine learning framework to determine the spread of COVID-19 in the USA using meteorological, social, and demographic factors. Int. J. Data Min. Model. Manag. 2020, 14, 89–109. [Google Scholar] [CrossRef]
- Onovo, A.; Atobatele, A.; Kalaiwo, A.; Obanubi, C.; James, E.; Gado, P.; Odezugo, G.; Ogundehin, D.; Magaji, D.; Russell, M. Using supervised machine learning and empirical Bayesian kriging to reveal correlates and patterns of COVID-19 disease outbreak in sub-Saharan Africa: Exploratory data analysis. MedRxiv 2020. [Google Scholar] [CrossRef]
- Bagabir, S.; Ibrahim, N.K.; Bagabir, H.; Ateeq, R. COVID-19 and Artificial Intelligence: Genome sequencing, drug development and vaccine discovery. J. Infect. Public Health 2022, 15, 289–296. [Google Scholar] [CrossRef]
- Bharadwaj, K.K.; Srivastava, A.; Panda, M.K.; Singh, Y.D.; Maharana, R.; Mandal, K.; Singh, B.M.; Singh, D.; Das, M.; Murmu, D.; et al. Computational intelligence in vaccine design against COVID-19. In Computational Intelligence Methods in COVID-19: Surveillance, Prevention, Prediction and Diagnosis; Springer: Berlin/Heidelberg, Germany, 2021; pp. 311–329. [Google Scholar]
- Ong, E.; Wong, M.U.; Huffman, A.; He, Y. COVID-19 coronavirus vaccine design using reverse vaccinology and machine learning. Front. Immunol. 2020, 11, 1581. [Google Scholar] [CrossRef]
- Keshavarzi Arshadi, A.; Webb, J.; Salem, M.; Cruz, E.; Calad-Thomson, S.; Ghadirian, N.; Collins, J.; Diez-Cecilia, E.; Kelly, B.; Goodarzi, H.; et al. Artificial intelligence for COVID-19 drug discovery and vaccine development. Front. Artif. Intell. 2020, 3, 65. [Google Scholar] [CrossRef]
- Mariappan, M.B.; Devi, K.; Venkataraman, Y.; Lim, M.K.; Theivendren, P. Using AI and ML to predict shipment times of therapeutics, diagnostics and vaccines in e-pharmacy supply chains during COVID-19 pandemic. Int. J. Logist. Manag. 2022; Epub ahead of print. [Google Scholar] [CrossRef]
- Tong, H.; Cao, C.; You, M.; Han, S.; Liu, Z.; Xiao, Y.; He, W.; Liu, C.; Peng, P.; Xue, Z.; et al. Artificial intelligence-assisted colorimetric lateral flow immunoassay for sensitive and quantitative detection of COVID-19 neutralizing antibody. Biosens. Bioelectron. 2022, 213, 114449. [Google Scholar] [CrossRef]
- Miner, A.S.; Laranjo, L.; Kocaballi, A.B. Chatbots in the fight against the COVID-19 pandemic. NPJ Digit. Med. 2020, 3, 1–4. [Google Scholar] [CrossRef] [PubMed]
- Shams, A.B.; Hoque Apu, E.; Rahman, A.; Sarker Raihan, M.M.; Siddika, N.; Preo, R.B.; Hussein, M.R.; Mostari, S.; Kabir, R. Web search engine misinformation notifier extension (SEMiNExt): A machine learning based approach during COVID-19 Pandemic. Healthcare 2021, 9, 156. [Google Scholar] [CrossRef] [PubMed]
- Mathieu, E.; Ritchie, H.; Ortiz-Ospina, E.; Roser, M.; Hasell, J.; Appel, C.; Giattino, C.; Rodés-Guirao, L. A global database of COVID-19 vaccinations. Nat. Hum. Behav. 2021, 5, 947–953. [Google Scholar] [CrossRef] [PubMed]
- COVID, C.; Team, V.B.C.I.; COVID, C.; Team, V.B.C.I.; COVID, C.; Team, V.B.C.I.; Birhane, M.; Bressler, S.; Chang, G.; Clark, T.; et al. COVID-19 Vaccine Breakthrough Infections Reported to CDC—United States, January 1–April 30, 2021. Morb. Mortal. Wkly. Rep. 2021, 70, 792. [Google Scholar]
- Krause, P.R.; Fleming, T.R.; Peto, R.; Longini, I.M.; Figueroa, J.P.; Sterne, J.A.; Cravioto, A.; Rees, H.; Higgins, J.P.; Boutron, I.; et al. Considerations in boosting COVID-19 vaccine immune responses. Lancet 2021, 398, 1377–1380. [Google Scholar] [CrossRef]
- Schafer, R.W.; Rabiner, L.R. Digital representations of speech signals. Proc. IEEE 1975, 63, 662–677. [Google Scholar] [CrossRef]
- Viel, C.; Viollet, S. Fast normalized cross-correlation for measuring distance to objects using optic flow, applied for helicopter obstacle detection. Measurement 2021, 172, 108911. [Google Scholar] [CrossRef]
- Friedman, J.; Hastie, T.; Tibshirani, R. The elements of Statistical Learning; Springer Series in Statistics; Springer: New York, NY, USA, 2001; Volume 1. [Google Scholar]
- Yao, L.; Fang, Z.; Xiao, Y.; Hou, J.; Fu, Z. An intelligent fault diagnosis method for lithium battery systems based on grid search support vector machine. Energy 2021, 214, 118866. [Google Scholar] [CrossRef]
- Li, G.; Wang, W.; Zhang, W.; Wang, Z.; Tu, H.; You, W. Grid search based multi-population particle swarm optimization algorithm for multimodal multi-objective optimization. Swarm Evol. Comput. 2021, 62, 100843. [Google Scholar] [CrossRef]
- Sun, Y.; Ding, S.; Zhang, Z.; Jia, W. An improved grid search algorithm to optimize SVR for prediction. Soft Comput. 2021, 25, 5633–5644. [Google Scholar] [CrossRef]
- Ghosal, S.; Sengupta, S.; Majumder, M.; Sinha, B. Linear Regression Analysis to predict the number of deaths in India due to SARS-CoV-2 at 6 weeks from day 0 (100 cases-March 14th 2020). Diabetes Metab. Syndr. Clin. Res. Rev. 2020, 14, 311–315. [Google Scholar] [CrossRef] [PubMed]
- Rath, S.; Tripathy, A.; Tripathy, A.R. Prediction of new active cases of coronavirus disease (COVID-19) pandemic using multiple linear regression model. Diabetes Metab. Syndr. Clin. Res. Rev. 2020, 14, 1467–1474. [Google Scholar] [CrossRef]
- Pedregosa, F.; Varoquaux, G.; Gramfort, A.; Michel, V.; Thirion, B.; Grisel, O.; Blondel, M.; Prettenhofer, P.; Weiss, R.; Dubourg, V.; et al. Scikit-learn: Machine learning in Python. J. Mach. Learn. Res. 2011, 12, 2825–2830. [Google Scholar]
- Araveeporn, A. The Higher-Order of Adaptive Lasso and Elastic Net Methods for Classification on High Dimensional Data. Mathematics 2021, 9, 1091. [Google Scholar] [CrossRef]
- Ghosh, P.; Azam, S.; Jonkman, M.; Karim, A.; Shamrat, F.J.M.; Ignatious, E.; Shultana, S.; Beeravolu, A.R.; De Boer, F. Efficient Prediction of Cardiovascular Disease Using Machine Learning Algorithms With Relief and LASSO Feature Selection Techniques. IEEE Access 2021, 9, 19304–19326. [Google Scholar] [CrossRef]
- Si, Y.; Kretsch, A.M.; Daigh, L.M.; Burk, M.J.; Mitchell, D.A. Cell-Free Biosynthesis to Evaluate Lasso Peptide Formation and Enzyme–Substrate Tolerance. J. Am. Chem. Soc. 2021, 143, 5917–5927. [Google Scholar] [CrossRef]
- Yazdi, M.; Golilarz, N.A.; Nedjati, A.; Adesina, K.A. An improved lasso regression model for evaluating the efficiency of intervention actions in a system reliability analysis. Neural Comput. Appl. 2021, 33, 7913–7928. [Google Scholar] [CrossRef]
- Connelly, L. Logistic regression. Medsurg Nurs. 2020, 29, 353–354. [Google Scholar]
- Nusinovici, S.; Tham, Y.C.; Yan, M.Y.C.; Ting, D.S.W.; Li, J.; Sabanayagam, C.; Wong, T.Y.; Cheng, C.Y. Logistic regression was as good as machine learning for predicting major chronic diseases. J. Clin. Epidemiol. 2020, 122, 56–69. [Google Scholar] [CrossRef]
- Chiappini, F.A.; Allegrini, F.; Goicoechea, H.C.; Olivieri, A.C. Sensitivity for Multivariate Calibration Based on Multilayer Perceptron Artificial Neural Networks. Anal. Chem. 2020, 92, 12265–12272. [Google Scholar] [CrossRef] [PubMed]
- Wang, H.; Moayedi, H.; Foong, L.K. Genetic algorithm hybridized with multilayer perceptron to have an economical slope stability design. Eng. Comput. 2020, 37, 3067–3078. [Google Scholar] [CrossRef]
- Wang, Y.; Li, Y.; Song, Y.; Rong, X. The influence of the activation function in a convolution neural network model of facial expression recognition. Appl. Sci. 2020, 10, 1897. [Google Scholar] [CrossRef]
- Ecer, F.; Ardabili, S.; Band, S.S.; Mosavi, A. Training multilayer perceptron with genetic algorithms and particle swarm optimization for modeling stock price index prediction. Entropy 2020, 22, 1239. [Google Scholar] [CrossRef]
- Chen, J.C.; Wang, Y.M. Comparing activation functions in modeling shoreline variation using multilayer perceptron neural network. Water 2020, 12, 1281. [Google Scholar] [CrossRef]
- Šegota, S.B.; Andelić, N.; Mrzljak, V.; Lorencin, I.; Kuric, I.; Car, Z. Utilization of multilayer perceptron for determining the inverse kinematics of an industrial robotic manipulator. Int. J. Adv. Robot. Syst. 2021, 18, 1729881420925283. [Google Scholar] [CrossRef]
- Bansal, N.; Defo, M.; Lacasse, M.A. Application of Support Vector Regression to the Prediction of the Long-Term Impacts of Climate Change on the Moisture Performance of Wood Frame and Massive Timber Walls. Buildings 2021, 11, 188. [Google Scholar] [CrossRef]
- Guo, X.; Zhou, W.; Shi, B.; Wang, X.; Du, A.; Ding, Y.; Tang, J.; Guo, F. An efficient multiple kernel support vector regression model for assessing dry weight of hemodialysis patients. Curr. Bioinform. 2021, 16, 284–293. [Google Scholar]
- Liantoni, F.; Agusti, A. Forecasting Bitcoin using Double Exponential Smoothing Method Based on Mean Absolute Percentage Error. JOIV Int. J. Informatics Vis. 2020, 4, 91–95. [Google Scholar] [CrossRef]
- Qiao, W.; Moayedi, H.; Foong, L.K. Nature-inspired hybrid techniques of IWO, DA, ES, GA, and ICA, validated through a k-fold validation process predicting monthly natural gas consumption. Energy Build. 2020, 217, 110023. [Google Scholar] [CrossRef]
- Lorencin, I.; Andelić, N.; Mrzljak, V.; Car, Z. Genetic algorithm approach to design of multi-layer perceptron for combined cycle power plant electrical power output estimation. Energies 2019, 12, 4352. [Google Scholar] [CrossRef]
- Marcot, B.G.; Hanea, A.M. What is an optimal value of k in k-fold cross-validation in discrete Bayesian network analysis? Comput. Stat. 2020, 36, 2009–2031. [Google Scholar] [CrossRef]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).