Improving the Road and Traffic Control Prediction Based on Fuzzy Logic Approach in Multiple Intersections

Abstract

Traffic congestion is a significant issue in many countries today. The suggested method is a novel control method based on multiple intersections considering the kind of traffic light and the duration of the green phase to determine the optimal balance at intersections by using fuzzy logic control, for which the balance should be adaptable to the unchanging behavior of time. It should reduce traffic volume in transport, average waits for each vehicle, and collisions between cars by controlling this balance in response to the typical behavior of time and randomness in traffic conditions. The proposed method is investigated at intersections using a sampling multi-agent system to set traffic light timings appropriately. The program is provided with many intersections, each of which is an independent entity exchanging information with the others. The stability per entity is proven separately. Simulation results show that Takagi–Sugeno (TS) fuzzy modeling performs better than Takagi–Sugeno (TS) fixed-time scheduling in decreasing the length of queueing times for vehicles.

1. Introduction

Nowadays, most cities face traffic congestion due to urban construction’s fast development. One of the main reasons for increasing traffic these days in the world can be an increase in the number of vehicles, which causes significant issues in major cities. An optimal traffic signal management strategy is the best option for improving transport infrastructure, making it fluid, adaptable and efficient [1,2].

Traffic signaling systems can be split into three types: those controlled by people, traditional and sensitive systems such as the traffic officer controlling traffic by hand gestures and periodically making verbal contact as the traffic officer’s instincts decide which car should move or stop [3]. An urban traffic control system manages traffic signal control and traffic grooming in an intelligent transportation system context. Traffic light control has become a critical element of traffic management [4]. Traffic signal controllers have been split into two types based on their process modes: timing signal controllers and adaptive signal controllers. The length of the cycles has been split in traffic control, such as green lights and red lights, which, at the same time, has adjusted adaptively from green lights to red lights in urban traffic. The literature has presented neural networks and fuzzy control models for designing signal controls to determine adjusted traffic lights [5].

In the urban areas of the world, various techniques have been used for traffic control. Still, the structure and efficient methods for controlling traffic signals in urban areas remain challenging. Nowadays, most studies use real-time traffic data such as queuing lengths detected by sensors in intersections [6]. Some control techniques such as fuzzy logic control and state feedback control have been presented to determine the effective green light period [7]. A fuzzy logic controller (FLC) has simulated skilled human traffic controllers responsible for resetting signals at over-saturated intersections during special events. A set of fuzzy rules determines whether a green phase should continue or be halted based on the real-time information provided by the fuzzy logic control center in [8].

Traffic congestion occurs when a vehicle population exceeds infrastructure capacity, thus leading to slow movements and queues. This is an evolutionary anomaly that extends over time. To improve infrastructure capacity and reduce travel time at the same time, optimizing intersection traffic light control and improving road users’ safety must be considered. Traffic signal controllers based on fuzzy logic have been successfully implemented in [9,10] by evaluating a real-time traffic signal regulation framework that can be developed utilizing agent technology and fuzzy logic. The suggested method deals with fuzzy traffic control based on a multi-agent system with attested stability, contrasting with recent studies that emphasize fuzzy controllers and multi-agent approaches in traffic management. The main contributions of this paper are as follows:

• We evaluate different definitions of state spaces for traffic signal control problems with the fuzzy logic control method.
• We consider and further integrate essential contextual factors that may affect route selection by employing a multi-agent system for road traffic decision-making.
• The aim is to reduce queue length and congestion at intersections and throughout the road network by improving intersection quality.

Section 2 describes an overview of urban traffic using different models; within Section 3, we present the proposed architecture of the framework, the agents’ organization and the specific roles of the various components. In Section 4, the simulation evaluates the efficiency of the proposed regulatory system based on the performance measures used. The end of the paper provides our conclusions and further work.

2. Related Work

Among the most important and influential elements of urban traffic, networks are signalized intersections and traffic signals are the most popular scheduling and traffic management instruments. A summary of several studies involving intelligent traffic signals with different methods and a multi-agent system is presented below. Pre-timed signals cannot control non-stationary traffic. It has been a while since interactive method control evolved into a movement in traffic management. Split Cycle Offset Optimization Technique (SCOOT) in the 1980s and the Sydney Coordinated Adaptive Traffic System (SCATS) design were the first adaptative traffic control techniques produced in the last decade of the last millennium in [11].

2.1. Urban Traffic Based on Multi Agent

Multi-agent signal control usually divides the road network into regions or subparts covering several intersections. There are several ways to model the organization of agents, in which the organizational structure determines the interactions, roles and forms of a community [12]. Urban traffic management has recently been focusing more on multi-agent systems. A multi-agent system alone cannot provide particular abilities necessary for disturbance management. Therefore, multi-agent systems integrate intelligent techniques to create intelligent traffic signal controllers. As an example, models optimize signal timing plans by combining multi-agent approaches with RL techniques; communication between the agents and the environment allows them to acquire knowledge and optimize their behavior. Q-learning is the most commonly employed model-free reinforcement learning method for intelligent traffic light control among multi-agent reinforcement learning researchers [13]. The delay is minimized by assuming a real-time-based response to traffic fluctuations in [14,15], in which an adaptive traffic signal control was designed utilizing multi-agent reinforcement learning for pre-allocation of the environment, which can be implemented with a non-deterministic environment model.

2.2. Urban Traffic Optimization by Using Fuzzy Logic Model

In the last few years, researchers have concentrated on discovering a way to minimize traffic congestion by modifying the timing and phase of the light signals. A fuzzy model was suggested for a separated signalized intersection, with results demonstrating that the presented model performs better than a fixed time control when calculating the average waiting time in [16]. Recently, additional focus has been placed on multi-agent-based systems in urban traffic management. The main goal is to determine traffic signals for each intersection individually with a predetermined cycle length. The phases of a traffic signal plan are based on a fixed cycle-based sequence split into phases [17,18,19,20,21]. The fuzzy logic control Sugeno technique was used to design an adaptive traffic light controller to determine the length of green time at an intersection. The results demonstrated that the traffic light with fuzzy logic control demonstrates better performance than a fixed-time control system [22]. A traffic light control framework was developed by combining fuzzy Q-learning and agent technology such that every time an agent makes a decision, it receives a reward. The number of vehicles was chosen as input. The main goal was the control created to schedule the green phase period to decrease the average delay time [23].

Adaptive fuzzy logic management has been designated for traffic control systems to deal with information uncertainty in thick traffic flows. By comparing the fixed-time traffic signals, the offered method was more effective at controlling intersections [24]. An area of interest has been employing intelligent techniques to make traffic routing decisions; a smart traffic light control was thus designed using fuzzy logic and a wireless sensor network to collect traffic while considering real-time data [25]. The use of a fuzzy logic-based real-time traffic monitoring system considering the dynamic control of traffic light phases and green time was suggested for managing traffic lights at isolated signalized intersections in real-time within the context of urban traffic [26]. A traffic signal was presented with deep reinforcement learning with the objective of modeling the control actions and the change of system states to design control signal timing plans, which could determine appropriate timing policies [27]. In [28], a traffic light controller was designed based on fuzzy logic to minimize average waiting time and queue length. While failing to consider heterogeneity by using neural traffic light control, the goal of managing the duration of green light intervals was attained. Other authors have applied a fuzzy inference rule-based method to train the neural network from time input and output data for the green light of a signal [29].

2.3. Urban Traffic with Considering Different Method

Wavelet neural networks have been used in unidirectional gradient descent algorithms for parameter optimization. These algorithms suffer from slow convergence and local optimum problems. Attention to traffic flow has been used in genetic algorithms and wavelet neural networks to improve prediction and optimization [30,31]. A developed strategy was predicted for traffic flow road transportation networks while considering limitation traffic data [32,33]. An autoregressive model simulation approach was used for traffic light control determination [31,32]. Simulation has been suggested based on a force-driven traffic simulation; however, they have missed vehicle dynamics and traffic control requirements. The paper presented [34,35] a theoretical mathematical model to study the density-based travel time for real-time vehicular dynamics, which was shown in intelligent transportation method applications where travel time is an essential element. To control a dynamic traffic light, domain experts utilized a convolutional neural network with reinforcement learning to control the traffic light by combining several features to improve the performance [36,37]. The authors of [38,39,40] used eight machine learning models to develop and analyse a suitable model for an isolated intersection. Traffic classification with input based on the selected models was developed to predict the traffic classification’s green time.

2.4. Traffic Light Control

Different strategies have been offered for minimizing traffic congestion at intersections based on intelligent traffic control in smart cities by using different techniques and methodologies to collect traffic data, such as wireless sensor networks (WSN), vehicular ad hoc Networks (VANETs), and image processing [41]. A virtual traffic light system has been presented for vehicle-to-vehicle distribution with the main objective of minimizing the time spent managing unregulated intersections. Additionally, a dynamic distributed solution to assist in automatic cyclical planning for vehicles approaching intersections to reduce wait times was proposed [42]. A traffic data algorithm was developed to plan phases of per intelligent traffic light cycle dynamically and efficiently based on real-time data collected using vehicular ad hoc networks (VANET). The goal was to create a dynamic and efficient traffic light with attention to green phase time per traffic, followed by considering real-time data in one intersection and the reality of emergency vehicles [43]. An intelligent traffic light-controlling algorithm was offered for vehicular networks. The suggested strategy was offered as an arterial traffic light control to design a traffic scheduling algorithm; the efficient plan phases of each isolated traffic light based on real-time traffic were followed. This adaptation of intelligent traffic light controlling (ITLC) was designed with open networks to schedule reports of neighborhood lights on an arterial street [44].

Increasing traffic volumes have posed many challenges over the past decades, and dynamic traffic light management is one of them. Thus, detecting, counting and classifying vehicles in real-time has become more complex. An intelligent traffic control system was implemented with real-time traffic statistics broadcasting to optimize the traffic control systems and convert traditional to intelligent lights by using an image processing algorithm for controlling traffic lights at intersections where cameras are placed. A timer control was used on the traffic thickness to acquire and process images in the road intersection [45].

Traffic data can be used for security purposes by using a routing service offered by this application. This has helped road users to choose the least congested routes. Each solution for the city’s congestion issues has specific features regardless of the technique used. Based on Table 1, it is apparent that researchers have often suggested traffic light control solutions for isolated intersections; regardless, realistic answers have been required strategies of coordination between intersections to avoid congestion at further neighbors’ intersections.

Table 1. Different urban traffic methods summarized.

Ref. No	Method	Goal	Technology	Type of Network
[46]	Computation management	Optimization, reduce traffic	Artificial intelligent	General network
[47]	Centralized simulated	Optimal vehicle, emission minimization	Internet of Things	General network
[48]	Adaptive control algorithm	Average waiting time	Wireless sensor networks	Isolated intersection
[49]	Image processing	Emission minimization	Internet of Things	Isolated intersection
[50]	Deployment of cybersecurity	Optimization, reduce traffic jam, vehicle stop minimization	Internet of things	General network
[51]	Deep reinforcement learning	Average travel distance, Average travel time	Artificial intelligent	General network

3. Methodology

Traffic signal control systems have been distributed spatially and functionally. Intersections are considered sub-sections of a network and are controlled by cooperative, autonomous, and intelligent agents. A multi-agent system can usually handle complex and distributed issues because agents have a more elevated abstraction than components and objects. There are two levels of collaboration within the suggested multi-agent system. Each signalized intersection is controlled by an intersection control group, which defines the signal control strategy. A phase layout strategy optimizes the requirements of the continuously changing surroundings. In contrast, the control of the entire intersection network is distributed between several intersection control groups that are coordinated collectively. Group members are physically close, and each kind of agent in the group plays a specific role within the distributed organism. Communication is allowed between agents within a group to build a shared perception of the environment presented in the network. Each agent has a specific role that allows the agent to better adapt to the tasks at hand. These roles map to agents’ characteristics, enabling them to become more efficient and master their roles. The agents work together to achieve a common goal: the local group is responsible for optimizing the traffic light signal at the local intersection. At the same time, the system is responsible for optimizing operations over the entire network, and the agents in the system are assigned sub-tasks to accomplish these goals. The agents’ behaviors and actions are synchronized and scheduled for high levels of performance and reliability. Arbitration is a fuzzy inference method containing rules for all agents to resolve conflicts.

As shown in Figure 1, control units at isolated intersections are considered agents. This figure then shows the presented multi-agent model, which has been used for eight intersections in traffic control and reducing the queue length utilizing fuzzy logic control. Optimal control actions (phase shift, cycle length change, the extension of green time, etc.) are received from the traffic states (waiting time, queue length, total delay). Feedback rewards are obtained iteratively by the agent and adjusted until optimal control is achieved for the aim of reducing queue length at intersections.

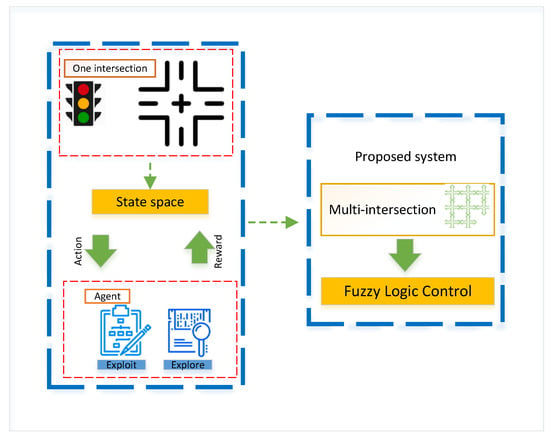
Figure 1. Proposed method framework for traffic light control.

3.1. Multi-Agent Signal Control

An agent-based control scheme involves multiple agents interacting to control specific processes. Negotiation may also be described as this interaction as each agent considers the other agents’ situation while pursuing its objectives. Hence, the agent’s preferences are usually balanced with other agents’ preferences when making a final decision. Each agent operates separately and locally in multi-agent systems rather than at a centralized level. Agents spend most of their time negotiating with those in their neighborhood. Distance determines neighborhoods, but other factors can also shape them.

3.2. Fuzzy Logic Control Method

One of the main principles presented so far is multi-agent control. The second is the algorithm chosen for providing control agents with the ability to make decisions. An input space is mapped to an output space in this issue; the input variables represent traffic conditions, and output variables represent decisions. A rule-based approach is suitable when an expert can describe the control task as a set of rules. These rules can sometimes be found, but their needs for activation tend to be vague. A fuzzy rule-based inference approach could be useful in these situations. Control system decisions are made with fuzzy inference. Signal control rules and conditions tend to be vague, and it is difficult to determine, for example, when a queue is long. The terms short and long queues can be defined as operating membership functions in fuzzy logic. The rule base can then be employed with vague arguments: extend green if the queue is long. The fuzzy logic algorithm is not explained in detail since the theory of fuzzy sets is referenced frequently. Logic based on binary parts can be incorporated into decision trees by following only one branch. Fuzzy inference operates a rule set that considers all rules at every step. Compared with binary logic-based rules, fuzzy inference produces smoother transitions between states. Fuzzy inference relies on rule-based calculations rather than relying on rules for reasoning. Thus, fuzzy membership functions are the results of such calculations. A defuzzification method must be used to create a crisp result value for a fuzzy algorithm. Fuzzy inference is similar to human reasoning in some ways. There is no requirement that the arguments be unit-compatible when using the rule base. The decision-making process can therefore take into account many factors. Ref. [52] started the field of fuzzy logic. Systems based on fuzzy logic and fuzzy-set approach are essential for soft computing and used mathematics applications. Using the Sugeno reasoning strategy is almost the same as operating Mamdani’s method. Ref. [53] showed the main difference is that the output (concentrations) are not fuzzy sets while constants or linear that the technique is credited to Takagi-Sugeno Kang. Sugeno’s membership function utilizes the singleton membership function with a membership phase of one for one crisp value and zero for another crisp matter. The paper suggests a fuzzy logic control Sugeno method in the adaptive control system. The system controls traffic lights according to a decision. Traffic following, which is based on how much green time is available, is used to determine the number of vehicles at the intersection. A fuzzy logic control system determines the time of green time by applying rules. The following Figure 2 illustrates the basic structure of a fuzzy logic control system.

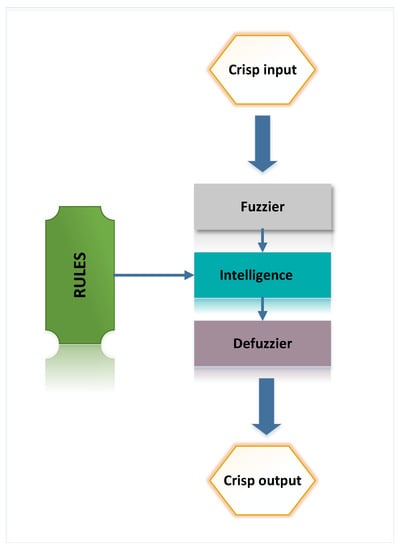
Figure 2. Basic design of fuzzy logic system control.

3.3. The Proposed Framework

The urban traffic control system’s functional design comprises several components to achieve optimal and adaptive road traffic regulation. It represents the standard components of a regulation’s functions, including captures, crossroads controllers, and traffic lights. We considered traffic lights that include the applications of elaborated regulatory strategy and phase control. Here at the start of this section, we have a mathematical model and then an analysis of multi-agent intersections.

3.4. Mathematical Model of an Intersection

Leg one and leg three in Figure 3 represent the first phase of a four-way intersection, while leg two and leg four represent the second phase. One of the main parameters in determining traffic flow in an intersection is the length of the vehicles’ queue, as described in Equation (1) [54].

$$Q_i(m+1)=Q_i\left(m\right)+q_i\left(m\right)-d_i\left(m\right)S_i\left(m\right)$$

(1)

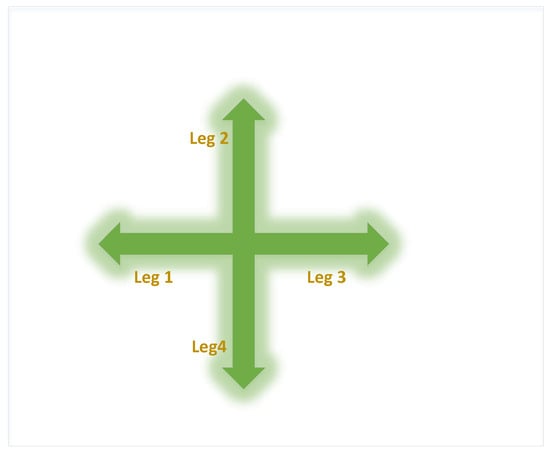
Figure 3. Signalized intersections with two phases.

In Equation (1), $Q_i$ is the length of the queue of vehicles, $d_i$ is the number of vehicles leaving the queue, $q_i$ is the number of vehicles entering the queue, and $S_i$ is the control signal that depicts the traffic light status in the legs. The state refers to either the presence of a green light and vehicle movement or a red light and the vehicle stopping. Here, $W_i$ in Equation (2) gives a total waiting time for vehicles if a sufficiently short discretized time interval is T [55].

$$W_i(m+1)=w_i\left(n\right)+T{Q}_i\left(m\right)-1/2T{d}_i\left(m\right)S_i\left(m\right)+1/2T{q}_i\left(m\right)$$

(2)

Equations (3) and (4) can be written to further clarify the intersection of state-space equations.

$$X(m+1)=AX\left(m\right)+B\left(m\right)S\left(m\right)+C\left(m\right)$$

(3)

$$Y\left(m\right)=CX\left(m\right)$$

(4)

In Equation (3), $X\left(m\right)$ shows the vector of variables of a model. $S\left(m\right)$ shows the vector control variables. Furthermore, in Equations (3) and (4) there are other matrices and vectors such as A, B, and C.

3.5. An Analysis of Multi-Agent Intersections

The multi-agent intersections shown in Figure 4 are connected, and the intersection consists of three lanes per link, with both approaches being two-way. All of the coefficients and parameters of the intersection differ in only the state-space equations, which are based on the Kronecker effect as per Equations (5) and (6). That was determined as a new state-space dynamic system based on the multi-agent system.

$$X(m+1)=(I_M\otimes A_i)X\left(m\right)+X\left(M\right)\otimes B_i)S\left(m\right)+C_i$$

(5)

$$Y\left(m\right)=CX\left(m\right)$$

(6)

Figure 4. Two-phase signalized intersection for the multi-agent system.

The Kronecker multiplication factor is based on two matrices, one of which can have any size; it can be described as multiplying matrix A in all B matrices. Even the Kronecker effect does not have removal effects. The Kronecker effect has been shown as ⊗.

3.6. Multi-Intersection Network Modeling by Fuzzy Controller

A fuzzy rule base is a set of rules based on IF-THEN combined with and/or operators representing expertise [56]. Input space can be mapped to output space using fuzzy logic [57]. With fuzzy logic, data input points can be mapped to values indicating membership or membership levels with fuzzy sets. A fuzzy set of variables is created as the first step in computing. The number of vehicles (low, medium, and high) and the degree of membership are indicated as input variables [58,59]. Various inputs can be used in the fuzzy controller, and different outputs can be produced because the fuzzy controller can take the number of different inputs with different outputs. This study uses three inputs and one output in the Takagi–Sugeno–Kang (TSK) fuzzy system. Controlling includes the length of the queue as well as the input and output vehicle. With attention to the proposed method, we have legs one and three in the first line (phase): $(Q_1+Q_3,Q_2+Q_4,d_1+d_3,q_1+q_3)$ and we have the following in the second line (phase) in the legs two and leg four: $(Q_1+Q_3,Q_2+Q_4,d_2+d_4,q_2+q_4)$. Fuzzy rules have the following general format:

$$\begin{array}{c}IF((Q_1+Q_3)IS{x}_1,(Q_2+Q_4)IS{x}_2,(d_m+d_n)IS{x}_3,(q_m+q_n)\\ IS{x}_4,Q_i\left(m\right)x_{5}AND{Q}_{i}IS{x}_{6}THEN\left(S_{i}ISY\right))\end{array}$$

(7)

$Q_1,Q_2,Q_3,Q_4$ show buffers, with each representing the relationship between intersections and the time between phases of green phase renewal $(S_1$ and $S_2)$. For fuzzy rules, the input variables are considered as the number of cars entering and outputting the queue when low (l), medium (m), and high (h). Thirty-seven rules are utilized in each controller, and intersections between buffers have been selected as low (l) and high (h). Here, there is one example. The rules of fuzzy controller for legs one and three in the one intersection are as follows:

$$\begin{array}{c}IF(Q_1+Q_{2}ISh,(d_1+d_2)ISh),\left((q_1+q_3)ISl\right),\\ \left(Q_{1}ISl\right),\left(Q_{1}ISl\right)AND\left(Q_{3}ISl\right)THEN\left(S_{1}IS1\right))\end{array}$$

(8)

The control signal at urban intersections generally consists of traffic lights that are green or red. During the green phase, vehicles can enter or exit, and those in the queue are only allowed to enter during the red phase. $X_{GREEN}=\left[\begin{array}{c}{Q}_{GREEN}\\ W_{GREEN}\end{array}\right]$ and $X_{RED}=\left[\begin{array}{c}{Q}_{RED}\\ W_{RED}\end{array}\right]$ are state vectors, where $GREEN$ and $RED$ show traffic light states. We considered a Lyapunov function to prove stability for a multi-intersection, where each intersection has attention to the Lyapunov function. This is shown in Equation (9).

$$v\left(X\right)={\left[\begin{array}{c}{X}_{GREEN}\\ X_{RED}\end{array}\right]}^t\left[\begin{array}{cc}{R}_1& 0\\ 0& R_2\end{array}\right]\left[\begin{array}{c}{X}_{GREEN}\\ X_{RED}\end{array}\right]$$

(9)

If R becomes positive and symmetric, then we have:

$$∆v\left(m\right)=v(m+1)-v\left(m\right)$$

(10)

By using ${\left(AB\right)}^t=B^t{A}^t$, we can obtain the Equation below:

$$\begin{array}{c}∆v\left(m\right)=X_{GREEN}^t(m+1)R_1{X}_{GREEN}(m+1)+X_{RED}^t{R}_2{X}_{RED}(m+1)-\\ X_{GREEN}^t\left(m\right)R_1{X}_{GREEN}\left(m\right)-X_{RED}^t\left(m\right)R_2{X}_{RED}\left(m\right)\end{array}$$

(11)

by regarding ${(A\otimes B)}^t=A^t\otimes B^t$ in Equation (9). Then we consider the fact that Equation (10) is as follows:

$$A_i^t{R}_i{A}_i-I=-Q$$

(12)

As seen in Equation (12), the Lyapunov function has a uniform difference.

$$\psi =\left\{\frac{X_{GREEN},X_{RED}|X_{RED}\ge \eta }{{\lambda }_{MIN}}\right\}$$

(13)

4. Results

The fuzzy control and selection time of $T=0.1$ were operated in a simulation in addition to the quadruple length decrease standard. We considered the values of urban traffic as a $\theta$ with a different condition. Table 2 shows simulation results for several traffic situations that show the values of other states in Table 2. In this study, the simulation was designed using MATLAB code.

Table 2. Values of $\theta$.

No	Type of Values	Value
(1)	Traffic flow position	$\theta$
(2)	Non-saturation	$\theta ⩾0.7$
(3)	Saturation	$0.4⩽\theta ⩽0.6$
(4)	Super-saturation	$0.1⩽\theta ⩽0.3$
(5)	Stable	$\theta =0$

4.1. Fixed Time Controller

A fixed-time controller repeats a phase arrangement according to a set length and sequence. The following chart shows an example of the simulation results for the number of vehicles waiting in the queue without controller intervention in fixed time control.

The number of vehicles in the first intersection is shown in Figure 5 using a fixed-time controller. The number of cars in traffic is raised in the different legs. The number of vehicles in the third leg is greater than in the other legs.

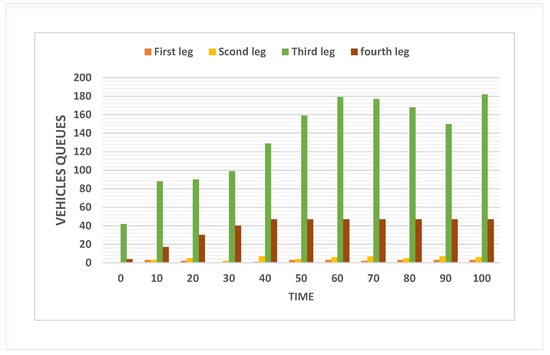
Figure 5. The length of the vehicle’s queue in the first intersection without the controller.

Control variables that are green or red indicator lights in the presence of a fuzzy controller, as demonstrated in the following Figure 6 for the length of the vehicle’s queue, are shown at the intersections with the fuzzy controller. These results showed that using a fuzzy controller decreases the length of queues in each leg compared with constant time control.

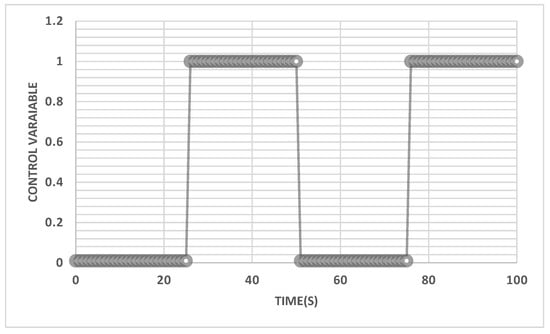
Figure 6. Control variables showing a green or red phase per leg.

4.2. Stable Fuzzy Logic Design on Multi Intersection

We determined optimal phase layouts by minimizing queue length through traffic light phase optimization considering the variable controller output $S_i$ by applying a fuzzy logic model that is as follows.

Figure 7 demonstrates the number of cars utilizing fuzzy logic control in the first intersection. The number of queues of cars in the first leg and the second leg has been changed with attention to the uncontrolled state using a fuzzy logic control.

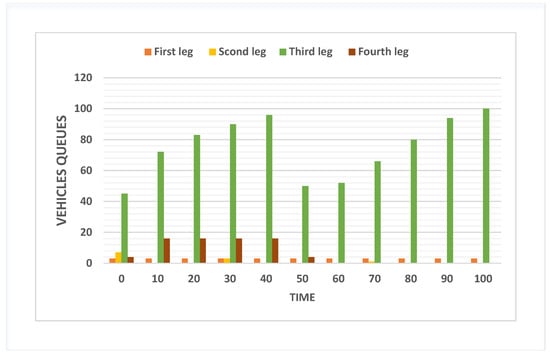
Figure 7. Using a fuzzy logic controller, we determine the length of the vehicle queue at the first intersection.

The proposed method can handle a multi-intersection, and the performance of the suggested approach is compared to fixed time without the controller in Figure 8. In low traffic, the offered method in the traffic signal optimization model improved compared to without the controller. We have seen decreased traffic using a fuzzy logic model equal to the fixed time in the medium traffic condition. Improvement values become more critical when traffic increases and the traffic congestion becomes worse; Figure 8 demonstrates the decreased vehicle queue length based on fixed time after utilizing fuzzy logic in high traffic.

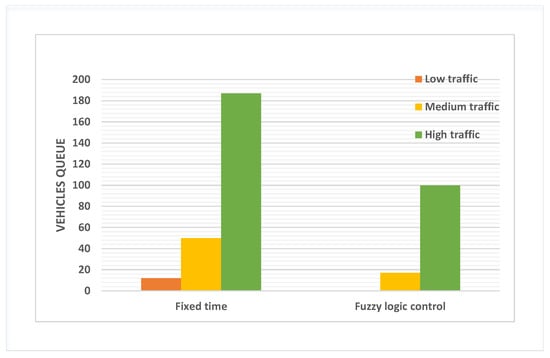
Figure 8. The comparison of average intersection considering the different conditions without a controller and with a controller.

4.3. Discussion

We compared the proposed method with different methods such as multi-agent deep reinforcement learning, genetic algorithm, and adaptive traffic control, considering the target and value of the intersection in every process; for example, two, three, six, and eight intersections are shown in Table 3. A new approach is presented in this article to discuss traffic lights at intersections that are controlled by traffic control systems. The problem in urban traffic has been the increased number of vehicles in the big cities. Congested intersections can be verified as one of the problems. A nonlinear model has been used based on traffic lights in urban traffic for managing traffic flow and reducing delay time by using a genetic algorithm that uses a mixed, nonlinear programming model; thus, a mixed, traffic-light-controlled junction’s traffic flow has been organized [60]. This paper has applied adaptive traffic control to multiple intersections to determine the best red and green times with attention to queue length, evacuation time, and capacity [61]. Furthermore, the paper suggested an Internet of Things for solving traffic issues based on deep reinforcement learning to optimize traffic lights and decrease traffic jams. The algorithm has improved urban traffic control performance by using a global approach to control traffic lights and vehicles [62]. An intelligent traffic signal control approach based on reinforcement learning with a Q-network approximator has been presented in this paper, which took into consideration traffic flow characteristics both in space and time. A Q-network has been offered to derive optimal control policies for signal control [63]. In our proposed method, we considered state space from multi intersections; after that, we applied model fuzzy control to optimize and reduce queue length in traffic jams based on a traffic light. The proposed method performs well according to our results because by using fuzzy logic, control systems can be more efficient, and human deductive reasoning can be emulated. Other studies have considered different intersections with different parameters to reduce traffic jams.

Table 3. The comparison with new related methods.

Ref. No	Utilized Method	Target	Limitation
[60]	Genetic algorithm	Minimizes the traffic waiting time	Two intersections
[61]	Adaptive traffic control system	Reduces and minimizes the average waiting time of vehicles	Four intersections
[62]	Multi-agent deep reinforcement learning	Reduces traffic jams	Six intersections
[63]	Reinforcement learning	The performance queue length and wait time	Eight intersections
Our method	Fuzzy logic control system	Reduces queue length and optimization	Eight intersections

5. Conclusions and Future Work

A fuzzy model was created in this article to develop and control traffic signals for multiple-agent intersections with connections between each other. The stability of this model was then demonstrated. Based on the theory of multi-functional systems, a fuzzy model was developed that considered adjacent intersections’ behavior. A fuzzy model was constructed based on the idea of multi-functional systems, with intersections considered for their effect on the system’s behavior as a whole. Based on state-space equations, a fuzzy controller that maximizes traffic volume decreases the queue of vehicles per phase compared with constant time. Based on simulations using fuzzy logic and Matlab, the proposed system significantly improved the traffic network’s queue length using a multi-agent organization. The simulation results demonstrated that the presented technique is efficient. Furthermore, we offer future work that should focus on the type of fuzzy sets and the fuzzy generalization machine. As in the Takagi–Sugeno framework, one could combine inputs linearly or mix fuzzy sets instead of triangulated outputs. Another study on fuzzy rules can be performed offline by employing real-life traffic data to extract fuzzy rules. Future research should investigate optimally managing communication failures and how these may affect regulation and traffic systems, mainly when many intersections are interested in the multi-intersection network. The traffic control system will be in use in other areas. This approach could be symbolic of traffic signal control by counting an intelligent path suggestion protocol that considers the close location of the vehicle as well as road traffic condition indicators. Meanwhile, a brilliant optimization method is needed to deal with design failures and consequences. Additionally, based on the dynamic model in the urban traffic, we can consider another type of fuzzy system design, such as the type-3 fuzzy logic system, for future study to predict traffic flow. Using a deep learned recurrent type-3 fuzzy logic system, a model and a prediction system for renewable energy on solar panels and wind turbines has been presented using the membership function and rule parameters tuned by a nonlinear structure [64]. We will use real data that integrate other technologies like machine learning to develop our method and ensure an ideal vehicle experience in cities. For example, a study has used real data from the busiest intersections in Bogor, Indonesia, to determine how to mitigate traffic congestion at a road intersection. The main objective of this work focused on the timing of traffic lights at junctions and considered road width variables by using a fuzzy logic model [65]. This is different from our approach because the work uses other features, and they did not mention how many intersections there are.