Jump and Initial-Sensitive Excessive Motion of a Class of Relative Rotation Systems and Their Control via Delayed Feedback
Abstract
:1. Introduction
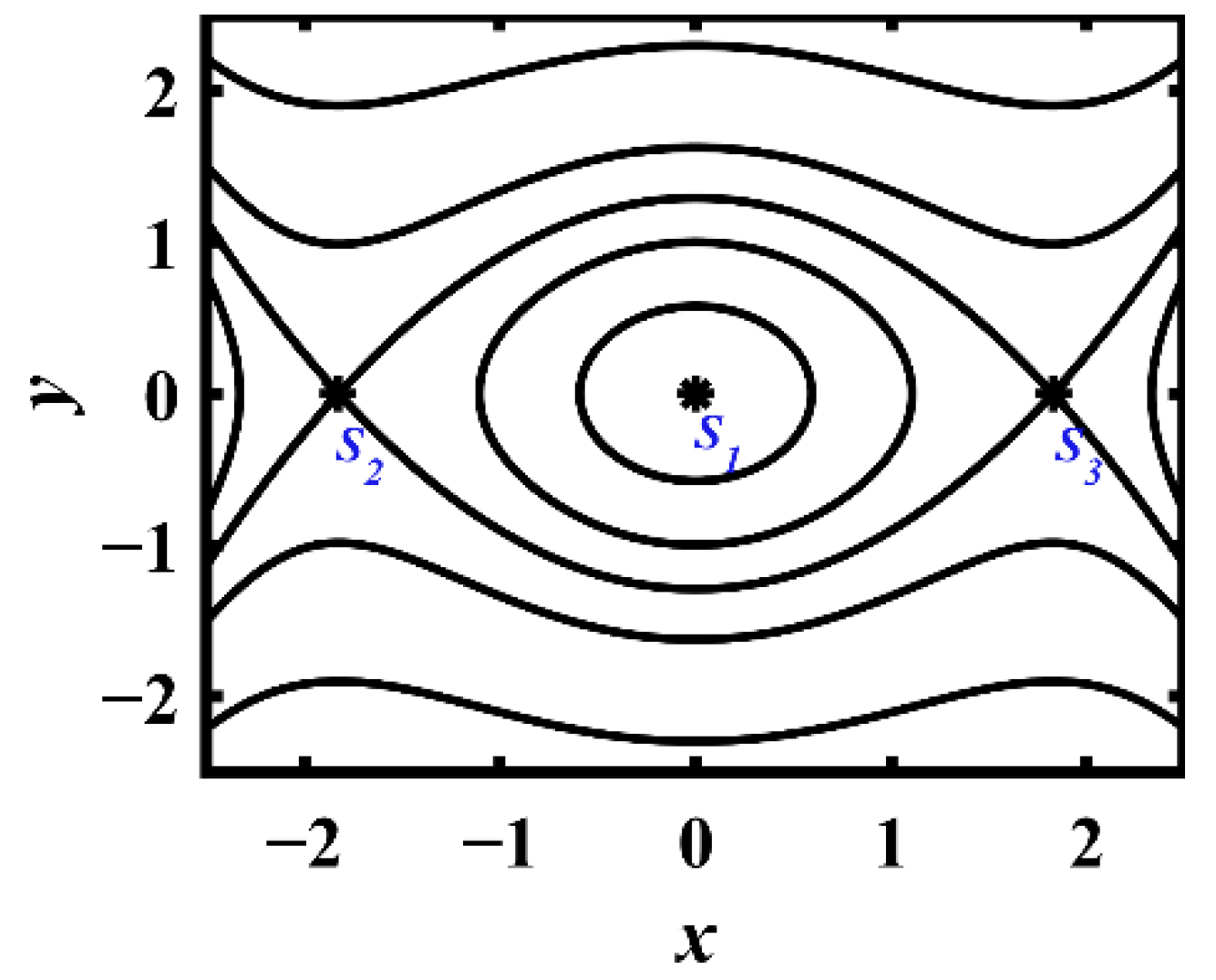
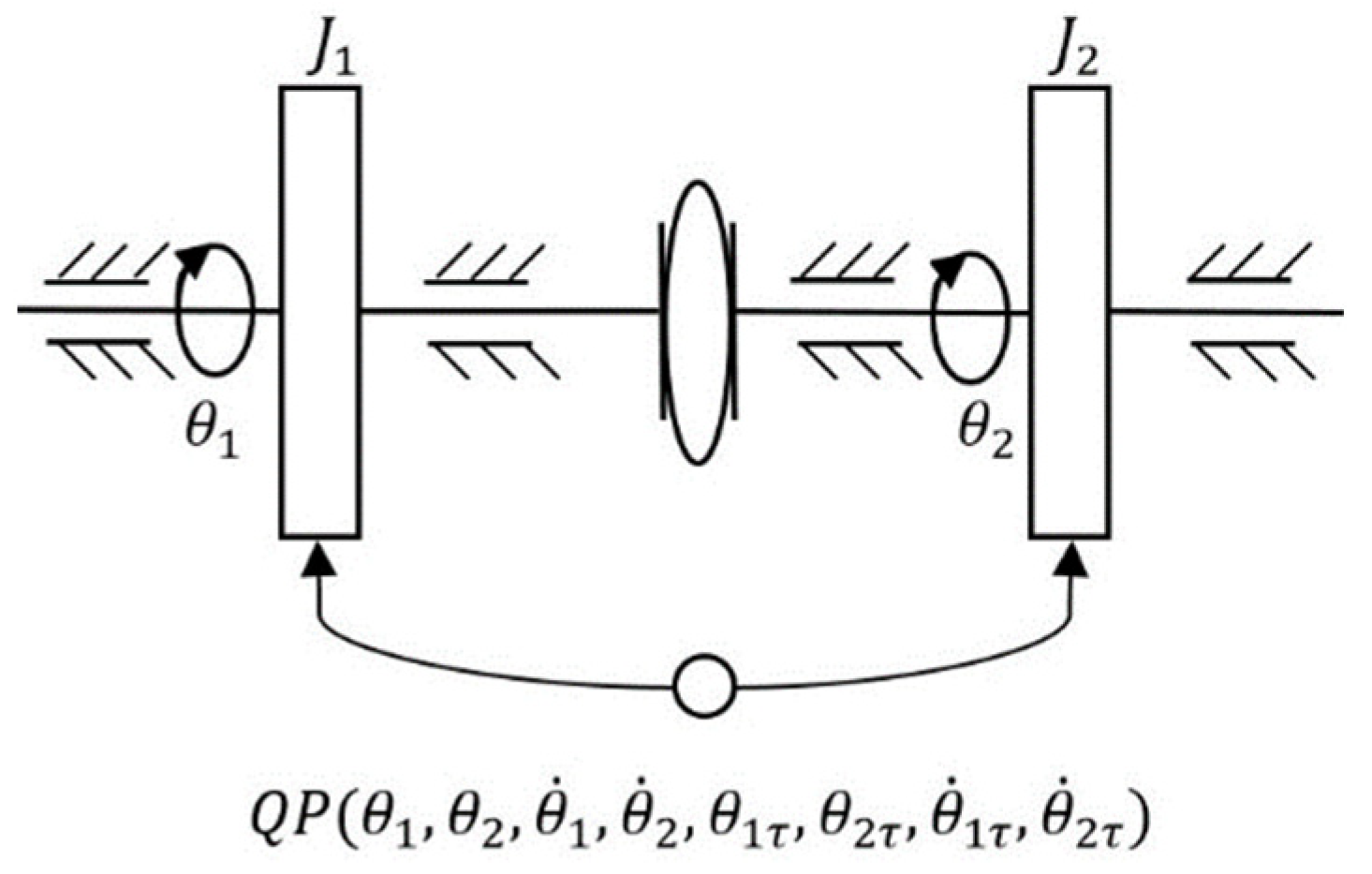
2. Dynamical Model and Unperturbed Dynamics
3. Complex Dynamics
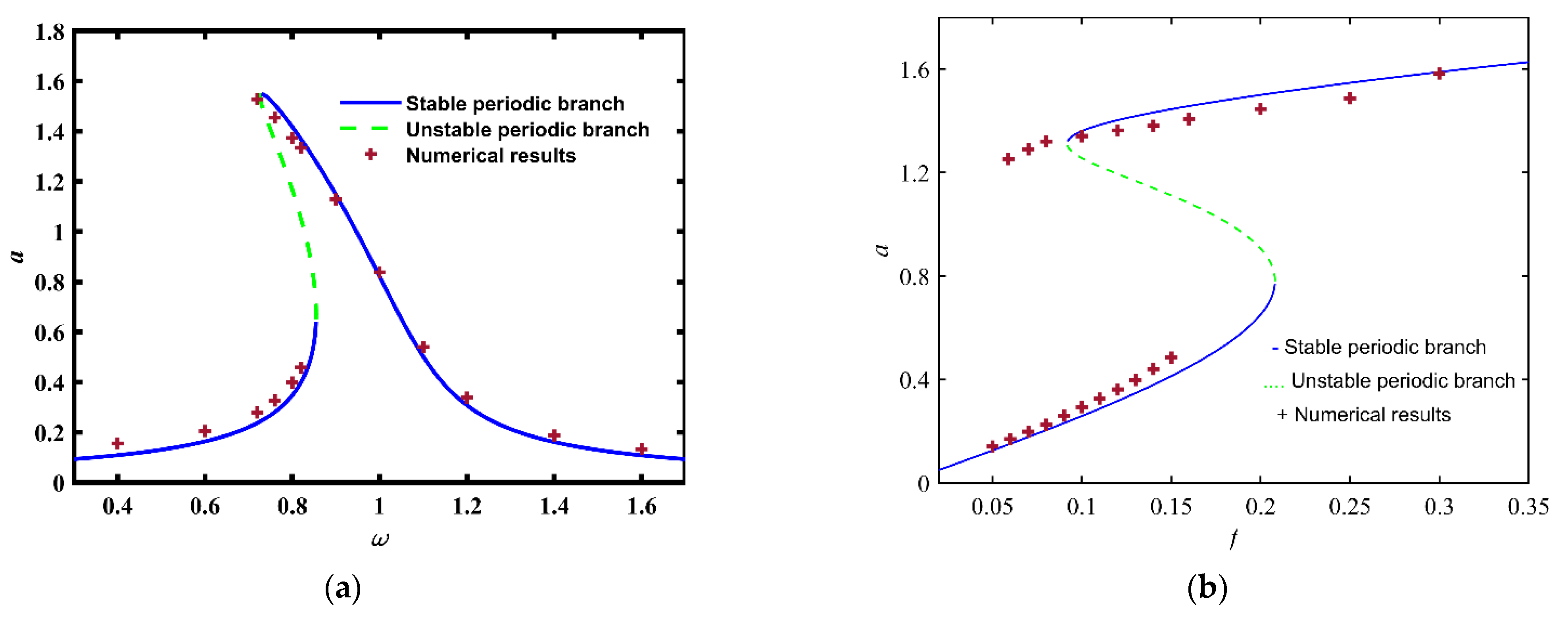
3.1. Multistability and Jump
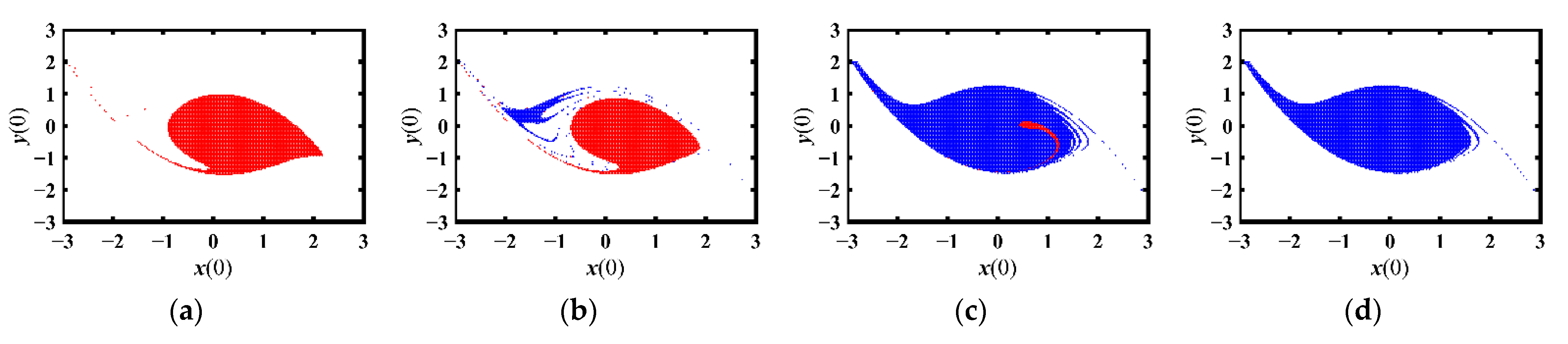
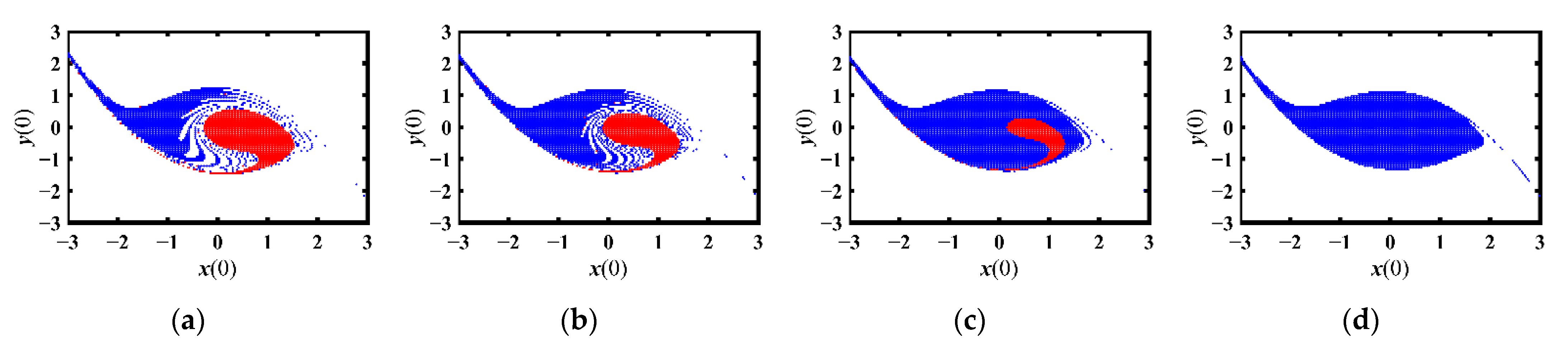
3.2. Initial-Sensitive Excessive Motion
4. Time-Delay Feedback to Control Complex Dynamics
4.1. Delayed Position Feedback Control
4.1.1. Primary Resonant Response and Stability of Solutions
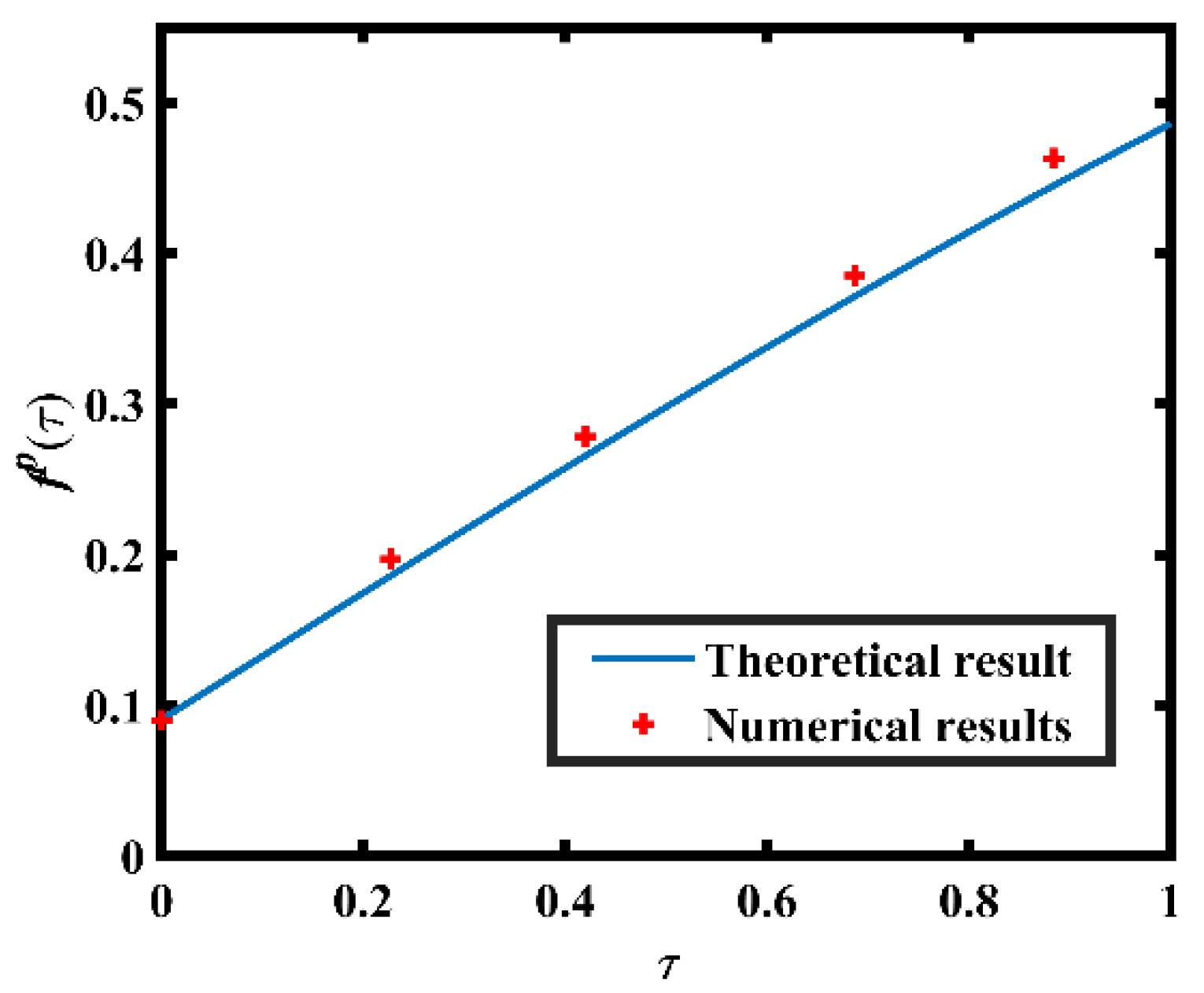
4.1.2. Heteroclinic Bifurcation
4.2. Delayed Velocity Feedback
4.2.1. Primary Resonant Response and Stability of Solutions
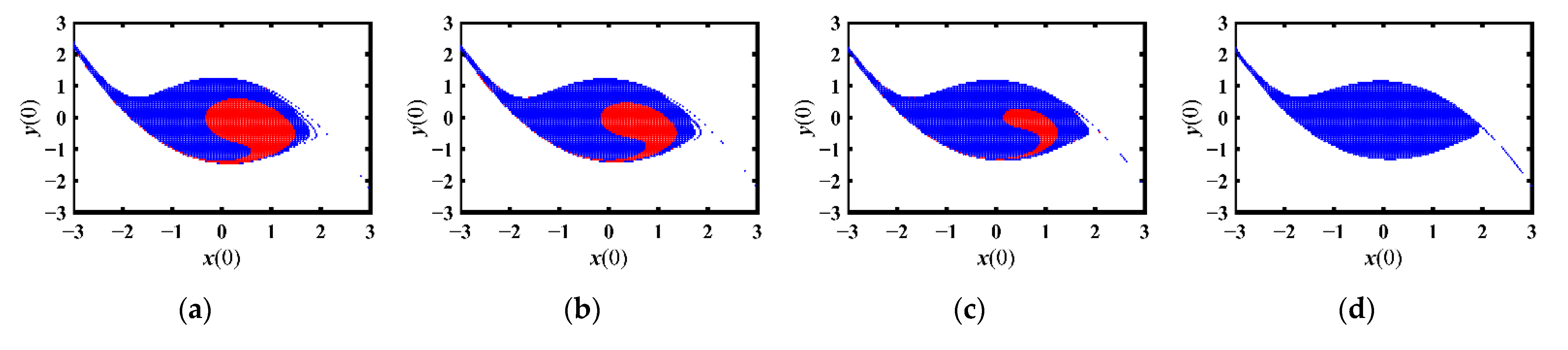
4.2.2. Heteroclinic Bifurcation under Delayed Velocity Feedback
5. Discussion
- (1)
- The variation of excitation may induce the coexistence of bistable periodic attractors, which can be ascribed to saddle-node bifurcation.
- (2)
- The increase of the excitation amplitude may cause initial-sensitive excessive motion, which can be due to heteroclinic bifurcation.
- (3)
- Under positive coefficients of the feedback gain, the delayed position feedback and the delayed velocity feedback can reduce saddle-node bifurcation and heteroclinic bifurcation so as to suppress jump and initial-sensitive excessive motion. Comparatively, the former can also reduce the amplitude of the response, while the latter may not; the former works well if time delay does not exceed the first stability switch of the trivial equilibrium, while the latter does not have that restriction.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Liang, Y.; Li, N. Optimal vibration control for nonlinear systems of tracked vehicle half-car suspensions. Int. J. Control. Autom. Syst. 2017, 15, 1675–1683. [Google Scholar] [CrossRef]
- Renson, L.; Noël, J.P. Complex dynamics of a nonlinear aerospace structure: Numerical continuation and normal modes. Nonlinear Dyn. 2015, 79, 1293–1309. [Google Scholar] [CrossRef] [Green Version]
- Shi, J.; Gou, X. Bifurcation and Erosion of Safe Basin for a Spur Gear System. Int. J. Bifurc. Chaos 2018, 28, 1830048. [Google Scholar] [CrossRef]
- Li, J.; Wu, H. Bifurcation, chaos, and their control in a wheelset model. Math. Methods Appl. Sci. 2020, 43, 7152–7174. [Google Scholar] [CrossRef]
- Luo, Z.; Wang, J. Research on vibration performance of the nonlinear combined support-flexible rotor system. Nonlinear Dyn. 2019, 98, 113–128. [Google Scholar] [CrossRef]
- Li, Y.; Luo, Z. Dynamic modeling and stability analysis of a rotor-bearing system with bolted-disk joint. Mech. Syst. Signal Process. 2021, 158, 107778. [Google Scholar] [CrossRef]
- Shi, P.; Liu, B. Chaotic motion of some relative rotation nonlinear dynamic system. Acta Phys. Sin. 2008, 57, 1321–1328. [Google Scholar]
- Li, Z.; Gou, X. Erosion and bifurcation of safety-attraction basin for multi-state meshing gear transmission system under tooth safety condition. J. Vbration Shock 2021, 40, 63–74. [Google Scholar]
- Wang, K.; Guan, X. Precise periodic solutions and uniqueness of periodic solutions of some relative rotation nonlinear dynamic system. Acta Phy. Sin. 2010, 59, 3648–3653. [Google Scholar] [CrossRef]
- Xiao, L.; Xuan, C. The periodic solution problem of a relative rotation nonlinear dynamic system with time-varying stiffness. Acta Phy. Sin. 2013, 62, 21–25. [Google Scholar]
- Li, X.; Yan, J. The periodic solution problem of a relative rotation nonlinear system with nonlinear elastic force and generalized damping force. Acta Phy. Sin. 2014, 63, 36–41. [Google Scholar]
- Shi, P.; Han, D. Chaos and chaotic control in a relative rotation nonlinear dynamical system under parametric excitation. Chin. Phys. B 2010, 19, 116–121. [Google Scholar]
- Verichev, N. Chaotic torsional vibration of imbalanced shaft driven by a limited power supply. J. Sound Vib. 2012, 331, 384–393. [Google Scholar] [CrossRef]
- Liu, B.; Zhao, H. Bifurcation and chaos of some relative rotation system with triple-well Mathieu-Duffing oscillator. Acta Phy. Sin. 2014, 63, 174502. [Google Scholar]
- Liu, S.; Tian, S. Chaos of a kind of nonlinear relative rotation system based on the effect of Coulomb friction. Acta Phy. Sin. 2015, 64, 247–254. [Google Scholar]
- Zhu, L.; Li, Z. Evolutionary mechanism of safety performance for spur gear pair based on meshing safety domain. Nonlinear Dyn. 2021, 104, 215–239. [Google Scholar] [CrossRef]
- Ju, J.; Wei, L. Dynamics and nonlinear feedback control for torsional vibration bifurcation in main transmission system of scraper conveyor direct-driven by high-power PMSM. Nonlinear Dyn. 2018, 93, 307–321. [Google Scholar] [CrossRef]
- Shang, H. Pull-in instability of a typical electrostatic MEMS resonator and its control by delayed feedback. Nonlinear Dyn. 2017, 90, 171–183. [Google Scholar] [CrossRef]
- Wang, Q.; Wu, H. The effect of fractional damping and time-delayed feedback on the stochastic resonance of asymmetric SD oscillator. Nonlinear Dyn. 2022, 107, 2099–2114. [Google Scholar] [CrossRef]
- Zhao, Y.; Li, C. The delayed feedback control to suppress the vibration in a torsional vibrating system. Acta Phy. Sin. 2011, 60, 417–425. [Google Scholar]
- Shang, H.; Han, Y. Suppression of chaos and basin erosion in a nonlinear relative rotation system by delayed position feedback. Acta Phy. Sin. 2014, 63, 88–95. [Google Scholar]
- Rezaei, M.; Khadem, E.S.; Friswell, I.M. Energy harvesting from the secondary resonances of a nonlinear piezoelectric beam under hard harmonic excitation. Meccanica 2020, 55, 1463–1479. [Google Scholar] [CrossRef]
- Siewe, S.M.; Hegazy, H.U. Homoclinic bifurcation and chaos control in MEMS resonators. Appl. Math. Model. 2011, 35, 5533–5552. [Google Scholar] [CrossRef]
- Danico, K.; Tanmoy, C.; Milan, C.; Sondipon, A.; Karličić, D.; Chatterjee, T.; Cajić, M.; Adhikari, S. Parametrically amplified Mathieu-Duffing nonlinear energy harvesters. J. Sound Vib. 2020, 488, 115677. [Google Scholar]
- Zhu, Y.; Shang, H. Multistability of the vibrating system of a micro resonator. Fractal Fract. 2022, 6, 141. [Google Scholar] [CrossRef]
- Rega, G.; Lenci, S. Dynamical integrity and control of nonlinear mechanical oscillators. J. Vib. Control 2008, 14, 159–179. [Google Scholar] [CrossRef] [Green Version]
- Liu, C.; Yan, Y.; Wang, W. Resonances and chaos of electrostatically actuated arch micro/nanoresonators with time delay velocity feedback. Chaos Solitons Fractals 2019, 10, 109512. [Google Scholar] [CrossRef]








Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Cui, Z.; Shang, H. Jump and Initial-Sensitive Excessive Motion of a Class of Relative Rotation Systems and Their Control via Delayed Feedback. Mathematics 2022, 10, 2676. https://doi.org/10.3390/math10152676
Cui Z, Shang H. Jump and Initial-Sensitive Excessive Motion of a Class of Relative Rotation Systems and Their Control via Delayed Feedback. Mathematics. 2022; 10(15):2676. https://doi.org/10.3390/math10152676
Chicago/Turabian StyleCui, Ziyin, and Huilin Shang. 2022. "Jump and Initial-Sensitive Excessive Motion of a Class of Relative Rotation Systems and Their Control via Delayed Feedback" Mathematics 10, no. 15: 2676. https://doi.org/10.3390/math10152676
APA StyleCui, Z., & Shang, H. (2022). Jump and Initial-Sensitive Excessive Motion of a Class of Relative Rotation Systems and Their Control via Delayed Feedback. Mathematics, 10(15), 2676. https://doi.org/10.3390/math10152676





